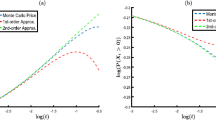Estimating the Hurst parameter from short term volatility swaps: a Malliavin calculus approach

Abstract

This paper is devoted to studying the difference between the fair strike of a volatility swap and the at-the-money implied volatility (ATMI) of a European call option. It is well known that the difference between these two quantities converges to zero as the time to maturity decreases. In this paper, we make use of a Malliavin calculus approach to derive an exact expression for this difference. This representation allows us to establish that the order of convergence is different in the correlated and uncorrelated cases, and that it depends on the behavior of the Malliavin derivative of the volatility process. In particular, we see that for volatilities driven by a fractional Brownian motion, this order depends on the corresponding Hurst parameter $H$. Moreover, in the case $H\geq 1/2$, we develop a model-free approximation formula for the volatility swap in terms of the ATMI and its skew.

1 Introduction

A volatility swap is a forward contract whose underlying is the future realized volatility of an asset price. It is well known (see for example Feinstein [11], Friz and Gatheral [12], Carr and Lee [6, 7]) that the difference between the ATMI of a vanilla option and the corresponding volatility swap price tends to zero as the time to maturity decreases. Moreover, the sign of the difference between the above two quantities is related to the skew of the implied volatility (see for example Demeterfi et al. [9] and Carr and Lee [6]).

This paper is devoted to contributing to the study of the link between volatility derivatives and the ATMI of vanilla options in the context of stochastic volatility models. Our analysis does not require a specific model and can be applied to the case of fractional volatility models, introduced by Comte and Renault [8] (with Hurst parameter $H>1/2$), to explain the long-time behavior of the implied volatility. Alòs et al. [4] proposed to consider volatility models with $H<1/2$ to explain the empirical short-time skew of the ATMI. Recently, fractional models with $H<1/2$ have been further studied by Fukasawa [13] and have been proved to be interesting as a tool to describe real market data (see for example Gatheral et al. [15]).

Even when the classical literature focuses on volatility models that are diffusion processes, several recent works include the case of fractional volatilities. Among them, we can quote the paper by Bergomi and Guyon [5], where the authors presented a vol-of-vol expansion of the ATMI around the variance swap. More recently, El Euch et al. [10] proved a small-time Edgeworth expansion of the density of the asset price, from which they deduced an expansion (again around the variance swap) of the ATMI, for models with Hurst parameter $H\in (0,\frac{1}{2} ]$.

Our approach uses Malliavin calculus techniques that allow us to find an explicit expression for the difference between the ATMI and the fair strike of the volatility swap in terms of the Malliavin derivative of the volatility process, both in the uncorrelated (see Proposition 3.1) and correlated (see Proposition 4.1) cases. As an application of these explicit decompositions, we compute the rate of convergence of this difference and see that this rate depends on the regularity properties of the Malliavin derivative. In particular, for models based on fractional Brownian motion, we prove that this difference is of the order $O(T^{1+2H})$ in the uncorrelated case, where $T$ denotes the time to maturity. In the correlated case, the difference is of the order $O( T^{2H})$ if $H\leq 1/2$, and of the order $O(T^{H+\frac{1}{2}})$ if $H>1/2$. These results give us a tool to estimate the Hurst parameter of fractional volatilities, as we see in the numerical examples in Sect. 5.

The paper is organized as follows. Section 2 is devoted to introducing the main concepts and notations. In Sect. 3, we prove a representation of the difference between the ATMI and the volatility swap in the case when the volatility process and the asset price are uncorrelated. This representation allows us to deduce the order of convergence of this difference, in terms of the Hurst parameter of the volatility process. Moreover, we prove a limit relationship between the implied volatility, its curvature and the volatility swap. In Sect. 4, we extend the results in Sect. 3 to the correlated case. Finally, some numerical examples of a fractional volatility model are presented in Sect. 5.

2 The main problem and notations

In this paper, we consider for the log-price of a stock under a risk-neutral probability measure $P$ the model

$$ X_{t}=X_{0}-\frac{1}{2}\int _{0}^{t}{\sigma _{s}^{2}}ds+\int _{0}^{t} \sigma _{s}( \rho dW_{s}+\sqrt{1-\rho ^{2}}dB_{s}) , \qquad t\in \lbrack 0,T]. $$

(2.1)

Here, $X_{0}$ is the current log-price, $W$ and $B$ are standard Brownian motions defined on a complete probability space $(\Omega , \mathcal{G},P)$, and $\sigma$ is a square-integrable (meaning $E[\int ^{T}_{0} \sigma _{s}^{2}ds] < \infty$) and right-continuous stochastic process adapted to the filtration generated by $W$. In the following, we denote by $\mathcal{F}^{W}$ and $\mathcal{F}^{B}$ the filtrations generated by $W$ and $B$ and define $\mathcal{F}:= \mathcal{F}^{W}\vee \mathcal{F}^{B}$. We assume the interest rate $r$ to be zero for the sake of simplicity. The arguments in this paper still hold if there exists a deterministic drift term in (2.1).

The price of a European call with strike price $K$ is given by the equality

$$ V_{t}=E_{t}[(e^{X_{T}}-K)^{+}], $$

where $E_{t}$ denotes the $\mathcal{F}_{t}$-conditional expectation with respect to $P$ (meaning that $E_{t}[Z]=E[Z|\mathcal{F}_{t}]$). In the sequel, we use the following notation:

• $v(t,Y_{t})=\sqrt{\frac{Y_{t}}{T-t}}$, where $Y_{t}=\int _{t}^{T}\sigma _{u}^{2}du$. We abbreviate it as $v_{t}= v(t,Y_{t})$. That is, $v$ represents the future average volatility, so that it is not an adapted process. Notice that $E_{t}[ v_{t}]$ is the fair strike of a volatility swap with maturity time $T$.

• $BS(t,T,x,k,\sigma )$ denotes the price of a European call option under the classical Black–Scholes model with constant volatility $\sigma$, current log stock price $x$, time to maturity $T-t$ and strike price $K=\exp (k)$. Recall that in this case,

  $$ BS(t,T,x,k,\sigma )=e^{x}N\big(d_{+}(k,\sigma )\big)-e^{k}N\big(d_{-}(k, \sigma )\big), $$

  where $N$ is the cumulative distribution function of the standard normal law and

  $$ d_{\pm }\left ( k,\sigma \right ) :=\frac{k^{*}_{t}-k}{\sigma \sqrt{T-t}}\pm \frac{\sigma }{2}\sqrt{T-t}, $$

  where $k^{*}_{t}$ denotes the at-the-money strike, which coincides with $x$ when the interest rate is zero.

• The inverse function $BS^{-1}(t, T, x, k, \cdot )$ of the Black–Scholes formula with respect to the volatility parameter is defined, for all $\lambda > 0$, via

  $$ BS \big(t, T, x, k,BS^{-1}(t, T, x, k,\lambda ) \big) = \lambda . $$

  We also use the simplified notation $BS^{-1}(k, \lambda ) := BS^{-1}(t,T,X _{t}, k, \lambda )$.

• For any fixed $t$, $T$, $X_{t}$, $k$, we define the implied volatility $I(t,T,X_{t},k)$ as the quantity such that

  $$ BS\big( t,T,X_{t},k,I( t,T,X_{t},k) \big) =V_{t}. $$

  Notice that $I(t, T,X_{t}, k) = BS^{-1}(t, T,X_{t}, k, V_{t})$ is the implied volatility for the model price $V_{t}$, which only depends on $t$, $T$, $X_{t}$, $k$.

• $H(t,T,x,k,\sigma ):=( \frac{\partial ^{3}}{\partial x^{3}}-\frac{ \partial ^{2}}{\partial x^{2}}) BS(t,T,x,k,\sigma )$.

We assume that the reader is familiar with the elementary results of the Malliavin calculus as given, for instance, in Nualart [16]. In the remainder of this paper, $\mathbb{D}_{W}^{1,2}$ denotes the domain of the Malliavin derivative operator $D^{W}$ with respect to the Brownian motion $W$. It is well known that $\mathbb{D}_{W} ^{1,2}$ is a dense subset of $L^{2}(\Omega )$ and that $D^{W}$ is a closed and unbounded operator from $\mathbb{D}_{W}^{1,2}$ to $L^{2}([0,T]\times \Omega )$. We also consider the iterated derivatives $D^{n,W}$ for $n>1$ whose domains are denoted by $\mathbb{D}_{W}^{n,2}$. We use the notation $\mathbb{L}_{W}^{n,2}=$$L^{2}([ 0,T] ; \mathbb{D}_{W}^{n,2})$.

We use the following anticipating Itô formula (see for example Alòs [2]).

Proposition 1

Assume (2.1) and$\sigma ^{2}\in \mathbb{L}^{1,2}_{W}$. Let$F:[0,T]\times \mathbb{R}^{2}\rightarrow \mathbb{R}$be a function in$C^{1,2} ([0,T]\times \mathbb{R}^{2})$such that for all$t\in [ 0,T]$, $F$and its partial derivatives evaluated in$( t,X_{t},Y_{t})$are bounded by one positive constant$C$. Then it follows that

$$\begin{aligned} F(t,X_{t},Y_{t}) =&F(0,X_{0},Y_{0})+\int _{0}^{t}{\partial _{s}F}(s,X _{s},Y_{s})ds-\int _{0}^{t}{\partial _{x}F}(s,X_{s},Y_{s}) \frac{\sigma _{s}^{2}}{2}ds \\ &{}+\int _{0}^{t}{\partial _{x}F}(s,X_{s},Y_{s})\sigma _{s}(\rho dW_{s}+\sqrt{1- \rho ^{2}}dB_{s}) \\ &{}-\int _{0}^{t}{\partial _{y}F}(s,X_{s},Y_{s})\sigma _{s}^{2}ds+\rho \int _{0}^{t}{\partial _{xy}^{2}F}(s,X_{s},Y_{s})\Theta _{s}ds \\ &{}+\frac{1}{2}\int _{0}^{t}{\partial _{xx}^{2}F}(s,X_{s},Y_{s})\sigma _{s}^{2}ds , \end{aligned}$$

(2.2)

where$\Theta _{s}:=(\int _{s}^{t}D^{W}_{s}\sigma _{r}^{2}dr)\sigma _{s}$.

3 The uncorrelated case

Let us consider the following hypotheses:

• (H1) There exist positive constants $a$, $b$ such that $a\leq \sigma _{t}\leq b$ for all $t\in [ 0,T]$.

• (H2) $\sigma ^{2}\in \mathbb{L}^{1,2}$.

The key tool in our analysis is the following relationship between the ATMI and the volatility swap fair strike.

Proposition 1

Consider the model (2.1) with$\rho =0$and assume that (H1) and (H2) hold. Then the at-the-money implied volatility admits the representation

$$\begin{aligned} &I( t,T,X_{t},k^{*}_{t}) \\ &=E_{t}[ v_{t}] - \frac{1}{32(T-t)} E_{t}\bigg[\int _{t}^{T} \frac{ \Psi _{r} }{( N^{\prime }( d_{+}(k^{*}_{t} ,\Psi _{r}) ) ) ^{2}} \\ & \phantom{E_{t}[ v_{t}] - : - \frac{1}{32(T-t)}\int _{t}^{T}aaa}\times \bigg( E_{r}\bigg[ N^{\prime }(d_{+}(k^{*}_{t},v_{t}) )\frac{\int _{r} ^{T}D_{r}^{W}\sigma _{s}^{2}ds}{v_{t}}\bigg] \bigg) ^{2}dr\bigg], \end{aligned}$$

where

$$\begin{aligned} \Lambda _{r} :=& E_{r}[ BS( t,T,X_{t},k^{*}_{t},v_{t}) ], \\ \Psi _{r} :=& BS^{-1}(k^{*}_{t}, \Lambda _{r}). \end{aligned}$$

Proof

Notice that in the uncorrelated case, the Hull and White formula gives us that the option price can be written as

$$ V_{t}=E_{t}[ BS( t,T,X_{t},k^{*}_{t},v_{t}) ] . $$

Then the implied volatility is such that

$$\begin{aligned} I( t,T,X_{t},k^{*}_{t}) =&BS^{-1}( k^{*}_{t},V_{t}) \\ =&E_{t}\big[ BS^{-1}\big(k^{*}_{t},E_{t}[ BS( t,T,X_{t},k^{*}_{t},v _{t}) ] \big)\big] \\ =&E_{t}\big[ BS^{-1}\big(k^{*}_{t},E_{t}[ BS( t,T,X_{t},k^{*}_{t},v _{t}) ] \big) \\ & \phantom{E_{t}\big[}-BS^{-1}\big(k^{*}_{t},BS( t,T,X_{t},k^{*}_{t},v _{t}) \big) \\ & \phantom{E_{t}\big[}+BS^{-1}\big(k^{*}_{t},BS( t,T,X_{t},k^{*}_{t},v _{t}) \big)\big] \\ =&E_{t}\big[ BS^{-1}\big(k^{*}_{t},E_{t}[ BS( t,T,X_{t},k^{*}_{t},v _{t}) ] \big) \\ & \phantom{E_{t}\big[}-BS^{-1}\big(k^{*}_{t},BS( t,T,X_{t},k^{*}_{t},v _{t}) \big)\big] +E_{t}[v_{t}]. \end{aligned}$$

Now, as in Alòs and León [3], we can write

$$ BS( t,T,X_{t},k^{*}_{t},v_{t}) =E_{t}[ BS( t,T,X_{t},k^{*}_{t},v_{t}) ] +\int _{t}^{T}U_{s}dW_{s}, $$

where $U_{s}$ can be computed by the Clark–Ocone formula and $W$ is the Brownian motion that drives the volatility process. Then

$$\begin{aligned} &{E_{t}\big[ BS^{-1}\big(k,E_{t}[ BS( t,T,X_{t},k^{*}_{t},v_{t}) ] \big)-BS^{-1}\big(k,BS( t,T,X_{t},k^{*}_{t},v_{t}) \big)\big] } \\ &= {E_{t}[ BS^{-1}(k^{*}_{t},\Lambda _{t} )-BS^{-1}(k^{*}_{t},\Lambda _{T} )] } \\ &=-E_{t}\left [\int _{t}^{T}( BS^{-1}) ^{\prime }( k^{*}_{t}, \Lambda _{r} ) U_{r}dW_{r} +\frac{1}{2}\int _{t}^{T}( BS^{-1}) ^{\prime \prime }( k^{*}_{t}, \Lambda _{r}) U_{r}^{2}dr\right ], \end{aligned}$$

(3.1)

where $(BS^{~{-1}})^{\prime }$ and $(BS^{~{-1}})^{\prime \prime }$ denote, respectively, the first and second derivatives of $BS^{-1}$ with respect to the last variable $\lambda$. Notice that

$$ U_{r} =E_{r}\big[ D_{r}^{W}\big( BS( t,T,X_{t},k^{*}_{t},v_{t}) \big) \big] =E_{r}\bigg[ \exp (X_{t})N^{\prime }\big(d_{+}(k^{*}_{t}, v_{t})\big) \frac{\int _{r}^{T}D_{r}^{W}\sigma _{s}^{2}ds}{2 \sqrt{T-t}\,v_{t}}\bigg], $$

which jointly with (H1) implies that

$$\begin{aligned} E_{t}\left [\int _{t}^{T}\big((BS^{-1})'(k^{*}_{t},\Lambda _{r})U_{r} \big)^{2} dr\right ] \le & \frac{\exp (2X_{t})}{4(T-t)}E_{t}\bigg[ \int _{t}^{T} \bigg(E_{r} \int _{r}^{T}D_{r}^{W}\sigma _{s}^{2}ds\bigg)^{2} dr \bigg] \\ \le & C(T,t). \end{aligned}$$

This gives that the expectation of the stochastic integral in (3.1) is zero. Then we get

$$\begin{aligned} & E_{t}\big[ BS^{-1}\big(X_{t},E_{t}[ BS( t,T,X_{t},k^{*}_{t},v_{t}) ] \big)-BS^{-1}\big(X_{t},BS( t,T,X_{t},k^{*}_{t},v_{t}) \big)\big] \\ &= -\frac{1}{2} E_{t}\bigg[ \int _{t}^{T}( BS^{-1}) ^{\prime \prime }( k^{*}_{t}, \Lambda _{r}) U_{r}^{2}dr\bigg]. \end{aligned}$$

Now, as

$$\begin{aligned} ( BS^{-1}) ^{\prime \prime }(k^{*}_{t},{\Lambda _{r}}) = \frac{\Psi _{r}}{4( \exp (X_{t})N^{\prime }(d_{+}( k^{*}_{t},\Psi _{r}) )) ^{2}}, \end{aligned}$$

(3.2)

the proof is complete. □

In order to prove our limit results, we need the following hypotheses.

• (H3) Hypothesis (H2) holds, and there exist two constants $\delta \in ( -\frac{1}{2},\frac{1}{2})$ and $C>0$ such that for any $0< r< s< T$,

  $$ E_{r}[ D_{r}^{W}\sigma _{s}^{2}] \leq C \left ( s-r\right ) ^{\delta }. $$

• (H4) Hypotheses (H2) and (H3) hold, and the term

  $$ \frac{1}{(T-t)^{3+2\delta }}E_{t}\bigg[\int _{t}^{T}\bigg( E_{r}\int _{r}^{T}D_{r}^{W}\sigma _{s}^{2}ds\bigg) ^{2}dr\bigg] $$

  has a finite a.s. limit as $T\rightarrow t$.

The following theorem gives us that with reasonable parameters, the difference between the volatility swap and the ATM implied volatility is very small, extending the results by Carr and Lee [7].

Theorem 2

Consider the model (2.1) with$\rho =0$and assume that hypotheses (H1)–(H4) hold. Then

$$\begin{aligned} &\lim _{T\rightarrow t}\frac{I( t,T,X_{t},k^{*}_{t}) -E_{t}[v_{t}] }{(T-t)^{2+2 \delta }} \\ &= -\frac{1}{32\sigma _{t}}\lim _{T\rightarrow t} \frac{1}{(T-t)^{3+2 \delta }}E_{t}\bigg[\int _{t}^{T}\bigg(E_{r}\int _{r}^{T}D_{r}^{W}\sigma _{s}^{2}ds\bigg) ^{2}dr\bigg] \qquad \textit{a.s.} \end{aligned}$$

Proof

Proposition 3.1 gives us that

$$\begin{aligned} &I( t,T,X_{t},k^{*}_{t}) \\ &=E_{t}[ v_{t}] - \frac{1}{32(T-t)} E_{t}\bigg[\int _{t}^{T}\frac{\Psi _{r}}{( N^{\prime }( d_{+}( k^{*}_{t},\Psi _{r}) ) ) ^{2}} \\ & \phantom{=:E_{t}[ v_{t}] - \frac{1}{32(T-t)} E_{t}\bigg[\int _{t}^{T}} \times \bigg( E_{r}\bigg[ N^{\prime }\big(d_{+}(k^{*}_{t},v_{t}) \big)\frac{\int _{r}^{T}D_{r}^{W}\sigma _{s}^{2}ds}{v_{t}}\bigg] \bigg) ^{2}dr\bigg]. \end{aligned}$$

Here, using similar arguments as in the proof of Proposition 3.1, we see that $\Psi _{r}$ can be expanded as

$$\begin{aligned} \Psi _{r} =&E_{r}[ \Psi _{r}] \\ =&E_{r}\bigg[ BS^{-1}\bigg(X_{t},\Lambda _{T}-\int _{r}^{T}U_{s}dW_{s} \bigg)\bigg] \\ =&E_{r}[ \Psi _{T}] -\frac{1}{2}E_{r}\left [\int _{r}^{T}( BS^{-1}) ^{\prime \prime }( k^{*}_{t},{\Lambda _{\theta }}) U_{\theta }^{2}d \theta \right ] \\ =&E_{r}[ v_{t}]-\frac{1}{2}E_{r}\left [ \int _{r}^{T}(BS^{-1}) ^{ \prime \prime }( k^{*}_{t},{\Lambda _{\theta }}) U_{\theta }^{2}d \theta \right ] . \end{aligned}$$

Notice that $( BS^{-1}) ^{\prime \prime }(k^{*}_{t},{\cdot })$ is bounded. This comes from hypothesis (H1) and (3.2). Moreover, (H1) and (H3) imply that

$$ U_{r}=E_{r}\bigg[ \exp (X_{t})N^{\prime }\big(d_{+}(k^{*}_{t}, v_{t}) \big)\frac{ \int _{r}^{T}D_{r}^{W}\sigma _{s}^{2}ds}{2\sqrt{T-t}\,v _{t}}\bigg] \leq C_{t}(T-t)^{\frac{1}{2}+\delta }, $$

where $C_{t}$ is a positive constant. Then we get

$$ \Psi _{r}=E_{r}[ v_{t}]+O\big((T-r)^{2+2\delta }\big) \qquad \text{a.s.,} $$

which jointly with (H1) and dominated convergence implies that

$$\begin{aligned} &\lim _{T\rightarrow t}\frac{I( t,T,X_{t},k^{*}_{t}) -E_{t}[ v_{t}] }{(T-t)^{2+2 \delta }} \\ &=- \frac{1}{32}\lim _{T\rightarrow t}\frac{1}{(T-t)^{3+2\delta }} \\ & \phantom{=:- \frac{1}{32}\lim _{T\rightarrow t}}\times E_{t}\bigg[\int _{t}^{T} \Psi _{r}\bigg( E_{r}\bigg[ \exp \Big( \frac{1}{8}( \Psi _{r}^{2}-v_{t}^{2}) (T-t) \Big) \frac{\int _{r}^{T}D_{r}^{W}\sigma _{s}^{2}ds}{v_{t}}\bigg] \bigg) ^{2}dr \bigg] \\ &=- \frac{1}{32\sigma _{t}}\lim _{T\rightarrow t}\frac{1}{(T-t)^{3+2 \delta }}E_{t}\bigg[ \int _{t}^{T}\bigg( E_{r}\int _{r}^{T}D_{r}^{W} \sigma _{s}^{2}ds\bigg) ^{2}dr\bigg]. \end{aligned}$$

Now the proof is complete. □

Corollary 3

Assume a fractional volatility model of the form$\sigma _{t}=f(B^{H} _{t})$, where$f\in \mathcal{C}_{b}^{1}$is a function with range in a compact set of$\mathbb{R}_{+}$and$B^{H}$is a fractional Brownian motion with Hurst parameter$H$ (see for example Alòs et al. [4]). Then (H1)–(H4) hold with$\delta =H-1/2$, and then Theorem3.2implies that

$$ I( t,T,X_{t},k^{*}_{t})-E_{t}[ v_{t}] =O\big(( T-t) ^{1+2H}\big) \qquad \textit{a.s. as}~T\to t. $$

Remark 4

Alòs and León [3, Corollary 3.10] show that under some regularity conditions,

$$\begin{aligned} &\lim _{T\rightarrow t}\frac{1}{(T-t)^{2\delta }}\frac{\partial ^{2}I}{ \partial k^{2}}(t,T,X_{t},k^{*}_{t}) \\ &=\frac{1}{4\sigma _{t}^{5}} \lim _{T\rightarrow t} \frac{1}{(T-t)^{3+2 \delta }}E_{t}\bigg[\int _{t}^{T}\bigg(E_{r}\int _{r}^{T}D_{r}^{W}\sigma _{s}^{2}ds\bigg) ^{2}dr\bigg] \qquad \text{a.s.} \end{aligned}$$

Then Theorem 3.2 gives us that in the uncorrelated case,

$$ \lim _{T\rightarrow t}\frac{I( t,T,X_{t},k^{*}_{t}) -E_{t}[ v_{t}] }{(T-t)^{2+2 \delta }}= -\frac{\sigma _{t}^{4}}{8}\lim _{T\rightarrow t}\frac{\frac{ \partial ^{2}I}{\partial k^{2}}( t,T,X_{t},k^{*}_{t}) }{(T-t)^{2\delta }} \qquad \text{a.s.} $$

That is,

$$ \lim _{T\rightarrow t}\frac{I( t,T,X_{t},k^{*}_{t}) -E_{t}[ v_{t}] }{(T-t)^{2+2 \delta }}= -\frac{1}{8}\lim _{T\rightarrow t}\frac{(I( t,T,X_{t},k^{*} _{t}))^{4}\frac{\partial ^{2}I}{\partial k^{2}}( t,T,X_{t},k^{*}_{t}) }{(T-t)^{2 \delta }} \qquad \text{a.s.} $$

Remark 5

Assume that (H3) holds with $\delta =0$ and that for every $t\in [ 0,T]$, there exists a random variable $D_{t}^{+}\sigma _{t} ^{2}$ such that

$$ \lim _{T\rightarrow t}\sup _{r\in [ t,T] } | E_{r}[ D_{r}^{W}\sigma _{s} ^{2}] -D_{t}^{+}\sigma _{t}^{2}| =0 \qquad \text{a.s.} $$

(3.3)

Then Theorem 3.2 gives us that a.s.,

$$\begin{aligned} &\lim _{T\rightarrow t}\frac{I( t,T,X_{t},k^{*}_{t}) -E_{t}[ v_{t}] }{(T-t)^{2}} \\ &=-\frac{( D_{t}^{+}\sigma _{t}^{2}) ^{2}}{96\sigma _{t}} \\ &\quad {}-\frac{1}{32\sigma _{t}}\lim _{T\rightarrow t}\frac{1}{(T-t)^{3}} \\ &\phantom{-\frac{1}{32\sigma _{t}}\lim _{T\rightarrow t}aai}\times E_{t} \bigg[\int _{t}^{T}\bigg( \Big( E_{r} \int _{r}^{T}D_{r}^{W}\sigma _{s} ^{2}ds \Big) ^{2}-\Big( \int _{r}^{T}D_{t}^{+}\sigma _{t}^{2}ds\Big) ^{2}\bigg) dr\bigg]. \end{aligned}$$

(3.4)

Now notice that

$$\begin{aligned} &E_{t}\bigg[\int _{t}^{T}\bigg( \Big( E_{r}\int _{r}^{T}D_{r}^{W}\sigma _{s} ^{2}ds\Big) ^{2}-\Big( \int _{r}^{T}D_{t}^{+}\sigma _{t}^{2}ds\Big) ^{2}\bigg) dr\bigg] \\ &=E_{t}\bigg[\int _{t}^{T}E_{r}\bigg[\bigg( \int _{r}^{T}D_{r}^{W} \sigma _{s}^{2}ds- \int _{r}^{T}D_{t}^{+}\sigma _{t}^{2}ds\bigg) \\ & \phantom{=:E_{t}\bigg[\int _{t}^{T}E_{r}\bigg[} \times \bigg(\int _{r}^{T}D_{r}^{W}\sigma _{s}^{2}ds+ \int _{r}^{T}D_{t} ^{+}\sigma _{t}^{2}ds\bigg) \bigg]dr\bigg], \end{aligned}$$

which jointly with (3.3) and (3.4) gives us that

$$ \lim _{T\rightarrow t}\frac{I( t,T,X_{t},k^{*}_{t}) -E_{t}[ v_{t}] }{(T-t)^{2}}=-\frac{( D_{t}^{+}\sigma _{t}^{2}) ^{2}}{96\sigma _{t}} \qquad \text{a.s.} $$

4 The correlated case

We now consider the following hypotheses:

(H2′):

$\sigma \in \mathbb{L}_{W}^{3,2}$.

(H3′):

Hypothesis (H2′) holds, and there exist two constants $\delta \in ( -\frac{1}{2},\frac{1}{2})$ and $C>0$ such that for any $0< r< s< T$,

$$\begin{aligned} E_{r}[ D_{r}^{W}\sigma _{s}^{2}] &\leq C( s-r) ^{\delta }, \\ E_{r}[ D_{\theta }^{W}D_{r}^{W}\sigma _{s}^{2}] &\leq C( s-r) ^{ \delta }( s-\theta ) ^{\delta }, \\ E_{r}[ D_{u}^{W}D_{\theta }^{W}D_{r}^{W}\sigma _{s}^{2}] &\leq C( s-r) ^{\delta }( s-\theta ) ^{\delta }( s-u) ^{\delta }. \end{aligned}$$

(H5):

Hypotheses (H1), (H2′), (H3′) and (H4) hold, and the terms

$$\begin{aligned} &\frac{1}{(T-t)^{2+\delta }}E_{t}\bigg[\int _{t}^{T} \int _{s}^{T}D_{s} ^{W}\sigma _{r}^{2}drds\bigg], \\ &\frac{1}{(T-t)^{4+2\delta }}E_{t} \bigg[\bigg(\int _{t}^{T} \int _{s} ^{T}D_{s}^{W}\sigma _{r}^{2}dr ds\bigg) ^{2}\bigg] , \\ &\frac{1}{(T-t)^{3+2\delta }}E_{t}\bigg[\int _{t}^{T}\bigg( \int _{s} ^{T} D_{s}^{W}\sigma _{r} dr\bigg) ^{2}ds\bigg], \\ &\frac{1}{(T-t)^{3+2\delta }}E_{t}\bigg[ \int _{t}^{T} \int _{s}^{T} \int _{r}^{T}D_{s}^{W}D_{r}^{W}\sigma _{u}^{2}du dr ds\bigg] \end{aligned}$$

all have finite a.s. limits as $T\rightarrow t$.

The following result gives us an exact decomposition for the at-the-money implied volatility. This is the main tool in this section.

Proposition 1

Consider the model (2.1) and assume that hypotheses (H1), (H2′) and (H3′) hold for some$\delta \in ( -\frac{1}{2},\frac{1}{2})$. Then

$$\begin{aligned} I( t,T,X_{t},k^{*}_{t}) =&I^{0}( t,T,X_{t},k^{*}_{t}) \\ &{}+\frac{\rho }{2}E_{t} \bigg[\int _{t}^{T}( BS^{-1}) ^{\prime }( k ^{\ast }_{t},\Gamma _{s}) H(s,T,X_{s},k^{*}_{t},v_{s})\Phi _{s}ds\bigg], \end{aligned}$$

(4.1)

where$I^{0}( t,T,X_{t},k^{*}_{t})$denotes the implied volatility in the uncorrelated case$\rho =0$,

$$ \Gamma _{s}:=E_{t}[ BS(t,T,X_{t},k^{*}_{t},v_{t})] +\frac{\rho }{2}E _{t}\left [\int _{t}^{s} H(r,T,X_{r},k^{*}_{t},v_{r})\Phi _{r}dr\right ], $$

and$\Phi _{t}:=\sigma _{t}\int _{t}^{T}D_{t}^{W}\sigma _{r}^{2}dr$.

Proof

We can write (see Alòs et al. [4])

$$ V_{t}=E_{t}[ BS(t,T,X_{t},k^{*}_{t},v_{t})] + A_{t}^{T}, $$

where

$$ A_{t}^{T}=\frac{\rho }{2}E_{t}\bigg[\int _{t}^{T}H(s,T,X_{s},k^{*}_{t},v _{s})\Phi _{s}ds\bigg]. $$

Thus,

$$ I( t,T,X_{t}, k_{t}^{*}) =BS^{-1}( k^{*}_{t},V_{t}) =E_{t}[ BS^{-1}(k ^{*}_{t},V_{t}^{0}+A_{t}^{T})] , $$

where $V_{t}^{0}:=E_{t}[ BS( t,T,X_{t},k_{t}^{*},v_{t})]$. Notice that because of the Hull and White formula, this expression coincides with the option price in the uncorrelated case $\rho = 0$. Then it follows that

$$\begin{aligned} &E_{t}[ BS^{-1}(k^{*}_{t},V_{t}^{0}+A_{t}^{T})-BS^{-1}(k^{*}_{t},V_{t}^{0})] \\ &=\frac{\rho }{2}E_{t}\left [\int _{t}^{T}( BS^{-1}) ^{\prime }( k_{t}^{*},\Gamma _{s}) H(s,T,X_{s},k^{*}_{t},v_{s})\Phi _{s}ds\right ], \end{aligned}$$

which proves (4.1). □

Theorem 3.2 and Proposition 4.1 allow us to prove the following result.

Theorem 2

Consider the model (2.1) and assume that hypotheses (H1), (H2′), (H3′), (H4) and (H5) hold for some$\delta \in ( -\frac{1}{2},\frac{1}{2})$. Then:

• If$\delta <0$, we have

  $$\begin{aligned} &\lim _{T\rightarrow t}\frac{I( t,T,X_{t},k^{*}_{t}) -E_{t}[v_{t}]}{(T-t)^{1+2\delta }} \\ &= \lim _{T\rightarrow t}\frac{3\rho ^{2}}{8\sigma _{t}^{3}(T-t)^{4+2 \delta }}E_{t}\bigg[\bigg(\int _{t}^{T}\int _{s}^{T}D_{s}^{W}\sigma _{r} ^{2}dr ds\bigg)^{2} \bigg] \\ &\quad {}-\lim _{T\rightarrow t} \frac{\rho ^{2}}{2\sigma _{t}(T-t)^{3+2\delta }}E_{t}\bigg[ \int _{t} ^{T}\bigg( \int _{s}^{T} D_{s}^{W}\sigma _{r} dr\bigg) ^{2}ds\bigg] \\ &\quad {}-\lim _{T\rightarrow t} \frac{\rho ^{2}}{2\sigma _{t}(T-t)^{3+2\delta }}E_{t}\bigg[\int _{t}^{T} \int _{s}^{T}\int _{r}^{T}D_{s}^{W}D_{r}^{W}\sigma _{u}^{2}du dr ds \bigg] \qquad \textit{a.s.} \end{aligned}$$

• If$\delta > 0$, we have

  $$\begin{aligned} \lim _{T\rightarrow t}\frac{I( t,T,X_{t},k^{*}_{t}) -E_{t}[v_{t}]}{(T-t)^{1+ \delta }} &=\lim _{T\rightarrow t}\frac{\rho }{4(T-t)^{2+\delta }} E_{t} \left [\int _{t}^{T}\! \int _{s}^{T} \!\!D_{s}^{W}\sigma _{r}^{2}dr ds\right ] \quad\ \textit{a.s.} \end{aligned}$$

• If$\delta =0$, we have

  $$\begin{aligned} &\lim _{T\rightarrow t}\frac{I( t,T,X_{t},k^{*}_{t}) -E_{t}[v_{t}]}{(T-t)} \\ &= \lim _{T\rightarrow t}\frac{3\rho ^{2}}{8\sigma _{t}^{3}(T-t)^{4 }}E _{t}\bigg[ \bigg(\int _{t}^{T}\int _{s}^{T}D_{s}^{W}\sigma _{r}^{2}dr ds \bigg)^{2}\bigg] \\ &\quad {}-\lim _{T\rightarrow t}\frac{\rho ^{2}}{2\sigma _{t}(T-t)^{3}}E_{t} \bigg[\int _{t}^{T}\bigg( \int _{s}^{T} D_{s}^{W}\sigma _{r} dr\bigg) ^{2}ds\bigg] \\ &\quad {}-\lim _{T\rightarrow t}\frac{\rho ^{2}}{2\sigma _{t}(T-t)^{3 }}E_{t} \bigg[\int _{t}^{T} \int _{s}^{T}\int _{r}^{T}D_{s}^{W}D_{r}^{W}\sigma _{u}^{2}du dr ds\bigg] \\ &\quad {}+\lim _{T\rightarrow t}\frac{\rho }{4(T-t)^{2}}E_{t}\bigg[\int _{t} ^{T} \int _{s}^{T}D_{s}^{W}\sigma _{r}^{2}dr ds\bigg] \qquad \textit{a.s.} \end{aligned}$$

Proof

The main idea of the proof is to see that $I( t,T,X_{t},k^{*}_{t}) -E[v _{t}]$ is a sum of terms of a.s. order $O((T-t)^{1+\delta })$, terms of a.s. order $O((T-t)^{1+2\delta })$ and a.s. higher-order terms. Then if $\delta <0$, we have $1+\delta >1+2\delta$ and the leading terms will be those of order $O((T-t)^{1+2\delta })$, while if $\delta >0$, the leading terms will be those of order $O((T-t)^{1+\delta })$. Notice that Proposition 4.1 gives us

$$ I( t,T,X_{t},k^{*}_{t}) -E[v_{t}]=T_{1}+T_{2}, $$

where

$$\begin{aligned} T_{1} =&I^{0}( t,T,X_{t},k^{*}_{t})-E[v_{t}], \\ T_{2} =&\frac{\rho }{2}E_{t}\left [\int _{t}^{T}( BS^{-1}) ^{\prime }( k_{t}^{*},\Gamma _{s}) H(s,T,X_{s},k^{*}_{t},v_{s})\Phi _{s}ds\right ]. \end{aligned}$$

We know from Theorem 3.2 that $T_{1}=O((T-t)^{2+2 \delta })$. Then the proof reduces to seeing that $T_{2}$ is a sum of terms of the orders $O((T-t)^{1+\delta })$ and $O((T-t)^{1+2\delta })$. To this end, we apply the anticipating Itô formula (2.2) to the process $H(s,T,X_{s},k^{*}_{t},v_{s})J_{s}$, where $J_{s}=\int _{s}^{T}( BS^{-1}) ^{\prime }( k_{t}^{*},\Gamma _{u})\Phi _{u}du$. Then taking conditional expectations, we get

$$\begin{aligned} 0 =&E_{t}\bigg[ H(t,T,X_{t},k^{*}_{t},v_{t})J_{t}+\int ^{T}_{t} H(s,T,X _{s},k^{*}_{t},v_{s}) dJ_{s} \\ & \phantom{E_{t}\Bigg[}+\int ^{T}_{t}\frac{\partial ^{2}}{\partial x \partial \sigma } H(s,T,X_{s},k^{*}_{t},v_{s}) J_{s} \frac{\partial v}{ \partial y} (D^{W}_{s} Y_{s}) \sigma _{s} ds \\ & \phantom{E_{t}\Bigg[}+\int ^{T}_{t} \frac{\partial }{\partial x} H(s,T,X _{s},k^{*}_{t},v_{s}) (D^{W}_{s} J_{s}) \sigma _{s} ds \\ & \phantom{E_{t}\Bigg[}+\int ^{T}_{t} \frac{\partial }{\partial t} H(s,T,X _{s},k^{*}_{t},v_{s})J_{s} ds \\ & \phantom{E_{t}\Bigg[}+\int ^{T}_{t} \frac{\partial }{\partial \sigma } H(s,T,X_{s},k^{*}_{t},v_{s})\frac{\partial v}{\partial t} J_{s}ds \\ & \phantom{E_{t}\Bigg[}+\int ^{T}_{t} \frac{\partial }{\partial \sigma } H(s,T,X_{s},k^{*}_{t},v_{s})\frac{\partial v}{\partial y} J_{s}dY _{s} \\ & \phantom{E_{t}\Bigg[}+\int ^{T}_{t} \frac{\partial }{\partial x} H(s,T,X _{s},k^{*}_{t},v_{s}) J_{s} dX_{s} \\ & \phantom{E_{t}\Bigg[}+\frac{1}{2}\int ^{T}_{t} \frac{\partial ^{2}}{ \partial x^{2}} H(s,T,X_{s},k^{*}_{t},v_{s}) J_{s} d\langle X\rangle _{s} \bigg]. \end{aligned}$$

Now, using the relationships

$$\begin{aligned} \frac{1}{\sigma (T-t)}\frac{\partial }{\partial \sigma }BS(t,T,x,k, \sigma ) =&\left (\frac{\partial ^{2}}{\partial x^{2}} - \frac{\partial }{\partial x}\right )BS(t,T,x,k,\sigma ), \\ \left (\frac{\partial }{\partial t} + \frac{1}{2}\sigma ^{2}\frac{ \partial ^{2}}{\partial x^{2}} - \frac{1}{2}\sigma ^{2} \frac{\partial }{\partial x} \right )BS(t,T,x,k,\sigma ) =&0, \\ D^{W}_{s} J_{s} =& \rho \int _{s}^{T}( BS^{-1}) ^{\prime }( k_{t}^{*}, \Gamma _{r})D^{W}_{s} \Phi _{r}dr, \\ D^{W}_{s} Y_{s} =& \rho \int ^{T}_{s} D^{W}_{s} \sigma ^{2}_{r} dr, \end{aligned}$$

we obtain

$$\begin{aligned} 0 =&E_{t}\bigg[ H(t,T,X_{t},k^{*}_{t},v_{t})J_{t}-\int _{t}^{T}H(s,T,X _{s},k^{*}_{t},v_{s})( BS^{-1}) ^{\prime }( X_{t},\Gamma _{s}) \Phi _{s}ds \\ & \phantom{E_{t}\Bigg[}+ \frac{\rho }{2} \int _{t}^{T} \left (\frac{ \partial ^{3}}{\partial x^{3}} - \frac{\partial ^{2}}{\partial x^{2}} \right ) H(s,T,X_{s},k^{*}_{t},v_{s})J_{s}\Phi _{s} ds \\ & \phantom{E_{t}\Bigg[}+ \rho \int _{t}^{T}\frac{\partial }{\partial x}H(s,T,X _{s},k^{*}_{t},v_{s})\left ( \int _{s}^{T}( BS^{-1}) ^{\prime }( k^{ \ast }_{t},\Gamma _{r}) ( D_{s}^{W}\Phi _{r}) dr\right ) \sigma _{s}ds \bigg], \end{aligned}$$

which implies that

$$\begin{aligned} T_{2} =&E_{t}\bigg[ \frac{\rho }{2} H(t,T,X_{t},k^{*}_{t},v_{t})J _{t} \\ & \phantom{E_{t}\Bigg[}+ \frac{\rho ^{2}}{4} \int _{t}^{T} \left (\frac{ \partial ^{3}}{\partial x^{3}} - \frac{\partial ^{2}}{\partial x^{2}} \right ) H(s,T,X_{s},k^{*}_{t},v_{s})J_{s}\Phi _{s} ds \\ & \phantom{E_{t}\Bigg[}+ \frac{\rho ^{2}}{2} \int _{t}^{T}\!\frac{\partial }{\partial x}H(s,T,X_{s},k^{*}_{t},v_{s})\left ( \int _{s}^{T}\!( BS^{-1}) ^{\prime }(k_{t}^{*},\Gamma _{r}) ( D_{s}^{W}\Phi _{r}) dr\right ) \sigma _{s}ds\bigg] \\ =&T_{2}^{1}+T_{2}^{2}+T_{2}^{3}. \end{aligned}$$

Now the proof is decomposed into three steps.

Step 1. Here we claim that $T_{2}^{1}$ is of the a.s. order $O((T-t)^{1+\delta })$. As

$$\begin{aligned} ( BS^{-1}) ^{\prime }( k_{t}^{*},\Gamma _{s}) &=\frac{1}{e^{X_{t}}N ^{\prime }(d_{+}( k_{t}^{*},BS^{-1}(k_{t}^{*},\Gamma _{s}))) \sqrt{T-t}}, \\ H(t,T,X_{t},k_{t}^{*},v_{t}) &=\frac{e^{X_{t}}N^{\prime }(d_{+}( k _{t}^{*},v_{t}) )}{v_{t}\sqrt{T-t}}\left ( 1-\frac{d_{+}( k_{t}^{*},v _{t}) }{v_{t}\sqrt{T-t}}\right ), \end{aligned}$$

we have that

$$\begin{aligned} &\lim _{T\rightarrow t}\frac{T_{2}^{1}}{(T-t)^{1+\delta }} \\ &=\lim _{T\to t}\frac{1}{(T-t)^{1+\delta }} E_{t}\bigg[ \frac{\rho }{2} H(t,T,X_{t},k^{*}_{t},v_{t})J_{t} \bigg] \\ &=\lim _{T\to t}\frac{\rho }{2(T-t)^{1+\delta }} E_{t}\bigg[ \frac{e ^{X_{t}}N^{\prime }(d_{+}( k^{*}_{t},v_{t}) )}{v_{t}\sqrt{T-t}} \bigg( 1-\frac{d_{+}( k^{*}_{t},v_{t})}{v_{t}\sqrt{T-t}}\bigg) \\ & \phantom{=:\lim _{T\to t}\frac{\rho }{2(T-t)^{1+\delta }} E_{t}\Bigg[} \times \int _{t}^{T}\frac{1}{e^{X_{t}}N^{\prime }(d_{+}( k_{t}^{*},BS ^{-1}(k_{t}^{*},\Gamma _{s}))) \sqrt{T-t}}\Phi _{s}ds \bigg] \\ &=\lim _{T\rightarrow t}\frac{\rho }{4(T-t)^{2+\delta }} E_{t}\left [\int _{t}^{T}\frac{\Phi _{s}}{v_{s}}ds\right ] \\ &=\lim _{T\rightarrow t}\frac{\rho }{4(T-t)^{2+\delta }}E_{t}\left [\int _{t}^{T}\frac{\sigma _{s}}{v_{s}}\int _{s}^{T}D_{s}^{W}\sigma _{r}^{2}dr ds\right ] \\ &=\lim _{T\rightarrow t}\frac{\rho }{4(T-t)^{2+\delta }}E_{t}\left [ \int _{t}^{T} \int _{s}^{T}D_{s}^{W}\sigma _{r}^{2}dr ds\right ] \qquad \text{a.s.} \end{aligned}$$

(4.2)

Step 2. In this step, we show that $T_{2}^{2}$ and $T_{2}^{3}$ are the sum of terms of a.s. order $O((T-t)^{1+2 \delta })$ plus terms of a.s. order $O((T-t)^{\frac{3}{2}+3\delta })$. We remark that we have $\frac{3}{2}+3\delta >\max {(1+\delta ,1+2\delta )}$. Applying again the anticipating Itô formula to the processes

$$ \left ( \frac{\partial ^{3}}{\partial x^{3}}-\frac{\partial ^{2} }{ \partial x^{2}}\right ) H(s,T,X_{s},k^{*}_{t},v_{s})Z_{s} \qquad \text{and} \qquad \frac{\partial H}{\partial x}(s,T,X_{s},k^{*}_{t},v_{s})R_{s}, $$

where

$$\begin{aligned} Z_{s} :=&\int _{s}^{T} \Phi _{u} J_{u} du, \\ R_{s} :=&\int _{s}^{T} \left (\int _{u}^{T}(BS^{-1}) ^{\prime }( k_{t} ^{*},\Gamma _{r}) ( D_{s}^{W}\Phi _{r}) dr\right ) \sigma _{u}du, \end{aligned}$$

we get

$$\begin{aligned} T_{2}^{2} =&\frac{\rho ^{2}}{4}E_{t}\bigg[ \left ( \frac{\partial ^{3}}{ \partial x^{3}}-\frac{\partial ^{2} }{\partial x^{2}}\right ) H(t,T,X _{t}, k_{t}^{*},v_{t})Z_{t} \\ & \phantom{\frac{\rho ^{2}}{4}E_{t}\Bigg[}+ \frac{\rho }{2}\int _{t} ^{T}\left ( \frac{\partial ^{3}}{\partial x^{3}}- \frac{\partial ^{2} }{ \partial x^{2}}\right )^{2} H(s,T,X_{s},k^{*}_{t},v_{s}) Z_{s}\Phi _{s} ds \\ & \phantom{\frac{\rho ^{2}}{4}E_{t}\Bigg[}+\rho \int _{t}^{T}\frac{ \partial }{\partial x}\left ( \frac{\partial ^{3}}{\partial x^{3}}- \frac{ \partial ^{2} }{\partial x^{2}}\right ) H(s,T,X_{s},k^{*}_{t},v_{s})(D _{s}^{W} Z_{s} ) \sigma _{s} ds\bigg] \end{aligned}$$

(4.3)

and

$$\begin{aligned} T_{2}^{3} =& \frac{\rho ^{2}}{2}E_{t}\bigg[\frac{\partial H}{\partial x}(t,T,X_{t},k^{*}_{t},v_{t})R_{t} \\ & \phantom{\frac{\rho ^{2}}{2}E_{t}\Bigg[} +\frac{\rho }{2}\int _{t}^{T} \left ( \frac{\partial ^{3}}{\partial x^{3}}-\frac{\partial ^{2} }{ \partial x^{2}}\right ) \frac{\partial H}{\partial x}(s,T,X_{s},k^{*} _{t},v_{s}) R_{s} \Phi _{s}ds \\ & \phantom{\frac{\rho ^{2}}{2}E_{t}\Bigg[} +\rho \int _{t}^{T}\frac{ \partial ^{2}H}{\partial x^{2}}(s,T,X_{s},k^{*}_{t},v_{s}) \\ & \phantom{\frac{\rho ^{2}}{2}E_{t}\Bigg[\frac{\partial H}{\partial x}(t,T} \times\left (\int _{s}^{T}\int _{r}^{T}( BS^{-1}) ^{\prime }( k_{t}^{*},\Gamma _{u}) ( D_{s}^{W}D_{r}^{W}\Phi _{u}) dudr\right ) \sigma _{s} ds\bigg]. \end{aligned}$$

(4.4)

Alòs et al. [4, Lemma 4.1] gives us that the last two terms in (4.3) and (4.4) are a.s. $O((T-t)^{\frac{3}{2}+3\delta })$. Now, as

$$\begin{aligned} \left ( \frac{\partial ^{3}}{\partial x^{3}}-\frac{\partial ^{2} }{ \partial x^{2}}\right ) H(t,T,X_{t},k^{*}_{t},v_{t}) =&-\frac{1}{16}\frac{e ^{X_{t}} N^{\prime }(d_{+}(k_{t}^{*},v_{t}))}{(v_{t}\sqrt{T-t}) ^{5}}\big( v_{t}^{4}(T-t)^{2}- 48\big), \\ \frac{\partial H}{\partial x}(t,T,X_{t},k^{*}_{t},v_{t}) =& \frac{1}{4} \frac{e^{X_{t}}N^{\prime }(d_{+}( k_{t}^{*},v_{t}) )}{( v _{t}\sqrt{T-t})^{3}} \big( v_{t}^{2}(T-t)-4\big), \end{aligned}$$

it follows that

$$\begin{aligned} &\lim _{T\rightarrow t}\frac{T_{2}^{2}}{(T-t)^{1+2\delta}} \\ &=\frac{\rho ^{2}}{4(T-t)^{1+2\delta }}E_{t}\biggl[ \biggl( \frac{ \partial ^{3}}{\partial x^{3}}-\frac{\partial ^{2} }{\partial x^{2}}\biggr)H(t,T,X _{t},k^{*}_{t},v_{t}) Z_{t}\biggr] \\ &=\frac{\rho ^{2}}{4(T-t)^{4+2\delta }}E_{t}\bigg[ {-}\frac{1}{16}\frac{e ^{X_{t}}N'(d_{+}(k_{t}^{*},v_{t})) }{v_{t}^{5}}\big( v_{t}^{4}(T-t)^{2}- 48\big) \\ &\phantom{\frac{\rho ^{2}}{4(T-t)^{4+2\delta }}E_{t}\Bigg[ -} \times \int _{t}^{T} \sigma _{s} \biggl(\int _{t}^{T}D_{s}^{W}\sigma _{r} ^{2}dr\biggr) \\ &\phantom{\frac{\rho ^{2}}{4(T-t)^{4+2\delta }}E_{t}\Bigg[ -\times \int _{t}^{T}} \times \biggl(\int _{s}^{T}\frac{\Phi _{r}}{e^{X_{t}}N^{\prime }(d_{+}( k^{*}_{t},BS^{-1}(k_{t}^{*},\Gamma _{r}))) }dr\biggr) ds \bigg] \\ &=\lim _{T\rightarrow t}\frac{3\rho ^{2}}{4\sigma _{t}^{5}(T-t)^{4+2 \delta }}E_{t} \biggl[\int _{t}^{T}\biggl( \int _{s}^{T}D_{s}^{W}\sigma _{r}^{2}dr\biggr) \biggl(\int _{s}^{T}\Phi _{r}dr\biggr) \sigma _{s}ds\biggr] \\ &=\lim _{T\rightarrow t}\frac{3\rho ^{2}}{4\sigma _{t}^{5}(T-t)^{4+2\delta }} \\ & \phantom{\lim _{T\rightarrow t}aa}\times E_{t}\biggl[\int _{t}^{T}\biggl( \int _{s}^{T}D_{s}^{W}\sigma _{r}^{2}dr\biggr) \biggl( \int _{s}^{T}\sigma _{r} \int _{r}^{T}D_{r} ^{W}\sigma _{\theta }^{2}d\theta dr\biggr) \sigma _{s}ds\biggr] \\ &=\lim _{T\rightarrow t}\frac{3\rho ^{2}}{4\sigma _{t}^{3}(T-t)^{4+2 \delta }}E_{t}\biggl[\int _{t}^{T}\biggl(\int _{s}^{T}D_{s}^{W}\sigma _{r}^{2}dr\biggr) \biggl( \int _{s}^{T}\int _{r}^{T}D_{r}^{W} \sigma _{\theta }^{2}d\theta dr\biggr) ds\biggr] \\ &=\lim _{T\rightarrow t}\frac{3\rho ^{2}}{8\sigma _{t}^{3}(T-t)^{4+2 \delta }}E_{t}\bigg[\biggl( \int _{t}^{T}\int _{s}^{T}D_{s}^{W}\sigma _{r}^{2} drds\biggr) ^{2}\bigg] \qquad \text{a.s.} \end{aligned}$$

(4.5)

and

$$\begin{aligned} &\lim _{T\rightarrow t}\frac{T_{2}^{3}}{(T-t)^{1+2\delta }} \\ &=\lim _{T\rightarrow t}\frac{\rho ^{2}}{2(T-t)^{1+2\delta }}E_{t} \left [\frac{\partial H}{\partial x}(t,T,X_{t},k^{*}_{t},v_{t})R_{t}\right ] \\ &=\lim _{T\rightarrow t}\frac{\rho ^{2}}{2(T-t)^{1+2\delta }}E_{t} \bigg[ \frac{1}{4}\frac{e^{X_{t}}N^{\prime }(d_{+}( k_{t}^{*},v_{t}) )}{( v_{t} \sqrt{T-t})^{3}}\big( v_{t}^{2}(T-t)-4\big) \\ & \phantom{\lim _{T\rightarrow t}\frac{\rho ^{2}}{2(T-t)^{1+2\delta }}E_{t}\Bigg[aa} \times \int _{t}^{T} \int _{s}^{T}\frac{1}{e^{X_{r}}N^{\prime }(d_{+}( k _{t}^{*},BS^{-1}(k_{t}^{*},\Gamma _{r}))) \sqrt{T-t}} \\ & \phantom{\lim _{T\rightarrow t}\frac{\rho ^{2}}{2(T-t)^{1+2\delta }}E_{t}\Bigg[\times \int _{t}^{T} \int _{s}^{T}aa} \times \bigg(D_{s}^{W}\Big(\sigma _{r} \int _{r}^{T}D_{s}^{W}\sigma _{u} ^{2}du\Big)\bigg) dr \sigma _{s}ds \bigg] \\ &=-\lim _{T\rightarrow t}\frac{\rho ^{2}}{2\sigma _{t}^{2}(T-t)^{3+2 \delta }} E_{t}\bigg[ \int _{t}^{T} \int _{s}^{T}D_{s}^{W}\sigma _{r} \int _{r}^{T}D_{r}^{W}\sigma _{u}^{2}du dr ds \\ & \phantom{-\lim _{T\rightarrow t}\frac{\rho ^{2}}{2\sigma _{t}^{2}(T-t)^{3+2\delta }} E_{t}\Bigg[aa}+\int _{t}^{T} \int _{s}^{T} \sigma _{r}\int _{r}^{T}D_{s} ^{W}D_{r}^{W}\sigma _{u}^{2}du dr ds \bigg] \\ &=-\lim _{T\rightarrow t}\frac{\rho ^{2}}{2\sigma _{t}(T-t)^{3+2\delta }}E_{t}\bigg[\int _{t}^{T}\biggl( \int _{s}^{T} D_{s}^{W}\sigma _{r} dr\biggr) ^{2}ds\bigg] \\ &\quad {}-\lim _{T\rightarrow t} \frac{\rho ^{2}}{2\sigma _{t}(T-t)^{3+2\delta }}E_{t}\biggl[\int _{t} ^{T} \int _{s}^{T} \int _{r}^{T}D_{s}^{W}D_{r}^{W}\sigma _{u}^{2}du dr ds\biggr] \qquad \text{a.s.} \end{aligned}$$

(4.6)

Step 3. From the results in the last steps, we deduce that $I( t,T,X_{t},k^{*}_{t}) -E[v_{t}]$ is the sum of terms of the orders $O((T-t)^{1+\delta })$, $O((T-t)^{1+2\delta })$ and higher-order terms. Then we conclude that for $\delta <0$, $I( t,T,X_{t},k^{*}_{t}) -E[v _{t}]$ is of the order $O((T-t)^{1+2\delta })$, and that if $\delta >0$, this difference is of the order $O((T-t)^{1+\delta })$. Taking into account (4.2), (4.5) and (4.6), the result follows. □

Corollary 3

Assume that$\sigma _{t}=f(B^{H}_{t})$, where$f\in \mathcal{C}_{b} ^{3}$with range in a compact set of$\mathbb{R}_{+}$and$(B^{H}_{t})$is a fractional Brownian motion with Hurst parameter$H$. Then$\delta =H-1/2$and Theorem4.2proves that in the correlated case,

• if$H\leq 1/2$, then$I(t,T,X_{t},k^{*}_{t}) -E_{t}[ v_{t}]=O((T-t)^{2H})$a.s. as$T \to t$;

• if$H\geq 1/2$, then$I( t,T,X_{t},k^{*}_{t}) -E_{t}[ v_{t}]=O((T-t)^{H+1/2})$a.s. as$T \to t$.

Notice that if we compare with Corollary 3.3, we see that the order of convergence is affected not only by the Hurst parameter, but also by the correlation. This result is in line with the results by Fukasawa [14], where it was established that the leverage effect (the negative correlation observed between the asset price and its volatility) plays a crucial role in the ATM short-time behavior of the implied volatility.

Remark 4

Theorem 4.2 gives us that if $\delta \geq 0$, a.s. as $\rho \to 0$,

$$ \lim _{T\rightarrow t}\frac{I( t,T,X_{t}, k_{t}^{*}) -E_{t}[v_{t}] }{(T-t)^{1+ \delta }} =\frac{\rho }{4}\lim _{T\rightarrow t}\frac{1}{(T-t)^{2+ \delta }}\int _{t}^{T} \int _{s}^{T}D_{s}^{W}\sigma _{r}^{2}dr ds+O(\rho ^{2}). $$

Now taking into account the representation of the short-time limit skew in terms of the Malliavin derivative of the volatility process (see Alòs et al. [4]), we get

$$ \lim _{T\rightarrow t}\frac{I( t,T,X_{t},k^{*}_{t}) -E_{t}[ v_{t}] }{(T-t)^{1+ \delta }}=\frac{\sigma _{t}^{2}}{2}\lim _{T\rightarrow t}\frac{\frac{ \partial I}{\partial k}( t,T,X_{t},k^{*}_{t}) }{(T-t)^{\delta }}+ O( \rho ^{2}) \qquad \text{a.s. as $\rho \to 0$.} $$

(4.7)

This equality is in line with the previous results in Carr and Lee [6, Sect. 6.5] on the impact of correlation on volatility swap prices. Moreover, (4.7) gives in the case $H\geq 1/2$ the model-free approximation formula

$$ E_{t}[ v_{t}] \approx I( t,T,X_{t},k^{*}_{t}) -\frac{I( t,T,X_{t},k _{t}^{*})^{2}}{2}\frac{\partial I}{\partial k}( t,T,X_{t},k^{*}_{t}) (T-t) , $$

(4.8)

which is similar to the model-free first-order vol-of-vol expansion around the variance swap by Bergomi and Guyon [5]. In the case $\delta <0$, the obtained limit expressions are more complex. Even when they would allow us to construct an approximation for the volatility swap fair strike, it is not easy to establish a model-free relationship between the fair strike of the volatility swap and the implied volatility skew.

Remark 5

Hypotheses (H1)–(H5) have been chosen for the sake of simplicity. The same results can be extended to other stochastic volatility models (see (5.1) in Sect. 5).

5 Numerical examples

Consider the model (2.1) whose volatility process is given in the form

$$ \sigma _{s} = \sigma _{0} \exp \left (\nu W_{s}^{H}- \frac{\nu ^{2}s^{2H}}{4H}\right ), \qquad s\in [0,T], $$

(5.1)

for some positive constants $\nu$ and $\sigma _{0}$ and where

$$\begin{aligned} W^{H}_{s} := \int ^{s}_{0}\frac{dW_{r}}{(s-r)^{\frac{1}{2}-H}} \end{aligned}$$

for some Hurst parameter $H \in (0,1)$. Also, we assume $t < T < \infty$. This model is similar to the fractional SABR model (see e.g. Akahori et al. [1]). We can prove that this model satisfies (H2′), (H4) and (H5). Nevertheless, it does not satisfy (H1) or (H3). In order to see that the results in Theorem 4.2 still hold, we can make use of an approximation argument. Let us define $\phi (x):=\sigma _{0}\exp (x)$. For every $n>1$, consider a function $\phi _{n}\in \mathcal{C}_{b}^{2}$ satisfying that $\phi _{n} (x)=\phi (x)$ for any $x\in [-n,n]$, $\phi _{n} (x) \in [\phi (-2n)\vee \phi (x), \phi (-n)]$ for $x\le -n$, and $\phi _{n} (x)\in [\phi (n),\phi (x)\wedge \phi (2n)]$ for $x\ge n$. We define

$$ \sigma _{s}^{n}:=\phi _{n}\left (\nu W_{s}^{H}-\frac{\nu ^{2}s^{2H}}{4H}\right ). $$

It is easy to see that $\sigma ^{n}$ satisfies (H1) and (H3′) with $\delta =H-\frac{1}{2}$. Then we can write (we consider $t=0$ for the sake of simplicity)

$$\begin{aligned} I( 0,T,X_{0},k^{*}_{0}) -E[v_{0}] &= I( 0,T,X_{0},k^{*}_{0}) -I^{n}( 0,T,X _{0},k^{*}_{0}) \\ & \phantom{=::}+ I^{n}(0,T,X_{0},k^{*}_{0}) -E[v^{n}_{0}] \\ & \phantom{=::}+E[v^{n}_{0}]-E[v_{0}] \\ &=: T_{1}+T_{2}+T_{3}, \end{aligned}$$

where $I^{n}$ and $E[v^{n}_{0}]$ denote, respectively, the implied volatility and the fair price of the volatility swap under the volatility process $\sigma ^{n}$. Now Theorem 4.2 gives us that (in the correlated case $\rho \neq 0$) $T_{2} = O(T^{2H})$ if $H\le \frac{1}{2}$, and $T_{2}=O(T^{H+\frac{1}{2}})$ if $H\geq \frac{1}{2}$. On the other hand,

$$ v_{0}^{n}=\sqrt{\frac{1}{T}\int ^{T}_{0} (\sigma _{s}^{n})^{2} ds}=\sqrt{ \frac{1}{T} \int _{0}^{T} \big(\phi _{n} (a_{s})\big)^{2}ds}, $$

where $a_{s}:=\nu W_{s}^{H}-\frac{\nu ^{2}s^{2H}}{4H}$. Now, as $\phi _{n}(x)\leq \max (\phi (x), \phi (-n))<\phi (x)+\phi (-n)$, $2(a^{2}+b^{2})\ge (a+b)^{2}$ and $\sqrt{a}+\sqrt{b} \ge \sqrt{a+b}$ for $a,b>0$, we get that

$$\begin{aligned} v_{0}^{n} \le & \sqrt{\frac{1}{T} \int _{0}^{T} \big(\phi (a_{s}) + \phi (-n)\big)^{2}ds} \\ \le & \sqrt{2}\bigg(\sqrt{\frac{1}{T} \int _{0}^{T} \big(\phi (a _{s})\big)^{2}ds} + \sqrt{\frac{1}{T}\int ^{T}_{0}\big(\phi (-n) \big)^{2}ds}\bigg) \\ =& \sqrt{2}\big(v_{0} + \phi (-n)\big). \end{aligned}$$

Then $|v_{0}^{n}-v_{0}|\leq (1+\sqrt{2})v_{0}+\sqrt{2}\phi (-n)$, which implies that

$$\begin{aligned} |T_{3}| \le & E [|v^{n}_{0} - v_{0}|] \\ \le & (1+\sqrt{2}) E\big[|v_{0} + \sigma _{0} \exp (-{n})| \mathbf{1}_{\{\sup _{s\in [0,T]} |\ln (\sigma _{s} /\sigma _{0})| >n\}} \big] \\ \leq & (1+\sqrt{2}) \Big(E\big[\big(v_{0} + \sigma _{0} \exp (- {n})\big)^{2} \big]\Big)^{\frac{1}{2}} \\ &\times \bigg(P\bigg[\sup _{s\in [0,T]}\bigg| \nu W_{s}^{H}-\frac{\nu ^{2}s^{2H}}{4H}\bigg|>n\bigg]\bigg)^{\frac{1}{2}}. \end{aligned}$$

(5.2)

Then if $T<1$, taking $n>\frac{\nu ^{2}}{2H}$, it follows that

$$ |T_{3}|\leq (1+\sqrt{2}) \Big(E\big[\big(v_{0} + \sigma _{0} \exp (- {n})\big)^{2} \big]\Big)^{\frac{1}{2}} \bigg( P\bigg[\sup _{s\in [0,T]} | W_{s}^{H} | >\frac{n}{2 \nu }\bigg]\bigg)^{\frac{1}{2}}. $$

Now Markov’s inequality gives

$$\begin{aligned} P\bigg[\sup _{s\in [0,T]}| W_{s}^{H} | >\frac{n}{2\nu }\bigg]\leq \bigg(\frac{2\nu }{n}\bigg)^{p} E \bigg[ \bigg(\sup _{s\in [0,T]}| W _{s}^{H}| \bigg)^{p}\bigg]. \end{aligned}$$

(5.3)

Moreover, by Nualart and Răşcanu [17, Lemma 7.4], we can easily deduce that for any $p>4$, there exists a positive constant $C_{1}$ such that

$$ E\bigg[\bigg(\sup _{s\in [0,T]} | W_{s}^{H} |\bigg)^{p}\bigg] \leq C _{1} T^{pH}. $$

This jointly with (5.2) and (5.3) gives $T_{3}=O(T^{\frac{pH}{2}})$. Then taking $p>4$, it follows that the order of this term is higher than the order of $T_{2}$. Next, by the mean value theorem, there exists a point $\xi \in (V^{n}_{0},V_{0})$ such that

$$ T_{1} = I(0,T,X_{0},k_{0}^{*}) - I^{n}(0,T,X_{0},k_{0}^{*}) = (BS^{-1})'(k _{0}^{*},\xi )(V_{0} - V^{n}_{0}), $$

where $V^{n}_{0}$ is the option premium with the approximated volatility $\sigma ^{n}$. Then we get

$$\begin{aligned} \lim _{T \to 0}\frac{I(0,T,X_{0},k^{*}_{0}) - I^{n}(0,T,X_{0},k^{*} _{0})}{T^{\alpha }} = C_{2} \lim _{T \to 0}\frac{V_{0} - V^{n}_{0}}{T ^{\alpha +\frac{1}{2}}} \qquad \text{a.s.} \end{aligned}$$

for any $\alpha$ and for some $C_{2}$. Now let us consider the following extension of the Hull and White formula (see Willard [19] and Romano and Touzi [18]):

$$\begin{aligned} V_{t} =& E_{t}\big[BS(t,T,\hat{X}_{t}, k_{t}^{*},\sqrt{1-\rho ^{2}} \,v_{t})\big], \\ V^{n}_{t} =& E_{t}\big[BS(t,T,\hat{X}^{n}_{t},k_{t}^{*},\sqrt{1- \rho ^{2}}\,v_{t}^{n})\big], \end{aligned}$$

where

$$\begin{aligned} \hat{X}_{t} &=X_{t}+\rho \int ^{T}_{t} \sigma _{s} dW_{s}-\frac{1}{2}\int _{t}^{T} (\sigma _{s})^{2} ds, \\ \hat{X}_{t}^{n} &=X_{t}+\rho \int ^{T}_{t} \sigma _{s}^{n} dW_{s}- \frac{1}{2}\int _{t}^{T}(\sigma ^{n}_{s})^{2}ds. \end{aligned}$$

Then similar arguments as for $T_{3}$ give that if $T<1$ and $n>\frac{\nu ^{2}}{2H}$,

$$\begin{aligned} |V_{0} - V^{n}_{0}| \le & E \big[ |e^{\hat{X}_{0}} - e^{\hat{X}^{n} _{0}} |\big] + E\big[ e^{\hat{X}_{0}} \sqrt{T(1-\rho ^{2})} | v_{0} - v_{0}^{n}| \big] \\ \le & \big(E \big[( e^{ \hat{X}_{0}} + e^{ \hat{X}^{n}_{0}})^{2} \big]\big)^{\frac{1}{2}} \big(E \big[ \mathbf{1}_{\{\sup _{s\in [0,T]} { |\ln (\sigma _{s} /\sigma _{0})| >n}\}} \big]\big)^{\frac{1}{2}} \\ &{}+ \sqrt{1-\rho ^{2}} (E [e^{2 \hat{X}_{0}}])^{\frac{1}{2}} \big(E \big[| v_{0} - v_{0}^{n}|^{2}\mathbf{1}_{\{\sup _{s\in [0,T]}{ |\ln ( \sigma _{s} /\sigma _{0})| >n}\}} \big]\big)^{\frac{1}{2}} \\ \le & \big(E \big[( e^{ \hat{X}_{0}} + e^{ \hat{X}^{n}_{0}})^{2} \big]\big)^{\frac{1}{2}} \big(E \big[ \mathbf{1}_{\{\sup _{s\in [0,T]} { |\ln (\sigma _{s} /\sigma _{0})| >n}\}} \big]\big)^{\frac{1}{2}} \\ &{}+ \sqrt{1-\rho ^{2}} (E [e^{2 \hat{X}_{0}}])^{\frac{1}{2}} \\ & \phantom{+}\times (1+\sqrt{2})\Big(E\big[\big(v_{0} + \sigma _{0} \exp (-{n})\big)^{2} \mathbf{1}_{\{\sup _{s\in [0,T]}{ |\ln (\sigma _{s} /\sigma _{0})| >n}\}} \big]\Big)^{\frac{1}{2}} \\ \le & C_{3} \bigg(P\bigg[\sup _{s\in [0,T]}\bigg|\nu W_{s}^{H}-\frac{ \nu ^{2}s^{2H}}{4H}\bigg|>n\bigg]\bigg)^{\frac{1}{4}} \\ \le & C_{3} \bigg( P\bigg[\sup _{s\in [0,T]} | W_{s}^{H}| >\frac{n}{2 \nu }\bigg]\bigg)^{\frac{1}{4}} \end{aligned}$$

for some $C_{3}>0$. Then Markov’s inequality gives

$$ |V_{0} - V^{n}_{0}| \leq C_{3} \left ( \frac{2\nu }{n} \right )^{ \frac{p}{4}} E\bigg[\bigg(\sup _{s\in [0,T]} | W_{s}^{H}|\bigg)^{p} \bigg]^{\frac{1}{4}}, $$

which implies that

$$ T_{1} =O(T^{\frac{pH}{4} - \frac{1}{2}}) \qquad \text{a.s.}, $$

and taking $p>\frac{8}{H}$, the order of $T_{1}$ is also higher than that of $T_{2}$.

5.1 Estimating the Hurst parameters

Hereafter, we use the parameters $\sigma _{0} = 10\%$, $\nu =0.2$, and the correlation between the asset price and its volatility is $\rho =-0.8$.

Let us consider a linear regression analysis with dependent variable

$$ \ln | I( 0,T,X_{0},k^{*}_{0})-E[ v_{0}] | $$

and independent variable $\ln T$. According to our previous results, the corresponding slope will be approximately $2H$ for $H\le 1/2$ and $1/2+H$ for $H > 1/2$. This gives us a tool to estimate the Hurst parameter of the fractional volatility model. In fact, if the obtained slope $a$ is less than 1, we estimate $H$ as $a/2$, while if $a\geq 1$, the Hurst parameter is estimated as $a-1/2$. In order to check the goodness of this methodology, we have checked it numerically for different Hurst parameters. The results have been compared with the estimate obtained from the fact that the skew is of the order $H- 1/2$ (which implies that a linear regression with dependent variable $\frac{\partial I}{\partial k}( 0,T,X_{0},k^{\ast }_{0})$ and independent variable $\ln T$ will have a slope equal to $H-1/2$).

First we obtain the ATM option premiums whose maturities are from 0.0001 to 0.5 by using Monte Carlo simulation with 500 time steps for one year (the number of partitions is max{500T, 100}) and $10^{9}$ trials. Then the ATM implied volatilities are calculated by the bisection method. The ATM skews $\frac{\partial I}{\partial k}$ are obtained by the difference method from the implied volatilities. The volatility swaps are also calculated by the Monte Carlo method. We apply the Black–Scholes model as control variate to the Monte Carlo simulations for calculating option premiums. The Hurst parameters are set as 0.1, 0.3, 0.5, 0.6 and 0.9. In order to estimate the Hurst parameters, we calculate the ATM implied volatilities, volatility swaps and ATM skews with these steps, and the results are shown in Table 1.

Table 1 ATM implied volatilities, volatility swaps and ATM skews

The linear regressions with dependent variable $\ln | I( 0,T,X_{0},k ^{*}_{0})-E[ v_{0}] |$ and independent variable $\ln T$ give us the slopes used for estimating the Hurst parameter. Moreover, we also estimate $H$ from the obtained skew. The results are summarised in Table 2.

Table 2 Hurst parameters obtained from linear regressions

Here $T \le x$ means that the maturities of the data which are used for the linear regression are less than or equal to $x$ years. For example, in the case of $T\le 0.2$, the linear regression analysis uses the data whose maturities are 0.2, 0.1, 0.01, 0.001, 0.0001. Furthermore, (A) shows the results estimated from the implied volatilities and volatility swaps, and (B) shows those estimated from the skews. In (A), the Hurst parameter estimates (the values in the estimated $H$ rows) are calculated by “$\mbox{slope}/2$” if the slope is less than 1, and by “$\hbox{slope} - 0.5$”, for slopes greater than 1. In (B), the Hurst parameter estimates are calculated by “$\hbox{slope} + 0.5$”.

The results show that most of the Hurst parameters are estimated accurately. In particular, the Hurst parameters estimated by skews are more precise than those estimated by implied volatilities and volatility swaps. However, volatility swaps and at-the-money implied volatilities are directly observable from the market, while the implied volatility skew needs to be computed from the implied volatility surface. We also notice that the estimates obtained from the implied volatilities and the volatility swaps tend to be more accurate when we only use very short times to maturity. The techniques presented in this paper could have a potential interest in FX markets, where volatility swaps are more popular than variance swaps and where maturities can be very short.

5.2 Approximation of volatility swaps

Even when formula (4.8) is only valid in the case $H\geq \frac{1}{2}$, Theorem 3.2 gives us that, in the uncorrelated case $\rho =0$, the ATM implied volatility (which coincides in this case with (4.8)) must be an accurate approximation for the volatility swap fair price. In this subsection, we compare the values of our formula (4.8) with those of the ATM implied volatility as the approximated values of volatility swaps. Tables 3 and 4 show the approximated volatility swaps using the ATM implied volatility (ATMI) and our correction (formula (4.8)) for $\rho =-0.8$ and $\rho =0$, respectively. The rows of “volatility swap” are the original volatility swap values obtained by the Monte Carlo simulation.

Table 3 Approximated volatility swaps ($\rho =-0.8$)

Table 4 Approximated volatility swaps ($\rho =0$)

The rows named “error” are calculated as

$$ \text{(approximated value $-$ volatility swap value)$/$(volatility swap value),} $$

and are expressed as a percentage.

In the correlated case (i.e., $\rho =-0.8$), we can see that all errors of the new approximation are lower than those obtained via the ATM implied volatility. In the uncorrelated case, as predicted and according to Carr and Lee [7], the differences between the volatility swap and the ATMI are much smaller than in the correlated case.