Crowdsourced top-k queries by pairwise preference judgments with confidence and budget control

Abstract

Crowdsourced query processing is an emerging technique that tackles computationally challenging problems by human intelligence. The basic idea is to decompose a computationally challenging problem into a set of human-friendly microtasks (e.g., pairwise comparisons) that are distributed to and answered by the crowd. The solution of the problem is then computed (e.g., by aggregation) based on the crowdsourced answers to the microtasks. In this work, we attempt to revisit the crowdsourced processing of the top-k queries, aiming at (1) securing the quality of crowdsourced comparisons by a certain confidence level and (2) minimizing the total monetary cost. To secure the quality of each paired comparison, we employ statistical tools to estimate the confidence interval from the collected judgments of the crowd, which is then used to guide the aggregated judgment. We propose novel frameworks, SPR and SPR$^+$, to address the crowdsourced top-k queries. Both SPR and SPR$^+$ are budget-aware, confidence-aware, and effective in producing high-quality top-k results. SPR requires as input a budget for each paired comparison, whereas SPR$^+$ requires only a total budget for the whole top-k task. Extensive experiments, conducted on four real datasets, demonstrate that our proposed methods outperform the other existing top-k processing techniques by a visible difference.

1 Introduction

Recently, crowdsourcing has been employed to process a variety of database queries, including the MAX queries [7, 8, 18, 22, 40], the JOIN queries [31, 42], and the top-k queries [25, 26, 29]. In this work, we focus on the crowdsourced top-k queries over a collection of data items, where humans are involved in deciding the orderings of items. Such crowdsourced top-k queries are particularly helpful in computer-hostile but human-friendly ranking tasks.

Examples. In the field of machine translation, it is an emerging requirement to find the best translations of a sentence among a set of candidate translations. This is a difficult task for computers since the judgment relies on advanced natural language skills. However, humans can easily point out the better translation of two candidates if they speak both languages. Thus, applications such as Google Translate¹, Duolingo², and Twitter³ etc. use crowdsourcing to rank the candidate translations. Other examples emerge in the field of public opinion analysis. For instance, finding the top-3 best-performing soccer players of the year is the ever interesting topic for soccer fans. For another instance, finding the top-10 best universities is always a yearly topic among graduating students. In these examples, the judgments typically rely on multi-source data integration and perceptual cognizance, which are more suitable for humans than machines. The answers to the top-k queries are essentially consensus rankings that reflect opinions of the crowd, especially those people with certain level of related knowledge (e.g., bilinguals, soccer fans, or graduating students). It is also worth noticing that the consensus rankings of the crowd are different from those fully statistics-based rankings, such as WhoScored⁴ or QS World University Rankings⁵, etc., thus having their own values in practice.

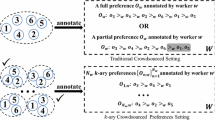
To process a crowdsourced top-k query, one needs to send out microtasks into the crowd, asking for judgments between data items (i.e., opinions on their relative ordering); there are several types of microtasks that can be designed. A straightforward way is to ask human workers to rank all or part of the items and then return the best k items by aggregating received rankings [31, 35]. These methods need complex user interface and are inconvenient for the human workers. Another way is to ask human workers to grade the items and then return the best k items in terms of their average ratings [31]. However, graded judgments are known to differ in scale across judges [41]. To make things worse for crowdsourcing, the graded judgments are hard to calibrate (e.g., to normalize the scores of each worker for fairness) as a worker may grade only a partial set of the items. Therefore, recent crowdsourced top-k query processing [7, 8, 17, 45] focuses on pairwise judgments, i.e., comparing two items at a time. In contrast to other alternatives, pairwise judgments are easier to answer and less prone to human error, requiring only relative preference judgments for paired items.

Determining the number of judgments (called workload hereinafter) needed for a pair of items is a hard problem. Intuitively, some comparisons are easy while others are difficult. A fixed workload could be either unthrifty or insufficient for many, if not most, of the comparisons. To address this problem, Busa-Fekete et al. [3] proposed to estimate the workload from pairwise binary judgments (i.e., yes-or-no answers). However, their solution demands large workloads as the confidence intervals⁶ [20] derived from binary samples are in general not tight enough.

In this work, we propose a new judgment model, entitled pairwise preference judgment, to tackle the problem discussed above. Our model can be viewed as a hybrid of graded judgments and pairwise binary judgments.

Fig. 1

Pairwise preference judgments

Figure 1 demonstrates an example interface for collecting pairwise preference judgments. A sliding bar is used to weigh the preference for a pair of items. Comparing to graded or pairwise binary judgments, pairwise preference judgments can derive tighter confidence intervals such that fewer workloads are needed to make judgments. Table 1 briefly summarizes the features of the three judgment models. Note that the relative order is easy to give (similar to that of the pairwise binary judgment), but the preference level is more difficult to grade (similar to that of the graded judgment). Therefore, the error of the pairwise preference judgment is moderate as compared with other two models.

Table 1 Features of different judgment models

For ease of discussion, we assume normally distributed preferences, following many existing solutions [1, 5, 37, 39]. Based on this assumption, we can readily derive the preference distribution between a pair of items from their judgments (see Fig. 1). Given a set of judgments and a confidence level $1-\alpha$, the confidence interval of the preference mean can be estimated by statistical tools such as Student’s t-distribution [20] and Stein’s estimation [38]. To distinguish a pair, we simply check the lower and the upper bounds of the interval against a neutral value (e.g., 0). For example, if the lower bound of the confidence interval with $\alpha =0.05$ is larger than 0, then we are more than $95\%$ confident that the right-hand-side item is better than the left-hand-side one (see Fig. 1). In other words, we can stop judging this pair if $95\%$ confidence is adequate for our application.

Given the confidence-based judgment model, our objective is to return the top-k items such that the monetary cost (i.e., the total workload) is minimized. Given N items, the best known workload complexity of finding the top-k items is $O\left( Nw\log k\right)$ by heap sort and $O\left( Nw+kw\log N\right)$ by tournament tree, where w is the expected workload for a paired comparison. These approaches overlook a property that the workload needed for a pair of items should be inversely proportional to their distance in the (unknown) true total order. As an example, in Fig. 2 the workload needed for $(o_a,o_b)$ is likely less than $(o_b,o_c)$.

Fig. 2

Select-Partition-Rank (SPR) top-k processing

In an earlier version of this work [23], we proposed a Select-Partition-Rank (SPR) framework that avoids comparing the items that are close to each other in the underlying total ordering (e.g., $o_b$ and $o_c$ in Fig. 2). Specifically, SPR iteratively (1) selects a representative reference r, (2) partitions items based on their relative ordering with respect to r to find the candidates of the top-k results, and (3) ranks the candidates via sorting. In order to minimize the total monetary cost, SPR manages to (1) reduce the total number of paired comparisons and (2) adaptively determine the number of judgments for each paired comparison with respect to some confidence level. Technically, SPR requires that the users specify a constant budget $B_{\text{ pair }}$ for each paired comparison. Two items are considered as ties if their relative ordering cannot be determined with at most $B_{\text{ pair }}$ judgments. The contributions of [23] are the following.

• 1. We considered the problem of crowdsourced top-k query processing with pairwise preference judgments. To the best of our knowledge, no one had ever investigated the problem before.

• 2. We proposed a novel pairwise preference judgment model, which allows the crowd workers to explicitly express their uncertainty on comparisons. Statistics tools are used to derive consensus judgments with confidence guarantees.

• 3. We developed a novel framework, SPR, to solve the crowdsourced top-k problem. By carefully choosing a good reference item r, SPR was able to avoid a large number of unnecessary comparisons.

• 4. We experimentally evaluated the performance of SPR on several real-world datasets. The results showed that SPR, compared with existing solutions, was very effective.

Having established the framework of SPR, we further realize that the users may still feel certain difficulties in practically applying SPR. For example, in order to find out the top-3 best-performing soccer players, a user has to tell SPR how much at maximum he is willing to pay for comparing any two soccer players. This may be difficult because there is no general instruction on how to choose a proper pairwise comparison budget $B_{\text{ pair }}$ for SPR and also because there is no trivial connection between $B_{\text{ pair }}$ and the total amount of money that the user eventually pays for the entire top-3 task. Such difficulties motivate a more user-friendly version of SPR, which should shift the somewhat technical focus on $B_{\text{ pair }}$ to a more practical consideration of overall budget control. Therefore, in this work, which is an extension of [23], we consider a different setting of the crowdsourced top-k problem, where we ask the users to provide a total budget, $B_{\text{ total }}$. An improved version of SPR, named SPR$^+$, is designed to solve this problem. SPR$^+$ allows users just to provide the total budget and tries the best to address the crowdsourced top-k query within the total budget, which is easy to use for general users.

To sum up, in this work, we make the following additional contributions.

• 1. We consider a more practical version of the crowdsourced top-k problem (Sect. 5). Instead of requiring a fixed budget $B_{\text{ pair }}$ for every paired comparison, the new problem setting requires as input a total budget $B_{\text{ total }}$ for the whole top-k ranking task. Comparing to the one studied in [23], the new problem setting is more natural and user-friendly in practice and thus has a wider range of applications.

• 2. We propose a more user-friendly version of SPR, named SPR$^+$, to solve the total-budget version of the crowdsourced top-k problem (Sect. 5.3). SPR$^+$ inherits the Select-Partition-Rank framework of SPR. Yet, the technical difference between SPR$^+$ and SPR is threefold. First, we adopt a bootstrapping technique to make deeper use of the collected individual judgments. Difficult comparisons may thus be foreseen and early terminated without actually spending an unnecessary amount of budget (Sect. 5.1). Second, we adopt a statistical hypothesis testing technique to implement indirect comparisons between items. The new technique contributes to the theoretical soundness of both SPR (Sect. 4.2.4) and SPR$^+$ (Sect. 5.2). More importantly, the hypothesis testing technique also makes the identification of the top-k candidates more effective in SPR$^+$ (Sect. 5.2). Last but not least, we propose a refinement procedure to fine-tune the top-k results in SPR$^+$ (Sect. 5.4).

• 3. We experimentally evaluate SPR$^+$ on real-world datasets (Sects. 6.4–6.5). The results show that the performance of SPR$^+$ is close to that of SPR if the same total amount of money is spent, which outperforms the state-of-the-art solutions. Given that SPR$^+$ is more natural and user-friendly, we argue that SPR$^+$ could be more practically useful.

The rest of the work is organized as follows. Related work and existing solutions are discussed in Sect. 2. Then, the pairwise preference judgment model as well as its superiority is introduced in Sect. 3. The pairwise-budget and total-budget versions of the top-k problem and their solutions, SPR and SPR$^+$, are elaborated in Sects. 4 and 5, respectively. Extensive experiments and analyses of the results can be found in Sect. 6. Finally, Sect. 7 concludes the work. Table 2 summarizes the notation used throughout this work for the ease of further discussions.

Table 2 Notation

2 Related work

2.1 Judgment models

Besides simple strategies such as majority voting or grading, advanced models were developed to draw a conclusion from multiple votes for comparing a pair of data items. Thurstone [39] proposed a model in which scores of items were assumed to be Gaussian random variables with known deviations but unknown means. Given the votes on a pair of items, Thurstone’s model is able to estimate the mean difference of their scores, based on which one item can be inferred superior to the other. Bradley and Terry [2] and Luce [30] proposed what is now known as the Bradley–Terry–Luce (BTL) model. The model assumes that item scores are Gumbel, instead of Gaussian, random variables. Similar to Thurstone’s model, the BTL model is also able to rank items based on votes. Busa-Feketes et al. [3] assumed that the judgment of a paired comparison was determined by the mean of a latent distribution over the items (e.g., the Bernoulli distribution). Therefore, from the answers of the workers, they estimated a confidence interval of the mean using the well-known Hoeffding inequality. A judgment could be made based on the relative position of the confidence interval with reference to a neutral value.

All the above models secure the quality of the answers but overlook a fact that the monetary cost is a major concern when processing a crowdsourced query. In this work, we ask the human workers to express their preferences in pairwise comparisons, which are much more informative in nature.

2.2 Crowdsourced top-k queries

Several studies are directly related to our work. Busa-Feketes et al. [3] proposed a preference-based racing algorithm to process the top-k queries, where a crowdsourced microtask was to ask for a vote between two items. They enumerated all the possible pairwise comparisons and calculated the confidence bounds using the Hoeffding inequality. Their objective was to find an accurate top-k set. Mohajer et al. [33] proposed an algorithm, combining tournament trees and max-heap, to solve the top-k problem. The algorithm first distributes the items into k groups. In each group, the max item is found by tournament. The max items are then fed into a max-heap. The top of the heap is thus the top-1 result. The algorithm then removes the top-1 item and updates the tournament tree and max-heap accordingly to find the top-2 item. The other top-k results are determined by repeating the above process. The above-mentioned methods are further discussed and evaluated in Sect. 6.

Some other studies are closely related to our work, but the proposed solutions are not directly comparable to ours due to technical differences in problem settings. Polychronopoulos et al. [35] studied the top-k query over a set of data items. Human workers were paid to rank small subsets of items, and then, these ranked lists were used to determine the global top-k list via median-rank aggregation [13]. Li et al. [26] also adopted a similar methodology to obtain the top-k ranked lists. The crowd workers were asked either to grade an item or to rank a small set of items. They developed a method to combine the ratings and rankings of items to generate the final top-k ranking. De Alfaro et al. [9] proposed a recursive algorithm to obtain the top-k list from a given set of items. Human workers were typically asked to select the max item out of a small set of items. The above-mentioned studies are different from ours in that they are not based on pairwise comparisons. Since there lacks widely accepted conversions between the costs/benefits of pairwise and non-pairwise comparisons, the above-mentioned top-k solutions are not directly comparable to our proposals.

Ciceri et al. [6] studied the top-k query over uncertain items. Each item was a multi-dimensional feature vector associated with a potential score, which was a weighted sum of its features. Due to the uncertainty in feature values or weights, the scores were uncertain and thus crowd workers were employed to compare items. By enumerating the possible orderings of items in a tree, the item pair that most significantly reduces the uncertainty is outsourced in each iteration. Their method is not directly comparable to ours because they require as input a prior estimation of the uncertainty of the item scores. Such estimations, if ever accessible, rely on case-by-case analyses of the target applications. Lin et al. [29] studied the top-k query over probabilistic data (i.e., $\left<\text {item, value, probability}\right>$ triplets). Their goal is to minimize the expected uncertainty of the final top-k ranking with a given budget. Lee et al. [25] addressed the crowdsourced top-k queries under latency constraints. They constructed a tournament tree of which the leaves contained item sets of various sizes. They aimed at minimizing both the height of the tree (i.e., the latency of the entire process) and the number of pairwise comparisons. Technically, they require a fixed worker error probability as a known input. Given a predefined partial order between items (i.e., a DAG of items), Dushkin et al. [12] aimed at minimizing the number of pairwise comparisons for finding the top-k items. Specifically, they proposed a heap-based solution, where pairwise comparisons between items were done by expert oracles. A single answer from an expert oracle sufficed to complete the judgment of two items. Comparing to our problem settings in this paper, the above-mentioned studies require as input additional information on the items (e.g., value probability, partial order, etc.). Those solutions are thus not directly applicable to our problem where their prerequisites are absent.

2.3 Crowdsourced max and ranking queries

Venetis et al. [40] studied the max query (i.e., top-1 query) over a set of items, with concerns on answer quality, monetary budget and time cost (i.e., the number of algorithmic steps to return the max item). A crowdsourced microtask was to ask a human worker to identify the best out of several items. Strategies for partitioning items and recovering the max were then analyzed with respect to different human error models. Guo et al. [18] investigated answering max queries by hiring human workers for pairwise comparisons. Given a set of items and a budget, they aimed at discovering the best item with the highest confidence. Answers from the human workers were collected to form a vote matrix, and then, the maximum likelihood techniques (e.g., Kemeny ranking [21]) and graph-based heuristics such as PageRank [34] were employed to infer the best item. Khan and García-Molina [22] considered a hybrid method to answer the max query. They first managed to identify a set of good candidates by asking the crowd to grade each of the items. Then, they sorted the candidates, via crowdsourced paired comparisons, to obtain the max item. Davidson et al. [7, 8] also considered such max queries. Pairwise votes from human workers were used to construct a tournament tree via a majority voting mechanism. Data items were randomly permuted as leaves. The tournament tree was tailored such that the number of crowdsourced microtasks for a comparison increased as the level approached the top. Under a proper error model, Davidson et al. showed that their solution might strike a balance between quality and cost.

Marcus et al. [31] aimed at sorting a given set of data items. Two types of microtasks were considered: One asked the workers to provide rankings of several items, and the other requested explicit ratings on items along. Ye and Doermann [44] considered sorting uncertain items, each of which was associated with an underlying score perturbed by a Gaussian noise. They crowdsourced both pairwise comparison tasks and rating tasks to maximize the information gain from a predefined budget. Based on the BTL model, Chen et al. [4] proposed solutions for aggregating votes on pairwise comparisons into a global ranking. They took a marginal perspective to solve the problem, aiming at finding (i) the best next pair of items to compare and (ii) the best human worker to do the comparison. Recently, Matsui et al. [32] considered worker quality in such sorting problems. They aggregated crowdsourced partial rankings based on the Spearman’s distance [10]. Gottlieb et al. [17] crowdsourced random paired comparisons and inferred an initial order. By excluding the ties and the easy pairs, another set of random paired comparisons were crowdsourced. The global ranking was the one minimizing the conflicts in the collected judgments. Dong et al. [11] studied the problem of ranking from crowdsourced pairwise comparisons, using a smoothed matrix manifold optimization technique based on the BTL model. Rajpal and Parameswaran [36] considered the ranking problem without budget control. They used a maximum likelihood method to find a globally consistent ranking from pairwise comparisons. Recently, Xu et al. [43] aimed at constructing a partial ranking, instead of a full ranking, from crowdsourced pairwise comparisons.

3 Preference judgment model

3.1 Comparison process and workloads

To compare items $o_i$ and $o_j$, a human worker provides a preference $v(o_i,o_j)\in [-1,1]$, of which the sign indicates the judgment intention and the absolute value describes the strength toward that intention. The comparison process $\textsc {Comp}\left( o_i,o_j\right)$ for items $o_i$ and $o_j$ is to draw a conclusion from a bag of $w_{i,j}$ (the workload) preference values $V_{i,j}=\{v_1(o_i,o_j),\dots ,v_{w_{i,j}}(o_i,o_j)\}$. Since the unit cost of collecting a human preference is fixed, the goal is to minimize the workload to save the cost.

We may assume that every data item $o_j$ is associated with a hidden score $s(o_j)$, and a human preference $v\left( o_i,o_j\right)$ is in principle monotonically proportional to the difference of the scores, $\Delta s_{i,j}=s(o_i)-s(o_j)$. Although such $\Delta s_{i,j}$ is unknown, we trust the human workers in that their preference values truly reflect $\Delta s_{i,j}$. Put in another way, the actual (unknown) difference of scores, $\Delta s_{i,j}$, determines a Gaussian distribution of human preference values between data items $o_i$ and $o_j$, i.e., $v\left( o_i,o_j\right) \sim \mathcal {N}\left( \mu _{i,j},\sigma ^2_{i,j}\right)$, where $\mu _{i,j}$ is proportional to $\Delta s_{i,j}$ and the variance $\sigma ^2_{i,j}$ reflects how difficult it is to choose between $o_i$ and $o_j$.

Since the mean $\mu _{i,j}$ is a monotonically increasing function of $\Delta s_{i,j}$, to conclude $s(o_i)<s(o_j)$ or $s(o_i)>s(o_j)$ we only need to test $\mu _{i,j}$ against 0. In particular, during the comparison process we aim at minimizing the number of samples required and estimating $\mu _{i,j}$ with a predefined confidence level of $1-\alpha$. Statistical tools for parameter estimation, such as Student’s t-distribution estimation [20] and Stein’s estimation [38], can thus be applied on the bag of samples $V_{i,j}$ to find the confidence interval of $\mu _{i,j}$ with $1-\alpha$ confidence. When the interval excludes 0, we are at least $1-\alpha$ confident to make a judgment between two items.

Student’s $\pmb {t}$-distribution estimation [20]. Let $n=w_{i,j}$ (the number of samples), and $\bar{v}_n$ and $S_n$ be the sample mean and sample standard deviation of $V_{i,j}$, respectively, i.e.,

$$\begin{aligned} \bar{v}_n=\frac{1}{n}\sum _{\ell =1}^{n}v_\ell \left( o_i,o_j\right) , \end{aligned}$$

and

$$\begin{aligned} S_n=\sqrt{\frac{1}{n-1}\sum _{\ell =1}^n\left( v_\ell \left( o_i,o_j\right) -\bar{v}_n\right) ^2}. \end{aligned}$$

Then, a $1-\alpha$ confidence interval of $\mu _{i,j}$ is given by

$$\begin{aligned} J(V_{i,j})=\left[ \bar{v}_n-\frac{t_{\frac{\alpha }{2}, n-1} S_n}{\sqrt{n}},\bar{v}_n+\frac{t_{\frac{\alpha }{2}, n-1}S_n}{\sqrt{n}}\right] , \end{aligned}$$

(1)

where $t_{\frac{\alpha }{2}, n-1}$ indicates the right-tail probability of size $\frac{\alpha }{2}$ of the t-distribution with $n-1$ degrees of freedom. Therefore, if the above interval does not contain 0 (the neutral value) then some conclusion can be made. For example, if $\bar{v}_{n}-t_{\frac{\alpha }{2}, n-1}\cdot \frac{S_n}{\sqrt{n}}>0$ then it is safe to conclude that $\mu _{i,j}>0$ and, as a consequence, $o_i\succ o_j$. As a general trend, with a larger workload, tighter bounds on $\mu _{i,j}$ can be obtained.

Algorithm 1 shows the core process of the estimation, StudentComp. By progressively calling StudentComp, crowd judgments are collected into V (Lines 1–2). Every time the set V is augmented, it is used to decide the relative ordering of $o_i$ and $o_j$ (Lines 3–5). If no decision can yet be made, $o_i$ and $o_j$ are said to be indistinguishable using the current set V, written as $o_i\approx _V o_j$ (Line 6). Note that it is also possible that items $o_i$ and $o_j$ are indistinguishable even after the consumption of the budget $B_{\text{ pair }}$.

Stein’s estimation [38]. Given a predefined interval width 2L, Stein proposed a method to estimate the number of samples n needed to conclude $\mu _{i,j}\in \left[ \bar{v}_n-L,\bar{v}_n+L\right]$ with confidence level $1-\alpha$. In its original form, the estimation takes two stages:

• 1. Get y (Gaussian) samples and calculate $S_y^2$, the sample variance. $S_y^2$ is thus a rough estimation of the true variance $\sigma _{i,j}^2$;

• 2. Set $y'\leftarrow \left\lceil t^2_{1 - \frac{\alpha }{2}, y-1}S_y^2 L^{-2} \right\rceil$. Then, $n=\max \{y,y'\}$ is the number of samples necessary to conclude $\mu _{i,j}\in \left[ \bar{v}_n-L,\bar{v}_n+L\right]$ with confidence level $1-\alpha$.

Recall that in our problem we simply want to find an interval $\left[ \bar{v}_n-L,\bar{v}_n+L\right]$ that excludes 0 with as few samples as possible. We may thus transform Stein’s original method into a progressive estimation on $\mu _{i,j}$.

Algorithm 2 shows the core process of Stein’s estimation. To compare items $o_i$ and $o_j$, we may repeatedly call SteinComp to collect judgments from the crowd. Note that during the process, we dynamically set L to be slightly smaller than $\left| \bar{v}\right|$ such that the interval $\left[ \bar{v}-L, \bar{v}+L\right]$ is always “adjacent” to 0.⁷ With this invariance, the algorithm terminates with a judgment as soon as the workload is sufficient (Lines 4-5). If no judgment can yet be made, then $o_i$ and $o_j$ are tying given V (Line 6). If $o_i$ and $o_j$ are still tying after the consumption of the budget $B_{\text{ pair }}$, they are considered to be a true tie, written as $o_i\approx _{B_{\text{ pair }}} o_j$.

3.2 Why preference judgment?

To demonstrate the effect of different judgment models, we empirically studied the number of microtasks needed to achieve certain confidence levels. Generally speaking, the confidence level can be achieved by fewer microtasks if the judgment model is more informative.

Our experiments were on an IMDb dataset, in which there were movies and users’ ratings (1$\sim$10) on movies. Detailed information of this dataset can be found in Sect. 6.1. We randomly picked 30 popular movies (with at least 100,000 ratings) from the dataset. The ground truth total order of the movies, $\Omega$, was decided based on their mean ratings. To simulate a pairwise preference judgment between movies $o_i$ and $o_j$, we sampled the ratings $s(o_i)$ and $s(o_j)$ from the corresponding histograms of ratings and set $v(o_i,o_j)=\frac{1}{10}\left( s(o_i)-s(o_j)\right)$, as detailed in Sect. 6.1. To simulate a pairwise binary judgment, we set $v(o_i,o_j)=1$ when $s(o_i)-s(o_j)>0$ and $v(o_i,o_j)=-1$ otherwise. (Non-informative cases of $s(o_i)=s(o_j)$ were ignored.)

Given the bag $V_{i,j}=\{v_1(o_i,o_j),\dots ,v_n(o_i,o_j)\}$ and a confidence level $1-\alpha$, we evaluated different $\textsc {Comp}\left( o_i,o_j\right)$ processes. Each $\textsc {Comp}\left( o_i,o_j\right)$ stopped when the estimated confidence reached $1-\alpha$. We ran each comparison process 100 times (setting $B_{\text{ pair }}=\infty$ and $I=30$) and recorded the average workload for each of the 435 paired comparisons. We also calculated the accuracy of each comparison model, which was the ratio of correctly compared pairs (i.e., comparison results that were consistent with $\Omega$) among all the 435 pairs.

Table 3 Accuracy and workload of different judgment models

Table 3 shows our findings. We first compare the preference judgment process to the binary judgment considered in [3]. To achieve the same confidence level, the workload needed for the preference judgment is 5.34 to 10.81 times lower than that of the binary judgment since more information leads to tighter confidence interval estimations. This indicates that the preference model is a better model to return the high-quality ranking results with relatively low monetary cost. The performance of the Student’s t-distribution estimation and the Stein’s estimation is very similar so that any of them can be used to process $\textsc {Comp}\left( o_i,o_j\right)$ for the bag of preferences $V_{i,j}$. A more theoretical analysis of this advantage can be found in Appendix D of [23].

We also evaluated the performance of the graded judgment. For each of the 30 items, we sampled $B_{\text{ pair }}$ ratings from its corresponding histogram and then used the average rating as the score of the item. Then, judgment was made by comparing the scores of items. The accuracy of such a comparison process is also reported in Table 3, with $B_{\text{ pair }}$ varying from 100 to 10,000.

The unit monetary cost of these judgments was more or less the same according to our empirical study on a real crowdsourcing platform Figure Eight (cf. Appendix B of [23]). Therefore, we conclude this section by arguing that the preference judgment model is potentially more effective and useful than the other models.

4 Answering crowdsourced top-k queries

Given a set of N items $\mathcal {O}=\left\{ o_1,o_2,\ldots ,o_N\right\}$, we want to find the k best items $\mathcal {O}^*=\left\{ o_1^*, o_2^*, \ldots , o_k^*\right\} \subset \mathcal {O}$ via pairwise comparisons, where $o_i^*$ is the ith best item. Assuming a unified cost per human worker per microtask, the total monetary cost (TMC) for finding the top-k items $\mathcal {O}^*$ depends on (i) the set of pairs to compare, $\mathcal {C}$, and (ii) the workload for each paired comparison in $\mathcal {C}$:

$$\begin{aligned} \text {TMC} = \sum _{\left( o_i,o_j\right) \in \mathcal {C}}w_{i,j}. \end{aligned}$$

Our goal is to minimize TMC while maintaining a good quality of $\mathcal {O}^*$. We carry out two objectives to that goal:

• 1. Microtask-level cost minimization, in which we manage to determine the workload $w_{i,j}$ of each comparison $\textsc {Comp}\left( o_i,o_j\right)$ subject to a confidence guarantee, and

• 2. Query-level cost minimization, in which we target toward minimizing the number of paired comparisons for finding $\mathcal {O}^*$.

We achieve the first objective via statistical estimations discussed in Sect. 3.1. As a matter of fact, the strength of a preference and the confidence level $1-\alpha$ suggest the difficulty in distinguishing items $o_i$ and $o_j$, and, intuitively, the workload needed should be proportional to the underlying difficulty of the corresponding comparison. The variance of effort in distinguishing different pairs of items makes the second objective hard to achieve. Traditional top-k algorithms assume that the comparison process $\textsc {Comp}\left( o_i,o_j\right)$ has unified cost in any pair of items, but this assumption is no longer held in crowdsourced top-k queries. Thus, simply minimizing the number of comparisons does not necessarily minimize the TMC. Note that, we assume that the answers from the same worker are independent over different comparisons. The dependency may exist in practice since a high-quality worker should have a consistent personal standard. However, this information is not considered in this work for simplicity.

4.1 An ideal solution

Before we propose our solution to the above crowdsourced top-k problem, we consider an interesting question: What is the infimum cost (i.e., the minimum possible cost) to answer a crowdsourced top-k query?

Fig. 3

Infimum cost

Let $\text {wrk}(o_i,o_j)$ be the expected workload to judge between data items $o_i$ and $o_j$, satisfying

$$\begin{aligned} \text {wrk}(o_i,o_j)\propto \frac{1}{|s(o_i)-s(o_j)|}. \end{aligned}$$

The above question is answered by the following lemma.

Lemma 1

[Infimum cost] Given a set of N items $\mathcal {O}$, the infimum cost to find the top-k list is

$$\begin{aligned} \text {TMC}_{\text {inf}}=\sum _{j=1}^{k-1}\text {wrk}(o^*_j,o^*_{j+1})+\sum _{j=k+1}^N\text {wrk}(o^*_j,o^*_k). \end{aligned}$$

Proof

To find the top-k list, it is sufficient and necessary to confirm (i) $o^*_1\succ o^*_2\succ \cdots \succ o^*_k$ and (ii) $o^*_k\succ o^*_j$ for any $j>k$. In the best case, the former costs $\sum _{j=1}^{k-1}\text {wrk}(o^*_j,o^*_{j+1})$, comparing adjacent top-k items. To establish the latter, note that every $o^*_j$ ($j>k$) must be compared to at least one item $o\in \mathcal {O}$ in order to be excluded from the top-k list. The lemma is trivially true when every $o^*_j$ is directly compared to $o=o^*_k$. We argue that comparing $o^*_j$ with $o\ne o^*_k$ is either wasteful or more expensive. Indeed, comparing $o^*_j$ to some $o\succ o^*_k$ does not exclude $o^*_j$ from the top-k list, and comparing $o^*_j$ to some o between $o^*_k$ and $o^*_j$ costs $\text {wrk}(o^*_j,o)\ge \text {wrk}(o^*_j,o^*_k)$ due to the fact that $|s(o^*_j)-s(o^*_k)|\ge |s(o^*_j)-s(o)|$.

Figure 3 illustrates the query processing with the infimum cost. Note that the infimum cost in Lemma 1 is theoretically achievable: We could be lucky to pick the right reference item $o^*_k$, thus after $N-k$ comparisons we prune $N-k$ non-result items. Then, when sorting the remaining k items, we may find that the items are already sorted.

4.2 Select-Partition-Rank (SPR)

Inspired by the discussion in Sect. 4.1, toward an efficient algorithm, any non-result item $o\in \mathcal {O}\setminus \mathcal {O}^*$ should be excluded as early as possible by comparing o with $o^*_k$. Without any prior knowledge on $o^*_k$, this is, of course, only if we are very lucky to pick $o^*_k$ by a wild guess. Fortunately, as will be shown later in Sect. 4.2.2, items succeeding but not far away from $o^*_k$ may also have strong pruning power. We define the sweet spot as the set of items $\left\{ o^*_{k},o^*_{k+1},\cdots ,o^*_{\lceil ck\rceil }\right\}$, where $c>1$ controls the size of the sweet spot ($ck\ll N$).

Fig. 4

Framework of SPR

We develop a randomized algorithm, SPR, to solve the crowdsourced top-k problem. Figure 4 and Algorithm 3 sketch the general idea of SPR. SPR first manages to identify a good reference item within the sweet spot with large probability via sampling (Fig. 4:1; Line 1). SPR then compares all the other items against the reference item and prunes non-result ones. After the comparison processes, we get three distinct groups: winners, ties, and losers, holding those items that are superior to, indistinguishable from, and inferior to the reference, respectively (Figure 4:2; Line 2). SPR then efficiently finds the top-k results by sorting certain part of the partition (Figure 4:3; Lines 3-9).

4.2.1 Selecting a reference

Given a set of N items, by a wild guess we have $\frac{j}{N}$ chance to hit an item r in the top-j set. When r is the max item in a set $\mathcal {X}\subset \mathcal {O}$ of x independent random samples (with putting back), the probability becomes

$$\begin{aligned} p_j(x)\overset{\text {\tiny def}}{=}\text {Pr}\left\{ \left. r \succeq o^*_j\right| x\right\} = 1 - \left( 1 - \frac{j}{N}\right) ^{x}. \end{aligned}$$

Note that this probability is monotonically increasing with respect to the choice of x. Our goal is to find a reference within the sweet spot. In other words, we want to find an item that can beat any item worse than $o^*_{ck}$ but, meanwhile, is itself no better than $o^*_k$. To that end, we consider the following (m, x)-sampling procedure.

(m, x)

-sampling. The (m, x)-sampling procedure takes m batches of independent samples from $\mathcal {O}$, with putting back, each containing x samples. Let $r_i$ be the max item of the ith batch $\mathcal {X}_i$ ($i=1,2,\cdots ,m$). The sampling procedure returns r, the median item of $r_1, r_2, \cdots , r_{m}$, as the final output. It can be shown that the (m, x)-sampling can find a reference r in the sweet spot with high probability.

Lemma 2

Consider a top-k query over N items. Let p be the ratio $\frac{k}{N}$.

If c is chosen such that $c>\frac{1}{p}\left( 1-2^{\frac{1}{\left\lceil \log _{1-p}2\right\rceil }}\right) \ge 1$, then there must exist an integer x within the range $\left( -\log _{1-cp}2,-\log _{1-p}2\right]$ such that $\lim _{m\rightarrow \infty }\text {Pr}\big \{o^*_k\succeq r\succeq o^*_{ck}\big |m,x\big \}=1$, where r is the reference determined by (m, x)-sampling. (Note that there is always a trivial bound of $c\le \frac{1}{p}$ due to $ck\le N$.)

Proof

Define $q_j(m,x)\overset{\text {\tiny def}}{=}\text {Pr}\left\{ \left. r \succeq o^*_j\right| m,x\right\}$, which is the probability of at least $\left\lceil \frac{m}{2}\right\rceil$ $r_i$’s being ranked before $o_j^*$ ($j=1,2,\cdots ,N$). Then,

$$\begin{aligned} q_j(m,x)=\sum _{i=0}^{\left\lfloor \frac{m}{2}\right\rfloor }{\left( {\begin{array}{c}m\\ i\end{array}}\right) } p_j^{m-i}(x)\left( 1-p_j(x)\right) ^i. \end{aligned}$$

For any fixed j and x, the Central Limit Theorem asserts that

Considering the fact that $\text {Pr}\left\{ \left. o^*_k\succeq r\succeq o^*_{ck}\right| m,x\right\} =q_{ck}(m,x)-q_{k-1}(m,x)$, it suffices to have some c and x such that $p_{k-1}(x)< p_k(x)\le \frac{1}{2}< p_{ck}(x)$. By solving this inequality, we obtain the range of c and x as specified in the lemma.

Balancing quality and cost. In practice, as one may imagine, there should be a balance between the quality of the reference and the cost of sampling. In general, we would like to restrict the cost such that it does not dominate the cost of the entire SPR algorithm. The sampling process takes $m(x-1)$ comparisons to find $r_1,r_2,\cdots ,r_m$, and then, any sorting or selection algorithm can be applied to find the median r. Since it takes N comparisons to partition the set of items (Line 2 of Algorithm 3), we solve an optimization problem for a good choice of integers m and x:

$$\begin{aligned} \max _{m,x}&\quad \text {Pr}\left\{ \left. o^*_k\succeq r\succeq o^*_{ck}\right| m,x\right\} \nonumber \\ \text {s.t.}&\quad m(x-1) + \mathcal {C}(\mathcal {A},m) \le N,\nonumber \\&\quad \frac{1}{p}\left( 1-2^{\frac{1}{\left\lceil \log _{1-p}2\right\rceil }}\right)<c\le \frac{1}{p},\nonumber \\&\quad -\log _{1-cp}2<x\le -\log _{1-p}2, \end{aligned}$$

(2)

where $\mathcal {C}(\mathcal {A},m)$ is an upper bound of the number of comparisons if algorithm $\mathcal {A}$ is used to find the median of m numbers. For example, $\mathcal {A}$ may refer to the bubble sort algorithm, which iteratively compares items with their predecessors in the current ranking. After the ith iteration, top-i items are guaranteed to be sorted at the leftmost (or rightmost, depending on the implementation) part of the array. This means that the median can be found in $\lceil \frac{m}{2}\rceil$ iterations. Therefore, when $m>1$,

$$\begin{aligned} \mathcal {C}(\mathcal {A},m)&=\sum _{i=1}^{\lceil \frac{m}{2}\rceil } (m-i) \le \frac{3}{8}(m^2-1). \end{aligned}$$

Similar analysis can be done for other choices of the algorithm $\mathcal {A}$.

Algorithm 4 summarizes the above discussions.

Let w be the expected workload to judge between two items. It takes O(Nw) microtasks to find a good reference.

4.2.2 Partitioning

With a proper reference r, SPR sequentially compares r with every other item. As a result, items $\mathcal {O}\setminus \{r\}$ are divided into three groups: winners $\mathcal {W}$, ties $\mathcal {T}$, and losers $\mathcal {L}$, consisting of the items that are superior to, indistinguishable from, and inferior to r, respectively. Ties are mainly due to practical considerations: Two items are considered tying if their relative ordering cannot yet be determined.

In Lemma 1, we have established that if $r=o^*_k$ then the cost for finding the top-k set (i.e., $\mathcal {W}\cup \{o^*_k\}$) is minimal. Let us suspend the discussion on ties for the moment, assuming that every pair of items $o_i$ and $o_j$ can be eventually separated via a workload of $\text {wrk}(o_i,o_j)$. We now show that, when r is in the sweet spot, it is still efficient in pruning non-result items.

Lemma 3

If the set $\mathcal {O}$ of N items are to be partitioned using $r=o^*_\ell$ ($\ell >k$), then finding the top-k list requires an infimum cost of

$$\begin{aligned} \text {TMC}_{\text {inf}}(o^*_\ell )=&\quad \sum _{j=1}^{k-1}\text {wrk}(o^*_j,o^*_{j+1})+\sum _{j=k+1}^{\ell }\text {wrk}(o^*_j,o^*_k)\\&+\sum _{j=\ell +1}^{N}\text {wrk}(o^*_j,o^*_\ell ). \end{aligned}$$

Specifically, $\text {TMC}_{\text {inf}}(o^*_k)=\text {TMC}_{\text {inf}}$ as in Lemma 1.

Proof

When using $o^*_\ell$ as the reference, to find the top-k list, it is sufficient and necessary to confirm (i) $o^*_1\succ o^*_2\succ \cdots \succ o^*_k$, (ii) $o^*_k\succ o^*_j$ for $k<j\le \ell$, and (iii) $o^*_\ell \succ o^*_j$ for $j>\ell$. $\text {TMC}_{\text {inf}}(o^*_\ell )$ is then the sum of the minimal cost of each of the three confirmations.

Lemma 4

When $k<\ell \ll N$, $\text {TMC}_{\text {inf}}(o^*_\ell )$ is monotonically increasing with respect to $\ell$.

Proof

For any $\ell '$ such that $\ell <\ell '\ll N$, from Lemma 3 it is easy to infer that

$$\begin{aligned}&\text {TMC}_{\text {inf}}(o^*_\ell )-\text {TMC}_{\text {inf}}(o^*_{\ell '})\\ =&\quad \sum _{j={\ell '}+1}^N\left( \text {wrk}(o^*_j,o^*_{\ell })-\text {wrk}(o^*_j,o^*_{\ell '})\right) \qquad (\le 0)\\&+\sum _{j=\ell +1}^{\ell '}\left( \text {wrk}(o^*_j,o^*_\ell )-\text {wrk}(o^*_j,o^*_k)\right) .\qquad (\ge 0) \end{aligned}$$

Since $\ell <\ell '\ll N$, the non-positive term clearly dominates the other, hence $\text {TMC}_{\text {inf}}(o^*_\ell )\le \text {TMC}_{\text {inf}}(o^*_{\ell '})$.

Lemmata 3 and 4 imply that a reference closer to $o^*_k$ is preferable. Given a reference r, Algorithm 5 follows this implication to efficiently prune non-result items. We take an incremental approach to split $\mathcal {O}$ into three sets $\mathcal {W}$, $\mathcal {T}$, and $\mathcal {L}$. At the beginning, every pair of items (o, r) for $o\ne r$ is considered a tie, as no comparison is ever made (Line 1). Then, for every item in $\mathcal {T}\setminus \{r\}$, we ask the crowd to provide one more preference feedback (if the budget still allows) and see whether any judgment can be made (Line 4). As the iteration proceeds, the confirmed winners and losers go to $\mathcal {W}$ and $\mathcal {L}$, respectively, leaving $\mathcal {T}$ being the set of true ties (Lines 5–6). With a good reference, which is guaranteed by SelectReference (Sect. 4.2.1), it is expected that the top-k items are all in $\mathcal {W}$ after the partitioning.

Complexity analysis. The partitioning step compares the reference r with all the other items and thus costs O(Nw), where w is the expected workload to judge between two items.

4.2.3 Sorting

Given a small set of top-k candidates, a sorting procedure can find the top-k list. The key observation here is that, based on their pairwise comparisons with the reference r, we may obtain a good initial ordering of those top-k candidates, and hence, any best-case linear sorting algorithm can find the top-k list efficiently.

In fact, for two items $o_i$ and $o_j$, we know that

$$\begin{aligned} o_i\succ o_j&\Leftrightarrow s(o_i)>s(o_j)\\&\Leftrightarrow \forall r: s(o_i)-s(r)>s(o_j)-s(r). \end{aligned}$$

Recall that, when comparing two items o and $o'$, workers’ feedbacks can be viewed as random samples drawn from a distribution, of which the mean $\mu _{o,{o'}}$ is proportional to $s(o)-s(o')$ and the standard deviation $\sigma _{o,{o'}}$ reflects the difficulty of the comparison. Hence, for any reference r,

$$\begin{aligned} s(o_i)\!>\!s(o_j)\Leftrightarrow s(o_i)\!-\!s(r)\!>\!s(o_j)\!-\!s(r)\Leftrightarrow \mu _{i,r}\!>\!\mu _{j,r}. \end{aligned}$$

While $\mu _{i,r}$ and $\mu _{j,r}$ are unknown, they can be estimated using $V_{i,r}$ and $V_{j,r}$, the bags of preference values collected from the workers. Specifically, given $V_{i,r}$ and $V_{j,r}$, we can define a heuristic ranking, $\succ _H$, between the items, such that $o_i \succ _H o_j$ if and only if $\hat{\mu }_{i,r}>\hat{\mu }_{j,r}$.

The ranking $\succ _H$ is heuristic because $o_i\succ _H o_j$ does not necessarily imply $o_i\succ o_j$ to a confidence level of $1-\alpha$. Nonetheless, the ranking $\succ _H$ may provide a good jumpstart to a best-case linear sorting algorithm, such that the confidence-aware ranking $\succ$ can be obtained with relatively small effort. It is worth mentioning that most divide-and-conquer methods such as quicksort and mergesort are not good for this task, since they do not take any advantage of the fact that the input is almost sorted. In contrast, bubble sort could be a good choice. Given an almost sorted input, bubble sort takes near-linear time to adjust the ordering. In crowdsourcing scenarios, all human preference feedback can be stored and the results of comparisons are always reusable. Hence, although a pair of items could be compared multiple times during the execution of bubble sort, it is not a performance bottleneck when the goal is to save as much monetary cost as possible.

Complexity analysis. Since r is in the sweet spot with high probability, the number of items to sort is fewer than ck. If we use a best-case linear sorting algorithm (say, bubble sort), the monetary cost of sorting is $O(c^2k^2w)$ in the average case, but O(ckw) if W is almost sorted. Therefore, the guaranteed overall cost of SPR is $O(\left( N+c^2k^2\right) \cdot w)$ but, in practice, it is often more close to $O((N+ck)\cdot w)$.

4.2.4 Changing the reference

Algorithm 5 views $\mathcal {W}$ and $\mathcal {T}$ as sets. In fact, it may further benefit from the heuristic ranking $\succ _H$ since there might be opportunities to change for a better reference.

Consider two items, $o_i$ and $o_j$, and a reference r. Suppose that, from the bags of comparisons $V_{i,r}$ and $V_{j,r}$, we know $o_i\succ _H o_j$. We want to confirm whether $o_i\succ o_j$ with a confidence level of $1-\alpha$. To do this, we run further statistical tests on $V_{i,r}$ and $V_{j,r}$. Recall that $V_{i,r}$ and $V_{j,r}$ are samples from distributions $\mathcal {N}\left( \mu _{i,r},\sigma _{i,r}^2\right)$ and $\mathcal {N}\left( \mu _{j,r},\sigma _{j,r}^2\right)$, respectively, where $\sigma _{i,r}\ne \sigma _{j,r}$ in general. Let the null hypothesis be

$$\begin{aligned} H_0: \mu _{i,r}\le \mu _{j,r},~\text {i.e.},~o_i\preceq o_j. \end{aligned}$$

Rejecting $H_0$ implies the acceptance of the alternative hypothesis

$$\begin{aligned} H_1: \mu _{i,r}>\mu _{j,r},~\text {i.e.},~o_i\succ o_j. \end{aligned}$$

We use the one-sided t-test. Let $n_{i,r}=\left| V_{i,r}\right|$ and $n_{j,r}=\left| V_{j,r}\right|$, and let $\left( \bar{x}_{i,r},S_{i,r}^2\right)$ and $\left( \bar{x}_{j,r},S_{j,r}^2\right)$ be the sample mean and sample variance of $V_{i,r}$ and $V_{j,r}$, respectively. Then, the t-value is

$$\begin{aligned} t = \frac{\bar{x}_{i,r}-\bar{x}_{j,r}}{\sqrt{\frac{S_{i,r}^2}{n_{i,r}}+\frac{S_{j,r}^2}{n_{j,r}}}}, \end{aligned}$$

and the degree of freedom, d, is

$$\begin{aligned} d=\frac{\left( \frac{S_{i,r}^2}{n_{i,r}}+\frac{S_{j,r}^2}{n_{j,r}}\right) ^2}{\frac{1}{n_{i,r}-1}\left( \frac{S_{i,r}^2}{n_{i,r}}\right) ^2+\frac{1}{n_{j,r}-1}\left( \frac{S_{j,r}^2}{n_{j,r}}\right) ^2}. \end{aligned}$$

We reject the null hypothesis $H_0$ if $t\ge t_{\alpha ,d}$. That is, when $t\ge t_{\alpha ,d}$, we have $1-\alpha$ confidence to conclude that $o_i\succ o_j$. The opposite judgment of $o_i\prec o_j$ can also be established analogously, by rejecting the null hypothesis $H_0$ of $o_i\succeq o_j$ when $t\le -t_{\alpha ,d}$.

Algorithm 6 shows the details of the hypothesis testing (HT) procedure. It is worth mentioning that the process of HT-Update is completely free of monetary cost, as it does not involve human workers.

HT allows indirect comparisons between items, which offers opportunities of changing for better references during partitioning. Indeed, Partition (Algorithm 5) may employ HT-Update as an optional sub-procedure whenever the size of $\mathcal {W}$ exceeds k during the process. In fact, we can try to use HT to find the kth best item $r'$ in $\mathcal {W}$, without any extra comparison between items in $\mathcal {W}$. Whenever such an $r'$ can be found, it satisfies $o^*_k\succeq r'\succ r$. According to Lemma 4, $r'$ is a better reference than r. With the new reference $r'$ and the updated partition $\left( \mathcal {W},\mathcal {T},\mathcal {L}\right)$, Partition continues until the final partition, with respect to $r'$, is obtained.

4.2.5 Latency analysis

The actual execution time of a crowdsourcing process depends on many factors such as the job publication/validation mechanisms of the platform, the availability of crowd workers, the difficulty of tasks, etc., which are not fully determined by the algorithm. Nonetheless, in this paper, we consider using latency as a metric for algorithms. To be precise, we consider the round model of latency [27]. That is, we measure the latency by the total number of task-publication rounds, assuming sufficient workers for parallel task processing in each round.

SPR is parallelism-friendly. The comparisons of different item pairs can be crowdsourced in parallel if they are independent, following the typical idea adopted in distributed algorithms. Specifically, the (m, x)-sampling procedure for finding a reference can be done in parallel since the microtasks are independent (see Sect. 4.2.1). Then, $\log x$ rounds are required to find the m max items, and another $\log m$ rounds are to sort the m candidates for selecting the median. The latency for selecting the reference is thus $\log x + \log m$. During partitioning, the reference can be compared with all the other items simultaneously, thus the latency is constant. Finally, all the items in $\mathcal {W}$ are sorted. The latency for sorting depends on the sorting algorithm. Recall that we use the bubble sort, a best-case linear sorting algorithm, to reduce the monetary cost (see Sect. 4.2.3). We may use the odd-even transportation sort algorithm, which can be regarded as a parallel version of bubble sort, to further reduce the latency. The total number of rounds for sorting is thus $|\mathcal {W}|=O(ck)$ in the worst case and $2=O(1)$ in the best case (i.e., $\mathcal {W}$ is already sorted). To sum up, the overall latency of SPR is $O\left( B_{\text{ pair }}\cdot (\log x + \log m + ck)\right)$ but, in practice, often close to $O\left( B_{\text{ pair }}\cdot (\log x + \log m)\right)$.

Microtask-level batch processing. To compare a pair of items, there is often latency between the distribution of microtasks and the collection of user feedbacks. At one extreme, every time only one microtask is sent into the crowd. Assume that w microtasks are sufficient and necessary to make a judgment. In this way, the monetary cost is w, which is minimized, but there is also a latency of w, which is often undesirable. At the other extreme, we can simply send $B_{\text{ pair }}$ microtasks into the crowd at once, minimizing the latency to 1 but increasing the monetary cost to $B_{\text{ pair }}$, which is often wasteful. To strike a balance between the monetary cost and the latency, we distribute microtasks in batches. Specifically, if we distribute $\eta$ microtasks at one time, then we reduce the latency to $\left\lceil w/\eta \right\rceil$, with an overhead cost of at most $\eta$.

5 SPR$^+$: a budget-bounded method

One problem with SPR is that it requires as input a budget $B_{\text{ pair }}$ for each paired comparison. Although this is also required by a wide range of existing studies (e.g., [4, 6, 8, 22, 32]), it is a bit difficult for a user to specify such a pairwise budget in practice. A more natural and practical scenario is that the user provides a total budget for the top-k query and relies on the platform/algorithm to make wise use of the budget.

In this section, we propose a budget-bounded version of the SPR algorithm, named SPR$^+$, which takes as input a total budget $B_{\text{ total }}$ and adaptively distributes $B_{\text{ total }}$ into pairwise comparisons such that the entire process is transparent to the user. The main idea here is also two-layered.⁸

• 1. Query-level cost adaptation. Since some of the paired comparisons are easy and some are difficult, the budget for a paired comparison should not be fixed but continuously changing as the process goes, such that eventually more budget could be assigned to more difficult comparisons.

• 2. Microtask-level cost adaptation. When comparing two items, the difficulty of the comparison could be estimated based on the judgments collected so far. Intuitively, judgments of an easier comparison tend to have a more consistent inner structure (i.e., different subsets of the judgments lead to similar conclusions).

Based on the above idea, the budget-bounded SPR$^+$ algorithm keeps the main framework of SPR and improves the pairwise comparison module (Sect. 5.1) and the partition module (Sect. 5.2).

5.1 Early termination of tied comparisons

The key idea of early termination is to “foresee” the tied comparisons before actually exhausting the budgets. Using the Stein’s estimation, the number of samples needed to compare a pair of items (i.e., to estimate the mean $\mu$ of some normal distribution $\mathcal {N}(\mu ,\sigma ^2)$) can be evaluated as $n=\max \{y,y'\}$, where y is the number of samples in the first stage and $y'=\left\lceil t_{1-\frac{\alpha }{2},y-1}^2S_y^2L^{-2}\right\rceil$ (see Sect. 3.1). It has been shown that the exact distribution of n is [15]:

$$\begin{aligned} \text {Pr}\left\{ n=y\right\} =\text {Pr}\left\{ {\chi }^2_{y-1}\le \frac{(y-1)y}{C_y}\right\} , \end{aligned}$$

and, for any integer $z>y$,

$$\begin{aligned} \text {Pr}\left\{ n\!=\!z\right\} \!=\!\text {Pr}\left\{ \frac{(y-1)(z-1)}{C_y}<{\chi }^2_{y-1}\le \frac{(y-1)z}{C_y}\right\} , \end{aligned}$$

where $\chi ^2_{y-1}$ is the $\chi ^2$-distribution with $y-1$ degrees of freedom and $C_y=t_{1-\frac{\alpha }{2},y-1}^2\sigma ^2L^{-2}$ is the optimal fixed-sample size required for the comparison, if the variance $\sigma ^2$ were known. Given the budget $B_{\text{ pair }}$ for a paired comparison, our idea of difficult comparison detection is to calculate the probability

$$\begin{aligned} \text {Pr}\left\{ n>B_{\text{ pair }}\right\}&=1-\text {Pr}\left\{ n=y\right\} -\sum \limits _{z=y+1}^{B_{\text {\tiny pair}}}\text {Pr}\left\{ n=z\right\} \nonumber \\&=1-\text {Pr}\left\{ {\chi }^2_{y-1}\le \frac{(y-1)B_{\text{ pair }}}{C_y}\right\} . \end{aligned}$$

(3)

Since the variance $\sigma ^2$ is unknown, we cannot directly compute $C_y$. One may think of bounding $\sigma ^2$ using the sample variance $S_y^2$ to some confidence level, so that there can be some estimations of $\text {Pr}\left\{ n>B_{\text{ pair }}\right\}$. Unfortunately, viewed as a function of $\sigma ^2$, $\text {Pr}\left\{ n>B_{\text{ pair }}\right\}$ could be very sensitive to the disturbance of $\sigma ^2$. Hence, even if the estimation of $\sigma ^2$ is accurate with respect to some confidence level, the estimated range of $\sigma ^2$ could still be too large to be practically useful.

To tackle the above difficulty, our idea is to view $\text {Pr}\left\{ n>B_{\text{ pair }}\right\}$ as a statistic of the distribution $\mathcal {N}(\mu ,\sigma ^2)$, i.e., the distribution from which the samples $V=\{v_1, v_2,\cdots ,v_y\}$ are drawn. The bootstrapping technique [14] can be used to accurately estimate $\text {Pr}\left\{ n>B_{\text{ pair }}\right\}$ by repeatedly resampling from the existing samples $V=\{v_1, v_2,\cdots ,v_y\}$. The details of the bootstrapping technique are shown in Algorithm 7.

The bootstrapping technique takes R resampling rounds. In each round, it takes a set $V_i$ of y samples (with replacement) from V (Line 2). Then, it evaluates Equation 3 using the sample variance of $V_i$ (Lines 3-4). After R rounds, the average probability $\bar{p}=\frac{1}{R}\sum _{i=1}^R p_i$ is considered as the final estimation of $\text {Pr}\{n>B_{\text{ pair }}\}$. The process then compares $\bar{p}$ against a threshold $\theta$ to determine whether or not $(o_i,o_j)$ is a difficult pair (Line 5).

Integrating the bootstrapping technique into SteinComp (Sect. 3.1), we may save cost via early termination of the difficult comparisons. The integrated comparison process, called BootstrapComp, is shown in Algorithm 8.

Like SteinComp, repeatedly calling BootstrapComp will progressively consume the budget $B_{\text{ pair }}$, during which process the items $o_i$ and $o_j$ might be distinguished by the crowd judgments (Line 4-5). BootstrapComp only differs SteinComp in Lines 6-7, where the probability $\text {Pr}\{n>B_{\text{ pair }}\}$ is estimated without actually consuming $B_{\text{ pair }}$. If $(o_i,o_j)$ is likely to be a tie under $B_{\text{ pair }}$, then the comparison process may terminate early with a judgment that $o_i\approx _{B_{\text {\tiny pair}}} o_j$.

5.2 More effective partitioning

We can use BootstrapComp to develop a more effective partitioning procedure, which we call Partition$^+$, as shown in Algorithm 9. Partition$^+$ preserves the basic methodology of Partition (Sect. 4.2.2), aiming at partitioning the item set $\mathcal {O}$ into three distinct sets of winners ($\mathcal {W}$), ties ($\mathcal {T}$), and losers ($\mathcal {L}$). Comparing to Partition of SPR, the advantages of Partition$^+$ are threefold.

First, Partition$^+$ implements a global budget control by accepting as input an available total budget $B_{\text{ total }}$ for the entire partitioning process. The budget for each paired comparison is adaptively calculated from (i) the remaining total budget and (ii) the estimated number of remaining comparisons (Lines 3 and 7). This strategy, although simple, is very effective in terms of budget allocation. In the beginning, when there are a large number of undistinguished items, the calculated budget for each paired comparison, $B_{\text{ pair }}$, is small. With such a small budget $B_{\text{ pair }}$, the easiest pairs of items might be distinguished. Then, as the confirmed winners and losers move from $\mathcal {T}$ to $\mathcal {W}$ and $\mathcal {L}$ (Line 6), more budget is allocated to the comparisons that are more difficult.

Second, Partition$^+$ uses BootstrapComp, instead of SteinComp, for paired comparisons (Line 5). As discussed in Sect. 5.1, with a small number of samples, BootstrapComp is able to detect those very difficult comparisons and, thereby, terminate the comparison at an early stage. Note that the budget for a comparison is dynamically changing. Thus, even if the comparison between $o_i$ and $o_j$ is early terminated due to insufficient budget $B_{\text{ pair }}$ (i.e., $o_i\approx _{B_{\text {\tiny pair}}} o_j$), the comparison may continue if there is a larger budget $B'_{\text {pair}}$ later on.

Finally, Partition$^+$ makes more use of the hypothesis testing technique (Lines 8–9 and 10–12) as discussed in Sect. 4.2.4. In particular, in order to handle the rare case of having chosen a very bad reference r (i.e., r is confirmed to be better than $o_k^*$ due to $|\mathcal {W}\cup \mathcal {T}|<k$), Partition$^+$ immediately searches the entire set of items for a better reference $r'$ (Lines 10–12). Like the case for $|\mathcal {W}|\ge k$ (Lines 8-9), here, as long as there exists such an $r'$, it is guaranteed that $o_k^*\succ r'$, thus $r'$ is a better reference than r. Note again that this process of changing the reference is free of monetary cost.

5.3 The SPR$^+$ algorithm

We conclude the discussions so far by presenting an enhanced version of SPR, named SPR$^+$, as shown in Algorithm 10. As can be seen, SPR$^+$ inherits the main framework of SPR, consisting of three major sub-procedures: Selecting the reference (Lines 1–4), Partitioning (Line 5), and Ranking (Lines 6–12). The major difference of SPR$^+$ from SPR is that the former takes as input a total budget $B_{\text{ total }}$ for the whole process instead of a budget $B_{\text{ pair }}$ for every paired comparison.

SPR$^+$ dynamically distributes the total budget $B_{\text{ total }}$ into the three sub-procedures (i.e., into the paired comparisons) by estimating the number of comparisons needed in the first two sub-procedures (Lines 1-2 of Algorithm 10 & Line 3 of Algorithm 9). In particular, it takes O(N) paired comparisons to determine the reference using (m, x)-sampling (Sect. 4.2.1). The partitioning process takes also O(N) paired comparisons using Algorithm 9. Generating the top-k list via ranking takes $O(|\mathcal {W}|^2)=O(c^2k^2)$ paired comparisons in the worst case if the odd-even transportation sort algorithm [24] is used. Therefore, the total estimated number of comparisons is $C = O(N)+O(N)+O(c^2k^2)=O(N+c^2k^2)$, which is in the same asymptotic order with SPR (see Sect. 4.2.3). Since the initial estimation, the number C always decreases as SPR$^+$ proceeds. As mentioned in Sect. 5.2, such a strategy adaptively assigns more budget to more difficult comparisons and is thus very effective in terms of budget allocation.

Let $w^+$ be the expected number of microtasks for a paired comparison using BootstrapComp. Then, the overall cost of SPR$^+$ is $O\left( \left( N+c^2k^2\right) \cdot w^+\right)$. Note that $w^+$ is different from w, the expected number of microtasks for a paired comparison in SPR (using SteinComp).

5.4 Further improving the Top-k List

Since the total budget $B_{\text{ total }}$ is dynamically allocated to each paired comparison, after selecting the reference, partitioning and ranking, there could still be budget remaining unspent, which could be used to further improve the top-k list.

Specifically, after the ranking procedure, we obtain a top-k list

$$\begin{aligned} o_1\diamond o_2\diamond o_3\diamond \cdots \diamond o_k, \end{aligned}$$

where the relation $\diamond$ is either superior-to ($\succ$) or indistinguishable-from ($\approx$). Since the top-k list is generated by a sorting procedure (Lines 6–12 of Algorithm 10), any two neighboring items must have been directly compared. All the $\succ$ relations are established with $1-\alpha$ confidence, whereas $\approx$ indicates that the two items cannot be distinguished with $1-\alpha$ confidence.

To further improve the ranking of $o_1,o_2,\cdots ,o_k$, one simple solution is to invest more money in comparing those pairs of items $(o_i,o_{i+1})$ where $o_i\approx o_{i+1}$. However, the comparison between $o_i$ and $o_{i+1}$ could be very difficult, given the fact that no judgment can ever be made so far. Therefore, we consider making use of the transitivity of $\succ$. In particular, if we observe a sequence of length $\ell$,

$$\begin{aligned} o_i\succ o_{i+1}\succ o_{i+2}\succ \cdots \succ o_{i+\ell -2}\approx o_{i+\ell -1}, \end{aligned}$$

and discover that $o_{i+\ell -1}\succ o_i$ by comparing $o_i$ and $o_{i+\ell -1}$, a local refinement can change the original ranking into

$$\begin{aligned} o_{i+\ell -1}\succ o_i\succ o_{i+1}\succ o_{i+2}\succ \cdots \succ o_{i+\ell -2}, \end{aligned}$$

eliminating the $\approx$ relation between $o_{i+\ell -2}$ and $o_{i+\ell -1}$. To understand the effect of the local refinement, we may think of item $o_{i+\ell -1}$ in the original ranking as being undervalued. Hence, by putting the undervalued item in a higher position in the list, the local refinement contributes to a better ranking.

In practice, we take a backward view to implement the above idea. Starting from a tie $o_i\approx o_{i+1}$, we scan backwards for the longest sequence (assuming a length of $\ell$) of the form

$$\begin{aligned} o_{i-\ell +2}\succ o_{i-\ell +3}\succ \cdots \succ o_{i-1}\succ o_i\approx o_{i+1}. \end{aligned}$$

Then, we compare $o_{i+1}$ with $o_{i-1},o_{i-2},\cdots ,o_{i-\ell +2}$, in order, to determine the correct position of $o_{i+1}$. The process is exactly the same as the insertion sort. Notice that the comparisons between items can either be done directly, by collecting more judgments from the crowd, or indirectly, by trying the HT technique (Sect. 4.2.4). The locally refined sequence is then placed back as a whole at its original position in the ranking, with possible new ties at its front and back ends. Then, a new round may start over to handle the rest of the ties in the ranking until all of them are eliminated or the budget is used up.

Given any top-k list $o_1\diamond o_2\diamond o_3\diamond \cdots \diamond o_k$ with multiple ties, it remains to decide which tie to handle next, regarding which here are two considerations: On the one hand, priority should be given to the more uncertain ties. Unlike the $\succ$ relations which are all at least $1-\alpha$ confident, the ties are associated with different levels of confidence. Consider a tie $o_i\approx o_j$ and the bag of judgments $V_{i,j}$ for comparing $o_i$ and $o_j$. By solving the Stein’s equation with respect to the confidence,

$$\begin{aligned} y'=\left\lceil t^2_{1 - \frac{x}{2}, y-1}S_y^2 L^{-2} \right\rceil , \end{aligned}$$

we obtain a solution $x=\alpha '$ with fixed $y=y'=|V_{i,j}|$. Let $\text {conf}(o_i,o_j)\overset{\text {\tiny def}}{=}1-\alpha '$. Then, the less $\text {conf}(o_i,o_j)$ is, the more uncertain the tie $o_i\approx o_j$ is. On the other hand, priority should also be given to the higher positions in the ranking since they are often more important. We may use a hyperbolic discounting scheme (e.g., $\text {imp}(t)\overset{\text {\tiny def}}{=}\frac{1}{1+t}$), to describe the importance of the tth position. Eventually, combining the confidence of the tie, $\text {conf}(o_i,o_j)$, and the position importance of the tie, $\text {imp}(t)$, there can actually be an ranking among the ties. Then, the next tie to be handled is therefore the first one in such a ranking.

6 Experiments

6.1 Datasets

We use four datasets in our experiments: IMDb, Book, Jester, and Photo. All the four datasets are from real-world applications. The first three are simulated, in the sense that the pairwise judgments between items are reasonably generated from the data (e.g., from users’ ratings on items). In contrast, the pairwise judgments in Photo are collected from an actual crowdsourcing platform. All the simulated and collected datasets are publicly available online.⁹

6.1.1 IMDb

The original dataset is collected from IMDb, containing 642,775 movies.¹⁰ IMDb allows its users to rate movies on a scale of 1 to 10. Each movie in the dataset is associated with its rating information. Specifically, for each movie $o_i$, the dataset provides (i) the total number of ratings casted by the users, $n_i$, (ii) a coded 10-bin histogram of the ratings, and (iii) a weighted rank. A coded 10-bin histogram is a sequence of 10 digits, $c_1c_2\cdots c_{10}$, where the code $c_j$ means that $10c_j\sim (10c_j+9)\%$ of the ratings to this movie are j ($j=1,2,\cdots ,10$). The weighted rank of the movie $o_i$ is defined as

$$\begin{aligned} \text {WeightedRank}(o_i) = \frac{\mu _i\cdot n_i+172500}{n_i+25000}, \end{aligned}$$

where $\mu _i$ is the mean rating of $o_i$.

Preprocessing. We select movies with more than 100,000 ratings from the original IMDb dataset. For each movie $o_i$, we calculate the mean rating $\mu _i$ from the total number of ratings, $n_i$, and the weighted rank value. After preprocessing, we obtain a dataset of 1225 movies, each associated with a mean rating and a coded 10-bin histogram of all its ratings. A total order of the movies is then determined by their mean ratings.

Simulating a comparison. To simulate a paired comparison from the IMDb dataset, we first transform the coded histogram $c_1c_2\cdots c_{10}$ into an ordinary histogram $p_1p_2\cdots p_{10}$ by setting $p_j = (10c_j+5)\%$, i.e., we use a single value $p_j$ to replace the code $c_j$, which represents a range of values from $10c_j\%$ to $(10c_j+9)\%$. To compare two movies $o_i$ and $o_j$, we sample two ratings, $s_i$ and $s_j$, from the corresponding transformed histograms. Then, $v(o_i,o_j)=\frac{1}{10}\left( s(o_i)-s(o_j)\right)$ can be regarded as the preference value of a human worker.

6.1.2 Book and Jester

The rest two datasets, Book and Jester, are both about users’ ratings on items (books or jokes).

The Book dataset [46] is collected from Book Crossing, a free online book club. The original dataset contains 340,556 books and 65,534 user ratings to the books. The ratings are at a scale of 1–10. In order to get statistically meaningful distributions of ratings, we filter out those books with less than 50 ratings. The remaining dataset contains 537 books and 50,192 ratings. A total order of the books can then be determined by the mean ratings of the books. For each book, we also have a 10-bin histogram of its ratings. Therefore, similar to what we do to IMDb, when comparing two books $o_i$ and $o_j$, we simulate the judgment based on the histograms of their ratings. Specifically, after sampling $s_i$ and $s_j$ from the rating histograms, we use $v(o_i,o_j)=\frac{1}{10}\left( s(o_i)-s(o_j)\right)$ as the preference value of a human worker.

The Jester dataset [16] is collected from the Jester online joke recommender system developed by UC Berkeley. The original dataset contains 100 jokes rated by 24,983 users where each user rated at least 36 jokes. The ratings are at a scale of $-\,10$ to 10. In order to simulate comparisons between jokes, we consider only the 7200 users in the dataset who have rated all the jokes. Each joke then has a mean rating of the 7200 ratings, based on which a total order of the jokes can be determined. We simulate a judgment between two jokes, $o_i$ and $o_j$, by picking a random user out of the 7200 users and using $v(o_i,o_j)=\frac{1}{20}\left( s(o_i)-s(o_j)\right)$ as a preference judgment, where $s(o_i)$ and $s(o_j)$ are the ratings given by the picked user.

6.1.3 Photo

This dataset is collected from a real crowdsourcing system, Figure Eight¹¹. We first collected a set of 200 photographs of university campuses (one photograph per university) from Google Images. Then, we collected 339,193 pairwise preference judgments from Figure Eight, at a rate of 0.1 US cent per judgment. The decision of which pairs of photographs to compare was basically uniformly random, but we managed to guarantee that each of the 19,900 possible pairs received at least ten judgments. For each paired comparison, we asked the workers to decide which university is more popular (in terms of comprehensive factors such as educational strength, academic support, cultural environment, scholarships, etc.). To do the comparison, a worker is expected to first recognize the universities from the photos and then provide his personal opinion. The available choices were at an eight-point Likert scale: “A(B) is definitely better,” “A(B) is much better,” “A(B) is better,” and “A(B) is slightly better.” We converted these choices to 0.875($-0.875$), 0.625($-0.625$), 0.375($-0.375$), and 0.125($-0.125$), respectively. Different from the other three datasets, we do not have a ground-truth total order in the Photo dataset. Indeed, although there are various university rankings such as the Academic Ranking of World Universities (ARWU)¹², the QS World University Rankings¹³, and the Times Higher Education World University Rankings¹⁴, etc., the consensus rankings of our interest are different from the above fully statistics-based ones.

6.2 Baselines, metrics, and default settings

We mainly compared our solutions, SPR and SPR$^+$, with the following baseline methods.

Infimum cost. Infimum cost is an ideal solution to find the top-k ranking (see Sect. 4.1). It is based on the following oracular assumptions:

• 1. It has luckily, but unknowingly, chosen the actual kth best item $o_k^*$ as the reference;

• 2. It compares $(o_1^*,o_2^*),(o_2^*,o_3^*),\ldots ,(o_{k-1}^*,o_k^*)$ to confirm the top-k ranking; and

• 3. It compares $(o_k^*,o_j^*)$ for any $j>k$ to exclude $o_j^*$ from the top-k results.

It is proved that Infimum Cost requires the minimum possible TMC to answer the top-k query.

Tournament tree. Tournament trees are widely adopted in crowdsourced top-k query processing [7, 8]. Tournament tree first randomly groups items into pairs. Winners of paired comparisons are promoted to upper levels of the tournament tree, until the best item reaches the root. The second best item can be identified by building a tournament tree over the items that ever directly lost to the best item. All k items can be found in a similar way progressively.

Heap sort. Heap sort is also a common technique to find top-k results. It first initializes a min-heap with k random items (i.e., top-k candidates) and then sequentially tests every other item against the top of the heap. Whenever an item is found better than the worst candidate in the heap, it expels the worst candidate from the heap and becomes a new top-k candidate.

Quick selection. Quick selection is a classic average-case linear recursive algorithm to find the kth best item (a.k.a. the kth order statistic) from a set of items. The algorithm finds the top-k items by partitioning the item set using the kth best item.

PBR. Proposed by Busa-Fekete et al. [3], the preference-based racing (PBR) algorithm compares all the pairs of items in an incremental manner. Specifically, in each iteration of PBR, each pair of items receives one more judgment and confidence intervals are updated. The algorithm terminates when the top-k items can be determined from the confidence intervals.

HBA. Proposed by Mohajer et al. [33], the heap-based algorithm (HBA) is a hybrid of tournament tree and heap sort. First, the entire set of items is divided into k groups. In each group, a tournament tree is built to find the best item within the group. A max-heap of the k best items is then built; the top of heap is thus the top-1 item. HBA repeats this process to find the other top-k results.

We use the following three metrics to evaluate the performance of the algorithms:

• TMC, which is the total monetary cost needed by an algorithm for answering the top-k query (i.e., generating a top-k ranked list).

• Latency, which is the number of iterations an algorithm needs for answering a top-k query. Note that within one iteration, multiple microtasks could be published and handled in parallel.

• NDCG (normalized discounted cumulative gain), which is a widely used metric for measuring the quality of the top-k result of an algorithm with respect to a known ground-truth ranking.

It is worth mentioning that the calculation of NDCG relies on precise ground-truth rankings. In our experiments, we have such ground-truth rankings for IMDb, Book, and Jester but not Photo (see Sect. 6.1). Since the ground truth is almost always unknown in practice, the logic of our experiments is that, if SPR/SPR$^+$ can achieve good NDCGs with less costs on IMDb, Book, and Jester, then it is reasonable to trust their accuracy and economic efficiency on Photo as well as other data from practical applications.

Investigated parameters and their evaluated ranges are listed in Table 4. Unless otherwise specified, in each experiment we vary one parameter and set the remaining ones to their defaults (shown in bold).

Table 4 Experiment parameters

6.3 Effectiveness of SPR

We first conducted a set of experiments on different datasets to compare the cost (i.e., TMC and latency) of SPR and the above-mentioned algorithms. The ideal infimum solution was also used as a reference. The experiments were done with default parameters, i.e., with query parameter $k=10$, confidence level $1-\alpha =0.98$, and budget $B_{\text{ pair }}=1000$ on each dataset.

The results are shown in Fig. 5. The x- and y-axes are TMC and latency, respectively. There is one figure for every dataset. (Note that the x-axis of Fig. 5a is in the logarithmic scale of base 2.) As can be seen, SPR is consistently the closest to the ideal infimum solution in all the cases.

Fig. 5

TMC and latency of SPR and the baselines

All the other solutions are times or even magnitudes more expensive than SPR, in terms of either TMC (e.g., quick selection and PBR) or latency (e.g., heap sort and HBA). Indeed, although quick selection is known as an average-linear algorithm for finding the kth best item, it is also known that the practical cost, in terms of number of comparisons, is usually high [19]. PBR maintains the confidence intervals based on the Hoeffding inequality [3]. Although the Hoeffding inequality empowers PBR with the ability of handling general, unknown distributions, it does not make much use of the model assumption on how comparisons were actually made and therefore typically requires much more answers from the crowd to make a confident judgment. For latency, we notice that it is difficult for heap sort to run in parallel. It can be shown that the overall latency heap sort is $O\left( B_{\text{ pair }}N\log k\right)$, which is asymptotically much more expensive than $O\left( B_{\text{ pair }}\log N\right)$ of tournament tree. HBA is a hybrid of tournament tree and heap sort and thus has an overall latency in between (with the heap sort steps being an obvious latency bottleneck). Such high TMC or latency costs make those baseline methods less competitive in practice. More experimental evaluations between SPR and the baseline methods can be found in the earlier version of this work [23].

6.4 Effectiveness of SPR$^+$

6.4.1 Effectiveness on simulated datasets

The next set of experiments is to evaluate the effectiveness of the budget control method SPR$^+$. To do this, we first ran SPR and recorded its TMC. Then, we used the recorded TMC of SPR as the input budget $B_{\text{ total }}$ of SPR$^+$. We compared the costs of SPR$^+$ and SPR (i.e., TMC and latency) and the qualities of their outcomes (i.e., NDCG of top-k ranked lists). The purpose was to demonstrate that, with approximately the same cost, SPR$^+$ achieved similar or even better top-k ranking results. We conducted the experiments on the simulated datasets (IMDb, Book, and Jester) under various parameter settings.

Figure 6 shows the trend of TMC and query latency by varying the query parameter k. The cost of the ideal infimum solution is also shown as a reference. Figure 6a, c shows that SPR$^+$ consumed similar or less cost. Indeed, the budget offered to SPR$^+$, $B_{\text{ total }}$, was exactly the TMC of SPR. By design, SPR$^+$ will use up the budget $B_{\text{ total }}$ to maximize the quality of the final top-k ranking. In particular, if there is remaining budget after the reference selection, partitioning and ranking phases, the budget will be used to refine the top-k ranking (Sect. 5.4). Therefore, SPR$^+$ and SPR typically have very close TMCs under our experiment setting, except for the simple cases where no much refinement is necessary (for example, when k is as small as 1 or 5 in the IMDb dataset). The refinement process might be at the expense of latency. As SPR$^+$ allocates the total budget $B_{\text{ total }}$ adaptively into its entire running process, the amount of budget left for final refinement depends on how much has been spent during the previous three procedures, which in turn depends on the difficulties of comparisons therein. Therefore, the relative latency overhead of SPR$^+$ over SPR is data-related and could be affected by query parameters. It can be seen that SPR$^+$ typically has a latency smaller than that of SPR, especially when $k\ge 15$ on IMDb and Book datasets, but there are still cases where SPR$^+$ requires more rounds to complete (e.g., $k=5$ on Book and $k\le 15$ on Jester). This could be because SPR$^+$ publishes less microtasks due to the use of bootstrapping and hypothesis testing techniques in the previous Select-Partition-Rank procedures. Since in all the cases SPR$^+$, given a budget of the TMC of SPR, costs no more than SPR does, a natural question is whether SPR$^+$ can also generate top-k rankings of the same or even better quality. Figure 7 shows the NDCG of the top-k results produced by SPR and SPR$^+$ on IMDb, Book, and Jester. As can be seen, SPR$^+$ achieves a visible improvement over SPR in most of the cases. Relating Fig. 7 with Fig. 6, it is clear that, comparing to SPR, SPR$^+$ produces better top-k results with the same or fewer amount of TMC.

Fig. 6

Cost of SPR and SPR$^+$ under varying k

Fig. 7

NDCG of SPR and SPR$^+$ under varying k

We also experimentally evaluated the impact of the total number of items, N, and the confidence level, $1-\alpha$, as they also affect the results of SPR$^+$. Although different datasets were already of different sizes (i.e., different N), we further investigated the effectiveness of SPR$^+$ under varying N in each dataset. Specifically, for each choice of N of each dataset, we kept the actual top-N items of that dataset and ran the algorithms on these N items. Figure 8 shows the TMC and query latency by varying N on IMDb, Book, and Jester, respectively. In all the cases, SPR$^+$ has nearly the same TMC with SPR, as expected. The pairwise comparisons in Book and Jester are in general more difficult than those in Movie data. Therefore, the refinement process may generate a bit larger latency than SPR does, but still, the latency values of SPR and SPR$^+$ are at the same level. In Fig. 9, it can be seen that the NDCG performance of SPR$^+$ is also at the same level of SPR, with clear dominance in the Book data.

Fig. 8

Cost of SPR and SPR$^+$ under varying N

Fig. 9

NDCG of SPR and SPR$^+$ under varying N

Similar results can be found when we vary the confidence level $1-\alpha$, as shown in Figs. 10 and 11.

Fig. 10

Cost of SPR and SPR$^+$ under varying confidence

Fig. 11

NDCG of SPR and SPR$^+$ under varying confidence

6.4.2 Effectiveness on real crowdsourced data

We also tested the proposed SPR and SPR$^+$ methods on the Photo dataset, of which the item comparisons were collected from a real crowdsourcing platform. Note that, since there is no ground-truth total order in the Photo dataset, the experiments mainly focused on TMC and latency.

Fig. 12

Cost of SPR and SPR$^+$ on Photo

Figure 12 shows the results. Comparing to the results on Movie, Book, and Jester datasets (Figs. 6, 8 and 10), we observe a clear gap between the TMCs of SPR and SPR$^+$. This indicates that the tasks of comparing universities are generally easy for human workers (i.e., there is clear consensus on which university should be more popular), so that SPR$^+$ does not have to consume all the budget $B_{\text{ total }}$ to generate a top-k ranking with confidence guarantees. Indeed, we observe that the variance of the collected judgments for Photo is typically lower than the variance of the simulated judgments on the other datasets.

6.4.3 Budget control as a feature of SPR$^+$

We conducted another set of experiments to demonstrate the feature of budget control of SPR$^+$. We first ran SPR by varying $B_{\text{ pair }}$, the budget for each paired comparison, from 100 to 4000. Then, we used the TMC cost of SPR at $B_{\text{ pair }}=4000$ as the total budget $B_{\text{ total }}$ of SPR$^+$. In particular, we fed SPR$^+$ with $\gamma B_{\text{ total }}$, where $\gamma$ is a discount ratio. Thus, by varying $\gamma$, we aimed to observe the performance of SPR$^+$ with respect to the change of the total budget.

Figure 13 shows the results of SPR with varying $B_{\text{ pair }}$. It is clear that, given the same fixed $B_{\text{ pair }}$, the TMCs of SPR on different datasets are significantly different. For example, with $B_{\text{ pair }}=500$, the TMCs on IMDb, Book, and Jester are 83,199.30, 62,095.42, and 23,877.58, respectively. Even considering the different sizes of the datasets (IMDb 1225, Book 537, and Jester 100), there is no systematic way to control the TMC using $B_{\text{ pair }}$.

Fig. 13

Ineffectiveness of SPR in budget control

Fig. 14

Effectiveness of SPR$^+$ in budget control

In this sense, we argue that SPR$^+$ is more natural and user-friendly by directly requesting a total budget $B_{\text{ total }}$ instead of a pairwise comparison budget $B_{\text{ pair }}$. In comparison, we set $B_{\text{ total }}=109778.24$ for IMDb, $B_{\text{ total }}=143262.11$ for Book and $B_{\text{ total }}=86346.32$ for Jester, which are the actual TMCs of SPR at $B_{\text{ pair }}=4000$ on these datasets. Figure 14 shows how SPR$^+$ performs with respect to the change of its total budget (i.e., with respect to varying $\gamma$). Specifically, on Book and Jester, $\gamma$ varies from 25 to 100%. The range on IMBb is a bit different, from 65 to 100, as 65% of $B_{\text{ total }}$ is merely 71,355.86, which is already slightly less than 72,128.93, the actual TMC of SPR with $B_{\text{ pair }}=100$. There can hardly be any meaningful result with an even less total budget. The performance of SPR is also plotted as a reference in Fig. 14. We observe that, on all the datasets, the quality of SPR$^+$ and SPR results are very close when the same amount of TMC is consumed. This indicates that SPR$^+$ is as effective as SPR, while SPR$^+$ has a more natural and systematic way in budget control.

6.4.4 The role of bootstrapping

An important component of SPR$^+$ is BootstrapComp (Sect. 5.1). This comparison model can be seen as an improvement over SteinComp (Sect. 3.1), which is capable of predicting whether two items are distinguishable under some budget, without actually spending up the budget. Therefore, an interesting and important question here is: Whether the predictions made by BootstrapComp are accurate.

To investigate the above question, given a dataset of N items, one way is to compare all the $\frac{N(N-1)}{2}$ pairs of items using both SteinComp and BootstrapComp. Here, the Stein’s comparison process SteinComp is used as a reference. We label a pair of items as “Difficult,” if the items are indistinguishable by SteinComp, and “Easy” otherwise. The effectiveness of BootstrapComp can then measured by the precision of its predictions on “Difficult” and “Easy,” i.e., the percentage of pairs of items, among all the $\frac{N(N-1)}{2}$, whose labels are correctly predicted.

We ran the above-designed experiments on each of the datasets under varying pairwise comparison budget $B_{\text{ pair }}$. Tables 5, 6, 7 and 8 show the precision of BootstrapComp under each choice of $B_{\text{ pair }}$ in each dataset. In addition to overall precision values, in each of the tables there are four columns of the form “X-Y,” meaning that the item pairs with a true label of “X” being predicted as “Y.” As can be seen in Tables 5-8, in all the cases, easy pairs were correctly identified as “Easy.” Most ($\ge 70\%$) of the difficult pairs were also correctly detected as “Difficult.” When the pairwise comparison budget $B_{\text{ pair }}$ increases, the overall precision was typically $\ge 95\%$. Considering the fact that SPR$^+$ already has a mechanism to avoid difficult comparisons, the results here confirm that BootstrapComp can precisely predict difficult pairs and thus may save the monetary cost by early terminating such comparisons.

Table 5 Precision of BootstrapComp on IMDb

Table 6 Precision of BootstrapComp on book

Table 7 Precision of BootstrapComp on Jester

Table 8 Precision of BootstrapComp on Photo

We have also conducted experiments to investigate the sensitivity of SPR$^+$ to the changes of bootstrapping parameters, i.e., the number of bootstrapping rounds R and the threshold $\theta$ (see Algorithm 7).

Sensitivity to the change of $\varvec{R}$. Figure 15 shows the NDCG of SPR$^+$ on IMDb, Book, and Jester, respectively, when varying the number of bootstrapping rounds R. As can be seen, there is no significant difference in NDCG when R goes from 100 to 1,000. This indicates that SPR$^+$ is insensitive to the changes of R.

Fig. 15

Sensitivity of SPR$^+$ to the change of R

Sensitivity to the change of $\varvec{\theta }$. Figure 16 shows the NDCG of SPR$^+$ on IMDb, Book, and Jester, respectively, when varying the variance threshold $\theta$. As can be seen, when $\theta$ goes from 0.90 to 0.99, there is no significant difference in the NDCG performance. Therefore, we argue that SPR$^+$ is also insensitive to the change of the bootstrapping threshold $\theta$.

Fig. 16

Sensitivity of SPR$^+$ to the change of $\theta$

To sum up, we conclude from this set of experiments that bootstrapping is useful and easy to use. The bootstrapping-based early termination recognizes easy and difficult comparisons with good precision (Tables 5–8) and is insensitive to its parameters (Figs. 15, 16). Therefore, in practice, we may simply set a sufficiently large R (e.g., $R=200$) to secure the statistical meaningfulness of the bootstrapping process.

6.5 Comparisons to other budget-bounded methods

In this set of experiments, we compare SPR$^+$ with a recent budget-bounded learning-to-rank method, margin-based maximum likelihood estimate (MLE), proposed by Xu et al. [43]. Strictly speaking, MLE is not a top-k solution in the sense that it generates not merely a top-k ranked list but also a partial order between all the items. Still, we are interested in this method because

• 1. MLE is budget-bounded, taking as input a total budget for the ranking task;

• 2. MLE aggregates pairwise judgments to form a partial order between items; and

• 3. MLE achieves good performance comparing to the other well applied learning-to-rank methods.

Given a total budget $B_{\text{ total }}$, MLE selects a set of item pairs and send them into the crowd for comparisons. For each paired comparison, the BTL model [2, 30] is used to produce the aggregated judgment from the feedback of the crowd. A maximum likelihood estimation process is then adopted to calculate the most likely underlying ordering of all the items that might generate the observed pairwise judgments.

Fig. 17

Performance of SPR$^+$ and MLE

Fig. 18

Crowdsourced top-k processing toolkit architecture

We offered the same total budget $B_{\text{ total }}$ to both SPR$^+$ and MLE and compared the quality of their top-k results on IMDb, Book, and Jester datasets. Figure 17 shows the results. Specifically, we varied the total budget $B_{\text{ total }}$ from 10,000 to 80,000 on each dataset. For MLE, we first calculated a partial order $\Omega _{\text {MLE}}$ with the total budget $B_{\text{ total }}$. Then, from the partial order $\Omega _{\text {MLE}}$, we induced the minimum set $W_{\text {MLE}}$ that guaranteed to include the top-k items under any total order consistent with $\Omega _{\text {MLE}}$. Finally, we broke the ties in $W_{\text {MLE}}$, if any, using the ground-truth total order of the dataset to obtain a final top-k ranked list. As can be seen in Fig. 17, when the total budget increases, the performance SPR$^{+}$ first increases and then becomes stable at a high level. In contrast, the NDCG results of MLE are consistently low. Indeed, MLE aims at optimizing the global partial order instead of the top-k ranking. A large portion of the budget is thus used to compare the non-top-k items. In fact, the top-k ranked lists we obtained were already of low quality as sets. Indeed, we measured the precision of the top-k ranked lists, which was defined as the ratio of the true top-k results in a top-k list. When $N=25$, the precision was 0.334$\,\sim \,$0.518 on IMDb, 0.267$\,\sim \,$0.466 on Book, and 0.328$\,\sim \,$0.512 on Jester. The precision was even lower when $N=100$, as less budget was dedicated to the comparisons with/among real top-k items.

6.6 Prototype system

We have implemented a prototype system of SPR [28], which can also be upgraded to support SPR$^+$. Figure 18 shows the architecture of the prototype system. At the core, there is the algorithm logic of SPR/SPR$^+$, which interacts with the crowdsourcing platform to publish microtasks and collect answers. The system manager monitors the entire running process of SPR/SPR$^+$ and presents the system status (e.g., progress, budget consumption status, exceptions, etc.) on a monitor interface (see Fig. 19).

7 Conclusion

In this work, we first discuss how the pairwise preference judgment helps to reduce the monetary cost of the comparison processes in crowdsourcing. According to our empirical studies, the pairwise preference judgment model outperforms the other two popular judgment models (i.e., the graded model and the pairwise binary model) as it achieves similar accuracy of comparisons via less number of microtasks. We propose novel frameworks, SPR and SPR$^+$, to address the crowdsourced top-k queries. Both SPR and SPR$^+$ are budget-aware and confidence-aware. SPR requires as input a budget for each paired comparisons, whereas SPR$^+$ requires only a total budget for the whole top-k task. Extensive experiments show that both SPR and SPR$^+$ outperform the other competitors in terms of the total monetary cost, the latency of query processing as well as the quality of the final top-k results.

Fig. 19

Monitor panel. The user specifies the total budget ($16) and the confidence level (90%). The pie chart shows the progress of the top-k processing as well as the costs incurred and estimated costs

In the future, we plan to further exploit the crowdsourced top-k queries by introducing other settings and optimization techniques. For instance, given some partial knowledge of the items [6], SPR and SPR$^+$ could select a reference more effectively so that the overall cost can be further reduced. We will also explore the statistical tools to enhance the performance of other crowdsourced queries (e.g., ranking, join, skyline, etc.).