Hydrodynamic damping enhancement by implementing a novel combined rigid-elastic heave plate

Abstract

Heave plates are structural components used for reducing the vibrations caused by environmental forces on marine and offshore structures by changing the hydrodynamic properties. The fact that the added mass increase via heave plates does not always lead to the structural response reduction underscores the role of damping in maintaining the vibration amplitude within allowable limits. In the present experimental study, a novel combined rigid-elastic design is used to improve the damping through the velocity increase in the elastic part and added mass creation in the central rigid part. The desired percentage of total added mass and damping can be adjusted by changing the rigid-to-elastic parts diameter ratio, which is the main scope of this experimental research. Frequency of vibration, which affects the elastic edge excited mode shapes, also affects the forming of the vortex shedding. Experimental tests show that the frequency increase generally causes high damping performance provided that the excited mode shapes are axisymmetric, which strongly depends on equivalent stiffness and mass.

1 Introduction

Offshore platforms are used for extracting oil from high potential energy resources in deep waters, and recently for renewable energy from wind. These platforms exhibit high dynamic response challenges due to the conditions during their lifetime. The dynamic response of platforms in the vertical plane should be kept a minimum. The practical approach is to attach a sharp and rigid plate at the bottom of the platform to decrease vibrations. These plates are used to alter the effective mass and dominant viscous damping of a structure. These hydrodynamic properties are dependent on the two well-known non-dimensional parameters, the Keulegan Carpenter number, $\text{KC}$, and frequency parameter, $\beta ,$ which are defined in Eqs. 1, 2 [1].

$$\text{KC} = \frac{2\uppi A}{D} ,$$

(1)

$$\beta = \frac{{D^{2} f }}{\vartheta } ,$$

(2)

Here $A$ and f are the oscillation amplitude and frequency, $D$ the disk diameter, and $\vartheta$ is the kinematic viscosity of the fluid. The effects of the mentioned parameters and some other factors on the hydrodynamic behavior of rigid heave plates have been studied by many researchers. These studies can be categorized into two main fields: researches on heave plates attached to the cylinder and isolated plates.

First, regarding the tests on plates attached to a cylinder, Thiagarajan and Troesch [2, 3] conducted experimental tests on a bare cylinder and a cylinder with a circular disk attached at the bottom. They showed that the dominant form drag on a plate attached to a cylinder is about two times larger than for the bare cylinder. The added mass increases when a disk is attached to the cylinder. However, when the plate is sufficiently separated from the cylinder, the added mass doubles in a forced vibration test [4]. Furthermore, the added mass seems to be more dependent on the heave plate diameter compared to the gap ratio over a $\text{KC}$ range of 0.2–1.4 [5]. Meanwhile, the disk thickness is also an active parameter on hydrodynamic coefficients, which was investigated by Tao and Cai [6] and Tao and Thiagarajan [7] for different shapes of appendage on a cylinder. They found that thinner disks demonstrate higher damping performance. Increasing the number of spaced disks attached to a cylinder is the other way to increase the damping and added mass significantly. For the spacing above a certain value, the vortex shedding interaction decreases, which in turn causes the added mass and damping to be independent of spacing [8,9,10].

Second, some researches are related to the effective factors on hydrodynamic characteristics of single or multiple plates without a cylinder. By conducting a series of experiments on square plates, Prislin et al. [11] concluded that the added mass is independent of Reynolds value beyond $10^{5}$. The tests on single and arrays of solid square plates by Li et al. [12] showed several results, namely, the independence of hydrodynamic coefficients from the frequency parameter ($0.2 < \text{KC} < 1.2, f < 1 \text{Hz}$), the independence of hydrodynamic forces from the spacing after a threshold value; and the independence of the drag coefficient from the edge shape. On the other hand, from a structural point of view, the heave plates should be stiffened. For this reason, Lopez-Pavon and Souto-Iglesias [13] showed experimentally and numerically that the added mass and the damping results of the flapped stiffened disk are, respectively, larger and lower than the values related to a plain disk. Moreover, perforation is an effective factor in the hydrodynamic behavior of plates. It has been shown that a higher perforation ratio leads to a larger drag and a lower added mass [14,15,16]. Most of the presented empirical formulas of the hydrodynamic coefficients have not included the effect of the cross-section type. Therefore, Zhang and Ishihara [17] suggested a new modified formula in this regard.

Finding the best conditions was the objective of almost all previously cited papers to improve the hydrodynamic characteristics of rigid heave plates. Based on the fact that the added mass increase cannot always lead to a better platform dynamic response [18, 19], a new design is suggested by amplifying the damping compared to the added mass in this study. It is expected that the velocity increase along the plate edges causes an increase in damping due to the high strength of the shed vortices. Accordingly, the elastic plate is a candidate that may result in different hydrodynamic characteristics when it oscillates in the fluid. It should be noted that some researches have been conducted experimentally and numerically for deriving the dynamic properties of metal plates, which are cited in the following. Hengstler and Dual [20] and Askari et al. [21] experimentally and numerically investigated the effect of the boundary proximity on the natural frequency of the plate in free vibration. The results revealed that by reducing the distance to the water surface, the natural frequency increases while the proximity to the bottom wall decreases it. Hengstler and Dual [20] also showed that damping decreases by disk closeness to the water surface while the nodal diameter number grows. Askari et al. [21] experimentally showed that there are larger values of damping ratio for a plate in water compared to a similar plate in the air. The cited researches show that there is not a clear strategy for deriving damping and added mass coefficients under forced vibration. Moreover, altering of the commonly used rigid heave plates with deformable elastic material may not be a realistic alternative due to the significant fatigue loads of the real operating conditions.

It is expected that an elastomer–rubber material with high fatigue resistance attached to the outer edge of a rigid plate can be a solution for the increase of damping. Besides, using rubber with a lower elastic modulus rather than metal creates the opportunity of a higher value of the outer edge deflection. Therefore, a combined disk is assembled by a rigid disk in the center and an elastic rubber plate around. The added mass and damping can be adjusted to result in the desired values by sharing the surface area between these two parts. The elastic rubber has a moving clamped boundary on the inner edge and free boundary condition on the outer edge. Therefore, the present study aims to experimentally investigate the hydrodynamic behavior of the combined disk under forced vibration versus the diameter ratio and excitation frequency through laboratory tests.

2 Experimental set-up

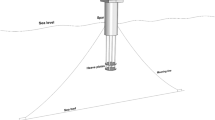
The tests were conducted at a wave tank of length (L), width (W) and height (H) of 8 m, 1 m, and 1 m, respectively, located in the Marine Ocean and Offshore Research (MOOR) laboratory at the University of Maine. The water depth ($H_{W}$) for all the tests is 0.9 m. Experiments were conducted on several isolated disks with combined rigid elastic design (CRED) when subject to forced sinusoidal oscillations parallel to their axes. The steps for tests on each case study are defined as follows.

First, CRED is assembled on threaded rod via two nuts and is attached to the load cells. Second, the load cell is connected to a screwdriver electric actuator (Parker ETH032), which was driven by a 750 W Parker servo motor (Parker BE341F). It generates forced harmonic vibration, as shown in Fig. 1. Third, when each CRED is vibrated at a specified frequency underwater, both of the force and displacement signals should be recorded. The hydrodynamic force applied on disk from the water was measured via two-load-cells placed between the actuator and the threaded rod. The recording of the force signal begins after a few oscillations when the signal is steady. The force sensors are LCPW ± 37.5 kg series with a precision of 0.02%. Simultaneously, a potentiometer (model P1010) is used for measuring the disk position during harmonic oscillations, as depicted in Fig. 1. A National instruments data acquisition system including a time controller (NI CRIO 9024) with a multi-channel card (NI 9205) and the Labview software are utilized for converting analog to digital and recording data at 1 kHz sampling rate. The final step is the technique to extract the added mass and damping coefficients, which is explained in the next section.

Fig. 1

Overall schematic of Tank and the details of equipment

3 Data analysis process

After the recording of the output data, the CRED hydrodynamic coefficients can be mathematically obtained by processing of the force and displacement signals. Based on Newton’s second law, as shown in Fig. 2, the equation of motion for an oscillating object in a fluid can be expressed as Eq.  3.

$$F_{\text{I}} \left( t \right) = F_{{\text{buoyancy }}} \left( t \right) + F_{{\text{fluid/body}}} \left( t \right) + F_{{\text{meas}}} - Mg,$$

(3)

$$F_{\text{I}} \left( t \right) = M\ddot{y}\left( t \right) = M*\left( { - A*\omega^{2} *\sin \left( {\omega t} \right)} \right) = - M\omega^{2} \left( {A*\sin \left( {\omega t} \right)} \right) = - M\omega^{2} y\left( t \right),$$

(4)

$$F_{{\text{buoy}}} \left( t \right) = \rho g\nabla ,$$

(5)

$$F_{{\text{fluid/body}}} \left( t \right) = - m_{\text{a}} \ddot{y}\left( t \right) - B\dot{y}\left( t \right) = - m_{\text{a}} \ddot{y}\left( t \right) - \frac{1}{2}\rho SC_{\text{d}} \dot{y}\left( t \right)\left| {\dot{y}\left( t \right)} \right|$$

(6)

where $F_{\text{I}}$ denotes the inertial force, $F_{{\text{buoy}}}$ the buoyancy force,$\nabla$ the submerged volume, $y\left( t \right)$ the displacement of the center of FRD or CRED, $M$ the total mass of FRD or CRED, threaded rod and lower part of the actuator, $F_{{\text{fluid/body}}}$ the hydrodynamic force applied on FRD/CRED from fluid, $m_{\text{a}}$ the added mass, $B$ the damping coefficient, $F_{{\text{meas}}}$ the measured force signal applied on the threaded rod attached to the disk. The Morison nonlinear drag force can be approximated as a linear term to simplify the extrapolation from small scale to full scale. The nonlinear form is originally included the difference and sum-frequency content, while the linear drag force is only a single frequency. The effects of difference and sum frequencies are considerable when the platform has, respectively, low and high stiffness in a specified direction. However, for heave direction in a platform like a spar, the stiffness is neither low nor high. Therefore linearization does not disrupt the results.

Fig. 2

Applied forces on CRED during harmonic oscillation in water

The effect of weight force due to M is seen as an averaged value in the signal of $F_{{\text{meas}}}$. It should be noted that for all cases, the buoyancy and weight forces cannot remove the effect of each other precisely at the center position of the vibration stroke. For this reason, there is a constant value in Eq. 7, which is defined as the weight of the disk and threaded rod at the mentioned position. Since $y\left( t \right)$ is harmonic, $F_{{\text{meas}}}$ is also expected to be a harmonic signal with a constant averaged value. This value should be removed such that the obtained signal “$F_{{\text{meas}}} - \text{constant}$” can be easily processed for deriving the unknown values of $m_{\text{a}}$, $B$.

$$F_{{\text{meas}}} = \left( {M + m_{\text{a}} } \right)\ddot{y}\left( t \right) + B\dot{y}\left( t \right) + C_{k} y\left( t \right) + \text{Constant}$$

(7)

Here $C_{k}$ is the hydrostatic coefficient. It can be seen that the right-hand side of Eq. 7 has a linear form versus the variables $\ddot{y}\left( t \right),\dot{y}\left( t \right)$, and $y\left( t \right)$, hence, $F_{{\text{meas}}}$ is considered linear. In practical conditions of data acquisition, some noises may disrupt the original signal. However, their effects are removed via filtration. This process for the displacement and force signals was performed by Butterworth low pass filter with a 25 Hz cut-off frequency via MATLAB software. The proper zero-phase digital filtering function in MATLAB software is used to compensate for the distortion effects of the filtering process.

A detailed analysis of the signals is conducted using MATLAB through which the acceleration and the velocity are obtained using the centered second-order numerical differentiation approximation. The added mass and damping coefficients are calculated by the least-squares method [1] that minimizes the error between $F_{{\text{meas}}}$ in Eq. 7 and the readings of $F_{{\text{meas}}}$. The values for the added mass and damping coefficients are the average of those coefficients, which have been calculated separately in each of the considered cycles. Each case study is tested over 32 cycles allowing a statistical analysis that yields a mean and standard deviation value for each coefficient. A windowing method similar to the process in the work of Moreno [22] is applied for all the obtained signal results. Damping is calculated from the velocity signal at each cycle via considering the velocity peak while the added mass coefficients are obtained from a window containing an acceleration peak. The error bars shown in Figs. 5 and 6 are the derived standard deviation through the window method. For the remaining figures, the error bars are neglected such that the figures are not messy. However, the corresponding error bars are similar to Figs. 5 and 6 and there is not a high specified value of standard deviation for data in curves.

The hydrodynamic coefficients for all the tests are made non-dimensional, as demonstrated in Eqs. 8, 9 based on a constant theoretical added mass value of a FRD, D = 0.2 m.

$$A^{\prime} = \frac{{m_{\text{a}} }}{{m_{{\text{ath}}} }} ,$$

(8)

$$B^{\prime} = \frac{B}{{2m_{{\text{ath}}} \omega }}$$

(9)

where $A^{\prime} {\text{and}} B^{\prime}$ are non-dimensional added mass and damping coefficients, respectively. $m_{{\text{ath}}} = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}\rho D^{3}$ is the theoretical added mass and $\omega$ is the vibration frequency. It should be noted that CRED outer diameter is the same for all CRED cases and consequently $m_{{\text{ath}}}$ is constant. This implies that the larger damping and added mass coefficients correspond to the larger hydrodynamic forces. Vibration amplitude, A, defined in the parameter of $\text{KC}$ for CRED is assumed to be the measured amplitude of the rigid part. It is noted that the deflection of the outer elastic edge automatically affects the $F_{{\text{fluid/body}}}$ and $F_{{\text{meas}}}$.

4 Model detail

A combined disk is assembled by attaching the co-axial rigid and flexible plate with different diameters. As shown in Figs. 3 and 4, different sizes of CRED are prepared for investigation of the effect of rigid to elastic diameter ratio, the excitation frequency and amplitude on the hydrodynamic coefficients. The rigid parts of all the CRED disks are connected to the elastic parts by small bolts as demonstrated in Figs. 3 and 4. The size of nuts and bolts is chosen such that they do not have a significant influence on the fluid streamlines around the disk.

Fig. 3

a Steel rigid plates before attaching to the elastic part. b Standard samples for tensile test

Fig. 4

a UCRED disks. b NCRED disks

The rigid part is steel, while the elastic part is from two different rubber materials, Urethane and Neoprene. The diameter ratio,$D_{{\text{rc}}}$, for CRED is defined as the rigid parts’ diameter,$D_{\text{R}}$, divided by the entire disk’s diameter,$D_{{\text{El}}}$. This means that $D_{{\text{rc}}}$ is set to 1 for a fully rigid disk (FRD). For Urethane CRED (UCRED), the thickness of the elastic part is different from the rigid part, while for the Neoprene CRED (NCRED), it is almost the same (Table 1). The distance of the disk from the free surface is defined as $d_{\text{S}}$, which is non-dimensionalized as $d_{{\text{Sr}}}$ through dividing by the CRED outer radius. For all the present tests, $d_{{\text{Sr}}} = 4.5.$ Young’s modulus of the elastic materials is obtained via a tensile test on small samples, as shown in Fig. 3. A detailed test matrix of all considered case studies is presented in Table 1.

Table 1 Text matrix of experiment

5 Results and discussion

Our previous work reported in Ref. [23] describes the validation work completed to ensure the accuracy of the experimental setup and the data analysis approach. Particularly, the added mass and damping results for a circular disk in isolation were compared against published data from [24, 25] and good agreement was observed. In this section, the results of different effective parameters, such as the diameter ratio and frequency are discussed. The submergence parameter is $d_{{\text{Sr}}} = 4.5$ in which the boundary effects can be neglected.

5.1 Effect of $D_{{\text{rc}}}$

The results of the hydrodynamic coefficients against $\text{KC}$ for the UCRED and NCRED are presented in Figs. 5 and 6 at different $D_{{\text{rc}}}$ and excitation frequency of $\beta = 4 \times 10^{4} ,f = 1 {\text{Hz }}$. Schematic of the deflection procedure and some of the excited mode shapes at different $\text{KC}, D_{{\text{rc}}}$ and frequencies are presented in Figs. 7, 8 and 9. There is nonlinearity in the curves of $B^{\prime} - {\text{KC and }}A^{\prime} - {\text{KC}}$ for both of the UCRED and NCRED compared to FRD curves. It can be seen that CRED cases have higher damping and lower added mass compared to FRD. When a UCRED and FRD are vibrated in a given amplitude, the elastic edge deflection causes the final displacement of the outer edge to be larger for CRED compared to FRD (Figs. 7 and 8a, e). This larger edge displacement induces the larger edge velocity for UCRED than for FRD. The larger velocity enhances the strength of the induced vortex, as investigated by many kinds of research [24, 26]. Despite the larger velocity for UCRED edge compared to the FRD edge, it is shown in Fig. 5a that the damping coefficients for cases with $D_{{\text{rc}}} = 0.8 {\text{and }}0.6$ are still lower than the FRD in a wide range of $\text{KC}$. The reason is related to the larger thickness of the elastic edge compared to the FRD edge, which affects the performance of the shed vortex from the edge [7]. For UCRED with $D_{{\text{rc}}} = 0.6$ the positive effect of the deflection finally overcomes on the negative effect of the large thickness. This consequently improves UCRED damping about 5–7% compared to FRD one for $\text{KC}$ larger than 1.2, as can be seen in Fig. 5. Furthermore, Fig. 7 shows a schematic view for the deflection procedure of a CRED compared to a FRD in four regions b and c of a vibration cycle.

Fig. 5

Non-dimensional damping (a) and added mass (b) coefficients versus $\text{KC}$ of UCRED at $\beta = 4 \times 10^{4}$

Fig. 6

Non-dimensional damping (a) and added mass (b) coefficients versus $\text{KC}$ of NCRED at $\beta = 4 \times 10^{4}$

Fig. 7

The displacement schematic for FRD compared to CRED in regions b and c of one complete oscillation cycle

Fig. 8

Some excited mode shapes of UCRED for different $D_{{\text{rc}}}$, $\text{KC}$,$\beta$ values in the condition of maximum deflection

Fig. 9

Some excited mode shapes of NCRED for different $D_{{\text{rc}}}$, $\text{KC}$,$\beta$ values in the condition of maximum deflection

The ability of the experiments to be duplicated has been investigated by a repeatability study. This was performed through testing in some cases FRD, UCRED, and NCRED at two medium and high KC values similar to the work of Moreno et al. [22]. Repeatability was also quantified at higher frequencies. Each of the experiments was repeated ten times. The results should be at a 95% confidence level based on the International Towing Tank Conference (ITTC) recommendations [27]. The obtained data reported the desired confidence level.

For interpretation of the deflection procedure, an equation can be developed to show the dependency of deflection to time and position. Strictly speaking, the dynamic equation, especially at high frequencies and large deflections, should be developed in a complete nonlinear form by considering the rubber material as a hyper elastic model. However, a simplified thin plate theory can approximately explain the observed deflection behavior by considering a constant elastic modulus. The dynamic equation for a fully elastic circular plate in the air has been presented in texts [28]. The elastic part of a CRED is an annular plate with clamped and free boundary conditions on its inner and outer edge, respectively. Based on Fig. 10) those equations can be modified to Eq. 10 for the vibration of an elastic annular plate in water with regard to a harmonic base excitation of the rigid part.

$$D S \nabla^{4} w + \rho h S\left( {\frac{{\partial^{2} w}}{{\partial t^{2} }} + \ddot{y}_{Q} } \right) = F_{{\text{fluid/body}}} \left( {r,\theta ,t} \right),$$

(10)

where $D$, S and w, respectively, define the flexural rigidity, the surface area of the annular plate and elastic plate deflection. $\rho$ is density and $F_{{\text{fluid/body}}} \left( {r,\theta ,t} \right)$ shows the hydrodynamic force.

Fig. 10

a Free body diagram of a CRED in water. b Equal simplified system equal to plate edge oscillation

Larger deflection for cases with lower $D_{{\text{rc}}}$ values is interpreted by an equivalent stiffness on the elastic-free edge. Regarding the formula for axisymmetric deflection [29] a simplified equivalent stiffness on the free edge can be calculated as shown in Eq. 11 based on its schematic view shown in Fig. 11. It should be noted that F is the total load which is uniformly distributed along the outer edge.

$$K_{{\text{eq}}} = \frac{F}{\delta } \cong \left( {\frac{1}{{0.1\frac{1}{{D_{r} }} - 0.1}}} \right)\frac{{Eh^{3} }}{{r_{{\text{El}}}^{2} }} 0.2 < D_{{\text{rc}}} < 0.8$$

(11)

The two-way fluid–structure interaction between elastic rubber and water requires fully coupled CFD-FEM analysis. However, the hydrodynamic forces are approximated to be harmonic as in Eq. 3. Therefore, according to Eq. 11, among all four cases for a CRED with $D_{{\text{rc}}} = 0.4, 0.6, 0.8, 1$, the maximum deflection is related to the case with the lowest stiffness, i.e., lowest $D_{{\text{rc}}}$. This then explains larger damping for cases with low $D_{{\text{rc}}}$ as presented in Figs. 5a and 6a.

Fig. 11

Equivalent stiffness for the outer edge of an annular elastic part in UCRED and NCRED with axisymmetric deflection

Added mass coefficients of UCRED introduce different trends as plotted in Fig. 5b. All the UCREDs show lower added mass compared to FRD. In the case with the lowest $D_{{\text{rc}}}$ value, 0.4, the added mass decreases about 25% in comparison with FRD at large $\text{KC} = 1.4 - 1.8$. The added mass reduction is expected due to the high deflection of the elastic edge that reduces the amount of acceleration imparted to the fluid. In fact, the input energy converted into internal energy. Therefore it is seen that both of the added mass and damping coefficients change for different $D_{{\text{rc}}}$ values in a certain $\text{KC}$.

The second type of CRED, Neoprene, has a higher elastic modulus,$E = 4.6 {\text{MPa}}$, compared to Urethane. The Neoprene thickness is 1.6 mm, close to the thickness of FRD, 1.85 mm. The NCRED thin edge, h = 1.6 mm, causes strong vortices compared to UCRED with h = 6 mm. In these conditions, it is expected that UCRED would have lower deflection and damping than NCRED due to small stiffness of the NCRED for the same values of $D_{{\text{rc}}}$,$r_{{\text{El}}}$ (Figs. 5a and 6a). The stiffness of CREDs in a given $D_{{\text{rc}}}$ and $r_{{\text{El}}}$ are only proportional to $Eh^{3}$ parameter as in Eq. 11. $Eh^{3}$ value for NCRED and UCRED is, respectively, 0.019 and 0.07, as shown in Table 1. Although the effect of decreasing UCRED thickness has not been studied in this research, one may expect in such a condition that the low stiffness of UCRED increases the damping provided that the deflection is axisymmetric. It is noted that there is the other specified condition in which only the outer edge of the UCRED edge is sharpened. In such a case, it is expected that sharpening the edge of UCRED improves vortex formation while the stiffness remains unchanged.

The thickness of FRD and NCRED are approximately the same. Hence, the elastic edge deflection can play a crucial role in damping even at small $\text{KC}$ and large $D_{{\text{rc}}}$ values. Figure 6 shows a considerable improvement in damping and a significant reduction in added mass for NCRED as $D_{{\text{rc}}}$ decrease compared to the UCRED data shown in Fig. 5.

The damping increase of UCRED or NCRED for $D_{{\text{rc}}} = 0.4$ is remarkable due to their smaller stiffness compared to cases with $D_{{\text{rc}}} = 0.6, 0.8, \;\text{and}\;1$ especially for small $\text{KC}$ values. Despite the increasing trend for damping against $\text{KC}$ at $D_{{\text{rc}}} = 0.4$ and small $\text{KCs}$, the slope suddenly decreases at large $\text{KC}$ values. This drop is more visible for NCRED in comparison to UCRED at $\text{KC}$ larger than 1.4. This slope reduction may be attributed to some reasons as follows:

• The hydrodynamic force for large $\text{KC}$ is not high enough to deflect the elastic edge at a low $\text{KC}$ range.

• The interaction of the induced vortexes from the opposite side of a CRED is more probable at large defections. Therefore, the vortexes cancel each other’s effects.

• Finally, it may be related to an exciting mode shape where all edge parts cannot be deflected simultaneously. Hence, the folded edge sequentially affects the edge vortex shedding mechanism. As depicted in Fig. 9a, b, and c, such a folded edge is more observed for the NCRED as will be explained in the following sections.

Generally, it is concluded that $D_{{\text{rc}}}$ reduction improves the damping in accompany with a decrease in added mass in the condition of the axisymmetric deflection. Therefore, the variation of $D_{{\text{rc}}}$ in CRED leads to a trade-off between added mass and damping coefficients, as observed in Figs. 5 and 6.

5.2 The axisymmetric deflection procedure of a CRED

The axisymmetric deflection procedure of the elastic part in a CRED can be analytically explained. For a given $D_{{\text{rc}}}$ value in CRED, the maximum deflection of the elastic part is accrued at the end of the stroke in an axisymmetric vibration. It is justified using a two-dimensional axisymmetric model instead of a general three-dimensional continuous vibration model. The dynamic equations are developed for a dynamical system as the annular elastic part of a CRED. According to Eq. 12, it can be again simplified to a single degree of freedom (SDOF) vibration for a point on the elastic outer edge, as shown in Fig. 10.

$$M_{eU} .\ddot{y}_{\text{U}} = - k_{eU} \left( {y_{\text{U}} - y_{\text{G}} } \right) - f_{{\text{eU}}} \left( t \right) \Rightarrow M_{eU} \ddot{w}_{U} + k_{eU} w_{U} = - \left( {M_{eU} + m_{a - eU} } \right)\ddot{y}_{\text{G}} - B_{eU} \dot{y}_{G}$$

(12)

Here $M_{eU} , k_{eU} ,f_{{\text{eU}}} \left( t \right),m_{a - eU} , and\, B_{eU}$ are the equivalent mass, stiffness, external force, added mass, and damping coefficients on point U, respectively. Since for SDOF system, the total mass of the real dynamical system is considered at a specified point, $M_{eU}$ is an equivalent mass instead of the distributed mass. It can be calculated based on the relation between the displacements of all points versus displacement of point U. Therefore, the dynamical properties of point U can be approximated by an analyzing a concentrated mass and spring at that point instead of analyzing a complicated mathematical form of a vibrating plate. The equivalent mass and stiffness are supposed to be a lumped mass and spring in point U in which they result in the same dynamical characteristics for point U instead of the real complicated form. The outer edge deflection relative to the inner edge displacement is defined as $w_{U}$ which is an effective factor in damping.

It is noted that $F_{{\text{fluid/body}}}$ is the total hydrodynamic force applied from fluid on both of the rigid and annular elastic plates. It is originally composed of two different parts with a phase difference of $\frac{{\uppi}}{2}$ which are defined as damping and inertia hydrodynamic forces. These parts can be approximated to be a function of the velocity and acceleration of disk ($\dot{y}_{G}$,$\ddot{y}_{\text{G}}$). $f_{{\text{eU}}} \left( t \right)$ is the equivalent concentrated force applied on point U which is originated from some part of the total $F_{{\text{fluid/body}}}$ applied to the annular elastic part. Therefore $f_{{\text{eU}}} \left( t \right)$ is included in terms of $m_{{\text{a} - eU}}$ and $B_{eU}$, which are indications of inertia and damping forces.

The right-hand side of Eq. 12 is interpreted as two harmonic excitation forces with different phases for an assumed absolute vibrational displacement, $w_{U}$. If the hydrodynamic forces are neglected as an oscillated case in air, hence, the phase difference of $w_{U}$ and $\ddot{y}_{\text{G}}$ is ${\uppi}$ in all the regions (a, b, c, d) of one complete cycle. It means that for the positive value of $y_{\text{G}}$ where $\ddot{y}_{\text{G}}$ is negative, region b, c of Fig. 10), $w_{U}$ is positive. In a similar trend $w_{U}$ has a negative direction opposite to $\ddot{y}_{\text{G}}$ in the region of (a) and (d). Consequently, the CRED edge displacement is larger than FRD one for a given amplitude applied from the actuator on the center part. Regarding the Eq. 12, the maximum deflection occurs at the stroke end of the harmonic vibration, in which the acceleration amplitude of the rigid part is maximum.

In hydro-elastic conditions, the hydrodynamic force affects the edge deformation differently. Equation (12) demonstrates that $w_{U}$ is in the same phase with the summation of inertia and damping terms $- \left\{ {\left( {M_{eU} + m_{{\text{a} - eU}} } \right)\ddot{y}_{\text{G}} + B_{eU} \dot{y}_{G} } \right\}$. Figure 10 (b) shows that both $\ddot{y}_{\text{G}}$ and $\dot{y}_{G}$ have the same sign in the region (a) and (c), therefore, the superposition of these terms results in a high deflection value. Figure 12 clarifies that there is a higher downward deflection in the region (a) during upward motion and also higher upward deflection in the region (c) for downward motion compared to the regions (b) and (d). However, the lower deflection in the regions (b) and (d) is due to the opposite effects of those terms. In the region (b) where UCRED is moving up, $\dot{y}_{G} > 0,\ddot{y}_{G} < 0$, the damping force tends to deflect the elastic edge downward while the inertia force causes the upward deflection. A similar interpretation can be expressed for the region (d). Hence, there is a phase difference between $w_{U}$ and $\dot{y}_{G}$ in the regions of b and d not equal to ${\uppi}$.

Fig. 12

Axisymmetric deflection of a UCRED with $D_{{\text{rc}}} = 0.4,\text{KC} = 1.8,\beta = 4 \times 10^{4} \left( {f = 1\;\text{Hz}} \right)$ for ten steps of one complete cycle in four regions (a, b, c, d)

As explained, Eq. 12 states that the inertia tends to deflect the elastic edge upward in regions (b) and (d) while Fig. 12 demonstrates that $w_{U}$ is downward. It means that the deflection is in the opposite direction of $\dot{y}_{G}$ in all regions. The reason can be related to this fact that the large defections in the region (a) and (c), due to superposition of the inertia and damping forces, cannot only be compensated by inertia force in regions (b) and (d), while the damping still tends to increase the deflection.

5.3 Effect of natural and excitation frequency

In most experiments, it is difficult to obtain $\beta$ and $\text{Re}$ numbers close to the corresponding values in real conditions. However, the influence of this factor on hydrodynamic coefficients of FRD, UCRED, and NCRED is studied for various $D_{{\text{rc}}}$ values in this section to the extent possible for $\beta = 4 \times 10^{4} ,8 \times 10^{4} ,1.2 \times 10^{5} ,$ corresponding to f = 1, 2, and 3 Hz. The results are depicted in Fig. 13, 14 and 15.

Fig. 13

Non-dimensional damping (a) and added mass (b) coefficients versus $\text{KC}$ FRD at $\beta = 4 - 8 \times 10^{4} \;\text{and} \;1.2 \times 10^{5}$

Fig. 14

UCRED non-dimensional damping (left) and Added mass (right) coefficients versus $\text{KC}$ at different $\beta$

Fig. 15

NCRED non-dimensional damping (left) and Added mass (right) coefficients versus $\text{KC}$ at different $\beta$

5.3.1 Effect of $\beta$ on FRD Hydrodynamic coefficients

It is expected that for FRD at $d_{{\text{Sr}}} = 4.5$, far from the boundaries, hydrodynamic coefficients would be independent of frequency [12,13,14, 30]. Figure 13 shows that for the FRD which is located above the deep water indication value of 2 [31], the hydrodynamic coefficients are frequency dependent. This dependency can be attributed to the fact that those published results were based on low frequencies, as expressed in Ref. [13], while the present study is for higher frequencies, as shown in Table 2. For a proper comparison, the defined parameters in Table 2 as $d_{\text{S}}$, $r_{\text{d}}$,$t_{\text{d}}$ and $D_{\text{d}}$ which introduces the disk submergence depth, equivalent radius, equivalent thickness, and equivalent diameter, respectively, are defined as those in the research of Lopez-Pavon and Souto-Iglesias [13]. The FRD damping changes significantly with frequency, especially in large $\text{KC}$ and $\beta$. It can be concluded that the frequency is the other key parameter on the FRD hydrodynamic properties similar to the results of Moreno et al. [22].

Table 2 Plate characteristics used in this study

5.3.2 Effect of the natural frequency on CRED hydrodynamic coefficients for a constant $\beta$

With a certain natural and excitation frequency, some modes with folded edges may be excited on a CRED, causing the deflection to be $\theta$ dependent. In this situation, the induced vortices cannot be developed strongly on a folded edge as the lower axisymmetric modes. Consequently, the damping for higher modes maybe even smaller than the lower mode. This point should be considered during the design steps of a CRED in which the excited mode should be around the resonance point of the first axisymmetric mode. Therefore, the effects of frequency variation on CRED hydrodynamic characteristics are different from those in FRD.

The elastic edge deflection and the resulted damping are dependent on the natural and excitation frequencies. In this section, the effect of the natural frequency variation on the hydrodynamic properties is investigated for a constant excitation frequency, $\beta$. The natural frequency of an elastic annular plate depends on the equivalent stiffness and mass. As expressed in Eq. 11, the stiffness of the CRED edge is approximated to be dependent on $D_{{\text{rc}}} ,\text{and}\, \frac{{Eh^{3} }}{{r_{{\text{El}}}^{2} }}$. Decreasing the width of the elastic annular plate, i.e. increase of $D_{{\text{rc}}}$ value, increases the total stiffness for a given $E$ and $h$. It means that for a specified CRED, UCRED or NCRED, $D_{{\text{rc}}}$ reduction decreases the natural frequency such that the higher modes are excited in a given $\text{KC}$ and $\beta$. Consequently, the higher mode shapes except the axisymmetric modes have a negative effect on the damping. This phenomenon can be clearly seen in Figs. 6a and 9c, e, and g for NCRED, $D_{{\text{rc}}}$ = 0.4, with the folded edge compared to $D_{{\text{rc}}}$ = 0.6 and 0.8, especially at large $\text{KC}$ values.

The other effective parameter on the natural frequency is the equivalent mass. Increase of the added mass by increasing of $\text{KC}$ in a given $D_{\text{rc}}$ and $\beta$ reduces the natural frequency. Hence, despite the constant excitation frequency, the higher modes can be observed with a gradual increase of $\text{KC}$. In these conditions, the disruption of the vortex formation is more probable compared to the low $\text{KC}$ regime. For example, NCRED with $D_{{\text{rc}}} = 0.4, \beta = 4 \times 10^{4} \left( {f = 1 \text{Hz}} \right)$ in Fig. 9b and c and UCRED with $D_{{\text{rc}}} = 0.4, \beta = 8 \times 10^{4} \left( {f = 2 \text{Hz}} \right)$ in Fig. 8b and c. The corresponding damping trends are observed in Figs. 6a and 14c.

At this step, the added mass properties are investigated. In most of the CREDs, with high stiffness, the hydrodynamic coefficients show a monotonic rise versus $\text{KC}$ for a given $D_{{\text{rc}}}$ and $\beta$ as illustrated in Figs. 5 and 6. However, Fig. 6b shows that the added mass has a decreasing trend in some CREDs with low stiffness as NCRED with $D_{{\text{rc}}} = 0.4$ for $\text{KC} < 1.2$. The related mode of this case can be observed in Fig. 9) and b. The reduction of the added mass against $\text{KC}$ is due to the conversion of the input energy into deflection (internal energy) instead of accelerating the surrounding fluid. Furthermore, for some CREDs, the applied force at large $\text{KC}$ cannot deflect the elastic edge as low $\text{KC}$. The input energy can accelerate more fluid volume compared to the low $\text{KC}$ conditions. Hence, the added mass curve slope at large $\text{KC}$ is considerably higher than the slop at small $\text{KC}$. Such a trend is obvious for UCRED with $D_{{\text{rc}}} = 0.4$ after $\text{KC} = 1.1$ as depicted in Fig. 5(b).

5.3.3 Effect of $\beta$ on UCRED hydrodynamic coefficients

The influence of other excitation frequencies, as $\beta = 8 \times 10^{4} ,\;\text{and}\; 1.2 \times 10^{5}$ in addition to $\beta = 4 \times 10^{4}$ on UCRED hydrodynamic coefficients, is examined hear. Generally, the increasing trend of damping against $\beta$ is clearly observed in Fig. 14a, b, and c for UCRED cases with high stiffness due to the strong vortexes at large $\beta$. This fact is satisfied provided that the UCRED with $D_{{\text{rc}}} = 0.8 ,0.6 \;{\text{and}}\; 0.4$ at $\beta = 4 \times 10^{4} ,8 \times 10^{4} ,\;\text{and}\; 1.2 \times 10^{5}$ is vibrated in an axisymmetric mode shape, as depicted in Fig. 8. However, in the case with $D_{{\text{rc}}} = 0.4$ which has the lowest stiffness among all $D_{{\text{rc}}}$ values, higher non-axisymmetric modes are observed at large frequencies $\beta = 8 \times 10^{4} ,\;\text{and}\; 1.2 \times 10^{5}$ for large $\text{KC}$, as presented in Fig. 8c and d. Considerable reduction in the slope of the UCRED damping curve versus $\text{KC}$ for $D_{{\text{rc}}} = 0.4, \beta = 8 \times 10^{4}$ is a result of these higher excited modes, Fig. 14c. The corresponding mode shapes are depicted in Fig. 8b and c. This is the reason why in Fig. 14c a monotonic rise for damping versus $\text{KC}$ are not seen for $D_{{\text{rc}}} = 0.4,\;\text{and}$ $\beta = 1.2 \times 10^{5}$ compared to the cases with $D_{{\text{rc}}} = 0.4,\beta = 4 \times 10^{4} ,\;{\text{and}}\; 8 \times 10^{4}$.

The UCRED added mass generally reduces at large frequencies for a given $D_{{\text{rc}}}$ and $\text{KC}$ due to the high deflection at large applied forces, Fig. 14d, e, and f. This reduction is more considerable at the lowest $D_{{\text{rc}}}$ value, 0.4. However, the added mass with $D_{{\text{rc}}}$ = 0.8 and $\beta = 8 \times 10^{4}$ is smaller than those with $D_{{\text{rc}}} = 0.8,\;\text{and}$ $\beta = 4 \times 10^{4}$. By increasing $\beta$ to $1.2 \times 10^{5}$ the added mass again decreases (Fig. 14d). Generally, when $\text{KC}$ is increased, the negative effect of the deflection on the CRED added mass is in contrast with the positive effect of the accelerating surrounding fluid. In most UCREDs, except cases with low $D_{{\text{rc}}}$ and large $\beta$, the positive effect overcomes in the negative one. Consequently, the added mass shows a monotonic rising trend versus $\text{KC}$, as depicted in Fig. 14d, e, and f.

5.3.4 Effect of $\beta$ on NCRED hydrodynamic coefficients

It is expected that $\beta$ would have a more significant influence on the NCRED hydrodynamic coefficients than on the UCRED ones. The reason is related to the low stiffness of NCRED compared to UCRED. Comparison of Figs. 14 and 15 clears that UCRED damping increases with increasing $\beta$ while NCRED damping trend is different, especially at small $D_{{\text{rc}}}$. NCRED damping increases as $\beta$ increases for $D_{{\text{rc}}} = 0.8$, as shown in Fig. 15a because the deflection and velocity grow and consequently, strong vortexes appear. Its dominant mode is axisymmetric as shown in Fig. 9g and h. It is demonstrated in Fig. 15b that the damping increases when $\beta$ changes from $4 \times 10^{4} {\text{to}} \;8 \times 10^{4}$ for $D_{{\text{rc}}} = 0.6$, with a first dominant mode in a combined mode (Fig. 9e, f). However, a drop in damping is seen at $\beta = 1.2 \times 10^{5}$ due to the second dominant mode, as can be seen in Fig. 15b. The lowest stiffness for $D_{{\text{rc}}} = 0.4$ is the reason for exciting the higher modes as shown in Fig. 9d, especially at large frequency of $\beta = 1.2 \times 10^{5}$. Figure 15c clears that the drastic drop in damping with the increasing of $\beta$ is the result of the excited higher mode. Such a drop occurs for NCRED cases with $D_{{\text{rc}}} = 0.6 {\text{and}} 0.4$ in all excited frequencies, as shown in Fig. 15b and c, while for UCRED with higher stiffness, it only happens for $D_{{\text{rc}}} = 0.4$ in the largest $\beta$ in Fig. 14c. The NCRED damping is larger than the UCRED one for $D_{{\text{rc}}}$ = 0.4 in low $\beta$ as presented in Fig. 5a and 6a. However, the higher excited modes of NCRED with $D_{{\text{rc}}}$ = 0.4 is a reason for damping drop compared to UCRED with $D_{{\text{rc}}}$ = 0.4 in large $\beta$, as depicted in Figs. 14c and 15c. The results clear that a monotonic increasing trend of damping versus $\text{KC}$ and $\beta$ can be achieved for a CRED with high stiffness in a wide range of $\text{KC}$ and $\beta$.

In a similar trend with UCRED, the NCRED added mass decreases as $\beta$ increases, as in Fig. 15d, e, and f while it differently changes $\text{with}\;\text{KC}$. It is observed in Fig. 15e and f that the slope of the added mass curve against $\text{KC}$ becomes negative for both $D_{{\text{rc}}} = 0.6\; {\text{and}}\; 0.4$ at $\beta = 8 \times 10^{4} ,1.2 \times 10^{5}$.

The hydrodynamic coefficients of FRD in most of the previously published research have been extracted at single excitation frequency, although the sea waves contain multiple frequency content. From a design point of view, the natural frequency of the body should not be in the vicinity of the peak frequency of the wave spectrum due to resonance vibration problems. Since the damping is highly dependent on the vibration amplitude (KC number), hence, in a specified condition in which resonance occurs, the damping plate affects the response considerably and decreases it. Generally, damping and added mass are weakly dependent on the excitation frequency for small value ranges of frequencies [12,13,14, 30]. Hence, most of the published researches have just investigated the $B^{\prime}$ and $A^{\prime}$ for a FRD attached to a platform column under a single frequency. In the experimental tests for a FRD attached to a cylinder, the single excitation frequency is selected to be around the structure natural frequency. This is for dominating the damping forces in the measured signal while the inertia forces are offset by restoring force [3]. It is concluded that in the other excitation frequencies which are away from the natural frequency the effect of damping plate on RAO is lower than for the natural frequency [32] while the damping due to the vortex shedding is still applied to the structures. For experimental tests on isolated FRD models without a specified structure, the excitation period has been approximated regarding the scaling of the dominant period of the sea waves (8–10) [12, 24]. In a real condition, the dominant period of the excitation wave is supposed to be around 8–10 s, which has been scaled by researchers to 1 s for a FRD model with dimension around D = 0.2 m. It is emphasized that the scaling of the frequency should be based on this fact that $\beta$ is kept constant for prototype and model. This point dictates that the frequency should be more than 1 s in the mentioned papers. For this reason, Moreno et al. [22] conducted experiments on the heave plate model under high excitation frequencies.

If the motion equation is linear, the obtained hydrodynamic coefficients of CRED under different single frequencies can be applied in the equations. Therefore the frequency response spectrum can be extracted. Moreover, some requirements should be respected during the initial design steps. If the wave excitation period is around the platform natural period the resonance occurs. In such a condition the designer can adjust the effective parameters on the axisymmetric natural period of the CRED such as E, h, and $D_{\text{rc}}$ around the wave excitation period. Consequently, the axisymmetric natural period of CRED is also around the platform natural period. This improves the resulted damping of CRED which decreases the platform response. However, in most of the time the designers can adjust the natural period of the platforms to be far away from the wave dominant period by changing of the equal stiffness and mass of the platform. For cases where the wave dominant period is far away from the natural period of the platform, the axisymmetric natural period of CRED should be only close to the wave excitation period for high damping performance as explained before. For the UCRED model of this study one may needs a scaling factor of $\lambda = \frac{1}{100}$ for the real size applications. Therefore the axisymmetric excitation period of the UCRED model, T _m= 1 s is scaled to T_p = 10 s for a large scale prototype. It is notable that this period is near the common wave dominant period (8–10 s). This period may be even around the natural period of a real platform when the designer cannot adjust the natural period of the structure to be far away from the wave excitation period.

The non-dimensional damping coefficients for CRED can be the same for model and prototype provided that all the dimensions as the diameter of the rigid disk, diameter ratio of rigid to elastic part and elastic module, etc. are scaled by the properly scaled factors. For instance, if the length scale factor is $\lambda$ the scaling factors for the elastic module and hydrodynamic forces from the water on CRED are $\lambda$ and $\lambda^{3}$. It means that the selected material for the scaled model is scaled to a stiffer material for the prototype that should be again in the range of the rubber materials which have high fatigue resistance.

The CRED damping of a model is supposed to be composed of the two separated parts. First, damping for an imagined FRD in which its vibration amplitude is the same as actuator vibration amplitude. Second, the damping of the other assumed FRD with a vibration amplitude equal to the edge deflection. For the first FRD, the non-dimensional damping of the model and prototype is kept the same as it has been proved by many researchers [3]. Regarding the second part, similar non-dimensional damping can be again obtained for the corresponding part in the prototype. This is because of the same deflection to the diameter ratio for the model and prototype. Finally, it can be concluded that the same non-dimensional damping for both of the model and prototype is derived based on Eq. 13.

$$B^{\prime}_{{\text{CRED} - p}} = \frac{{B_{1 - p} + B_{2 - p} }}{{2m_{{\text{ath}}} \omega_{p} }} = B^{\prime}_{1 - p} + B^{\prime}_{2 - p} \approx \left[ {\alpha_{1} + \left( {\frac{2\uppi A}{{D_{p} }}} \right)\alpha_{2} } \right] + \left[ {\left( {\frac{{2\uppi \delta_{p} }}{{D_{p} }}} \right)\alpha_{2} } \right] \approx B^{\prime}_{1 - m} + \left[ {\left( {\frac{{2\uppi \delta_{m} }}{{D_{m} }}} \right)\alpha_{2} } \right] \approx B^{\prime}_{1 - m} + B^{\prime}_{2 - m} \approx B^{\prime}_{{\text{CRED} - m}}$$

(13)

The index p and m are related to the corresponding parameters of the prototype and model. $\alpha_{1}$ and $\alpha_{2}$ are offset and slope values of the damping curves versus $\text{KC}$. This simplified approximation has been basically derived with regard to the linear governing equation. If the nonlinearity is high, which brings complexity to the problem, more detailed researches are required to cover all aspects.

6 Conclusion

For improving the damping characteristics, a novel CRED has been proposed as a substitution for FRD. Different parameters as $D_{{\text{rc}}}$, $\text{KC}$ and $\beta$ affect the hydrodynamic behavior of heave plates. The variation of hydrodynamic characteristics of a CRED has been investigated experimentally in terms of the changes in the effective variables. The main outcomes are listed below, which help the designer to find the optimum condition for the desired hydrodynamic coefficients:

• 1. Due to the velocity increase of the elastic edge in a CRED compared to the rigid edge of FRD, CRED damping is higher than for the FRD in a given outer diameter.

• 2. The decrease in $D_{{\text{rc}}}$ can generally increase the CRED damping for a given $\text{ KC}$ and $\beta$ which is simultaneous with a reduction in added mass when CRED is deflected in axisymmetric mode. The reduction is originated from this fact that the deflected elastic edge of CRED has the low capability to accelerate surrounding fluid particles compared to FRD.

• 3. The natural frequency of a CRED for a given $D_{{\text{rc}}}$ and $\beta$ in fluid change with the increase of $\text{ KC}$. This is due to the added mass increase, which decreases the natural frequency. Hence the higher mode shapes can be excited with folds on the outer edge, which consequently decreases the damping. This point should be considered in the design steps of a CRED.

• 4. Larger damping can be obtained for a low stiffness CRED compared to high stiffness CRED and FRD at small $\text{ KC}$ and $\beta$ while a drastic drop may occur at large $\text{ KC}$ and $\beta$. The reason is that at high values of $\text{ KC}$ and $\beta$ the equal mass of the vibrating system increases through the added mass increase. As a result, the natural frequency reduces, which in turn excites higher mode shape with folded edge. This fact decreases the resulted damping.

• 5. A monotonic rise in $B^{\prime} - \text{KC}$ curve of a CRED with high stiffness is achieved in a wide range of $\text{ KC}$ and $\beta$, especially at large $\text{ KC}$ and $\beta$ compared to low stiffness CRED. This is because of the higher excited mode shapes in the latter case at large $\text{ KC}$ and $\beta$ which in turn decrease the damping.

• 6. High damping achievements requires that the CRED excited modes are only around the resonance point of the first axisymmetric mode. Asymmetric modes cause the shedding of the vortex from the outer edge disrupt. This disruption considerably reduces the induced damping force.