Numerical study of roughness model effect including low-Reynolds number model and wall function method at actual ship scale

Abstract

A numerical study of roughness effects at an actual ship scale is performed. Low-Reynolds number roughness models based on the two-equation turbulence model are employed, meanwhile, a wall function method is also developed. First, the roughness models are examined for the 2D flat plate case at the Reynolds numbers of $1.0 \times 10^7$, $1.0 \times 10^8$ and $1.0\times 10^9.$ The resistance coefficient increases with roughness height and uncertainty analysis of the resistance coefficient is performed. Additionally, the distributions of the non-dimensional velocities $u^+$ based on the non-dimensional heights $y^+$ of the low-Reynolds number models and the wall function method are compared for changing the roughness height. Next, the roughness models and wall function method are applied to the flows around a ship at full scale. The tanker hull form with the flow measurement result from an the actual sea test is selected. The propulsive condition with the free surface effect is achieved by the propeller model. The velocity contours are compared with the measured results of the actual ship. The results of the roughness models show good agreement in comparison with the smooth surface condition. The wall function method leads to reduced grid uncertainty with respect to the resistance coefficient and shows agreement with the measured velocity contours. Consequently, the wall function method is better at full scale.

1 Introduction

Estimation of ship performance at full scale is a key issue in the field of hydrodynamics. Several projects have been carried out to grasp the phenomena while focusing on the flows around an actual ship. The wake flows of several ships are being measured using the laser Doppler velocimeter (LDV) of the European Project EFFORT (European Full-scale FlOw Research and Technology). The project also involves gathering existing data, including the results for a container ship [1] that has the LDV measurement results. Recently, the particle image velocimetry (PIV) technique has been utilized for the measurement of an actual ship. Kleinwachter et al. performed PIV measurement for a roll-on/roll-off container ship with a ship length of approximately 186 m [2]. The total wake field is simultaneously obtained at multiple points by the PIV system. The shaft torque and power of a general cargo ship are measured in the workshop [3]. The actual ship hull form is also measured by a 3D laser scanner system.

Numerical simulation based on computational fluid dynamics (CFD) is also widely utilized in the field of hydrodynamics. The Reynolds averaged Navier–Stokes (RANS) simulation is applied to the case at an actual ship scale. Visonneau et al. computed the flows around a ship with complex appendages, including a nozzle around the propeller, a headbox and a propeller shaft with V-brackets [4]. The unstructured RANSE solver is utilized, and the axial wake fields in front of the propeller are compared with the full-scale experimental results obtained by the EFFORT project. The scale effects on the axial velocity contours are also discussed. Starke et al. compared the computed results with the measured data in all cases of the EFFORT project [5]. The linear turbulence models are examined and the accuracy of the estimation is examined while considering the relation between the flow features and the ship shapes. The same configuration including the complex appendages, the propeller shaft with V-brackets, and so on is also selected. Although the wake pattern due to the shaft exhibits a difference from the measured result, the boundary layer thickness is reasonably predicted. All of the previous numerical results exclude the roughness effect of the body surfaces.

The roughness effect of the body surfaces plays an important role at an actual ship scale. The body surface of an actual ship has roughness that comes from the paints, welding lines, and wavy shapes due to the hull and other structures. Starke et al. estimated the shaft power of a general cargo ship [3] using CFD simulation combined with the empirical frictional line and roughness allowance and conclude that the roughness allowance plays an important role in the accuracy of the estimation [6]. Eça and Hoekstra investigated the roughness models for the k-$\omega$ SST model. The low-Reynolds number roughness models proposed by Wilcox [7] and Knopp et al. [8] are examined using the 2D flat plate cases at high Reynolds numbers. The uncertainties based on the grid resolutions are described in detail with changing roughness height. The automatic wall functions [9] are also tested in the same 2D flat plate cases. The velocity profiles of the wall function model show agreement with the assumed analytical profiles and the resistance coefficients of the low-Reynolds number roughness models and wall function model show good agreement with the semi-empirical formula. Castro et al. [10] perform numerical simulations at the model and full scales. The propulsion condition with the free surface effect is achieved by the discretized propeller and the roughness of the hull surface is accounted for using the roughness effect in the wall function model. The roughness effect on the resistance coefficient is examined by changing the roughness height and the skin friction correction and the resistance coefficient are compared with the results based on ITTC correlation and procedures. Moreover, the scale effect, especially for the boundary layer thickness, is discussed and the positive point that comes from the thinner boundary layer at full scale is described.

In this work, the roughness effect at an actual ship scale is examined using the structured solver with the overset grid method. Low-Reynolds number roughness models [7, 11] are employed. The boundary condition of the frequency $\omega$ is changed in both models using the function based on a non-dimensionalized roughness height. A wall function method that can cope with the roughness effect is also developed. The analytical wall function using the empirical formula can be found, e.g., [9], however, the function has very complex expressions and the possibility to cause the numerical instability, and it is based on the empirical formula even in the analytical form. The present approach is a very simple expression based on the mixing length which is based on the assumption of local equilibrium with the correction formula suggested by Cebeci [12] and the roughness effect is accounted for by the kinetic energy on the boundary condition of the frequency $\omega$. First, the present methods are tested in the 2D flat plate cases. The Reynolds numbers are set as $1.0 \times 10^7$, $1.0 \times 10^8$ and $1.0\times 10^9$ to fit in the range of an actual ship scale. Uncertainty analysis based on the FS method [13] is performed using three computational grids with changing division numbers of the grids. The velocity profiles with changing roughness height are depicted in comparison with the analytical profiles. Next, the flows around the tanker hull [14] that has the flow measurement data from an actual sea test are selected and the roughness effect is examined. The propulsive condition including the free surface effect is achieved by the propeller model. The distributions of the non-dimensionalized roughness height and shear stress on the body surfaces are revealed and uncertainty analysis regarding the resistance coefficients is carried out. Finally, we conclude the present study.

2 Numerical method

2.1 Governing equations

The governing equation is the incompressible three-dimensional Reynolds-averaged Navier–Stokes equation using the artificial compressibility approach to couple pressure and velocities.

$$\begin{aligned}&\frac{\partial {\varvec{q}}}{\partial t} +\frac{\partial ({\varvec{e}}-{\varvec{e}}^{v})}{\partial x} +\frac{\partial ({\varvec{f}}-{\varvec{f}}^{v})}{\partial y} +\frac{\partial ({\varvec{g}}-{\varvec{g}}^{v})}{\partial z}-{{\varvec{H}}}=0\nonumber \\&\quad {{\varvec{q}}}=[ \begin{array}{cccc} p &{} u &{} v &{} w \\ \end{array} ]^{T}, \end{aligned}$$

(1)

Equation 1 is non-dimensionalized by the reference density $\rho _0$, reference velocity $U_0$, and reference length $L_0$. (u, v, w) represent the velocities in the (x, y, z) directions, respectively. Temporal time is expressed by t. The pressure p is modified in the next equation for free surface flows.

$$\begin{aligned} p=p^*+\frac{z}{F_n^2}, \end{aligned}$$

(2)

where $p^*$ is the pressure in the computational domain, $F_n$ is the Froude number, and z is the vertical coordinate from the static water plane($z=0$). The gravity term is included with the pressure in this modification.

The convective terms ${{\varvec{e}}}$, ${{\varvec{f}}}$ and ${{\varvec{g}}}$, viscous terms ${{\varvec{e}}}^{{\varvec{v}}}$, ${{\varvec{f}}}^{{\varvec{v}}}$ and ${{\varvec{g}}}^{{\varvec{v}}}$ and additional body force term ${{\varvec{H}}}$ are defined as follows:

$$\begin{aligned} {{\varvec{e}}}= & {} \left[ \!\!\begin{array}{c} \beta u\\ uu+p\\ uv \\ uw \\ \end{array} \!\!\right] , \ {{\varvec{f}}}=\left[ \!\!\begin{array}{c} \beta v\\ vu \\ vv+p\\ vw \\ \end{array} \!\!\right] , \ {{\varvec{g}}}=\left[ \!\!\begin{array}{c} \beta w\\ wu \\ wv \\ ww+p\\ \end{array}\!\! \right] , \nonumber \\ {{\varvec{e}}}^{v}= & {} \left[ \!\!\begin{array}{c} 0\\ \tau _{xx}\\ \tau _{xy}\\ \tau _{zx}\\ \end{array}\!\!\right] , \ {{\varvec{f}}}^{v}=\left[ \!\!\begin{array}{c} 0\\ \tau _{xy}\\ \tau _{yy}\\ \tau _{yz}\\ \end{array}\!\!\right] , \ {{\varvec{g}}}^{v}=\left[ \!\!\begin{array}{c} 0\\ \tau _{zx}\\ \tau _{yz}\\ \tau _{zz}\\ \end{array}\!\!\right] , \ {{\varvec{H}}}=\left[ \!\!\begin{array}{c} 0\\ f_x\\ f_y\\ f_z\\ \end{array}\!\!\right] , \end{aligned}$$

(3)

where $\beta$ is a parameter of the artificial compressibility approach and $\beta =1.0$ is given in the present computation. $\tau _{ij}$ is defined as $\tau _{ij}= \frac{1}{R} \left( \frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right) -\overline{u^\prime _iu^\prime _j}$, R is the Reynolds number, $\nu$ is the kinematic viscosity coefficient, and $-\overline{u^\prime _iu^\prime _j}$ is the Reynolds stress component, which is determined by the $k-\omega \;SST$ model.

The integral and discretized form of Eq. 1 is expressed as Eq. 4 using the finite volume method for a structured grid with a cell-centered layout.

$$\begin{aligned}&\frac{\partial V_{i,j,k} {\varvec{q_{i,j,k}}}}{\partial t}-{V_{i,j,k}}{{\varvec{H}}_{i,j,k}} \nonumber \\&\quad +[{\varvec{E}}-{\varvec{E_v}}]^{i+1/2}_{i-1/2}+[{\varvec{F}} -{\varvec{F_v}}]^{j+1/2}_{j-1/2}\nonumber \\&\quad +[{\varvec{G}}-{\varvec{G_v}}]^{k+1/2}_{k-1/2}=0, \end{aligned}$$

(4)

where $\pm 1/2$ indicates the directions of each cell face, ${\varvec{E}}$, ${\varvec{F}}$ and ${\varvec{G}}$ are convective fluxes, and ${\varvec{E_v}}$, ${\varvec{F_v}}$ and ${\varvec{G_v}}$ are viscous fluxes.

An in-house structured CFD solver [15] is employed. The details of the solver can be found in [15], where a summary is provided. Inviscid fluxes are evaluated by the third-order upwind scheme based on the flux-difference splitting of Roe. The evaluation of viscous fluxes is second-order accurate. The first-order Euler implicit scheme is employed for the temporal step. The linear equation system is solved by the symmetric Gauss–Seidel (SGS) method.

For free surface treatment, an interface capturing method with a single phase level-set approach is employed. The propeller effects are accounted for according to the body forces derived from the propeller model [15], which is based on potential theory.

2.2 Applying the overset grid method

The weight values for the overset interpolation are determined by an in-house system [16]. The details of the system can be found in [16] and a summary is provided below.

• 1. The priority of the computational grid is set.

• 2. The cells of a lower-priority grid and those inside a body are identified (referred to herein as in-wall cells).

• 3. Receptor cells for which the flow variables must be interpolated from donor cells are defined. Two layers of cells on a higher-priority grid and facing the outer boundary are set as receptor cells to satisfy the third-order discretization of the NS solver. Additionally, two cells that neighbor the in-wall cells, cells of a lower-priority grid and cells inside the domain of a higher-priority grid are also set as the receptor cells.

• 4. The weight values for the overset interpolation are determined by solving the inverse problem based on the Ferguson spline interpolation.

Flow variables of the receptor cell are updated when the boundary condition is set. The forces and moments are integrated on the higher-priority grid to eliminate the overlapped regions on body surfaces. First, the cell face of the lower-priority grid is divided into small faces. Second, the small faces are projected to the cell face of the higher-priority grid using the normal vector of the higher-priority face. Then, the 2D solid angle is calculated and the small faces are determined to be inside or outside of the higher-priority face. If a small face is in the higher-priority face, then the area ratio is set to zero. Finally, the area ratio is integrated on the higher-priority face and then used to integrate the forces and moments on the lower-priority face.

2.3 Roughness model for the low-Reynolds number model

Roughness effects are accounted for by roughness models based on two models. The model proposed by Wilcox [7, 17] is named as model1 and the model proposed by Hellsten [11] is named as model2 hereafter. The non-dimensionalized roughness height is defined using frictional velocity $u_\tau$ and roughness height $h_{\text {r}}$ as follows:

$$\begin{aligned} h_{\text {r}}^{+}=\frac{u_\tau h_{\text {r}}}{\nu }. \end{aligned}$$

(5)

The non-dimensionalized form of Eq. 5 is given as follows:

$$\begin{aligned} h_{\text {r}}^{+}=u_\tau h_{\text {r}} R. \end{aligned}$$

(6)

The non-dimensionalized roughness height is limited to $h_{\text {r}}^+<400$ in model1 and the function $S_{\text {R}}$ is introduced.

$$\begin{aligned} S_{\text {R}}=\left\{ \begin{array}{ll} \left( \frac{200}{\max (h_{\text {r}}^+,h_{\min }^+)} \right) ^2 &{}\quad h_{\text {r}}^+\le 5 \\ \frac{100}{h_{\text {r}}^+}+\left[ \left( \frac{200}{h_{\text {r}}^+} \right) ^2-\frac{100}{h_{\text {r}}^+}\right] {\text {e}}^{5-h_{\text {r}}^+} &{}\quad h_{\text {r}}^+ > 5 \end{array} \right. \end{aligned}$$

(7)

where the new variable $h_{\min }^{+}$ is employed in the above equation based on model2, which is proposed by Hellsten to ensure the function meets the smooth surface condition and $h_{\min }^{+}$ is defined as $h_{\min }^+=9.6y_1^{+0.85}$, which is based on the first computational cell adjacent to the wall surface and non-dimensionalzed height $y_1^{+}$.

The function $S_{\text {R}}$ is introduced in the model2 as follows:

$$\begin{aligned} S_{\text {R}}=\left\{ \begin{array}{ll} \left( \frac{50}{\max (h_{\text {r}}^+,h_{\min }^+)} \right) ^2 &{} h_{\text {r}}^+< 25 \\ \frac{100}{h_{\text {r}}^+} &{} h_{\text {r}}^+ \ge 25 \end{array} \right. \end{aligned}$$

(8)

where $h_{\min }^+=2.4y_1^{+0.85}$ is applied.

The boundary condition of $\omega$ on a wall surface is given as follows:

$$\begin{aligned} \omega =\frac{u_\tau ^2}{\nu }S_{\text {R}}. \end{aligned}$$

(9)

The non-dimensionalized form of Eq. 9 is given as follows:

$$\begin{aligned} \omega =u_\tau ^2 S_{\text {R}} R \end{aligned}$$

(10)

The reference velocity profile proposed by Apsley [9] is used in the present study.

$$\begin{aligned}&u^+=y^+_{v0}+\frac{1}{\kappa }\ln \left( \frac{1+\kappa (y^+-y^+_v)}{1+\kappa (y^+_{v0}-y^+_v)} \right) \end{aligned}$$

(11)

$$\begin{aligned}&y^+_v=\left\{ \begin{array}{ll} C-\frac{1}{\kappa }\ln (\kappa ) &{}\;\; C-\frac{1}{\kappa } \ln (\kappa )\ge 0\\ \frac{1}{\kappa }\left( 1-{\text {e}}^{-\kappa \left( C-\frac{1}{\kappa }\ln (\kappa )\right) }\right) &{}\;\; C-\frac{1}{\kappa }\ln (\kappa )<0\\ \end{array} \right. \end{aligned}$$

(12)

$$\begin{aligned}&C=8-\frac{1}{\kappa } \ln (h_{\text {r}}^++3.152) \end{aligned}$$

(13)

$$\begin{aligned}&y_{v0}^+=\max (y_v^+,0), \end{aligned}$$

(14)

where $\kappa$ is assumed as 0.41.

2.4 Roughness model for the wall function

The shear stress can be obtained with the following equation applying the wall function.

$$\begin{aligned} \tau _w=c_\mu ^{1/4} k_{\text {p}}^{1/2} \frac{\kappa U_{\text {p}}}{\ln \left( \frac{E y^+}{\left( 1+C_{\text {s}} h_{\text {r}}^+\right) } \right) }, \end{aligned}$$

(15)

where $k_{\text {p}}$ is the turbulent kinetic energy at the first point away from a wall surface and the second term is based on the correction formula to account for the roughness effect suggested by Cebeci [12]. $c_{\mu }$ is 0.09, $\hbox {E}=9.8$, $\kappa =0.41$ and $C_{\text {s}}=0.3$, based on the assumption of local equilibrium. $U_{\text {p}}$ is the wall parallel component at the first point away from a wall surface.

The boundary condition of the specific frequency $\omega$ on a wall surface is determined by the condition of the dissipation rate $\epsilon$ as follows:

$$\begin{aligned} \epsilon= & {} \frac{C_\mu ^{3/4} k_{\text {p}}^{3/2}}{\kappa y_{\text {p}}} \end{aligned}$$

(16)

$$\begin{aligned} \omega= & {} \frac{\epsilon }{C_\mu k}, \end{aligned}$$

(17)

where $y_{\text {p}}$ is the distance from the wall surface at the first cell center position.

2.5 Uncertainty analysis

Uncertainty analysis based on the Richardson extrapolation method with the FS method [13] is performed. The grid discretization uncertainty due to the steady condition of the present study is evaluated and three systematic grids with uniform refinement ratio $r_G=\sqrt{2}$ are utilized. Once the solutions $S_3$, $S_2$ and $S_1$ from the coarse grid to the fine grid are obtained, the solution changes are defined as $\epsilon _{12}=S_2-S_1$ and $\epsilon _{23}=S_3-S_2$. The convergence ratio R is $\epsilon _{12}/\epsilon _{23}$ and R takes a monotonic convergence with $0<\epsilon _{12}/\epsilon _{23}<1$. The order of accuracy p and the error $\delta _{\text {RE}}$ are defined as follows:

$$\begin{aligned} p=\frac{\ln (\epsilon _{23}/\epsilon _{12})}{\ln (r_G)}, \quad \delta _{\text {RE}}=S_1-S_0=\frac{\epsilon _{12}}{r_G^p-1}. \end{aligned}$$

(18)

The uncertainty is estimated by the following equation using the variable $P=p/p_{\text {th}}$. The theoretical accuracy $p_{\text {th}}$ is assumed to be $p_{\text {th}}=2$.

$$\begin{aligned} U_{\text {SN}}=\left\{ \begin{array}{ll} (2.45-0.85P)|\delta _{\text {RE}}|, &{}\;\;\; 0<P\le 1 \\ (16.4P-14.8)|\delta _{\text {RE}}|, &{}\;\;\; P>1 \end{array} \right. \end{aligned}$$

(19)

3 Computational results for the 2D flat plate case

A 2D flat plate case is selected as the fundamental test case. The Reynolds number is set as $1.0\times 10^7$, $1.0\times 10^8$ and $1.0\times 10^9$ based on the plate length L as the reference length. The space between the first cell center and wall surface satisfies $y^+\le 1$ in the low-Reynolds number models. Table 1 shows the three resolutions of the computational grids. Figure  1 shows the computational grids, the boundary conditions and the definitions of directions of the divisions. The uniform inflow condition is set at the inflow boundary faces. The distance between the wall surface and the top boundary is 0.1 L. The resistance coefficients are non-dimensionalized by $\rho U^2_0 S$ where S is the plate area and converge to the fourth digit. Therefore, the iterative error can be negligible in comparison with the grid uncertainty $U_{\text {G}}$. The value estimated by the empirical formula [18] is utilized as the reference. The empirical formula [18] can be applied to the case with the roughness and the certain limitation for the roughness height exists as $150< L/h_{\text {r}} < 1.5\times 10^{7}$. If larger roughness height is given to the relation [18], unfortunately, the frictional coefficient becomes lower than the value of the smooth surface condition due to the limit of the application. On the other hand, the present roughness models ensure the function meets the smooth surface condition and the present study focuses on the roughness effect. Consequently, the roughness heights are selected in the following at the range to meet the present purpose.

$$\begin{aligned} C_{\text {D}}=\left( 2.635+0.618 \ln \frac{L}{h_{\text {r}}}\right) ^{-2.57}. \end{aligned}$$

(20)

Table 1 Division number of computational grids

Fig. 1

Computational grids and boundary conditions

Table 2 shows the resistance coefficient with changing non-dimensionalized distance $y^+$ and minimum spacing on the wall at $R=1.0\times 10^7$ obtained using the wall function method. Although the resistance coefficient takes a higher value at the lower range of $y^+$, the influence of the minimum spacing on the wall is relatively small in every case of changing the roughness height. The non-dimensionalized distance $y^+$ is set as 200 for the 2D flat plate cases.

Table 2 Resistance coefficient with changing roughness height and minimum spacing on the wall ($\times 10^{-3}, R=1.0\times 10^7$)

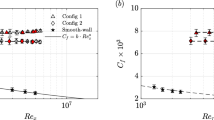
Table 3 shows a comparison of the resistance coefficients of model1 with changing roughness height from $h_{\text {r}}=1\times 10^{-5}$ to $h_{\text {r}}=7.5\times 10^{-5}$ and the grid resolutions at the Reynolds number $R=1.0\times 10^7$. The roughness height is non-dimensionalized by the plate length L The resulting uncertainty is in the range of approximately 1% of the solution of the fine grid, thus the uncertainty takes a small value when using the present computational grids. Although the computed results are slightly higher than the value of the empirical formula, the resistance coefficient increases with the roughness height. Table 3 shows similar results for model2. The uncertainty is less than 1% of the solution of the fine grid. Comparing the results of model1 and model2, the resistance coefficient of model2 becomes larger than that of model1 at $h_{\text {r}}=1\times 10^{-5}$ and the values of model2 are smaller than those of model1 at $2.5\times 10^{-5}$ and $5\times 10^{-5}$ (Table 4). The results of model1 and model2 are the same at $7.5\times 10^{-5}$. Table 5 shows a comparison of the resistance coefficients of the wall function method. Although the resulting uncertainty is in the range from 7 to 17% of the solution of the fine grid, the differences between the three grids are limited to within 1%. The results of the wall function method are from 1 to 3% higher than the results of the low-Reynolds number model2 and the resistance coefficient increases with roughness height, similar to the results of the empirical formula.

Table 3 Resistance coefficient (model1, $\times 10^{-3}, R=1.0\times 10^7$)

Table 4 Resistance coefficient (model2, $\times 10^{-3}, R=1.0\times 10^7$)

Table 5 Resistance coefficient (wall function, $\times 10^{-3}, R=1.0\times 10^7$)

Figure 2 shows the distributions of $u^+$ and $y^+$ with changing roughness height at positions $x/L=0.5$ and $x/L=0.9$ of model2 and the wall function method. The results of model1 are the same as the results of model2, then the results of model1 are omitted. For reference, the correlations based on the smooth surface condition and Eq. 11 with roughness $h_{\text {r}}=7.5\times 10^{-5}$ are also shown in Fig. 2. The velocity distributions change logarithmically with the roughness height in both results, and the first point away from a wall surface of the wall function method is located at $y^+=200$, which is intended. The velocities at positions $x/L=0.5$ and $x/L=0.9$ exhibit the same distribution in the logarithmic region and differences can be found in the outer region.

Fig. 2

Comparison of $y^+$ and $u^+$ at $R=1.0\times 10^7$ (left: low-Reynolds number model, right: wall function)

Table 6 shows the results of model1 at $R=1.0\times 10^8$ with changing non-dimensionalized roughness height from $h_{\text {r}}=1\times 10^{-6}$ to $h_{\text {r}}=7.5\times 10^{-6}$. The uncertainty becomes larger than that at the Reynolds number $R=1.0\times 10^7$ and the resistance coefficient takes a value similar to that of the empirical formula. Table 7 shows the results of model2. The resistance coefficient of model2 exhibits a similar tendency to that in the case of $R=1.0\times 10^7$. Table 8 shows the resistance coefficient of the wall function method. The resulting uncertainty is a small value of approximately 1%. The difference between the value of the wall function method and the value of the empirical formula is approximately 2% and the difference between the value of the wall function method and the value of model2 is within 5%.

Table 6 Resistance coefficient (model1, $\times 10^{-3}, R=1.0\times 10^8$)

Table 7 Resistance coefficient (model2, $\times 10^{-3}, R=1.0\times 10^8$)

Table 8 Resistance coefficient (wall function, $\times 10^{-3}, R=1.0\times 10^8$)

Figure 3 shows the non-dimensionalized velocity distributions of model2 and the wall function method. For reference, the correlation based on Eq. 11 at $h_{\text {r}}=7.5\times 10^{-6}$ is shown. The computed results show a similar distribution to that in the case where $R=1.0\times 10^7$.

Fig. 3

Comparison of $y^+$ and $u^+$ at $R=1.0\times 10^8$ (left: low-Reynolds number model, right: wall function)

Finally, Table 9 shows the results of model1 at $R=1.0\times 10^9$ with changing non-dimensionalized roughness height from $h_{\text {r}}=1\times 10^{-7}$ to $h_{\text {r}}=7.5\times 10^{-7}$. The uncertainty becomes smaller than that at the Reynolds number $R=1.0\times 10^8$. Table 10 shows the results of model2. The resistance coefficient of model2 takes a larger value than the results of model1 in the range up to $h_{\text {r}}=2.5\times 10^{-7}$, then the relation shows the opposite trend. Table 11 shows the resistance of the wall function method. The resulting uncertainty is a small value less than 1%.

Table 9 Resistance coefficient (model1, $\times 10^{-3}, R=1.0\times 10^9$)

Table 10 Resistance coefficient (model2, $\times 10^{-3}, R=1.0\times 10^9$)

Table 11 Resistance coefficient (wall function, $\times 10^{-3}, R=1.0\times 10^9$)

Figure 4 shows the $u^+$ and $y^+$ distributions of model2 and the wall function method. The computed results show a similar distribution to those in the cases $R=1.0\times 10^7$ and $R=1.0\times 10^8$, except that the logarithmic region becomes wider than the results of $R=1.0\times 10^7$ and $R=1.0\times 10^8$. The first point away from a wall surface with the wall function is again located at $y^+=200$, and the distributions follow a curve similar to the results of model2.

Fig. 4

Comparison of $y^+$ and $u^+$ at $R=1.0\times 10^9$(left: low-Reynolds number model, right: wall function)

Figure 5 shows the distributions of $h_{\text {r}}^+$ of model2 and the wall function method on the flat plate for the condition of $h_{\text {r}}=7.5\times 10^{-7}$ and $R=1.0\times 10^9$. $h_{\text {r}}^+$ takes a larger value near the front end of the flat plate, then the value becomes almost constant with $h_{\text {r}}^+=25$ over the surface in both results. The value of model2 is within the model limitation of $h_{\text {r}}^+<400$.

Fig. 5

Non-dimensionalized roughness height on the wall ($h_{\text {r}}=7.5\times 10^{-7}$, $R=1.0\times 10^9$, top:low-Reynolds number model, bottom: wall function)

4 Flows around an actual ship

A numerical study with/without the roughness effect is performed for the case of a tanker hull [14] with flow measurement data for the actual ship. The principal particulars of the ship and propeller are shown in Tables 12 and 13. The computations are carried out under the propulsive condition with the free surface effect. The Reynolds number based on the ship length L is $R=2.43\times 10^9$ and the Froude number is Fn = 0.153. The propulsive condition is achieved using the propeller model [15]. The propeller rotational speed is varied to adjust the propeller thrust to the resistance of the ship. The roughness value is set as $150\times 10^{-6}$ m based on the ITTC recommended procedure [19]. The roughness on the hull and rudder surfaces comes from the paint, welding lines, waving of surfaces due to the structural components, fouling and so on. Unfortunately, the roughness data do not exist on the present case, therefore the typical value for the roughness height is selected from the ITTC recommended procedure.

Table 12 Principal particulars of the ship at full scale

Table 13 Principal particulars of the propeller at full scale

Table 14 shows the division number of the computational grids in each direction. The grids are arranged according to the priority of the overset interpolation. The computational grid consists of the hull grid, the rudder grid and two rectangular grids, including the refinement grid near the aft part of the ship hull and the grid covering the whole domain. The space between the first cell center and wall surface satisfies $y^+\le 1$ for the low-Reynolds number model. The $y^+$ value is set as 100 for the wall function method and the division number KM of the hull grid for the direction of a boundary layer is changed while the other division numbers are maintained. Figure 6 shows a global view of the computational grids with the boundary conditions and the grids near the aft part of the ship.

Table 14 Division numbers of the computational grids

Fig. 6

Computational grid (top: global view, bottom: near aft part of hull)

Figure 7 shows the axial velocity contour with/without the roughness effect at the propeller plane in the towing condition obtained using the low-Reynolds number models. The results based on the three grid are also shown. The region within which the axial velocity is less than 0.3 spreads according to the grid resolution. The axial velocity with the roughness effect becomes lower than that in the smooth surface condition, and the difference between the roughness models is relatively small.

Fig. 7

Axial velocity contour (top: coarse grid, mid: medium grid, bottom: fine grid)

Figures 8 and 9 show comparisons with the measured data for the actual ship. The position is $x/L=0.9553$ from the fore perpendicular position on the port side. The position locates one propeller diameter before the propeller position, and the ship hull so-called as the V-shape which the flow separation becomes smaller than the U-shape in general, especially, at the full scale. Consequently, the present results seem to be less affected by the propeller. The results with the roughness effect of the low-Reynolds number models and wall function method show agreement with the measured data, especially for the range $u/U=0.5$–0.7. The results of the smooth surface condition differ from the measured data in the one contour range. The differences between the results of the low-Reynolds number models and wall function method with changing the grid resolutions are relatively small and the differences between the results of the low-Reynolds number models can be negligible.

Fig. 8

Comparison of axial velocity contours with measured results (low-Reynolds number models top:coarse grid, middle:medium grid, bottom:fine grid)

Fig. 9

Comparison of axial velocity contours with measured results (wall function, top:coarse grid, middle:medium grid, bottom:fine grid)

Figure 10 shows the distribution of the non-dimensionalized roughness height $h_{\text {r}}^+$ on the body surfaces. $h_{\text {r}}^+$ takes small values near the fore and stern ends and $h_{\text {r}}^+$ is distributed on the body surface with a value near 40. The difference between the port and starboard sides is relatively small. The non-dimensionalized roughness height on the rudder surface, which is positioned behind the propeller, takes a higher value than the $h_{\text {r}}^+$ on the hull surface. The difference between the port and starboard sides on the rudder surface can be observed to be affected by the propeller rotational flow. Figure 11 shows the non-dimensionalized shear stress $\tau _{\text {f}}$ distribution on the body surfaces. The $\tau _{\text {f}}$ distribution is similar to the distribution of the non-dimensionalized roughness height, and the shear stress exhibits higher values in the area where $h_{\text {r}}^+$ takes higher values. The distribution of the non-dimensional velocity $u^+$ at the bottom of the hull and at the midship $x/L=0$ and center line $y/L=0$ is shown is Fig. 12. The correlation based on Eq. 11 is also shown in Fig. 12. The difference between the low-Reynolds number models is negligible: thus, the result of model2 is shown in Fig. 12. The non-dimensional velocities obtained with model2 and the wall function method decrease in comparison with the velocities of the smooth surface condition. The non-dimensional velocities with roughness decrease according to the rise of the frictional velocity due to the roughness effect. The $y^+$ value is maintained at 1.0 for model2 and the first point away from a wall surface with the wall function is located at $y^+=100$, which is intended.

Finally, the resistance coefficients are shown in Tables 15, 16 and 17. All the coefficients are non-dimensionalized by $\frac{1}{2}\rho U^2_0 S$ where S is the wetted surface area including the hull and rudder surfaces. The rudder has approximately 6% of the total resistance in all cases. An uncertainty analysis for the total, frictional and pressure resistance coefficients is performed. In here, the iterative error can be negligible comparing with the grid uncertainty as similar with the 2D flat plate cases. The resistance coefficients of the low-Reynolds number models are close for both models and the uncertainties of the total and pressure resistance coefficients take slightly larger values. Although the total and pressure resistance coefficients of the wall function method become smaller than the results of the low-Reynolds number models, the resulting uncertainty values are small. The frictional resistance coefficient of all models and methods are close and the uncertainty values become small. The frictional resistance coefficient based on Eq. 20 is $1.837 \times 10^{-3}$ which is slightly smaller than the values of the present computations. The uncertainties of the total and pressure resistance coefficients of the low-Reynolds number models remain higher and the values decrease with increasing division number of the grid, thus both coefficients are expected to be close to the results of the wall function method. The wall function method yields reasonable results for the velocity contours and resistance coefficients with smaller uncertainties and the method requires smaller division of the computational grid in comparison with the low-Reynolds number models. Consequently, the wall function method is a better method of computation on the actual ship scale with the roughness effect.

Fig. 10

Non-dimensional roughness on the hull and rudder surfaces

Fig. 11

Non-dimensional shear stress on the hull and rudder surfaces

Fig. 12

Comparison of $y^+$ and $u^+$ at $x/L=0$ and $y/L=0$

Table 15 Comparison of resistance coefficients (model1)

Table 16 Comparison of resistance coefficients (model2)

Table 17 Comparison of resistance coefficients (wall function)

5 Conclusions

A numerical study of the roughness effect at the actual ship scale is performed. Roughness models of the low-Reynolds number turbulence model are developed. The models are based on the non-dimensionalized roughness height and the boundary condition of the frequency $\omega$ is corrected using the function for the roughness effect. A wall function to account for the roughness effect is also developed based on the assumption of local equilibrium. The low-Reynolds number models and wall function method are examined with respect to the computation of the 2D flat plate case at the actual ship scale. The resistance coefficients of the low-Reynolds number models increase with the roughness height similar to the value of the empirical formula. An uncertainty analysis is performed using the FS method and the division numbers of the three different computational grids increase with the uniform refinement ratio $\sqrt{2}$. The uncertainties decrease for high Reynolds numbers and the differences between the computational grids are limited to within 1%. The velocity profiles based on $y^+$ and $u^+$ are compared for changing roughness height. The velocity distributions mainly change logarithmically with the roughness height. The influence of the minimum spacing on the wall of the wall function method is relatively small in every case with changing roughness height. The wall function method also works properly with changing roughness height and Reynolds number. The uncertainties in the resistance coefficient of the wall function method reach larger values than those of the low-Reynolds number models at the Reynolds number $1.0\times 10^{7}$ and the uncertainties become smaller at higher Reynolds numbers. $y^+$, which is the first point away from a wall surface of the wall function method, is precisely located at the intended point.

The roughness models and wall function method are applied to the computation of flows around an actual ship, which has the flow measurement data from an actual sea test. The roughness value is given as $150\times 10^{-6}$ m based on the ITTC recommended procedure. The self-propelled condition with the free surface effect is achieved by the propeller model and the single phase level-set method. The overset grid method is applied and three computational grids for the hull with different division numbers are prepared to examine the effect of the grid resolution on the flows around the hull. Although room for the further study including the equivalent sand grain roughness remained, the results for the roughness effect using the typical value based on the ITTC recommended procedure clearly exhibited an agreement with the measured data from the actual sea test compared with the smooth surface condition. The difference between the three computational grids is relatively small with respect to the velocity contours and the distinction of the low-Reynolds number models can be negligible. Detailed analyses, which include the distributions of the non-dimensionalized roughness height $h_{\text {r}}^+$ and shear stress $\tau _{\text {f}}$, are carried out. The relation between $h_{\text {r}}^+$ and $\tau _{\text {f}}$ is revealed. Finally, an uncertainty analysis is performed with respect to the resistance coefficients. The uncertainties in the total and pressure resistance coefficients of the low-Reynolds number models take slightly larger values compared with the results of the wall function method. Consequently, the wall function method is a better method for computation at the actual ship scale with the roughness effect.