1 Introduction

For ships navigating across large oceans considerations about the present weather conditions are essential for safe and efficient operations. The highly dynamic environment exposes the ship to loads from wind, waves and currents. To ensure safe passage, arrival on time, minimized operational costs and minimal environmental impact it is important that the route of the ship is optimized with regard to the weather.

Numerical route optimization, or weather routing, is proven to be successful in reducing travel times in ocean yacht racing, in minimizing operational costs [1, 2] and in reducing encountered wave heights [3]. The two main problem areas in the field of numerical weather routing are the modelling of added resistance due to wind and waves and the reliability of the weather forecasts on which the optimization is based. This paper deals with the latter problem by investigating the use of ensemble weather forecasts.

The standard weather forecast, here referred to as a deterministic forecast, is typically computed by first calculating the current state of the weather from observational data collected by weather stations and satellites. The calculated representation of the weather is called the analysis. The analysis then serves as the initial condition from which a numerical model of the atmosphere is integrated in time. The analysis can also refer to a set of consecutive analysis steps used as a record for the true development of the weather. In this paper the term ’verified weather’ is used instead to avoid confusion. The progression in time of the deterministic forecast is naturally strongly dependent on the initial condition (the analysis).

As an alternative, or a complement, to the deterministic forecast one can produce what is called an ensemble forecast. The ensemble forecast is a large set of deterministic forecasts that are generated by performing the same integration in time but using slightly perturbed initial conditions, resulting in a set of forecasts that thus evolve differently over time. The individual forecasts in the ensemble are called ensemble members, and the ensemble member that is derived from the unperturbed initial value is called the control member. All of the forecasts in the ensemble are typically considered equally likely to realise. The spread of the ensemble members is called the ensemble spread and can be used to asses how stable the current weather conditions are and thus indicate the uncertainty of the deterministic forecast. A large spread at a given time in the forecast indicates high uncertainty and vice versa. A good introduction to ensemble weather forecasts is provided by the National Oceanic and Atmospheric Administration (NOAA) online [4].

Several approaches have been proposed for using ensemble weather forecasts for route optimization. In [1], Saetra provided important information about the relationship between ensemble spread and routing performance, confirming that the application of ensemble forecasts to weather routing has merit. Hoffschildt [5] and Saetra [1] evaluated several approaches to route optimization using ensemble weather forecasts; however, none of those performed better than methods based on the deterministic forecast.

Allsopp, Philpott and Mason [6, 7] presented a method based on a dynamic programming approach to solve a minimum time routing problem under consideration of uncertainties. The method is similar to the Bellman method [5] but expands the state space to include the weather scenario. The weather scenarios are part of a branching tree of scenarios with specified probabilities associated with each branch. The method is implemented for a yacht racing problem where the only objective is time, but the method could be expanded to more complicated problems. Treby [8] used a different dynamic program to solve the same problem.

Harries et al. [9] introduced a novel approach to route optimization that uses a genetic algorithm to generate Pareto optimal solutions to a multi-objective routing problem. In addition to varying the route, the velocity profile along the route was also varied, making the problem more complex. Hinnenthal [10], together with Saetra [11] and Clauss [12], later expanded this method to make use of ensemble forecasts by introducing a concept of Robustness (see Sect. 3.2) to evaluate the sensitivity of the routes to changes in the weather.

The ensemble forecast is a relatively new approach to weather forecasting, first being put to use in the 1990s; therefore, the potential applications and benefits to weather routing have not yet been fully explored. Although the papers referenced here provide evaluations of several methods, comparisons of the performance in realised weather of routes computed using deterministic and ensemble weather forecasts are performed only in [1] and [5].

1.1 The contribution of this paper

This paper compares the results of using a standard, or deterministic, weather forecast and an ensemble weather forecast for numerical weather routing. The comparison focuses on two important performance factors as objectives for the optimization: arrival on time and fuel consumption. Routing using the ensemble forecast implements the robustness measure, introduced in [11], to ensure that the optimized routes are not sensitive to the weather developing differently than predicted by the deterministic weather forecast. The performance of the routes, optimized using the deterministic and ensemble weather forecasts, respectively, is evaluated in the verified weather, i.e. the weather that realised and not the forecasted weather. The scope of the evaluation presented in this paper is to assess the qualitative differences between using deterministic and ensemble weather forecasts for numerical weather routing. Further, this comparison only investigates one possible method of using ensemble weather forecasts for weather routing. To perform the comparison a route optimization method is implemented that can handle both types of forecasts. The optimization method is presented in some detail for completeness. The continuation of this paper is divided in to the following parts: first, an overview of the methodology employed for the comparison performed in this paper is given. Second, the optimization algorithm used for weather routing using both deterministic and ensemble forecasts is presented. Third, the test cases used for this paper are detailed along with some additional implementation details. Fourth, results from the comparison are presented and discussed. Fifth, the authors present their conclusions and thoughts on future work.

2 Methodology

To compare routing using deterministic and ensemble forecasts the following methodology is used. Also see Fig. 1:

  • A problem is formulated in terms of point of departure, point of destination, arrival time and ship characteristics. This is referred to as a ‘case’.

  • A set of Pareto optimal (see Sect. 3.1) routes is computed using the deterministic weather forecast as input to the optimization algorithm.

  • A second set of Pareto optimal routes is computed using the ensemble weather forecast as input to the optimization algorithm.

  • The realised performance of both routes is re-evaluated using the verified weather. That is, a journey along the route is simulated using the realised weather and the realised performance is calculated.

  • The results of the two different routings are compared with respect to late arrival and fuel consumption.

Fig. 1
figure 1

Structure of the comparison of weather routing using deterministic and ensemble weather forecasts

Full size image

Routing using the deterministic and ensemble forecast is performed using the same optimization algorithm. The difference is that the additional data available when optimizing with the ensemble forecast allows for the introduction of a new objective, namely robustness. The robustness objective, how it is computed and other details about the optimization algorithm, are presented below.

The verified weather is constructed from the initial time steps of the control members of the ensemble forecasts issued each day for the duration of the voyage. This can be considered to be a close approximation of the weather which would be observed during the voyage. By re-evaluating the routes in the verified weather the realised performance of the different routes from the ensemble and deterministic routings can be determined.

3 Optimization

The optimization method used here is a dynamic programming algorithm that finds the Pareto optimal paths through a graph under constraints. For an introduction to dynamic programming methods and shortest path problems see [13, 14] and for a treatment of dynamic programming and route optimization see [15]. For a thorough presentation of multi criterion shortest path algorithms see [16–18] and for a presentation of resource constrained shortest path problems see [19]. Although dynamic programming methods have been used for route optimization of ships for a long time the use of multi-objective optimization methods does not appear to be common. In [20] a method similar to the one presented here is introduced, but there are some important differences. Most notably the algorithm presented in the present paper stores only Pareto optimal solutions as opposed to the floating state technique used in [20]. Further, the method presented in this paper is adapted for use with ensemble weather forecasts.

The handling of constraints has been left out of the description of the algorithm below for brevity. The only constraints considered in this paper are arrival on time and maximum engine power output (an additional constraint is imposed for routing using ensemble weather forecasts, see below). The arrival on time constraint is handled by treating travel time as a Resource by the method described in [19] and the achievable engine power constraint is handled by the performance calculations, see Sect. 3.3. As dynamic programming methods are common for solving optimal path problems and widely known, the presentation here will be in relation to the weather routing problem with focus on the adaptation for use with ensemble weather forecasts. The rest of this section is divided into five parts. First, an introduction is given to the concept of Pareto optimality. Second, the robustness concept is introduced and discussed. Third, the concept of a performance model is introduced briefly. Fourth, the dynamic programming algorithm is presented. Finally, the adaptation of the optimization method for use with ensemble weather forecasts is presented.

3.1 Pareto optimality

The concept of Pareto optimality originates from the field of economics and game theory. It is named after Vilfredo Pareto and will here be explained shortly.

Let \(\bar{f}(\bar{x}) = (f_1(\bar{x}), f_2(\bar{x}), \ldots f_n(\bar{x}))\) be the function to optimize, for example by minimization of all of the functions, \(\displaystyle \min _{\bar{x}} f_i(\bar{x})\), for all \(i\). However it is not clear what constitutes an optimal solution since, presumably, not all functions \(f_i(\bar{x})\) will have a global minimum for the same value of \(\bar{x}\). One commonly used approach is to create a weighted sum of the different functions \(f_i\). This allows for the computation of one solution which is optimal for the given set of weights, but the problem of specifying the weights remains. An alternative approach is to generate a set of optimal solutions, the Pareto optimal solutions.

To define Pareto optimality the concept called dominance is introduced. Let \(\bar{x}'\) and \(\bar{x}''\) be two different candidate solutions to the optimization problem. Then the solution \(\bar{x}'\) dominates solution \(\bar{x}''\) if and only if the following holds:

$$\begin{aligned} (\forall i : f_i(\bar{x}^{\prime }) \le f_i(\bar{x}^{\prime \prime })) \wedge (\exists i : f_i(\bar{x}^{\prime }) < f_i(\bar{x}^{\prime \prime })). \end{aligned}$$

That is, the solution \(\bar{x}'\) is at least as good as \(\bar{x}''\) for all functions \(f_i\), and strictly better for at least one function \(f_j\). A solution is Pareto optimal if no other feasible solution dominates it. Of course, the sign of the inequality in the definition of dominance depends on whether maximization or minimization of the objective \(f_i(\bar{x})\) is desired. The set of all Pareto optimal solutions is called the Pareto frontier.

3.2 Robustness

Robustness, in the field of optimization, is a property of a solution to an optimization problem which describes how resistant the solution is to errors in the data used in the optimization process. If the constraints, or other properties of the problem, used for the optimization are changed slightly the proposed solution may no longer be the optimal one, or even a feasible solution. Methods for determining the robustness of a solution often use random perturbations of some of the values assumed for the problem which are considered to be representative of the likely error. In this paper a similar approach, introduced by Hinnenthal and Saetra in [11], is used. The ensemble weather forecast is used to represent all possible outcomes of the weather and is used to compute the robustness of solutions. This method is preferable to random variations of the deterministic weather forecast since it computes the robustness using only possible developments of the weather. The computation of the robustness of a solution is simple. The performance of a solution is evaluated, using the same performance model used by the optimization routine, for all of the ensemble members. The constraints imposed during the optimization are also evaluated using all the different ensemble members. The robustness evaluation results in a set of binary values, one for each ensemble member, which indicates whether the proposed solution is feasible in that forecast or not. From each ensemble member, in which the solution is feasible, there is also information about the performance in terms of fuel consumption, which can be used to compute the average expected fuel consumption. The value of this robustness measure has not been thoroughly studied, but intuitively it is a reasonable measure. If we assume that one of the ensemble members will be equal to the true evolution of the weather, it is reasonable to state that a route with high robustness will be more likely to remain feasible in the realised weather than one with low robustness. The robustness of a route can be viewed as a measure of safety, if proper safety constraints are imposed, but it is more useful as a measure of how likely it is that a route has to be significantly altered, in course or speed, due to the development of the weather along the route.

This method for calculating the robustness can be used to determine the robustness of a route optimized using the deterministic forecast if the ensemble forecast is available. If the optimization is instead performed using the ensemble forecast, the robustness of the solution may be included as an objective of the optimization and it is thus possible to ensure solutions which have good performance and are robust with regard to changes in the weather. This is the method used for weather routing using the ensemble forecast in this paper.

3.3 Performance model

The optimization of routes is based on performance predictions based on forecasted weather and ship characteristics. These calculations are handled by a performance model which calculates the resistance acting on the vessel from information about wind, waves and the ship speed. The calculated resistance value is used to determine engine load and fuel consumption. More information on the specific performance model used in this paper is presented below, in Sect. 4.

3.4 The basic algorithm

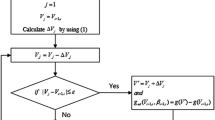
The algorithm resembles the classic Bellman–Ford–Moore shortest path algorithm [21–23] and other label setting algorithms. These algorithms work by assigning and correcting labels for each of the vertices in the graph, an example graph used by the optimization method can be seen in Fig. 3. Unlike single-objective label setting algorithms the presented algorithm saves all the Pareto optimal labels for each vertex instead of just one label. This collection of labels is referred to as the Pareto optimal set of labels. A label is a solution to a sub-problem, namely the routing problem from the start vertex to the vertex associated with the label, and contains a set of values for the different objectives upon reaching the vertex, e.g. time of arrival and fuel consumption. The label also contains information about which vertex preceded the current vertex so that one can reconstruct the entire route from the labels of the goal vertex when the algorithm has finished. The presented algorithm only works for directed acyclic graphs.

Below a step-by-step description of the algorithm follows. The description is quite general and is applicable for any number of objectives.

  1. 1.

    Initiation.

    1. 1.1.

      Generate an appropriate graph covering the area of interest, with one vertex at the point of departure and one at the destination.

    2. 1.2.

      Set the Pareto optimal set of labels to empty for each vertex.

    3. 1.3.

      Designate the vertex corresponding to the point of departure to Current.

    4. 1.4.

      Add a label corresponding to the initial conditions to the Pareto optimal set of labels of Current.

  2. 2.

    Evaluate edges from Current to neighbours.

    1. 2.1.

      Do the following for each neighbour of Current and each label in the Pareto optimal set of labels of Current.

      1. 2.1.1.

        Create a candidate label by evaluating the journey between the Current vertex and the selected neighbour, starting at the time specified in the selected label, using the ship performance model.

      2. 2.1.2.

        Add this candidate label to the Pareto optimal set of labels of the neighbour if the candidate label is not dominated in that set. If the candidate label is added to the set remove all labels in the set that are dominated by it, thus maintaining a Pareto optimal set.

  3. 3.

    Select next vertex for evaluation.

    1. 3.1.

      Select one of the vertices in the graph which has had all edges leading to it evaluated already.

    2. 3.2.

      Set this vertex to Current.

    3. 3.3.

      If Current is the vertex corresponding to the destination (the goal vertex) go to 4, else go to 2.

  4. 4.

    Generate the Pareto optimal solutions to the routing problem from the Pareto optimal labels of Current.

Steps 2 and 3 above form the recursive part of the algorithm and are illustrated in Fig. 2 where two edges leading to the same vertex are evaluated and a Pareto optimal set of labels for that vertex is established. In (a) the edges leading to vertices A and B have already been evaluated and a Pareto optimal set of labels (labels marked by ‘o’) exist for both. In (b) the algorithm selects A as the next vertex to be evaluated and proceeds to evaluate the travel between A and C (indicated by the black edge) starting from each of the conditions in the labels of A. This generates a set of candidate labels (candidate labels marked by ‘x’) of C. All candidates are kept since none is dominated by any other and the initial set of labels of C was empty [these labels can be seen marked with an ‘o’ in (c)]. In (c) B is selected as the Current vertex and the algorithm proceeds to evaluate the edge between B and C and a new set of candidate labels of C are found. This time one of the candidates is dominated by one of the existing labels of C (dominated labels marked as red) and is, therefore, not added to the Pareto optimal set of labels of C. Also, one of the existing labels of C is dominated by one of the candidate labels and is, therefore, removed from the Pareto optimal set of labels. Now, in (d), remains only the final Pareto optimal set of labels of C, since all edges leading to C have been evaluated and no changes can be made. All edges leading away from C (not shown in the illustration) may now be evaluated, i.e. C may be set as Current by the algorithm.

Since edge costs are time dependent and fuel consumption rates depend on the speed at which the vessel travels it is important to allow for variations in velocity during the optimization. To include variation of velocity each evaluation along an edge is performed for a discrete set of velocities, each evaluation generating a candidate label.

Fig. 2
figure 2

Illustration of the recursive part of the optimization algorithm for a problem with two objectives. Detailed description may be found in Sect. 3.4 a Initial state. b Evaluation of edge AC. c Evaluation of edge BC. d Final state

Full size image

3.5 Adaptation for use with ensemble forecasts

The adaptation of the presented optimization algorithm for use with ensemble forecasts is relatively straightforward. The Robustness, as introduced in [11] and defined above, is included as an objective which is to be maximized. To evaluate the robustness of a candidate label the voyage along the edge is simulated in all ensemble members separately. In some members the voyage will be infeasible due to some constraint and the number of members in which the voyage is feasible is the Robustness of the candidate label. The fuel consumption of the route may be calculated as the arithmetic mean of the fuel consumption over the feasible members. Each label stores which ensemble members it was feasible in and when it is evaluated for travel to the next vertex only those members in which it was previously feasible are used to determine robustness and fuel consumption of the resulting candidate label. Thus the robustness of a candidate label will be less than or equal to the robustness of the label from which it originated.

With the adaptations above some special care has to be taken when determining the Pareto optimality of a label; a simple greater than or equal to comparison of the robustness objective may cause the algorithm to miss some Pareto optimal solutions. This can easily be demonstrated. Consider two different labels at the same vertex. They both have the same arrival time and fuel consumption, but one has a higher robustness. Since one clearly dominates the other only the solution with the higher robustness should be kept. However, this may not be the label which will result in the most robust solution, since the two labels may be feasible in different ensemble members. For example, label A is feasible in members 1–30 and label B is feasible in members 31–50. Label A is clearly more robust, but as the evaluation is continued it might be that members 1–30 forecast severe weather for the continuation of the journey and members 31–50 forecast calm weather. Then it would have been better to keep label B for further evaluation. This also affects other objectives, such as the average fuel consumption over the feasible members; consider again two labels (A and B) of the same vertex. They have the same arrival time and the same robustness, A being feasible in members 1–25 and B in members 26–50, they do, however, have different fuel consumption. If label A has a lower fuel consumption than label B, then label A clearly dominates label B. However, if the weather predicted by members 26–50 forecast calmer weather it would have been better to keep label B in the set of labels.

To address this issue a change in the domination criterion used for the ensemble routing is required. Instead of doing a simple greater than or equal to comparison for the robustness objective the set of ensemble members in which the labels are feasible is used to determine domination (together with the normal greater than or equal to condition of the other objectives). If the set of feasible members of one label is a subset to the feasible members of the other label, then, and only then is the robustness of the first label considered to be less than that of the second. For the final vertex the normal greater than or equal to criterion can be used since the route ends there. This method of comparing robustness results in more labels being kept for each vertex in the graph; the set of labels will contain labels that are not Pareto optimal solutions to the sub-problem as defined above. However, the additional labels are potential candidates to the set of Pareto optimal solutions to the full routing problem. Since more labels are kept for each vertex the computation time is increased. Introducing a lower limit for the robustness will help to keep the computation time within reasonable limits. Such a limit will not affect the usefulness of the optimization as there will always be some lower limit of robustness desired by the decision maker.

The above solution is equivalent to replacing the robustness objective with a binary feasibility objective for each of the ensemble members and using the standard Pareto-optimality definition alongside a constraint on the sum over those objectives to ensure a minimal robustness level. The reason for using the robustness objective instead is that it is more intuitive and has been used previously in, for example, [10].

4 Test cases and test details

To perform the comparison of deterministic and ensemble weather routing the presented optimization algorithm is implemented in Matlab® using a ship performance model, provided by Seaware AB. The performance model is based on Holtrop-Mennen [24] for calm water resistance, the approximative methods presented in [25] for the added resistance from waves and a propulsion model of the engine and propeller system developed in-house. The performance model considers wind speed and direction, and the significant height, direction and mean period of wind waves and swell when evaluating the added resistance. The ship modelled in the tests is a panamax container carrier with a design displacement of 68,000 tons, the length between perpendiculars is 275 m and the design speed of the vessel is 18 knots. As this study only focuses on the qualitative difference between deterministic and ensemble routing the accuracy of the performance model is of limited importance as long as the performance characteristics that are modelled by the performance model are representative of some vessel of similar size and engine power.

To compare the results from deterministic routing and ensemble routing several test cases are considered. For each test case two route optimizations are performed: one with the deterministic weather forecast and one with the ensemble weather forecast. Then the realised performance of the routes from both routings is evaluated in the verified weather. For this re-evaluation in the verified weather the speed profile along the route, provided by the routing solution, is not followed strictly; if the required engine power is not achievable, due to greater than predicted resistance, the speed will be reduced until the voyage is possible. If a reduction in speed is needed the speed profile for the remainder of the route is updated to attempt to compensate for the delay. The adjustment in speed is proportional to the current lateness. That is, the speed for all remaining legs of the route is increased by a factor proportional to the current deviation from the predicted arrival at the current location. The flexibility of the speed used during the re-evaluation in the verified weather is included to more accurately capture the realistic operation of a vessel travelling with a set arrival time.

No re-routing is performed during the re-evaluation of the voyage in the verified weather and the ship is forced to sail along the route dictated by the routing procedure. This is of course not representative of real-life operations, but it is deemed sufficient for this qualitative study.

All weather forecasts used for this study are products of the European Centre for Medium Ranged Weather Forecasts, ECMWF, and contain 51 ensemble members including the control. For the evaluation performed in this paper the control member of the ensemble forecast is used for the deterministic routing instead of the operational forecast, and the verified weather is constructed from the control members of consecutive forecasts.

No explicit modelling of safety or comfort is performed for the tests presented in this paper and the only constraints on the optimization are arrival before the latest allowed arrival time, 180 h after departure, and achievable engine power output. For the ensemble routing a minimum robustness of 80 % is used as an additional constraint. That is, routes must be feasible in at least 80 % of the ensemble members. The ensemble forecasts used in this paper contain 51 members but as the control member is used as a deterministic reference only 50 members are used for the ensemble routing, which translates to a minimum robustness of 40 members. The test cases used are listed in Table 1 and the graph used for the optimization is illustrated in Fig. 3. The speeds allowed during the optimization are 70, 80, 90, 100 and 110 % of the design speed.

Table 1 Definition of test cases \(T_{\rm max}\) is the latest allowed time of arrival in hours after departure
Full size table
Fig. 3
figure 3

The graph used by the optimization algorithm for test cases 3–8, the graph used for test cases 1 and 2 has a similar structure but is located further south. The number of possible different geographical routes through the graph is roughly 45,000 and the number of different possible routes including a choice of five different speeds for each edge is roughly \(10^{13}\). The map projection is equidistant conic

Full size image

5 Results

The results of the comparison between deterministic and ensemble routing are broken down into three parts. First, the routing results and the re-evaluated results from both deterministic and ensemble routing are presented for two representative test cases. Second, an evaluation of the risk of late arrival for all test cases is presented. Third, an evaluation of fuel consumption prediction error is presented for all test cases.

5.1 Routing results

The test cases are divided into two groups: the first four use weather data from winter months and the last four use weather data from summer months. The weather for test cases 1–4 is generally harsher than the weather for test cases 5–8. The difference between the deterministic and ensemble routing results is small for test cases 5–8 as the weather is relatively stable and the ensemble members do not diverge drastically or predict harsh weather. For test cases 1–4 the difference is much more pronounced, as is the difference between predicted results and re-evaluated results. In Fig. 4 the predicted performance for routes from both deterministic and ensemble routing, as well as the re-evaluated performance of those routes, is presented for two representative test cases.

The predicted performance of the solutions calculated by the deterministic routing is generally better than the predicted performance of the solutions calculated by the ensemble routing. The re-evaluated performance of the routes indicates no such clear advantage, except that the routes which achieve the fastest arrival times are from the deterministic routing. Since the ensemble routing is constrained to solutions with a robustness greater than or equal to 40 it will generally not find solutions with as fast arrival times as the deterministic routing.

The ensemble solutions constitute a three-dimensional Pareto front, with the additional objective being robustness, which produces a ‘cloud’ of solutions in the 2D-plots in Fig. 4. Ensemble solutions that appear to be dominated by other ensemble solutions are in fact more robust and thus not dominated. When the solutions are re-evaluated in the verified weather the results are no longer a Pareto front as the values for fuel consumption and arrival time changes for each solution.

Fig. 4
figure 4

Routing results and re-evaluation results for test cases 3 and 8. Each data point is the result from one of the routes from the deterministic or ensemble routings

Full size image

5.2 Arrival on time

In Figs. 5 and 6, histograms of the lateness of routes from both deterministic and ensemble routings are presented for all the test cases. Here lateness is defined as the difference between predicted arrival time and achieved arrival time for a route. In Table 2 the arithmetic mean and the median of the lateness of the deterministic and ensemble routing solutions are presented.

The results clearly show that the ensemble routing solutions have a significantly lower risk of arriving late for all test cases. The histograms show that the weight of the distribution for the ensemble solution is shifted to the left (lower lateness) compared to the distribution for the deterministic solution. For test cases 7 and 8, where the overall lateness is quite small, there are still solutions from the deterministic routing with a significant lateness, up to 5 hours. By looking at the routing and re-evaluation results in Fig. 4 it is clear that the minimum time routes from the deterministic routing are too optimistic, when re-evaluated in the verified weather the routes achieve a significantly later arrival time. The mean and median lateness presented in Table 2 quantifies the difference between deterministic and ensemble routing and shows that ensemble routing performs better for all test cases and that for at least test cases 3 and 4 the difference is very significant. Since the deterministic routing is not limited by the robustness constraint it will in general generate more routes with earlier arrival times and, as discussed above, these routes are likely to be too optimistic. However, these routes are not the only ones to contribute to the difference in the risk of arriving late between the set of solutions from the two routings. Test case 3 serves as a good example to illustrate this; the difference in lateness is significant and the fastest route from the deterministic routing estimates arrival times as early as 157 h after departure, whereas the fastest solutions from the ensemble routing estimates arrival at 168 h after departure (see Fig. 4). Intuitively it is this difference that should account for most of the difference in lateness; however, if only solutions with arrival times between 180 and 170 h after departure are considered (see Fig. 7) there is still a significant difference in lateness. For the ensemble solutions the mean and median lateness for this restricted set of solutions is roughly the same. For the deterministic solutions the mean and median lateness are higher, increased from 7.5 to 7.8 and from 7.9 to 9.7 h, respectively. Most notably the routes that are most late are among these ‘slower’ routes: two routes from the deterministic routing which predict arrival around 178 h after departure and achieve an arrival time around 192 h after departure in the verified weather, a lateness of roughly 14 h.

Fig. 5
figure 5

Histograms comparing lateness of solutions from ensemble and deterministic routing results re-evaluated in verified weather. Test cases 1–4. Note that the scaling of the horizontal axis is different for all plots

Full size image
Table 2 Arithmetic mean and median value of lateness for deterministic and ensemble routing solutions
Full size table
Fig. 6
figure 6

Histograms comparing lateness of solutions from ensemble and deterministic routing results re-evaluated in verified weather. Test cases 5–8. Note that the scaling of the horizontal axis is different for all plots

Full size image
Fig. 7
figure 7

Histogram of lateness for test case 3. Only solutions with estimated arrival times between 170 and 180 hours after departure are included

Full size image

5.3 Fuel consumption

In Table 3 the mean absolute percentage error (MAPE) of the fuel consumption prediction is presented for all test cases. The percentage error is calculated as the difference between predicted fuel consumption and fuel consumption in the verified weather divided by the fuel consumption in the verified weather. The MAPE is the arithmetic mean of the absolute values of the percentage errors. In Table 4 the same values are presented but only for routes that achieved their estimated arrival time. As the speed correction used during the re-evaluation is somewhat simplistic no, or very few, routes achieve their arrival time perfectly for some of the test cases, and a small lateness (1 h) is tolerated for this comparison.

The results presented in Tables 3 and 4 indicate that the ensemble routing method is slightly better at estimating the fuel consumption of a voyage. The likely cause of the difference in fuel consumption prediction error is that the average fuel consumption over several ensemble members, in which the route is feasible, is a better estimator than using only the deterministic forecast. However, there is reason to be cautious about such conclusions as the errors are calculated for different sets of routes for the deterministic and ensemble estimations.

Table 3 Mean absolute percentage error for fuel consumption prediction
Full size table
Table 4 Mean absolute percentage error for fuel consumption prediction of routes that achieved an arrival time no more than 1 h greater than predicted. No solutions achieved requisite arrival time for test case 3
Full size table

5.4 Error sources

The following discussion is intended to highlight some of the more important sources of uncertainty and their effect on the results but is not a complete list of possible error sources.

The same resolution is used in both the deterministic and ensemble routing to avoid different resolutions affecting the results of the comparison. It can be argued that the deterministic routing should be allowed a higher resolution since it requires less time to compute the solutions, but since the focus here is on the overall potential benefits of ensemble routing this is not considered.

As no modelling of safety or comfort is performed for this study the only constraints that affect the optimization are arrival on time and achievable engine power. This is likely to bias the results toward the deterministic routing as robustness will be less important, although to what extent is not investigated. For example, if a comfort constraint related to slamming is introduced, there will likely be more cases where the ship is forced to slow down to conform to the constraint for routes determined by the deterministic routing than the ensemble routing. It is important that future studies consider more constraints than the ones used in this paper.

The test cases used for this paper treat voyages that take approximately one week to complete. During the evaluation of the voyage in the verified weather no re-routing is performed, only speed adjustments due to constraints on the power output of the engine. This is not a realistic representation of how weather routing is used, especially for voyages through rough weather, and will likely bias the results in favour of ensemble routing.

6 Conclusion and future work

The goal of this paper was to explore the potential of using ensemble weather forecasts for weather routing of ocean going vessels. To achieve this goal a method for route optimization is developed with the necessary adaptations for ensemble routing. The method is based on a dynamic programming algorithm and computes Pareto optimal solutions to a multi-objective routing problem. The method is adapted for use with ensemble weather forecasts by adding Robustness as an additional objective and using the average of the fuel consumption predicted in several ensemble members as an estimator for fuel consumption instead of using only the fuel consumption predicted using the deterministic forecast.

Eight test cases are used to study the difference in performance between routes from deterministic and ensemble weather routing. The routes calculated by the deterministic and ensemble routings are re-evaluated in verified weather to estimate the realised performance of the routes. During the re-evaluation the speed of a route is adapted to ensure that the engine power constraint is not violated and to attempt to compensate for any potential delay.

Two performance factors were considered when comparing the routes from the deterministic and ensemble routings, risk of late arrival and error in fuel consumption prediction. For both these measures the ensemble routing performs better in all test cases, and for two of the test cases the risk of late arrival is significantly lower for the routes from the ensemble routing. The potential of ensemble routing techniques to reduce the risk of late arrival is concluded to be very promising, as arrival on time is important for planning purposes and can affect the operational costs significantly.

For future exploration of the possible benefits of ensemble routing it is important to include re-routing during the voyage. Also it is important to introduce a more complete set of constraints on the operation of the vessel, including safety and comfort levels. Future studies should also consider several different vessels as sensitivity to weather varies widely depending on the size and type of the vessel.

As performing route optimization using the entire ensemble forecast may be too costly in terms of computational effort an exploration of alternative methods of utilizing the data from ensemble forecasts for weather routing is interesting. One such method could be post processing of routing results from a deterministic routing by re-evaluating the performance of the routes in the ensemble forecast. A post-processing using the ensemble forecast will require significantly less computational effort than routing using the full ensemble and may provide the decision maker with important information about the performance and risk associated with different routes.

Another interesting area of research is to study the possible application of stochastic programming techniques to weather routing using ensemble weather forecasts, in particular studying two-stage (or multi-stage) optimization based on clustered ensemble weather forecasts. This is closely linked to the work of Allsopp, Philpott and Mason [6, 7]. The availability of clustered sea weather forecasts is at the time limited, but the possible benefits and relative simplicity of these methods make them an interesting area of study.