Taxation, capital accumulation, environment and unemployment in an efficiency wage model

Abstract

We develop an aggregate growth model with environmental pollution and unemployment equilibrium to be explained by efficiency wage hypothesis. Environmental quality is degraded due to emissions generated from production and is improved by abatement expenditure. The efficiency of a worker varies positively with its wage, unemployment rate and environmental quality. In the short-run equilibrium, an exogenous improvement in environmental quality given the capital stock lowers efficiency wage rate and unemployment rate but raises the rental rate on capital and the level of output; and an exogenous increase in capital stock given the environmental quality raises efficiency wage rate and level of output but lowers rental rate on capital and unemployment rate. Capital stock and environmental quality accumulate over time. A proportional tax is imposed on the rental income on capital to finance the abatement expenditure; and households’ savings is invested. An increase in the tax rate raises the capital stock, national income and the environmental quality but lowers the unemployment rate in the long run equilibrium.

1 Introduction

There are various alternative theories to explain unemployment in a macro economic model; and ‘Efficiency Wage hypothesis’ is one of them. According to the traditional version of this efficiency wage hypothesis, the efficiency of a worker varies positively with her wage rate and the unemployment rate in the labour market. A higher wage rate motivates the labourer to work hard. A higher unemployment rate lowers the marginal disutility of work effort in the presence of a threat of firing; and this, in turn, makes the labourer more disciplined and hardworking. Many models in the existing literature introduce unemployment problem using efficiency wage framework.¹ A few of them are intertemporal in nature; and attempts to explain the interaction between economic growth and unemployment.² However, majority of these existing efficiency wage models do not consider the problem of environmental pollution. Introducing efficiency wage hypothesis into a dynamic model with environmental pollution and capital accumulation, one can easily study the interaction among capital accumulation, unemployment and environment; and can also analyse simultaneous effects of different policies on all these macro economic variables. Unfortunately no existing model takes care of this interaction. On the other hand, many dynamic models deal with the interaction between economic growth and environmental pollution.³ However, none of these models consider the problem of unemployment.

It is always important to analyse this interaction between unemployment and environment because many developed countries and developing countries in the world suffer from both the unemployment problem and the environmental pollution problem. In less developed countries, many underemployed workers are employed in labour intensive informal sectors; and productions in these sectors generate substantial emissions leading to pollution of air and water.⁴ Unemployed workers and dishonest businessmen often earn income destroying natural resources. Thus growing unemployment degrades the quality of environment through the growth of anti social as well as informal economic activities. The agricultural sector in a less developed economy contributes substantially to national employment. However, application of scientific farming with chemical fertilizers, pesticides and insecticides etc. not only raises the agricultural productivity and level of employment but also leads to water pollution in lakes and canals.

A few works introduce environmental pollution in efficiency wage models. Albert and Meckl (2001) and Schneider (1997) develop models with efficiency wage and green tax to improve environment. However, their models are static and short-run equilibrium models; and hence do not focus on capital accumulation and economic growth. Lai et al. (2002) is the only dynamic model in this context. However, in Lai et al. (2002), we find an intertemporal analysis without capital accumulation. Moreover, environmental quality does not directly enter into the efficiency function of labour in these models.

We develop an one sector dynamic model with an unemployment equilibrium to be explained by the efficiency wage hypothesis.⁵ Only one commodity is produced with capital and labour as inputs; and labour is measured in efficiency unit. The special property of the present model is that efficiency of labour varies positively not only with the wage rate and the unemployment rate but also with the quality of environment; and this property follows from the rational behaviour of the worker who derives utility from environmental quality as well as from consumption and when these two arguments in the utility function are complementary to each other. So the motivation of the worker to work hard is also improved because the improvement in the environmental quality raises her marginal utility of consumption which, in turn, raises her marginal benefit of working harder. This efficiency enhancing effect of environment is missing in the existing efficiency wage models.⁶

Environmental quality is defined as a combined stock of natural gifts consisting of fresh air, pure water, fertility of land, plants, animals etc.; and we ignore the problem of aggregation of these different natural gifts in this theoretical exercise. It may be treated as an aggregate public durable consumption good of the worker available free of cost. Emission generated from the production sector is a flow variable and is different from this stock of environmental quality. This environmental quality changes over time; and emission from production causes intertemporal degradation of environmental quality while an abatement activity leads to its upgradation. Many existing models treat environmental quality as a stock variable making it different from emission which is a flow variable.⁷ However, many other models assume environmental quality to be identical to emission; and hence it is treated as a flow variable there.⁸ The distinction between environment stock and emission flow makes sense in a dynamic intertemporal model.

In this paper, our goal is to make a dynamic long run equilibrium analysis with intertemporal accumulation of capital as well as of environmental quality. The model takes care of the negative effect of production activity on environmental degradation assuming that the level of emission is proportional to the level of output. Proportional tax is imposed on the rental income on capital; and the tax revenue is spent to finance abatement activities. The change in environmental quality is defined as the old emission removed by abatement activity plus the natural improvement of environmental quality minus the present emission generated by production. So the environmental quality changes over time⁹ due to negative environmental effects of production activity and positive effects of abatement activity. Capital accumulation which is the source of economic growth also takes place over time through investment of savings. These two features justify the dynamic long run equilibrium analysis to be done at the end.

We derive a few interesting results from this model. First, an exogenous improvement in the environmental quality given the capital stock lowers the efficiency wage rate and unemployment rate but raises the rental rate on capital and the level of output in the new short run equilibrium. Second, an exogenous increase in the capital stock given the environmental quality raises efficiency wage rate and level of output but lowers rental rate on capital and unemployment rate in the new short run equilibrium. Third, an exogenous increase in the tax rate on rental income on capital raises capital stock, national income and environmental quality but lowers unemployment rate in the new long run equilibrium when tax revenue is utilized to finance abatement expenditure. This third result is valid not only in the exogenous saving model but also in the endogenous savings model. The first and the third result can not be obtained from traditional efficiency wage models where labour efficiency is independent of environmental quality.

Capital income taxation as a policy instrument is chosen from the view point of equity.¹⁰ Abatement expenditure is productive in this model because labour efficiency varies positively with environmental quality; and so an improvement in environmental quality leads to a redistribution of income in favour of the capitalists raising the rental rate on capital and lowering the efficiency wage rate of labour. Abatement activities cause improvement in environmental quality. Thus our analysis attempts to justify a policy combination of taxing capitalists income and utilizing the tax revenue to finance abatement expenditure. However, this justification can not be made in the absence of any efficiency enhancing effect of environment. Existing efficiency wage models do not incorporate the efficiency enhancing effect of environment.

Micro foundation of the efficiency function is provided in Sect. 2. We develop the basic short run equilibrium model in Sect. 3. In Sect. 4, we introduce intertemporal accumulation of capital and degradation of environmental quality to make the model dynamic. Savings rate is assumed to be exogenous with capitalists and workers having different savings propensities. We analyse properties of long-run equilibrium in sub-Sect. 4.1; and study comparative steady-state effects in subsection 4.2. The Ramsey savings problem is solved in subsection 4.3 using a representative household framework. Section 5 is used to make concluding remarks.

2 Efficiency function

In this section, we provide the micro foundation of the efficiency function of labour. This efficiency function is derived from utility maximizing behaviour of the worker who derives utility from consumption and environmental quality and derives disutility from effort. Here the stock of environmental quality enters into the utility function as an argument and provides a flow of consumption services to the worker. However, the worker does not derive any disutility from the flow of emission generated by the production sector.

Let ${\overline{\text{C}}}$ be the expected consumption level of the worker and ${\Omega }\left( {{\overline{\text{C}}},{\text{E}}} \right)$ be his utility function and ${\text{V}}\left( {\text{e}} \right)$ be the disutility function where ${\text{e}}$ is his effort level and ${\text{E}}$ stands for the stock of environmental quality. Here, $0 \le {\text{e}} \le 1$. Maximum effort permissible physically is normalized to unity. We assume following restrictions to be satisfied: (i) ${\Omega }_{1} > 0$, ${\Omega }_{2} > 0$, ${\Omega }_{11} \le 0$, ${\Omega }_{22} < 0$, ${\Omega }_{12} > 0$ and (ii) ${\text{V}^{\prime}}\left( {\text{e}} \right) > 0$, ${\text{V}^{\prime\prime}}\left( {\text{e}} \right) > 0$. Here, ${\Omega }_{12} > 0$ implies that consumption and environmental quality are complementary. ${\Omega }_{11} \le 0$ implies that the worker is not a risk-lover. Also ${\text{V}}\left( {\text{e}} \right)$ is independent of ${\text{E}}$. Hence the marginal disutility of effort, ${\text{V}^{\prime}}\left( {\text{e}} \right)$, is independent of environmental quality.

The objective of the worker is to maximize the net utility given by

$$ {\text{Z}} = {\Omega }\left( {{\overline{\text{C}}},{\text{E}}} \right) - {\text{V}}\left( {\text{e}} \right) $$

with respect to the choice of effort, ${\text{e}}$, as well as with respect to the rate of savings. Here

$$ {\overline{\text{C}}} = \left( {1 - {\text{s}}} \right){\overline{\text{Y}}} $$

where ${\overline{\text{Y}}}$ represents the expected level of income and ${\text{s}}$ represents the savings rate. Here expected income consists of expected wage income as well as of non wage income. Hence,

$$ {\overline{\text{Y}}} = {\text{pw}} + \left( {1 - {\text{p}}} \right){\text{w}}^{{\text{a}}} + {\text{w}}^{{\text{n}}} $$

where ${\text{w}}$ is the wage income and ${\text{w}}^{{\text{n}}}$ is the non wage income. $\left( {1 - {\text{p}}} \right)$ is the probability that the worker will be monitored and fired if caught shirking; and ${\text{w}}^{{\text{a}}}$ is the alternative expected wage income if the worker is fired. We assume that this probability, $\left( {1-{\text{p}}} \right)$, is lower (higher) when his effort level is higher (lower). Mathematically, ${\text{p}} = {\text{p}}\left( {\text{e}} \right)$ with ${\text{p}^{\prime}}\left( {\text{e}} \right) > 0$.

Also ${\text{p}}\left( 0 \right) = 0$ and ${\text{p}}\left( 1 \right) = 1$. Here, ${\text{p}^{\prime\prime}}\left( {\text{e}} \right) < 0$ is a simplifying assumption. The alternative expected wage income after being fired is given by.

${\text{w}}^{{\text{a}}} = \left( {1 - {\text{u}}} \right){\text{w}}^{*} + {\text{ub}}$.

Here u is the unemployment rate defined as the level of unemployment divided by the total number of workers. This unemployment rate denotes the probability of remaining unemployed after losing the job. The actual wage rate in the alternative job is denoted by ${\text{w}}^{*}$; and ${\text{b}}$ stands for the rate of unemployment allowance.

Using all these four equations, we have

$$ {\overline{\text{C}}} = \left( {1 - {\text{s}}} \right)\left\{ {{\text{p}}\left( {\text{e}} \right)\left[ {{\text{w}} - {\text{w}}^{*} + {\text{u}}\left( {{\text{w}}^{*} - {\text{b}}} \right)} \right] + \left( {1 - {\text{u}}} \right){\text{w}}^{*} + {\text{ub}} + {\text{w}}^{{\text{n}}} } \right\} $$

and

$$ {\text{Z}} = {\Omega }\left( {\left( {1 - {\text{s}}} \right)\left\{ {{\text{p}}\left( {\text{e}} \right)\left[ {{\text{w}} - {\text{w}}^{*} + {\text{u}}\left( {{\text{w}}^{*} - {\text{b}}} \right)} \right] + \left( {1 - {\text{u}}} \right){\text{w}}^{*} + {\text{ub}} + {\text{w}}^{{\text{n}}} } \right\},{\text{E}}} \right) - {\text{V}}\left( {\text{e}} \right). $$

We assume the savings rate, ${\text{s}}$, to be exogenously given.¹¹ Savings finances future consumption. So, in an one period model, endogenous allocation of income between consumption and savings does not make sense. It makes sense in a multiperiod life time utility maximization model. So, in the present section, ${\text{Z}}$ is to be maximized with respect to ${\text{e}}$ only; and the first-order condition of maximization is given by

$$ \left( {1 - {\text{s}}} \right){\Omega }_{1} {\text{p}^{\prime}}\left( {\text{e}} \right)\left\{ {\left( {{\text{w}} - {\text{w}}^{*} } \right) + {\text{u}}\left( {{\text{w}}^{*} - {\text{b}}} \right)} \right\} = {\text{V}^{\prime}}\left( {\text{e}} \right). $$

Here the right hand side represents marginal disutility of effort and the left hand side represents marginal utility of effort. ${\Omega }_{1}$ represents marginal utility of expected consumption and $\left( {1 - {\text{s}}} \right){\text{p}^{\prime}}\left( {\text{e}} \right)\left\{ {\left( {{\text{w}} - {\text{w}}^{*} } \right) + {\text{u}}\left( {{\text{w}}^{*} - {\text{b}}} \right)} \right\}$ stands for the marginal contribution of effort on expected consumption. Additional effort leads to additional income; and this, in turn, leads to additional consumption and additional utility.

The second order condition of maximization is always satisfied because

$${\text{D}} = \left( {1 - {\text{s}}} \right)\left[ {\left( {{\Omega }_{11} {\text{p}^{\prime}}\left( {\text{e}} \right) + {\Omega }_{1} {\text{p}^{\prime\prime}}\left( {\text{e}} \right)} \right)\left\{ {\left( {{\text{w}} - {\text{w}}^{*} } \right) + {\text{u}}\left( {{\text{w}}^{*} - {\text{b}}} \right)} \right\} - {\text{V}^{\prime\prime}}\left( {\text{e}} \right)} \right] < 0.$$

Here ${\text{w}} \ge {\text{w}}^{*} > b$, by assumption. Also $0 < {\text{s}} < 1$. For ${\Omega }_{11} \le 0$, ${\text{D}}$ is always negative because ${\text{p}^{\prime\prime}}\left( {\text{e}} \right) < 0$ and ${\text{V}^{\prime\prime}}\left( {\text{e}} \right) > 0$. Here consumption is uncertain. ${\Omega }_{11} = 0( < 0)$ implies that worker is risk neutral (averter). Utility defined over expected consumption makes sense when the worker is risk neutral.

From the first order condition of maximization, we have

$${\text{Dde}} + {\Omega }_{12} {\text{dE}} = - \left( {1 - {\text{s}}} \right)\left( {{\text{p}^{\prime}}\left( {\text{e}} \right){\Omega }_{1} + {\text{p}}\left( {\text{e}} \right){\text{V}^{\prime}}\left( {\text{e}} \right)\frac{{{\Omega }_{11} }}{{{\Omega }_{1} }}} \right)\left\{ {{\text{dw}} - {\text{udb}} + \left( {{\text{w}}^{*} - {\text{b}}} \right){\text{du}}} \right\}.$$

Here $\left( { - \frac{{{\Omega }_{11} }}{{{\Omega }_{1} }}} \right)$ represents the absolute rate of risk aversion.

We assume that no allowance is paid to unemployed workers. So ${\text{b}} = 0$. Hence, with ${\Omega }_{11} = 0$, i.e., with risk-neutrality assumption, we have

$$ \frac{{{\text{de}}}}{{{\text{dw}}}} = - \frac{{\left( {1 - {\text{s}}} \right){\Omega }_{1} {\text{p}^{\prime}}\left( {\text{e}} \right)}}{{\text{D}}} > 0, $$

and

$$\frac{{{\text{de}}}}{{{\text{du}}}} = - \frac{{\left( {1 - {\text{s}}} \right){\Omega }_{1} {\text{p}^{\prime}}\left( {\text{e}} \right){\text{w}}^{*} }}{{\text{D}}} > 0.$$

So an increase in the wage rate and/or unemployment rate generates a positive effect on the optimum level of effort of the risk-neutral worker.

Mathematical signs of $\frac{{{\text{de}}}}{{{\text{dw}}}}$ and $\frac{{{\text{de}}}}{{{\text{du}}}}$ remain unchanged when ${\Omega }_{11} < 0$ but is very low, i.e., when the worker is risk averter but the degree of risk aversion is very low. However, when the degree of risk aversion is very high, these signs may be reversed.

It can be easily shown that

$$ \frac{{{\text{de}}}}{{{\text{dE}}}} = - \frac{{{\Omega }_{12} \left( . \right)}}{{\text{D}}} > 0\, {\text{if}}\,\,{{\Omega }}_{12} > 0; $$

and this sign is independent of whether ${\Omega }_{11}$ is negative or zero. So, regardless of risk neutrality or risk aversion, an improvement in the environmental quality always raises the optimum level of effort of the worker.

If ${\Omega }_{1}$ is independent of ${\overline{\text{C}}}$, i.e., if ${\Omega }_{11} = 0$, then a change in the non-wage income, ${\text{w}}^{{\text{n}}}$, does not affect the equilibrium condition. So optimum effort level, ${\text{e}}$, is independent of non-wage income, ${\text{w}}^{{\text{n}}}$, when the worker is risk neutral.

However, when ${\Omega }_{11} < 0$, then

$$\frac{{{\text{de}}}}{{{\text{dw}}^{{\text{n}}} }} = - \frac{{{\Omega }_{11} \left( {1 - {\text{s}}} \right){\text{V}^{\prime}}\left( {\text{e}} \right)}}{{{\text{D}\Omega }_{1} }} < 0. $$

Hence an increase in the non-wage income must have a negative effect on the optimum level of effort when the worker is risk averter.

If ${\text{e}}^{*}$ is the equilibrium effort level of the worker, then

$$ {\text{e}}^{*} = {\text{e}}^{*} \left( {{\text{w}},{\text{E}},{\text{u}},{\text{w}}^{{\text{n}}} } \right) $$

is the optimum effort function and this is called the labour efficiency function in this model. From this labour efficiency function, we can easily establish the following proposition.

Proposition 1

Efficiency of labour varies positively with the wage rate as well as with the unemployment rate when the worker is risk neutral and also when the degree of risk aversion of the worker is positive but is very low. It also varies positively with the environmental quality if environmental quality and consumption are complementary in workers preference. It varies inversely with (is independent of) the non wage income when the worker is risk averter (neutral).

We provide intuitive explanations behind the proposition. An exogenous increase in the wage rate means an increase in the higher return on her effort and indirectly means an increase in the cost of her shirking. So she must work hard following an increase in the wage rate. Similarly an increase in the unemployment rate means a decrease in her expected income from the alternative source which, in turn, implies an increase in the cost of shirking. So she puts a higher effort in her workplace when she faces a higher unemployment rate in the labour market. An improvement in the environmental quality raises the marginal utility of consumption of the worker when consumption and environmental quality are complementary in workers’s preference. So the worker works hard to earn more following an improvement in environmental quality.

An increase in non wage income acts like a risk free gift income to the worker; and so it discourages the risk averter worker to work hard when wage income is uncertain. However, it does not affect the effort choice of the risk-neutral worker because the risk neutral worker is indifferent between risky income and risk free income. This negative effect¹² of non wage income on labour efficiency is very small when ${\Omega }_{11}$ is very low; and so, for the sake of simplicity, we ignore this effect in this paper assuming risk-neutrality. The worker is assumed to save and to earn rental income in the dynamic model to be developed in Sect. 4; and so an analysis of the role of non wage income on labour efficiency is important in this mico-foundation section.

It may be noted that efficiency of labour varies inversely with the quality of environment when ${\Omega }_{12}<0$, i.e., when consumption and environmental quality are substitutes. However, we do not consider this case. There may be a substitution between effort and environmental quality in the disutility function. The labour efficiency varies positively with environmental quality when it is substitute to leisure. However, if leisure and environmental quality are complementary, then also an improvement in environmental quality demotivates the worker from working hard. So our special result that labour efficiency varies positively with environmental quality is conditional on the assumption that environmental quality is complementary to consumption and not to leisure.

Disutility function is also independent of the level of emission in this case. However, if the marginal disutility of effort varies positively with the level of emission, then the level of production may have a negative effect on the efficiency of labour because production sector generates emission.

Entry of environmental quality as an argument in the labour efficiency function creates an indirect positive effect of environment on productivity. Many authors like Nordhaus (1992), Bovenberg and Smulders (1995), Greiner (2005), Gupta and Barman (2009, 2010) etc. introduce environment as a productive input in the aggregate production function without providing any micro foundation of this positive effect. Our exercise provides the required micro foundation through derivation of the efficiency function of labour; and this has not been done earlier.

3 The short run equilibrium model

The transitional dynamic phase of every dynamic model consists of a series of short run equilibria defined at different points of time. In the short-run equilibrium of the present model, we solve for equilibrium values of variables like factor prices, intersectoral factor allocations and level of output of different sectors. These values are obtained at a given point of time in terms of given values of stock variables like capital stock and environmental quality. These equilibrium values change over time when capital stock and environmental quality change over time.

We consider a decentralized economy with only one production sector and with two factors of production called labour and capital and also with all exchanges taking place in competitive markets. The production function obeys all standard neo-classical properties including constant returns to scale. Capital stock is exogenously given in the short run, i.e., at a particular point of time, but changes over time. So it plays the role of a parameter in the short run. Labour is measured in efficiency unit; and number of workers is given and time independent. Wage rate is perfectly flexible in both the directions. However, there exists unemployment in the labour market; and this unemployment equilibrium is explained by efficiency wage hypothesis,¹³ according to which, the efficiency of a worker in general varies positively with the wage rate and unemployment rate.¹⁴ The special property of this model is that the efficiency of labour varies positively also with the quality of environment; and this efficiency function is already derived in Sect. 2 of this paper. This quality of environment is also exogenously given in the short run, i.e., at a given point of time. However, it accumulates over time. An exogenous improvement in the quality of environment raises the efficiency of labour by raising the marginal utility of consumption of the worker. Rental rate on capital is perfectly flexible and this flexibility ensures full utilization of capital stock. All markets are perfectly competitive. The representative firm maximizes profit; and so all profit maximizing input–output coefficients in the production technology depend on the wage-rental ratio. The representative consumer maximizes utility subject to the budget constraint. Production sector generates emission; and the flow of emission varies positively and proportionately with the level of output. This flow of emission does not affect the efficiency of labour instantaneously. However this emission affects the rate of degradation of environmental quality over time; and this change in environmental quality generates an intertemporal effect on the change in efficiency of labour.

We use following notations.

• ${\text{P}} = 1$ = Price of the product.

• ${\text{e}}$ = Efficiency of labour.

• $\frac{{\text{w}}}{{\text{e}}}$ = Wage rate per efficiency unit of labour.

• ${\text{r}}$ = Rate of return on capital.

• ${\text{X}}$ = Level of output.

• ${\text{L}}$ = Number of workers.

• ${\text{eL}}$ = Labour endowment in efficiency unit.

• ${\text{K}}$ = Capital endowment.

• ${\text{u}}$ = Unemployment rate.

• ${\text{eL}}\left( {1 - {\text{u}}} \right)$ = Labour employment in efficiency unit.

• ${\text{a}}_{{\text{K}}} = \frac{{\text{K}}}{{\text{X}}}$ = Profit maximizing capital output ratio.

• ${\text{a}}_{{\text{L}}} = \frac{{{\text{eL}}\left( {1 - {\text{u}}} \right)}}{{\text{X}}}$ = Profit maximizing employment output ratio, labour being expressed in efficiency unit.

• ${\text{E}}$ = Quality of environment.

• ${\uptheta }_{{\text{j}}}$ = Distributive share of ${\text{j}}$ th factor for ${\text{j}}$ = ${\text{L}}$, ${\text{K}}$.

• ${\upsigma }$ = $\left[ {\frac{{\partial \left( {\frac{{{\mathbf{a}}_{{\mathbf{K}}} }}{{{\mathbf{a}}_{{\mathbf{L}}} }}} \right)}}{{\partial \left( {\frac{{{\raise0.7ex\hbox{${\mathbf{w}}$} \!\mathord{\left/ {\vphantom {{\mathbf{w}} {\mathbf{e}}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\mathbf{e}}$}}}}{{\mathbf{r}}}} \right)}}} \right]\left[ {\frac{{\frac{{{\raise0.7ex\hbox{${\mathbf{w}}$} \!\mathord{\left/ {\vphantom {{\mathbf{w}} {\mathbf{e}}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\mathbf{e}}$}}}}{{\mathbf{r}}}}}{{\frac{{{\mathbf{a}}_{{\mathbf{K}}} }}{{{\mathbf{a}}_{{\mathbf{L}}} }}}}} \right] =$ Technical elasticity of substitution between labour (measured in efficiency unit) and capital.

• ${\hat{\text{z}}}$ = $\frac{{{\text{dz}}}}{{\text{z}}}$ = Relative change in ${\text{z}}$ where ${\text{z}}$ is any variable.

Following equations describe the short-run equilibrium of this model.

$$ 1 = {\text{a}}_{{\text{L}}} \left( {\frac{{\text{w}}}{{\text{e}}}} \right) + {\text{a}}_{{\text{K}}} {\text{r}}{.} $$

(1)

$$ {\text{e}} = {\text{e}}\left( {{\text{w}},{\text{E}},{\text{u}}} \right)\;\;{\text{with}}\;\;{\text{e}}_{{\text{m}}} > 0 \;{\text{and}}\;{\text{e}}_{{{\text{mm}}}} < 0 \;{\text{for}}\;{\text{m}} = 1,2,3. $$

(2)

Here ${\text{e}}_{{\text{m}}}$ is the marginal efficiency with respect to the ${\text{m}}$th argument; and ${\text{e}}_{{{\text{mm}}}}$ is the rate of change in that marginal efficiency.

$$ \frac{{\partial {\text{e}}}}{{\partial {\text{w}}}}\frac{{\text{w}}}{{\text{e}}} = {\text{e}}_{1} \frac{{\text{w}}}{{\text{e}}} = 1. $$

(3)

$$ {\text{a}}_{{\text{K}}} {\text{X}} = {\text{K}}{.} $$

(4)

$$ {\text{a}}_{{\text{L}}} {\text{X}} = {\text{L}}\left( {1 - {\text{u}}} \right){\text{e}}{.} $$

(5)

Here Eq. (1) stands for the profit maximizing condition of a competitive firm. Price of the product is normalized to unity in an one commodity model. Price is equal to marginal cost in competitive equilibrium; and marginal cost is equal to average cost when there is constant to returns to scale in production technology. Derivation of this Eq. (1) is described in “Appendix A”. Equation (2) stands for the efficiency function of labour. Efficiency of labour is a positive and concave function¹⁵ in terms of its every argument. It is the optimum effort function of an utility maximizing worker derived in the presence of her threat of firing when she shirks; and its derivation has already been analysed in Sect. 2. Effective unit cost of employing labour is $\left( {\frac{{\text{w}}}{{\text{e}}}} \right)$; and this unit cost is to be minimized with respect to wage rate, ${\text{w}}$. The first-order condition of unit cost minimization is given by Eq. (3). It is similar to Solow (1979) condition which implies that wage elasticity of labour efficiency is equal to unity. Equation (4) stands for capital market equilibrium condition and this equilibrium is automatically attained by the flexibility of rental rate on capital. Equation (5) represents unemployment adjusted labour market equilibrium condition. Profit maximizing factor output coefficients, ${\text{a}}_{{\text{K}}}$ and ${\text{a}}_{{\text{L}}}$, are functions of factor-price ratio, $\frac{{\left( {\frac{{\text{w}}}{{\text{e}}}} \right)}}{{\text{r}}}$.

There are five unknowns in this short run equilibrium model: ${\text{w}}$, ${\text{e}}$, ${\text{r}}$,${\text{ u}}$ and ${\text{X}}$. Three parameters are given by ${\text{E}}$, ${\text{L}}$, and ${\text{K}}$. These five unknowns are solved simultaneously by these five equations. Equations (1), (2), (3) and (5) solve for equilibrium values of ${\text{w}}$, ${\text{e}}$, ${\text{r}}$ and ${\text{ u}}$. Then values of ${\text{a}}_{{\text{K}}}$ and ${\text{a}}_{{\text{L}}}$ are also endogenously determined because each of these two coefficients is a function of $\frac{{\left( {\frac{{\text{w}}}{{\text{e}}}} \right)}}{{\text{r}}}$. Finally, Eq. (4) solves for the equilibrium value of output, ${\text{X}}$. Multiplying both sides of Eq. (4) by ${\text{r}}$ and of Eq. (5) by $\left( {\frac{{\text{w}}}{{\text{e}}}} \right)$ and then using Eq. (1), we have

$${\text{X}} = {\text{rK}} + {\text{wL}}\left( {1 - {\text{u}}} \right). $$

This proves the equality between national income at product price and national income at factor cost.

3.1 Change in parameters

Only ${\text{K}}$ and ${\text{E}}$ change over time but ${\text{L}}$ is time independent by assumption. Here we analyse the effect of an exogenous change in environmental quality, ${\text{E}}$, and in capital endowment, ${\text{K}}$,one by one, keeping other parameters fixed.

We define following two notations.

${\upvarepsilon }_{{\text{E}}} =$ Elasticity of labour efficiency with respect to environmental quality.

${\upvarepsilon }_{{\text{u}}}$ = Elasticity of labour efficiency with respect to unemployment rate.

In our model, ${\upvarepsilon }_{{\text{E}}} > 0$ because an improvement in environmental quality raises labour efficiency. In the existing efficiency wage models, ${\upvarepsilon }_{{\text{E}}} = 0$. However, ${\upvarepsilon }_{{\text{u}}}$ is always positive in any efficiency wage model.

Using Eqs. (1) to (5), we obtain¹⁶ following equations.

$$ \widehat{{\text{w}}} = \frac{1}{\Delta }\left\{ { - {\uptheta }_{{\text{K}}} {\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}\widehat{{\text{E}}} + \left. {{\uptheta }_{{\text{K}}} {\upvarepsilon }_{{\text{u}}} \widehat{{\text{K}}}} \right\}} \right.. $$

(6)

$$ \widehat{{\text{e}}} = \frac{{\left( {1 + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right)}}{\Delta }\left\{ { - {\uptheta }_{{\text{K}}} {\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}\widehat{{\text{E}}} + \left. {{\uptheta }_{{\text{K}}} {\upvarepsilon }_{{\text{u}}} \widehat{{\text{K}}}} \right\}} \right.. $$

(7)

$$ {\hat{\text{r}}} = - \frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\left( {{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}\widehat{{\text{E}}}\left. { - {\upvarepsilon }_{{\text{u}}} \widehat{{\text{K}}}} \right)} \right.. $$

(8)

$$ \widehat{{\text{u}}} = \frac{1}{\Delta }\left[ { - {\upvarepsilon }_{{\text{E}}} \left\{ { - {\sigma e}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \left. { + {\uptheta }_{{\text{K}}} \left( {1 + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right)} \right\}\widehat{{\text{E}}} + {\uptheta }_{{\text{K}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}} {\widehat{{\text{K}}}}\right.} \right]. $$

(9)

$$ \widehat{{\text{X}}} = \frac{1}{\Delta }\left[ { - {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} {\uptheta }_{{\text{L}}} {\upsigma }\frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}}\widehat{{\text{E}}}} \right. + \left\{ { - {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{K}}} \left( {{\upvarepsilon }_{{\text{u}}} {\upsigma } + \frac{{\text{u}}}{{\left( {1- {\text{u}}} \right)}}} \right)} \right. + \left. {\left. {{\uptheta }_{{\text{K}}} {\upvarepsilon }_{{\text{u}}} \left( {1 + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right)} \right\}\widehat{{\text{K}}}} \right]. $$

(10)

Here,

$$\Delta = - {\upvarepsilon }_{{\text{u}}} {\sigma e}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}} + {\upvarepsilon }_{{\text{u}}} {\uptheta }_{{\text{K}}} \left\{ {\left( {1 + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right) - {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\frac{{\text{u}}}{{{\upvarepsilon }_{{\text{u}}} \left( {1 - {\text{u}}} \right)}}} \right\}.$$

$\Delta$ represents the elasticity of substitution between capital and labour when labour is measured in efficiency unit and when efficiency wage is paid to workers. In a flexible wage full employment model with exogenous labour efficiency, $\Delta = {\upsigma }$. Here, ${\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}$ is the elasticity of marginal efficiency with respect to wage rate when efficiency wage is paid to the worker.

We assume that $\left( {1 + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right) > 0$. This assumption implies that the elasticity of marginal efficiency with respect to wage rate is less-than unity when efficiency wage is paid to the worker. $\Delta > 0$ in this case¹⁷ because $- {\uptheta }_{{\text{L}}} < 0$, ${\uptheta }_{{\text{K}}} > 0$, ${\upsigma } > 0$ and ${\text{e}}_{11} < 0$.

Now, from Eqs. (6) to (10), we have

$\frac{{\widehat{{\text{w}}}}}{{\widehat{{\text{E}}}}} = - \frac{{{\uptheta }_{{\text{K}}} {\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}}}{\Delta } \le 0$ for ${\upvarepsilon }_{{\text{E}}} \ge 0$;

$$ \begin{aligned} &\frac{{\widehat{{\text{w}}}}}{{\widehat{{\text{K}}}}} = \frac{{{\uptheta }_{{\text{K}}} {\upvarepsilon }_{{\text{u}}} }}{\Delta } > 0; \\& \frac{{{\hat{\text{e}}}}}{{\widehat{{\text{E}}}}} = - \frac{{\left( {1 + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right)}}{\Delta }{\uptheta }_{{\text{K}}} {\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}} \le 0\;\;{\text{for}}\;\;{\upvarepsilon }_{{\text{E}}} \ge 0; \\ & \frac{{{\hat{\text{e}}}}}{{\widehat{{\text{K}}}}} = \frac{{\left( {1 + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right)}}{\Delta }{\uptheta }_{{\text{K}}} {\upvarepsilon }_{{\text{u}}} > 0; \\ &\frac{{{\hat{\text{r}}}}}{{\widehat{{\text{E}}}}} = - \frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}} \ge 0\;\;{\text{for}}\;\;{\upvarepsilon }_{{\text{E}}} \ge 0;\\ &\frac{{{\hat{\text{r}}}}}{{\widehat{{\text{K}}}}} = \frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} < 0;\\ &\frac{{{\hat{\text{u}}}}}{{\widehat{{\text{E}}}}} = - \frac{1}{\Delta }{\upvarepsilon }_{{\text{E}}} \left\{ { - {\sigma e}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\left. { + {\uptheta }_{{\text{K}}} \left( {1 + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right)} \right\} \le 0} \right.\;\;{\text{for}}\;\;{\upvarepsilon }_{{\text{E}}} \ge 0; \\ &\frac{{{\hat{\text{u}}}}}{{\widehat{{\text{K}}}}} = \frac{1}{\Delta }{\uptheta }_{{\text{K}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}} < 0; \\ &\frac{{\widehat{{\text{X}}}}}{{\widehat{{\text{E}}}}} = - \frac{1}{\Delta }{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} {\uptheta }_{{\text{L}}} {\upsigma }\frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}} \ge 0\;\;{\text{for}}\;\;{\upvarepsilon }_{{\text{E}}} \ge 0; \\ &\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}} = \frac{1}{\Delta }\left\{ { - {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{k}}} \left( {{\upvarepsilon }_{{\text{u}}} {\upsigma } + \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}} \right)} \right. + {\uptheta }_{{\text{K}}} \left. {{\upvarepsilon }_{{\text{u}}} \left( {1 + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right)} \right\} > 0; \\ &\text{and} \\ &\frac{{\widehat{{{\text{e}}\left( {1 - {\text{u}}} \right)}}}}{{{\hat{\text{E}}}}} = \frac{1}{\Delta }{\upvarepsilon }_{{\text{E}}} \left\{ { - {\sigma e}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}} + {\uptheta }_{{\text{K}}} \left( {1 + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right)\left( {{\text{e}} - {\text{u}}} \right)} \right\} > 0\;\;{\text{for}}\;\;{\text{e}} \ge {\text{u}}{.}\end{aligned} $$

Here magnitudes of $\frac{{{\hat{\text{u}}}}}{{{\hat{\text{E}}}}}$, $\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}$ and $\frac{{{\hat{\text{X}}}}}{{{\hat{\text{E}}}}}$ vary positively with the value of ${\upsigma }$; and other expressions are independent of the value of ${\upsigma }$. However their signs do not depend on the value of ${\upsigma }$. So, from these expressions, it is clear that an exogenous increase in capital stock, ${\text{K}}$, raises ${\text{w}}$, ${\text{e}}$ and ${\text{X}}$ but lowers ${\text{r}}$ and ${\text{u}}$. Mathematical signs of derivatives with respect to ${\text{K}}$ are independent of whether ${\upvarepsilon }_{{\text{E}}} > 0$ or ${\upvarepsilon }_{{\text{E}}} = 0$. However, an increase in environmental quality, ${\text{E}}$, lowers ${\text{w}}$, ${\text{e}}$ and ${\text{u}}$ but raises ${\text{r}}$ and ${\text{X}}$ only when ${\upvarepsilon }_{{\text{E}}} > 0$, i.e., when environment has a positive efficiency enhancing effect. In the existing efficiency wage literature, ${\upvarepsilon }_{{\text{E}}} = 0$; and hence expressions of these derivatives with respect to ${\text{E}}$ clearly show that

$$ \frac{{{\hat{\text{w}}}}}{{{\hat{\text{E}}}}} = \frac{{{\hat{\text{e}}}}}{{{\hat{\text{E}}}}} = \frac{{{\hat{\text{r}}}}}{{{\hat{\text{E}}}}} = \frac{{{\hat{\text{u}}}}}{{{\hat{\text{E}}}}} = { }\frac{{{\hat{\text{X}}}}}{{{\hat{\text{E}}}}} = 0 $$

when ${\upvarepsilon }_{{\text{E}}} = 0$. So, in the existing efficiency wage models with ${\upvarepsilon }_{{\text{E}}} = 0$, an exogenous change in the environmental quality, ${\text{E}}$, does not affect short-run equilibrium values of ${\text{w}}$, ${\text{e}}$, ${\text{r}}$,${\text{ u}}$ and ${\text{X}}$.

Also from Eqs. (6) and (7), we have

$$ {\hat{\text{w}}} - {\hat{\text{e}}} = \frac{{{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}}}{\Delta }\left[ {\left. {{\uptheta }_{{\text{K}}} \left( {{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}{\hat{\text{E}}}\left. { - {\upvarepsilon }_{{\text{u}}} \widehat{{\text{K}}}} \right)} \right.} \right]} \right. $$

(11)

and this Eq. (11) implies that

$\frac{{{\hat{\text{w}}} - {\hat{\text{e}}}}}{{{\hat{\text{E}}}}} \le 0$ for ${\upvarepsilon }_{{\text{E}}} \ge 0$ with ${\hat{\text{K}}} = 0$

and

$\frac{{{\hat{\text{w}}} - {\hat{\text{e}}}}}{{{\hat{\text{K}}}}} > 0$ for ${\upvarepsilon }_{{\text{u}}} > 0$ with ${\hat{\text{E}}} = 0$.

So the efficiency wage rate, $\frac{{\text{w}}}{{\text{e}}}$, varies inversely with (is independent of) the environmental quality, ${\text{E}}$, if the efficiency enhancing effect of environment is present (absent). However, ${\upvarepsilon }_{{\text{u}}}$ is always positive. So this efficiency wage rate always varies directly with the capital stock, ${\text{K}}$, regardless of the presence or absence of efficiency enhancing effect of environment.

Using Eqs. (6)–(11), we can now establish the following proposition.

Proposition 2

In the short-run equilibrium, (i) an exogenous improvement in the environmental quality given the capital stock lowers (does not affect) the efficiency wage rate and the unemployment rate but raises (does not affect) the rental rate on capital and the level of output in the presence (absence) of efficiency enhancing effect of environment; and (ii) an exogenous increase in capital stock given the environmental quality always raises efficiency wage rate and level of output but lowers rental rate on capital and unemployment rate.

We now attempt to provide an intuitive explanation behind this proposition. An improvement in the environmental quality generates a positive externality to the health capital and the utility function of the worker and thus motivates her to work hard. This leads to an increase in the efficiency of labour given the unemployment rate and the wage rate. This is called the efficiency enhancing effect of environment. So the efficiency wage rate falls and labour becomes relatively cheaper. So employers demand for labour is increased lowering the unemployment rate because keeping unemployment in the labour market is the labour disciplining device of the employer. On the other hand, a fall in the unemployment rate lowers the efficiency of labour. However, this second negative effect is stronger than the first positive effect. So the net effect on labour efficiency is negative. Since labour and capital are complementary to each others, demand for capital is also increased. So the rental rate on capital goes up. However, total labour endowment in efficiency unit to be used in production is increased because unemployment rate is reduced. The negative net effect on labour efficiency is outweighed by the positive effect resulting from a fall in the unemployment rate. This raises the level of output. However, this mechanism does not work in the absence of an efficiency enhancing effect of environment because neither unemployment rate nor efficiency is changed in that case. The existing literature on efficiency wage theory unfortunately fails to incorporate this efficiency enhancing effect of environment.

An increase in capital stock lowers the rental rate on capital in the new capital market equilibrium. So the efficiency wage rate is increased to satisfy the profit maximizing condition of the firm because product price is given. Labour and capital are complementary to each others; and so demand for labour is also increased which, in turn, lowers the unemployment rate and raises the wage rate. The fall in the unemployment rate lowers labour efficiency but the rise in the wage rate raises it; and the second effect is stronger than the first effect. So total labour employment in efficiency unit is increased. Full utilization of additional capital and that increase in labour employment in efficiency unit cause expansion of output. However, this mechanism is also valid even in the absence of efficiency enhancing effect of environment.

So an improvement in environmental quality has an income redistribution effect in favour of capitalists because it raises the rental rate on capital but lowers the efficiency wage rate in the presence of an efficiency enhancing effect of environment. Abatement activities of the government lead to an upgradation of environmental quality over time. So, in the context of financing these abatement activities through tax-revenue, one may justify the choice of capital income taxation on the ground of equity.

4 The dynamic analysis

The dynamic model consists of all equations of the short-run equilibrium model and of a few additional equations of motion generated from the intertemporal movement of stock variables. Here we justify the economics behind those additional equations of motion. Capital stock and environmental quality change over time. So the short-run equilibrium values of all variables change over time; and this is how a dynamic system moves over time.

We assume that the government imposes a proportional tax on rental income of capital¹⁸ at the rate, $\uptau$; and this tax revenue is spent to finance abatement expenditure. The choice of this tax is justified by the fact that capital income tax is an important source of tax revenue in many developed and developing countries. Also abatement activities redistribute income in favour of capital in this model. There are two sources of intertemporal improvement of environmental quality. One is the natural rate of improvement and another is the abatement activity to be financed by tax revenue. In the public economics literature, there exists substantial works dealing with general equilibrium effects of corporate income taxes on resource allocation and on capital accumulation. However, use of this tax revenue to finance abatement expenditure is generally not considered in those models with a few works being exceptions¹⁹; and those few works neither focus on the effects of capital income taxation nor study the implication of unemployment problems. Like Solow (1956) model, we assume that entire savings is invested; and, like Kaldor (1957) model, we assume that workers and capitalists have different propensities to save. Existing capital stock depreciates over time at a constant rate. However, we ignore the intertemporal growth of the number of workers in this model²⁰; and hence number of workers is normalized to unity. A constant and positive rate of depreciation of capital is enough to ensure the existence of a long run equilibrium. We also consider an exogenous savings model in this section. Environmental quality is degraded due to expansion of output because we assume that production sector is the source of emission.²¹

Equations (12) and (13) presented below describe the intertemporal rate of change in capital stock and the rate of change in environmental quality respectively.

$$ {\dot{\text{K}}} = {\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right){\text{rK}} + {\text{s}}_{{\text{w}}} \left( {1 - {\text{u}}} \right){\text{wL}} - {{\updelta K;}} $$

(12)

and

$$ {\dot{\text{E}}} = {{\uptau {\text{rK}}}} - {\upalpha \text{X}} + {\uppi \text{E}}{.} $$

(13)

Here ${\updelta }$ represents the constant rate of depreciation of capital stock. ${\uptau }$ represents the tax rate on rental income capital. Hence $\left( {1 - {\uptau }} \right){\text{rK}}$ represents post tax rental income on capital; and ${{\uptau rK}}$ stands for tax revenue spent as abatement expenditure. ${\uppi }$ represents constant relative rate of natural improvement of environment. ${\upalpha }$ represents the rate of emission generated per unit of output. By assumption, one unit of abatement expenditure can remove one unit of emission; and Eq. (13) implies that change in environmental quality is defined as the difference between old emission removed by abatement and new emission generated from production plus the natural absolute rate of improvement of environment. Upgradation of environmental quality must take place over time when the accumulated past emission removed by abatement expenditure plus the natural rate of improvement of environmental quality exceeds the rate of new emission generated by production. First term in the right hand side of Eq. (12) represents aggregate savings (investment). Here ${\text{s}}_{{\text{p}}}$ and ${\text{s}}_{{\text{w}}}$ represent constant marginal propensities to save of capitalists and workers respectively. Equation (12) is a definitional identity which implies that net investment is equal to gross investment minus depreciation.

In Solow (1956) model, all individuals-workers and capitalists- are identical. They do not differ in terms of savings propensities. Hence ${\text{s}}_{{\text{p}}} = {\text{s}}_{{\text{w}}} = {\text{s}}$; and so Eq. (12) is reduced to.

$${\dot{\text{K}}} = {\text{s}}\left( {{\text{X}}-{{\uptau \text{rK}}}} \right)-{\updelta \text{K}}.$$

4.1 Long-run equilibrium

In the long-run equilibrium, capital stock and environmental quality do not change over time. Consequently short run equilibrium values of all flow variables become time-independent in the long run equilibrium. We have ${\dot{\text{K}}} = {\dot{\text{E}}} = 0$ in the long-run equilibrium; and hence, from Eqs. (12) and (13), we find

$$ {\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right){\text{rK}} + {\text{s}}_{{\text{w}}} \left( {1 - {\text{u}}} \right){\text{wL}} = {{\updelta {K};}} $$

(14)

and

$$ {{\uptau \text{rK}}} = {\upalpha \text{X}} - {\uppi \text{E}}{.} $$

(15)

These Eqs. (14) and (15) solve for long run equilibrium values of ${\text{K}}$ and ${\text{E}}$. From comparative static results presented in the short run equilibrium model, we find that ${\text{w}}$, ${\text{u}}$, ${\text{r}}$ and ${\text{X}}$ are determined in terms of ${\text{K}}$ and ${\text{E}}$. Hence Eqs. (14) and (15) solve for long run equilibrium values of ${\text{K}}$ and ${\text{E}}$ given by $\left( {{\text{K}}^{*} ,{\text{ E}}^{*} } \right)$. These values are determined in terms of parameters- ${\text{s}}_{{\text{p}}}$, ${\text{s}}_{{\text{w}}}$, ${\uptau }$, ${\upalpha }$, ${\updelta }$ and ${\uppi }$; and the tax rate, ${\uptau }$, is the only policy parameter in this model.

From Eqs. (14) and (15), it can be shown that,

$$ \left. {\frac{{{\text{dE}}}}{{{\text{dK}}}}} \right|_{{{\dot{\text{K}}} = 0}} = \frac{{\text{E}}}{{\text{K}}}\frac{{{\upvarepsilon }_{{\text{u}}} }}{{{\upvarepsilon }_{{\text{E}}} }}\frac{{\left( {1 - {\text{u}}} \right)}}{{\text{u}}} > 0\;\;{\text{for}}\;\;{\upvarepsilon }_{{\text{E}}} > 0; $$

(16)

and

$$ \left. {\frac{{{\text{dE}}}}{{{\text{dK}}}}} \right|_{{{\dot{\text{E}}} = 0}} = \frac{{\left\{ {\left( {\frac{{{\upalpha \text{X}} - {\uppi \text{E}}}}{{\text{K}}}} \right)\frac{1}{\Delta }{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} {\uptheta }_{{\text{L}}} \left( {{\upsigma } - 1} \right) + \frac{{{\uppi \text{E}}}}{{\text{K}}}\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}} \right\}}}{{\left\{ {\left( {\frac{{{\upalpha \text{X}}}}{{\text{E}}} - {\uppi }} \right)\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}\left( {{\upsigma } - 1} \right) + {\uppi }\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}} + \frac{{\uppi }}{\Delta }{\upsigma \text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} \left( {{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}} - {\upvarepsilon }_{{\text{u}}} } \right)} \right\}}}. $$

If ${\upsigma } = 1$, i.e., if the production function is Cobb–Douglas, then

$$ \left. {\frac{{{\text{dE}}}}{{{\text{dK}}}}} \right|_{{{\dot{\text{E}}} = 0}} = \frac{{\frac{{\text{E}}}{{\text{K}}}\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}}}{{\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}} + \frac{1}{\Delta }{\sigma e}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} \left( {{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}} - {\upvarepsilon }_{{\text{u}}} } \right)}}. $$

(17)

Here the numerator is always positive and the denominator may be negative only if ${\upvarepsilon }_{{\text{E}}} {\text{u}} > {\upvarepsilon }_{{\text{u}}} \left( {1 - {\text{u}}} \right)$ and only if $\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}$ is very low. Hence ${\dot{\text{E}}} = 0$ locus slopes negatively in this case; and we assume ${\upvarepsilon }_{{\text{E}}} {\text{u}} > {\upvarepsilon }_{{\text{u}}} \left( {1 - {\text{u}}} \right)$ to get the negative slope of ${\dot{\text{E}}} = 0$ locus.

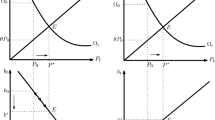
However, with ${\upvarepsilon }_{{\text{E}}} > 0$, ${\dot{\text{K}}} = 0$ stationary locus is always positively sloped. Both the loci are drawn in the phase diagram given by Fig. 1. So the existence of a unique long run equilibrium point, T, is ensured. In the conventional efficiency wage model, ${\upvarepsilon }_{{\text{E}}} = 0$. If ${\upvarepsilon }_{{\text{E}}} = 0$, then ${\dot{\text{K}}} = 0$ locus is a vertical straight line. However, existence and uniqueness properties of long-run equilibrium are not disturbed even if ${\upvarepsilon }_{{\text{E}}} = 0$.

Fig. 1

Long run equilibrium

The stability analysis of this long run equilibrium point is done in “Appendix C”; and it is found that this unique long run equilibrium is stable if, ${\upvarepsilon }_{{\text{E}}} {\text{u}} > {\upvarepsilon }_{{\text{u}}} \left( {1 - {\text{u}}} \right)$ and if $\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}$ is very low; i.e., if ${\dot{\text{E}}} = 0$ stationary locus slopes negatively. Determinant of the Jacobian matrix of this 2 × 2 dynamic system described by Eqs. (12) and (13) takes a positive sign if ${\upvarepsilon }_{{\text{E}}} {\text{u}} > {\upvarepsilon }_{{\text{u}}} \left( {1 - {\text{u}}} \right)$ and its trace is likely to be negative when $\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}$ is positive but is very low. If ${\upvarepsilon }_{{\text{E}}} {\text{u}} < {\upvarepsilon }_{{\text{u}}} \left( {1 - {\text{u}}} \right)$, then the Jacobian determinant takes a negative sign and then the long run equilibrium is a saddle point. This saddle point stability property is independent of the value of $\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}$. However, if ${\upvarepsilon }_{{\text{E}}} {\text{u}} > {\upvarepsilon }_{{\text{u}}} \left( {1 - {\text{u}}} \right)$ and if $\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}$ is high, then the equilibrium may be unstable. Here, $\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}$ represents the capital elasticity of output.

We have the following proposition here.

Proposition 3

The long run equilibrium is stable (unstable) if ${\upvarepsilon }_{{\text{E}}} > \frac{{\left( {1 - {\text{u}}} \right)}}{{\text{u}}}{\upvarepsilon }_{{\text{u}}}$ and if capital elasticity of output is positive but low (high). This equilibrium is a saddle point when ${\upvarepsilon }_{{\text{E}}} < \frac{{\left( {1 - {\text{u}}} \right)}}{{\text{u}}}{\upvarepsilon }_{{\text{u}}}$.

It may be noted that properties of long run equilibrium are independent of the values of ${\text{s}}_{{\text{w}}}$ and ${\text{s}}_{{\text{p}}}$. Same results will be obtained even if we have the Solow (1956) savings function where ${\text{s}}_{{\text{p}}} = {\text{s}}_{{\text{w}}}$. However, the efficiency enhancing effect of environment plays a very important role to obtain the stability property of the long run equilibrium.

4.2 Comparative steady state effects

Our objective is to analyse long run effects of capital income taxation on capital accumulation unemployment and environment. So, we now turn to analyse comparative steady state effects with respect to an increase in tax rate, ${\uptau }$, when the unique long-run equilibrium is stable.

From Eqs. (14) and (15), it can be shown that²²

$$\frac{{{\rm{dK}}}}{{{{\text{d}\uptau }}}} = {\rm{rK}}\frac{{\frac{{{{{\uptheta }}_{\rm{L}}}}}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left\{ {{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}{\rm{E}}\left( {{{\uppi \text{E}}} - {{\updelta \text{K}}}} \right) - {{\uppi }}{{{\upvarepsilon }}_{\rm{u}}}} \right\} + {{\uppi }}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}} + \frac{1}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}\frac{1}{{\rm{E}}}\left( {{{\upsigma }} - 1} \right)\left\{ { - {{\rm{s}}_{\rm{w}}}{\rm{wL}}\left( {1 - {\rm{u}}} \right) + \left( {{{\upalpha \text{X}}} - {{\uppi \text{E}}}} \right){{{\uptheta }}_{\rm{L}}}} \right\}}}{{{{\uppi }}\left( {{{{\upvarepsilon }}_{\rm{u}}} - {{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}} \right)\frac{1}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left\{ {{{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right){\rm{r}}{{{\uptheta }}_{\rm{L}}} - \left. {{{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right\}\left\{ {\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}} - \frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{L}}}{{{\upvarepsilon }}_{\rm{u}}}} \right\}} \right.}};$$

(18)

and

$$ \frac{{{\text{dE}}}}{{{\text{d}\uptau}}} = - {\text{rK}}\frac{{\frac{1}{\Delta }{{\updelta \uptheta }}_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} - \frac{{{\uppi \text{E}}}}{{\text{K}}}\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}} + \frac{1}{\Delta }{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} \frac{1}{{\text{K}}}\left( {{\upsigma } - 1} \right)\left\{ {{\text{s}}_{{\text{w}}} {\text{wL}}\left( {1 - {\text{u}}} \right) - \left( {{\upalpha \text{X}} - {\uppi \text{E}}} \right){\uptheta }_{{\text{L}}} } \right\}}}{{{\uppi }\left( {{\upvarepsilon }_{{\text{u}}} - {\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}} \right)\frac{1}{\Delta }{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\left\{ {{\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right){{r\uptheta }}_{{\text{L}}} - \left. {{\text{s}}_{{\text{w}}} \frac{{{\text{wL}}}}{{\text{K}}}\left( {1 - {\text{u}}} \right)\left( { - {\upsigma } + {\uptheta }_{{\text{K}}} } \right)} \right\}\left\{ {\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}} - \frac{1}{\Delta }{\upvarepsilon }_{{\text{u}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} {\upvarepsilon }_{{\text{u}}} } \right\}} \right.}}. $$

(19)

We now assume that ${\upsigma } = 1$; i.e., the production function is Cobb–Douglas. If ${\upsigma } = 1$, then from Eqs. (18) and (19), we obtain

$$\frac{{{\rm{dK}}}}{{{{\text{d}\uptau }}}} = {\rm{rK}}\frac{{\frac{{{{{\uptheta }}_{\rm{L}}}}}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left\{ {{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}{\rm{E}}\left( {{{\uppi \text{E}}} - {{\updelta \text{K}}}} \right) - {{\uppi }}{{{\upvarepsilon }}_{\rm{u}}}} \right\} + {{\uppi }}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}}}{{\left( {{{{\upvarepsilon }}_{\rm{u}}} - {{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}} \right)\frac{{{\uppi }}}{\Delta }{{\updelta }}{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( {\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}} - \frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{L}}}{{{\upvarepsilon }}_{\rm{u}}}} \right)}};$$

(20)

and

$$ \frac{{{\text{dE}}}}{{{\text{d}\uptau}}} = - {\text{rK}}\frac{{\frac{1}{\Delta }{{\updelta \uptheta }}_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} - \frac{{{\uppi \text{E}}}}{{\text{K}}}\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}}}{{\left( {{\upvarepsilon }_{{\text{u}}} - {\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}} \right)\frac{{\uppi }}{\Delta }{{\updelta \uptheta }}_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\left( {\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}} - \frac{1}{\Delta }{\upvarepsilon }_{{\text{u}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} {\upvarepsilon }_{{\text{u}}} } \right)}}. $$

(21)

Denominators in the right hand side of both Eqs. (20) and (21) are positive because the equilibrium is stable. In Eq. (21), the numerator is always positive; and so $\frac{{{\text{dE}}}}{{{\text{d}\uptau}}}$ is always positive. However, the numerator in the right hand side of Eq. (20) is positive if ${\uppi \text{E}} < \updelta K$. Hence $\frac{{{\text{dK}}}}{{{\text{d}\uptau}}} > 0$ if ${\uppi \text{E}} < \updelta \text{K}$. So an increase in the tax rate, ${\uptau }$, on capital income raises the long run equilibrium value of ${\text{K}}$ when the long run equilibrium value of $\frac{{\text{K}}}{{\text{E}}}$ exceeds $\frac{{\uppi }}{{\updelta }}$. Using Eqs. (14) and (15) we have

${\updelta \text{K}} > \uppi \text{E}\mathop \Rightarrow \limits^{ } {\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right){\text{rK}} + {\text{s}}_{{\text{w}}} \left( {1 - {\text{u}}} \right){\text{wL}} > {\upalpha \text{X}} - {{\uptau \text{rK}}}$.

Since $0 < {\text{s}}_{{\text{p}}} < 1$, this inequality is always true when

$\frac{{{\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right){\text{rK}} + {\text{s}}_{{\text{w}}} \left( {1 - {\text{u}}} \right){\text{wL}}}}{{\text{X}}} > {\upalpha }$,

i.e., when the aggregate savings income ratio exceeds the emission output coefficient. Savings generates capital accumulation through investment. It is a positive effect. However, emission generated from production produces a negative effect. It causes a misuse of this investible fund channelling the productive savings into abatement expenditure to maintain the ecological balance. Hence ${\updelta \text{K}} > \uppi \text{E}$ implies that the positive effect of savings dominates the negative effect of emission in the long run equilibrium.

Also we have

$$ \frac{{{\text{dX}}}}{{{\text{d}\uptau}}} = \frac{{{\text{rK}}}}{{\upalpha }} + \frac{{{\text{rK}}}}{{\upalpha }}\left( {1 + \frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} } \right)\frac{{{\text{dK}}}}{{{\text{d}\uptau}}} + \frac{{\uppi }}{{\upalpha }}\frac{{{\text{dE}}}}{{{\text{d}\uptau}}}. $$

(22)

Hence

$\frac{{{\text{dX}}}}{{{\text{d}\uptau}}} > 0$ if $\frac{{{\text{dK}}}}{{{\text{d}\uptau}}} > 0$.

This is so because

$\Delta > - {\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}}$.

So an increase in the tax rate on capital income raises national income in the new long run equilibrium. There is a direct increase due to rise in the tax rate. Also there is an indirect increase due to capital accumulation as well as due to improvement in the environmental quality. The first term in the right hand side of Eq. (22) represents its direct increase due to rise in the tax rate. The second term represents its increase through capital accumulation and the third term stands for the increase through improvement in the environmental quality.

Finally, using Eqs. (9), (20) and (21), we have

$$ \frac{{{\text{du}}}}{{{\text{d}\uptau}}} = \frac{{\text{u}}}{\Delta }\left[ {{\uptheta }_{{\text{K}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\frac{1}{{\text{K}}}\frac{{{\text{dK}}}}{{{\text{d}\uptau}}} - {\upvarepsilon }_{{\text{E}}} \left. {\left\{ { - {\sigma e}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right. + {\uptheta }_{{\text{K}}} \left( {1 + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right)} \right\}\frac{{{\text{dE}}}}{{{\text{d}\uptau}}}} \right]. $$

(23)

Here, the expression $\frac{{{\text{du}}}}{{{\text{d}\uptau}}}$ is negative because both $\frac{{{\text{dE}}}}{{{\text{d}\uptau}}}$ and $\frac{{{\text{dK}}}}{{{\text{d}\uptau}}}$ are positive, and ${\uptheta }_{{\text{K}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\frac{1}{{\text{K}}} < 0$, $- {\upvarepsilon }_{{\text{E}}} \left. {\left\{ { - {\sigma e}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right. + {\uptheta }_{{\text{K}}} \left( {1 + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right)} \right\} < 0$. The first term stands for the effect on unemployment via capital accumulation. The increase in the tax rate raises capital stock in the new long run equilibrium. Tax revenue is spent to finance abatement expenditure. This leads to an upgradation of environment. So efficiency of labour is improved; and this raises rental rate on capital and thus gross investment. So capital stock is increased in the long run equilibrium. The second term in the right hand side of Eq. (23) represents the efficiency enhancing effect of environment on unemployment. Additional taxation upgrades environmental quality in the new long run equilibrium. Unemployment rate and environmental quality are two substitute arguments in the labour efficiency function. So unemployment rate is reduced. So an increase in the tax rate on capital income lowers unemployment rate through capital accumulation as well as through upgradation of environmental quality. In traditional efficiency wage models, there is no efficiency enhancing effect of environment. So unemployment effect of additional taxation through environment upgradation is also nil in those models. Only the unemployment effect through capital accumulation exists there.

This analysis leads to the following proposition.

Proposition 4

If ${\uppi \text{E}} < \updelta \text{K}$, ${\upvarepsilon }_{{\text{E}}} {\text{u}} > {\upvarepsilon }_{{\text{u}}} \left( {1 - {\text{u}}} \right)$ and if $\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}$ is very low, then an exogenous increase in the tax rate on rental income of capital raises the capital stock, national income and the environmental quality but lowers unemployment rate in the new long run equilibrium when the tax revenue is used to finance abatement expenditure.

The intuition behind the result summarized in proposition 4 is given below. As the tax rate is increased, additional fund is made available to finance abatement expenditure, given the initial long run equilibrium. So environmental quality starts improving over time; and this raises efficiency of labour. However, the increase in the tax rate on rental income produces two conflicting effects on capital accumulation. On the one hand, it lowers the post-tax rental income with given rental rate in the initial long equilibrium. On the other hand, it raises the rental rate on capital through improvement in environmental quality but lowers the wage rate. Both wage earners and capitalists save; and entire savings is invested. Gross investment is increased because income redistribution in favour of capitalists generates more savings and because the second effect on rental income dominates the first effect. The second effect dominates the first effect if the gross investment income ratio exceeds the emission output coefficient. This produces a net positive effect on the time path of capital accumulation. Capital accumulation and improvement in labour efficiency through environmental upgradation must raise national income. Capital accumulation raises wage rate through increases in the demand for labour. Both wage rate and environmental quality are substitutes to unemployment rate in the labour efficiency function. So the employment rate is increased by profit maximizing employers in the new long run equilibrium leading to a decline in the unemployment rate in the labour market. In a standard dynamic model without efficiency enhancing effect of environmental quality and without tax financed abatement expenditure, the second effect does not exist. So we do not get any favourable effect of additional taxation on capital income in such a model.

It may be noted that signs and magnitudes of all these comparative steady state effects are independent of the values of ${\text{s}}_{{\text{p}}}$ and ${\text{s}}_{{\text{w}}}$. So same results are obtained with a Solow (1956) savings function where ${\text{s}}_{{\text{p}}} = {\text{s}}_{{\text{w}}} = {\text{s}}$.

4.3 Ramsey problem

We solve the Ramsey problem using the representative household framework; and so we assume that all identical households save at the same rate, i.e., ${\text{s}}_{{\text{p}}} = {\text{s}}_{{\text{w}}} = {\text{s}}$. Entire capital stock is equally distributed among them. The representative household derives utility from consumption and environmental quality but derives disutility from effort. All restrictions imposed on the utility function in Sect. 2 are also valid here. The household maximizes the life time utility defined as the discounted present value of utility over the infinite time horizon. It is given by

$\mathop \int \limits_{0}^{\infty } \left[ {{\Omega }\left( {{\overline{\text{C}}},{\text{ E}}} \right) - {\text{V}}\left( {\text{e}} \right)} \right]{\text{e}}^{{ - {\rho t}}} {\text{dt}}$ with ${\uprho } > 0$.

For the sake of simplicity, we choose a specific functional from of the utility function, ${\Omega }\left( {{\overline{\text{C}}},{\text{ E}}} \right)$. It is given by

$${\Omega }\left( {{\overline{\text{C}}},{\text{ E}}} \right) = \frac{{\left( {{\overline{\text{C}}}^{{\upmu }} {\text{E}}^{{1 - {\upmu }}} } \right)^{1 - \vartheta } - 1}}{1 - \vartheta }$$

with $0 < {\upmu } < 1$ with $0 < \vartheta < 1.$

Here

$${\Omega }_{11} = {\upmu }\left( {{\upmu }\left( {1 - \vartheta } \right) - 1} \right){\overline{\text{C}}}^{{{\upmu }\left( {1 - \vartheta } \right) - 2}} {\text{E}}^{{\left( {1 - {\upmu }} \right)\left( {1 - \vartheta } \right)}} < 0;$$

$${\Omega }_{22} = \left( {1 - {\upmu }} \right)\left( {\left( {1 - {\upmu }} \right)\left( {1 - \vartheta } \right) - 1} \right){\overline{\text{C}}}^{{{\upmu }\left( {1 - \vartheta } \right)}} {\text{E}}^{{\left( {1 - {\upmu }} \right)\left( {1-\vartheta } \right)-2}} < 0;$$

and

$${\Omega }_{12} = {\upmu }\left( {1 - {\upmu }} \right)\left( {1 - \vartheta } \right){\overline{\text{C}}}^{{{\upmu }\left( {1 - \vartheta } \right) - 1}} {\text{E}}^{{\left( {1 - {\upmu }} \right)\left( {1 - \vartheta } \right) - 1}} > 0.$$

Here $\vartheta$ stands for the elasticity of marginal utility with respect to consumption. ${\uprho }$ is the constant rate of discount. ${\Omega }_{12} > 0$ ensures that consumption and environmental quality are complementary.

$$ {\overline{\text{C}}} = \left( {1 - {\text{s}}} \right){\overline{\text{Y}}} $$

is the expected level of consumption of the household and ${\overline{\text{Y}}}$ is her expected level of income. Here

$$ {\overline{\text{Y}}} = \left[ {{\text{p}}\left( {\text{e}} \right){\text{w}} + \left( {1 - {\text{p}}\left( {\text{e}} \right)} \right)\left( {1 - {\text{u}}} \right){\text{w}}^{*} + {\text{w}}^{{\text{n}}} } \right] $$

where

$${\text{w}}^{{\text{n}}} = \left( {1 - {\uptau }} \right){\text{rK}}.$$

Notations- ${\text{s}}$, ${\text{e}}$, ${\text{p}}\left( {\text{e}} \right)$, ${\Omega }$, ${\text{V}}$, ${\text{w}}^{*}$ and ${\text{w}}^{{\text{n}}}$ are already defined in Sect. 2. Expressions of ${\overline{\text{C}}}$ and ${{\overline{\text{Y}} }}$ are also taken from Sect. 2.

This objective functional is to be maximized with respect to the savings rate, ${\text{s}}$, as well as with respect to the level of effort, ${\text{e}}$; and the alternative wage income, ${\text{w}}^{*}$, is treated as a parameter in the optimization process even though its value is to be determined in the general equilibrium.

The equation of motion faced by the household is given by

$${\dot{\text{K}}} = {{\text{s}\overline{\text{Y}}}} - {\delta K}.$$

Here, ${\text{K}}$ is the state variable; and ${\text{s}}$ and ${\text{e}}$ are two control variables of this optimal control problem. Environmental quality, ${\text{E}}$, is treated as an externality to the optimization problem. So the household can not maximize the objective functional with respect to E.

The value of ${\text{w}}^{*}$ is determined endogenously in the general equilibrium equating expected wage income of the representative household to the actual average wage income of the economy. So

$${\text{p}}\left( {\text{e}} \right){\text{w}} + \left( {1 - {\text{p}}\left( {\text{e}} \right)} \right)\left( {1 - {\text{u}}} \right){\text{w}}^{*} = {\text{w}}\left( {1 - {\text{u}}} \right)$$

.

All individuals are identical and only wage income is uncertain. So expected wage income is equal to actual average wage income in the long run.

So ${\text{w}}^{*} \le {\text{w}}$ for ${\text{u}} \ge 0$. Also, in the general equilibrium, expected consumption, ${\overline{\text{C}}}$, is equal to actual consumption, ${\text{C}}$; and hence, ${\overline{\text{Y}}} = {\text{Y}}$.

We assume the existence of an interior solution to the optimization problem. Along the life time utility maximization path of the representative household, and, with endogenous value of ${\text{w}}^{*}$ in the general equilibrium, optimal time path of ${\text{K}}$ and ${\text{C}}$ satisfy following equations of motions.²³

$$ \frac{{{\dot{\text{C}}}}}{{\text{C}}} = \frac{{{\text{r}}\left( {1 - {\uptau }} \right) - {\updelta } - {\uprho }}}{{1 - {\upmu }\left( {1 - \vartheta } \right)}} - \frac{{\left( {1 - {\upmu }} \right)\left( {1 - \vartheta } \right)}}{{{\upmu }\left( {1 - \vartheta } \right) - 1}}\frac{{{\dot{\text{E}}}}}{{\text{E}}}; $$

(24)

and

$$ {\dot{\text{K}}} = {\text{wL}}\left( {1 - {\text{u}}} \right) + {\text{rK}} - {{\uptau \text{rK}}} - {\text{C}} - {\delta \text{K}}{.} $$

(25)

Equation (24) implies that the rate of growth of consumption varies positively with the rate of upgradation of environmental quality. We assume that, ${\upmu }\left( {1 - \vartheta } \right) < 1$; and this assumption ensures that ${\Omega }_{11} < 0$, i.e., utility function is concave in terms of ${\text{C}}$. Here, ${\Omega }_{11} = 0$ only if ${\upmu }\left( {1 - \vartheta } \right) = 1$; but Eq. (24) does not make sense in that case. So we can not work out this Ramsey model assuming that ${\Omega }_{11} = 0$ even though we can derive the labour efficiency function in Sect. 2 in that case.

Optimal time path of effort level, ${\text{e}}$, satisfies the following condition.

$$ {\upmu \text{C}}^{{{\upmu }\left( {1 - \vartheta } \right) - 1}} {\text{E}}^{{\left( {1 - {\upmu }} \right)\left( {1 - \vartheta } \right)}} {\text{p}^{\prime}}\left( {\text{e}} \right)\left[ {\frac{{{\text{wu}}}}{{1 - {\text{p}}\left( {\text{e}} \right)}}} \right] = {\text{V}^{\prime}}\left( {\text{e}} \right). $$

(26)

Equation (26) implies that marginal utility of effort obtained through consumption is equal to the marginal disutility of effort. The labour efficiency function is derived from this Eq. (26). So the time path of labour efficiency, $\mathrm{e}$, is conditional on the time path of $\mathrm{E}$, $\mathrm{C}$ and $\mathrm{u}$. The time path of $\mathrm{u}$ is conditional on the time path of $\mathrm{K}$ and $\mathrm{E}$.

From Eq. (26), we have²⁴

$$ \frac{{{\dot{\text{e}}}}}{{\text{e}}} = \frac{{\left\{ {{\upmu }\left( {1 - \vartheta } \right) - 1} \right\}\frac{{{\dot{\text{C}}}}}{{\text{C}}} + \frac{{{\upvarepsilon }_{{\text{E}}} }}{\Delta }\left[ {\left\{ { - {\sigma e}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right.\left. { + {\uptheta }_{{\text{K}}} \left( {1 + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right)} \right\} + {\uptheta }_{{\text{K}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}} + \left( {1 - {\upmu }} \right)\left( {1 - \vartheta } \right)} \right]\frac{{{\dot{\text{E}}}}}{{\text{E}}} + \frac{1}{\Delta }{\uptheta }_{{\text{K}}} \left( {{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}} + {\upvarepsilon }_{{\text{u}}} } \right)\frac{{{\dot{\text{K}}}}}{{\text{K}}}}}{{\frac{{\text{e}}}{{{\text{V}^{\prime}}\left( {\text{e}} \right)}}{\text{V}^{\prime\prime}}\left( {\text{e}} \right) - \left( {\frac{{{\text{p}^{\prime}}\left( {\text{e}} \right){\text{e}}}}{{\left( {1 - {\text{p}}\left( {\text{e}} \right)} \right)}} + \frac{{{\text{p}^{\prime\prime}}\left( {\text{e}} \right){\text{e}}}}{{{\text{p}^{\prime}}\left( {\text{e}} \right)}}} \right)}}. $$

(27)

So, in Eq. (27), $\frac{{{\dot{\text{e}}}}}{{\text{e}}}$ depends on $\frac{{{\dot{\text{K}}}}}{{\text{K}}}$, $\frac{{{\dot{\text{E}}}}}{{\text{E}}}$ and $\frac{{{\dot{\text{C}}}}}{{\text{C}}}$. When,

$$\frac{{{\dot{\text{C}}}}}{{\text{C}}} = \frac{{{\dot{\text{E}}}}}{{\text{E}}} = \frac{{{\dot{\text{K}}}}}{{\text{K}}} = 0,$$

we have, $\frac{{{\dot{\text{e}}}}}{{\text{e}}} = 0$. So Eq. (27) is not an independent equation of motion of the dynamic system. Equations (24), (25) and (13) are three independent equations of motion.

The equation of motion describing the intertemporal change in the environmental quality is given by Eq. (13), i.e.,

$${\dot{\text{E}}} = {{\uptau \text{rK}}} - {\upalpha \text{X}} + {\uppi \text{E}}.$$

Number of workers, ${\text{L}}$, does change over time. Hence Eq. (5) is also valid in this case.

In the long run equilibrium, ${\dot{\text{K}}} = {\dot{\text{E}}} = {\dot{\text{C}}} = 0$. Here Eq. (24) with ${\dot{\text{C}}} = 0$ and ${\dot{\text{E}}} = 0$ solves for the optimum value of ${\text{r}}$ in terms of the tax rate, ${\uptau }$; and ${\text{r}}$ is a function of ${\text{K}}$ and ${\text{E}}$. Thus ${\dot{\text{C}}} = 0$ and ${\dot{\text{E}}} = 0$ equations obtained from Eqs. (24) and (13) solve for equilibrium values of ${\text{K}}$ and ${\text{E}}$. ${\dot{\text{K}}} = 0$ equation solves for the equilibrium value of ${\text{C}}$. Equation (26) solves for the equilibrium value of ${\text{e}}$. Equation (5) solves for the equilibrium value of ${\text{u}}$. These values are also obtained in terms of the exogenous value of the tax rate, ${\uptau }$.

Stability analysis of the long run equilibrium is done using only three independent equations of motion given by Eqs. (13), (24) and (25). The long-run equilibrium is either saddle point stable or unstable.²⁵ When ${\upvarepsilon }_{{\text{E}}} {\text{u}} > {\upvarepsilon }_{{\text{u}}} \left( {1 - {\text{u}}} \right)$, a necessary condition for saddle point stability is given by

$\left( {{\uptheta }_{{\text{K}}} + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right) > 0.$

We can work out comparative steady-state effects with respect to change in the tax rate,${\uptau }$, on the equilibrium values of ${\text{K}}$ and ${\text{E}}$ when the production function is Cobb–Douglas. The comparative steady state effects are analysed²⁶ when the equilibrium is saddle point stable; and the results are summarized in the following proposition.

Proposition 5

An exogenous increase in the tax rate on rental income on capital stock raises the volume of capital stock and the level of environmental quality but lowers the unemployment rate in the new long run equilibrium if $\left( {{\uptheta }_{{\text{K}}} + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right) > 0$ and if ${\upvarepsilon }_{{\text{E}}} {\text{u}} > {\upvarepsilon }_{{\text{u}}} \left( {1 - {\text{u}}} \right)$.

So, looking at propositions 4 and 5, we find that comparative steady state results on ${\text{K}}$, ${\text{E}}$ and ${\text{u}}$ in the endogenous savings model are qualitatively similar to corresponding results obtained in the exogenous savings model. Our focus in this paper is on the comparative steady-state effects with respect to change in the tax rate.

5 Conclusion

We develop an aggregate model of economic growth and environmental pollution with only one production sector and with capital and labour as two factors. Unemployment exists in the labour market due to wage rigidity explained by the efficiency wage hypothesis. The special feature of this efficiency wage hypothesis is the efficiency enhancing effect of environment which is not considered by earlier efficiency wage models. Abatement expenditure designed to remove pollution is financed by the tax revenue obtained from a tax imposed on capital income.

We derive a few interesting results from this model. First, an exogenous improvement in environmental quality lowers efficiency wage rate and unemployment rate but raises the rental rate on capital and the level of output in the short run equilibrium. Such a result can not be obtained in earlier models as they do not consider the efficiency enhancing effect of environment. Second, an exogenous increase in capital stock raises efficiency wage rate, and the level of output but lowers the rental rate on capital and unemployment rate in the short run equilibrium. This result is easily obtained from earlier efficiency wage models because it is independent of the efficiency-enhancing effect of environment. Third, an increase in the tax rate on rental income raises the capital stock, national income and the environmental quality but lowers unemployment rate in the new long run equilibrium when tax revenue is utilized to finance abatement expenditure. This third result is not only obtained in the exogenous savings growth model but also obtained in the endogenous savings growth model where the representative household solves a Ramsey problem. However, this result can not be obtained when labour efficiency is independent of environmental quality.

Our results are not necessarily conditional only on the use of the capital income taxation even though we have justified the use of this tax on the ground of equity. If the production function is Cobb–Douglas, then both rental income on capital and labour income are proportional to total income in the competitive world. So, with Cobb–Douglas production function, we get similar comparative steady state results with respect to change in the tax rate even if taxation on rental income on capital is replaced by that on total income or on labour income. In the Cobb–Douglas world, relative competitive output shares of both the factors remains unchanged; and so the defence of capital income taxation on the ground of equity loses its strength in this case. An efficiency based analysis of alternative taxes appears to be of importance even though the present paper does not deal with that problem.

However, our model fails to consider many important aspects of reality. We ignore the financing of abatement expenditure from private sources. Utilization of tax revenue as investment to public capital accumulation is also ignored. We do not distinguish between skilled worker and unskilled worker; and this distinction is important because expansion of knowledge makes the workers aware of the benefits of environmental upgradation. We do not incorporate anti-social sector rooted from unemployment problem even though anti-social activities produce negative effects on capital accumulation as well as on environment. Due to technical complications, we analyse an exogenous growth model and do not focus on the sources of endogenous growth. Even though we solve the Ramsey problem of the household in one of the different sections, we do not analyse the properties of Ramsey-optimal tax policy of the government. However, we plan to remove all these limitations of the present exercise in our future works.

Appendices

Appendix (A)

The production function is given by

$${\text{X}} = {\text{F}}\left( {{\text{eL}},{\text{ K}}} \right);$$

where

$$ {\text{e}} = {\text{e}}\left( {{\text{w}},{\text{u}},{\text{E}}} \right) $$

is the labour efficiency function.

Profit maximizing conditions of a competitive firm are given by

$$ {\text{F}}_{1} = \frac{{\text{w}}}{{\text{e}}} $$

and ${\text{F}}_{2} = {\text{r}}$.

Since the production function satisfies constant returns to scale, from Eulers theorem, we have

$${\text{X}} = {\text{F}}_{1} {\text{ eL}} + {\text{F}}_{2} {\text{K}}.$$

So, using profit maximizing conditions, we have

$$ {\text{X}} = \frac{{\text{w}}}{{\text{e}}}{\text{ eL}} + {\text{rK}} $$

$$ \Rightarrow \frac{{\text{w}}}{{\text{e}}}{\text{ a}}_{{\text{L}}} + {\text{ra}}_{{\text{K}}} = 1 $$

where ${\text{a}}_{{\text{L}}} = \frac{{{\text{eL}}}}{{\text{X}}}$ and ${\text{a}}_{{\text{K}}} = \frac{{\text{K}}}{{\text{X}}}$ are the two input of output coefficients. Since the production function satisfies CRS, ${\text{a}}_{{\text{L}}}$ and ${\text{a}}_{{\text{K}}}$ are functions of capital-labour ratio, $\frac{{\text{K}}}{{{\text{eL}}}}$. Again profit maximizing conditions ensure that $\frac{{\text{K}}}{{{\text{eL}}}}$ is a function of factor price ratio, $\frac{{{\raise0.7ex\hbox{${\text{w}}$} \!\mathord{\left/ {\vphantom {{\text{w}} {\text{e}}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\text{e}}$}}}}{{\text{r}}}$. Hence ${\text{a}}_{{\text{L}}}$ and ${\text{a}}_{{\text{K}}}$ are also functions of $\frac{{{\raise0.7ex\hbox{${\text{w}}$} \!\mathord{\left/ {\vphantom {{\text{w}} {\text{e}}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\text{e}}$}}}}{{\text{r}}}$.

Appendix (B)

From Eqs. (1) and (2), we have

$$ {\uptheta }_{{\text{L}}} {\hat{\text{w}}} - {\uptheta }_{{\text{L}}} {\hat{\text{e}}} + {\uptheta }_{{\text{K}}} {\hat{\text{r}}} = 0; $$

(28)

and

$$ {\hat{\text{w}}} - {\hat{\text{e}}} + {\upvarepsilon }_{{\text{u}}} {\hat{\text{u}}} = - {\upvarepsilon }_{{\text{E}}} {\hat{\text{E}}}{.} $$

(29)

From Eq. (3), we obtain

$$ \frac{{\partial^{2} {\text{e}}}}{{\partial {\text{w}}^{2} }}\frac{{{\text{dw}}}}{{\text{w}}}\frac{{\left( {\text{w}} \right)^{2} }}{{\text{e}}} + \frac{{\partial {\text{e}}}}{{\partial {\text{w}}}}\frac{{{\text{dw}}}}{{\text{w}}}\frac{{\text{w}}}{{\text{e}}} - \frac{{\partial {\text{e}}}}{{\partial {\text{w}}}}\frac{{\text{w}}}{{{\text{e}}^{2} }}\left[ {\frac{{\partial {\text{e}}}}{{\partial {\text{w}}}}\frac{{{\text{dw}}}}{{\text{w}}}{\text{w}} + \frac{{\partial {\text{e}}}}{{\partial {\text{u}}}}\frac{{{\text{du}}}}{{\text{u}}}{\text{u}} + \frac{{\partial {\text{e}}}}{{\partial {\text{E}}}}\frac{{{\text{dE}}}}{{\text{E}}}{\text{E}}} \right] = 0. $$

(30)

Using Eqs. (3) and (30), we have

$$ {\text{e}}_{11} \frac{{\left( {\text{w}} \right)^{2} }}{{\text{e}}}{\hat{\text{w}}} - {\upvarepsilon }_{{\text{u}}} {\hat{\text{u}}} = {\upvarepsilon }_{{\text{E}}} {\hat{\text{E}}}{.} $$

(31)

where ${\upvarepsilon }_{{\text{u}}} = \frac{{\partial {\text{e}}}}{{\partial {\text{u}}}}\frac{{\text{u}}}{{\text{e}}} > 0$, ${\upvarepsilon }_{{\text{E}}} = \frac{{\partial {\text{e}}}}{{\partial {\text{E}}}}\frac{{\text{E}}}{{\text{e}}} > 0$ and ${\text{e}}_{11} = \frac{{\partial^{2} {\text{e}}}}{{\partial {\text{w}}^{2} }} < 0$.

From Eq. (4), we have

$$ {\uptheta }_{{\text{L}}} {{\sigma \hat{\text{W}}}} - {\uptheta }_{{\text{L}}} {{\sigma \hat{\text{e}}}} - {\uptheta }_{{\text{L}}} {{\sigma \hat{\text{r}}}} + {\hat{\text{X}}} = {\hat{\text{K}}}{.} $$

(32)

From Eq. (5), we obtain

$$ - {\uptheta }_{{\text{K}}} {{\sigma \hat{\text{W}}}} - \left( { - {\uptheta }_{{\text{K}}} {\upsigma } + 1} \right){\hat{\text{e}}} + {\uptheta }_{{\text{K}}} {{\sigma \hat{\text{r}}}} + \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}{\hat{\text{u}}} + {\hat{\text{X}}} = 0. $$

(33)

Using Eqs. (28), (29) and equations (31) to (33), we have

$$ {\hat{\text{w}}} = \frac{1}{\Delta }\left\{ { - {\uptheta }_{{\text{K}}} {\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}{\hat{\text{E}}} + {\uptheta }_{{\text{K}}} {\upvarepsilon }_{{\text{u}}} {\hat{\text{K}}}} \right\}. $$

(34)

$$ {\hat{\text{e}}} = \frac{{\left( {1 + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right)}}{\Delta }\left\{ { - {\uptheta }_{{\text{K}}} {\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}{\hat{\text{E}}} + {\uptheta }_{{\text{K}}} {\upvarepsilon }_{{\text{u}}} {\hat{\text{K}}}} \right\}. $$

(35)

$$ {\hat{\text{r}}} = \frac{1}{\Delta }\left[ { - {\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\left( {{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}{\hat{\text{E}}} - {\upvarepsilon }_{{\text{u}}} {\hat{\text{K}}}} \right)} \right]. $$

(36)

$$ {\hat{\text{u}}} = \frac{1}{\Delta }\left[ { - {\upvarepsilon }_{{\text{E}}} \left\{ { - {\sigma e}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \left. { + {\uptheta }_{{\text{K}}} \left( {1 + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right)} \right\}{\hat{\text{E}}} + {\uptheta }_{{\text{K}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}} {{\hat{\text{K}}}}\right.} \right]; $$

(37)

and

$$ {\hat{\text{X}}} = \frac{1}{\Delta }\left[ { - {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} {\uptheta }_{{\text{L}}} {\upsigma }\frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}{\hat{\text{E}}} + \left\{ { - {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{K}}} \left( {{\upvarepsilon }_{{\text{u}}} {\upsigma } + \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}} \right) + {\uptheta }_{{\text{K}}} {\upvarepsilon }_{{\text{u}}} \left( {1 + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} {{\hat{\text{K}}}} \right)} \right\}} \right]; $$

(38)

where,

$$ \Delta = - {\upvarepsilon }_{{\text{u}}} {\sigma e}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}} + {\upvarepsilon }_{{\text{u}}} {\uptheta }_{{\text{K}}} \left\{ {\left( {1 + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right) - {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\frac{{\text{u}}}{{{\upvarepsilon }_{{\text{u}}} \left( {1 - {\text{u}}} \right)}}} \right\}. $$

Equations (34) to (38) are same as Eqs. (6) to (10) in the body of the paper.

Appendix (C)

3.1 C.1 Slopes of stationary loci

We derive the slopes of two stationary loci $\dot{\mathrm{K}}=0$ and $\dot{\mathrm{E}}=0$ in this section.

Equations (12) and (13) presented below describe the rate of change in capital stock and the rate of change in environmental quality respectively.

$$ {\dot{\text{K}}} = {\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right){\text{rK}} + {\text{s}}_{{\text{w}}} \left( {1 - {\text{u}}} \right){\text{wL}} - {{\updelta K;}} $$

(12)

and

$$ {\dot{\text{E}}} = {{\uptau \text{rK}}} - {\upalpha \text{X}} + {\uppi \text{E}}{.} $$

(13)

We have ${\dot{\text{K}}} = {\dot{\text{E}}} = 0$; and hence, from Eqs. (12) and (13), we find that

$$ {\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right){\text{rK}} + {\text{s}}_{{\text{w}}} \left( {1 - {\text{u}}} \right){\text{wL}} = {{\updelta K;}} $$

(14)

and

$$ {{\uptau \text{rK}}} = {\upalpha \text{X}} - {\uppi \text{E}}{.} $$

(15)

From Eq. (14), we have

$$ \begin{aligned} & \left\{ {{\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right){\text{r}} + {\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right){\text{K}}\frac{{\partial {\text{r}}}}{{\partial {\text{K}}}} - {\text{s}}_{{\text{w}}} {\text{wL}}\frac{{\partial {\text{u}}}}{{\partial {\text{K}}}} + {\text{s}}_{{\text{w}}} \left( {1 - {\text{u}}} \right){\text{L}}\frac{{\partial {\text{w}}}}{{\partial {\text{K}}}} - {\updelta }} \right\}{\text{dK}} \hfill \\ & = - \left\{ {{\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right){\text{K}}\frac{{\partial {\text{r}}}}{{\partial {\text{E}}}} - {\text{s}}_{{\text{w}}} {\text{wL}}\frac{{\partial {\text{u}}}}{{\partial {\text{E}}}} + {\text{s}}_{{\text{w}}} \left( {1 - {\text{u}}} \right){\text{L}}\frac{{\partial {\text{w}}}}{{\partial {\text{E}}}}} \right\}{\text{dE}} \hfill \\ \end{aligned} $$

(39)

Using Eqs. (14) and (39), we have

$$ \begin{aligned} &\left\{ {{\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right){\text{K}}\frac{{\partial {\text{r}}}}{{\partial {\text{K}}}} - {\text{s}}_{{\text{w}}} \frac{{{\text{wL}}}}{{\text{K}}}\left( {1 - {\text{u}}} \right) - {\text{s}}_{{\text{w}}} {\text{wL}}\frac{{\partial {\text{u}}}}{{\partial {\text{K}}}} + {\text{s}}_{{\text{w}}} \left( {1 - {\text{u}}} \right){\text{L}}\frac{{\partial {\text{w}}}}{{\partial {\text{K}}}}} \right\}{\text{dK}}\;\;\;\left( {\text{using steady state condition}} \right) \hfill \\ & = - \left\{ {{\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right){\text{K}}\frac{{\partial {\text{r}}}}{{\partial {\text{E}}}} - {\text{s}}_{{\text{w}}} {\text{wL}}\frac{{\partial {\text{u}}}}{{\partial {\text{E}}}} + {\text{s}}_{{\text{w}}} \left( {1 - {\text{u}}} \right){\text{L}}\frac{{\partial {\text{w}}}}{{\partial {\text{E}}}}} \right\}{\text{dE}} \hfill \\ & \mathop \Rightarrow \limits^{ } \left[ {{\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right)\frac{{{\text{rK}}}}{{\text{K}}}\frac{{{\hat{\text{r}}}}}{{{\hat{\text{K}}}}} - {\text{s}}_{{\text{w}}} \left\{ {\frac{{{\text{wL}}}}{{\text{K}}}\left( {1 - {\text{u}}} \right) + \frac{{{\text{wL}}}}{{\text{K}}}{\text{u}}\frac{{{\hat{\text{u}}}}}{{{\hat{\text{K}}}}} - \left( {1 - {\text{u}}} \right)\frac{{{\text{wL}}}}{{\text{K}}}\frac{{{\hat{\text{w}}}}}{{{\hat{\text{K}}}}}} \right\}} \right]{\text{dK}} \hfill \\ & = - \left[ {{\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right)\frac{{{\text{rK}}}}{{\text{E}}}\frac{{{\hat{\text{r}}}}}{{{\hat{\text{E}}}}} + {\text{s}}_{{\text{w}}} \left\{ {\frac{{{\text{wL}}}}{{\text{E}}}\left( {1 - {\text{u}}} \right)\frac{{{\hat{\text{w}}}}}{{{\hat{\text{E}}}}} - \frac{{{\text{wL}}}}{{\text{E}}}{\text{u}}\frac{{{\hat{\text{u}}}}}{{{\hat{\text{E}}}}}} \right\}} \right]. \hfill \\ \end{aligned} $$

(40)

Using Eqs. (6), (8), (9) and (40), we obtain

$$ \begin{aligned}& \Rightarrow \left[ {{{\rm{s}}_{\rm{p}}}\left( {1 - { {\uptau }}} \right)\frac{{{\rm{rK}}}}{{\rm{K}}}\frac{1}{\Delta }{{ {\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{ {\upvarepsilon }}_{\rm{u}}} - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left\{ {\left( {1 - {\rm{u}}} \right) + {\rm{u}}\frac{1}{\Delta }{{ {\uptheta }}_{\rm{K}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}} - \left( {1 - {\rm{u}}} \right)\frac{{{{ {\uptheta }}_{\rm{K}}}{{ {\upvarepsilon }}_{\rm{u}}}}}{\Delta }} \right\}} \right]{\rm{dK}} \\& = - \left[ { - {{\rm{s}}_{\rm{p}}}\left( {1 - { {\uptau }}} \right)\frac{{{\rm{rK}}}}{{\rm{E}}}\frac{1}{\Delta }{{ {\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{ {\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}} \right. \\& \left. { +\, {{\rm{s}}_{\rm{w}}}\left[ { - \frac{{{\rm{wL}}}}{{\rm{E}}}\left( {1 - {\rm{u}}} \right)\frac{{{{{\uptheta }}_{\rm{K}}}{{ {\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}}}{\Delta }} \right.\left. { + \frac{{{\rm{wL}}}}{{\rm{E}}}{\rm{u}}\frac{1}{\Delta }{{ {\upvarepsilon }}_{\rm{E}}}\left\{ { - { {\upsigma }}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left. { + {{ {\uptheta }}_{\rm{K}}}\left( {1 + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right)} \right\}} \right.} \right]} \right]{\rm{dE}} \\& \Rightarrow \left[ {{{\rm{s}}_{\rm{p}}}\left( {1 - { {\uptau }}} \right)\frac{{{\rm{rK}}}}{{\rm{K}}}\frac{1}{\Delta }{{ {\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{ {\upvarepsilon }}_{\rm{u}}}} \right. - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\left\{ {1 - \frac{1}{\Delta }\left\{ {{{ {\upvarepsilon }}_{\rm{u}}}{{ {\uptheta }}_{\rm{K}}}\left( {1 - {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\frac{{\rm{u}}}{{{{ {\upvarepsilon }}_{\rm{u}}}\left( {1 - {\rm{u}}} \right)}}} \right)} \right.} \right. \\& \left. {\left. {\left. { - {{ {\upvarepsilon }}_{\rm{u}}}{ {\upsigma }}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}} + {{ {\upvarepsilon }}_{\rm{u}}}{{ {\uptheta }}_{\rm{K}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}} + {{ {\upvarepsilon }}_{\rm{u}}}{ {\upsigma }}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}} - {{ {\upvarepsilon }}_{\rm{u}}}{{ {\uptheta }}_{\rm{K}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right\}} \right\}} \right]{\rm{dK}} \\& = - \left[ { - {{\rm{s}}_{\rm{p}}}\left( {1 - { {\uptau }}} \right)\frac{{{\rm{rK}}}}{{\rm{E}}}\frac{1}{\Delta }{{ {\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{ {\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}} \right. \\& + {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{E}}}\frac{1}{\Delta }\left[ { - {{ {\uptheta }}_{\rm{K}}}{{ {\upvarepsilon }}_{\rm{E}}}{\rm{u}}} \right.\left. { + {\rm{u}}{{ {\upvarepsilon }}_{\rm{E}}}\left\{ { - { {\upsigma }}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left. { + {{ {\uptheta }}_{\rm{K}}}\left( {1 + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right)} \right\}} \right.} \right]{\rm{dE}}\\& \Rightarrow \left[ {{{\rm{s}}_{\rm{p}}}\left( {1 - { {\uptau }}} \right)\frac{{{\rm{rK}}}}{{\rm{K}}}\frac{1}{\Delta }{{ {\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{ {\upvarepsilon }}_{\rm{u}}}} \right. - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\left\{ {1 - \frac{1}{\Delta }\left\{ { - {{ {\upvarepsilon }}_{\rm{u}}}{ {\upsigma }}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}} + {{ {\upvarepsilon }}_{\rm{u}}}{{ {\uptheta }}_{\rm{K}}}\left\{ {\left( {1 + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right)} \right.} \right.} \right.\\& \left. {\left. {\left. {\left. { - {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\frac{{\rm{u}}}{{{{ {\upvarepsilon }}_{\rm{u}}}\left( {1 - {\rm{u}}} \right)}}} \right\} + {{ {\upvarepsilon }}_{\rm{u}}}{ {\upsigma }}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}} - {{{\upvarepsilon }}_{\rm{u}}}{{{\theta }}_{\rm{K}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right\}} \right\}} \right]{\rm{dK}}\\& = - \left[ { - {{\rm{s}}_{\rm{p}}}\left( {1 - {{\tau }}} \right)\frac{{{\rm{rK}}}}{{\rm{E}}}\frac{1}{\Delta }{{{\theta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}} \right.\\& + {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{E}}}\frac{1}{\Delta }\left[ { - {{{\theta }}_{\rm{K}}}{{{\upvarepsilon }}_{\rm{E}}}{\rm{u}}} \right.\left. { + {\rm{u}}{{{\upvarepsilon }}_{\rm{E}}}\left\{ { - {{\upsigma }}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left. { + {{{\theta }}_{\rm{K}}}\left( {1 + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right)} \right\}} \right.} \right]{\rm{dE}}\\& \Rightarrow \left[ {{{\rm{s}}_{\rm{p}}}\left( {1 - {{\tau }}} \right)\frac{{{\rm{rK}}}}{{\rm{K}}}\frac{1}{\Delta }{{{\theta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}} \right. - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\left\{ {1 - \frac{1}{\Delta }\left\{ {\Delta \left. {\left. {\left. { - {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( { - {{\upsigma }} + {{{\theta }}_{\rm{K}}}} \right)} \right\}} \right\}} \right]{\rm{dK}}} \right.} \right.\\& (from \,\,\, definition \,\,\, of \,\,\, \Delta \,\,\, from \,\,\, static \,\,\, model)\\& = - \left[ { - {{\rm{s}}_{\rm{p}}}\left( {1 - {{\tau }}} \right)\frac{{{\rm{rK}}}}{{\rm{E}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}} \right.\left. { + {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{E}}}\frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{E}}}{\rm{u}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right]{\rm{dE}}\\& \Rightarrow \left[ {{{\rm{s}}_{\rm{p}}}\left( {1 - {{\tau }}} \right)\frac{{{\rm{rK}}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}} \right. - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\left\{ {1 - 1 + \frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left. {\left. {\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right\}} \right]{\rm{dK}}} \right.\\& = - \left[ { - {{\rm{s}}_{\rm{p}}}\left( {1 - {{\tau }}} \right)\frac{{{\rm{rK}}}}{{\rm{E}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}} \right.\left. { + {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{E}}}\frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{E}}}{\rm{u}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right]{\rm{dE}} \\& \Rightarrow \left[ {{{\rm{s}}_{\rm{p}}}\left( {1 - {{\tau }}} \right)\frac{{{\rm{rK}}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}} \right. - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left. {\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right]{\rm{dK}}\\& = - \left[ { - {{\rm{s}}_{\rm{p}}}\left( {1 - {{\tau }}} \right)\frac{{{\rm{rK}}}}{{\rm{E}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}} \right.\left. { + {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{E}}}\frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{E}}}{\rm{u}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right]{\rm{dE}} \\& \Rightarrow \left[ {{{\rm{s}}_{\rm{p}}}\left( {1 - {{\tau }}} \right)\frac{{{\rm{rK}}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}} \right. - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left. {\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right]{\rm{dK}}\\& = \left[ {{{\rm{s}}_{\rm{p}}}\left( {1 - {{\tau }}} \right)\frac{{{\rm{rK}}}}{{\rm{E}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}} \right.\left. { - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{E}}}\frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{E}}}{\rm{u}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right]{\rm{dE}}\\& {\left. { \Rightarrow \frac{{{\rm{dE}}}}{{{\rm{dK}}}}} \right|_{{ {\dot \rm {K}}} = 0}} = \frac{{\rm{E}}}{{\rm{K}}}\frac{{{{{\upvarepsilon }}_{\rm{u}}}}}{{{{{\upvarepsilon }}_{\rm{E}}}}}\frac{{\left( {1 - {\rm{u}}} \right)}}{{\rm{u}}}\frac{{\left[ {{{\rm{s}}_{\rm{p}}}\left( {1 - {{\tau }}} \right){\rm{r}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}\frac{1}{{\rm{E}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\frac{1}{{\left( {1 - {\rm{u}}} \right)}}} \right. - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{{\rm{KE}}}}\frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left. {\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right]}}{{\left[ {{{\rm{s}}_{\rm{p}}}\left( {1 - {{\tau }}} \right){\rm{r}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}\frac{1}{{\rm{E}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\frac{1}{{\left( {1 - {\rm{u}}} \right)}}} \right. - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{{\rm{KE}}}}\frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left. {\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right]}}\\& \Rightarrow {\left. {\frac{{{\bf{dE}}}}{{{\bf{dK}}}}} \right|_{{\bf{\dot K}} = 0}} = \frac{{\bf{E}}}{{\bf{K}}}\frac{{{{\bf{\varepsilon }}_{\bf{u}}}}}{{{{\bf{\varepsilon }}_{\bf{E}}}}}\frac{{\left( {1 - {\bf{u}}} \right)}}{{\bf{u}}}.\end{aligned}$$

So the slope of $\dot{\mathrm{K}}=0$ stationary locus is positive and is independent of the value of $\upsigma$.

From Eq. (15), we have

$$ \begin{aligned} &\left( {{\uptau \text{K}}\frac{{\partial {\text{r}}}}{{\partial {\text{E}}}} - {\upalpha }\frac{{\partial {\text{X}}}}{{\partial {\text{E}}}} + {\uppi }} \right){\text{dE}} = - \left( {{\uptau \text{r}} + {\uptau \text{K}}\frac{{\partial {\text{r}}}}{{\partial {\text{K}}}} - {\upalpha }\frac{{\partial {\text{X}}}}{{\partial {\text{K}}}}} \right){\text{dK}} \hfill \\ & \mathop \Rightarrow \limits^{ } \left( {\frac{{{\uptau \text{X}}}}{{\text{r}}}\frac{{\text{r}}}{{\text{E}}}\frac{{{\hat{\text{r}}}}}{{{\hat{\text{E}}}}} - {\upalpha }\frac{{\text{X}}}{{\text{E}}}\frac{{{\hat{\text{X}}}}}{{{\hat{\text{E}}}}} + {\uppi }} \right){\text{dE}} = - \left( {{\uptau \text{r}} + \frac{{{\uptau \text{K}}}}{{\text{r}}}\frac{{\text{r}}}{{\text{K}}}\frac{{{\hat{\text{r}}}}}{{{\hat{\text{K}}}}} - \frac{{{\upalpha \text{X}}}}{{\text{K}}}\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}} \right){\text{dK}} \hfill \\ & \mathop \Rightarrow \limits^{ } \left\{ {\left( {\frac{{{\upalpha \text{X}}}}{{\text{E}}} - {\uppi }} \right)\left( {\frac{{{\hat{\text{r}}}}}{{{\hat{\text{E}}}}} - \frac{{{\hat{\text{X}}}}}{{{\hat{\text{E}}}}}} \right) + {\uppi }\left( {1 - \frac{{{\hat{\text{X}}}}}{{{\hat{\text{E}}}}}} \right)} \right\}{\text{dE}} = - \left\{ {\left( {\frac{{{\upalpha \text{X}} - {\uppi \text{E}}}}{{\text{K}}}} \right)\left( {1 + \frac{{{\hat{\text{r}}}}}{{{\hat{\text{K}}}}} - \frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}} \right) - \frac{{{\uppi \text{E}}}}{{\text{K}}}\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}} \right\}{\text{dK}}{.} \hfill \\ \end{aligned} $$

(41)

Using Eqs. (15) and (41), we have

$$ \mathop \Rightarrow \limits^{ } \left\{ {\left( {\frac{{{\alpha X}}}{{\text{E}}} - {\uppi }} \right)\left( {\frac{{{\hat{\text{r}}}}}{{{\hat{\text{E}}}}} - \frac{{{\hat{\text{X}}}}}{{{\hat{\text{E}}}}}} \right) + {\uppi }\left( {1 - \frac{{{\hat{\text{X}}}}}{{{\hat{\text{E}}}}}} \right)} \right\}{\text{dE}} = \left\{ { - \left( {\frac{{{\upalpha \text{X}} - {\uppi \text{E}}}}{{\text{K}}}} \right)\left( {1 + \frac{{{\hat{\text{r}}}}}{{{\hat{\text{K}}}}} - \frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}} \right) + \frac{{{\uppi \text{E}}}}{{\text{K}}}\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}} \right\}{\text{dK}}{.} $$

(42)

Using Eqs. (8), (10) and (42), we obtain

$$\begin{aligned} &\Rightarrow \left\{ {\left( {\frac{{{{\upalpha \text{X}}}}}{{\rm{E}}} - {{\uppi }}} \right)\left( { - \frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}} + \frac{1}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}{{{\uptheta }}_{\rm{L}}}{{\upsigma }}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}} \right) + {{\uppi }}\left( {1 - \frac{{{\hat{\rm X}}}}{{{\hat{\rm E}}}}} \right)} \right\}{\rm{dE}}\\& = \left[ { - \left( {\frac{{{{\upalpha \text{X}}} - {{\uppi \text{E}}}}}{{\rm{K}}}} \right)\left\{ {1 + \frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}} - \frac{1}{\Delta }\left\{ { - {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{k}}}\left( {{{{\upvarepsilon }}_{\rm{u}}}{{\upsigma }} + \frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}} \right)} \right. + {{{\uptheta }}_{\rm{K}}}\left. {{{{\upvarepsilon }}_{\rm{u}}}\left( {1 + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right)} \right\}} \right\}} \right.\\& \quad \left. { + \frac{{{\uppi \text{E}}}}{{\rm{K}}}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}} \right]{\rm{dK}}\\& \Rightarrow \left\{ {\left( {\frac{{{{\upalpha \text{X}}}}}{{\rm{E}}} - {{\uppi }}} \right)\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}\left( {{{\upsigma }} - 1} \right) + {{\uppi }}\left( {1 - \frac{{{\hat{\rm X}}}}{{{\hat{\rm E}}}}} \right)} \right\}{\rm{dE}}\\& = \left[ { - \left( {\frac{{{{\upalpha \text{X}}} - {{\uppi \text{E}}}}}{{\rm{K}}}} \right)} \right.\left[ {1 - \frac{1}{\Delta }\left[ {{{{\upvarepsilon }}_{\rm{u}}}{{{\uptheta }}_{\rm{K}}}\left\{ {\left( {1 + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right)} \right.} \right.} \right.\left. { - {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\frac{{\rm{u}}}{{{{{\upvarepsilon }}_{\rm{u}}}\left( {1 - {\rm{u}}} \right)}}} \right\}\\& \quad - {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}{{{\uptheta }}_{\rm{k}}}{{\upsigma }}\left. {\left. { - {{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}} \right]} \right] + \left. {\frac{{{{\uppi \text{E}}}}}{{\rm{K}}}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}} \right]{\rm{dK}}\\& \Rightarrow \left\{ {\left( {\frac{{{{\upalpha X}}}}{{\rm{E}}} - {{\uppi }}} \right)\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}\left( {{{\upsigma }} - 1} \right) + {{\uppi }}\left( {1 - \frac{{{\hat{\rm X}}}}{{{\hat{\rm E}}}}} \right)} \right\}{\rm{dE}}\\& = \left[ { - \left( {\frac{{{{\upalpha \text{X}}} - {{\uppi \text{E}}}}}{{\rm{K}}}} \right)} \right.\left[ {1 - \frac{1}{\Delta }\left[ {{{{\upvarepsilon }}_{\rm{u}}}{{{\uptheta }}_{\rm{K}}}\left\{ {\left( {1 + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right)} \right.} \right.} \right.\left. { - {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\frac{{\rm{u}}}{{{{{\upvarepsilon }}_{\rm{u}}}\left( {1 - {\rm{u}}} \right)}}} \right\} - {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}{{\upsigma }} + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}{{\upsigma }}\\& \quad - {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}{{{\uptheta }}_{\rm{k}}}{{\upsigma }}\left. {\left. { - {{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}} \right]} \right] + \left. {\frac{{{{\uppi \text{E}}}}}{{\rm{K}}}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}} \right]{\rm{dK}}\\& \Rightarrow \left\{ {\left( {\frac{{{{\upalpha \text{X}}}}}{{\rm{E}}} - {{\uppi }}} \right)\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}\left( {{{\upsigma }} - 1} \right) + {{\uppi }}\left( {1 - \frac{{{\hat{\rm X}}}}{{{\hat{\rm E}}}}} \right)} \right\}{\rm{dE}}\\& = \left[ { - \left( {\frac{{{{\upalpha \text{X}}} - {{\uppi \text{E}}}}}{{\rm{K}}}} \right)} \right.\left[ {1 - \frac{1}{\Delta }\left[ \Delta \right.} \right. + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}{{\upsigma }}\left. {\left( {1 - {{{\uptheta }}_{\rm{K}}}} \right)\left. { - {{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}} \right]} \right] + \left. {\frac{{{{\uppi \text{E}}}}}{{\rm{K}}}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}} \right]{\rm{dK}}\\& (from \,\,\, definition \,\,\, of \,\,\, \Delta \,\,\, from \,\,\, static \,\,\, model)\\& \Rightarrow \left\{ {\left( {\frac{{{{\upalpha \text{X}}}}}{{\rm{E}}} - {{\uppi }}} \right)\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}\left( {{{\upsigma }} - 1} \right) + {{\uppi }}\left( {1 - \frac{{{\hat{\rm X}}}}{{{\hat{\rm E}}}}} \right)} \right\}{\rm{dE}}\\& = \left[ { - \left( {\frac{{{{\upalpha \text{X}}} - {{\uppi \text{E}}}}}{{\rm{K}}}} \right)} \right.\left[ {1 - \frac{1}{\Delta }\left[ \Delta \right.} \right. + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}{{\upsigma }}\left. {{{{\uptheta }}_{\rm{L}}}\left. { - {{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}} \right]} \right] + \left. {\frac{{{{\uppi \text{E}}}}}{{\rm{K}}}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}} \right]{\rm{dK}}\\& \Rightarrow \left\{ {\left( {\frac{{{{\upalpha \text{X}}}}}{{\rm{E}}} - {{\uppi }}} \right)\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}\left( {{{\upsigma }} - 1} \right) + {{\uppi }}\left( {1 - \frac{{{\hat{\rm X}}}}{{{\hat{\rm E}}}}} \right)} \right\}{\rm{dE}}\\& = \left[ { - \left( {\frac{{{{\upalpha \text{X}}} - {{\uppi \text{E}}}}}{{\rm{K}}}} \right)} \right.\left[ {1 - \frac{1}{\Delta }\left[ \Delta \right.} \right. + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}{{\upsigma }}\left. {\left. {{{{\uptheta }}_{\rm{L}}}\left( {{{\upsigma }} - 1} \right)} \right]} \right] + \left. {\frac{{{{\uppi \text{E}}}}}{{\rm{K}}}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}} \right]{\rm{dK}}\\& \Rightarrow \left\{ {\left( {\frac{{{{\upalpha \text{X}}}}}{{\rm{E}}} - {{\uppi }}} \right)\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}\left( {{{\upsigma }} - 1} \right) + {{\uppi }}\left( {1 - \frac{{{\hat{\rm X}}}}{{{\hat{\rm E}}}}} \right)} \right\}{\rm{dE}}\\& = \left\{ {\left( {\frac{{{{\upalpha \text{X}}} - {{\uppi \text{E}}}}}{{\rm{K}}}} \right)\frac{1}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}{{{\uptheta }}_{\rm{L}}}\left( {{{\upsigma }} - 1} \right) + \frac{{{{\uppi \text{E}}}}}{{\rm{K}}}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}} \right\}{\rm{dK}}\\& {\left. {\frac{{{\rm{dE}}}}{{{\rm{dK}}}}} \right|_{{\dot{\rm E}} = 0}} = \frac{{\left\{ {\left( {\frac{{{{\upalpha \text{X}}} - {{\uppi \text{E}}}}}{{\rm{K}}}} \right)\frac{1}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}{{{\uptheta }}_{\rm{L}}}\left( {{{\upsigma }} - 1} \right) + \frac{{{{\uppi \text{E}}}}}{{\rm{K}}}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}} \right\}}}{{\left\{ {\left( {\frac{{{{\upalpha \text{X}}}}}{{\rm{E}}} - {{\uppi }}} \right)\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}\left( {{{\upsigma }} - 1} \right) + {{\uppi }}\left( {1 - \frac{{{\hat{\rm X}}}}{{{\hat{\rm E}}}}} \right)} \right\}}} \end{aligned} .$$

(43)

Now,

$$ \begin{aligned} &1 - \frac{{{\hat{\text{X}}}}}{{{\hat{\text{E}}}}} \hfill \\ & = 1 + \frac{1}{\Delta }{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} {\uptheta }_{{\text{L}}} {\upsigma }\frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}} \hfill \\& = \frac{{\Delta + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} {\uptheta }_{{\text{L}}} {\upsigma }\frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}}}{\Delta } \hfill \\& = \frac{{ - {\upvarepsilon }_{{\text{u}}} {\sigma e}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}} + {\upvarepsilon }_{{\text{u}}} {\uptheta }_{{\text{K}}} \left\{ {\left( {1 + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right) - {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\frac{{\text{u}}}{{{\upvarepsilon }_{{\text{u}}} \left( {1 - {\text{u}}} \right)}}} \right\} + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} {\uptheta }_{{\text{L}}} {\upsigma }\frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}}}{\Delta }~~(from \quad definition \quad of \quad from \quad static \quad model) \hfill \\& = \frac{1}{\Delta }\left[ { - {\upvarepsilon }_{{\text{u}}} {\sigma e}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{K}}} - {\upvarepsilon }_{{\text{u}}} {\sigma e}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} + {\upvarepsilon }_{{\text{u}}} {\uptheta }_{{\text{K}}} \left\{ {\left( {1 + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right) - {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\frac{{\text{u}}}{{{\upvarepsilon }_{{\text{u}}} \left( {1 - {\text{u}}} \right)}}} \right\}} \right. \hfill \\& \quad \left. { + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} {\uptheta }_{{\text{L}}} {\upsigma }\frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}} \right] \hfill \\ &= \frac{1}{\Delta }\left[ { - {\upvarepsilon }_{{\text{u}}} {\sigma e}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{K}}} - {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{K}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}} + {\upvarepsilon }_{{\text{u}}} {\uptheta }_{{\text{K}}} \left( {1 + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right) - {\upvarepsilon }_{{\text{u}}} {\sigma e}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} } \right. \hfill \\ & \quad \left. {+ {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} {\uptheta }_{{\text{L}}} {\upsigma }\frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}} \right] \hfill \\ &= \frac{1}{\Delta }\left[ { - {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\left( {{\upvarepsilon }_{{\text{u}}} {\uptheta }_{{\text{K}}} {\upsigma } + \frac{{{\uptheta }_{{\text{K}}} {\text{u}}}}{{\left( {1 - {\text{u}}} \right)}}} \right) + {\uptheta }_{{\text{K}}} {\upvarepsilon }_{{\text{u}}} \left( {1 + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right) + {\sigma e}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} \left( { - {\upvarepsilon }_{{\text{u}}} + {\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}} \right)} \right] \hfill \\ &= \frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}} + \frac{1}{\Delta }{\sigma e}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} \left( {{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}} - {\upvarepsilon }_{{\text{u}}} } \right) \hfill \\ \end{aligned} $$

Now from Eq. (19), we have

$\left. {\frac{{{\text{dE}}}}{{{\text{dK}}}}} \right|_{{{\dot{\text{E}}} = 0}} = \frac{{\left\{ {\left( {\frac{{{\upalpha \text{X}} - {\uppi \text{E}}}}{{\text{K}}}} \right)\frac{1}{\Delta }{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} {\uptheta }_{{\text{L}}} \left( {{\upsigma } - 1} \right) + \frac{{{\uppi \text{E}}}}{{\text{K}}}\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}} \right\}}}{{\left\{ {\left( {\frac{{{\alpha X}}}{{\text{E}}} - {\uppi }} \right)\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}\left( {{\upsigma } - 1} \right) + {\uppi }\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}} + \frac{{\uppi }}{\Delta }{\sigma e}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} \left( {{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}} - {\upvarepsilon }_{{\text{u}}} } \right)} \right\}}}$.

If ${\upsigma } = 1$, then

$\left. {\frac{{{\mathbf{dE}}}}{{{\mathbf{dK}}}}} \right|_{{{\dot{\mathbf{E}}} = 0}} = \frac{{\frac{{\mathbf{E}}}{{\mathbf{K}}}\frac{{{\hat{\mathbf{X}}}}}{{{\hat{\mathbf{K}}}}}}}{{\frac{{{\hat{\mathbf{X}}}}}{{{\hat{\mathbf{K}}}}} + \frac{1}{\Delta }{\mathbf{\sigma e}}_{11} \frac{{{\mathbf{w}}^{2} }}{{\mathbf{e}}}{{\varvec{\uptheta}}}_{{\mathbf{L}}} \left( {{{\varvec{\upvarepsilon}}}_{{\mathbf{E}}} \frac{{\mathbf{u}}}{{\left( {1 - {\mathbf{u}}} \right)}} - {{\varvec{\upvarepsilon}}}_{{\mathbf{u}}} } \right)}}$ .

Here the numerator is always positive and the denominator may be negative only if

${\upvarepsilon }_{{\text{E}}} {\text{u}} > {\upvarepsilon }_{{\text{u}}} \left( {1 - {\text{u}}} \right)$.

Only in this case, second term of the denominator is negative. If $\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}$ is very low, this denominator may be negative and hence ${\dot{\text{E}}} = 0$ locus may slope negatively.

C.2 Stability analysis of the long-run equilibrium

Jacobian matrix corresponding to the differential Eqs. (14) and (15) is given by.

${\text{J}} = \left[ {\begin{array}{*{20}c} {\frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{K}}}}} & {\frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{E}}}}} \\ {\frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{K}}}}} & {\frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{E}}}}} \\ \end{array} } \right]$.

Using Eq. (12), we have

$$ \frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{K}}}} = {\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right){\text{r}} + {\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right){\text{K}}\frac{{\partial {\text{r}}}}{{\partial {\text{K}}}} - {\text{s}}_{{\text{w}}} {\text{wL}}\frac{{\partial {\text{u}}}}{{\partial {\text{K}}}} + {\text{s}}_{{\text{w}}} \left( {1 - {\text{u}}} \right){\text{L}}\frac{{\partial {\text{w}}}}{{\partial {\text{K}}}} - {\updelta }{.} $$

(44)

Using Eqs. (14) and (39), we have

$$ \begin{gathered} \frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{K}}}} = {\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right){\text{K}}\frac{{\partial {\text{r}}}}{{\partial {\text{K}}}} - {\text{s}}_{{\text{w}}} \frac{{{\text{wL}}}}{{\text{K}}}\left( {1 - {\text{u}}} \right) - {\text{s}}_{{\text{w}}} {\text{wL}}\frac{{\partial {\text{u}}}}{{\partial {\text{K}}}} + {\text{s}}_{{\text{w}}} \left( {1 - {\text{u}}} \right){\text{L}}\frac{{\partial {\text{w}}}}{{\partial {\text{K}}}} \hfill \\ \mathop \Rightarrow \limits^{ } \frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{K}}}} = {\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right)\frac{{{\text{rK}}}}{{\text{K}}}\frac{{{\hat{\text{r}}}}}{{{\hat{\text{K}}}}} - {\text{s}}_{{\text{w}}} \left[ {\frac{{{\text{wL}}}}{{\text{K}}}\left( {1 - {\text{u}}} \right) + \frac{{{\text{wL}}}}{{\text{K}}}{\text{u}}\frac{{{\hat{\text{u}}}}}{{{\hat{\text{K}}}}} - \left( {1 - {\text{u}}} \right)\frac{{{\text{wL}}}}{{\text{K}}}\frac{{{\hat{\text{w}}}}}{{{\hat{\text{K}}}}}} \right]. \hfill \\ \end{gathered} $$

(45)

Using Eqs. (6), (8), (9) and (45), we obtain

$$\begin{aligned} &\frac{{\partial {\dot{\rm K}}}}{{\partial {\rm{K}}}} = {{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right)\frac{{{\rm{rK}}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}} - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left[ {\left( {1 - {\rm{u}}} \right) + {\rm{u}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{K}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}} - \left( {1 - {\rm{u}}} \right)\frac{{{{{\uptheta }}_{\rm{K}}}{{{\upvarepsilon }}_{\rm{u}}}}}{\Delta }} \right]\\& \Rightarrow \frac{{\partial {\dot{\rm K}}}}{{\partial {\rm{K}}}} = {{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right)\frac{{{\rm{rK}}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}} - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left[ {\left( {1 - {\rm{u}}} \right) + {\rm{u}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{K}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}} - \left( {1 - {\rm{u}}} \right)\frac{{{{{\uptheta }}_{\rm{K}}}{{{\upvarepsilon }}_{\rm{u}}}}}{\Delta }} \right]\\& \Rightarrow \frac{{\partial {\dot{\rm K}}}}{{\partial {\rm{K}}}} = {{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right)\frac{{{\rm{rK}}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}} - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\left\{ {1 - \frac{1}{\Delta }\left\{ {{{{\upvarepsilon }}_{\rm{u}}}{{{\uptheta }}_{\rm{K}}}\left( {1 - {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\frac{{\rm{u}}}{{{{{\upvarepsilon }}_{\rm{u}}}\left( {1 - {\rm{u}}} \right)}}} \right)} \right.} \right.\\& \left. {\left. { - {{{\upvarepsilon }}_{\rm{u}}}{{\upsigma }}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}} + {{{\upvarepsilon }}_{\rm{u}}}{{{\uptheta }}_{\rm{K}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}} + {{{\upvarepsilon }}_{\rm{u}}}{{\upsigma }}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}} - {{{\upvarepsilon }}_{\rm{u}}}{{{\uptheta }}_{\rm{K}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right\}} \right\}\\& \Rightarrow \frac{{\partial {\dot{\rm K}}}}{{\partial {\rm{K}}}} = {{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right)\frac{{{\rm{rK}}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}} - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\left\{ {1 - \frac{1}{\Delta }\left\{ { - {{{\upvarepsilon }}_{\rm{u}}}{{\upsigma }}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}} + {{{\upvarepsilon }}_{\rm{u}}}{{{\uptheta }}_{\rm{K}}}\left\{ {\left( {1 + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right)} \right.} \right.} \right.\\& \left. {\left. {\left. { - {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\frac{{\rm{u}}}{{{{{\upvarepsilon }}_{\rm{u}}}\left( {1 - {\rm{u}}} \right)}}} \right\} + {{{\upvarepsilon }}_{\rm{u}}}{{\upsigma }}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}} - {{{\upvarepsilon }}_{\rm{u}}}{{{\uptheta }}_{\rm{K}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right\}} \right\}\\& \Rightarrow \frac{{\partial {\dot{\rm K}}}}{{\partial {\rm{K}}}} = {{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right)\frac{{{\rm{rK}}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}} - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\left\{ {1 - \frac{1}{\Delta }\left\{ {\Delta \left. {\left. { - {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right\}} \right\}} \right.} \right.\\ & (from \quad definition \quad of \quad \Delta \quad from \quad static \quad model)\\& \Rightarrow \frac{{\partial {\dot{\rm K}}}}{{\partial {\rm{K}}}} = {{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right)\frac{{{\rm{rK}}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}} - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\left\{ {1 - 1 + \frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right\}\\& \Rightarrow \frac{{\partial {\dot{\rm K}}}}{{\partial {\rm{K}}}} = {{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right)\frac{{{\rm{rK}}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}} - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right).\end{aligned}$$

(46)

If ${\upsigma } = 1$, then

$$ \frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{K}}}} = {\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right)\frac{{{\text{rK}}}}{{\text{K}}}\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} + {\text{s}}_{{\text{w}}} \frac{{{\text{wL}}}}{{\text{K}}}\left( {1 - {\text{u}}} \right)\frac{1}{\Delta }{\upvarepsilon }_{{\text{u}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} $$

$$ \mathop \Rightarrow \limits^{ } \frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{K}}}} = \frac{1}{\Delta }{\uptheta }_{{\text{L}}} \frac{1}{{\text{K}}}{\delta e}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} \left\{ {{\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right){\text{rK}} + {\text{s}}_{{\text{w}}} \left( {1 - {\text{u}}} \right){\text{wL}}} \right\} $$

$$\Rightarrow \frac{{\partial {\dot{\mathbf{K}}}}}{{\partial {\mathbf{K}}}} = \frac{1}{\Delta }{{\varvec{\uptheta}}}_{{\mathbf{L}}} {\boldsymbol{\delta} \mathbf{e}}_{11} \frac{{{\mathbf{w}}^{2} }}{{\mathbf{e}}}{{\varvec{\upvarepsilon}}}_{{\mathbf{u}}} < 0. ~~(\text{Using} ~~\text{Eq}. ~(14))$$

Using Eq. (12), we have

$$ \begin{gathered} \frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{E}}}} = {\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right){\text{K}}\frac{{\partial {\text{r}}}}{{\partial {\text{E}}}} - {\text{s}}_{{\text{w}}} {\text{wL}}\frac{{\partial {\text{u}}}}{{\partial {\text{E}}}} + {\text{s}}_{{\text{w}}} \left( {1 - {\text{u}}} \right){\text{L}}\frac{{\partial {\text{w}}}}{{\partial {\text{E}}}} \hfill \\ \mathop \Rightarrow \limits^{ } \frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{E}}}} = {\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right)\frac{{{\text{rK}}}}{{\text{E}}}\frac{{{\hat{\text{r}}}}}{{{\hat{\text{E}}}}} + {\text{s}}_{{\text{w}}} \left[ {\frac{{{\text{wL}}}}{{\text{E}}}\left( {1 - {\text{u}}} \right)\frac{{{\hat{\text{w}}}}}{{{\hat{\text{E}}}}} - \frac{{{\text{wL}}}}{{\text{E}}}{\text{u}}\frac{{{\hat{\text{u}}}}}{{{\hat{\text{E}}}}}} \right]. \hfill \\ \end{gathered} $$

(47)

Using Eqs. (6), (8), (9) and (43), we obtain

$$ \begin{aligned} & \frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{E}}}} = - {\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right)\frac{{{\text{rK}}}}{{\text{E}}}\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}} \hfill \\ &\quad+ {\text{s}}_{{\text{w}}} \left[ { - \frac{{{\text{wL}}}}{{\text{E}}}\left( {1 - {\text{u}}} \right)\frac{{{\uptheta }_{{\text{K}}} {\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}}}{\Delta }} \right.\left. { + \frac{{{\text{wL}}}}{{\text{E}}}{\text{u}}\frac{1}{\Delta }{\upvarepsilon }_{{\text{E}}} \left\{ { - {\sigma e}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\left. { + {\uptheta }_{{\text{K}}} \left( {1 + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right)} \right\}} \right.} \right] \hfill \\ & \mathop \Rightarrow \limits^{ } \frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{E}}}} = - {\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right)\frac{{{\text{rK}}}}{{\text{E}}}\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}} \hfill \\ & \quad + {\text{s}}_{{\text{w}}} \frac{{{\text{wL}}}}{{\text{E}}}\frac{1}{\Delta }\left[ { - {\uptheta }_{{\text{K}}} {\upvarepsilon }_{{\text{E}}} {\text{u}}} \right.\left. { + {{\text{u}\upvarepsilon }}_{{\text{E}}} \left\{ { - {\sigma e}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\left. { + {\uptheta }_{{\text{K}}} \left( {1 + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right)} \right\}} \right.} \right] \hfill \\ & \mathop \Rightarrow \limits^{ } \frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{E}}}} = - {\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right)\frac{{{\text{rK}}}}{{\text{E}}}\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}} + {\text{s}}_{{\text{w}}} \frac{{{\text{wL}}}}{{\text{E}}}\frac{1}{\Delta }{\upvarepsilon }_{{\text{E}}} {\text{ue}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\left( { - {\upsigma } + {\uptheta }_{{\text{K}}} } \right). \hfill \\ \end{aligned} $$

(48)

If ${\upsigma } = 1$, then

$$\begin{aligned} &\frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{K}}}} = {\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right)\frac{{{\text{rK}}}}{{\text{K}}}\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} + {\text{s}}_{{\text{w}}} \frac{{{\text{wL}}}}{{\text{K}}}\left( {1 - {\text{u}}} \right)\frac{1}{\Delta }{\upvarepsilon }_{{\text{u}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} \\ & \Rightarrow \frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{K}}}} = \frac{1}{\Delta }{\uptheta }_{{\text{L}}} \frac{1}{{\text{K}}}{\delta e}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} \left\{ {{\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right){\text{rK}} + {\text{s}}_{{\text{w}}} \left( {1 - {\text{u}}} \right){\text{wL}}} \right\} \\ &\Rightarrow \frac{{\partial {\dot{\mathbf{K}}}}}{{\partial {\mathbf{K}}}} = \frac{1}{\Delta }{{\varvec{\uptheta}}}_{{\mathbf{L}}} {\boldsymbol{\delta} e}_{11} \frac{{{\mathbf{w}}^{2} }}{{\mathbf{e}}}{{\varvec{\upvarepsilon}}}_{{\mathbf{u}}} > 0. \, (\text{Using}~~ \text{Eq}.~~ (14)) \end{aligned}$$

Using Eq. (13), we have

$$ \begin{aligned} &\frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{K}}}} = {\uptau \text{r}} + {\uptau \text{K}}\frac{{\partial {\text{r}}}}{{\partial {\text{K}}}} - {\upalpha }\frac{{\partial {\text{X}}}}{{\partial {\text{K}}}} \hfill \\ &\Rightarrow \frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{K}}}} = {\uptau \text{r}} + \frac{{{\uptau \text{K}}}}{{\text{r}}}\frac{{\text{r}}}{{\text{K}}}\frac{{{\hat{\text{r}}}}}{{{\hat{\text{K}}}}} - \frac{{{\upalpha \text{X}}}}{{\text{K}}}\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}. \hfill \\ \end{aligned} $$

(49)

From Eq. (15) and (49), we obtain

$$ \frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{K}}}} = \left( {\frac{{{\upalpha \text{X}} - {\uppi \text{E}}}}{{\text{K}}}} \right)\left( {1 + \frac{{{\hat{\text{r}}}}}{{{\hat{\text{K}}}}} - \frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}} \right) - \frac{{{\uppi \text{E}}}}{{\text{K}}}\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}. $$

(50)

From Eq. (8), (10) and (50), we have

$$\begin{aligned}&\frac{{\partial {\dot{\rm E}}}}{{\partial {\rm{K}}}} = \left( {\frac{{{{\upalpha \text{X}}} - {{\uppi \text{E}}}}}{{\rm{K}}}} \right)\left\{ {1 + \frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{ {\upvarepsilon }}_{\rm{u}}} - \frac{1}{\Delta }\left\{ { - {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{k}}}\left( {{{{\varepsilon }}_{\rm{u}}}{{\upsigma }} + \frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}} \right)} \right. + {{{\uptheta }}_{\rm{K}}}\left. {{{{\upvarepsilon }}_{\rm{u}}}\left( {1 + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right)} \right\}} \right\}\\& \quad - \frac{{{{\uppi \text{E}}}}}{{\rm{K}}}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}\\& \Rightarrow \frac{{\partial {\dot{\rm E}}}}{{\partial {\rm{K}}}} = \left( {\frac{{{{\upalpha \text{X}}} - {{\uppi \text{E}}}}}{{\rm{K}}}} \right)\left[ {1 - \frac{1}{\Delta }\left[ {{{{\upvarepsilon }}_{\rm{u}}}{{{\uptheta }}_{\rm{K}}}\left\{ {\left( {1 + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right)} \right.} \right.} \right.\left. { - {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\frac{{\rm{u}}}{{{{{\upvarepsilon }}_{\rm{u}}}\left( {1 - {\rm{u}}} \right)}}} \right\}\\&\quad - {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}{{{\uptheta }}_{\rm{k}}}{{\upsigma }}\left. {\left. { - {{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}} \right]} \right] - \frac{{{{\uppi \text{E}}}}}{{\rm{K}}}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}\\& \Rightarrow \frac{{\partial {\dot{\rm E}}}}{{\partial {\rm{K}}}} = \left( {\frac{{{{\upalpha \text{X}}} - {{\uppi \text{E}}}}}{{\rm{K}}}} \right)\left[ {1 - \frac{1}{\Delta }\left[ {{{{\upvarepsilon }}_{\rm{u}}}{{{\uptheta }}_{\rm{K}}}\left\{ {\left( {1 + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right)} \right.} \right.} \right.\left. { - {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\frac{{\rm{u}}}{{{{{\upvarepsilon }}_{\rm{u}}}\left( {1 - {\rm{u}}} \right)}}} \right\} - {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}{{\upsigma }} + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}{{\upsigma }}\\& \quad - {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}{{{\uptheta }}_{\rm{k}}}{ {\upsigma }}\left. {\left. { - {{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}} \right]} \right] - \frac{{{{\uppi \text{E}}}}}{{\rm{K}}}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}\\& \Rightarrow \frac{{\partial {\dot{\rm E}}}}{{\partial {\rm{K}}}} = \left( {\frac{{{{\upalpha \text{X}}} - {{\uppi \text{E}}}}}{{\rm{K}}}} \right)\left[ {1 - \frac{1}{\Delta }\left[ \Delta + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}{{\upsigma }} {\left( {1 - {{{\uptheta }}_{\rm{K}}}} \right)\left. { - {{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}} \right]} \right]} \right. - \frac{{{{\uppi \text{E}}}}}{{\rm{K}}}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}\\& \Rightarrow \frac{{\partial {\dot{\rm E}}}}{{\partial {\rm{K}}}} = \left( {\frac{{{{\upalpha \text{X}}} - {{\uppi \text{E}}}}}{{\rm{K}}}} \right)\left[ {1 - \frac{1}{\Delta }\left[ \Delta + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}{{\upsigma }} {{{{\uptheta }}_{\rm{L}}}\left. { - {{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}} \right]} \right]} \right. - \frac{{{{\uppi \text{E}}}}}{{\rm{K}}}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}\\& \Rightarrow \frac{{\partial {\dot{\rm E}}}}{{\partial {\rm{K}}}} = \left( {\frac{{{{\upalpha \text{X}}} - {{\uppi \text{E}}}}}{{\rm{K}}}} \right)\left[ {1 - \frac{1}{\Delta }\left[ \Delta {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}{{\upsigma }} {{{{\uptheta }}_{\rm{L}}}\left( {{{\upsigma }} - 1} \right)} \right]} \right] - \frac{{{{\uppi \text{E}}}}}{{\rm{K}}}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}\\& \Rightarrow \frac{{\partial {\dot{\rm E}}}}{{\partial {\rm{K}}}} = - \left( {\frac{{{{\upalpha \text{X}}} - {{\uppi \text{E}}}}}{{\rm{K}}}} \right)\frac{1}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}{{{\uptheta }}_{\rm{L}}}\left( {{{\upsigma }} - 1} \right) - \frac{{{{\uppi \text{E}}}}}{{\rm{K}}}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}.\end{aligned}$$

If ${\upsigma } = 1,$ then.

$$\frac{{\partial {\dot{\mathbf{E}}}}}{{\partial {\mathbf{K}}}} = - \frac{{{\mathbf{\pi E}}}}{{\mathbf{K}}}\frac{{{\hat{\mathbf{X}}}}}{{{\hat{\mathbf{K}}}}} < 0.$$

Using Eq. (13), we have

$$ \begin{aligned} &\frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{E}}}} = {\uptau \text{K}}\frac{{\partial {\text{r}}}}{{\partial {\text{E}}}} - {\upalpha }\frac{{\partial {\text{X}}}}{{\partial {\text{E}}}} + {\uppi } \\ & \mathop \Rightarrow \limits^{ } \frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{E}}}} = \frac{{{\uptau X}}}{{\text{r}}}\frac{{\text{r}}}{{\text{E}}}\frac{{{\hat{\text{r}}}}}{{{\hat{\text{E}}}}} - {\upalpha }\frac{{\text{X}}}{{\text{E}}}\frac{{{\hat{\text{X}}}}}{{{\hat{\text{E}}}}} + {\uppi } \\ & \mathop \Rightarrow \limits^{ } \frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{E}}}} = \left( {\frac{{{\upalpha \text{X}}}}{{\text{E}}} - {\uppi }} \right)\left( {\frac{{{\hat{\text{r}}}}}{{{\hat{\text{E}}}}} - \frac{{{\hat{\text{X}}}}}{{{\hat{\text{E}}}}}} \right) + {\uppi }\left( {1 - \frac{{{\hat{\text{X}}}}}{{{\hat{\text{E}}}}}} \right). \end{aligned}$$

(51)

From Eq. (15) and (51), we obtain

$$ \begin{aligned}& \frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{E}}}} = \left( {\frac{{{\upalpha \text{X}}}}{{\text{E}}} - {\uppi }} \right)\left( {\frac{{{\hat{\text{r}}}}}{{{\hat{\text{E}}}}} - \frac{{{\hat{\text{X}}}}}{{{\hat{\text{E}}}}}} \right) + {\uppi }\left( {1 - \frac{{{\hat{\text{X}}}}}{{{\hat{\text{E}}}}}} \right) \hfill \\ & \Rightarrow \frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{E}}}} = \left( {\frac{{{\upalpha \text{X}}}}{{\text{E}}} - {\uppi }} \right)\left( { - \frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}} + \frac{1}{\Delta }{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} {\uptheta }_{{\text{L}}} {\upsigma }\frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}} \right) + {\uppi }\left( {1 - \frac{{{\hat{\text{X}}}}}{{{\hat{\text{E}}}}}} \right) \hfill \\ & \Rightarrow \frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{E}}}} = \left( {\frac{{{\upalpha \text{X}}}}{{\text{E}}} - {\uppi }} \right)\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}\left( {{\upsigma } - 1} \right) + {\uppi }\left( {1 - \frac{{{\hat{\text{X}}}}}{{{\hat{\text{E}}}}}} \right) \hfill \\ & \Rightarrow \frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{E}}}} = \left( {\frac{{{\upalpha \text{X}}}}{{\text{E}}} - {\uppi }} \right)\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}\left( {{\upsigma } - 1} \right) + {\uppi }\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}} + \frac{{\uppi }}{\Delta }{\sigma e}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} \left( {{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}} - {\upvarepsilon }_{{\text{u}}} } \right). \hfill \\ \end{aligned} $$

If ${\upsigma } = 1$, then

$\frac{{\partial {\dot{\mathbf{E}}}}}{{\partial {\mathbf{E}}}} = {{\varvec{\uppi}}}\frac{{{\hat{\mathbf{X}}}}}{{{\hat{\mathbf{K}}}}} + \frac{{{\varvec{\uppi}}}}{\Delta }{\mathbf{e}}_{11} \frac{{{\mathbf{w}}^{2} }}{{\mathbf{e}}}{{\varvec{\uptheta}}}_{{\mathbf{L}}} \left( {{{\varvec{\upvarepsilon}}}_{{\mathbf{E}}} \frac{{\mathbf{u}}}{{\left( {1 - {\mathbf{u}}} \right)}} - {{\varvec{\upvarepsilon}}}_{{\mathbf{u}}} } \right).$

Here, $\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}} > 0$. However, if ${\upvarepsilon }_{{\text{E}}} {\text{u}} > {\upvarepsilon }_{{\text{u}}} \left( {1 - {\text{u}}} \right)$ and if $\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}$ is very low, then $\frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{E}}}}$ may be negative.

Jacobian Determinant, ${\text{J}}$, is given by

$$\begin{aligned}&{\rm{J}} = \left\{ {{{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right)\frac{{{\rm{rK}}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}} - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right\}\\& \left\{ {\left( {\frac{{{\alpha {\rm X}}}}{{\rm{E}}} - {{\uppi }}} \right)\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}\left( {{{\upsigma }} - 1} \right) + {{\uppi }}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}} + \frac{{{\uppi }}}{\Delta }{{\upsigma }}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{L}}}\left( {{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}} - {{{\upvarepsilon }}_{\rm{u}}}} \right)} \right\} + \\& \left\{ { - {{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right)\frac{{{\rm{rK}}}}{{\rm{E}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}} + {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{E}}}\frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{E}}}{\rm{u}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right\}\\& \left\{ {\left( {\frac{{{\alpha{\rm X}} - {{\uppi E}}}}{{\rm{K}}}} \right)\frac{1}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}{{{\uptheta }}_{\rm{L}}}\left( {{{\upsigma }} - 1} \right) + \frac{{{{\uppi E}}}}{{\rm{K}}}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}} \right\}\\& = \left\{ {{{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right)\frac{{{\rm{rK}}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}} - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right\}\\& \left\{ {{{\uppi }}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}} + \frac{{{\uppi }}}{\Delta }{{\upsigma }}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{L}}}\left( {{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}} - {{{\upvarepsilon }}_{\rm{u}}}} \right)} \right\} + \\& \left\{ { - {{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right)\frac{{{\rm{rK}}}}{{\rm{E}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}} + {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{E}}}\frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{E}}}{\rm{u}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right\}\frac{{{{\uppi E}}}}{{\rm{K}}}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}\\& = {{\uppi }}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}\left\{ {{{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right)\frac{{\rm{r}}}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}} - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right.\\& \left. { - {{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right)\frac{{{\rm{rK}}}}{{\rm{E}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}} + {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{E}}}\frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{E}}}{\rm{u}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right\} + \\& \frac{{{\uppi }}}{\Delta }{{\upsigma }}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{L}}}\left( {{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}} - {{{\upvarepsilon }}_{\rm{u}}}} \right)\\& \left\{ {{{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right)\frac{{\rm{r}}}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}} - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right\}\\& = {{\uppi }}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}\left\{ {{{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right)\frac{{\rm{r}}}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( {{{{\upvarepsilon }}_{\rm{u}}} - {{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}} \right) - \left. {{{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\frac{1}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)\left( {{{{\upvarepsilon }}_{\rm{u}}} - {{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}} \right)} \right\}} \right.\\& + \frac{{{\uppi }}}{\Delta }{{\upsigma }}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{L}}}\left( {{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}} - {{{\upvarepsilon }}_{\rm{u}}}} \right)\\& \left\{ {{{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right)\frac{{\rm{r}}}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}} - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right\}\\& = {{\uppi }}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}\left( {{{{\upvarepsilon }}_{\rm{u}}} - {{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}} \right)\left\{ {{{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right)\frac{{\rm{r}}}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}} - \left. {{{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\frac{1}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right\}} \right.\\& - \frac{{{\uppi }}}{\Delta }{{\upsigma }}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{L}}}\left( {{{{\upvarepsilon }}_{\rm{u}}} - {{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}} \right)\\& \left\{ {{{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right)\frac{{\rm{r}}}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}} - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right\}\\& = {{\uppi }}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}\left( {{{{\upvarepsilon }}_{\rm{u}}} - {{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}} \right)\left\{ {{{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right)\frac{{\rm{r}}}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}} - \left. {{{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\frac{1}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right\}} \right.\\& - \frac{{{\uppi }}}{\Delta }{{\upsigma }}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{L}}}{{{\upvarepsilon }}_{\rm{u}}}\left( {{{{\upvarepsilon }}_{\rm{u}}} - {{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}} \right)\\& \left\{ {{{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right)\frac{{\rm{r}}}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}} - \left. {{{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\frac{1}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right\}} \right.\\& = {{\uppi }}\left( {{{{\upvarepsilon }}_{\rm{u}}} - {{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}} \right)\left\{ {{{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right)\frac{{\rm{r}}}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}} - \left. {{{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\frac{1}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right\}} \right.\\& \left\{ {\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}} - \frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{L}}}{{{\upvarepsilon }}_{\rm{u}}}} \right\}\\& = {{\uppi }}\left( {{{{\upvarepsilon }}_{\rm{u}}} - {{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}} \right)\frac{1}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left\{ {{{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right){\rm{r}}{{{\uptheta }}_{\rm{L}}} - \left. {{{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right\}} \right.\\& \left\{ {\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}} - \frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{L}}}{{{\upvarepsilon }}_{\rm{u}}}} \right\}\end{aligned}$$

If ${\upsigma } = 1$, then

$$ \begin{aligned} &\Rightarrow {\text{J}} = {\uppi }\left( {{\upvarepsilon }_{{\text{u}}} - {\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}} \right)\frac{1}{\Delta }{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} \frac{1}{{\text{K}}}\left\{ {{\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right){\text{rk}} + \left. {{\text{s}}_{{\text{w}}} \left( {1 - {\text{u}}} \right){\text{wL}}} \right\}} \right. \\ & \left\{ {\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}} - \frac{1}{\Delta }{\upvarepsilon }_{{\text{u}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} {\upvarepsilon }_{{\text{u}}} } \right\} \end{aligned} $$

$\mathop \Rightarrow \limits^{ } {\mathbf{J}} = \left( {{{\varvec{\upvarepsilon}}}_{{\mathbf{u}}} - {{\varvec{\upvarepsilon}}}_{{\mathbf{E}}} \frac{{\mathbf{u}}}{{\left( {1 - {\mathbf{u}}} \right)}}} \right)\frac{{{\varvec{\uppi}}}}{\Delta }{\mathbf{\delta \theta }}_{{\mathbf{L}}} {\mathbf{e}}_{11} \frac{{{\mathbf{w}}^{2} }}{{\mathbf{e}}}\left( {\frac{{{\hat{\mathbf{X}}}}}{{{\hat{\mathbf{K}}}}} - \frac{1}{\Delta }{{\varvec{\upvarepsilon}}}_{{\mathbf{u}}} {\mathbf{e}}_{11} \frac{{{\mathbf{w}}^{2} }}{{\mathbf{e}}}{{\varvec{\uptheta}}}_{{\mathbf{L}}} {{\varvec{\upvarepsilon}}}_{{\mathbf{u}}} } \right) > 0$ (Using Eq. (14))

if ${\upvarepsilon }_{{\text{E}}} {\text{u}} > {\upvarepsilon }_{{\text{u}}} \left( {1 - {\text{u}}} \right)$.

Trace of Jacobian Matrix is $= \frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{K}}}} + \frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{E}}}}$.

Here,

$$ \begin{aligned} &\frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{K}}}} + \frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{E}}}} \hfill \\ & = {\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right)\frac{{{\text{rK}}}}{{\text{K}}}\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} - {\text{s}}_{{\text{w}}} \frac{{{\text{wL}}}}{{\text{K}}}\left( {1 - {\text{u}}} \right)\frac{1}{\Delta }{\upvarepsilon }_{{\text{u}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\left( { - {\upsigma } + {\uptheta }_{{\text{K}}} } \right) \hfill \\ &\quad + \left( {\frac{{{\upalpha \text{X}}}}{{\text{E}}} - {\uppi }} \right)\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}\left( {{\upsigma } - 1} \right) + {\uppi }\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}} + \frac{{\uppi }}{\Delta }{\sigma e}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} \left( {{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}} - {\upvarepsilon }_{{\text{u}}} } \right) \hfill \\ \end{aligned} $$

If ${\upsigma } = 1$, then

Trace of Jacobian Matrix

$$= \frac{1}{\Delta }{{\varvec{\uptheta}}}_{{\mathbf{L}}} {\mathbf{\delta e}}_{11} \frac{{{\mathbf{w}}^{2} }}{{\mathbf{e}}}{{\varvec{\upvarepsilon}}}_{{\mathbf{u}}} + {{\varvec{\uppi}}}\frac{{{\hat{\mathbf{X}}}}}{{{\hat{\mathbf{K}}}}} + \frac{{{\varvec{\uppi}}}}{\Delta }{\mathbf{e}}_{11} \frac{{{\mathbf{w}}^{2} }}{{\mathbf{e}}}{{\varvec{\uptheta}}}_{{\mathbf{L}}} \left( {{{\varvec{\upvarepsilon}}}_{{\mathbf{E}}} \frac{{\mathbf{u}}}{{\left( {1 - {\mathbf{u}}} \right)}} - {{\varvec{\upvarepsilon}}}_{{\mathbf{u}}} } \right).$$

Here the first term is always negative and the third term is also negative if

${\upvarepsilon }_{{\text{E}}} {\text{u}} > {\upvarepsilon }_{{\text{u}}} \left( {1 - {\text{u}}} \right)$.

However, the second term, ${\uppi }\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}} > 0$. If $\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}$ is very low, then trace may be negative and the steady state equilibrium may be stable.

Appendix (D)

From Eq. (14), we have

$$ \begin{aligned} &\left\{ {{\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right){\text{r}} + {\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right){\text{K}}\frac{{\partial {\text{r}}}}{{\partial {\text{K}}}} - {\text{s}}_{{\text{w}}} {\text{wL}}\frac{{\partial {\text{u}}}}{{\partial {\text{K}}}} + {\text{s}}_{{\text{w}}} \left( {1 - {\text{u}}} \right){\text{L}}\frac{{\partial {\text{w}}}}{{\partial {\text{K}}}} - {\updelta }} \right\}\frac{{{\text{dK}}}}{{{\text{d}\uptau}}} \hfill \\&\quad + \left\{ {{\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right){\text{K}}\frac{{\partial {\text{r}}}}{{\partial {\text{E}}}} - {\text{s}}_{{\text{w}}} {\text{wL}}\frac{{\partial {\text{u}}}}{{\partial {\text{E}}}} + {\text{s}}_{{\text{w}}} \left( {1 - {\text{u}}} \right){\text{L}}\frac{{\partial {\text{w}}}}{{\partial {\text{E}}}}} \right\}\frac{{{\text{dE}}}}{{{\text{d}\uptau}}} = {\text{rK}} \hfill \\ \end{aligned} $$

(52)

Using Eqs. (6), (8), (9) and (40), we obtain

$$ \begin{aligned}& \left[ {{\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right)\frac{{{\text{rK}}}}{{\text{K}}}\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} } - {\text{s}}_{{\text{w}}} \frac{{{\text{wL}}}}{{\text{K}}}\left( {1 - {\text{u}}} \right)\frac{1}{\Delta }{\upvarepsilon }_{{\text{u}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}} {\left( { - {\upsigma } + {\uptheta }_{{\text{K}}} } \right)} \right]\frac{{{\text{dK}}}}{{{\text{d}\uptau}}} \hfill \\ & - \left[ {{\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right)\frac{{{\text{rK}}}}{{\text{E}}}\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}} \right.\left. { - {\text{s}}_{{\text{w}}} \frac{{{\text{wL}}}}{{\text{E}}}\frac{1}{\Delta }{\upvarepsilon }_{{\text{E}}} {\text{ue}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\left( { - {\upsigma } + {\uptheta }_{{\text{K}}} } \right)} \right]\frac{{{\text{dE}}}}{{{\text{d}\uptau}}} = {\text{rK}} \hfill \\ &\mathop \Rightarrow \limits^{ } \left[ {\frac{1}{\Delta }{{\updelta \uptheta }}_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} } + {\text{s}}_{{\text{w}}} \frac{{{\text{wL}}}}{{\text{K}}}\left( {1 - {\text{u}}} \right)\frac{1}{\Delta }{\upvarepsilon }_{{\text{u}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}} {\left( {{\upsigma } - 1} \right)} \right]\frac{{{\text{dK}}}}{{{\text{d}\uptau}}} \hfill \\ &- \left[ {\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}} \right.\left. {\frac{{{\delta K}}}{{\text{E}}} + {\text{s}}_{{\text{w}}} \frac{{{\text{wL}}}}{{\text{E}}}\frac{1}{\Delta }{\upvarepsilon }_{{\text{E}}} {\text{ue}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\left( {{\upsigma } - 1} \right)} \right]\frac{{{\text{dE}}}}{{{\text{d}\uptau}}} = {\text{rK}}. \hfill \\ \end{aligned} $$

(53)

From Eq. (15), we have

$$ \left( {{\tau \text{r}} + {\tau \text{K}}\frac{{\partial {\text{r}}}}{{\partial {\text{K}}}} - {\upalpha }\frac{{\partial {\text{X}}}}{{\partial {\text{K}}}}} \right)\frac{{{\text{dK}}}}{{{\text{d}\uptau}}} + \left( {{\tau \text{K}}\frac{{\partial {\text{r}}}}{{\partial {\text{E}}}} - {\upalpha }\frac{{\partial {\text{X}}}}{{\partial {\text{E}}}} + {\uppi }} \right)\frac{{{\text{dE}}}}{{{\text{d}\uptau}}} = - {\text{rK}}{.} $$

(54)

Using Eqs. (8), (10) and (41), we obtain

$$ \begin{aligned} &- \left\{ {\left( {\frac{{{\alpha X} - {\uppi \text{E}}}}{{\text{K}}}} \right)\frac{1}{\Delta }{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} {\uptheta }_{{\text{L}}} \left( {{\upsigma } - 1} \right) + \frac{{{\uppi \text{E}}}}{{\text{K}}}\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}} \right\}\frac{{{\text{dK}}}}{{{\text{d}\uptau}}} \hfill \\ &+ \left\{ {\left( {\frac{{{\alpha X}}}{{\text{E}}} - {\uppi }} \right)\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}\left( {{\upsigma } - 1} \right) + {\uppi }\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}} + \frac{{\uppi }}{\Delta }{\sigma e}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} \left( {{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}} - {\upvarepsilon }_{{\text{u}}} } \right)} \right\}\frac{{{\text{dE}}}}{{{\text{d}\uptau}}} = - {\text{rK}}{.} \hfill \\ \end{aligned} $$

(55)

Using Eqs. (53) and (56), we have

$$\frac{{{\rm{dK}}}}{{{\rm{d}\uptau }}} = {\rm{rK}}\frac{{\frac{{{{{\uptheta }}_{\rm{L}}}}}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left\{ {{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}{\rm{E}}\left( {{{\uppi \text{E}}} - {{\updelta \text{K}}}} \right) - {{\uppi }}{{{\upvarepsilon }}_{\rm{u}}}} \right\} + {{\uppi }}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}} + \frac{1}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}\frac{1}{{\rm{E}}}\left( {{{\upsigma }} - 1} \right)\left\{ { - {{\rm{s}}_{\rm{w}}}{\rm{wL}}\left( {1 - {\rm{u}}} \right) + \left( {{{\upalpha \text{X}}} - {{\uppi \text{E}}}} \right){{{\uptheta }}_{\rm{L}}}} \right\}}}{{{{\uppi }}\left( {{{{\upvarepsilon }}_{\rm{u}}} - {{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}} \right)\frac{1}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left\{ {{{\rm{s}}_{\rm{p}}}\left( {1 - {{\uptau }}} \right){\rm{r}}{{{\uptheta }}_{\rm{L}}} - {{\rm{s}}_{\rm{w}}}\frac{{{\rm{wL}}}}{{\rm{K}}}\left( {1 - {\rm{u}}} \right)\left( { - {{\upsigma }} + {{{\uptheta }}_{\rm{K}}}} \right)} \right\}\left\{ {\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}} - \frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{L}}}{{{\upvarepsilon }}_{\rm{u}}}} \right\}}};$$

(56)

and

$$ \frac{{{\text{dE}}}}{{{\text{d}\uptau }}} = - {\text{rK}}\frac{{\frac{1}{\Delta }{{\updelta \uptheta }}_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} - \frac{{{\uppi \text{E}}}}{{\text{K}}}\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}} + \frac{1}{\Delta }{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} \frac{1}{{\text{K}}}\left( {{\upsigma } - 1} \right)\left\{ {{\text{s}}_{{\text{w}}} {\text{wL}}\left( {1 - {\text{u}}} \right) - \left( {{\upalpha \text{X}} - {\uppi \text{E}}} \right){\uptheta }_{{\text{L}}} } \right\}}}{{{\uppi }\left( {{\upvarepsilon }_{{\text{u}}} - {\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}} \right)\frac{1}{\Delta }{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\left\{ {{\text{s}}_{{\text{p}}} \left( {1 - {\uptau }} \right){{\text{r} \uptheta }}_{{\text{L}}} - \left. {{\text{s}}_{{\text{w}}} \frac{{{\text{wL}}}}{{\text{K}}}\left( {1 - {\text{u}}} \right)\left( { - {\upsigma } + {\uptheta }_{{\text{K}}} } \right)} \right\}\left\{ {\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}} - \frac{1}{\Delta }{\upvarepsilon }_{{\text{u}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} {\upvarepsilon }_{{\text{u}}} } \right\}} \right.}}. $$

(57)

Equations (56) and (57) are same as Eqs. (18) and (19) in the body of the paper.

If ${\upsigma } = 1$.

then from equations (56) and (57), we obtain

$$\frac{{{\rm{dK}}}}{{{\rm{d}\uptau }}} = {\rm{rK}}\frac{{\frac{{{{{\uptheta }}_{\rm{L}}}}}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left\{ {{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}{\rm{E}}\left( {{{\uppi E}} - {{\updelta K}}} \right) - {{\uppi }}{{{\upvarepsilon }}_{\rm{u}}}} \right\} + {{\uppi }}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}}}{{\left( {{{{\upvarepsilon }}_{\rm{u}}} - {{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}} \right)\frac{{{\uppi }}}{\Delta }{{\updelta }}{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( {\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}} - \frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{L}}}{{{\upvarepsilon }}_{\rm{u}}}} \right)}};$$

(58)

and

$$ \frac{{{\text{dE}}}}{{{\text{d}\uptau}}} = - {\text{rK}}\frac{{\frac{1}{\Delta }{{\updelta \theta }}_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} - \frac{{{\uppi E}}}{{\text{K}}}\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}}}{{\left( {{\upvarepsilon }_{{\text{u}}} - {\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}} \right)\frac{{\uppi }}{\Delta }{{\updelta \uptheta }}_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\left( {\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}} - \frac{1}{\Delta }{\upvarepsilon }_{{\text{u}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} {\upvarepsilon }_{{\text{u}}} } \right)}}. $$

(59)

Equations (58) and (59) are same as Eqs. (20) and (21) in the body of the paper.

From Eq. (9), we have

$$ \begin{aligned} & {\hat{\text{u}}} = \frac{1}{\Delta }\left[ { - {\upvarepsilon }_{{\text{E}}} \left\{ { - {\upsigma \text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right.} \right.\left. { + {\uptheta }_{{\text{K}}} \left( {1 + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right)} \right\}{\hat{\text{E}}} + {\uptheta }_{{\text{K}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\left. {{\hat{\text{K}}}} \right] \hfill \\ & \Rightarrow \frac{{{\text{du}}}}{{{\text{d}\uptau}}} = \frac{{\text{u}}}{\Delta }\left[ { - {\upvarepsilon }_{{\text{E}}} \left\{ { - {\upsigma \text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right.} \right.\left. { + {\uptheta }_{{\text{K}}} \left( {1 + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right)} \right\}\frac{1}{{\text{E}}}\frac{{{\text{dE}}}}{{{\text{d}\uptau}}} + {\uptheta }_{{\text{K}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\left. {\frac{1}{{\text{K}}}\frac{{{\text{dK}}}}{{{\text{d}\uptau}}}} \right]. \hfill \\ \end{aligned} $$

(60)

Using equations (58)–(60), we obtain

$$\frac{{{\rm{du}}}}{{{\rm{d}\uptau }}} = \frac{{\rm{u}}}{\Delta }\left[ {{{{\uptheta }}_{\rm{K}}}{{\rm{e}}_{11}}} {\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{\rm{r}}\frac{{\frac{{{{{\uptheta }}_{\rm{L}}}}}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left\{ {{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}{\rm{E}}\left( {{{\uppi \text{E}}} - {{\updelta \text{K}}}} \right) - {{\uppi }}{{{\upvarepsilon }}_{\rm{u}}}} \right\} + {{\uppi }}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}}}{{\left( {{{{\upvarepsilon }}_{\rm{u}}} - {{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1 - {\rm{u}}} \right)}}} \right)\frac{{{\uppi }}}{\Delta }{{\updelta }}{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( {\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}} - \frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{L}}}{{{\upvarepsilon }}_{\rm{u}}}} \right)}}} \right] $$

Equation (60) is same as Eq. (23) in the body of the paper.

Appendix (E)

6.1 E.1 Ramsey Problem

6.1.1 Rate of Growth of Consumption

The representative consumer maximizes $\mathop \int \limits_{0}^{ \propto } \left[ {\frac{{\left( {{\text{C}}^{{\upmu }} {\text{E}}^{{1 - {\upmu }}} } \right)^{1 - \vartheta } - 1}}{1 - \vartheta } - {\text{V}}\left( {\text{e}} \right)} \right]{\text{e}}^{{ - {\rho t}}} {\text{dt}}$ subject to the equation of motion given by

$$ {\dot{\text{K}}} = {\text{sY}} - {\delta K}{.} $$

(61)

${\text{K}}\left( 0 \right)$ is given. ${\text{K}}$ is the state variable; and ${\text{s}}$ and ${\text{e}}$ are two control variables.

The Current value Hamiltonian to be maximized at each point of time is given by

$${\rm{H}} = \left[ {\frac{{{{\left( {{{{\bar{\rm C}}}^{{\upmu }}}{{\rm{E}}^{1-{{\upmu }}}}} \right)}^{1-\vartheta }}-1}}{{1-\vartheta }}-{\rm{V}}\left( {\rm{e}} \right)} \right]{{\rm{e}}^{-{{\uprho \text{t}}}}} + {\rm{q}}{{\rm{e}}^{-{{\uprho \text{t}}}}}{\dot{\rm K}};$$

(62)

where, ${\text{q}}$ is the co-state variable.

Using equations (61) and (62) and the expression of ${\overline{\text{Y}}}$, we have

$$ \begin{aligned} &{\text{H}} = \frac{{\left( {{\overline{\text{C}}}^{{\upmu }} {\text{E}}^{{1 - {\upmu }}} } \right)^{1 - \vartheta } - 1}}{1 - \vartheta }{\text{e}}^{{ - {\rho t}}} + {\text{qe}}^{{ - {\rho t}}} \left\{ {\left( {{\overline{\text{Y}}} - {\overline{\text{C}}}} \right) - {{\updelta K }}} \right\} - {\text{V}}\left( {\text{e}} \right){\text{e}}^{{ - {\rho t}}} , \hfill \\ & \Rightarrow {\text{H}} = \frac{{\left( {{\overline{\text{C}}}^{{\upmu }} {\text{E}}^{{1 - {\upmu }}} } \right)^{1 - \vartheta } - 1}}{1 - \vartheta }{\text{e}}^{{ - {\rho t}}} + {\text{qe}}^{{ - {\rho t}}} \left[ {{\text{p}}\left( {\text{e}} \right){\text{w}} + \left( {1 - {\text{p}}\left( {\text{e}} \right)} \right)\left( {1 - {\text{u}}} \right){\text{w}}^{*} + \left( {1 - {\uptau }} \right){\text{rK}}} \right] \hfill \\ & - {\text{qe}}^{{ - {\rho t}}} {{\uptau rK}} - {\text{qe}}^{{ - {\rho t}}} {\overline{\text{C}}} - {{\updelta Kqe}}^{{ - {\rho t}}} . \hfill \\ \end{aligned} $$

(63)

The representative consumer is a taker of, ${\text{r}}$ and ${\text{w}}$ and ${\text{w}}^{*}$. ${\text{H}}$ is to be maximized with respect to ${\text{s}}$ and ${\text{e}}$. Since ${\overline{\text{C}}}$ is a function of ${\text{s}}$ and ${\text{e}}$, we obtain the same solution maximizing ${\text{H}}$ with respect to ${\overline{\text{C}}}$ and ${\text{e}}$. The first order interior optimality condition with respect to ${\overline{\text{C}}}$ is given by

$$ \begin{gathered} \left[ {{{\upmu \overline{\text{C}}}}^{{{\upmu }\left( {1 - \vartheta } \right) - 1}} {\text{E}}^{{\left( {1 - {\upmu }} \right)\left( {1 - \vartheta } \right)}} - {\text{q}}} \right]{\text{e}}^{{ - {\rho t}}} = 0, \hfill \\ \Rightarrow {{\upmu \overline{\text{C}}}}^{{{\upmu }\left( {1 - \vartheta } \right) - 1}} {\text{E}}^{{\left( {1 - {\upmu }} \right)\left( {1 - \vartheta } \right)}} = {\text{q}}. \hfill \\ \end{gathered} $$

(64)

Similarly the first order interior optimality condition with respect to ${\text{e}}$ is given by

$$ \left[ {\left( {1 - {\text{s}}} \right){{\upmu \overline{\text{C}}}}^{{{\upmu }\left( {1 - \vartheta } \right) - 1}} {\text{E}}^{{\left( {1 - {\upmu }} \right)\left( {1 - \vartheta } \right)}} + {\text{qs}}} \right]\frac{{\partial {\overline{\text{Y}}}}}{{\partial {\text{e}}}} = {\text{V}^{\prime}}\left( {\text{e}} \right), $$

(65)

where

$$ \frac{{\partial {\overline{\text{Y}}}}}{{\partial {\text{e}}}} = {\text{p}^{\prime}}\left( {\text{e}} \right)\left[ {{\text{w}} - {\text{w}}^{*} + {\text{w}}^{*} {\text{u}}} \right]. $$

From equation (65) and using ${\text{C}} = {\overline{\text{C}}}$ in the general equilibrium, we have

$$ \frac{{{\dot{\text{C}}}}}{{\text{C}}} = \frac{1}{{\left( {{\upmu }\left( {1 - \vartheta } \right) - 1} \right)}}\frac{{{\dot{\text{q}}}}}{{\text{q}}} - \frac{{\left( {1 - {\upmu }} \right)\left( {1 - \vartheta } \right)}}{{\left( {{\upmu }\left( {1 - \vartheta } \right) - 1} \right)}}\frac{{{\dot{\text{E}}}}}{{\text{E}}}. $$

(66)

Optimum time path of the co-state variable satisfies the following differential equation.

$$ \begin{aligned} & {\dot{\text{q}}} = {\rho q} - \frac{{\partial {\text{He}}^{{{\rho t}}} }}{{\partial {\text{K}}}}, \hfill \\ & \mathop \Rightarrow \limits_{ } \frac{{{\dot{\text{q}}}}}{{\text{q}}} = {\uprho } + {\updelta } - {\text{r}}\left( {1 - {\uptau }} \right) \hfill \\ \end{aligned} $$

(67)

Using equations (66) and (67), we obtain

$$ \frac{{{\dot{\text{C}}}}}{{\text{C}}} = \frac{{{\text{r}}\left( {1 - {\uptau }} \right) - {\updelta } - {\uprho }}}{{1 - {\upmu }\left( {1 - \vartheta } \right)}} - \frac{{\left( {1 - {\upmu }} \right)\left( {1 - \vartheta } \right)}}{{\left( {{\upmu }\left( {1 - \vartheta } \right) - 1} \right)}}\frac{{{\dot{\text{E}}}}}{{\text{E}}}. $$

(68)

Equation (68) is same as Eq. (24) in the body of the paper.

Using equations (64) and (65) and the expression of $\frac{{\partial {\overline{\text{Y}}}}}{{\partial {\text{c}}}}$ and ${\text{C}} = {\overline{\text{C}}}$, we have

$$ {\upmu \text{C}}^{{{\upmu }\left( {1 - \vartheta } \right) - 1}} {\text{E}}^{{\left( {1 - {\upmu }} \right)\left( {1 - \vartheta } \right)}} {\text{p}^{\prime}}\left( {\text{e}} \right)\left[ {{\text{w}} - {\text{w}}^{*} + {\text{uw}}^{*} } \right] = {\text{V}^{\prime}}\left( {\text{e}} \right). $$

(69)

In the general equilibrium

$$ {\text{w}}^{*} \left( {1 - {\text{u}}} \right) = \frac{{{\text{w}}\left[ {1 - {\text{u}} - {\text{p}}\left( {\text{e}} \right)} \right]}}{{1 - {\text{p}}\left( {\text{e}} \right)}}. $$

So from equation (69), we have

$$ {\mu C}^{{{\upmu }\left( {1 - \vartheta } \right) - 1}} {\text{E}}^{{\left( {1 - {\upmu }} \right)\left( {1 - \vartheta } \right)}} {\text{p}^{\prime}}\left( {\text{e}} \right)\left[ {\frac{{{\text{wu}}}}{{1 - {\text{p}}\left( {\text{e}} \right)}}} \right] = {\text{V}^{\prime}}\left( {\text{e}} \right). $$

(70)

Equation (70) is same as Eq. (26) in the body of the paper.

From equation (70), we have

$$ \left[ {\left( {{\upmu }\left( {1 - \vartheta } \right) - 1} \right)} \right]\frac{{{\dot{\text{c}}}}}{{\text{c}}} + \left( {1 - {\upmu }} \right)\left( {1 - \vartheta } \right)\frac{{{\dot{\text{E}}}}}{{\text{E}}} + \frac{{{\dot{\text{u}}}}}{{\text{u}}} + \frac{{{\dot{\text{w}}}}}{{\text{w}}} = \frac{{\text{e}}}{{{\text{V}^{\prime}}\left( {\text{e}} \right)}}{\text{V}^{\prime\prime}}\left( {\text{e}} \right)\frac{{{\dot{\text{e}}}}}{{\text{e}}} - \frac{{{\text{p}^{\prime}}\left( {\text{e}} \right){\text{e}}}}{{\left( {1 - {\text{p}}\left( {\text{e}} \right)} \right)}}\frac{{{\dot{\text{e}}}}}{{\text{e}}} - \frac{{{\text{p}^{\prime\prime}}\left( {\text{e}} \right){\text{e}}}}{{{\text{p}^{\prime}}\left( {\text{e}} \right)}}\frac{{{\dot{\text{e}}}}}{{\text{e}}}. $$

(71)

Using equations (68) and (71), we have,

$$ \begin{aligned} & {\updelta } + {\uprho } - {\text{r}}\left( {1 - {\uptau }} \right) + \frac{{{\dot{\text{u}}}}}{{\text{u}}} + \frac{{{\dot{\text{w}}}}}{{\text{w}}} = \frac{{\text{e}}}{{{\text{V}^{\prime}}\left( {\text{e}} \right)}}{\text{V}^{\prime\prime}}\left( {\text{e}} \right)\frac{{{\dot{\text{e}}}}}{{\text{e}}} - \frac{{{\text{p}^{\prime}}\left( {\text{e}} \right){\text{e}}}}{{\left( {1 - {\text{p}}\left( {\text{e}} \right)} \right)}}\frac{{{\dot{\text{e}}}}}{{\text{e}}} - \frac{{{\text{p}^{\prime\prime}}\left( {\text{e}} \right){\text{e}}}}{{{\text{p}^{\prime}}\left( {\text{e}} \right)}}\frac{{{\dot{\text{e}}}}}{{\text{e}}}, \hfill \\ &\Rightarrow \frac{{{\dot{\text{e}}}}}{{\text{e}}} = \frac{{{\updelta } + {\uprho } - {\text{r}}\left( {1 - {\uptau }} \right) + \frac{{{\dot{\text{u}}}}}{{\text{u}}} + \frac{{{\dot{\text{w}}}}}{{\text{w}}}}}{{\frac{{\text{e}}}{{{\text{V}^{\prime}}\left( {\text{e}} \right)}}{\text{V}^{\prime\prime}}\left( {\text{e}} \right) - \left( {\frac{{{\text{p}^{\prime}}\left( {\text{e}} \right){\text{e}}}}{{\left( {1 - {\text{p}}\left( {\text{e}} \right)} \right)}} + \frac{{{\text{p}^{\prime\prime}}\left( {\text{e}} \right){\text{e}}}}{{{\text{p}^{\prime}}\left( {\text{e}} \right)}}} \right)}} \hfill \\ \end{aligned} $$

(72)

Using Eqs. (6) and (72), we have

$$ \frac{{{\dot{\text{e}}}}}{{\text{e}}} = \frac{{{\updelta } + {\uprho }-{\text{r}}\left( {1-{\uptau }} \right) + \frac{{{\dot{\text{u}}}}}{{\text{u}}} + \frac{1}{\Delta }\left\{ {-{\uptheta }_{{\text{K}}} {\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}}\frac{{{\dot{\text{E}}}}}{{\text{E}}} + \left. {{\uptheta }_{{\text{K}}} {\upvarepsilon }_{{\text{u}}} \frac{{{\dot{\text{K}}}}}{{\text{K}}}} \right\}} \right.}}{{\frac{{\text{e}}}{{{\text{V}^{\prime}}\left( {\text{e}} \right)}}{\text{V}^{\prime\prime}}\left( {\text{e}} \right)-\left( {\frac{{{\text{p}^{\prime}}\left( {\text{e}} \right){\text{e}}}}{{\left( {1-{\text{p}}\left( {\text{e}} \right)} \right)}} + \frac{{{\text{p}^{\prime\prime}}\left( {\text{e}} \right){\text{e}}}}{{{\text{p}^{\prime}}\left( {\text{e}} \right)}}} \right)}}. $$

(73)

Using Eq. (9), we get

$$ \frac{{{\dot{\text{u}}}}}{{\text{u}}} = \frac{1}{\Delta }\left[ {-{\upvarepsilon }_{{\text{E}}} \left\{ {-{\sigma e}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right.} \right.\left. { + {\uptheta }_{{\text{K}}} \left( {1 + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right)} \right\}\frac{{{\dot{\text{E}}}}}{{\text{E}}} + {\uptheta }_{{\text{K}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\left. {\frac{{{\dot{\text{K}}}}}{{\text{K}}}} \right]. $$

(74)

Using equations (68), (73) and (74), we have

$$\begin{aligned} & \frac{{{\dot{\rm e}}}}{{\rm{e}}} = \frac{{\left\{ {{{\upmu }}\left( {1-\vartheta } \right)-1} \right\}\left( {\frac{{\left( {1-{{\upmu }}} \right)\left( {1-\vartheta } \right)}}{{\left( {{{\upmu }}\left( {1-\vartheta } \right)-1} \right)}}\frac{{{\dot{\rm E}}}}{{\rm{E}}} + \frac{{{\dot{\rm C}}}}{{\rm{C}}}} \right) + \frac{1}{\Delta }\left[ {-{{{\upvarepsilon }}_{\rm{E}}}\left\{ {-{{\upsigma }}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right.} \right.\left. { + {{{\uptheta }}_{\rm{K}}}\left( {1 + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right)} \right\}\frac{{{\dot{\rm E}}}}{{\rm{E}}} + {{{\uptheta }}_{\rm{K}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left. {\frac{{{\dot{\rm K}}}}{{\rm{K}}}} \right] + \frac{1}{\Delta }\left\{ {-{{{\uptheta }}_{\rm{K}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1-{\rm{u}}} \right)}}\frac{{{\dot{\rm E}}}}{{\rm{E}}} + \left. {{{{\uptheta }}_{\rm{K}}}{{{\upvarepsilon }}_{\rm{u}}}\frac{{{\dot{\rm K}}}}{{\rm{K}}}} \right\}} \right.}}{{\frac{{\rm{e}}}{{{\rm{V'}}\left( {\rm{e}} \right)}}{\rm{V}^{\prime\prime}}\left( {\rm{e}} \right)-\left( {\frac{{{\rm{p}^{\prime}}\left( {\rm{e}} \right){\rm{e}}}}{{\left( {1-{\rm{p}}\left( {\rm{e}} \right)} \right)}} + \frac{{{\rm{p}^{\prime\prime}}\left( {\rm{e}} \right){\rm{e}}}}{{{\rm{p}{\prime}}\left( {\rm{e}} \right)}}} \right)}},\\& \mathop \Rightarrow \limits_{\rm{~}} \frac{{{\dot{\rm e}}}}{{\rm{e}}} = \frac{{\left\{ {{{\upmu }}\left( {1-\vartheta } \right)-1} \right\}\left( {\frac{{\left( {1-{{\upmu }}} \right)\left( {1-\vartheta } \right)}}{{\left( {{{\upmu }}\left( {1-\vartheta } \right)-1} \right)}}\frac{{{\dot{\rm E}}}}{{\rm{E}}} + \frac{{{\dot{\rm C}}}}{{\rm{C}}}} \right) + \frac{{{{{\upvarepsilon }}_{\rm{E}}}}}{\Delta }\left[ {\left\{ {-{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right.\left. { + {{{\uptheta }}_{\rm{K}}}\left( {1 + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right)} \right\} + {{{\uptheta }}_{\rm{K}}}\frac{{\rm{u}}}{{\left( {1-{\rm{u}}} \right)}}} \right]\frac{{{\dot{\rm E}}}}{{\rm{E}}} + \frac{1}{\Delta }{{{\uptheta }}_{\rm{K}}}\left( {{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}} + {{{\upvarepsilon }}_{\rm{u}}}} \right)\frac{{{\dot{\rm K}}}}{{\rm{K}}}}}{{\frac{{\rm{e}}}{{{\rm{V}^{\prime}}\left( {\rm{e}} \right)}}{\rm{V}^{\prime\prime}}\left( {\rm{e}} \right)-\left( {\frac{{{\rm{p}^{\prime}}\left( {\rm{e}} \right){\rm{e}}}}{{\left( {1-{\rm{p}}\left( {\rm{e}} \right)} \right)}} + \frac{{{\rm{p}^{\prime\prime}}\left( {\rm{e}} \right){\rm{e}}}}{{{\rm{p}^{\prime}}\left( {\rm{e}} \right)}}} \right)}}\;\quad \left[ {{\rm{with}~~\upsigma } = 1} \right],\\& \mathop \Rightarrow \limits_{\rm{~}} \frac{{{\dot{\rm e}}}}{{\rm{e}}} = \frac{{\left\{ {{{\upmu }}\left( {1-\vartheta } \right)-1} \right\}\frac{{{\dot{\rm C}}}}{{\rm{C}}} + \frac{{{{{\upvarepsilon }}_{\rm{E}}}}}{\Delta }\left[ {\left\{ {-{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right.\left. { + {{{\uptheta }}_{\rm{K}}}\left( {1 + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right)} \right\} + {{{\uptheta }}_{\rm{K}}}\frac{{\rm{u}}}{{\left( {1-{\rm{u}}} \right)}} + \left( {1-{{\upmu }}} \right)\left( {1-\vartheta } \right)} \right]\frac{{{\dot{\rm E}}}}{{\rm{E}}} + \frac{1}{\Delta }{{{\uptheta }}_{\rm{K}}}\left( {{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}} + {{{\upvarepsilon }}_{\rm{u}}}} \right)\frac{{{\dot{\rm K}}}}{{\rm{K}}}}}{{\frac{{\rm{e}}}{{{\rm{V'}}\left( {\rm{e}} \right)}}{\rm{V}^{\prime\prime}}\left( {\rm{e}} \right)-\left( {\frac{{{\rm{p}^{\prime}}\left( {\rm{e}} \right){\rm{e}}}}{{\left( {1-{\rm{p}}\left( {\rm{e}} \right)} \right)}} + \frac{{{\rm{p}^{\prime\prime}}\left( {\rm{e}} \right){\rm{e}}}}{{{\rm{p}^\prime}\left( {\rm{e}} \right)}}} \right)}}.\end{aligned}$$

(75)

Equation (76) is same as Eq. (27) in the body of the paper.

6.2 E.2 Stability of long-run equilibrium

While analysing stability of long run equilibrium, we use three independent equations of motion given by (24), (25) and (13). These equations of motion are given by

$$ \begin{aligned} & {\dot{\text{C}}} = \frac{{{\text{r}}\left( {1-{\uptau }} \right)-{\updelta }-{\uprho }}}{{1-{\upmu }\left( {1-\vartheta } \right)}}{\text{C}}-\frac{{\left( {1-{\upmu }} \right)\left( {1-\vartheta } \right)}}{{{\upmu }\left( {1-\vartheta } \right)-1}}{\text{C}}\frac{{{\dot{\text{E}}}}}{{\text{E}}}, \hfill \\ & \Rightarrow {\dot{\text{C}}} = \frac{{{\text{r}}\left( {1-{\uptau }} \right)-{\updelta }-{\uprho }}}{{1-{\upmu }\left( {1-\vartheta } \right)}}{\text{C}}-\frac{{\left( {1-{\upmu }} \right)\left( {1-\vartheta } \right)}}{{{\upmu }\left( {1-\vartheta } \right)-1}}\frac{{\text{C}}}{{\text{E}}}\left( {{{\uptau \text{rK}}}-{\upalpha \text{X}} + {\uppi \text{E}}} \right) \hfill \\ \end{aligned} $$

and

$\begin{aligned}&{\dot{\text{K}}} = {\text{s}}\left( {{\text{X}}-{{\uptau \text{rK}}}} \right)-{{\updelta \text{K},}} \hfill \\ & \Rightarrow {\dot{\text{K}}} = \left( {1-\frac{{\text{C}}}{{{\text{X}}-{{\uptau \text{rK}}}}}} \right)\left( {{\text{X}}-{{\uptau \text{rK}}}} \right)-{\updelta \text{K}}. \hfill \\ & \mathop \Rightarrow \limits_{ } {\dot{\text{K}}} = {\text{X}}-{{\uptau \text{rK}}}-{\text{C}}-{{\updelta \text{K};}} \hfill \\ \end{aligned}$

and

${\dot{\text{E}}} = {{\uptau \text{rK}}}-{\upalpha \text{X}} + {\uppi \text{E}}$.

The stability properties of the long-run equilibrium depends on the sign of latent roots of the Jacobian matrix corresponding to those three equations of motion. The Jacobian matrix is given by.

${\text{J}} = \left[ {\begin{array}{*{20}c} {\frac{{\partial {\dot{\text{C}}}}}{{\partial {\text{C}}}}} & {\frac{{\partial {\dot{\text{C}}}}}{{\partial {\text{K}}}}} & {\frac{{\partial {\dot{\text{C}}}}}{{\partial {\text{E}}}}} \\ {\frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{C}}}}} & {\frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{K}}}}} & {\frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{E}}}}} \\ {\frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{C}}}}} & {\frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{K}}}}} & {\frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{E}}}}} \\ \end{array} } \right]$.

We assume ${\upsigma } = 1$, i.e., the production function is Cobb–Douglas. Using Eqs. (7A), (10A), (16)–(18) and long-run equilibrium conditions, we have

$\begin{aligned} & \frac{{\partial {\dot{\text{C}}}}}{{\partial {\text{c}}}} = 0; \\ & \frac{{\partial {\dot{\text{C}}}}}{{\partial {\text{K}}}} = {\text{C}}\frac{{\left( {1-{\uptau }} \right)}}{{1-{\upmu }\left( {1-\vartheta } \right)}}\frac{{\text{r}}}{{\text{K}}}\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} + \frac{{\left( {1-{\upmu }} \right)\left( {1-\vartheta } \right)}}{{{\upmu }\left( {1-\vartheta } \right)-1}}\frac{{\text{C}}}{{\text{E}}}\frac{{{\uppi \text{E}}}}{{\text{K}}}\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}; \\ & \frac{{\partial {\dot{\text{C}}}}}{{\partial {\text{E}}}} =-{\text{C}}\frac{{\left( {1-{\uptau }} \right)}}{{1-{\upmu }\left( {1-\vartheta } \right)}}\frac{{\text{r}}}{{\text{E}}}\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}}-\frac{{\left( {1-{\upmu }} \right)\left( {1-\vartheta } \right)}}{{{\upmu }\left( {1-\vartheta } \right)-1}}\frac{{\text{C}}}{{\text{E}}}\left\{ {{\uppi }\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}} + \frac{{\uppi }}{\Delta }{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} \left( {{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}}-{\upvarepsilon }_{{\text{u}}} } \right)} \right\}; \\ & \frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{C}}}} =-1 < 0; \\ & \frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{K}}}} = \frac{{\text{X}}}{{\text{K}}}\frac{1}{\Delta }\left\{ {-{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{k}}} \left( {{\upvarepsilon }_{{\text{u}}} + \frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}}} \right)} \right. + {\uptheta }_{{\text{K}}} \left. {{\upvarepsilon }_{{\text{u}}} \left( {1 + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right)} \right\}-{\uptau \text{r}}\left( {1 + \frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} } \right)-{\updelta }; \\ & \frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{E}}}} =-\frac{{{\text{rK}}}}{{\text{E}}}\left( {1-{\uptau }} \right)\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}} > 0; \\ & \frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{C}}}} = 0; \\ & \frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{K}}}} =-\frac{{{\uppi \text{E}}}}{{\text{K}}}\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}} < 0 \\ & \text{and} \\ & \frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{E}}}} = {\uppi }\frac{{\widehat{{{\text{pX}}}}}}{{{\hat{\text{K}}}}} + \frac{{\uppi }}{\Delta }{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} \left( {{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}}-{\upvarepsilon }_{{\text{u}}} } \right) < 0. \end{aligned}$

The determinant corresponding to this Jacobian matrix is given by

$$\begin{aligned} & {\rm{Det}}\left( {\rm{J}} \right) = \left[ {{\rm{C}}\frac{{\left( {1-{{\uptau }}} \right)}}{{1-{{\upmu }}\left( {1-\vartheta } \right)}}\frac{{\rm{r}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}} + \frac{{\left( {1-{{\upmu }}} \right)\left( {1-\vartheta } \right)}}{{{{\upmu }}\left( {1-\vartheta } \right)-1}}\frac{{\rm{C}}}{{\rm{E}}}\frac{{{{\uppi \text{E}}}}}{{\rm{K}}}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}} \right]\left[ {{{\uppi }}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}} + \frac{{{\uppi }}}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{L}}}\left( {{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1-{\rm{u}}} \right)}}-{{{\upvarepsilon }}_{\rm{u}}}} \right)} \right]\\& -\left[ {{\rm{C}}\frac{{\left( {1-{{\uptau }}} \right)}}{{1-{{\upmu }}\left( {1-\vartheta } \right)}}\frac{{\rm{r}}}{{\rm{E}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1-{\rm{u}}} \right)}} + \frac{{\left( {1-{{\upmu }}} \right)\left( {1-\vartheta } \right)}}{{{{\upmu }}\left( {1-\vartheta } \right)-1}}\frac{{\rm{C}}}{{\rm{E}}}\left\{ {{{\uppi }}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}} + \frac{{{\uppi }}}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{L}}}\left( {{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1-{\rm{u}}} \right)}}-{{{\upvarepsilon }}_{\rm{u}}}} \right)} \right\}} \right]\frac{{{{\uppi \text{E}}}}}{{\rm{K}}}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}\\& = {\rm{C}}\frac{{\left( {1-{{\uptau }}} \right)}}{{1-{{\upmu }}\left( {1-\vartheta } \right)}}\frac{{\rm{r}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}\left[ {{{\uppi }}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}} + \frac{{{\uppi }}}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{L}}}\left( {{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1-{\rm{u}}} \right)}}-{{{\upvarepsilon }}_{\rm{u}}}} \right)} \right]\\& -{\rm{C}}\frac{{\left( {1-{{\uptau }}} \right)}}{{1-{{\upmu }}\left( {1-\vartheta } \right)}}\frac{{\rm{r}}}{{\rm{E}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1-{\rm{u}}} \right)}}\frac{{{{\uppi \text{E}}}}}{{\rm{K}}}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}\\& = {\rm{C}}\frac{{\left( {1-{{\uptau }}} \right)}}{{1-{{\upmu }}\left( {1-\vartheta } \right)}}\frac{{\rm{r}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}{{\uppi }}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}} + {\rm{C}}\frac{{\left( {1-{{\uptau }}} \right)}}{{1-{{\upmu }}\left( {1-\vartheta } \right)}}\frac{{\rm{r}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}\frac{{{\uppi }}}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{L}}}\left( {{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1-{\rm{u}}} \right)}}-{{{\upvarepsilon }}_{\rm{u}}}} \right)\\& -{\rm{C}}\frac{{\left( {1-{{\uptau }}} \right)}}{{1-{{\upmu }}\left( {1-\vartheta } \right)}}\frac{{\rm{r}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1-{\rm{u}}} \right)}}{{\uppi }}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}\\& = {\rm{C}}\frac{{\left( {1-{{\uptau }}} \right)}}{{1-{{\upmu }}\left( {1-\vartheta } \right)}}\frac{{\rm{r}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\upvarepsilon }}_{\rm{u}}}\frac{{{\uppi }}}{\Delta }{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{L}}}\left( {{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1-{\rm{u}}} \right)}}-{{{\upvarepsilon }}_{\rm{u}}}} \right)\\& -{\rm{C}}\frac{{\left( {1-{{\uptau }}} \right)}}{\vartheta }\frac{{\rm{r}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{\uppi }}\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}}\left( {{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1-{\rm{u}}} \right)}}-{{{\upvarepsilon }}_{\rm{u}}}} \right)\\& =-{\rm{C}}\frac{{\left( {1-{{\uptau }}} \right)}}{{1-{{\upmu }}\left( {1-\vartheta } \right)}}\frac{{\rm{r}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( {{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1-{\rm{u}}} \right)}}-{{{\upvarepsilon }}_{\rm{u}}}} \right){{\uppi }}\left( {\frac{{{\hat{\rm X}}}}{{{\hat{\rm K}}}} + \frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{L}}}} \right)\\& =-{\rm{C}}\frac{{\left( {1-{{\uptau }}} \right)}}{{1-{{\upmu }}\left( {1-\vartheta } \right)}}\frac{{\rm{r}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( {{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1-{\rm{u}}} \right)}}-{{{\upvarepsilon }}_{\rm{u}}}} \right){{\uppi }}\left[ {\frac{1}{\Delta }\left\{ {-{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{k}}}\left( {{{{\upvarepsilon }}_{\rm{u}}} + \frac{{\rm{u}}}{{\left( {1-{\rm{u}}} \right)}}} \right)} \right.} \right.\\& + {{{\uptheta }}_{\rm{K}}}\left. {{{{\upvarepsilon }}_{\rm{u}}}\left( {1 + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right)} \right\}\left. { + \frac{1}{\Delta }{{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{L}}}} \right]\\& =-{\rm{C}}\frac{{\left( {1-{{\uptau }}} \right)}}{{1-{{\upmu }}\left( {1-\vartheta } \right)}}\frac{{\rm{r}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( {{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1-{\rm{u}}} \right)}}-{{{\upvarepsilon }}_{\rm{u}}}} \right)\frac{{{\uppi }}}{\Delta }\left[ {\left\{ {-{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{k}}}\left( {{{{\upvarepsilon }}_{\rm{u}}} + \frac{{\rm{u}}}{{\left( {1-{\rm{u}}} \right)}}} \right)} \right.} \right.\\& + {{{\uptheta }}_{\rm{K}}}\left. {{{{\upvarepsilon }}_{\rm{u}}}\left( {1 + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right)} \right\}\left. { + {{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{L}}}} \right]\\& =-{\rm{C}}\frac{{\left( {1-{{\uptau }}} \right)}}{{1-{{\upmu }}\left( {1-\vartheta } \right)}}\frac{{\rm{r}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( {{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1-{\rm{u}}} \right)}}-{{{\upvarepsilon }}_{\rm{u}}}} \right)\frac{{{\uppi }}}{\Delta }\left\{ {-{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{k}}}\left( {{{{\upvarepsilon }}_{\rm{u}}} + \frac{{\rm{u}}}{{\left( {1-{\rm{u}}} \right)}}} \right)} \right. + {{{\uptheta }}_{\rm{K}}}{{{\upvarepsilon }}_{\rm{u}}} + \left. {{{{\upvarepsilon }}_{\rm{u}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right\}\\& =-{\rm{C}}\frac{{\left( {1-{{\uptau }}} \right)}}{{1-{{\upmu }}\left( {1-\vartheta } \right)}}\frac{{\rm{r}}}{{\rm{K}}}\frac{1}{\Delta }{{{\uptheta }}_{\rm{L}}}{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}\left( {{{{\upvarepsilon }}_{\rm{E}}}\frac{{\rm{u}}}{{\left( {1-{\rm{u}}} \right)}}-{{{\upvarepsilon }}_{\rm{u}}}} \right)\frac{{{\uppi }}}{\Delta }\left\{ {-{{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}{{{\uptheta }}_{\rm{K}}}\left( {{{{\upvarepsilon }}_{\rm{u}}} + \frac{{\rm{u}}}{{\left( {1-{\rm{u}}} \right)}}} \right)} \right. + \left. {{{{\upvarepsilon }}_{\rm{u}}}\left( {{{{\uptheta }}_{\rm{K}}} + {{\rm{e}}_{11}}\frac{{{{\rm{w}}^2}}}{{\rm{e}}}} \right)} \right\}.\end{aligned}$$

When ${\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}} > {\upvarepsilon }_{{\text{u}}}$, ${\text{Det}}\left( {\text{J}} \right)$ is positive if $\left( {{\uptheta }_{{\text{K}}} + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right) > 0$; and we assume this to be true.

If the determinant of ${\text{J}}$ is positive, then either all three latent roots are positive or two roots are negative and one root is positive.

Trace of the Jacobian matrix is given by

$$ \begin{aligned} & {\text{Tr}}\left( {\text{J}} \right) = \frac{{\text{X}}}{{\text{K}}}\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}-{\tau r}\left( {1 + \frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} } \right)-{\updelta } + {\uppi }\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}} + \frac{{\uppi }}{\Delta }{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} \left( {{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}}-{\upvarepsilon }_{{\text{u}}} } \right) \hfill \\ &= \frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}\left( {\frac{{\text{X}}}{{\text{K}}} + {\uppi }} \right)-{\tau r}\left( {1 + \frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} } \right)-{\updelta } + \frac{{\uppi }}{\Delta }{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} \left( {{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}}-{\upvarepsilon }_{{\text{u}}} } \right) \hfill \\ &= \frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}\left( {\frac{{\text{X}}}{{\text{K}}} + {\uppi }} \right)-{\tau r}\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}}-\frac{{\uppi }}{\Delta }{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} {\upvarepsilon }_{{\text{u}}}-{\tau r}-{\updelta } + \frac{{\uppi }}{\Delta }{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} {\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}} \hfill \\& = \frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}\left( {\frac{{\text{X}}}{{\text{K}}} + {\uppi }} \right)-\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} \left( {{\tau r} + {\uppi }} \right)-{\tau r}-{\updelta } + \frac{{\uppi }}{\Delta }{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} {\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}} \hfill \\ \end{aligned} $$

Here $\left\{ {\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}\left( {\frac{{\text{X}}}{{\text{K}}} + {\uppi }} \right)-\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} \left( {{\uptau \text{r}} + {\uppi }} \right)} \right\} > 0 \,{\text{and}}\, \left\{ {-{\uptau \text{r}}-{\updelta } + \frac{{\uppi }}{\Delta }{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} {\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}}} \right\} < 0$. So, Trace of the Jacobian matrix is indeterminate in sign.

In order to determine the sign of the latent roots of the ${\text{J}}$ matrix we apply the Routh-Hurwitz Theorem. The characteristic equation obtained from ${\text{J}}$ matrix is given by

$$ - {{\rm{v}}^3} + {\rm{Tr}}\left( {\rm{J}} \right){{\rm{v}}^2} - {\rm{M}}\left( {\rm{J}} \right){\rm{v}} + {\rm{Det}}\left( {\rm{v}} \right) = 0,$$

(76)

where ${\text{v}}$ is the latent root.

Here,

$$ {\text{M}}\left( {\text{J}} \right) = \left\lceil {\begin{array}{*{20}c} {\frac{{\partial {\dot{\text{C}}}}}{{\partial {\text{c}}}}} & {\frac{{\partial {\dot{\text{C}}}}}{{\partial {\text{K}}}}} \\ {\frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{C}}}}} & {\frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{K}}}}} \\ \end{array} } \right\rceil + \left\lceil {\begin{array}{*{20}c} {\frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{K}}}}} & {\frac{{\partial {\dot{\text{K}}}}}{{\partial {\text{E}}}}} \\ {\frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{K}}}}} & {\frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{E}}}}} \\ \end{array} } \right\rceil + \left\lceil {\begin{array}{*{20}c} {\frac{{\partial {\dot{\text{C}}}}}{{\partial {\text{c}}}}} & {\frac{{\partial {\dot{\text{C}}}}}{{\partial {\text{E}}}}} \\ {\frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{C}}}}} & {\frac{{\partial {\dot{\text{E}}}}}{{\partial {\text{E}}}}} \\ \end{array} } \right\rceil $$

The sign of ${\text{M}}\left( {\text{J}} \right)$ is ambiguous.

The number of positive roots in the characteristic equation (72) is equal to the number of variations of signs in the scheme

$$ \left\{ { - 1,{\text{ Tr}}\left( {\text{J}} \right), - {\text{M}}\left( {\text{J}} \right) + \frac{{{\text{Det}}\left( {\text{J}} \right)}}{{{\text{Tr}}\left( {\text{J}} \right)}},{\text{Det}}\left( {\text{J}} \right)} \right\}. $$

(77)

If the sign of ${\text{M}}\left( {\text{J}} \right)$ is ambiguous, then sign of $- {\text{M}}\left( {\text{J}} \right) + \frac{{{\text{Det}}\left( {\text{J}} \right)}}{{{\text{Tr}}\left( {\text{J}} \right)}}$ is also ambiguous. Hence the number of positive latent roots can not be obtained in this way.

The number of negative roots will determine the nature of transitional paths around the long-run equilibrium point. In this model, we have two state variables, ${\text{K}}$ and ${\text{E}}$, and only one control variable, ${\text{C}}$. The properties of transitional dynamics depends on the relationship between the number of state variables and the number of negative latent roots. The long run equilibrium is saddle point stable (unstable) if the number of negative latent roots is equal to (less than) the number of state variables. However, it faces indeterminacy with infinite number of transitional path when number of negative latent roots is greater than the number of state variables.²⁷ We consider four alternative cases.

Case (i): Trace is positive and $- {\text{M}}\left( {\text{J}} \right) + \frac{{{\text{Det}}\left( {\text{J}} \right)}}{{{\text{Tr}}\left( {\text{J}} \right)}}$ is positive.

We have only one variation in sign in the scheme (76) in this case. So the characteristic equation (77) has only one positive root and two negative roots; and thus the number of negative latent roots is equal to the number of state variables. Hence the long-run equilibrium point satisfies saddle point stability in this case.

Case (ii): Trace is positive and $- {\text{M}}\left( {\text{J}} \right) + \frac{{{\text{Det}}\left( {\text{J}} \right)}}{{{\text{Tr}}\left( {\text{J}} \right)}}$ is negative.

We have three variations in sign in the scheme (76). So the characteristic equation (77) has all three positive latent roots. So the number of negative latent roots being zero falls short of the number of state variables. So the long-run equilibrium is unstable in this case.

Case (iii): Trace negative and $- {\text{M}}\left( {\text{J}} \right) + \frac{{{\text{Det}}\left( {\text{J}} \right)}}{{{\text{Tr}}\left( {\text{J}} \right)}}$ is positive.

We have only one variation in sign in the scheme (76) in this case. So the characteristic equation (77) has only one positive root and two negative roots; and thus the number of negative latent roots is equal to the number of state variables. Hence the long-run equilibrium point satisfies saddle point stability in this case.

Case (iv): Trace negative; $- {\text{M}}\left( {\text{J}} \right) + \frac{{{\text{Det}}\left( {\text{J}} \right)}}{{{\text{Tr}}\left( {\text{J}} \right)}}$ is negative.

We have only one variation in sign in the scheme (76) in this case. So the characteristic equation (77) has only one positive root and two negative roots; and thus the number of negative latent roots is equal to the number of state variables. Hence the long-run equilibrium point satisfies saddle point stability in this case.

6.3 E.3 Comparative steady state effects

We analyse comparative steady state effects on ${\text{K}}$, ${\text{E}}$ and ${\text{u}}$ with respect to change in ${\uptau }$ when the equilibrium is saddle point stable. ${\text{C}}$ is a jump variable; and its value can be thrown on the saddle path.

From Eq. (24), i.e., with ${\dot{\text{C}}} = 0$ and ${\dot{\text{E}}} = 0$, we have

$$ {\text{C}}\frac{{\left( {1 - {\uptau }} \right)}}{{1 - {\upmu }\left( {1 - \vartheta } \right)}}\frac{{\text{r}}}{{\text{K}}}\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} \frac{{{\text{dK}}}}{{{\text{d}\uptau}}} - {\text{C}}\frac{{\left( {1 - {\uptau }} \right)}}{{1 - {\upmu }\left( {1 - \vartheta } \right)}}\frac{{\text{r}}}{{\text{E}}}\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}\frac{{{\text{dE}}}}{{{\text{d}\uptau}}} = \frac{{{\text{rC}}}}{{1 - {\upmu }\left( {1 - \vartheta } \right)}}. $$

(78)

From Eq. (13), with ${\dot{\text{E}}} = 0$, we have

$$ - \frac{{{\uppi \text{E}}}}{{\text{K}}}\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}}\frac{{{\text{dK}}}}{{{\text{d}\uptau}}} + \left\{ {{\uppi }\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}} + \frac{{\uppi }}{\Delta }{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} \left( {{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}} - {\upvarepsilon }_{{\text{u}}} } \right)} \right\}\frac{{{\text{dE}}}}{{{\text{d}\uptau}}} = - {\text{rK}}{.} $$

(79)

Using equations (79) and (80), we have

$$ \begin{gathered} \frac{{{\text{dK}}}}{{{\text{d}\uptau }}} =-\frac{{{\text{rC}}\frac{1}{{1-{\upmu }\left( {1-\vartheta } \right)}}\left[ {\left\{ {{\uppi }\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}} + \frac{{\uppi }}{\Delta }{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} \left( {{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}}-{\upvarepsilon }_{{\text{u}}} } \right)} \right\}-{\text{K}}\left( {1-{\uptau }} \right)\frac{{\text{r}}}{{\text{E}}}\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}}} \right]}}{{{\text{C}}\frac{{\left( {1-{\uptau }} \right)}}{{1-{\upmu }\left( {1-\vartheta } \right)}}\frac{{\text{r}}}{{\text{K}}}\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\left( {{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}}-{\upvarepsilon }_{{\text{u}}} } \right)\frac{{\uppi }}{\Delta }\left\{ {-{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{K}}} \left( {{\upvarepsilon }_{{\text{u}}} + \frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}}} \right)} \right. + \left. {{\upvarepsilon }_{{\text{u}}} \left( {{\uptheta }_{{\text{K}}} + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right)} \right\}}} \hfill \\ \mathop \Rightarrow \limits_{ } \frac{{{\text{dK}}}}{{{\text{d}\uptau}}} =-\frac{{{\text{rC}}\frac{1}{{1-{\upmu }\left( {1-\vartheta } \right)}}\left[ {{\uppi }\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}} + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} {\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}}\frac{1}{\Delta }\frac{1}{{\text{E}}}\left\{ {{\uppi \text{E}}-\left( {1-{\uptau }} \right){\text{rK}}} \right\}} \right]}}{{{\text{C}}\frac{{\left( {1-{\uptau }} \right)}}{{1-{\upmu }\left( {1-\vartheta } \right)}}\frac{{\text{r}}}{{\text{K}}}\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\left( {{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}}-{\upvarepsilon }_{{\text{u}}} } \right)\frac{{\uppi }}{\Delta }\left\{ {-{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{K}}} \left( {{\upvarepsilon }_{{\text{u}}} + \frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}}} \right)} \right. + \left. {{\upvarepsilon }_{{\text{u}}} \left( {{\uptheta }_{{\text{K}}} + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right)} \right\}}} \hfill \\ \mathop \Rightarrow \limits_{ } \frac{{{\text{dK}}}}{{{\text{d}\uptau}}} =-\frac{{{\text{rC}}\frac{1}{{1-{\upmu }\left( {1-\vartheta } \right)}}\left[ {{\uppi }\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}} + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{L}}} {\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}}\frac{1}{\Delta }\frac{1}{{\text{E}}}\left\{ {{\uppi \text{E}}-\left( {{\updelta } + {\uprho }} \right){\text{K}}} \right\}} \right]}}{{{\text{C}}\frac{{\left( {1-{\uptau }} \right)}}{{1-{\upmu }\left( {1-\vartheta } \right)}}\frac{{\text{r}}}{{\text{K}}}\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\left( {{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}}-{\upvarepsilon }_{{\text{u}}} } \right)\frac{{\uppi }}{\Delta }\left\{ {-{\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{K}}} \left( {{\upvarepsilon }_{{\text{u}}} + \frac{{\text{u}}}{{\left( {1-{\text{u}}} \right)}}} \right)} \right. + \left. {{\upvarepsilon }_{{\text{u}}} \left( {{\uptheta }_{{\text{K}}} + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right)} \right\}}}; \hfill \\ \end{gathered} $$

(80)

and

$$ \frac{{{\text{dE}}}}{{{\text{d}\uptau}}} =-\frac{{{\text{rC}}\frac{1}{{1 - {\upmu }\left( {1 - \vartheta } \right)}}\left[ {\frac{{{\uppi \text{E}}}}{{\text{K}}}\frac{{{\hat{\text{X}}}}}{{{\hat{\text{K}}}}} - {\text{K}}\left( {1-{\uptau }} \right)\frac{{\text{r}}}{{\text{K}}}\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\upvarepsilon }_{{\text{u}}} } \right]}}{{{\text{C}}\frac{{\left( {1 - {\uptau }} \right)}}{{1 - {\upmu }\left( {1 - \vartheta } \right)}}\frac{{\text{r}}}{{\text{K}}}\frac{1}{\Delta }{\uptheta }_{{\text{L}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\left( {{\upvarepsilon }_{{\text{E}}} \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}} - {\upvarepsilon }_{{\text{u}}} } \right)\frac{{\uppi }}{\Delta }\left\{ { - {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}{\uptheta }_{{\text{K}}} \left( {{\upvarepsilon }_{{\text{u}}} + \frac{{\text{u}}}{{\left( {1 - {\text{u}}} \right)}}} \right)} \right. + \left. {{\upvarepsilon }_{{\text{u}}} \left( {{\uptheta }_{{\text{K}}} + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right)} \right\}}}. $$

(81)

For both equation (80) and (81) denominators in the RHS are negative if $\left( {{\uptheta }_{{\text{K}}} + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right) > 0$ and ${\upvarepsilon }_{{\text{E}}} {\text{u}} > {\upvarepsilon }_{{\text{u}}} \left( {1 - {\text{u}}} \right)$. Numerator of (81) is always positive. Numerator of (81) is positive if ${\uppi \text{E}} < \left( {{\updelta } + {\uprho }} \right){\text{K}}$. Hence, under these conditions, $\frac{{{\text{dK}}}}{{{\text{d}\uptau}}} > 0$ and $\frac{{{\text{dE}}}}{{{\text{d}\uptau}}} > 0$.

Using equation (60), we obtain

$$ \frac{{{\text{du}}}}{{{\text{d}\uptau }}} = \frac{{\text{u}}}{\Delta }\left[ { - {\upvarepsilon }_{{\text{E}}} \left\{ { - {\upsigma \text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right.} \right.\left. { + {\uptheta }_{{\text{K}}} \left( {1 + {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}} \right)} \right\}\frac{1}{{\text{E}}}\frac{{{\text{dE}}}}{{{\text{d}\uptau }}} + {\uptheta }_{{\text{K}}} {\text{e}}_{11} \frac{{{\text{w}}^{2} }}{{\text{e}}}\left. {\frac{1}{{\text{K}}}\frac{{{\text{dK}}}}{{{\text{d}\uptau }}}} \right]. $$

(82)

Here also $\frac{{{\text{du}}}}{{\text{d}\uptau }} < 0$, as $\frac{{{\text{dE}}}}{{{\text{d}\uptau }}} > 0$ and $\frac{{{\text{dK}}}}{{{\text{d}\uptau }}} > 0$.

Appendix F

If we assume full employment in the model of the body of the paper; then term ${\upvarepsilon }_{\mathrm{u}}=0$. Then, without using Solow (1979) condition i.e. assuming that ${\upvarepsilon }_{{\text{w}}} \ne 1$, Eqs. (28), (29), (32) and (33) are modified as follows

$$ {\uptheta }_{{\text{L}}} {\hat{\text{w}}} - {\uptheta }_{{\text{L}}} {\hat{\text{e}}} + {\uptheta }_{{\text{K}}} {\hat{\text{r}}} = 0; $$

(83)

$$ {\upvarepsilon }_{{\text{w}}} {\hat{\text{w}}} - {\hat{\text{e}}} = - {\upvarepsilon }_{{\text{E}}} {{\hat{\text{E}}}} ;$$

(84)

$$ {\uptheta }_{{\text{L}}} {{\upsigma \hat{\text{W}}}} - {\uptheta }_{{\text{L}}} {{\upsigma \hat{\text{e}}}} - {\uptheta }_{{\text{L}}} {{\upsigma \hat{\text{r}}}} + {\hat{\text{X}}} = {{\hat{\text{K}};}} $$

(85)

and

$$ - {\uptheta }_{{\text{K}}} {{\upsigma \hat{\text{W}}}} - \left( { - {\uptheta }_{{\text{K}}} {\upsigma } + 1} \right){\hat{\text{e}}} + {\uptheta }_{{\text{K}}} {{\upsigma \hat{\text{r}}}} + {\hat{\text{X}}} = 0. $$

(86)

From Eqs. (83), (84), (85) and (86), we have

$$ \Delta = {\upsigma } + {\upvarepsilon }_{{\text{w}}} \left\{ { - {\upsigma } + {\uptheta }_{{\text{K}}} } \right\}. $$

(87)

Following equations describe the flexible wage full employment model with exogenous labour efficiency.

$$ 1 = {\text{a}}_{{\text{L}}} {\text{w}} + {\text{a}}_{{\text{K}}} {\text{r}}{.} $$

(88)

$$ {\text{a}}_{{\text{K}}} {\text{X}} = {\text{K}}{.} $$

(89)

$$ {\text{a}}_{{\text{L}}} {\text{X}} = {\text{L}}{.} $$

(90)

Here ${\upvarepsilon }_{{\text{w}}} = 0$; and hence from Eq. (87) we have

$$ \Delta = {\upsigma }{.} $$

(91)