Price control and privatization in a mixed duopoly with a public social enterprise

Abstract

We explore the issue of the optimal degree of privatization for a public firm that does not need to care about its rival’s profit completely. We find that the optimal privatization of a public social enterprise under exogenous price control depends on the level of the regulated price. Namely, when the regulated price is low (medium, high), the optimal privatization is partial privatization (complete privatization, completely public owned). If the price control is optimized by maximizing social welfare, then the optimal privatization is complete privatization. For the case of the traditionally defined public firm, its optimal privatization is completely public owned when the price control is exogenously given. If the price control is endogenously determined, then privatization policy is redundant.

1 Introduction

Public firms are very common in many countries and usually play important roles in some industries, such as telecommunications, media, transportation, education, postal, energy, and health. Since 1980s, many governments have put great efforts in public firm privatization to improve production or management efficiency (Cremer et al. 1989; De Fraja and Delbono 1989; George and Manna 1996; Matsumura 1998; Mukherjee and Suetrong 2009; Aiura and Sanjo 2010; Mukherjee and Sinha 2014). In the very recent research, Colombo (2016) indicates that privatization can influence private firms’ incentive of collusion and Chen (2017) considers that privatization can improve the public firm’s production efficiency and call it the efficiency-enhancing effect. We thus see nowadays that many public and private firms simultaneously provide goods or services in these industries, bringing about a kind of market structure called mixed oligopoly.

Some models in the literature related to mixed oligopoly consider that a public firm’s objective function is the weighted average of the public firm’s profit and social welfare (Cremer et al. 1989; De Fraja and Delbono 1989). Such a setting seems implausible because it implies that the public firm is benefited whenever its rival’s profit rises. Matsumura (1998) presumes that public firms care more about consumer surplus and places a higher weight on consumer surplus in setting the public firm’s objective function. Nabin et al. (2014) define that a public firm’s objective function includes only the public firm’s profit and consumer surplus. Herr (2011) assumes that the objective function of a public hospital consists of the hospital’s profit and its market share.

In this paper we use the idea of Nabin et al. (2014) and the literature related to CSR (Corporate Social Responsibility) to define the objective function of public firm [see Brand and Grothe (2015), Chang et al. (2014), Goering (2012), Lambertini and Tampieri (2011), and Xu (2014)]. Concretely, we designate that the objective function of public firm contains only the public firm’s profit and the consumer surplus and call such public firm the public social enterprise. Note that the profit of the public firm’s rival is excluded in the public firm’s objective function. In contrast, we denote the public firms defined by De Fraja and Delbono (1989) as traditional public firms.

Some mixed oligopolistic industries (e.g. telecommunications, transportation, energy, and health) are regulated through price controls in many countries. Aiura and Sanjo (2010) analyze the optimal privatization policy under the condition of (exogenous) price control. Herr (2011) and Sanjo (2009) propose mixed duopoly models to study competition in the health industry under the existence of (endogenous) price control.¹ This paper proposes a model of mixed oligopoly under price control to analyze the optimal privatization policy. Furthermore, we consider both cases of exogenous and endogenous price controls. In comparison with the models in the existing literature (George and Manna 1996 or Mukherjee and Sinha 2014), our model is different in the setting of the public firm’s objective function and the consideration of price control.

In this paper, we show that given the same production and investment efficiency, the optimal privatization of a public social enterprise under exogenous price control depends on the level of the regulated price. Namely, when the regulated price is low (medium, high), the optimal privatization is partial privatization (complete privatization, completely public owned). If the price control is optimized by maximizing social welfare, then the optimal privatization is complete privatization. For the case of the traditionally defined public firm, its optimal privatization is completely public owned when the price control is exogenously given. If the price control is endogenously determined, then privatization policy is redundant. In the next section, we propose the basic model and proceed with the equilibrium analysis and the social optimization analysis. Section 3 analyzes quality competition between public and private firms. Section 4 studies the optimal privatization for a public social firm. We extend the discussion in Sect. 5 and offer a conclusion in the final section.

2 Basic model and first-best outcome

Consider a linear market, represented by the interval [0, 1], where consumers are spread uniformly with density 1. Each consumer demands one unit of the product provided by the public firm or the private firm. The public firm, indexed by A, is located at the left end-point (i.e. 0) in the linear market; as well as, the private firm, indexed by B, is located at the right end-point (i.e. 1). Assume that the utility of a consumer located at point $x\in \left[ {0, 1} \right]$ purchasing the product from A or B is given by:

$$\begin{aligned} u_{Ax} =v+q_{_A} -tx-M, \end{aligned}$$

(1.1)

$$\begin{aligned} u_{Bx} =v+q_{_B} -t\left( {1-x} \right) -M, \end{aligned}$$

(1.2)

where v is the reservation benefit of consuming the product that is assumed to be sufficiently large so that the market is fully covered. Each firm i supplies the product with the quality level $q_i >0$. We can regard $x\in \left[ {0, 1} \right]$ as the consumer’s congenital preference, and t is the unit disutility generated by x, called the freight rate. M is the price of the product that is regulated by the government. In the case of no subsidization, the consumer should pay M for consuming the product.²

By (1.1) and (1.2), we derive the demand functions of firm A and firm B respectively:

$$\begin{aligned} n_{A} ={\hat{x}}=\frac{1}{2}+\frac{q_{_A} -q_{_B} }{2t}, \end{aligned}$$

(2.1)

$$\begin{aligned} n_B =1-{\hat{x}}=\frac{1}{2}+\frac{q_{_B} -q_{_A} }{2t}, \end{aligned}$$

(2.2)

where ${\hat{x}}$ is the marginal consumer. We then derive the overall consumer surplus (denote by CS) as:

$$\begin{aligned} CS=\mathop \int \nolimits _0^{\hat{x} } u_A dx+\mathop \int \nolimits _{\hat{x}}^1 u_B dx=v+n_{A} q_{_A} +n_B q_{_B} -T-M, \end{aligned}$$

(3)

where $T\equiv t\left[ {\mathop \int \nolimits _0^{\hat{x} } xdx+\mathop \int \nolimits _{\hat{x} }^1 \left( {1-x} \right) dx} \right]$ is the aggregate disutility (called the total transportation cost), which is generated by consumers’ congenital preferences.

Because of price regulation, the two firms compete in quality. For simplicity, we assume that the production costs of the two firms are zero, and the cost of quality improving is $q_i ^{2}/2$.³ Hence, firms’ profits can be written as:

$$\begin{aligned} \pi _i =M\cdot n_i -\frac{q_i^{2}}{2},i=A,B, \end{aligned}$$

(4)

By (3) and (4), we derive the social welfare function as:

$$\begin{aligned} W= & {} \mathop \sum \limits _{i=A,B} \pi _i +CS=\left[ {M-\frac{1}{2}\mathop \sum \limits _{i=A,B} q_i^{2}} \right] \nonumber \\&+\left[ {v+\mathop \sum \limits _{i=A,B} n_i q_i -T-M} \right] . \end{aligned}$$

(5)

Ever since De Fraja and Delbono (1989), the public firm’s objective function is assumed to be the weighted average of its profit and the social welfare. Since the setting is implausible as we have mentioned, we think that it is more appropriate to modify the public firm’s objective function to be the weighted average of its profit and the consumer surplus. Moreover, we consider a more generalized setting. Let parameter $\beta \in \left[ {0,1} \right]$, called the type-parameter, measure the degree of caring about the rival’s profit. The larger $\beta$ is, the more the public firm cares about its rival’s profit. Hence, when $\beta$ equals 1, the public firm’s objective function is the same as the traditional defined public firm’s objective function—that is, the weighted average of its profit and the social welfare. Such a firm is called thetraditional-type public firm. When $\beta$ is zero, the public firm’s objective function is the weighted average of its profit and the consumer surplus. We name the firm the public social enterprise (or PSE-type public firm). No matter the value of $\beta$, we still call firm A as the public firm for convenience. Therefore, the objective function of firm A can be written as:

$$\begin{aligned} H^{A}=\rho \pi _A +\left( {1-\rho } \right) \left( {\pi _A +\beta \pi _B +CS} \right) , \end{aligned}$$

(6.1)

where $\rho \in \left[ {0,1} \right]$ denotes the degree of privatization of firm A. The objective function of the private firm is:

$$\begin{aligned} H^{B}=\pi _B . \end{aligned}$$

(6.2)

We examine two cases: the regulated price is exogenously given (e.g. for historical or political reasons), and is endogenously determined by the government. The timing of the game is as follows. In the first stage, the government decides the degree of privatization of the public firm in the former case, or the degree of privatization and the regulated price simultaneously in the latter case. In the second stage, the firms are engaged in quality competition. The game is solved by backward induction.

Note that there are two distinctions between our approach and the traditional privatization literature. First, the product price is regulated. Second, we consider a more generalized objective function of the public firm. Namely, the public firm could be the traditional-type (i.e., $\beta =1)$ that pursues the weighted average of its profit and social welfare, the PSE-type (i.e., $\beta =0)$ that maximizes the weighted average of its profit and consumer surplus, or in-between these two types (i.e. $0<\beta <1)$.

In order to know whether the equilibrium is desirable from the viewpoint of the social welfare, we need to derive the first-best outcome (hereafter, FB) that can be obtained through assuming that the quality levels are also determined by the government. Differentiating Eq. (5) with respect to $q_i$, we have:

$$\begin{aligned} \frac{\partial W}{\partial q_i }= & {} -q_i +\left[ {\left( {n_i +q_i \frac{\partial n_i }{\partial q_i }} \right) +q_j \frac{\partial n_j }{\partial q_i }+t\left( {\frac{\partial n_i }{\partial q_i }n_j +n_i \frac{\partial n_j }{\partial q_i }} \right) } \right] \\= & {} -q_i +n_i , i,j=A,B, i \ne j. \end{aligned}$$

The first term of the right-hand side in the above equation is the cost when the firms invest for enhancing their product quality levels, and we call it the investment cost effect, which is negative. The second term includes the variation of consumers’ utility and the total transportation cost, and we call it the consumer surplus effect, which is positive. It can clearly be seen that the social optimum quality is to let the quality levels completely convert into each firm’s market share; $q_i =n_i$.

Solving the two first-order conditions simultaneously, we obtain the socially optimal quality levels as:

$$\begin{aligned} q_i^{FB}=\frac{1}{2}, \quad i=A,B. \end{aligned}$$

Superscript FB represents the equilibrium outcome for social optimum. We assume the freight rate $t>1$ to satisfy the second-order and stability conditions.⁴ Substituting $q_i^{FB}$ into Eq. (5), the optimal social welfare is $W^{FB}=v-\left( {t-1} \right) /4$. Obviously, the optimal social welfare is not affected by the regulated price. The results are summarized as follows;

Lemma 1

The first-best outcome is $q_i ^{FB}=\frac{1}{2}, n_i ^{FB}=\frac{1}{2},i=A,B$, and $W^{FB}=v-\left( {t-1} \right) /4$.

3 Quality competition

Given firm A’s privatization degree and the regulated price M, the two firms compete in quality in the second stage. The first-order conditions for maximizing Eqs. (6.1) and (6.2) with respect to $q_{_{A}}$ and $q_{_B}$ are⁵:

$$\begin{aligned} H_A^A =\frac{\partial H^{A}}{\partial q_{_A} }=\left[ {\frac{M}{2t}-q_{_A} } \right] +\left( {1-\rho } \right) \left[ {\frac{1}{2}+\frac{\left( {q_{_A} -q_{_B} } \right) }{2t}-\beta \frac{M}{2t}} \right] , \end{aligned}$$

(7.1)

$$\begin{aligned} H_B^B =\frac{\partial H^{B}}{\partial q_{_B} }=\frac{M}{2t}-q_{_B} . \end{aligned}$$

(7.2)

The second-order and stability conditions are established.⁶ The first bracket, $M/2t-q_{_A}$, in the right-hand side of Eq. (7.1) is the direct effect of firm A’s quality decision on its own profit. The term, $1/2+\left( {q_{_A} -q_{_B} } \right) /2t$, in the second bracket, is the effect of firm A’s quality decision on consumers’ surplus, i.e. $\partial CS/\partial q_{_A}$. The term, $-\beta M/2t$ is the effect of firm A’s quality decision on firm B’s profit, i.e. $\beta \cdot \partial \pi _B /\partial q_{_A}$. The larger $\beta$ is, the more firm A cares about firm B’s profit, the less firm A invests in quality.

From the two equations, we obtain the optimal quality levels:

$$\begin{aligned} q_{_A} =\frac{M}{2t}+\frac{\left( {1-\rho } \right) }{\Delta }\left( {t-\beta M} \right) , \end{aligned}$$

(8.1)

$$\begin{aligned} q_{_B} =\frac{M}{2t}, \end{aligned}$$

(8.2)

where $\Delta \equiv 2t-1+\rho >0$. Intuitively, comparing with the traditional-type public firm ($\beta =1$), if firm A does not concern firm B’s profit (i.e. $\beta =0$), then firm A is willing to invest more in quality. In addition, from Eq. (8.1), we see that, as long as $\rho <1$ (namely, firm A is not a purely private firm), then a higher $\beta$ implies a lower $q_{_A}$, perhaps even less than $q_{_B}$. Finally, when $\beta =t/M$, the effect from consumer surplus and that from caring about the profit of firm B cancel each other out. This leads to the same quality level, $q_{_A} =q_{_B}$. Summarizing the above results, we have Proposition 1.

Proposition 1

Given $\rho <1$, when the public firm cares more about its rival’s profit, the public firm invests less on its quality level. If $\beta >t/M$, then the product quality of the public firm is less than that of the private firm.

When $\beta =0$, the public firm provides higher quality than the private firm does, because the public firm cares about the consumer surplus beside its own profit. When $\beta >0$, the public firm concerns its rival’s profit, and so the public firm will reduce the quality level to mitigate the competition with its rival. For the case of $\beta =1$, firm A is a traditional-type public firm, and once upon the regulated price is large enough, say $M>t$, firm A invests in its product quality even less than firm B does. Figure  1 shows the result by reaction functions.

Fig. 1

The reaction functions of quality competition ($\beta >t/M$)

In Fig. 1, $R_B$ is the reaction function of firm B. It depends on the regulated price M and the freight rate t, but is independent of the quality level of product A. An increase of firm A’s product quality can crowd out firm B’s output and further lower firm B’s profit. Moreover, the firms’ average revenues are controlled by the government (i.e. through the regulated price), and they are not influenced by the quality level of product A. $R_A$ is the reaction function of firm A, and its slope is $-\Delta /\left( {1-\rho } \right) <0$. Note that firm A’s objective function includes part of firm B’s profit. Therefore, from firm A’s point of view, the quality levels of the two firms are strategic substitutes. When firm B increases its product quality, the best response of firm A is to lower its product quality. As to which firm provides a higher quality level, it depends on whether the intersection of the two reaction curves is above the $45^{{\circ }}$ line or not. When $\beta =1$ and $M=t$, the two reaction functions cross on the $45^{{\circ }}$ line, and the equilibrium quality levels of the two firms are the same.

There is a large strand of literature discussing quality competition in mixed oligopoly industries, but we focus on the portion related to price control. Herr (2011) considers asymmetric production costs and assumes the objective function of a public hospital consists of the hospital’s profit and its market share. In his model, if the production costs are symmetric, then the public hospital always invests in a higher quality level. Our model can be viewed as a generalization of the model of Herr (2011).⁷

Some comparative statics can be examined as follows. From Eqs. (8.1) and (8.2), we have:

$$\begin{aligned} \frac{\partial q_{_A} }{\partial \rho }=-\frac{2t\left( {t-\beta M} \right) }{\Delta ^{2}}\frac{>}{<}0 \quad \hbox { iff }\quad \beta \frac{>}{<}\frac{t}{M}; \quad \quad \quad \quad \quad \quad \quad \frac{\partial q_{_B} }{\partial \rho }=0; \end{aligned}$$

(9.1)

$$\begin{aligned} \frac{\partial q_{_A} }{\partial \beta }=-\frac{\left( {1-\rho } \right) M}{\Delta }\le 0; \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \frac{\partial q_{_B} }{\partial \beta }=0; \end{aligned}$$

(9.2)

$$\begin{aligned} \frac{\partial q_{_A} }{\partial M}=\frac{1}{2t}-\frac{\left( {1-\rho } \right) \beta }{\Delta }\frac{>}{<}0 \quad \hbox { iff }\quad \beta \frac{<}{>}\frac{\Delta }{2t\left( {1-\rho } \right) }; \,\,\quad \quad \qquad \frac{\partial q_{_B} }{\partial M}=\frac{1}{2t}>0. \end{aligned}$$

(9.3)

Equation (9.1) shows that the direction of firm A’s quality change depends on the type-parameter $\beta$. When $\rho$ increases, as firm A is closer to being a pure private firm, its strategy approaches firm B’s strategy. When $\beta$ is small (large), the initial quality level of firm A is higher (lower) than firm B; nonetheless, as $\rho$ increases, firm A tends to invest less (more), and becoming close to the quality investment of firm B.

Equation (9.2) indicates that if firm A cares more about firm B’s profit, then firm A tends to reduce its quality level in order to avoid grabbing too much profit from firm B. From Fig. 1, it is easy to see that $R_A$ shifts inward and $R_B$ remains unchanged when $\beta$ increases. This implies that $q_{_A}$ decreases as $\beta$ increases.

The intuition behind Eq. (9.3) can be explained as follows. From Fig. 1, we can observe that when M increases (decreases), $R_B$ will rise (fall), and $R_A$ will shift outward (inward). This leads to a definite increase in $q_{_B}$, but an ambiguous movement in $q_{_A}$. As firm A is a public social enterprise, improving the quality level can extract more consumers from firm B and brings about the following consequences. (i) The consumers gain higher utilities from purchasing the product from A. (ii) Firm B’s profit is reduced. Given $\beta$ is small, the quality of firm A’s product increases as the regulated price increases because firm A relatively cares more on (i). When $\beta$ is larger, firm A that concerns more on the effect of (ii) tends to lower its product quality as the regulated price is raised.

We next discuss the issue of corner solution. Substituting (8.1) and (8.2) into Eqs. (2.1) and (2.2), we have $n_{A} =\left[ {2t^{2}-\left( {1-\rho } \right) \beta M} \right] /2t\Delta$ and $n_B =\left[ {2t\left( {t+\Delta } \right) +\left( {1-\rho } \right) \beta M} \right] /2t\Delta$, respectively. Based on the setting of the basic model, the demand for the two firms must be between 0 and 1. This requires the following constraint:

$$\begin{aligned} M\le \frac{2t^{2}}{\left( {1-\rho } \right) \beta }. \end{aligned}$$

(10)

If the constraint is satisfied, then the equilibrium quality levels of the two firms are (8.1) and (8.2), respectively. Otherwise, the equilibrium outcomes become:

$$\begin{aligned} q_{_A} =0, \quad q_{_B} =\frac{t}{\left( {1-\rho } \right) \beta }; \quad \quad n_{A} =0, \quad n_B =1. \end{aligned}$$

(11)

The related discussion is in “Appendix”.

4 Optimal degree of privatization and social welfare

If the regulated price is determined by historical or political factors, then it can be regarded as exogenously given. On the other hand, if the regulated price depends on the social welfare generated from this industry, then the regulated price should be endogenously determined. We respectively discuss the optimal degree of privatization for the cases of exogenously and endogenously regulated prices in the following two subsections.

4.1 Exogenously regulated price

Substituting Eqs. (8.1) and (8.2) into Eq. (5) and then differentiating W with respect to $\rho$, we have:

$$\begin{aligned} \frac{\partial W}{\partial \rho }= & {} \frac{\partial q_{_A} }{\partial \rho }\left( {n_{A} -q_{_A} } \right) \nonumber \\&+\,\frac{\partial n_{A} }{\partial \rho }\left[ {\left( {q_{_A} -tn_{A} } \right) -\left( {q_{_B} -tn_B } \right) } \right] =\frac{\partial q_{_A} }{\partial \rho }\left( {n_{A} -q_{_A} } \right) . \end{aligned}$$

(12)

The optimal degree of privatization can be derived from $\partial q_{_A} /\partial \rho =0$ or $n_{A} -q_{_A} =0$. From Eq. (9.1), we find that if $\beta =t/M$, then $\partial q_{_A} /\partial \rho =0$, and the optimal degree of privatization can be any value. The possible interior solution of the optimal degree of privatization can be derived by $\left( {n_{A} -q_{_A} } \right) =0$, and it yields⁸:

$$\begin{aligned} \rho ^{*}=\frac{\left( {1-\beta } \right) \left( {2t-1} \right) M}{2t\left( {t-\beta M} \right) -\left( {1-\beta } \right) M}. \end{aligned}$$

(13)

Note that if $M= t$, then $\rho ^{*}=1$. If $M< t$, then the optimal degree of privatization, Eq. (13), is between 0 and 1; hence, Eq. (13) is the optimal interior solution. If $M>t$, then $n_{A}$ is always smaller than $q_{_A}$;⁹ thus, the optimal degree of privatization should be either 0 or 1, depending on the sign of $\partial q_{_A} /\partial \rho$. From (9.1) we know that if $M<t/\beta$, then $\partial q_{_A} /\partial \rho <0$, and so the first-order condition will be larger than zero; the optimal degree of privatization $\rho ^{*}=1$; conversely, if $M>t/\beta$, then $\partial q_{_A} /\partial \rho$ is positive, and the first-order condition will become negative; $\rho ^{*}=0$. The following proposition summarizes the results.

Proposition 2

In the case of exogenously regulated price M, the optimal degree of privatization is: (i) partial privatization $\rho ^{*}=\frac{\left( {1-\beta } \right) \left( {2t-1} \right) M}{2t\left( {t-\beta M} \right) -\left( {1-\beta } \right) M}$ if $M<t$ ; (ii) completely privatized $\rho ^{*}=1$ if $M\in \left[ {t,\frac{t}{\beta }} \right)$; (iii) completely public-owned $\rho ^{*}=0$ if $M>\frac{t}{\beta }$ ; and (iv) $\rho ^{*}=any value$ if $M=\frac{t}{\beta }.$

The results in Proposition 2 are illustrated in the upper figure in Fig. 2, and the related economic intuition can be explained as follows. Let us start from considering the traditional-type public firm, $\beta =1$. The first-order condition can be simplified to $\left( {n_{A} -q_{_A} } \right) =\rho \left( {t-M} \right) /\Delta$, and$\rho ^{*}=0$; which is completely public-owned.¹⁰ When $\beta <1$, if $\rho =0$, then the public firm’s objective function will deviate from the social welfare function. That is why the government needs to adjust the optimal privatization policy so as to ensure the optimal condition $\left( {n_{A} -q_{_A} } \right) =0$ is satisfied - namely, the value is shown in (i) of Proposition 2. However, $n_{A}$ is always smaller than $q_{_A}$ when $M>t$, implying that Eq. (12) cannot be zero by adjusting the degree of privatization. How the government determines the degree of privatization depends on how the degree of privatization affects the quality levels of the two firms.

First of all, when $t/\beta>M>t$, both qualities chosen by the firms are higher than the first-best outcome, and the quality of firm A is higher than that of firm B. Hence, for the government, a rise in the degree of privatization can reduce firm A’s investment, and it not only can decrease the investment cost but also lead the two firms to exhibit symmetry so as to decrease the total transportation cost. This is why the result (ii) in Proposition 2 is complete privatization.

Why is the result (iii) (i.e. completely public owned) exactly opposite to the result (ii)? It is because firm A’s product quality is lower than that of firm B when $M>t/\beta$. Although an increase in firmA’s investment can decrease the total transportation cost, the sum of investment costs of the two firms is too high. Therefore, the government lets firm A remain completely public owned, and it pushes firm B’s investment reaches the condition $q_{_B} =n_B$.

Note that, in the case of $\beta =0$, the constraint (10) always satisfied, it means that the optimal degree of privatization will be either partial privatization or completely privatized. And the results (iii) and (iv) will not appear since none of firms will be driven out the market. The intuition is completely included in the case of $\beta <1$ in previous paragraphs.

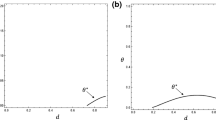
Substituting the optimal degree of privatization into Eq. (5) and together with Lemma 1, we derive the results of the corresponding social welfare levels that are sated in Proposition 3. We also depict the social welfare levels under different regulated prices in the lower figure of Fig. 2.

Proposition 3

Given the optimal degree of privatization is partial privatization, the social welfare is $W^{*1}=W^{FB}-\left( {t-1} \right) \left( {t-M} \right) ^{2}/4t^{2}\left( {2t-1} \right)$ with slope $\left( {\left( {t-1} \right) \left( {t-M} \right) } \right) /\left( {2t^{2} \left( {2t-1} \right) } \right) >0$; if the optimal degree of privatization is completely privatized, the social welfare is $W^{*2}=W^{FB}-\left( {t-M} \right) ^{2}/4t^{2}$ with slope $\left( {t-M} \right) /\left( {2t^{2}} \right) <0$ ; if the optimal degree of privatization is completely public-owned, the social welfare is $W^{*3}=W^{*1}-\left( {1-\beta } \right) ^{2}M^{2}/4t\left( {2t-1} \right)$ with slope $\left( {t-1} \right) \left( {t-M} \right) /2t^{2}\left( {2t-1} \right) -\left( {1-\beta } \right) ^{2}M/2t\left( {2t-1} \right) <0$ or $W^{*4}=W^{FB}-\left[ {\left( {1-\beta } \right) /2\beta } \right] ^{2}-\left( {2t+1} \right) \left( {t-1} \right) /4\beta ^{2}$ with slope zero.

Fig. 2

The optimal degree of privatization and social welfare level under different regulated prices

By Lemma 1, we know $W^{FB}=v-\left( {t-1} \right) /4$. It is easy to see that $W^{*1}$ and $W^{*2}$ depicted in Fig. 2 are the social welfare levels respectively corresponding to the results of (i) partial privatization and (ii) complete privatization. Regarding the social welfare level corresponding to result (iii), we need to consider the situation of market structure. Namely, if the regulated price is larger than $2t^{2}/\beta$, and if firm A is nationalized, then inequality (10) does not hold, and the equilibrium results is (11). Hence, $W^{*3}$ represents the social welfare level when firm A stays in the market, and $W^{*4}$ corresponds to the situation whereby firm A exits. In fact, Fig. 2 illustrates the relationship between the regulated prices and the social welfare levels under corresponding optimal privatization policies.

According to the above analysis, we find that the government privatization policy varies with the quality discrepancy of the two firms. If the public firm cares more about its rival’s profit (i.e. $\beta >t/M)$, tending to invest less in quality, then the government reduces the public firm’s investment through full nationalization. On one hand, this could save investment costs for the public firm, and on the other hand, it enables the investment by the private firm. Conversely, if the public firm is not concerned about its rival’s profit (i.e.$\beta <t/M)$ much, tending to produce higher quality, then the government raises the degree of privatization to discourage the public firm’s investment incentive, thus decreasing the total transportation cost and the public firm’s investment cost.

One last point is worth mentioning here. When $\beta <t/M$, Proposition 2 indicates two results: partial privatization and complete privatization. The main reason is due to the level of the regulated price; when M is too small, even the government has the incentive to raise the degree of privatization, but the quality of the private firm is too low. In order to allow consumers to enjoy higher quality product, the government prevents the public firm from choosing too low quality under partial privatization.

4.2 Endogenously regulated price

Aside from the degree of privatization$\rho$, the government can also in accordance with the social welfare set the regulated price in an attempt to reach the first-best outcome (shown in Lemma 1). The first-order condition of $\rho$ is already shown by Eq. (12), and the other condition is given by differentiating W with respect to M, as follows¹¹:

$$\begin{aligned} W_M =\frac{\partial W}{\partial M}=\mathop \sum \limits _{i=A,B} \left[ {\frac{\partial q_i }{\partial M}\left( {n_i -q_i } \right) } \right] . \end{aligned}$$

(14)

These two first-order conditions can be rearranged as:

$$\begin{aligned}&\frac{\partial W}{\partial \rho }=-\frac{2t\left( {t-\beta M} \right) }{\Delta ^{2}}\left[ {\frac{2t\rho \left( {t-\beta M} \right) -\left( {1-\beta } \right) M\Delta }{2t\Delta }} \right] ,\\&\frac{\partial W}{\partial M}=\frac{1}{2t^{2}\Delta ^{2}}\left\{ {\left( {t-M} \right) {\Phi }\left( {\rho ;\beta ,t} \right) -t\left( {1-\beta } \right) \left( {1-\rho } \right) \left[ {\left( {1-\beta } \right) \Delta +2\rho \beta t} \right] } \right\} , \end{aligned}$$

where ${ \Phi }\left( {\rho ;\beta ,t} \right) >0$.¹² We can easily see that if $\beta =1$, $M=t$ satisfies the two first-order conditions, and there is no need for another policy to implement the first-best outcome. However, if $\beta <1$, then it requires an additional policy to set $\rho =1$. The optimal privatization and price policies are $\left\{ {M^{**},\rho ^{**}} \right\} =\left\{ {t,1} \right\}$.¹³ We can now present the next proposition.

Proposition 4

If the public firm belongs to the traditional-type (i.e. $\beta =1$), then the government only needs to determine the regulated price $M^{**}=t$, and the privatization policy is redundant. However, if the public firm does not fully take its rival’s profit into account (i.e. $0\le \beta <1$) and given the same regulated price $M^{**}=t$, then the optimal privatization policy is to transform the public firm into a pure private firm (i.e. $\rho ^{**}=1$).

In the literature, for a traditional-type public firm, if the market price is controlled by the government and if the public firm does not exhibit inefficiency in all aspects versus the private firm, then intuitively the government will not necessarily privatize the public firm. We confirm this result in Proposition 2. If the government maximizes social welfare to choose the regulated price, then the first-best outcome can be achieved, and as long as $M^{**}=t$, there is no need to use the privatization policy. However, if the regulated price is determined by historical or political factors instead of depending on the social welfare, then in most situations the privatization policy cannot implement the first-best outcome since the privatization policy only influences the strategy of the public firm and not the private firm.

In regards to the case that the public firm does not fully take the rival’s profit into account (i.e. $\beta <1)$, the optimal regulated price $M^{**}=t$ can induce the private firm’s quality to achieve the first-best outcome. Nevertheless, the public firm invests more than the first-best outcome, because the public firm is concerned about its profit and the consumer surplus more so than the social welfare. For this reason, the government is willing to completely privatize firm A (i.e. $\rho ^{{**}}=1)$, so that the regulated price can force the quality of firm A to reach the first-best outcome.

5 Extended discussion

In this section, we discuss three extended cases. One is that the freight rate exactly equals 1, the second is that the government subsidizes consumers (or firms). Finally, we add one parameter to study the case that the public firm cares more about the consumer surplus.

5.1 The freight rate equal to one

Adopting a Hotelling linear transportation model to analyze quality competition, researchers usually suppose the unit of transportation cost is strictly larger than 1 (i.e. the freight rate $t>1)$, so as to ensure the existence, uniqueness, and stability of the social optimum (i.e. first-best outcome). When $t=1$, we find that the stability condition of the social optimum exactly equals zero, so that any pairs of qualities that satisfy the equation $\mathop \sum \nolimits _{i=A,B} q_i =1$ are all the first-best outcome. In this paper, all pairs of two firms’ product qualities given by (8.1) and (8.2) meet the social optimum, as long as the regulated price is $2\rho /\left[ {\left( {1+\rho } \right) -\left( {1-\rho } \right) \beta } \right]$ [derived from Eq. (14)]. This indicates that, in the special case of $t=1$, whether or not the public firm cares about the rival’s profit, the government can implement the social optimum through price control.

5.2 Subsidization

Aiura and Sanjo (2010) and Sanjo (2009) consider the healthcare market and suppose that a patient who received the medical service only needs to pay part of the medical fee and the rest is paid by the central government. We refer to their model to discuss the case in which the government subsidizes consumers who purchase the product. Consumers do not need to pay the full price, and the government pays the remaining amount due to vulnerable security, justice, consumer protection, and other policy considerations. Those expenditures do not require any balance in this industry, just like in the healthcare market.

We first rewrite the consumer utility function as follows:

$$\begin{aligned} u_A =v+q_{_A} -tx-sM, \end{aligned}$$

(15.1)

$$\begin{aligned} u_B =v+q_{_B} -t\left( {1-x} \right) -sM, \end{aligned}$$

(15.2)

where $s\in \left[ {0,1} \right]$ is exogenously given and represents the proportion borne by the consumer. We call it the co-payment rate. The social welfare, which is created from this industry, is now equivalent to the original social welfare (5) plus the government subsidy, which is diverted from elsewhere:

$$\begin{aligned} W'= & {} \left[ {M - \frac{1}{2}\mathop \sum \limits _{i = A,B} {q_i}^2} \right] \nonumber \\&+ \left[ {v + \mathop \sum \limits _{i = A,B} {n_i}{q_i} - T - sM} \right] = W + \left( {1 - s} \right) M \end{aligned}$$

(16)

where the first term in the right-hand side of the second equal sign in the above equation is original to social welfare (5), and the second term is the extra government subsidy. As for the game stages, they are roughly the same as before, except that the government’s objective function is no longer Eq. (5), but instead ${W}'$ of Eq. (16).

If the regulated price is exogenously given, then the optimal privatization policy will be the same as in Proposition 2, since differentiating ${W}'$ with respect to $\rho$ will derive the same first-order condition, which is Eq. (12). We thus want to know the difference in the optimal privatization policy between whether there is an extra government subsidy or not. Differentiating Eq. (16) with respect to $\rho$ is Eq. (12), but the first-order condition of M changes to:

$$\begin{aligned} W_M^{'} = \frac{{\partial W'}}{{\partial M}} = \left( {1 - s} \right) + \mathop \sum \limits _{i = A,B} \left[ {\frac{{\partial {q_i}^*}}{{\partial M}}\left( {{n_i}^* - {q_i}^*} \right) } \right] \end{aligned}$$

(17)

¹⁴ Comparing with Eq. (14), the above condition appends one more term $\left( {1-s} \right)$, implying the government will set a higher regulated price, i.e. larger than $M^{**}$. Hence, from Proposition 2 and Fig. 2, Corresponding to a higher regulated price, we thus know that the optimal degree of privatization will be either 0 or 1. Moreover, if s is small, then the government will tend to employ a larger regulated price, meaning that for a smaller co-payment rate, the government prefers more to let firm A remain a completely public owned firm.

What about if the government subsidizes the firms? From the viewpoint of policy execution, the government can (indirectly) subsidize the firms through setting a higher regulated price. Hence, the policy of subsidizing firms should be already incorporated in the government’s consideration of price regulation.

5.3 A more generalized model of the public firm’s objective function

As Matsumura (1998) mentions that the public firm may cares more about consumer surplus, in this subsection, let us consider the public firm’s objective function now to be $H^{A}=\rho \pi _A +\left( {1-\rho } \right) \left( {\pi _A +\beta \pi _B +\gamma CS} \right)$, where $\beta \le 1$ and $\gamma \ge 1$.¹⁵ The larger value of $\gamma$, the public firm cares more about the consumer surplus. We then derive

$$\begin{aligned} q_{_A} ^{g}=\frac{M}{2t}+\frac{\left( {1-\rho } \right) }{{\Lambda }}\left( {\gamma t-\beta M} \right) , \end{aligned}$$

(18)

where superscript g represents the outcomes of this model, and ${\Lambda }\equiv 2t-{\upgamma }\left( {1-\rho } \right)$. Suppose that t is large enough such that ${\Lambda }>0$. In this case, the public firm will choose a higher quality. Moreover, in the case of exogenously regulated price, if the regulated price is sufficiently low, i.e. $M\le t$, the optimal degree of privatization is:

$$\begin{aligned} \rho ^{g}=\frac{\left( {{\upgamma }-\beta } \right) \left( {2t-1} \right) M+2t\left( {t-M} \right) \left( {{\upgamma }-1} \right) }{2t\left( {{\upgamma }t-\beta M} \right) -\left( {{\upgamma }-\beta } \right) M}. \end{aligned}$$

(19)

Note that $\rho ^{g}-\rho ^{*}>0$. Differentiating Eq. (19) with respect to ${\upgamma }$, we obtain $\partial \rho ^{g}/\partial \gamma =2t\left( {2t^{2}-M} \right) \left( {t-M} \right) /\left[ {2t\left( {{\upgamma }t-\beta M} \right) -\left( {{\upgamma }-\beta } \right) M} \right] ^{2}>0$. Therefore, we see that if the public firm cares more about consumer surplus, then the quality of the product provided by the public firm will be raised. This induces the government to choose a higher privatization rate. Also, the interval of regulated price (i.e. $t\le M\le \gamma t/\beta )$ that corresponding to completely privatization becomes larger than that of the basic model (i.e. $t\le M\le t/\beta )$.

Regarding the case of endogenously regulated price, as long as one of weight average parameters (i.e. $\beta$ and $\gamma )$ does not equal to one, then the optimal regulated price and privatization are $\left\{ {M^{g},\rho ^{g}} \right\} =\left\{ {M^{**},\rho ^{**}} \right\} =\left\{ {t,1} \right\}$. The intuition is the same as Proposition 4.¹⁶

6 Conclusion

Many studies in the literature related to mixed oligopoly suppose that the public firm’s objective function is the weighted average of its own profit and social welfare, thus finding that it is not necessary for the government to privatize a public firm if the public firm is as efficient as the private firm in all aspects. However, in reality, especially for an oligopoly where only a few private firms and the public firm compete in the same market, it seems implausible for the government to still ask the public firm to care about it rivals’ profits. In view of this, we propose a generalized parameter to connect the PSE-type and the traditional-type public firm and utilize a mixed oligopolistic model to analyze the optimal privatization policy. We find the following: when the regulated price is exogenously determined, if the public firm is not a traditional-type public firm, then even though it has the same efficiency as the private firm the government may fully privatize it; but if the regulated price is endogenously determined, then full privatization is the unique optimal policy. However, if the public firm is a traditional-type public firm, no matter whether the regulated price is endogenous or exogenous, full privatization is the optimal policy.

When the market price is commonly controlled by the government, if the public firm does not show inefficiency in all aspects versus the private firm, then the public firm in general should provide a higher quality level. The PSE-type public firm conceived herein meets the general thinking and thus it is a reasonable explanation that the public firm’s objective function is not necessarily the social welfare. Therefore, one direction for a future extension of research based on the PSE-type public firm is to re-examine the results in the literature related to mixed oligopoly. Furthermore, because this paper only discusses the situation when the market price is under control, other extended directions can encompass the case that firms can freely price their products, or the that the government can only control the price of the public firm. Lastly, we define the PSE-type public firm’s objective function as the weighted average of its profit and the consumer surplus, but therein the consumer surplus is the surplus obtained by all consumers. Thus, one extension is to alter the contents of consumer surplus, e.g. including only the surplus derived by the consumers who purchase the product or service from the public firm.

Appendix: The discussion for the issue of corner solution of quality competition

Substituting (8.1) and (8.2) into Eqs. (2.1) and (2.2), we have $n_{A} =\left[ {2t^{2}-\left( {1-\rho } \right) \beta M} \right] /2t\Delta$ and $n_B =\left[ {2t\left( {t+\Delta } \right) +\left( {1-\rho } \right) \beta M} \right] /2t\Delta$, respectively. Based on the setting of the basic model, the demand for the two firms must be between 0 and 1. This requires the constraint: $M\le \frac{2t^{2}}{\left( {1-\rho } \right) \beta }$. If the constraint is satisfied, then the equilibrium quality levels of the two firms are (8.1) and (8.2), respectively. Otherwise, given the quality level of firm A in (8.1), no consumer will purchase product A. Figure 3 illustrates such a situation.

Fig. 3

The reaction functions of quality competition (corner solution)

Note that the reaction functions of the quality levels shift outward when M increases. If M rises to $M{\prime }$ and $M{\prime }>2t^{2}/[\left( {1-\rho } \right) \beta ]$, $R_A$ will shift to $R_A {\prime }$ and $R_B$ will rise to $R_B {\prime }$. However, the two new reaction functions fail to intersect, as shown in Fig. 2. Therefore, firm A’s best response is to completely abandon investing in product quality. Substituting $M=2t^{2}/\left[ {\left( {1-\rho } \right) \beta } \right]$ into (8.2), we derive that the optimal quality level of firm B in such a situation is $t/\left[ {\left( {1-\rho } \right) \beta } \right]$. This indicates that if inequality (10) does not hold, then the equilibrium outcomes become:

$$\begin{aligned} q_{_A} =0, \quad q_{_B} =\frac{t}{\left( {1-\rho } \right) \beta }; \quad \quad n_{A} =0, \quad n_B =1. \end{aligned}$$