Higher-order finite strip method (H-FSM) with nonlocal strain gradient theory for analyzing bending and free vibration of orthotropic nanoplates

Abstract

This paper develops a size-dependent Kirchhoff plate model for bending and free vibration analyses using a semi-analytical higher-order finite strip method (H-FSM) based on the nonlocal strain gradient theory (NSGT). To satisfy the various longitudinal boundary conditions, the continuous trigonometric function series and the interpolation polynomial functions are employed in the transverse direction. In solving nanoplate problems using the H-FSM, the higher-order polynomial shape functions (higher-order Hermitian shape functions) are utilized to evaluate the second derivatives, in addition to the displacement and first derivative. The stiffness and mass matrices, and force vector of the nanoplates are derived using the weighted residual method. A numerical study is conducted to investigate the impact of different factors, such as boundary conditions, nonlocal and strain gradient parameters, aspect ratio, and types of transverse loading. The Navier solution is utilized to analyze the effects of material length scale parameters on bending and free vibration responses of nanoplates for preliminary comparisons. The numerical results show that, when the transverse load on the nanoplate is uniform or hydrostatic and the plate has a CCCC boundary condition, the nonlocal effect does not affect the deflection results and is the same as the obtained results in the local mode.

1 Introduction

Nanostructures have exceptional properties and have found numerous applications in various fields such as aerospace, automotive, biomedical, mechanical, and civil engineering. Ignoring the nano-scale effects on mechanical properties may lead to incorrect designs and solutions [1]. However, conducting experimental measurements at the nano-scale is challenging and expensive, leading to the development of molecular dynamics and continuum-based modeling. Although classical continuum mechanics models are computationally less expensive, they do not consider inter-atomic forces and atomic length scale parameters, resulting in inaccurate results. Continuum theories that can capture size effects of materials at small sizes have gained significant attention in the research community for achieving more precise results. Several alternative theories to classical elasticity have been proposed to account for material length scale parameters, including nonlocal elasticity theory [2], strain gradient theories [3, 4], modified couple stress theory [5], and nonlocal strain gradient theory [6].

The nonlocal theory of Eringen [2] is a continuum theory that can accurately capture small-scale effects and the behavior of structures of all sizes. This theory assumes that stress at a point is a function of the strain field at all neighboring points in the continuum body, making it useful for analyzing nanostructures. Numerous studies have utilized this theory to investigate the scaling effects on the buckling, bending, and vibration behaviors of nanostructures, including nonlocal nonlinear analysis of functionally graded and laminated composite plates subjected to various loads [7,8,9,10], the nonlinear post-critical temperature-deflection behavior [11], investigation of the buckling and vibration behavior of imperfect nanoplates [12], stability and free vibration analysis of orthotropic single-layered graphene sheets [13], and porosity-dependent analysis of functionally graded sandwich nanoplates [14]. Other studies have investigated the buckling of compressed Bernoulli–Euler nano-beams [15], compared differential and integral formulations for boundary value problems in nonlocal elasticity [16], and investigated the deflection and temperature distribution of nanobeams [17] also, bending, buckling, and vibration analysis of functionally graded (FG) nanobeam [18]. Additional investigations on stress-driven nonlocal elasticity theory have been conducted and are referenced in a review article by Shariati et al. [19], and Nuhu and Babaei [20].

The theory of gradient elasticity [3, 21] suggests that materials should be treated as collections of atoms with higher-order deformation mechanisms at a small scale, and stress must consider additional strain gradient terms. The literature shows that nonlocal models and strain gradient models describe distinct size-dependent mechanical characteristics of materials at a small scale. Aifantis’s model [21], which involves only one gradient coefficient with length dimensions, has attracted considerable attention in gradient elasticity and led to the publication of numerous papers based on this theory. Several studies have investigated the mechanical behavior of isotropic nanoplates [22,23,24], cross-ply and angle-ply of Kirchhoff nanoplates [25], thin laminated composite nanoplates [26,27,28,29], transient analysis of functionally graded microplates [30], a neural network approach of isotropic nanoplates [31] using strain gradient theory, and nonlinear analysis of porous functionally graded composite microplates with and without cutouts [32], also bending of orthotropic nanoplates reinforced by defective graphene sheets [33]. These studies have explored bending, buckling, and free vibration behaviors of various nanoplates under different conditions using finite element and analytical methods.

The nonlocal strain gradient theory [6, 34] combines the effects of both nonlocal and strain gradient parameters to consider both stiffness softening and stiffness enhancement effects in small-scale materials. This theory has been successfully applied and developed for nanobeams, nanoplates, and nanoshells. Lim et al. [6] formulated this theory by introducing two parameters into classical continuum mechanics. This theory considers both the non-gradient nonlocal stress field [2] and the higher-order pure strain gradient stress field [21].

Several studies have investigated various aspects of nanostructure mechanics using nonlocal strain gradient theory are mentioned. For example, Rajabi and Hosseini-Hashemi [35] examined the free vibration of orthotropic nanoplates, while Karami et al. explored hygrothermal wave propagation in viscoelastic graphene [36] and resonance behavior of a three-directional functionally graded material [37]. A nonlocal strain gradient plate model to investigate the vibration of double-layered graphene sheets was developed by Ebrahimi and Barati [38], and the effects of hygrothermal and electromagnetic fields on smart piezomagnetic nanoplates was studied by Abazid [39]. Khazaei and Mohammadimehr [40] analyzed the deflection and buckling of porous nanocomposite piezoelectric plates, and Farajpour et al. [41] investigated the bending and transverse vibration of rectangular nanoplates. In addition, Chu et al. [42] investigated the thermally-induced dynamic behaviors of functionally graded flexoelectric nanobeams, and Malikan et al. [43] studied the torsional critical stability of a single-walled composite nano-shell exposed to a magnetic field. A nonlocal model for thermal buckling analysis of functionally graded nanobeams by was developed Fang et al. [44], and Xiao and Dai [45] proposed a size-dependent beam model for bending of bi-semi-tubes.

Abdelrahman et al. [46] developed a non-classical dynamic finite element model for perforated nanobeam structures, and Dangi et al. [47] considered the combined effect of nonlocality, strain gradient, and surface stresses on natural frequencies of functionally graded nanobeams. Additionally, Fan et al. [48] studied the nonlinear buckling and post-buckling analysis of micro/nano-plates made of a porous functionally graded material, while Tang and Qing [49] investigated the buckling and free vibration response of functionally graded Timoshenko beams using a nonlocal strain gradient integral model. Mohammadian and Hosseini [50] analyzed axial vibration of functionally graded carbon nanotube reinforced composite microrods, and Wang et al. [51] studied the buckling of bi-directional functionally graded nanotubes. Furthermore, Li et al. [52] investigated the free vibration of a piezoelectric nanoribbon, while Tanzadeh and Amoushahi [53] developed a buckling analysis of orthotropic nanoplates. Wu et al. [54] studied the free and forced vibrations of nonplanar imperfect nanobeams, Boyina and Piska [55] investigated wave propagation in viscoelastic Timoshenko nanobeams and buckling analysis of functionally graded Euler–Bernoulli beam subjected to thermo-mechanical loads was depeloped by Boyina et al. [56].

Recent research has explored the effects of material length scales on structures at micro- and nano-scales. This paper introduces the higher-order finite strip method for the first time for analyzing nanoplates using the nonlocal strain gradient theory. This theory incorporates two material length scale parameters that can capture changes in the stiffness of nanoscale structures. The strain gradient effect increases the order of the governing differential equation for nanoplates, causing the conventional Hermite shape function to become inadequate. Higher-order shape functions are necessary for accurate results, and fewer strips are required for convergence. As a result, using the higher-order finite strip method with nonlocal strain gradient theory is an efficient approach for examining nanoplates. Furthermore, the proposed relation demonstrates that simply supported nanoplates will have responses equivalent to locally available responses if the non-local parameter equals the second power of the strain gradient parameter. Numerical results show that the nonlocal effect does not impact deflection results for nanoplates subjected to uniform or hydrostatic transverse loads and with CCCC boundary conditions. The paper is divided into several sections. In Sect. 2, the higher order finite strip method is used to explain the kinematics of deformation and governing equation for thin isotropic and orthotropic Kirchhoff nanoplates based on nonlocal strain gradient theory. Section 3 proposes an analytical Navier formulation for isotropic and orthotropic nanoplates. Section 4 presents numerical results for bending and free vibration problems, demonstrating the effectiveness of the proposed H-FSM formulations in comparison to analytical results. Finally, Sect. 5 provides concluding remarks.

2 Higher-order finite strip method for isotropic and orthotropic nanoplates

In this section, a novel approach for analyzing nanoplates is presented, which considers the effects of material length scales and utilizes higher-order shape functions to enhance accuracy and convergence. The approach presented here is the higher-order finite strip method for isotropic and orthotropic nanoplates, which employs the nonlocal strain gradient theory. By deriving the governing equation, the method is shown to be capable of capturing both the reduction and increase in the stiffness of structures at the nanoscale.

2.1 Nonlocal strain gradient theory and the governing equation

According to Lim et al. [6] theory, the nonlocal strain gradient theory considers non-local stress field and strain gradient effects by introducing two scale parameters. The stress field, according to this theory, includes not only the non-local elastic stress field but also the strains gradient field, i.e., [6]:

$${t}_{ij}={\sigma }_{ij}^{(0)}-\nabla {\sigma }_{ij}^{(1)}$$

(1)

The laplacian operator $\nabla$ is applied to obtain the total stress, represented as ${t}_{ij}$. The classical nonlocal stress ${\sigma }_{ij}^{(0)}$ and the higher-order nonlocal stress ${\sigma }_{ij}^{(1)}$ are related to the strain ${\varepsilon }_{kl}$ and $\nabla {\varepsilon }_{kl}$ defined as [6]

$${\sigma }_{ij}^{(0)}={\int }_{V}{C}_{ijkl}{\alpha }_{0}\left(\left|x-{x}{\prime}\right|,{\mu }_{0}\right){\varepsilon }_{kl}{\prime}({x}{\prime})dV({x}{\prime})$$

(2a)

$${\sigma }_{ij}^{(1)}={l}^{2}{\int }_{V}{C}_{ijkl}{\alpha }_{1}\left(\left|x-{x}{\prime}\right|,{\mu }_{1}\right)\nabla {\varepsilon }_{kl}{\prime}({x}{\prime})dV({x}{\prime})$$

(2b)

where, the elastic coefficient ${C}_{ijkl}$ is accompanied by the nonlocal effects captured by ${\mu }_{0}={\left({e}_{0} a\right)}^{2}$ and ${\mu }_{1}={\left({e}_{1} a\right)}^{2}$, and the strain gradient effects captured by $l$. The attenuation kernel functions ${\alpha }_{0}(|x-{x}{\prime}|,{\mu }_{0})$, and ${\alpha }_{1}(|x-{x}{\prime}|,{\mu }_{1})$ are nonlocal functions that satisfy the developed conditions by Eringen [57] and incorporate the nonlocal effects of strain and the first-order strain gradient field into constitutive equations.

Considering the findings from the previous discussion, the following form represents the differential form of the constitutive relation for size-dependent nanoplates based on the nonlocal strain gradient theory [6]:

$$\left(1-{\mu }_{1}{\nabla }^{2}\right)\left(1-{\mu }_{0}{\nabla }^{2}\right) {t}_{ij} ={C}_{ijkl} {\left(1-{\mu }_{1}{\nabla }^{2}\right) \varepsilon }_{kl}-{C}_{ijkl} {l}^{2}{\left(1-{\mu }_{0}{\nabla }^{2}\right) {\nabla }^{2}\varepsilon }_{kl}$$

(3)

where ${\nabla }^{2}={\partial }^{2}/\partial {x}^{2}$ +${\partial }^{2}/\partial {y}^{2}$. Including, ${\mu }_{0}={\mu }_{1}=\mu$, canceling $\left(1-\mu {\nabla }^{2}\right)$ from two sides of equation, and factoring, ${C}_{ijkl} {\varepsilon }_{kl},$ on the right-hand side, the general constitutive relation in Eq. (3), can be condensed in this way:

$$\left(1-\mu {\nabla }^{2}\right){t}_{ij} ={C}_{ijkl} {\left(1-{l}^{2}{\nabla }^{2}\right) \varepsilon }_{kl}$$

(4)

In the current theory, the displacement field under the Kirchhoff assumptions at an arbitrary point is shown as follows [58]:

$$\begin{gathered} u\left( {x,y,z,t} \right) = u\left( {x,y,t} \right) - z\frac{{\partial w\left( {x,y,t} \right)}}{\partial x} \hfill \\ v\left( {x,y,z,t} \right) = v\left( {x,y,t} \right) - z\frac{{\partial w\left( {x,y,t} \right)}}{\partial y} \hfill \\ w\left( {x,y,z,t} \right) = w\left( {x,y,t} \right) \hfill \\ \end{gathered}$$

(5)

Here, $u$, $v,$ and $w$ specify the displacement components of an arbitrary point in the mid-plane along the coordinates $x$, $y,$ and $z$ directions, respectively, and $t$ denotes the time.

Finally, the above differential constitutive equation for an orthotropic nanoplate can be expressed by:

$$\begin{gathered} \left( {1 - \mu \nabla^{2} } \right)\left\{ {\begin{array}{*{20}c} {t_{xx} } \\ {t_{yy} } \\ {t_{xy} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {C_{11} } & {C_{12} } & 0 \\ {C_{12} } & {C_{22} } & 0 \\ 0 & 0 & {C_{66} } \\ \end{array} } \right]\left( {1 - l^{2} \nabla^{2} } \right)\left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {\gamma_{xy} } \\ \end{array} } \right\} \hfill \\ C_{11} = \frac{{E_{1} }}{{1 - v_{12} v_{21} }}, C_{12} = \frac{{v_{12} E_{2} }}{{1 - v_{12} v_{21} }}, C_{22} = \frac{{E_{2} }}{{1 - v_{12} v_{21} }}, C_{66} = G_{12} = \frac{{E_{1} }}{{2\left( {1 + v_{12} } \right)}} \hfill \\ \end{gathered}$$

(6)

In which ${E}_{1}$ and ${E}_{2}$ refer to Young’s moduli in directions $x$ and $y$ of the orthotropic plate; ${G}_{12}$ is the shear moduli, and ${v}_{12}$ and ${v}_{21}$ are Poisson’s ratios. Also, the moduli of elasticity and Poisson’s ratios are related by ${v}_{12}{{E}_{2}=v}_{21}{E}_{1}.$

The strains based on the classic plate theory (CPT) as a function of the displacements are written as follows [59]:

$$\left\{\begin{array}{c}{\varepsilon }_{xx}\\ \\ {\varepsilon }_{yy}\\ \\ {\gamma }_{xy}\end{array}\right\}=\left\{\begin{array}{c}\frac{\partial u}{\partial x}\\ \begin{array}{c}\frac{\partial v}{\partial y}\\ \frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}\end{array}\end{array}\right\}-z\left\{\begin{array}{c}\frac{{\partial }^{2}w}{\partial {x}^{2}}\\ \frac{{\partial }^{2}w}{\begin{array}{c}\partial {y}^{2}\\ 2\frac{{\partial }^{2}w}{\partial x\partial y}\end{array}}\end{array}\right\}$$

(7)

In the following, by integrating the total stresses, resultants of forces and moments of a thin plate are obtained

$${N}_{ij}={\int }_{-h/2}^{h/2}{t}_{ij} dz; i=j=x,y$$

(8)

$${M}_{ij}={\int }_{-h/2}^{h/2}{t}_{ij} z dz; i=j=x,y$$

(9)

where $h$ denotes the thickness of the plate. Using Eqs. (6), (7), and (9), moment resultants in terms of displacements for an orthotropic nanoplate based on the nonlocal strain gradient theory (NSGT) can be written as

$$\left(1-\mu {\nabla }^{2}\right)\left\{\begin{array}{c}{M}_{xx}\\ {M}_{yy}\\ {M}_{xy}\end{array}\right\}=-\left[\begin{array}{ccc}{D}_{11}& {D}_{12}& 0\\ {D}_{12}& {D}_{22}& 0\\ 0& 0& {D}_{66}\end{array}\right](1-{l}^{2}{\nabla }^{2})\left\{\begin{array}{c}\frac{{\partial }^{2}w}{\partial x}\\ \frac{{\partial }^{2}w}{\partial {y}^{2}}\\ 2\frac{{\partial }^{2}w}{\partial x\partial y}\end{array}\right\}$$

(10)

where, rigidities for orthotropic plates are [58],

$${D}_{11}=\frac{{E}_{1}{h}^{3}}{12(1-{v}_{12}{v}_{21})}; {D}_{22}=\frac{{E}_{2}{h}^{3}}{12(1-{v}_{12}{v}_{21})}; {D}_{12}=\frac{{{v}_{12}E}_{2}{h}^{3}}{12(1-{v}_{12}{v}_{21})}; {D}_{66}=\frac{{G}_{12}{h}^{3}}{12}$$

(11)

And for an isotropic plate, it is only necessary to set [58]

$${E}_{1}={E}_{2}=E; {v}_{12}={v}_{21}=v; {G}_{12}=G=\frac{E}{2(1+v)}$$

(12)

where $E$ and $v$ are the moduli of elasticity and the Poisson’s ratio for the isotropic nanoplates. The following equilibrium equation, based on the classical plate theory (CPT), is written as [58]

$$\frac{{\partial }^{2}{M}_{xx}}{\partial {x}^{2}}+2\frac{{\partial }^{2}{M}_{yy}}{\partial x\partial y}+\frac{{\partial }^{2}{M}_{xy}}{\partial {y}^{2}}+q+\frac{\partial }{\partial x}\left({N}_{x}\frac{\partial w}{\partial x}+{N}_{xy}\frac{\partial w}{\partial y}\right)+\frac{\partial }{\partial y}\left({N}_{y}\frac{\partial w}{\partial y}+{N}_{xy}\frac{\partial w}{\partial x}\right)={I}_{0}\frac{{\partial }^{2}w}{\partial {t}^{2}}-{I}_{2}\left(\frac{{\partial }^{4}w}{\partial {x}^{2}\partial {t}^{2}}+\frac{{\partial }^{4}w}{\partial {y}^{2}\partial {t}^{2}}\right)$$

(13)

where, ${I}_{0}=\rho h$ and ${I}_{2}=\rho {h}^{3}/12$ are translational and rotational inertias, respectively. In which $\rho$ is the mass density. Also, $q$ is the transverse load, as shown in Fig. 1, for uniformly distributed loading, and the different load functions are presented in Table 1, and ${N}_{x}$, ${N}_{y},$ and ${N}_{xy}$ are in-plane loads. Considering $w\left(x,y,t\right)=w\left(x,y\right){e}^{i\omega t}$ and using Eq. (10), it can obtain the nonlocal strain gradient governing the differential equation for bending, vibration, and buckling of orthotropic nanoplates as shown.

Fig. 1

Continuum nanoplate model under transverse loads

Table 1 Different transverse loading and values of ${q}_{mn}$ [58]

$$\left(1-{l}^{2}{\nabla }^{2}\right)\left[{D}_{11}\frac{{\partial }^{4}w}{\partial {x}^{4}}+2{(D}_{12}+2{D}_{66})\frac{{\partial }^{4}w}{\partial {x}^{2}\partial {y}^{2}}+{D}_{22}\frac{{\partial }^{4}w}{\partial {y}^{4}}\right]+\left(1-\mu {\nabla }^{2}\right)\left[-q-\frac{\partial }{\partial x}\left({N}_{x}\frac{\partial w}{\partial x}+{N}_{xy}\frac{\partial w}{\partial y}\right)-\frac{\partial }{\partial y}\left({N}_{xy}\frac{\partial w}{\partial x}+{N}_{y}\frac{\partial w}{\partial y}\right)-{I}_{0}{\omega }^{2}w+{I}_{2}{\omega }^{2}\left(\frac{{\partial }^{2}w}{\partial {x}^{2}}+\frac{{\partial }^{2}w}{\partial {y}^{2}}\right)\right]=0$$

(14)

This study examines the static and free vibration analyses of nanoplates, where buckling loads ${N}_{x}, {N}_{y}$, and ${N}_{xy}$ are neglected. The governing equation for orthotropic nanoplates in Eq. (14) is derived using the nonlocal theory with $l=0$, the strain gradient theory with $\mu =0$, and the local theory with $l=\mu =0$.

2.2 Development of a finite strip formulation for nanoplates

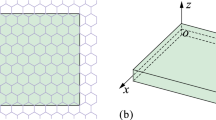
The ordinary finite strip method is considered for analyzing rectangular nanoplates where two opposite edges in the longitudinal directions ($y$ direction) are assumed to be different boundary conditions. The other two edges in the transverse direction ($x$ direction) can have arbitrary boundary conditions. The displacement functions are supposed to be polynomials in the transverse direction, while in the longitudinal direction, the basic trigonometric functions are considered. This approach allows the discretization of the rectangular plate in finite longitudinal strips. In this strip, the transverse curvature amplitude is also used as a nodal displacement parameter in addition to the standard deflection and rotation variables.

Using Hamilton’s principle, the governing equation of orthotropic nanoplates can be derived from the virtual work of stress/moment resultants. However, this approach only provides an incomplete set of boundary conditions for the sixth-order equation (Eq. (14)) with higher-order strain gradient terms. Because of this, numerical solutions such as finite element (FE) and finite strip (FS) formulations that are based on this method necessitate only C¹ continuity but generate an unsymmetric stiffness matrix. Nevertheless, the weak form of the governing equations results in a symmetric stiffness matrix, necessitates C² continuity of the finite strip formulation, and demands a proper set of boundary conditions. By performing integration by parts of non-local terms, the symmetric weak form of the equation can be derived, which necessitates additional boundary conditions. The symmetric weak form and complete set of boundary conditions can also be obtained by starting from the weighted residual statement corresponding to Eq. (14) [22].

Since the governing equation in Eq. (14) has the highest derivative of $w$ with respect to $x$ in the essential boundary conditions of order 2, the finite strip method used in this study needs to meet the C² continuity requirement. In Fig. 2, the degrees of freedom at each node line are selected as the lateral displacement $w$, its rotation $\theta$, and curvature $\chi$ (i.e., the first and second partial derivatives of $w$ with respect to $x$). These parameters can be represented using the generalized displacement parameters.

Fig. 2

Higher-order rectangular strip with two nodal lines (HO2)

$$w(x,y)=\sum_{p=1}^{r}\left({H}_{1}\left(x\right){w}_{1p}+{H}_{2}\left(x\right){\theta }_{1p}+{H}_{3}\left(x\right){\chi }_{1p}{+H}_{4}(x){w}_{2p}+{H}_{5}(x){\theta }_{2p}+{H}_{6}(x){\chi }_{2p}\right){Y}_{p}(y)$$

(15)

As shown in Fig. 2, ${w}_{ip}$, ${\theta }_{ip}$, and ${\chi }_{ip}(i=\text{1,2})$ are deflections, rotations, and curvatures at nodal line $i$ for the ${p}^{th}$ mode, so Eq. (15) can be rewritten in the vector form as

$$w\left( {x,y,t} \right) = \mathop \sum \limits_{p = 1}^{r} {\mathbf{H}} Y_{p} \left( y \right) {{\varvec{\Delta}}}_{p} e^{i\omega t}$$

(16)

where ${Y}_{p}(y)$ the trigonometric shape function, is presented in Table 1, ${{\varvec{\Delta}}}_{p}$ is the DOF vector of one strip at ${p}^{th}$ mode as shown in Eq. (17), also, $\omega$ is the natural frequency, and $t$ is time.

$${{\varvec{\Delta}}}_{p}={\left[\begin{array}{cccccc}{w}_{1}& {\theta }_{1}& {\chi }_{1}& {w}_{2}& {\theta }_{2}& {\chi }_{2}\end{array}\right]}_{p}^{T}$$

(17)

In which ${\theta }_{i}={\left(\frac{\partial w}{\partial x}\right)}_{i}$, ${\theta }_{j}={\left(\frac{\partial w}{\partial x}\right)}_{j}$ and${\chi }_{i}={\left(\frac{{\partial }^{2}w}{\partial {x}^{2}}\right)}_{i}$,${\chi }_{j}={\left(\frac{{\partial }^{2}w}{\partial {x}^{2}}\right)}_{j}$. The total DOF vector for each finite strip could be expressed as:

$${\varvec{\Delta}}={\left[\begin{array}{cccc}{{\varvec{\Delta}}}_{p=1}& {{\varvec{\Delta}}}_{p=2}& \cdots & {{\varvec{\Delta}}}_{p=r}\end{array}\right]}^{T}$$

(18)

As previously stated, a 6-term polynomial is used to approximate $H$ in this strip. In order to satisfy the continuity and differentiability requirements between elements, the quintic variation of $H$ is utilized.

$$H\left(x\right)={\alpha }_{1}+{\alpha }_{2}x+{\alpha }_{3}{x}^{2}+{\alpha }_{4}{x}^{3}+{\alpha }_{5}{x}^{4}+{\alpha }_{6}{x}^{5}$$

(19)

The local coordinates of the 2-noded line strip are denoted by $x$ in the polynomial approximation of $H$, where $x$ belongs to the interval $[0,{a}_{s}]$. The constants ${\alpha }_{j}, j=1,\dots ,6$ are determined and grouped in the vector α to meet the differentiability and interelement continuity requirements. The values of $w$, $\theta$, and, $\chi$ at each noded line, which are represented by $H$, $dH/dx$, and ${d}^{2}H/d{x}^{2}$, are computed at $x=0,{a}_{s}$ and are set equal to their nodal values collected in the vector ${{\varvec{\Delta}}}_{p}$. This process results in a system of 6 algebraic equations that allow the computation of the constants ${\alpha }_{j}$. This system can be represented in a compact matrix form.

$${{\varvec{\Delta}}}_{p}=\widehat{\mathbf{A}}{\varvec{\upalpha}}$$

(20)

The coefficients of the vector ${\varvec{\upalpha}}$, which depend on the node coordinates, can be obtained through matrix inversion of the known coefficient matrix $\widehat{\mathbf{A}}$.

$${\varvec{\upalpha}}={\widehat{\mathbf{A}}}^{-1}{{\varvec{\Delta}}}_{p}$$

(21)

After computing the constants ${\alpha }_{j}$, the solution is substituted into the initial approximation of $H$ given in Eq. (3). Each term of the solution multiplied by ${\Delta }_{pj}$ represents an interpolating function ${H}_{j}\left(x\right)$ associated with that degree of freedom. This results in six functions that can be used for further analysis.

$${\mathbf{H}}_{p}={\left\{\begin{array}{c}{H}_{1}\\ {H}_{2}\\ {H}_{3}\\ {H}_{4}\\ {H}_{5}\\ {H}_{6}\end{array}\right\}}^{T}{Y}_{p}\left(y\right)={\left\{\begin{array}{c}\left(1-10{\xi }^{3}+15{\xi }^{4}-6{\xi }^{5}\right)\\ {a}_{s}\left(\xi -6{\xi }^{3}+8{\xi }^{4}-3{\xi }^{5}\right)\\ 0.5{a}_{s}^{2}\left({\xi }^{2}-{3\xi }^{3}+3{\xi }^{4}-{\xi }^{5}\right)\\ \left(10{\xi }^{3}-15{\xi }^{4}+6{\xi }^{5}\right)\\ {a}_{s}\left(-4{\xi }^{3}+7{\xi }^{4}-3{\xi }^{5}\right)\\ 0.5{a}_{s}^{2}\left({\xi }^{3}-{\xi }^{4}+{\xi }^{5}\right)\end{array}\right\}}^{T}{Y}_{p}\left(y\right)$$

(22)

In which, $\xi =x/{a}_{s}$, ${a}_{s}$ is the width of the strip.

By disregarding the buckling load terms $({N}_{x},{N}_{y},{N}_{xy})$ and using the definition of $w$ from Eq. (16), the sixth-order governing equation in Eq. (14) can be used to derive the linear algebra static and eigenvalue free vibration equations of nanoplates. This is accomplished by applying the method of weighted residuals.

$$\left(\mathbf{K}-{{\varvec{\omega}}}^{2}\mathbf{M}\right){\varvec{\Delta}}=0$$

(23a)

$$\mathbf{K}{\varvec{\Delta}}=\mathbf{F}$$

(23b)

In which ${\varvec{\Delta}}$ is the eigenvector for the free vibration problem and nodal displacements vector for the bending problem; $\mathbf{K}$ includes global local and nonlocal (associated with strain gradient) stiffness matrices, $\mathbf{M}$ includes local and nonlocal (associated with Eringen nonlocality) mass matrices and $\mathbf{F}$ is related to local and nonlocal (also associated with Eringen nonlocality) force vectors.

In the present study, using the higher-order finite strip procedure, the element stiffness and mass matrices, also force vectors, are calculated, and according to the compatibility equations along the nodal lines, these matrices are assembled, and the global stiffness and mass matrices and global force vector on the whole plate are obtained. Finally, by properly applying the boundary conditions and then as an eigenvalue problem, fundamental frequencies and by linear solution deflection of nanoplate could be calculated.

The stiffness matrix of a higher-order strip corresponding to $m$^th and $n$^th modes, ${\left(\mathbf{K}\right)}_{mn}^{e}$, is expressed as

$$\begin{aligned} \left( {\mathbf{K}} \right)_{mn}^{e} & = \left( {{\mathbf{K}}^{L} } \right)_{mn}^{e} + l^{2} \left( {{\mathbf{K}}^{NL} } \right)_{mn}^{e} \\ = & \mathop \int \limits_{0}^{b} \mathop \int \limits_{0}^{{a_{s} }} \left( {\left[ {\begin{array}{*{20}c} {\frac{{\partial^{2} {\mathbf{H}}_{m} }}{{\partial x^{2} }}} & {\frac{{\partial^{2} {\mathbf{H}}_{m} }}{{\partial y^{2} }}} & {2\frac{{\partial^{2} {\mathbf{H}}_{m} }}{\partial x\partial y}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {D_{11} } & {D_{12} } & 0 \\ {D_{12} } & {D_{22} } & 0 \\ 0 & 0 & {D_{66} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\frac{{\partial^{2} {\mathbf{H}}_{n} }}{{\partial x^{2} }}} \\ {\frac{{\partial^{2} {\mathbf{H}}_{n} }}{{\partial y^{2} }}} \\ {2\frac{{\partial^{2} {\mathbf{H}}_{n} }}{\partial x\partial y}} \\ \end{array} } \right]} \right)dxdy \\ & + l^{2} \mathop \int \limits_{0}^{b} \mathop \int \limits_{0}^{{a_{s} }} \left( {\left[ {\begin{array}{*{20}c} {\frac{{\partial^{3} {\mathbf{H}}_{m} }}{{\partial x^{3} }}} & {\frac{{\partial^{3} {\mathbf{H}}_{m} }}{{\partial x\partial y^{2} }}} & {\frac{{\partial^{3} {\mathbf{H}}_{m} }}{{\partial y^{3} }}} & {\frac{{\partial^{3} {\mathbf{H}}_{m} }}{{\partial x^{2} \partial y}}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {D_{11} } & {D_{12} } & 0 & 0 \\ {D_{12} } & {D_{22} + 2D_{66} } & 0 & 0 \\ 0 & 0 & {D_{22} } & {D_{12} } \\ 0 & 0 & {D_{12} } & {D_{11} + 2D_{66} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\frac{{\partial^{3} {\mathbf{H}}_{n} }}{{\partial x^{3} }}} \\ {\frac{{\partial^{3} {\mathbf{H}}_{n} }}{{\partial x\partial y^{2} }}} \\ {\frac{{\partial^{3} {\mathbf{H}}_{n} }}{{\partial y^{3} }}} \\ {\frac{{\partial^{3} {\mathbf{H}}_{n} }}{{\partial x^{2} \partial y}}} \\ \end{array} } \right]} \right)dxdy \\ \end{aligned}$$

(24)

The mass matrix of the strip, ${\left(\mathbf{M}\right)}_{mn}^{e}$ is also defined as

$$\begin{aligned}{\left(\mathbf{M}\right)}_{mn}^{e}&={\left({\mathbf{M}}^{L}\right)}_{mn}^{e}+\mu {\left({\mathbf{M}}^{NL}\right)}_{mn}^{e}\\ &=\mathop\int \limits_{0}^{b}\mathop\int\limits_{0}^{{a}_{s}} \left({\mathbf{H}}_{m}^{T}{{I}_{0}{\varvec{H}}}_{n}+\left[\begin{array}{cc}\frac{\partial {\mathbf{H}}_{m}}{\partial x} \frac{\partial {\mathbf{H}}_{m}}{\partial y}\end{array}\right]{I}_{2}\left[\begin{array}{c}\frac{\partial {\mathbf{H}}_{n}}{\partial x}\\ \frac{\partial {\mathbf{H}}_{n}}{\partial y}\end{array}\right]\right)dxdy\\ &\quad+\mu {\int }_{0}^{b}{\int }_{0}^{{a}_{s}}\left(\left[\begin{array}{cc}\frac{\partial {\mathbf{H}}_{m}}{\partial x}& \frac{\partial {\mathbf{H}}_{m}}{\partial y}\end{array}\right]{I}_{0}\left[\begin{array}{c}\frac{\partial {\mathbf{H}}_{n}}{\partial x}\\ \frac{\partial {\mathbf{H}}_{n}}{\partial y}\end{array}\right]+\left[\begin{array}{cc}\frac{\partial {\mathbf{H}}_{m}}{\partial x}& \frac{\partial {\mathbf{H}}_{m}}{\partial y}\end{array}\right]\left[\begin{array}{cc}{I}_{2}& {I}_{2}\\ {I}_{2}& {I}_{2}\end{array}\right]\left[\begin{array}{c}\frac{\partial {\mathbf{H}}_{n}}{\partial x}\\ \frac{\partial {\mathbf{H}}_{n}}{\partial y}\end{array}\right]\right)dxdy\end{aligned}$$

(25)

Also, ${\left(\mathbf{F}\right)}_{mn}^{e}$ is shown as

$${\left(\mathbf{F}\right)}_{m}^{e}={\left({\mathbf{F}}^{L}\right)}_{m}^{e}+\mu {\left({\mathbf{F}}^{NL}\right)}_{m}^{e}={\int }_{0}^{b}{\int }_{0}^{{a}_{s}} { q\left(x,y\right)\mathbf{H}}_{{\varvec{m}}}^{T}dxdy+\mu {\int }_{0}^{b}{\int }_{0}^{{a}_{s}}-{\nabla }^{2}q\left(x,y\right){\mathbf{H}}_{{\varvec{m}}}^{T}dxdy$$

(26)

When transverse applied load $q\left(x,y\right)={q}_{0}$, the force vector ${\left(\mathbf{F}\right)}_{m}^{e}$ simplified rewritten as

$${\left(\mathbf{F}\right)}_{m}^{e}={q}_{0}{\int }_{0}^{b}{\int }_{0}^{{a}_{s}} { \mathbf{H}}_{{\varvec{m}}}^{T}dxdy+\mu {q}_{0}{\int }_{0}^{b}{\int }_{0}^{{a}_{s}}-\left(\frac{{\partial }^{2}{\mathbf{H}}_{m}}{\partial {x}^{2}}+\frac{{\partial }^{2}{\mathbf{H}}_{m}}{\partial {y}^{2}}\right)dxdy$$

(27)

Finally, by considering, Eq. (23a), the fundamental frequency ($\omega$) and transverse displacement of the nanoplates are calculated by solving the eigenvalue problem and linear solution, as shown in Eqs. (28a) and Eq. (28b), respectively.

$$\text{det}\left|\mathbf{K}-{{\varvec{\omega}}}^{2}\mathbf{M}\right|=0$$

(28a)

$$\mathbf{K}{\varvec{\Delta}}=\mathbf{F}$$

(28b)

3 Analytical solution of isotropic and orthotropic nanoplates

This section presents analytical solutions for the static and free vibration analyses of isotropic and orthotropic nanoplates.

3.1 Static analysis

The analytical solution is derived for the bending of simply-supported thin orthotropic nanoplates using nonlocal strain gradient theory to compare with the present higher-order semi-analytical finite strip method. Navier’s approach is used to express the transverse displacement w, which satisfies both local and nonlocal boundary conditions, including $w={M}_{xx}=0$ at $x=0,a$ and $w={M}_{yy}=0$ at $y=0,b$, while the nonlocal boundary conditions are ${\partial }^{2}w/\partial {x}^{2}=0$ at $x=0,a$ and ${\partial }^{2}w/\partial {y}^{2}=0$ at $y=0,b$ [60], in small-scale problems [58].

$$w\left( {x,y,t} \right) = \sum\limits_{m = 1}^{\infty } {\,\sum\limits_{n = 1}^{\infty } {W_{mn} \sin \alpha x \, \sin \beta y \Phi \left( {\omega_{mn} t} \right)} }$$

(29)

where ${W}_{mn}$ is the amplitude and ${\omega }_{mn}$ is the natural frequency of transverse vibration, also. $\alpha =\frac{m\pi x}{a}$, $\beta =\frac{m\pi y}{b}$ The lateral load $q$ is also expanded into a double sine series as:

$$q\left(x,y\right)=\sum_{m=1}^{\infty }\sum_{n=1}^{\infty }{q}_{mn}\text{ sin}\alpha x\text{ sin}\beta y$$

(30)

where

$${q}_{mn}=\frac{4}{ab}\int^{b}_{0}\int^{a}_{0}q(x,y) \text{ sin}\alpha x \text{ sin}\beta y$$

(31)

Setting in-plane loads ${N}_{xx}= {N}_{yy}= {N}_{xy}=0$, and $\Phi ({\omega }_{mn}t) =1,$ and substituting the expression of $w$, Eq. (29), in the equation of motion (Eq. (14)), the static deflection of orthotropic nanoplates for different lateral load $q(x,y)$ could be expressed as:

$${W}_{mn}=\frac{{q}_{mn}}{{d}_{mn}}$$

(32a)

$$\begin{gathered} d_{mn} = K_{0} + l^{2} K_{2} \hfill \\ K_{0} = D_{11} \alpha^{4} + 2\left( {D_{12} + 2D_{66} } \right)\alpha^{2} \beta^{2} + D_{22} \beta^{4} \hfill \\ K_{2} = D_{11} (\alpha^{2} + \alpha^{4} \beta^{2} ) + 2\left( {D_{12} + 2D_{66} } \right)\left( {\alpha^{4} \beta^{2} + \alpha^{2} \beta^{4} } \right) + D_{22} (\alpha^{2} \beta^{4} + \beta^{4} ) \hfill \\ \end{gathered}$$

(32b)

, whereas for nanoplates with an isotropic material

$${W}_{mn}=\frac{{q}_{mn}(1+\mu \lambda )}{D{\lambda }^{2}(1+{l}^{2}\lambda )}$$

(33a)

$${d}_{mn}=D{\lambda }^{2}\left(1+{l}^{2}\lambda \right),\cdot \cdot \cdot \cdot \cdot \lambda =\left({\alpha }^{2}+{\beta }^{2}\right)$$

(33b)

The corresponding expression for the classical case (local mode) can be obtained, if in Eq. (33a), nonlocal and strain gradient parameters are set to zero ($l=\mu =0)$.

$${W}_{mn}=\frac{{q}_{mn}}{D{\lambda }^{2}}$$

(34)

For the case of a square plate with $a=b$, and $m=n=1$, the relation between nonlocal and local normalized central deflection if $\mu ={\left({e}_{0}{l}_{i}\right)}^{2}$ can be obtained:

$${w}_{c}^{\text{NSGT}}=\left(\frac{1+\mu \lambda }{1+{l}^{2}\lambda }\right){w}_{c}^{\text{Local}}=\left(\frac{1+2{\pi }^{2}{\left(\frac{{e}_{0}{l}_{i}}{a}\right)}^{2} }{1+2{\pi }^{2}{\left(\frac{l}{a}\right)}^{2}}\right){w}_{c}^{\text{Local}}$$

(35)

A nonlinear relationship can be observed between the deflection of the nanoplate and the increase in values of $(l/a)$, indicating a decrease in deflection. On the other hand, an increase in deflection of the nanoplate is observed with an increase in values of $(\frac{{e}_{0}{l}_{i}}{a})$, also in a nonlinear way. The coefficients ${q}_{mn}$ corresponding to various transverse loads are listed in Table 1.

3.2 Free vibration analysis

By setting $q=0$, in-plane loads ${N}_{xx}= {N}_{yy}= {N}_{xy}=0$ and $\Phi \left({\omega }_{mn}t\right)={e}^{i{\omega }_{mn}t}$, in Eq. (14) the expression for natural frequencies of orthotropic nanoplates is derived as:

$${\omega }_{mn}^{2}=\frac{{K}_{0}+{l}^{2}{K}_{2}}{({I}_{0}+{I}_{2}\lambda )+\mu ({I}_{0}\lambda +{I}_{2}{\lambda }^{2})}=\frac{{K}_{0}+{l}^{2}{K}_{2}}{({I}_{0}+{I}_{2}\lambda )(1+\mu \lambda )}$$

(36)

whereas, for nanoplates with an isotropic material,

$${\omega }_{mn}^{2}=\frac{D{\lambda }^{2}(1+{l}^{2}\lambda )}{({I}_{0}+{I}_{2}\lambda )(1+\mu \lambda )}$$

(37)

For the special case of a square plate with side $a$ and, $m=n=1$, one has the form

$${\omega }_{11}=\left(\frac{2{\pi }^{2}}{{a}^{2}}\right)\sqrt{\frac{D}{\left({I}_{0}+{I}_{2}\left(\frac{2{\pi }^{2}}{{a}^{2}}\right)\right)}}\sqrt{\frac{1+{l}^{2}\left(\frac{2{\pi }^{2}}{{a}^{2}}\right)}{1+\mu \left(\frac{2{\pi }^{2}}{{a}^{2}}\right)}}$$

(38)

If $\mu ={\left({e}_{0}{l}_{i}\right)}^{2}$

$${\omega }_{11}=\left(\frac{2{\pi }^{2}}{{a}^{2}}\right)\sqrt{\frac{D}{\left({I}_{0}+{I}_{2}\left(\frac{2{\pi }^{2}}{{a}^{2}}\right)\right)}}\sqrt{\frac{1+2{\pi }^{2}{\left(\frac{l}{a}\right)}^{2}}{1+2{\pi }^{2}{\left(\frac{{e}_{0}{l}_{i}}{a}\right)}^{2}}}$$

(39)

Therefore, the nondimensional nonlocal fundamental frequency when ${\omega }_{11}^{\text{Local}}=\left(\frac{2{\pi }^{2}}{{a}^{2}}\right)\sqrt{D/\left({I}_{0}+{I}_{2}\left(\frac{2{\pi }^{2}}{{a}^{2}}\right)\right)}$ is

$${\omega }_{11}^{\text{NSGT}}={\omega }_{11}^{\text{Local}}\sqrt{\frac{1+2{\pi }^{2}{\left(\frac{l}{a}\right)}^{2}}{1+2{\pi }^{2}{\left(\frac{{e}_{0}{l}_{i}}{a}\right)}^{2}}}$$

(40)

Increasing the strain gradient parameter $(l)$ results in an increase in frequency, while increasing the nonlocal parameter $(\mu )$ leads to a decrease in frequency.

4 Numerical results

Various numerical examples are provided to analyze the bending and free vibration of isotropic and orthotropic nanoplates using the nonlocal strain gradient theory based on the classic plate theory (CPT). The examples consider different length-to-thickness ratios, types of transverse loading, and boundary conditions. The number of degrees of freedom for each finite longitudinal strip is $6r$, where $r$ represents the number of deformation modes along the longitudinal direction. The dimensions of the nanoplates, represented as $a, b,$ and $h$, stand for the plate width, length, and thickness, respectively. These values are used consistently in all tables and figures.

The nanoplates analyzed in this study have dimensions of $a=10 \text{\,nm}$, $b=10 \text{\,nm}$, and $h=0.34 \text{\,nm}$ [61]. For isotropic nanoplates, material properties of $E=1.1 \text{TPa}, \nu =0.3$, and mass density $\rho =2300 \text{kg}/{\text{m}}^{3}$ are used. For orthotropic nanoplates, Poisson’s ratio is set to ${\nu }_{12}=0.25$, and for the modulus ratio ${E}_{1}/{E}_{2}=1$, the shear modulus is ${G}_{12}=0.4{E}_{2}$. For other modulus ratios, the value of ${G}_{12}$ is set to $0.5{E}_{2}$.To access the same results for isotropic plates with Poisson’s ratio ($\nu =0.25$), with orthotropic plates with ${E}_{1}/{E}_{2}=1$, the shear modulus is taken ${G}_{12}=0.4{E}_{2}$. To obtain equivalent outcomes for isotropic plates having Poisson’s ratio ($\nu =0.25$) and orthotropic plates having a modulus ratio of ${E}_{1}/{E}_{2}=1$, ${G}_{12}$ is set to $0.4{E}_{2}$.

Non–dimensional transverse displacement and fundamental frequency for orthotropic nanoplates are expressed by the following equations:

$$\begin{gathered} \overline{w} = w_{0} \frac{{D_{22} }}{{q_{0} a^{4} }},\check{w} = w_{0} \left( {\frac{{E_{2} h^{3} }}{{q_{0} a^{4} }}} \right){\text{while for isotropic material}},D_{22} = D \hfill \\ \overline{\omega } = \omega_{cr} \left( {\frac{{a^{2} }}{{\pi^{2} }}} \right)\sqrt {\frac{\rho h}{{D_{11} }}} ; \hat{\omega } = \omega_{cr} b^{2} \sqrt {\frac{\rho }{{E_{2} h^{2} }}} \hfill \\ \end{gathered}$$

(41)

where $D=\frac{E{h}^{3}}{12\left(1-{\nu }^{2}\right)}$. In this higher-order finite strip method, different boundary conditions in the longitudinal direction and the transverse direction are considered. Different end conditions for the two other edges in the transverse direction are given in Table 2 and for the two opposite edges in the longitudinal direction, trigonometric functions are chosen are shown in Table 3. Note that the essential boundary conditions specified in this table are just constrained conditions. Also, the different boundary conditions that are considered for the plate, as shown in Fig. 3, are simply supported (S), clamped (C), and free (F).

Table 2 Different essential boundary conditions in the transverse direction [22]

Table 3 Different shape functions in the longitudinal direction [62]

Fig. 3

Nanoplate subjected to the different types of transverse loading. a Uniform (UL), b concentrated (CL), c hydrostatic (HL), d parabolic (PL), e single sinusoidal (SSL), f double sinusoidal (DSL)

4.1 Bending results of the isotropic and orthotropic nanoplates

For verification, the non-dimensional transverse deflection $\overline{w }=1000 {w}_{0}(a/2,b/2)(D/{qa}^{4} )$ of simply supported isotropic square nanoplate for different strain gradient parameters ($l=0, 0.2, 0.5, 1$) are shown in Table 4. The obtained results are based on the use of different numbers of strips considering nine modes ($r=9$). The analysis shows that increasing the number of strips is effective up to five strips, beyond which no significant effect is observed. Therefore, for the following analysis, five strips and one mode ($r=1$) are used unless otherwise specified. It should be mentioned that the plate’s four edges are assumed to be simply supported unless mentioned otherwise. The deflection of the nanoplate is seen to decrease with an increase in the strain gradient length scale parameter$(l)$. This is due to the stiffening of the nanoplate as this parameter increases, which is reflected in the stiffness matrix. These results are consistent with previously published work and support the accuracy and dependability of the H-FSM.

Table 4 The non-dimensional transverse deflections $\overline{w }=1000 {w}_{0}(a/2,b/2)(D/{qa}^{4} )$ in isotropic square simply-supported (SSSS) plates subjected to uniformly distributed load, $[\mu =0]$

Table 5 presents the non-dimensional transverse deflections $\check{w} = w_{0} \left( {a/2,b/2} \right)\left( {E_{2} h^{3} /q_{0} a^{4} } \right)$ of square and rectangular plates under various types of loads, including single sinusoidal (SSL), double sinusoidal (DSL), uniform (UL), hydrostatic (HL), parabolic (PL), and concentrated load (CL). For concentrated load, the non-dimensional transverse deflection is considered $\check{w} = w_{0} \left( {a/2,b/2} \right)\left( {E_{2} h^{3} /Pa^{2} } \right)$. The results show the effect of different types of loads on the non-dimensional transverse deflection and provide valuable insights into the behavior of square and rectangular plates under various loading conditions. It is noticeable from the table that the results obtained in this study exhibit remarkable conformity with the previously published work conducted by Reddy [58]. Additionally, the proposed formulation in Eq. (34) which is based on the Navier solution is also presented in this study.

Table 5 The nondimensional transverse deflections $\check{w} = w_{0} \left( {a/2,b/2} \right)\left( {E_{2} h^{3} /q_{0} a^{4} } \right)$ of isotropic and orthotropic (${E}_{1}/{E}_{2} = 25, {G}_{12} =0.5{E}_{2}, {\nu }_{12} = 0.25$) rectangular plates subjected to different types of loads, $(\mu =0, l=0)$

The effects of nonlocal and strain gradient parameters on the non-dimensional deflection of simply-supported rectangular plates under uniform loading are presented in Table 6. It is observed that by increasing the aspect ratio after $b/a=5$, maximum deflection does not change. This situation also exists in non-local (Eringen nonlocal and strain gradient) problems. The interesting point is that in the non-local mode when $\mu =1$ and $l=1$, the results are the same as in the local mode. This was also mentioned in the relationship presented in Navier’s formula, and Eq. (35) confirms this issue. The lowest deflection occurs when strain gradient length scale parameter $l$ is maximum and nonlocal parameter $\mu$ is minimum, because as observed in the table, increasing $l$ increases the stiffness of the plate but increasing $\mu$ decreases the stiffness of the plate. In other words, $l$ has a hardening effect and $\mu$ has a softening effect.

Table 6 The effect of nonlocal and strain gradient parameters on the non-nondimensional deflection $\overline{w }=100{w}_{0}(a/2,b/2)(D/{qa}^{4} )$ of simply-supported isotropic rectangular plates subjected to uniformly distributed load

Table 7 presents the nondimensional deflection for different aspect ratios of isotropic and orthotropic CSSS plates under uniformly distributed load. The table reveals that an increase in the value of ${E}_{1}/{E}_{2}$ leads to a significant reduction in deflection. Moreover, increasing the stiffness of the edges and aspect ratio of the plate results in a decrease in the influence of nonlocal and strain gradient parameters.

Table 7 Effect of nonlocal and strain gradient length scale parameters ($\mu$ and$l$) on the non-dimensional deflections of isotropic and orthotropic $\overline{w }={w}_{0}(a/2,b/2)({D}_{22}/{{q}_{0}L}^{4} )$ rectangular plates with side $x = 0$ clamped, side $x = a$ simply0supported, and sides $y = 0, b$ simply supported (CSSS), subjected to uniformly distributed load, ($b/a\le 1$:${{qL}^{4}qb}^{4}$,$b/a>1$: ${qL}^{4}={qa}^{4}),r=9$

Table 8 presents the maximum non-dimensional deflection $\overline{w }=1000{w}_{0}(x,y)(D/{qa}^{4} )$ of a rectangular isotropic nanoplate with various boundary conditions (SSSS, CCSS, FFSS, CFSS, and CCCC) under a uniformly distributed transverse load and different $b/a$ ratios. The aim of this study is to investigate the effect of the strain gradient parameter ($l$) on the maximum deflection. The results indicate that the present H-FSM agrees well with [23] based on the Levy solution. Moreover, increasing the strain gradient parameter $l$ results in a decrease in the maximum transverse displacement for all cases.

Table 8 The non-dimensional transverse deflections $\overline{w }={1000w}_{0}(x,y)D/{qa}^{4}$ of isotropic square plates with various boundary conditions and subjected to uniformly distributed load

The Effect of nonlocal and strain gradient length scale parameters ($\mu$ and$l$) are presented in Table 9–13 on the non-dimensional deflection $\overline{w }=1000{w}_{0}(a/2,b/2)(D/{qa}^{4} )$ of isotropic Kirchhoff nanoplate subjected to uniform, sinusoidal and concentrated load with different combinations of simply-supported (S) and clamped (C) boundary conditions on the edges $x = 0, a$ and$y = 0, b$.

Table 9 The non-dimensional deflection $\overline{w }=100{w}_{0}(a/2,b/2)(D/{qa}^{4} )$ of isotropic square nanoplates with different boundary conditions subjected to uniformly distributed load (UL)

Table 10 The non-dimensional deflection $\overline{w }=100{w}_{0}(a/2,b/2)(D/{qa}^{4} )$ of isotropic square nanoplates with different boundary conditions subjected to uniformly distributed load (SL)

Table 11 The non-dimensional frequencies ${\overline{\omega }=\omega }_{cr} ({a}^{2}/{\pi }^{2})\sqrt{\rho h/{D}_{11}}$ of simply-supported SSSS isotropic and orthotropic plates

Table 12 Effect of plate aspect ratio ($b/a$) and modulus ratio (${E}_{1}/{E}_{2})$ on the non-dimensional frequencies ${{\overline{\omega }}_{n}=\omega }_{n} {a}^{2}\sqrt{\rho h/{D}_{11}}$ of orthotropic rectangular SSCF plates

Table 13 Effect of boundary conditions and strain gradient parameter ($l$) on the non-dimensional frequencies ${\overline{\omega }=\omega }_{cr} {a}^{2}\sqrt{\rho h/D}$ of isotropic ($\nu = 0.3$) square nanoplates

Figure 4 illustrates the non-dimensional deflection $\overline{w }=100{w}_{0}(a/2,b/2)(D/{qa}^{4} )$ of an isotropic square nanoplate at $y=b/2$ under various types of loads including uniform, hydrostatic, sinusoidal, and concentrated load, with CCCC boundary condition. The plot shows how the deflection varies for different types of loads and highlights the differences between them.

Fig. 4

The non-dimensional deflection $\overline{w }=100{w}_{0}\left(x,b/2\right)\left(\text{D}/{{q}_{0}a}^{4}\right)$ of isotropic square CCCC nanoplates subjected to: a UL, b HL, c DSL, d CL

On the edges $y=0, b$, the used shape function for the CC boundary condition is ${Y}_{m}(y)=\text{sin}(m\pi y/b)(\text{sin}(\pi y/b)$ and for applying the CC boundary condition on the edges $x=0, a$, $w$, and its first derivative to $x$ as mentioned in Table 3, should be constrained. The force vector is typically separated into two parts: local and non-local. In the non-local part, for uniform or hydrostatic load distributions in the x direction, only the degrees of freedom that are constrained on the edges $x = 0, a$ have nonzero terms in the first term of the force vector calculation for CC boundary condition. Once these constraints are applied to the force vector, the nonzero terms are eliminated, resulting in a zero-force vector. The second non-local term also yields a zero-force vector due to trigonometric properties.

Hence, it can be observed that the deflection results for a nanoplate with CCCC boundary conditions under uniform or hydrostatic transverse loads remain unaffected by the nonlocal parameter ($\mu$), indicating that the nonlocal effect has no significant impact on the results in such cases. This can be verified by referring to Table 9 and Fig. 4, which illustrate that the deflection values remain the same as those obtained in the local mode.

For different boundary conditions the non-dimensional transverse deflection $\overline{w }=100{w}_{0}(x,y)(D/{qa}^{4})$ of isotropic square nanoplates with nonlocal and strain gradient parameters $\mu =l=1$ subjected to double sinusoidal load (DSL) are depicted in Fig. 5.

Fig. 5

The non-dimensional deflection $\overline{w }=100{w}_{0}(x,y)(D/{qa}^{4} )$ of isotropic square nanoplates with nonlocal and strain gradient parameters $\mu =1, l=1$ subjected to double sinusoidal load (DSL) for different boundary conditions: a SSSS, b CCCC, c CCCF, d CFCF, e FFSC, f FFCF

4.2 Free vibration results of the isotropic and orthotropic nanoplates

The non-dimensional frequencies, ${\overline{\omega }=\omega }_{cr} ({a}^{2}/{\pi }^{2})\sqrt{\rho h/{D}_{11}}$, of isotropic ($\nu =0.25$) plates and orthotropic (${G}_{12}=0.5{E}_{2}, {\nu }_{12}=0.25$) plates for modulus ratios ${E}_{1}/{E}_{2} =3,10, 25$ are presented in Table 11. The first natural frequency of vibration of the plate increases as the ratio of the moduli ${E}_{1}/{E}_{2}$ increases. The effect of rotary inertia ${I}_{2}$ on the frequency is negligible for thin plates because ${I}_{2}$ is proportional to the third power of the thickness. The proposed equation in Eq. (36) based on the Navier solution indicates that ${I}_{2}$ has a decreasing effect on the frequency. As the aspect ratio ($b/a$) of the plate increases, the frequency of vibration decreases. On the other hand, orthotropy, which is characterized by the modulus ratio ${E}_{1}/{E}_{2}$, increases the frequency of vibration.

Table 12 displays the frequencies at which orthotropic plates with SSCF boundary condition vibrate. The boundary condition has C and F boundary conditions on the edges $x=0$ and $a$, respectively. The table shows the first six modes of vibration for orthotropic plates with modulus ratios ${E}_{1}/{E}_{2} = 3, 10$ and aspect ratios $b/a= 0.5, 1.0, 1.5 \text{and} 2$. The modulus ratio ${E}_{1}/{E}_{2}$ has a more significant impact on the natural frequencies of the fundamental and lower modes of vibration, whereas the effect is almost negligible on higher modes of vibration.

The non-dimensional frequencies ${\overline{\omega }=\omega }_{cr} {a}^{2}\sqrt{\rho h/D}$ of isotropic nanoplate for different strain gradient parameters ($l=0, 0.2, 0.5, 1$) are presented in Table 13, for SSCC, SSFF, SSCF, and CCCC boundary conditions. This table presents the natural frequencies of rectangular nanoplates with different boundary conditions and values of the strain gradient parameter ($l$) and edge stiffness. The results indicate that increasing both the strain gradient parameter and the edges stiffness leads to an increase in the frequency of vibration. This is because the plate becomes stiffer due to the applied constraint on support moment and stress resultants. It can also be observed that the CCCC boundary condition has the highest stiffness, while SSFF has the lowest. The results obtained in this study have good agreement with Babu and Patel’s FEM-based studies [61], but with less computational effort and a smaller number of elements.

Table 14 presents the influence of boundary condition, nonlocal, and strain gradient parameters ($\mu ,l$) on the non-dimensional fundamental frequency (${\overline{\omega }=\omega }_{cr} {a}^{2}\sqrt{\rho h/D}$) of square isotropic nanoplates. The results show that increasing the strain gradient parameter and the edges stiffness of the plate leads to an increase in the fundamental frequency due to the stiffer plate resulting from the applied constraint on support moment and stress resultants. However, the nonlocal parameter ($\mu$) has a softening effect, resulting in a decrease in frequency. It is also observed that as the strain gradient parameter ($l$) increases, the results for CC and SC boundary conditions at $y=0,b$ converge to the same values.

Table 14 The effect of clamped (C) and simply-supported (S) boundary conditions in the four edges and nonlocal parameter and strain gradient parameters on the non-dimensional frequencies ${\overline{\omega }=\omega }_{cr} {b}^{2}\sqrt{\rho h/D}$ of isotropic ($\nu$ = 0.3) square nanoplate

The first six mode shapes and natural frequencies of isotropic square nanoplates with CCCC boundary conditions are shown in Fig. 6 The values presented in the figure are obtained by considering nonlocal and strain gradient parameters $\mu =4$ and $l=1$, and using the non-dimensional fundamental frequency $\overline{\omega }={\omega }_{\text{cr}}{a}^{2}\sqrt{\rho h/D}$ with two series terms ($r=2$). The mode shapes and corresponding frequencies are plotted in the figure, providing a visual representation of the vibration behavior of the nanoplates under these conditions.

Fig. 6

First six mode shape of an isotropic square CCCC nanoplate with nonlocal and strain gradient parameters $\mu =4, l=1$ and non-dimensional fundamental frequencies $\overline{\omega }={\omega }_{\text{cr}}{a}^{2}\sqrt{\rho h/D}$, ($r=2$)

Figure 7 shows plots of the non-dimensional fundamental frequency ${\overline{\omega }=\omega }_{cr} {a}^{2}\sqrt{\rho h/{D}_{11}}$ versus aspect ratios $b/a$, nonlocal parameter ($\mu =\text{0,1},\text{2.25,4}$), and strain gradient parameter ($l=0)$ of isotropic and orthotropic simply-supported SSSS nanoplates. The natural frequency increases with the degree of orthotropy ${E}_{1}/{E}_{2}$, but for long nanoplates, the results approach to frequency of a plate strip (${\overline{\omega }}_{11}=1.0$). In the high nonlocal parameter ($\mu =4)$, the aspect ratio almost has no effect on the frequency of isotopic nanoplates.

Fig. 7

The effect of the modulus ratio (${E}_{1}/{E}_{2}$) on the fundamental frequencies ${\overline{\omega }=\omega }_{cr} {a}^{2}\sqrt{\rho h/{D}_{11}}$ of simply supported SSSS isotropic and orthotropic nanoplates ($l=0$). a $\mu =0$, b $\mu =1$, c $\mu =2.25$, d $\mu =4$

The non-dimensional fundamental frequencies ${\overline{\omega }=\omega }_{cr} {a}^{2}\sqrt{\rho h/{D}_{11}}$ versus aspect ratios $b/a$, for different nonlocal parameters ($\mu =0, 1, 2.25, 4$) and strain gradient parameters ($l=0, 0.2, 0.5, 1)$ of isotropic clamped nanoplates are depicted in Fig. 8. The natural frequency of plate increases when the strain gradient parameter ($l$) increases and the nonlocal parameter ($\mu$) decreases. However, the effect of the nonlocal parameter on the frequency is more significant compared to the effect of the strain gradient parameter. In other words, changing the nonlocal parameter has a greater impact on the natural frequency of the system than changing the strain gradient parameter.

Fig. 8

The effect of strain gradient parameter ($l$) on the fundamental frequency ${\overline{\omega }=\omega }_{cr} {a}^{2}\sqrt{\rho h/D}$ versus aspect ratio ($b/a$) of isotropic CCCC nanoplate. a $\mu =0$, b $\mu =1$, c $\mu =2.25$, d $\mu =4$

5 Conclusions

The article presents a novel semi-analytical higher-order finite strip method for analyzing the bending and free vibration of isotropic and orthotropic nanoplates based on the nonlocal strain gradient theory (NSGT). The study investigates the effects of various factors such as boundary conditions, nonlocal and strain gradient parameters, aspect ratio, and different types of transverse loading and boundary conditions. The results demonstrate the suitability of the proposed method for analyzing the behavior of nanoplates and provide valuable insights that can be useful in designing and engineering nanoplates for various applications.

The deflection of nanoplates is influenced by the strain gradient and nonlocal effects. Increasing the strain gradient length scale parameter decreases deflection, while increasing the nonlocal parameter increases deflection. Aspect ratio affects the difference between local and non-local results, with larger aspect ratios resulting in smaller differences. The nonlocal effect is more significant for aspect ratios smaller than one, and disappears for aspect ratios larger than two, while the strain gradient effect remains. Increasing the modulus ratio and stiffness of edges reduces the effect of nonlocal and strain gradient parameters. Nonlocal effect is negligible for uniform or hydrostatic transverse loads and CCCC boundary conditions, with deflection results like those in local mode.

Increasing the strain gradient parameter and stiffness of edges increased the fundamental frequency of isotropic nanoplates due to increased stiffness from support moment and stress resultants. The aspect ratio had an inverse relationship with the frequency, while orthotropy had a positive effect, especially in lower modes. The degree of orthotropy affected the frequency, but for long plates, the results were close to that of a plate strip ${\overline{\omega }}_{11}=1.0$. In high nonlocal parameters, the aspect ratio had almost no effect on the frequency. Increasing the strain gradient parameter and decreasing the nonlocal parameter increased the natural frequency, but the frequency was more sensitive to the nonlocal effect.