1 Introduction

The Nonlocal theory and the modified couple stress theory represent distinct approaches aimed at elucidating the size-dependent behaviors of materials, particularly in micro/nanostructures. The Nonlocal theory emphasizes the incorporation of long-range interatomic cohesive forces, whereas the modified couple stress theory introduces an equilibrium requirement for moments of couples. This results in notable advantages, including a symmetric couple stress tensor and a singular material length scale parameter. These stipulations enable the strain energy function to be solely dependent on the strain and the symmetric component of the stress tensor. Consequently, among various theories considering stiffness enhancement, such as strain gradient, modified strain gradient, couple stress, and modified couple stress theories, the modified couple stress theory emerges as noteworthy.

Alireza Babaei and Arash Rahmani [1] conducted a study on the vibration analysis of a rotating gyroscope subjected to thermal stress using the displacement field via modified coupled stress method. Their research involved vibration procedure of a Timoshenko microbeam, considering temperature dependency and a parameter representing a length scale beyond classical measures [2]. Farajollah Zare Jouneghani et al. [3] used Ritz formulation to investigate the elasticity of non-uniform composite laminated beams due to modified couple stress interaction. Many studies delve into various aspects of microscale and nanoscale mechanics, employing the modified couple stress theory to analyze the behavior of composite microplates, microbeams, carbon nanotubes, and fiber-metal laminates. The analyses presented contribute to the understanding of size-dependent phenomena and couple stress mechanical properties at these scales, offering insights into the design and optimization of advanced materials and structures [4,5,6,7]. Kumar et al.[8] analyzed photo-thermal excitation in semiconducting mediums within the framework of the dual-phase lag theory, considering nonlocal effects. In Zenkour's other studies [9], the author discussed the refined two-temperature multiphase lags theory for the thermo-mechanical response of microbeams, as well as a multiphase-lag model of coupled thermoelasticity. Mohammad Jamshidi and Jafar Ghazanfarian [10] conducted a dual-phase lag analysis of a CNT–MoS2–ZrO2–SiO2–Si nano-transistor and arteriole within a multilayered skin. Kumar et al. [11] investigated the significance of memory-dependent derivative approach in analyzing thermoelastic damping in micromechanical resonators. Zhang et al. [12] investigated Adjustable characteristics of propagating waves in one-dimensional arrays made up of tubular structures, encompassing compression to rarefaction. Ramagiri Manjula [13] conducted research on torsional elastic waves in a thermoelastic cylinder with voids. Dual-phase lag thermoelastic damping in nonlocal nanobeams was improved by Borjalilou et al. [14]. Finally, Zhai Fang-Man and Li-Qun Cao [15] scrutinized the parallel algorithm in multistate for the heat conduction equation with dual-phase lag in composite materials. In a separate study, Pourasghar and Chen [16] utilized the dual-phase lag to test heat propagation. Gao et al. [17] employed the element-wise differential method utilizing local least-squares techniques. To solve heat transport equations in composite materials, Zhou et al. [18] developed Green’s functions in three dimensional anisotropic bimaterial for transient heat transport. Thermoelasticity was explored by Roy Choudhuri [19] through the three-phase lag thermoelastic equation, while Namayandeh et al. [20] analyzed thermal stress propagation in anisotropic and isotropic cylindrical structures. Tiwari and Mukhopadhyay [21]analyzed harmonic plane wave propagation in fractional order thermoelasticity, focusing on the fractional order heat conduction equation. Tiwari and Abouelregal [22] studied thermo-viscoelastic transversely isotropic rotating hollow cylinders using a three-phase lag thermoelastic model and fractional Kelvin–Voigt type approach. Tiwari et al. [23] explored memory response in generalized thermoelastic mediums within the context of dual-phase lag thermoelasticity with nonlocal effect.

Biswas and Abo-Dahab [24] studied the interactions of magneto-electro-thermoelasticity within initially stressed orthotropic materials using the type II Green-Naghdi model. Tiwari et al. [25] studied thermoelastic vibrations of nanobeams subjected to varying axial loads and ramp type heating, applying the Moore–Gibson–Thompson generalized theory of thermoelasticity. Zhu et al. [26] examined a dynamic system operating within a two-dimensional time slice and multiple phases for the monitoring of batch processes, while Othman and Abbas [27] examined the thermal shock phenomenon in a homogeneously isotropic hollow cylinder considering energy leakage. In recent investigations, researchers have concentrated on the thermal vibration analysis of diverse geometrical structures, including panel, triangle micro wire porous micro-tubes and carbon nanostructures, exhibiting different mechanical characteristics [28,29,30,31]. These studies employed the modified couple stress theory [32, 33]. Kumar and Mukhopadhyay [34] conducted an analysis of thermoelastic damping in micro plate resonators with size-dependent characteristics, employing both the modified couple stress theory and the heat transport with three-phase lag. Hu et al. [35] employed numerical methods to study functionally graded curved Timoshenko microbeams, integrating isogeometric Analysis (IGA) and the modified couple stress theory. Additionally, Jomehzadeh et al. [36] explored the vibrations influenced by size variations in microplates based on the couple stress in new form.

The current thermoelasticity model focuses on analyzing the propagation of thermoelastic waves in a composite hollow circular cylinder with an LEMV/CFRP interface layer. It utilizes a modified nonlocal couple stress theory and higher order time derivatives to derive the governing equations. These equations are then solved using linear elasticity theory to obtain frequency equations for the external surface of the cylinder under traction-free conditions, while ensuring continuity conditions at the boundaries. The study investigates how variations in wave number and thickness impact the frequency, temperature, and displacements in the field. To assess the effects of different thermoelasticity theories and nonlocal coupled stress parameters, tables and graphs are employed for comparison and estimation.

2 Formulation of the problem

Following[37], the governing equations of thermoelastic media using a novel refined size-dependent couple stress theory without body related forces are given by.

$${\varrho }_{ij}\left(\left(1-{\epsilon }^{2}{\nabla }^{2}\right){\overrightarrow{F}}_{r}\right)={c}_{ijkl}{\varsigma }_{kl}+\frac{1}{2}{e}_{ijk}{m}_{lkl}-{\beta }_{ij}T,$$
$${c}_{ijkl}{{\varsigma }_{kl}}_{,j }+\frac{1}{2}{e}_{ijk}{m}_{lk,lj}-{\beta }_{ij}{T}_{,j}=\left(1-{\epsilon }^{2}{\nabla }^{2}\right){\overrightarrow{F}}_{r}\rho {u}_{,tt},$$
$${K}_{ij}{T}_{,ij}-\rho {C}_{v}{T}_{t}={\beta }_{ij}{T}_{0},$$

where \({\varsigma }_{kl}=\frac{1}{2}({u}_{i,j}+{u}_{j,i})\) \({m}_{ij}=2m{\nu }^{2}{\varsigma }_{ij}\), u, v, w is displacement components, \({c}_{ijkl}\) is elastic parameters, \({\varrho }_{ij}\) is the components of stress, \({\varsigma }_{ij}\) is the components of strain, \({e}_{ijk}\) is alternate tensor, \({m}_{ij}\) is couple stress modulli, \(\rho \) is the density, \({K}_{ij}\) is the thermal conductivity, \({c}_{v}\) is specific heat capacity, \({T}_{0}\) is equilibrium temperature. Here, \(\epsilon ={e}_{0}{a}_{0}\) is the elastic nonlocal parameter, \({a}_{0}\) is the internal characteristic length and \({e}_{0}\) is a material constant.

The current density from the \({J}_{x}=\frac{{\sigma }_{0}{\mu }_{0}{H}_{0}}{1+{m}^{2}} \, (m{u}_{,t}-{w}_{,t}\)) and \({J}_{z}=\frac{{\sigma }_{0}{\mu }_{0}{H}_{0}}{1+{m}^{2}}({u}_{,t}+m{w}_{,t})\) can be computed from the Lorentz’s force \({\overrightarrow{F}}_{i}={\mu }_{0}{\left(\overrightarrow{J }\times {\overrightarrow{H}}_{0}\right)}_{i}\) in which\(\overrightarrow{j}=\frac{{\sigma }_{0}}{1+{m}^{2}}(\overrightarrow{E}+{\mu }_{o}\left(\overrightarrow{\dot{u}} \times \overrightarrow{H}-\frac{1}{e{n}_{e}}\overrightarrow{j} \times {\overrightarrow{H}}_{0}\right))\), where \({\sigma }_{0}\) is the electrical conductivity, \(m(={\omega }_{e}{t}_{e}\)) is the Hall parameter, \({\omega }_{e}\) is the electronic frequency, \({t}_{e}\) is the electron collision time, e is the charge of an electron, and ne is the number of density of electrons.

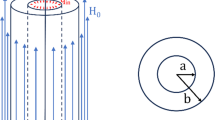
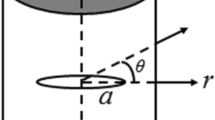
Here, we examine a thermally elastic body with homogeneity and transverse isotropy, initially at a uniform temperature \(T_{ \circ }\), while considering the influence of nonlocal couple stress. The analysis employs a cylindrical polar coordinate system (r, θ, z) characterized by symmetry about the z-axis.

$$ \begin{aligned}&\frac{{c}_{11}}{1-{\epsilon }^{2}{\nabla }^{2}}\left({{u}^{l}}_{,rr}+{r}^{-1}{{u}^{l}}_{,r}-{r}^{-2}u\right)+\frac{{c}_{44}}{1-{\epsilon }^{2}{\nabla }^{2}}{{u}^{l}}_{,zz}+\left({c}_{44}+{c}_{13}\right){{w}^{l}}_{,rz}\\ & \qquad +\frac{m{\nu }^{2}}{4(1-{\epsilon }^{2}{\nabla }^{2})}\left(-{u}_{,rrzz}^{l}+{w}_{,rrrz}-{u}_{,zzzz}+{w}_{,rzzz}\right) \\ & \qquad -\frac{1}{1-{\epsilon }^{2}{\nabla }^{2}}{\beta }_{1}{T}_{,r}+\left(1-{\epsilon }^{2}{\nabla }^{2}\right)\frac{{\mu }_{0}^{2}{H}_{0}^{2}{\sigma }^{2}}{1+{m}^{2}}\left({u}_{,t}+m{w}_{,t}\right)=\left(1-{\epsilon }^{2}{\nabla }^{2}\right)\rho {{u}^{l}}_{,tt}. \end{aligned} $$
(1)
$$\begin{aligned}&\frac{{c}_{44}}{1-{\epsilon }^{2}{\nabla }^{2}}\left({{w}^{l}}_{,rr}+{r}^{-1}{{w}^{l}}_{,r}\right)+{r}^{-1}\frac{\left({c}_{44}+{c}_{13}\right)}{1-{\epsilon }^{2}{\nabla }^{2}}\left({{u}^{l}}_{,z}\right)+\frac{{(c}_{44}+{c}_{13})}{1-{\epsilon }^{2}{\nabla }^{2}}{{u}^{l}}_{,rz}\\ & \quad +{c}_{33}{{w}^{l}}_{,zz}+\frac{1}{4}\frac{m{\nu }^{2}}{1-{\epsilon }^{2}{\nabla }^{2}}\left({-u}_{,rrrz}+{w}_{,rrrr}-{r}^{-1}{u}_{,rrz}+{r}^{-1}{w}_{,rrr}\right)\\ & \quad +\frac{1}{4}\frac{m{v}^{2}}{1-{\epsilon }^{2}{\nabla }^{2}}({u}_{,rrrz}-{w}_{,rrzz}+{r}^{-1}{u}_{,zzz}-{r}^{-1}{w}_{,rrz}-{\beta }_{3}{T}_{,z}\\ & \quad+\left(1-{\epsilon }^{2}{\nabla }^{2}\right)\frac{{\mu }_{0}^{2}{H}_{0}^{2}{\sigma }^{2}}{1+{m}^{2}}\left({u}_{,t}+m{w}_{,t}\right)=\left(1-{\epsilon }^{2}{\nabla }^{2}\right)\rho {{w}^{l}}_{,tt}.\end{aligned}$$
(2)

The heat transport equation is taken as [38]

$$\begin{aligned}&\left(1+\sum_{n=1}^{N}\frac{{\tau }_{\theta }^{n}}{n!}\frac{{\partial }^{n}}{\partial {t}^{n}} \right)\left[{K}_{1}\left({T}_{,rr}^{l}+{r}^{-1}{{T}^{l}}_{,r}+{r}^{-2}{{T}^{l}}_{,\theta \theta }\right)+{K}_{3}{{T}^{l}}_{,zz}\right]\\ & \quad= \left(\delta +{\tau }_{0} \frac{\partial }{\partial t}+\sum_{n=2}^{N}\frac{{\tau }_{q}^{n}}{n!}\frac{{\partial }^{n}}{\partial {t}^{n}} \right)\left[\rho {c}_{v}{T}_{,t}+{T}_{0}{\left({\beta }_{1}\left({u}_{,r}^{l}+{r}^{-1}{{v}^{l}}_{,\theta }+{r}^{-1}{u}^{l}\right)+{ \beta }_{3}{{w}^{l}}_{,z}\right)}_{,t}\right].\end{aligned}$$
(3)

The phase lag of the heat flux and temperature gradient denoted as \({\tau }_{\theta }\) and \({\tau }_{q}\) are defined. The parameter N signifies the refined generalized theory requirements.

For Eqs. (1), (2) and (3), the solution is as [37]

$${u}^{l}\left(r,z,t\right)=\left({{U}^{l}}_{,r}\right){\text{exp}}i\left(kz+pt\right),$$
$${w}^{l}\left(r,z,t\right)=\left(\frac{i}{h}\right){W}^{l}{\text{exp}}i\left(kz+pt\right),$$
$${T}^{l}\left(r,z,t\right)=\left(\frac{{c}_{44}}{{{\beta }_{3}h}^{2}}\right){T}^{l}{\text{exp}}i\left(kz+pt\right),$$
(4)

Here, \(i=\sqrt{-1}\), k is the wave number, \(\omega \) is the frequency; \({U}^{l},{W}^{l},,{T}^{l}\) are all displacement potentials, electric conduction and thermal change. By introducing the dimensionless quantities such as,

$$ \begin{aligned} ~x & = \frac{r}{h},\;~\zeta = kh~,\Omega ^{2} = \frac{{\rho p^{2} a^{2} \left( {1 - \int ^{2} \nabla ^{2} } \right)^{2} }}{{c_{{44}} }},\bar{c}_{{11}} = {\raise0.7ex\hbox{${c_{{11}} \left( {1 - \epsilon ^{2} \nabla ^{2} } \right)}$} \!\mathord{\left/ {\vphantom {{c_{{11}} \left( {1 - \epsilon ^{2} \nabla ^{2} } \right)} {c_{{44}} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${c_{{44}} }$}},\bar{c}_{{13}} = {\raise0.7ex\hbox{${c_{{13}} \left( {1 - \epsilon ^{2} \nabla ^{2} } \right)}$} \!\mathord{\left/ {\vphantom {{c_{{13}} \left( {1 - \epsilon ^{2} \nabla ^{2} } \right)} {c_{{44}} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${c_{{44}} }$}}, \\ ~\bar{c}_{{33}} & = {\raise0.7ex\hbox{${c_{{33}} \left( {1 - \epsilon ^{2} \nabla ^{2} } \right)}$} \!\mathord{\left/ {\vphantom {{c_{{33}} \left( {1 - \epsilon ^{2} \nabla ^{2} } \right)} {c_{{44}} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${c_{{44}} }$}},~\bar{c}_{{66}} = {\raise0.7ex\hbox{${c_{{66}} \left( {1 - \epsilon ^{2} \nabla ^{2} } \right)}$} \!\mathord{\left/ {\vphantom {{c_{{66}} \left( {1 - \epsilon ^{2} \nabla ^{2} } \right)} {c_{{44}} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${c_{{44}} }$}}\bar{\beta } = {\raise0.7ex\hbox{${\beta _{1} \left( {1 - \epsilon ^{2} \nabla ^{2} } \right)}$} \!\mathord{\left/ {\vphantom {{\beta _{1} \left( {1 - \epsilon ^{2} \nabla ^{2} } \right)} {\beta _{3} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\beta _{3} }$}} \\ \bar{m} & = \frac{m}{{4c_{{44}} }},\;~\bar{K}_{i} = \frac{{\left( {\rho c_{{44}} } \right)^{{\frac{1}{2}}} }}{{\beta _{3}^{2} T_{0} a\Omega }}K_{i} ,\;\bar{d} = \rho c_{v} c_{{44}} /\beta _{3}^{2} T_{0} ,\;~N = \frac{{\left( {1 - \epsilon ^{2} \nabla ^{2} } \right)^{2} }}{{c_{{44}} }}\frac{{\mu _{0}^{2} H_{0}^{2} \sigma ^{2} }}{{1 + m^{2} }} \\ \end{aligned} $$

, \(\overline{m }=\frac{m}{4{c}_{44}}\),\({\overline{K} }_{i}=\frac{{\left(\rho {c}_{44}\right)}^{\frac{1}{2}}}{{\beta }_{3}^{2}{T}_{0}a\Omega }{K}_{i}\), \(\overline{d }=\rho {c}_{v}{c}_{44}/{\beta }_{3}^{2}{T}_{0}\),\(N=\frac{{\left(1-{\epsilon }^{2}{\nabla }^{2}\right)}^{2}}{{c}_{44}}\frac{{\mu }_{0}^{2}{H}_{0}^{2}{\sigma }^{2}}{1+{m}^{2}}\)

Loading Eq. (4) in to the Eqs. (1)–(3) yields.

$$ \begin{aligned} & \left[ {\left( {\overline{c}_{11} + \overline{m}\nu^{2} \zeta^{2} /h^{2} } \right)D^{2} + \overline{c}_{11} x^{ - 1} D + \left( { - \zeta^{2} - \left( {ch} \right)^{2} - \overline{m}\nu^{2} \zeta^{2} k^{2} } \right) - iNp} \right]U^{l} \\ & \quad + \left[ {\left( {\zeta \left( {1 + \overline{c}_{13} } \right) + \overline{m}\nu^{2} /h^{2} } \right)D^{2} + (\zeta \left( {1 + \overline{c}_{13} + \overline{m}k^{2} \nu^{2} } \right) + Nm\left( \frac{p}{h} \right)} \right]W^{l} + \overline{\beta }T^{l} = 0. \\ \end{aligned} $$
(5)
$$\begin{aligned}&\left[\frac{\overline{m}{\nu }^{2}k}{2h}{D}^{4}-\frac{\overline{m}{\nu }^{2}k}{h{x}^{2}}{D}^{3}-\left(\zeta \left(1+{\overline{c} }_{13}\right)\right){D}^{2}-\overline{m}{\nu }^{2}{\zeta }^{2}-iNp\right]{U}^{l}\\&\quad+\left[-\frac{\overline{m}{\nu }^{2}}{{h}^{2}} {D}^{4}-\frac{\overline{m}{\nu }^{2}{x}^{-1}}{{h}^{2}} {D}^{3}+\left({\overline{c} }_{44}-\overline{m}{\nu }^{2}{k}^{2}+\zeta {x}^{-1}\right){D}^{2}\right. \\&\quad \left.-{\overline{c} }_{44}{x}^{-1}D+\left(\zeta {\overline{c} }_{33}-{\left(ch\right)}^{2}\right)+Nm\left(\frac{p}{h}\right)\right]{W}^{l}+\overline{\beta }{T}^{l}=0.\end{aligned}$$
(6)
$$\begin{aligned}&\overline{\beta }\left[\delta +{\tau }_{0}(i\omega )+\sum_{n=2}^{N}{\left(i\omega \right)}^{n} {\tau }_{q}^{n}/n!\right] {U}^{l}+\zeta \left[\delta +{\tau }_{0}(i\omega )+\sum_{n=2}^{N}{\left(i\omega \right)}^{n} {\tau }_{q}^{n}/n!\right]\\&\quad{W}^{l}+ \frac{\delta (1+\sum_{n=1}^{N}\frac{{\tau }_{\theta }^{n}}{n!} (i{\omega }^{n})}{\left[\delta +{\tau }_{0}(i\omega )+\sum_{n=2}^{N}{\left(i\omega \right)}^{n} {\tau }_{q}^{n}/n!\right]}\\&\quad \times\left[i{\overline{K} }_{1}{D}^{2}+i{\overline{K} }_{1}{x}^{-1}D+i{\overline{K} }_{3}\zeta \right]{T}^{l}=0.\end{aligned}$$
(7)

The system of Eqs. (5) to (7) results in a non-trivial solution.

$${(P}_{1}{D}^{8}+{P}_{2}{D}^{6}+{P}_{3}{D}^{4}+{P}_{4}{D}^{2}+{P}_{5})\left({U}^{l} {W}^{l},{T}^{l}\right)=0.$$
(8)

After decoupling the Eq. (8) in to biquadrate form, the symmetric mode solutions are

$${U}^{l}=\sum_{j=1}^{3}{{A}^{l}}_{j}{\mathfrak{J}}_{0}\left({{\alpha }^{l}}_{j}x\right)+{B}_{j}^{l}{\mathfrak{R}}_{0}(\left({{\alpha }^{l}}_{j}x\right),$$
$${W}^{l}=\sum_{j=1}^{3}{{{a}^{l}}_{j}{A}^{l}}_{j}{\mathfrak{J}}_{0}\left({{\alpha }^{l}}_{j}x\right)+{B}_{j}^{l}{\mathfrak{R}}_{0}(\left({{\alpha }^{l}}_{j}x\right),$$
$$ T^{l} = \mathop \sum \limits_{j = 1}^{3} b^{l}_{j} A^{l}_{j } \mathfrak{J}_{0} \left( {\alpha^{l}_{j} x} \right) + B_{j}^{l} \Re_{0} (\left( {\alpha^{l}_{j} x} \right). $$

The arbitrary constants \({a}_{j}^{l}\) and \({b}_{j}^{l}\) are given by

$$ \begin{aligned} & \left[ {\left( {\overline{c}_{11} + \overline{m}\nu^{2} \zeta^{2} /h^{2} } \right)\left( {\alpha_{j} } \right)^{2} + \overline{c}_{11} x^{ - 1} \alpha_{j} + \left( { - \zeta^{2} - \left( {ch} \right)^{2} - \overline{m}\nu^{2} \zeta^{2} k^{2} } \right)} \right]U^{l} \\ & \quad + \left[ {\left( {\zeta \left( {1 + \overline{c}_{13} } \right) + \overline{m}\nu^{2} /h^{2} } \right)\left( {\alpha_{j} } \right)^{2} + (\zeta \left( {1 + \overline{c}_{13} + \overline{m}k^{2} \nu^{2} } \right) + Nm\left( \frac{p}{h} \right)} \right]W^{l} + \overline{\beta }T^{l} = 0. \\ \end{aligned} $$
$$\begin{aligned}&\left[\frac{\overline{m}{\nu }^{2}k}{2h}{({\alpha }_{j})}^{4}-\frac{\overline{m}{\nu }^{2}k}{h{x}^{2}}{({\alpha }_{j})}^{3}-\left(\zeta \left(1+{\overline{c} }_{13}\right)\right){({\alpha }_{j})}^{2}-\overline{m}{\nu }^{2}{\zeta }^{2}\right]{U}^{l}\\&\quad+\left[-\frac{\overline{m}{\nu }^{2}}{{h}^{2}} {\left({\alpha }_{j}\right)}^{4}-\frac{\overline{m}{\nu }^{2}{x}^{-1}}{{h}^{2}} {\left({\alpha }_{j}\right)}^{3}+\left({\overline{c} }_{44}-\overline{m}{\nu }^{2}{k}^{2}+\zeta {x}^{-1}\right){\left({\alpha }_{j}\right)}^{2}\right. \\ & \quad \left.-{\overline{c} }_{44}{x}^{-1}\left({\alpha }_{j}\right)+\left(\zeta {\overline{c} }_{33}-{\left(ch\right)}^{2}\right)+Nm(\frac{p}{h})\vphantom{\frac{\overline{m}{\nu }^{2}{x}^{-1}}{{h}^{2}}}\right]{W}^{l}+\overline{\beta }{T}^{l}=0.\end{aligned}$$

3 Solution for linear elastic materials with voids

The displacement equations of motion and equation of equilibrated inertia for an isotropic LEMV are [37]

$$\left(\lambda +2\mu \right)\left({u}_{,rr}+{r}^{-1}{u}_{,r}-{r}^{-2}u\right)+\mu {u}_{,zz}+\left(\lambda +\mu \right){w}_{,zz}+\beta {\mathrm{\aleph }}_{,r}=\rho {u}_{,tt},$$
$$\left(\lambda +\mu \right)\left({u}_{,rz}+{r}^{-1}{u}_{,z}\right)+\mu \left({w}_{,rr}+{r}^{-1}{w}_{,r}\right)+\left(\lambda +2\mu \right){w}_{,zz}+\beta {\mathrm{\aleph }}_{,z}=\rho {w}_{,tt},$$
$$-\beta \left({u}_{,r}+{r}^{-1}u\right)-\beta {w}_{,z}+\alpha \left({\mathrm{\aleph }}_{,rr}+{r}^{-1}{\mathrm{\aleph }}_{,r}+{\mathrm{\aleph }}_{,zz}\right)-\delta k{\mathrm{\aleph }}_{,tt}-\omega {\mathrm{\aleph }}_{,t}-\xi \mathrm{\aleph }=0.$$
(9)

\(u,v,w\) represents displacements components along \(r, \theta ,\) and z directions,\(\alpha ,\beta ,\xi ,\omega \) and \(k\) are LEMV material constants characterizing the core in the equilibrated inertial state, \(\rho \) is the density, and \(\lambda , \mu \) are the lame constants, and \(\aleph \) is the new kinematical variable associated with another material without voids. The stress in the LEMV core materials is

$${\varrho }_{rr}=\left(\lambda +2\mu \right){u}_{,r}+\lambda {r}^{-1}u+\lambda {w}_{,z}+\beta \mathrm{\aleph },$$
$${\varrho }_{rz}=\mu \left({u}_{,r}+{w}_{,r}\right),$$

And Eq. (9) is giving the following solution

$${u}^{l}={{U}^{l}}_{,r}expi\left(kz+pt\right),$$
$${w}^{l}=\left(\frac{i}{h}\right){W}^{l}expi\left(kz+pt\right),$$
$${\mathrm{\aleph }}^{l}=\left(\frac{1}{{h}^{2}}\right){\mathrm{\aleph }}^{l}expi\left(kz+pt\right).$$
(10)

The solution of Eq. (9) can be reached by the following determinant

$$\left|\begin{array}{c@{\quad}c@{\quad}c}\left(\lambda +2\mu \right){\nabla }^{2}+{F}_{1}& -{F}_{2}& {F}_{3}\\ {F}_{2}{\nabla }^{2}& \overline{\mu }{ \nabla }^{2}+{F}_{4}& {F}_{5}\\ -{F}_{3}{\nabla }^{2}& {F}_{5}& \alpha {\nabla }^{2}+{F}_{6}\end{array}\right|\left(U,W,\mathrm{\aleph }\right)=0.$$
(11)

where \({\nabla }^{2}=\frac{{\partial }^{2}}{\partial {x}^{2}}+\frac{1}{x}\frac{\partial }{\partial x}\), \({F}_{1}=\frac{\rho }{{\rho }^{1}}{\left(ch\right)}^{2}-\overline{\mu }{\epsilon }^{2}\), \({F}_{2}=(\overline{\lambda }+\overline{\mu })\epsilon \) , \({F}_{3}=\overline{\beta },{F}_{4}=\frac{\rho }{{\rho }^{1}}{\left(ch\right)}^{2}-(\overline{\lambda }+\overline{\mu }){\epsilon }^{2}\),\({F}_{5}=\overline{\beta }\epsilon \), \({F}_{6}=\frac{\rho }{{\rho }^{1}}{\left(ch\right)}^{2}\overline{k }-\overline{\alpha }{\epsilon }^{2}-i\overline{\omega }\left(ch\right)-\overline{\xi }\) and \(\overline{\lambda }=\frac{\lambda }{{c}_{44}^{l}}, \overline{\mu }=\frac{\mu }{{c}_{44}^{l}}\),\(\overline{\alpha }=\frac{\alpha }{{h}^{2}{c}_{44}^{l}}\), \(\overline{\beta }=\frac{\beta }{{c}_{44}^{l}}\),\(\overline{\xi }=\frac{\xi }{{c}_{44}^{l}}\), \(\overline{\omega }=(\frac{\omega }{h}\))\({\left({c}_{44}^{l}\rho \right)}^{\frac{1}{2}}\overline{K }=k/{h}^{2}\).

Equation (11) is rewritten as:

$$\left({\nabla }^{6}+P{\nabla }^{4}+Q{\nabla }^{2}+R\right)\left(U,W,\aleph \right)=0.$$
(12)

Hence, the solution of Eq. (12) is,

$$U=\sum_{j=1}^{3}\left[{A}_{j}{\mathfrak{J}}_{n}\left({\alpha }_{j}x\right)+{B}_{j}{\mathfrak{R}}_{n}\left({\alpha }_{j}x\right)\right],$$
$$W=\sum_{j=1}^{3}{d}_{j}\left[{A}_{j}{\mathfrak{J}}_{n}\left({\alpha }_{j}x\right)+{B}_{j}{\mathfrak{R}}_{n}\left({\alpha }_{j}x\right)\right],$$
$$\aleph =\sum_{j=1}^{3}{e}_{j}\left[{A}_{j}{\mathfrak{J}}_{n}\left({\alpha }_{j}x\right)+{B}_{j}{\mathfrak{R}}_{n}\left({\alpha }_{j}x\right)\right],$$
(13)

\({\left({\alpha }_{j}x\right)}^{2}\) are the roots of the equation when replacing \({\nabla }^{2}=-{\left({\alpha }_{j}x\right)}^{2}.\) The arbitrary constant \({d}_{j}\) and \({e}_{j}\) are obtained from.

$${F}_{2}{\nabla }^{2}+\left(\overline{\mu }{\nabla }^{2}+{F}_{4}\right){d}_{j}+{F}_{5}{e}_{j}=0,$$
$$-{F}_{3}{\nabla }^{2}+{F}_{5}{d}_{j}+\left(\alpha {\nabla }^{2}+{F}_{6}\right){e}_{j}=0.$$
(14)

The CFRP solution is reached through \(\aleph \)= 0 and \(\lambda ={c}_{12},\mu =\frac{\left({c}_{11}-{c}_{12}\right)}{2}\).

4 Boundary conditions at the interface and equations for frequency

The preliminary conditions at the interface are

  1. (i)

    \({\varrho }_{rr}^{l}={\varrho }_{rz}^{l}={T}^{l}=0 \ \mathrm{ with } \ l=\mathrm{1,3}.\)

  2. (ii)

    \({\varrho }_{rr}^{l}, {\varrho }_{rz}^{l}={\varrho }_{rz}^{l} ,{u}^{l}=u ,{w}^{l}=w ,{T}^{l}=0 ,\mathrm{with } \ l=\mathrm{1,2},3.\)

The frequency equation is formulated:

$$ \left| {\left( {{\Gamma }_{i,j} } \right)} \right| = 0,\;\left( {{\text{i}},{\text{j}}\, = \,{1},{2},{3},.....,{18}} \right), $$

where

$$\Gamma \left(1,j\right)=2{\overline{c} }_{66}\left(\frac{{\alpha }_{j}^{1}}{{x}_{0}}\right){\mathfrak{J}}_{1}\left({\alpha }_{j}^{1}{x}_{0}\right)-\left[{\overline{c} }_{11}{\left({\alpha }_{j}^{1}\right)}^{2}+{\overline{c} }_{13}\zeta {a}_{j}^{1}-\overline{\beta }{b}_{j}^{1}\right]{\mathfrak{J}}_{0}({\alpha }_{j}^{1}{x}_{0}) ,$$
$$\Gamma \left(2,j\right)=\left(\zeta +{a}_{j}\right)\left({\alpha }_{j}^{1}\right){\mathfrak{J}}_{1}\left({\alpha }_{j}^{1}{x}_{0}\right),$$
$$\Gamma \left(3,j\right)=\frac{{b}_{j}^{1}}{{x}_{0}}{\mathfrak{J}}_{0}\left({\alpha }_{j}^{1}{x}_{0}\right)-\left({\alpha }_{j}^{1}{x}_{0}\right){\mathfrak{J}}_{1}\left({\alpha }_{j}^{1}{x}_{0}\right).$$
$$\Gamma \left(4,j\right)=2{\overline{c} }_{66}\left(\frac{{\alpha }_{j}^{1}}{{x}_{1}}\right){\mathfrak{J}}_{1}\left({\alpha }_{j}^{1}{x}_{1}\right)-\left[{\overline{c} }_{11}{\left({\alpha }_{j}^{1}\right)}^{2}+{\overline{c} }_{13}\zeta {a}_{j}^{1}-\overline{\beta }{b}_{j}^{1}\right]{\mathfrak{J}}_{0}({\alpha }_{j}^{1}{x}_{1}) ,$$
$$\Gamma \left(4,j+6\right)=-\left[2\overline{\mathrm{\rm M} }\left(\frac{{\alpha }_{j}^{1}}{{x}_{1}}\right){\mathfrak{J}}_{1}\left({\alpha }_{j}^{1}{x}_{1}\right)+\left[-\left(\overline{\Lambda }+\overline{\mathrm{\rm M} }\right){\left({\alpha }_{j}^{1}\right)}^{2}+{\beta }^{2}{f}_{j}^{2}\right]{\mathfrak{J}}_{0}\left({\alpha }_{j}^{2}{x}_{1}\right)\right],$$
$$\Gamma \left(5,j\right)=\left(\zeta +{d}_{j}^{2}\right)\left({\alpha }_{j}^{1}\right){\mathfrak{J}}_{1}\left({\alpha }_{j}^{1}{x}_{1}\right),$$
$$\Gamma \left(5,j+6\right)=-\mu \left(-\left(\zeta +{a}_{j}^{1}\right)\right)\left({\alpha }_{j}^{1}\right){\mathfrak{J}}_{1}\left({\alpha }_{j}^{1}{x}_{1}\right),$$
$$\Gamma \left(6,j\right)=-\left({\alpha }_{j}^{1}\right){\mathfrak{J}}_{1}\left({\alpha }_{j}^{1}{x}_{1}\right),$$
$$\Gamma \left(6,j+6\right)=-\left({\alpha }_{j}\right){\mathfrak{J}}_{1}\left({\alpha }_{j}{x}_{1}\right),$$
$$\Gamma \left(7,j\right)={a}_{j}^{1}{\mathfrak{J}}_{1}\left({\alpha }_{j}{x}_{1}\right),$$
$$\Gamma \left(8,j\right)={b}_{j}^{1}{\mathfrak{J}}_{1}\left({\alpha }_{j}^{1}{x}_{1}\right),$$
$$\Gamma \left(9,j\right)={c}_{j}^{1}{/{x}_{1} \mathfrak{J}}_{0}\left({\alpha }_{j}^{1}{x}_{1}\right)-({\alpha }_{j}^{1}){/{x}_{1} \mathfrak{J}}_{1}\left({\alpha }_{j}^{1}{x}_{1}\right)$$

5 Particular cases

  1. I.

    If \({\tau }_{0}={\tau }_{\theta }={\tau }_{q}=0\) and δ = 1, then, Eq. (3) results coupled thermoelasticity (CTE) theory with hall current.

  2. ii.

    If \({\tau }_{q},{\tau }_{\theta }\) → 0, δ = 1 and \({\tau }_{0}\) > 0, then Eq. (3) results Lord–Shulman (LS) theory with hall current.

  3. iii.

    If \({\tau }_{q},{\tau }_{\theta }\) → 0, δ = 0 and \({\tau }_{0}\) = 1, then Eq. (3) results Green–Naghdi (GN III) theory with hall current.

  4. iv.

    If \({\tau }_{0}>{\tau }_{\theta }\ge 0\) and δ = 1, then Eq. (3) results Simple-Phase Lag (SPL) theory with hall current.

  5. v.

    If \({\tau }_{q}={\tau }_{0}>{\tau }_{\theta }\ge 0\) and δ = 1, \(N\ge 1\), then Eq. (3) results Refined-Phase Lags (RPL) theory with hall current.

6 Numerical computation

For numerical calculations, we consider copper as the transversely isotropic material. The physical data for a single crystal of copper are provided by: [37]

\({C}_{11}=18.78\times {10}^{10} \ \mathrm{Kg }{{\text{m}}}^{-1}{{\text{s}}}^{-2},\) \({C}_{12}=8.76\times {10}^{10} \ \mathrm{Kg }{{\text{m}}}^{-1}{{\text{s}}}^{-2},\) \({C}_{13}=8.0\times {10}^{10} \ \mathrm{Kg }{{\text{m}}}^{-1}{{\text{s}}}^{-2},\) \({C}_{33}=17.2\times {10}^{10} \ {\text{Kg}}{\mathrm{ m}}^{-1}{\mathrm{ s}}^{-2},\) \({C}_{44}=5.06\times {10}^{10} \ \mathrm{Kg }{{\text{m}}}^{-1 }{{\text{s}}}^{-2},\) \({C}_{v}=0.6331\times {10}^{3} \ \mathrm{J K}{{\text{g}}}^{-1}{\mathrm{ K}}^{-1}{, \beta }_{1}=2.98\times {10}^{-5}{ {\text{K}}}^{-1},\) \({\beta }_{3}=2.4\times {10}^{-5}{ {\text{K}}}^{-1}\), \({T}_{0}=293 {\text{K}}\), \(\rho =8.954\times {10}^{3} \ {\text{Kg}}{\mathrm{ m}}^{-3}\), \({K}_{1}=0.433\times {10}^{3} \ {{\text{Wm}}}^{1} {{\text{K}}}^{-1}\), \({K}_{3}=0.433\times {10}^{3} \ {{\text{Wm}}}^{1} {{\text{K}}}^{-1}\), \( G=0.\)

The graphs of the physical quantities are plotted with a fixed wave number (0–1) and thickness (0–2). Tables 1 and 2 compare the non-dimensional frequency values obtained from various thermoelasticity theories for LEMV/CFRP cylinders of different thermal expansion coefficients with and without influence of non-local couple stress parameter. The tables show that the non-dimensional frequency increases with an amplified values of wave number for all thermoelasticity theories. However, the frequency values slightly vary within these models. Tables 3 and 4 show the radial, axial, and temperature changes of LEMV and CFRP layered cylinders with stress-free conditions for various thermoelasticity theories against increasing values of wave number with and without influence of non-local couple stress parameter. The tables reveal that the radial and axial distributions follow a growing trend as the wave number increases, while the temperature distribution of the composite hollow cylinders decreases with an increasing wave number. However, significant changes are observed in different thermoelasticity theories. Based on this analysis, thermoelastic hollow LEMV cylinders perform better with the multiphase lagging model in both cases of with and without influence of non-local couple stress parameter. The current results relating to the multilayered composite cylinder using non-local parameter in the case of vanishing non-local parameter, the results of thermal distributions in the multilayered composite cylinder are concord with the results of thermal distributions in the hollow cylinder is obtained by Zenkour [38] (Table 5).

Table 1 Changes in CFRP layer by different non-local parameter
Full size table
Table 2 Changes in LEMV layer by different non-local parameter
Full size table
Table 3 Changes in radial, axial and temperature in LEMV composite with \(\in \ = 0.03\)
Full size table
Table 4 Changes in radial, axial and temperature in CFRP composite with \(\in \ = 0.03\)
Full size table
Table 5 Comparison of dimensionless temperature distribution
Full size table

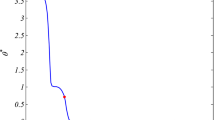
Figures 1 and 2 represent effects of radial and axial displacements against growing values of wavenumber with influence of various thermoelastic theories. From this, both axial and radial displacements maintain unique nature for starting values of wave number, but for higher values, its little variation observed. In Fig. 3, effects of temperature distribution against increasing values of wavenumber with influence of various thermoelastic theories and it shows that temperature distribution maintain decreasing nature against growing values of wave number. In Fig. 4, variations of couple stress against increasing values of wavenumber with influence of various thermoelastic theories and it maintains oscillatory nature for growing values of wave number. The hall current effect against wave number with various thermoelastic theories is represented in Fig. 5; from this observation, hall current maintains different nature for MPL model for lower values of wave number, but for higher values, it maintains unique nature in all models.

Fig. 1
figure 1

Plot of radial displacement on wave number across different thermoelastic theories in composite LEMV hollow cylinders

Full size image
Fig. 2
figure 2

Plot of axial distributaion on wave number across different thermoelastic theories in composite LEMV hollow cylinders

Full size image
Fig. 3
figure 3

Plot of temperature distribution on wave number across different thermoelastic theories in composite LEMV hollow cylinders

Full size image
Fig. 4
figure 4

Plot of couple stress on wave number across different thermoelastic theories in composite LEMV hollow cylinders

Full size image
Fig. 5
figure 5

Plot of Hall current on wave number across different thermoelastic theories in composite LEMV hollow cylinders

Full size image

Figures 6 and 7 characterize effects of radial and axial stress against growing values of thickness with influence of various thermoelastic theories. From this, radial stress keeps increasing nature for increasing values of thickness, but axial stress preserves decreasing nature for lower values of thickness, and for higher values, it keeps similar nature in all thermoelastic theories. In Fig. 8, effects of temperature distribution against increasing values of thickness with influence of various thermoelastic theories and it shows that temperature distribution maintain decreasing nature against growing values of thickness. In Fig. 9, variations of couple stress against increasing values of thickness with influence of various thermoelastic theories and it maintains oscillatory nature for growing values of thickness at the same time couple stress preserve slight variation in MPL model. The hall current effect against thickness with various thermoelastic theories is represented in Fig. 10; from this observation, hall current maintains different nature for MPL model compare to other thermoelastic theories.

Fig. 6
figure 6

Plot of radial stress on wave number across different thermoelastic theories in composite LEMV hollow cylinders

Full size image
Fig. 7
figure 7

Plot of axial stress on thickness across different thermoelastic theories in composite LEMV hollow cylinders

Full size image
Fig. 8
figure 8

Plot of temperature distribution on thickness across different thermoelastic theories in composite LEMV hollow cylinders

Full size image
Fig. 9
figure 9

Plot of couple stress on thickness across different thermoelastic theories in composite LEMV hollow cylinders

Full size image
Fig.10
figure 10

Plot of Hall current on thickness across different thermoelastic theories in composite LEMV hollow cylinders

Full size image

7 Conclusion

This article conducts a study on the wave propagation of a composite circular hollow cylinder composed of LEMV and CFRP. The investigation employs modified nonlocal couple stress and multiphase-lag thermoelasticity theories to analyze the behavior of the hollow cylinder. To achieve this, a set of three coupled partial differential equations defines the equations of motion and heat conduction, which are solved exactly. By comparing different thermoelasticity theories, the study explores the influence of the wavenumber and thickness on the characteristics of wave propagation. Among the investigated theories, the multiphase-lag thermoelasticity theory yielded the most precise outcomes, particularly when assessing the influence of nonlocal couple stress. Furthermore, the study rooted into the effects of adjusting the modified nonlocal couple stress parameter, which was observed to greatly affect the frequency and distribution of displacements. These discoveries hold considerable importance in comprehending the nonlocal dynamic response of transversely isotropic thermoelastic cylinders, which have broad applications across diverse industries.