1 Introduction

The exceptional physical and mechanical attributes of graphene and its derivatives have attracted significant interest in the advancement of high-performance and multifunctional composite materials and structures [1]. Zhao et al. [2] found that the addition of 1.8 vol% of graphene to polyvinyl alcohol (PVA) resulted in a considerable enhancement of the tensile strength and Young's modulus, with an increase of 150% and nearly 10 times, respectively. By utilizing atomistic modeling, Rahman and Haque [3] and Sun et al. [4] also observed a significant improvement in the elastic properties of graphene-reinforced composites. Apart from enhancing the mechanical performance of composites, graphene fillers can also improve their electrical and dielectric properties simultaneously [5, 6]. Cui et al. [7] measured the dielectric permittivity of graphene nanoplatelet (GPL)/polyvinylidene fluoride (PVDF) composites and reported a peak dielectric constant of 2080 at 1000 Hz with the addition of 12.5 vol% graphene. Experiment conducted by Mehmood et al. [8] indicated a considerable improvement in the dielectric properties of GPLs/Ni-Co-Nd spinel composites with the incorporation of 2.5 wt% of GPLs.

In addition to examining the material properties, it has been discovered that the incorporation of graphene into composite structures can lead to remarkable enhancements in their structural behaviors [9,10,11,12,13,14]. Over the past few years, the concept of functionally graded graphene nanoplatelet-reinforced composites (FG-GPLRC) has emerged as a means to optimize the efficacy of graphene fillers [15], and a large number of works have reported the structural behavior of FG-GPLRC. Yang et al. [16, 17] found a significant increase in both the critical buckling load and the post-buckling of FG-GPLRC beam by adding a small quantity of GPL. Feng et al. [18, 19] explored the nonlinear free vibration and nonlinear bending of FG-GPLRC beams and found that placing more GPLs near the top and bottom surfaces of the beam are the most effective ways to strengthen stiffness. Based on the first-order shear deformation theory, Malekzadeh et al. [20] investigated the free vibration of FG-GPLRC annular plates which embedded in piezoelectric layers. Nguyen et al. [21] carried out a study on the static and dynamic responses of FG-GPLRC plates based on refined plate theory and NURBS-based isogeometric analysis. Ma et al. [22] analyzed the free vibration of FG-GPLRC piezoelectric plates with the plate theory incorporating a modified interlaminar shear stress field. Nikrad et al. [23] investigated the nonlinear thermal stability responses of FG-GPLRC laminated plates with embedded circular and elliptical delamination. Karami et al. [24] carried out an analysis on the forced resonant vibration of FG-GPLRC doubly curved shells within the framework of third-order shear deformation shell theory. Ye et al. [25] presented a study on the nonlinear forced vibration of FG-GPLRC cylindrical shells by implementing Galerkin method. In recent years, the composites can exhibit negative Poisson's ratio characteristics when the graphene is designed to be graphene origami, which has great influences on the vibration characteristics of FG beam structures. Zhao et al. [26,27,28] investigated the nonlinear bending and vibration of FG graphene origami-enabled auxetic metamaterial beams. Murari et al. [29, 30] presented the nonlinear vibration and post-buckling analyses of FG graphene origami-enabled metamaterial beams in fluid.

The aforementioned FG-GPLRC structures are often operating in complex environments, including the subjection to different dynamic loadings in various engineering applications, and it is challenging to completely avoid the occurrence of structural damage. The presence of cracks in an engineering structure may significantly reduce the local stiffness and strength of the structure and affect structural performance accordingly [31, 32]. Several studies have been devoted to the structural behavior analysis of cracked FG-GPLRC beam. For example, Song et al. [33] examined the characteristics of linear free vibration and elastic buckling behaviors of FG-GPLRC beams with a single edge crack and located on an elastic foundation. Kou et al. [34] investigated the free vibration of FG-GPLRC beams with open edged cracks via a meshfree boundary-domain integral equation method. Tam et al. [35] employed the finite element method (FEM) to analyze the nonlinear bending behaviors of three types of FG-GPLRC beams with an open edge crack. Mao et al. [36] analyzed free vibration of edge-cracked FG-GPLRC piezoelectric beam by applying Ritz procedure and Newmark average acceleration method.

Despite the numerous studies have been conducted on cracked FG-GPLRC structures, the work is solely focused on mechanical properties, with no consideration of the electrical properties of FG-GPLRC. As previously stated, GPL fillers can significantly enhance the physical property of composites, such as the electrical conductivity and the dielectric permittivity. Such physical properties of FG-GPLRC can be utilized for sensing, monitoring and actively tuning the impact of cracks on the structural performance. However, to the best of the authors’ knowledge, the effects of such physical properties on the structural behaviors of the cracked FG-GPLRC beams have not been investigated.

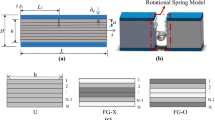
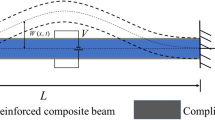
In this work, the nonlinear vibration of cracked FG-GPLRC beam with dielectric properties and damping is numerically investigated. Figure 1 exhibits the diagram of cracked FG-GPLRC beam, with L, b and h being the length, width, and height, respectively. Assuming that the crack is perpendicular to the upper surface of the FG-GPLRC laminated beam, and the crack depth and location are represented by a and L1, respectively. W(x, t) represents the displacement of the middle plane of the beam and V is the applied voltage. To enable active tuning and structural behavior monitoring using the applied electric field, compliant electrodes in the form of a thin layer of silver paste are applied to both the top and bottom surfaces of the beam. The effective material properties of the composites are determined by EMT and rule of mixture. Governing equations are established based on Timoshenko beam theory and nonlinear von Kármán strain–displacement relationship. Utilizing differential quadrature (DQ) and direct iterative methods, the governing equations are numerically solved. Comprehensive numerical results demonstrate that FG-GPLRC structures with dielectric properties can achieve self-sensing and structural health monitoring capabilities for the damage detection and safety assessment.

Fig. 1
figure 1

Schematic of FG-GPLRC dielectric beam with an edge crack subjected to electrical field and mechanical excitation

Full size image

2 Effective Properties of FG-GPLRC

Figure 2 illustrates five different distribution profiles, namely profiles U, X, O, A and V, in the present study. Profile U denotes the uniform distribution of GPL throughout the thickness, while profiles X and O exhibit a linear increase and decrease of GPL concentration from the midplane toward the top and bottom surfaces of the beam, respectively. In the case of profiles A and V, the GPL concentration uniformly increases and decreases from the top to the bottom of the beam, respectively.

Fig. 2
figure 2

Five GPL distribution profiles a U; b X; c O; d A; e V

Full size image

The volume fraction of GPLs in each individual layer, denoted as φk, is computed as follows

$$ \begin{gathered} U:\;\varphi_{k} = \varphi_{avg} \hfill \\ X:\;\varphi_{k} = \frac{{Z - 2 - \left( {Z - 2\left| {Z + 1 - 2k} \right|} \right)S_{g} }}{Z - 2}\varphi_{avg} \hfill \\ O:\;\varphi_{k} = \frac{{Z - 2 + \left( {Z - 2\left| {Z + 1 - 2k} \right|} \right)S_{g} }}{Z - 2}\varphi_{avg} \hfill \\ A:\;\varphi_{k} = \frac{{Z - 1 + \left( {2k - Z - 1} \right)S_{g} }}{Z - 1}\varphi_{avg} \hfill \\ V:\;\varphi_{k} = \frac{{Z - 1 - \left( {2k - Z - 1} \right)S_{g} }}{Z - 1}\varphi_{avg} \hfill \\ \end{gathered} $$
(1)

where Z denotes the total number of layers, the scaling factor Sg is given by (φmax–φmin)/(φmax + φmin), where φmax and φmin are the maximum and minimum volume fraction of GPLs. φavg is the average volume fraction of the FG-GPLRC, which can be defined by the total weight fraction of GPLs (fGPL).

Considering that this work covers not only the mechanical properties of the composite but also its electrical properties, EMT [37] is employed to obtain the elastic modulus and dielectric permittivity of the composites for structural analysis.

The material properties of the composite GPLRC can be determined by [37, 38]

$$ \left( {1 - \varphi_{k} } \right)\frac{{L_{{m}} - L_{{{e}k}} }}{{L_{{m}} + \left( {{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}} \right)\left( {L_{{m}} - L_{{{e}k}} } \right)}} + \frac{1}{3}\varphi_{k} \sum_{r = 1}^{3} {\frac{{L_{r} - L_{{{e}k}} }}{{L_{{{e}_{k} }} + S_{rr} \left( {L_{r} - L_{{{e}k}} } \right)}}} = 0 $$
(2)

where L represents the moduli tensor, which can be elastic modulus of the mechanical property and complex electrical conductivity of the physical property. The subscript “e” stands for effective medium, and Srr is the r.th component of Eshelby tensor of the filler, expressed as [39]

$$ \left\{ \begin{gathered} S_{11} = S_{22} = \frac{\alpha }{{2\left( {1 - \alpha^{2} } \right)^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} }}\left[ {\arccos \alpha - \alpha \left( {1 - \alpha^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \right] \hfill \\ S_{33} = 1 - 2S_{11} \hfill \\ \end{gathered} \right. $$
(3)

where α = tGPL/DGPL with tGPL and DGPL being the thickness and diameter of the GPL, respectively.

For the mechanical properties of GPLRC, Eq. (2) can be represented as

$$ \left( {1 - \varphi_{k} } \right)\frac{{E_{{m}} - E_{{{e}k}} }}{{E_{{m}} + \left( {{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}} \right)\left( {E_{{m}} - E_{{{e}k}} } \right)}} + \frac{1}{3}\varphi_{k} \sum_{r = 1}^{3} {\frac{{E_{r} - E_{{{e}k}} }}{{E_{{{e}k}} + S_{rr} \left( {E_{r} - E_{{{e}k}} } \right)}}} = 0 $$
(4)

where Ee denotes the effective elastic modulus of composite. An interphase coating the filler is introduced to address the imperfect bonding between GPL and matrix. Hence, Er is replaced by the ones of the coated filler \(E_{r}^{{\left( {\varvec{c}} \right)}}\), i.e.,

$$ \begin{array}{*{20}c} {E_{r}^{{\left( {\text{c}} \right)}} = E_{0}^{{\left( {\text{int}} \right)}} \left[ {1 + \frac{{\left( {1 - \varphi_{{\text{int}}} } \right)\left( {E_{r} - E_{0}^{{\left( {\text{int}} \right)}} } \right)}}{{\varphi_{{\text{int}}} S_{rr} \left( {E_{r} - E_{0}^{{\left( {\text{int}} \right)}} } \right) + E_{0}^{{\left( {\text{int}} \right)}} }}} \right]} & {r = 1,2,3} \\ \end{array} $$
(5)

where \(E_{0}^{{\left( {\text{int}} \right)}}\) denotes the elastic modulus of the interphase and φint is the volume fraction of the interphase.

For the electrical properties of GPLRC, the moduli tensors can be replaced by the complex electrical conductivity, and then Eq. (2) becomes

$$ \left( {1 - \varphi_{k} } \right)\frac{{\sigma_{{m}}^{*} - \sigma_{{{e}k}}^{{*}} }}{{\sigma_{{\text{m}}}^{*} + \left( {{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3}} \right)\left( {\sigma_{{m}}^{*} - \sigma_{{{e}k}}^{{*}} } \right)}} + \frac{1}{3}\varphi_{k} \sum_{r = 1}^{3} {\frac{{\sigma_{r}^{*} - \sigma_{{{e}k}}^{*} }}{{\sigma_{{{e}k}}^{{*}} + S_{rr} \left( {\sigma_{r}^{*} - \sigma_{{{e}k}}^{{*}} } \right)}}} = 0 $$
(6)

where σ* m, σ* e and σ* r represent the complex electrical conductivity of the matrix, the composites and the rth component of the filler, respectively. The complex electrical conductivity σ* can be further expressed as σ* = σ + 2πifACε, where fAC is the AC frequency (in Hz) and ε is the dielectric permittivity of the composites.

Similarly, with the consideration of the interphase, the electrical conductivity and the dielectric permittivity of GPLs are modified as [37, 38]

$$ \begin{array}{*{20}c} {\left\{ \begin{gathered} \sigma_{r}^{{\left( {c} \right)}} = \sigma_{0}^{{\left( {\text{int}} \right)}} \left[ {1 + \frac{{\left( {1 - \varphi_{{\text{int}}} } \right)\left( {\sigma_{r} - \sigma_{0}^{{\left( {\text{int}} \right)}} } \right)}}{{\varphi_{{\text{int}}} S_{rr} \left( {\sigma_{r} - \sigma_{0}^{{\left( {\text{int}} \right)}} } \right) + \sigma_{0}^{{\left( {\text{int}} \right)}} }}} \right] \hfill \\ \varepsilon_{r}^{{\left( {c} \right)}} = \varepsilon_{0}^{{\left( {\text{int}} \right)}} \left[ {1 + \frac{{\left( {1 - \varphi_{{\text{int}}} } \right)\left( {\varepsilon_{r} - \varepsilon_{0}^{{\left( {\text{int}} \right)}} } \right)}}{{\varphi_{{\text{int}}} S_{rr} \left( {\varepsilon_{r} - \varepsilon_{0}^{{\left( {\text{int}} \right)}} } \right) + \varepsilon_{0}^{{\left( {\text{int}} \right)}} }}} \right] \hfill \\ \end{gathered} \right.} & {r = 1,2,3} \\ \end{array} $$
(7)

where σ(int) 0 and ε(int) 0 represent the electrical conductivity and dielectric permittivity of interphase, respectively.

Considering the interfacial electron hopping, Maxwell–Wagner–Sillars (MWS) polarization [40, 41] and the AC frequency facilitated effects [37, 42], σ(int) 0 and ε(int) 0 in Eq. (7) are modified as the ones in [37].

The rule of mixture is used to estimate Poisson’s ratio and density, i.e.,

$$ \left\{ \begin{gathered} \nu_{{{\text{e}}k}} = \left( {1 - \varphi_{k} } \right)\nu_{{m}} + \varphi_{k} \nu_{{f}} \hfill \\ \rho_{{{\text{e}}k}} = \left( {1 - \varphi_{k} } \right)\rho_{{m}} + \varphi_{k} \rho_{{f}} \hfill \\ \end{gathered} \right. $$
(8)

where νm and νf are, respectively, the Poisson’s ratio of matrix and filler, ρm and ρf are, respectively, the mass density of matrix and filler.

3 Governing equations

3.1 Equivalent spring model

Considering an open edge crack that is perpendicular to the surface of the FG-GPLRC beam, it can be modeled by a massless elastic rotational spring with KT being the spring stiffness as shown in Fig. 3.

Fig. 3
figure 3

Schematic of the rotational spring model

Full size image

The Griffith energy balance shows that the elastic work done by the bending moment is used to generate a new crack surface [43], i.e.,

$$ \frac{1}{2}Md\psi_{12} = Gda $$
(9)

where M is the bending moment at the crack and ψ12 is the relative angle of rotation of the two parts of the spring connection. G represents the energy release rate, which can be expressed as

$$ G = \left( {1 - \nu^{2} } \right)\frac{{\pi \xi^{2} a}}{E} $$
(10)

where ξ stands for the tensile stress of the infinite plate, E and ν represent the elastic modulus and Poisson’s ratio of the material, respectively. By introducing the stress intensity factor (SIF) KI, Eq. (10) becomes

$$ G = \left( {1 - \nu^{2} } \right)\frac{{K_{{\text{I}}}^{2} }}{E} $$
(11)

Substituting Eq. (11) and \(d\psi_{12} = MdC\) into Eq. (9), we can have

$$ \frac{{1 - \nu^{2} }}{E}K_{{\text{I}}}^{2} = \frac{{M^{2} }}{2}\frac{dC}{{da}} $$
(12)

where C denotes the spring flexibility. For finite structures, the SIF is determined by the following equation

$$ K_{{\text{I}}} = \frac{{6M\sqrt {\pi a} }}{{h^{2} }}F\left( a \right) $$
(13)

Substituting Eq. (13) into Eq. (12) followed by integration, we have

$$ C = \frac{72\pi }{{h^{4} }}\left[ {\sum_{k = 1}^{\vartheta } {\int_{{Z_{{{\text{b}}\left( k \right)}} }}^{{Z_{{{\text{t}}\left( k \right)}} }} {\frac{{1 - \nu^{2} }}{E}aF^{2} \left( a \right)da} } + \int_{{Z_{{{\text{t}}\left( \vartheta \right)}} }}^{a} {\frac{{\left( {1 - \nu^{2} } \right)}}{E}aF^{2} \left( a \right)da} } \right] $$
(14)

where ϑ denotes the layer number that crack penetrates through and spring stiffness is defined as KT = 1/C.

3.2 Constitutive equation

The displacement field of the composite beam in the segment i can be expressed by using the Timoshenko beam theory as

$$ \begin{array}{*{20}c} {\left\{ \begin{gathered} \tilde{u}_{i} \left( {x_{i} ,z,t} \right) = u_{i} \left( {x_{i} ,t} \right) - z\psi_{i} \left( {x_{i} ,t} \right) \hfill \\ \tilde{w}_{i} \left( {x_{i} ,z,t} \right) = w_{i} \left( {x_{i} ,t} \right) \hfill \\ \end{gathered} \right.} & {i = 1{,2}} \\ \end{array} $$
(15)

where ui(xi,t) and wi(xi,t) represent the displacements of the beam in axial and transverse directions, respectively, ψi(xi,t) is the rotation angle of the middle plane of the beam and t represents time.

Utilizing von Kármán nonlinear strain–displacement relation, the strains are

$$ \left\{ \begin{gathered} \varepsilon_{ixx} = \frac{{\partial \tilde{u}_{i} }}{{\partial x_{i} }} + \frac{1}{2}\left( {\frac{{\partial \tilde{w}_{i} }}{{\partial x_{i} }}} \right)^{2} = \frac{{\partial u_{i} }}{{\partial x_{i} }} + \frac{1}{2}\left( {\frac{{\partial w_{i} }}{{\partial x_{i} }}} \right)^{2} - z\frac{{\partial \psi_{i} }}{{\partial x_{i} }} \hfill \\ \gamma_{ixz} = \frac{{\partial \tilde{u}_{i} }}{\partial z} + \frac{{\partial \tilde{w}_{i} }}{{\partial x_{i} }} = - \psi_{i} + \frac{{\partial w_{i} }}{{\partial x_{i} }} \hfill \\ \end{gathered} \right. $$
(16)

In the present work, Kelvin–Voigt model will be used to consider the internal damping. The Kelvin–Voigt model consists of a spring and a damper in parallel. Then the constitutive relationship between stress and strain in the i.th layer of the composite becomes [44]

$$ \left\{ \begin{gathered} \tilde{\sigma }_{ixxk} = \frac{{E_{{{\text{e}}k}} }}{{1 - \nu_{{{\text{e}}k}}^{2} }}\left( {\varepsilon_{ixx} + \varepsilon_{0} + \beta_{1} \dot{\varepsilon }_{ixx} } \right) - \sigma_{k}^{{\text{E}}} \hfill \\ \tilde{\tau }_{ixzk} = \frac{{E_{{{\text{e}}k}} }}{{2\left( {1 + \nu_{{{\text{e}}k}} } \right)}}\left( {\gamma_{ixz} + \beta_{2} \dot{\gamma }_{ixz} } \right) \hfill \\ \end{gathered} \right. $$
(17)

where β1 and β2 denote the tensile and shear proportionality constants of the internal damping, respectively, ε0 denotes the pre-strain in the longitudinal direction of the beam. \(\sigma_{k}^{{\text{E}}}\) denotes the electrostatic stress, which can be determined as

$$ \sigma_{k}^{{\text{E}}} = \frac{{V_{k}^{2} }}{{h_{k}^{2} }}\varepsilon_{{{\text{e}}k}} $$
(18)

where εek represents the effective dielectric permittivity of the kth layer of the composite beam.

The axial force, bending moment and shear force of the beam are expressed as

$$ \left\{ \begin{gathered} N_{ix} = \sum_{k = 1}^{Z} {\int_{{H_{{{\text{b}}\left( k \right)}} }}^{{H_{{{\text{t}}\left( k \right)}} }} {\tilde{\sigma }_{ixxk} dz} } = A_{11} \varepsilon_{0} + A_{11} \left[ {\frac{{\partial u_{i} }}{{\partial x_{i} }} + \frac{1}{2}\left( {\frac{{\partial w_{i} }}{{\partial x_{i} }}} \right)^{2} } \right] - B_{11} \frac{{\partial \psi_{i} }}{{\partial x_{i} }} + \beta_{1} A_{11} \left( {\frac{{\partial \dot{u}_{i} }}{{\partial x_{i} }} + \frac{{\partial w_{i} }}{{\partial x_{i} }}\frac{{\partial \dot{w}_{i} }}{{\partial x_{i} }}} \right) - \beta_{1} B_{11} \frac{{\partial \dot{\psi }_{i} }}{{\partial x_{i} }} - N_{i11}^{{\text{E}}} \hfill \\ M_{ix} = \sum_{k = 1}^{Z} {\int_{{H_{{{\text{b}}\left( k \right)}} }}^{{H_{{{\text{t}}\left( k \right)}} }} {\tilde{\sigma }_{ixxk} zdz} } = B_{11} \varepsilon_{0} + B_{11} \left[ {\frac{{\partial u_{i} }}{{\partial x_{i} }} + \frac{1}{2}\left( {\frac{{\partial w_{i} }}{{\partial x_{i} }}} \right)^{2} } \right] - D_{11} \frac{{\partial \psi_{i} }}{{\partial x_{i} }} + \beta_{1} B_{11} \left( {\frac{{\partial \dot{u}_{i} }}{{\partial x_{i} }} + \frac{{\partial w_{i} }}{{\partial x_{i} }}\frac{{\partial \dot{w}_{i} }}{{\partial x_{i} }}} \right) - \beta_{1} D_{11} \frac{{\partial \dot{\psi }_{i} }}{{\partial x_{i} }} - M_{i11}^{{\text{E}}} \hfill \\ Q_{ix} = \sum_{k = 1}^{Z} {\int_{{H_{{{\text{b}}\left( k \right)}} }}^{{H_{{{\text{t}}\left( k \right)}} }} {k_{s} \tilde{\tau }_{ixzk} dz} } = A_{55} \left( { - \psi_{i} + \frac{{\partial w_{i} }}{{\partial x_{i} }}} \right) + \beta_{2} A_{55} \left( { - \dot{\psi }_{i} + \frac{{\partial \dot{w}_{i} }}{{\partial x_{i} }}} \right) \hfill \\ \end{gathered} \right. $$
(19)

where Hb(k) and Ht(k) denote the coordinates of the bottom and top of the kth layer, respectively. A11, B11, D11 and A55 represent stiffness coefficients. NE i11 and ME i11 are, respectively, the electrostatic axial force and bending moment, determined as

$$ \begin{gathered} \left\{ {A_{11} ,B_{11} ,D_{11} } \right\} = \sum_{k = 1}^{Z} {\int_{{H_{{{\text{b}}\left( k \right)}} }}^{{H_{{{\text{t}}\left( k \right)}} }} {\frac{{E_{{{\text{e}}k}} }}{{1 - \nu_{{{\text{e}}k}}^{2} }}\left\{ {1,z,z^{2} } \right\}dz} } \hfill \\ A_{55} = \sum_{k = 1}^{Z} {\int_{{H_{{{\text{b}}\left( k \right)}} }}^{{H_{{{\text{t}}\left( k \right)}} }} {\frac{{k_{s} E_{{{\text{e}}k}} }}{{2\left( {1 + \nu_{{{\text{e}}k}} } \right)}}dz} } \hfill \\ \left\{ {N_{i11}^{{\text{E}}} ,M_{i11}^{{\text{E}}} } \right\} = \sum_{k = 1}^{Z} {\int_{{H_{{{\text{b}}\left( k \right)}} }}^{{H_{{{\text{t}}\left( k \right)}} }} {\frac{{V_{ik}^{2} }}{{H_{k}^{2} }}\varepsilon_{{{\text{e}}ik}} \left\{ {1,z} \right\}dz} } \hfill \\ \end{gathered} $$
(20)

where ks = 5/6 is the shear correction factor pertaining to the composite beam considered in present work.

While estimating the electrical properties, the FG-GPLRC beam can be regarded as a resistive series model [45], from which the voltage Vk can be calculated for each layer. The electrical conductivity and resistance are related as

$$ \sigma_{{\text{e}}} = \frac{l}{RS} $$
(21)

where l, S and R denote the length between the electrodes, the electrode area and the resistance, respectively, σe represents the conductivity of the material. Then, the resistance of the kth layer in the series system is

$$ R_{k} = \frac{{H_{k} }}{{\sigma_{{{\text{e}}k}} L}} $$
(22)

where Hk represents the thickness of each individual layer of functionally graded structure. In this study, it is assumed that each layer has the same thickness, i.e., Hk = h/Z. According to Ampere’s law, one can have

$$ I = \frac{U}{R} = \frac{V}{{R_{{{\text{overall}}}} }} = \frac{V}{{\sum_{k = 1}^{Z} {\frac{1}{{R_{k} }}} }} $$
(23)

Then the voltage across each resistor can be expressed as

$$ V_{k} = IR_{k} = \frac{{VhR_{k} }}{{ZL\sum_{k = 1}^{Z} {\sigma_{{{\text{e}}k}} } }} = \frac{{Vh^{2} }}{{Z^{2} L^{2} }}\frac{1}{{\sigma_{{{\text{e}}k}} \sum_{k = 1}^{Z} {\sigma_{{{\text{e}}k}} } }} $$
(24)

The cracked FG-GPLRC beam can be equivalent to the configuration illustrated in Fig. 4. When subjected to the applied electric field, the multilayer structure can be simulated as a parallel system comprising two resistances that are connected in series. Therefore, the voltage across each resistor can be obtained from Eqs. (21)–(24) as

$$ V_{ik} = \frac{{Vh^{2} }}{{Z^{2} L_{i}^{2} }}\frac{1}{{\sigma_{{i{\text{e}}k}} \sum_{k = 1}^{Z} {\sigma_{{i{\text{e}}k}} } }} $$
(25)
Fig. 4
figure 4

Schematic of equivalent resistance model of FG-GPLRC beam with an edge crack

Full size image

3.3 Energy integrals

The virtual strain energy of the FG-GPLRC beam can be written as

$$ \begin{aligned} \delta \Pi_{{\text{U}}} &= \sum_{i = 1}^{2} {\int_{0}^{{L_{i} }} {\sum_{k = 1}^{Z} {\int_{{H_{{{\text{b}}\left( k \right)}} }}^{{H_{{{\text{t}}\left( k \right)}} }} {\left( {\tilde{\sigma }_{ixxk} \delta \varepsilon_{ixx} + \tilde{\tau }_{ixzk} \delta \gamma_{ixz} } \right)dz} } dx_{i} } } + \delta \left[ {\frac{1}{2}K_{{\text{T}}} \left( {\Delta \psi } \right)^{2} } \right] \\ &= - \sum_{i = 1}^{2} {\int_{0}^{{L_{i} }} {\frac{{\partial N_{ix} }}{{\partial x_{i} }}\delta u_{i} dx_{i} } } - \sum_{i = 1}^{2} {\int_{0}^{{L_{i} }} {\left[ {\frac{\partial }{{\partial x_{i} }}\left( {N_{ix} \frac{{\partial w_{i} }}{{\partial x_{i} }}} \right) + \frac{{\partial Q_{ix} }}{{\partial x_{i} }}} \right]\delta w_{i} dx_{i} } } \\&\quad+ \sum_{i = 1}^{2} {\int_{0}^{{L_{i} }} {\left( {\frac{{\partial M_{ix} }}{{\partial x_{i} }} - Q_{ix} } \right)\delta \psi_{i} dx_{i} } } \\ \end{aligned} $$
(26)

The virtual kinetic energy of the beam can be determined as

$$ \begin{aligned} \delta \Pi_{{\text{T}}} &= \frac{1}{2}\delta \sum_{i = 1}^{2} {\int_{0}^{{L_{i} }} {\sum_{k = 1}^{{N_{i} }} {\int_{{H_{{{\text{b}}\left( k \right)}} }}^{{H_{{{\text{t}}\left( k \right)}} }} {\rho_{{{\text{e}}k}} \left[ {\left( {\frac{{\partial \tilde{u}_{i} }}{\partial t}} \right)^{2} + \left( {\frac{{\partial \tilde{w}_{i} }}{\partial t}} \right)^{2} + \left( {z\frac{{\partial \psi_{i} }}{\partial t}} \right)^{2} } \right]dz} } dx_{i} } } \\ &= \sum_{i = 1}^{2} {\int_{0}^{{L_{i} }} {\left[ {I_{1} \left( {\frac{{\partial u_{i} }}{\partial t}\frac{{\partial \delta u_{i} }}{\partial t} + \frac{{\partial w_{i} }}{\partial t}\frac{{\partial \delta w_{i} }}{\partial t}} \right) - I_{2} \left( {\frac{{\partial \psi_{i} }}{\partial t}\frac{{\partial \delta u_{i} }}{\partial t} + \frac{{\partial u_{i} }}{\partial t}\frac{{\partial \delta \psi_{i} }}{\partial t}} \right) + 2I_{3} \frac{{\partial \psi_{i} }}{\partial t}\frac{{\partial \delta \psi_{i} }}{\partial t}} \right]dx_{i} } } \\ \end{aligned} $$
(27)

where I1, I2 and I3 are inertial coefficients, i.e.,

$$ \left\{ {I_{1} ,I_{2} ,I_{3} } \right\} = \sum_{k = 1}^{Z} {\int_{{H_{{{\text{b}}\left( k \right)}} }}^{{H_{{{\text{t}}\left( k \right)}} }} {\rho_{{{\text{e}}k}} \left\{ {1,z,z^{2} } \right\}dz} } $$
(28)

Employing Hamilton’s principle, we have

$$ \int_{0}^{t} {\left( {\delta \Pi_{{T}} - \delta \Pi_{{U}} } \right)dt} = 0 $$
(29)

and then the governing equations for the vibration of the beam are

$$ \begin{array}{*{20}c} {\left\{ \begin{gathered} \frac{{\partial N_{ix} }}{{\partial x_{i} }} = I_{1} \frac{{\partial^{2} u_{i} }}{{\partial t^{2} }} - I_{2} \frac{{\partial^{2} \psi_{i} }}{{\partial t^{2} }} \hfill \\ \frac{{\partial \left( {N_{ix} \frac{{\partial w_{i} }}{{\partial x_{i} }}} \right)}}{{\partial x_{i} }} + \frac{{\partial Q_{ix} }}{{\partial x_{i} }} = I_{1} \frac{{\partial^{2} w_{i} }}{{\partial t^{2} }} \hfill \\ \frac{{\partial M_{ix} }}{{\partial x_{i} }} - Q_{ix} = I_{2} \frac{{\partial^{2} u_{i} }}{{\partial t^{2} }} - 2I_{3} \frac{{\partial^{2} \psi_{i} }}{{\partial t^{2} }} \hfill \\ \end{gathered} \right.} & {i = 1,2} \\ \end{array} $$
(30)

Substituting Eq. (19) into Eq. (30), we have

$$ \left\{ \begin{gathered} A_{11} \left( {\frac{{\partial^{2} u_{i} }}{{\partial x_{i}^{2} }} + \frac{{\partial w_{i} }}{{\partial x_{i} }}\frac{{\partial^{2} w_{i} }}{{\partial x_{i}^{2} }}} \right) - B_{11} \frac{{\partial^{2} \psi_{i} }}{{\partial x_{i}^{2} }} + \beta_{1} A_{11} \left( {\frac{{\partial^{2} \dot{u}_{i} }}{{\partial x_{i}^{2} }} + \frac{{\partial \dot{w}_{i} }}{{\partial x_{i} }}\frac{{\partial^{2} w_{i} }}{{\partial x_{i}^{2} }} + \frac{{\partial w_{i} }}{{\partial x_{i} }}\frac{{\partial^{2} \dot{w}_{i} }}{{\partial x_{i}^{2} }}} \right) - \beta_{1} B_{11} \frac{{\partial^{2} \dot{\psi }_{i} }}{{\partial x_{i}^{2} }} = I_{1} \frac{{\partial^{2} u_{i} }}{{\partial t^{2} }} - I_{2} \frac{{\partial^{2} \psi_{i} }}{{\partial t^{2} }} \hfill \\ A_{11} \varepsilon_{0} \frac{{\partial^{2} w_{i} }}{{\partial x_{i}^{2} }} + A_{11} \left[ {\frac{{\partial^{2} u_{i} }}{{\partial x_{i}^{2} }}\frac{{\partial w_{i} }}{{\partial x_{i} }} + \frac{{\partial^{2} w_{i} }}{{\partial x_{i}^{2} }}\frac{{\partial u_{i} }}{{\partial x_{i} }} + \frac{3}{2}\left( {\frac{{\partial w_{i} }}{{\partial x_{i} }}} \right)^{2} \frac{{\partial^{2} w_{i} }}{{\partial x_{i}^{2} }}} \right] - B_{11} \left( {\frac{{\partial^{2} \psi_{i} }}{{\partial x_{i}^{2} }}\frac{{\partial w_{i} }}{{\partial x_{i} }} + \frac{{\partial^{2} w_{i} }}{{\partial x_{i}^{2} }}\frac{{\partial \psi_{i} }}{{\partial x_{i} }}} \right) - N_{11}^{{\text{E}}} \frac{{\partial^{2} w_{i} }}{{\partial x_{i}^{2} }} \hfill \\ + \beta_{1} A_{11} \left[ {\frac{{\partial^{2} \dot{u}_{i} }}{{\partial x_{i}^{2} }}\frac{{\partial w_{i} }}{{\partial x_{i} }} + \frac{{\partial^{2} w_{i} }}{{\partial x_{i}^{2} }}\frac{{\partial \dot{u}_{i} }}{{\partial x_{i} }} + 2\frac{{\partial w_{i} }}{{\partial x_{i} }}\frac{{\partial^{2} w_{i} }}{{\partial x_{i}^{2} }}\frac{{\partial \dot{w}_{i} }}{{\partial x_{i} }} + \left( {\frac{{\partial w_{i} }}{{\partial x_{i} }}} \right)^{2} \frac{{\partial^{2} \dot{w}_{i} }}{{\partial x_{i}^{2} }}} \right] - \beta_{1} B_{11} \left( {\frac{{\partial^{2} \dot{\psi }_{i} }}{{\partial x_{i}^{2} }}\frac{{\partial w_{i} }}{{\partial x_{i} }} + \frac{{\partial^{2} w_{i} }}{{\partial x_{i}^{2} }}\frac{{\partial \dot{\psi }_{i} }}{{\partial x_{i} }}} \right) \hfill \\ + A_{55} \left( { - \frac{{\partial \psi_{i} }}{{\partial x_{i} }} + \frac{{\partial^{2} w_{i} }}{{\partial x_{i}^{2} }}} \right) + \beta_{2} A_{55} \left( { - \frac{{\partial \dot{\psi }_{i} }}{{\partial x_{i} }} + \frac{{\partial^{2} \dot{w}_{i} }}{{\partial x_{i}^{2} }}} \right) = I_{1} \frac{{\partial^{2} w_{i} }}{{\partial t^{2} }} \hfill \\ B_{11} \left( {\frac{{\partial^{2} u_{i} }}{{\partial x_{i}^{2} }} + \frac{{\partial w_{i} }}{{\partial x_{i} }}\frac{{\partial^{2} w_{i} }}{{\partial x_{i}^{2} }}} \right) - D_{11} \frac{{\partial^{2} \psi_{i} }}{{\partial x_{i}^{2} }} + \beta_{1} B_{11} \left( {\frac{{\partial^{2} \dot{u}_{i} }}{{\partial x_{i}^{2} }} + \frac{{\partial \dot{w}_{i} }}{{\partial x_{i} }}\frac{{\partial^{2} w_{i} }}{{\partial x_{i}^{2} }} + \frac{{\partial w_{i} }}{{\partial x_{i} }}\frac{{\partial^{2} \dot{w}_{i} }}{{\partial x_{i}^{2} }}} \right) \hfill \\ - \beta_{1} D_{11} \frac{{\partial^{2} \psi_{i} }}{{\partial x_{i}^{2} }} - A_{55} \left( { - \psi_{i} + \frac{{\partial w_{i} }}{{\partial x_{i} }}} \right) - \beta_{2} A_{55} \left( { - \dot{\psi }_{i} + \frac{{\partial \dot{w}_{i} }}{{\partial x_{i} }}} \right) = I_{2} \frac{{\partial^{2} u_{i} }}{{\partial t^{2} }} - 2I_{3} \frac{{\partial^{2} \psi_{i} }}{{\partial t^{2} }} \hfill \\ \end{gathered} \right. $$
(31)

For considered boundary conditions, i.e., clamped (C) end and hinged (H) end, we have

$$ u_{i} = 0,w_{i} = 0,\psi_{i} = 0\;\left( {\text{C end}} \right) $$
(32)

and

$$ u_{i} = 0,w_{i} = 0,M_{i} = 0\;\left( {\text{H end}} \right) $$
(33)

It is necessary to reintegrate the above two parts into a unified solution. Thus, the matching conditions at the crack need to be considered along with the boundary conditions, and we have

$$ \left\{ \begin{gathered} u_{{1N_{1} }} = u_{21} ,w_{{1N_{1} }} = w_{21} ,N_{1x} = N_{2x} \hfill \\ N_{1x} \frac{{\partial w_{1} }}{{\partial x_{1} }} + Q_{1x} = N_{2x} \frac{{\partial w_{2} }}{{\partial x_{2} }} + Q_{2x} \hfill \\ M_{1x} = M_{2x} = K_{{\text{T}}} \left( {\psi_{1} - \psi_{2} } \right) \hfill \\ \end{gathered} \right. $$
(34)

4 Solution

To normalize the governing equations, the following definitions are introduced

$$ \begin{gathered} X_{i} = \frac{{x_{i} }}{{L_{i} }},U_{i} = \frac{{u_{i} }}{h},W_{i} = \frac{{w_{i} }}{h},\Psi_{i} = \psi_{i} ,\eta_{i} = \frac{{L_{i} }}{h},\kappa = \frac{L}{h} \hfill \\ A_{110} = \frac{{E_{{\text{m}}} }}{{1 - \nu_{{\text{m}}}^{2} }}h,I_{10} = \rho_{{\text{m}}} h,\left\{ {i_{1} ,i_{2} ,i_{3} } \right\} = \left\{ {\frac{{I_{1} }}{{I_{10} }},\frac{{I_{2} }}{{I_{10} h}},\frac{{I_{3} }}{{I_{10} h^{2} }}} \right\} \hfill \\ \left\{ {a_{11} ,a_{55} ,b_{11} ,d_{11} ,\overline{N}_{11}^{{\text{E}}} ,\overline{M}_{11}^{{\text{E}}} ,\overline{K}_{{\text{T}}} } \right\} = \left\{ {\frac{{A_{11} }}{{A_{110} }},\frac{{A_{55} }}{{A_{110} }},\frac{{B_{11} }}{{A_{110} h}},\frac{{D_{11} }}{{A_{110} h^{2} }},\frac{{N_{11}^{{\text{E}}} }}{{A_{110} }},\frac{{M_{11}^{{\text{E}}} }}{{A_{110} h}},\frac{{K_{{\text{T}}} }}{{A_{110} h}}} \right\} \hfill \\ T = \frac{t}{L}\sqrt {\frac{{A_{110} }}{{I_{10} }}} ,\left\{ {c_{1} ,c_{2} } \right\} = \left\{ {\frac{{\beta_{1} }}{L}\sqrt {\frac{{A_{110} }}{{I_{10} }}} ,\frac{{\beta_{2} }}{L}\sqrt {\frac{{A_{110} }}{{I_{10} }}} } \right\} \hfill \\ \end{gathered} $$
(35)

Substituting Eq. (35) into Eq. (31), the dimensionless governing equation is obtained as

$$ \left\{ \begin{gathered} a_{11} \left( {\frac{{\partial^{2} U_{i} }}{{\partial X_{i}^{2} }} + \frac{1}{{\eta_{i} }}\frac{{\partial W_{i} }}{{\partial X_{i} }}\frac{{\partial^{2} W_{i} }}{{\partial X_{i}^{2} }}} \right) - b_{11} \frac{{\partial^{2} \Psi_{i} }}{{\partial X_{i}^{2} }} + c_{1} a_{11} \left( {\frac{{\partial^{2} \dot{U}_{i} }}{{\partial X_{i}^{2} }} + \frac{1}{{\eta_{i} }}\frac{{\partial \dot{W}_{i} }}{{\partial X_{i} }}\frac{{\partial^{2} W_{i} }}{{\partial X_{i}^{2} }} + \frac{1}{{\eta_{i} }}\frac{{\partial W_{i} }}{{\partial X_{i} }}\frac{{\partial^{2} \dot{W}_{i} }}{{\partial X_{i}^{2} }}} \right) - c_{1} b_{11} \frac{{\partial^{2} \dot{\Psi }_{i} }}{{\partial X_{i}^{2} }} = i_{1} \frac{{\eta_{i}^{2} }}{{\kappa^{2} }}\frac{{\partial^{2} U_{i} }}{{\partial T^{2} }} - i_{2} \frac{{\eta_{i}^{2} }}{{\kappa^{2} }}\frac{{\partial^{2} \Psi_{i} }}{{\partial T^{2} }} \hfill \\ a_{11} \varepsilon_{0} \frac{{\partial^{2} W_{i} }}{{\partial X_{i}^{2} }} + a_{11} \left[ {\frac{1}{{\eta_{i} }}\frac{{\partial^{2} U_{i} }}{{\partial X_{i}^{2} }}\frac{{\partial W_{i} }}{{\partial X_{i} }} + \frac{1}{{\eta_{i} }}\frac{{\partial^{2} W_{i} }}{{\partial X_{i}^{2} }}\frac{{\partial U_{i} }}{{\partial X_{i} }} + \frac{3}{{2\eta_{i}^{2} }}\left( {\frac{{\partial W_{i} }}{{\partial X_{i} }}} \right)^{2} \frac{{\partial^{2} W_{i} }}{{\partial X_{i}^{2} }}} \right] - \frac{{b_{11} }}{{\eta_{i} }}\left( {\frac{{\partial^{2} \Psi_{i} }}{{\partial X_{i}^{2} }}\frac{{\partial W_{i} }}{{\partial X_{i} }} + \frac{{\partial^{2} W_{i} }}{{\partial X_{i}^{2} }}\frac{{\partial \Psi_{i} }}{{\partial X_{i} }}} \right) - \overline{N}_{11}^{{\text{E}}} \frac{{\partial^{2} W_{i} }}{{\partial X_{i}^{2} }} \hfill \\ + c_{1} a_{11} \left[ {\frac{1}{{\eta_{i} }}\frac{{\partial^{2} \dot{U}_{i} }}{{\partial X_{i}^{2} }}\frac{{\partial W_{i} }}{{\partial X_{i} }} + \frac{1}{{\eta_{i} }}\frac{{\partial^{2} W_{i} }}{{\partial X_{i}^{2} }}\frac{{\partial \dot{U}_{i} }}{{\partial X_{i} }} + \frac{2}{{\eta_{i}^{2} }}\frac{{\partial W_{i} }}{{\partial X_{i} }}\frac{{\partial^{2} W_{i} }}{{\partial X_{i}^{2} }}\frac{{\partial \dot{W}_{i} }}{{\partial X_{i} }} + \frac{1}{{\eta_{i}^{2} }}\left( {\frac{{\partial W_{i} }}{{\partial X_{i} }}} \right)^{2} \frac{{\partial^{2} \dot{W}_{i} }}{{\partial X_{i}^{2} }}} \right] - \frac{{c_{1} b_{11} }}{{\eta_{i} }}\left( {\frac{{\partial^{2} \dot{\Psi }_{i} }}{{\partial X_{i}^{2} }}\frac{{\partial W_{i} }}{{\partial X_{i} }} + \frac{{\partial^{2} W_{i} }}{{\partial X_{i}^{2} }}\frac{{\partial \dot{\Psi }_{i} }}{{\partial X_{i} }}} \right) \hfill \\ + a_{55} \left( { - \eta_{i} \frac{{\partial \Psi_{i} }}{{\partial X_{i} }} + \frac{{\partial^{2} W_{i} }}{{\partial X_{i}^{2} }}} \right) + c_{2} a_{55} \left( { - \eta_{i} \frac{{\partial \dot{\Psi }_{i} }}{{\partial X_{i} }} + \frac{{\partial^{2} \dot{W}_{i} }}{{\partial X_{i}^{2} }}} \right) = i_{1} \frac{{\eta_{i}^{2} }}{{\kappa^{2} }}\frac{{\partial^{2} W_{i} }}{{\partial T^{2} }} \hfill \\ b_{11} \left( {\frac{{\partial^{2} U_{i} }}{{\partial X_{i}^{2} }} + \frac{1}{{\eta_{i} }}\frac{{\partial W_{i} }}{{\partial X_{i} }}\frac{{\partial^{2} W_{i} }}{{\partial X_{i}^{2} }}} \right) - d_{11} \frac{{\partial^{2} \Psi_{i} }}{{\partial X_{i}^{2} }} + c_{1} b_{11} \left( {\frac{{\partial^{2} \dot{U}_{i} }}{{\partial X_{i}^{2} }} + \frac{1}{{\eta_{i} }}\frac{{\partial \dot{W}_{i} }}{{\partial X_{i} }}\frac{{\partial^{2} W_{i} }}{{\partial X_{i}^{2} }} + \frac{1}{{\eta_{i} }}\frac{{\partial W_{i} }}{{\partial X_{i} }}\frac{{\partial^{2} \dot{W}_{i} }}{{\partial X_{i}^{2} }}} \right) \hfill \\ - c_{1} d_{11} \frac{{\partial^{2} \dot{\Psi }_{i} }}{{\partial X_{i}^{2} }} - a_{55} \eta_{i}^{2} \left( { - \psi_{i} + \frac{1}{{\eta_{i} }}\frac{{\partial W_{i} }}{{\partial X_{i} }}} \right) - c_{2} a_{55} \eta_{i}^{2} \left( { - \dot{\Psi }_{i} + \frac{1}{{\eta_{i} }}\frac{{\partial \dot{W}_{i} }}{{\partial X_{i} }}} \right) = i_{2} \frac{{\eta_{i}^{2} }}{{\kappa^{2} }}\frac{{\partial^{2} U_{i} }}{{\partial T^{2} }} - 2i_{3} \frac{{\eta_{i}^{2} }}{{\kappa^{2} }}\frac{{\partial^{2} \Psi_{i} }}{{\partial T^{2} }} \hfill \\ \end{gathered} \right. $$
(36)

The dimensionless governing equations will be discretized using DQ method for numerical solution, and the resulting expressions for the displacements and their derivatives are

$$ \left\{ \begin{gathered} \left\{ {U_{i} \left( {X_{i} ,T} \right),W_{i} \left( {X_{i} ,T} \right),\Psi_{i} \left( {X_{i} ,T} \right)} \right\} = \sum_{n = 1}^{{N_{i} }} {l_{in} \left( {X_{i} } \right)\left\{ {U_{in} \left( T \right),W_{in} \left( T \right),\Psi_{in} \left( T \right)} \right\}} \hfill \\ \left. {\frac{{\partial^{\varsigma } }}{{\partial X_{i}^{\varsigma } }}\left\{ {U_{i} \left( {X_{i} ,T} \right),W_{i} \left( {X_{i} ,T} \right),\Psi_{i} \left( {X_{i} ,T} \right)} \right\}} \right|_{{X_{i} = X_{ij} }} = \sum_{n = 1}^{{N_{i} }} {\lambda_{ijn}^{\left( \varsigma \right)} \left\{ {U_{in} \left( T \right),W_{in} \left( T \right),\Psi_{in} \left( T \right)} \right\}} \hfill \\ \end{gathered} \right. $$
(37)

where Ni denotes the total number of grid points along the longitudinal direction of the beam, {Uin, Win, Ψin} is the displacement vector when Xi = Xij, and lin(Xi) and \(\lambda_{ijn}^{\left( \varsigma \right)}\) are, respectively, the Lagrange interpolating polynomial and its corresponding weighting coefficients of the ϛ.th derivative when Xi = Xij. The distribution of the grid points is given as [46]

$$ \begin{array}{*{20}c} {X_{ij} = \frac{1}{2}\left\{ {1 - \cos \left[ {\frac{{\pi \left( {j - 1} \right)}}{{N_{i} - 1}}} \right]} \right\}} & {j = 1,2, \cdots ,} \\ \end{array} N_{i} $$
(38)

Substituting Eqs. (34) and (37) into Eq. (36) gives

$$ \left\{ \begin{gathered} U_{{1N_{1} }} = U_{{21}} ,W_{{1N_{1} }} = W_{{21}} \hfill \\ a_{{11}} \left[ {\frac{1}{{\eta _{1} }}\sum_{{n = 1}}^{{N_{1} }} {\lambda _{{1N_{1} n}}^{{\left( 1 \right)}} U_{{1n}} } + \frac{1}{{2\eta _{1}^{2} }}\left( {\sum_{{n = 1}}^{{N_{1} }} {\lambda _{{1N_{1} n}}^{{\left( 1 \right)}} W_{{1n}} } } \right)^{2} } \right] - \frac{{b_{{11}} }}{{\eta _{1} }}\sum_{{n = 1}}^{{N_{1} }} {\lambda _{{1N_{1} n}}^{{\left( 1 \right)}} \Psi _{{1n}} } \hfill \\ + c_{1} a_{{11}} \left( {\frac{1}{{\eta _{1} }}\sum_{{n = 1}}^{{N_{1} }} {\lambda _{{1N_{1} n}}^{{\left( 1 \right)}} \dot{U}_{{1n}} } + \frac{1}{{\eta _{1}^{2} }}\sum_{{n = 1}}^{{N_{1} }} {\lambda _{{1N_{1} n}}^{{\left( 1 \right)}} W_{{1n}} } \sum_{{n = 1}}^{{N_{1} }} {\lambda _{{1N_{1} n}}^{{\left( 1 \right)}} \dot{W}_{{1n}} } } \right) - \frac{{c_{1} b_{{11}} }}{{\eta _{1} }}\sum_{{n = 1}}^{{N_{1} }} {\lambda _{{1N_{1} n}}^{{\left( 1 \right)}} \dot{\Psi }_{{1n}} } \hfill \\ = a_{{11}} \left[ {\frac{1}{{\eta _{2} }}\sum_{{n = 1}}^{{N_{2} }} {\lambda _{{21n}}^{{\left( 1 \right)}} U_{{2n}} } + \frac{1}{{2\eta _{2}^{2} }}\left( {\sum_{{n = 1}}^{{N_{2} }} {\lambda _{{21n}}^{{\left( 1 \right)}} W_{{2n}} } } \right)^{2} } \right] - \frac{{b_{{11}} }}{{\eta _{2} }}\sum_{{n = 1}}^{{N_{2} }} {\lambda _{{21n}}^{{\left( 1 \right)}} \Psi _{{2n}} } \hfill \\ + c_{1} a_{{11}} \left( {\frac{1}{{\eta _{2} }}\sum_{{n = 1}}^{{N_{2} }} {\lambda _{{21n}}^{{\left( 1 \right)}} \dot{U}_{{2n}} } + \frac{1}{{\eta _{2}^{2} }}\sum_{{n = 1}}^{{N_{2} }} {\lambda _{{21n}}^{{\left( 1 \right)}} W_{{2n}} } \sum_{{n = 1}}^{{N_{2} }} {\lambda _{{21n}}^{{\left( 1 \right)}} \dot{W}_{{2n}} } } \right) - \frac{{c_{1} b_{{11}} }}{{\eta _{2} }}\sum_{{n = 1}}^{{N_{2} }} {\lambda _{{21n}}^{{\left( 1 \right)}} \dot{\Psi }_{{2n}} } \hfill \\ \left\{ {\frac{{a_{{11}} \varepsilon _{0} - \bar{N}_{{11}}^{{\text{E}}} }}{{\eta _{1} }} + \frac{{a_{{11}} }}{{\eta _{1}^{2} }}\left[ {\sum_{{n = 1}}^{{N_{1} }} {\lambda _{{1N_{1} n}}^{{\left( 1 \right)}} U_{{1n}} } + \frac{1}{{2\eta _{1} }}\left( {\sum_{{n = 1}}^{{N_{1} }} {\lambda _{{1N_{1} n}}^{{\left( 1 \right)}} W_{{1n}} } } \right)^{2} } \right] + \frac{{c_{1} a_{{11}} }}{{\eta _{1}^{2} }}\left( {\sum_{{n = 1}}^{{N_{1} }} {\lambda _{{1N_{1} n}}^{{\left( 1 \right)}} \dot{U}_{{1n}} } + \frac{1}{{\eta _{1} }}\sum_{{n = 1}}^{{N_{1} }} {\lambda _{{1N_{1} n}}^{{\left( 1 \right)}} W_{{1n}} } \sum_{{n = 1}}^{{N_{1} }} {\lambda _{{1N_{1} n}}^{{\left( 1 \right)}} \dot{W}_{{1n}} } } \right)} \right\}\sum_{{n = 1}}^{{N_{1} }} {\lambda _{{1N_{1} n}}^{{\left( 1 \right)}} W_{{1n}} } \hfill \\ - \left[ {\frac{{b_{{11}} }}{{\eta _{1}^{2} }}\sum_{{n = 1}}^{{N_{1} }} {\lambda _{{1N_{1} n}}^{{\left( 1 \right)}} \Psi _{{1n}} } + \frac{{c_{1} b_{{11}} }}{{\eta _{1}^{2} }}\sum_{{n = 1}}^{{N_{1} }} {\lambda _{{1N_{1} n}}^{{\left( 1 \right)}} \Psi _{{1n}} } } \right]\sum_{{n = 1}}^{{N_{1} }} {\lambda _{{1N_{1} n}}^{{\left( 1 \right)}} W_{{1n}} } + a_{{55}} \left( { - \Psi _{{1N_{1} }} + \frac{1}{{\eta _{1} }}\sum_{{n = 1}}^{{N_{1} }} {\lambda _{{1N_{1} n}}^{{\left( 1 \right)}} W_{{1n}} } } \right) + c_{2} a_{{55}} \left( { - \dot{\Psi }_{{1N_{1} }} + \frac{1}{{\eta _{1} }}\sum_{{n = 1}}^{{N_{1} }} {\lambda _{{1N_{1} n}}^{{\left( 1 \right)}} \dot{W}_{{1n}} } } \right) \hfill \\ = \left\{ {\frac{{a_{{11}} \varepsilon _{0} - \bar{N}_{{11}}^{{\text{E}}} }}{{\eta _{2} }} + \frac{{a_{{11}} }}{{\eta _{2}^{2} }}\left[ {\sum_{{n = 1}}^{{N_{2} }} {\lambda _{{21n}}^{{\left( 1 \right)}} U_{{2n}} } + \frac{1}{{2\eta _{2} }}\left( {\sum_{{n = 1}}^{{N_{2} }} {\lambda _{{21n}}^{{\left( 1 \right)}} W_{{2n}} } } \right)^{2} } \right] + \frac{{c_{1} a_{{11}} }}{{\eta _{2}^{2} }}\left( {\sum_{{n = 1}}^{{N_{2} }} {\lambda _{{21n}}^{{\left( 1 \right)}} \dot{U}_{{2n}} } + \frac{1}{{\eta _{2} }}\sum_{{n = 1}}^{{N_{2} }} {\lambda _{{21n}}^{{\left( 1 \right)}} W_{{2n}} } \sum_{{n = 1}}^{{N_{2} }} {\lambda _{{21n}}^{{\left( 1 \right)}} \dot{W}_{{2n}} } } \right)} \right\}\sum_{{n = 1}}^{{N_{2} }} {\lambda _{{21n}}^{{\left( 1 \right)}} W_{{2n}} } \hfill \\ - \left[ {\frac{{b_{{11}} }}{{\eta _{2}^{2} }}\sum_{{n = 1}}^{{N_{2} }} {\lambda _{{21n}}^{{\left( 1 \right)}} \Psi _{{2n}} } + \frac{{c_{1} b_{{11}} }}{{\eta _{2}^{2} }}\sum_{{n = 1}}^{{N_{2} }} {\lambda _{{21n}}^{{\left( 1 \right)}} \dot{\Psi }_{{2n}} } } \right]\sum_{{n = 1}}^{{N_{2} }} {\lambda _{{21n}}^{{\left( 1 \right)}} W_{{2n}} } + a_{{55}} \left( { - \Psi _{{21}} + \frac{1}{{\eta _{2} }}\sum_{{n = 1}}^{{N_{2} }} {\lambda _{{21n}}^{{\left( 1 \right)}} W_{{2n}} } } \right) + c_{2} a_{{55}} \left( { - \dot{\Psi }_{{21}} + \frac{1}{{\eta _{2} }}\sum_{{n = 1}}^{{N_{2} }} {\lambda _{{21n}}^{{\left( 1 \right)}} \dot{W}_{{2n}} } } \right) \hfill \\ b_{{11}} \varepsilon _{0} + \frac{{b_{{11}} }}{{\eta _{1} }}\left[ {\sum_{{n = 1}}^{{N_{1} }} {\lambda _{{1N_{1} n}}^{{\left( 1 \right)}} U_{{1n}} } + \frac{1}{{2\eta _{1} }}\left( {\sum_{{n = 1}}^{{N_{1} }} {\lambda _{{1N_{1} n}}^{{\left( 1 \right)}} W_{{1n}} } } \right)^{2} } \right] + \frac{{c_{1} b_{{11}} }}{{\eta _{1} }}\left( {\sum_{{n = 1}}^{{N_{1} }} {\lambda _{{1N_{1} n}}^{{\left( 1 \right)}} \dot{U}_{{1n}} } + \frac{1}{{\eta _{1} }}\sum_{{n = 1}}^{{N_{1} }} {\lambda _{{1N_{1} n}}^{{\left( 1 \right)}} W_{{1n}} } \sum_{{n = 1}}^{{N_{1} }} {\lambda _{{1N_{1} n}}^{{\left( 1 \right)}} \dot{W}_{{1n}} } } \right) \hfill \\ - \frac{{d_{{11}} }}{{\eta _{1} }}\sum_{{n = 1}}^{{N_{1} }} {\lambda _{{1N_{1} n}}^{{\left( 1 \right)}} \Psi _{{1n}} } - \frac{{c_{1} d_{{11}} }}{{\eta _{1} }}\sum_{{n = 1}}^{{N_{1} }} {\lambda _{{1N_{1} n}}^{{\left( 1 \right)}} \dot{\Psi }_{{1n}} } - \bar{M}_{{11}}^{{\text{E}}} = \bar{K}_{{\text{T}}} \left( {\Psi _{{21}} - \Psi _{{1N_{1} }} } \right) \hfill \\ b_{{11}} \varepsilon _{0} + \frac{{b_{{11}} }}{{\eta _{2} }}\left[ {\sum_{{n = 1}}^{{N_{2} }} {\lambda _{{21n}}^{{\left( 1 \right)}} U_{{2n}} } + \frac{1}{{2\eta _{2} }}\left( {\sum_{{n = 1}}^{{N_{2} }} {\lambda _{{21n}}^{{\left( 1 \right)}} W_{{2n}} } } \right)^{2} } \right] + \frac{{c_{1} b_{{11}} }}{{\eta _{2} }}\left( {\sum_{{n = 1}}^{{N_{2} }} {\lambda _{{21n}}^{{\left( 1 \right)}} \dot{U}_{{2n}} } + \frac{1}{{\eta _{2} }}\sum_{{n = 1}}^{{N_{2} }} {\lambda _{{21n}}^{{\left( 1 \right)}} W_{{2n}} } \sum_{{n = 1}}^{{N_{2} }} {\lambda _{{21n}}^{{\left( 1 \right)}} \dot{W}_{{2n}} } } \right) \hfill \\ - \frac{{d_{{11}} }}{{\eta _{2} }}\sum_{{n = 1}}^{{N_{2} }} {\lambda _{{21n}}^{{\left( 1 \right)}} \Psi _{{2n}} } - \frac{{c_{1} d_{{11}} }}{{\eta _{2} }}\sum_{{n = 1}}^{{N_{2} }} {\lambda _{{21n}}^{{\left( 1 \right)}} \dot{\Psi }_{{2n}} } - \bar{M}_{{11}}^{{\text{E}}} - \bar{M}_{{11}}^{{\text{T}}} = \bar{K}_{{\text{T}}} \left( {\psi _{{21}} - \psi _{{1N_{1} }} } \right) \hfill \\ \end{gathered} \right. $$
(39)

Correspondingly, the boundary condition becomes

$$ U_{ij} = 0,W_{ij} = 0,\Psi_{ij} = 0\;\left( {\text{C end}} \right) $$
(40)

and

$$ \left\{ \begin{gathered} U_{ij} = 0,W_{ij} = 0 \hfill \\ b_{11} \varepsilon_{0} + b_{11} \left[ {\frac{1}{{\eta_{i} }}\sum_{n = 1}^{{N_{i} }} {\lambda_{ijn}^{\left( 1 \right)} U_{in} } + \frac{1}{2}\frac{1}{{\eta_{i}^{2} }}\left( {\sum_{n = 1}^{{N_{i} }} {\lambda_{ijn}^{\left( 1 \right)} W_{in} } } \right)^{2} } \right] - d_{11} \frac{1}{{\eta_{i} }}\sum_{n = 1}^{{N_{i} }} {\lambda_{ijn}^{\left( 1 \right)} \Psi_{in} } \hfill \\ + c_{1} b_{11} \left( {\frac{1}{{\eta_{i} }}\sum_{n = 1}^{{N_{i} }} {\lambda_{ijn}^{\left( 1 \right)} \dot{U}_{in} } + \frac{1}{{\eta_{i}^{2} }}\sum_{n = 1}^{{N_{i} }} {\lambda_{ijn}^{\left( 1 \right)} W_{in} } \sum_{n = 1}^{{N_{i} }} {\lambda_{ijn}^{\left( 1 \right)} \dot{W}_{in} } } \right) - c_{1} d_{11} \frac{1}{{\eta_{i} }}\sum_{n = 1}^{{N_{i} }} {\lambda_{ijn}^{\left( 1 \right)} \dot{\Psi }_{in} } - \overline{M}_{11}^{{\text{E}}} = 0 \hfill \\ \end{gathered} \right.\;\left( {\text{H end}} \right) $$
(41)

Equation (39) can be further written as

$$ {\mathbf{M}}_{i} {\ddot{{\mathbf{d}}}}_{i} + \left[ {{\mathbf{C}}_{{i{\text{L}}}} +{\mathbf{ C}}_{{i{\text{NLd}}}} \left( {{\mathbf{d}}_{i} } \right)} \right]{\dot{\mathbf{d}}}_{i} + \left[ {{\mathbf{K}}_{{i{\text{L}}}} +{\mathbf{ K}}_{{i{\text{NL}}}} \left( {{\mathbf{d}}_{i} } \right) + {\mathbf{C}}_{{i{\text{NLv}}}} \left( {{\dot{\mathbf{d}}}_{i} } \right)} \right]{\mathbf{d}}_{i} = {\varvec{0}} $$
(42)

where

$$ {\mathbf{M}}_{i} = \frac{{\eta_{i}^{2} }}{{\kappa^{2} }}\left[ {\begin{array}{*{20}c} { - i_{1} {\mathbf{I}}} &\quad {\mathbf{0}} &\quad {i_{2} {\mathbf{I}}} \\ {\mathbf{0}} &\quad { - i_{1} {\mathbf{I}}} &\quad {\mathbf{0}} \\ {i_{2} {\mathbf{I}}} &\quad {\mathbf{0}} &\quad { - 2i_{3} {\mathbf{I}}} \\ \end{array} } \right] $$
(43)
$$ {\mathbf{C}}_{{i{\text{L}}}} = \left[ {\begin{array}{*{20}l} {c_{1} a_{{11}} \user2{\lambda }_{i}^{{(2)}} } \hfill &\quad {\mathbf{0}} \hfill &\quad { - c_{1} b_{{11}} \user2{\lambda }_{i}^{{(2)}} } \hfill \\ {\mathbf{0}} \hfill &\quad {c_{1} a_{{55}} \user2{\lambda }_{i}^{{(2)}} } \hfill &\quad { - c_{1} \eta _{i} \user2{\alpha }_{{55}} \user2{\lambda }_{i}^{{(1)}} } \hfill \\ { - c_{1} b_{{11}} \user2{\lambda }_{i}^{{(2)}} } \hfill &\quad {c_{1} \eta _{i} \user2{\alpha }_{{55}} \user2{\lambda }_{i}^{{(1)}} } \hfill &\quad { - c_{1} d_{{11}} \user2{\lambda }_{i}^{{(2)}} - c_{1} \eta _{i}^{2} \user2{\alpha }_{{55}} \user2{I}} \hfill \\ \end{array} } \right] $$
(44)
$$ {\mathbf{C}}_{{i{\text{NLd}}}} \left( {{\mathbf{d}}_{i} } \right) = \left[ {\begin{array}{*{20}c} {\mathbf{0}} &\quad {{\mathbf{C}}_{{i{\text{NLd}}}}^{12} } &\quad {\mathbf{0}} \\ {{\mathbf{C}}_{{i{\text{NLd}}}}^{21} } &\quad {{\mathbf{C}}_{{i{\text{NLd}}}}^{22} } &\quad {{\mathbf{C}}_{{i{\text{NLd}}}}^{23} } \\ {\mathbf{0}} &\quad {{\mathbf{C}}_{{i{\text{NLd}}}}^{32} } &\quad {\mathbf{0}} \\ \end{array} } \right] $$
(45)
$$ {\mathbf{K}}_{{i{\text{L}}}} = \left[ {\begin{array}{*{20}c} {a_{11} {{\varvec{\uplambda}}}_{i}^{\left( 2 \right)} } &\quad {\mathbf{0}} &\quad { - b_{11} {{\varvec{\uplambda}}}_{i}^{\left( 2 \right)} } \\ {\mathbf{0}} &\quad {\left( {a_{11} \varepsilon_{0} - \overline{N}_{11}^{{\text{E}}} } \right){{\varvec{\uplambda}}}_{i}^{\left( 2 \right)} + a_{55} {{\varvec{\uplambda}}}_{i}^{\left( 2 \right)} } &\quad { - \eta_{i} a_{55} {{\varvec{\uplambda}}}_{i}^{\left( 1 \right)} } \\ { - b_{11} {{\varvec{\uplambda}}}_{i}^{\left( 2 \right)} } &\quad {\eta_{i} a_{55} {{\varvec{\uplambda}}}_{i}^{\left( 1 \right)} } &\quad {d_{11} {{\varvec{\uplambda}}}_{i}^{\left( 2 \right)} - \eta_{i}^{2} a_{55} {\mathbf{I}}} \\ \end{array} } \right] $$
(46)
$$ {\mathbf{K}}_{{i{\text{NL}}}} \left( {{\mathbf{d}}_{i} } \right) = \left[ {\begin{array}{*{20}c} {\mathbf{0}} &\quad {{\mathbf{K}}_{{i{\text{NL}}}}^{12} } &\quad {\mathbf{0}} \\ {{\mathbf{K}}_{{i{\text{NL}}}}^{21} } &\quad {{\mathbf{K}}_{{i{\text{NL}}}}^{22} \left( 1 \right) + {\mathbf{K}}_{{i{\text{NL}}}}^{22} \left( 2 \right)} &\quad {{\mathbf{K}}_{{i{\text{NL}}}}^{23} } \\ {\mathbf{0}} &\quad {{\mathbf{K}}_{{i{\text{NL}}}}^{32} } &\quad {\mathbf{0}} \\ \end{array} } \right] $$
(47)

and

$$ {\mathbf{C}}_{{i{\text{NLv}}}} \left( {{\dot{\mathbf{d}}}_{i} } \right) = \left[ {\begin{array}{*{20}c} {\mathbf{0}} &\quad {{\mathbf{C}}_{{i{\text{NLv}}}}^{12} } &\quad {\mathbf{0}} \\ {\mathbf{0}} &\quad {{\mathbf{C}}_{{i{\text{NLv}}}}^{22} \left( 1 \right) + {\mathbf{C}}_{{i{\text{NLv}}}}^{22} \left( 2 \right)} &\quad {\mathbf{0}} \\ {\mathbf{0}} &\quad {{\mathbf{C}}_{{i{\text{NLv}}}}^{32} } &\quad {\mathbf{0}} \\ \end{array} } \right] $$
(48)

where I denotes the identity matrix. The expressions for K12 iNL, K21 iNL, K22 iNL(1), K22 iNL(2), K23 iNL and K32 iNL are listed in appendix A, C12 iNLv, C22 iNLv(1), C22 iNLv(2) and C32 iNLv are listed in appendix B, and C12 iNLd, C21 iNLd, C22 iNLd, C23 iNLd and C32 iNLd are listed in appendix C.

By rearranging the field equations within the structure of the generalized eigenvalue problem, Eq. (42) can be transformed into

$$ \left[ {\begin{array}{*{20}c} {\mathbf{0}} &\quad { - {\mathbf{I}}} \\ {{\mathbf{K}}_{{i{\text{L}}}} + {\mathbf{K}}_{{i{\text{NL}}}} \left( {\mathbf{d}} \right) + {\mathbf{C}}_{{i{\text{NL - v}}}} \left( {{\dot{\mathbf{d}}}} \right)} &\quad {{\mathbf{C}}_{{i{\text{L}}}} + {\mathbf{C}}_{{i{\text{NL - d}}}} \left( {\mathbf{d}} \right)} \\ \end{array} } \right]{\mathbf{q}} = \left[ {\begin{array}{*{20}c} { - {\mathbf{I}}} &\quad {\mathbf{0}} \\ {\mathbf{0}} &\quad { - {\mathbf{M}}_{i} } \\ \end{array} } \right]{\dot{\mathbf{q}}} $$
(49)

where \({\mathbf{q}}{ = }\left[ {{\mathbf{d}},{\dot{\mathbf{d}}}} \right]^{T}\) denotes the state vector of the system.

Applying state-space transformation and direct iterative method, the nonlinear frequency can be obtained as following:

Step 1. Neglecting nonlinear stiffness and damping matrices, a linear eigenvalue problem is obtained, whose linear eigenvalues λD_L and eigenvectors ψD_L are extracted as initial values.

Step 2. Scale the eigenvectors until the amplitude corresponding to the eigenvectors is equal to the maximum dimensionless amplitude Wmax.

Step 3. The obtained eigenvectors are substituted into the nonlinear stiffness matrix and damping matrix, which yields new nonlinear eigenvalues λD_NL and eigenvectors ψD_NL from Eq. (49).

Step 4. Repeating steps 2 to 3 until the eigenvalues λD_NL converge.

The eigenvalues λ as involved in steps 1 and 3 can be expressed in complex form as

$$ \lambda = \chi \pm i\omega_{{\text{D}}} $$
(50)

where the real part χ is the parameter related to the damping ratio and the imaginary part ωD denotes the damped natural frequency. Particularly, ωD denotes the linear damped natural frequency ωD_L in step 1 while it denotes the nonlinear damped natural frequency ωD_NL in step 3.

5 Results and discussion

Unless specifically stated, the following parameters will be adopted in the subsequent numerical calculations [5, 37]:

  1. 1.

    The dimensions of the beam are L = 1 × 10−2 m and h = 5 × 10−4 m, respectively. The depth and location of the crack are a/h = 0.5 and L1/L = 0.5, respectively;

  2. 2.

    The dimensionless initial amplitude is Wmax = 0.5, and the initial pre-strain is ε0 = 0.0001;

  3. 3.

    The average weight fraction of GPLs is fGPL = 1.5%, and the concentration gradient scaling factor Sg is set to 0.1. The thickness of the GPL is tGPL = 5 × 10−8 m, and the aspect ratio of GPL is assumed to be DGPL/tGPL = 300;

  4. 4.

    For the PVDF matrix, the mass density is ρm = 1780 kg/m3, the Poisson’s ratio is νm = 0.35, the elastic modulus is Em = 1.44 GPa, the electrical conductivity is σm = 3.5 × 10−9 S/m, and the dielectric permittivity is εm = 5 × 8.85 × 10−12 F/m;

  5. 5.

    The parameters used for GPL filler are ρf = 2200 kg/m3, νf = 0.175, E1 = E2 = 1.01 TPa, E3 = 101 TPa, σ1 = σ2 = 8.32 × 104 S/m, σ3 = 83.2 S/m, ε1 = ε2 = 1.3275 × 10−10 F/m and ε3 = 8.894 × 10−11 F/m;

5.1 Calculation of stress intensity factor (SIF) by ABAQUS

Among the three basic models for cracking, i.e., opening (type I), sliding (type II) and tearing (type III), type I is the most commonly employed in practical engineering. In this section, the SIF of type I crack is calculated using the J-Contour integral in ABAQUS software, and the established model and grid distribution are depicted in Fig. 5. To simulate the tensile state of the crack plane, a pair of directional bending moments measuring 10 N·m is applied at both ends of the beam. The grid consists of 2710 CPS4 quadrilateral elements, with the requirement to define singular elements around the crack tip.

Fig. 5
figure 5

ABAQUS model of FG-GPLRC beam with edge crack under pure bending moment

Full size image

The analysis of the dimensionless SIF of cracked FG-GPLRC beam is conducted by the finite element software. This analysis involves various factors, such as aspect ratio and weight fraction of GPL, FG distribution profiles, scaling factor and crack depth. The detailed results are presented in Appendix D.

5.2 Convergence study and validation

Table 1 presents the convergence of the total number of layers (Z) with different FG distribution profiles and crack depths. The applied voltage is fixed as VDC = 20 V. It can be seen that the results converge gradually as Z increases and exhibit a negligible difference when the number of layers is larger than 10 regardless of the FG distribution profiles and crack depth. To balance accuracy and computational efficiency, 10 layers will be used for subsequent analysis.

Table 1 Convergence study on total number of layers (N1 = N2 = 13)
Full size table

The convergence of the number of grid points in two segments of cracked FG-GPLRC beam is studied in Table 2. It is found that when the number of grid points in both parts is more than 11, the results converge. Therefore, N1 = N2 = 11 will be used for subsequent calculation.

Table 2 Convergence study on the number of grid points of the beam (Z = 10)
Full size table

To validate the proposed model that incorporates the Kelvin–Voigt damping, Fig. 6 exhibits the comparison between the existing results and previously reported ones for the first the frequencies of the first three modes [44]. The involved material properties and geometric dimensions are set to be the same values as in the reference and a cantilever beam structure is employed with β1 = β2 = β. The comparison demonstrates that the existing results are in good agreement with the previously reported ones.

Fig. 6
figure 6

Comparison of the frequencies of the Kelvin–Voigt damping model

Full size image

Table 3 tabulates the comparison of fundamental frequency ratios (ωD_L/ωD_L0) of the cracked FG-GPLRC beams with different distribution profiles, where ωD_L and ωD_L0 denote the fundamental frequencies of cracked and intact beams, respectively. The parameters involved are h = 0.12 m, a/h = 0.3, L/h = 10 and fGPL = 0.6 wt%. As can be seen from the table, our results agree well with the existing ones.

Table 3 Comparison of frequency ratio of cracked FG-GPLRC beam
Full size table

The effect of crack location on the fundamental frequency ratio of the FG-GPLRC beam with profile X is investigated in Fig. 7. The crack depth is a/h = 0.2. The present results are in excellent agreement with the ones in previous study once again. It is worth noting that when the crack is at the end of the H boundary, the crack has limited effect on the frequency. In contrast, when the crack is close to the C boundary end, the frequency is weakened significantly. When there is symmetric boundary condition, the crack located at the mid-span of the beam reduces the frequency the most.

Fig. 7
figure 7

Comparison of frequency ratio of cracked FG-GPLRC beam with different boundary conditions

Full size image

5.3 Parametric study

Figure 8 presents the effect of location of crack on frequency ratio ωD_L/ωD_L0 of cracked FG-GPLRC beam. It is obvious that the fundamental frequency ratio is related to the crack location. When the crack location is closed to L1/L = 0.2 or 0.8, the frequency ratio of the cracked beam does not change with the crack depth. This is due to the eigenvectors of the free vibration of the intact FG-GPLRC beam reaching the extreme rotational displacements in these two sections. As expected, when the crack depth increases, the cracked beam becomes more vulnerable as evidenced by the decrease in the frequency ratio. In addition, it can be observed that the frequency ratio of the cracked FG-GPLRC beam decreases as the applied voltage increases, especially when the crack location is closer to the mid-span, suggesting that cracks in the mid-span region have a more significant effect on the stiffness of the beams.

Fig. 8
figure 8

Effect of location of crack on fundamental frequency ratio ωD_L/ωD_L0 of cracked FG-GPLRC beam a VDC = 20 V; b VDC = 40 V

Full size image

Figure 9 investigates the dependency of the fundamental frequency ratio of cracked FG-GPLRC beam on the scaling factor considering four distribution profiles. It is evident that the frequency ratios of the beams with profiles O and A always increase with the increase of the scaling factor, regardless of the voltage applied. In contrast, it is quite different for the beam with profiles X and V. For example, when there is no applied voltage, the frequency ratio exhibits a decrease as the scaling factor increases. For profile X, when a voltage of 40 V is applied, the frequency ratio first increases with the scaling factor and then starts to decrease and converge to the case without voltage. Slightly different from the variation of profile X, the frequency ratio of the beam with profile V first decreases with the scaling factor. Then the frequency ratio undergoes a similar trend as profile X. The above observation can be explained by the competing effects of the scaling factor and the applied voltage on the stiffness of the cracked FG-GPLRC beam subjected to different FG distribution profiles.

Fig. 9
figure 9

Effect of scaling factor on fundamental frequency ratio ωD_L/ωD_L0 of cracked FG-GPLRC beam

Full size image

Figure 10 demonstrates the variation of the fundamental frequency ratio of the cracked FG-GPLRC beam with DC voltages and AC frequencies. In Fig. 10a, the frequency ratio of the cracked FG-GPLRC beam decreases as the voltage increases, which is particularly pronounced in the beam with profile U. This observation suggests that the utilization of FG distribution profiles enables the cracked FG-GPLRC beams to be more stable subjected to electrostatic stresses. As seen from Fig. 10b, the frequency ratio of the cracked FG-GPLRC beam with profile U is more significantly affected by AC frequency than the other four distribution profiles, especially when the AC frequency is around 103 Hz. Based on the above phenomena, the cracked FG-GPLRC beam with dielectric properties demonstrates the capability of self-sensing and structural health monitoring.

Fig. 10
figure 10

Effects of a applied voltage and b AC frequency on fundamental frequency ratio ωD_L/ωD_L0 of cracked FG-GPLRC beam

Full size image

The influence of the GPL aspect ratio on the frequency ratio of the cracked FG-GPLRC beam is studied in Fig. 11, which involves different Kelvin–Voigt damping coefficients. Seen From Fig. 11a, the frequency ratio curves with different damping coefficients intersect at the same point with the increase of the GPL aspect ratio, and this intersection point moves as the GPL aspect ratio increases or the voltage decreases. The intersection point observed in Fig. 11a also shifts by changing the functionally graded distribution as observed in Fig. 11b. In addition, the frequency ratio increases first and then decreases with the increase of GPL aspect ratio for relatively large damping coefficients, i.e., β = 1.5 × 10–5 s. This can be attributed to the increased stiffness of the structure due to the increase of GPL aspect ratio. For larger aspect ratio, the beam becomes more sensitive to the applied voltage, surpassing the enhancing effect induced by the increase in GPL aspect ratio.

Fig. 11
figure 11

Effect of GPL aspect ratio on fundamental frequency ratio ωD_L/ωD_L0 of cracked FG-GPLRC beam a Profile X; b VDC = 20 V

Full size image

Figure 12 displays the effect of the Kelvin–Voigt damping coefficient on the frequency ratio of the cracked FG-GPLRC beam with different DC voltages and GPL concentrations. It is apparent that an increase in the damping coefficient leads to accelerated increase in the frequency ratio and decrease in the sensitivity of the cracked FG-GPLRC beam to voltage. Similar to the findings presented in Fig. 11, the curves representing different GPL concentrations at the same voltage have intersecting points as the damping coefficient increases. Furthermore, an increasing voltage enables the convergence point to shift toward the upper right direction.

Fig. 12
figure 12

Effect of Kelvin–Voigt damping on fundamental frequency ratio ωD_L/ωD_L0 of cracked FG-GPLRC beam

Full size image

Figure 13 depicts the effect of the crack location on nonlinear frequency ratio ωD_NL/ωD_L of the cracked FG-GPLRC beam. The frequency ratio, which is symmetric with respect to the crack location, increases as the crack depth increases, indicating an increasing nonlinearity of the cracked FG-GPLRC beam. Furthermore, when the applied voltage increases, a noticeable rise in the frequency ratio of the cracked FG-GPLRC is observed, particularly in the case of FG-GPLRC beams with deeper cracks, suggesting that the cracked FG-GPLRC beams with lower stiffness are more susceptible to voltage regulation.

Fig. 13
figure 13

Effect of crack location on nonlinear frequency ratio ωD_NL/ωD_L of cracked FG-GPLRC beam a VDC = 0 V; b VDC = 20 V; c VDC = 40 V; d VDC = 80 V

Full size image

Figure 14 plots the effect of dimensionless initial amplitude on frequency ratio of the cracked FG-GPLRC beam. The frequency ratio increases as the dimensionless amplitude increases as expected, indicating an increasing nonlinearity of the system. It is worth noting that altering the shear damping coefficient β2 has limited effect on the nonlinearity of the cracked FG-GPLRC beam, while the increase of the tensile damping coefficient β1 results in the decreased frequency ratio and nonlinearity. The above observation demonstrates the tensile damping coefficient exhibits a stronger energy dissipation effect on the nonlinear vibration of the cracked FG-GPLRC beam than the shear damping coefficient.

Fig. 14
figure 14

Effect of dimensionless initial amplitude on nonlinear frequency ratio ωD_NL/ωD_L of cracked FG-GPLRC beam

Full size image

Figure 15 demonstrates the effect of GPL concentration on frequency ratio of the cracked FG-GPLRC beam. When there is no applied voltage, the frequency ratio decreases with the increase of GPL concentration, and larger damping coefficient leads to smaller frequency ratio. With the application of applied voltage, a notable increase in the frequency ratios is observed as the GPL concentration surpasses a specific threshold, i.e., fGPL = 0.9%. Moreover, the frequency ratios of the cracked beams with different damping coefficients intersect at a point when the GPL concentration further increases, and the frequency ratios with larger damping coefficients becomes larger as the GPL concentration keeps increasing.

Fig. 15
figure 15

Effect of GPL concentration on nonlinear frequency ratio ωD_NL/ωD_L of cracked FG-GPLRC beam

Full size image

6 Conclusions

In this paper, a numerical study on the damped nonlinear vibration of the cracked FG-GPLRC dielectric beam is carried out. Governing equations are derived using the Timoshenko beam theory and the nonlinear von Kármán strain–displacement relationship. A massless rotational spring model is employed to model the edge crack, and the SIF at the crack tip is then calculated using finite element method. DQ and direct iterative methods are utilized to solve the nonlinear system. The following conclusions can be obtained:

  1. (1)

    As the applied voltage increases, the fundamental frequency ratio ωD_L/ωD_L0 of the cracked FG-GPLRC beam decreases, while nonlinear frequency ratio ωD_NL/ωD_L increases. Two specific crack locations are observed where the frequency ratio of the beam is independent on crack depth.

  2. (2)

    The frequency ratio of the cracked FG-GPLRC beam with profile U is more sensitive to the variations in applied voltage and AC frequency compared to the ones with other profiles, suggesting that the FG distribution profiles enable the cracked FG-GPLRC beams to be more stable when subjected to the external electric field.

  3. (3)

    With the application of external electric field, the cracked FG-GPLRC beam with different damping coefficients generates a consistent frequency ratio as the concentration and aspect ratio of GPL increases. For the two damping coefficients considered, the tensile damping coefficient demonstrates a more pronounced energy dissipation effect on the nonlinear vibration of the beam than the shear damping coefficient.