Abstract
We develop a general nonlinear theory of thermo-electrodynamics. We show that two theories constructed in our previous works, namely the linear theory of thermo-electrodynamics and the nonlinear theory of electromagnetism, can be obtained from the general nonlinear theory proposed in the present paper. We also make some assumptions about how our model can be used to describe the fields corresponding to strong and weak interactions. Our approach is based on using of the Cosserat continuum of a special type as a mechanical model and some analogues between mechanical and physical quantities.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
It is well known that, until the late nineteenth century, the idea of using mechanical models to describe physical processes was dominant in science. Many mechanical models of thermal, electrical, magnetic and electromagnetic processes were proposed at that time. These models are known as the ether models, see [1]. Such famous scientists as Volta, Ampère, Poisson, Ørsted, Young, Fresnel, Stokes, Navier, Cauchy, Green, Strutt, Neumann, Weber, Gauss, Riemann, Thomson, Maxwell, Helmholtz, Kirchhoff, FitzGerald et al contributed to the creation of the ether models. It is important to note that all mathematical models of the ether constructed in the nineteenth century are based on translational degrees of freedom. Such models can be found in the studies published at the turn of the 20th/21st centuries, when the interest in mechanical models of physical processes began to revive, see, e.g., [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27]. At the same time, some scientists of the nineteenth century, e.g., Kelvin, Fitzgerald and Maxwell, came up with an idea of using models based on rotational degrees of freedom [1]. In the 20th and 21st centuries, the description of electromechanical and magnetomechanical effects using continuum models with rotational degrees of freedom was performed in works of many authors. We can refer, e.g., to one-component continuum models [28,29,30,31,32,33,34,35] and two-component continuum models [36,37,38,39]. We can also refer to [40,41,42], where analogues between curved beams and electrical circuits are used to design the multi-physics metamaterials.
Zhilin was the first scientist of twentieth century who created models of physical processes based on continua with rotational degrees of freedom and who called these models the ether models. In 1996, Zhilin gave the lecture “Reality and mechanics” at XXIII Summer School “Nonlinear Oscillations in Mechanical Systems” (St. Petersburg, Russia), where he showed that based on the continuum possessing only rotation degrees of freedom one can obtain the Schrödinger equation and the Klein–Gordon equation. In 2000, Zhilin gave the lecture “The main direction of the development of mechanics for XXI century” at XXVIII Summer School–Conference “Advanced Problems in Mechanics” (St. Petersburg, Russia), where he presented a continuum model with only rotation degrees of freedom as a model of electromagnetic field in vacuum. Both lectures were published in [11]. In 2005, Zhilin created a nonlinear theory of electromagnetic field, which was published in [43, 44]. A brief outline of the above Zhilin works can be found in [45]; the biography and scientific contributions of Zhilin are presented in [46,47,48]. Beginning in 2010, we have published a series of works [49,50,51,52,53,54,55] developing Zhilin’s ideas applied to modeling thermodynamic processes and a series of works [56,57,58,59,60,61,62,63,64] developing Zhilin’s ideas applied to modeling electromagnetic processes and mutual influence of thermodynamic and electromagnetic processes. The idea of describing physical phenomena using mechanical models based on rotational degrees of freedom was also developed by other authors, see [65,66,67,68,69]. A discussion of various models of the ether, both classical and modern, can be found in [70].
Papers [60, 63, 64] are directly related to the subject of the present study, so we discuss the results of these papers in more detail. In [64], we have proposed a linear theory of thermo-electrodynamics, which is based on the Cosserat continuum of a special type. This theory describes electric, magnetic and thermal effects in dielectrics and in conductors. In contrast to Maxwell’s electrodynamics, the proposed theory is in agreement with Kirchhoff’s laws for electrical circuits. In addition, the proposed theory describes the mutual influence of thermal and electromagnetic processes. In the framework of the theory, we have obtained the entropy balance equation and the heat conduction equation containing Joule heat. We have also obtained the generalized Maxwell–Faraday equation containing the temperature gradient. Thus, the proposed theory contains three mutually orthogonal vectors: the electric field vector, the magnetic field vector and the temperature gradient. This is in agreement with two experimentally observed effects: the Ettingshausen effect and the Nernst–Ettingshausen effect. In [60], we have proposed a nonlinear theory of electromagnetism. In this paper, we show that the proposed theory can be based on two different models. Both the models are based on the Cosserat continuum, but one of them assumes the true moment stress tensor to be antisymmetric, whereas another model assumes the energy moment stress tensor to be antisymmetric. In the case of the linear theory, the difference between these models disappears. The study performed in [60] did not allow us to give preference to one of the aforesaid models. In [63], we have developed and generalized the nonlinear theory based on these models. As a result, we not only have introduced mechanical analogues of all known quantities characterizing the state of electromagnetic field, but also have introduced some additional quantities: a voltage density vector, a magnetic charge density vector, a magnetic flux tensor, an electromagnetic current density tensor, and an electromagnetic induction tensor. In the framework of this theory, we have generalized Maxwell’s first equation writing it in tensor form. We have also generalized the charge balance equation writing it in tensor form, so that the trace of this equation gives us the electric charge balance equation, and the vector invariant of this equation gives us the magnetic charge balance equation. Despite the significant development of the theory, we could not find convincing arguments in favor of one of our models. In [63], we concluded that only a further generalization of the theory would allow us to choose between the two models.
The purpose of the present study is to create a general nonlinear theory of thermo-electrodynamics, from which we can obtain, as special cases, the linear theory of thermo-electrodynamics developed in [64], and the nonlinear theory of electromagnetism developed in [63]. It is important to note that attempt to combine the linear theory of thermo-electrodynamics [64] and the nonlinear theory of electromagnetism [63] shows that only the model based on the use of the true moment stress tensor allows this to be done. Thus, in the present paper we make a choice between the two models. In addition, we make some assumptions about how our model can describe the fields corresponding to strong and weak interactions.
2 The classical nonlinear theory of the elastic Cosserat continuum
2.1 Kinematics of the continuum
There are two approaches to describe the kinematics of continua: the material (Lagrangian) description [71,72,73] and the spatial (Eulerian) description [74,75,76]. Below, we employ the spatial description. Let vector \({\textbf{r}}\) identify the position of some point of space. We introduce the following notations: \({\textbf{v}}({\textbf{r}},t)\) is the velocity vector field; \({\textbf{u}}({\textbf{r}}, t)\) is the displacement vector field; \({\textbf{P}}({\textbf{r}}, t)\) is the rotation tensor field, and \(\varvec{\omega }({\textbf{r}},t)\) is the angular velocity vector field. In the spatial description, the kinematic relations have the form
Here the operator \({\displaystyle \frac{\delta \,\,}{\delta t} \,}\) is the material time derivative, and the operator \({\displaystyle \frac{\textrm{d} \,\,}{\textrm{d} t}\,}\) is the total time derivative. In order to clarify the concept of the total time derivative [77, 78], it is necessary to introduce the frame of reference. Let us imagine in a point O three rigidly connected, mutually orthogonal pointers (“arrows”), \({\textbf{e}}_1\), \({\textbf{e}}_2\), \({\textbf{e}}_3\). The set \( \{O,\, {\textbf{e}}_1,\, {\textbf{e}}_2,\, {\textbf{e}}_3\} \) is called a “frame.” The body of reference is defined by a frame to which a set of points (in space) have been added, whereby a rigid body motion of all the points together with the frame is allowed. The position of the points is labeled relatively to the frame by establishing the reference coordinate system \(x_1,\,x_2,\,x_3\) with origin O: \(\,{\textbf{r}}_* = x_1 {\textbf{e}}_1 + x_2 {\textbf{e}}_2 + x_3 {\textbf{e}}_3\), where \(\, -\infty<(x_1,\,x_2,\,x_3)<+\infty \). The frame and the reference coordinate system determine the reference body. They are “immutable.” In order to describe motion, we must be able to measure not only distance but also time. Hence, we need a “clock.” The reference body with a “clock” is called the “frame of reference.” Let \(f(x_1,\,x_2,\,x_3,\,t)\) be a function of the reference coordinates and of time. By the definition, the total time derivative of f is
under the condition that the reference coordinates \(x_1,\,x_2,\,x_3\) are held constant and there is an increment in the function only because of the increment in time. We note that in addition to the reference coordinate system one is free to choose any mathematical coordinate system in which the equations are specified. However, the reference coordinate system is a distinctive one since it determines the frame of reference. Let \(f(x(x_1,\,x_2,\,x_3,\,t),\,y(x_1,\,x_2,\,x_3,\,t),\,z(x_1,\,x_2,\,x_3,\,t),\,t)\) be a composite function of several variables, namely x, y, z. Then the total time derivative of f is
In accordance with Eq. (3), the total time derivative is the partial derivative with the reference coordinates held constant.
2.2 Inertia characteristics and dynamic structures of the continuum
Within the spatial description, it is customary to refer the inertia characteristics to an elementary volume fixed in space and containing an ensemble of particles. As the medium moves, different particles pass through the elementary volume, with each of these particles having its own mass and tensor of inertia. That is why, the question arises as to how the tensor of inertia of the elementary volume can be introduced. Here we use the approach that is discussed in detail in [79,80,81,82,83,84]. We introduce the following notations: \(\rho ({\textbf{r}},t)\) is the mass density of the continuum at a given point of space at the current time; \({\textbf{J}}({\textbf{r}},t)\) is the specific inertia tensor of the particles which occupy an elementary fixed volume \({\mathscr {V}}\) in space near the point identified by the position vector \({\textbf{r}}\) at the current time. Following the ideas of [79,80,81,82,83,84,85], we define \(\rho \) and \({\textbf{J}}\) as
where N is the number of particles in the elementary volume, and these particles possess masses \(m_i\) and inertia tensors \(\hat{{\textbf{J}}}_i\). Further, we consider an isotropic continuum. Therefore, we assume that
where \(J({\textbf{r}},t)\) is the specific moment of inertia, \({\textbf{E}}\) is the second-rank identity tensor.
The kinetic energy, the linear momentum vector and the angular momentum vector constitute the dynamic structures of the continuum. The specific kinetic energy of the continuum has the form
The specific linear momentum and the specific angular momentum of the continuum are
where the specific angular momentum is calculated with respect to the origin of the reference frame. We note that the first term in the expression for the specific angular momentum is called the specific moment of momentum and the second term is called the specific proper angular momentum.
2.3 The balance equations
Below we formulate four balance equations: the mass balance equation, the first law of the Eulerian dynamics, the second law of the Eulerian dynamics, and the energy balance equation. The mass balance equation can be written as:
In order to formulate the first and the second laws of the Eulerian dynamics, we need to introduce the stress vector \(\varvec{\tau }_n\) and the moment stress vector \({\textbf{T}}_n\) modeling the surrounding medium influence on the surface \({\mathscr {S}}\) of the elementary volume \({\mathscr {V}}\). By standard reasoning, we introduce the concept of stress tensor \(\varvec{\tau }\) associated with the stress vector \(\varvec{\tau }_n\) and the concept of moment stress tensor \({\textbf{T}}\) associated with the moment stress vector \({\textbf{T}}_n\). These tensors are defined by the relations \(\varvec{\tau }_n = {\textbf{n}} \cdot \varvec{\tau }\) and \({\textbf{T}}_n = {\textbf{n}} \cdot {\textbf{T}}\) where \({\textbf{n}}\) denotes the unit outer normal vector to the surface \({\mathscr {S}}\). We note that the stress tensor \(\varvec{\tau }\) and the moment stress tensor \({\textbf{T}}\) have the meaning of the Cauchy stress tensors or, what is the same thing, the true stress tensors. Now, we can write the first law of the Eulerian dynamics (the linear momentum balance equation) and the second law of the Eulerian dynamics (the angular momentum balance equation) as
where \({\textbf{f}}\) is the external force per unit mass, \({\textbf{L}}\) is the external moment per unit mass, \((\ )_{\times }\) denotes the vector invariant of a tensor that is defined for an arbitrary dyad as \(({\textbf{a}} {\textbf{b}})_{\times } = {\textbf{a}} \times {\textbf{b}}\).
Now, we turn to the energy balance equation. Assuming that the energy supply from external sources is absent, we formulate the energy balance equation as
where \({\mathscr {U}}\) is the specific internal energy. By standard reasoning, taking into account Eqs. (6), (8), (9), we can reduce Eq. (10) to the local form
where the double contraction is defined as \({\textbf{a}} {\textbf{b}} \cdot \cdot \, {\textbf{c}} {\textbf{d}} = ({\textbf{b}} \cdot {\textbf{c}})({\textbf{a}} \cdot {\textbf{d}})\), the cross product of a second-rank tensor and a vector is defined as follows: if \({\textbf{A}} = {\textbf{a}} {\textbf{b}}\) then \({\textbf{A}} \times {\textbf{c}} = {\textbf{a}} {\textbf{b}} \times {\textbf{c}} = {\textbf{a}} ({\textbf{b}} \times {\textbf{c}})\). Further, we use the energy balance equation (11) to define the concept of strain tensors and to obtain the Cauchy–Green relations.
2.4 The strain tensors
In modern literature, one can find different definitions of the strain tensors. Below we use the definitions adopted in [11, 43, 86, 87].
Definition 1
The tensors on which the stress tensor and the moment stress tensor perform work are called the strain tensors. Namely, the tensor on which the stress tensor performs work is called the stretch tensor; the tensor on which the moment stress tensor performs work is called the wryness tensor.
For convenience and brevity, we introduce the stretch tensor \({\textbf{g}}\) and the wryness tensor \(\varvec{\varTheta }\) by the formulas
and then, we show that these are the quantities that appear in the energy balance equation. In order to show the difference in properties of the stretch tensor and the wryness tensor, we consider some consequences of Eq. (12). It is not difficult to see that the stretch tensor satisfies the equation
which is known as the strain compatibility equation. The wryness tensor satisfies the equation
which also has the meaning of the strain compatibility equation. The proof of Eq. (14) based on the second equation in (12) can be found in [60]. The distinguish between Eq. (13) and Eq. (14) is evident. We emphasize that it is this difference that is the main reason that we create mechanical models of the electromagnetic field based on a continuum with rotational degrees of freedom. Taking the trace of Eq. (14)
Taking the vector invariant of Eq. (14) gives
We note that Eqs. (15), (16) play an important role in the proposed model of electromagnetic field.
As shown in [11, 43], the velocity gradient and the angular velocity gradient are related to the stretch tensor and the wryness tensor as
If translational velocity \({\textbf{v}}\) is assumed to be equal to zero, from Eqs. (14), (17) it follows that
In order to prove Eq. (18), it is sufficient to take the time derivative of Eq. (14), to take the curl of the second equation in (17), and eliminate the time derivative of \(\nabla \cdot \varvec{\varTheta }\) from the obtained equations. Taking the trace of Eq. (18), we arrive at
Taking the vector invariant of Eq. (18) yields
We refer to Eqs. (14), (15), (16) and Eqs. (18), (19), (20) in Sect. 5.4, where we briefly outline the nonlinear theory of non-conductive materials.
2.5 The reduced energy balance equation and the Cauchy–Green relations
In order to transform the energy balance equation (11) to a form convenient for obtaining the Cauchy–Green relations, we introduce the energy stress tensor \(\varvec{\tau }_e\) and the energy moment stress tensor \({\textbf{T}}_e\) as
and also the energy stretch tensor \({\textbf{g}}_e\) and the energy wryness tensor \(\varvec{\varTheta }_e\) as
Then, taking into account Eqs. (17), (21), (22), we can reduce Eq. (11) to the form
This form of the energy balance equation is called the reduced energy balance equation. The transformations needed to go from Eqs. (11) to (23) can be found in [53]. Thus, we have proved that Eq. (12) actually introduces the strain tensors, and it becomes clear why tensors (21) are called the energy stress tensor and the energy moment stress tensor and also why tensors (22) are called the energy stretch tensor and the energy wryness tensor.
The energy balance equation (23) allows us to determine the arguments of the function \({\mathscr {U}}\). If the continuum is assumed to be elastic, then from Eq. (23) it follows that the specific internal energy is the function of two arguments, the energy stretch tensor and the energy wryness tensor: \({\mathscr {U}} = {\mathscr {U}}\bigl ({\textbf{g}}_e,\,\varvec{\varTheta }_e\bigr )\). Since in the case of elastic continuum the stress tensor and the moment stress tensors do not depend of the strain rates, by standard reasoning we arrive at the Cauchy–Green relations
In order to obtain the constitutive equations, it is necessary to specify the function \({\mathscr {U}}\bigl ({\textbf{g}}_e,\, \varvec{\varTheta }_e \bigr )\). Indeed, the conditions of stability of the material impose certain restrictions upon the choice of function \({\mathscr {U}}\bigl ({\textbf{g}}_e,\, \varvec{\varTheta }_e \bigr )\).
Now, we have the closed system of equations (1), (8), (9), (12), (21), (22), (24) that describes the classical elastic Cosserat continuum.
The above method of derivation of the constitutive equations is convenient if we deal with arbitrary stress tensors and an arbitrary moment stress tensors. This method is also convenient if we impose some restrictions on the energy stress tensor \(\varvec{\tau }_e\) and the energy moment stress tensor \({\textbf{T}}_e\). However, if we impose some restrictions on the true stress tensor \(\varvec{\tau }\) and true moment stress tensor \({\textbf{T}}\) the method of derivation of the constitutive equations needs to be modified.
Now, we return to the energy balance equation (11). In order to represent this equation in a form convenient for obtaining new Cauchy–Green relations, we introduce the following quantities characterizing the stresses:
and the following quantities characterizing the strains:
Taking into account Eqs. (17), (25), (26), we can reduce Eq. (11) to the form
The derivation of Eq. (27) can be found in “Appendix A.” If the continuum is assumed to be elastic, then from Eq. (27) it follows that \({\mathscr {U}} = {\mathscr {U}}\bigl ({\textbf{g}}_r,\,\varvec{\varTheta }_r\bigr )\). By standard reasoning, we arrive at the Cauchy–Green relations
Specifying the function \({\mathscr {U}}\bigl ({\textbf{g}}_r,\, \varvec{\varTheta }_r \bigr )\), we can obtain the constitutive equations. As a result, we have an alternative form of the closed system of equations describing the classical elastic Cosserat continuum, namely Eqs. (1), (8), (9), (12), (25), (26), (28).
We note that \({\textbf{g}}_r = {\textbf{g}}_e\), but \(\varvec{\tau }_r\) does not coincide with \(\varvec{\tau }_e\). Furthermore, in contrast to tensor \(\varvec{\tau }_e\), tensor \(\varvec{\tau }_r\) depends not only on the stress tensor \(\varvec{\tau }\), but also on the moment stress tensor \({\textbf{T}}\). We also note that tensor \({\textbf{T}}_r\) and tensor \(\varvec{\varTheta }_r\) are in fact the rotated tensor \({\textbf{T}}\) and the rotated tensor \(\varvec{\varTheta }\), respectively. Therefore, tensor \({\textbf{T}}_r\) possesses the same properties as tensor \({\textbf{T}}\). If tensor \({\textbf{T}}\) is symmetric, then tensor \({\textbf{T}}_r\) is also symmetric. If \({\textbf{T}}\) is antisymmetric, then \({\textbf{T}}_r\) is also antisymmetric. That is why, the method of derivation of the constitutive equations based on the energy balance equation (27) is convenient if we impose some restrictions on the true moment stress tensor \({\textbf{T}}\).
3 A modified nonlinear theory of the elastic Cosserat continuum
3.1 Non-geometric interpretation of the strain tensors
The system of equations describing the behavior of the Cosserat continuum consists of the mass balance equation, two equations of motion (the first and the second laws of the Eulerian dynamics), the constitutive equations, the kinematics relations and the equations for the strain tensors. Material parameters are contained in the constitutive equations. All other equations have the same form for any materials. In contrast to the mass balance equation and the equations of motion, which can be written in both differential form and integral form, the kinematics relations and the equations for the strain tensors are always formulated in differential form. All of the above refers to the classical approach.
In [88], we have proposed a new approach to the definition of the stretch tensor for the continuum possessing only translational degrees of freedom. In [64, 89], we have developed this approach for the linear Cosserat continuum possessing only rotational degrees of freedom. Now, we develop this approach as applied to the nonlinear Cosserat continuum, which has both rotational and translational degrees of freedom. The main feature of our approach is that we do not consider the strain tensors to be purely geometric characteristics. An important circumstance is that the strain tensors satisfy not only the differential equations, but also the integral equations having the form of balance equations. Below we prove this assertion.
We start with the equations directly relating the gradients of the translational and angular velocities to the strain tensors. Our goal is to obtain the integral form of these equations. In order to do so, we transform Eq. (17) by using the definition of the material time derivative given by Eq. (1) to the form
The derivation of Eq. (29) can be found in “Appendix B.” Now, we rewrite Eq. (29) as
where the third-rank tensors \({\textbf{J}}_g\) and \({\textbf{J}}_\varTheta \), and the second-rank tensor \(\varvec{\varpi }\) have the form
Integrating Eq. (30) over the fixed volume \({\mathscr {V}}\) and using the divergence theorem yields
It is evident that both equations in (30) and both equations in (32) have the form of balance equations. The first equations in (30) and (32) are the local and the integral forms of the stretch tensor balance equation. The second equations in (30) and (32) are the local and the integral forms of the wryness tensor balance equation. The third-rank tensors \({\textbf{J}}_g\) and \({\textbf{J}}_\varTheta \) play the role of the fluxes of the stretch tensor and the wryness tensor, respectively. The second-rank tensor \(\varvec{\varpi }\) plays the role of the rate of production of the wryness tensor. In order to clarify the physical meaning of vectors \({\textbf{v}} \cdot {\textbf{g}}\) and \({\textbf{v}} \cdot \varvec{\varTheta } - \varvec{\omega }\), which determine the flux tensors \({\textbf{J}}_g\) and \({\textbf{J}}_\varTheta \), we turn to the kinematics relations (1). In view of Eq. (12), the kinematics relations can be rewritten as
Since the total time derivative of some quantity characterizes the rate of change of this quantity at a given point of space, from Eq. (33) it follows that vector \({\textbf{v}} \cdot {\textbf{g}}\) characterizes the rate of change of the displacement vector field at a given point of space, and vector \(\varvec{\omega } - {\textbf{v}} \cdot \varvec{\varTheta }\) characterizes the rate of change of the rotation tensor field at a given point of space. We note that both equations in (33) can be considered as balance equations where fluxes are equal to zero. In this case, the right-hand sides of these equations can be treated as the rate of production of the displacement vector and the rate of production of the rotation tensor, respectively.
Thus, we have obtained the balance equations for the strain tensors, the displacement vector and the rotation tensor. As a result, these quantities become, in some sense, similar to such quantities as mass, momentum, angular momentum and energy. However, since the balance equations for the strain tensors, the displacement vector and the rotation tensor are obtained by identical transformations, these quantities have not lost their geometric meaning.
3.2 Modified balance equations for the strain tensors
It is known that the balance equation for some quantity can contain a term having the meaning of the rate of supply of this quantity from an external source. It seems logical to us to add such terms to the balance equation for the stretch tensor and to the balance equation for the wryness tensor. In [88], we have done so in the case of the continuum possessing only translational degrees of freedom, where we have modified the stretch tensor balance equation. In [64], we have applied this idea in the case of the linear Cosserat continuum possessing only rotational degrees of freedom, where we have modified the wryness tensor balance equation. Now, we are going to develop this idea as applied to the case of the nonlinear Cosserat continuum possessing rotational and translational degrees of freedom.
Let us modify the balance equations (30) as follows:
where the additional terms \(\varvec{\varUpsilon }_g\) and \(\varvec{\varUpsilon }_\varTheta \) are the rate of supply of the stretch tensor from an external source and the rate of supply of the wryness tensor from an external source, respectively. As stated in [88], these additional terms can be used, i.e., for modeling chemical reactions which result in changes in mechanical states and mechanical properties of solids, and also for describing phase transitions and structural changes that occur both with a change in mass and without a change in mass. Furthermore, these terms provide additional opportunities to take into account the interrelation of thermal and mechanical processes.
In view of Eq. (31), we can rewrite Eq. (34) as
We pay attention to an important circumstance. If we replace Eq. (29) by Eq. (35), then we must either reject kinematics relations (1) or reject geometric relations (12). Here we reject Eq. (12). In this case, we should consider the first and the second equations in (35) as definitions of the stretch tensor and the wryness tensor, respectively; and also we should consider the first and the second equations in (1) as definitions of the displacement vector and the rotation tensor, respectively. With this approach, the velocity vector and the angular velocity vector play the role of the main variables. Since we reject Eq. (12), equations (1) and (33) become non-equivalent. This is due to the fact that kinematics relations (33) were obtained from kinematics relations (1) in view of geometric relations (12). Thus, now we can use the kinematics relations only in the form of Eq. (1).
Let us reduce Eq. (35) to the form containing the material time derivatives of the stretch tensor and the wryness tensor. We emphasize that we cannot just add the term \(\varvec{\varUpsilon }_g\) to the first equation in (17) and the term \(\varvec{\varUpsilon }_\varTheta \) to the second equation in (17). This is because differential equations (29) were obtained from differential equations (17) in view of geometric relations (12). Now, we cannot use geometric relations (12) since they are not valid. After simple transformations, see “Appendix B,” we obtain
Here the double cross product is defined as \({\textbf{a}} {\textbf{b}} \times \times \, {\textbf{c}} {\textbf{d}} = ({\textbf{b}} \times {\textbf{c}})({\textbf{a}} \times {\textbf{d}})\). We note that Eq. (36) can be written as
where tensors \(\varvec{\varUpsilon }_g^*\) and \(\varvec{\varUpsilon }_\varTheta ^*\) play the role of the source terms. These tensors are related to the source terms \(\varvec{\varUpsilon }_g\) and \(\varvec{\varUpsilon }_\varTheta \) by the formulas
It is easy to see that both equations in (37) differ from the corresponding equations in (17) only by the presence of the source terms \(\varvec{\varUpsilon }_g^*\) and \(\varvec{\varUpsilon }_\varTheta ^*\).
Now, it is not clear to us which source terms are preferable to use when constructing the theory of the generalized Cosserat continuum: \(\varvec{\varUpsilon }_g\) and \(\varvec{\varUpsilon }_\varTheta \) or \(\varvec{\varUpsilon }_g^*\) and \(\varvec{\varUpsilon }_\varTheta ^*\). However, we do not need to address this issue now, since below we consider a model based only on rotational degrees of freedom. In such a case, \(\varvec{\varUpsilon }_g^* = \varvec{\varUpsilon }_g\) and \(\varvec{\varUpsilon }_\varTheta ^* = \varvec{\varUpsilon }_\varTheta \).
3.3 The reduced energy balance equation in the case of the modified strain tensors
In the case of the modified strain tensors, the integral form of the energy balance equation (10) and the local form of the energy balance equation (11) remain valid since these equations do not depend on the strain tensors. Now, we transform the energy balance equation (11) in view of Eq. (37). If we use the energy strain tensors \({\textbf{g}}_e\) and \(\varvec{\varTheta }_e\), we obtain
If we use the strain tensors \({\textbf{g}}_r\) and \(\varvec{\varTheta }_r\), we arrive at the following equation
The derivation of Eqs. (39) and (40) can be found in “Appendix C.” It is easy to see that the right-hand sides of Eqs. (39) and (40) contain the additional terms compared with Eqs. (23) and (27), respectively. Because of these additional terms, Eqs. (39) and (40) do not allow us to determine the arguments of the function \({\mathscr {U}}\), even if the continuum is assumed to be elastic. This means that using Eq. (39) or Eq. (40) as a starting point we cannot arrive at the Cauchy–Green relations (24) or the Cauchy–Green relations (28), respectively.
Further, for simplicity sake, we assume that
We note that the source terms \(\varvec{\varUpsilon }_g^*\) and \(\varvec{\varUpsilon }_\varTheta ^*\) should be specified by constitutive equations, which can be chosen arbitrary. Scalar equation (41) can be considered as an equation specifying one component of tensor \(\varvec{\varUpsilon }_g^*\) or one component of tensor \(\varvec{\varUpsilon }_\varTheta ^*\). The physical meaning of this equation is that it imposes a restriction on the energy exchange caused by the source terms \(\varvec{\varUpsilon }_g^*\) and \(\varvec{\varUpsilon }_\varTheta ^*\). If the source terms satisfy this equation, then the energy of the considered continuum can be redistributed between its degrees of freedom, but the energy exchange due to \(\varvec{\varUpsilon }_g^*\) and \(\varvec{\varUpsilon }_\varTheta ^*\) between the considered continuum and its surrounding is absent. Indeed, in view of Eq. (41), the energy balance equation (39) turns into Eq. (23), and the energy balance equation (40) turns into Eq. (27). In this special case, the above reasoning regarding the Cauchy–Green relations remains valid. Namely, if the continuum is elastic, i.e., \({\mathscr {U}} = {\mathscr {U}}\bigl ({\textbf{g}}_e,\, \varvec{\varTheta }_e \bigr )\) or \({\mathscr {U}} = {\mathscr {U}}\bigl ({\textbf{g}}_r,\, \varvec{\varTheta }_r \bigr )\), then the Cauchy–Green relations take the form of Eq. (24) or Eq. (28), respectively. Below we consider only the special case given by Eq. (41).
Thus, we arrive at two nonlinear theories of the modified elastic Cosserat continuum. The first theory is described by Eqs. (1), (8), (9), (21), (22), (24), (37), (38) under restriction (41). The second theory is described by Eqs. (1), (8), (9), (25), (26), (28), (37), (38) under restriction (41). We note that we consider the modified Cosserat continuum to be elastic due to the Cauchy–Green relations (24) and (28), which allow us to obtain the constitutive equations as in the case of an elastic material. However, thanks to a special choice of the constitutive equations for tensors \(\varvec{\varUpsilon }_g^*\) and \(\varvec{\varUpsilon }_\varTheta ^*\), the modified Cosserat continuum can possess some properties of a viscoelastic continuum. This peculiarity of the modified Cosserat continuum is very important for further physical interpretations.
4 The Cosserat continuum of a special type
4.1 The modified theory of the Cosserat continuum possessing only rotational degrees of freedom
Below, we outline a simplified version of the theory presented in Sect. 3. The simplification consists in rejecting translational degrees of freedom in the modified theory of the Cosserat continuum. In other words, below we assume that \(\,{\textbf{v}} = 0\), \(\,{\textbf{u}} = 0\), \(\,{\textbf{g}} = {\textbf{E}}\), \(\,\rho = \textrm{const}\,\), and \(\,\varvec{\varUpsilon }_g = 0\). In this case, the material time derivative coincides with the total time derivative, the mass balance equation and the stretch tensor balance equation turn into identities.
The kinematics relation between the rotation tensor and the angular velocity vector (1) takes the form
The angular momentum balance equation (9) is written as
The wryness tensor balance equation (36) is reduced to the form
The simplifying restriction (41) turns into the equation
An additional simplification of the theory consists in the assumption that the specific internal energy does not depend on tensor \({\textbf{g}}_e = {\textbf{g}}_r\). In this case, two types of the Cauchy–Green relations are simplified as follows. The Cauchy–Green relations (24) are reduced to the form
The Cauchy–Green relations (28) are written as
Certainly, the system of the basic equations includes either Eq. (46) or Eq. (47).
The linear momentum balance equation (9) takes the form of the quasi-static equation
In order to close the system of equations, we should specify the external moment \(\rho {\textbf{L}}\), tensor \(\varvec{\varUpsilon }_\varTheta \), characterizing the rate of supply of the wryness tensor from an external source, and either the specific internal energy \({\mathscr {U}} = {\mathscr {U}}\bigl (\varvec{\varTheta }_e\bigr )\) or the specific internal energy \({\mathscr {U}} = {\mathscr {U}}\bigl (\varvec{\varTheta }_r\bigr )\).
We note that, in the case of the Cauchy–Green relations (46), the stress tensor \(\varvec{\tau }\) is equal to zero. Then, according to Eq. (48), the external force \({\textbf{f}}\) must be equal to zero. In the case of the Cauchy–Green relations (47), the stress tensor \(\varvec{\tau }\) is completely determined by the quantities associated with rotational degrees of freedom, and it is not equal to zero. Thus, although the theory ignores translational degrees of freedom, it includes nonzero stress tensor \(\varvec{\tau }\). In this case, the linear momentum balance equation (48) determines the external force \({\textbf{f}}\) at which translational motion of the continuum is absent. Thus, the presence of the external force \({\textbf{f}}\) in the linear momentum balance equation (48) allows us to avoid any theoretical contradictions between the expression for \(\varvec{\tau }\) and assumption \({\textbf{v}} = 0\). Certainly, it would be more correct to take into account translational degrees of freedom rather than introduce such an external force. We are going to include translational degrees of freedom in our model in future research. But in this paper, we focus our attention on other issues and therefore avoid overcomplicating the model, which is already quite complex.
4.2 The choice between two models
In [60, 63], we consider two nonlinear models, where we use the classical equation relating the wryness tensor to the angular velocity vector, i.e., the equation without the term characterizing the rate of supply of the wryness tensor from an external source. Constructing one of these models, we assume that
Constructing another model, we assume that
In all our previous works, where we compare the equations of the Cosserat continuum with the equations of electrodynamics and thermodynamics, we eliminate the rotation tensor and obtain the system of the basic equations that includes the angular momentum balance equation, the equation relating the wryness tensor to the angular velocity vector, and the constitutive equations. When we impose the restriction on the true moment stress tensor, see Eq. (50), we use vector \({\textbf{M}}\), tensor \(\varvec{\varTheta }\), vector \(\varvec{\omega }\) and vector \(\varvec{{\mathcal {K}}} = \rho J \varvec{\omega }\) as the main variables, and we match these quantities to electrodynamic ones. When we impose the restriction on the energy moment stress tensor, see Eq. (49), we use vector \({\textbf{M}}_e\), tensor \(\varvec{\varTheta }_e\), vector \(\varvec{\varOmega } = {\textbf{P}}^T \cdot \varvec{\omega }\) and vector \(\varvec{{\mathcal {K}}}_e = \rho J \varvec{\varOmega }\) as the main variables, and we match these quantities to electrodynamic ones. In [60, 63], we could not give preference to one of the models since we arrived at the same results when using each of them. In [64], where we firstly added the rate of supply of the wryness tensor from an external source to the wryness tensor balance equation, we considered the linear approximation. In the linear case, the true moment stress tensor coincides with the energy moment stress tensor, so we do not face the problem of choosing between the two models.
Now, the question arises: can we generalize the nonlinear models proposed and developed in [60, 63] to the case of the modified definition of the wryness tensor, given by Eq. (44)? In fact, the question is whether we can eliminate the rotation tensor from the system of basic equations, so that the result would be a closed system of equations in variables \({\textbf{M}}\), \(\varvec{\varTheta }\), \(\varvec{\omega }\), \(\varvec{{\mathcal {K}}}\) in the case of restriction (50) or in variables \({\textbf{M}}_e\), \(\varvec{\varTheta }_e\), \(\varvec{\varOmega }\), \(\varvec{{\mathcal {K}}}_e\) in the case of restriction (49). The problem is as follows. If we add the source term to the wryness tensor balance equation, we can no longer use the relation \(\nabla {\textbf{P}} = \varvec{\varTheta } \times {\textbf{P}}\). At the same time, if we rewrite the angular momentum balance equation in terms of variables \({\textbf{M}}_e\), \(\varvec{\varTheta }_e\), \(\varvec{\varOmega }\), \(\varvec{{\mathcal {K}}}_e\), we can eliminate the rotation tensor from this equation only if we use the relation \(\nabla {\textbf{P}} = \varvec{\varTheta } \times {\textbf{P}}\). This fact is shown in “Appendix D.” Thus, in the case of the nonlinear model with the source term in the wryness tensor balance equation, we cannot eliminate the rotation tensor from the system of the basic equations if we impose restrictions on the energy moment stress tensor. That is why, below we consider only the model based on restrictions imposed on the true moment stress tensor.
4.3 Assumptions regarding the constitutive equations
Now, we are going to make a few additional assumptions regarding the Cosserat continuum without translational degrees of freedom, which is presented in the previous section. These assumptions allow us to obtain an original model based on the Cosserat continuum. Below, in Sect. 5, we give a physical interpretation of the proposed model by introducing thermodynamic and electrodynamic analogues of mechanical quantities.
Hypothesis 1 The moment stress tensor \({\textbf{T}}\) has the following structure:
where the scalar quantity T characterizes the spherical part of tensor \({\textbf{T}}\) and the vector quantity \({\textbf{M}}\) characterizes the antisymmetric part of tensor \({\textbf{T}}\).
Hypothesis 2 The source term in the balance equation for the wryness tensor \(\varvec{\varTheta }\) has the following structure:
where the scalar quantity \(\varUpsilon _\varTheta \) characterizes the spherical part of tensor \(\varvec{\varUpsilon }_\varTheta \) and the vector quantity \(\varvec{\varUpsilon }_\varPsi \) characterizes the antisymmetric part of tensor \(\varvec{\varUpsilon }_\varTheta \).
In fact, we choose the structure of the source term in the wryness tensor balance equation (44) by the analogy with the structure of the moment stress tensor.
Hypothesis 3 The spherical part of the source term \(\varvec{\varUpsilon }_\varTheta \) is related to its antisymmetric part as
This equation has the same physical meaning as Eq. (45).
Hypothesis 4 The specific internal energy has the following form:
where \(U_*\), \(T_*\) and \(\varTheta _*\) are the reference values of U, T and \(\varTheta \), respectively, constants \(C_\varTheta \) and \(C_\varPsi \) are the stiffness parameters.
In view of Eq. (54), we obtain the following constitutive equations:
Derivation of these constitutive equations can be found in “Appendix E.”
Hypothesis 5 Vector \(\varvec{\varUpsilon }_\varPsi \) characterizing the antisymmetric part of the source term \(\varvec{\varUpsilon }_\varTheta \) is proportional to vector \({\textbf{M}}\) characterizing the antisymmetric part of the moment stress tensor:
where parameter \(\kappa \) is assumed to be constant.
Constitutive equation (56) was firstly used in [64]. In the cited paper, it is shown that, adopting constitutive equation (56), we arrive at the model that is in some sense similar to Maxwell’s model of a viscoelastic continuum based on rotational degrees of freedom, which was used in [62]. We also refer to [89], where different approaches to construction of mathematical models of viscoelastic materials are discussed.
Hypothesis 6 The external moment \(\rho {\textbf{L}}\) is the moment of linear viscous damping proportional to the proper angular momentum:
Here \(\varvec{{\mathcal {K}}}\) is the proper angular momentum per unit volume, \(\beta \) is the coefficient of damping. Coefficient \(\beta \) is assumed to be constant.
The external moment \(\rho {\textbf{L}}\) given by Eq. (57) models the dissipation of energy of the continuum. This dissipation is caused by the interaction of the considered continuum with some other continuum, which is ignored in the proposed model. The structure of moment \(\rho {\textbf{L}}\) is chosen in accordance with the results obtained by solving two model problems, see [50, 51].
4.4 The system of the basic equations
Here, we present the system of the basic equations that we are going to discuss in the next sections. The angular momentum balance equation rewritten in terms of the proper angular momentum \(\varvec{{\mathcal {K}}}\) and quantities T, \({\textbf{M}}\) determining the moment stress tensor, takes the form
In virtue of Eq. (52), the balance equation for the wryness tensor is written as
The constitutive equations are
The expression for the spherical part of the source term, which follows from Eq. (53), has the form
Thus, we have the closed system of equations describing the physically linear, but geometrically nonlinear theory of the Cosserat continuum of a special type.
4.5 Consequences of the wryness tensor balance equations
Now, we consider some consequences of Eq. (59) relating the wryness tensor to the angular velocity vector. Taking the trace of Eq. (59) yields
Taking into account Eq. (62), we can transform Eq. (59) to the form
The transformation can be found in “Appendix F.” We note that Eq. (63) is equivalent to Eq. (59). Indeed, if we know tensor \(\varvec{\varTheta }\), we can find tensor \(\varvec{\varTheta } - \textrm{tr}\,{\varvec{\varTheta }}\, {\textbf{E}}\), and vice versa. Taking the vector invariant of Eq. (59) gives
We will discuss the physical meaning of Eqs. (62), (63), (64) and all other equations given in this section after introducing thermodynamic and electrodynamic analogues of mechanical quantities.
Now, we turn to less obvious consequences of Eq. (59). First of all, performing some transformations of Eq. (59), see “Appendix F,” we obtain
Taking the trace of Eq. (65) gives
Taking the vector invariant of Eq. (65) yields
We note that the left-hand side of Eq. (66) contains the second scalar invariant of tensor \(\varvec{\varTheta }\). The left-hand side of Eq. (67) contains vector quantity \(\varvec{\varTheta } \cdot \varvec{\varTheta }_\times \), which is also invariant of tensor \(\varvec{\varTheta }\). By an invariant of the second-rank tensor, we mean a scalar or vector quantity, which does not depend on the choice of basis. Further, we use term “the first vector invariant” of tensor \(\varvec{\varTheta }\) for vector \(\varvec{\varTheta }_\times \) and term “the second vector invariant” of tensor \(\varvec{\varTheta }\) for vector \(\varvec{\varTheta } \cdot \varvec{\varTheta }_\times \). Although these terms are not generally accepted, we believe that they are quite relevant, as they reflect the essence of these quantities.
Next, performing some additional transformations of Eq. (59) and taking into account Eq. (65), see “Appendix F,” we arrive at
Taking the trace of Eq. (68), we obtain
Adding up Eq. (66) and Eq. (69) yields
Taking the vector invariant of Eq. (68), we get
Adding up Eqs. (67) and (71) gives
All the above equations are used in order to give a physical interpretation of the mechanical model proposed in the present paper.
5 A physical interpretation of the proposed theory
5.1 Mechanical analogues of thermodynamic and electromagnetic quantities
Following [49,50,51,52], we interpret quantity T, characterizing the spherical part of the moment stress tensor, as a mechanical analogue of absolute temperature \(T_a\) and trace of the wryness tensor as a mechanical analogue of entropy per unit volume \(\varTheta _a\). Thus, we have
where a is the normalization factor. In the literature on classical thermodynamics and continuum mechanics, specific entropy is often used. If we deal with the ponderable matter, entropy per unit volume \(\varTheta _a\) and specific entropy \(\vartheta _a\) are related to each other as \(\varTheta _a = \varrho \vartheta _a\), where \(\varrho \) is the mass density of the ponderable matter, not the mass density of the ether. In the present paper, we ignore translational degrees of freedom associated with the ether and we ignore all mechanical processes associated with the ponderable matter. This means that both the mass density of the ether \(\rho \) and the mass density of the ponderable matter \(\varrho \) are considered to be constant. That is why, without loss of generality, we can write all known thermodynamic formulas using the entropy per unit volume instead of the specific entropy.
Following [56, 57, 60], we introduce the analogues of electromagnetic quantities as follows: the moment stress vector \({\textbf{M}}\) is the analogue of the electric field vector \(\varvec{{\mathscr {E}}}\); the volume density of proper angular momentum \(\varvec{{\mathcal {K}}}\) is the analogue of the magnetic induction vector \(\varvec{{\mathscr {B}}}\); the vector invariant of the wryness tensor \(\varvec{\varTheta }_\times \) is the analogue of the electric induction vector \(\varvec{{\mathscr {D}}}\); the angular velocity vector \(\varvec{\omega }\) is the analogue of the magnetic field vector \(\varvec{{\mathscr {H}}}\). Thus, we have the relations
where \(\chi \) is the normalization factor. In addition, following [62, 64], we introduce some additional analogues. We consider vector \(\varvec{\varUpsilon }_\varPsi \), characterizing the antisymmetric part of the source term in the wryness tensor balance equation, as the analogue of the conducting current density vector \(\varvec{{\mathscr {J}}}_c\); the external moment per unit volume \(\rho {\textbf{L}}\) as the analogue of the conducting voltage density vector \(\varvec{{\mathscr {V}}}_c\); the angular velocity vector \(\varvec{\omega }\) as the analogue of the entropy flux vector \({\textbf{h}}_\varTheta \); and scalar \(\varUpsilon _\varTheta \), characterizing the spherical part of the source term in the wryness tensor balance equation, as the analogue of the entropy production per unit volume per unit time \(q_\varTheta \). Thus, we have
The physical meaning of the quantities in the first, third and fourth equations in (75) is clear. The appearance of vector \(\varvec{\omega }\) simultaneously in the third equation in (75) and in the fourth equation in (74) needs to be explained. It will be done in Sect. 5.3. The treatment of the source term \(\varUpsilon _\varTheta \) as the entropy production requires \(\varUpsilon _\varTheta \) to be non-negative. This condition is satisfied due to the hypotheses given by Eqs. (53), (56). Now, we focus our attention on the conducting voltage density vector \(\varvec{{\mathscr {V}}}_c\). This is a quantity specific for electrodynamics developed on the basis of our mechanical model. In the proposed version of electrodynamics, vector \(\varvec{{\mathscr {V}}}_c\) is presented in the modified Maxwell–Faraday equation (Maxwell’s second equation). Vector \(\varvec{{\mathscr {V}}}_c\) plays the same role in this equation as vector \(\varvec{{\mathscr {J}}}_c\) plays in Maxwell’s first equation. The simplest constitutive equation for the conducting voltage density vector \(\varvec{{\mathscr {V}}}_c\) is similar to Ohm’s law for the conducting current density vector \(\varvec{{\mathscr {J}}}_c\). The only difference is that vector \(\varvec{{\mathscr {V}}}_c\) is proportional to the magnetic field vector \(\varvec{{\mathscr {H}}}\), whereas vector \(\varvec{{\mathscr {J}}}_c\) is proportional to the electric field vector \(\varvec{{\mathscr {E}}}\). Due to the presence of vector \(\varvec{{\mathscr {V}}}_c\) in the modified Maxwell–Faraday equation, the linearized equations of out electrodynamics are three-dimensional analogues of Kirchhoff’s laws for electrical circuits. In addition, due to the presence of vector \(\varvec{{\mathscr {V}}}_c\) the linearized equations of our electrodynamics can be reduced to the three-dimensional analogue of the telegraph equation, which is usually used to describe the electromagnetic processes in transmission lines. All the equations mentioned above can be found in Sect. 5.3. A more detailed explanation of the physical meaning of vector \(\varvec{{\mathscr {V}}}_c\) can be found in [62, 64].
Now, following [60, 63], we introduce the analogue of the electric charge density \({\mathscr {Q}}\), the analogue of the positive electric charge density \({\mathscr {Q}}^+\) and the analogue of the negative electric charge density \({\mathscr {Q}}^-\) as
where index s denotes the symmetric part of a tensor. Next, following [63], we introduce four physical concepts, which are absent in classical electrodynamics, but play an important role in the proposed theory.
-
\(\varvec{{\mathscr {Q}}}_m\) is the magnetic charge density vector. It is introduced by the analogy with the electric charge density. Just like the electric charge density, the magnetic charge density vector satisfies the conservation law and the Gauss law.
-
\(\varvec{{\mathscr {D}}}_m\) is the entropy and electromagnetic induction tensor. It is introduced by the analogy with the electric induction vector. Just like the electric induction vector is presented in the Gauss law for the electric charge density, the entropy and electromagnetic induction tensor is presented in the Gauss law for the magnetic charge density vector.
-
\(\varvec{{\mathscr {J}}}_m\) is the electromagnetic current density tensor. It is introduced by the analogy with the electric current density vector. Just like the electric current density vector is presented in the conservation law for the electric charge density, the electromagnetic current density tensor is presented in the conservation law for the magnetic charge density vector.
-
\(\varvec{{\mathscr {H}}}_m\) is the magnetic flux tensor. It is the third-rank tensor, which can be represented by means if the magnetic field vector and the unit tensor. The physical meaning of the magnetic flux tensor will be discussed below.
In [63], we define the aforementioned quantities \(\varvec{{\mathscr {Q}}}_m\), \(\varvec{{\mathscr {D}}}_m\), \(\varvec{{\mathscr {J}}}_m\) and \(\varvec{{\mathscr {H}}}_m\) as
In addition, following [60, 63], we introduce the analogue of the internal current density vector \(\varvec{{\mathscr {J}}}_I\) and the analogue of the internal voltage density vector \(\varvec{{\mathscr {V}}}_I\) as
As will be shown in Sect. 5.4, vectors \(\varvec{{\mathscr {J}}}_I\) and \(\varvec{{\mathscr {V}}}_I\) play the same role in Maxwell’s first and second equations as vectors \(\varvec{{\mathscr {J}}}_c\) and \(\varvec{{\mathscr {V}}}_c\), respectively, and in this sense \(\varvec{{\mathscr {J}}}_I\) is the current density vector and \(\varvec{{\mathscr {V}}}_I\) is the voltage current density vector. However, it is important not to confuse the internal current density vector \(\varvec{\mathscr {J}}_I\) with the conducting current density vector \(\varvec{{\mathscr {J}}}_c\) and also the internal voltage density vector \(\varvec{{\mathscr {V}}}_I\) with the conducting voltage density vector \(\varvec{{\mathscr {V}}}_c\), because these vectors are defined by different formulas and have different physical meaning. In contrast to vectors \(\varvec{{\mathscr {J}}}_c\) and \(\varvec{{\mathscr {V}}}_c\), vectors \(\varvec{{\mathscr {J}}}_I\) and \(\varvec{{\mathscr {V}}}_I\) are not specified by constitutive equations containing material constants. As seen from Eqs. (73), (74), (77), (78), vectors \(\varvec{{\mathscr {J}}}_I\) and \(\varvec{{\mathscr {V}}}_I\) are nonlinear characteristics of electromagnetic field, which are completely determined by the entropy and electromagnetic induction tensor \(\varvec{{\mathscr {D}}}_m\) and a number of well-known electrodynamic and thermodynamic quantities:
We emphasize that vector \(\varvec{{\mathscr {J}}}_I\) is proportional to the magnetic field vector \(\varvec{{\mathscr {H}}}\), whereas vector \(\varvec{{\mathscr {J}}}_c\) is proportional to the electric field vector \(\varvec{{\mathscr {E}}}\). Similarly, vector \(\varvec{{\mathscr {V}}}_I\) is proportional to the electric field vector \(\varvec{{\mathscr {E}}}\), whereas vector \(\varvec{{\mathscr {V}}}_c\) is proportional to the magnetic field vector \(\varvec{{\mathscr {H}}}\). The fact that vector \(\varvec{{\mathscr {J}}}_I\) is proportional to the magnetic field vector \(\varvec{{\mathscr {H}}}\) gives us reason to suppose that the internal current density vector \(\varvec{{\mathscr {J}}}_I\) is in some sense related to the so-called Ampère molecular currents, i.e., the currents that take place inside atoms and are responsible for magnetic effects at the macro level. In this case, it seems logical to associate the internal voltage density vector \(\varvec{{\mathscr {V}}}_I\) with molecular voltages that characterize the electric states of atoms, in which the molecular currents take place. However, it should be noted that classical Maxwell’s equations do not contain terms responsible for permanent magnets, do not contain the Ampère molecular currents, and do not contain vectors \(\varvec{{\mathscr {J}}}_I\) and \(\varvec{{\mathscr {V}}}_I\). Therefore, when discussing the internal currents inherent our model, we can assume these currents are something similar to the Ampère molecular currents, but we cannot say with certainty that these currents are exactly the Ampère molecular currents. The distinction between vector \(\varvec{{\mathscr {J}}}_c\) and vector \(\varvec{{\mathscr {J}}}_I\) and also the distinction between vector \(\varvec{{\mathscr {V}}}_c\) and vector \(\varvec{{\mathscr {V}}}_I\) are discussed in more detail in Sect. 5.5, where we focus our attention on the role played by these vectors in differential equations of the proposed theory.
We are deeply convinced that quantities \(\varvec{{\mathscr {Q}}}_m\), \(\varvec{{\mathscr {D}}}_m\), \(\varvec{{\mathscr {J}}}_m\), \(\varvec{{\mathscr {H}}}_m\), which are absent in classical electrodynamics, are the real physical quantities, and differential equations relating these quantities to each other (see Sect. 5.4) describe real physical processes and phenomena. In our opinion, the magnetic charge density vector \(\varvec{{\mathscr {Q}}}_m\) characterizes a property inherent in some elementary particles and a state of microscopic permanent magnets, just as the electric charge density \({\mathscr {Q}}\) characterizes a property inherent in the charged elementary particles and a state of the charged microscopic bodies. We believe that the influence of the magnetic charge density vector \(\varvec{{\mathscr {Q}}}_m\) on the magnetization is performed by means of the entropy and electromagnetic induction tensor \(\varvec{{\mathscr {D}}}_m\). In [63], we discuss in detail our guesses about how exactly this influence might occur. In addition, we note that the magnetic charge density vector \(\varvec{{\mathscr {Q}}}_m\) has nothing to do with magnetic monopoles, which are discussed in various literary sources. We are convinced that magnetic charges should be described by vector quantities, not by scalars. This is what fundamentally distinguishes our approach to describing magnetic phenomena from the known approaches.
In order to explain the name of tensor \(\varvec{{\mathscr {D}}}_m\) and its physical meaning, we give two algebraic relations following from Eqs. (73), (74), (77):
In accordance with Eq. (80), tensor \(\varvec{{\mathscr {D}}}_m\) includes the entropy per unit volume \(\varTheta _a\) and the electric induction vector \(\varvec{{\mathscr {D}}}\). Let us represent tensor \(\varvec{{\mathscr {D}}}_m\) in the form
where \(\varvec{{\mathscr {D}}}_m^s\) is the symmetric part of tensor \(\varvec{{\mathscr {D}}}_m\). Equation (81) makes it obvious that, besides the entropy per unit volume \(\varTheta _a\) and the electric induction vector \(\varvec{\mathscr {D}}\), tensor \(\varvec{{\mathscr {D}}}_m\) also includes some additional characteristics of electromagnetic field and/or thermal field, which are contained in the deviator of its symmetric part. As seen from Eq. (79), these additional characteristics influence on vectors \(\varvec{{\mathscr {J}}}_I\) and \(\varvec{{\mathscr {V}}}_I\), which play an important role in electrodynamic processes. As it will be shown in Sect. 5.4, tensor \(\varvec{{\mathscr {D}}}_m\) is related to the magnetic charge density vector \(\varvec{\mathscr {Q}}_m\) by a differential equation having the form of the Gauss law. In other words, tensor \(\varvec{{\mathscr {D}}}_m\) and vector \(\varvec{{\mathscr {Q}}}_m\) are related to each other by the equation similar to that relates the electric induction vector \(\varvec{{\mathscr {D}}}\) and the electric charge density \({\mathscr {Q}}\).
In order to explain the physical meaning of tensors \(\varvec{{\mathscr {J}}}_m\) and \(\varvec{{\mathscr {H}}}_m\), we give several algebraic relations, which follow from Eqs. (73), (74), (77):
As seen from Eq. (82), the electromagnetic current density tensor \(\varvec{{\mathscr {J}}}_m\), as well as the internal current density vector \(\varvec{\mathscr {J}}_I\), is proportional to the magnetic field vector \(\varvec{{\mathscr {H}}}\), and the antisymmetric part of tensor \(\varvec{{\mathscr {J}}}_m\) is completely determined by vector \(\varvec{{\mathscr {J}}}_I\). Therefore, we can consider tensor \(\varvec{{\mathscr {J}}}_m\) as a generalization of vector \(\varvec{{\mathscr {J}}}_I\). As it will be shown in Sect. 5.4, the magnetic charge density vector \(\varvec{{\mathscr {Q}}}_m\) satisfies the conservation law, where tensor \(\varvec{{\mathscr {J}}}_m\) plays the role of the current density tensor. As seen from the last equation in (82), the third-rank tensor \(\varvec{{\mathscr {H}}}_m\) is completely determined by the magnetic field vector \(\varvec{{\mathscr {H}}}\). This tensor is introduced in order to formulate a generalized Maxwell’s first equation, which relates to each other tensors \(\varvec{{\mathscr {H}}}\), \(\varvec{{\mathscr {J}}}_m\) and \(\varvec{{\mathscr {D}}}_m\), see Sect. 5.4.
Finally, we introduce three more physical quantities that take our theory beyond the thermo-electrodynamics. They are a generalized charge density tensor \(\varvec{{\mathscr {Q}}}_g\), a generalized induction tensor \(\varvec{{\mathscr {D}}}_g\), and a generalized current density tensor \(\varvec{{\mathscr {J}}}_g\). In the framework of our mechanical model, we define these quantities as
In order to clarify the physical meaning of the introduced quantities, we pay attention to relations between the charge densities
relations between the inductions
and relations between the current densities
Thus, tensor \(\varvec{{\mathscr {Q}}}_g\) can be treated as the generalized charge density tensor because it contains the electric charge density and the magnetic charge density vector; tensor \(\varvec{{\mathscr {D}}}_g\) can be treated as the generalized induction tensor because it contains the electric induction vector and the electromagnetic induction tensor; tensor \(\varvec{{\mathscr {J}}}_g\) can be treated as the generalized current density tensor because it contains the internal current density vector and the electromagnetic current density tensor. Differential equations relating quantities \(\varvec{\mathscr {Q}}_g\), \(\varvec{{\mathscr {D}}}_g\), \(\varvec{{\mathscr {J}}}_g\) will be discussed in Sects. 5.6 and 5.4. In Sect. 5.4, we also discuss a quantum mechanical interpretation of tensors \(\varvec{\mathscr {Q}}_g\), \(\varvec{{\mathscr {D}}}_g\), \(\varvec{{\mathscr {J}}}_g\).
In this section, we have introduced a lot of quantities related to the wryness tensor. These quantities are not independent. Some of the algebraic equations relating these quantities to each other are given above, all other equations can be found in “Appendix G.” In the main text of the paper, we mention the relations, the physical meaning of which is quite clear. These are, e.g., the relation between the electric charge density and the generalized charge density tensor, the relation between the magnetic charge density vector and the generalized charge density tensor, the relation between the entropy and the entropy per unit volume and the entropy electromagnetic induction tensor, the relation between the electric induction vector and the entropy and electromagnetic induction tensor. At the same time, there are a number of relations the physical meaning of which remains vague. We believe that in the future these relations may be useful for explaining certain physical phenomena. That is why, we present such relations in “Appendix G.”
5.2 The basic equations in terms of physical quantities
Now, we rewrite the basic equations presented in Sect. 4.4 in terms in physical quantities using the analogues suggested in Sect. 5.1.
In virtue of Eqs. (73), (74), (75), (78), (77), the angular momentum balance equation (58) can be rewritten as
where the internal voltage density vector \(\varvec{\mathscr {V}}_I\) has the form
As mentioned above, the wryness tensor balance equation (59) can be replaced by the equivalent equation (63). In view of Eqs. (74), (75), (77), the wryness tensor balance equation (63) takes the form
where the magnetic flux tensor \(\varvec{{\mathscr {H}}}_m\) and the electromagnetic current density tensor \(\varvec{{\mathscr {J}}}_m\) can be represented as
In view of Eqs. (73), (74), (75), the constitutive equations (60) take the form
and Eq. (61) can be rewritten as
Although Eqs. (87), (88), (89), (90), (91), (92) contain electrodynamic and thermodynamic quantities, these equations are not very similar to the equations of electrodynamics and thermodynamics. Therefore, we start by considering two special cases. The first one is the linear thermo-electrodynamics of conductive media. The second one is a nonlinear thermo-electrodynamics of non-conductive media. Under certain simplifying assumptions, both theories can be reduced to the well-known equations of thermodynamics and electrodynamics. After discussing the special cases, we will return to the system of equations (87), (88), (89), (90), (91), (92) and discuss a number of its consequences, which clarify the physical meaning of the basic equations.
5.3 The linear theory describing thermal and electromagnetic processes in conductive media
In this section, we show that the basic equations of the linear theory describing thermal and electromagnetic processes in conductive media can be obtained by linearizing the equations presented in the previous section. We also show that all other equations of the linear theory can be obtained in view of the analogues given in Sect. 5.1 as mathematical consequences of the basic equations.
We start with Eq. (89). In the linear approximation this equation is written as
Let us divide Eq. (93) into three parts: the antisymmetric part, the deviator of the symmetric part and the spherical part. The antisymmetric part of Eq. (93) is determined by the vector invariant of this equation. In view of the second equation in (88) and the first equation in (90), it takes the form
Equation (94) coincides with Maxwell’s first equation
if the electric current density vector \(\varvec{{\mathscr {J}}}\) is assumed to be the conducting current density vector \(\varvec{{\mathscr {J}}}_c\).
In view of Eq. (90), the deviator of the symmetric part of Eq. (93) can be written as
Equation (96) allows us to find \(\textrm{dev}\,\varvec{{\mathscr {D}}}_m\) if we know magnetic field vector \(\varvec{{\mathscr {H}}}\).
The spherical part of Eq. (93) is characterized by the trace of this equation. Taking into account Eqs. (73), (75), (77), we can transform the trace of Eq. (93) to the form
Equation (97) is the entropy balance equation. This equation is well known and can be found in the literature on non-equilibrium thermodynamics and continuum mechanics. We emphasize that we obtain Eq. (97) using the analogue for the angular velocity vector \(\varvec{\omega }\) given by the third equation in (75), and we obtain Eq. (94) using the analogue for the angular velocity vector \(\varvec{\omega }\) given by the last equation in (74). Comparing the third equation in (75) and the last equation in (74) we see that
At first glance, Eq. (98) seems strange. However, the entropy balance equation contains only the potential part of the entropy flux vector \({\textbf{h}}_\varTheta \), whereas Maxwell’s first equation contains only the vortex part of the magnetic field vector \(\varvec{{\mathscr {H}}}\). Therefore, there is no contradiction in Eq. (98).
Now, we turn to Eq. (87). In the linear approximation, this equation takes the form
If we suppose that \(T_a = \textrm{const}\) or the term containing \(\nabla T_a\) can be ignored for some other reason, we can reduce Eq. (99) to the form
Comparing Eq. (100) with the Maxwell–Faraday equation (Maxwell’s second equation)
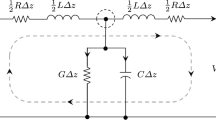
we see that Eq. (100) contains two terms that constitute the Maxwell–Faraday equation, and also the conducting voltage density vector \(\varvec{{\mathscr {V}}}_c\). The presence of the terms constituting the Maxwell–Faraday equation allows us to treat Eq. (100) as the generalized Maxwell–Faraday equation. We note that the conducting voltage density vector \(\varvec{{\mathscr {V}}}_c\) plays the same role in the generalized Maxwell–Faraday equation (100) as the conducting current density vector \(\varvec{{\mathscr {J}}}_c\) plays in Maxwell’s first equation (94). Below, we show that due to the presence of vector \(\varvec{{\mathscr {V}}}_c\) in Eq. (100), the system of equations (94), (100) can be considered as a three-dimensional analogue of Kirchhoff’s laws for electrical circuits.
Let us return to Eq. (99). On the one hand, we can consider this equation as the generalized Maxwell–Faraday equation that takes into account thermal effects. On the other hand, in view of Eq. (98) and also the third and the last equations in (91), we can rewrite Eq. (99) in terms of the entropy flux vector \({\textbf{h}}_\varTheta \) as
In virtue of the relation between the entropy flux vector \({\textbf{h}}_\varTheta \) and the heat flux vector \({\textbf{h}}\), which has the form \({\textbf{h}} = T_a {\textbf{h}}_\varTheta \) when the linear approximation is considered, Eq. (102) can be rewritten as
If we neglect the last term on the right-hand side of Eq. (103), this equation takes the form of the Maxwell–Cattaneo–Vernotte law relating the heat flux vector to the temperature gradient
where \(\tau _h\) is the heat flux relaxation constant, \(\lambda \) is the thermal conductivity.
In order to determine the parameters of our model we should compare the constitutive equations obtained in the framework of our model with the well-known constitutive equations. We start with the comparison of the first three equations in (91) with the constitutive equations
where \(\varrho \) is the density of mass of a material, \(c_v\) is the specific heat at constant volume; \(\varepsilon _0\) and \(\mu _0\) are the permittivity and the permeability of vacuum; \(\varepsilon \) and \(\mu \) are the relative permittivity and the relative permeability of a material. As a result, we have the following expressions for the parameters characterizing the elastic and inertia properties of the mechanical model:
Comparing the coefficients in Eqs. (103) and (104), we infer that
We note that from Eq. (107) it follows that
On the one hand, Eq. (108) gives the temperature dependence of the heat flux relaxation constant. On the other hand, this equation allows us to find the fundamental constant \(\chi ^2/a^2\) if we have reliable experimental data on the values of the heat flux relaxation constant in a wide temperature range. Unfortunately, no such data is currently available.
Next, we take into account Ohm’s law
where \(\sigma \) is the electrical conductivity, and the Wiedemann–Franz law
where L is the Lorenz number, which is a fundamental constant, i.e., the constant which cannot depend on any parameters of a material. Following [64], we introduce two different electrical conductivities, \(\sigma _d\) and \(\sigma _c\), such that \(\sigma _d\) is the coefficient in Ohm’s law and \(\sigma _c\) is presented in the Wiedemann–Franz law. Thus, instead of Eqs. (109), (110), we have
Comparing the fourth equation in (91) with the first equation in (111) and eliminating \(\lambda \) from the second equation in (107) by means of the second equation in (111), we obtain the following expressions for the parameters characterizing the viscous properties of the mechanical model:
In view of Eqs. (106), (112), the last two constitutive equations in (91) take the form
Let us compare the constitutive equations (113) with each other. The first equations relates the conducting current density vector \(\varvec{\mathscr {J}}_c\) to the electric field vector \(\varvec{{\mathscr {E}}}\) and contains the electrical conductivity \(\sigma _d\); the second one relates the conducting voltage density vector \(\varvec{\mathscr {V}}_c\) to the magnetic field vector \(\varvec{{\mathscr {H}}}\) and contains the electrical conductivity \(\sigma _c\). These equations are, in fact, Ohm’s law for the electric current density and the analogue of Ohm’s law for the electric voltage density, respectively. In order to clarify the physical meaning of parameters \(\sigma _d\) and \(\sigma _c\), we rewrite Eqs. (94) and (100) taking into account the constitutive equations (113). As a result, we have
We draw attention to that equations (114) have the same structure as Kirchhoff’s laws for electrical circuits
where z is the spatial coordinate, I is the electric current, V is the electric voltage, \({\mathcal {L}}\) is the inductance, \({\mathcal {C}}\) is the capacitance, \({\mathcal {G}}\) is the shunt conductance, \({\mathcal {R}}\) is the series resistance. If we suppose that the magnetic field vector \(\varvec{{\mathscr {H}}}\) matches the electric current I and the electric field vector \(\varvec{{\mathscr {E}}}\) matches the electric voltage V, then we can infer that
We emphasize that it is precisely due to the presence of vector \(\varvec{{\mathscr {V}}}_c\) in the generalized Maxwell–Faraday equation (100), our theory turns out to be in agreement with Kirchhoff’s laws for electrical circuits.
If we eliminate I from system (115), we arrive at the telegraph equation
Equation (117) is well known and widely used to describe the electromagnetic processes in transmission lines.
If we eliminate vector \(\varvec{{\mathscr {H}}}\) from system (114) and ignore the potential part of the electric field vector assuming that \(\nabla \cdot \varvec{{\mathscr {E}}} = 0\), then we obtain
It is evident that Eq. (118) is the three-dimensional analogue of the telegraph equation (117). At the same time, from classical Maxwell’s equations it follows the simpler equation
Both Eqs. (118) and (119) are valid for the vortex part of the electric field vector since they are obtained under the assumption \(\nabla \cdot \varvec{{\mathscr {E}}} = 0\). In order to derive the equation for the potential part of vector \(\varvec{{\mathscr {E}}}\), we should take the divergence of Eq. (114). As a result, we have
It is easy to see that Eq. (120) for \(\nabla \cdot \varvec{{\mathscr {E}}}\) is not the wave equation and it does not contain derivatives with respect to the space coordinates at all. This means that \(\nabla \cdot \varvec{{\mathscr {E}}}\) propagates in space instantly.
Now, we return to Eq. (102) for the entropy flux vector \({\textbf{h}}_\varTheta \). In view of Eqs. (106), (107), this equation takes the form
Taking the divergence of Eq. (121), eliminating \(\nabla \cdot {\textbf{h}}_\varTheta \) from the obtained equation by means of the entropy balance equation (97) and taking into account the first constitutive equation in (105), we arrive at the hyperbolic-type heat conduction equation
Using the approximate form of Eq. (92), namely
we can rewrite Eq. (122) as
Thus, we obtain the hyperbolic-type heat conduction equation with Joule heat \(\varvec{{\mathscr {E}}} \cdot \varvec{\mathscr {J}}_c\). If \(\tau _h \rightarrow 0\), Eq. (124) turns into the classical heat conduction equation with Joule heat.
In addition, we give two equations, which relate the divergence of the magnetic induction vector to thermodynamic quantities. The first one follows from Eqs. (97), (98) and the third equation in (105). It has the form
The second one can be obtained from Eq. (125) in view of the first equation in (105) and Eq. (123). It is written as
As seen from Eq. (126), we can obtain the well-known equation \(\nabla \cdot \varvec{{\mathscr {B}}} = 0\) if we suppose that \({\displaystyle \frac{d T_a}{d t} = \frac{\varvec{{\mathscr {E}}} \cdot \varvec{\mathscr {J}}_c}{\varrho c_v}}\). The physical meaning of this relation is that Joule heat is completely spent on changing the temperature at a given point in space.
Summing up the results of this section, we draw attention to the important features of the proposed linear theory of thermo-electrodynamics. First, the entropy balance equation (97) contains the source term (123) that describes the conversion of electrical energy into thermal energy due to Joule heat. Second, the generalized Maxwell–Faraday equation (100) contains the electric voltage density \(\varvec{{\mathscr {V}}}_c\). Thanks to this, the generalized Maxwell’s equations are in agreement with Kirchhoff’s laws for electrical circuits. Third, the generalized Maxwell–Faraday equation (99) contains the temperature gradient, the constitutive equation for the heat flux vector (103) contains the curl of the electric field vector, and the potential part of the magnetic induction vector is related to the thermodynamic quantities by Eqs. (125), (126). This opens up new possibilities for describing thermoelectric, thermomagnetic, and thermoelectromagnetic effects. A more detailed description of the linear theory of thermo-electrodynamics can be found in [64].
5.4 The nonlinear theory describing electromagnetic and thermal processes in non-conductive media
In this section, we briefly outline the nonlinear theory that can be obtained from the equations presented in Sect. 5.2 by neglecting the dissipative terms, i.e., by assuming that
Under assumptions (127), the last two equations in (91) and Eq. (92) take the form
Thus, in this section, we consider the conservative theory that follows from the general theory under the conditions (128).
We start with the closed system of equations of the theory of thermo-electrodynamics of non-conductive media. This system can be obtained from Eqs. (87), (88), (89), (90), (91), (92) in virtue of Eq. (128). This system includes two balance equations
three constitutive equations
and also five algebraic equations expressing auxiliary variables in terms of the main variables
We note that the nonlinear electrodynamics developed in [63] can be obtained from the system of equations (129), (130), (131) if \(T_a = T_a^*\) and at the same time \(c_v \rightarrow \infty \). We emphasize that all equations given in this section are important because their consideration allows us to substantiate why our theory can be treated as thermo-electrodynamics. At the same time, only Eqs. (129), (130), (131) should be used in order to solve specific problems of thermo-electrodynamics. All other equations are not needed to solve the problems because these equations are not independent and can be obtained from Eqs. (129), (130), (131).
Now, we turn to Eq. (89). In view of Eq. (128), this equation is reduced to the form
We divide the tensor equation (132) into three parts, as done above for the linear theory of conductive media. The antisymmetric part of Eq. (132) is determined by its vector invariant. In view of the second equation in (88) and the first equation in (90), the vector invariant of Eq. (132) takes the form
Equation (133) coincides with Maxwell’s first equation (101) if the electric current density vector \(\varvec{{\mathscr {J}}}\) is assumed to be the internal current density vector \(\varvec{{\mathscr {J}}}_I\). Next, in view of Eq. (90), the deviator of the symmetric part of Eq. (132) is written as
Finally, in order to find the spherical part of Eq. (132), we take the trace of this equation. Taking into account the analogues between physical and mechanical quantities given by Eqs. (73), (74), (75), (77) and the algebraic relations between physical quantities given in “Appendix G,” we can rewrite the obtained equation in terms of thermodynamic quantities as
Equation (135) is the entropy balance equation. It differs from the entropy balance equation (97) obtained in the linear theory of conductive media only by the source term. In the case of conductive media, the source term \(q_\varTheta \) is proportional to Joule heat, see Eq. (92). In the case of the nonlinear theory of non-conductive media, the source term \({\displaystyle \frac{a}{\chi ^2}\,\varvec{{\mathscr {D}}} \cdot \varvec{{\mathscr {H}}}}\) characterizes the entropy production due to nonlinear electromagnetic processes. The entropy flux vector \({\textbf{h}}_\varTheta \) in Eq. (135) is related to the magnetic field vector \(\varvec{{\mathscr {H}}}\) by Eq. (98) as in the linear theory of conductive media.
Next, we turn to Eq. (87). In virtue of assumption (128) this equation takes the form
The structure of Eq. (136) coincides with the structure of Eq. (99) obtained in the linear theory of conductive media. The only difference between these equations consists in that Eq. (136) contains the internal voltage density vector \(\varvec{{\mathscr {V}}}_I\), whereas Eq. (99) contains the conducting voltage density vector \(\varvec{{\mathscr {V}}}_c\). All other terms in Eq. (99) and Eq. (136) are the same. In previous section, we show that Eq. (99) can be treated as the generalized Maxwell–Faraday equation. Therefore, we believe that Eq. (136) can also be treated as the generalized Maxwell–Faraday equation. In addition, we consider the thermodynamic interpretation of Eq. (136). Taking into account Eqs. (98), (105), (107), we rewrite Eq. (136) as
In fact, Eq. (137) is the constitutive equation for the entropy flux vector \({\textbf{h}}_\varTheta \). Comparing Eq. (137) with Eq. (121) obtained in the linear theory of conductive media, we see that these equations differ from each other in that Eq. (121) contains the term proportional to \({\textbf{h}}_\varTheta \) and does not contain the term proportional to \(\varvec{{\mathscr {V}}}_I\), while Eq. (137), on the contrary, contains the term proportional to \(\varvec{{\mathscr {V}}}_I\) and does not contain the term proportional to \({\textbf{h}}_\varTheta \). The absence of the term proportional to \({\textbf{h}}_\varTheta \) in Eq. (137) is due to the fact that the problem is conservative. The presence of the term proportional to \(\varvec{{\mathscr {V}}}_I\) in Eq. (137) is due to the fact that the problem is nonlinear.
Next, we take the divergence of Eq. (137) and eliminate \(\nabla \cdot {\textbf{h}}_\varTheta \) from the obtained equation by means of the entropy balance equation (135). Taking into account the first equation in (105) and Eq. (108), we transform the obtained equation to the form
Equation (138) is an analogue of the heat conduction equation (124) obtained in the linear theory of conductive media. However, Eq. (138) is the wave equation. This is not surprising since we consider the conservative problem. We note that Eq. (138) does not contain Joule heat, but it contains two other terms of electrodynamic nature, which are actually external factors causing thermal processes. In addition, we pay attention to two equations, which relate the divergence of the magnetic induction vector to thermodynamic quantities. The first one follows from Eq. (135) in view of Eq. (98) and the third equation in (105). It has the form
The second equation can be obtained from Eq. (139) in view of the first equation in (105). It is written as
The well-known equation \(\nabla \cdot \varvec{{\mathscr {B}}} = 0\) can be obtained from Eq. (139) under the assumption that \({\displaystyle \frac{d \varTheta _a}{d t} = - \frac{a}{\chi ^2}\,\varvec{{\mathscr {D}}} \cdot \varvec{{\mathscr {H}}}}\). The physical meaning of this relation is that the entropy change at a given point in space is completely determined by nonlinear electromagnetic effects in this point in space. Comparing Eq. (140) with Eq. (126) obtained in the linear theory of conductive media, we see that the only difference is that Eq. (140) contains \(\varvec{{\mathscr {D}}} \cdot \varvec{{\mathscr {H}}}\) instead of Joule heat, which is contained in Eq. (126).
Now, we return Eq. (89) and consider some of its consequences. We recall that Eq. (89) is actually the wryness tensor balance equation. In this section, we are dealing with the special case of our theory where the source terms in the wryness tensor balance equation are ignored. Therefore, we consider the consequences the wryness tensor balance equation given by Eqs. (15), (16), (19), (20). Let us rewrite these equations in terms of physical quantities. In virtue of the analogues (74), (76), (78), (77), we can rewrite Eqs. (15), (16) as
and we can also rewrite Eqs. (19), (20) as
It is easy to see that the first equation in (141) is the Gauss law for electric field, and the first equation in (142) is the electric charge conservation law. By analogy, we can interpret the second equation in (141) as the Gauss law for electromagnetic field, and second equation in (142) as the magnetic charge conservation law. This is the interpretation adopted in [63]. It is important to note that there are no analogues of Eqs. (141), (142) in the linear theory of conductive media. The reason is that the mechanical analogues of scalar quantity \({\mathscr {Q}}\), vectors \(\varvec{{\mathscr {Q}}}_m\) and \(\varvec{{\mathscr {J}}}_I\), and tensor \(\varvec{{\mathscr {J}}}_m\) are the nonlinear functions of the main mechanical variables \(\varvec{\varTheta }\) and \(\varvec{\omega }\). Due to this circumstance, in the case of the linear theory of non-conductive media, the first equation in (141) is reduced to equation \(\nabla \cdot \varvec{{\mathscr {D}}} = 0\), which means the absence of the electric charge, the second equation in (141) is reduced to equation \(\nabla \cdot \varvec{{\mathscr {D}}}_m^T = 0\), which means the absence of the magnetic charge vector, and both equations in (142) turn into identities of \(0 = 0\) type.
In Sect. 5.1, we have introduced the generalized charge density tensor \(\varvec{{\mathscr {Q}}}_g\), the generalized induction tensor \(\varvec{{\mathscr {D}}}_g\), and the generalized current density tensor \(\varvec{{\mathscr {J}}}_g\), see Eq. (83) relating these quantities to the mechanical quantities. Now, we are going to explain the meaning of these physical quantities by analyzing the structure of the equations that are satisfied by them. In view of Eq. (83), we can rewrite Eqs. (14), (18) as
The first equation in (143) has the same structure as the Gauss law for electric field and the Gauss law for electromagnetic field, see Eq. (141). The second equation in (143) has the same structure as the electric charge conservation law and the magnetic charge conservation law, see Eq. (142). The above gives us reason to interpret \(\varvec{{\mathscr {Q}}}_g\) as the generalized charge density tensor, \(\varvec{{\mathscr {D}}}_g\) as the generalized induction tensor, and \(\varvec{{\mathscr {J}}}_g\) as the generalized current density tensor. Now, we take into account relations between physical quantities. First of all, we draw attention to the algebraic equations for the current densities:
As seen from Eq. (144), all current densities are not independent quantities, but they are expressed as the dot and cross products of the magnetic field vector \(\varvec{{\mathscr {H}}}\) and the induction tensors. To be exact, the transposed electromagnetic current density tensor \(\varvec{{\mathscr {J}}}_m\) is proportional to the generalized induction tensor \(\varvec{{\mathscr {D}}}_g\), in the same way as the internal current density vector \(\varvec{{\mathscr {J}}}_I\) is proportional to the entropy and electromagnetic induction tensor \(\varvec{{\mathscr {D}}}_m\). Thus, the second and third equations in (144) explain the meaning of the generalized induction tensor \(\varvec{{\mathscr {D}}}_g\). Next, we note that the electric charge density \({\mathscr {Q}}\) and the magnetic charge density vector \(\varvec{{\mathscr {Q}}}_m\) are contained in the generalized charge density tensor \(\varvec{{\mathscr {Q}}}_g\):
Here \(\varvec{{\mathscr {Q}}}_g^s\) is the symmetric part of tensor \(\varvec{{\mathscr {Q}}}_g\). The last formula in (145) gives us an additional argument in favor of the treatment of tensor \(\varvec{{\mathscr {Q}}}_g\) as the generalized charge density tensor.
Now, we try to match the quantum mechanical characteristics of particles to the physical quantities introduced in the framework of our model. We note that it is very difficult, if not impossible, to suggest algebraic relations between quantum mechanical quantities and mechanical quantities and then substantiate the validity of the proposed relationships by comparing the obtained differential equations with the known ones, in the same way as it was done in the case of thermo-electrodynamics. This is due to the fact that, on the one hand, mechanics and quantum mechanics use different mathematical tools, and on the other hand, the foundations of these two sciences are conceptually different. Nevertheless, we can make some general assumptions about analogies between quantum mechanical charges and quantities characterizing \(\textrm{dev}\,\varvec{{\mathscr {Q}}}_g^s\). However, it is important to pay attention to the differences between the quantities associated with \(\textrm{dev}\,\varvec{\mathscr {Q}}_g^s\) in our model and the corresponding quantities introduced in quantum mechanics. In our model, \(\textrm{dev}\,\varvec{\mathscr {Q}}_g^s\) and its associated quantities characterize the current state of the continuum and are arbitrary functions of space coordinates and time. On the contrary, quantum mechanical quantities characterize some properties of elementary particles and take on only certain values, which are defined by numbers or words. Within the framework of our model, we can speak of particles, quasi-particles or virtual particles only if some physical quantities characterizing the current state of the continuum are localized in very small regions of space. So, we represent tensor \(\textrm{dev}\,\varvec{{\mathscr {Q}}}_g^s\) as
where \({\textbf{e}}_r\), \({\textbf{e}}_g\), \({\textbf{e}}_b\) are mutually orthogonal unit vectors (eigenvectors of \(\textrm{dev}\,\varvec{{\mathscr {Q}}}_g^s\)), and \({\mathscr {Q}}_r \le {\mathscr {Q}}_g \le {\mathscr {Q}}_b\). We suppose that quantities \({\mathscr {Q}}_r\), \({\mathscr {Q}}_g\), \({\mathscr {Q}}_b\) can be treated as the color charges. Since \(\textrm{tr}\, (\textrm{dev}\,\varvec{{\mathscr {Q}}}_g^s) = 0\), we have
Equation (147) can be interpreted as the fact that the combination of three different color charges gives the colorless charge. It is well known that color charge is a property of quarks and gluons. Due to a phenomenon known as color confinement, quarks and gluons are never found in isolation. Quarks can be found only within composite particles called hadrons; gluons bind quarks in hadrons. Hadrons are the colorless particles. Thus, the interpretation of color charges, given in the framework of our model by Eqs. (146), (147), is qualitatively in agreement with the quantum mechanical interpretation. We emphasize that \({\mathscr {Q}}_r\), \({\mathscr {Q}}_g\), \({\mathscr {Q}}_b\) can be positive or negative. We do not associate the signs of these quantities with the concepts of particle and anti-particle. Within the framework of our model, we can speak of particles and anti-particles, meaning the positive or negative of another scalar invariant of tensor \(\varvec{{\mathscr {Q}}}_g\). This scalar invariant can be, e.g., \(\textrm{Det}\,\varvec{{\mathscr {Q}}}_g\), \(\textrm{Det}\,\varvec{{\mathscr {Q}}}_g^s\), \(\textrm{Det}\,(\textrm{dev}\,\varvec{{\mathscr {Q}}}_g^s)\). We can suggest mechanical interpretation of other quantum characteristics. For example, if we represent the symmetric part of tensor \(\varvec{\mathscr {D}}_m\) as
we can rewrite tensor \(\textrm{dev}\,\varvec{{\mathscr {Q}}}_g^s\) in the form
and interpret six quantities \({\mathscr {Q}}_{ij}\) as six flavors of quarks. We can also use the representation
or the representation
and associate quantities \({\mathscr {Q}}_m^{(r)}\), \({\mathscr {Q}}_m^{(g)}\), \({\mathscr {Q}}_m^{(b)}\) or quantities \({\mathscr {Q}}_m^{(1)}\), \({\mathscr {Q}}_m^{(2)}\), \({\mathscr {Q}}_m^{(3)}\) with some quantum characteristics.
Here we have briefly outlined some ideas regarding the description of quantum mechanical charges from the point of view of rational mechanics. A more detailed discussion of this topic is beyond the scope of this work.
5.5 Maxwell’s equations and thermal processes in the nonlinear theory of conductive media
In this section, we consider some equations that follow from the basic equations of the nonlinear theory of conductive media presented in Sect. 5.2. We compare these equations with the corresponding equations obtained in the framework of the linear theory of conductive media and in the framework of the nonlinear theory of non-conductive media.
Let us take the vector invariant of Eq. (89) and reduce the obtained equation in view of the second equation in (88) and the first equation in (90). As a result, we have
Equation (152) coincides with Maxwell’s first equation (101) if the electric current density vector \(\varvec{{\mathscr {J}}}\) is assumed to be the sum of the conducting current density vector \(\varvec{{\mathscr {J}}}_c\) and the internal current density vector \(\varvec{{\mathscr {J}}}_I\). We note that Maxwell’s first equation in the linear theory of conductive media contains only the conducting current density vector \(\varvec{{\mathscr {J}}}_c\), whereas Maxwell’s first equation in the nonlinear theory of non-conductive media contains only the internal current density vector \(\varvec{{\mathscr {J}}}_I\). Now, we discuss the differences between vector \(\varvec{{\mathscr {J}}}_c\) and vector \(\varvec{{\mathscr {J}}}_I\). We start with the equations
The first equation in (153) is the constitutive equation, which is given in Sect. 5.3, see Eq. (113). In fact, the first equation in (153) is Ohm’s law. That is why, we interpret \(\varvec{{\mathscr {J}}}_c\) as the conducting current density vector. The second equation in (153) is not a constitutive equation because it contains only the fundamental constant \(\chi \) and does not contain any material constants. This equation can be obtained from the second equation in (133) in view of Eq. (90). It is easy to see that \(\varvec{{\mathscr {J}}}_I\) is represented as the algebraic function of the quantities associated with magnetic field, namely the magnetic field vector \(\varvec{{\mathscr {H}}}\) and the entropy and electromagnetic induction tensor \(\varvec{{\mathscr {D}}}_m\), which in turn is related to the magnetic charge vector \(\varvec{{\mathscr {Q}}}_m\), see Eq. (141). That is why, we believe that the internal current density vector \(\varvec{{\mathscr {J}}}_I\) is associated with magnetic processes.
Let us take the trace of Eq. (89) and reduce the obtained equation in virtue of the second equation in (88) and Eqs. (90), (92), (98). As a result, we arrive at the entropy balance equation
The second term on the right-hand side of Eq. (154) has the meaning of the entropy production due to Joule heat \(\varvec{{\mathscr {E}}} \cdot \varvec{{\mathscr {J}}}_c\). We emphasize that Joule heat depends on the conducting current density vector \(\varvec{{\mathscr {J}}}_c\) and does not depend of the internal current density vector \(\varvec{{\mathscr {J}}}_I\). The last term on the right-hand side of Eq. (154) also has the meaning of the entropy production, but it is associated with interplay of electric and magnetic processes. We note that, in the case of the linear theory of conductive media, the source term in the entropy balance equation is completely determined by Joule heat, whereas in the case of the nonlinear theory of non-conductive media, the source term is completely determined by the last term on the right-hand side of Eq. (154). Entropy production due to Joule heat is always positive. The last term on the right-hand side of Eq. (154) can be either positive or negative. As a result, the total entropy production can also be either positive or negative. Negative entropy production means violation of the second law of thermodynamics. The difficulties with the second law of thermodynamics are well known, see, e.g., [90,91,92,93]. In particular, they always arise when the hyperbolic-type heat conduction equation is used [94].
Thus, on the one hand, the trace of Eq. (89) is the entropy balance equation. On the other hand, the vector invariant of Eq. (89) is Maxwell’s first equation, and due to this reason we interpret Eq. (89) as generalized Maxwell’s first equation. However, in fact, Eq. (89) describes both electromagnetic and thermal processes. Equation (89) contains two physical quantities, tensor \(\varvec{{\mathscr {D}}}_m\) and tensor \(\varvec{{\mathscr {J}}}_m\), that were first introduced in our models. We try to explain the names of these quantities. The trace of tensor \(\varvec{{\mathscr {D}}}_m\) is proportional to the entropy per unit volume \(\varTheta _a\), the vector invariant of tensor \(\varvec{{\mathscr {D}}}_m\) equals to the electric induction vector \(\varvec{{\mathscr {D}}}\), and the potential part of tensor \(\varvec{{\mathscr {D}}}_m^T\) is associated with the magnetic charge density vector \(\varvec{{\mathscr {Q}}}_m\). That is why, we call tensor \(\varvec{{\mathscr {D}}}_m\) the entropy and electromagnetic induction tensor. The vector invariant of tensor \(\varvec{{\mathscr {J}}}_m\) equals to the internal current density vector \(\varvec{{\mathscr {J}}}_I\), tensor \(\varvec{{\mathscr {J}}}_m\) is proportional to the magnetic field vector \(\varvec{{\mathscr {H}}}\), and the potential part of tensor \(\varvec{{\mathscr {J}}}_m^T\) is associated with the magnetic charge conservation law. That is why, we call tensor \(\varvec{{\mathscr {J}}}_m\) the electromagnetic current density tensor.
Now, we consider Eq. (87). If we ignore thermal effects, this equation takes the form
where vector \(\varvec{{\mathscr {V}}}_c\) and vector \(\varvec{{\mathscr {V}}}_I\) are determined as
Equation (155) is the generalized Maxwell–Faraday equation. This equation differs from the classical Maxwell–Faraday equation by the presence of vectors \(\varvec{{\mathscr {V}}}_c\) and \(\varvec{{\mathscr {V}}}_I\). It is easy to see that Eq. (155) has the exactly same structure as Maxwell’s first equation (152), and vector \(\varvec{{\mathscr {V}}}_c + \varvec{{\mathscr {V}}}_I\) plays the same role in Eq. (155) as vector \(\varvec{{\mathscr {J}}}_c + \varvec{{\mathscr {J}}}_I\) plays in Eq. (152). In order to clarify the physical meaning of vector \(\varvec{{\mathscr {V}}}_c\) and vector \(\varvec{{\mathscr {V}}}_I\), we turn to Eq. (156). The first equation in (156) is the constitutive equation, which is given in Sect. 5.3, see Eq. (113). This equation is similar to the first equation in (153), i.e., it is similar to Ohm’s law for the conducting current density vector \(\varvec{\mathscr {J}}_c\). That is why, we interpret vector \(\varvec{{\mathscr {V}}}_c\) as the conducting voltage density vector and the first equation in (156) as the analogue of Ohm’s law for the conducting voltage density. The second equation in (156) can be obtained from Eq. (88) if the term containing absolute temperature \(T_a\) is ignored. This equation, as well as the second equation in (153), is not a constitutive equation because it does not contain any material constants. Comparing the second equation in (153) and the second equation in (156), we see that both vector \(\varvec{{\mathscr {J}}}_I\) and vector \(\varvec{\mathscr {V}}_I\) are proportional to the entropy and electromagnetic induction tensor \(\varvec{{\mathscr {D}}}_m\). We note that the generalized Maxwell–Faraday equation contains only the conducting voltage density vector \(\varvec{{\mathscr {V}}}_c\) in the case of the linear theory of conductive media, and it contains only the internal voltage density vector \(\varvec{{\mathscr {V}}}_I\) in the case of the nonlinear theory of non-conductive media.
Let us return to Eq. (87), which includes five vectors: the electric field vector, the magnetic induction vector, the temperature gradient, and also vectors \(\varvec{{\mathscr {V}}}_c\) and \(\varvec{{\mathscr {V}}}_I\). In our theory, this equation plays a dual role. On the one hand, Eq. (87) can be treated as the generalized Maxwell–Faraday equation. The presence of the temperature gradient in this equation should not be surprising, since it agrees with experimental facts discovered by Ettingshausen and Nernst. We mean the Ettingshausen effect (if there is a current in a conductor and a magnetic field normal to it, one observes a temperature gradient normal to the current and magnetic field) and the Nernst–Ettingshausen effect (if a conductive sample undergoes the influence of a magnetic field and a temperature gradient normal to the magnetic field, one observes an electric field directed perpendicular to both the magnetic field and the temperature gradient). On the other hand, Eq. (87) can be treated as the generalized Maxwell–Cattaneo–Vernotte law, which contains the internal voltage density vector \(\varvec{{\mathscr {V}}}_I\) and the curl of the electric field vector. Indeed, taking into account Eqs. (98), (113), we can rewrite Eq. (87) as
Equation (157) is the generalization of Eq. (121) obtained in the framework of the linear theory of conductive media and Eq. (137) obtained in the framework of the nonlinear theory of non-conductive media. Equation (157) is derived in the same way as Eqs. (121) and (137). Taking the divergence of Eq. (157), eliminating \(\nabla \cdot {\textbf{h}}_\varTheta \) from the obtained equation in virtue of the entropy balance equation (154) and taking into account the first constitutive equation in (113), we obtain
Equation (158) is the hyperbolic-type heat conduction equation, and all terms on the right-hand side of this equation play the role of heat production due to different electromagnetic effects.
In our opinion, there is no contradiction in the two above interpretations of Eq. (87) because only the vortex parts of the magnetic induction vector \(\varvec{{\mathscr {B}}}\), of the magnetic field vector \(\varvec{{\mathscr {H}}}\) and of the electric voltage density vector \(\varvec{{\mathscr {V}}}\) have the electrodynamic meaning, whereas their potential parts have the thermodynamic meaning. Moreover, we believe that Eq. (87) opens up new possibilities for describing thermoelectric, thermomagnetic, and thermoelectromagnetic effects.
5.6 Equations relating charges, currents and inductions in the nonlinear theory of conductive media
In this section we discuss the physical analogues of some consequences of the wryness tensor balance equation, which are presented in Sect. 4.5. First of all, we rewrite Eqs. (65), (66), (67) in terms of physical quantities taking into account the analogues between physical and mechanical quantities given in Sect. 5.1. Equation (65) takes the form
Let us compare Eq. (159) with the second equation in (143), which is valid in the case of non-conductive media and has the meaning of the conservation law for the generalized charge density tensor \(\varvec{\mathscr {Q}}_g\). We see that Eq. (159) differs from the second equation in (143) by a number of terms, which play the role of the source terms. Thus, Eq. (159) generalizing the second equation in (143) to the case of conductive media is the balance law, not the conservation one. Rewriting Eq. (66) in terms of physical quantities, we arrive at the electric charge balance equation
which generalizes the electric charge conservation law, given by the first equation in (142). Rewriting Eq. (67) in terms of physical quantities, we obtain the magnetic charge balance equation
which generalizes the magnetic charge conservation law, given by the second equation in (142). Comparing Eq. (160) with the electric charge conservation law and Eq. (161) with the magnetic charge conservation law, we see that the difference is that Eqs. (160), (161) contain the source terms.
The magnetic charge density vector \(\varvec{{\mathscr {Q}}}_m\), as well as the generalized charge density tensor \(\varvec{\mathscr {Q}}_g\), are quantities inherent only in our theory. Therefore, the presence or absence of source terms in the equations for these quantities is unlikely to cause any emotions in the reader. The electric charge density \({\mathscr {Q}}\) is well-known quantity, and it is generally accepted that the electric charge is conserved. Therefore, the presence of the source term in the equation for the electric charge is likely to surprise the reader. Perhaps this causes not just surprise, but disagreement and even complete rejection. Nevertheless, we can refer to literary sources, the authors of which suggest the possibility of violating the charge conservation law, see [11, 95,96,97,98,99]. We have to admit that there are very few such literary sources. Therefore, instead of analyzing the ideas of authors who admit that the charge conservation law is violated, we focus on the question of what the charge conservation law actually means. We start with quotation from [100, p. 18–3]: “The laws of physics have no answer to the question: ‘What happens if a charge is suddenly created at this point—what electromagnetic effects are produced?’ No answer can be given because our equations say it doesn’t happen. If it were to happen, we would need new laws, but we cannot say what they would be. We have not had the chance to observe how a world without charge conservation behaves. According to our equations, if you suddenly place a charge at some point, you had to carry it there from somewhere else. In that case, we can say what would happen.” In modern physics, three different statements can be found: 1) the charge conservation law is a law of nature; 2) the charge conservation law is a fundamental law; 3) the charge conservation law is a fundamental law of nature. In the above quotation, Feynman talks about equations, and this leads us to think that he most likely considers the charge conservation law to be a fundamental law. This means that if we observe a violation of the charge conservation law, we should not believe this, but we should think that we have not taken into account some charges. The important thing to note is that, in classical electrodynamics, the charge conservation law is a consequence of Maxwell’s equations, and it is the solvability condition for Maxwell’s equations. Therefore, we cannot change the charge conservation law without first changing Maxwell’s equations. Thus, in the framework of classical electrodynamics, the charge conservation law is a fundamental law and it cannot be changed. If we modify Maxwell’s equations, the charge conservation law ceases to be a fundamental law in the sense mentioned above. In this case we can discuss the charge conservation law only as a law of nature.
Now, we turn to the question of what exactly is measured in conductive media when measuring charge? To answer this question we quote from [101, p. 46]: “In our experiments with electric fields, we made use of field decay (discharging of condensers) to gain some particular insights; it led us to several important phenomena: First to influence, then to the location of mobile charges on the outer surfaces of conductors, and finally to the currents which flow through a conductor during discharge. This latter phenomenon now brings us closer to an important goal, the quantitative measurement of electric charges in electrical units.” We also quote from [101, p. 48]: “From this we may deduce that the current impulse \(\int I \textrm{d}t\) associated with the decay or production of the field is a measure of the electric charges Q associated with the field. We can measure electric charges Q by determining a current impulse.” Finally, we give one more quotation from [101, p. 51,52]: “In all of the electric fields that we have considered thus far, the field lines had ends, and electric charges were found to be sitting at those ends. Therefore, a quantitative relation between charge Q and electric field strength E is to be expected. We search for it experimentally by looking at the geometrically simplest field, our old friend the homogeneous field of a parallel-plate condenser. Let the area of each of its plates be A, the voltage between them be U, and their spacing l. Then the magnitude of the electric field between the plates is \(E = U/l\).... We repeat these measurements several times with various values of the plate area A and the field strength \(E = U/l\). The result of all these measurements is \(Q/A = \varepsilon _0 E\), or, in words: The surface density Q/A of the charge on the condenser plates is proportional to the electric field strength E (\(\varepsilon _0\) is a constant of proportionality). We find the same simple relation for the surface density Q/A of the influence charges.... The surface density of these influence charges has its own name; it is called the displacement density D, with \(D = Q/A\).” In the above quotation, term ‘displacement density’ is used for the electric induction. As can be seen from the above quotes, the measurement of electric charge is identified with the measurement of electric current and the electric charge itself is identified with the electric induction. This means that, in the considered case, the experimentally established charge conservation law expresses the relationship between the electric current and the electric induction. Next, the following questions arise. What is electric charge according to the conventional wisdom? How is this concept defined in theoretical physics? The most common definition is: “Electric charge is the basic physical property of matter that causes it to experience a force when kept in an electric or magnetic field.” In fact, this definition of electric charge is based on the Coulomb force, or what is the same thing, on the Gauss law for electric field. In other words, when speaking of electric charge, one actually speaks of a quantity directly related to the electric induction. Thus, discussing the views of theoretical physics, we again come to what is said in the above quotations from [101].
Now, we return to our theory. Taking into account the analogues between physical and mechanical quantities given in Sect. 5.1, we rewrite Eq. (70) as
If we follow ideas of [101] and identify the electric charge density \({\mathscr {Q}}\) with \(\nabla \cdot \varvec{\mathscr {D}}\), then we can treat Eq. (162) as the electric charge conservation law. We draw attention to the fact that the right-hand side of Eq. (162) is the divergence of the total electric current density vector \(\varvec{{\mathscr {J}}}_I + \varvec{{\mathscr {J}}}_c\). At the same time, the right-hand side of the electric charge balance equation (160) contains the divergence of only the internal current density vector \(\varvec{{\mathscr {J}}}_I\) and the source term that depends on the conducting current density vector \(\varvec{{\mathscr {J}}}_c\) along with some other quantities. Let us turn to the analogous equations for the magnetic charge density vector. In view of the analogues between physical and mechanical quantities, Eq. (72) takes the form
If we identify the magnetic charge density vector \(\varvec{{\mathscr {Q}}}_m\) with \(\nabla \cdot \varvec{\mathscr {D}}_m^T\), then we can treat Eq. (163) as the magnetic charge conservation law since the right-hand side of this equation is the divergence of some tensor. We emphasize that, in contrast to Eq. (163), the right-hand side of Eq. (161) contains not only divergence of tensor \(\varvec{{\mathscr {J}}}_m^T\), but also a number of the source terms. That is why, Eq. (161) is the balance equation, not a conservation law. Thus, in the framework of our model, we have obtained the conservation laws (162) and (163) for quantities \(\nabla \cdot \varvec{{\mathscr {D}}}\) and \(\nabla \cdot \varvec{{\mathscr {D}}}_m^T\), respectively. At the same time, we have obtained the balance equations (160) and (161) for the electric charge density \({\mathscr {Q}}\) and the magnetic charge density vector \(\varvec{{\mathscr {Q}}}_m\), respectively, and these equations are not the conservation laws. Obviously, this means that in the case of conductive media quantities \(\nabla \cdot \varvec{{\mathscr {D}}}\) and \({\mathscr {Q}}\), and also \(\nabla \cdot \varvec{\mathscr {D}}_m^T\) and \(\varvec{{\mathscr {Q}}}_m\) are not related to each other by the Gauss laws given by Eq. (141). Below, we consider equations that generalize the Gauss laws to the case of conductive media in framework of our model.
In view of the analogues between physical and mechanical quantities given in Sect. 5.1, Eq. (68) takes the form
Equation (164) generalizes the Gauss law (143) relating the generalized induction tensor \(\varvec{{\mathscr {D}}}_g\) to the generalized charge density tensor \(\varvec{{\mathscr {Q}}}_g\) in the case of non-conductive media. At first glance, it seems that Eq. (164) and Eq. (143) have nothing in common with each other. Nevertheless, we show how one can obtain Eq. (143) from Eq. (164). If we neglect the conductivity of matter, i.e., we assume that \(\varvec{{\mathscr {J}}}_c = 0\) and \(q_\varTheta = 0\), then Eq. (164) takes the form
Let us make a change of variables
where \({\textbf{X}}_g\) is a new variable, \({\textbf{P}}_g^T\) is the rotation tensor, which will be determined below. Taking into account Eq. (166), we can rewrite Eq. (165) as
Here \(\varvec{\omega }_g\) is the angular velocity vector corresponding to the rotation tensor \({\textbf{P}}_g\). Now, we determine tensor \({\textbf{P}}_g\) as follows
In view of Eq. (168), we can reduce Eq. (167) to the form
If we make additional assumption \(\left. \left( \nabla \cdot \varvec{{\mathscr {D}}}_g - \varvec{\mathscr {Q}}_g\right) \right| _{t=0} = 0\), then we have
Thus, in view of notation (166), we arrive at the Gauss law (143). Let us return to Eq. (164). Using Eqs. (166), (168) and the following notation for the right-hand side of Eq. (164)
we rewrite Eq. (164) as
Taking into account Eq. (166), the last equation in (172) can be rewritten as
Equation (173) is more like a generalization of the Gauss law than Eq. (164). However, it is the same equation, just written in a different form.
Next, taking into account the analogues between physical and mechanical quantities, we can rewrite Eq. (69) as
Equation (174) generalizes the first equation in (141), which is the Gauss law for electric field in the case of non-conductive media. It is important to note that \({\mathscr {Q}} = \textrm{tr}\,\varvec{{\mathscr {Q}}}_g\), \(\nabla \cdot \varvec{{\mathscr {D}}} = \textrm{tr}\,\left( \nabla \cdot \varvec{{\mathscr {D}}}_g\right) \) and Eq. (174) can be obtained by taking the trace of Eq. (164). Therefore, in order to obtain another form of Eq. (174) it is sufficient to take the trace of Eq. (173). As a result, we arrive at the following equation
If we assume that \(\varvec{{\mathscr {J}}}_c = 0\) and \(q_\varTheta = 0\), from Eq. (171) it follows that \({\textbf{Y}}_g = 0\). If, in addition, \(\left. {\textbf{X}}_g\right| _{t=0}\) is assumed to be equal to zero, Eq. (175) reduces to the first equation in (141), i.e., to the classical form of the Gauss law for electric field.
Finally, taking into account the analogues between physical and mechanical quantities, we can rewrite Eq. (71) as
Equation (176) generalizes the second equation in (141), which is the Gauss law for electromagnetic field in the case of non-conductive media. Since \(\varvec{{\mathscr {Q}}}_m = \left( \varvec{\mathscr {Q}}_g\right) _\times \), \(\nabla \cdot \varvec{{\mathscr {D}}}_m^T = \left( \nabla \cdot \varvec{{\mathscr {D}}}_g\right) _\times \) and Eq. (176) can be obtained by taking the vector invariant of Eq. (164), in order to obtain another form of Eq. (176) it is sufficient to take the vector invariant of Eq. (173). As a result, we have
If \(\varvec{{\mathscr {J}}}_c = 0\), \(q_\varTheta = 0\) and \(\left. {\textbf{X}}_g\right| _{t=0} = 0\), then Eq. (177) reduces to the second equation in (141), i.e., to the Gauss law for electromagnetic field in the case of non-conductive media.
Thus, in the case of conductive media, our approach leads to rather complicated equations (164), (174), (176) instead of the Gauss laws. The Gauss laws containing the generalized charge density tensor \(\varvec{{\mathscr {Q}}}_g\) and the magnetic charge density vector \(\varvec{{\mathscr {Q}}}_m\), as well as the corresponding generalized equations, are new equations inherent only in our theory. The generalized Gauss law for electric field (174) is also a new equation inherent only in our theory.
The Gauss law for electric field is well known. Therefore the question arises whether its violation is possible from the point of view of modern physics. To clarify this issue we quote from [100]. The first quotation from [100, p. 5–5]: “The validity of Gauss’ law depends upon the inverse square law of Coulomb. If the force law were not exactly the inverse square, it would not be true that the field inside a uniformly charged sphere would be exactly zero.” The second quotation from [100, p. 5–6]: “If we write that the electrostatic force depends on \(r^{-2+\epsilon }\), we can place an upper bound on \(\epsilon \). By this method Maxwell determined that \(\epsilon \) was less than 1/10, 000. The experiment was repeated and improved upon in 1936 by Plimpton and Laughton. They found that Coulomb’s exponent differs from two by less than one part in a billion. Now that brings up an interesting question: How accurate do we know this Coulomb law to be in various circumstances? The experiments we just described measure the dependence of the field on distance for distances of some tens of centimeters. But what about the distances inside an atom—in the hydrogen atom, for instance, where we believe the electron is attracted to the nucleus by the same inverse square law? It is true that quantum mechanics must be used for the mechanical part of the behavior of the electron, but the force is the usual electrostatic one. In the formulation of the problem, the potential energy of an electron must be known as a function of distance from the nucleus, and Coulomb’s law gives a potential which varies inversely with the first power of the distance. How accurately is the exponent known for such small distances? As a result of very careful measurements in 1947 by Lamb and Retherford on the relative positions of the energy levels of hydrogen, we know that the exponent is correct again to one part in a billion on the atomic scale—that is, at distances of the order of one angstrom (\(10^{-8}\) centimeter).” The third quotation from [100, p. 5–7]: “From measurements in nuclear physics it is found that there are electrostatic forces at typical nuclear distances—at about \(10^{-13}\) centimeter—and that they still vary approximately as the inverse square.... How about \(10^{-14}\) centimeter? This range can be investigated by bombarding protons with very energetic electrons and observing how they are scattered. Results to date seem to indicate that the law fails at these distances. The electrical force seems to be about 10 times too weak at distances less than \(10^{-14}\) centimeter. Now there are two possible explanations. One is that the Coulomb law does not work at such small distances; the other is that our objects, the electrons and protons, are not point charges. Perhaps either the electron or proton, or both, is some kind of a smear. Most physicists prefer to think that the charge of the proton is smeared.” And finally, the fourth quotation from [100, pp. 12–12]: “Our currently most complete theory of electrodynamics does indeed have its difficulties at very short distances. So it is possible, in principle, that these equations are smoothed-out versions of something. They appear to be correct at distances down to about \(10^{-14}\) cm, but then they begin to look wrong. It is possible that there is some as yet undiscovered underlying ‘machinery’, and that the details of an underlying complexity are hidden in the smooth-looking equations—as is so in the ‘smooth’ diffusion of neutrons. But no one has yet formulated a successful theory that works that way. Strangely enough, it turns out (for reasons that we do not at all understand) that the combination of relativity and quantum mechanics as we know them seems to forbid the invention of an equation that is fundamentally different from \({\displaystyle \nabla \cdot (k \nabla \phi ) = - \frac{\rho _{free}}{\epsilon _0}}\), and which does not at the same time lead to some kind of contradiction. Not simply a disagreement with experiment, but an internal contradiction. As, for example, the prediction that the sum of the probabilities of all possible occurrences is not equal to unity, or that energies may sometimes come out as complex numbers, or some other such idiocy. No one has yet made up a theory of electricity for which \({\displaystyle \nabla ^2 \phi = - \frac{\rho }{\epsilon _0}}\) is understood as a smoothed-out approximation to a mechanism underneath, and which does not lead ultimately to some kind of an absurdity. But, it must be added, it is also true that the assumption that \({\displaystyle \nabla ^2 \phi = - \frac{\rho }{\epsilon _0}}\) is valid for all distances, no matter how small, leads to absurdities of its own (the electrical energy of an electron is infinite)—absurdities from which no one yet knows an escape.” We emphasize that Feynman, in fact, discuss the question of whether it is possible to change the electrostatic potential. He does not discuss the time dependence of the electrostatic potential. We also emphasize that the above quotes from Feynman’s book discuss the interaction of charges separated by empty space and the Gauss law for electric field in vacuum. Feynman discusses the Gauss law as applied to conductive media in [100, pp. 5–7]: “Now consider the interior of a charged conducting object. (By ‘interior’ we mean in the metal itself.) Since the metal is a conductor, the interior field must be zero, and so the gradient of the potential \(\phi \) is zero. That means that \(\phi \) does not vary from point to point. Every conductor is an equipotential region, and its surface is an equipotential surface. Since in a conducting material the electric field is everywhere zero, the divergence of \({\textbf{E}}\) is zero, and by Gauss’ law the charge density in the interior of the conductor must be zero. If there can be no charges in a conductor, how can it ever be charged? What do we mean when we say a conductor is ‘charged’? Where are the charges? The answer is that they reside at the surface of the conductor, where there are strong forces to keep them from leaving—they are not completely ‘free’. When we study solid-state physics, we shall find that the excess charge of any conductor is on the average within one or two atomic layers of the surface. For our present purposes, it is accurate enough to say that if any charge is put on, or in, a conductor it all accumulates on the surface; there is no charge in the interior of a conductor.” In the above quotation, Feynman expresses the conventional wisdom. Below, we give several quotations from [102], confirming and supplementing what Feynman said. The first quotation from [102, p. 126]: “ A perfect conductor is a macroscopic model for real conducting matter with the property that static electric fields are completely excluded from its interior. Since \(\epsilon _0 \nabla \cdot {\textbf{E}}({\textbf{r}}) = \rho ({\textbf{r}})\), a precise definition of a perfect conductor is that both the macroscopic electric field and the macroscopic charge density vanish everywhere inside its volume. This definition implies that all excess charge accumulates on the surface of a conductor in the form of a surface charge density \(\sigma ({\textbf{r}}_S)\).” The second quotation from [102, p. 127]: “Electrostatic induction in a real metal does not involve any long-range displacement of charge. Equilibrium is re-established by tiny perturbations of the conduction electron wave functions at every point in the conductor. When summed over all occupied states, the corresponding perturbed charge density Lorentz averages to zero at all interior points.” The third quotation from [102, p. 133]: “Conductors have the unique ability to screen or shield a suitably placed sample from the effects of an electric field. By this we mean that a conductor interposed between a sample and a source of electric field generally reduces (and ideally eliminates) the field at the position of the sample.” And the fourth quotation from [102, p. 149]: “This screening length \(\ell \) varies from \(~10^{-10}\) m for a good metal to \(~10^{-8}\) m for a biological plasma, \(~10^{-5}\) m for a laboratory plasma, and 10 m for an astrophysical plasma.” Thus, on the one hand, the Gauss law in vacuum is considered to be correct at distances down to about \(10^{-14}\) cm, and on the other hand, it is well known that, the electrostatic field in conductive media decays at a distance of the order of \(~10^{-8}\) cm. The question arises as to whether the electrostatic field near the boundary of the conductive medium is described by the Gauss law or by some other law. It would seem that if the electrostatic field is described by the Gauss law, then it should penetrate into the charged body, and not decay to zero near the surface. The fact that the electrostatic field in conductive media decays to zero at much shorter distances than in vacuum or in dielectrics can be explained either by assuming that the electrostatic field in conductors is not described by the Gauss law, or by assuming that permittivity of conductors is several orders of magnitude greater than permittivity of dielectrics. We cannot compare the permittivities of conductors and dielectrics because there is no information about the values of permittivity of conductors in handbooks. Moreover, in the scientific literature there is no information about the possibility of determining the values of permittivity of conductors by electrostatic experiments. All known methods of determining the values of permittivity of conductors are based on the study of wave processes at the conductor–dielectric interface. These experiments (or their interpretation accepted in modern literature) give very strange results, according to which the values of the real part of permittivity of conductors are negative throughout the frequency range below the terahertz one, see [103]. The use of such permittivity values in the Gauss law leads to absurd results, such as attraction of charges having the same signs and repulsion of charges having opposite signs. Therefore, it seems logical to assume that in the case of conductive media, the Gauss law needs to be modified. Ideas regarding modification of the Gauss law by including time dependence in it were expressed by Gauss himself, see [1]. Later, these ideas were developed by Riemann, see [1]. Weber developed an original theory based on the generalized Coulomb’s law, which includes dependence not only on distance, but also on the relative velocity and relative acceleration of interacting charges, see [1]. It should be noted that applications of Weber’s theory can be found in modern literature, see, e.g., [104,105,106,107,108]. Our ideas differ from the ideas of Gauss, Riemann and Weber. However, there is something in common between our ideas and the ideas of the authors mentioned above, which is that some terms containing time derivatives appear in equations of “electrostatics.” In other words, in the case of conductive media, equations of electrostatics turn into equations describing certain relaxation processes.
5.7 Some ideas concerning strong and weak interactions
There are four types of interactions between elementary particles: gravitational, electromagnetic, strong and weak. Now we focus on strong and weak interactions. Particle physics introduces such characteristics of particles as color charge, isospin, weak isospin, flavour, etc. All these characteristics are somehow related to strong and weak interactions.
Strong interaction (other names: color interaction, nuclear interaction) is the interaction that is responsible for the connection between quarks in hadrons and for the attraction between nucleons (protons and neutrons) in nuclei. From the point of view of strong interaction, proton and neutron are the same particles. There is a model according to which any nucleon has isospin equal to 1/2, and the projection of isospin in a special isotopic space can be either \(+1/2\) or \(-1/2\). If the projection of isospin is \(+1/2\), then the nucleon is a proton. If the projection of isospin is \(-1/2\), then the nucleon is a neutron. According to the concepts of modern physics, strong interaction exists only between quarks, and it occurs through the exchange of gluons. Color charge, which is attributed to gluons and quarks, is related to strong interaction. Quarks have their own color: “red,” “green,” “blue” or “anti-red,” “anti-green,” “anti-blue” (such quarks are usually called anti-quarks). Quarks are also characterized by flavors. The are six flavors: u (“Up quark”), d (“Down quark”), s (“Strange quark”), c (“Charm quark”), b (“Beauty quark”), t (“Truth quark”). Three quarks of different colors constitute baryons, which are “white” (colorless) particles. Two quarks, one of which has any color and another one has the matching anti-color, constitute mesons, which are also “white” particles. All mesons are unstable. Color charges of gluons are characterized by various combinations of colors and anti-colors. There are eight gluons, among them six color ones and two colorless ones.
In [63], we discuss an interpretation of strong interaction in the framework of our model. Here, we quote from [63]: “It is known that the Coulomb force is defined as the product of the charge and the electric field vector. Since the electric field vector is proportional to the electric induction vector, the Coulomb force actually turns to be proportional to the product of the charge and the electric induction vector. Taking into account the analogy between the proposed concepts of electric charge and magnetic charge vector and also between the electric induction vector and the entropy and electromagnetic induction tensor, we can hypothesize the existence of forces (and possibly moments) that are proportional to the dot product of the magnetic charge vector \(\varvec{{\mathscr {Q}}}_m\) and the entropy and electromagnetic induction tensor \(\varvec{{\mathscr {D}}}_m\). We would venture to suggest that these forces (and possibly moments) characterize the strong interaction. We can put forward two arguments in favor of our hypothesis. The first argument is that the forces characterizing the strong interaction are not central, and hence, they must be generated not by scalar charges, but by vector ones. The second argument is as follows. According to the concepts of modern physics, the strong interaction binds protons and neutrons to create atomic nuclei and holds quarks together to form hadrons. At the same time, in accordance with the concepts of modern physics, elementary particles possess magnetic dipole moments, i.e., they behave like tiny magnets and produce magnetic field. It seems logical to suggest that two vector characteristics: the magnetic dipole moment introduced in classical physics and the magnetic charge vector introduced in our theory, in some sense correspond to each other. It seems also logical to suggest that protons and neutrons create atomic nuclei due to magnetic properties of elementary particles. Hence, we can suppose that the magnetic charge density vector \(\varvec{{\mathscr {Q}}}_m\) and the entropy and electromagnetic induction tensor \(\varvec{{\mathscr {D}}}_m\) are responsible for the strong interaction.” In addition to what has been said, we also assume that strong interaction can depend on the deviator of the symmetric part of the generalized charge density tensor \(\varvec{{\mathscr {Q}}}_g\). To be exact, we assume that forces (and possibly moments) responsible for strong interaction are proportional to the double dot product of two tensors: the deviator of the symmetric part of the second rank tensor \(\varvec{{\mathscr {Q}}}_g\) and the third rank tensor \(\varvec{{\mathscr {D}}}_g\), which is called the generalized induction tensor and related to the generalized charge density tensor \(\varvec{{\mathscr {Q}}}_g\) by the first equation in (143). In other words, these forces (and possibly moments) depend on color charges located at some point in space and the field generated by color charges located at another point in space. Such an interpretation of strong interaction is in agreement with quantum mechanical concept, in accordance to which particles possessing color charges are responsible for strong interaction. At this stage in the development of our theory, we cannot describe strong interaction in more detail for several reasons. Firstly, in order to describe strong interaction, it is necessary to add translational degrees of freedom to our model. Secondly, we have no certainty in the question of whether strong interaction is described only by forces or by forces and moments. Thirdly, now we cannot say with certainty which components of the generalized charge density tensor are responsible for strong interaction. However, we have confidence in that strong interaction is an elastic interaction; it is described by forces (and possibly moments) depending on the generalized charge density tensor (or some its components) and the generalized induction tensor (or its potential part); mathematical formulas describing strong interaction must be in some sense similar to the Coulomb force.
Weak interaction is the interaction that is responsible for the nuclear fission and nuclear fusion. According to the concepts of modern physics, weak interaction exists between all known elementary particles. Weak interaction was first described by Enrico Fermi in terms of the so-called four-fermion contact interaction. Sheldon Glashow, Abdus Salam and Steven Weinberg later showed that electromagnetic interaction and weak interaction are two aspects of a single interaction. The term electroweak interaction is used for this interaction. There are two types of weak interaction. The first type is the so-called “charged-current interaction,” in which the weakly interacting fermions form a current with total electric charge that is nonzero. The second type is the so-called “neutral-current interaction,” in which the weakly interacting fermions form a current with total electric charge of zero. Particle physics introduces weak isospin, which is associated with weak interaction in the same way as isospin is associated with strong interaction. All fermions have a weak isospin equal to 1/2. There are pairs of particles that are the same from the point of view of weak interaction. Fermions of one pair differ from each other by the projection of weak isospin. As in the case of isospin, the projection of weak isospin can be either \(+1/2\) or \(-1/2\). It is important to note that weak interaction does not produce bound states, nor does it involve binding energy. This is what distinguishes the weak interaction from three other fundamental interactions. Weak interaction can lead to the decay of massive particles into lighter ones. This type of decay is called weak decay. An important special case of weak decay is neutron beta-decay. Despite the short range and relative smallness, the weak interaction is important for a number of natural processes. In particular, it is the weak interaction that is responsible for thermonuclear reactions, which are the main sources of energy for most stars.
Now, we turn to an interpretation of weak interaction in the framework of our model. The important thing to note is that, in contrast to strong interaction, weak interaction does not produce bound states. From the point of view of a mechanical model, this can be treated as that the corresponding forces (and possibly moments) are not elastic. In order to explain this statement, we discuss two different model of the same process. First, we consider a two-component model. Let us suppose that particles of ponderable matter are immersed in some infinite elastic medium (the ether or, what is the same thing, the thermo-electromagnetic field). Particles of ponderable matter interact with this medium by elastic forces (and possibly moments) and influence each other through this medium. At the same time, some part of the particle energy is lost due to interaction with the infinite elastic medium (the ether). It cannot be ruled out that some part of the ether energy can be absorbed by particles of ponderable matter. Thus, if we consider a two component continuum consisting of ponderable matter and the ether, we deal with only elastic interactions. Next, we consider a one-component model. In fact, we deal with a continuum, which models ponderable matter, and we take into account the ether only by means of forces (and possibly moments) acting on particles of ponderable matter. It is clear that we should introduce not only elastic, but also inelastic forces (and possibly moments). In such a case, the elastic forces (and possibly moments) produce bound states, whereas the inelastic forces (and possibly moments) are responsible for processes associated with the exchange of energy between ponderable matter and the ether. We believe that the elastic forces (and possibly moments) are associated with strong interaction, whereas the inelastic forces (and possibly moments) are associated with weak interaction. We pay attention to the fact that the quantum mechanical description of weak interaction is based on the concept of currents, not charges. This fact leads us to the idea that, within the framework of our model, the forces (and possibly moments) responsible for weak interaction should be specified as functions of some current densities. We emphasize that, in our model, the mechanical analogues of the internal current density vector \(\varvec{{\mathscr {J}}}_I\), the electromagnetic current density tensor \(\varvec{{\mathscr {J}}}_m\) and the generalized current density tensor \(\varvec{{\mathscr {J}}}_g\) are proportional to the angular velocity vector. In many cases, though not all, the dependence of interactions on velocities, in particular angular velocities, results in energy dissipation, which is an indication that the interactions are inelastic. Thus, \(\varvec{\mathscr {J}}_I\), \(\varvec{{\mathscr {J}}}_m\) and \(\varvec{{\mathscr {J}}}_g\) can be precisely those quantities on which inelastic interactions can depend. Thus, our idea regarding inelastic nature of weak interaction together with the fact that the quantum mechanics uses the concept of currents for describing weak interaction give us reason to believe that weak interaction can depend on one of the current densities \(\varvec{{\mathscr {J}}}_I\), \(\varvec{\mathscr {J}}_m\), \(\varvec{{\mathscr {J}}}_g\). In addition, we pay attention to the fact that, according to the modern quantum mechanical concept, weak interaction is part of the electroweak interaction. This fact, in turn, leads us to the idea that the current density responsible for weak interaction must be related to the electric charge density. In accordance with the charge conservation law (142), the current density vector related to the electric charge density is the internal current density vector \(\varvec{{\mathscr {J}}}_I\). The potential part of vector \(\varvec{{\mathscr {J}}}_I\) can be associated with either a positive charge or a negative charge, and hence, the potential part of vector \(\varvec{{\mathscr {J}}}_I\) can be treated as the density of either a positive current or a negative current. At the same time, the vortex part of vector \(\varvec{{\mathscr {J}}}_I\) is not related to the electric charge density, and hence, the vortex part of vector \(\varvec{{\mathscr {J}}}_I\) can be treated as the density of a neutral current. Thus, we have some additional reason to believe that the forces (and possibly moments) responsible for weak interaction can depend on the internal current density vector \(\varvec{{\mathscr {J}}}_I\).
According to concepts of quantum mechanics, an interaction occurs when two particles (usually fermions) exchange bosons that carry the interaction. Quantum mechanics introduces many hypothetical and short-lived particles that are thought to be involved in interactions. In many cases, the conservation laws are fulfilled only due to the participation of some hypothetical and short-lived particles in the interactions. Thus, these hypothetical and short-lived particles play an important role in quantum mechanics. Our ideas concerning the description of strong and weak interactions do not coincide with the concepts of quantum mechanics, but do not contradict these concepts either. When describing the interactions, we use the approach of classical mechanics, according to which any interactions (forces and moments) are specified by constitutive equations or are determined as a result of solving differential equations. From the point of view of classical mechanics, it does not matter how these interactions occur in nature: with direct contact or with the help of intermediate particles. And even more so, it does not matter what happens to the intermediate particles in the process or as a result of interactions. Thus, the difference between our approach to describing fundamental interactions and the quantum mechanical approach is in some sense similar to the difference between classical thermodynamics and kinetic theory. Classical thermodynamics and kinetic theory are two sciences that study the same natural phenomena, but use different fundamental principles and different mathematical methods. These two sciences exist independently of each other and do not contradict each other. The same can be said when comparing our approach with the quantum mechanical one.
6 Summary and outlook
In this paper, we present the general nonlinear theory of thermo-electrodynamics. We have shown that from the general theory we can obtain, as special cases, the linear theory of thermo-electrodynamics developed in [64] and the nonlinear theory of electromagnetism developed in [63]. This result is important from the theoretical point of view because it means that the two theories, which have been developed independently from each other, are in agreement with each other. Certainly, the proposed theory is not free from shortcomings. Firstly, this theory is valid only for immobile media and it needs to be generalized to the case of moving media. Secondly, in the present paper, we make some assumptions about how to describe strong and weak interactions in the framework of our model, however this can be done only after our model takes into account force interactions in addition to the moment interactions. To develop our theory in both directions, we need to add translational degrees of freedom to our model. This will be the topic of future research.
References
Whittaker, E.: A History of the Theories of Aether and Electricity. The Classical Theories. Thomas Nelson and Sons Ltd, London (1910)
Jaswon, M.A.: Mechanical interpretation of Maxwell’s equations. Nature 224, 1303–1304 (1969)
Kelly, E.M.: Vacuum electromagnetics derived exclusively from the properties of an ideal fluid. Nuovo Cim. B 32(1), 117–137 (1976)
Theocharis, T.: On Maxwell’s ether. Lett. Nuovo Cim. 36, 325–332 (1983)
Winterberg, F.: Maxwell’s equations and Einstein-gravity in the Planck aether model of a unified field theory. Z. Naturforsch. 45a, 1102–1116 (1990)
Winterberg, F.: The Planck aether model for a unified theory of elementary particles. Int. J. Theor. Phys. 33(6), 1275–1314 (1994)
Winterberg, F.: Derivation of quantum mechanics from the Boltzmann equation for the Planck aether. Int. J. Theor. Phys. 34(10), 2145–2164 (1995)
Winterberg, F.: Planck mass plasma vacuum conjecture. Z. Naturforsch. 58a, 231–267 (2003)
Zhilin, P.A.: Reality and mechanics. In: Proceedings of XXIII Summer School “Nonlinear Oscillations in Mechanical Systems”, St. Petersburg, Russia, pp. 6–49 (1996) (in Russian)
Zhilin, P.A.: Classical and modified electrodynamics. In: Proceedings of International Conference “New Ideas in Natural Sciences”, St. Petersburg. Russia. Part I—Physics, pp. 73–82 (1996)
Zhilin, P.A.: Advanced Problems in Mechanics, vol. 2. Institute for Problems in Mechanical Engineering, St. Petersburg (2006)
Larson, D.J.: A derivation of Maxwell’s equations from a simple two-component solid-mechanical aether. Phys. Essays 11(4), 524–530 (1998)
Zareski, D.: The elastic interpretation of electrodynamics. Found. Phys. Lett. 14, 447–469 (2001)
Dmitriyev, V.P.: Electrodynamics and elasticity. Am. J. Phys. 71(9), 952–953 (2003)
Dmitriyev, V.P.: Mechanical model of the Lorentz force and Coulomb interaction. Cent. Eur. J. Phys. 6(3), 711–716 (2008)
Christov, C.I.: Maxwell-Lorentz electrodynamics as a manifestation of the dynamics of a viscoelastic metacontinuum. Math. Comput. Simul. 74(2–3), 93–104 (2007)
Christov, C.I.: On the nonlinear continuum mechanics of space and the notion of luminiferous medium. Nonlinear Anal. 71, e2028–e2044 (2009)
Christov, C.I.: The concept of a quasi-particle and the non-probabilistic interpretation of wave mechanics. Math. Comput. Simul. 80(1), 91–101 (2009)
Christov, C.I.: Frame indifferent formulation of Maxwell’s elastic-fluid model and the rational continuum mechanics of the electromagnetic field. Mech. Res. Commun. 38(4), 334–339 (2011)
Wang, X.S.: Derivation of Maxwell’s equations based on a continuum mechanical model of vacuum and a singularity model of electric charges. Prog. Phys. 2, 111–120 (2008)
Lin, T.-W., Lin, H.: Newton’s laws of motion based substantial aether theory for electro-magnetic wave. J. Mech. 30(4), 435–442 (2014)
Magnitskii, N.A.: Mathematical theory of physical vacuum. Commun. Nonlinear Sci. Numer. Simul. 16, 2438–2444 (2011)
Magnitskii, N.A.: Fundamentals of the theory of compressible oscillating ether. J. Phys. Conf. Ser. 1141, 012052 (2018)
Magnitskii, N.A.: Theory of compressible oscillating ether. Results Phys. 12, 1436–1445 (2019)
Wang, L.J.: Ether dynamics and unification of gravitational and electromagnetic forces. Glob. J. Sci. Front. Res. A Phys. Space Sci. 20(A13), 1–16 (2020)
Simeonov, L.S.: Mechanical model of Maxwell’s equations and of Lorentz transformations. Found. Phys. 52(52) (2022)
Krivtsov, A.M.: Dynamics of matter and energy. Z. Angew. Math. Mech. 103(4), e202100496 (2023)
Dixon, R.C., Eringen, A.C.: A dynamical theory of polar elastic dielectrics—I. Int. J. Eng. Sci. 2, 359–377 (1964)
Dixon, R.C., Eringen, A.C.: A dynamical theory of polar elastic dielectrics—II. Int. J. Eng. Sci. 3, 379–398 (1965)
Treugolov, I.G.: Moment theory of electromagnetic effects in anisotropic solids. Appl. Math. Mech. 53(6), 992–997 (1989)
Grekova, E., Zhilin, P.: Basic equations of Kelvin’s medium and analogy with ferromagnets. J. Elast. 64, 29–70 (2001)
Grekova, E.F.: Ferromagnets and Kelvin’s medium: basic equations and wave processes. J. Comput. Acoust. 9(2), 427–446 (2001)
Ivanova, E.A., Krivtsov, A.M., Zhilin, P.A.: Description of rotational molecular spectra by means of an approach based on rational mechanics. Z. Angew. Math. Mech. 87(2), 139–149 (2007)
Ivanova, E.A., Kolpakov, Ya.E.: Piezo-effect in polar materials using moment theory. J. Appl. Mech. Tech. Phys. 54(6), 989–1002 (2013)
Ivanova, E.A., Kolpakov, Ya.E.: A description of piezoelectric effect in non-polar materials taking into account the quadrupole moments. Z. Angew. Math. Mech. 96(9), 1033–1048 (2016)
Tiersten, H.F.: Coupled magnetomechanical equations for magnetically saturated insulators. J. Math. Phys. 5(9), 1298–1318 (1964)
Maugin, G.A.: Continuum Mechanics of Electromagnetic Solids. Elsevier, Oxford (1988)
Eringen, A.C., Maugin, G.A.: Electrodynamics of Continua. Springer, New York (1990)
Fomethe, A., Maugin, G.A.: Material forces in thermoelastic ferromagnets. Contin. Mech. Thermodyn. Issue 8, 275–292 (1996)
Silvio, A., Dell’Isola, F., Porfiri, M.: A revival of electric analogs for vibrating mechanical systems aimed to their efficient control by PZT actuators. Int. J. Solids Struct. 39(20), 5295–5324 (2002)
Ugo, A., Dell’Isola, F., Porfiri, M.: Piezoelectric passive distributed controllers for beam flexural vibrations. J. Vib. Control 10(5), 625–659 (2004)
Darleux, R., Lossouarn, B., Giorgio, I., dell’Isola, F., Deü, J.F.: Electrical analogs of curved beams and application to piezoelectric network damping. Math. Mech. Solids (2021)
Zhilin, P.A.: In: Ivanova, E.A., Altenbach, H., Vilchevskaya, E.N., Gavrilov, S.N., Grekova, E.F., Krivtsov, A.M. (eds.) Rational Continuum Mechanics. Polytechnic University Publishing House, St. Petersburg (2012) (in Russian)
Zhilin, P.A.: Modeling of the electromagnetic field based on rational mechanics approach. Z. Angew. Math. Mech. 103(4), e202302004 (2023)
Müller, W.H., Rickert, W., Vilchevskaya, E.N.: Thence the moment of momentum. Z. Angew. Math. Mech. 100(5), e202000117 (2020)
Altenbach, H., Indeitsev, D., Ivanova, E., Krvitsov, A.: In memory of Pavel Andreevich Zhilin (1942–2005). Z. Angew. Math. Mech. 87(2), 79–80 (2007)
Altenbach, H., Eremeyev, V., Indeitsev, D., Ivanova, E., Krvitsov, A.: On the contributions of Pavel Andreevich Zhilin to Mechanics. Tech. Mech. 29(2), 115–134 (2009)
Altenbach, H., Ivanova, E.A.: Zhilin, Pavel Andreevich. In: Altenbach, H., Öchsner, A. (eds.) Encyclopedia of Continuum Mechanics. Springer, Berlin (2020)
Ivanova, E.A.: Derivation of theory of thermoviscoelasticity by means of two-component medium. Acta Mech. 215, 261–286 (2010)
Ivanova, E.A.: On one model of generalized continuum and its thermodynamical interpretation. In: Altenbach, H., Maugin, G.A., Erofeev, V. (eds.) Mechanics of Generalized Continua, pp. 151–174. Springer, Berlin (2011)
Ivanova, E.A.: Derivation of theory of thermoviscoelasticity by means of two-component Cosserat continuum. Tech. Mech. 32, 273–286 (2012)
Ivanova, E.A.: Description of mechanism of thermal conduction and internal damping by means of two-component Cosserat continuum. Acta Mech. 225, 757–795 (2014)
Ivanova, E.A.: Description of nonlinear thermal effects by means of a two-component Cosserat continuum. Acta Mech. 228, 2299–2346 (2017)
Vitokhin, E.Y., Ivanova, E.A.: Dispersion relations for the hyperbolic thermal conductivity, thermoelasticity and thermoviscoelasticity. Contin. Mech. Thermodyn. 29, 1219–1240 (2017)
Ivanova, E.A.: Thermal effects by means of two-component Cosserat continuum. In: Altenbach, H., Öchsner, A. (eds.) Encyclopedia of Continuum Mechanics. Springer, Berlin (2020)
Ivanova, E.A.: A new model of a micropolar continuum and some electromagnetic analogies. Acta Mech. 226, 697–721 (2015)
Ivanova, E.A.: On a micropolar continuum approach to some problems of thermo- and electrodynamics. Acta Mech. 230, 1685–1715 (2019)
Ivanova, E.A.: Towards micropolar continuum theory describing some problems of thermo and electrodynamics. In: Altenbach, H., Irschik, H., Matveenko, V.P. (eds.) Contributions to Advanced Dynamics and Continuum Mechanics, pp. 111–129. Springer, Berlin (2019)
Ivanova, E.A., Matias, D.V.: Coupled problems in thermodynamics. In: Altenbach, H., Öchsner, A. (eds.) State of the Art and Future Trends in Material Modeling, pp. 151–172. Springer, Berlin (2019)
Ivanova, E.A.: Modeling of electrodynamic processes by means of mechanical analogies. Z. Angew. Math. Mech. 101(4), e202000076 (2021)
Ivanova, E.A.: On a new theory of the Cosserat continuum with applications in electrodynamics. In: Altenbach, H., Bauer, S., Eremeyev, V.A., Mikhasev, G.I., Morozov, N.F. (eds.) Recent Approaches in the Theory of Plates and Plate-Like Structures. Advanced Structured Materials, vol. 151, pp. 75–87. Springer, Cham (2022)
Ivanova, E.A.: Modeling of thermal and electrical conductivities by means of a viscoelastic Cosserat continuum. Contin. Mech. Thermodyn. 34, 555–586 (2022)
Ivanova, E.A.: Modeling of physical fields by means of the Cosserat continuum. Z. Angew. Math. Mech. 103(4), e202100333 (2023)
Ivanova, E.A.: A new approach to modeling of thermal and electrical conductivities by means of the Cosserat continuum. Contin. Mech. Thermodyn. 34, 1313–1342 (2022)
Garrigues-Baixauli, J.: Relation between the gravitational and magnetic fields. J. Phys. Math. 7(2), 1000169 (2016)
Garrigues-Baixauli, J.: Wave-particle duality as a classic phenomenon. Int. Sci. Res. Org. J. ISROJ 2(1), 20–24 (2017)
Garrigues-Baixauli, J.: Discrete model of electron. Appl. Phys. Res. 11(6), 36–55 (2019)
Garrigues-Baixauli, J.: Is space absolute? Hadronic J. 43, 217–240 (2020)
Unzicker, A.: Nonlinear continuum mechanics with defects resembles electrodynamics–A comeback of the aether? Z. Angew. Math. Mech. 103(4), e202100280 (2023)
Müller, W.H., Vilchevskaya, E.N., Eremeyev, V.A.: Electrodynamics from the viewpoint of modern continuum theory—a review. Z. Angew. Math. Mech. 103(4), e202200179 (2023)
Malvern, E.: Introduction to the Mechanics of a Continuous Medium. Prentice-Hall, Englewood Cliffs (1969)
Truesdell, C.: A First Course in Rational Continuum Mechanics. Academic Press, The John Hopkins University, Maryland (1977)
Eringen, C.: Mechanics of Continua. Robert E. Krieger Publishing Company, Huntington (1980)
Batchelor, G.: An Introduction to Fluid Dynamics. Cambridge University Press, Cambridge (1970)
Loitsyansky, L.G.: Fluid Mechanics. Nauka, Moscow (1987). ((In Russian))
Daily, J., Harleman, D.: Fluid Dynamics. Addison-Wesley, Massachusetts (1966)
Ivanova, E.A., Vilchevskaya, E.N., Müller, W.H.: Time derivatives in material and spatial description—what are the differences and why do they concern us? In: Naumenko, K., Aßmus, M. (eds.) Advanced Methods of Continuum Mechanics for Materials and Structures, pp. 3–28. Springer, Berlin (2016)
Ivanova, E.A., Vilchevskaya, E.N., Müller, W.H.: A study of objective time derivatives in material and spatial description. In: Altenbach, H., Goldstein, R., Murashkin, E. (eds.) Mechanics for Materials and Technologies. Advanced Structured Materials, vol. 46, pp. 195–229. Springer, Cham (2017)
Ivanova, E.A., Vilchevskaya, E.N.: Micropolar continuum in spatial description. Contin. Mech. Thermodyn. 28(6), 1759–1780 (2016)
Müller, W.H., Vilchevskaya, E.N., Weiss, W.: Micropolar theory with production of rotational inertia: a farewell to material description. Phys. Mesomech. 20(3), 250–262 (2017)
Müller, W.H., Vilchevskaya, E.N.: Micropolar theory from the viewpoint of mesoscopic and mixture theories. Phys. Mesomech. 20(3), 263–279 (2017)
Vilchevskaya, E.N.: On Micropolar Theory with Inertia Production. In: Altenbach, H., Öchsner, A. (eds.) State of the Art and Future Trends in Material Modeling, pp. 421–442. Springer, Berlin (2019)
Vilchevskaya, E.N., Müller, W.H.: Modeling of orientational polarization within the framework of extended micropolar theory. Contin. Mech. Thermodyn. 33, 1263–1279 (2021)
Fomicheva, M., Vilchevskaya, E.N., Bessonov, N., et al.: Micropolar medium in a funnel-shaped crusher. Contin. Mech. Thermodyn. 33, 1347–1362 (2021)
Ivanova, E.A., Vilchevskaya, E.N.: A note on dependence of the inertia tensor on the strain measures. Contin. Mech. Thermodyn. 35(4), 141–158 (2023)
Altenbach, H., Naumenko, K., Zhilin, P.A.: A micro-polar theory for binary media with application to phase-transitional flow of fiber suspensions. Contin. Mech. Thermodyn. 15(6), 539–570 (2003)
Zhilin, P.A.: Applied Mechanics. Foundations of Shells Theory. Tutorial Book. Politechnic University Publishing House, St. Petersburg (2006). ((In Russian))
Ivanova, E.A., Jatar Montaño, L.E.: A new approach to solving the solid mechanics problems with matter supply. Contin. Mech. Thermodyn. 33, 1829–1855 (2021)
Ivanova, E.A.: Two approaches to modeling viscoelastic Cosserat continua. In: Altenbach, H., Berezovski, A., dell’Isola, F., Porubov, A. (eds.) Sixty Shades of Generalized Continua. Advanced Structured Materials, vol. 170, pp. 345–360. Springer, Cham (2023)
Ostoja-Starzewski, M.: Second law violations, continuum mechanics, and permeability. Contin. Mech. Thermodyn. 28, 489–501 (2016)
Ostoja-Starzewski, M.: Admitting spontaneous violations of the second law in continuum thermomechanics. Entropy 19(2), 78 (2017)
Raghavan, B.V., Karimi, P., Ostoja-Starzewski, M.: Stochastic characteristics and second law violations of atomic fluids in Couette flow. Physica A 496, 90–107 (2018)
Laudani, R., Ostoja-Starzewski, M.: Spontaneous negative entropy increments in granular flows. ASME J. Appl. Mech. 88(3), 031010 (2021)
Baik, C., Lavine, A.S.: On hyperbolic heat conduction equation and the second law of thermodynamics. Trans. ASME. J. Heat Transf. 117, 256–263 (1995)
Hively, L.M., Giakos, G.C.: Toward a more complete electrodynamic theory. Int. J. Signal Imaging Syst. Eng. 5(1), 3–10 (2012)
Keil, R., et al.: Optical simulation of charge conservation violation and Majorana dynamics. Optica 2(5), 454–459 (2015)
Bednik, G., Zyuzin, A.A., Burkov, A.A.: New J. Phys. 18, 085002 (2016)
Gratus, J., Kinsler, P., McCall, M.W.: Evaporating black-holes, wormholes, and vacuum polarisation: must they always conserve charge? Found. Phys. 49, 330–350 (2019)
Gratus, J., Kinsler, P., McCall, M.W.: Temporary singularities and axions: an analytic solution that challenges charge conservation. Ann. Phys. 533, 2000565 (2021)
Feynman, R.P., Leighton, R.B., Sands, M.: The Feynman Lectures on Physics. Mainly Electromagnetism and Matter, vol. 2. Addison-Wesley, London (1964)
Lüders, K., Pohl, R.O. (eds.): Pohl’s Introduction to Physics. Electrodynamics and Optics, vol. 2. Springer, Cham (2018)
Zangwill, A.: Modern Electrodynamics. Cambridge University Press, New York (2012)
Ordal, M.A., et al.: Optical properties of the metals Al Co, Cu, Au, Fe, Pb, Ni, Pd, Pt, Ag, Ti, and W in the infrared and far infrared. Appl. Opt. 22(7), 1099–1120 (1983)
Assis, A.K.T.: Deriving Ampere’s law from Weber’s law. Hadronic J. 13, 441–451 (1990)
Assis, A.K.T., Silva, H.T.: Comparison between Weber’s electrodynamics and classical electrodynamics. Pramana 55, 393–404 (2000)
Torres-Silva, H., López-Bonilla, J., López-Vázquez, R., Rivera-Rebolledo, J.: Weber’s electrodynamics for the hydrogen atom. Indones. J. Appl. Phys. 5, 39–46 (2015)
Kühn, S.: Experimental investigation of an unusual induction effect and its interpretation as a necessary consequence of Weber electrodynamics. J. Electr. Eng. 72(6), 366–373 (2021)
Baumgärtel, C., Maher, S.: Foundations of electromagnetism: a review of Wilhelm Weber’s electrodynamic force law. Foundations 2(4), 949–980 (2022)
Acknowledgements
The author is deeply grateful to V. A. Kuzkin and E. N. Vilchevskaya for useful discussions on the paper. The study was supported by the Russian Science Foundation grant No. 23-11-00363, https://rscf.ru/project/23-11-00363/.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
A Transformation of the energy balance equation
Let us rewrite Eq. (17) as
In view of Eq. (178), the energy balance equation (11) takes the form
Next, we transform Eq. (179) as follows
In view of identity \({\textbf{E}} \times \varvec{\omega } = \varvec{\omega } \times {\textbf{E}}\) and the properties of the double dot product, Eq. (180) can be reduced to the form
Performing some transformation of Eq. (181), we arrive at
B Transformation of the strain balance equations
We start with the equations for the stretch tensor \({\textbf{g}}\). It is easy to see that the first equation in (17) can be rewritten as
Taking into account the first equation in (12) we can show that \(\nabla \times {\textbf{g}} = 0\). In this case, the last equation in (183) turns to the first equation in (29).
Analogously, the first equation in (35) can be transformed as
The last equation in (184) is, in fact, the first equation in (36).
Now, we turn to the equations for the wryness tensor \(\varvec{\varTheta }\). The second equation in (17) can be rewritten as
Taking into account the second equation in (12) we can show that \({\displaystyle \nabla \times \varvec{\varTheta } = \frac{1}{2}\,\varvec{\varTheta }^T \!\times \times \, \varvec{\varTheta }}\). In this case, the last equation in (185) takes the form
It is easy to see that the last equation in (186) coincides with the second equation in (29).
Next, we transform the second equation in (35) as follows
The last equation in (187) is the second equation in (36).
C The energy balance equation in the case of the modified strain tensors
Let us rewrite Eq. (37) as
Inserting Eq. (188) in the energy balance equation (11), we obtain
After simple transformations Eq. (189) can be rewritten as
Next, performing the same transformations as in [53], we obtain Eq. (39). Performing the same transformations as in “Appendix A,” we reduce Eq. (190) to the form
This equation coincides with Eq. (40).
D Transformation of the angular momentum balance equation
If we use restriction (49), we should consider the model based on the energy moment stress tensor. In this case the angular momentum balance equation (43) takes the form
In virtue the relations \({\textbf{T}} = {\textbf{T}}_e \cdot {\textbf{P}}^T\) and \(\varvec{\omega } = \varvec{\varOmega } \cdot {\textbf{P}}^T\), we can rewrite Eq. (192) as
Let us take the dot product of Eq. (193) on tensor \({\textbf{P}}\) and perform some simple transformations in view of the kinematic relation (42). As a result, we have
where we use the notation \(\varvec{{\mathcal {K}}}_e = \rho J \varvec{\varOmega }\) and \(\rho {\textbf{L}}_e = \rho {\textbf{L}} \cdot {\textbf{P}}\). We can specify the constitutive equation for the external moment \(\rho {\textbf{L}}\), e.g., as the linear function of \(\varvec{\omega }\). In this case, the constitutive equation for \(\rho {\textbf{L}}_e\) will be the linear function of \(\varvec{\varOmega }\). Thus, choosing \({\textbf{M}}_e\), \(\varvec{{\mathcal {K}}}_e\), \(\varvec{\varOmega }\) and \(\varvec{\varTheta }_e\) as the basic variables, we have transformed the angular momentum balance equation to the form, where only one term contains the rotation tensor. Now, we show that we can rewrite the expression \(\left( \nabla \times {\textbf{P}}^T\right) \cdot {\textbf{P}}\) in terms of tensor \(\varvec{\varTheta }_e\) only if we use the equation \(\nabla {\textbf{P}} = \varvec{\varTheta } \times {\textbf{P}}\). Let us rewrite this equation as
Then, we can perform the following transformations:
We emphasize that the last transformations are valid only in virtue of equation \(\nabla {\textbf{P}} = \varvec{\varTheta } \times {\textbf{P}}\):
If we reject the first equation in (196) we cannot use the second equation in (196), and hence we cannot eliminate tensor \({\textbf{P}}\) from Eq. (194).
E Derivation of the constitutive equations
Let us start with the energy balance equation (27), where \(\varvec{\tau }_r\), \({\textbf{T}}_r\) are given by Eq. (25), and \({\textbf{g}}_r\), \(\varvec{\varTheta }_r\) are given by Eq. (26). We assume that the structure of tensor \({\textbf{T}}\) is determined by Eq. (51). In this case tensors \(\varvec{\tau }_r\), \({\textbf{T}}_r\) take the form
In view of the second equation in (197), we can rewrite Eq. (27) as
After simple transformations Eq. (198) takes the form
where
We assume that the continuum is elastic. In this case, from Eq. (27) it follows that \(U = U\bigl ({\textbf{g}}_r,\,\varTheta ,\,\varvec{\varPsi }_r\bigr )\). In addition, we assume that the internal energy does no depend on \({\textbf{g}}_r\). Then, by standard reasoning, we arrive at the Cauchy–Green relations
Next, we assume that function \(\rho U\bigl (\varTheta ,\,\varvec{\varPsi }_r\bigr )\) is specified by Eq. (54). Then, from Eq. (201) it follows
Taking into account Eqs. (197), (200), we can transform Eq. (202) to the form of Eq. (55).
F Derivation of equations for the wryness tensor
Multiplying Eq. (62) by the unit tensor and calculating the difference of Eq. (59) and the obtained equation, we arrive at the equation
Next, we perform the following transformation:
In view of the last transformation, Eq. (203) takes the form of Eq. (63).
Let us take the double cross product of tensor \(\varvec{\varTheta }^T\) and Eq. (59), then take the double cross product of transposed Eq. (44) and tensor \(\varvec{\varTheta }\). Adding up the obtained equations, we obtain
Taking into account the identity \({\textbf{A}}^T \!\times \times \, {\textbf{B}} = {\textbf{B}}^T \!\times \times \, {\textbf{A}}\), which is valid for arbitrary tensors \({\textbf{A}}\) and \({\textbf{B}}\), we rewrite Eq. (204) as
The first term on the right-hand side of Eq. (205) can be transformed as follows:
The second term on the right-hand side of Eq. (205) can be rewritten as
In view of these identities Eq. (205) takes the form
If the source term \(\varvec{\varUpsilon }_\varTheta \) has the form of Eq. (52), then
Let us perform the following transformation:
Then Eq. (207) takes the form
Inserting Eq. (208) in Eq. (206), we arrive at Eq. (65).
Now, we take the curl of Eq. (59). As a result, we have
Calculating the difference of Eq. (209) and Eq. (206) yields
If the source term \(\varvec{\varUpsilon }_\varTheta \) is given by Eq. (52), then
Inserting Eqs. (208), (211) in Eq. (210), we arrive at Eq. (68).
Now, we turn to equations that were used in our previous models, see [60, 63], and we show how these equations can be obtained from the above equations. If we suppose that \(\varUpsilon _\varTheta = 0\) and \(\varvec{\varUpsilon }_\varPsi = 0\), then Eq. (68) takes the form
Using the notation
we can rewrite Eq. (212) as
Let us represent \({\textbf{X}}\) as \({\textbf{X}} = {\textbf{Y}} \cdot {\textbf{P}}^T\), where \({\textbf{P}}\) is the rotation tensor corresponding to the angular velocity vector \(\varvec{\omega }\), i.e., \({\displaystyle \frac{d {\textbf{P}}}{d t} = \varvec{\omega } \times {\textbf{P}}}\). Then Eq. (214) takes the form
If \(\left. {\textbf{X}}\right| _{t=0} = 0\), and hence, \(\left. {\textbf{Y}}\right| _{t=0} = 0\), from Eq. (215) follows that \({\textbf{Y}} = 0\), and hence, \({\textbf{X}} = 0\). Thus, solving Eq. (212) with the initial condition \({\displaystyle \left. \left( \nabla \times \varvec{\varTheta } - \frac{1}{2}\, \varvec{\varTheta }^T \!\times \times \, \varvec{\varTheta }\right) \right| _{t=0} = 0}\), we obtain Eq. (14).
G Algebraic relations between physical quantities
Relations between the charge densities \({\mathscr {Q}}\), \(\varvec{{\mathscr {Q}}}_m\) and \(\varvec{{\mathscr {Q}}}_g\), between the inductions \(\varvec{{\mathscr {D}}}\), \(\varvec{\mathscr {D}}_m\), \(\varvec{{\mathscr {D}}}_g\) and the entropy per unit volume \(\varTheta _a\) have the form
Expressions for the electric charge density \({\mathscr {Q}}\) and the magnetic charge density vector \(\varvec{{\mathscr {Q}}}_m\) in terms of the entropy and electromagnetic induction tensor \(\varvec{{\mathscr {D}}}_m\), the electric induction vector \(\varvec{{\mathscr {D}}}\) and the entropy per unit volume \(\varTheta _a\) are
Two expressions for the generalized charge density tensor \(\varvec{{\mathscr {Q}}}_g\) in terms of the entropy and electromagnetic induction tensor \(\varvec{{\mathscr {D}}}_m\) and the entropy per unit volume \(\varTheta _a\) have the form
Relations between the current densities have the form
Two expressions for the electromagnetic current density tensor \(\varvec{{\mathscr {J}}}_m\) are
Two additional relations containing the electromagnetic current density tensor are written as
Expressions for the internal current density vector \(\varvec{{\mathscr {J}}}_I\) and the internal voltage density vector \(\varvec{{\mathscr {V}}}_I\) have the form
Three additional relations containing the magnetic field vector are
We remind the reader that \(\varvec{{\mathscr {H}}}_m\) is the magnetic flux tensor, \(\varvec{{\mathscr {D}}}_g\) is the generalized induction tensor, \(\varvec{{\mathscr {J}}}_g\) is the generalized current density tensor, and \({\textbf{h}}_\varTheta \) is the entropy flux vector.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Ivanova, E.A. Thermo-electrodynamics of conductive media based on the nonlinear viscoelastic Cosserat continuum of a special type. Acta Mech 234, 6205–6249 (2023). https://doi.org/10.1007/s00707-023-03688-y
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00707-023-03688-y