On Rayleigh-type surface wave in incompressible nematic elastomers

Abstract

In this paper, the propagation of a Rayleigh-type wave is explored in a half-space of an incompressible nematic elastomer with a uniform director aligned orthogonal to the surface. The nematic elastomer is idealized so as to fit within the framework of linear viscoelasticity theory. The governing equations of nematic elastomers are subjected to the Tiersten-type impedance boundary conditions. An explicit secular equation of the Rayleigh wave is obtained which depends upon the non-dimensional anisotropy parameter, impedance parameters, frequency, rubber relaxation time, director rotation times, and the dynamic soft elasticity of nematic elastomers. The numerical computations of the Rayleigh wave speed are restricted for the case of ideal nematic rubbers. The Rayleigh wave speed is illustrated graphically to observe the effects of non-dimensional anisotropy parameter, frequency, impedance parameters, rubber relaxation time, and director rotation times.

1 Introduction

Liquid crystalline elastomers have been an object of growing interest in recent years due to their potential applications in the fields of optics, coatings of materials, artificial muscles, light scattering electro-optical switches, and display materials [1,2,3,4]. Nematic elastomers are unusual materials that simultaneously combine the elastic properties of rubbers with the anisotropy of liquid crystals. They consist of networks of elastic solid chains formed by the cross-linking of nematic crystalline molecules as the elements of their main chains and /or pendant side groups. Due to this structure, any stress on the polymer network influences the nematic order of the nematic, and, conversely, any change in the orientational order will affect the mechanical shape of the elastomer. This interplay between elastic and orientational changes is responsible for many fascinating properties of such materials that are different from the classical elastic solids and liquid crystals. The unusual static and dynamical mechanical properties of liquid crystal elastomers have been discussed by various researchers including Warner and Terentjev [5], Kupfer and Finkelmann [6, 7], Brand et al. [8], Finkelmann et al. [9], Bladon et al. [10, 11], Martinoty et al. [12], and Anderson et al. [13].

Soft elasticity is a remarkable ability of nematic elastomers to exhibit large deformations under small applied forces. Golubovic and Lubensky [14] investigated the soft elasticity on phenomenological grounds within continuum theory. The theory on soft elasticity of nematic elastomers was developed by many researchers; notably among them are Teixeira and Warner [15], Uchida [16], Carlson et. al. [17], Stenull and Lubensky [18, 19], and Fried and Sellers [20]. Oscillating dynamic-mechanical properties of liquid crystalline elastomers were studied by Gallani et al. [21]. Terentjev and Warner [22] investigated the basic properties of nematic rubbers and developed a theory of linear viscoelasticity of nematic elastomers in hydrodynamic (low frequency) limit.

The wave propagation phenomenon in nematic elastomers has potential applications in the fields of acoustics. It is also used in frequency-dependent and direction-dependent smart materials. Based on linear viscoelastic theory of nematic elastomers in the low-frequency limit, Terentjev et al. [23] showed an unusual dispersion and anomalous anisotropy of shear acoustic waves due to soft elasticity combined with the Leslie–Ericksen version of dissipation function. Fradkin et al. [24] studied the spectral and polarization properties of acoustic waves propagating in nematic liquid-crystalline rubber materials. Thereafter, the linear viscoelastic theory of nematic elastomers was applied in various other studies. For example, Singh [25] illustrated the dependence of reflection coefficients on incident angle, frequency, elastic constants, relaxation times, and director angle. Zakharov and Kaptsov [26, 27] and Zakharov [28, 29] studied the wave propagation in elastic bodies with nematic coatings. Yang et al. [30] obtained characteristic equations for Rayleigh waves in nematic elastomers and numerically analyzed the dispersion and attenuation properties of the Rayleigh waves. Yang et al. [31] explored the potential application of nematic elastomers in the band tuning and investigated the band structures in two kinds of nematic elastomer phononic crystals. Recently, Zhao et al. [32] and Zhao and Liu [33, 34] applied the linear viscoelastic theory of nematic elastomers for beams and plates.

In the context of Rayleigh waves, it is assumed that the traction vanishes on the surface. A traction-free surface is described by Neumann boundary conditions. Impedance boundary conditions mean a linear combination of the unknown function, and their derivatives are prescribed on the boundary. These types of boundary conditions are used in the fields of acoustics and electromagnetism and are not common in seismology or geophysics. In the context of the theory of elasticity, Tiersten [35] derived impedance-like boundary conditions to simulate the effect of a thin layer of a different material over an elastic half-space. These boundary conditions specify tractions in terms of displacement and its derivatives. Malischewsky [36] applied Tiersten’s boundary conditions and obtained a secular equation for Rayleigh waves. Thereafter, Rayleigh waves with impedance boundary conditions have been investigated in different materials by Godoy et al. [37], Vinh and Hue [38, 39], Singh [40], and Vinh and Xuan [41].

Being a type of generic surface wave, the Rayleigh waves are extensively used for estimation of material properties. Yang et al. [30] have studied the propagation characteristics of Rayleigh waves in a compressible half-space of nematic elastomers in the context of viscoelastic theory in low frequency limit. The propagation of the Rayleigh wave in nematic elastomers may find many applications in various fields including acoustics, mechanical damping, and materials science. The main objective of this paper is to study the propagation of Rayleigh-type wave in a half-space of nematic elastomer which is assumed as incompressible. The assumption of incompressibility in the present problem seems realistic as most rubbers and liquid crystal elastomers are found nearly volume conserving (for example, Saccomandi and Ogden [42]). In Sect. 2, the governing equations of linear viscoelasticity of nematic elastomers are expressed in terms of a scalar potential function for an incompressible case, where the effects of Frank elasticity on the director gradient are not considered. In Sect. 3, the specialized governing equation is solved by a traditional approach as given in Ogden and Vinh [43]. With the use of relevant impedance boundary conditions at the surface of nematic elastomer half-space, an irrational secular equation for Rayleigh wave is obtained. The secular equation is also reduced for the isotropic limit in Sect. 4. In Sect. 5, the effects of impedance parameters, frequency, chain anisotropy parameter, non-dimensional anisotropy parameter, rubber relaxation time, and director rotation times on wave speed are illustrated graphically for the specific forms of elastic moduli and coupling constants in the theory of ideal nematic rubbers. A conclusion of the results is given in Sect. 6.

2 Governing field equations

Following de Gennes [1], Warner and Terentjev [44] and neglecting the effects of Frank elasticity on the director gradient, the equations of motion for a viscous nematic solid are obtained as

$$\begin{aligned}{} & {} \nabla ~ . ~\mathbf{\sigma } = \rho {\partial }_{tt}{} \textbf{u}, \end{aligned}$$

(1)

$$\begin{aligned}{} & {} \textbf{n} \times [(d_1 + {\gamma }_1 {\partial }_t) \textbf{n} \times \mathbf{\Theta } + (d_2 + {\gamma }_2 {\partial }_t) \textbf{n} . \mathbf{\epsilon }] = \textbf{0}, \end{aligned}$$

(2)

where $\mathbf{\sigma }$ is the symmetric part of the stress tensor, $\mathbf{\epsilon }$ is the symmetric part of the strain tensor, $\partial _t$ and $\partial _{tt}$ denote partial time derivatives, $\rho$ is the mass density, $\textbf{u}$ is the displacement vector, $\mathbf \Theta = \mathbf \Omega - [\textbf{n} \times \mathbf{\delta n}]$ is relative rotation vector, $\textbf{n}$ is an undistorted nematic director, $\mathbf{\Omega } = \frac{1}{2} curl~\textbf{u}$ is the antisymmetric part of strain, and $\gamma _j = d_j \tau _j$, (j = 1, 2) and $d_1, d_2$ are coupling constants.

For a given coordinate system $Ox_1x_2x_3$, the half-space $(x_3 \ge 0)$ is assumed to be occupied by an incompressible viscous nematic solid. The coordinate axis $x_3$ is chosen along undistorted director $\textbf{n}$. Then, the components of the viscoelastic symmetric stress tensor are

$$\begin{aligned}{} & {} {\sigma }_{11} + p = (1 + {\tau }_R {\partial }_t) (c_{11} {\epsilon }_{11} + c_{12} {\epsilon }_{22} + c_{13} {\epsilon }_{33}), \end{aligned}$$

(3)

$$\begin{aligned}{} & {} {\sigma }_{22} + p = (1 + {\tau }_R {\partial }_t)(c_{12} {\epsilon }_{11} + c_{11} {\epsilon }_{22} + c_{13} {\epsilon }_{33}),\end{aligned}$$

(4)

$$\begin{aligned}{} & {} {\sigma }_{33} + p = (1 + {\tau }_R {\partial }_t)(c_{13} {\epsilon }_{11} + c_{13} {\epsilon }_{22} + c_{33} {\epsilon }_{33}),\end{aligned}$$

(5)

$$\begin{aligned}{} & {} {\sigma }_{12} = {\sigma }_{21} = 2 (1 + {\tau }_R {\partial }_t) c_{66} {\epsilon }_{12},\end{aligned}$$

(6)

$$\begin{aligned}{} & {} {\sigma }_{13} = 2 (1 + {\tau }_R {\partial }_t) c_{44} {\epsilon }_{13} -(1/2)d_2 (1 + {\tau }_2 {\partial }_t) {\Theta }_2,\end{aligned}$$

(7)

$$\begin{aligned}{} & {} {\sigma }_{23} = 2 (1 + {\tau }_R {\partial }_t) c_{44} {\epsilon }_{23} +(1/2)d_2 (1 + {\tau }_2 {\partial }_t) {\Theta }_1, \end{aligned}$$

(8)

where $p~=~p(x_1,~x_2,~x_3,~t)$ is the hydrostatic pressure associated with the incompressibility constraints, $e_{ik} = (1/2)[u_{i,k} + u_{k,i}]$ is linear symmetric strain, ${\epsilon }_{ik} = e_{ik} - (1/3) tr [\textbf{e}] {\delta }_{ik}$ is the traceless part of linear symmetric strain, $c_{ij},~(i, j = 1, 2, 3)$ are elastic constants , ${\tau }_R$ is characteristic time of rubber relaxation, and ${\tau }_1, {\tau }_2$ are director rotation times. Following Fradkin et al. [24], the entropy production density function will remain positive if

$$\begin{aligned} {{\tau }_2}^2 \le \frac{8 C_5 d_1}{{d_2}^2} {\tau }_R {\tau }_1, \end{aligned}$$

(9)

where $C_5$ is the shear modulus.

Now, we specialize the governing equations in $x_1-x_3$ plane for an incompressible nematic elastomer half-space occupying the region $x_3 \ge 0$. We assume a two-dimensional motion in the $(x_1, x_3)$ plane such that the displacement components are taken as

$$\begin{aligned} u_i = u_i(x_1, x_3, t),~(i = 1, 3),~~u_2 = 0, \end{aligned}$$

(10)

where t is time. For an incompressible material, we have

$$\begin{aligned} u_{1,1} + u_{3,3}=0, \end{aligned}$$

(11)

where the commas in subscript indicate the differentiation with respect to spatial variables $x_k$.

Following Ogden and Vinh [43], a scalar function $\psi (x_1,~x_3,~t)$ exists such that

$$\begin{aligned} u_1=\psi _{,3},~~u_3=-\psi _{,1}. \end{aligned}$$

(12)

Making use of Eqs. (3), (5), (7), and (12) in Eqs. (1) and (2) and eliminating p, the following equation in $\psi$ is obtained:

$$\begin{aligned} \gamma \psi _{,1111} + 2 \beta \psi _{,1133} + \gamma \psi _{,3333}=\rho (\partial _{tt}\psi _{,11}+ \partial _{tt} \psi _{,33}), \end{aligned}$$

(13)

where the differential operators $\gamma$ and $\beta$ are given by

$$\begin{aligned} \gamma= & {} (1 + {\tau }_R {\partial }_t) c_{44} - (1/4) d_1 d_2 (1 + {\tau }_1 {\partial }_t) (1 + {\tau }_2 {\partial }_t), \end{aligned}$$

(14)

$$\begin{aligned} \beta= & {} (1/2)(1 + {\tau }_R {\partial }_t) (c_{11} + c_{33} - 2 c_{13} - 2 c_{44})\nonumber \\{} & {} + (1/4) d_1 d_2 (1 + {\tau }_1 {\partial }_t) (1 + {\tau }_2 {\partial }_t). \end{aligned}$$

(15)

For the strain energy of the material to be positive semi-definite, all elastic constants are positive, and

$$\begin{aligned} c_{11} + c_{33} - 2c_{13}~>~0. \end{aligned}$$

(16)

3 Rayleigh waves

We consider the propagation of a Rayleigh wave along $x_1$-axis and decaying in the $x_3$-direction as follows:

$$\begin{aligned} u_i \rightarrow 0~~(i=1, 3)~~as~~x_3 \rightarrow +\infty . \end{aligned}$$

(17)

From Eqs. (12) and (17), the decay condition becomes

$$\begin{aligned} \psi (x_1,x_3,t)\rightarrow 0~~as~~x_3\rightarrow +\infty . \end{aligned}$$

(18)

According to Ogden and Vinh [42], the scalar function $\psi (x_1, x_3, t)$ representing the Rayleigh wave propagation is assumed as

$$\begin{aligned} \psi (x_1,x_3,t)=\phi (z)e^{ik(x_1-vt)} \end{aligned}$$

(19)

where $z=k x_3,$ and k is the complex wavenumber such that $Re(k)\ge 0$ to ensure the propagation of the wave in positive $x_1$ direction. v is a complex parameter such that $Re(v) = \omega /Re(k)$ where $\omega$ is circular frequency. The value of Im(k) will determine the attenuation of the Rayleigh wave.

Using Eq. (19), Eq. (13) becomes

$$\begin{aligned} \gamma ^{*} \phi ^{''''}(z) - (2\beta ^{*}- \rho v^2)\phi ^{''}(z) + (\gamma ^{*} - \rho v^2) \phi (z)=0, \end{aligned}$$

(20)

where a prime indicates differentiation with respect to z,  and

$$\begin{aligned} \gamma ^*= & {} (1 - \iota \omega {\tau }_R) c_{44} - (1/4) d_1 d_2 (1 - \iota \omega {\tau }_1) (1 - \iota \omega {\tau }_2), \end{aligned}$$

(21)

$$\begin{aligned} \beta ^*= & {} (1/2)(1 - \iota \omega {\tau }_R) (c_{11} + c_{33} - 2 c_{13} - 2 c_{44})\nonumber \\{} & {} + (1/4) d_1 d_2 (1 - \iota \omega {\tau }_1) (1 - \iota \omega {\tau }_2). \end{aligned}$$

(22)

From Eqs. (18) and (19), it follows that

$$\begin{aligned} \phi (z)\rightarrow 0~~as~~z\rightarrow +\infty . \end{aligned}$$

(23)

Then, the general solution $\phi (z)$ of Eq. (20) satisfying the radiation condition (23) is obtained as

$$\begin{aligned} \phi (z)=Ae^{-m_1z}+Be^{-m_2z} \end{aligned}$$

(24)

where the constants A and B are to be determined. Here, $m_1$ and $m_2$ are the roots of the following equation:

$$\begin{aligned} m^4-({\eta }^2 + \xi - 1) m^2 + {\eta }^2 = 0, \end{aligned}$$

(25)

such that $Re(m_1)>0, Re(m_2) > 0,$ and where

$$\begin{aligned} {\eta }^2 = 1 - ({\rho v^2}/{\gamma ^*}),~~\xi = 2\beta ^*/\gamma ^*. \end{aligned}$$

(26)

It follows from Eq. (25) that

$$\begin{aligned} m_1^2 + m_2^2= {\eta }^2 + \xi - 1,~~m_1^2 m_2^2= {\eta }^2. \end{aligned}$$

(27)

For the existence of Rayleigh wave, the real parts of the complex roots $m_1$ and $m_2$ of Eq. (25) used in solution (24) must be positive. Then, the expressions for $m_1+m_2$ and $m_1 m_2$ are obtained from Eq. (27) as

$$\begin{aligned} m_1 + m_2= \sqrt{{\eta }^2 + 2 \eta + \xi - 1},~~m_1 m_2= \eta . \end{aligned}$$

(28)

Tiersten [35] introduced special boundary conditions on the surface in order to simulate the elastic behavior of a thin layer over a half-space. Malischewsky [36] expressed these conditions in terms of stresses and displacements. In the two-dimensional case, these types of boundary conditions on surface $x_3=0$ of nematic elastomer half-space may be written in the following form:

$$\begin{aligned} \sigma _{13} + \omega U (1 + {\tau }_R {\partial }_t) u_1 = 0,~~\sigma _{33} + \omega W (1 + {\tau }_R {\partial }_t) u_3 = 0, \end{aligned}$$

(29)

where U and W are shear and normal impedance parameters. The impedance parameters U and W are of dimensions of stress/velocity. In the context of Tiersten’s theory, these parameters have specific values as functions of the thickness of the thin layer, the elastic parameters, and the frequency. For $U = 0$ and $W = 0$, the boundary conditions (29) reduce to the well-known traction-free boundary conditions. If U and W tend to infinity, then fixed faced boundary is obtained.

Using Eqs. (5), (7), (12) and eliminating p, the boundary conditions (29) at $x_3 = 0$ are expressed in terms of $\psi$ as

$$\begin{aligned}{} & {} \left[ (1 + {\tau }_R {\partial }_t) (1 + {\tau }_1 {\partial }_t) c_{44}\right. \nonumber \\{} & {} \quad -\left. \frac{1}{4} \frac{{d_2}^2}{d_1} (1 + {\tau }_2 {\partial }_t)^{2}] (\psi _{,33}-\psi _{,11}) + (1 + {\tau }_R {\partial }_t) (1 + {\tau }_1 {\partial }_t) \omega U \psi _{,3}\right] = 0, \end{aligned}$$

(30)

$$\begin{aligned}{} & {} \gamma \psi _{,333} + (2 \beta + \gamma ) \psi _{,113} + \omega W (1 + {\tau }_R {\partial }_t) \psi _{,11}-\rho {\partial }_{tt}{\psi }_{,3}=0. \end{aligned}$$

(31)

With the help of Eq. (19), the boundary conditions (30) and (31) are written in terms of $\phi$ as

$$\begin{aligned}{} & {} (1 - \iota \omega {\tau }_R) \{{c^R}_{44}(\omega ) [\phi ^{''}(0) + \phi (0)] + v U \phi ^{'}(0)\} = 0, \end{aligned}$$

(32)

$$\begin{aligned}{} & {} \gamma \phi ^{'''}(0) - (2\beta ^* + \gamma ^* - \rho v^2) \phi ^{'}(0)-v W (1 - \iota \omega {\tau }_R) \phi (0) = 0, \end{aligned}$$

(33)

where

$$\begin{aligned} {c^R}_{44} (\omega ) = c_{44} - \frac{1}{4} \frac{{d_2}^2}{d_1} \frac{{(1 - \iota \omega {\tau }_2)}^2}{(1 - \iota \omega {\tau }_1)(1 - \iota \omega {\tau }_R)}. \end{aligned}$$

(34)

The solution (24) satisfies the boundary conditions (32) and (33) to obtain the following homogeneous system of equations:

$$\begin{aligned}{} & {} (1 - \iota \omega {\tau }_R) [{c^R}_{44}(\omega ) ( 1 + m_1^2) + v U m_1] A\nonumber \\{} & {} \quad + (1 - \iota \omega {\tau }_R) [{c^R}_{44}(\omega ) ( 1 + m_2^2) + v U m_2] B = 0, \end{aligned}$$

(35)

$$\begin{aligned}{} & {} [\gamma m_1^3 - (2\beta ^* + \gamma ^* - \rho v^2) m_1-v W (1 - \iota \omega {\tau }_R)]A\nonumber \\{} & {} \quad + [\gamma m_2^3 - (2\beta ^* + \gamma ^* - \rho v^2) m_2-v W (1 - \iota \omega {\tau }_R)]B = 0. \end{aligned}$$

(36)

For a non-trivial solution of the homogeneous system of Eqs. (35) and (36), the determinant of the coefficients of A and B vanishes. After removing the factor $(m_2-m_1)$ and using Eqs. (27) and (28), we obtain

$$\begin{aligned} \eta ^3 + \eta ^2 + (\xi + 1) \eta - 1 + \sqrt{{\eta }^2 + 2 \eta + \xi - 1} (a^* e^* \eta + b^* d^*) + a^* b^* d^* e^* = 0, \end{aligned}$$

(37)

where

$$\begin{aligned} a^* = \sqrt{\frac{\rho v^2}{{c^R}_{44}(\omega )}},~b^* = \sqrt{\frac{\rho v^2}{\gamma ^*}},~d^* = \frac{W (1 - \iota \omega {\tau }_R)}{\sqrt{\rho \gamma ^*}},~e^* = \frac{U}{\sqrt{\rho \gamma ^*}}. \end{aligned}$$

(38)

Equation (37) gives a dimensionless secular equation of Rayleigh waves along the surface of an incompressible viscous nematic elastomer half-space with impedance boundary conditions.

For $d^* = 0, e^* = 0$, Eq. (37) reduces to

$$\begin{aligned} \eta ^3 + \eta ^2 + (\xi + 1) \eta - 1 =0, \end{aligned}$$

(39)

which is a dimensionless secular equation of Rayleigh wave along the surface of an incompressible nematic elastomer half-space whose surface is subjected to traction-free boundary conditions. Equation (39) is in agreement with the secular equation as obtained by Ogden and Vinh [43].

4 Isotropic viscoelastic limit

In the isotropic viscoelastic limit, $d_1 \rightarrow 0,~~d_2 \rightarrow 0,~~c_{11} = c_{33} \rightarrow \lambda + 2\mu ,~~c_{13} \rightarrow \lambda ,~~c_{44} \rightarrow \mu$, ($\lambda$ and $\mu$ are Lamé’s coefficients), and hence $\beta ^* = \gamma ^* = {c^R}_{44} \rightarrow \mu (1 - \iota \omega \tau _R), {\eta } \rightarrow \sqrt{1-\frac{\rho v^2}{\mu (1 - \iota \omega \tau _R)}}$ and $\xi \rightarrow 2$, and then, the frequency equation (37) reduces to

$$\begin{aligned} \eta ^3 + \eta ^2 + 3 \eta - 1 + \sqrt{{\eta }^2 + 2 \eta + 1} (a^* e^* \eta + b^* d^*) + a^* b^* d^* e^* = 0, \end{aligned}$$

(40)

where

$$\begin{aligned} a^* = \sqrt{\frac{\rho v^2}{\mu ^*}},~b^* = \sqrt{\frac{\rho v^2}{\mu ^*}},~d^* = \frac{W(1 - \iota \omega \tau _R)}{\sqrt{\rho \mu ^* }},~e^* = \frac{U}{\sqrt{\rho \mu ^* }},~\mu ^*=\mu (1 - \iota \omega \tau _R). \end{aligned}$$

(41)

Equation (40) is a dimensionless secular equation of Rayleigh waves in an incompressible isotropic viscoelastic half-space with impedance boundary conditions.

5 Numerical results and discussion

For the purpose of numerical computations, the following specific forms of elastic moduli and coupling constants are taken in the theory of ideal nematic rubbers as [24]

$$\begin{aligned}{} & {} c_{44} = 2 C_5,~~c_{11} = B + (4/3) \mu -(4/3) C_2, \end{aligned}$$

(42)

$$\begin{aligned}{} & {} c_{13} = B - (2/3) \mu + (2/3) C_2,~~c_{33} = B + (4/3) \mu +(8/3) C_2. \end{aligned}$$

(43)

$$\begin{aligned}{} & {} C_{5} = \frac{1}{8} \mu \frac{{(r + 1)}^2}{r},~~d_1 = \mu \frac{{(r - 1)}^2}{r},~~ d_2 = \frac{(1 - r^2)}{r},~~{c_{44}}^{R} (0) = 0. \end{aligned}$$

(44)

where B is bulk modulus, $C_2$ is an elastic constant, and r is the chain anisotropy parameter. The principal constants $\rho = 1000\,{\textrm{kg}}\,{\textrm{m}}^{-3},~~B = 10^{10}\,{\textrm{Pa}},~~\mu = 10^{5}\,{\textrm{Pa}},$ and $C_2 =\mu /2$ given by Fradkin et al. [24] are considered for numerical computations of the Rayleigh wave speed. Nematic elastomers are reduced to isotropic viscoelastic materials for anisotropy chain parameter $r = 1$. Terentjev and Warner [23] investigated the director rotation time, ${\tau }_1$, and it was experimentally measured by Schonstein et al. [45] and Schmidtke et al. [46] as ${\tau }_1 \thicksim 10^{-1}-10^{-2}$s. The characteristic time of rubber relaxation ${\tau }_R$ is of the order of Rouse time of the corresponding polymer chains, which is taken as ${\tau }_R \thicksim 10^{-5}-10^{-6}$s.

The secular Eq. (37) of Rayleigh wave is a relationship between the complex wave speed v, circular frequency $\omega$, non-dimensional anisotropy parameter $\xi$, impedance parameters U and W, rubber relaxation time $\tau _R$, and director rotation times $\tau _1$ and $\tau _2$. Equation (37) in revised version is an irrational equation due to the presence of the radical in it. It is not easy to solve this equation algebraically. Therefore, the equation is rationalized into an implicit equation. The six complex roots of the implicit equation contain few extraneous roots due to rationalization. These roots are resolved to satisfy the decay condition for Rayleigh surface waves. Four extraneous roots are identified which do not satisfy Eq. (37) and are filtered out. Two roots with positive real parts are identified which satisfy Eq. (37) and which define the existence and propagation of Rayleigh waves. One of the roots with positive real part satisfying the secular Eq. (37) is considered for numerical simulations.

If we write $v^{-1} = c^{-1} + i \omega Q$ such that $k =P + i Q$, then $c = \omega /P$ is the speed of propagation, and Q is the attenuation coefficient. The speed of propagation $c = Re(v)$ of the Rayleigh wave is illustrated graphically against the non-dimensional anisotropy parameter $\xi$, impedance parameter U, chain anisotropy parameter r, rubber relaxation time $\tau _R$, and director rotation time $\tau _1$ in Figs. 1, 2, 3, 4, and 5.

Fig. 1

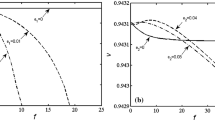
a The variation of Rayleigh wave speed with respect to the non-dimensional anisotropy parameter $\xi$ for different values of shear impedance parameter U when $W = 0$, $\omega = 100$ s$^{-1}$, $r = 3$, $\tau _1 = 10^{-2} s$, and $\tau _R = 10^{-6} s$. b The variation of Rayleigh wave speed with respect to the shear impedance parameter U for different values of anisotropy parameter $\xi$ when $W = 0$, $\omega = 100$ s$^{-1}$, $r = 3$, $\tau _1 = 10^{-2} s$, and $\tau _R = 10^{-6} s$. c The variation of Rayleigh wave speed with respect to the non-dimensional anisotropy parameter $\xi$ for different values of chain anisotropy parameter r when $U = 0$, $W = 0$, $\omega = 100$ s$^{-1}$, $\tau _1 = 10^{-2} s$, and $\tau _R = 10^{-6} s$

Fig. 2

a The variation of Rayleigh wave speed with respect to the shear impedance parameter U for different values of frequency $\omega$ when $W = 0$, $r = 3$, $\tau _1 = 10^{-2} s$, and $\tau _R = 10^{-6} s$. b The variation of Rayleigh wave speed with respect to the frequency $\omega$ for different values of shear impedance parameter U when $W = 0$, $r = 3$, $\tau _1 = 10^{-2} s,$ and $\tau _R = 10^{-6} s$

Fig. 3

a The variation of Rayleigh wave speed with respect to the chain anisotropy parameter r for different values of frequency $\omega$ when $U = 100$, $W = 100$, $\tau _1 = 10^{-2} s,$ and $\tau _R = 10^{-6}$ s. b The variation of Rayleigh wave speed with respect to the chain anisotropy parameter r for different values of shear impedance parameter U when $\omega = 100 s^{-1}$, $W = 0$, $\tau _1 = 10^{-2} s$, and $\tau _R = 10^{-6} s$

Fig. 4

a The variation of Rayleigh wave speed with respect to the rubber relaxation time $\tau _R$ for different values of shear impedance parameter U when $\omega = 100 s^{-1}$, $W = 100$, $r = 3$, and $\tau _1 = 10^{-2} s$. b The variation of Rayleigh wave speed with respect to the rubber relaxation time $\tau _R$ for different values of frequency $\omega$ when $U = 100$, $W = 100$, $r = 3$, and $\tau _1 = 10^{-2} s$

Fig. 5

a The variation of Rayleigh wave speed with respect to the director rotation time $\tau _1$ for different values of shear impedance parameter U when $\omega = 100 s^{-1}$, $W = 100$, $r = 3$, and $\tau _R = 10^{-6} s$. b The variation of Rayleigh wave speed with respect to the director rotation time $\tau _1$ for different values of frequency $\omega$ when $U = 100$, $W = 100$, $r = 3$, and $\tau _R = 10^{-6} s$

Fig. 6

a The variation of attenuation coefficient Q against the non-dimensional anisotropy parameter $\xi$. b The variation of attenuation coefficient Q against the circular frequency $\omega$

The wave speed c against the non-dimensional anisotropy parameter $\xi$ is illustrated graphically in Fig. 1a for three different values of shear impedance parameter U. In the absence of impedance parameters (i.e., for traction-free boundary case), the speed is $2.6361 \times 10^3\,{\mathrm{m. s}}^{-1}$ at $\xi = 0$, and it increases very sharply to a value $3.209 \times 10^3\,{\mathrm{m. s}}^{-1}$ at $\xi = 2$ (isotropic limit) and then increases slowly to $3.2688 \times 10^3\,{\mathrm{m. s}}^{-1}$ at $\xi = 10$. These values of speeds at each $\xi$ decrease on increasing the shear impedance parameter U. The effect of shear impedance parameter U is found significant in the range $0 \le \xi \le 2$, and it becomes relatively low beyond $\xi = 2$. Again, the variations in Fig. 1b show that the wave speed decreases with the increase in the value of shear impedance parameter U, and the rate of decrease becomes relatively low as we increase the value of $\xi$. The variation of the speed against the non-dimensional anisotropy parameter $\xi$ is also shown in Fig. 1c for three different values of the chain anisotropy parameter r. The speed in the range $0 \le \xi \le 2$ increases at each value of $\xi$ as the chain anisotropy parameter r increases.

The speed c is also illustrated graphically against the shear impedance parameter U for three different values of the circular frequency $\omega$. As shown in Fig. 2a, the speed decreases slowly with increasing value of U for a given $\omega$. The variations in Fig. 2b show that the speed increases very sharply against the circular frequency $\omega$ for a given value of shear impedance parameter U.

The speed variations with respect to the chain anisotropy parameter r for three different values of frequency $\omega$ are illustrated in Fig. 3a. For $r =1$, the Rayleigh wave speed corresponds to pure isotropic viscoelastic material with no director relaxation. For $\omega = 100, 200,$ and 300, it has value $9.7958\,{\mathrm{m. s}}^{-1}$ at $r = 1.001,$ and it increases sharply with increasing value of r. The rate of increase in speed is observed more for higher values of frequency. The speed variations against chain anisotropy parameter r in Fig. 3b for three different values of shear impedance parameter U show a decrease in wave speed as the value of shear impedance parameter U increases.

The speed variations against the rubber relaxation time $\tau _R$ in Fig. 4a, b show that the wave speed decreases by increasing the rubber relaxation time $\tau _R$ for given values of shear impedance parameter U and circular frequency $\omega$. However, the rate of decrease in speed is observed faster for higher values of U or $\omega$.

The speed variations against the director rotation time $\tau _1$ are given in Fig. 5a, b for three different values of shear impedance parameter U and circular frequency $\omega$. For given U or $\omega$, the wave speed increases sharply as $\tau _1$ increases. The rate of increase in speed becomes relatively slow as U increases but the rate of increase in speed becomes relatively faster on increasing the value of $\omega$.

The attenuation of the Rayleigh wave is also examined against the non-dimensional anisotropy parameter $\xi$ and circular frequency in Fig. 6a, b, respectively. The attenuation coefficient Q decreases exponentially against $\xi$ and $\omega$

6 Conclusions

The secular equation of Rayleigh wave is derived in an incompressible nematic elastomer half-space with impedance boundary conditions. This secular equation provides a relation between the wave speed, frequency, rubber relaxation time, director rotation times, non-dimensional anisotropy parameter, chain anisotropy parameters, shear and normal impedance parameters. A specific material in the theory of ideal nematic rubbers is taken to compute the Rayleigh wave speed. The numerical results are illustrated graphically. Some important theoretical predictions from the numerical results are observed as follows:

• (i) The speed of Rayleigh wave increases sharply with anisotropy parameter $\xi$. The presence of shear impedance parameter U affects the rate of increase relatively at low values of $\xi$. The wave speed decreases along with an increase in shear impedance parameter U. The rate of decrease in wave speed becomes relatively slow with increasing values of anisotropy parameter $\xi$.

• (ii) The speed increases sharply with the increase in the value of frequency $\omega$ for a given value of shear impedance parameter U.

• (iii) The speed increases sharply with increasing value of chain anisotropy parameter r. The rate of increase in speed becomes relatively faster as we increase the value of frequency $\omega$. The speed variation for $r = 1$ corresponds to pure isotropic viscoelastic material with no director relaxation.

• (iv) The speed decreases by increasing the value of rubber relaxation time $\tau _R$. The rate of decrease in speed becomes relatively faster as we increase the value of frequency $\omega$ or shear impedance parameter U.

• (v) The speed increases sharply with an increase in the value of director rotation time $\tau _1$. This rate of increase becomes relatively faster for higher values of frequency $\omega$.

• (vi) The speed is also computed with respect to normal impedance parameter W. It is observed that the wave speed is independent of W.

• (vii) The present results for the incompressible case are different from the compressible case studied by Yang et al. [30]. In the present study, the main focus is on the dependence of Rayleigh wave speed on non-dimensional anisotropy parameter $\xi$ and shear impedance parameters U. On comparing the speed variations in Fig. 2b and Fig. 2 [30], the dependence of wave speed on the circular frequency $\omega$ is observed similar in both compressible and incompressible cases. The effect of incompressibility is also observed in the comparison of variations in these Figures.