1 Introduction

Sandwich structures have been used for many applications in structural engineering such as wind turbine blades, space vehicles, helicopter blades, airplanes, and road transport vehicles. However, they have some limitations such as constant frequency and damping properties.

Smart materials are a kind of functional material which can respond to the environmental excitations in a controlled fashion. Magnetorheological (MR) materials are smart materials whose rheological properties can be controlled by the application of external electric/magnetic fields. They have been studied in several researches especially in the last decades [1,2,3,4,5,6,7,8,9,10,11,12]. The mechanical properties of these materials such as damping factor and shear modulus can be modified by changing the magnetic field intensity; then, the vibration characteristics of the structure can be changed by applying an appropriate magnetic field intensity.

MR elastomers (MREs) can sustain large deformations in tension, compression and shear modes due to solid features and flexible texture. Their handling and storage are easier under the actuation of the magnetic field, and they show quicker response than MR fluids [13]. Yalcintas and Dai [14] investigated the vibration control capabilities of adaptive structures based on MR and ER (Electro-Rheological) materials, and show that by using the MR material, the natural frequencies are almost two times higher than those for ER-based structures. Nayak et al. [15] studied the dynamic analysis and parametric instability of the magnetorheological elastomer (MRE) sandwich beams subjected to a periodic axial load and magnetic field under various boundary conditions. They reported 30% greater vibration reduction of an MRE-embedded cantilever sandwich beam in comparison to that of a sandwich beam with a viscoelastic material core.

The theoretical and experimental investigation of the dynamic characteristics and instability of the MRE sandwich beams subjected to a periodic axial load and magnetic field was presented by Li et al. [16] and Nayak et al. [17, 18] too. Other theoretical and experimental investigation with special emphasis on the research and development of MRE devices and their applications was presented [19,20,21,22]. Navazi et al. [23] investigated the dynamic characteristics of a doubly tapered magnetorheological rotating sandwich beam based on the Euler–Bernoulli theory and reported the effects of different parameters such as rotating speed, magnetic field and taper ratio.

The free vibration analysis of a rotating MRE-based sandwich beam with rectangular cross section along the edgewise direction is studied by Bornassi et al. [24]. In this study the elastic skins of the beam are analyzed using the Euler–Bernoulli beam theory and the shear strains in the MRE layer are considered for developing the dynamic model of the system. In addition to the effects of rotary and bending inertia of this layer are investigated and finally, the effects of different parameters on the natural frequencies and damping capability of the MRE sandwich beam are presented.

Recently, de Souza Eloy et al. [25] studied numerically and experimentally the free and forced vibration of sandwich beams with carbon/epoxy composite skin and a honeycomb core filled with MR elastomer in the various proportions of magneto/elastomer under several magnetic field intensities. The experimental results showed that the natural frequencies and vibration amplitude of the sandwich beam shifted by applying a magnetic field.

Although investigation of the effects of magnetoelastic loads is one of the important issue in dynamic behavior of magnetorheological sandwich beam, there are few researcher that analyzed the vibration characteristics of this type of beam by considering the magnetoelastic load effects [26, 27]. Rokn-Abadi et al. [28] investigated the effects of magnetoelastic loads on free vibration characteristics of the magnetorheological-based sandwich beam. For these means, the structural governing equations are derived using the Hamilton principle and solved by the finite element method. They studied the effects of variation in the parameters such as magnetic field intensity and the thickness of the core and top layers on the deviation of the first natural frequency and the corresponding loss factor.

In recent years, functionally graded materials (FGMs) have attracted considerable interest as heat-shielding materials for various advanced purpose [29,30,31]. Functionally graded materials are advanced composites, and their mechanical properties vary smoothly from one surface to the other. Unlike fiber-matrix composites which have a mismatch of mechanical properties across an interface of two discrete materials bonded together and may result in rebounding at high temperature, gradually varying the material properties of FGMs can avoid or remove this problem [32]. Moreover, FGMs allow for spatial optimization by grading the volume fractions of two or more constituents to improve the response of structures. If properly designed, FGMs can offer various advantages such as reduction of thermal stresses, minimization of stress concentration or intensity factors and attenuation of stress waves. Hence, FGMs have gained potential applications in a wide variety of engineering components or systems which include the rocking-motor casing, armor plating, heat-engine components, packaging encapsulants, thermoelectric generators, and human implants, just to name a few [33].

Ke and Wang [34] showed that the effect of the size of materials on dynamic stability of FG microbeams can only be considered when the length scale parameter has the same value as that of beam thickness. Piovan and Machado [35] suggested that dynamically unstable regions of thin wall FG beams vary inversely with elastic stiffness. Kolakowski [36] did inspection about the dynamic stability of trapezoidal FGM beams. The relation between static and dynamic bucklings of structure and primary and secondary local buckling was given. Fazzolari [37] examined vibration and stability of FG beams. Using different mathematical theories, various material parameters were taken into account to study frequency and buckling load of FG beams. At 2018 Zhang et al. [38] presented an overview of the existing literature on stability, buckling, and free vibration analysis of FGM carried out by numerous authors in the past decade.

Besides, using the functionally graded materials (FGM) on structural elements in high temperature environments can help to effectively reduce the possible failures that are induced by thermo or combined thermo-mechanical loadings. These materials that made from a mixture of metals and ceramics, are one of the advanced composites [39].

A novel analytical model based on combined (cubic, sinusoidal and exponential) higher order quasi-3D formulation developed to examine flexural and free vibrational response on the various FG-plate resting on elastic foundation by Bouafia et al. [40]. The analytical solution obtained on the basis of the both Hamilton's principle and Navier's technique. In this work the parametric studies performed to show the effects of the material distribution, inhomogeneity index, elastic foundation parameters, geometry and dimension ratios on displacements, stresses and naturel frequencies of the simply supported FG-plates.

Kouider et al. [41] presented an original four-variable quasi-3D shear deformation theory for the static and free vibration analysis of new type of sandwich plates with both FG face sheets and FGM hard core. Their formulation which takes into account both the transverse shear and normal deformation, predicted the natural frequencies with the same degree of accuracy as that of 3D elasticity solutions and given a good result of displacements and stress compared with others Quasi-3D theories.

Several theoretical and experimental studies have been done to analyze the mechanical behavior of FGM structural beam too [42, 43], but there are few studies about vibration analysis of functionally graded adaptive sandwich structures with electrorheological or magnetorheological fluid core [44].

The investigation of bending response of a simply supported functionally graded (FG) viscoelastic sandwich beam with elastic core resting on Pasternak’s elastic foundations is presented by Zenkour et al. [45]. In this study the numerical results for deflections and stresses obtained using the refined sinusoidal shear deformation beam theory and the effects of material distribution, span-to-thickness ratio, foundation stiffness and time parameter are investigated. Allahverdizadeh et al. [46,47,48] studied the Vibration characteristics of Functionally Graded Electro-Rheological (FGER) sandwich beams. They presented the effects of functionally graded materials volume fraction index, rotating speed, electric field and thickness of the viscoelastic core on the natural frequencies and modal loss factors of the FGER beam.

On the other hand, there is a lot of research about the vibration characteristics and behavior of functionally graded sandwich plates [49,50,51,52,53,54,55,56], and beams in thermal environment [57, 58].

Tahir et al. [59] investigated the wave propagation of porous functionally graded sandwich plate in a hygrothermal environment by using the six different porosity models to express the porosities’ distribution factor and uniformity. Their numerical results obtained by solving an eigenvalue problem and eventually, the effects of core‐to‐thickness ratio, FGM power index, porosity volume fraction, temperature, and moisture change illustrated and discussed. In the same year, the bending behavior of an advanced functionally graded ceramic–metal plate subjected to a hygrothermo-mechanical load and resting on a viscoelastic foundation studied by using a simple higher-order integral shear deformation theory by Mudhaffar et al. [60]. A three-parameter viscous foundation model used to study the bending response utilizing the damping coefficient in addition to Winkler’s and Pasternak’s parameters for the first time in their work. Another similar work done by Merazka et al. [61] resting on elastic foundations and the effects of the temperature, moisture concentration, elastic foundation parameters, shear deformation, geometrical parameters, and power-law-index on the dimensionless deflections, axial and transverse shear stresses of the FG-plate presented and discussed. Zaitoun et al. [62] presented the buckling response of a functionally graded sandwich plate on a viscoelastic foundation and exposed to hygrothermal conditions. They showed a parametric study of the effect of the damping coefficient along with the aspect ratio, moisture condition, power-law index, and temperature variation over the buckling temperature of the FG sandwich plate on the viscoelastic foundation.

Xiang and Yang [63] investigated the free and forced vibration of a laminated FGM Timoshenko beam of variable thickness under heat conduction. Numerical results in their work are presented in both tabular and graphical forms for various laminated functionally graded beams, showing that vibration frequencies, mode shapes and dynamic response are significantly influenced by the thickness variation, temperature change, slenderness ratio, volume fraction index, the thickness of the functionally graded layer, and the end support conditions. The thermo–mechanical vibration of FG sandwich beams under variable elastic foundation was studied by Pradhan and Murmu [64]. In their study, the Euler–Bernoulli beam theory was adopted and the DQM was used to solve the governing differential equations. free vibration of a FG beam subjected to thermal environment based on a unified higher order shear deformation theory were studied by Mahi et al. [65]. Shen and Wang based on a higher-order shear deformation beam theory, investigated the vibration and nonlinear bending of FG material beams resting on elastic foundations in thermal environments [66]. The free vibration of functionally graded beams with various boundary conditions resting on a two-parameter elastic foundation in a thermal environment is studied using the third order shear deformation beam theory by Zahedinejad [67].

However, to the best of our knowledge, there are few available studies in the literature to analyze the mechanical and dynamical behavior of FGM structural with viscoelastic core and functionally graded material constraining layer under heat condition. Therefore, the investigation of the FGMR sandwich beam in the sense of vibration analysis and heat condition, is the main purpose of the present work. Jonson and Mohanty [68] analyzed the buckling and free vibration of a sandwich plate with viscoelastic core and functionally graded material constraining lamina under high temperature environment. They used the first-order shear deformation theory and various parametric studies such as effect of aspect ratio, core thickness ratio and volume fraction index on static and dynamic behavior of the sandwich plate are examined. Simultaneously, the influence of porosity on the flexural and free vibration responses of functionally graded plates in thermal environment by using a new mathematical model to incorporate the effects of porosity in the FGM plate are studied by Gupta and Talha [69].

In this paper the effect of temperature and magnetoelastic loads on free vibration of a FGMR elastomer sandwich beam under heat conduction is studied. For this purpose, first, the method of combining the two type of materials (FGM and MRE) that use simultaneously in beam structure will be studied. Then, how to extract the governing equations of this type of beam will be explained. In the following, the effect of some parameters on dynamic behavior of a sandwich beam with MR core and FGM constraining layers under temperature environment will be studied by solving the equations and examining the results.

The thermal gradient due to one-dimensional through-thickness steady heat conduction is considered. The governing equations of motion of the system are achieved using assumed modes method and Hamilton’s principle, and the frequencies are obtained by eigenvalue analysis. Finally, the results are validated with the analytical and numerical studies in the literature.

In the following, first, the effects of magnetic field intensity on natural frequency and modal loss factor of the FGMR beam are studied. Then, the influence of temperature distribution on the vibration of FGMR sandwich beam is shown for different boundary condition and volume fraction index. Finally, the effect of slenderness ratio on fundamental frequency of FGMR beam is presented.

The results show that the dynamic behavior is significantly influenced by the effects of FGM distribution, applied magnetic field, the temperature and magnetoelastic loads, for different boundary conditions.

2 Dynamic model of sandwich beam

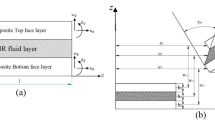
We consider a sandwich beam with three layers, the elastomer core and two functionally graded (FGM) layers, as shown in Fig. 1. The core is made of magnetorheological elastomer, and the face layers are graded from ceramic to meatal. So that the top and bottom surface of sandwich beam is made of pure ceramic. The beam has a length L and a width B. The vertical position of the bottom, the two interface between the layers and the top are denoted by \({h}_{0}\), \({h}_{1}\), \({h}_{2}\) and \({h}_{3}\), respectively. The bottom, top and core layer thicknesses are \({h}_{{\rm b}}\), \({h}_{{\rm t}}\) and \({h}_{{\rm c}}\), respectively.

Fig. 1
figure 1

Configuration of functionally graded beam with MR core

Full size image

To investigate the dynamic behavior of the sandwich beam, according to Fig. 2, it will be assumed that shear strains in the face plates are negligible and that longitudinal direct stresses in the core are negligible. The thickness of all layers is very small compared to the length of the beam and there is no slippage and delamination between the FGM layers and the magnetorheological elastomer layer. Transverse direct strains in both core and face plates are also neglected, so that the transverse displacement w at a section does not vary along the beam’s thickness [70].

Fig. 2
figure 2

Kinematic relationships of deflected beam [71]

Full size image

In Fig. 2, the \({u}_{{\rm b}}\), \({u}_{{\rm t}}\) and \({u}_{{\rm c}}\) are the longitudinal displacements of the mid-plane of the bottom, top and core layers, respectively, in the x-direction.

It is also assumed that the displacement field relationships, strain–displacement relations and constitutive equations are linear. The geometric nonlinear model is usually recommended when the large deformation is between ten or fifteen percent of the beam length. According to the dimensions of the beam and the transverse displacement in this paper, the use of a linear model can be justified.

On the other hand, the investigation of the free vibration and linear natural frequencies is the purpose of this study. Therefore, a linear model in which the nonlinear curvature terms have been omitted, will be used.

2.1 Displacement fields

According to the mentioned assumptions, the longitudinal and transverse displacements of the top and bottom layers at a material point (x, z) can be expressed as [72]:

$${u}_{{\rm b}}\left(x,{z}_{{\rm b}},t\right)={u}_{{\rm b}}\left(x,t\right)-{z}_{{\rm b}}\frac{\partial w}{\partial x}\left(x,t\right),$$
(1)
$${u}_{{\rm t}}\left(x,{z}_{{\rm t}},t\right)={u}_{{\rm t}}\left(x,t\right)-{z}_{{\rm t}}\frac{\partial w}{\partial x}\left(x,t\right),$$
(2)
$${w}_{{\rm t}}\left(x,{z}_{{\rm t}},t\right)={w}_{{\rm b}}\left(x,{z}_{{\rm b}},t\right)=w\left(x,t\right).$$
(3)

In the above equations, t represents the time and the \({z}_{{\rm b}}, {z}_{{\rm t}}\) are the local distance from mid-plane of bottom and top layers, respectively.

From the geometry of the deflected beam (Fig. 2), the shear strain in the MRE core can be expressed as [70]

$${\gamma }_{{\rm c}}=\frac{\partial w}{\partial x}+\frac{\partial {u}_{{\rm c}}}{\partial z},$$
(4)

where

$$\frac{\partial {u}_{{\rm c}}}{\partial z}=\frac{\left({h}_{{\rm b}}+{h}_{{\rm t}}\right)}{2{h}_{{\rm c}}}\frac{\partial w}{\partial x}+\frac{\left({u}_{{\rm t}}-{u}_{{\rm b}}\right)}{{h}_{{\rm c}}}.$$
(5)

Using Eqs. (4) and (5), the shear strain of the core layer can be rewritten as

$${\left({\gamma }_{{\rm c}}\right)}_{xz}=\frac{\partial w}{\partial x}+\frac{\partial {u}_{{\rm c}}}{\partial z}=\frac{S}{{h}_{{\rm c}}}\frac{\partial w}{\partial x}+\frac{\left({u}_{{\rm t}}-{u}_{{\rm b}}\right)}{{h}_{{\rm c}}},$$
(6)

where \(S={h}_{{\rm c}}+\left(\left({h}_{{\rm b}}+{h}_{{\rm t}}\right)/2\right)\). In the pre-yield region, the MR materials exhibit viscoelastic behavior, which can be explained by the linear viscoelastic theory as

$$\tau ={G}_{{\rm c}}^{*}\gamma ,$$
(7)

where \(\tau\) is the shear stress and \({G}_{{\rm c}}^{*}\) is the complex modulus. So, the field-dependent complex modulus can be obtained from [73]

$${G}_{{\rm c}}^{*}={G}^{^{\prime}}\left(1+{\eta }_{{\rm c}}\right),$$
(8)

where \({G}^{^{\prime}}\) and \({\eta }_{{\rm c}}\) are the shear storage modulus and the loss factor of the viscoelastic material, respectively.

Eventually the linear strain associated with the displacements in any FGM layer can be defined as

$${\left({\varepsilon }_{xx}\right)}_{{\rm b}}=\frac{\partial {u}_{{\rm b}}\left(x,t\right)}{\partial x}-{z}_{{\rm b}}\frac{{\partial }^{2}w\left(x,t\right)}{{\partial x}^{2}} ,$$
(9)
$${\left({\varepsilon }_{xx}\right)}_{{\rm t}}=\frac{\partial {u}_{{\rm t}}\left(x,t\right)}{\partial x}-{z}_{{\rm t}}\frac{{\partial }^{2}w\left(x,t\right)}{{\partial x}^{2}},$$
(10)

where the b and t subscripts are pertinent to the bottom and top layers, respectively.

The normal stress \({\sigma }_{x}\) is given by the linear elastic constitutive law according to functionally graded materials (FGM), as [56]

$${\left({\sigma }_{xx}\right)}_{i}=\frac{{E}_{i}\left({z}_{i}\right)}{1-{\nu }_{i}^{2}}\left[{\left({\varepsilon }_{xx}\right)}_{i}-\alpha \left({z}_{i}\right)\Delta T\left({z}_{i}\right)\right] ,\quad i=t,b ,$$
(11)

where \(E, \nu , \alpha\) and \(\Delta T\) are the elastic modulus, Poisson’s ratio, coefficient of thermal expansion and temperature change, respectively.

2.2 Sandwich FGM beam

The material composition of the two FGM layers follows a power law distribution along the z-axis so that the volume fractions of the material phases involved in both layers is given by [46]:

$$\begin{aligned} \begin{array}{ll}{V}^{\left(1\right)}\left(z\right)={\left(\frac{z}{{h}_{{\rm b}}}+\frac{1}{2}\right)}^{e},&\quad {h}_{0}\le z\le {h}_{1},\\ {V}^{\left(2\right)}\left(z\right)=0 ,&\quad {h}_{1}\le z\le {h}_{2},\\ {V}^{\left(3\right)}\left(z\right)={\left(\frac{z}{{h}_{{\rm t}}}+\frac{1}{2}\right)}^{e} , &\quad {h}_{2}\le z\le {h}_{3},\\ \end{array}\end{aligned}$$
(12)

where e is the nonnegative volume fraction index and \({V}^{\left(n\right)}\left(z\right)\) is the volume fractions of the ceramic at each layer. An effective generic material property \({P}^{\left(n\right)}\) of FGM layer n (n = 1, 3), such as the coefficient of thermal expansion \(\alpha\), the coefficient of thermal conductivity \(\kappa\), and the modulus of elasticity E, can be defined as [56]

$${P}^{\left(n\right)}\left(z,T\right)={P}_{m}\left(T\right)+\left({P}_{{\rm c}}\left(T\right)-{P}_{m}\left(T\right)\right){V}^{\left(n\right)}\left(z\right).$$
(13)

In which the subscripts m and c refer to the metal and ceramic constituents, so that \({P}_{m}\) and \({P}_{{\rm c}}\) denote the temperature-dependent properties of the metal and ceramic, respectively.

2.3 Thermal conditions

Consider a sandwich beam with FGM and MR layers in which the temperature of the bottom and top surfaces of this beam are \({T}_{{\rm b}}\) and \({T}_{{\rm t}}\), respectively (Fig. 1). As the FG materials are most commonly used in high temperature environments in which significant changes in material properties are to be expected, the material properties of an FGM beam layers are both position and temperature-dependent. Note that the material properties of the MR layer are not dependent to temperature. Thus, it is essential to consider this temperature-dependence for reliable and accurate prediction of the structural response. The material properties are temperature-dependent and are obtained using the following expression [31]:

$$P\left(T\right)={P}_{0}\left({P}_{-1}{T}^{-1}+1+{P}_{1}T+{P}_{2}{T}^{2}+{P}_{3}{T}^{3}\right), $$
(14)

In which \(T={T}_{0}+\Delta T\), \({T}_{0}\) =300 K (room temperature), and \(\Delta T\) is the temperature change. Also the\({P}_{0}\), \({P}_{-1}\),\({P}_{1}\), \({P}_{2}\) and \({P}_{3}\) are temperature-dependent coefficient and are unique to each constituent. The temperature field assumed to be uniform over the beam surface. Suppose that the beam only is subjected to a one-dimensional temperature change \(\Delta T\) in the thickness direction. The ceramic-rich top surface in \({h}_{3}\) is exposed to temperature \({T}_{{\rm t}}\) and the ceramic-rich bottom surface in \({h}_{0}\) is held at temperature\({T}_{{\rm b}}\). The nonlinear temperature distribution along the thickness can be obtained by solving the steady-state heat transfer equation as [49]

$$-\frac{\hbox{d}}{\hbox{d}z}\left[\kappa \frac{\hbox{d}T}{\hbox{d}z}\right]=0$$
(15)

with the following thermal boundary conditions:

$$T\left(z\right)\left|{ }_{z={h}_{{\rm c}}/2+{h}_{{\rm t}}}\right.={T}_{{\rm t}},\quad T\left(z\right)\left|{ }_{z=-\left({h}_{{\rm c}}/2+{h}_{{\rm b}}\right)}\right.={T}_{{\rm b}}. $$
(16)

Also the continuity requirements at the two FGM substrate interfaces are

$${T}^{\left(1\right)}\left|{ }_{z=-{h}_{{\rm c}}/2}\right.={T}^{\left(2\right)}\left|{ }_{z=-{h}_{{\rm c}}/2}\right.,\quad {T}^{\left(2\right)}\left|{ }_{z={h}_{{\rm c}}/2}\right.={T}^{\left(3\right)}\left|{ }_{z={h}_{{\rm c}}/2}\right. ,$$
(17a)
$${\kappa }^{\left(1\right)}\frac{\hbox{d}T}{\hbox{d}z}\left|{ }_{{ }_{z=-{h}_{{\rm c}}/2}}\right.={\kappa }^{\left(2\right)}\frac{\hbox{d}T}{\hbox{d}z}\left|{ }_{{ }_{z=-{h}_{{\rm c}}/2}}\right.,\quad {\kappa }^{\left(2\right)}\frac{\hbox{d}T}{\hbox{d}z}\left|{ }_{{ }_{z={h}_{{\rm c}}/2}}\right.= {\kappa }^{\left(3\right)}\frac{\hbox{d}T}{\hbox{d}z}\left|{ }_{{ }_{z={h}_{{\rm c}}/2}}\right. ,$$
(17b)

where (\({T}^{\left(1\right)}, {T}^{\left(2\right)}, {T}^{\left(3\right)}\)) and (\({\kappa }^{\left(1\right)}, {\kappa }^{\left(2\right)}, {\kappa }^{\left(3\right)}\)) are the temperature distribution and thermal conductivity coefficients of the lower FGM layer, the MR substrate, and the upper FGM layer, respectively. Using the above boundary conditions, the temperature distribution can be written as [74]

$${T}^{\left(n\right)}\left(z\right)={T}_{{\rm b}}+\left({T}_{{\rm t}}-{T}_{{\rm b}}\right){\Psi }^{n},\quad {{n}}=1, 2, 3,$$
(18)

where

$${\Psi }^{1}=\frac{{\int }_{{h}_{0}}^{z}\left(1/{{\kappa}^{(1)}(z)}\right)\hbox{d}z}{{\sum }_{n=1}^{3}{\int }_{{h}_{n-1}}^{{h}_{n}}\left(1/{{\kappa}^{(n)}(z)}\right)\hbox{d}z},\quad {h}_{0}\le z\le {h}_{1},$$
(19a)
$${\Psi }^{2}=\frac{{\int }_{{h}_{0}}^{{h}_{1}}\left(1/{{\kappa}^{(1)}(z)}\right)\hbox{d}z+{\int }_{{h}_{1}}^{z}\left(1/{{\kappa}^{(2)}(z)}\right)\hbox{d}z}{{\sum }_{n=1}^{3}{\int }_{{h}_{n-1}}^{{h}_{n}}\left(1/{{\kappa}^{(n)}(z)}\right)\hbox{d}z} ,\quad {h}_{1}\le z\le {h}_{2},$$
(19b)
$${\Psi }^{3}=\frac{{\int }_{{h}_{0}}^{{h}_{1}}\left(1/{{\kappa}^{(1)}(z)}\right)\hbox{d}z+{\int }_{{h}_{1}}^{{h}_{2}}\left(1/{{\kappa}^{(2)}(z)}\right)\hbox{d}z+{\int }_{{h}_{2}}^{z}\left(1/{{\kappa}^{(3)}(z)}\right)\hbox{d}z}{{\sum }_{n=1}^{3}{\int }_{{h}_{n-1}}^{{h}_{n}}\left(1/{{\kappa}^{(n)}(z)}\right)\hbox{d}z} ,\quad {h}_{2}\le z\le {h}_{3},$$
(19c)

The temperature at the positions \({h}_{1}\) and \({h}_{2}\) is \({T}_{1}\) and \({T}_{2}\) respectively (Fig. 1) and is as follows

$${T}_{1}={T}_{{\rm b}}+\left({T}_{{\rm t}}-{T}_{{\rm b}}\right)\frac{{\int }_{{h}_{0}}^{{h}_{1}}\left(1/{{\kappa}^{(1)}(z)}\right)\hbox{d}z}{{\sum }_{n=1}^{3}{\int }_{{h}_{n-1}}^{{h}_{n}}\left(1/{{\kappa}^{(n)}(z)}\right)\hbox{d}z},$$
(20)
$${T}_{2}={T}_{{\rm b}}+\left({T}_{{\rm t}}-{T}_{{\rm b}}\right)\frac{{\int }_{{h}_{0}}^{{h}_{1}}\left(1/{{\kappa}^{(1)}(z)}\right)\hbox{d}z+{\int }_{{h}_{1}}^{{h}_{2}}\left(1/{{\kappa}^{(2)}(z)}\right)\hbox{d}z}{{\sum }_{n=1}^{3}{\int }_{{h}_{n-1}}^{{h}_{n}}\left(1/{{\kappa}^{(n)}(z)}\right)\hbox{d}z}.$$
(21)

2.4 Governing equations and analysis method

To derive the equations of motion of the FGMR-based sandwich beam, Hamilton’s principle is applied. This method is expressed as [10]

$${\int }_{{t}_{1}}^{{t}_{2}}\delta \left(U-T+W\right)dt=0 ,$$
(22)

where t is the time, \({t}_{1}\) and \({t}_{2}\) are the initial and end times, respectively. Furthermore, δ is the first variation and T, U, and W indicate kinetic energy, potential energy, and external work done by the magnetoelastic loads, respectively. The total strain energy of the FGRM beam can be represented as

$$U={U}_{{\rm d}}+{U}_{{\rm T}},$$
(23)

where \({U}_{{\rm d}}\) is the strain energy due to the mechanical stresses and \({U}_{{\rm T}}\) is the strain energy caused by the initial stresses due to temperature rise. For the strain energy due to the mechanical stresses we have

$${U}_{{\rm d}}=\frac{1}{2}{\int }_{0}^{L}{\int }_{A}\left({\sigma }_{xx}{\varepsilon }_{xx}+{\tau }_{xz}{\gamma }_{xz}\right)\hbox{d}A\hbox{d}x .$$
(24)

By using Eqs. (9), 10 and (11) for the FGM layers, and Eqs. (6) and (7) for the MR layer, and applying integrations in the lateral direction (y direction), this equation can be expressed as follows:

$${U}_{{\rm d}}=\frac{B}{2}\left[{D}_{{\rm t}}^{1}{\int }_{0}^{L}{\left(\frac{\partial {u}_{{\rm t}}}{\partial x}\right)}^{2}+{D}_{{\rm b}}^{1}{\int }_{0}^{L}{\left(\frac{\partial {u}_{{\rm b}}}{\partial x}\right)}^{2}+\left({D}_{{\rm t}}^{3}+{D}_{{\rm b}}^{3}\right){\int }_{0}^{L}{\left(\frac{{\partial }^{2}w}{{\partial x}^{2}}\right)}^{2}-2{D}_{{\rm t}}^{2}{\int }_{0}^{L}\frac{\partial {u}_{{\rm t}}}{\partial x}\frac{{\partial }^{2}w}{{\partial x}^{2}}-2{D}_{{\rm b}}^{2}{\int }_{0}^{L}\frac{\partial {u}_{{\rm b}}}{\partial x}\frac{{\partial }^{2}w}{{\partial x}^{2}}\right]\hbox{d}x+\frac{1}{2}{\int }_{0}^{L}{G}_{{\rm c}}^{*}{A}_{{\rm c}}{{\gamma }_{{\rm c}}}^{2}\hbox{d}x , $$
(25)

where the coefficients \({D}_{{\rm t}}^{i}\) and \({D}_{{\rm b}}^{i}\) (i = 1, 2, 3) are given in the Appendix.

The strain energies due to the thermal load can be expressed as [49]

$${U}_{{\rm T}}=\frac{1}{2}{\int }_{0}^{L}{\int }_{A}\left(-\frac{E\left(z,T\right)\alpha \left(z,T\right)}{1-\nu \left(z,T\right)}{\Delta T\left(z\right)d}_{xx}\right)\hbox{d}A\hbox{d}x ,$$
(26)

where

$${d}_{xx}={\left(\frac{\partial {u}_{{\rm b}}\left(x,{z}_{{\rm b}},t\right)}{\partial x}\right)}^{2}+{\left(\frac{\partial {u}_{{\rm t}}\left(x,{z}_{{\rm b}},t\right)}{\partial x}\right)}^{2}+{\left(\frac{\partial w\left(x,t\right)}{\partial x}\right)}^{2}. $$
(27)

By applying integrations in the lateral direction, this equation can be expressed as follow

$${U}_{{\rm T}}=\frac{B}{2}\left[{\Lambda }_{{\rm t}}^{1}{\int }_{0}^{L}{\left(\frac{\partial {u}_{{\rm t}}}{\partial x}\right)}^{2}+{\Lambda }_{{\rm b}}^{1}{\int }_{0}^{L}{\left(\frac{\partial {u}_{{\rm b}}}{\partial x}\right)}^{2}+\left({\Lambda }_{{\rm t}}^{3}+{\Lambda }_{{\rm b}}^{3}\right){\int }_{0}^{L}{\left(\frac{{\partial }^{2}w}{{\partial x}^{2}}\right)}^{2}-2{\Lambda }_{{\rm t}}^{2}{\int }_{0}^{L}\frac{\partial {u}_{{\rm t}}}{\partial x}\frac{{\partial }^{2}w}{{\partial x}^{2}}-2{\Lambda }_{{\rm t}}^{2}{\int }_{0}^{L}\frac{\partial {u}_{{\rm b}}}{\partial x}\frac{{\partial }^{2}w}{{\partial x}^{2}}+\left({\Lambda }_{{\rm t}}^{1}+{\Lambda }_{{\rm b}}^{1}\right){\int }_{0}^{L}{\left(\frac{\partial w}{\partial x}\right)}^{2}\right]\hbox{d}x , $$
(28)

where the coefficients \({\Lambda }_{{\rm t}}^{i}\) and \({\Lambda }_{{\rm b}}^{i}\) (i = 1, 2, 3) are given in the Appendix. The total kinetic energy of the FGRM beam can be represented as

$$T={T}_{1}+{T}_{2},$$
(29)

where \({T}_{1}\) is the kinetic energy that arises from the edgewise bending motion and longitudinal deformation of the bottom and top FGM layers that can be expressed as

$${T}_{1}=\frac{1}{2}{\int }_{0}^{L}{\int }_{A}{\rho }_{i}\left({z}_{i}\right)\left({\left(\frac{\partial {u}_{i}\left(x,{z}_{{\rm b}},t\right)}{\partial t}\right)}^{2}+{\left(\frac{\partial w\left(x,t\right)}{\partial t}\right)}^{2}\right)\hbox{d}A\hbox{d}x ,\quad i=t,b , $$
(30)

where \({\rho }_{{\rm b}}\) and \({\rho }_{{\rm t}}\) are the mass density of bottom and top of the FGM layers, respectively. By expanding the equation and applying integrations in the lateral direction (y-direction), we get

$${T}_{1}=\frac{B}{2}\left[{F}_{{\rm t}}^{1}{\int }_{0}^{L}{\left(\frac{\partial {u}_{{\rm t}}}{\partial t}\right)}^{2}+{F}_{{\rm b}}^{1}{\int }_{0}^{L}{\left(\frac{\partial {u}_{{\rm b}}}{\partial t}\right)}^{2}+\left({F}_{{\rm t}}^{1}+{F}_{{\rm b}}^{1}\right){\int }_{0}^{L}{\left(\frac{\partial w}{\partial t}\right)}^{2}+\left({F}_{{\rm t}}^{3}+{F}_{{\rm b}}^{3}\right){\int }_{0}^{L}{\left(\frac{{\partial }^{2}w}{\partial t\partial x}\right)}^{2}-2{F}_{{\rm t}}^{2}{\int }_{0}^{L}\frac{\partial {u}_{{\rm t}}}{\partial t}\frac{{\partial }^{2}w}{\partial t\partial x}-2{F}_{{\rm b}}^{2}{\int }_{0}^{L}\frac{\partial {u}_{{\rm b}}}{\partial t}\frac{{\partial }^{2}w}{\partial t\partial x}\right]\hbox{d}x . $$
(31)

The coefficients \({{F}}_{{\rm t}}^{i}\) and \({{F}}_{{\rm b}}^{i}\) (i = 1, 2, 3) are given in the Appendix.

The kinetic energy due to rotational deformation and transverse displacement of the MR segment can be expressed as

$${T}_{2}=\frac{1}{2}{\int }_{0}^{L}{\int }_{A}{\rho }_{{\rm c}}{I}_{{\rm c}}{\left(\frac{\partial {\gamma }_{{\rm c}}}{\partial t}\right)}^{2}\hbox{d}A\hbox{d}x+\frac{1}{2}{\int }_{0}^{L}{\int }_{A}{\rho }_{{\rm c}}\left({\left(\frac{\partial w\left(x,t\right)}{\partial t}\right)}^{2}\right)\hbox{d}A\hbox{d}x , $$
(32)

where \({\rho }_{{\rm c}}\) and \({I}_{{\rm c}}\) are the mass density and the second moment of inertia of the MR layer, respectively.

The applied magnetic field can yield magnetoelastic loads in the top and bottom layers. The non-conservative work done owing to the magnetoelastic loads is given by [20]

$${W}_{nc}={\int }_{0}^{L}\left({n}_{{\rm t}}{u}_{{\rm t}}+{n}_{{\rm b}}{u}_{{\rm b}}+\left({m}_{{\rm t}}+{m}_{{\rm b}}\right)\frac{\partial w\left(x,t\right)}{\partial x}\right)\hbox{d}x , $$
(33)

where \({n}_{{\rm t}}\) and \({n}_{{\rm b}}\) are the magnetoelastic force, and \({m}_{{\rm t}}\) and \({m}_{{\rm b}}\) are the magnetoelastic distributed moment in the top and bottom skins, respectively, which can be expressed as [20]

$${n}_{i}=\frac{{B}_{0}^{2}b{h}_{i}}{{\mu }_{ei}}\left(\frac{{\partial }^{2}{u}_{i}}{{\partial x}^{2}}\right) ,\quad i=b, \, t ,$$
(34)
$${m}_{i}=\frac{{B}_{0}^{2}b{h}_{i}}{{\mu }_{0}}\left(\frac{\pi }{2ln\frac{x}{L-x}}\left(\frac{\partial {u}_{i}}{\partial x}\right)-\frac{{h}_{i}}{2\pi }ln\frac{x}{x-L}\left(\frac{{\partial }^{2}w}{{\partial x}^{2}}\right)+\frac{\partial w}{\partial x}\right)-\frac{{B}_{0}^{2}b{h}_{i}^{3}}{{12\mu }_{ei}}\left(\frac{{\partial }^{3}w}{{\partial x}^{3}}\right) ,\quad i=b,t , $$
(35)

where \({B}_{0}\) is the magnetic field intensity, \({\mu }_{0}\) is the permeability of the air gap and \({\mu }_{ei} (i=b, \, t)\) is the average permeability of ceramic and metal at any FGM layers, respectively.

By substituting the potential energy, kinetic energy, and the work done by the magnetoelastic loads into Hamilton’s principle (22), the governing equation for the FGMR sandwich beam under heat conduction can be expressed.

In the following, assumed mode method is used to solve the coupled equations by using the following relationships for transverse and longitudinal displacements:

$$w\left(x,t\right)=\sum_{i=1}^{{N}_{w}}{\psi }_{i}\left(x\right){\eta }_{i}\left(t\right), $$
(36)
$${u}_{{\rm b}}\left(x,t\right)={\sum }_{i=1}^{{N}_{{u}_{{\rm b}}}}{\varphi }_{i}\left(x\right){\delta }_{i}\left(t\right), $$
(37)
$${u}_{{\rm t}}\left(x,t\right)={\sum }_{i=1}^{{N}_{{u}_{{\rm t}}}}{\varphi }_{i}\left(x\right){\varepsilon }_{i}\left(t\right), $$
(38)

where \({\psi }_{i}\left(x\right)\) and \({\varphi }_{i}\left(x\right)\) are, respectively, the transverse and longitudinal principle vibration mode shape of the Euler–Bernoulli beam, and \({\eta }_{i}\left(t\right)\), \({\delta }_{i}\left(t\right)\) and \({\varepsilon }_{i}\left(t\right)\) are the generalized coordinates of the system. \({N}_{w}\), \({N}_{{u}_{{\rm b}}}\) and \({N}_{{u}_{{\rm t}}}\) are the number of corresponding modes used in transverse and longitudinal direction.

By substituting Eqs. (36)–(38) into Eq. (22) and after some manipulations, the global governing equations of the sFGMR sandwich beam are obtained as

$$\mathbf{M}\ddot{\mathbf{q}}+\mathbf{K}\mathbf{q}=0 ,$$
(39)

where \({\varvec{q}}=\left[{\eta }_{1}\cdots {\eta }_{{N}_{w}}, {\varepsilon }_{1}\cdots {\varepsilon }_{{N}_{{u}_{{\rm t}}}}, {\delta }_{1}\cdots {\delta }_{{N}_{{u}_{{\rm b}}}}\right]\) is the vector of generalized coordinates and M and K are the structural mass and stiffness matrices, respectively, that are defined as

$$\mathbf{M}=\left[\begin{array}{ccc}{\mathbf{M}}_{11}& {\mathbf{M}}_{12}& {\mathbf{M}}_{13}\\ {\mathbf{M}}_{21}& {\mathbf{M}}_{22}& {\mathbf{M}}_{23}\\ {\mathbf{M}}_{31}& {\mathbf{M}}_{32}& {\mathbf{M}}_{33}\end{array}\right],\quad {\varvec{K}}=\left[\begin{array}{ccc}{\mathbf{K}}_{11}& {\mathbf{K}}_{12}& {\mathbf{K}}_{13}\\ {\mathbf{K}}_{21}& {\mathbf{K}}_{22}& {\mathbf{K}}_{23}\\ {\mathbf{K}}_{31}& {\mathbf{K}}_{32}& {\mathbf{K}}_{33}\end{array}\right] .$$
(40)

The expressions for the mass and stiffness matrices of the above equation are given in the Appendix.

Assuming harmonic motion \({\varvec{r}}={{\varvec{r}}}_{0}^{\boldsymbol{*}}\hbox{exp}\left({\rm i}pt\right)\), where \({{\varvec{r}}}_{0}^{\boldsymbol{*}}\) and p are the eigenvectors and eigenvalues of the system and \(i=\sqrt{-1}\), the equation of motion of the beam is transformed into a standard eigenvalue problem as

$${\varvec{K}}{{\varvec{r}}}_{0}^{\boldsymbol{*}}={p}^{2}{\varvec{M}}{{\varvec{r}}}_{0}^{\boldsymbol{*}}. $$
(41)

Eventually, the natural frequency and modal loss factor of the FGRM beam can be obtained as

$$\omega =\sqrt{{\rm Re}\left({p}^{2}\right)}, $$
(42)
$$\eta =\frac{\hbox{Im}\left({p}^{2}\right)}{\hbox{Re}\left({p}^{2}\right)}.$$
(43)

3 Validation

To investigate the behavior and determine the effect of magnetoelastic loads and temperature dependency on the vibration and damping behavior of FGMR sandwich beam, a computer code was developed. To evaluate the accuracy of the code, the results from this study are verified by comparing the results with those available in the literature for several cases.

First of all, the first three natural frequencies of MRE-embedded cantilever sandwich beam with magnetoelastic effects are compared with analytical (Nayak et al. [15]) and finite element method results (Nayak et al. [18] and Rokn-Abadi et al. [28]) in Table 1.

Table 1 Comparison of the first three natural frequencies for different magnetic field intensities
Full size table

The comparisons show that the natural frequencies obtained by the present method are in good agreement with the numerical and analytical existing results but there is still a slight difference. The relative difference in the values of the free vibration natural frequencies determined with the use of different reference for this type of cantilever sandwich beam is equal to 0.06% and increases to 3.7% for the first frequency and is equal to 0.01% that increases to 6.1% for the second natural frequency. The differences for the three natural frequency are from 0.04 up to 8.09%. There are no significant differences in the frequency values obtained from the proposed description and from other available references. This could be due to the solve method or to consider number of terms of total kinetic and potential energy equations. Also the key approximation involved in the Guyan reduction that all of the inertia of slave coordinates are ignored.

In the second investigation, the first four natural frequencies of the MR sandwich beam are compared with those reported by Nayak et al. [17] and Rokn abadi et al. [28] for three different boundary conditions; clamped-free, simply supported, and clamped–clamped boundary conditions. Comparison of these results and their difference show in Table 2. It is seen that the natural frequencies obtained by the present work have a good agreement with the results in the literature.

Table 2 Comparison of the first four natural frequencies for three different boundary conditions
Full size table

In Table 3 another validity of the present formulations for the FGM beam under heat condition is demonstrated by comparing the non-dimensional natural frequency corresponding to the first and fifth modes under cantilever, hinged–hinged and clamped–clamped conditions with considering the elastic core for the sandwich beam [63]. The constituent material properties of the FG beam have been chosen from this reference. For Timoshenko beam theory and for used value of index volume fraction in this reference, good agreement is observed between the results of the present work and Ref. [63], especially for low frequencies. Using the Timoshenko beam theory and stocky beam model [75] in this reference causes higher differences at high frequencies.

Table 3 Dimensionless natural frequencies of laminated FGM beams under heat condition \(\left(L/H=10, {T}_{{\rm t}}={T}_{{\rm b}}=50\,{^\circ{\rm C}}, e=2\right)\)
Full size table

4 Results and discussion

The vibration characteristics of the FGRM sandwich beam are influenced by various parameters such as the magnetic field intensity, temperature changes, the geometry of the beam, volume fraction index of FGM layers, boundary conditions, and thickness of any layer. The free vibration of the FGMR sandwich beam with elastomer core in the edgewise direction, is studied in this section. The FG material chosen in this study is a mixture of Titanium alloy (Ti–4V–6Al) and Zirconia (ZrO2) as presented in Table 4 [67].

Table 4 Temperature-dependent coefficients of elastic modulus E (Pa), coefficient of thermal expansion α (\({K}^{-1}\)), mass density ρ (\(Kg/{m}^{3}\)), thermal conductivity \(\kappa\) (\(W/mK\)), and Poisson’s ratio \(\nu\), of FGM layers [67]
Full size table

The other temperature independent parameters and material properties of the FGMR beam are listed in Table 5.

Table 5 Geometry and properties of the FGMR elastomer sandwich beam
Full size table

For the core layer, a natural rubber-based MRE containing 80% iron particles directed along the magnetic field lines (z-axis) is used in this study. The shear storage modulus and loss factor of the MR elastomer used in this investigation are presented as [18]

$${G}^{^{\prime}}=\left(-6.9395{B}_{0}^{6}-9.1077{B}_{0}^{5}+71.797{B}_{0}^{4}-93.422{B}_{0}^{3}+38.778{B}_{0}^{2}+2.43B_{0}+2.7006\right)\,\hbox{MPa}, $$
(44)
$${\eta }_{{\rm c}}=5.3485{B}_{0}^{6}-17.787{B}_{0}^{5}+22.148{B}_{0}^{4}-12.185{B}_{0}^{3}+2.3522{B}_{0}^{2}+0.1526B_{0}+0.228 .$$
(45)

The first eight natural frequencies and loss factors of the cantilever sandwich beam are, respectively, presented in Tables 6 and 7 for different number of modes to study the convergence of the results. It can be seen that about eight modes are sufficient to reach the desired convergence.

Table 6 Convergence study of the natural frequencies for cantilever FGRM sandwich beam (B0 = 0, ΔT = 0, e = 2)
Full size table
Table 7 Convergence study of the loss factors for cantilever FGRM sandwich beam (B0 = 0, ΔT = 0, e = 2\()\)
Full size table

4.1 Effect of magnetic field intensity

The effects of magnetic field intensity on natural frequency and modal loss factor of the FGMR beam are studied in this section. Variation of the first natural frequencies and first modal loss factor with applied magnetic field and different values of volume fraction index for clamped-free (cantilever), simply supported, and clamped–clamped boundary conditions are indicated in Figs. 3, 4, and 5, respectively. It is obvious that the natural frequencies and modal loss factors increase with increasing the magnetic field intensity from 0 to 0.6 Tesla. Also, the volume fraction index of the FGM layers has significant effect on the vibrational characteristics of the sandwich beam. The increase in the volume fraction index causes the increase in the volumetric percentage of metallic constituent in the FGM layers. This causes that the natural frequencies decrease by increasing volume fraction index, but the natural frequencies increase by increasing volume fraction index, for every boundary condition.

Fig. 3
figure 3

Variation of the first natural frequencies (a) and first loss factors with applied magnetic field (\(B_{0}\)) for different values of volume fraction index and Cantilever condition

Full size image
Fig. 4
figure 4

Variation of the first natural frequencies (a) and first loss factors with applied magnetic field (\(B_{0}\)) for different values of volume fraction index and simply supported condition

Full size image
Fig. 5
figure 5

Variation of the first natural frequencies (a) and first loss factors with applied magnetic field (\(B_{0}\)) for different values of volume fraction index and clamped–clamped condition

Full size image

Also, for simply supported boundary condition, the loss factor reaches about ninety percent of its maximum value at about 0.23 Tesla, for each volume fraction index. This point can be useful and important for design, especially reaching a high magnetic field intensity is not possible.

4.2 Effect of temperature and slenderness ratio

In this section the influence of temperature distribution on the vibration of FGMR sandwich beam has been shown for different boundary condition and volume fraction index. It is assumed that the temperature of the bottom surface is constant and equal to ambient temperature (T = 300 K) and the temperature of the top surface changes only. As is evident from Figs. 6, 7 and 8 for clamped-free, simply supported, and clamped–clamped boundary conditions, when the top surface temperature increases from 300 to 600 K, the first fundamental frequencies decrease with increasing temperature since the stiffness deteriorates in this process. Also, as is evident from the figures, the natural frequencies decrease by increasing volume fraction index, for each boundary condition.

Fig. 6
figure 6

Variation of the first natural frequencies with variation of top surface temperature for different values of volume fraction index and cantilever condition (\(B_{0}=0.4\))

Full size image
Fig. 7
figure 7

Variation of the first natural frequencies with variation of top surface temperature for different values of volume fraction index and simply supported condition (\(B_{0}=0.2\))

Full size image
Fig. 8
figure 8

Variation of the first natural frequencies with variation of top surface temperature for different values of volume fraction index and clamped- clamped condition (\(B_{0}=0.2\))

Full size image

Also the effect of the slenderness ratio on the fundamental frequency of the FGMR beam is presented in Fig. 9. The results are presented for cantilever, clamped–clamped and hinged–hinged FGRM sandwich beams. As expected, the beam with a smaller slenderness ratio has a higher fundamental frequency.

Fig. 9
figure 9

Effect of the slenderness ratio on the first frequency of FGMR beam under heat condition (Tb=300, ΔT=50, B0=0.3, e=1)

Full size image

5 Conclusions

In this study, the effects of temperature dependency and magnetoelastic loads on the free vibration of an FGMR elastomer sandwich beam with magnetorheological core and Functionally Graded Material (FGM) constraining lamina under high temperature environment, are investigated. The material properties of FGM layers are assumed to be temperature-dependent and vary continuously through-the-thickness according to a simple power-law distribution in terms of the volume fractions of the constituents. Also, it is assumed that the beam may be clamped, hinged, or free at its ends and is subjected to one-dimensional steady heat conduction in the thickness direction. The classical Hamilton’s principle and the assumed mode method are used to set up the equations of motion and the modal frequencies and loss factors of the three-layer sandwich beam are obtained by eigenvalue analysis of the system. The results are validated in comparison with the existing results in the literature. Finally, the effects of the applied magnetic field, volume fraction index, temperature change, and slenderness ratio are studied for different boundary conditions.

It was demonstrated that the magnetic field changes the stiffness and damping properties of the sandwich beam. Therefore, the natural frequencies and the modal loss factors of the system can be controlled by changing the intensity of magnetic field. Also it was concluded that the temperature rise has more significant effect on the frequency parameters.

The other most important points are summarized as follows:

  •   The natural frequencies and corresponding modal loss factors of FGRM sandwich beam, increases with the increase in the magnetic field intensities for each amount of volume fraction index and boundary condition.

  •   The rise in the external temperature reduces the fundamental frequencies for simply-supported, Cantilever, and clamped–clamped boundary conditions of FGRM beam.

  •   For all boundary conditions, the frequency decreases as increases in the volume fraction index, whereas the mode loss factors increase. So, the volume fraction is an essential parameter in structural component design.

  •   The beam slenderness ratio, and the end support condition significantly affect the dynamic behavior of FGRM sandwich beam. The beam with a smaller slenderness ratio has a higher fundamental frequency.

Concluding it can be said that the sandwich beam or panel structure that made of FGM and MR materials has two functional performances. One, due to the magnetorheological material and them properties, we can control of vibration behavior in the turbomachine’s blades. On the other hand, due to ceramic in the functionally graded materials as heat-shielding materials we can prevent damage to the middle layer. Also, due to the metal in the functionally graded materials, we can reduce the possible failures induced by mechanical load or fatigue.

Generally, it can be said that using the functionally graded material and MR material simultaneously on sandwich structural elements in the high temperature environments reduces the possible failures that are induced by thermo or combined thermo-mechanical loadings.