1 Introduction

The art of mathematical modeling of mechanical systems is based on the correct estimation of the acting forces and torques that affect the dynamics and provide qualitative and quantitative properties of motion. In those cases where the acting forces can be considered known and time invariant, the estimations are based on calculating the absolute values of forces and torques. In cases of time-varying forces and torques, such estimates are not enough. Important quantitative characteristics of variable force factors are their mean values. A comparison of the mean values of acting forces often reveals the main ones, and the rest can be classified as disturbances. However, numerous well-known examples of the analysis of the mechanical systems behavior indicate that disturbances with zero mean values are not necessarily insignificant. Therefore, neglecting such disturbances is unacceptable in many problems. At the same time, their account often significantly complicates analytical qualitative analysis of the mechanical system behavior [1,2,3,4,5,6]. Hence, on the one hand, there is a significant interest of specialists in problems of the dynamics of systems subjected to perturbations with zero mean values, and on the other hand, these complex problems are not well understood, and therefore the stream of publications on this topic continues [7,8,9,10,11,12]. Attitude stabilization of a spacecraft is one of the typical nonlinear problems, usually complicated by the presence of numerous nonstationary disturbances, including those with zero mean values. This problem is relevant in many astronautical and engineering applications [1, 12,13,14,15,16]. This article is dedicated to this specific problem. It is worth mentioning that a similar problem was earlier considered in our paper [17], but with other assumptions concerning disturbances and control torques.

2 Statement of the problem

Let a rigid body rotating around its mass center O with angular velocity \(\vec \omega \) be given. Denote by \(Ox_1x_2x_3\) the principal central axes of inertia of the body. The attitude motion of the body under a control torque \(\vec L\) is described by the Euler equations [1]

$$\begin{aligned} {\mathbf {J}} {\dot{\vec \omega }} + \vec \omega \times {\mathbf {J}} \vec \omega =\vec L. \end{aligned}$$
(1)

Here, \({\mathbf {J}}=\hbox \mathrm{diag} \{A_1,A_2,A_3\}\) is inertia tensor of the body in the axes \(Ox_1 x_2 x_3\).

Consider two right triples of mutually orthogonal unit vectors \(\vec \xi _1\), \(\vec \xi _2\), \(\vec \xi _3\) and \(\vec \eta _1\), \(\vec \eta _2\), \(\vec \eta _3\). Let vectors \(\vec \xi _1\), \(\vec \xi _2\), \(\vec \xi _3\) be constant in the inertial frame, and vectors \(\vec \eta _1\), \(\vec \eta _2\), \(\vec \eta _3\) be constant in the body-fixed frame. Thus, vectors \(\vec \xi _1\), \(\vec \xi _2\), \(\vec \xi _3\) rotate with respect to the system \(Ox_1 x_2 x_3\) with the angular velocity \(-\vec {\omega }\). Hence, we obtain the Poisson kinematic equations

$$\begin{aligned} \dot{\vec {\xi }}_i=- \vec \omega \times \vec {\xi }_i, \quad i=1,2,3. \end{aligned}$$
(2)

It is worth noting that the systems (1), (2) may describe a wide variety of objects such as aircraft, satellite, submarine, missile, and quadcopter (Fig. 1) [1, 18,19,20].

Fig. 1
figure 1

Quadcopter attitude motion and angles \(\phi \), \(\theta \), \(\psi \)

Full size image

Let torque \(\vec L\) be the sum of a dissipative component \(\vec L_d\) and a restoring one \(\vec L_r\): \(\vec L=\vec L_d+\vec L_r\). We will assume that the dissipative torque is linear with respect to \(\vec \omega \) [21, 22] and it is defined by the formula

$$\begin{aligned} \vec L_d=h \mathbf {B}\vec \omega , \end{aligned}$$
(3)

where \(\mathbf {B}\) is a constant symmetric and negative definite matrix, h is a positive parameter. The restoring torque \(\vec L_r\) should be chosen such that the torque \(\vec L\) provides triaxial stabilization of the body, i.e., the system of Eqs. (1), (2) should admit the asymptotically stable equilibrium position

$$\begin{aligned} \vec {\omega }= \vec {0}, \qquad \vec {\xi }_i= \vec {\eta }_i, \quad i=1,2,3. \end{aligned}$$
(4)

It is known (for example, see [19]), that the torque \(\vec L_r\) can be defined by the formula

$$\begin{aligned} \vec L_r= -c f^\nu (\vec \xi _1,\vec \xi _2) \left( a_1 \vec \xi _1\times \vec \eta _1+a_2 \vec \xi _2\times \vec \eta _2\right) . \end{aligned}$$
(5)

Here, c, \(a_1\), \(a_2\) are positive constants,

$$\begin{aligned} f(\vec \xi _1,\vec \xi _2)= \left( {a_1} \Vert \vec \xi _1- \vec \eta _1\Vert ^2+{a_2} \Vert \vec \xi _2- \vec \eta _2\Vert ^2\right) /2, \end{aligned}$$

\(\nu \ge 0\), and \(\Vert \cdot \Vert \) is the Euclidean norm of a vector.

In the present paper, we consider the case where, along with the control torque \(\vec L\), a nonstationary perturbing torque \(\vec {L}_p\) acts on the body.

3 Construction of a strict Lyapunov function for the unperturbed system

Consider the unperturbed system composed of the Poisson kinematic Eq. (2) and the Euler dynamic equations

$$\begin{aligned} {\mathbf {J}} {\dot{\vec \omega }} + \vec \omega \times {\mathbf {J}} \vec \omega =\vec L_d+\vec L_r, \end{aligned}$$
(6)

where dissipative and restoring torques are defined by the formulae (3) and (5), respectively.

Stability of the equilibrium position (4) for the system (2), (6) was proved in [19]. However, it is worth mentioning that results of [19] are based on construction of a weak Lyapunov function. The derivative of this function along the solutions of the considered system is only nonnegative. Such Lyapunov functions are not well applicable to robustness analysis of nonlinear systems, since their negative semi-definite derivatives could become positive under arbitrarily small perturbations [23, 24].

In [20, 25], an approach was developed to transform the weak Lyapunov function constructed in [19] into a strict one (a function with negative definite derivative) [26, 27]. At the same time, it should be noted that the approach of [20, 25] can be used only for the case of linear restoring torque. Moreover, this approach is not effective for the investigation of the problem studied in the present paper. Therefore, we will propose another construction of a strict Lyapunov function for the system (2), (6).

Choose a Lyapunov function candidate as follows:

$$\begin{aligned} V\left( \vec \omega ,\vec \xi _1,\vec \xi _2\right)= & {} \dfrac{\lambda }{2} {\vec \omega }^\top {\mathbf {J}} \vec \omega +\dfrac{a_1}{2} \Vert \vec {\xi }_1- \vec {\eta }_1\Vert ^2 +\dfrac{a_2}{2} \Vert \vec {\xi }_2- \vec {\eta }_2\Vert ^2\nonumber \\&-\dfrac{1}{h} \left( a_1 \vec \xi _1\times \vec \eta _1+a_2 \vec \xi _2\times \vec \eta _2\right) ^\top \mathbf {B}^{-1} {\mathbf {J}} \vec \omega . \end{aligned}$$
(7)

Here, \(\lambda \) is an auxiliary positive parameter. Then,

$$\begin{aligned}&\lambda c_1 \Vert \vec \omega \Vert ^2 +\dfrac{a_1}{2} \Vert \vec {\xi }_1- \vec {\eta }_1\Vert ^2 +\dfrac{a_2}{2} \Vert \vec {\xi }_2- \vec {\eta }_2\Vert ^2\\&\quad -\frac{c_3}{h} \Vert \vec \omega \Vert \left( \Vert \vec {\xi }_1- \vec {\eta }_1\Vert + \Vert \vec {\xi }_2- \vec {\eta }_2\Vert \right) \le V\left( \vec \omega ,\vec \xi _1,\vec \xi _2\right) \\&\quad \le \lambda c_2 \Vert \vec \omega \Vert ^2 +\dfrac{a_1}{2} \Vert \vec {\xi }_1- \vec {\eta }_1\Vert ^2 +\dfrac{a_2}{2} \Vert \vec {\xi }_2- \vec {\eta }_2\Vert ^2 +\frac{c_3}{h} \Vert \vec \omega \Vert \left( \Vert \vec {\xi }_1- \vec {\eta }_1\Vert + \Vert \vec {\xi }_2- \vec {\eta }_2\Vert \right) , \end{aligned}$$

where \(c_1, c_2, c_3\) are positive constants.

Differentiating the function (7) along the solutions of (2), (6), we obtain

$$\begin{aligned} \dot{V}= & {} \lambda h {\vec \omega }^\top {\mathbf {B}} \vec \omega -\lambda c f^\nu {\vec \omega }^\top \left( a_1 \vec \xi _1\times \vec \eta _1+a_2 \vec \xi _2\times \vec \eta _2\right) \\&+\dfrac{1}{h}\bigl (a_1 (\vec \omega \times \vec \xi _1)\times \vec \eta _1+a_2 (\vec \omega \times \vec \xi _2)\times \vec \eta _2)^\top \mathbf {B}^{-1} {\mathbf {J}} \vec \omega \\&+\dfrac{1}{h} \left( a_1 \vec \xi _1\times \vec \eta _1+a_2 \vec \xi _2\times \vec \eta _2\right) ^\top \mathbf {B}^{-1}(\vec \omega \times ({\mathbf {J}}\vec \omega ))\\&+\dfrac{c}{h} f^\nu \left( a_1 \vec \xi _1\times \vec \eta _1+a_2 \vec \xi _2\times \vec \eta _2\right) ^\top \mathbf {B}^{-1} \left( a_1 \vec \xi _1\times \vec \eta _1+a_2 \vec \xi _2\times \vec \eta _2\right) . \end{aligned}$$

The matrix \(\mathbf {B}\) is negative definite. Therefore, the inequality

$$\begin{aligned} \dot{V}\le & {} -\left( \lambda h c_4-\dfrac{c_5}{h}\right) \Vert \vec \omega \Vert ^2 -\dfrac{c_6}{h} f^\nu \left\| a_1 \vec \xi _1\times \vec \eta _1 +a_2 \vec \xi _2\times \vec \eta _2 \right\| ^2\\&+\dfrac{c_7}{h} \Vert \vec \omega \Vert ^2 \left( \Vert \vec \xi _1- \vec \eta _1\Vert + \Vert \vec \xi _2- \vec \eta _2\Vert \right) +\lambda c_8 \Vert \vec \omega \Vert \left( \Vert \vec \xi _1- \vec \eta _1\Vert + \Vert \vec \xi _2- \vec \eta _2\Vert \right) ^{2\nu +1} \end{aligned}$$

holds. Here, \(c_i>0\), \(i=4,\ldots ,8\).

Choose a number \(\varepsilon \in (0,1)\). In [28], it was proved that there exists \(\delta >0\) such that

$$\begin{aligned} \left\| a_1 \vec \xi _1\times \vec \eta _1 +a_2 \vec \xi _2\times \vec \eta _2 \right\| ^2\ge \varepsilon \left( a^2_1 \Vert \vec \xi _1- \vec \eta _1\Vert ^2 +a^2_2 \Vert \vec \xi _2-\vec \eta _2\Vert ^2 \right) \end{aligned}$$

for \(\Vert \vec \xi _1- \vec \eta _1\Vert ^2 +\Vert \vec \xi _2-\vec \eta _2\Vert ^2<\delta ^2\). Hence,

$$\begin{aligned} \dot{V}\le & {} -\left( \lambda h c_4-\dfrac{c_6}{h} \right) \Vert \vec \omega \Vert ^2 -\dfrac{c_9}{h} \left( \Vert \vec \xi _1- \vec \eta _1\Vert ^2+ \Vert \vec \xi _2- \vec \eta _2\Vert ^2 \right) ^{\nu +1}\\&+\dfrac{c_7}{h} \Vert \vec \omega \Vert ^2 \left( \Vert \vec \xi _1- \vec \eta _1\Vert + \Vert \vec \xi _2- \vec \eta _2\Vert \right) +\lambda c_8 \Vert \vec \omega \Vert \left( \Vert \vec \xi _1- \vec \eta _1\Vert + \Vert \vec \xi _2- \vec \eta _2\Vert \right) ^{2\nu +1} \end{aligned}$$

for \(\Vert \vec \xi _1- \vec \eta _1\Vert ^2 +\Vert \vec \xi _2-\vec \eta _2\Vert ^2<\delta ^2\), where \(c_9=\mathrm{const}>0\).

As a result, we obtain that there exist positive numbers \(\lambda \), h, \(\bar{\delta }\) such that

$$\begin{aligned}&\frac{1}{2} \lambda c_1 \Vert \vec \omega \Vert ^2 +\dfrac{a_1}{4} \Vert \vec {\xi }_1- \vec {\eta }_1\Vert ^2 +\dfrac{a_2}{4} \Vert \vec {\xi }_2- \vec {\eta }_2\Vert ^2\\&\quad \le V\left( \vec \omega ,\vec \xi _1,\vec \xi _2\right) \le 2 \lambda c_2 \Vert \vec \omega \Vert ^2 +{a_1} \Vert \vec {\xi }_1- \vec {\eta }_1\Vert ^2 +{a_2} \Vert \vec {\xi }_2- \vec {\eta }_2\Vert ^2,\\&\quad \dot{V}\le -\frac{1}{2} \lambda h c_4 \Vert \vec \omega \Vert ^2 -\dfrac{c_9}{2h} \left( \Vert \vec \xi _1- \vec \eta _1\Vert ^2+ \Vert \vec \xi _2- \vec \eta _2\Vert ^2 \right) ^{\nu +1} \end{aligned}$$

for \(\vec \omega \in \mathbb R^3\), \(\Vert \vec \xi _1- \vec \eta _1\Vert ^2 +\Vert \vec \xi _2-\vec \eta _2\Vert ^2<{\bar{\delta }}^2\).

It is worth noting that, in the case where \(\nu =0\), value of \(\lambda \) should be sufficiently small and the value of h should be sufficiently large, whereas, in the case where \(\nu >0\), h may be an arbitrary positive number and \(\lambda \) should be sufficiently large.

Thus, for an appropriate choice of \(\lambda \) and h, (7) is a strict Lyapunov function for the unperturbed system (2), (6).

In what follows, using the approach developed in [29,30,31] and taking into account structure and properties of the nonstationary torque \(\vec L_p\), we will propose some modifications of the function (7) to derive conditions ensuring asymptotic stability of the equilibrium position (4) of the perturbed system.

4 Linear restoring and perturbing torques

Let \(\nu =0\) and \(\vec L_p=\mathbf {D}_1(t)(\vec \xi _1- \vec \eta _1) +\mathbf {D}_2(t)(\vec \xi _2- \vec \eta _2)\). Here matrices \(\mathbf {D}_1(t), \mathbf {D}_2(t)\in \mathbb R^{3\times 3}\) are continuous and bounded for \(t\in [0,+\infty )\). Then, the system (1) takes the form

$$\begin{aligned} {\mathbf {J}} {\dot{\vec \omega }} + \vec \omega \times {\mathbf {J}} \vec \omega= & {} h \mathbf {B}\vec \omega -a_1 \vec \xi _1\times \vec \eta _1\nonumber \\&-a_2 \vec \xi _2\times \vec \eta _2 +\mathbf {D}_1(t)(\vec \xi _1- \vec \eta _1) +\mathbf {D}_2(t)(\vec \xi _2- \vec \eta _2). \end{aligned}$$
(8)

Thus, we consider the case where restoring and perturbing torques are linear.

Let us determine conditions under which perturbations do not disturb asymptotic stability of the equilibrium position (4).

Consider the derivative of the Lyapunov function (7) with respect to the system (2), (8). If \(\lambda \) and \(\bar{\delta }\) are sufficiently small and h is sufficiently large, then the inequalities

$$\begin{aligned}&\dot{V}\le -\frac{1}{2} \lambda h c_4 \Vert \vec \omega \Vert ^2 -\dfrac{c_9}{2h} \left( \Vert \vec \xi _1- \vec \eta _1\Vert ^2+ \Vert \vec \xi _2- \vec \eta _2\Vert ^2 \right) \nonumber \\&\qquad +\lambda \vec \omega ^\top \vec L_p -\dfrac{1}{h} \left( a_1 \vec \xi _1\times \vec \eta _1+a_2 \vec \xi _2\times \vec \eta _2\right) ^\top \mathbf {B}^{-1}\vec L_p\nonumber \\&\quad \le -\frac{1}{3} \lambda h c_4 \Vert \vec \omega \Vert ^2 -\dfrac{c_9}{3h} \left( \Vert \vec \xi _1- \vec \eta _1\Vert ^2+ \Vert \vec \xi _2- \vec \eta _2\Vert ^2 \right) \nonumber \\&\qquad -\dfrac{1}{h} \left( a_1 \vec \xi _1\times \vec \eta _1+a_2 \vec \xi _2\times \vec \eta _2\right) ^\top \mathbf {B}^{-1}\vec L_p \end{aligned}$$
(9)

hold for \(\vec \omega \in \mathbb R^3\), \(\Vert \vec \xi _1- \vec \eta _1\Vert ^2 +\Vert \vec \xi _2-\vec \eta _2\Vert ^2<{\bar{\delta }}^2\).

Theorem 1

Let the matrices

$$\begin{aligned} \int \limits _0^{t} \!\mathbf {D}_i(s) \, ds, \quad i=1,2, \end{aligned}$$
(10)

be bounded for \(t\in [0,+\infty )\). Then, there exists a number \(h_0>0\) such that the equilibrium position (4) of the system (2), (8) is uniformly asymptotically stable for any \(h\ge h_0\).

Proof

Modify the Lyapunov function (7) as follows:

$$\begin{aligned} V_1\left( t,\vec \omega ,\vec \xi _1,\vec \xi _2\right)= & {} V\left( \vec \omega ,\vec \xi _1,\vec \xi _2\right) +\dfrac{1}{h} \bigl (a_1 \vec \xi _1\times \vec \eta _1\\&+a_2 \vec \xi _2\times \vec \eta _2\bigr )^\top \mathbf {B}^{-1} \sum _{i=1}^2 \int \limits _0^{t} \mathbf {D}_i(s)\,ds \, (\vec \xi _i- \vec \eta _i). \end{aligned}$$

Using the results of the previous Section and the inequalities (9), it is easy to verify that one can choose and fix sufficiently small values of \(\lambda \) and \(\bar{\delta }\) and after that find \(h_0>0\) such that if \(h\ge h_0\), \(\Vert \vec \xi _1- \vec \eta _1\Vert ^2 +\Vert \vec \xi _2-\vec \eta _2\Vert ^2<{\bar{\delta }}^2\), then the function \(V_1\left( t,\vec \omega ,\vec \xi _1,\vec \xi _2\right) \) and its derivative with respect to the system (2), (8) satisfy the estimates

$$\begin{aligned}&\frac{1}{2} \lambda c_1 \Vert \vec \omega \Vert ^2 +\dfrac{a_1}{4} \Vert \vec {\xi }_1- \vec {\eta }_1\Vert ^2 +\dfrac{a_2}{4} \Vert \vec {\xi }_2- \vec {\eta }_2\Vert ^2\\&\qquad -\frac{b_1}{h} \left( \Vert \vec \xi _1- \vec \eta _1\Vert ^2 +\Vert \vec \xi _2-\vec \eta _2\Vert ^2\right) \le V_1\left( t,\vec \omega ,\vec \xi _1,\vec \xi _2\right) \\&\quad \le 2 \lambda c_2 \Vert \vec \omega \Vert ^2 +{a_1} \Vert \vec {\xi }_1- \vec {\eta }_1\Vert ^2 +{a_2} \Vert \vec {\xi }_2- \vec {\eta }_2\Vert ^2 +\frac{b_1}{h} \left( \Vert \vec \xi _1- \vec \eta _1\Vert ^2 +\Vert \vec \xi _2-\vec \eta _2\Vert ^2\right) ,\\&\quad \dot{V}_1\le -\frac{1}{3} \lambda h c_4 \Vert \vec \omega \Vert ^2 -\dfrac{c_9}{3h} \left( \Vert \vec \xi _1- \vec \eta _1\Vert ^2+ \Vert \vec \xi _2- \vec \eta _2\Vert ^2 \right) \\&\qquad +\frac{b_2}{h} \Vert \vec \omega \Vert \left( \Vert \vec \xi _1- \vec \eta _1\Vert +\Vert \vec \xi _2-\vec \eta _2\Vert \right) , \end{aligned}$$

where \(b_1\), \(b_2\) are positive constants.

Hence, for sufficiently large values of \(h_0\), the inequalities

$$\begin{aligned}&\frac{1}{2} \lambda c_1 \Vert \vec \omega \Vert ^2 +\dfrac{a_1}{8} \Vert \vec {\xi }_1- \vec {\eta }_1\Vert ^2 +\dfrac{a_2}{8} \Vert \vec {\xi }_2- \vec {\eta }_2\Vert ^2\\&\quad \le V_1\left( t,\vec \omega ,\vec \xi _1,\vec \xi _2\right) \le 2 \left( \lambda c_2 \Vert \vec \omega \Vert ^2 +{a_1} \Vert \vec {\xi }_1- \vec {\eta }_1\Vert ^2 +{a_2} \Vert \vec {\xi }_2- \vec {\eta }_2\Vert ^2\right) ,\\&\quad \dot{V}_1\le -\frac{1}{4} \lambda h c_4 \Vert \vec \omega \Vert ^2 -\dfrac{c_9}{4h} \left( \Vert \vec \xi _1- \vec \eta _1\Vert ^2+ \Vert \vec \xi _2- \vec \eta _2\Vert ^2 \right) \end{aligned}$$

hold for \(h\ge h_0\), \(t\ge 0\), \(\vec \omega \in \mathbb R^3\), \(\Vert \vec \xi _1- \vec \eta _1\Vert ^2 +\Vert \vec \xi _2-\vec \eta _2\Vert ^2<{\bar{\delta }}^2\).

Thus, all the assumptions of the theorem on the uniform asymptotic stability (see [32]) are fulfilled for the function \(V_1\left( t,\vec \omega ,\vec \xi _1,\vec \xi _2\right) \). \(\square \)

Remark 1

For instance, the assumption of Theorem 1 on boundedness of the matrices (10) is fulfilled if entries of these matrices are periodic functions with zero mean values.

The next theorem gives us stability conditions for a wider class of perturbed systems.

Theorem 2

Let

$$\begin{aligned} \frac{1}{T} \int \limits _t^{t+T} \!\mathbf {D}_i(s) \, ds \rightarrow \mathbf {0} \ \ \ { as} \ \ \ T\rightarrow +\infty , \ \ \ i=1,2, \end{aligned}$$
(11)

uniformly with respect to \(t\in [0,+\infty )\). Then, there exists a number \(h_0>0\) such that the equilibrium position (4) of the system (2), (8) is uniformly asymptotically stable for any \(h\ge h_0\).

Proof

In this case, we will use the following modification of the Lyapunov function (7):

$$\begin{aligned} V_2\left( t,\vec \omega ,\vec \xi _1,\vec \xi _2\right)= & {} V\left( \vec \omega ,\vec \xi _1,\vec \xi _2\right) +\dfrac{1}{h} \bigl (a_1 \vec \xi _1\times \vec \eta _1\\&+a_2 \vec \xi _2\times \vec \eta _2\bigr )^\top \mathbf {B}^{-1} \sum _{i=1}^2 \int \limits _0^{t} e^{\alpha (s-t)} \mathbf {D}_i(s)\,ds \, (\vec \xi _i- \vec \eta _i), \end{aligned}$$

where \(\alpha \) is a positive parameter.

Under an appropriate choice of \(\lambda \), \(h_0\), \(\bar{\delta }\), we obtain

$$\begin{aligned}&\frac{1}{2} \lambda c_1 \Vert \vec \omega \Vert ^2 +\dfrac{a_1}{4} \Vert \vec {\xi }_1- \vec {\eta }_1\Vert ^2 +\dfrac{a_2}{4} \Vert \vec {\xi }_2- \vec {\eta }_2\Vert ^2 \\&\qquad -\frac{b_3}{\alpha h} \left( \Vert \vec \xi _1- \vec \eta _1\Vert ^2 +\Vert \vec \xi _2-\vec \eta _2\Vert ^2\right) \le V_2\left( t,\vec \omega ,\vec \xi _1,\vec \xi _2\right) \\&\quad \le 2 \lambda c_2 \Vert \vec \omega \Vert ^2 +{a_1} \Vert \vec {\xi }_1- \vec {\eta }_1\Vert ^2 +{a_2} \Vert \vec {\xi }_2- \vec {\eta }_2\Vert ^2 +\frac{b_3}{\alpha h} \left( \Vert \vec \xi _1- \vec \eta _1\Vert ^2 +\Vert \vec \xi _2-\vec \eta _2\Vert ^2\right) , \\&\quad \dot{V}_2\le -\frac{1}{3} \lambda h c_4 \Vert \vec \omega \Vert ^2 -\dfrac{c_9}{3h} \left( \Vert \vec \xi _1- \vec \eta _1\Vert ^2+ \Vert \vec \xi _2- \vec \eta _2\Vert ^{2} \right) \\&\qquad +\frac{b_4}{\alpha h}\Vert \vec \omega \Vert \left( \Vert \vec \xi _1- \vec \eta _1\Vert +\Vert \vec \xi _2-\vec \eta _2\Vert \right) \\&\qquad +\frac{\alpha b_5}{h} \sum _{i=1}^2 \left\| \int \limits _0^{t} e^{\alpha (s-t)} \mathbf {D}_i(s)\,ds\right\| \left( \Vert \vec \xi _1- \vec \eta _1\Vert ^2+ \Vert \vec \xi _2- \vec \eta _2\Vert ^{2} \right) , \end{aligned}$$

where \(b_3\), \(b_4\), \(b_5\) are positive constants.

In [33], it was proved that

$$\begin{aligned} \alpha \int \limits _0^{t} e^{\alpha (s-t)} \mathbf {D}_i(s)\,ds \rightarrow \mathbf {0} \ \ \ \mathrm{as} \ \ \ \alpha \rightarrow 0, \ \ \ i=1,2, \end{aligned}$$

uniformly with respect to \(t\in [0,+\infty )\). Therefore, there exists \(\alpha >0\) such that

$$\begin{aligned} 6 b_5 \alpha \sum _{i=1}^2 \left\| \int \limits _0^{t} e^{\alpha (s-t)} \mathbf {D}_i(s)\,ds\right\| <c_9 \end{aligned}$$

for \(t\in [0,+\infty )\).

Then, for fixed values of \(\lambda \), \(\bar{\delta }\), \(\alpha \), one can find a sufficiently large number \(h_0\) such that

$$\begin{aligned}&\frac{1}{2} \lambda c_1 \Vert \vec \omega \Vert ^2 +\dfrac{a_1}{8} \Vert \vec {\xi }_1- \vec {\eta }_1\Vert ^2 +\dfrac{a_2}{8} \Vert \vec {\xi }_2- \vec {\eta }_2\Vert ^2 \\&\quad \le V_2\left( t,\vec \omega ,\vec \xi _1,\vec \xi _2\right) \le 2 \left( \lambda c_2 \Vert \vec \omega \Vert ^2 +{a_1} \Vert \vec {\xi }_1- \vec {\eta }_1\Vert ^2 +{a_2} \Vert \vec {\xi }_2- \vec {\eta }_2\Vert ^2\right) , \\&\quad \dot{V}_2\le -\frac{1}{4} \lambda h c_4 \Vert \vec \omega \Vert ^2 -\dfrac{c_9}{8h} \left( \Vert \vec \xi _1- \vec \eta _1\Vert ^2+ \Vert \vec \xi _2- \vec \eta _2\Vert ^2 \right) \end{aligned}$$

for \(h\ge h_0\), \(t\ge 0\), \(\vec \omega \in \mathbb R^3\), \(\Vert \vec \xi _1- \vec \eta _1\Vert ^2 +\Vert \vec \xi _2-\vec \eta _2\Vert ^2<{\bar{\delta }}^2\). \(\square \)

Remark 2

The conditions (11) are fulfilled if entries of the matrices \(\mathbf {D}_1(t)\), \(\mathbf {D}_2(t)\) are almost periodic functions with zero mean values. It is known (see [34]), that, for such matrices, the integrals (10) may be unbounded.

Remark 3

It is worth noting that Theorem 1 is a special case of Theorem 2. However, Theorem 1 possesses own meaning, since the proof of the theorem gives us less conservative restrictions on the parameter h than those in the proof of Theorem 2.

5 Purely nonlinear restoring and perturbing torques

Next, assume that \(\nu >0\) and the perturbing torque has the form \(\vec L_p=\mathbf {D}(t)\,\vec G(\vec \xi _1- \vec \eta _1,\vec \xi _2- \vec \eta _2)\), where the matrix \(\mathbf {D}(t)\in \mathbb R^{3\times m}\) is continuous and bounded for \(t\in [0,+\infty )\) and components of the vector \(\vec G(\vec u,\vec v)\in \mathbb R^{m}\) are continuously differentiable for \(\vec u,\vec v\in \mathbb R^3\) homogeneous functions of the order \(2\nu +1\). Hence, we consider the system

$$\begin{aligned} {\mathbf {J}} {\dot{\vec \omega }} + \vec \omega \times {\mathbf {J}} \vec \omega= & {} -c f^\nu (\vec \xi _1,\vec \xi _2) \left( a_1 \vec \xi _1\times \vec \eta _1+a_2 \vec \xi _2\times \vec \eta _2\right) \nonumber \\&+h \mathbf {B}\vec \omega +\mathbf {D}(t)\vec G(\vec \xi _1- \vec \eta _1,\vec \xi _2- \vec \eta _2). \end{aligned}$$
(12)

In this case, restoring and perturbing torques are purely nonlinear and homogeneous vector functions, and the homogeneity order of \(\vec L_r\) coincides with that of \(\vec L_p\).

Remark 4

It is known (see [35,36,37,38]), that, in numerous models of mechanical systems, strong nonlinear restoring forces with real-valued powers should be taken into consideration. Such forces can be related both to physical configurations and purely nonlinear material properties [3, 39]. In addition, power-law characteristics of restoring forces provide smooth approximations of non-smooth forces [38].

The aim of the present Section is to show that, for purely nonlinear restoring and disturbing torques, the asymptotic stability of the equilibrium position (4) can be guaranteed under less conservative conditions than for linear torques.

For an arbitrarily chosen \(h>0\), one can find \(\lambda _0>0\) and \(\bar{\delta }>0\) such that the derivative of the Lyapunov function (7) with respect to the system (2), (12) satisfies for \(\lambda \ge \lambda _0\), \(\vec \omega \in \mathbb R^3\), \(\Vert \vec \xi _1- \vec \eta _1\Vert ^2 +\Vert \vec \xi _2-\vec \eta _2\Vert ^2<{\bar{\delta }}^2\) the inequality

$$\begin{aligned} \dot{V}\le & {} -\dfrac{1}{3} \lambda h c_4 \Vert \vec \omega \Vert ^2 -\dfrac{c_9}{3h} \left( \Vert \vec \xi _1- \vec \eta _1\Vert ^2+ \Vert \vec \xi _2- \vec \eta _2\Vert ^2 \right) ^{\nu +1}\\&-\dfrac{1}{h} \left( a_1 \vec \xi _1\times \vec \eta _1+a_2 \vec \xi _2\times \vec \eta _2\right) ^\top \mathbf {B}^{-1}\vec L_p. \end{aligned}$$

Theorem 3

Let the matrix \(\int _0^{t} \!\mathbf {D}(s) \, ds\) be bounded for \(t\in [0,+\infty )\). Then the equilibrium position (4) of the system (2), (12) is uniformly asymptotically stable for any \(h>0\).

Proof

Choose and fix an arbitrary positive value of the parameter h. Construct a Lyapunov function by the formula

$$\begin{aligned} V_3\left( t,\vec \omega ,\vec \xi _1,\vec \xi _2\right)= & {} V\left( \vec \omega ,\vec \xi _1,\vec \xi _2\right) \\&+\dfrac{1}{h} \bigl (a_1 \vec \xi _1\times \vec \eta _1 +a_2 \vec \xi _2\times \vec \eta _2\bigr )^\top \mathbf {B}^{-1} \int \limits _0^{t} \mathbf {D}(s)\,ds \, \vec G(\vec \xi _1- \vec \eta _1,\vec \xi _2- \vec \eta _2). \end{aligned}$$

If \(\lambda \) is sufficiently large and \(\bar{\delta }\) is sufficiently small, then the function \(V_1\left( t,\vec \omega ,\vec \xi _1,\vec \xi _2\right) \) and its derivative with respect to the system (2), (8) satisfy the estimates

$$\begin{aligned}&\frac{1}{2} \lambda c_1 \Vert \vec \omega \Vert ^2 +\dfrac{a_1}{4} \Vert \vec {\xi }_1- \vec {\eta }_1\Vert ^2 +\dfrac{a_2}{4} \Vert \vec {\xi }_2- \vec {\eta }_2\Vert ^2\\&\qquad -\frac{b_1}{h} \left( \Vert \vec \xi _1- \vec \eta _1\Vert ^2 +\Vert \vec \xi _2-\vec \eta _2\Vert ^2\right) ^{\nu +1} \le V_3\left( t,\vec \omega ,\vec \xi _1,\vec \xi _2\right) \\&\quad \le 2 \lambda c_2 \Vert \vec \omega \Vert ^2 +{a_1} \Vert \vec {\xi }_1- \vec {\eta }_1\Vert ^2 +{a_2} \Vert \vec {\xi }_2- \vec {\eta }_2\Vert ^2 +\frac{b_1}{h} \left( \Vert \vec \xi _1- \vec \eta _1\Vert ^2 +\Vert \vec \xi _2-\vec \eta _2\Vert ^2\right) ^{\nu +1},\\&\quad \dot{V}_3\le -\frac{1}{3} \lambda h c_4 \Vert \vec \omega \Vert ^2 -\dfrac{c_9}{3h} \left( \Vert \vec \xi _1- \vec \eta _1\Vert ^2+ \Vert \vec \xi _2- \vec \eta _2\Vert ^2 \right) ^{\nu +1}\\&\qquad +\frac{b_2}{h} \Vert \vec \omega \Vert \left( \Vert \vec \xi _1- \vec \eta _1\Vert +\Vert \vec \xi _2-\vec \eta _2\Vert \right) ^{2\nu +1} \end{aligned}$$

for \(t\ge 0\), \(\vec \omega \in \mathbb R^3\), \(\Vert \vec \xi _1- \vec \eta _1\Vert ^2 +\Vert \vec \xi _2-\vec \eta _2\Vert ^2<{\bar{\delta }}^2\). Here \(b_1\) and \(b_2\) are positive constants.

Using properties of homogeneous functions (see [40, 41]), it can be proved the existence of a number \(\delta _0>0\) such that the estimates

$$\begin{aligned}&\frac{1}{2} \lambda c_1 \Vert \vec \omega \Vert ^2 +\dfrac{a_1}{8} \Vert \vec {\xi }_1- \vec {\eta }_1\Vert ^2 +\dfrac{a_2}{8} \Vert \vec {\xi }_2- \vec {\eta }_2\Vert ^2\\&\quad \le V_3\left( t,\vec \omega ,\vec \xi _1,\vec \xi _2\right) \le 2 \left( \lambda c_2 \Vert \vec \omega \Vert ^2 +{a_1} \Vert \vec {\xi }_1- \vec {\eta }_1\Vert ^2 +{a_2} \Vert \vec {\xi }_2- \vec {\eta }_2\Vert ^2\right) ,\\&\quad \dot{V}_3\le -\frac{1}{4} \lambda h c_4 \Vert \vec \omega \Vert ^2 -\dfrac{c_9}{4h} \left( \Vert \vec \xi _1- \vec \eta _1\Vert ^2+ \Vert \vec \xi _2- \vec \eta _2\Vert ^2 \right) ^{\nu +1} \end{aligned}$$

hold for \(t\ge 0\), \(\vec \omega \in \mathbb R^3\), \(\Vert \vec \xi _1- \vec \eta _1\Vert ^2 +\Vert \vec \xi _2-\vec \eta _2\Vert ^2<{\delta _0}^2\). \(\square \)

Theorem 4

Let

$$\begin{aligned} \frac{1}{T} \int \limits _t^{t+T} \!\mathbf {D}(s) \, ds \rightarrow \mathbf {0} \ \ \ { as} \ \ \ T\rightarrow +\infty \end{aligned}$$

uniformly with respect to \(t\in [0,+\infty )\). Then, the equilibrium position (4) of the system (2), (12) is uniformly asymptotically stable for any \(h>0\).

Proof

Let h be a fixed positive number. Consider the Lyapunov function

$$\begin{aligned} V_4\left( t,\vec \omega ,\vec \xi _1,\vec \xi _2\right)= & {} V\left( \vec \omega ,\vec \xi _1,\vec \xi _2\right) +\dfrac{1}{h} \bigl (a_1 \vec \xi _1\times \vec \eta _1\\&+a_2 \vec \xi _2\times \vec \eta _2\bigr )^\top \mathbf {B}^{-1} \int \limits _0^{t} e^{\alpha (s-t)} \mathbf {D}(s)\,ds \, \vec G(\vec \xi _1- \vec \eta _1,\vec \xi _2- \vec \eta _2), \end{aligned}$$

where \(\alpha =\mathrm{const}>0\).

If \(\lambda \) is sufficiently large and \(\bar{\delta }\) is sufficiently small, then

$$\begin{aligned}&\frac{1}{2} \lambda c_1 \Vert \vec \omega \Vert ^2 +\dfrac{a_1}{4} \Vert \vec {\xi }_1- \vec {\eta }_1\Vert ^2 +\dfrac{a_2}{4} \Vert \vec {\xi }_2- \vec {\eta }_2\Vert ^2\\&\qquad -\frac{b_3}{\alpha h} \left( \Vert \vec \xi _1- \vec \eta _1\Vert ^2 +\Vert \vec \xi _2-\vec \eta _2\Vert ^2\right) ^{\nu +1} \le V_4\left( t,\vec \omega ,\vec \xi _1,\vec \xi _2\right) \\&\quad \le 2 \lambda c_2 \Vert \vec \omega \Vert ^2 +{a_1} \Vert \vec {\xi }_1- \vec {\eta }_1\Vert ^2 +{a_2} \Vert \vec {\xi }_2- \vec {\eta }_2\Vert ^2 +\frac{b_3}{\alpha h} \left( \Vert \vec \xi _1- \vec \eta _1\Vert ^2 +\Vert \vec \xi _2-\vec \eta _2\Vert ^2\right) ^{\nu +1},\\&\quad \dot{V}_4\le -\frac{1}{3} \lambda h c_4 \Vert \vec \omega \Vert ^2 -\dfrac{c_9}{3h} \left( \Vert \vec \xi _1- \vec \eta _1\Vert ^2+ \Vert \vec \xi _2- \vec \eta _2\Vert ^{2} \right) ^{\nu +1}\\&\qquad +\frac{b_4}{\alpha h}\Vert \vec \omega \Vert \left( \Vert \vec \xi _1- \vec \eta _1\Vert +\Vert \vec \xi _2-\vec \eta _2\Vert \right) ^{2\nu +1}\\&\qquad +\frac{\alpha b_5}{h} \left\| \int \limits _0^{t} e^{\alpha (s-t)} \mathbf {D}(s)\,ds\right\| \left( \Vert \vec \xi _1- \vec \eta _1\Vert ^2+ \Vert \vec \xi _2- \vec \eta _2\Vert ^{2} \right) ^{\nu +1}. \end{aligned}$$

Here, \(b_3\), \(b_4\), \(b_5\) are positive constants.

Similarly to the proof of Theorem 2, choose \(\alpha >0\) such that

$$\begin{aligned} 6 b_5 \alpha \left\| \int \limits _0^{t} e^{\alpha (s-t)} \mathbf {D}(s)\,ds\right\| <c_9 \end{aligned}$$

for \(t\in [0,+\infty )\). Then, for sufficiently small values of \(\bar{\delta }\), we obtain

$$\begin{aligned}&\frac{1}{2} \lambda c_1 \Vert \vec \omega \Vert ^2 +\dfrac{a_1}{8} \Vert \vec {\xi }_1- \vec {\eta }_1\Vert ^2 +\dfrac{a_2}{8} \Vert \vec {\xi }_2- \vec {\eta }_2\Vert ^2\\&\quad \le V_4\left( t,\vec \omega ,\vec \xi _1,\vec \xi _2\right) \le 2 \left( \lambda c_2 \Vert \vec \omega \Vert ^2 +{a_1} \Vert \vec {\xi }_1- \vec {\eta }_1\Vert ^2 +{a_2} \Vert \vec {\xi }_2- \vec {\eta }_2\Vert ^2\right) ,\\&\quad \dot{V}_4\le -\frac{1}{4} \lambda h c_4 \Vert \vec \omega \Vert ^2 -\dfrac{c_9}{4h} \left( \Vert \vec \xi _1- \vec \eta _1\Vert ^2+ \Vert \vec \xi _2- \vec \eta _2\Vert ^2 \right) ^{\nu +1} \end{aligned}$$

for \(t\ge 0\), \(\vec \omega \in \mathbb R^3\), \(\Vert \vec \xi _1- \vec \eta _1\Vert ^2 +\Vert \vec \xi _2-\vec \eta _2\Vert ^2<{\bar{\delta }}^2\). \(\square \)

Remark 5

Theorem 3 is a special case of Theorem 4. However, the proof of Theorem 3 permits us to derive a wider estimate of attraction domain of the equilibrium position than that which can be obtained with the aid of the proof of Theorem 4.

Remark 6

Compared with Theorems 1 and 2, Theorems 3 and 4 guarantee the asymptotic stability of the equilibrium position (4) for any \(h>0\).

6 Computer modeling and discussion

The aim of the present paper is to provide a constructive approach to robustness analysis in the problem of attitude control for a rigid body subjected to nonstationary disturbing torques with zero mean values. It is worth noting that the disturbing torques (linear and nonlinear) are not assumed to be small in magnitude. For this reason, the obtained results seem to be attractive from the practical point of view.

The suggested approach is based on construction of a strict Lyapunov functions for the system governing the rigid body attitude dynamics. Theorems 1–4 ensure conditions under which perturbations do not disturb asymptotic stability of the programmed attitude motion.

In this Section, we illustrate Theorems 1–4 by means of a numerical simulation with the use of Maple-2019 tools for the numerical integration of differential equations.

Let the inertial parameters of a rigid body be given as: \(A_1=20\), \(A_2=24\), \(A_3=16\). Here and in what follows all parameters are taken in International System of Units. The programmed orientation (4) of the body is such that “aircraft” angles \(\varphi \), \(\theta \), \(\psi \) in the inertial coordinate system are all equal to zero. The disturbing torque is taken in the form \(\vec L_p=\mathbf {D}(t)\,\vec G(\vec \xi _1- \vec \eta _1,\vec \xi _2- \vec \eta _2)\), where

$$\begin{aligned} \mathbf {D}(t)={\mathrm{diag}}\{\sin t +\cos (\sqrt{3}\,t), \sin 2t +\cos (\sqrt{2}\,t), \sin 3t +\cos t\}, \end{aligned}$$
$$\begin{aligned} \vec G(\vec \xi _1- \vec \eta _1,\vec \xi _2- \vec \eta _2) = \left( \left( \Vert \vec \xi _1- \vec \eta _1\Vert ^2 +\Vert \vec \xi _2- \vec \eta _2\Vert ^2\right) /2\right) ^{\nu }(\vec \xi _1- \vec \eta _1 +\vec \xi _2- \vec \eta _2). \end{aligned}$$

Choose the matrix \(\mathbf {B}\) of dissipative torque in the form \(\mathbf {B}=-\mathrm {diag}\{1, 1, 1\}\). Let \(a_1=1\), \(a_2=1\), \(c=1\). Consider the control process governed by the system (2), (12) for different values of h and \(\nu \) and the same initial conditions \(\varphi (0)=0.4\), \(\theta (0)=0.4\), \(\psi (0)=-0.4\), \(\omega _1(0)=\omega _2(0)=\omega _3(0)=0.2\).

First, we take \(h=0.1\) and \(\nu =0\). In this case disturbing and control torques are linear, the dissipative torque is small, and the process doesn’t converge to the programmed motion as can be seen from Fig. 2.

Fig. 2
figure 2

Angles time history, \(h=0.1\), \(\nu =0\)

Full size image

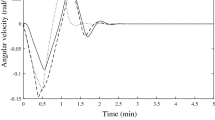
In accordance with Theorems 1 and 2, there exists a number \(h_0>0\) such that the programmed motion is uniformly asymptotically stable for any \(h\ge h_0\). In our case \(h_0 =0.4\) is appropriate as it can be seen from Fig. 3. where the stabilization process is shown.

Fig. 3
figure 3

Angles time history, \(h=0.4\), \(\nu =0\)

Full size image
Fig. 4
figure 4

Angles time history, \(h=0.1\), \(\nu =0.5\)

Full size image

At the same time, Theorems 3 and 4 give us the possibility to reach the goal of a stabilization process without dissipative torque increasing. This possibility is based on applying the nonlinear restoring torque (\(\nu >0\)). As is shown in Fig. 4. asymptotic stability is achieved at \(\nu =0.5\) even for \(h=0.1\).

We believe that our approach to the Lyapunov stability analysis in the problem of attitude control for a rigid body subjected to nonstationary disturbing torques with zero mean values is rather effective, and it can be exploited for the problem of satellite attitude stabilization with the use of electrodynamic attitude control system [28, 42, 43]. As is known, a satellite that moves in the Earth’s gravitational and magnetic fields [44, 45] is subjected to a lot of disturbing torques [18, 46,47,48]. From the mathematical point of view, the majority of these torques can be modeled by almost periodic functions of time with zero mean values [49]. The magnitudes of these torques are often close to each other, and, generally speaking, they are not negligibly small [1]. For this reason, the usage of well-known perturbation methods faces difficulties in such problems, and the methods based on the application of Lyapunov functions seem to be promising.