Local linear Timoshenko rod

Abstract

In this article, we consider a variant of the Simo–Reissner theory for a rod but restrict the study to two-dimensional motion where the rod undergoes flexure, shear and extension but not torsion. Linear elastic behaviour is assumed to formulate constitutive equations; the constitutive equations of the Timoshenko theory adapted for extension and large rotation. We call the model the local linear Timoshenko rod model. We show that this model serves as a framework for a class of simpler mathematical models for slender solids in various applications. The advantage is that the more general model can be used to evaluate and compare the simpler models.

1 Introduction

The dynamical analysis of (possibly) large motion of elastic rods undergoing flexure, shear, extension and torsion remains a significant challenge. To appreciate the extent of this challenge, one may read the introduction to the article [1]. It is also instructive to read [2,3,4]. The term rod, above, refers to objects modelled as one-dimensional continua, e.g. strings, beams, cables, hoses, etc. For a list of applications, see [4] and especially [1]. According to [4], the most general model is referred to as a Cosserat rod which is in line with the general model in [3]. The authors of [1] place the emphasis on theories and refer to Kirchhoff–Love theory versus Simo–Reissner theory.

In this article, we consider the Simo–Reissner theory for a rod but restrict the study to two-dimensional motion where the rod undergoes flexure, shear and extension but not torsion. The theory is further simplified by the assumption of linear elastic behaviour to formulate constitutive equations. Since the Timoshenko theory provides an excellent approximation for three-dimensional elastic behaviour with plane stress (explained in the next paragraph), we adapt the constitutive equations for application to large rotations. We call the model the local linear Timoshenko (rod) model or simply the LLT model. We will show that this model serves as a framework for a class of simpler mathematical models for slender solids in various applications. The advantage is that the more general model can be used to evaluate and compare the simpler models.

The analysis of a three-dimensional beam in [5] provides a solid theoretical derivation (as far as a derivation is possible) for the linear Timoshenko beam model. In [6], it is shown that the Timoshenko beam model compares very well to a three-dimensional beam model using numerical experiments. In the same article, results of physical experiments are also used to demonstrate that both models are strikingly realistic. The article [7] may also be considered.

Initially, the idea was to consider the possibly large motion of a rod, but with small strains (a variation of the Simo–Reissner theory). Then, some justification using three-dimensional theory as in [5] was considered. Comparison to the model in [2] was first considered but not done because the approach in [2] is fundamentally different. However, the same authors used the material description of motion in Section 3 of [8]. This fact facilitated comparison. To prepare the final version of this article, the articles [8,9,10] were studied. This leads to a significant improvement.

In the next section, equations of motion for a rod are derived from the conservation laws for momentum and angular momentum. The result is not new but necessary to clarify the connection between the three-dimensional solid and the rod model. The equations of motion for planar motion follow by simply imposing the constraint.

As mentioned, the LLT model is obtained by using linear constitutive equations for large motion. The necessary preparation is done in Sect. 3 where displacements, angles of rotation and tangent and normal vectors are defined. No use is made of a moving reference system and sketches are not used to define displacements or angles. Instead, the use of elementary differential geometry enables one to give unambiguous definitions and absolute clarity. The model is in Sect. 4.

In Sect. 5, additional motivation for the LLT model is provided by applying three-dimensional elasticity to a thin disc in the beam. In the same section, the articles [8, 10] are compared to the LLT model.

In Sect. 6, approximations of the LLT model for small vibrations are investigated. Linear and nonlinear models are derived. The derivation of the models in [11, 12], from the LLT model, is new. Two adapted versions of the linear Timoshenko model, with axial force, are also derived from the LLT model instead of merely inserting the force in the linear model.

In Sect. 7, the variational form for the linear and nonlinear Timoshenko models is derived and the finite element approximation of solutions of problems is briefly discussed. In Sect. 8, the weak variational forms are derived and existence of solutions for the adapted (linear) Timoshenko model is then proved. Eigenvalues and eigenfunctions are used in Sect. 9 to compare the different Adapted Timoshenko models. Finally, a conclusion is given in Sect. 10.

A preliminary communication, Locally linear Timoshenko beam model (UPWT 2016/06) on this research, was posted on the website of the Department of Mathematics and Applied Mathematics, University of Pretoria, South Africa.

2 Dynamics of a rod

2.1 Conservation laws

As mentioned, the term rod in this article refers to a one-dimensional continuum as in [3] where a rigorous (and general) description can be found. In a simplified approach, we also use the material description of motion where the reference configuration is the undeformed state of the solid and is denoted by ${{\mathcal {B}}}$. It is assumed that the solid has the following property in the undeformed state: there exists a straight line segment in ${{\mathcal {B}}}$ such that every cross section perpendicular to this line has its centroid on the line. (This straight line is referred to as the axis.) We choose coordinates for the reference configuration in such a way that the axis is the line $y = z = 0$.

It is assumed that every cross section executes a rigid motion as is commonly done (see, e.g. [2, 4, 8,9,10, 12]). To be specific, assume that the position of a point $X = (x,y,z)$ in ${\mathcal {B}}$ at time t is given by

$$\begin{aligned} {\overline{R}}(X,t) = {\bar{r}}_0(x,t) + y {\bar{e}}_y(x,t) + z{\bar{e}}_z(x,t), \end{aligned}$$

(2.1)

where ${\bar{e}}_y$ and ${\bar{e}}_z$ are mutually orthogonal unit vectors. This implies that ${\bar{e}}_y$ and ${\bar{e}}_z$ “move with the cross section" and a cross section remains plane during the motion. Clearly, ${\bar{r}}_0(x,t)$ is the position of the centroid (x, 0, 0) of a cross section at time t and the position of X relative to the centroid is ${\bar{r}}(X,t) = y{\bar{e}}_y(x,t) + z{\bar{e}}_z(x,t)$. The normal vector ${\bar{e}}_y \times {\bar{e}}_z$ is denoted by ${\bar{e}}_x$.

Let ${{\mathcal {R}}}$ be the part of ${{\mathcal {B}}}$ between $x = a$ and $x = b$. The velocity of the point $X=(x,y,z)$ at time t is ${\bar{v}} = \partial _t {\bar{r}}_0 + \partial _t {\bar{r}} = \partial _t {\bar{r}}_0 + y \partial _t {\bar{e}}_y + z \partial _t {\bar{e}}_z.$ If the density $\rho$ is constant, then the momentum of ${{\mathcal {R}}}$ is

$$\begin{aligned} \int _{{\mathcal {R}}}\ \rho {\bar{v}}(\cdot ,t)\ \mathrm{d}V = \rho \int _a^b~A(x)\partial _t {\bar{r}}_0(x,t)\ \mathrm{d}x, \end{aligned}$$

where A(x) is the area of the cross section. The angular momentum of ${{\mathcal {R}}}$ about ${\bar{0}}$ is

$$\begin{aligned} \int _{{\mathcal {R}}}~{\overline{R}} \times \rho \bar{v} \mathrm{d}V= & {} \rho \int _a^b~A(x){\bar{r}}_0(x,t) \times \partial _t {\bar{r}}_0(x,t)~\mathrm{d}x \nonumber \\&+ \rho \int _a^b \int _{{\mathcal {D}}}~{\bar{r}}(X,t)\times \partial _t {\bar{r}}(X,t)~\mathrm{d}A\mathrm{d}x, \end{aligned}$$

where ${{\mathcal {D}}} = {{\mathcal {D}}}(x)$ denotes the relevant cross section.

2.2 The one-dimensional model

The boundary of ${{\mathcal {R}}}$ consists of three parts: the cross sections ${{\mathcal {D}}}(a)$ and ${{\mathcal {D}}}(b)$ and part of the outer surface of the solid between the cross sections. Assuming that cross sections undergo rigid motion, the traction on an arbitrary cross section ${{\mathcal {D}}}(c)$ is equivalent to a force $\overline{F}(c,t)$ acting at the centroid ${\bar{r}}_0(c,t)$ and a couple ${\overline{M}}(c,t)$. The following function convention is used: ${\overline{F}}(c,t)$ and ${\overline{M}}(c,t)$ are the force and couple acting on the part of the solid where $x \le c$. Consequently, the forces exerted on ${{\mathcal {R}}}$ are ${\bar{F}}(b,t)$ and $-\overline{F}(a,t)$ and the couples are ${\overline{M}}(b,t)$ and $-\overline{M}(a,t)$.

From a mathematical point of view, we now have a one-dimensional model for the solid ${{\mathcal {B}}}$ which we call a rod (or Cosserat rod). The reference configuration is $[0,\ell ]$ where $\ell$ is the length of the axis.

2.2.1 Conservation of momentum

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}t}~\int _a^b~\rho A \partial _t {\bar{r}}_0(x,t)~\mathrm{d}x = \overline{F}(b,t) - {\overline{F}}(a,t) + \int _a^b~ \bar{P}(x,t)~ \mathrm{d}x, \end{aligned}$$

where P is the load.

It is useful to introduce the following notation (recalling that $\rho$ is constant):

$$\begin{aligned} {\overline{H}}(x,t) = \rho \int _{{\mathcal {D}}}~{\bar{r}} \times \partial _t\bar{r} \mathrm{d}A. \end{aligned}$$

(2.2)

The quantity ${\overline{H}}(x,t)$ is referred to as the angular momentum density (about the centroid).

2.2.2 Conservation of angular momentum

$$\begin{aligned}&\frac{\mathrm{d}}{\mathrm{d}t}~\int _a^b~\rho A {\bar{r}}_0(x,t) \times \partial _t {\bar{r}}_0(x,t) \mathrm{d}x + \frac{\mathrm{d}}{\mathrm{d}t}~\int _a^b~ {\overline{H}}(x,t)~\mathrm{d}x \\&\quad = {\bar{r}}_0(b,t) \times {\overline{F}}(b,t) - {\bar{r}}_0(a,t) \times {\overline{F}}(a,t) + {\overline{M}}(b,t) - {\overline{M}}(a,t) \\&\qquad + \int _a^b~{\bar{r}}_0(x,t) \times {\overline{P}}(x,t)~\mathrm{d}x. \end{aligned}$$

From the conservation laws, following the usual approach, we derive the equations of motion:

$$\begin{aligned} \rho A \partial ^2_t {\bar{r}}_0= & {} \partial _x {\overline{F}} + {\overline{P}}, \end{aligned}$$

(2.3)

$$\begin{aligned} \partial _t {\overline{H}}= & {} \partial _x {\bar{r}}_0 \times {\overline{F}} + \partial _x {\overline{M}}. \end{aligned}$$

(2.4)

To derive the second equation of motion first prove that

$$\begin{aligned} \rho A {\bar{r}}_0 \times \partial ^2_t {\bar{r}}_0 + \partial _t {\overline{H}} = \partial _x ({\bar{r}}_0 \times {\overline{F}}) + \partial _x {\overline{M}} + {\bar{r}}_0 \times {\overline{P}}. \end{aligned}$$

The result follows by combining this result with Eq. (2.3).

Eqs. (2.3) and (2.4) correspond to Eqs. (2.11) and (2.12) in [3] where they are referred to as the classical forms of the equations of motion. The system is given by Eq. (8) in [4], where references are provided regarding the derivation. More detail on the angular momentum density is provided in [3, 4], but it is not required for this paper.

3 Planar motion

Recall (from Eq. (2.1)) that the position of a point (x, y, z) at time t is given by

$$\begin{aligned} {\overline{R}}(x,y,z,t) = {\bar{r}}_0(x,t) + y {\bar{e}}_y(x,t) + z{\bar{e}}_z(x,t), \end{aligned}$$

where ${\bar{e}}_x$, ${\bar{e}}_y$ and ${\bar{e}}_z$ “move with the cross section”. Let $\{{\bar{e}}_1, {\bar{e}}_2, \bar{e}_3\}$ denote an orthonormal set “fixed” in space forming a right-handed triad. For planar motion assume that

$$\begin{aligned} {\bar{r}}_0(x,t) = r_1(x,t) {\bar{e}}_1 + r_2(x,t) {\bar{e}}_2 \end{aligned}$$

and ${\bar{e}}_z(t) = {\bar{e}}_3$ for each t. Note that the motion of each point is in a plane perpendicular to ${\bar{e}}_3$.

Since the tangent vector is

$$\begin{aligned} \partial _x {\bar{r}}_0(x,t) = \partial _x r_1(x,t) {\bar{e}}_1 + \partial _x r_2(x,t) {\bar{e}}_2, \end{aligned}$$

it follows that the angle $\theta (x,t)$ of the tangent vector with the direction of ${\bar{e}}_1$ satisfies

$$\begin{aligned} \cos \theta= & {} \Vert \partial _x \bar{r}_0\Vert ^{-1}\partial _x r_1, \end{aligned}$$

(3.1)

$$\begin{aligned} \sin \theta= & {} \Vert \partial _x \bar{r}_0\Vert ^{-1}\partial _x r_2. \end{aligned}$$

(3.2)

Fig. 1

Diagram of relevant angles and vectors

The unit tangent vector ${\bar{e}}_T$ and another useful vector $\bar{e}_\theta$ are given by

$$\begin{aligned} \bar{e}_T(x,t)= & {} \cos \theta (x,t) {\bar{e}}_1 + \sin \theta (x,t) {\bar{e}}_2\\ {\bar{e}}_\theta (x,t)= & {} - \sin \theta (x,t) {\bar{e}}_1 + \cos \theta (x,t) {\bar{e}}_2. \end{aligned}$$

It is clear that cross sections rotate about the $z-$axis. The angle of rotation $\phi$ is defined by $\cos \phi = {\bar{e}}_x \cdot \bar{e}_1$ and $\sin \phi = {\bar{e}}_y \cdot {\bar{e}}_2$. Consequently,

$$\begin{aligned} {\bar{e}}_y(x,t)= & {} - \sin \phi (x,t) {\bar{e}}_1 + \cos \phi (x,t) {\bar{e}}_2, \\ {\bar{e}}_x(x,t)= & {} \cos \phi (x,t) {\bar{e}}_1 + \sin \phi (x,t) {\bar{e}}_2. \end{aligned}$$

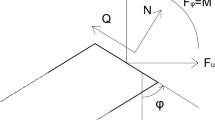
Since $\bar{e}_y \times \bar{e}_x = - \bar{e}_3 = - \bar{e}_z$, it follows that ${\bar{e}}_y \times {\bar{e}}_z = {\bar{e}}_x$, the unit normal to the cross section, as required. Also, $\phi$ is equal to the angle between a cross section and ${\bar{e}}_2$ and the angle between the normal vector and ${\bar{e}}_1$. It follows from elementary trigonometry that $\theta - \phi$ is the angle between the normal vector to the cross section and tangent vector, see Fig. 1.

Recall the angular density ${\overline{H}}$ defined in Eq. (2.2). For planar motion, it is necessary that ${\overline{H}} = H {\bar{e}}_z$. If ${{\mathcal {D}}}$ is symmetric with respect to the $y-$axis, then an elementary calculation shows that the angular momentum density is

$$\begin{aligned} {\overline{H}}(x,t) = \rho I~\partial _t \phi (x,t){\bar{e}}_3, \end{aligned}$$

(3.3)

where I is the area moment of inertia about the $z-$axis.

To derive the equations of motion for planar motion, use Eqs. (2.3) and (2.4) together with

$$\begin{aligned} \partial _t^2 {\bar{r}}_0 = \partial _t^2 r_1 {\bar{e}}_1 + \partial _t^2 r_2 {\bar{e}}_2 ~~~ \text {and} ~~~ \partial _t {\overline{H}} = \rho I~\partial _t^2 \phi {\bar{e}}_3. \end{aligned}$$

3.1 Equations of motion for planar motion

$$\begin{aligned} \rho A \partial ^2_t r_1= & {} \partial _x F_1 + P_1, \end{aligned}$$

(3.4)

$$\begin{aligned} \rho A \partial ^2_t r_2= & {} \partial _x F_2 + P_2, \end{aligned}$$

(3.5)

$$\begin{aligned} \rho I \partial ^2_t \phi= & {} \partial _x r_1 F_2 - \partial _x r_2 F_1 + \partial _x M_3. \end{aligned}$$

(3.6)

Remark

The equations of motion above also apply to the model in Section 3 of [8]. If $\partial ^2_t r_1=0$, $\partial ^2_t r_2=0$ and $\partial ^2_t \phi =0$ then we have a static problem as in [10]. (The function ${\overline{R}}$ above corresponds to the function r defined by Eq. (1) in [10].)

4 Local linear approximation

4.1 Constitutive equations

To obtain a mathematical model, the equations of motion (3.4), (3.5) and (3.6) must be supplemented with constitutive equations. If it is assumed that the motion is locally linear, then a natural choice for shear and bending are the constitutive equations of the Timoshenko theory (see, e.g. [5,6,7, 13,14,15]). For the longitudinal strain, Hooke’s law in its simplest form is used. However, the axial force is not equal to $F_1$ and the shear force is not equal to $F_2$ due to the rotation of the tangent vector. In fact

$$\begin{aligned} F_1= & {} S \cos \theta - V \sin \theta , \end{aligned}$$

(4.1)

$$\begin{aligned} F_2= & {} S \sin \theta + V \cos \theta , \end{aligned}$$

(4.2)

where S denotes the axial force and V the shear force.

In the Timoshenko theory, the angle between the tangent vector and the normal to the cross section is considered to be the “average" shear strain. Assuming that the strains are small, the following constitutive equations are used:

$$\begin{aligned} M ~=~ M_3= & {} EI \partial _x \phi , \end{aligned}$$

(4.3)

$$\begin{aligned} V= & {} \kappa ^2AG(\theta - \phi ). \end{aligned}$$

(4.4)

In the equations above, E is Young’s modulus, I the area moment of inertia, $\kappa ^2$ the shear coefficient, A the area of a cross section and G the shear modulus. (In the linear case, $\theta$ is approximated by $\partial _x w$.)

To account for extension and compression, note that

$$\begin{aligned} (\partial _x s)^2 = \Vert \partial _x r_0\Vert ^2 = (\partial _x r_1)^2 + (\partial _x r_2)^2, \end{aligned}$$

(4.5)

where s is the arc length function. The axial rod strain is defined to be

$$\begin{aligned} \epsilon _s = \partial _x s - 1. \end{aligned}$$

(4.6)

(The actual strain is discussed in Sect. 5.) We assume the simplest form of Hooke’s law:

$$\begin{aligned} S= & {} AE\epsilon _s, \end{aligned}$$

(4.7)

If the constitutive equations above as well as (4.1) and (4.2) are substituted into the equations of motion, (3.4), (3.5) and (3.6), the model problem is in general nonlinear.

Although the rod (or beam) strains $\epsilon _s$, $\partial _x \phi$ and $\partial _x s - 1$ are a natural adjustment for large rotations of beams where linear elasticity is commonly used, it is prudent to consider the theory in [16]. To avoid confusion, we use a subscript “R" for the beam strains used by Reissner. The strains are $\varepsilon _R$, $\kappa _R$ and $\gamma _R$ for stretching, bending and shear, respectively. The result in [16] is (for an initially straight rod)

$$\begin{aligned} \varepsilon _R= & {} \partial _x s \cos (\theta -\phi )-1, \end{aligned}$$

(4.8)

$$\begin{aligned} \gamma _R= & {} \partial _x s \sin (\theta -\phi ), \end{aligned}$$

(4.9)

$$\begin{aligned} \kappa _R= & {} \partial _x \phi , \end{aligned}$$

(4.10)

using the notation of the present paper. Assuming that $\cos (\theta -\phi ) \approx 1$ in (4.8) and $\partial _x s \approx 1$ and $\sin (\theta -\phi ) \approx \theta -\phi$ in (4.9) the strains correspond to those used in this paper, i.e. $\varepsilon _R \approx \epsilon _s$ and $\gamma _R \approx \theta -\phi$. Using the multi-dimensional strains to motivate the strains in (4.3), (4.4) and (4.6) are considered in Sect. 5.

Recall that small strains are required for linear elasticity. Therefore, the quantities $\partial _x s - 1$ and $\theta - \phi$ must be small, but the rod “strain" $\partial _x \phi$ is not dimensionless and cannot be considered. However, $y\partial _x \phi$ is dimensionless and one may require that $h\partial _x \phi$ be small where h denotes the diameter of the cross section in the direction of ${\bar{e}}_y$.

4.1.1 Dimensionless form

For the different mathematical models and comparisons of them, it is convenient to introduce notation for the displacement. Let $u(x,t)=r_1(x,t)-x$ and $w(x,t)=r_2(x,t)$. (The displacement is relative to the line segment through the points represented by $\bar{0}$ and $\ell {\bar{e}}_1$.)

Set

$$\begin{aligned} \tau = \frac{t}{T},\ \xi =\frac{x}{\ell },\ u^*(\xi ,\tau )=\frac{u(x,t)}{\ell }, ~ \text {and}, ~ w^*(\xi , \tau ) = \frac{w(x,t)}{\ell }, \end{aligned}$$

where T needs to be specified. Since $\phi$ is dimensionless, it follows that

$$\begin{aligned} \phi ^*(\xi , \tau ) = \phi (x,t). \end{aligned}$$

Next, the forces, force densities and moments are scaled by $AG\kappa ^2$, $AG\kappa ^2 \ell ^{-1}$ and $AG\kappa ^2 \ell$, respectively. For example,

$$\begin{aligned} F_i^*(\xi ,\tau )=\frac{F_i(x,t)}{AG\kappa ^2}, ~~~ P_i^*(\xi ,\tau )=\frac{\ell P_i(x,t)}{AG\kappa ^2 }, ~ \text {and}, ~ M^*(\xi ,\tau )=\frac{M(x,t)}{AG\kappa ^2 \ell }. \end{aligned}$$

The dimensionless form of Eq. (3.4) is

$$\begin{aligned} \frac{\rho \ell ^2}{G\kappa ^2T^2} \partial ^2_\tau u^*= & {} \partial _\xi F_1^* + P^*_1. \end{aligned}$$

Using the choice

$$\begin{aligned} T = \ell \sqrt{\frac{\rho }{G\kappa ^2}}, \end{aligned}$$

this equation of motion in original notation now reads

$$\begin{aligned} \partial ^2_t u= & {} \partial _x F_1 + P_1. \end{aligned}$$

Similarly, the other two equations of motion in dimensionless form using the original notation are

$$\begin{aligned} \partial ^2_t w= & {} \partial _x F_2 + P_2, \\ \frac{1}{\alpha } \partial ^2_t \phi= & {} (1+\partial _x u) F_2 - \partial _x w F_1 + \partial _x M, \end{aligned}$$

where $\displaystyle \alpha = \frac{A \ell ^2}{I}.$ Let $\displaystyle \beta =\frac{AG\kappa ^2 \ell ^2}{EI}$ and $\displaystyle \gamma = \frac{\beta }{\alpha } = \frac{G\kappa ^2}{E}$, then the constitutive equations (4.3), (4.4) and (4.7) become

$$\begin{aligned} M = \frac{1}{\beta } \partial _x \phi , \qquad V = \theta - \phi , \qquad S = \frac{1}{\gamma }(\partial _x s - 1). \end{aligned}$$

Equations (3.1), (3.2), (4.1) and (4.2) convert trivially to dimensionless form and the other equation (4.5) is effectively in dimensionless form. The complete model problem is presented in Sect. 4.2, using the original notation.

The parameters $\alpha$ and $\beta$ are subject to large variations but $\gamma$ range between $\frac{1}{6}$ and $\frac{1}{2}$, see, e.g. [7, 17] and the references there in.

Recall that the strains $\theta - \phi$, $\partial _x s - 1$ and $h\partial _x \phi$ must be small. But now both h and $\partial _x \phi$ are dimensionless and $\partial _x \phi$ may be an order larger than the above-mentioned strains if $h < \frac{1}{10}$. Consider for example a beam where $I= \frac{1}{12} bh^3$, then $h^2 = 12/\alpha = 1/100$ for $\alpha = 1200.$

Remark

Due to the scaling, dimensionless forces larger than $10^{-2}$ should be considered large.

4.2 Local linear Timoshenko rod model

The complete mathematical model is presented here for convenience.

Equations of motion:

$$\begin{aligned} \partial ^2_t u= & {} \partial _x F_1 + P_1, \end{aligned}$$

(4.11)

$$\begin{aligned} \partial ^2_t w= & {} \partial _x F_2 + P_2, \end{aligned}$$

(4.12)

$$\begin{aligned} \frac{1}{\alpha } \partial ^2_t \phi= & {} (1+\partial _x u) F_2 - \partial _x w F_1 + \partial _x M, \end{aligned}$$

(4.13)

with

$$\begin{aligned} F_1= & {} S \cos \theta - V \sin \theta , \end{aligned}$$

(4.14)

$$\begin{aligned} F_2= & {} S \sin \theta + V \cos \theta \end{aligned}$$

(4.15)

and $\partial _x s$ and $\theta$ defined by

$$\begin{aligned} (\partial _x s)^2= & {} (1+\partial _x u)^2 + (\partial _x w)^2, \end{aligned}$$

(4.16)

$$\begin{aligned} \cos \theta= & {} (\partial _x s)^{-1}(1+\partial _x u), \end{aligned}$$

(4.17)

$$\begin{aligned} \sin \theta= & {} (\partial _x s)^{-1}\partial _x w. \end{aligned}$$

(4.18)

The constitutive equations are

$$\begin{aligned} M= & {} \frac{1}{\beta } \partial _x \phi , \end{aligned}$$

(4.19)

$$\begin{aligned} V= & {} \theta - \phi , \end{aligned}$$

(4.20)

$$\begin{aligned} S= & {} \frac{1}{\gamma }(\partial _x s - 1). \end{aligned}$$

(4.21)

The model above differs from the models in Sections 2 and 3 of [8]. The equations of motion are effectively the same as in Sect. 3, but the strains differ as we explain in Sect. 5.

Usually, constitutive equations are substituted into the equations of motion to yield partial differential equations. Following the usual approach, one would attempt to substitute $F_1$, $F_2$ and M into Eqs. (4.11), (4.12) and (4.13). This is not advisable and fortunately not necessary. Inspection of Eqs. (4.14) to (4.21) leads to the conclusion that $F_1$, $F_2$ and M are well defined in terms of u, w and $\phi$. The model may be referred to as “well formulated”.

Although the LLT model has various applications to rods, our main concern in the rest of this paper will be beams. (It is not possible to give a precise criterion for a rod to be a beam, but the parameters $\alpha$ and $\beta$ should not be too large.)

Boundary conditions  The modelling assumptions are as follows. The force F and the moment M are both zero at a free end. $M = 0$ at a pinned end where u and w are fixed, while at a clamped end, u, w and $\phi$ are fixed. (Note that $F = 0$ implies that $S = V = 0$.)

Three configurations are considered for which the boundary conditions are stated below.

Cantilever beam  At the clamped end

$$\begin{aligned} u(0,t) = w(0,t) = \phi (0,t) = 0. \end{aligned}$$

(4.22)

At the free end, the boundary conditions are

$$\begin{aligned} F_1(1,t) = F_2(1,t) = M(1,t) = 0. \end{aligned}$$

(4.23)

Pinned–pinned beam  At both endpoints, u, w and M are zero, i.e.

$$\begin{aligned} u(0,t)= & {} w(0,t)=u(1,t)=w(1,t)=0, \end{aligned}$$

(4.24)

$$\begin{aligned} M(0,t)= & {} M(1,t)=0. \end{aligned}$$

(4.25)

Pivoted beam  The boundary conditions are the same as for the Cantilever beam except that $\phi (0,t)=0$ is replaced by $M(0,t)=0$.

For each model problem, the initial values for u, w, $\phi$, $\partial _t u$, $\partial _t w$ and $\partial _t \phi$ must be prescribed. Simulations were done using a finite element approximation, and acceptable results were obtained. See Sect. 7 for further discussion.

4.3 Simplified models

4.3.1 Pivoted beam with constant angular velocity

Consider a beam pivoted at $\mathbf{0}$. The boundary conditions are

$$\begin{aligned} u(0,t)= & {} w(0,t) = 0, \\ M(0,t)= & {} F_1(1,t) = F_2(1,t) = M(1,t) = 0. \end{aligned}$$

Suppose the force P is equal to zero and the beam is rotating with constant angular velocity $\omega$. Let $\bar{R}(x,y,z,t) = g(x)(\cos (\omega t) \bar{e}_1 + \sin (\omega t) \bar{e}_2)$ with $\omega$ constant. Consequently, $u(x,t) = g(x)\cos (\omega t)$, $w(x,t) = g(x)\sin (\omega t)$, and $\theta (t) = \omega t$.

Now, suppose the expressions for u, w and $\theta$ are substituted into (4.11) to (4.15). From Eqs. (4.11) and (4.12), it follows that $\partial _xV = 0$ and both equations reduce to $-\omega ^2 g(x) = S'(x)$.

The shear force V is equal to zero due to the boundary condition at the free end. This implies that $\theta = \phi$ and since $\partial _x \phi = 0$, it follows that $M = 0$. Substituting the results into (4.13) shows that the equation is satisfied. The left hand side of the equation is clearly zero as well as the last term. For the other terms note that

$$\begin{aligned} \partial _x(g(x) \cos \omega t)S \sin \omega t - \partial _x(g(x) \sin \omega t)S \cos \omega t = 0. \end{aligned}$$

It follows from Eq. (4.16) that $\partial _x s = g'$. Note that Eqs. (4.17) and (4.18) are satisfied. It follows from Eq. (4.21) and the results for s and S above that

$$\begin{aligned} g'' = \partial ^2_x s = \gamma S' = -\gamma \omega ^2 g. \end{aligned}$$

From the boundary condition for u(0, t) and since $S(1) = 0$, the boundary conditions for g are $g(0) = 0$ and $g'(1) = 1$. A unique solution exists for g, and hence, a solution for the original problem is obtained.

4.3.2 Nonlinear models without shear

Since (4.20) cannot be used, the shear force V is not known. The model is not “well formulated” in the way the LLT model is. In the linear case, V can be eliminated before $\phi$ is replaced by $\partial _x w$, but this is not possible here. The shear force is implicitly defined and there is no easy way to deal with it. Since the LLT model is our concern, this model is not considered any further.

5 Multi-dimensional considerations regarding strains

Reissner [16] stated that physical experiments are necessary to establish constitutive equations. Irschik and Gerstmayr did not fully agree with this point of view. In the articles [9, 10], the authors showed that the problem regarding experiments can be overcome (at least partially) using the multi-dimensional theory of continuum mechanics.

In this section, we present a justification for the constitutive equations of the LLT model using those of the three-dimensional theory of linear elasticity. We also compare our theory to the theories in [8,9,10]. It is necessary to bear in mind that assumptions must be made; a one-dimensional model cannot be derived rigorously from a multi-dimensional model.

5.1 Local linear Timoshenko model

Recall that the reference configuration for the one-dimensional model (the axis of the rod) is the line segment between ${\bar{0}}$ and $\ell {\bar{e}}_1$. By assumption, every cross section executes a rigid rotation where the normal vector ${\bar{e}}_x$ is rotated through the angle $\phi (x,t)$. The displacement of the “disc” ${{\mathcal {R}}}$ (defined in Sect. 2.1) consists of three displacements. First the centroid of ${{\mathcal {D}}}(a)$ is moved to ${\bar{r}}_0(a,t)$, then ${{\mathcal {R}}}$ is rigidly rotated through the angle $\theta (a,t)$, and lastly, it is allowed to undergo deformation. Recall from Sect. 3 that

$$\begin{aligned} {\bar{R}}(x,y,z,t) = {\bar{r}}_0(x,t) + y {\bar{e}}_y(x,t) + z {\bar{e}}_z. \end{aligned}$$

(5.1)

If $b-a$ is sufficiently small it is assumed that ${\bar{r}}_0$ can be written as

$$\begin{aligned} {\bar{r}}_0(x,t) = {\bar{r}}_0(a,t) + (x-a+d(x,t)){\bar{e}}_T(x,t). \end{aligned}$$

(5.2)

(In [8], a different possibility is considered.) Also

$$\begin{aligned} y {\bar{e}}_y(x,t) = y(-\sin \psi {\bar{e}}_T(x,t)+ \cos \psi \bar{e}_\theta (x,t)), \end{aligned}$$

where $\psi (x,t) =\phi (x,t) -\theta (a,t)$. As a consequence

$$\begin{aligned} {\bar{R}}(x,y,z,t) = {\bar{r}}_0(a,t) + u_1(x,y,t) {\bar{e}}_T(x,t) + u_2(x,y,t)y {\bar{e}}_\theta (x,t) + z {\bar{e}}_z, \end{aligned}$$

(5.3)

where

$$\begin{aligned} u_1(x,y,z,t)= & {} x-a + d(x,t) - y \sin (\psi (x,t)),\\ u_2(x,y,z,t)= & {} y \cos (\psi (x,t)) \ \text {and}\\ u_3(x,y,z,t)= & {} z. \end{aligned}$$

Next the (Fréchet) derivative of the vector ${\bar{u}}$ is computed. The result, using a prime for the derivative w.r.t. x, is

$$\begin{aligned}{}[\nabla {\bar{u}}]= & {} \left[ \begin{array}{lll} 1 + d' - y \psi '\cos \psi &{} -\sin \psi &{} 0 \\ -y\psi '\sin \psi &{} \cos \psi &{} 0 \\ 0 &{} 0 &{} 1 \end{array}\right] . \end{aligned}$$

(5.4)

The derivative ${{\mathcal {F}}}$ of ${\bar{R}}(\cdot ,t)$ satisfies

$$\begin{aligned} {{\mathcal {F}}} = R_\theta ^T[ \nabla {\bar{u}}], \end{aligned}$$

where the matrix representation of $R_\theta$ is

$$\begin{aligned}{}[R_\theta ] = \left[ \begin{array}{l@{\quad }l@{\quad }l} \cos \theta &{} \quad \sin \theta &{} \quad 0 \\ -\sin \theta &{} \quad \cos \theta &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad 1 \end{array}\right] . \end{aligned}$$

(5.5)

To proceed, we use the polar decomposition ${{\mathcal {F}}} = RU$. The rotation R can be factored as $R = R_\theta ^T R_1$. We assume that both $R_1 - I$ and $U-I$ are small. Consequently,

$$\begin{aligned} R_1 U = I + Y \end{aligned}$$

with Y small. The rotation $R_\theta$, however, may be large and there is no restriction on the magnitude of $\theta$. Let ${{\mathcal {E}}} = \frac{1}{2}(Y + Y^T)$ and $\Omega = \frac{1}{2}(Y - Y^T)$, then

$$\begin{aligned} (I + \Omega )(I + {{\mathcal {E}}}) = I + {{\mathcal {E}}} + \Omega + \Omega {{\mathcal {E}}} \approx I + Y. \end{aligned}$$

Therefore,

$$\begin{aligned} {{\mathcal {F}}} \approx R_\theta (I + \Omega )(I + {{\mathcal {E}}}), \end{aligned}$$

where $I + \Omega$ and $I + {{\mathcal {E}}}$ are approximations for $R_1$ and U.

Assuming that $\psi '$ and $\psi$ are sufficiently small, the approximation for (5.4) is

$$\begin{aligned}{}[\nabla u] \approx \left[ \begin{array}{l@{\quad }l@{\quad }l} 1 + d' - y \psi ' &{} \quad - \psi &{} \quad 0 \\ 0 &{} \quad 1 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad 1 \end{array}\right] =I+Y. \end{aligned}$$

Using the definition ${{\mathcal {E}}} = \frac{1}{2}(Y + Y^T)$ for strain, it follows that the matrix representation for the strain is given by

$$\begin{aligned}{}[{{\mathcal {E}}}] \approx \frac{1}{2}\left[ \begin{array}{l@{\quad }l@{\quad }l} 2(d' - y \psi ') &{} \quad - \psi &{} \quad 0 \\ - \psi &{} \quad 0 &{} \quad 0 \\ 0 &{} \quad 0 &{} \quad 0 \end{array}\right] . \end{aligned}$$

It is assumed that $\psi$, $\psi '$ and $d'$ are small. (The angle of the infinitesimal rotation $I + \Omega$ is $\psi /2$.)

The infinitesimal theory of linear elasticity with strain given by ${{\mathcal {E}}}$ can now be used. The rigidly rotated disc ${{\mathcal {R}}}$ now serves as reference configuration with basis $\{{\bar{e}}_T(a,t),\bar{e}_\theta (a,t),{\bar{e}}_3\}$. The point $x{\bar{e}}_1 + y{\bar{e}}_2 + z\bar{e}_3$ is now at ${\bar{r}}_0(a,t) + (x-a){\bar{e}}_T + y{\bar{e}}_\theta + z{\bar{e}}_3$. It is convenient to refer to it as the point $\xi \bar{e}_\xi + \eta {\bar{e}}_\eta + z{\bar{e}}_3$ or $(\xi ,\eta ,z)$ with $\xi = x-a$ and $\eta =y$. We assume plane stress; more precisely, $\sigma _{\xi \xi }$ and $\sigma _{\xi \eta }$ are the only nonzero stress components. By Hooke’s law, the only relevant strains are the axial strain and the shear strain: $\epsilon _{\xi \xi } = \displaystyle {\frac{\sigma _{\xi \xi }}{E}}$ and $\epsilon _{\xi \eta } = \displaystyle {\frac{2(1 + \nu ) \sigma _{\xi \eta }}{E}}.$ (This is in agreement with the Timoshenko assumptions and [10].) Combining the results above produces

$$\begin{aligned} \sigma _{\xi \xi }= & {} E(d' - y \psi '),\\ \sigma _{\xi \eta }= & {} G(- \psi ). \end{aligned}$$

Integrating over a cross section (orthogonal to ${\bar{e}}_T$) yields the normal force N, shear force Q and the bending moment M:

$$\begin{aligned} N= & {} E\int (d' - y \psi ')\, \mathrm{d}A = EA d', \end{aligned}$$

(5.6)

$$\begin{aligned} Q= & {} G \int (-\psi ) \, \mathrm{d}A = G A(-\psi ), \end{aligned}$$

(5.7)

$$\begin{aligned} M= & {} -E \int y(d' - y \psi ') \, \mathrm{d}A = E \psi ' \int y^2 \, \mathrm{d}A = EI\psi '. \end{aligned}$$

(5.8)

Note that $d'=\partial _x s -1= \epsilon _s$ and hence Eq. (5.6) above corresponds to (4.7). (It also follows that $\epsilon _s$ is equal to the mean of $\epsilon _{\xi \xi }$.) Since $\psi =\phi -\theta$, (5.7) does correspond to (4.4) but without the factor $\kappa ^2$. To obtain the correction, it is necessary to consider the warping of the cross section (see, e.g. [5]). The simple form of Eq. (5.8) is due to the symmetry assumption in Sect. 3. Since $\psi (x,t)=\phi (x,t)-\theta (a,t)$, $\partial _x\psi = \partial _x\phi$ and (5.8) corresponds to (4.3). The notation N and Q for the forces in the equations above corresponds to the notation in [9, 10, 16], but we use S for N and V for Q in the rest of this paper. It follows that the internal force is ${\overline{F}} = S {\bar{e}}_T + V {\bar{e}}_\theta$ which explains Eqs. (4.1) and (4.2).

5.2 Theory of Simo and Vu Quoc

The theory in [8] also starts with Eq. (5.1), but the form for ${\bar{r}}_0$ differs significantly from (5.2):

$$\begin{aligned} {\bar{r}}_0(x,t) = [x + u_1(x,t)]{\bar{e}}_1 + u_2(x,t){\bar{e}}_2. \end{aligned}$$

Observe the additional term $u_2{\bar{e}}_2$. The relevant strains for purpose of comparison are discussed in Sect. 3.3: A vector strain $\varvec{{\tilde{\gamma }}}=\Gamma _1 {\bar{e}}_x + \Gamma _2 {\bar{e}}_y$ and scalar $\kappa =\partial _x \phi$. Only $\varvec{{\tilde{\gamma }}}$ is motivated by multi-dimensional considerations. For this purpose, the two-dimensional rotation $R_\phi$ with matrix representation $[R_\phi ] = \left[ \begin{array}{ll} \cos \phi &{} \sin \phi \\ -\sin \phi &{} \cos \phi \end{array}\right] ,$ is required. The authors present the following “physically reasonable definition of the strains” $\Gamma _i$:

$$\begin{aligned} \left[ \begin{array}{l} \Gamma _1 \\ \Gamma _2 \end{array}\right] = [R_\phi ]^T \left[ \begin{array}{l} 1 + u'_1 - \cos \phi \\ u'_2 -\sin \phi \end{array}\right] . \end{aligned}$$

(5.9)

Consequently, ${\overline{F}} = [R_\phi ][C] \left[ \begin{array}{c} \Gamma _1 \\ \Gamma _2 \end{array}\right]$ where $[C] = \displaystyle {\left[ \begin{array}{ll} EA &{} 0 \\ 0 &{} GA_s \end{array}\right] }$. Note that the strains $\Gamma _i$ are constant over a cross section. It is clear from the definition of the strains that this model differs from the LLT model.

The authors effectively assume Eq. (4.3) (also Eq. (5.8)), $M=EI\partial _x\phi$, as can be seen by inspection of the formulation of the elastic potential energy.

Applications of the theory above are in [18]. The LLT model can also be used for some of these applications.

5.3 Theory of Irschik and Gerstmayr

The local linear model is a special case of the nonlinear model in [10]; hence, the article is of special interest. The authors consider the equilibrium of a beam that is “bent, sheared and stretched by external forces and moments”. They restrict the situation to plane deformations and static conditions. It is assumed that the deformed configuration is described by

$$\begin{aligned} r(x,y,z) = r_0(x) + y e_y(x) + z e_z. \end{aligned}$$

Note that this is a static version of Eq. (5.1). To obtain constitutive equations, the authors combine the Green strain tensor G and second Piola–Kirchhoff stress tensor. To define G, one starts with the deformation gradient ${{\mathcal {F}}} = \nabla r$ and then defines $G = \frac{1}{2}(C - I)$, where $C = {{\mathcal {F}}}^T\mathcal{F}$.

Comparing the “virtual work considerations” with the calculation of forces and moments for the LLT model, it is clear that the factor $\partial _x s$ plays a prominent role. (Note that $e = {\bar{e}}_T$ and $\Lambda _{x0} = \partial _x s$ in [10].) Recall the assumption that $\partial _x s - 1$ should be small.

The theory in [10] is applied to a static beam problem consisting of a hyper-elastic material. The LLT theory is not suitable for this application. Neither is the theory in [8] suitable for this application, since it cannot account for finite non-rigid rotations.

Superficially, there is a connection between the theory in [9] and the approach followed by [8]. But the rotation $R_\phi$ is in general not the same as the rotation R in the polar decomposition. The question arises whether there is in fact some connection.

6 Small vibrations

For small vibrations, it is usually assumed that $\partial _x u$ and $\partial _x w$ are small or $\theta$ is small. It is necessary to be careful since such assumptions may lead to contradictions.

First, just assume that $\theta$ is sufficiently small to justify the assumptions $\cos \theta \approx 1$ and $\sin \theta \approx \theta$. Then, (4.17) implies that $\partial _x s = 1 + \partial _x u$. Next, assume that $\partial _x u$ and $\partial _x w$ are sufficiently small for $(\partial _x u)^2$ and $(\partial _x w)^2$ to be neglected. Then,

$$\begin{aligned} \partial _x s= & {} \sqrt{1 + 2\partial _x u + (\partial _x u)^2 + (\partial _x w)^2}\\\approx & {} 1 + \partial _x u + \frac{1}{2}(\partial _x u)^2 + \frac{1}{2}(\partial _x w)^2. \end{aligned}$$

But the assumption is that $\partial _x u$ and $\partial _x w$ are small, and hence, $(\partial _x u)^2$ and $(\partial _x w)^2$ may be neglected. This leads to the assumption

$$\begin{aligned} \partial _x s = 1 + \partial _x u, \end{aligned}$$

(6.1)

and the result is the same as when the assumption $\theta$ small was used. Instead of (6.1), the assumption

$$\begin{aligned} \partial _x s = 1 + \partial _x u + \frac{1}{2}(\partial _x w)^2 \end{aligned}$$

(6.2)

is often used (see, e.g. [11, 12, 19]).

In the rest of this section, more additional assumptions will be made which may lead to unrealistic mathematical models. However, the solutions of the simplified models can be compared to those of the LLT model.

6.1 A significant nonlinear model for small vibrations

If $\sin \theta$ and $\cos \theta$ are replaced by $\theta$ and 1, respectively, then Eqs. (4.14) and (4.15) reduce to $F_1 = S - V \theta$ and $F_2 = S \theta + V.$ Note that the computations in (4.16) to (4.18) still need to be done. Further approximation where $\theta = \partial _x w$ avoids this complication without rendering the model less applicable. For the simplified model assume that

$$\begin{aligned} F_1= & {} S - V \partial _x w, \end{aligned}$$

(6.3)

$$\begin{aligned} F_2= & {} S \partial _x w + V. \end{aligned}$$

(6.4)

The constitutive equation (4.21) must be replaced by either (6.1) or (6.2), but the other constitutive equations remain the same. Note that the system is still nonlinear.

Consider the substitution of (6.3) and (6.4) into the equation of motion (4.13):

$$\begin{aligned} \frac{1}{\alpha } \partial ^2_t \phi= & {} (1+\partial _x u) (S \partial _x w + V) - \partial _x w (S - V \partial _x w) + \partial _x M \\= & {} V + \partial _x u(S \partial _x w + V) + V (\partial _x w)^2 + \partial _x M. \end{aligned}$$

By assumption, $\partial _x u$ and $\partial _x w$ are small and due to the scaling S and V are substantially less than one for linear elasticity, hence $S \partial _x u \partial _x w$ and $V(\partial _x w)^2$ may be neglected. However, one should be more careful with the terms $\partial _xuV$ and $\partial _xwS$. It is notable that the term $\partial _x uV$ originating in (3.6) is absent in the other articles we studied.

Model SLLT Small vibrations

Equations of motion:

$$\begin{aligned} \partial ^2_t u= & {} \partial _x (S - V \partial _x w) + P_1, \end{aligned}$$

(6.5)

$$\begin{aligned} \partial ^2_t w= & {} \partial _x (S\partial _x w + V) + P_2, \end{aligned}$$

(6.6)

$$\begin{aligned} \frac{1}{\alpha } \partial ^2_t \phi= & {} (1 + \partial _x u)V + \partial _x M, \end{aligned}$$

(6.7)

with constitutive equations

$$\begin{aligned} M= & {} \frac{1}{\beta } \partial _x \phi , \end{aligned}$$

(6.8)

$$\begin{aligned} V= & {} \partial _x w - \phi , \end{aligned}$$

(6.9)

$$\begin{aligned} S= & {} \frac{1}{\gamma }\partial _x u \end{aligned}$$

(6.10)

$$\begin{aligned} \text {or} \quad S= & {} \frac{1}{\gamma }\partial _x u + \frac{1}{2\gamma }(\partial _x w)^2. \end{aligned}$$

(6.11)

The boundary conditions are one of the following.

Cantilever beam:

$$\begin{aligned} u(0,t)= & {} w(0,t) = \phi (0,t) = 0. \end{aligned}$$

(6.12)

$$\begin{aligned} S(1,t)= & {} V(1,t) = M(1,t) = 0. \end{aligned}$$

(6.13)

Pinned–pinned beam:

$$\begin{aligned} u(0,t)= & {} w(0,t)=u(1,t)=w(1,t)=0 \end{aligned}$$

(6.14)

$$\begin{aligned} M(0,t)= & {} M(1,t)=0. \end{aligned}$$

(6.15)

Pivoted beam: The boundary conditions are the same as for the Cantilever beam except that $\phi (0,t)=0$ is replaced by $M(0,t)=0$.

For each model problem, the initial values for u, w, $\phi$, $\partial _t u$, $\partial _t w$ and $\partial _t \phi$ must be prescribed.

Remark

A solution for the pivoted beam model may develop large displacements violating the assumptions made.

Despite the additional assumptions made, the system is still nonlinear. It is notable that quite a number of simpler models can be derived from Model SLLT. We consider transverse vibration in the next subsection and models without shear in Sect. 6.5.

6.2 Transverse vibration

If the term $-V\partial _x w$ in (6.5) is neglected and Eq. (6.10) used, then it is possible to decouple longitudinal and transverse vibration.

Model LLT-T Transverse vibrations

Equations of motion:

$$\begin{aligned} \partial ^2_t u= & {} \partial _x S + P_1, \end{aligned}$$

(6.16)

$$\begin{aligned} \partial ^2_t w= & {} \partial _x (S\partial _x w) + \partial _x V + P_2, \end{aligned}$$

(6.17)

$$\begin{aligned} \frac{1}{\alpha }\partial ^2_t \phi= & {} (1 + \partial _x u)V + \partial _x M. \end{aligned}$$

(6.18)

The constitutive equations (excluding (6.11)) and boundary conditions remain unchanged.

It appears as if the system is still nonlinear but if the boundary conditions for u and S do not involve the other variables, the system decouples. For example, boundary conditions for u and S are $u(0,t) = S(1,t) = 0$ for the cantilever and $u(0,t) = u(1,t) = 0$ for a hinged-hinged beam. Consequently, since $\partial _x u = \gamma S$, (6.16) becomes the wave equation with homogeneous boundary conditions. Once u and S are known, Eqs. (6.17) and (6.18) constitute a nonhomogeneous linear system. Due to the time dependent coefficients $\partial _x u$ and S, we have forced vibrations (even when $P_2=0$). A special case of this linear system is considered in the next subsection.

If the Constitutive Equation (6.11) is used, then pure transverse oscillations are only possible when $\partial _x S = 0$ as shown in Sect. 6.4.

6.3 Adapted linear Timoshenko model

Consider the linear model for transverse vibrations. In some realistic applications, $\partial _t P_1 = 0$, and then, $\partial _t S = 0$ since there is no boundary forcing. Equation (6.16) reduces to

$$\begin{aligned} 0= & {} \partial _x S + P_1. \end{aligned}$$

(6.19)

Since $\partial _x u = \gamma S$, both u and the force S are uniquely determined and the model for transverse vibrations is linear.

Model Tim-Ad1   Adapted linear Timoshenko model

The model is given by (6.19) and

$$\begin{aligned} \partial ^2_t w= & {} \partial _x (S\partial _x w) + \partial _x V + P_2, \end{aligned}$$

(6.20)

$$\begin{aligned} \frac{1}{\alpha }\partial ^2_t \phi= & {} \gamma SV + V + \partial _x M. \end{aligned}$$

(6.21)

The constitutive equations and boundary conditions remain unchanged.

The model above is a variation on the well-known linear Timoshenko beam model. It can be used to model vertical structures like buildings or industrial chimneys. An alternative adapted Timoshenko model is possible, and therefore, the two models are numbered for easy reference.

As mentioned before, forces and force densities are small but to neglect the term $\partial _x w S$ altogether may be a mistake. However, the approximation

$$\begin{aligned} (1+ \gamma S)V = V \end{aligned}$$

(6.22)

may be considered. Indeed, the term $\gamma S V$ is absent in other articles we studied. Justification for this assumption is investigated in Sect. 9. Model Tim-Ad1 is symmetric if $\gamma SV$ is neglected as explained in Sect. 8.

6.3.1 Alternative linear model

Assuming that longitudinal oscillations may be ignored in the Local linear Timoshenko model (in Sect. 4) and that the transverse vibrations are sufficiently small, one obtains another linear approximation. Simply let $F_1 = S$ and $F_2 = V$ in Eqs. (4.11) to (4.13) to obtain another linear model.

The equations of motion are

$$\begin{aligned} \partial ^2_t w= & {} \partial _x V + P_2, \end{aligned}$$

(6.23)

$$\begin{aligned} \frac{1}{\alpha }\partial ^2_t \phi= & {} (1 + \gamma S)V -S\partial _x w + \partial _x M. \end{aligned}$$

(6.24)

The constitutive equations and the boundary conditions are the same as for the SLLT beam model in Sect. 6.1.

This model was considered in [20]. Due to the symmetry, one may prefer Model Tim-Ad1 but further investigation is called for. Another question is whether the difference is serious. In this regard, it should be noted that the models become identical if the shear is eliminated to derive the Raleigh or Euler–Bernoulli models (see Sect. 6.5).

The alternative model above is almost symmetric. Note that

$$\begin{aligned} (1 + \gamma S)V -S\partial _x w + \partial _x M = V + \gamma SV - SV - S\phi + \partial _x M. \end{aligned}$$

Model Tim-Ad2 Alternative formulation

$$\begin{aligned} \partial ^2_t w= & {} \partial _x V + P_2, \end{aligned}$$

(6.25)

$$\begin{aligned} \frac{1}{\alpha }\partial ^2_t \phi= & {} V + (\gamma -1)SV - S\phi + \partial _x M. \end{aligned}$$

(6.26)

This model is also symmetric if SV is neglected.

6.4 Nonlinear Timoshenko model of Sapir and Reiss

In [11], the authors derive a nonlinear Timoshenko beam model similar to Model LLT-T. However, the nonlinearity arises due to the fact that they use (6.11) as a constitutive equation. Their aim was to study the transient motion of a buckled column using nonlinear Timoshenko beam theory. The authors provide a derivation for their model in an appendix. They start with nonlinear plane strain displacement relations and then make simplifying assumptions eventually leading to a nonlinear Timoshenko model.

In terms of the notation of this section, they assume that $\partial ^2_t u$ and $\partial _x uV$ may be neglected in Model LLT-T and that $P_1=P_2=\partial _x S = 0$. Consequently,

$$\begin{aligned} \partial ^2_t w= & {} S\partial ^2_x w+ \partial _x V, \end{aligned}$$

(6.27)

$$\begin{aligned} \frac{1}{\alpha }\partial ^2_t \phi= & {} V + \partial _x M. \end{aligned}$$

(6.28)

These are Eqs. (A.15b) and (A.15c) in [11]. Note that this model is linear if $\partial _xS=0$ and (6.10) is used. This is to be expected from the way that the shear strain displacements are linearized in the derivation of the model in [11]. However, in [11] it is assumed that

$$\begin{aligned} S= & {} \frac{1}{\gamma }(\partial _x s-1) = \frac{1}{\gamma }\left( \partial _x u + \frac{1}{2}(\partial _x w)^2\right) . \end{aligned}$$

(6.29)

Since $\partial _x S = 0$, it follows that

$$\begin{aligned} S(t)= & {} \frac{1}{\gamma }(u(1) - u(0)) + \frac{1}{2\gamma }\int _0^1(\partial _x w(\cdot ,t))^2. \end{aligned}$$

(6.30)

The boundary conditions for the pinned–pinned case (or hinged ends) are

$$\begin{aligned} w(0,t)= & {} \partial _x \phi (0,t) = w(1,t) = \partial _x \phi (1,t) = 0. \end{aligned}$$

The problem above with $w(\cdot ,0)$, $\phi (\cdot ,0)$, $\partial _t w(\cdot ,0)$ and $\partial _t \phi (\cdot ,0)$ prescribed has a unique weak solution, see, e.g. [21]. An algorithm based on FEM is developed in [22] where the authors also derive error estimates.

6.4.1 Nonlinear fourth-order Timoshenko beam equation

In [11], the authors preferred a single partial differential equation formulation for the model, which they derived by eliminating V and $\phi$. First, eliminating the angular acceleration in (6.28) yields

$$\begin{aligned} \partial ^4_t w - \partial ^2_t(S\partial ^2_x w) - \partial ^2_t \partial ^2_x w + \alpha \partial _x V + \alpha \partial ^2_x M = 0. \end{aligned}$$

Now $\alpha \partial _x M = \gamma \partial ^2_x \phi = \gamma \partial ^3_x w - \gamma \partial ^2_x V$ so that V and its partial derivatives can be eliminated using (6.27)

$$\begin{aligned}&\partial ^4_t w - \partial ^2_t(S\partial ^2_x w) - \partial ^2_t \partial ^2_x w - \gamma \partial ^2_x \partial ^2_t w + \alpha \partial ^2_t w \nonumber \\&\quad + \gamma (1 + S)\partial ^4_x w - \alpha S\partial ^2_x w = 0. \end{aligned}$$

(6.31)

A nonlinear fourth-order Timoshenko beam equation is also derived in [23]. The author claims that the partial differential equation above is a special case of his model.

Remark

The nonlinear Timoshenko system is not equivalent to Eq. (6.31). If the pair $(w,\phi )$ is a solution of the system (6.27)–(6.28) and sufficiently smooth, then w is a solution of (6.31). But, having a solution of this partial differential equation does not enable one to compute the shear force V or angle $\phi$.

6.5 Beam models without shear

In this subsection, it is shown how a number of published models for beams can be obtained from Model SLLT by eliminating shear. Recall that dimensionless forces are small. Using the approximation (6.22) in (6.7) yields

$$\begin{aligned} \frac{1}{\alpha }\partial ^2_t \phi= & {} V + \partial _x M. \end{aligned}$$

(6.32)

Combining this equation with (6.6) to eliminate V produces the equation of motion

$$\begin{aligned} \partial ^2_t w -\frac{1}{\alpha }\partial ^2_t \partial _x\phi= & {} \partial _x(\partial _x w S) - \partial ^2_x M + P_2. \end{aligned}$$

(6.33)

Assuming that $\phi = \partial _x w$, then $M = \frac{1}{\beta }\partial ^2_x w$ and substitution of both into Eq. (6.33) yields

$$\begin{aligned} \partial ^2_t w -\frac{1}{\alpha }\partial ^2_t \partial ^2_x w= & {} \partial _x(\partial _x w S) - \frac{1}{\beta }\partial ^4_x w + P_2. \end{aligned}$$

(6.34)

If the constitutive equation for S is (6.29), then the partial differential equation is nonlinear. This equation together with (6.5) (in Model SLLT) is the same as the system in [12] to model longitudinal and transverse vibrations.

If the constitutive equation in (6.10) is used or S is constant, then (6.34) is linear and models a Rayleigh beam with axial force. It models an Euler–Bernoulli beam if the term $-\frac{1}{\alpha }\partial ^2_t \partial ^2_x w$ is neglected.

A special case of the model in [12] is when $\partial _t P_1=0$ (as in Sect. 6.3). This is the case in [19] where the transverse vibration of a vertical structure is modelled and $P_1$ is due to gravity.

7 Variational forms

In this section, the different model problems presented in Sect. 6 are written in variational form. The variational form can be used for theory and for finite element approximations.

7.1 The local linear Timoshenko model for small vibrations

The variational form for the SLLT model is derived starting with the equations of motion. There are three cases, formulated in Sect. 4.2.

Cantilever beam: The forced boundary conditions for the test functions are $v(0) = z(0) = \psi (0) = 0$ and the space of test functions is defined as

$$\begin{aligned} T_1[0,1] = \{ y \in C^1 ~|~ y(0) = 0 \}. \end{aligned}$$

The problem is to find the functions u, w and $\phi$ such that $u(\cdot ,t)$, $w(\cdot ,t)$ and $\phi (\cdot ,t)$ are in $T_1[0,1]$ for all $t>0$ and the following hold:

$$\begin{aligned} \int _0^1 \partial ^2_t u(\cdot ,t) v&= -\int _0^1\big (S-V(\cdot ,t)\partial _x w(\cdot ,t)\big ) v' + \int _0^1 P_1(\cdot ,t) v, \end{aligned}$$

(7.1)

$$\begin{aligned} \int _0^1 \partial ^2_t w(\cdot ,t) z&= -\int _0^1 \big (S\partial _x w(\cdot ,t)+V(\cdot ,t)\big ) z' + \int _0^1 P_2(\cdot ,t) z, \end{aligned}$$

(7.2)

$$\begin{aligned} \int _0^1 \frac{1}{\alpha } \partial ^2_t \phi (\cdot ,t) \psi&= \int _0^1 \big (1 + \partial _x u(\cdot ,t)\big ) V(\cdot ,t) \psi - \int _0^1 M(\cdot ,t) \psi ' \end{aligned}$$

(7.3)

for all $\langle v, z, \psi \rangle \in T_1[0,1] \times T_1[0,1] \times T_1[0,1]$.

Equations (7.1), (7.2) and (7.3) are the variational equations of motion. This together with Eqs. (6.8) to (6.11) produces the system in variational form. For the model problem, one must prescribe initial values for u, w, $\phi$, $\partial _t u$, $\partial _t w$ and $\partial _t \phi$. Denote these by $u_0,~w_0,~\phi _0,~u_d,~w_d$ and $\phi _d$, respectively.

Pinned–pinned beam: A space of test functions for a pinned–pinned beam is defined as

$$\begin{aligned} T_2[0,1] = \{ y \in C^1 ~|~ y(0) = y(1) = 0 \}. \end{aligned}$$

The problem is to find the functions u, w and $\phi$ such that $u(\cdot ,t)$, $w(\cdot ,t) \in T_2[0,1]$ and $\phi (\cdot ,t) \in C^1[0,1]$ for all $t>0$ and Eqs. (7.1), (7.2) and (7.3) hold for all $\langle v, z, \psi \rangle \in T_2[0,1] \times T_2[0,1] \times C^1[0,1]$.

Pivoted beam: The problem is to find the functions u, w and $\phi$ such that $u(\cdot ,t)$, $w(\cdot ,t) \in T_1[0,1]$ and $\phi (\cdot ,t) \in C^1[0,1]$ for all $t>0$ and Eqs. (7.1), (7.2) and (7.3) hold for all $\langle v, z, \psi \rangle \in T_1[0,1] \times T_1[0,1] \times C^1[0,1]$.

Recall that initial conditions need to be specified, see Sect. 6.1.

Simulations were done using a finite element approximation and acceptable numerical results were obtained.

Using the variational form of the model problem, it is easy to formulate the finite element approximation problem. Simulations were done to approximate the motion of the rod. As was the case with the LLT model, numerical experiments indicated that the approximations converge. For small initial data, the approximation for the nonlinear problem compared well with the exact solution of the corresponding linear problem (relative differences were less than $10^{-4}$). However, more numerical experiments are required as well as an analysis of the algorithm.

7.2 Transverse vibration

For transverse vibrations, everything stays the same, except that the term $V(\cdot ,t)\partial _x w(\cdot ,t)$ in Eq. (7.1) is neglected, and therefore, we have

$$\begin{aligned} \int _0^1 \partial ^2_t u(\cdot ,t) v&= -\int _0^1 S v' + \int _0^1 P_1(\cdot ,t) v. \end{aligned}$$

(7.4)

The boundary conditions do not change, and consequently, the test functions do not change either.

7.3 Adapted Timoshenko models

Recall from Sect. 6.3 that u and S are uniquely determined. The model problems can be considered as special cases of transverse vibration where Eq. (7.4) is omitted. The spaces of test functions are the same as before. We present the cantilever beam here.

7.4 Model problem Tim-Ad1 in variational form

Find the functions w and $\phi$ such that $w(\cdot ,t)$ and $\phi (\cdot ,t)$ are in $T_1[0,1]$ for all $t>0$ and the following hold:

$$\begin{aligned} \int _0^1 \partial ^2_t w(\cdot ,t) v&= -\int _0^1S\partial _x w(\cdot ,t) v'-\int _0^1 V(\cdot ,t) v' + \int _0^1 Q(\cdot ,t) v, \end{aligned}$$

(7.5)

$$\begin{aligned} \int _0^1 \frac{1}{\alpha } \partial ^2_t \phi (\cdot ,t) \psi&= \int _0^1 \big (1+\gamma S\big ) V(\cdot ,t) \psi - \int _0^1 M(\cdot ,t) \psi ' \end{aligned}$$

(7.6)

for all $\langle v, \psi \rangle \in T_1[0,1] \times T_1[0,1]$.

Using the variational forms, existence of solutions for the adapted Timoshenko models is considered in the next section.

8 Weak variational forms and existence for the adapted Timoshenko models

8.1 Weak variational forms

To derive the weak variational form for Problem Tim-Ad1, add Eqs. (7.5) and (7.6):

$$\begin{aligned} \int ^1_0 \partial _t^2 w (\cdot ,t) v + \dfrac{1}{\alpha } \int ^1_0 \partial _t^2 \phi (\cdot ,t) \psi&= \int ^1_0 V(\cdot ,t) (\psi - v') - \int ^1_0 S \partial _x w(\cdot ,t) v' \nonumber \\&\quad + \int ^1_0 \gamma S V(\cdot ,t) \psi - \int ^1_0 M(\cdot ,t) \psi ' + \int _0^1 Q(\cdot ,t) v. \end{aligned}$$

(8.1)

Let u denote the pair $\langle w, \phi \rangle$ and define the following bilinear forms.

For $u_i$ and $v_i$ in $\mathcal {L}^2(0,1)$,

$$\begin{aligned} c(u,v) = \int _0^1 u_1v_1 + \int _0^1 \frac{1}{\alpha }~u_2 v_2. \end{aligned}$$

For $u_i$ and $v_i$ in $T_1[0,1]$,

$$\begin{aligned} b_T(u,v)&= \int _0^{1} \frac{1}{\beta } u_2'v_2' + \int _0^{1} (u_1'-u_2)(v_1'-v_2), \end{aligned}$$

(8.2)

$$\begin{aligned} b_1(u,v)&= b_T(u,v) + \int _0^1 S u_1' v_1', \end{aligned}$$

(8.3)

$$\begin{aligned} b_{1,\gamma }(u,v)&= b_1(u,v) - \int _0^{1} \gamma S(u_1'-u_2) v_2. \end{aligned}$$

(8.4)

Using the bilinear forms, the variational Eq. (8.1) can be written as

$$\begin{aligned} c(\partial _t^2 u(\cdot ,t),v) + b_{1,\gamma }( u(\cdot ,t),v) = (Q (\cdot ,t),v_1), \end{aligned}$$

(8.5)

where (f, g) denote $\int ^1_0 fg$.

To write the model problem in weak variational form, suitable function spaces are needed. The necessary product spaces are defined by $X = {{\mathcal {L}}}^2(0,1) \times {{\mathcal {L}}}^2(0,1)$ and $H^1 = H^1(0,1) \times H^1(0,1)$. An element $y \in X$ is written as $y = \langle y_1,y_2\rangle$ and the inner product for $\mathcal {L}^2(0,1)$ is denoted by $(\cdot ,\cdot )$. A natural inner product for X is

$$\begin{aligned} (x,y)_{X}=(x_1,y_1)+(x_2,y_2), \end{aligned}$$

and the corresponding norm is denoted by $\Vert \cdot \Vert _{X}$. The natural inner product for the product space $H^1$ is

$$\begin{aligned} (x,y)_{H^1}=(x_1,y_1)_1+(x_2,y_2)_1 \end{aligned}$$

and the corresponding norm is denoted by $\Vert \cdot \Vert _{H^1}$.

The bilinear form c is clearly an inner product for X, which induces a norm $\Vert u\Vert _{W} = \sqrt{c(u,u)}$. The vector space X equipped with this inner product is referred to as the inertia space W. Obviously, the norms $\Vert \cdot \Vert _W$ and $\Vert \cdot \Vert _X$ are equivalent.

Let $V_1(0,1)$ be the closure of $T_1[0,1]$ in $H^1(0,1)$ and $V_2(0,1)$ be the closure of $T_2[0,1]$. The product space V is defined as either $V_1 \times V_1$ or $V_2 \times H^1$. To proceed, it is necessary for $b_1$ to be an inner product for the space V. The different cases are treated in the next section. The space V equipped with the inner product $b_1$ is referred to as the energy space with associated norm $\Vert u\Vert _{V} = \sqrt{b_1(u,u)}$.

Due to the fact that $C^{\infty }_0(0,1)$ is dense in $\mathcal{L}^2(0,1)$, the following result is obvious.

Proposition 8.1

V is a dense subset of W.

Notation Let $q_X$ be the mapping $t \rightarrow \langle Q(\cdot ,t),0 \rangle$.

From the definition of the bilinear form $b_{1,\gamma }$, it is now possible to define the weak variational form for the Timoshenko beam problem.

Problem Tim-Ad1 Weak variational form

Find u such that for each $t>0$, $u(t) \in V$, $u'(t) \in V$, $u''(t) \in W$ and

$$\begin{aligned} c(u''(t),v) + b_{1,\gamma }(u(t),v) = (q_X(t),v)_{X} ~~ \text {for each}~~ v \in V, \end{aligned}$$

(8.6)

with $u(0) = u_0=\langle w_0,\phi _0 \rangle$ and $u'(0) = u_d=\langle w_d,\phi _d \rangle$.

All that is required for the alternative linear problem, is to define alternative bilinear forms:

$$\begin{aligned} b_2(u,v)&= b_T(u,v) + \int _0^{1} Su_2v_2 \quad \text {and} \end{aligned}$$

(8.7)

$$\begin{aligned} b_{2,\gamma }(u,v)&= b_2(u,v) - \int _0^{1} \gamma S(u_1'-u_2) v_2. \end{aligned}$$

(8.8)

Problem Tim-Ad2 Weak variational form

Find u such that for each $t>0$, $u(t) \in V$, $u'(t) \in V$, $u''(t) \in W$ and

$$\begin{aligned} c(u''(t),v) + b_{2,\gamma }(u(t),v) = (q_X(t),v)_{X} ~~ \text {for each}~~ v \in V, \end{aligned}$$

(8.9)

with $u(0) = u_0=\langle w_0,\phi _0 \rangle$ and $u'(0) = u_d=\langle w_d,\phi _d \rangle$.

8.2 Existence theory

The weak variational form of the model problems in this paper is a special case of the general linear second-order hyperbolic problem considered in [20] (given here for convenience): Find $u \in C^1([0, \infty ), X)$ such that, for all $t>0$, $u(t) \in V$, $u'(t) \in V$ and $u''(t) \in W$, and

$$\begin{aligned} c(u''(t),v) + a(u'(t),v) + b(u(t),v) = (f(t),v)_X \quad \text {for all} \ v \in V, \end{aligned}$$

with $u(0) = u_0$, $u'(0) = u_1$.

For the model problems in this paper, there is no damping, and consequently, the bilinear form a in the equation above is equal to 0. This is a special case of weak damping.

The following assumptions are made in [20] (also in [24]):

A1:

V is dense in W and W is dense in X.

A2:

There exists a positive constant $C_W$ such that $\Vert w \Vert _X \le C_W \Vert w \Vert _W \ \forall \ w \in ~W$.

A3:

There exists a positive constant $C_V$ such that $\Vert v \Vert _W \le C_V\Vert v \Vert _V \ \forall \ v \in V$.

For the existence result, the following important subspace of V is needed.

Definition

The space $E_b$

$$\begin{aligned} E_b = \{x \in V ~|~ \text {there exists a}~y \in W~\text {such that}~c(y,v) = b(x,v)~\text {for all}~v \in V\}. \end{aligned}$$

The following result is Theorem 2.3 in [20] (and also Theorem 2 in [24]), slightly rephrased.

Theorem 8.1

Suppose b is the inner product for the space V and Assumptions A1 to A3 hold. Let J be an interval containing zero. If $f \in C^1(J,X)$, then there exists a unique solution

$$\begin{aligned} u \in C^1(J,V) \cap C^2(J,W) \end{aligned}$$

for the general linear second-order hyperbolic problem with no damping for each $u_0 \in E_b$ and $u_1 \in V$. If $f=0$ then $u \in C^1((- \infty , \infty ), V) \cap (( - \infty , \infty ),W)$.

This result cannot be used in cases where the bilinear form b is not symmetric. In the article [20] however, it is shown that the symmetry of b is not necessary provided that b is the sum of $(u,v)_V$ (inner product for V) and another “suitably bounded” bilinear form ${\hat{b}}$ (Assumption A5). To be more specific: If $b(u,v) = (u,v)_V + {\hat{b}}(u,v)$, then it is required that $|{\hat{b}}(u,v)| \le k \Vert u\Vert _V \Vert v\Vert _W$ for some constant $k<C^{-1}_V$. As an application the authors used a mathematical model that is a version of Model Tim-Ad2.

Remark

Other existence results are available in the literature, e.g. [25, 26]. The results from [20, 24] are convenient for our problems, since it is given in terms of bilinear forms.

8.3 Application to symmetric problems

In this subsection, we consider a special case of the weak variational forms for problems Tim-Ad1 and Tim-Ad2 where the terms $\gamma SV$ and $(\gamma -1)SV$ are omitted.

Although it is well known that the bilinear form $b_T$ for the standard Timoshenko model is positive definite and an inner product for V, it is often not explicitly mentioned. It can for example be inferred from the estimates in [27]. It is stated and proved in [20]. In the articles mentioned above and others, beams that are clamped on one or both sides are considered. We were unable to find a direct proof for the pinned–pinned case in the literature but an indirect proof is provided in the Appendix of [28]. The result can be formulated as

Proposition 8.2

The bilinear form $b_T$ is an inner product for V and there exists a constant $c_T$ such that

$$\begin{aligned} b_T(u,u) \ge c_T\Vert u\Vert ^2_W \quad \text {for each} \ u \in V. \end{aligned}$$

(8.10)

Next, if $(Su'_1,u'_1) > -c_\alpha \Vert u'_1\Vert ^2$ where $c_\alpha < \displaystyle \frac{c_T}{2\alpha + 2c_T}$, then

$$\begin{aligned} \frac{b_1(u,u)}{b_T(u,u)}> \frac{c_T -2L(c_T + \alpha )}{c_T} > 0\quad \text {for each} ~ u \in V. \end{aligned}$$

(8.11)

Combining (8.10) and (8.11) yields the next result.

Proposition 8.3

If $\ (Su'_1,u'_1) > -c_\alpha \Vert u'_1\Vert ^2$, then the bilinear form $b_1$ is an inner product for V.

The inequality above is a stability condition which is trivially satisfied when $S\ge 0$. The following result is immediate.

Corollary 8.1

The norms $\Vert \cdot \Vert _V$ and $\Vert \cdot \Vert _{H^1}$ are equivalent on V.

It is clear from Sect. 8.1 that Assumptions A1 to A3 are satisfied for Problem Tim-Ad1 when $b_{1,\gamma }$ is replaced by $b_1$. The existence of a unique solution for the weak variational form follows, provided that $q_X$ is continuously differentiable w.r.t. the norm of X, which requires ${\tilde{q}}$ to be continuously differentiable with respect to the norm of $\mathcal {L}^2(0,1)$. If that condition is satisfied, Theorem 8.1 applies.

8.4 Application to the nonsymmetric problem

In this subsection, we consider Problem Tim-Ad1 as formulated in Sects. 6.3 and 8.1. Recall that $b_{1,\gamma } = b_1 + b_\gamma$ where

$$\begin{aligned} b_\gamma (u,v) = -\int _0^1 \gamma S(u'_1-u_2)v_2. \end{aligned}$$

(8.12)

Assume that the axial force S satisfies the stability condition in Proposition 8.3 effecting $b_1$ to be an inner product for V. To apply Theorem 2.3 in [20], it is necessary to prove that $|b_\gamma (u,v)| \le C \Vert u\Vert _V\Vert v\Vert _W$ for a suitable constant C (see Sect. 8.2). It is not difficult to derive such an estimate but C must be less than the minimum of the Rayleigh quotient associated with $b_1$.

Assuming that the stability condition is met, there exists a positive constant $c_1$ such that

$$\begin{aligned} b_1(u,u) \ge c_1\Vert u\Vert ^2_W \quad \text {for each} \ u \in V. \end{aligned}$$

(8.13)

Now, $|b_\gamma (u,v)| \le \mu \sqrt{\alpha }\Vert u\Vert _V \Vert v\Vert _W$ where $\mu = \sup |S|$. Consequently, Assumption A5 (in [20]) is satisfied if $\mu \sqrt{\alpha }< c_1$ and the existence theorem can be applied. From the above, it is clear that the required assumption on $b_{1,\gamma }$ is satisfied and that the existence theorem from [20] can be applied to Problem Tim-Ad1. As before, the existence of a unique solution for the weak variational form follows, provided that $q_X$ is smooth enough (see end of previous subsection).

The result is not entirely satisfactory; the condition for the existence of a solution should depend on the sign of the axial force S as for the symmetric problems. The result in this subsection is due to Assumption A5 in [20]; it may be that the condition is not necessary (although sufficient).

9 Comparison of the adapted linear Timoshenko models

9.1 Using eigenvalues to compare models

It is widely accepted (if not always explicitly mentioned) that the essential information about a vibration model is contained in its sequence of eigenfunctions and corresponding eigenvalues. See for example the books [14, 29, 30] and articles [6, 31, 32]. It is a fact that many comparisons of models rely on comparison of eigenvalues. A good example is the article [6]. In the article, natural frequencies for a beam are determined by physical experiments and compared to numerical values for a three-dimensional model obtained via the finite element method. The results are then compared to those for the Timoshenko theory.

Justification of the method to use eigenvalues to compare vibration models is based on the convergence of partial sums for a solution to the actual solution (see, e.g. [32]). As demonstrated in the article, the convergence results rely on the existence of a complete orthonormal sequence of eigenfunctions. We are not aware of a theory that provides these facts directly for a Timoshenko beam (let alone the variations in Sect. 6.3). The theory in [32] indicates how such results can be obtained. One can also use the theory for second order elliptic operators in [33] as a guide.

Note that the discussion above concerns symmetric problems. In the previous section, a distinction was made between symmetric and nonsymmetric dynamic problems. The corresponding eigenvalue problems inherit the symmetry or lack thereof. Consider for example the variational form of Problem Tim-Ad1 with $b_{1,\gamma }$ replaced by $b_1$. The corresponding eigenvalue problem in variational form is to find $u \in V$ such that

$$\begin{aligned} b_1(u,v) = \lambda c(u,v) \quad \text { for each} \ v \in V. \end{aligned}$$

Eigenvalues and eigenfunctions can be calculated using FEM. The theory mentioned above applies to the weak variational form due to the fact that both $b_1$ and c are symmetric. However, it must be verified that Assumptions A1 to A3 hold and also that a bounded sequence in V contains a convergent subsequence in W.

If S is a constant then the results in [17] can be used despite the fact that $S=0$ in the article. The proofs remain valid provided that $-1<S<1$. All the eigenvalues are simple for a cantilever beam and a pinned–pinned beam. It is possible to calculate all eigenvalues and eigenfunctions and guarantee the error. The eigenfunctions are pairs $\langle w,\phi \rangle$ where both w and $\phi$ are linear combinations of $\sinh \mu x$, $\cosh \mu x$, $\sin \omega x$ and $\cos \omega x$ with $\mu$ and $\omega$ uniquely determined by the relevant eigenvalue $\lambda$.

9.2 Application to the adapted Timoshenko models

In this subsection, the method in [17] is applied to the eigenvalue problems for the adapted Timoshenko models. First, consider the assumption in Eq. (6.22). This assumption amounts to neglecting the term $\gamma SV$ or $\partial _x uV$. As mentioned before, this “problematic term” is, as far a we could determine, missing in the literature. Our first objective is to evaluate the contribution of this term. To start, consider the eigenvalue problem associated with model Tim-Ad1:

$$\begin{aligned} -Sw'' - w'' + \phi '= & {} \lambda w , \end{aligned}$$

(9.1)

$$\begin{aligned} - \frac{1}{\beta }\phi ''- \gamma S(w' - \phi ) - (w' - \phi )= & {} \frac{\lambda }{\alpha } \phi . \end{aligned}$$

(9.2)

We compare the eigenvalues and eigenfunctions for the case above with those for the problem where the term $- \gamma S(w' - \phi )$ is neglected. The boundary conditions for both a cantilever and a pinned–pinned beam were considered. The numerical experiments were carried out for various values of S in the range $-10^{-1}< S < 10^{-1}$. (Recall the condition $-1< S < 1$ and also the fact that $S = \pm 10^{-1}$ should be considered as large.) In our experiments, the relative differences turned out to be less than $1 \%$. However, only a limited number of modes can be investigated and we calculated the first four in each case.

Next, consider the eigenvalue problems for the two versions of model Tim-Ad2 which are determined by the equations

$$\begin{aligned} - w'' + \phi '&= \lambda w , \end{aligned}$$

(9.3)

$$\begin{aligned} - \frac{1}{\beta }\phi ''- \gamma S(w' - \phi ) - (w' - \phi ) + Sw'&= \frac{\lambda }{\alpha } \phi . \end{aligned}$$

(9.4)

$$\begin{aligned} - \frac{1}{\beta }\phi ''- (\gamma - 1) S(w' - \phi ) - (w' - \phi ) + S\phi&= \frac{\lambda }{\alpha } \phi . \end{aligned}$$

(9.5)

The eigenvalue problem for the nonsymmetric case is determined by Eqs. (9.3) and (9.4), while (9.3) and (9.5) hold for the symmetric case. We investigated the effect of neglecting the term $- \gamma S(w' - \phi )$ in Eq. (9.4) and $(1 - \gamma ) S(w' - \phi )$ in Eq. (9.5). In a few samples, these terms did not affect the results significantly as was the case for model Tim-Ad1. Also, due to their simplicity, the simplified models are more likely to be used in applications.

In other experiments, we compared models Tim-Ad1 and Tim-Ad2 (nonsymmetric). Numerical experiments were carried out for various values of S, again in the range $-10^{-1}< S < 10^{-1}$. The boundary conditions for both a cantilever and pinned–pinned beam were considered. In our experiments, the relative differences turned out to be less than $1 \%$ for the axial force in the range $-10^{-2}< S < 10^{-2}$. However, for $S = \pm 10^{-1}$ the relative differences jumped to approximately 5% or more. The same experiments were carried out to compare the symmetric and nonsymmetric cases for model Tim-Ad2. The results were similar to those for the preceding set of experiments.

Critical load   For the pinned–pinned beam, $\lambda = \alpha$ is an eigenvalue with corresponding eigenfunction $\langle w(x),\phi (x)\rangle = \langle 0,1\rangle$. All the other eigenfunctions can be written as $\langle w_k(x),\phi _k(x)\rangle = \langle \sin k\pi x,A_k\cos k\pi x\rangle$ where, for model Tim-Ad1,

$$\begin{aligned} (1+S)k^2 \pi ^2 - k \pi A_k= & {} \lambda _k, \\ \frac{1}{\beta }k^2 \pi ^2A_k - (k \pi - A_k) - \gamma S(k \pi - A_k)= & {} \frac{\lambda _k}{\alpha } A_k. \end{aligned}$$

Setting $\lambda _1 = 0$, one can solve for the load S. It is the lesser root of $\displaystyle {\gamma S^2 + \frac{\pi ^2 + \beta }{\beta }S + \frac{\pi ^2}{\beta } = 0}$, i.e. $\displaystyle {S_{crit} \approx -\frac{\pi ^2}{\beta } + \left( \frac{\pi ^2}{\beta }\right) ^2}$ for $\gamma = 1/4$. For this load one expects that an associated nonlinear problem will yield buckled states. If the problematic term is left out (as described above), then

$\displaystyle {S_{crit} = -\frac{\pi ^2}{\beta + \pi ^2}}$. For both cases of model Tim-Ad2, $\displaystyle {S_{crit} = -\frac{\pi ^2}{\beta }}$.

10 Conclusion

In this article, we derived a mathematical model for large planar motion of elastic rods which undergo flexure, shear and extension but not torsion. (We use the term rod for one-dimensional solids, i.e. beams, cables, ropes, hoses. etc.) Since the Timoshenko theory provides an excellent approximation for three-dimensional elastic behaviour with plane stress, we adapted the constitutive equations for application to large rotations to complete the model, which we call the local linear Timoshenko rod (LLT) model. We demonstrated that this model serves as a framework for a class of simpler mathematical models for slender solids in various applications with the advantage that the more general model can be used to evaluate and compare the simpler models.

In Sect. 5, the infinitesimal theory of linear elasticity is applied to a thin disc in the beam to motivate the constitutive equations. The polar decomposition theorem is then used to motivate the co-existence of large rigid rotations and small strains. In the same section, the LLT model was compared to the models in [8, 10]. The static case was considered in [10], but the constitutive equations are fully nonlinear and a generalization of those in the LLT model. The LLT model shares some properties of the model in [8], but there are important differences, e.g. the strains in [8] do not reflect the Timoshenko kinematical assumption (see [10]).

A mathematical model for small vibrations of an elastic rod is also developed (from the LLT model) where flexure, shear and extension are still taken into account. This model, which is still nonlinear, also serves as a framework for a class of simpler models for small vibrations. A number of linear and nonlinear models are included of which some feature in articles published by other authors.

Variational forms and the implementation of the finite element method are discussed briefly. Some numerical experiments were carried out with encouraging results. Further work is in progress and results should be ready for publication soon. Analysis of the algorithms is a challenge where it is difficult to predict the outcome.

A section on weak variational forms and the existence of solutions for different linear Timoshenko model problems with axial loads is new. In another section, these models are compared using eigenvalues and eigenfunctions.