Rayleigh waves in a nonlocal thermoelastic layer lying over a nonlocal thermoelastic half-space

Abstract

The paper deals with Rayleigh wave propagation in a nonlocal thermoelastic layer, and the layer is lying over a nonlocal thermoelastic half-space. The problem is treated in the context of Eringen’s nonlocal thermoelasticity and Green–Naghdi model type III of hyperbolic thermoelasticity. The frequency equation of Rayleigh waves is derived, and different cases are also discussed. The effect of the nonlocal parameter on phase velocity, attenuation coefficient, specific loss, and penetration depth is presented graphically.

1 Introduction

The theory of nonlocal elasticity has attracted the attention of many authors because of its early success in solving an old problem in fracture mechanics. The nonlocal elasticity solution of Eringen [1, 2] showed that the stress at the tip of a crack is finite; it rises to a maximum and then diminishes with the distance from the crack tip. Eringen [3, 4] found the nonlocal solution of the discrete dislocation problem. Nonlocal field theories contain very interesting physics, in fact, all physics, excluding quantum effects and elementary particle physics. This can be extended further to include the nonlocal mixture theory, diffusion, and other allied phenomena.

Some nonclassical thermoelasticity theories have been developed depending on the strategies to incorporate additional atomistic features based on Eringen’s nonlocal elasticity theory [5] which is now well established. In the local elasticity model, Eringen [5] assumed that the stress field at a particular point in an elastic continuum not only depends on the strain field but also on strains at all other points of the body. Altan [6] studied the uniqueness in the linear theory of nonlocal elasticity. The nonlocal elasticity models characterized by the presence of nonlocality residuals of fields have been proposed by Eringen and Edelen [7]. Eringen extended the concept of nonlocality to various other fields in his works cited in [8,9,10].

Nonlocal elasticity theories are now well established and are being applied to the problems of wave propagation in elastic and thermoelastic solids. Pramanik and Biswas [11] investigated the propagation of Rayleigh surface waves in nonlocal thermoelastic solids. Biswas [12] considered the propagation of Rayleigh surface waves in a porous nonlocal thermoelastic orthotropic medium. Khurana and Tomar [13] studied wave propagation in a nonlocal microstretch solid. Jun et al. [14] discussed nonlocal thermoelasticity based on nonlocal heat conduction and nonlocal elasticity. Khurana and Tomar [15] investigated Rayleigh-type waves in a nonlocal micropolar solid half-space.

The generalized thermoelasticity theories have been developed with the aim of removing the paradox of infinite speed of heat propagation inherent in the classical coupled dynamical thermoelasticity theory (Biot [16]). Many new theories have been proposed to take care of this physical absurdity. Lord and Shulman [17] first modified Fourier’s law by introducing the term representing the thermal relaxation time. The heat equation associated with this theory is a hyperbolic type and hence eliminates the paradox of infinite speed of thermal propagation. Then, Green and Lindsay [18] developed a more general theory of thermoelasticity in which Fourier’s law of heat conduction is unchanged, whereas the classical energy equation and Duhamel–Neumann’s relations are modified by introducing two constitutive constants having the dimensions of time. Later, Green and Naghdi [19,20,21] developed three models for generalized thermoelasticity of homogeneous isotropic materials, which are labelled as models I, II, and III. Green–Naghdi model type II is known as thermoelasticity without energy dissipation, and Green–Naghdi type III model is known as thermoelasticity with energy dissipation. Detailed information regarding these theories can be found in [22, 23].

Dwan and Chakraborty [24] proposed Rayleigh waves in the context of Green-Lindsay’s model of generalized thermoelasticity theory, and Rossikin and Shitikova [25] discussed nonstationary Rayleigh waves in the thermally insulated surfaces of some thermoelastic bodies of revolution. Singh et al. [26] considered propagation of the Rayleigh wave in an initially stressed transversely isotropic magneto-thermoelastic half-space with dual-phase-lag model. Biswas et al. [27] investigated Rayleigh surface wave propagation in orthotropic thermoelastic solids under three-phase-lag model. Biswas and Abo-Dahab [28] considered the effect of phase lags on Rayleigh waves in an initially stressed magneto-thermoelastic orthotropic medium. Abd-Alla and Al-Dawy [29] considered the effect of thermal relaxation times on Rayleigh waves in a generalized thermoelastic medium. Wojnar [30] examined Rayleigh waves in a thermoelastic medium with relaxation times. Biswas [31] reported Stroh analysis of Rayleigh waves in an anisotropic thermoelastic medium with three-phase-lag model. Biswas and Mukhopadhyay [32] employed the eigenfunction expansion method to characterize Rayleigh wave propagation in an orthotropic medium with three-phase-lag model.

In this article, Rayleigh wave propagation in an isotropic thermoelastic layer lying over an isotropic thermoelastic half-space is investigated. The problem is treated in the context of Green–Naghdi model type III based on Eringen’s nonlocal thermoelasticity. Different frequency equations are derived as special cases which agree with the existing literature. In order to illustrate the theoretical developments, the computer simulated results with respect to phase velocity, attenuation coefficient, specific loss, and penetration depth are presented graphically.

2 Derivation of the model

We shall first establish the constitutive relations and field equations for a nonlocal thermoelastic medium with Green–Naghdi model type III of generalized thermoelasticity.

Consider a thermoelastic body having volume V, bounded by the surface S and occupying region B in $R^{3}$ at time t. Let the position of a typical point of B in the unbounded state be $X_{i}$ and the position of the corresponding point in the deformed state be $x_{i}$. The displacement components $u_{i}$ of the particle are given by $u_{i} =x_{i} -X_{i}$.

Let us denote the strain tensor by $e_{ij}$. In the linear theory, the Lagrangian strain tensor reduces to

$$\begin{aligned} e_{ij} =\frac{1}{2}\left( {u_{i,j} +u_{j,i} } \right) . \end{aligned}$$

Suppose $\theta =T-T_{0}$, where $T_{0}$ is the temperature of the material in its natural state assumed to be such that $\left| {\frac{\theta }{T_{0} }} \right|<<1$ and T is the absolute temperature of the material.

Within the context of linear theory and assuming that the initial body is free from stresses, we take the set of basic variables at two neighbouring points $\mathrm{\mathbf{x}}$ and $\mathrm{\mathbf{{x}'}}$, respectively, as

$$\begin{aligned}&\Pi =\left\{ {e_{ij} \left( {\mathrm{\mathbf{x}}} \right) ,\theta \left( {\mathrm{\mathbf{x}}} \right) } \right\} \nonumber \\&\hbox {and }{\Pi }'=\left\{ {e_{ij} \left( {\mathrm{\mathbf{{x}'}}} \right) ,\theta \left( {\mathrm{\mathbf{{x}'}}} \right) } \right\} . \end{aligned}$$

(1)

The strain energy function W for nonlocal thermoelastic materials can be written as

$$\begin{aligned} 2W=C_{ijkl} e_{ij} \left( {\mathrm{\mathbf{x}}} \right) e_{kl} \left( {\mathrm{\mathbf{{x}'}}} \right) -\beta _{ij} \left[ {e_{ij} \left( {\mathrm{\mathbf{x}}} \right) \theta \left( {\mathrm{\mathbf{{x}'}}} \right) +e_{ij} \left( {\mathrm{\mathbf{{x}'}}} \right) \theta \left( {\mathrm{\mathbf{x}}} \right) } \right] -a\theta \left( {\mathrm{\mathbf{x}}} \right) \theta \left( {\mathrm{\mathbf{{x}'}}} \right) \end{aligned}$$

(2)

where the constitutive coefficients $C_{ijkl} ,a,\beta _{ij}$ are prescribed functions of $\mathrm{\mathbf{x}}$ and $\mathrm{\mathbf{{x}'}}$. $C_{ijkl}$ are the elastic constants, $\beta _{ij}$ are the thermal moduli, $e_{ij}$ are the strain components, and $a=\frac{\rho C_{v} }{T_{0} }.$

We adopt the following symmetries in the constitutive coefficients as

$$\begin{aligned} C_{ijkl} \left( {\mathrm{\mathbf{x,{x}'}}} \right) =C_{klij} \left( {\mathrm{\mathbf{x,{x}'}}} \right) =C_{jikl} \left( {\mathrm{\mathbf{x,{x}'}}} \right) , \beta _{ij} \left( {\mathrm{\mathbf{x,{x}'}}} \right) =\beta _{ji} \left( {\mathrm{\mathbf{x,{x}'}}} \right) . \end{aligned}$$

Following Eringen [1], the constitutive relations are obtained from

$$\begin{aligned} \Gamma =\int \limits _V {\left[ {\frac{\partial W}{\partial \Pi }+\left( {\frac{\partial W}{\partial {\Pi }'}} \right) ^{s}} \right] } \mathrm{d}V\left( {\mathrm{\mathbf{{x}'}}} \right) \end{aligned}$$

(3)

where the superscript ‘s’ represents the symmetry of that quantity with respect to interchange of $\mathrm{\mathbf{x}}$ and $\mathrm{\mathbf{{x}'}}$. The set $\Gamma =\left\{ {\tau _{ij} ,-\eta } \right\}$ is an ordered set with the set $\Pi$.

Thus, the force stress tensor $\tau _{ij}$ and the specific entropy $\eta$ are obtained from relations (2) and (3) as

$$\begin{aligned} \tau _{ij}= & {} \int \limits _V {\left[ {C_{ijkl} \left( {\mathrm{\mathbf{x,{x}'}}} \right) e_{kl} \left( {\mathrm{\mathbf{{x}'}}} \right) -\beta _{ij} \left( {\mathrm{\mathbf{x,{x}'}}} \right) \theta \left( {\mathrm{\mathbf{{x}'}}} \right) } \right] } \mathrm{d}V\left( {\mathrm{\mathbf{{x}'}}} \right) , \end{aligned}$$

(4)

$$\begin{aligned} \rho \eta= & {} \int \limits _V {\left[ {\beta _{ij} \left( {\mathrm{\mathbf{x,{x}'}}} \right) e_{ij} \left( {\mathrm{\mathbf{{x}'}}} \right) +a\theta \left( {\mathrm{\mathbf{{x}'}}} \right) } \right] } \mathrm{d}V\left( {\mathrm{\mathbf{{x}'}}} \right) . \end{aligned}$$

(5)

For a centro-symmetric isotropic material, the constitutive coefficients reduce to

$$\begin{aligned} C_{ijkl} =\lambda \left( {\mathrm{\mathbf{x,{x}'}}} \right) \delta _{ij} \delta _{kl} +2\mu \left( {\mathrm{\mathbf{x,{x}'}}} \right) \delta _{ik} \delta _{jl} , \beta _{ij} =\beta \left( {\mathrm{\mathbf{x,{x}'}}} \right) \end{aligned}$$

where the material coefficients $\lambda ,\mu ,\beta$ are functions of $\left| {\mathrm{\mathbf{x}}-\mathrm{\mathbf{{x}'}}} \right|$.

Hence, the constitutive relations (4)–(5) become

$$\begin{aligned} \tau _{ij}= & {} \int \limits _V {\left[ {\lambda \left( {\left| {\mathrm{\mathbf{x}}-\mathrm{\mathbf{{x}'}}} \right| } \right) \delta _{ij} e_{kk} \left( {\mathrm{\mathbf{{x}'}}} \right) +2\mu \left( {\left| {\mathrm{\mathbf{x}}-\mathrm{\mathbf{{x}'}}} \right| } \right) e_{ij} \left( {\mathrm{\mathbf{{x}'}}} \right) -\beta \left( {\left| {\mathrm{\mathbf{x}}-\mathrm{\mathbf{{x}'}}} \right| } \right) \theta \left( {\mathrm{\mathbf{{x}'}}} \right) } \right] } \mathrm{d}V\left( {\mathrm{\mathbf{{x}'}}} \right) , \end{aligned}$$

(6)

$$\begin{aligned} \rho \eta= & {} \int \limits _V {\left[ {\beta \left( {\left| {\mathrm{\mathbf{x}}-\mathrm{\mathbf{{x}'}}} \right| } \right) e_{ij} \left( {\mathrm{\mathbf{{x}'}}} \right) +a\left( {\left| {\mathrm{\mathbf{x}}-\mathrm{\mathbf{{x}'}}} \right| } \right) \theta \left( {\mathrm{\mathbf{{x}'}}} \right) } \right] } \mathrm{d}V\left( {\mathrm{\mathbf{{x}'}}} \right) . \end{aligned}$$

(7)

For most of the materials, the cohesive zone is very small, and within that zone the intermolecular forces decrease rapidly with distance from the reference point. Hence, we consider that all constitutive coefficients attenuate with distance, e.g.

$$\begin{aligned} \mathop {\lim }\limits _{\left( {\left| {\mathrm{\mathbf{x}}-\mathrm{\mathbf{{x}'}}} \right| } \right) \rightarrow \infty } \lambda \left( {\left| {\mathrm{\mathbf{x}}-\mathrm{\mathbf{{x}'}}} \right| } \right) \rightarrow 0. \end{aligned}$$

We also consider that all the constitutive coefficients attenuate the same degree and they attain their maxima at $\mathrm{\mathbf{x}}=\mathrm{\mathbf{{x}'}}$.

Therefore, we can take the following relations between nonlocal and local coefficients:

$$\begin{aligned} \frac{\lambda \left( {\left| {\mathrm{\mathbf{x}}-\mathrm{\mathbf{{x}'}}} \right| } \right) }{\lambda _{0} }=\frac{\mu \left( {\left| {\mathrm{\mathbf{x}}-\mathrm{\mathbf{{x}'}}} \right| } \right) }{\mu _{0} }=\frac{\beta \left( {\left| {\mathrm{\mathbf{x}}-\mathrm{\mathbf{{x}'}}} \right| } \right) }{\beta _{0} }=\frac{a\left( {\left| {\mathrm{\mathbf{x}}-\mathrm{\mathbf{{x}'}}} \right| } \right) }{a_{0} }=G\left( {\left| {\mathrm{\mathbf{x}}-\mathrm{\mathbf{{x}'}}} \right| } \right) ; \end{aligned}$$

(8)

here, the quantities in the denominator are Lamé constants coefficients. $\lambda _{0} ,\mu _{0}$ are well-known Lame’s constants, $\beta _{0} =\left( {3\lambda _{0} +2\mu _{0} } \right) \alpha _{t} ,\alpha _{t}$ is the coefficient of linear thermal expansion, a is thermal constant, $\delta _{ij}$ is the Kronecker delta function, and the function $G\left( {\left| {\mathrm{\mathbf{x}}-\mathrm{\mathbf{{x}'}}} \right| } \right)$ is a nonlocal kernel representing the effect of distant interactions of material points between $\mathrm{\mathbf{x}}$ and $\mathrm{\mathbf{{x}'}}$.

Also, the integral of the nonlocal kernel $G\left( {\left| {\mathrm{\mathbf{x}}-\mathrm{\mathbf{{x}'}}} \right| } \right)$ over the domain of integration is unity, i.e.

$$\begin{aligned} \int \limits _V {G\left( {\left| {\mathrm{\mathbf{x}}-\mathrm{\mathbf{{x}'}}} \right| } \right) } \mathrm{d}V=1. \end{aligned}$$

Hence, the kernel function G behaves as a Dirac delta function over the domain of influence. The function G attains its peak at $\left| {\mathrm{\mathbf{x}}-\mathrm{\mathbf{{x}'}}} \right| =0$ and generally decays with increasing $\left| {\mathrm{\mathbf{x}}-\mathrm{\mathbf{{x}'}}} \right|$.

Eringen [5] has already shown that the function G satisfies the relation

$$\begin{aligned} \left( {1-\varepsilon ^{2}\nabla ^{2}} \right) G\left( {\left| {\mathrm{\mathbf{x}}-\mathrm{\mathbf{{x}'}}} \right| } \right) =\delta \left( {\left| {\mathrm{\mathbf{x}}-\mathrm{\mathbf{{x}'}}} \right| } \right) \end{aligned}$$

(9)

where $\varepsilon =e_{0} a_{cl}$ is the elastic nonlocal parameter [1, 5], $a_{cl}$ being the internal characteristic length, and $e_{0}$ is a material constant. The internal characteristic length $a_{cl}$ is the interatomic distance, e.g. length of C–C bond (0.142 nm in Carbon nanotube).

Applying the operator $\left( {1-\varepsilon ^{2}\nabla ^{2}} \right)$ on the constitutive relations (6), (7), owing to the relation (8) and the property (9), we obtain (after suppressing the subscript ‘0’ from the constitutive coefficients)

$$\begin{aligned}&\left( {1-\varepsilon ^{2}\nabla ^{2}} \right) \tau _{ij} =\tau _{ij}^{L} =\left\{ {2\mu e_{ij} \left( {\mathrm{\mathbf{x}}} \right) +\left[ {\lambda e_{kk} \left( {\mathrm{\mathbf{x}}} \right) -\beta \theta \left( {\mathrm{\mathbf{x}}} \right) } \right] \delta _{ij} } \right\} , \end{aligned}$$

(10)

$$\begin{aligned}&\left( {1-\varepsilon ^{2}\nabla ^{2}} \right) \rho \eta =\left( {\rho \eta } \right) ^{L}=\left[ {\beta e_{kk} \left( {\mathrm{\mathbf{x}}} \right) +a\theta \left( {\mathrm{\mathbf{x}}} \right) } \right] , \end{aligned}$$

(11)

wherein the formula

$$\begin{aligned} \int {f\left( x \right) } \delta \left( {x-a} \right) \mathrm{d}x=f\left( a \right) \end{aligned}$$

(12)

has been employed. The quantities $\tau _{ij}^{L}$, and $\left( {\rho \eta } \right) ^{L}$ correspond to the local thermoelastic solid.

The fourier law for the GN-III model in nonlocal thermoelasticity becomes:

$$\begin{aligned} \left( {1-\varepsilon ^{2}\nabla ^{2}} \right) \dot{{q}}_{i} =\dot{{q}}_{i}^{L} =-\left( {K\dot{{\theta }}_{,i} +K^{*}\theta _{,i} } \right) \end{aligned}$$

(13)

where $q_{i}$ are the components of the heat flux vector, K is the thermal conductivity, and $K^{*}$ is the material constant characteristic of the theory.

3 Basic equations

The constitutive equations for isotropic thermoelastic material become:

(a) The energy equation for the linear theory of a thermoelastic material:

$$\begin{aligned} -\rho T_{0} \dot{{\eta }}=q_{i,i}; \end{aligned}$$

(14)

(b) The equations of motion (in the absence of body force):

$$\begin{aligned} \tau _{ij,j} =\rho \ddot{{u}}_{i} \end{aligned}$$

(15)

where $\rho$ is the mass density.

From the constitutive relations (10) and (11), Fourier’s law (13), the energy equation (14), and the equation of motion (15), we obtain the field equations in terms of the displacement and temperature for a homogeneous isotropic nonlocal thermoelastic material in the absence of body forces as

$$\begin{aligned}&\left( {\lambda +\mu } \right) u_{j,ij} +\mu u_{i,jj} -\beta \theta _{,i} =\left( {1-\varepsilon ^{2}\nabla ^{2}} \right) \rho \ddot{{u}}_{i}, \end{aligned}$$

(16)

$$\begin{aligned}&K\nabla ^{2}\dot{{\theta }}+K^{*}\nabla ^{2}\theta =\rho C_{v} \ddot{{T}}+\beta T_{0} \ddot{{e}} \end{aligned}$$

(17)

where $aT_{0} =\rho C_{v} ,C_{v}$ is the specific heat at constant strain.

From Eq. (10), we get the stress components as

$$\begin{aligned} \left( {1-\varepsilon ^{2}\nabla ^{2}} \right) \tau _{ij} =\tau _{ij}^{L} =\lambda e_{kk} \delta _{ij} +2\mu e_{ij} -\beta \theta \delta _{ij}. \end{aligned}$$

(18)

4 Formulation of the problem in a nonlocal thermoelastic layer

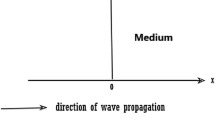
Let us consider a medium which consists of a nonlocal, homogeneous and isotropic layer of a constant thickness H lying over a nonlocal, homogeneous, and isotropic thermoelastic half space (Fig. 1).

Let us consider a plane harmonic surface wave which propagates along the x-axis and which is polarised in the $\left( {x,z} \right)$ plane.

We take ${\vec {u}}_{1} =\left( {u_{1} ,0,w_{1} } \right)$ as the displacement vector in the layer, $\lambda _{1} ,\mu _{1}$ are Lamé constants in the layer, $\beta _{1}$ is the thermal modulus in the layer, $\rho _{1}$ is the mass density of the thermoelastic layer, $\theta _{1}$ is the temperature above reference temperature of the layer, $K_{1}$ is the thermal conductivity of thermoelastic layer, $K_{1}^{*}$ is the material constant characteristic of the theory for the layer, $C_{v}$ is the specific heat at constant strain, and $\left( {\tau _{ij} } \right) _{1}$ are the stress components in the layer.

The basic governing equations of a nonlocal thermoelastic layer with Green–Naghdi type III model are obtained as

$$\begin{aligned}&\left( {\lambda _{1} +2\mu _{1} } \right) \frac{\partial ^{2}u_{1} }{\partial x^{2}}+\mu _{1} \frac{\partial ^{2}u_{1} }{\partial z^{2}}+\left( {\lambda _{1} +\mu _{1} } \right) \frac{\partial ^{2}w_{1} }{\partial x\partial z}-\beta _{1} \frac{\partial \theta _{1} }{\partial x}=\left( {1-\varepsilon ^{2}\nabla ^{2}} \right) \rho _{1} \ddot{{u}}_{1}, \end{aligned}$$

(19)

$$\begin{aligned}&\left( {\lambda _{1} +2\mu _{1} } \right) \frac{\partial ^{2}w_{1} }{\partial x^{2}}+\mu _{1} \frac{\partial ^{2}w_{1} }{\partial z^{2}}+\left( {\lambda _{1} +\mu _{1} } \right) \frac{\partial ^{2}u_{1} }{\partial x\partial z}-\beta _{1} \frac{\partial \theta _{1} }{\partial z}=\left( {1-\varepsilon ^{2}\nabla ^{2}} \right) \rho _{1} \ddot{{w}}_{1}, \end{aligned}$$

(20)

$$\begin{aligned}&K_{1}^{*} \nabla ^{2}\theta _{1} +K_{1} \nabla ^{2}\dot{{\theta }}_{1} =\rho _{1} C_{v} \ddot{{\theta }}_{1} +\beta _{1} T_{0} \ddot{{e}}. \end{aligned}$$

(21)

We define the dimensionless quantities as follows:

$$\begin{aligned} \left( {{x}',{z}',{\varepsilon }'} \right)= & {} \frac{\omega _{1}^{*} }{c_{1} }\left( {x,z,\varepsilon } \right) ,\, \left( {{u}'_{1} ,{w}'_{1} } \right) =\frac{\omega _{1}^{*} }{c_{1} }\left( {u_{1} ,w_{1} } \right) ,\, {\theta }'_{1} =\frac{\beta _{1} \theta _{1} }{\rho _{1} c_{1}^{2} },\, {t}'=\omega _{1}^{*} t, \left( {\tau _{ij} } \right) _{1}^{\prime }=\frac{\left( {\tau _{ij} } \right) _{1} }{\beta _{1} T_{0} },\\ m_{1}= & {} \frac{\mu _{1} }{\lambda _{1} +2\mu _{1} }, \,m_{2} =\frac{\lambda _{1} +\mu _{1} }{\lambda _{1} +2\mu _{1} },\, m_{3} =\frac{\beta _{1}^{2} T_{0} \omega _{1}^{*} }{\rho _{1} K_{1}^{*} },\, m_{4} =\frac{K_{1} \omega _{1}^{*} }{K_{1}^{*} },\, m_{5} =\frac{\lambda _{1} }{\lambda _{1} +2\mu _{1} } \end{aligned}$$

where $\omega _{1}^{*} =\frac{\rho _{1} C_{v} c_{1}^{2} }{K_{1}^{*} }$ and $c_{1} =\sqrt{\frac{\lambda _{1} +2\mu _{1} }{\rho _{1} }}$ are the characteristic frequency and longitudinal wave velocity in the layer, respectively.

Using nondimensional quantities in Eqs. (19), (20), and (21) and dropping primes, we get

$$\begin{aligned}&\frac{\partial ^{2}u_{1} }{\partial x^{2}}+m_{1} \frac{\partial ^{2}u_{1} }{\partial z^{2}}+m_{2} \frac{\partial ^{2}w_{1} }{\partial x\partial z}-\frac{\partial \theta _{1} }{\partial x}=\left( {1-\varepsilon ^{2}\nabla ^{2}} \right) \ddot{{u}}_{1}, \end{aligned}$$

(22)

$$\begin{aligned}&\frac{\partial ^{2}w_{1} }{\partial x^{2}}+m_{1} \frac{\partial ^{2}w_{1} }{\partial z^{2}}+m_{2} \frac{\partial ^{2}u_{1} }{\partial x\partial z}-\frac{\partial \theta _{1} }{\partial z}=\left( {1-\varepsilon ^{2}\nabla ^{2}} \right) \ddot{{w}}_{1}, \end{aligned}$$

(23)

$$\begin{aligned}&\nabla ^{2}\theta _{1} +m_{4} \nabla ^{2}\dot{{\theta }}_{1} =\ddot{{\theta }}_{1} +m_{3} \ddot{{e}}. \end{aligned}$$

(24)

5 Formulation of the problem in a nonlocal thermoelastic half-space

We take ${\vec {u}}_{2} =\left( {u_{2} ,0,w_{2} } \right)$ as the displacement vector in the half-space, $\lambda _{2} ,\mu _{2}$ are Lamé constants in the half-space , $\beta _{2}$ is the thermal modulus for the thermoelastic half-space, $\rho _{2}$ is the mass density of the thermoelastic half-space, $\theta _{2}$ is the temperature above reference temperature of the half-space, $K_{2}$ is the thermal conductivity of the thermoelastic half-space, $K_{2}^{*}$ is the material constant characteristic of the theory for the half-space, ${C}'_{v}$ is the specific heat at constant strain, and $\left( {\tau _{ij} } \right) _{2}$ are the stress components in the half-space.

The basic governing equations of a nonlocal thermoelastic half-space with Green–Naghdi type III model are obtained as

$$\begin{aligned}&\left( {\lambda _{2} +2\mu _{2} } \right) \frac{\partial ^{2}u_{2} }{\partial x^{2}}+\mu _{2} \frac{\partial ^{2}u_{2} }{\partial z^{2}}+\left( {\lambda _{2} +\mu _{2} } \right) \frac{\partial ^{2}w_{2} }{\partial x\partial z}-\beta _{2} \frac{\partial \theta _{2} }{\partial x}=\left( {1-\varepsilon ^{2}\nabla ^{2}} \right) \rho _{2} \ddot{{u}}_{2}, \end{aligned}$$

(25)

$$\begin{aligned}&\left( {\lambda _{2} +2\mu _{2} } \right) \frac{\partial ^{2}w_{2} }{\partial x^{2}}+\mu _{2} \frac{\partial ^{2}w_{2} }{\partial z^{2}}+\left( {\lambda _{2} +\mu _{2} } \right) \frac{\partial ^{2}u_{2} }{\partial x\partial z}-\beta _{2} \frac{\partial \theta _{2} }{\partial z}=\left( {1-\varepsilon ^{2}\nabla ^{2}} \right) \rho _{2} \ddot{{w}}_{2}, \end{aligned}$$

(26)

$$\begin{aligned}&K_{2}^{*} \nabla ^{2}\theta _{2} +K_{2} \nabla ^{2}\dot{{\theta }}_{2} =\rho _{2} {C}'_{v} \ddot{{\theta }}_{2} +\beta _{2} T_{0} \ddot{{e}}. \end{aligned}$$

(27)

We define the dimensionless quantities as follows:

$$\begin{aligned}&\left( {{x}',{z}',{\varepsilon }'} \right) =\frac{\omega ^{*}}{c_{2} }\left( {x,z,\varepsilon } \right) ,\, \left( {{u}'_{2} ,{w}'_{2} } \right) =\frac{\omega ^{*}}{c_{2} }\left( {u_{2} ,w_{2} } \right) ,\, {\theta }'_{2} =\frac{\beta _{2} \theta _{2} }{\rho _{2} c_{2}^{2} }, \,{t}'=\omega ^{*}t, \left( {\tau _{ij} } \right) _{2}^{\prime }=\frac{\left( {\tau _{ij} } \right) _{2} }{\beta _{2} T_{0} }, \\&r_{1} =\frac{\mu _{2} }{\lambda _{2} +2\mu _{2} }, \,r_{2} =\frac{\lambda _{2} +\mu _{2} }{\lambda _{2} +2\mu _{2} },\, r_{3} =\frac{\beta _{2}^{2} T_{0} \omega ^{*}}{\rho _{2} K_{2}^{*} },\, r_{4} =\frac{K_{2} \omega ^{*}}{K_{2}^{*} },\, r_{5} =\frac{\lambda _{2} }{\lambda _{2} +2\mu _{2} } \end{aligned}$$

where $\omega ^{*}=\frac{\rho _{2} {C}'_{v} c_{2}^{2} }{K_{2}^{*} }$ and $c_{2} =\sqrt{\frac{\lambda _{2} +2\mu _{2} }{\rho _{2} }}$ are the characteristic frequency and longitudinal wave velocity in the half-space, respectively.

Using nondimensional quantities in Eqs. (25), (26), and (27), and dropping primes, we get

$$\begin{aligned}&\frac{\partial ^{2}u_{2} }{\partial x^{2}}+r_{1} \frac{\partial ^{2}u_{2} }{\partial z^{2}}+r_{2} \frac{\partial ^{2}w_{2} }{\partial x\partial z}-\frac{\partial \theta _{2} }{\partial x}=\left( {1-\varepsilon ^{2}\nabla ^{2}} \right) \ddot{{u}}_{2}, \end{aligned}$$

(28)

$$\begin{aligned}&\frac{\partial ^{2}w_{2} }{\partial x^{2}}+r_{1} \frac{\partial ^{2}w_{2} }{\partial z^{2}}+r_{2} \frac{\partial ^{2}u_{2} }{\partial x\partial z}-\frac{\partial \theta _{2} }{\partial z}=\left( {1-\varepsilon ^{2}\nabla ^{2}} \right) \ddot{{w}}_{2}, \end{aligned}$$

(29)

$$\begin{aligned}&\nabla ^{2}\theta _{2} +r_{4} \nabla ^{2}\dot{{\theta }}_{2} =\ddot{{\theta }}_{2} +r_{3} \ddot{{e}}. \end{aligned}$$

(30)

6 Boundary conditions

Now we add boundary conditions which determine the properties of the wave field at the boundaries.

• (a) Surface of the layer $z=0:$ We assume the surface of the layer to be traction free and temperature free:

  • (i) $\left( {\tau _{xz} } \right) _{1} =0$

    $$\begin{aligned} \hbox {which gives }\left( {\tau _{xz} } \right) _{1}^{L} =0, \end{aligned}$$

    (31)

  • (ii) $\left( {\tau _{zz} } \right) _{1} =0$,

    $$\begin{aligned} \hbox {which gives }\left( {\tau _{zz} } \right) _{1}^{L} =0, \end{aligned}$$

    (32)
  • (iii)
    $$\begin{aligned} \theta _{1} =0. \end{aligned}$$

    (33)

• (b) Interface between the layer and the half-space $z=H:$ We require all displacement and stress components to be continuous across this interface:

  • (iv)
    $$\begin{aligned} u_{1} =u_{2}, \end{aligned}$$

    (34)
  • (v)
    $$\begin{aligned} w_{1} =w_{2}, \end{aligned}$$

    (35)
  • (vi)
    $$\begin{aligned} \left( {\tau _{xz} } \right) _{1}= & {} \left( {\tau _{xz} } \right) _{2},\\ \left( {1-\varepsilon ^{2}\nabla ^{2}} \right) \left( {\tau _{xz} } \right) _{1}= & {} \left( {1-\varepsilon ^{2}\nabla ^{2}} \right) \left( {\tau _{xz} } \right) _{2}. \end{aligned}$$

    We have

    $$\begin{aligned} \left( {\tau _{xz} } \right) _{1}^{L} =\left( {\tau _{xz} } \right) _{2}^{L}, \end{aligned}$$

    (36)
  • (vii)
    $$\begin{aligned} \left( {\tau _{zz} } \right) _{1}= & {} \left( {\tau _{zz} } \right) _{2},\\ \left( {1-\varepsilon ^{2}\nabla ^{2}} \right) \left( {\tau _{zz} } \right) _{1}= & {} \left( {1-\varepsilon ^{2}\nabla ^{2}} \right) \left( {\tau _{zz} } \right) _{2}, \end{aligned}$$

    We have

    $$\begin{aligned} \left( {\tau _{zz} } \right) _{1}^{L} =\left( {\tau _{zz} } \right) _{2}^{L}, \end{aligned}$$

    (37)
  • (viii)
    $$\begin{aligned} \theta _{1} =\theta _{2}. \end{aligned}$$

    (38)

• (c) Infinite depth $z\rightarrow \infty :$ We require the displacements and temperature to diminish to zero at large depths,

  $$\begin{aligned} u_{2} \rightarrow 0,\,w_{2} \rightarrow 0,\,\theta _{2} \rightarrow 0. \end{aligned}$$

  This condition guarantees that the wave under consideration will have the character of a surface wave.

7 Solution of the problem in a nonlocal thermoelastic layer

For Rayleigh wave propagation in the layer along the $x-$direction, we take

$$\begin{aligned} \left( {u_{1} ,w_{1} ,\theta _{1} } \right) \left( {x,z,t} \right) =\left( {f_{1} ,g_{1} ,h_{1} } \right) \left( z \right) \exp \left[ {i\left( {kx-\omega t} \right) } \right] \end{aligned}$$

(39)

where $\omega =kc$ is the angular frequency of Rayleigh waves, c is the phase velocity, and k is the wave number.

Using Eq. (39) in Eqs. (22), (23), and (24), we get

$$\begin{aligned}&\left( {m_{1} -\varepsilon ^{2}\omega ^{2}} \right) D^{2}f_{1} +\left[ {\left( {1+\varepsilon ^{2}k^{2}} \right) \omega ^{2}-k^{2}} \right] f_{1} +ikm_{2} Dg_{1} -ikh_{1} =0, \end{aligned}$$

(40)

$$\begin{aligned}&\left( {1-\varepsilon ^{2}\omega ^{2}} \right) D^{2}g_{1} +\left[ {\left( {1+\varepsilon ^{2}k^{2}} \right) \omega ^{2}-m_{1} k^{2}} \right] g_{1} +ikm_{2} Df_{1} -Dh_{1} =0, \end{aligned}$$

(41)

$$\begin{aligned}&\left( {1-i\omega m_{4} } \right) D^{2}h_{1} +\left[ {\omega ^{2}-\left( {1-i\omega m_{4} } \right) k^{2}} \right] h_{1} +ikm_{3} \omega ^{2}f_{1} +m_{3} \omega ^{2}Dg_{1} =0 \end{aligned}$$

(42)

where $D\equiv \frac{d}{dz}$.

Eliminating $f_{1}$ and $h_{1}$ from Eqs. (40), (41), and (42), we get

$$\begin{aligned} \left( {AD^{6}+BD^{4}+CD^{2}+E} \right) g_{1} \left( z \right) =0. \end{aligned}$$

In a similar way, we can write

$$\begin{aligned} \left( {AD^{6}+BD^{4}+CD^{2}+E} \right) \left( {f_{1} \left( z \right) ,g_{1} \left( z \right) ,h_{1} \left( z \right) } \right) =0 \end{aligned}$$

(43)

in which

$$\begin{aligned} A= & {} n_{5} n_{8} \left( {n_{3} -n_{4} n_{5} } \right) ,\\ B= & {} \left( {n_{3} -n_{4} n_{5} } \right) \left( {n_{5} n_{9} +n_{6} n_{8} +n_{11} } \right) -n_{4} n_{5} n_{6} n_{8} ,\\ C= & {} n_{6} n_{9} \left( {n_{3} -n_{4} n_{5} } \right) -n_{4} n_{6} \left( {n_{5} n_{9} +n_{6} n_{8} +n_{11} } \right) ,\\ E= & {} -n_{4} n_{6}^{2} n_{9} , \end{aligned}$$

where $n_{1} =\left( {m_{1} -\varepsilon ^{2}\omega ^{2}} \right) ,n_{2} =\left[ {\left( {1+\varepsilon ^{2}k^{2}} \right) \omega ^{2}-k^{2}} \right] ,n_{3} =ikm_{2} ,n_{4} =ik,n_{5} =\left( {1-\varepsilon ^{2}\omega ^{2}} \right) ,$

$$\begin{aligned}&n_{6} =\left[ {\left( {1+\varepsilon ^{2}k^{2}} \right) \omega ^{2}-m_{1} k^{2}} \right] , n_{7} =ikm_{2} , n_{8} =\left( {1-i\omega m_{4} } \right) , n_{9} =\left[ {\omega ^{2}-\left( {1-i\omega m_{4} } \right) k^{2}} \right] , \\&n_{10} =ikm_{3} , n_{11} =m_{3} \omega ^{2}. \end{aligned}$$

From Eq. (43), we get

$$\begin{aligned} \left( {D^{2}+\eta _{1}^{2} } \right) \left( {D^{2}+\eta _{2}^{2} } \right) \left( {D^{2}+\eta _{3}^{2} } \right) \left[ {f_{1} \left( z \right) ,g_{1} \left( z \right) ,h_{1} \left( z \right) } \right] =0. \end{aligned}$$

(44)

Now we obtain

$$\begin{aligned}&f_{1} \left( z \right) =\sum \limits _{n=1}^3 {A_{n} } \cos \eta _{n} z+\sum \limits _{n=1}^3 {B_{n} \sin \eta _{n} z} , \end{aligned}$$

(45)

$$\begin{aligned}&g_{1} \left( z \right) =\sum \limits _{n=1}^3 {C_{n} } \cos \eta _{n} z+\sum \limits _{n=1}^3 {D_{n} \sin \eta _{n} z}, \end{aligned}$$

(46)

$$\begin{aligned}&h_{1} \left( z \right) =\sum \limits _{n=1}^3 {E_{n} } \cos \eta _{n} z+\sum \limits _{n=1}^3 {F_{n} \sin \eta _{n} z}. \end{aligned}$$

(47)

Now the displacements and temperature are obtained as

$$\begin{aligned} u_{1} \left( {x,z,t} \right) =\left[ {\sum \limits _{n=1}^3 {A_{n} } \cos \eta _{n} z+\sum \limits _{n=1}^3 {B_{n} \sin \eta _{n} z} } \right] \exp \left[ {i\left( {kx-\omega t} \right) } \right] , \end{aligned}$$

(48)

$$\begin{aligned} w_{1} \left( {x,z,t} \right) =\left[ {\sum \limits _{n=1}^3 {C_{n} } \cos \eta _{n} z+\sum \limits _{n=1}^3 {D_{n} \sin \eta _{n} z} } \right] \exp \left[ {i\left( {kx-\omega t} \right) } \right] , \end{aligned}$$

(49)

$$\begin{aligned} \theta _{1} \left( {x,z,t} \right) =\left[ {\sum \limits _{n=1}^3 {E_{n} } \cos \eta _{n} z+\sum \limits _{n=1}^3 {F_{n} \sin \eta _{n} z} } \right] \exp \left[ {i\left( {kx-\omega t} \right) } \right] \end{aligned}$$

(50)

where we take $C_{n} =c_{n} A_{n} ,D_{n} =d_{n} B_{n} ,E_{n} =e_{n} A_{n} ,F_{n} =f_{n} B_{n}$.

The stresses are obtained as follows:

$$\begin{aligned} \left( {\tau _{xx} } \right) _{1}^{L}= & {} \frac{\partial u_{1} }{\partial x}+m_{5} \frac{\partial w_{1} }{\partial z}-\theta _{1}\\= & {} \left[ \sum \limits _{n=1}^3 \left( {ikA_{n} +m_{5} \eta _{n} d_{n} B_{n} -e_{n} A_{n} } \right) \cos \eta _{n} z\right. \\&\left. +\sum \limits _{n=1}^3 {\left( {ikB_{n} -m_{5} \eta _{n} c_{n} A_{n} -f_{n} B_{n} } \right) \sin \eta _{n} z} \right] \exp \left[ {i\left( {kx-\omega t} \right) } \right] ,\\ \left( {\tau _{xz} } \right) _{1}^{L}= & {} \frac{\partial u_{1} }{\partial z}+\frac{\partial w_{1} }{\partial x}\\= & {} \left[ {\sum \limits _{n=1}^3 {\left( {\eta _{n} B_{n} +ikc_{n} A_{n} } \right) \cos \eta _{n} z+\sum \limits _{n=1}^3 {\left( {-\eta _{n} A_{n} +ikd_{n} B_{n} } \right) \sin \eta _{n} z} } } \right] \exp \left[ {i\left( {kx-\omega t} \right) } \right] ,\\ \left( {\tau _{zz} } \right) _{1}^{L}= & {} \frac{\partial w_{1} }{\partial z}+m_{5} \frac{\partial u_{1} }{\partial x}-\theta _{1}\\= & {} \left[ {\sum \limits _{n=1}^3 {\left( {im_{5} A_{n} -e_{n} A_{n} +d_{n} \eta _{n} B_{n} } \right) \cos \eta _{n} z+\sum \limits _{n=1}^3 {\left( {ikm_{5} B_{n} -\eta _{n} c_{n} A_{n} -f_{n} B_{n} } \right) \sin \eta _{n} z} } } \right] \\&\times \exp \left[ {i\left( {kx-\omega t} \right) } \right] . \end{aligned}$$

8 Solution of the problem in the nonlocal thermoelastic half-space

For Rayleigh wave propagation in the half-space along x-direction, we take

$$\begin{aligned} \left( {u_{2} ,w_{2} ,\theta _{2} } \right) \left( {x,z,t} \right) =\left( {f_{2} ,g_{2} ,h_{2} } \right) \left( z \right) \exp \left[ {i\left( {kx-\omega t} \right) } \right] . \end{aligned}$$

(51)

Using Eq. (51) in Eqs. (28), (29), and (30), we get

$$\begin{aligned}&\left( {r_{1} -\varepsilon ^{2}\omega ^{2}} \right) D^{2}f_{2} +\left[ {\left( {1+\varepsilon ^{2}k^{2}} \right) \omega ^{2}-k^{2}} \right] f_{2} +ikr_{2} Dg_{2} -ikh_{2} =0, \end{aligned}$$

(52)

$$\begin{aligned}&\left( {1-\varepsilon ^{2}\omega ^{2}} \right) D^{2}g_{2} +\left[ {\left( {1+\varepsilon ^{2}k^{2}} \right) \omega ^{2}-r_{1} k^{2}} \right] g_{2} +ikr_{2} Df_{2} -Dh_{2} =0, \end{aligned}$$

(53)

$$\begin{aligned}&\left( {1-i\omega r_{4} } \right) D^{2}h_{2} +\left[ {\omega ^{2}-\left( {1-i\omega r_{4} } \right) k^{2}} \right] h_{2} +ikr_{3} \omega ^{2}f_{2} +r_{3} \omega ^{2}Dg_{2} =0 \end{aligned}$$

(54)

where $D\equiv \frac{\mathrm{d}}{\mathrm{d}z}$.

Eliminating $f_{2}$ and $h_{2}$ from Eqs. (52), (53), and (54), we get

$$\begin{aligned} \left( {{A}'D^{6}+{B}'D^{4}+{C}'D^{2}+{E}'} \right) g_{2} \left( z \right) =0. \end{aligned}$$

In a similar way, we can write

$$\begin{aligned} \left( {{A}'D^{6}+{B}'D^{4}+{C}'D^{2}+{E}'} \right) \left( {f_{2} \left( z \right) ,g_{2} \left( z \right) ,h_{2} \left( z \right) } \right) =0 \end{aligned}$$

(55)

in which

$$\begin{aligned} {A}'= & {} s_{5} s_{8} \left( {s_{3} -s_{4} s_{5} } \right) ,\\ {B}'= & {} \left( {s_{3} -s_{4} s_{5} } \right) \left( {s_{5} s_{9} +s_{6} s_{8} +s_{11} } \right) -s_{4} s_{5} s_{6} s_{8} ,\\ {C}'= & {} s_{6} s_{9} \left( {s_{3} -s_{4} s_{5} } \right) -s_{4} s_{6} \left( {s_{5} s_{9} +s_{6} s_{8} +s_{11} } \right) ,\\ {E}'= & {} -s_{4} s_{6}^{2} s_{9} , \end{aligned}$$

where

$$\begin{aligned}&s_{1} =\left( {r_{1} -\varepsilon ^{2}\omega ^{2}} \right) ,s_{2} =\left[ {\left( {1+\varepsilon ^{2}k^{2}} \right) \omega ^{2}-k^{2}} \right] ,s_{3} =ikr_{2} ,s_{4} =ik,s_{5} =\left( {1-\varepsilon ^{2}\omega ^{2}} \right) ,\\&s_{6} =\left[ {\left( {1+\varepsilon ^{2}k^{2}} \right) \omega ^{2}-r_{2} k^{2}} \right] , s_{7} =ikr_{2} , s_{8} =\left( {1-i\omega r_{4} } \right) , s_{9} =\left[ {\omega ^{2}-\left( {1-i\omega r_{4} } \right) k^{2}} \right] ,\\&s_{10} =ikr_{3} , s_{11} =r_{3} \omega ^{2}. \end{aligned}$$

From Eq. (55), we get

$$\begin{aligned}&\left( {D^{2}-k_{1}^{2} } \right) \left( {D^{2}-k_{2}^{2} } \right) \left( {D^{2}-k_{3}^{2} } \right) \left[ {f_{2} \left( z \right) ,g_{2} \left( z \right) ,h_{2} \left( z \right) } \right] =0,\nonumber \\&f_{2} \left( z \right) =\sum \limits _{n=1}^3 {X_{n} \exp \left( {-k_{n} z} \right) } +\sum \limits _{n=1}^3 {L_{n} } \exp \left( {k_{n} z} \right) ,\nonumber \\&g_{2} \left( z \right) =\sum \limits _{n=1}^3 {Y_{n} \exp \left( {-k_{n} z} \right) } +\sum \limits _{n=1}^3 {M_{n} } \exp \left( {k_{n} z} \right) ,\nonumber \\&h_{2} \left( z \right) =\sum \limits _{n=1}^3 {Z_{n} \exp \left( {-k_{n} z} \right) } +\sum \limits _{n=1}^3 {N_{n} } \exp \left( {k_{n} z} \right) . \end{aligned}$$

(56)

For bounded solution at $z\rightarrow \infty$, we take $L_{n} =M_{n} =N_{n} =0$.

So, we get

$$\begin{aligned} f_{2} \left( z \right) =\sum \limits _{n=1}^3 {X_{n} \exp \left( {-k_{n} z} \right) }, \end{aligned}$$

(57)

$$\begin{aligned} g_{2} \left( z \right) =\sum \limits _{n=1}^3 {Y_{n} \exp \left( {-k_{n} z} \right) }, \end{aligned}$$

(58)

$$\begin{aligned} h_{2} \left( z \right) =\sum \limits _{n=1}^3 {Z_{n} \exp \left( {-k_{n} z} \right) }. \end{aligned}$$

(59)

Using Eqs. (57)–(59) in Eqs. (52)–(54), we get

$$\begin{aligned} Y_{n} =y_{n} X_{n} , \quad Z_{n} =z_{n} X_{n} \end{aligned}$$

where

$$\begin{aligned} y_{n}= & {} \frac{k_{n} \left[ {s_{1} k_{n}^{2} +\left( {s_{2} -s_{4} s_{7} } \right) } \right] }{\left[ {\left( {s_{3} -s_{4} s_{5} } \right) k_{n}^{2} -s_{4} s_{6} } \right] },\\ z_{n}= & {} \frac{s_{1} s_{11} k_{n}^{2} +\left( {s_{2} s_{11} -s_{3} s_{10} } \right) }{s_{3} s_{6} k_{n}^{2} +\left( {s_{3} s_{9} +s_{4} s_{11} } \right) }. \end{aligned}$$

Now replacing z by $\left( {z-H} \right)$, we get displacements, temperature, and stresses as follows:

$$\begin{aligned} u_{2}= & {} \sum \limits _{n=1}^3 {X_{n} } \exp \left[ {-k_{n} \left( {z-H} \right) } \right] \exp \left[ {i\left( {kx-\omega t} \right) } \right] , \end{aligned}$$

(60)

$$\begin{aligned} w_{2}= & {} \sum \limits _{n=1}^3 {y_{n} X_{n} } \exp \left[ {-k_{n} \left( {z-H} \right) } \right] \exp \left[ {i\left( {kx-\omega t} \right) } \right] , \end{aligned}$$

(61)

$$\begin{aligned} \theta _{2}= & {} \sum \limits _{n=1}^3 {z_{n} X_{n} } \exp \left[ {-k_{n} \left( {z-H} \right) } \right] \exp \left[ {i\left( {kx-\omega t} \right) } \right] , \nonumber \\ \left( {\tau _{xx} } \right) _{2}^{L}= & {} \frac{\partial u_{2} }{\partial x}+r_{5} \frac{\partial w_{2} }{\partial z}-\theta _{2}\nonumber \\= & {} \sum \limits _{n=1}^3 {\left( {ik-r_{5} y_{n} k_{n} -z_{n} } \right) } X_{n} \exp \left[ {-k_{n} \left( {z-H} \right) } \right] \exp \left[ {i\left( {kx-\omega t} \right) } \right] ,\nonumber \\ \left( {\tau _{xz} } \right) _{2}^{L}= & {} \frac{\partial u_{2} }{\partial z}+\frac{\partial w_{2} }{\partial x}\nonumber \\= & {} \sum \limits _{n=1}^3 {\left( {iky_{n} -k_{n} } \right) }X_n \exp \left[ {-k_{n} \left( {z-H} \right) } \right] \exp \left[ {i\left( {kx-\omega t} \right) } \right] ,\nonumber \\ \left( {\tau _{zz} } \right) _{2}^{L}= & {} \frac{\partial w_{2} }{\partial z}+r_{5} \frac{\partial u_{2} }{\partial x}-\theta _{2}\nonumber \\= & {} \sum \limits _{n=1}^3 {\left( {ikr_{5} -k_{n} y_{n} -z_{n} } \right) } X_n \exp \left[ {-k_{n} \left( {z-H} \right) } \right] \exp \left[ {i\left( {kx-\omega t} \right) } \right] . \end{aligned}$$

(62)

9 Derivation of the frequency equation

Using the boundary conditions (31), (32), and (33), we get

$$\begin{aligned}&\sum \limits _{n=1}^3 {\left( {\eta _{n} B_{n} +ikc_{n} A_{n} } \right) } =0, \end{aligned}$$

(63)

$$\begin{aligned}&\sum \limits _{n=1}^3 {\left[ {\left( {ikm_{5} -e_{n} } \right) A_{n} +d_{n} \eta _{n} B_{n} } \right] } =0, \end{aligned}$$

(64)

$$\begin{aligned}&\sum \limits _{n=1}^3 {e_{n} A_{n} =0}. \end{aligned}$$

(65)

From Eq. (63), we get

$$\begin{aligned} B_{n} =\delta _{n} A_{n} \end{aligned}$$

(66)

in which $\delta _{n} =-\frac{ikc_{n} }{\eta _{n} }$.

From Eq. (65), we get

$$\begin{aligned} A_{3} =-\frac{e_{1} }{e_{3} }A_{1} -\frac{e_{2} }{e_{3} }A_{2}. \end{aligned}$$

(67)

Using Eq. (66) and Eqs. (45)–(47) in Eqs. (40)–(42), we get

$$\begin{aligned} c_{n}= & {} \frac{n_{6} +\left( {n_{7} -f_{n} } \right) \eta _{n} \delta _{n} }{n_{5} \eta _{n}^{2} }, d_{n} =\frac{\left( {n_{7} \eta _{n} -e_{n} \eta _{n} -n_{6} \delta _{n} } \right) }{n_{5} \eta _{n}^{2} \delta _{n} },\\ e_{n}= & {} f_{n} =\frac{\left( {n_{2} n_{11} +n_{3} n_{10} } \right) -n_{1} n_{11} \eta _{n}^{2} }{\left( {n_{4} n_{11} -n_{3} n_{9} } \right) +n_{3} n_{8} \eta _{n}^{2} }, \end{aligned}$$

Using the boundary conditions (34)–(38), we get

$$\begin{aligned}&\alpha _{1} A_{1} +\alpha _{2} A_{2} -X_{1} -X_{2} -X_{3} =0, \end{aligned}$$

(68)

$$\begin{aligned}&\gamma _{1} A_{1} +\gamma _{2} A_{2} -y_{1} X_{1} -y_{2} X_{2} -y_{3} X_{3} =0, \end{aligned}$$

(69)

$$\begin{aligned}&l_{1} A_{1} +l_{2} A_{2} -l_{3} X_{1} -l_{4} X_{2} -l_{5} X_{3} =0, \end{aligned}$$

(70)

$$\begin{aligned}&p_{1} A_{1} +p_{2} A_{2} -p_{3} X_{1} -p_{4} X_{2} -p_{5} X_{3} =0, \end{aligned}$$

(71)

$$\begin{aligned}&q_{1} A_{1} +q_{2} A_{2} -z_{1} X_{1} -z_{2} X_{2} -z_{3} X_{3} =0. \end{aligned}$$

(72)

We have five homogeneous equations in terms of five unknowns. The system of equations has a nontrivial solution if

$$\begin{aligned} \left| {{\begin{array}{*{20}c} {\alpha _{1} } &{}\quad {\alpha _{2} } &{}\quad {-1} &{}\quad {-1} &{}\quad {-1} \\ {\gamma _{1} } &{}\quad {\gamma _{2} } &{}\quad {-y_{1} } &{}\quad {-y_{2} } &{}\quad {-y_{3} } \\ {l_{1} } &{}\quad {l_{2} } &{}\quad {-l_{3} } &{}\quad {-l_{4} } &{}\quad {-l_{5} } \\ {p_{1} } &{}\quad {p_{2} } &{}\quad {-p_{3} } &{}\quad {-p_{4} } &{}\quad {-p_{5} } \\ {q_{1} } &{}\quad {q_{2} } &{}\quad {-z_{1} } &{}\quad {-z_{2} } &{}\quad {-z_{3} } \\ \end{array} }} \right| =0. \end{aligned}$$

Expanding the determinant, we get

$$\begin{aligned} \alpha _{1} P_{1} -\alpha _{2} P_{2} -P_{3} +P_{4} -P_{5} =0 \end{aligned}$$

(73)

in which $P_{n} \left( {n=1,2,\ldots ,5} \right)$ are mentioned in the Appendix.

Equation (73) is the frequency equation of Rayleigh waves in a nonlocal thermoelastic layer lying over a nonlocal thermoelastic half-space.

10 Discussion of the frequency equation

Considering various particular values of the parameters, we can obtain the following different results in an isotropic medium:

• (a) The frequency equation reduces to the case of the theory of classical coupled thermoelasticity (C T) when we put $K_{1}^{*} =K_{2}^{*} =0.$

• (b) The frequency equation reduces to the case of GN model type II when we put $K_{1} =K_{2} =0$.

• (c) The frequency equation reduces to the case of local thermoelasticity if we put $\varepsilon =0$.

• (d) In the absence of a temperature field, the frequency equation of Rayleigh waves in a local elastic thermoelastic layer agrees with that of Singhal and Sahu [33].

11 Solution of the frequency equation

In general, wavenumber (k) and hence phase velocity (c) are complex quantities. If we take

$$\begin{aligned} c^{-1}=V^{-1}+i\omega ^{-1}Q, \end{aligned}$$

(74)

the wavenumber can be expressed as $k=R+iQ$ where $R=\frac{\omega }{V}$ in which V and Q are real. V is the propagation speed, and Q is the attenuation coefficient of Rayleigh waves.

12 Specific loss

The specific loss (SL) is the ratio of energy $(\Delta W)$ dissipated in taking specimen through cycle, to elastic energy (W) stored in a specimen when the strain is at maximum. The specific loss is the most direct way of defining internal friction for a material (Puri and Cowin [34]). For a sinusoidal surface wave of small amplitude, Kolsky [35] shows that the specific loss $\frac{\Delta W}{W}$ equals $4\pi$ times the absolute value of the ratio of imaginary part of k to the real part of k, that is ,

$$\begin{aligned} \hbox {SL}=\frac{\Delta W}{W}=4\pi \left| {\frac{\hbox {Im}(k)}{\hbox {Re}(k)}} \right| =4\pi \left| {\frac{VQ}{\omega }} \right| . \end{aligned}$$

13 Special cases

In the absence of a layer, i.e., if we take $H=0$ then the frequency of Rayleigh waves reduces to the frequency equation of Rayleigh waves in case of a thermoelastic half-space. We discuss some special cases of the frequency equation in a local thermoelastic half-space as follows:

Case (1) The frequency equation of surface waves in an isotropic half-space with classical coupled thermoelasticity is obtained as follows:

$$\begin{aligned} \left[ {\left( {2-\frac{c^{2}}{c_{3}^{2} }} \right) ^{2}\left( {\gamma _{1} +\gamma _{2} } \right) -4\gamma _{3} \left( {\gamma _{1} \gamma _{2} +1-\frac{k^{2}c^{2}}{c_{2}^{2} }} \right) } \right] =0 \end{aligned}$$

(75)

Equation (75) is similar to the result obtained in Nowinski [36], where $\gamma _{1}^{2} =1-\frac{\xi _{1}^{2} }{k^{2}},\gamma _{2}^{2} =1-\frac{\xi _{2}^{2} }{k^{2}},\gamma _{3}^{2} =1-\frac{\zeta ^{2}}{k^{2}},\zeta ^{2}=\frac{k^{2}c^{2}}{c_{3}^{2} }$, and $\xi _{1}^{2}$ and $\xi _{2}^{2}$ are the roots of the biquadratic equation

$$\begin{aligned} \xi ^{4}-\left[ {\frac{k^{2}c^{2}}{c_{3}^{2} }+(1+\kappa )\frac{ikc\rho _{2} {C}'_{v} }{K_{2} }} \right] \xi ^{2}+\frac{ik^{3}c^{3}\rho _{2} {C}'_{v} }{K_{2} c_{2}^{2} }=0 \end{aligned}$$

(76)

in which $\kappa =\frac{T_{0} \beta _{2}^{2} }{\rho _{2}^{2} c_{2}^{2} {C}'_{v} }$ and $c_{2}^{2} =\frac{\lambda _{2} +2\mu _{2} }{\rho _{2} },c_{3}^{2} =\frac{\mu _{2} }{\rho _{2} }$.

The results of the paper for an isotropic half-space with classical coupled thermoelasticity agree with Abd-Alla and Al-Dawy [29] and Wojnar [30].

Fig. 1

Geometry of the problem

Case (2) If we take $K_{2}^{*} =0$ and if we add a thermal relaxation time, then the paper agrees with the results of Abd-Alla and Al-Dawy [29], Nayfeh and Nemat-Nasser [37] and Agrawal [38] in case of the Lord–Shulman model.

Case (3) If we take $K_{2}^{*} =0$ and if we add two thermal relaxation times, then the paper agrees with the results of Abd-Alla and Al-Dawy [29], Wojnar [30], and Agarwal [38] in case of Green–Lindsay model.

Case (4) Neglecting thermal parameters, i.e. when there is no coupling between temperature and strain field, the frequency equation of Rayleigh waves in an isotropic elastic half-space is obtained as

$$\begin{aligned} \left( {2-\frac{c^{2}}{c_{3}^{2} }} \right) ^{2}=4\left( {1-\frac{c^{2}}{c_{2}^{2} }} \right) ^{\frac{1}{2}}\left( {1-\frac{c^{2}}{c_{3}^{2} }} \right) ^{\frac{1}{2}} \end{aligned}$$

(77)

where $c_{2}^{2} =\frac{\lambda _{2} +2\mu _{2} }{\rho _{2} },c_{3}^{2} =\frac{\mu _{2} }{\rho _{2} }$.

14 Numerical discussion

For numerical computation, we take the data values of copper material as follows (Biswas [39]):

$$\begin{aligned} \lambda _{1}= & {} \lambda _{2} =7.76\times 10^{10}\,\hbox {Kg}\,\hbox {m}^{-1}\,\text{ s}^{-2},\mu _{1} =\mu _{2} =3.86\times 10^{10}\hbox {Kg}\,\hbox {m}^{-1}\,\hbox {s}^{-2},\\ \beta _{1}= & {} \beta _{2} =1.78\times 10^{-5}\,\hbox {K}^{-1}, \quad \rho _{1} =\rho _{2} =8954\,\text{ Kg }\,\text{ m}^{-3}\text{, }K_{1} =K_{2} =386\,\text{ W }\,\text{ m}^{-1}\,\text{ K}^{-\text{1 }},\\ K_{1}^{*}= & {} K_{2}^{*} =124\text{ W }\,\text{ m}^{-1}\,\text{ K}^{-1}\,\text{ s}^{-\text{1 }},T_{0} =293\text{ K },\\ C_{v}= & {} {C}'_{v} =383.1\text{ J }\,\text{ Kg}^{-1}\,\text{ K}^{-1}\text{, }H=2\text{ m },e_{0} =0.39,a_{cl} =0.5\times 10^{-9}\text{ m. } \end{aligned}$$

Fig. 2

Variation of phase velocity with respect to frequency

Fig. 3

Variation of attenuation coefficient with respect to frequency

Fig. 4

Variation of penetration depth with respect to frequency

Fig. 5

Variation of specific loss with respect to frequency

In Fig. 2, the variation of phase velocity with respect to frequency is presented. It is observed that the phase velocity increases with the increase in frequency. The phase velocity for local thermoelastic medium is larger than the phase velocity for a nonlocal thermoelastic medium.

In Fig. 3, the variation of the attenuation coefficient with respect to frequency is presented. It is observed that the attenuation coefficient decreases with the increase in frequency. The attenuation coefficient for a local thermoelastic medium is larger than the attenuation coefficient for a nonlocal thermoelastic medium.

In Fig. 4, the variation of penetration depth with respect to frequency is presented. It is observed that the penetration depth increases with the increase in frequency. The penetration depth for nonlocal thermoelastic medium is larger than the penetration depth for a local thermoelastic medium.

In Fig. 5, the variation of specific loss with respect to frequency is presented. It is observed that the specific loss decreases with the increase in frequency. The specific loss for a nonlocal thermoelastic medium is larger than the specific loss for a local thermoelastic medium.

15 Conclusions

In this article, Rayleigh wave propagation in a nonlocal thermoelastic layer lying over a nonlocal thermoelastic half-space is investigated with the Green–Naghdi model type III based on Eringen’s nonlocal thermoelasticity theory. The frequency equation of a Rayleigh wave is derived, and different cases are discussed. Different characteristics of wave propagation are computed numerically and presented graphically.

From the theoretical and numerical discussion, we can conclude the following remarks:

• (a) Phase velocity and penetration depth of Rayleigh waves increase with the increase in frequency.

• (b) Attenuation coefficient and specific loss of Rayleigh waves decrease with the increase in frequency.

• (c) Phase velocity and attenuation coefficient for a local thermoelastic medium are larger than phase velocity and attenuation coefficient for a nonlocal thermoelastic medium.

• (d) Penetration depth and specific loss for a nonlocal thermoelastic medium are larger than penetration depth and specific loss for a local thermoelastic medium.

Appendix

$$\begin{aligned} \alpha _{1}= & {} \delta _{1} \sin \eta _{1} H+\cos \eta _{1} H-\frac{e_{1} }{e_{3} }\left( {\delta _{3} \sin \eta _{3} H+\cos \eta _{3} H} \right) ,\\ \alpha _{2}= & {} \delta _{2} \sin \eta _{2} H+\cos \eta _{2} H-\frac{e_{2} }{e_{3} }\left( {\delta _{3} \sin \eta _{3} H+\cos \eta _{3} H} \right) ,\\ \gamma _{1}= & {} c_{1} \cos \eta _{1} H+d_{1} \delta _{1} \sin \eta _{1} H-\frac{e_{1} }{e_{3} }\left( {c_{3} \cos \eta _{3} H+d_{3} \delta _{3} \sin \eta _{3} H} \right) ,\\ \gamma _{2}= & {} c_{2} \cos \eta _{2} H+d_{2} \delta _{2} \sin \eta _{2} H-\frac{e_{2} }{e_{3} }\left( {c_{3} \cos \eta _{3} H+d_{3} \delta _{3} \sin \eta _{3} H} \right) ,\\ l_{1}= & {} \left( {ikc_{1} +\delta _{1} \eta _{1} } \right) \cos \eta _{1} H+\left( {ikd_{1} \delta _{1} -\eta _{1} } \right) \sin \eta _{1} H\\&-\frac{e_{1} }{e_{3} }\left[ {\left( {ikc_{3} +\delta _{3} \eta _{3} } \right) \cos \eta _{3} H+\left( {ikd_{3} \delta _{3} -\eta _{3} } \right) \sin \eta _{3} H} \right] ,\\ l_{2}= & {} \left( {ikc_{2} +\delta _{2} \eta _{2} } \right) \cos \eta _{2} H+\left( {ikd_{2} \delta _{2} -\eta _{2} } \right) \sin \eta _{2} H\\&-\frac{e_{2} }{e_{3} }\left[ {\left( {ikc_{3} +\delta _{3} \eta _{3} } \right) \cos \eta _{3} H+\left( {ikd_{3} \delta _{3} -\eta _{3} } \right) \sin \eta _{3} H} \right] ,\\ l_{3}= & {} iky_{1} -k_{1} ,\\ l_{4}= & {} iky_{2} -k_{2} ,\\ l_{5}= & {} iky_{3} -k_{3} ,\\ p_{1}= & {} \left( {ikm_{5} -e_{1} +d_{1} \eta _{1} \delta _{1} } \right) \cos \eta _{1} H+\left( {-c_{1} \eta _{1} +ikm_{5} \delta _{1} -f_{1} \delta _{1} } \right) \sin \eta _{1} H\\&-\frac{e_{1} }{e_{3} }\left[ {\begin{array}{l} \left( {ikm_{5} -e_{3} -d_{3} \delta _{3} \eta _{3} } \right) \cos \eta _{3} H \\ +\left( {-c_{3} \eta _{3} +ikm_{5} \delta _{3} -f_{3} \delta _{3} } \right) \sin \eta _{3} H \\ \end{array}} \right] ,\\ p_{2}= & {} \left( {ikm_{5} -e_{2} +d_{2} \eta _{2} \delta _{2} } \right) \cos \eta _{2} H+\left( {-c_{2} \eta _{2} +ikm_{5} \delta _{2} -f_{2} \delta _{2} } \right) \sin \eta _{2} H\\&-\frac{e_{2} }{e_{3} }\left[ {\begin{array}{l} \left( {ikm_{5} -e_{3} -d_{3} \delta _{3} \eta _{3} } \right) \cos \eta _{3} H \\ +\left( {-c_{3} \eta _{3} +ikm_{5} \delta _{3} -f_{3} \delta _{3} } \right) \sin \eta _{3} H \\ \end{array}} \right] ,\\ p_{3}= & {} ikr_{5} -k_{1} y_{1} -z_{1} ,\\ p_{4}= & {} ikr_{5} -k_{2} y_{2} -z_{2} ,\\ p_{5}= & {} ikr_{5} -k_{3} y_{3} -z_{3} ,\\ q_{1}= & {} e_{1} \cos \eta _{1} H+f_{1} \delta _{1} \sin \eta _{1} H-\frac{e_{1} }{e_{3} }\left( {e_{3} \cos \eta _{3} H+f_{3} \delta _{3} \sin \eta _{3} H} \right) ,\\ q_{2}= & {} e_{2} \cos \eta _{2} H+f_{2} \delta _{2} \sin \eta _{2} H-\frac{e_{2} }{e_{3} }\left( {e_{3} \cos \eta _{3} H+f_{3} \delta _{3} \sin \eta _{3} H} \right) ,\\ P_{1}= & {} \gamma _{2} \left\{ {-l_{3} \left( {p_{4} z_{3} -z_{2} p_{5} } \right) +l_{4} \left( {p_{3} z_{3} -z_{1} p_{5} } \right) +l_{5} \left( {p_{3} z_{2} -z_{1} p_{4} } \right) } \right\} \\&+y_{1} \left\{ {l_{2} \left( {z_{3} p_{4} -z_{2} p_{5} } \right) +l_{4} \left( {-p_{2} z_{3} +q_{2} p_{5} } \right) -l_{5} \left( {-p_{2} z_{2} +p_{4} q_{2} } \right) } \right\} \\&-y_{2} \left\{ {l_{2} \left( {z_{3} p_{3} -z_{1} p_{5} } \right) +l_{3} \left( {-p_{2} z_{3} +p_{5} q_{2} } \right) -l_{5} \left( {-p_{2} z_{1} +q_{2} p_{3} } \right) } \right\} \\&+y_{3} \left\{ {l_{2} \left( {p_{3} z_{2} -p_{4} z_{1} } \right) +l_{3} \left( {-p_{2} z_{2} +p_{4} q_{2} } \right) -l_{4} \left( {-p_{2} z_{1} +p_{3} q_{2} } \right) } \right\} ,\\ P_{2}= & {} \gamma _{1} \left\{ {-l_{3} \left( {p_{4} z_{3} -z_{2} p_{5} } \right) +l_{4} \left( {p_{3} z_{3} -z_{1} p_{5} } \right) +l_{5} \left( {p_{3} z_{2} -z_{1} p_{4} } \right) } \right\} \\&+y_{1} \left\{ {l_{1} \left( {z_{3} p_{4} -z_{2} p_{5} } \right) +l_{4} \left( {-p_{1} z_{3} +q_{1} p_{5} } \right) -l_{5} \left( {-p_{1} z_{2} +p_{4} q_{1} } \right) } \right\} \\&-y_{2} \left\{ {l_{1} \left( {z_{3} p_{3} -z_{1} p_{5} } \right) +l_{3} \left( {-p_{1} z_{3} +p_{5} q_{1} } \right) -l_{5} \left( {-p_{1} z_{1} +q_{1} p_{3} } \right) } \right\} \\&+y_{3} \left\{ {l_{1} \left( {p_{3} z_{2} -p_{4} z_{1} } \right) +l_{3} \left( {-p_{1} z_{2} +p_{4} q_{1} } \right) -l_{4} \left( {-p_{1} z_{1} +p_{3} q_{1} } \right) } \right\} , \\ P_{3}= & {} \gamma _{1} \left\{ {l_{2} \left( {p_{4} z_{3} -z_{2} p_{5} } \right) +l_{4} \left( {-p_{2} z_{3} +q_{2} p_{5} } \right) -l_{5} \left( {-p_{2} z_{2} +q_{2} p_{4} } \right) } \right\} \\&-\gamma _{2} \left\{ {l_{1} \left( {z_{3} p_{4} -z_{2} p_{5} } \right) +l_{4} \left( {-p_{1} z_{3} +q_{1} p_{5} } \right) -l_{5} \left( {-p_{1} z_{2} +p_{4} q_{1} } \right) } \right\} \\&-y_{2} \left\{ {l_{1} \left( {z_{3} p_{2} +q_{2} p_{5} } \right) -l_{2} \left( {-p_{1} z_{3} +p_{5} q_{1} } \right) -l_{5} \left( {p_{1} q_{2} -q_{1} p_{2} } \right) } \right\} \\&+y_{3} \left\{ {l_{1} \left( {-p_{2} z_{2} +p_{4} q_{2} } \right) -l_{2} \left( {-p_{1} z_{2} +p_{4} q_{1} } \right) -l_{4} \left( {p_{1} q_{2} -p_{2} q_{1} } \right) } \right\} , \\ P_{4}= & {} \gamma _{1} \left\{ {l_{2} \left( {p_{3} z_{3} -z_{1} p_{5} } \right) +l_{3} \left( {-p_{2} z_{3} +q_{2} p_{5} } \right) -l_{5} \left( {-p_{2} z_{1} +q_{2} p_{3} } \right) } \right\} \\&-\gamma _{2} \left\{ {l_{1} \left( {z_{3} p_{3} -z_{1} p_{5} } \right) +l_{3} \left( {-p_{1} z_{3} +q_{1} p_{5} } \right) -l_{5} \left( {-p_{1} z_{1} +p_{3} q_{1} } \right) } \right\} \\&-y_{1} \left\{ {l_{1} \left( {-z_{3} p_{2} +q_{2} p_{5} } \right) -l_{2} \left( {-p_{1} z_{3} +p_{5} q_{1} } \right) -l_{5} \left( {p_{1} q_{2} -q_{1} p_{2} } \right) } \right\} \\&+y_{3} \left\{ {l_{1} \left( {-p_{2} z_{1} +p_{3} q_{2} } \right) -l_{2} \left( {-p_{1} z_{1} +p_{3} q_{1} } \right) -l_{3} \left( {p_{1} q_{2} -p_{2} q_{1} } \right) } \right\} , \\ P_{5}= & {} \gamma _{1} \left\{ {l_{2} \left( {p_{3} z-p_{4} z_{1} } \right) +l_{3} \left( {-p_{2} z_{2} +q_{2} p_{4} } \right) -l_{4} \left( {-p_{2} z_{1} +q_{2} p_{3} } \right) } \right\} \\&-\gamma _{2} \left\{ {l_{1} \left( {z_{3} p_{2} -p_{4} z_{1} } \right) +l_{3} \left( {-p_{1} z_{2} +q_{1} p_{4} } \right) -l_{4} \left( {-p_{1} z_{1} +p_{3} q_{1} } \right) } \right\} \\&-y_{1} \left\{ {l_{1} \left( {-z_{2} p_{2} +q_{2} p_{4} } \right) -l_{2} \left( {-p_{1} z_{2} +p_{4} q_{1} } \right) -l_{4} \left( {p_{1} q_{2} -q_{1} p_{2} } \right) } \right\} \\&+y_{2} \left\{ {l_{1} \left( {-p_{2} z_{1} +p_{3} q_{2} } \right) -l_{2} \left( {-p_{1} z_{1} +p_{3} q_{1} } \right) -l_{3} \left( {p_{1} q_{2} -p_{2} q_{1} } \right) } \right\} . \end{aligned}$$