Maxwell homogenization scheme for piezoelectric composites with arbitrarily-oriented spheroidal inhomogeneities

Abstract

In this work, the effective electro-elastic properties of piezoelectric composites are computed using the Maxwell homogenization method (MHM). The composites are made by several families of spheroidal inhomogeneities embedded in a homogeneous infinite medium (matrix). Each family of spheroidal inhomogeneities is made of the same material, and all the inhomogeneities have identical size and shape and are randomly oriented. The inhomogeneities and matrix materials exhibit piezoelectric transversely isotropic symmetry. It is shown that the shape of the “effective inclusion” substantially affects the effective piezoelectric properties. A new and simple form to calculate the aspect ratio of effective inclusion is presented. The effect on the overall piezoelectric properties due to the orientation of the inhomogeneities and different families of piezoelectric inhomogeneities is discussed. The MHM approach is applied in two examples, material with inhomogeneities having scatter orientation and composites with two different families of spheroidal inhomogeneities.

1 Introduction

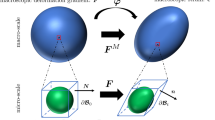
The Maxwell homogenization method (MHM) is a homogenization technique that is applicable to cases of anisotropic multiphase composites with a good accuracy degree. This approach can be applied in order to obtain the effective electro-elastic properties of a composite made by a matrix material occupying the region $V^{0}$ with properties $\mathbf{L }^{0}$ and containing spheroidal inhomogeneities with properties $\mathbf{L }^{1}$ and volume fraction $\theta = V^{1}/V^{0}$, where $V^{1}$ is the volume occupied by the inhomogeneities. We will assume that there is a spheroidal region $V^{e}$ of the heterogeneous medium placed into the matrix material and large enough to contain a representative number of spheroidal inhomogeneities (see Fig. 1), called effective inclusion. This construction is subjected to external fields acting on every inhomogeneity. (The inhomogeneities do not interact.) The asymptotic far field of the perturbation generated by the inhomogeneities inside $V^{e}$ is proportional to the sum of far fields generated by the inhomogeneities. The perturbation field induced by the inhomogeneities far from the center of $V^{e}$ is equal to the field produced by the entire region $V^{e}$ considered as an individual inhomogeneity with effective unknown properties $\bar{\mathbf {L}}$.

The Maxwell scheme was first proposed to calculate the effective electrical conductivity of a matrix of conductivity $k_{0}$ containing spherical inhomogeneities of conductivity $k_{1}$ [1]. The authors in Ref. [2] considered the Maxwell homogenization technique for the propagation of seismic waves in a material containing randomly oriented identical spheroidal inhomogeneities. The authors in Ref. [3] developed a similar method to the Maxwell scheme for multiphase composites containing randomly oriented ellipsoidal inhomogeneities. When “Maxwell’s scheme for elastic properties” was introduced for the first time [4], it was used to study the problem of randomly localized spheres. The authors in Ref. [5] addressed the problem about the shape of the “effective inclusion.” The authors showed that for the case of a material containing aligned identical ellipsoidal inhomogeneities it has to match the shape of the individual inhomogeneities.

A fundamental question of the MHM is the determination of the aspect ratio $\delta _{e}$ of the effective inclusion. In Ref. [6], the uncertainty related to the shape of the effective inclusion is discussed; however, the authors did not provide explicit recommendations regarding the choice of the shape for the more general scenario. Later, in Ref. [7] the hypothesis that allows to evaluate the shape of the effective inclusion in the transversely isotropic composites was explicitly formulated. The author shows that this parameter must reflect the form of each inhomogeneity; otherwise, the predictions of the effective properties can lose physical meaning. This approach was very successful. The authors of Ref. [8] illustrate that this hypothesis allows to optimize Maxwell’s scheme, and in Ref. [9], this approach was addressed to consider composites with anisotropic constituents.

Recently, a previous work [10] has only focused on the extension of Maxwell’s homogenization scheme for piezoelectric composites containing parallel aligned spheroidal inhomogeneities along the $x_{3}$ axis of the composite. The authors reported a simple way to obtain the effective overall electro-elastic properties of biphasic and tri-phasic composites. In addition, numerical measurements of the electromechanical coupling factor and the effective hydrostatic charge were performed in a tri-phasic composite made by Araldite-D matrix containing fiber reinforcements of PZT-7A* and porous of two different geometrical shapes. However, the dependence of the behavior of the effective moduli on the orientations of the reinforcements inside the matrix was not analyzed. The novelty of the present work is based on the analysis of the relation between the behavior of the effective moduli and the orientations of the reinforcements inside the matrix by means of probability functions, which allow to examine the effective performance of composites and generalize the approach presented in Ref. [10]. Self-consistent variational bounds are given in Ref. [11] for the effective electro-elastic properties of heterogeneous piezoelectric solids. These bounds are based on a generalization of the Hashin–Shtrikman variational principles. Numerical calculations were presented, and comparisons with real measurements were made for composites with different microstructural geometries.

During the last few years, there has been a growing interest in materials with high electrical or thermal conductivity and dielectric permittivity, such as graphene–polymer nanocomposites or graphite nanoplatelet/epoxy composites due to their wide range of applications. Several theories have been proposed to estimate the effectiveness and efficiency of the electromagnetic interference shielding in these composites. A method to produce thin graphite nanoplatelet/epoxy composites with a thickness of 20–50 nm is developed in Ref. [12]. The dependence of the thermal conductivity on the volume fraction of graphite nanoplatelet and the dependence of the dielectric constant on the frequency were studied. The behavior of the dielectric properties, the loss factor, and the conductivity in reduced graphite oxide/polypropylene composites was studied against the frequency in Ref. [13]. Additionally, the dependence of the dielectric permittivity on the volume fraction of reduced graphene oxide was compared with experimental measurements showing a good accuracy. The temperature dependence of the dielectric permittivity for different frequency values showed that for the lowest frequency the composite gets the highest temperature value; moreover, the effective dielectric permittivity increases as the temperature increases. A study about the electromagnetic interference shielding efficiency and the effective dielectric permittivity of highly aligned graphene/polymer nanocomposites has been given in Ref. [14]. A theory of the continuum, based on the effective medium method, is formulated in Ref. [15] to calculate the electrical conductivity, dielectric permittivity, and magnetic permeability in a highly porous graphene composite foam. This process allows to evaluate the effectiveness of the electromagnetic interference shielding of lightweight foams. The Maxwell–Wagner–Sillars polarization mechanism was implemented, too, and it was shown that the electrical conductivity had the strongest influence on the effectiveness of the electromagnetic shielding. Recently, the authors of Refs. [16, 17] presented a model based on the effective medium theory. The proposed model takes into account interface effects, electron tunneling, Maxwell–Wagner–Sillars polarization, Dyre’s frequency-assisted electron hopping, and Debye’s dielectric relaxation. All these effects are incorporated to estimate the effectiveness of the electromagnetic interference shielding. By the proposed model, the calculations of the frequency-dependent effective electric conductivity and dielectric permittivity and the frequency-independent magnetic permeability in graphene–polymer nanocomposites can be taken into account. The authors also found that the effective conductivity increases remarkably in the high frequency range, while the dielectric permittivity decreases. The theories presented in Refs. [12,13,14] were based on the original Maxwell far-field matching framework developed in Ref. [18] and first applied to the electrical conductivity of CNT and graphene–polymer nanocomposites with electron tunneling and percolation threshold by the authors of Refs. [19, 20]. A dynamical approach to the models of Mori–Tanaka (for aligned ellipsoidal inclusions) and Ponte Castañeda–Willis (for both aligned and randomly ellipsoidal inclusions) is developed in Ref. [18]. Even when the Mori–Tanaka moduli were not obtained for randomly aligned inclusions, the author points out that in the case of isotropic constituents it is worthwhile, because the moduli always lie at or within the Hashin–Shtrikman bounds. A continuum model proposed in Ref. [19] is applied to the predictions of the electrical conductivity of carbon nanotubes as well as the study about the effect of anisotropy of the conductivity in axial and transverse directions. It is remarkable that the axial conductivity is the main property that affects the transport process even when the transverse conductivity has the lowest value. Calculations of magnetoelectric coupling coefficients and voltage coefficients can be found [20] by a model based on Mori–Tanaka scheme for the perfect interface case, and then, a thin layer between the inclusion and the matrix is introduced to study the imperfect contact scenario. Moreover, comparisons with experimental data for the magnetoelectric voltage coefficient are made, with a good accuracy between the predictions and the experimental results.

Fig. 1

Schematic diagram of Maxwell’s homogenization method. Effective properties of a composite (a) are calculated by setting equal the effects produced by the set of inhomogeneities embedded in the matrix material (b) and by a fictitious domain having yet unknown effective properties (c)

The performance of composite materials is highly affected by the inhomogeneity’s spatial arrangement and orientation. The work in Ref. [21] stated that the inhomogeneities are usually neither perfectly parallel, nor perfectly randomly oriented, but have a certain orientation distribution, which is one of the primary factors affecting the overall mechanical properties. The present paper focuses on the integration of the characteristics of the inhomogeneity’s orientation into MHM, to consider the orientation distribution of non-spherical inhomogeneities in heterogeneous materials. The authors of Refs. [22, 23] take into account the random orientation of fibers by applying an average induced strain approach to composites with 3D randomly oriented short fibers. In Ref. [24], a theoretical scheme in which the fiber orientation distribution was allowed to be arbitrarily specified is presented. These authors first introduced an orientation distribution function (ODF) defined over the full Euler space. Many specific ODFs have been discussed in the literature.

In the present paper, the extension of Maxwell’s scheme to the piezoelectric composites given by authors of Ref. [10] is used. To the best of our knowledge, a theoretical model describing the electromechanical behavior of multiphase piezoelectric composites has not been proposed and the effect of arbitrary-oriented inhomogeneities has not been addressed. In this work, the effective electro-elastic properties of a material reinforced with spheroidal inhomogeneities considering the orientation distribution of the inhomogeneities that may vary from perfectly aligned to randomly oriented ones are calculated by the MHM. In Sect. 2.2, the equation to calculate the overall electro-elastic properties of composites with more than one type of inhomogeneities is presented. The method is addressed to media with only one type of inhomogeneity and whose orientation is governed by an ODF as described in Sect. 3. Also, the effect of different ODFs in the overall electro-elastic properties is discussed in Sect. 3. The numerical predictions of the MHM are presented for the case of fiber-reinforced composites in Sect. 4, and the conclusions are presented in Sect. 5. In “Appendix A,” the tensorial basis representation of an arbitrarily oriented inhomogeneity is developed. “Appendix B” provides explicit tensorial expressions for the case of spheroidal inhomogeneities.

2 Basic equations of piezoelectricity and Maxwell’s approach

The aim of this Section is to give an overview on piezoelectricity, to provide the essential ideas of Maxwell’s scheme, and to describe the numerical implementation of the effective equations of the present model.

2.1 Piezoelectric laws

Let $C_{ijkl}$ be the fourth-rank stiffness tensor of an elastic composite having transversely isotropic symmetry and satisfying the index relations $C_{ijkl}=C_{jikl}=C_{ijlk}=C_{klij}$. Using the two-index Voigt notation and by the following relations:

$$\begin{aligned} (ij) \rightarrow \alpha | (kl) \rightarrow \beta |&(11) \rightarrow 1 | (22) \rightarrow 2 | (33) \rightarrow 3 | (23),(32) \rightarrow 4 | (13),(31) \rightarrow 5 | (12),(21) \rightarrow 6, \end{aligned}$$

the fourth-rank stiffness tensor $C_{ijkl}$ can be reduced to the following $6 \times 6$ matrix:

$$\begin{aligned} C_{ijkl}= C_{\alpha \beta } = \begin{pmatrix} C_{11} &{}\quad C_{12} &{}\quad C_{13} &{}\quad 0 &{}\quad 0 &{}\quad 0\\ C_{12} &{}\quad C_{11} &{}\quad C_{13} &{}\quad 0 &{}\quad 0 &{}\quad 0\\ C_{13} &{}\quad C_{13} &{}\quad C_{33} &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad C_{44} &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad C_{44} &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad C_{66}\\ \end{pmatrix}, \quad C_{66} = \dfrac{C_{11}-C_{12}}{2}. \end{aligned}$$

Let now $e_{ijk}$ and $\eta _{ij}$ be the third-rank piezoelectric and the second-rank dielectric permittivity tensors, respectively, where $e_{ijk} = e_{ikj}$ holds. Following the Voigt notation, the third-rank piezoelectric tensor and the second-rank dielectric permittivity tensor can be written in matrix form as

$$\begin{aligned} {\mathbf {e}}^{t} = \begin{pmatrix} 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad e_{15} &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0 &{}\quad e_{15} &{}\quad 0 &{}\quad 0\\ e_{31} &{}\quad e_{31} &{}\quad e_{33} &{}\quad 0 &{}\quad 0 &{}\quad 0\\ \end{pmatrix}, \quad {\varvec{\eta }} = \begin{pmatrix} \eta _{11} &{}\quad 0 &{}\quad 0\\ 0 &{}\quad \eta _{11} &{}\quad 0\\ 0 &{}\quad 0 &{}\quad \eta _{33}\\ \end{pmatrix}, \end{aligned}$$

and using now the following index relations:

$$\begin{aligned} (pq) \rightarrow \upsilon | (41),(14) \rightarrow 7 | (42),(24) \rightarrow 8 | (43),(34) \rightarrow 9 | \upsilon = 7, 8, 9, \end{aligned}$$

the electro-elastic tensor ${\mathbf {L}}$ for piezoelectric composites of 6mm class can be reduced to a matrix of $9 \times 9$ as follows:

$$\begin{aligned} {\mathbf {L}} = \begin{pmatrix} C_{\alpha \beta } &{}\quad e_{ipq}\\ e_{pqi}^{t} &{}\quad -\eta _{pq}\\ \end{pmatrix}. \end{aligned}$$

For piezoelectric solids, the interdependence between mechanical and electrical variables implies a coupling between the elastic and electromagnetic waves,

$$\begin{aligned} \sigma _{ij}(x)&= C_{ijkl}(x) s_{kl}(x) - e_{ijk}(x) E_{k}(x), \\ D_{i}(x)&= e_{ikl}^{t}(x) s_{kl}(x) + \eta _{ik}(x) E_{k}(x), \\ E_{k}(x)&= - \Phi _{,k}(x), \, s_{kl}(x) = \dfrac{u_{k,l}(x) + u_{l,k}(x)}{2}, \end{aligned}$$

where $a_{,j}$ means $\dfrac{\partial a}{\partial x_{j}}$, $E_{k}$ the electric field, $\Phi$ the electric potential, and $\sigma _{ij}$ and $s_{kl}$ the second-order stress and strain tensors, respectively. $u_{k}$ is the displacement, $D_{i}$ is the electric displacement, and $x = (x_{1},x_{2},x_{3})$ is a point in the three-dimensional space. Under constant external strain $s^{0}$ and electric $E^{0}$ fields applied to the medium, the stress field given by the stress tensor represents an equilibrium state with the body forces $f_{i}(x)$ in the whole composite. Then, Newton’s second law for the equilibrium condition of the stress field and Gauss’s law imply the following:

$$\begin{aligned} \sigma _{ij,j}(x) + f_{i}(x) = 0, \quad D_{i,i}(x) = 0. \end{aligned}$$

Finally, for an isolated solid, the body forces $f_{i}(x) = 0$ are zero; therefore, the following relations must hold:

$$\begin{aligned}&\Big [C_{ijkl}(x) s_{kl}(x) - e_{ijk}(x) E_{k,j}(x) \Big ]_{,j}=0,\\&\Big [e_{ikl}^{t}(x) s_{kl}(x) + \eta _{ik}(x) E_{k}(x) \Big ]_{,i}=0. \end{aligned}$$

2.2 Maxwell homogenization scheme

A heterogeneous medium is considered to be composed of a solid matrix with properties ${\mathbf {L}}^{0}$, where n different types of inhomogeneities are embedded. Each type of inhomogeneityr has properties ${\mathbf {L}}^{r}$, as well as the same form, size, and orientation. The symmetry centers $\mathbf{x }^{'}$ are randomly distributed for each inhomogeneity. The properties ${\mathbf {L}}$ in the composite depend on the position $\mathbf{x }$, and taking the values ${\mathbf {L}}^{r}$ when the position $\mathbf{x }$ is in the volume $V_{r}$ occupied by the inhomogeneity and the values ${\mathbf {L}}^{0}$ if the point $\mathbf{x }$ is in the matrix, the following is obtained:

$$\begin{aligned} {\mathbf {L}}({\mathbf {x}})={\mathbf {L}}^{0}+\sum _{r=1}^{n} \left( {\mathbf {L}}^{r}-{\mathbf {L}}^{0}\right) V_{r}({\mathbf {x}}), \quad V_{r}({\mathbf {x}})= {\left\{ \begin{array}{ll} 1, &{}\quad \text {if } {{\mathbf {x}} \in } \text { type } r \text { inhomogeneity} \\ 0, &{}\quad \text {other case} \end{array}\right. } \end{aligned}$$

(2.1)

where $V_{r}({\mathbf {x}})$ is the characteristic function of the volume occupied by the inhomogeneity of type r, with $r=1,2,3,\ldots ,n$. The matrix ${\mathbf {L}}$ represents the electro-elastic properties of transversely isotropic piezoelectric materials with hexagonal symmetry, and it is a linear transformation ($9\times 9$ matrix) which transforms the stress vector ${\varvec{\Sigma }} = ({\varvec{\sigma }},{\mathbf {D}}) = (\sigma _{11}, \sigma _{22}, \sigma _{33}, \sigma _{23}, \sigma _{13}, \sigma _{12}, D_{1}, D_{2}, D_{3})$ into the strain vector ${\mathbf {Z}} = ({\mathbf {s}},{\mathbf {E}}) = (s_{11}, s_{22}, s_{33}, 2s_{23}, 2s_{13}, 2s_{12}, E_{1}, E_{2}, E_{3})$,

$$\begin{aligned} {\varvec{\Sigma }}={\mathbf {L}}{\mathbf {Z}}, \qquad {\mathbf {L}}_{9\times 9} = \begin{bmatrix} {\mathbf {C}}_{6\times 6}&\quad {\mathbf {e}}_{6\times 3} \\ {\mathbf {e}}^{T}_{3\times 6}&\quad -{\varvec{\eta }}_{3\times 3} \end{bmatrix}. \end{aligned}$$

(2.2)

Following a similar notation as that of Ref. [25], Eq. (2.2) is the matrix form of the constitutive equations of a homogeneous piezoelectric material under isothermal conditions. The above equations couple the mechanical properties: the strain ${{\varvec{s}}}$, the stress ${\varvec{\sigma }}$, and the elastic moduli tensor ${\mathbf {C}}$, with the electric variables such as the electric field ${\mathbf {E}}$, the electric displacement field ${\mathbf {D}}$, the piezoelectric tensor ${\mathbf {e}}$, and the dielectric tensor ${\varvec{\eta }}$. The superscript T denotes the transpose.

The effective electro-elastic properties $\bar{{\mathbf {L}}}$ of a multiphase composite are given as a function of the matrix properties ${\mathbf {L}}^{0}$, the properties of each family of inhomogeneities $\theta _{r}$ (volume fraction), $\delta _{r}$ (aspect ratio), ${\mathbf {L}}^{r}$ and the effective inclusion’s aspect ratio $\delta _{e}$,

$$\begin{aligned} \bar{{\mathbf {L}}} = {\mathbf {L}}^{0} + \left[ \left( \sum _{r=1}^{N}\theta _{r} {\mathbf {N}}^{(r)}\right) ^{-1} + {\mathbf {Q}}^{(e)}\right] ^{-1}, \quad {\mathbf {N}}^{(r)} = \left( {\mathbf {L}}^{r} - {\mathbf {L}}^{0}\right) \left[ {\mathbf {I}} + {\mathbf {Q}}^{(r)} ({\mathbf {L}}^{r}-{\mathbf {L}}^{0})\right] ^{-1}. \end{aligned}$$

(2.3)

Here, the superscript (r) indicates the type of inhomogeneity and is not an exponent. ${\mathbf {I}}$ is a unitary matrix of rank 9, and the function ${\mathbf {Q}}^{(e)}$ depends on the effective inclusion’s aspect ratio $\delta _{e}$ and the properties of the matrix ${\mathbf {L}}^{0}$. The selection of an explicit expression for $\delta _{e}$ is discussed in Sect. 4.

2.3 Hill tensor Q for spheroidal inhomogeneities

The matrix ${\mathbf {Q}}^{(r)}$ is expressed in terms of the second derivatives of the electro-elastic Green’s function (a $4\times 4$ matrix with components $G_{li}({\mathbf {x}})$, $G_{l4}({\mathbf {x}})$, $G_{4i}({\mathbf {x}})$ and $G_{44}({\mathbf {x}})$), which is derived following the authors of Refs. [26,27,28]:

$$\begin{aligned} {\mathbf {Q}}^{(r)} = -\int _{V_{r}} \begin{bmatrix} G_{li,jk}({\mathbf {x}}-{\mathbf {x}}^{'})&\quad G_{l4,jk}({\mathbf {x}}-{\mathbf {x}}^{'}) \\ G_{4i,jk}({\mathbf {x}}-{\mathbf {x}}^{'})&\quad -G_{44,jk}({\mathbf {x}}-{\mathbf {x}}^{'}) \end{bmatrix} \mathrm {d}{\mathbf {x}}^{'} = \begin{bmatrix} S^{(r)}_{x(klij)}&\quad S^{(r)}_{,x(k4ij)} \\ M^{(r)}_{x(kl4j)}&\quad M^{(r)}_{,x(k44j)} \end{bmatrix} \end{aligned}$$

(2.4)

where $V_{r}$ represents the spheroids, with $a_{r}$ and $c_{r}$ being the spheroid semiminor and semimajor axes, respectively. The tensors ${\mathbf {S}}^{(r)}_{x}$, ${\mathbf {M}}^{(r)}_{x}$, ${\mathbf {S}}^{(r)}_{,x}$, and ${\mathbf {M}}^{(r)}_{,x}$ are averaged over the inhomogeneity domain of the second partial derivative of the Green’s function (a detailed discussion is given in Ref. [10]),

$$\begin{aligned} S^{(r)}_{x(klij)}&= \frac{1}{4\pi } \int _{|{\varvec{\zeta }}|=1} \mathrm {d}\Omega ({\varvec{\zeta }})\,\zeta _{k} ({\bar{\Gamma }}_{li}({\varvec{\zeta }}))^{-1} \zeta _{j}\bigg |_{(ij),(kl)}, \end{aligned}$$

(2.5)

$$\begin{aligned} S^{(r)}_{,x(k4ij)}&= \frac{1}{4\pi } \int _{|{\varvec{\zeta }}|=1} \mathrm {d}\Omega ({\varvec{\zeta }})\,\zeta _{k} \frac{\gamma _{l}({\varvec{\zeta }}) ({\bar{\Gamma }}_{li}({\varvec{\zeta }}))^{-1}}{\epsilon ({\varvec{\zeta }})} \zeta _{j}\bigg |_{(ij)}, \end{aligned}$$

(2.6)

$$\begin{aligned} M^{(r)}_{,x(k44j)}&= \frac{1}{4\pi } \int _{|{\varvec{\zeta }}|=1} \mathrm {d}\Omega ({\varvec{\zeta }}) \frac{\zeta _{k}\zeta _{j}}{\epsilon ({\varvec{\zeta }})+ \gamma _{i}({\varvec{\zeta }}) (\Gamma _{il}({\varvec{\zeta }}))^{-1} \gamma _{l}({\varvec{\zeta }})}, \end{aligned}$$

(2.7)

and the tensor ${\mathbf {M}}^{(r)}_{x}$ is the transpose of ${\mathbf {S}}^{(r)}_{,x}$. The notation (ij) represents a symmetry with respect to the pair of indexes i, j. The integrals are calculated over the unit sphere, and ${\varvec{\zeta }}$ is a unit vector in spherical coordinates ${\varvec{\zeta }}=(\sin \phi \cos \varphi ,\sin \phi \sin \varphi ,\cos \phi )$, where $\zeta _{3}=\cos \phi = u$, and the azimuthal coordinate $\varphi$ and the latitude $\phi$ take values between $\varphi \in (0,2\pi )$ and $\phi \in (-\frac{\pi }{2},\frac{\pi }{2})$, respectively. $\Gamma _{ik}({\varvec{\zeta }})$, ${{\bar{\Gamma }}}_{ik}({\varvec{\zeta }})$ are $3\times 3$ symmetric matrices, $\gamma _{k}({\varvec{\zeta }})$ is a $3\times 1$ vector, and $\epsilon ({\varvec{\zeta }})$ is a negative scalar. $\Gamma _{ik}({\varvec{\zeta }})$, ${{\bar{\Gamma }}}_{ik}({\varvec{\zeta }})$, $\gamma _{k}({\varvec{\zeta }})$, and $\epsilon ({\varvec{\zeta }})$ are defined by

$$\begin{aligned} \Gamma _{ik}({\varvec{\zeta }}) = C^{0}_{ijkl}\zeta _{j}\zeta _{l}, \quad \gamma _{k}({\varvec{\zeta }}) = e^{0}_{jkl}\zeta _{j}\zeta _{l}, \quad \epsilon ({\varvec{\zeta }})= \epsilon ^{0}_{jl}\zeta _{j} \zeta _{l}, \quad {{\bar{\Gamma }}}_{ik}({\varvec{\zeta }}) = \Gamma _{ik}({\varvec{\zeta }})+ \frac{\gamma _{i}^{T}({\varvec{\zeta }})\; \gamma _{k}({\varvec{\zeta }})}{\epsilon ({\varvec{\zeta }})}. \end{aligned}$$

(2.8)

The components of the tensors ${\mathbf {S}}^{(r)}_{x}$, ${\mathbf {S}}^{(r)}_{,x}$, and ${\mathbf {M}}^{(r)}_{,x}$ depend strongly on the type r of the inhomogeneity’s geometry $V_{r}$, by the aspect ratio parameter $\delta _{r} = c_{r}/a_{r}$. The inhomogeneity is an oblate spheroid if the fraction $\delta _{r}$ is smaller than 1, or a prolate spheroid if $\delta _{r}$ is larger than 1. Particularly, if $\delta _{r}<<1$ the inhomogeneities are considered as disks, if $\delta _{r}>>1$ they are considered as fibers, and if $\delta _{r}=1$ they are spheres. The components of the tensors ${\mathbf {S}}^{(r)}_{x}$, ${\mathbf {S}}^{(r)}_{,x}$, and ${\mathbf {M}}^{(r)}_{,x}$ are given in Appendix A.

3 Randomly oriented distributions of spheroidal inhomogeneities

3.1 Overview

During the analysis of a fiber-reinforced composite in Ref. [29], an ODF independent of the Euler angles $\phi$, $\theta$, and $\varphi$ is assumed,

$$\begin{aligned} P(\phi ,\theta ,\varphi ) = P(\phi )P(\theta )P(\varphi ), \qquad 0\le \phi \le \pi ,\, 0\le \theta \le \pi ,\, 0\le \varphi \le \pi , \end{aligned}$$

(3.1)

where $P(\phi )$ is a trigonometric distribution, and $P(\theta )$, $P(\varphi )$ are Gaussian distributions obtained by a quantitative image analysis of SEM pictures,

$$\begin{aligned} \begin{aligned} P(\phi )&= \frac{2 + \cos 2\phi }{2\pi }, \quad P(\theta )&= \sqrt{\frac{2}{\pi }}\exp \left( \frac{-(\theta - \pi /2)^{2}}{2}\right) , \quad P(\varphi )&= \sqrt{\frac{2}{\pi }}\exp \left( \frac{-(\varphi - \pi /2)^{2}}{2}\right) . \end{aligned} \end{aligned}$$

(3.2)

Moreover, in Ref. [30] the effects of misoriented inhomogeneities on the effective thermal conductivity of a transversely isotropic composite are considered. An ODF is introduced, where the distribution is described by a parameter $\lambda$ as follows:

$$\begin{aligned} P(\theta ) = 1 - \exp (\lambda \theta ) \end{aligned}$$

(3.3)

where highly oriented inhomogeneities are described by large values of $\lambda$ ($\lambda \rightarrow \infty$) and a completely random distribution of inhomogeneities is given by $\lambda = 0$. The effect of the inhomogeneity’s distribution function on the effective thermo-mechanical properties of fiber-reinforced composites is discussed in Ref. [31]. The following exponential ODF is assumed:

$$\begin{aligned} P(\theta ) = \exp (-\theta ^{2}/2\lambda ^{2}). \end{aligned}$$

(3.4)

Additionally, in Ref. [32] the following two-parameter ODF is used:

$$\begin{aligned} P(\theta ) = \frac{\sin ^{2p - 1}\theta \; \cos ^{2q - 1}\theta }{\int _{\theta _\mathrm{min}}^{\theta _\mathrm{max}} \sin ^{2p - 1}\theta \; \cos ^{2q - 1}\theta \mathrm {d}\theta }, \qquad 0\le \theta _\mathrm{min}\le \theta \le \theta _\mathrm{max}\le \pi /2 \end{aligned}$$

(3.5)

where p and q are shape parameters. Also, the use of the following ODF is suggested in Ref. [33]:

$$\begin{aligned} P_{\lambda }(\varphi ) = \frac{1}{2\pi } \left[ (\lambda ^{2} + 1) \exp (-\lambda \varphi ) + \lambda \exp (-\lambda \pi /2)\right] , \end{aligned}$$

(3.6)

to calculate the effective elastic properties in composites with transversely isotropic orientation distribution of cracks. This function was used later in Ref. [7] to discuss the way in which the aspect ratios of the effective inclusion have to be chosen in the framework of the Maxwell scheme. Also, Eq. (3.6) was used in Ref. [34] to calculate viscoelastic properties of short-fiber-reinforced composites, and it was also used in Ref. [35] to calculate the effective elastic properties of polymer-fiber-reinforced concrete.

An ODF is introduced in Ref. [36], to consider the anisotropy due to all the families of pores and/or mineral constituents in rock-like composites,

$$\begin{aligned} P_{\sigma }(\varphi ) = \frac{1}{2\pi } \frac{\sigma \cosh (\sigma \cos \varphi )}{\sinh \sigma }, \end{aligned}$$

(3.7)

where $\sigma$ is the parameter accounting for the degree of the preferred alignment. The specific choice of an ODF is mostly related to computational cost, because its form does not affect significantly the overall elastic and conductive properties of a composite, as shown in Ref. [37].

3.2 Random distribution of reinforcements by the present model

An oriented or anisotropic distribution of spheroidal inhomogeneities in a transversely isotropic piezoelectric material can be considered by introducing an orientation distribution function (ODF) which allows to incorporate the anisotropy due to the inhomogeneities of the system. An ODF can be denoted by $P(\phi ,\theta )$ and represents a probability density function defined on the upper semi-sphere $\Phi$ of unit radius and subjected to the normalization condition. The contributions of all the families of inhomogeneities to the overall electro-elastic properties are taken into account by integrating over the unit sphere,

$$\begin{aligned} \int _{0}^{2\pi }\mathrm {d}\theta \int _{0}^{\pi /2}\mathrm {d}\phi P(\phi ,\theta )\sin \phi = 1, \end{aligned}$$

(3.8)

where the two angles $0\le \phi \le \pi /2$ and $0\le \theta \le 2\pi$ define the unit vector $m_{i}$ along the spheroid’s symmetry axis, as shown in Fig. 2,

$$\begin{aligned} m_{i}=(\cos \theta \sin \phi ,\sin \theta \sin \phi ,\cos \phi ). \end{aligned}$$

(3.9)

Fig. 2

Orientational distribution function $P_{\lambda }$ at $\lambda =1$

The distribution orientation that lies between the random and the parallel distribution can be considered by specifying the following probability density $P(\phi ,\theta ) = P(\phi )$. (Its independence on $\theta$ implies a transverse isotropy, where $x_{3}$ is the symmetry axis.) Following Refs. [7, 33, 36], the ODFs given by Eqs. (3.6) and (3.7) can be considered. These equations are governed by the parameters $\lambda \ge 0$ and $\sigma \ge 0$, respectively.

Figure 3a shows the dependence of $P_{\lambda }(\phi )$ on $\phi$ for several values of $\lambda$, and Fig. 3b shows the function $P_{\sigma }(\phi )$ for several values of $\sigma$. The parallel orientation statistics ($\phi = 0$) is an extreme case and corresponds to $\lambda \rightarrow \infty$ and $\sigma \rightarrow \infty$. Another extreme case is the random orientation statistics (any value of $\phi$ has the same probability) which corresponds to $\lambda = 0$ and $\sigma = 0$. Both ODFs cover two important limiting cases: slightly perturbed parallel orientations (large values of the parameter) and weakly expressed orientation preference (small parameter values). Figure 3c shows the dependence of $P_{\lambda }(\phi )$ on $\lambda$ for several values of $\phi$ (the probability change for obtaining fibers with specific orientation as $\lambda$ increases), and Fig. 3d shows the dependence of $P_{\sigma }(\phi )$ on $\sigma$, for several values of $\phi$. Notice that the orientation distribution given by $P_{\lambda }(\phi )$ and $P_{\sigma }(\phi )$ for the same parameter value $\lambda = \sigma$ is different. Then, the effect of changing $P_{\lambda }(\phi )$ with $P_{\sigma }(\phi )$ in the electro-elastic effective properties is difficult to compare.

Fig. 3

Plots of $P_{\lambda }$ and $P_{\sigma }$ against the angle $\phi$ for several values of $\lambda$ (a) and $\sigma$ (b). The dependence of $P_{\lambda }$ and $P_{\sigma }$ on the scatter parameters $\lambda$ (c) and $\sigma$ (d) for several values of the angle $\phi$ is also shown

Considering identical oblate spheroidal inhomogeneities with the orientation distribution that is between the fully random and the perfectly parallel ones (preferential orientation with scatter) and taking into account all the inhomogeneities with different orientations, the tensor ${\mathbf {N}}^{(p)} = \sum {\mathbf {N}}(\phi ^{(0)},\theta ^{(0)})$, where $p = \lambda , \sigma$ represents the election of $P_{\lambda }(\phi )$ or $P_{\sigma }(\phi )$, and $\phi ^{(0)},\theta ^{(0)}$ are related to an inhomogeneity’s specific orientation $m_{i}^{(0)}(\phi ^{(0)},\theta ^{(0)})$. For computational convenience, summation over the inhomogeneities can be replaced by the integration over orientations,

$$\begin{aligned} {\mathbf {N}}^{(p)} = \int _{\Phi }P_{p}(\phi ) {\mathbf {N}}(\phi ,\theta )\sin \phi \mathrm {d}\phi \mathrm {d}\theta = \int _{0}^{\pi /2}\mathrm {d}\phi P_{p}(\phi )\sin \phi \int _{0}^{2\pi }\mathrm {d}\theta {\mathbf {N}}(\phi ,\theta ), \qquad p = \lambda ,\, \sigma , \end{aligned}$$

(3.10)

where the tensor ${\mathbf {N}}$ has hexagonal symmetry and therefore can be represented by the tensorial basis described in Ref. [38]. ${\mathbf {N}}^{(\lambda )}$ as described in Eq. (3.10) has the same symmetry and can be represented in this basis, and its components are obtained in Appendix A.

The Maxwell scheme can be applied to a composite in which one family of inhomogeneities with an oriented distribution is embedded in a matrix material. The relation given by Eq. (2.3) has to be replaced with the following expression:

$$\begin{aligned} \bar{{\mathbf {L}}} = {\mathbf {L}}^{0} + \theta \left[ \left( {\mathbf {N}}^{p} \right) ^{-1} + \theta {\mathbf {Q}}^{(e)}\right] ^{-1} \end{aligned}$$

(3.11)

where ${\mathbf {N}}^{p}$ has the information related to the orientation. In this case, there is no problem with the election of the effective inclusion’s aspect ratio $\delta _{e}$ because there is only one type of inhomogeneity with aspect ratio $\delta$, then $\delta _{e} = \delta$.

4 Numerical results

The goal of this Section is primarily to illustrate the effective electro-elastic properties of composites with more than one family of inhomogeneities. Another goal is to illustrate the effect of the inhomogeneity’s orientation on the overall properties of piezoelectric composites. The orientation of the inhomogeneities is given by the parameter $\lambda$ by (ODF) $P_{\lambda }(\phi )$. Additionally, the dependence of the effective electro-elastic moduli on the aspect ratio $\delta _{e}$ of the effective inclusion for different scatter parameter values $\lambda$ and volume fraction $\theta$ is presented. The electro-elastic properties of the materials which are the composite constituents are given in Table 1. These values are taken from Refs. [39,40,41].

Table 1 Materials’ electro-elastic properties

Fig. 4

Comparison between the effects of $P_{\lambda }(\phi )$ and $P_{\sigma }(\phi )$ on the electro-elastic effective coefficients for porous PZT-7A

This Section presents numerical results for biphasic and tri-phasic composites. The biphasic composite is made by only one family of inhomogeneities embedded in a matrix material. Particularly, porous composites are considered when the pores of the matrix are constituted by inhomogeneities. The tri-phasic composite is made by two families of inhomogeneities embedded in a matrix.

The electro-elastic effective properties ${\bar{C}}_{44}$, ${\bar{e}}_{15}$, ${\bar{\eta }}_{11}$, and ${\bar{\eta }}_{33}$ are plotted against ODF parameters in Fig. 4. With the logarithmic scale for $\lambda$ and $\sigma$, it is possible to probe the entire inhomogeneity’s orientation distribution given by $P_{\lambda }(\phi )$ and $P_{\sigma }(\phi )$, respectively. A porous PZT-7A ceramic is considered with porosity $\theta _{1} = 0.1$. The elastic effective coefficient ${\bar{C}}_{44}$ and the piezoelectric effective property ${\bar{e}}_{15}$ are shown in Fig. 4a, b. The effective permittivities ${\bar{\eta }}_{11}$ and ${\bar{\eta }}_{33}$ are plotted in Fig. 4c, d. Notice that each effective coefficient is affected differently by the change in orientation distribution. For example, an increment in ${\bar{C}}_{44}$ is obtained by raising $\lambda -\sigma$. A decrease in ${\bar{e}}_{15}$ by lowering the values of $\lambda -\sigma$ is observed as well. Also, both ODFs have the same behavior for the aligned and randomly oriented inhomogeneity’s limiting cases. The predictions for intermediate scenarios (between these limit cases) are in close agreement; therefore, the choice of an ODF does not dramatically affect the overall electro-elastic properties.

The effects of the aspect ratio $\delta _{e}$ of the effective inclusion on the effective properties of composites are displayed in Fig. 5. The elastic stiffness ${\bar{C}}_{33}$ and piezoelectric coefficients ${\bar{e}}_{33}$ are plotted against the effective aspect ratio $\delta _{e}$ of the inhomogeneities at different values of the degree of the preferred alignment $\lambda$, by considering four different porosities $\theta _{1}=0.1,\;0.2,\;0.3,\;0.4$ for a PZT-7A ceramic with a porous aspect ratio $\delta = 0.1$. As observed in Ref. [7], for elastic composites, the effective inclusion’s aspect ratio affects significantly the effective piezoelectric coefficients. Beyond the point where $\lambda = 100$, the orientation distribution can be considered as a parallel one; the electro-elastic properties are not observed to change for values of $\lambda =100$. The coefficients ${\bar{C}}_{33}$ and ${\bar{e}}_{33}$ become negative (lose physical meaning) for different values of $\delta _{e}$. The limit case $\lambda = 100$ is most affected by the variation of $\delta _{e}$, and the case $\lambda = 0$ has the lowest correlation with $\delta _{e}$. This behavior is not exclusive for these properties at those concentrations; it can be observed for all electro-elastic properties independently of the value of $\lambda$.

Fig. 5

Plots of the stiffness ${\bar{C}}_{33}$ and piezoelectric moduli ${\bar{e}}_{33}$ against the aspect ratio $\delta _{e}$ of the effective inclusion for four porosities $\theta _{1}$ in a PZT-7A ceramic. Completely random orientation of pores $\lambda = 0$ is shown in (a) and (b) and parallel distribution $\lambda = 100$ in (e) and (f)

The stiffness ${\bar{C}}_{33}$ and the piezoelectric coefficients ${\bar{e}}_{33}$ are plotted in Fig. 6, against the porosity $\theta _{1}$ of a PZT-7A ceramic at different values of the preferred alignment $\lambda$ and with four effective inclusion’s aspect ratios $\delta _{e}$. The pores have an aspect ratio of $\delta = 0.1$. The curve for $\delta _{e} = \delta = 0.1$ is the only that has physical meaning. The effective properties become negative with an increment of $\theta _{1}$, and this trend is observed to be stronger for $\delta _{e}>>\delta$. The numerical experiments show that the effective electro-elastic properties lose physical meaning (become negative) when $\delta _{e}$ is different from $\delta$, independently of the inhomogeneity’s orientation $\lambda$. The effective inclusion must be selected as a spheroid with the same aspect ratio as the inhomogeneities $\delta _{e} = \delta$, as observed in Refs. [7, 10].

Fig. 6

Stiffness ${\bar{C}}_{33}$ and piezoelectric moduli ${\bar{e}}_{33}$ as functions of the porosity $\theta$ for PZT-7A ceramic containing pores with orientation scatter at different values of the effective inclusion’s aspect ratio $\delta _{e}$ and the scatter parameter $\lambda$. Completely random orientation $\lambda = 0$ is shown in (a) and (b), and parallel distribution of porous $\lambda = 100$ in (e) and (f)

Figure 7 shows a comparison between the effective constants for different tri-phasic piezoelectric composites. Each composite is made by an Araldite-D matrix in which long fibers of PZT-7A and other ceramics, like PZT-4, PZT-5, and $\hbox {BaTiO}_{{3}}$, are embedded. The volume fraction of PZT-4, PZT-5, and $\hbox {BaTiO}_{{3}}$ is fixed at $\theta _{2} = 0.3$, and the volume fraction of PZT-7A varies from $\theta _{PZT-7A} = 0$ to $\theta _{PZT-7A} = 0.6$. The total volume fraction is $\theta = \theta _{PZT-7A} + \theta _{2}$. The aspect ratio of the effective inclusion is $\delta _{e} = 1000$ because the inhomogeneities are fibers. For the anti-plane coefficients ${\bar{C}}_{44}$, ${\bar{e}}_{15}$, and ${\bar{\eta }}_{11}$, the theoretical predictions are practically the same for the three composites in the whole range of the volume fraction $0\le \theta \le 0.9$, since the observed differences are negligible.

Fig. 7

Dependency of the electro-elastic coefficients on the volumetric fraction $\theta _{PZT-7A}$ in tri-phasic composites made by fibers of PZT-7A, PZT-4, PZT-5, and $\hbox {BaTiO}_{{3}}$ at $\theta _{2} = 0.3$ embedded in an Araldite-D matrix

Fig. 8

Plots of the electro-elastic coefficients as functions of the PZT-4 volume fraction $\theta _{d}$ in a tri-phasic composite made by disks of PZT-4 and fibers of PZT-7A embedded in an Araldite-D matrix for different fiber volume fractions $\theta _{f}$

In Fig. 8, the effective electro-elastic properties of a tri-phasic piezoelectric composite made by long fibers ($\delta = 1000$) of PZT-7A and disks ($\delta = 0.1$) of PZT-4 embedded in an Araldite-D matrix are plotted against the PZT-4 disk volumetric fraction $\theta _{d}$ for three different PZT-7A fiber volumetric fractions $\theta _{f}$. The total volumetric fraction is $\theta = \theta _{f} + \theta _{d}$, and to avoid percolation, the range of $\theta _{d}$ is $0<\theta _{d}<0.4$. The aspect ratio of the effective inclusion is $\delta _{e} = \theta _{f}\delta _{f} + \theta _{d}\delta _{d}$. The anisotropy of ${\mathbf {Q}}^{(e)}$ is the same as the anisotropy of $\sum _{r=1}^{N}\theta _{r}{\mathbf {N}}^{(r)}$ and $\sum _{r=1}^{N}\theta _{r}{\mathbf {Q}}^{(r)}$. With this selection of $\delta _{e}$, a condition is obtained for the physical consistence of the model. The authors of Refs. [7, 10] state that for composites with transversely isotropic microstructure, where the symmetry axis coincides with the $Ox_{3}$ axis of the Cartesian coordinate system, the effective inclusion is an oblate spheroid with aspect ratio $\delta _{e} = \sum _{r=1}^{N}\theta _{r} N^{(r)}_{3333}/N^{(r)}_{1111}$, if this fraction is smaller than 1, or a prolate spheroid with aspect ratio $\delta _{e}=\sum _{r=1}^{N}\theta _{r}Q^{(r)}_{3333}/Q^{(r)}_{1111}$, if this fraction is larger than or equal to 1. The calculation of $\delta _{e}$ as previously discussed is avoided because it is more computationally expensive than $\delta _{e} = \theta _{f}\delta _{f} + \theta _{d}\delta _{d}$, even in the tri-phasic scenario.

5 Conclusions

The present paper provides an analysis of piezoelectric composites and the behavior of the static effective properties using the Maxwell homogenization method. As a novel contribution, the electro-elastic coefficients in composites with more than one family of inhomogeneities are obtained with the Maxwell scheme. The results are presented for three-phase composites which are made by two types of piezoelectric reinforcements embedded in a non-piezoelectric matrix. MHM is extended to piezoelectric composites with arbitrarily-oriented inhomogeneities whose distribution orientations are given by two different probability densities. The question of the shape of the effective inclusion is treated. The present model poses a novel way to compute the aspect ratio of the effective inclusion. The components of the tensorial integral functions are given in explicit form.

The Maxwell scheme is applied to composites in which the inhomogeneities of a given family have an orientation distribution. Two different ODFs are considered, $P_{\lambda }(\phi )$ and $P_{\sigma }(\phi )$, where both reflect the transverse isotropy with respect to the symmetry axis $Ox_{3}$. $P_{\lambda }(\phi )$ and $P_{\sigma }(\phi )$ are governed by the parameters $\lambda \ge 0$ and $\sigma \ge 0$, respectively. Orientations between a random $\lambda ,\sigma =0$ and the parallel $\lambda ,\sigma \rightarrow \infty$ were considered. The components of the average electro-elastic properties over the inhomogeneities are given in explicit form. The selection of $P_{\lambda }(\phi )$ and $P_{\sigma }(\phi )$ does not affect the effective properties of piezoelectric composites.

The static effective properties of piezoelectric composites are significantly affected by the geometry of the effective inclusion. It is shown that an inappropriate choice of the aspect ratio $\delta _{e}$ of the effective inclusion may lead to effective electro-elastic properties that have no physical meaning. $\delta _{e}$ has to be of ellipsoidal shape and with the same aspect ratio than the inhomogeneities $\delta _{e} = \delta$ for aligned inhomogeneities in biphasic composites. Finally, the effective inclusion’s aspect ratio can be selected as $\delta _{e} = \sum \nolimits _{i=1}^{N}\theta _{i}\delta _{i}$ for N different families of inhomogeneities.

Appendices

Appendix A. ${\mathbf {T}}$, ${\mathbf {U}}$, ${\mathbf {t}}$ tensor bases representation

The electro-elastic properties of a piezoelectric transversely isotropic material can be represented in the form

$$\begin{aligned} \begin{aligned} {\mathbf {C}}(\phi ,\theta )&= C_{11} {\mathbf {T}}^{1}(\phi ,\theta ) + C_{12} ({\mathbf {T}}^{2}(\phi ,\theta ) - {\mathbf {T}}^{1}(\phi ,\theta ))\\&\quad + C_{13} ({\mathbf {T}}^{3}(\phi ,\theta ) + {\mathbf {T}}^{4}(\phi ,\theta )) + 4C_{44} {\mathbf {T}}^{5}(\phi ,\theta ) + C_{33} {\mathbf {T}}^{6}(\phi ,\theta ), \\ \mathbf {e(\phi ,\theta )}&= e_{31} {\mathbf {U}}^{1}(\phi ,\theta ) + e_{15} {\mathbf {U}}^{2}(\phi ,\theta ) + e_{33} {\mathbf {U}}^{3}(\phi ,\theta ), \\ {\varvec{\epsilon }} (\phi ,\theta )&= \epsilon _{33} {\mathbf {t}}^{1}(\phi ,\theta ) + \epsilon _{11} {\mathbf {t}}^{2}(\phi ,\theta ) \end{aligned} \end{aligned}$$

(A.1)

where $C_{11}$, $C_{12}$, $C_{13}$, $C_{33}$, $C_{44}$ are five independent elastic moduli of the transversely isotropic medium, $e_{31}$, $e_{15}$, $e_{33}$ are three piezoelectric constants, and $\epsilon _{33}$, $\epsilon _{11}$ are two permittivities. The quantities ${\mathbf {T}}^{i}(\phi ,\theta )$, ${\mathbf {U}}^{i}(\phi ,\theta )$, ${\mathbf {t}}^{i}(\phi ,\theta )$ are the elements of the tensor basis defined in Ref. [38] as follows:

$$\begin{aligned} \begin{aligned} T_{ijkl}^{1}(\phi ,\theta )&= \frac{1}{2}(\theta _{ik}\theta _{lj} + \theta _{il}\theta _{kj}), \qquad T_{ijkl}^{2}(\phi ,\theta ) = \theta _{ij}\theta _{kl}, \\ T_{ijkl}^{3}(\phi ,\theta )&= \theta _{ij}m_{k}m_{l}, \qquad T_{ijkl}^{4}(\phi ,\theta ) = m_{i}m_{j}\theta _{kl}, \\ T_{ijkl}^{5}(\phi ,\theta )&= \frac{1}{4}\left( \theta _{ik}m_{l}m_{j}+ \theta _{il}m_{k}m_{j}+\theta _{jk}m_{l}m_{i} + \theta _{jl} m_{k}m_{i}\right) , \\ T_{ijkl}^{6}(\phi ,\theta )&= m_{i}m_{j}m_{k}m_{l}, \\ U_{ijk}^{1}(\phi ,\theta )&= \theta _{ij}m_{k}, \qquad U_{ijk}^{2}(\phi ,\theta ) = m_{i}\theta _{jk}+m_{j}\theta _{ik}, \qquad U_{ijk}^{3}(\phi ,\theta ) = m_{i}m_{j}m_{k}, \\ t_{ij}^{1}(\phi ,\theta )&= m_{i}m_{j}, \qquad t_{ij}^{2}(\phi ,\theta ) = \theta _{ij}, \\ \theta _{ij}(\phi ,\theta )&= \delta _{ij}-m_{i}(\phi ,\theta )m_{j}(\phi ,\theta ) \end{aligned} \end{aligned}$$

(A.2)

where $m_{i}(\phi ,\varphi ) = (\cos \theta \sin \phi ,\sin \theta \sin \phi ,\cos \phi )$ is the unit vector along the symmetry axis of the material and is defined by Eq. (3.9).

The average electro-elastic properties of a composite in which the inhomogeneities have arbitrary orientations are given by integrating over the different orientations,

$$\begin{aligned} \begin{aligned} {\mathbf {C}}^{p}&= \int _{0}^{\pi /2}\mathrm {d}\phi \, P_{p}(\phi )\sin \phi \left\{ \int _{0}^{2\pi }\mathrm {d}\theta \Big [C_{11}{\mathbf {T}}^{1}(\phi ,\theta ) + C_{12} \left( {\mathbf {T}}^{2}(\phi ,\theta ) - {\mathbf {T}}^{1}(\phi ,\theta )\right) \right. \\&\quad \left. +\, C_{13} ({\mathbf {T}}^{3}(\phi ,\theta ) + {\mathbf {T}}^{4}(\phi ,\theta )) + 4C_{44} {\mathbf {T}}^{5}(\phi ,\theta ) + C_{66} {\mathbf {T}}^{6}(\phi ,\theta )\Big ]\right\} , \\ {\mathbf {e}}^{p}&= \int _{0}^{\pi /2}\mathrm {d}\phi \, P_{p}(\phi )\sin \phi \int _{0}^{2\pi }\mathrm {d}\theta \Big [e_{31}{\mathbf {U}}^{1}(\phi ,\theta ) + e_{15} {\mathbf {U}}^{2}(\phi ,\theta ) + e_{33} {\mathbf {U}}^{3}(\phi ,\theta )\Big ], \\ {\varvec{\epsilon }} ^{p}&= \int _{0}^{\pi /2}\mathrm {d}\phi \, P_{p}(\phi )\sin \phi \int _{0}^{2\pi }\mathrm {d}\theta \Big [\epsilon _{33} {\mathbf {t}}^{1}(\phi ,\theta ) + \epsilon _{11} {\mathbf {t}}^{2}(\phi ,\theta )\Big ], \end{aligned} \end{aligned}$$

(A.3)

after taking into account Eqs. (A.1) and (3.10). The functions $P_{\lambda }(\phi )$ and $P_{\sigma }(\phi )$ described in Eqs. (3.6) and (3.7), respectively, are represented by the function $P_{p}(\phi )$. The components of ${\mathbf {C}}^{p}$, ${\mathbf {e}}^{p}$, and ${\varvec{\epsilon }}^{p}$ are given by

$$\begin{aligned} \begin{aligned} C_{11}^{(p)}&= g_{11}(p) C_{11} + g_{12}(p) C_{13} + \frac{3}{8}g_{6}(p) C_{33} + 2g_{12}(p) C_{44}, \\ C_{12}^{(p)}&= \frac{1}{8}g_{6}(p) C_{11} + (1-2g_{1}(p)) C_{12} + g_{10}(p) C_{13} + \frac{1}{8}g_{6}(p) C_{33} -\frac{1}{2}g_{6}(p) C_{44}, \\ C_{13}^{(p)}&= g_{4}(p) C_{11} + g_{1}(p) C_{12} + g_{5}(p) C_{13} + g_{4}(p) C_{33} - 4g_{4}(p) C_{44}, \\ C_{33}^{(p)}&= g_{6}(p) C_{11} + 4g_{4}(p) C_{13} + g_{7}(p) C_{33} + 8g_{4}(p) C_{44}, \\ C_{44}^{(p)}&= g_{8}(p) C_{11} - \frac{1}{2}g_{1}(p) C_{12} - 2g_{4}(p) C_{13} + g_{4}(p) C_{33} + g_{9}(p) C_{44}, \\ e_{31}^{(p)}&= (g_{2}(p) + g_{3}(p)) e_{31} - 2g_{2}(p) e_{15} + g_{2}(p) e_{33}, \\ e_{15}^{(p)}&= - g_{2}(p) e_{31} + g_{3}(p) e_{15} + g_{2}(p) e_{33}, \\ e_{33}^{(p)}&= 2g_{2}(p) e_{31} + 4g_{2}(p) e_{15} + g_{3}(p) e_{33}, \\ \epsilon _{11}^{(p)}&= (1 - g_{1}(p)) \epsilon _{11} + g_{1}(p) \epsilon _{33}, \\ \epsilon _{33}^{(p)}&= 2g_{1}(p) \epsilon _{11} + (1 - 2g_{1}(p)) \epsilon _{33}. \end{aligned} \end{aligned}$$

(A.4)

When $p = \lambda$, the functions $g_{i}(\lambda )$ are defined as

$$\begin{aligned} \begin{aligned} g_{1}(\lambda )&= \frac{3}{9+\lambda ^{2}}-\lambda e^{-\frac{\pi }{2}\lambda }\frac{3+\lambda ^{2}}{6(9+\lambda ^{2})}, \\ g_{2}(\lambda )&= \frac{e^{-\frac{\pi }{2}\lambda }\bigg (40+ 24e^{\frac{\pi }{2}\lambda }(1+\lambda ^{2})+\lambda (64+\lambda ( 44+\lambda (20+\lambda (4+\lambda ))))\bigg )}{8(4+\lambda ^{2})(16+\lambda ^{2})}, \\ g_{3}(\lambda )&= \frac{e^{-\frac{\pi }{2}\lambda }\bigg (24+ 4e^{\frac{\pi }{2}\lambda }(1+\lambda ^{2})(10+\lambda ^{2})+ \lambda (64+\lambda (24+20\lambda +\lambda ^{3}))\bigg )}{4(4+\lambda ^{2})(16+\lambda ^{2})}, \\ g_{4}(\lambda )&= \frac{3(5+\lambda ^{2})}{(9+\lambda ^{2})(25+\lambda ^{2})}+\lambda e^{-\frac{\pi }{2}\lambda }\frac{12+(1+\lambda ^{2}) (18+\lambda ^{2})}{15(9+\lambda ^{2})(25+\lambda ^{2})}, \\ g_{5}(\lambda )&= \frac{96+(1+\lambda ^{2})(24+\lambda ^{2})}{(9+\lambda ^{2})(25+\lambda ^{2})}+\lambda e^{-\frac{\pi }{2}\lambda }\frac{192+(1+\lambda ^{2}) (63+\lambda ^{2})}{30(9+\lambda ^{2})(25+\lambda ^{2})}, \\ g_{6}(\lambda )&= \frac{1800}{15(9+\lambda ^{2})(25+\lambda ^{2})} -\lambda e^{-\frac{\pi }{2}\lambda }\frac{435+178\lambda ^{2}+ 7\lambda ^{4}}{15(9+\lambda ^{2})(25+\lambda ^{2})}, \\ g_{7}(\lambda )&= \frac{24+(1+\lambda ^{2})(21+\lambda ^{2})}{(9+\lambda ^{2})(25+\lambda ^{2})}+\lambda e^{-\frac{\pi }{2}\lambda }\frac{72+(1+\lambda ^{2}) (33+\lambda ^{2})}{5(9+\lambda ^{2})(25+\lambda ^{2})}, \\ g_{8}(\lambda )&= \frac{3(35+3\lambda ^{2})}{2(9+\lambda ^{2})(25+\lambda ^{2})}-\lambda e^{-\frac{\pi }{2}\lambda }\frac{192+(1+\lambda ^{2}) (63+\lambda ^{2})}{60(9+\lambda ^{2})(25+\lambda ^{2})}, \\ g_{9}(\lambda )&= \frac{10+\lambda ^{2}}{25+\lambda ^{2}}-\lambda e^{-\frac{\pi }{2}\lambda }\frac{-5+\lambda ^{2}}{10(25+\lambda ^{2})}, \\ g_{10}(\lambda )&= \frac{6(20+\lambda ^{2})}{(9+\lambda ^{2})(25+\lambda ^{2})}-\lambda e^{-\frac{\pi }{2}\lambda }\frac{1065+382\lambda ^{2}+ 13\lambda ^{4}}{60(9+\lambda ^{2})(25+\lambda ^{2})}, \\ g_{11}(\lambda )&= \frac{93+(1+\lambda ^{2})(27+\lambda ^{2})}{(9+\lambda ^{2})(25+\lambda ^{2})}+\lambda e^{-\frac{\pi }{2}\lambda }\frac{1695+586\lambda ^{2}+ 19\lambda ^{4}}{120(9+\lambda ^{2})(25+\lambda ^{2})}, \\ g_{12}(\lambda )&= \frac{6(10+\lambda ^{2})}{(9+\lambda ^{2})(25+\lambda ^{2})}+\lambda e^{-\frac{\pi }{2}\lambda }\frac{-195-26\lambda ^{2}+ \lambda ^{4}}{60(9+\lambda ^{2})(25+\lambda ^{2})}. \end{aligned} \end{aligned}$$

(A.5)

For $p = \sigma$, the functions $g_{i}(\sigma )$ are defined as follows:

$$\begin{aligned} g_{1}(\sigma )= & {} \frac{\sigma \coth \sigma - 1}{\sigma ^{2}}, \nonumber \\ g_{2}(\sigma )= & {} \text {csch}\sigma \frac{\sigma ^{2} + 2(3 + \sigma ^{2})\cosh \sigma - 6\sigma \sinh \sigma - 6}{2\sigma ^{3}},\nonumber \\ g_{3}(\sigma )= & {} \frac{6\sigma + \sigma ^{3} -3(2 + \sigma ^{2}) \coth \sigma + 6\text {csch}\sigma }{\sigma ^{3}},\nonumber \\ g_{4}(\sigma )= & {} \frac{-12 - 5\sigma ^{2} - \sigma (12 + \sigma ^{2}) \coth \sigma }{\sigma ^{4}},\nonumber \\ g_{5}(\sigma )= & {} (8 + \sigma ^{2})\frac{3 + \sigma ^{2} - 3\sigma \coth \sigma }{\sigma ^{4}},\nonumber \\ g_{6}(\sigma )= & {} \frac{24 + 8\sigma ^{2} - 24\sigma \coth \sigma }{\sigma ^{4}},\\ g_{7}(\sigma )= & {} \frac{24 + 12\sigma ^{2} + \sigma ^{4} - 4\sigma (6 + \sigma ^{2})\coth \sigma }{\sigma ^{4}},\nonumber \\ g_{8}(\sigma )= & {} \frac{-24 - 11\sigma ^{2} + 3\sigma (8 + \sigma ^{2}) \coth \sigma }{2\sigma ^{4}},\nonumber \\ g_{9}(\sigma )= & {} \frac{48 + 21\sigma ^{2} + \sigma ^{4} - \sigma (48 + 5\sigma ^{2})\coth \sigma }{\sigma ^{4}},\nonumber \\ g_{10}(\sigma )= & {} \frac{-6 - 4\sigma ^{2} + 2\sigma (3 + \sigma ^{2}) \coth \sigma }{\sigma ^{4}},\nonumber \\ g_{11}(\sigma )= & {} \frac{9 + 5\sigma ^{2} + \sigma ^{4} - \sigma (9 + 2\sigma ^{2})\coth \sigma }{\sigma ^{4}},\nonumber \\ g_{12}(\sigma )= & {} 2\frac{-9 - 4\sigma ^{2} + \sigma (9 + \sigma ^{2}) \coth \sigma }{\sigma ^{4}}.\nonumber \end{aligned}$$

(A.6)

Taking the limit of parallel orientations $p\rightarrow \infty$, the components of $\mathbf{C }^{(p)}$, $\mathbf{e }^{(p)}$, ${\varvec{\epsilon }}^{(p)}$ have the following form:

$$\begin{aligned} \begin{aligned} \lim \limits _{p\rightarrow \infty } C_{11}^{(p)}&= C_{11}, \qquad \lim \limits _{p\rightarrow \infty } C_{12}^{(p)} = C_{12}, \qquad \lim \limits _{p\rightarrow \infty } C_{13}^{(p)} = C_{13}, \qquad \lim \limits _{p\rightarrow \infty } C_{33}^{(p)} = C_{33}, \\ \lim \limits _{p\rightarrow \infty } C_{44}^{(p)}&= C_{44}, \qquad \lim \limits _{p\rightarrow \infty } e_{31}^{(p)} = e_{31}, \qquad \lim \limits _{p\rightarrow \infty } e_{15}^{(p)} = e_{15}, \qquad \lim \limits _{p\rightarrow \infty } e_{33}^{(p)} = e_{33}, \\ \lim \limits _{p\rightarrow \infty } \epsilon _{11}^{(p)}&= \epsilon _{11}, \qquad \lim \limits _{p\rightarrow \infty } \epsilon _{33}^{(p)} = \epsilon _{33}, \end{aligned} \end{aligned}$$

(A.7)

after substitution of $g_{i}(\lambda )$ or $g_{i}(\sigma )$ into Eq. (A.4). The limits in Eq. (A.7) are in agreement with the representation of a transversely isotropic medium $\mathbf{C }(0,\theta )$, $\mathbf{e }(0,\theta )$, ${\varvec{\epsilon }}(0,\theta )$ in the tensor basis given by Eq. (A.2).

Appendix B. Components of the tensors $\bar{{\mathbf {S}}}^{(r)}_{x}$, $\bar{{\mathbf {M}}}^{(r)}_{x}$, $\bar{{\mathbf {S}}}^{(r)}_{,x}$, and $\bar{{\mathbf {M}}}^{(r)}_{,x}$.

The tensor ${\mathbf {S}}^{(r)}_{x}$ is given by Eq. (2.5). Due to the $\varphi$ and u dependence in Eq. (2.5), the only non-vanishing components of $S^{(r)}_{x(klij)}$ are $S^{(r)}_{x(1111)} = S^{(r)}_{x(2222)}$, $S^{(r)}_{x(1122)} = S^{(r)}_{x(2211)}$, $S^{(r)}_{x(3333)}$, $S^{(r)}_{x(1133)} = S^{(r)}_{x(2233)} = S^{(r)}_{x(3311)} = S^{(r)}_{x(3322)}$, $S^{(r)}_{x(2323)} = S^{(r)}_{x(2332)} = S^{(r)}_{x(3223)} = S^{(r)}_{x(3232)} = S^{(r)}_{x(1313)} =S^{(r)}_{x(1331)} = S^{(r)}_{x(3113)} = S^{(r)}_{x(3131)}$ and $S^{(r)}_{x(1212)} = S^{(r)}_{x(1221)} = S^{(r)}_{x(2112)} = S^{(r)}_{x(2121)}$. Then, using the Voigt two-index notation,

$$\begin{aligned} S^{(r)}_{x(11)}&= \int _{-1}^{1}\mathrm {d}u\, \frac{1-u^{2}}{4\pi |{\bar{\Gamma }}_{li}|} \Big (\Lambda _{c}(\Lambda _{a}+3\Gamma _{b})- \Lambda ^{2}_{ac}\Big ), \end{aligned}$$

(B. 1)

$$\begin{aligned} S^{(r)}_{x(12)}&= \int _{-1}^{1}\mathrm {d}u\, \frac{1-u^{2}}{4\pi |{\bar{\Gamma }}_{li}|} \Big (\Lambda ^{2}_{ac}- \Lambda _{ab}\Lambda _{c}\Big ), \end{aligned}$$

(B. 2)

$$\begin{aligned} S^{(r)}_{x(13)}&= \int _{-1}^{1}\mathrm {d}u\, \frac{u\sqrt{1-u^{2}}}{4\pi |{\bar{\Gamma }}_{li}|} \Lambda _{ac}\Big (\Lambda _{ab}-\Lambda _{a}- 3\Gamma _{b}\Big ), \end{aligned}$$

(B. 3)

$$\begin{aligned} S^{(r)}_{x(33)}&= \int _{-1}^{1}\mathrm {d}u\, \frac{u^{2}}{4\pi |{\bar{\Gamma }}_{li}|} \Big (\Lambda ^{2}_{a}-\Lambda ^{2}_{ab}+ 6\Lambda _{a}\Gamma _{b}+\Gamma ^{2}_{b}\Big ), \end{aligned}$$

(B. 4)

$$\begin{aligned} S^{(r)}_{x(44)}&= \int _{-1}^{1}\mathrm {d}u\, \frac{1-u^{2}}{8\pi |{\bar{\Gamma }}_{li}|} \Big (\Lambda ^{2}_{a}-\Lambda ^{2}_{ab}+ 6\Lambda _{a}\Gamma _{b}+\Gamma ^{2}_{b}\Big ) \nonumber \\&\quad + \int _{-1}^{1}\mathrm {d}u\, \frac{u\sqrt{1-u^{2}}}{2\pi |{\bar{\Gamma }}_{li}|} \Lambda _{ac}\Big (\Lambda _{ab}-\Lambda _{a}- 3\Gamma ^{0}_{b}\Big ) \nonumber \\&\quad +\int _{-1}^{1}\mathrm {d}u\, \frac{u^{2}}{\pi |{\bar{\Gamma }}_{li}|} \Big (\Lambda _{c}(\Lambda _{a}+\Gamma _{b})- \Lambda ^{2}_{ac}\Big ), \end{aligned}$$

(B. 5)

$$\begin{aligned} S^{(r)}_{x(66)}&= \int _{-1}^{1}\mathrm {d}u\, \frac{1-u^{2}}{8\pi |{\bar{\Gamma }}_{li}|} \Big (\Lambda _{c}(\Lambda _{a}+3\Gamma _{b}+ \Lambda _{ab})-2\Lambda ^{2}_{ac}\Big ). \end{aligned}$$

(B. 6)

Here, the determinant $|{\bar{\Gamma }}_{li}|$ of ${\bar{\Gamma }}_{li}$ is given by

$$\begin{aligned} |{\bar{\Gamma }}_{li}| = -\frac{\Gamma _{b}}{\epsilon }\Big (2\Gamma _{ac}\gamma _{a}\gamma _{c}- \Gamma _{a}\gamma ^{2}_{c}+ \epsilon \Gamma ^{2}_{ac}-\Gamma _{c} \Big (\gamma ^{2}_{a}+\epsilon \Gamma _{a}\Big )\Big ) \end{aligned}$$

(B. 7)

where $\Lambda _{a}({\varvec{\zeta }})$, $\Lambda _{ab}({\varvec{\zeta }})$, $\Lambda _{ac}({\varvec{\zeta }})$, $\Lambda _{c}({\varvec{\zeta }})$, $\Gamma _{a}({\varvec{\zeta }})$, $\Gamma _{b}({\varvec{\zeta }})$, $\Gamma _{c}({\varvec{\zeta }})$, $\Gamma _{ab}({\varvec{\zeta }})$, $\Gamma _{ac}({\varvec{\zeta }})$, $\gamma _{a}({\varvec{\zeta }})$, $\gamma _{c}({\varvec{\zeta }})$, and $\epsilon ({\varvec{\zeta }})$ are given by

$$\begin{aligned} \begin{aligned} \Lambda _{a}({\varvec{\zeta }})&= \Gamma _{a}({\varvec{\zeta }})+ \frac{\gamma _{a}^{2}({\varvec{\zeta }})}{\epsilon ({\varvec{\zeta }})},&\Lambda _{ab}({\varvec{\zeta }})&= \Gamma _{ab}({\varvec{\zeta }}) +\frac{\gamma _{a}^{2}({\varvec{\zeta }})}{\epsilon ({\varvec{\zeta }})}, \\ \Lambda _{ac}({\varvec{\zeta }})&= \Gamma _{ac}({\varvec{\zeta }})+ \frac{\gamma _{a}({\varvec{\zeta }}) \gamma _{c}({\varvec{\zeta }})}{\epsilon ({\varvec{\zeta }})},&\Lambda _{c}({\varvec{\zeta }})&= \Gamma _{c}({\varvec{\zeta }})+ \frac{\gamma _{c}^{2}({\varvec{\zeta }})}{\epsilon ({\varvec{\zeta }})}, \\ \Gamma _{a}({\varvec{\zeta }})&= \frac{1}{a^{2}_{r}}\left( C^{0}_{11}(1-u^{2})+ \frac{C^{0}_{44} u^{2}}{\delta ^{2}_{r}}\right) ,&\Gamma _{ab}({\varvec{\zeta }})&= \frac{C^{0}_{11}+C^{0}_{12}}{2 a^{2}_{r}}(1-u^{2}), \\ \Gamma _{b}({\varvec{\zeta }})&= \frac{1}{a^{2}_{r}}\left( C^{0}_{66}(1-u^{2})+ \frac{C^{0}_{44} u^{2}}{\delta ^{2}_{r}}\right) ,&\Gamma _{ac}({\varvec{\zeta }})&= \frac{C^{0}_{13}+C^{0}_{44}}{a^{2}_{r}\delta _{r}} u\sqrt{1-u^{2}}, \\ \Gamma _{c}({\varvec{\zeta }})&= \frac{1}{a^{2}_{r}}\left( C^{0}_{44}(1-u^{2})+ \frac{C^{0}_{33} u^{2}}{\delta ^{2}_{r}}\right) ,&\gamma _{a}({\varvec{\zeta }})&= \frac{e^{0}_{31}+e^{0}_{15}}{a^{2}_{r}\delta _{r}} u\sqrt{1-u^{2}}, \\ \gamma _{c}({\varvec{\zeta }})&= \frac{1}{a^{2}_{r}}\left( e^{0}_{15}(1-u^{2})+ \frac{e^{0}_{33} u^{2}}{\delta ^{2}_{r}}\right) ,&\epsilon ({\varvec{\zeta }})&= \frac{1}{a^{2}_{r}}\left( \epsilon ^{0}_{11}(1-u^{2})+ \frac{\epsilon ^{0}_{33} u^{2}}{\delta ^{2}_{r}}\right) . \end{aligned} \end{aligned}$$

(B. 8)

The tensor ${\mathbf {S}}^{(r)}_{,x}$ is obtained from Eq. (2.6). The only nonzero components of $S^{(r)}_{,x(k4ij)}$ are $S^{(r)}_{,x(1413)} = S^{(r)}_{,x(2423)} = S^{(r)}_{,x(1431)} = S^{(r)}_{,x(2432)}$, $S^{(r)}_{,x(3411)} = S^{(r)}_{x(3422)}$, and $S^{(r)}_{,x(3433)}$, due to the $\varphi$ and u dependence in Eq. (2.6). Then, in Voigt’s notation,

$$\begin{aligned} S^{(r)}_{,x(31)}&= \int _{-1}^{1}\mathrm {d}u\, \frac{u\sqrt{1-u^{2}}}{4\pi \epsilon |{\bar{\Gamma }}_{li}|} \bigg (\Lambda _{a}-\Lambda _{ab}+3\Gamma _{b}\bigg ) \bigg (\Lambda _{c}\gamma _{a} - \Lambda _{ac}\gamma _{c}\bigg ), \end{aligned}$$

(B. 9)

$$\begin{aligned} S^{(r)}_{,x(15)}&= \int _{-1}^{1}\mathrm {d}u\, \frac{u\sqrt{1-u^{2}}}{\pi \epsilon |{\bar{\Gamma }}_{li}|} \bigg (\Lambda _{a}-\Lambda _{ab}+3\Gamma _{b}\bigg ) \bigg (\Lambda _{c}\gamma _{a}- \Lambda _{ac}\gamma _{c}\bigg ) \nonumber \\&\quad +\int _{-1}^{1}\mathrm {d}u\, \frac{1-u^{2}}{4\pi \epsilon |{\bar{\Gamma }}_{li}|} \gamma _{c}\bigg (\Lambda ^{2}_{a}- \Lambda ^{2}_{ab}+6\Lambda _{a}\Gamma _{b} +\Gamma ^{2}_{b}\bigg ) \nonumber \\&\quad +\int _{-1}^{1}\mathrm {d}u\,\frac{1-u^{2}}{2\pi \epsilon |{\bar{\Gamma }}_{li}|}\Lambda _{ac}\gamma _{a} \bigg (\Lambda _{ab}-\Lambda _{a}-3\Gamma _{b}\bigg ), \end{aligned}$$

(B. 10)

$$\begin{aligned} S^{(r)}_{,x(33)}&= \int _{-1}^{1}\mathrm {d}u\, \frac{u^{2}}{4\pi \epsilon |{\bar{\Gamma }}_{li}|} \gamma _{c}\bigg (\Lambda ^{2}_{a}- \Lambda ^{2}_{ab}+6\Lambda _{a}\Gamma _{b} +\Gamma ^{2}_{b}\bigg ) \nonumber \\&\quad +\int _{-1}^{1}\mathrm {d}u\, \frac{u^{2}}{4\pi \epsilon |{\bar{\Gamma }}_{li}|} 2\Lambda _{ac}\gamma _{a}\bigg (\Lambda _{ab}- \Lambda _{a}-3\Gamma _{b}\bigg ). \end{aligned}$$

(B. 11)

The tensor ${\mathbf {M}}^{(r)}_{,x}$ is given by Eq. (2.7). Due to the $\varphi$ and u dependence in Eq. (2.7), the only nonzero components of $M^{(r)}_{,x(k44j)}$ are $M^{(r)}_{,x(1441)} = M^{(r)}_{,x(2442)}$ and $M^{(r)}_{,x(3443)}$. Then

$$\begin{aligned} M^{(r)}_{,x(11)}&= \int _{-1}^{1}\mathrm {d}u\frac{1-u^{2}}{4} \bigg (\epsilon -\frac{\Gamma _{b}}{|\Gamma _{ij}|} \Big (\gamma _{c}(2\Gamma _{ac}\gamma _{a}- \Gamma _{a}\gamma _{c})- \Gamma _{c}\gamma ^{2}_{a}\Big )\bigg )^{-1}, \end{aligned}$$

(B. 12)

$$\begin{aligned} M^{(r)}_{,x(33)}&= \int _{-1}^{1}\mathrm {d}u\frac{u^{2}}{2} \bigg (\epsilon -\frac{\Gamma _{b}}{|\Gamma _{ij}|} \Big (\gamma _{c}(2\Gamma _{ac}\gamma _{a}- \Gamma _{a}\gamma _{c})- \Gamma _{c}\gamma ^{2}_{a}\Big )\bigg )^{-1}. \end{aligned}$$

(B. 13)

Here, the determinant $|\Gamma _{li}|$ of $\Gamma _{li}$ is written as

$$\begin{aligned} |\Gamma _{li}| = -\Gamma _{b}\Big ( \Gamma ^{2}_{ac}-\Gamma _{a}\Gamma _{c}\Big ). \end{aligned}$$

(B. 14)