1 Introduction

Several types of tumour therapy including chemotherapy and radiotherapy are utilized to treat cancer disease. However, the research work suggests that elevated temperature can have the ability to damage cancerous cells without the issue of harmful toxicity and radiations [1]. The biomedical researchers suggest that in any type of hyperthermia, the prime objective is to deliver a specific amount of energy to the infected portion of the cancer tumour with the appropriate control of energy propagation to ensure the eradication of malignant cells with un-alteration of healthy tissues [2]. The regional hyperthermia therapy (RHT) is a kind of therapeutic treatment for malignant diseases in deeper tissues, i.e. larger size of tumour. It can be achieved by increasing the perfusion in organs by heating of blood or by irrigation of body cavities [3]. The dual phase lag (DPL) theory was first developed by Xu et al. [4], and it is on the basis of local thermal equilibrium (LTE) in the arterio-vascular region in the human body. This theory does not consider the local vascular geometry, and it is developed with the absence of the energy interaction among the branches of arteriole–venule structure. The DPL model is derived from the classical model (Fourier’s law of heat conduction) with the consideration of different relaxation times [5]. To renovate more realistic bioheat models, Xuan and Roetzel [6] and Roetzel and Xuan [7] proposed that the entire anatomical architecture of biological tissue is distinguished into two distinct regions: vascular regime (blood vessels) and extravascular regime (solid matrix) (refer Fig. 1); and the two regimes characterize as fluid saturated porous medium. These two regimes can be identified based on the volume average theory (VAT) which is termed as local thermal non-equilibrium (LTNE) approach. In many practical applications associated with the hyper-porous structures with a variable temperature difference between fluid and solid media, LTE approach might not be an appropriate one, whereas LTNE scheme is globally acceptable having an accurate analysis [8]. Alazmi and Vafai [9] and Khaled and Vafai [10] strongly suggested in their works that the implementation of porous media theory in biological heat transfer arena is most appropriate to avail the thermal non-equilibrium to exist between blood and peripheral tissues. Nakayama and Kuwahara [11] evolved the mathematical development of bioheat equations based on the volume average theory. Mahzoob and Vafai [12] carried out a comprehensive research work on the analytical modelling of LTNE bioheat equations in relation with the hyperthermia. Yuan [13] investigated an equivalent heat transfer coefficient between tissue and blood by the numerical simulation of biological porous media model. Zhang [14] developed bioheat governing differential equations based on LTNE approach in a most pertinent form with accurate mathematical expressions of two relaxation time lags. Afrin et al. [15] presented a numerical simulation for laser-irradiated living tissues, effects of laser exposure time as well as laser irradiance, and coupling factors. Yuan et al. [16] presented a numerical analysis of the spherical bioheat model with spherical tissues. Liu and Chen [17] solved the LTNE bioheat model with a hybrid application of Laplace transform method and modified discretization method. The coupling factors between blood and tissue, and porosity and phase lag times were investigated, separately. Hooshmand et al. [18] solved LTNE bioheat energy equation by the separation of variables. They used Duhamel’s integral method for both absorbing and scattering tissues with the laser interaction. Jasiński et al. [19] conducted a numerical study of thermal processes in soft tissues subjected to laser irradiation. Liu and Chen [20] analysed the thermal behaviour of laser-irradiated living tissues by implementing a hybrid approach based on the Laplace transform method and modified discretization method. Monte and Haji-Sheikh [21] developed analytical solutions by the Green’s function to focus on the results for the effects of thermal therapy.

Fig. 1
figure 1

Schematic diagram of tissue–vascular architecture with boundary conditions imposed for the present research work

Full size image

The above-mentioned research work was developed based on the constant initial condition of skin tissue. However, in the medical science of bio-thermomechanics, it is obvious that there is always thermal response in living tissues propagated in a spatial domain [22] due to the highly non-homogeneous anatomical structure of the human body. Dutta and Kundu [23,24,25] successfully established the concept of spatially based mathematical formulation of bioheat modelling with LTE approach for the hyperthermia therapy in order to develop an accurate study.

Encouraged by the advantageous LTNE approach, in this study two-dimensional mathematical modelling of LTNE bioheat model subject to RHT has been established. Here, it is demonstrated that no analysis exists for the multi-dimensional heat flow based on LTNE approach (from the authors’ best knowledge). However, in a physical domain, there is always possibility to transfer heat in multi-dimensional mode in tissues. In addition, when the bi-dimensional approach is dominant, the spatial domain of interest is large. From the biomedical point of view, it can be well applicable in case of RHT where a larger therapeutic area is preferred for the treatment of a large cancerous tumour. In the present study, a hybrid analytical scheme comprising ‘shift of variables’ and ‘finite integral transform (FIT)’ has been employed to determine the thermal response of LTNE 2-D DPL bioheat model. The external heat sources have been imposed as ‘constant’ and ‘sinusoidal’ at the exposed surface of the skin tissue, and other boundaries are considered to be at zero temperature gradient due to the absence of net heat transfer across these boundaries from the symmetric aspect. A comparative study has been conducted to analyse the benefits of thermobiological characteristics of the oscillating heat source over the constant heat source on the basis of the treatment protocol. The isotherms have been generated to visualize the thermal propagation in skin tissues, and it enables to predict the heat flow in the physical tissue domain. The present mathematical modelling has been endeavoured to validate with the published experimental work [34]. Based on the literature survey conducted, Hooshmand et al. [18] and Monte and Haji-Sheikh [21] have provided the exact solution of an LTNE bioheat model by the classical analytical scheme. In the current research work, initiatives have been taken to establish an exact solution by a hybrid method with appropriate (realistic) initial and boundary conditions to generate the thermal response in LTNE bioheat model applicable to the regional hyperthermia therapy along with the influence of several therapeutically dependent parameters.

2 Mathematical genesis

Nakayama and Kuwahara [11] identified that blood and tissue temperatures are different as the equilibrium concept of heat propagation is irrational. Therefore, two-temperature models (separately for fluid and solid medium) are incorporated in the concept of LTNE in arterio-vascular structure. The mathematical development of the two-temperature model can be presented for blood phase and tissue phase as [10, 11]

$$\begin{aligned} \epsilon \rho _{\mathrm{b}} {c}_\mathrm{b} \left[ {{\partial {T}_\mathrm{b} }/{\partial {t}}+\vec {\mathrm{v}}\cdot \nabla {T}_{\mathrm{b}} } \right] =\varepsilon {k}_{\mathrm{b}} \nabla ^{2}{T}_{\mathrm{b}} +{G}\left( {{T}_\mathrm{t} -{T}_{\mathrm{b}} } \right) +\varepsilon {q}_\mathrm{S} ;{\hbox {for blood phase}} \end{aligned}$$
(1)

and

$$\begin{aligned} \left( {1-\varepsilon } \right) \rho _{\mathrm{t}} {{c}}_{\mathrm{t}} \left( {{\partial {T}_{\mathrm{t}} }/{\partial {t}}} \right) =\left( {1-\varepsilon } \right) {{k}}_{\mathrm{t}} \nabla ^{2}{T}_{\mathrm{t}} +{G}\left( {{T}_{\mathrm{b}} -{T}_{\mathrm{t}} } \right) +\left( {1-\varepsilon } \right) {{q}}_{\mathrm{m}} +\left( {1-\varepsilon } \right) {{q}}_{\mathrm{S}} ;{\hbox {for tissue phase}}. \end{aligned}$$
(2)

According to the local thermal equilibrium (LTE) approach, the blood perfusion term is represented by \(\omega _{\mathrm{b}} \rho _{\mathrm{b}} {{c}}_{\mathrm{b}} \left( {{T}_{\mathrm{b}} -{T}_{\mathrm{t}} } \right) \) in which \(\omega _{\mathrm{b}}\) is defined as blood perfusion rate (\({s}^{-1})\) of the tissue [7]. But in the LTNE approach, the significant impact from blood flow direction, thermal diffusion, vascular geometry, and size has been accounted by the convective heat transfer coefficient \({h}_{\mathrm{b}}\) and specific area of the blood vessel in tissue \({a}_{\mathrm{b}}\). The specific term which correlates blood flow, thermal diffusion, and size of the vascular geometry is termed as the ‘coupling factor’, and mathematically, it can be expressed as \({G}={a}_{\mathrm{b}} {h}_{\mathrm{b}} +\omega _{\mathrm{b}} {{c}}_{\mathrm{b}} \) [refer Eqs. (1) and (2)] [14], and it denotes the energy exchange between blood (perfused inside the vessel) and surrounding tissue. The coupling factor can also be illustrated as a lumped convection–perfusion parameter [14]. The coupling factor is one of the most significant evolutions of LTNE bioheat approach over LTE bioheat modelling due to the consideration of vascular geometry along with the impact of blood perfusion rate. For more precise estimation, for a bundle of vascular tubes of diameter \({{d}}_{\mathrm {pore}} \), the specific area and heat transfer coefficients are postulated as \({{a}}_{\mathrm{b}} ={4\varepsilon }/{{{d}}_{\mathrm {pore}} } \) and \({{h}}_{\mathrm{b}} ={Nu}\left( {{{{k}}_{\mathrm{b}} }/{{{d}}_{\mathrm{pore}} }} \right) \), respectively [11]. Implementing the consideration of \({{a}}_{\mathrm{b}} \) and \({{h}}_{\mathrm{b}} \), the modified form of the coupling factor becomes:

$$\begin{aligned} {G}=\left( {{4\varepsilon {{k}}_{\mathrm{b}} }/{{{d}}_{\mathrm{pore}}^2 }} \right) {Nu}+\omega _{\mathrm{b}} {{c}}_{\mathrm{b}}. \end{aligned}$$
(3)

In LTE bioheat models, the velocity of the flow field has not been considered in the model formulation as it was assumed to be constant. But considering the practical aspects, blood velocity is not necessarily constant, and also its magnitude and direction are very complex to estimate. The blood flow rate changes rapidly due to size variation of arteries and vessels. In the LTNE bioheat model, the blood velocity has been incorporated (refer Eq. (1)). Though the blood velocity is coupled, for the mathematical modelling it is very difficult to predict the blood velocity inside the human body. So for the modification of the blood velocity term, Minkowycz et al. [26] proposed a new theory where the directional blood flow is accounted by convective heat transfer between blood and vessels, and mathematically, it can be formulated as

$$\begin{aligned} -\varepsilon \rho _{\mathrm{b}} {{c}}_{\mathrm{b}} \left( {\vec {{v}}\cdot \nabla {T}_{\mathrm{t}} } \right) \approx {G}\left( {{T}_{\mathrm{b}} -{T}_{\mathrm{t}} } \right) . \end{aligned}$$
(4)

The second term in Eq. (1) composed of blood velocity is replaced by using Eq. (4). Now the governing differential equation of LTNE DPL bioheat model has been derived in the form of tissue temperature [coupling Eqs. (1) and (2)] as proposed by Zhang [14] with the help of a theory developed by Minkowycz et al. [26] as referred in Eq. (4), and it can be mathematically represented as

$$\begin{aligned} \tau _{\mathrm {q}} \frac{\partial ^{2}{T}_{\mathrm {t}} }{\partial {t}^{2}}+\frac{\partial {T}_{\mathrm {t}} }{\partial {t}}= & {} \alpha _{\mathrm {eff}} \left[ {\nabla ^{2}{T}_{\mathrm {t}} +\tau _{\mathrm {T}} \frac{\partial }{\partial {t}}\left( {\nabla ^{2}{T}_{\mathrm {t}} } \right) } \right] +\frac{{G}}{\left( {\rho {c}} \right) _{\mathrm {eff}} }\left( {{T}_{\mathrm {b}} -{T}_{\mathrm {t}} } \right) \nonumber \\&+\frac{\left( {1-\varepsilon } \right) {{q}}_{\mathrm {m}} +{q_S}}{\left( {\rho {c}} \right) _{\mathrm {eff}} }+\frac{\varepsilon \rho _{\mathrm {b}} {{c}}_{\mathrm {b}} }{{G}\left( {\rho \mathrm {c}} \right) _{\mathrm {eff}} }\left[ {\left( {1-\varepsilon } \right) \frac{\partial {{q}}_{\mathrm {m}} }{\partial {t}}+\frac{\partial {{q}}_{\mathrm {S}} }{\partial {t}}} \right] \end{aligned}$$
(5)

where the constitutional parameters are correlated as follows:

$$\begin{aligned} \tau _{\mathrm{q}}= & {} \frac{\varepsilon \left( {1-\varepsilon } \right) \rho _{\mathrm{b}} {{c}}_{\mathrm{b}} \rho _{\mathrm{t}} {{c}}_{\mathrm{t}} }{{G}\left( {\rho {c}} \right) _{\mathrm{eff}} }; \quad \tau _{\mathrm{T}} =\frac{\varepsilon \left( {1-\varepsilon } \right) \rho _{\mathrm{b}} {{c}}_{\mathrm{b}} {{k}}_{\mathrm{t}} }{{{Gk}}_{\mathrm{eff}} }; \quad \left( {\rho {c}} \right) _{\mathrm{eff}} =\varepsilon \rho _{\mathrm{b}} {{c}}_{\mathrm{b}} +\left( {1-\varepsilon } \right) \rho _{\mathrm{t}} {{c}}_{\mathrm{t}} ; \nonumber \\ {{k}}_{\mathrm{eff}}= & {} \varepsilon {{k}}_{\mathrm{b}} +\left( {1-\varepsilon } \right) {{k}}_{\mathrm{t}} ;{\hbox {and}}\alpha _{\mathrm{eff}} =\frac{{{k}}_{\mathrm{eff}} }{\left( {\rho {c}} \right) _{\mathrm{eff}} }. \end{aligned}$$
(6)

Assuming \({q}_{\mathrm{m}}\) = constant and \({q}_{\mathrm{S}} = 0\) [23], the dimensionless form of Eq. (5) can be addressed in the following:

$$\begin{aligned} \frac{\partial ^{2}\theta _{\mathrm{t}} }{\partial {X}^{2}}+\frac{\partial ^{2}\theta _{\mathrm{t}} }{\partial {Y}^{2}}+{{Ve}}_{\mathrm{T}}^2 \frac{\partial ^{3}\theta _{\mathrm{t}} }{\partial {F}\partial {X}^{2}}+{{Ve}}_{\mathrm{T}}^2 \frac{\partial ^{3}\theta _{\mathrm{t}} }{\partial {F}\partial {Y}^{2}}-{{Ve}}_{\mathrm{q}}^2 \frac{\partial ^{2}\theta _{\mathrm{t}} }{\partial {F}^{2}}-\frac{\partial \theta _{\mathrm{t}} }{\partial {F}}-\beta ^{2}\theta _{\mathrm{t}} +\left( {1-\varepsilon } \right) {{Q}}_{\mathrm{m}}^*=0, \end{aligned}$$
(7)

and the dimensionless variables are defined as

$$\begin{aligned} \theta _{\mathrm{t}}= & {} \frac{{T}_{\mathrm{t}} -{T}_{\mathrm{b}} }{{T}_{\mathrm{r}} -{T}_{\mathrm{b}} }; \quad \beta =\sqrt{\frac{{GL}^{2}}{{{k}}_{\mathrm{eff}} } }; \quad {{Q}}_{\mathrm{m}}^*=\frac{{{q}}_{\mathrm{m}} {L}^{2}}{{{k}}_{\mathrm{eff}} \left( {{T}_{\mathrm{r}} -{T}_{\mathrm{b}} } \right) }; \quad {F}=\frac{\alpha _{\mathrm{eff}} {t}}{{L}^{2}}; \quad {{Ve}}_{\mathrm{q}} =\sqrt{\frac{\alpha _{\mathrm{eff}} \tau _{\mathrm{q}} }{{L}{ }^2}}; \nonumber \\&{{Ve}}_{\mathrm{T}} =\sqrt{\frac{\alpha _{\mathrm{eff}} \tau _{\mathrm{T}} }{{L}{ }^2}}; \quad {X}=\frac{{x}}{{L}};{\hbox {and}}\,{Y}=\frac{{y}}{{L}}. \end{aligned}$$
(8)

The initial conditions for solving Eq. (7) have been predefined in non-dimensional form as

$$\begin{aligned} {\hbox {at}}\,\,{F}= & {} 0,\,\, \theta _{\mathrm{t}} \left( {{X, Y},\;0} \right) =\theta _{\mathrm {steady}} \left( {{X},\;{Y}} \right) ; \end{aligned}$$
(9.1)
$$\begin{aligned} {\hbox {at }}\,\,{F}= & {} 0, {\partial \theta _{\mathrm{t}} }/{\partial {F}}=0. \end{aligned}$$
(9.2)

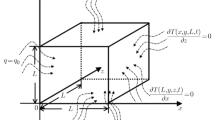
Here, it can be noted that the initial temperature of the physical domain before the therapeutic time can be considered as a steady temperature, and this temperature as a function of spatial coordinates in the direction of heat flow occurred for the metabolic heat generated in living tissues. In the duration of hyperthermia treatment, the skin surface is under therapeutic conditions, and an external heat flux (in the form of both constant and oscillating) has been imposed on the exposed skin surface (at \(x = 0\)). In other boundaries (at \(x = L\), \(y = 0\), and \(y = L\)), zero temperature gradient has been imposed (refer Fig. 1). Apart from the exposed surface at \(x = 0\), other three unexposed boundary surfaces are seated at the inner core section of the tissue. Obviously, there is no chance for convective–conductive heat transfer at these unexposed surfaces. Again due to rigorous microscopic and macroscopic energy exchange inside the human body, a constant temperature (boundary condition of first kind) boundary condition at the inner core may be a mathematical case study but wouldn’t be feasible enough from the practical point of view. Hence, zero thermal gradients (boundary condition of second kind) would be a better choice for the selection of boundary conditions at the inner core sections of tissue due to the line of symmetry for heat conduction, and it also signifies the possibility of maximum or minimum temperature at the boundaries influenced by the external heat flux. Several authors [15, 17, 18, 20] have used the aforesaid boundary conditions at the inner core section of the skin tissue. Mathematically, the non-dimensional forms of boundary conditions for the solution of Eq. (7) are taken as

$$\begin{aligned} {{\hbox {in}}\, X{\hbox {-direction}}}, \left\{ {{\begin{array}{ll} {{X}=0;}&{} \quad {{\partial \theta _{\mathrm{t}} }/{\partial {X}}=-{Q}} \\ {{X}=1 ;}&{}\quad {{\partial \theta _{\mathrm{t}} }/{\partial {X}}=0} \\ \end{array} }} \right. \end{aligned}$$
(10.1)

and

$$\begin{aligned} {{\hbox {in}}\, Y{\hbox {-direction}}} \left\{ {{\begin{array}{ll} {{Y}=0 ;}&{}\quad {{\partial \theta _{\mathrm{t}} }/{\partial {Y}}=0} \\ {{Y}=1 ;}&{}\quad {{\partial \theta _{\mathrm{t}} }/{\partial {Y}}=0} \\ \end{array} }} \right. \end{aligned}$$
(10.2)

where

$$\begin{aligned} {Q}={{qL}}/{{k}({T}_{\mathrm{r}} -{T}_{\mathrm{b}} )}; \quad {q}=\left\{ {{\begin{array}{l} {{{q}}_0 } \\ {{{q}}_0 \sin ({{W}}_{\mathrm{n}} {F}+\phi )} \\ \end{array} }} \right. ; \quad {and}\,\,{{W}}_{\mathrm{n}} ={\omega _{\mathrm{n}} {L}^{2}}/\alpha . \end{aligned}$$
(10.3)

In order to determine the initial temperature in skin tissues, \(\theta _{\mathrm {Steady}} \left( {{X},\;{Y}} \right) \) [as scripted in Eq. (9.1)], the governing equation can be written from Eq. (7) with the independent time as

$$\begin{aligned} \frac{\partial ^{2}\theta _{\mathrm{steady}} }{\partial {X}^{2}}+\frac{\partial ^{2}\theta _{\mathrm{steady}} }{\partial {Y}^{2}}-\beta ^{2}\theta _{\mathrm{steady}} +\left( {1-\varepsilon } \right) {{Q}}_{\mathrm{m}}^*=0. \end{aligned}$$
(11)

Equation (11) is an expression of 2-D steady-state LTNE bioheat model. Before the application of therapeutic exposure, it is assumed that the skin surface is exposed to the surrounding ambience, and obviously the convective heat transfer takes place from the body to the surrounding. Therefore, for the solution, Eq. (11) is subjected to the following non-therapeutic boundary conditions expressed in dimensionless form below:

$$\begin{aligned} {\hbox {along}\, X\hbox {-direction}, }\left\{ {{\begin{array}{lc} {{X}=0 ;}&{}\quad {\frac{\partial \theta _{\mathrm{steady}} }{\partial {X}}={Bi}\left( {\theta _{\mathrm{steady}} -\theta _{\mathrm{c}} } \right) } \\ {{X}=1 ;}&{}\quad {\frac{\partial \theta _{\mathrm{steady}} }{\partial {X}}=0} \\ \end{array} }} \right. \end{aligned}$$
(12.1)

and

$$\begin{aligned} {\hbox {along}\, Y\hbox {-direction}, }\left\{ {{\begin{array}{lc} {{Y}=0 ;}&{}\quad {\frac{\partial \theta _{\mathrm{steady}} }{\partial {Y}}=0} \\ {{Y}=1 ;}&{}\quad {\frac{\partial \theta _{\mathrm{steady}} }{\partial {Y}}=0} \\ \end{array} }} \right. \end{aligned}$$
(12.2)

where

$$\begin{aligned} \theta _{\mathrm{c}} =\frac{\left( {{T}_\infty -{T}_{\mathrm{b}} } \right) }{\left( {{T}_{\mathrm{r}} -{T}_\infty } \right) }, \quad {Bi}=\frac{{hL}}{{k}},\,\text { and }\,\theta _{\mathrm{Steady}} =\frac{\left( {{T}_{\mathrm{steady}} -{T}_{\mathrm{b}} } \right) }{\left( {{T}_{\mathrm{r}} -{T}_{\mathrm{b}} } \right) }. \end{aligned}$$
(12.3)

To solve Eq. (11) with the predefined boundary conditions as mentioned in Eqs. (12.1,2), it has been realized that the solution of \(\theta _{\mathrm{Steady}} \left( {{X},{Y}} \right) \) would be impossible with the help of a classical analytical method due to a similar kind of boundary conditions imposed along the Y-direction [24]. Hence, to get a converged solution, the following approximate relation has been implemented:

$$\begin{aligned} \theta _{\mathrm{Steady}} \left( {{X,Y}} \right) =\mu \left( {X} \right) +\delta \left( {{X,Y}} \right) +\exp \left( {-\beta {X}} \right) +\exp \left( {-\beta {Y}} \right) . \end{aligned}$$
(13)

Equation (11) can be reformed with the implementation of Eq. (13) as

$$\begin{aligned} \frac{\partial ^{2}\mu }{\partial {X}^{2}}-\beta ^{2}\mu +\left( {1-\varepsilon } \right) {{Q}}_{\mathrm{m}}^*=0 \end{aligned}$$
(14.1)

and

$$\begin{aligned} \frac{\partial ^{2}\delta }{\partial {X}^{2}}+\frac{\partial ^{2}\delta }{\partial {Y}^{2}}-\beta ^{2}\delta =0. \end{aligned}$$
(14.2)

The solution of Eq. (14.1) with imposed non-therapeutic boundary conditions [refer Eqs. (12.1) and (12.2)] is obtained in the following:

$$\begin{aligned} \mu \left( {X} \right) ={A}\cosh \left( {\beta {X}} \right) +{B}\sinh \left( {\beta {X}} \right) +\left( {1-\varepsilon } \right) \frac{{{Q}}_{\mathrm{m}}^*}{\beta ^{2}} \end{aligned}$$
(15)

where

$$\begin{aligned} {A}=\frac{\beta \exp \left( {-\beta } \right) -\left( {\frac{{Bi} {{Q}}_{\mathrm{m}}^*}{\beta ^{2}}+\beta } \right) \cosh \left( \beta \right) }{\beta \sinh \left( \beta \right) +{Bi}\cosh \left( \beta \right) }; \quad {B}=\frac{{Bi}}{\beta }\left\{ {{A}+\left( {1-\varepsilon } \right) \frac{{{Q}}_{\mathrm{m}}^*}{\beta ^{2}}} \right\} +1. \end{aligned}$$
(16)

Now for solving Eq. (14.2), the following set of variables has been considered:

$$\begin{aligned} \delta \left( {{X,Y}} \right) =\eta \left( {X} \right) \xi \left( {Y} \right) . \end{aligned}$$
(17)

Applying Eq. (17) in Eq. (14.2), it can be rearranged as follows:

$$\begin{aligned} \frac{\partial ^{2}\eta }{\partial {X}^{2}}-\frac{\beta ^{2}}{2}\eta =0 \end{aligned}$$
(18.1)

and

$$\begin{aligned} \frac{\partial ^{2}\xi }{\partial {Y}^{2}}-\frac{\beta ^{2}}{2}\xi =0. \end{aligned}$$
(18.2)

The solution of Eqs. (18.1,2) can be presented with the boundary conditions mentioned in Eqs. (12.1) and (12.2), respectively, as follows:

$$\begin{aligned} \eta \left( {X} \right) ={D}\cosh \left( {\beta _{\mathrm{k}} {X}} \right) +{E}\sinh \left( {\beta _{\mathrm{k}} {X}} \right) \end{aligned}$$
(19.1)

and

$$\begin{aligned} \xi \left( {Y} \right) ={g}\cosh \left( {\beta _{\mathrm{k}} {Y}} \right) +\sqrt{2}\sinh \left( {\beta _{\mathrm{k}} {Y}} \right) \end{aligned}$$
(19.2)

where

$$\begin{aligned} {D}= & {} -\frac{\sqrt{2} {Bi}\left( {1-\theta _{\mathrm{C}} } \right) \cosh \left( {\beta _{\mathrm{k}} } \right) }{\beta \sinh \left( {\beta _{\mathrm{k}} } \right) +\sqrt{2} {Bi}\cosh \left( {\beta _{\mathrm{k}} } \right) } ; \quad {E}=\frac{\sqrt{2} {Bi}}{\beta }\left[ {{D}+1-\theta _{\mathrm{C}} } \right] ; \nonumber \\&{g}=\sqrt{2}\left\{ {\frac{\exp \left( {-\beta } \right) }{\sinh \left( {\beta _{\mathrm{k}} } \right) }-\coth \left( {\beta _{\mathrm{k}} } \right) } \right\} ;\text { and }\,\beta _{\mathrm{k}} =\beta /{\sqrt{2}}. \end{aligned}$$
(20)

Hence, from Eq. (17),

$$\begin{aligned} \delta \left( {{X,Y}} \right) =\left\{ {{D}\cosh \left( {\beta _{\mathrm{k}} {X}} \right) +{E}\sinh \left( {\beta _{\mathrm{k}} {X}} \right) } \right\} \left\{ {{g}\cosh \left( {\beta _{\mathrm{k}} {Y}} \right) +\sqrt{2}\sinh \left( {\beta _{\mathrm{k}} {Y}} \right) } \right\} . \end{aligned}$$
(21)

Now from Eqs. (13), (15), and (21), one obtains

$$\begin{aligned} \theta _{\mathrm{Steady}} \left( {{X,Y}} \right)= & {} {A}\cosh \left( {\beta {X}} \right) +{B}\sinh \left( {\beta {X}} \right) +\left( {1-\varepsilon } \right) \frac{{{Q}}_{\mathrm{m}}^*}{\beta ^{2}}\nonumber \\&+\left\{ {{D}\cosh \left( {\beta _{\mathrm{k}} {X}} \right) +{E}\sinh \left( {\beta _{\mathrm{k}} {X}} \right) } \right\} \left\{ {{g}\cosh \left( {\beta _{\mathrm{k}} {Y}} \right) +\sqrt{2}\sinh \left( {\beta _{\mathrm{k}} {Y}} \right) } \right\} \nonumber \\&+\exp \left( {-\beta {X}} \right) +\exp \left( {-\beta {Y}} \right) . \end{aligned}$$
(22)

It is to mention that Eq. (22) is a steady-state temperature in tissues before the therapeutic application, and therefore, this temperature can be used as an initial condition to determine the transient temperature response in cancerous tumours during the hyperthermia treatment.

3 Solution methodology by hybrid analytical scheme

We have employed a hybrid analytical scheme to solve Eq. (7) (LTNE DPL model) with the prescribed initial and boundary conditions [refer Eqs. (22), (10.1) and (10.2)]. For this, we have taken the following set of variables:

$$\begin{aligned} \theta _{\mathrm{t}} \left( {{X,Y,F}} \right) =\Theta \left( X \right) +\Psi \left( {{X,Y,F}} \right) . \end{aligned}$$
(23)

Combining Eqs. (7) and (23), we have

$$\begin{aligned} \frac{\partial ^{2}\Theta }{\partial {X}^{2}}-\beta ^{2}\Theta +\left( {1-\varepsilon } \right) {{Q}}_{\mathrm{m}}^*=0 \end{aligned}$$
(24.1)

and

$$\begin{aligned} \frac{\partial ^{2}\Psi }{\partial {X}^{2}}+\frac{\partial ^{2}\Psi }{\partial {Y}^{2}}+{{Ve}}_{\mathrm{T}}^2 \frac{\partial ^{3}\Psi }{\partial {F}\partial {X}^{2}}+{{Ve}}_{\mathrm{T}}^2 \frac{\partial ^{3}\Psi }{\partial {F}\partial {Y}^{2}}-{{Ve}}_{\mathrm{q}}^2 \frac{\partial ^{2}\Psi }{\partial {F}^{2}}-\frac{\partial \Psi }{\partial {F}}-\beta ^{2}\Psi =0. \end{aligned}$$
(24.2)

The solution of Eq. (24.1) can be delineated as

$$\begin{aligned} \Theta \left( X \right) =\frac{{Q}}{\beta } \left[ {\frac{\cosh \left( {\beta {X}} \right) }{\tanh \left( \beta \right) }-\sinh \left( {\beta {X}} \right) } \right] +\left( {1-\varepsilon } \right) \frac{{{Q}}_{\mathrm{m}}^*}{\beta ^{2}}. \end{aligned}$$
(25)

The mathematical expression given in Eq. (24.2) consists of higher-order mixed partial derivatives (third and fourth terms). The idea behind the implementation of finite integral transform (FIT) is to eliminate the higher-order spatial functions, and subsequently, it will be converted into a lower-order partial differential equation with the proper set of eigenfunctions. Some of the notable research papers on the applications of FIT approach are mentioned here: analytical solution of LTE 2-D DPL bioheat modelling [27], exact bending solutions of fully clamped orthotropic rectangular thin plates [28], and hybrid integral transform of LTE Fourier bioheat modelling [29]. The pair of double finite integral transform can be written as follows [30]:

$$\begin{aligned} {\Psi }''\left( {{m,n,F}} \right) =\int \limits _{X=0}^1 {\int \limits _{Y=0}^1 {\Psi \left( {{X,Y,F}} \right) \cos \left( {{m}\pi {X}} \right) \cos \left( {{n}\pi {Y}} \right) } } {{\hbox {d}}X{\hbox {d}}Y}. \end{aligned}$$
(26)

With the help of the inverse theorem, the function \(\Psi \left( {{X,Y,F}} \right) \) can be found as [30],

$$\begin{aligned} \Psi \left( {{X,Y,F}} \right) =4\sum \limits _{m=0}^\infty {\sum \limits _{n=0}^\infty {{\Psi }''\left( {{m,n,F}} \right) \cos \left( {{m}\pi {X}} \right) \cos \left( {{n}\pi {Y}} \right) } }. \end{aligned}$$
(27)

The appointment of the eigenfunction is dependent on the set of boundary conditions. For the Neumann (second kind) boundary condition, the eigenfunction is of the order of ‘cosine form’, whereas for the Dirichlet (first kind) boundary conditions, it is of ‘sine form’. In the present 2-D analysis, the imposed boundary conditions are of Neumann condition (refer Eqs. (10.1) and (10.2)) [30]. Hence, the eigenfunction is used in the order of ‘cosine form’.

Now applying FIT approach to Eq. (24.2) with respect to ‘X’ and keeping ‘Y’ constant, it gives

$$\begin{aligned}&\int \limits _{X=0}^1 {\frac{\partial ^{2}\Psi }{\partial {X}^{2}}\cos \left( {{m}\pi {X}} \right) {{\hbox {d}}X}+} \int \limits _{\mathrm{X=0}}^1 {\frac{\partial ^{2}\Psi }{\partial {Y}^{2}}\cos \left( {{m}\pi {X}} \right) {{\hbox {d}}X}} +{{Ve}}_{\mathrm{T}}^2 \frac{\partial }{\partial {F}}\left[ {\int \limits _{X=0}^1 {\frac{\partial ^{2}\Psi }{\partial {X}^{2}}\cos \left( {{m}\pi {X}} \right) {{\hbox {d}}X}} } \right] \nonumber \\&\quad +{{Ve}}_{\mathrm{T}}^2 \frac{\partial }{\partial {F}}\left[ {\int \limits _{\mathrm{X=0}}^1 {\frac{\partial ^{2}\Psi }{\partial {Y}^{2}}\cos \left( {{m}\pi {X}} \right) {{\hbox {d}}X}} } \right] -{{Ve}}_{\mathrm{q}}^2 \int \limits _{X=0}^1 {\frac{\partial ^{2}\Psi }{\partial {F}^{2}}\cos \left( {{m}\pi {X}} \right) {{\hbox {d}}X}} -\int \limits _{\mathrm{X=0}}^1 {\frac{\partial \Psi }{\partial {F}}\cos \left( {{m}\pi {X}} \right) {{\hbox {d}}X}} \nonumber \\&\quad -\beta ^{2}\int \limits _{X=0}^1 {\Psi \cos \left( {{m}\pi {X}} \right) {{\hbox {d}}X}} =0. \end{aligned}$$
(28)

With some intermediate steps of integral operations, Eq. (28) can be obtained as

$$\begin{aligned}&\frac{\partial ^{2}{\Psi }'\left( {{m,Y,F}} \right) }{\partial {Y}^{2}}-{m}^{2}\pi ^{2} {{Ve}}_{\mathrm{T}}^2 \frac{\partial {\Psi }'\left( {{m,Y,F}} \right) }{\partial {F}}+{{Ve}}_{\mathrm{T}}^2 \frac{\partial ^{3}{\Psi }'\left( {{m,Y,F}} \right) }{\partial {F}\partial {Y}^{2}}-{{Ve}}_{\mathrm{q}}^2 \frac{\partial ^{2}{\Psi }'\left( {{m,Y,F}} \right) }{\partial {F}^{2}} \nonumber \\&\quad -{{Ve}}_{\mathrm{q}}^2 \frac{\partial ^{2}{\Psi }'\left( {{m,Y,F}} \right) }{\partial {F}^{2}}-\frac{\partial {\Psi }'\left( {{m,Y,F}} \right) }{\partial {F}}-\left( {{m}^{2}\pi ^{2}+\beta ^{2}} \right) {\Psi }'\left( {{m,Y,F}} \right) =0 \end{aligned}$$
(29)

where the transformed function \({\Psi }'\left( {{m,Y,F}} \right) \) as referred in Eq. (29) is

$$\begin{aligned} {\Psi }'\left( {{m,Y,F}} \right) =\int \limits _{\mathrm{X=}0}^1 {\Psi \left( {{X,Y,F}} \right) \cos \left( {{m}\pi {X}} \right) {{\hbox {d}}X}}. \end{aligned}$$
(30)

Again applying FIT approach in Eq. (29) with respect to ‘Y’, we obtain

$$\begin{aligned}&\int \limits _{Y=0}^1 {\frac{\partial ^{2}{\Psi }'}{\partial {Y}^{2}}\cos \left( {{n}\pi {Y}} \right) {{\hbox {d}}Y}-{{Ve}}_{\mathrm{T}}^2 {m}^{2}\pi ^{2}\frac{\partial }{\partial {F}}} \int \limits _{Y=0}^1 {{\Psi }'\cos \left( {{n}\pi {Y}} \right) {{\hbox {d}}Y}} +{{Ve}}_{\mathrm{T}}^2 \frac{\partial }{\partial {F}}\int \limits _{Y=0}^1 {\frac{\partial ^{2}{\Psi }'}{\partial {Y}^{2}}\cos \left( {{n}\pi {Y}} \right) {{\hbox {d}}Y}} \nonumber \\&\quad -{Ve}_{\mathrm{q}}^2 \frac{\partial ^{2}}{\partial {F}^{2}}\int \limits _{Y=0}^1 {{\Psi }'\cos \left( {{n}\pi {Y}} \right) {{\hbox {d}}Y}} -\frac{\partial }{\partial {F}}\int \limits _{Y=0}^1 {{\Psi }'\cos \left( {{n}\pi {Y}} \right) {{\hbox {d}}Y}} -\left( {\beta ^{2}+{m}^{2}\pi ^{2}} \right) \int \limits _{Y=0}^1 {{\Psi }'\cos \left( {{n}\pi {Y}} \right) {{\hbox {d}}Y}} =0.\nonumber \\ \end{aligned}$$
(31)

After rearranging, the final form of Eq. (31) can be written as

$$\begin{aligned}&{{Ve}}_{\mathrm{q}}^2 \frac{{d}^{2}{\Psi }''\left( {{m,n,F}} \right) }{{dF}^{2}}+\left( {{m}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +{n}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +1} \right) \frac{{d}{\Psi }''\left( {{m,n,F}} \right) }{{dF}}\nonumber \\&\quad +\left( {m}^{2}\pi ^{2}+{n}^{2}\pi ^{2}+\beta ^{2} \right) {\Psi }''\left( {{m,n,F}} \right) =0 \end{aligned}$$
(32)

where

$$\begin{aligned} {\Psi }''\left( {{m,n,F}} \right) =\int \limits _{Y=0}^1 {{\Psi }'\left( {{m,Y,F}} \right) \cos \left( {{n}\pi {Y}} \right) {{\hbox {d}}Y}}. \end{aligned}$$
(33)

Here, it can be noted that Eq. (24.2) is converted into Eq. (32) with the help of FIT approach. It has been noticed in Eq. (32) that it is a linear second-order homogeneous differential equation, and third-order terms (available in Eq. (24.2)) have completely vanished. Now from Eq. (32), the characteristic equation is determined as

$$\begin{aligned} {{Ve}}_{\mathrm{q}}^2 \Omega ^{2}+\left( {{m}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +{n}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +1} \right) \Omega +\left( {{m}^{2}\pi ^{2}+{n}^{2}\pi ^{2}+\beta ^{2}} \right) =0 \end{aligned}$$
(34)

where

$$\begin{aligned} \Omega =\frac{{d}{\Psi }''\left( {{m,n,F}} \right) }{{dF}}. \end{aligned}$$
(35)

The roots of characteristic equation are obtained from Eq. (34) in the following:

$$\begin{aligned} \Omega =-\frac{\left( {{m}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +{n}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +1} \right) }{2{{Ve}}_{\mathrm{q}}^2 }\pm \sqrt{\frac{\left( {{m}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +{n}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +1} \right) ^{2}-4{{Ve}}_{\mathrm{q}}^2 \left( {{m}^{2}\pi ^{2}+{n}^{2}\pi ^{2}+\beta ^{2}} \right) }{2{{Ve}}_{\mathrm{q}}^2 }}.\nonumber \\ \end{aligned}$$
(36)

For solving Eq. (32), three different distinct roots have appeared from Eq. (36), and three conditions have been used to determine \({\Psi }''\left( {{m,n,F}} \right) \) in the following.

1st condition:\(\left( {{m}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +{n}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +1} \right) ^{2}-4{{Ve}}_{\mathrm{q}}^2 \left( {{m}^{2}\pi ^{2}+{n}^{2}\pi ^{2}+\beta ^{2}} \right) >0\) (for two different real roots).

Based on the standard procedure of solving the second-order linear ordinary differential equation, for two distinct real roots from Eq. (36) and using the first condition, the solution of Eq. (32) is written as [31]:

$$\begin{aligned} {\Psi }''\left( {{m,n,F}} \right) =\exp \left\{ {-\frac{\left( {{m}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +{n}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +1} \right) }{2 {{Ve}}_{\mathrm{q}}^2 }{F}} \right\} \left( {{{C}}_1 \cosh \left( {{JF}} \right) +{{C}}_2 \sinh \left( {{JF}} \right) } \right) \end{aligned}$$
(37)

where

$$\begin{aligned} {J}=\frac{\sqrt{\left( {{m}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +{n}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +1} \right) ^{2}-4{{Ve}}_{\mathrm{q}}^2 \left( {{m}^{2}\pi ^{2}+{n}^{2}\pi ^{2}+\beta ^{2}} \right) }}{2 {{Ve}}_{\mathrm{q}}^2 }. \end{aligned}$$
(38)

Now based on the inverse theorem concept of FIT expressed in Eq. (27), Eq. (37) is redefined as

$$\begin{aligned} \Psi \left( {{X,Y,F}} \right)= & {} 4\sum \limits _{m=0}^\infty \sum \limits _{n=0}^\infty \exp \left\{ {-\frac{\left( {{m}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +{n}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +1} \right) }{2 {{Ve}}_{\mathrm{q}}^2 }{F}} \right\} \left( {{C}}_1 \cosh \left( {{JF}} \right) \right. \nonumber \\&\left. +{{C}}_2 \sinh \left( {{JF}} \right) \right) \cos \left( {{m}\pi {X}} \right) \cos \left( {{n}\pi {Y}} \right) . \end{aligned}$$
(39)

To find out the unknown constants \({C}_{{1}}\) and \({C}_{{2}}\) from Eq. (39), Eq. (9.2) can be used. The shift of variables as depicted in Eq. (23) gives

$$\begin{aligned} {at }{F}=0 ,\quad \frac{\partial \Psi }{\partial {F}}=0. \end{aligned}$$
(40)

Now from Eqs. (39) and (40),

$$\begin{aligned} {{C}}_2 =-\frac{\left( {{m}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +{n}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +1} \right) }{2 {{JVe}}_{\mathrm{q}}^2 }{C}{ }_1. \end{aligned}$$
(41)

Implementing Eq. (41) on Eq. (39) delivers

$$\begin{aligned} \Psi \left( {{X,Y,F}} \right)= & {} 4\sum \limits _{m=0}^\infty {\sum \limits _{n=0}^\infty {\exp \left\{ {-\frac{\left( {{m}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +{n}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +1} \right) }{2 {{Ve}}_{\mathrm{q}}^2 }{F}} \right\} } }\nonumber \\&{{C}}_1 \left[ {\cosh \left( {{JF}} \right) +\left\{ {-\frac{\left( {{m}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +{n}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +1} \right) }{2 {{JVe}}_{\mathrm{q}}^2 }} \right\} \sinh \left( {{JF}} \right) } \right] \nonumber \\&\quad \cos \left( {{m}\pi {X}} \right) \cos \left( {{n}\pi {Y}} \right) . \end{aligned}$$
(42)

For finding out the unknown constant \({C}_{{1}}\) from Eq. (42), the initial condition (see Eq. (9.1)) is applied according to Eq. (23) as

$$\begin{aligned} {at }{F}=0 ,\quad \Psi \left( {{X,Y,0}} \right) =\theta _{\mathrm{Steady}} \left( {{X,Y,0}} \right) -\Theta \left( {X} \right) . \end{aligned}$$
(43)

Implementing Eqs. (22) and (25) on Eq. (43) gives

$$\begin{aligned}&\sum \limits _{m=0}^\infty {\sum \limits _{n=0}^\infty {{{C}}_1 \cos \left( {{m}\pi {X}} \right) \cos \left( {{n}\pi {Y}} \right) ={A}\cosh \left( {\beta {X}} \right) +{B}\sinh \left( {\beta {X}} \right) +\left( {1-\varepsilon } \right) \frac{{{Q}}_{\mathrm{m}}^*}{\beta ^{2}}} }\nonumber \\&\quad +\left\{ {{D}\cosh \left( {\beta _{\mathrm{k}} {X}} \right) +{E}\sinh \left( {\beta _{\mathrm{k}} {X}} \right) } \right\} \left\{ {{g}\cosh \left( {\beta _{\mathrm{k}} {Y}} \right) +\sqrt{2}\sinh \left( {\beta _{\mathrm{k}} {Y}} \right) } \right\} +\exp \left( {-\beta {X}} \right) +\exp \left( {-\beta {Y}} \right) \nonumber \\&\quad -\frac{{Q}}{\beta } \left[ {\frac{\cosh \left( {\beta {X}} \right) }{\tanh \left( \beta \right) }-\sinh \left( {\beta {X}} \right) } \right] -\left( {1-\varepsilon } \right) \frac{{{Q}}_{\mathrm{m}}^*}{\beta ^{2}}. \end{aligned}$$
(44)

To find out the unknown constant \({C}_{{1}}\), the orthogonal property relations [31, 32] can be implemented by multiplying \(\int \limits _{X=0}^1 {\cos \left( {{m}\pi {X}} \right) {{\hbox {d}}X}} \) and \(\int \limits _{Y=0}^1 {\cos \left( {{n}\pi {Y}} \right) {{\hbox {d}}Y}} \)on both sides of Eq. (44), and this gives

$$\begin{aligned}&\sum \limits _{m=0}^\infty \sum \limits _{n=0}^\infty \int \limits _{X=0}^1 {\int \limits _{Y=0}^1 {{{C}}_1 \cos ^{2}\left( {{m}\pi {X}} \right) \cos ^{2}\left( {{n}\pi {Y}} \right) } } {{\hbox {d}}X{\hbox {d}}Y}\nonumber \\&\quad = \int \limits _{X=0}^1 {\int \limits _{Y=0}^1 {\left[ {\left\{ {{A}\cosh \left( {\beta {X}} \right) +{B}\sinh \left( {\beta {X}} \right) +\left( {1-\varepsilon } \right) \frac{{{Q}}_{\mathrm{m}}^*}{\beta ^{2}}} \right\} } \right. } } \nonumber \\&\quad +\left\{ {\left( {{D}\cosh \left( {\beta _{\mathrm{k}} {X}} \right) +{E}\sinh \left( {\beta _{\mathrm{k}} {X}} \right) } \right) \left( {{g}\cosh \left( {\beta _{\mathrm{k}} {Y}} \right) +\sqrt{2}\sinh \left( {\beta _{\mathrm{k}} {Y}} \right) } \right) } \right\} +\exp \left( {-\beta {X}} \right) +\exp \left( {-\beta {Y}} \right) \nonumber \\&\quad \left. {-\frac{{Q}}{\beta }\left\{ {\frac{\cosh \left( {\beta {X}} \right) }{\tanh \left( \beta \right) }-\sinh \left( {\beta {X}} \right) } \right\} -\left( {1-\varepsilon } \right) \frac{{{Q}}_{\mathrm{m}}^*}{\beta ^{2}}} \right] \cos \left( {{m}\pi {X}} \right) \cos \left( {{n}\pi {Y}} \right) {{\hbox {d}}X{\hbox {d}}Y}. \end{aligned}$$
(45)

Now proceeding with the integral operations in Eq. (45), the mathematical expression of \({C}_{{1}}\) can be represented as follows:

$$\begin{aligned} {{C}}_1= & {} \left[ {{D} {g}\frac{\beta _{\mathrm{k}} \sinh \left( {\beta _{\mathrm{k}} } \right) \cos \left( {{m}\pi } \right) }{\beta _{\mathrm{k}}^2 +{m}^{2}\pi ^{2}}\frac{\beta _{\mathrm{k}} \sinh \left( {\beta _{\mathrm{k}} } \right) \cos \left( {{n}\pi } \right) }{\beta _{\mathrm{k}}^2 +{n}^{2}\pi ^{2}}} \right] \nonumber \\&+\left[ {{g} {E}\frac{\beta _{\mathrm{k}} \cosh \left( {\beta _{\mathrm{k}} } \right) \cos \left( {{m}\pi } \right) -\beta _{\mathrm{k}} }{\beta _{\mathrm{k}}^2 +{m}^{2}\pi ^{2}}\frac{\beta _{\mathrm{k}} \sinh \left( {\beta _{\mathrm{k}} } \right) \cos \left( {{n}\pi } \right) }{\beta _{\mathrm{k}}^2 +{n}^{2}\pi ^{2}}} \right] \nonumber \\&+\left[ {\sqrt{2} {D}\frac{\beta _{\mathrm{k}} \sinh \left( {\beta _{\mathrm{k}} } \right) \cos \left( {{m}\pi } \right) }{\beta _{\mathrm{k}}^2 +{m}^{2}\pi ^{2}}\frac{\beta _{\mathrm{k}} \cosh \left( {\beta _{\mathrm{k}} } \right) \cos \left( {{n}\pi } \right) -\beta _{\mathrm{k}} }{\beta _{\mathrm{k}}^2 +{n}^{2}\pi ^{2}}} \right] \nonumber \\&+\left[ {\sqrt{2} {E}\frac{\beta _{\mathrm{k}} \cosh \left( {\beta _{\mathrm{k}} } \right) \cos \left( {{m}\pi } \right) -\beta _{\mathrm{k}} }{\beta _{\mathrm{k}}^2 +{m}^{2}\pi ^{2}}\frac{\beta _{\mathrm{k}} \cosh \left( {\beta _{\mathrm{k}} } \right) \cos \left( {{n}\pi } \right) -\beta _{\mathrm{k}} }{\beta _{\mathrm{k}}^2 +{n}^{2}\pi ^{2}}} \right] . \end{aligned}$$
(46)

Hence, for the 1st condition, the transient thermal response of the skin tissue can be depicted mathematically as

$$\begin{aligned} \theta _{\mathrm{t}} \left( {{X,Y,F}} \right)= & {} \frac{{Q}}{\beta } \left[ {\frac{\cosh \left( {\beta {X}} \right) }{\tanh \left( \beta \right) }-\sinh \left( {\beta {X}} \right) } \right] +\left( {1-\varepsilon } \right) \frac{{{Q}}_{\mathrm{m}}^*}{\beta ^{2}}\nonumber \\&+4\sum \limits _{m=0}^\infty {\sum \limits _{n=0}^\infty {\exp \left\{ {-\frac{\left( {{m}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +{n}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +1} \right) }{2 {{Ve}}_{\mathrm{q}}^2 }{F}} \right\} } }\nonumber \\&{{C}}_1 \left[ {\cosh \left( {{JF}} \right) +\left\{ {-\frac{\left( {{m}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +{n}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +1} \right) }{2 {{JVe}}_{\mathrm{q}}^2 }} \right\} \sinh \left( {{JF}} \right) } \right] \cos \left( {{m}\pi {X}} \right) \cos \left( {{n}\pi {Y}} \right) .\nonumber \\ \end{aligned}$$
(47)

2nd condition:\(\left( {{m}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +{n}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +1} \right) ^{2}-4{{Ve}}_{\mathrm{q}}^2 \left( {{m}^{2}\pi ^{2}+{n}^{2}\pi ^{2}+\beta ^{2}} \right) =0\) (for two repeated roots).

The solution of Eq. (32) (second-order linear ordinary differential equation) for two similar roots is expressed as [31]

$$\begin{aligned} {\Psi }''\left( {{m,n,F}} \right) =\exp \left\{ {-\frac{\left( {{m}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +{n}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +1} \right) }{2 {{Ve}}_{\mathrm{q}}^2 }{F}} \right\} \left( {{{C}}_3 +{{C}}_4 {F}} \right) . \end{aligned}$$
(48)

From the inversion theorem as stated in Eq. (27), Eq. (48) can be represented as follows:

$$\begin{aligned} \Psi \left( {{X,Y,F}} \right) =4\sum \limits _{m=0}^\infty {\sum \limits _{n=0}^\infty {\exp \left\{ {-\frac{\left( {{m}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +{n}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +1} \right) }{2 {{Ve}}_{\mathrm{q}}^2 }{F}} \right\} \left( {{{C}}_3 +{{C}}_4 {F}} \right) \cos \left( {{m}\pi {X}} \right) \cos \left( {{n}\pi {Y}} \right) } }.\nonumber \\ \end{aligned}$$
(49)

Now to find out the unknown constants \({C}_{{3}}\) and \({C}_{{4}}\) from Eq. (49), Eq. (9.2) has been utilized. This provides

$$\begin{aligned} {{C}}_4 =-\frac{\left( {{m}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +{n}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +1} \right) }{2 {{Ve}}_{\mathrm{q}}^2 }{{C}}_3. \end{aligned}$$
(50)

To find out the unknown constant \({C}_{{3}}\), the same procedure has been followed as considered in the first condition (refer Eqs. (43)–(46)), and it has been found that \({{C}}_3 ={{C}}_1 \). Hence, the transient thermal response of the skin tissue can be expressed mathematically for the second condition as

$$\begin{aligned} \theta _{\mathrm{t}} \left( {{X,Y,F}} \right)= & {} \frac{{Q}}{\beta } \left[ {\frac{\cosh \left( {\beta X} \right) }{\tanh \left( \beta \right) }-\sinh \left( {\beta {X}} \right) } \right] +\left( {1-\varepsilon } \right) \frac{{{Q}}_{\mathrm{m}}^*}{\beta ^{2}}\nonumber \\&+4\sum \limits _{m=0}^\infty {\sum \limits _{n=0}^\infty {\exp \left\{ {-\frac{\left( {{m}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +{n}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +1} \right) }{2 {{Ve}}_{\mathrm{q}}^2 }{F}} \right\} } }\nonumber \\&\quad {{C}}_1 \left\{ {1-\left( {-\frac{\left( {{m}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +{n}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +1} \right) }{2 {{Ve}}_{\mathrm{q}}^2 }} \right) {F}} \right\} \cos \left( {{m}\pi {X}} \right) \cos \left( {{n}\pi {Y}} \right) . \end{aligned}$$
(51)

3rd condition:\(\left( {{m}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +{n}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +1} \right) ^{2}-4{{Ve}}_{\mathrm{q}}^2 \left( {{m}^{2}\pi ^{2}+{n}^{2}\pi ^{2}+\beta ^{2}} \right) <0\) (for no real roots).

The solution of Eq. (32) of the second-order linear ordinary differential equation for non-real (imaginary) roots is [31]

$$\begin{aligned} {\Psi }''\left( {{m,n,F}} \right) =\exp \left\{ {-\frac{\left( {{m}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +{n}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +1} \right) }{2 {{Ve}}_{\mathrm{q}}^2 }{F}} \right\} \left( {{{C}}_5 \cos \left( {{JF}} \right) +{{C}}_6 \sin \left( {{JF}} \right) } \right) . \end{aligned}$$
(52)

Combining Eqs. (27) and (52), we obtain,

$$\begin{aligned} \Psi \left( {{X,Y,F}} \right) =4\sum \limits _{m=0}^\infty {\sum \limits _{n=0}^\infty {\exp \left\{ {-\frac{\left( {{m}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +{n}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +1} \right) }{2 {{Ve}}_{\mathrm{q}}^2 }{F}} \right\} \left( {{{C}}_5 \cos \left( {{JF}} \right) +{{C}}_6 \sin \left( {{JF}} \right) } \right) } } \end{aligned}$$
(53)

Again the application of Eqs. (9.2) and (53) yields,

$$\begin{aligned} {{C}}_6 =-\frac{\left( {{m}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +{n}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +1} \right) }{2 {{JVe}}_{\mathrm{q}}^2 }{C}{ }_5. \end{aligned}$$
(54)

In a similar way, by the application of the initial condition (refer Eq. (9.1)) along with the orthogonal property relation as depicted for the first and second conditions, the unknown constant \({C}_{{5}}\) is found exactly similar to \({C}_{{1}}\). Thus,

$$\begin{aligned} {{C}}_5 ={{C}}_1. \end{aligned}$$
(55)

Then, the transient tissue temperature is obtained for the third condition as

$$\begin{aligned} \theta _{\mathrm{t}} \left( {{X,Y,F}} \right)= & {} \frac{{Q}}{\beta } \left[ {\frac{\cosh \left( {\beta {X}} \right) }{\tanh \left( \beta \right) }-\sinh \left( {\beta {X}} \right) } \right] +\left( {1-\varepsilon } \right) \frac{{{Q}}_{\mathrm{m}}^*}{\beta ^{2}}\nonumber \\&+4\sum \limits _{m=0}^\infty {\sum \limits _{n=0}^\infty {\exp \left\{ {-\frac{\left( {{m}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +{n}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +1} \right) }{2 {{Ve}}_{\mathrm{q}}^2 }{F}} \right\} } }\nonumber \\&{{C}}_1 \left[ {\cos \left( {{JF}} \right) +\left\{ {-\frac{\left( {{m}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +{n}^{2}\pi ^{2}{{Ve}}_{\mathrm{T}}^2 +1} \right) }{2 {{JVe}}_{\mathrm{q}}^2 }} \right\} \sin \left( {{JF}} \right) } \right] \cos \left( {{m}\pi {X}} \right) \cos \left( {{n}\pi {Y}} \right) .\nonumber \\ \end{aligned}$$
(56)

It can be highlighted from the combined form of Eqs. (47), (51), and (56) that the solution of the 2-D transient tissue temperature \(\theta _{\mathrm{t}}\) on the basis of LTNE bioheat model is dependent on several therapeutic variables such as blood perfusion parameter (\(\beta \)), two different thermal relaxation time lags (\({Ve}_{{\mathrm{q}}}\) and \({Ve}_{\mathrm{T}})\), porosity factor (\(\varepsilon )\), imposed external heat flux (Q), constant metabolic heat generation rate (\({Q}_{{\mathrm{m}}}\)*), and therapeutic exposure time (F). Now the impact of these dependent variables on the 2-D thermal response in viewpoint of the regional hyperthermia treatment is analysed and the sustainability of such analysis in relation to the thermal therapy is discussed in the following Sections.

Table 1 Constant thermogeometric properties as input variables bestowed in the present hybrid analytical computation
Full size table
Fig. 2
figure 2

a Comparison of present theoretical research work on human body with published experimental research work [34] on pig, and b error distribution of thermal response with time between present theoretical work and published experimental work [34]

Full size image
Fig. 3
figure 3

Isotherms generated in physical domain for constant heat flux of \({{q}}_0 =50\, \hbox {W\,m}^{-2}\) at \(\omega _{\mathrm{b}} =0.1 \,\hbox {s}^{-1}\), \(\varepsilon =0.005\), \({{d}}_{\mathrm{pore}} =0.001\,\hbox {m}\), \({Nu}=1\) for different therapeutic exposures

Full size image
Fig. 4
figure 4

Thermal contour in physical domain of skin tissue for sinusoidal heat flux of \({q}={{q}}_0 \sin (\omega _{\mathrm{n}} {t}+\varphi )\) at \({{q}}_0 =50\,\mathrm{W\,m}^{-2}\),\(\omega _{\mathrm{b}} =0.1 \,\mathrm{s}^{-1}\), \(\varepsilon =0.005\), \({{d}}_{\mathrm{pore}} =0.001\,\mathrm{m}\), \(\omega _{\mathrm{n}} =0.1\,\mathrm{rad\,s}^{-1}\), \(\varphi =0.01 \mathrm{rad}\), and \({Nu}=1\) for different therapeutic exposures

Full size image
Fig. 5
figure 5

Spatiotemporal 3-D surface evolution of thermal response for \({q} = {q}_{{0}}\)

Full size image
Fig. 6
figure 6

Spatiotemporal 3-D surface evolution of thermal response for \({q} = {q}_{{0}}\) sin(\(\omega _{\mathrm{n}}{t}+\varphi \))

Full size image

4 Results and discussion

The most significant disadvantage of chemotherapy are treatment-related side effects. According to National Cancer Institute [33], individuals undergoing chemo frequently report experiencing additional symptoms such as nausea, vomiting, loss of appetite, constipation, or diarrhoea. The most challenging part of chemo patients is to adapt with the induced impacts of toxicity of cytotoxic drugs on human immune system. Thus, from the sustainability point of view, chemotherapy treatment may be a bit questionable. But the research work carried out on hyperthermia indicates that it doesn’t have any report of toxic effects on the patients’ body. Malignant cells are particularly vulnerable by heating. In vivo studies suggest that the temperature in the range of 40–44 \(^{\circ }{\hbox {C}}\) causes selective damage to the tumours [3]. Protein denaturation is the prime molecular event to be occurred in this temperature range led by hyperthermia. The thermal dose to be targeted for a particular malignant tissue inside the human body is based on the heat energy alone. The combined effort of particular thermal dose and the specific predefined therapeutic exposure (heating time) accomplishes the successful hyperthermia therapy.

Particularly, the regional hyperthermia therapy is much more complex than the localized heating due to a wide variation in therapeutic properties of body tissues. Since in regional hyperthermia energy is delivered to the deep-seated diseased tumour in a focused manner, energy is also delivered to the adjacent normal tissues. Under such prevailing conditions, the selective heating of tumours is feasible only when the heat dissipation by blood flow through the normal tissue is higher than the malignant tissue [1, 2]. Preserving all these biological rationales in mind, we have incorporated a large structure of tissue \(100\, {\hbox {mm}}\times 100 \,{\hbox {mm}}\) to justify the aspect of regional hyperthermia. Here, it can be noted from Eq. (7) that \(\tau _{\mathrm{q}}\) and \(\tau _{\mathrm{T}}\) are purely dependent on thermophysical properties of tissue and blood, porosity, and coupling factor. Hence, depending upon the magnitude of these variables, thermal relaxation time lags are determined as output variables, whereas for LTE bioheat models, \(\tau _{\mathrm{q}}\) and \(\tau _{\mathrm{T}}\) values are to be assumed based on the realistic data [4]. The thermophysical properties of human tissue and blood are considered in the present study as [13]: \(\rho _{\mathrm{t}}=\rho _{\mathrm{b}} = 1050 \,{\hbox {kg\,m}}^{-3}\), \({k}_{{\mathrm{t}}} = {k}_{{\mathrm{b}}} = 0.5 {\hbox {Wm}}^{-1}\,^\circ {\hbox {C}}^{-1}\), and \({c}_{{\mathrm{t}}} = {c}_{{\mathrm{b}}} = 3770\, {\hbox {J\,kg}}^{-1}\, ^\circ {\hbox {C}}^{-1}\). Several other input therapeutic variables are given in Table 1. The results have been generated in such a manner that the sustainability of the regional hyperthermia therapy would be rationalized by implementing the two-temperature energy model as proposed by LTNE approach.

The first objective of this research work is to validate the present output with the published results. From the literature survey, it has been already noticed that most of the theoretical 2-D bioheat models are created based on localized hyperthermia not targeting the RHT. Hence, we have focused on the experimental research work. Again the literature review indicates that currently no research work exists on living tissues of human body subjected to thermal therapies. Though a few experimental studies have been conducted on artificial tissue phantom, the thermophysical properties of living tissue and dead tissue (immediately after rigour mortis) are entirely different, and it would not be so logical to compare with these research outputs. In these instances, the temperature measurement has been carried out on tissue phantom. Ware et al. [34] developed a hyperthermia device to provide the thermal dose for cancer surgery, and the experimentation has been conducted on pig by using the ‘pancreatic ductal adenocarcinoma’ (PDAC) model. This research work assessed that a mild hyperthermia therapy with the temperature range of 41–\(46\,^{\circ }{\hbox {C}}\) would be better for eradicating cancerous cells by preserving the healthy cells. As the experimental work on live tissues is being considered to be real-time data, we have plotted the temperature distribution curve with the therapeutic exposure time for the present work and results generated by Ware et al. [34]. Figure 2a indicates that the variation in thermal response of the present 2-D analytical modelling is in line with the experimental output. This validation would also be a useful comparison of the bioheat modelling of flesh products. A minute deviation of temperature distribution in Fig. 2a is observed as the real-time data consist of many nonlinearities which is very difficult to capture in the theoretical investigation. For the validation purpose, the therapeutic variables with constant heat flux are considered as \({{d}}_{\mathrm{pore}} =0.001\,{m}\), \(\omega _{\mathrm{b}} =0.15\, {s}^{-1}\), \(\varepsilon =0.005\), \({Bi}=0.1\), \({Nu}=0.05\) at the location of \({x}=0.05\,{\mathrm{m}}\) and \({y}=0.05\,{\mathrm{m}}\). Based on these input variables, the thermal relaxation time lags and coupling factor have been found from Eq. (6) as: \(\tau _{\mathrm{q}} =\tau _{\mathrm{T}} =12.38{s}\) and \({G}=965.5\, \hbox {W} {m}^{-3\,o}\hbox {C}^{-1}\). In Fig. 2b, the error distribution of tissue temperature between the present and the published work [34] is displayed, and it has been noted that the maximum temperature deviation is 2.26%. However, the present work emphasized the therapeutic heating exposure of longer time duration with both the constant and sinusoidal heating for the lower peak temperature of entire surgery as well as better assurance of less damage of healthy tissues inside the human body. Hence, from the graphical representation depicted in Fig. 2, it can be highlighted that the present analytical model is best suited with the real-time analysis, and the correctness of the in-house computer programming (carried out in FORTRAN language) is also well justified keeping the experimental work [34] as the benchmark.

We have created 3-D surface isotherms for different therapeutic exposure times for both the constant and sinusoidal heat flux. This observation has been studied to understand the two-dimensional temperature field produced during RHT. In Fig. 3 for maintaining a constant heat flux at the therapeutic surface, it can be noted that the temperature gradually drops along the inner core of the malignant tissue. Obviously, a higher dimension impact is available due to the large size of the tissue as heat propagates in both x- and y-directions. Also it has been noticed that the temperature profile of the entire tissue has been decreased with the increase in therapeutic heating time (tends to be stabilized). It is clear that thermal contour lines are perpendicular to the boundaries at \({x=L} \left( {0\le {y}\le {L}} \right) \), \( {y}=0 \;\left( {0\le {x}\le {L}} \right) \), and \( {y=L} \;\left( {0\le {x}\le {L}} \right) \). From the mathematical and physical points of view, this trend shows the correctness of the present model because all the boundary conditions at their boundaries satisfy zero temperature gradient except at the therapeutic surface boundary. At \({x=0}\;\left( {0\le {y}\le {L}} \right) \), the therapeutic boundary condition (nonzero temperature gradient) has been imposed, and it shows that the curves incline at the boundary. For the results depicted in Fig. 3, the input therapeutic variables are taken as \({{q}}_0 =50\,\hbox {W}\,\hbox {m}^{-2} \), \(\omega _{\mathrm{b}} =0.1\,\hbox {s}^{-1} \), \(\varepsilon =0.005 \), \({{d}}_{\mathrm{pore}} =0.001\,\hbox {m} \), and \({Nu}=1 \). Based on these variables, the thermal relaxation times and coupling factor are determined (based on Eq. (6)) as \(\tau _{\mathrm{q}} =1.897{s}\), \(\tau _{\mathrm{T}} =1.897\) s, and \({G}=10376.99 {\hbox {W\,m}}^{-3\,{\circ }}{\hbox {C}}^{-1}\).

In Fig. 4 for the oscillating heat flux, the same physical phenomena as illustrated in Fig. 3 are examined, and a slight variation in the contour curves is obtained. Finally, based on the boundary conditions used for the present work, it can be highlighted that the isotherms are correctly generated in the x- and y-directions of the physical domain of a malignant tissue. The fundamental objective behind implementing oscillating (sinusoidal) heat flux is to ensure the safety of healthy tissues inside the human body. Due of waveform heating, a specific portion of the tissue is not exposed to fixed temperature for a certain period. If temperature oscillates, then chances of development of thermal injuries inside the human body reduces. This study may also help to validate the present mathematical model. For the research output given in Fig. 4, the input therapeutic variables are used as \({{q}}_0 =50\,{\hbox {W\,m}}^{-2} \), \(\omega _{\mathrm{b}} =0.1\,\hbox {s}^{-1} \), \(\varepsilon =0.005 \), \({{d}}_{\mathrm{pore}} =0.001\,\hbox {m} \), \({Nu}=1 \), \(\omega _{\mathrm{n}} =0.1\,{\hbox {rad}}\,{\hbox {s}}^{-1} \), and \(\varphi =0.01\,{\hbox {rad}} \). Based on these variables, the thermal relaxation times, and the coupling factor are evaluated (based on Eq. (6)) as \(\tau _{\mathrm{q}} =1.897\,\hbox {s} \), \(\tau _{\mathrm{T}} =1.897\,\hbox {s} \), and \({G}=10376.99\,{\hbox {W\,m}}^{-3}\,^\circ {\hbox {C}}^{-1}\). From Figs. 3 and 4, it can also be highlighted that for the prediction of temperature response under the regional hyperthermia treatment, the present 2-D model will have an ability to determine the temperature response correctly in comparison with the existing 1-D model [25]. Finally, as the present 2-D model has predicted an accurate result for the temperature, it can be used in the practical implementation for knowing the actual heat propagation in living tissues with a predefined external heat source to provide the proper treatment protocol in destructing malignant tumours.

The final objective of this research work is to analyse the spatiotemporal behaviour of thermal response in the physical domain for both constant and sinusoidal heat flux imposed on the skin surface. For this study, input therapeutic variables are \({{d}}_{\mathrm{pore}} =0.001\,\hbox {m} \), \(\omega _{\mathrm{b}} =0.15\,\hbox {s}^{-1} \),  \({Bi}=0.1 \), \({Nu}=0.05 \), and \(\varepsilon =0.005 \) (for other process variables, refer Table 1). Figure 5a depicts the temperature distribution for the constant heat flux along the x-direction at \(y = 0.05\) m, and Fig. 5b represents the thermal response along the y-direction at \(x = 0.05\) m. The temperature range has been found as 38–44 \(^{\circ }\mathrm{C}\) and 40–41.\(4\,^{\circ }{\hbox {C}}\) along x-direction and y-direction, respectively. In both cases, thermal oscillations have been observed, and prime causes is implementation of LTNE approach which is the modified version of DPL bioheat model. As two thermal relaxation time lags are involved, it is evident to produce hyperbolic characteristics of thermal behaviour [4]. From such spatiotemporal investigation of thermal behaviour, it has been noticed that temperature along y-axis deviates around 1.8–2\(\,^{\circ }{\hbox {C}}\) in the physical domain of skin tissue, and this can suggest that the consideration of two-dimensional modelling is essential rather than 1-D analysis for more accurate and appropriate analysis. The magnitude of temperature deviation is higher along x-direction (\(6\,^{\circ }{\hbox {C}}\)) due to the involvement of external heating along this direction. In Fig. 6 the same phenomenon is observed for sinusoidal heat flux where the oscillating parameters are taken as \(\omega _{\mathrm{n}} =0.1\,\hbox {rad}\,{s}^{-1}\)and \(\varphi =0.5\,\hbox {rad}\). It has been noticed that the nature of the temperature field remains same with a longer therapeutic exposure due to the impingement of the sinusoidal nature of the heat flux on the boundary surface as compared to the constant heat flux. Such oscillating kind of therapeutic heating might be preferable for a prolonged period of thermal therapy with the moderate temperature range as exposed in the present work, and it will help to reduce the possibility of collateral damage of skin tissue induced by thermal injury. The coupling factor and the relaxation times in the present analysis with both the constant and oscillating heat flux have been determined as \(\tau _{\mathrm{q}} =\tau _{\mathrm{T}} =18.48\,\hbox {s} \) and \({G}=1065.5\,\hbox {W\,m}^{-3{{\circ }}}{\mathrm{C}}^{-1} \).

5 Conclusions

The concluding statements can be summarized based on the research output as follows:

  1. (a)

    It has been attempted to establish the exact analytical solution of the temperature distribution of LTNE DPL bioheat model in the bi-dimensional form subjected to the regional hyperthermia therapy. The implementation of the present hybrid scheme comprising ‘shift of variables’ and ‘finite integral transform’ has been well justified and validated.

  2. (b)

    The concept of implementing the porous media approach in the skin tissue is more realistic due to its highly non-homogeneous structure, and this work completes the successful application with the spatially dependent initial condition as suggested by the medical science. It has been noticed in the present research work that the larger the blood vessels (pore diameter), the higher the impact of LTNE modelling. The higher the porosity, the better the DPL waveform has been found. Such aspects actually glorify the acceptance of the LTNE modelling over the LTE modelling in the arena of biological heat transfer.

  3. (c)

    We have proposed the concept of a medium range of tissue heating 38–44 \(^{\circ }{\hbox {C}}\) with the prolonged treatment time to avoid internal injury (tissue trauma). In case of the regional hyperthermia, first of all the size of the affected tissue is very large, and the location is interior of the body as compared to the localized hyperthermia [3]. So the external energy to be delivered to a particular organ has to pass through several healthy (non-malignant) tissues. To avoid any possibility of tissue trauma or thermal damage, we strongly recommend maintaining the temperature range of 38–44 \(^{\circ }{\hbox {C}}\) for the regional hyperthermia therapy. The results indicate that the larger skin tissue would be preferred for the LTNE model. The sinusoidal heat flux is proved to be a better alternative than the constant heat flux when a longer therapeutic exposure is necessary to kill the cancer cells completely.