A partition statistic for partitions with even parts distinct

Abstract

Andrews, Hirschhorn, and Sellers studied the partition function ped(n) which enumerates the number of partitions of n with even parts distinct, and obtained a number of interesting congruences. This paper aims to introduce a partition statistic to investigate the partition function ped(n). We give combinatorial interpretations for some properties of ped(n) including the infinite families of congruences given by Andrews et al.

1 Introduction

A partition $\lambda$ of a positive integer n is a finite non-increasing sequence of positive integers $\lambda =(\lambda _1,\ldots , \lambda _l)$ such that $|\lambda |=\sum _{i=1}^{l}\lambda _i=n$. The Ferrers graph of a partition $\lambda$ is a set of coordinates in the bottom right quadrant of the plane where the i-th row contains $\lambda _i$ dots. We denote by $\lambda '$ the conjugate of $\lambda$, which is the partition whose graph is obtained by reflecting the Ferrers graph of $\lambda$ about the main diagonal. For example, we give $\lambda =(4,4,2,2,1)$ and its conjugate partition $\lambda '=(5,4,2,2)$ in Fig. 1.

Fig. 1

Ferrers graph of partitions $\lambda =(4,4,2,2,1)$ and $\lambda '=(5,4,2,2)$

Let p(n) denote the ordinary partition function. The partition statistic crank defined by Andrews and Garvan [2, 6] can be used to provide combinatorial interpretations for Ramanujan’s famous congruences

$$\begin{aligned} p(5n+4)&\equiv 0 \pmod {5}, \nonumber \\ p(7n+5)&\equiv 0 \pmod {7},\nonumber \\ p(11n+6)&\equiv 0\pmod {11}. \end{aligned}$$

(1.1)

The crank of a partition $\lambda \ne (1)$ is defined as follows:

$$\begin{aligned} c(\lambda )=\left\{ \begin{array}{ll} \lambda _1,\ \ if\ \ n_1(\lambda )=0,\\ \mu (\lambda )-n_1(\lambda ), \ \ if \ n_1(\lambda )>0, \end{array}\right. \end{aligned}$$

where $n_1(\lambda )$ denotes the number of parts equal to one in $\lambda$ and $\mu (\lambda )$ denotes the number of parts in $\lambda$ larger than $n_1(\lambda )$. Let M(m, n) enumerate partitions of n with crank m. It should be pointed out that when $\lambda =(1)$,

$$\begin{aligned} M(0,1)=-1, \ \ M(-1,1)=M(1,1)=1. \end{aligned}$$

Andrews and Garvan [2, 6] established the generating function of M(m, n) as given by

$$\begin{aligned} \sum _{n=0}^{\infty }\sum _{m=-\infty }^{\infty } M(m,n)z^mq^n =\frac{(q;q)_\infty }{(zq;q)_\infty (z^{-1}q;q)_\infty }. \end{aligned}$$

(1.2)

Here and throughout this paper, $(a;q)_\infty$ stands for the q-shifted factorial

$$\begin{aligned} (a;q)_{\infty }=\prod _{n=1}^{\infty }(1-aq^{n-1}),\,\, |q|<1, \end{aligned}$$

and for any positive integer k,

$$\begin{aligned} f_k=(q^k;q^k)_{\infty }. \end{aligned}$$

Let M(m, t, n) denote the number of partitions of n with crank congruent to m modulo t. In 1990, Garvan [7] presented a graceful refinement of the congruence (1.1)

$$\begin{aligned} M(m,2,5n+4)\equiv 0 \pmod {5},\ \ m=0,1, \end{aligned}$$

together with the combinatorial interpretation

$$\begin{aligned} M(m+2k,10,5n+4)=\frac{M(m,2,5n+4)}{5},\ \ 0\le k\le 4,m=0,1. \end{aligned}$$

Let ped(n) be the function that enumerates partitions of n with even parts distinct. Obviously,

$$\begin{aligned} \sum _{n=0}^{\infty }ped(n)q^n =\frac{(-q^2;q^2)_{\infty }}{(q;q^2)_{\infty }}. \end{aligned}$$

The sequence ${ped(n)}_{n\ge 0}$ is well known and can be seen in [11, A001935], as well as other combinatorial interpretations. In 2010, Andrews, Hirschhorn, and Sellers [3] proved the following congruences.

Theorem 1.1

For $\alpha ,n \ge 0$,

$$\begin{aligned} ped\left( 3^{2\alpha +2}n+\frac{11\cdot 3^{2\alpha +1}-1}{8}\right)&\equiv 0\pmod {2},\\ ped\left( 3^{2\alpha +2}n+\frac{19\cdot 3^{2\alpha +1}-1}{8}\right)&\equiv 0\pmod {2}. \end{aligned}$$

Theorem 1.2

For $n \ge 0$,

$$\begin{aligned} ped(9n+4)&\equiv 0\pmod {4},\end{aligned}$$

(1.3)

$$\begin{aligned} ped(9n+7)&\equiv 0\pmod {12}. \end{aligned}$$

(1.4)

In 2017, Merca [9] provided a simple criterion for deciding the parity of ped(n).

Theorem 1.3

The number of partitions of n with distinct even parts is odd if and only if n is a triangular number.

In this paper, we aim at introducing a partition statistic which we call ped-crank to study the partition function ped(n). Let $M_{ped}(m,n)$ denote the number of partitions of n with even parts distinct with ped-crank m, and let

$$\begin{aligned} M_{ped}(m,t,n)=\sum _{k\equiv m\pmod {t}} M_{ped}(k,n). \end{aligned}$$

(1.5)

The main results of this paper are summarized below.

Theorem 1.4

For $\alpha ,n \ge 0$,

$$\begin{aligned} M_{ped}\left( 0,6,3^{2\alpha +2}n+\frac{11\cdot 3^{2\alpha +1}-1}{8}\right)&= M_{ped}\left( 3,6,3^{2\alpha +2}n+\frac{11\cdot 3^{2\alpha +1}-1}{8}\right) ,\\ M_{ped}\left( 1,6,3^{2\alpha +2}n+\frac{11\cdot 3^{2\alpha +1}-1}{8}\right)&= M_{ped}\left( 2,6,3^{2\alpha +2}n+\frac{11\cdot 3^{2\alpha +1}-1}{8}\right) ,\\ M_{ped}\left( 0,6,3^{2\alpha +2}n+\frac{19\cdot 3^{2\alpha +1}-1}{8}\right)&= M_{ped}\left( 3,6,3^{2\alpha +2}n+\frac{19\cdot 3^{2\alpha +1}-1}{8}\right) ,\\ M_{ped}\left( 1,6,3^{2\alpha +2}n+\frac{19\cdot 3^{2\alpha +1}-1}{8}\right)&= M_{ped}\left( 2,6,3^{2\alpha +2}n+\frac{19\cdot 3^{2\alpha +1}-1}{8}\right) . \end{aligned}$$

Any of the following three corollaries deduced from Theorem 1.4 provides a combinatorial interpretation or a refinement of Theorem 1.1. When $\alpha =0$, combining Corollary 1.5 and Corollary 1.6 refines (1.3). Meanwhile, Corollary 1.7 combinatorially interprets (1.3).

Corollary 1.5

For $m=0,1,2$ and $\alpha ,n \ge 0$,

$$\begin{aligned} M_{ped}\left( m,6,3^{2\alpha +2}n+\frac{11\cdot 3^{2\alpha +1}-1}{8}\right)&=\frac{M_{ped}\left( m,3,3^{2\alpha +2}n+\frac{11\cdot 3^{2\alpha +1}-1}{8}\right) }{2},\\ M_{ped}\left( m,6,3^{2\alpha +2}n+\frac{19\cdot 3^{2\alpha +1}-1}{8}\right)&=\frac{M_{ped}\left( m,3,3^{2\alpha +2}n+\frac{19\cdot 3^{2\alpha +1}-1}{8}\right) }{2}. \end{aligned}$$

Corollary 1.6

For $\alpha ,n \ge 0$,

$$\begin{aligned} M_{ped}\left( 3,12,3^{2\alpha +2}n+\frac{11\cdot 3^{2\alpha +1}-1}{8}\right) =\,&\frac{M_{ped}\left( 0,3,3^{2\alpha +2}n+\frac{11\cdot 3^{2\alpha +1}-1}{8}\right) }{4},\\ M_{ped}\left( 3,12,3^{2\alpha +2}n+\frac{19\cdot 3^{2\alpha +1}-1}{8}\right) =\,&\frac{M_{ped}\left( 0,3,3^{2\alpha +2}n+\frac{19\cdot 3^{2\alpha +1}-1}{8}\right) }{4}. \end{aligned}$$

Corollary 1.7

For $\alpha ,n \ge 0$,

$$\begin{aligned} M_{ped}\left( 1,4,3^{2\alpha +2}n+\frac{11\cdot 3^{2\alpha +1}-1}{8}\right)&=\frac{ped\left( 3^{2\alpha +2}n+\frac{11\cdot 3^{2\alpha +1}-1}{8}\right) }{4}, \\ M_{ped}\left( 1,4,3^{2\alpha +2}n+\frac{19\cdot 3^{2\alpha +1}-1}{8}\right)&=\frac{ped\left( 3^{2\alpha +2}n+\frac{19\cdot 3^{2\alpha +1}-1}{8}\right) }{4}. \end{aligned}$$

Theorem 1.8

If n cannot be written as a sum of a triangular number and a square of even integer, we have

$$\begin{aligned} M_{ped}(0,4,n)&=M_{ped}(2,4,n). \end{aligned}$$

Moreover, $M_{ped}(0,n)$ is odd if and only if n is a triangular number.

Theorem 1.9

For $m=0,1,2,3,4,5$ and $n\ge 0$,

$$\begin{aligned} M_{ped}(m,6,9n+7)=\,&\frac{ped(9n+7)}{6}, \nonumber \\ M_{ped}(3,12,9n+7) =\,&\frac{ped(9n+7)}{12}. \end{aligned}$$

(1.6)

It is worth mentioning that Theorem 1.8 not only combinatorially interprets but also refines Theorem 1.3, and (1.6) provides a combinatorial interpretation for (1.4).

2 Definition of the ped-crank

In this section, we shall define the ped-crank of partitions with even parts distinct based on Glaisher’s bijection and a modified version $\varphi$ of the Wright map established by Seo and Yee [10].

We first give a quick overview of Glaisher’s bijection and the Frobenius symbol. Let $D_n$ denote the set of distinct partitions, and let $O_n$ denote the set of odd partitions of n respectively. Glaisher’s bijection $\phi$: $O_n\rightarrow D_n$ is defined as follows. Let $\lambda =(1^{m_1}3^{m_3}\ldots )\in O_n$ be an odd partition. For every odd i, let $\phi (\lambda )$ contain part $i\cdot 2^r$, if and only if the integer $m_i$ written in binary has 1 at the r-th position. In the other direction, let $\psi$: $D_n\rightarrow O_n$ be defined by an iterative procedure. Start with $\lambda =(\lambda _1,\lambda _2,\ldots )\in D_n$. Substitute every even part $\lambda _i$ with two parts $\lambda _i/2$. Repeat until the resulting partition has no even parts.

The Frobenius symbol of n is a two-rowed array [1, 14]

$$\begin{aligned} F=\left( \begin{array}{ccccc} \alpha _1 &{} \quad \alpha _2 &{} \cdots &{} \alpha _\ell \\ \beta _1 &{} \quad \beta _2 &{} \cdots &{} \beta _\ell \end{array}\right) , \end{aligned}$$

where $\alpha _1>\alpha _2>\ldots >\alpha _{\ell }\ge 0$, $\beta _1>\beta _2>\ldots >\beta _{\ell }\ge 0$ and $n=|\alpha |+|\beta |+\ell$. If we express an ordinary partition by Ferrers graph, it is easy to see that $\alpha _i$ form rows to the right of the diagonal and $\beta _i$ form columns below the diagonal. Thus the Frobenius symbol is another representation of an ordinary partition. For instance, the Frobenius symbol for (8, 7, 4, 3, 1) is

$$\begin{aligned} \left( \begin{array}{ccccc} 7 &{}\quad 5 &{} \quad 1 \\ 4 &{}\quad 2 &{}\quad 1 \end{array}\right) . \end{aligned}$$

Giving a real number c, we define $c\lambda$ as the partition whose parts are c times each part of $\lambda$. For example, let $\lambda =(4,2,2)$. We have $4\lambda =(16,8,8)$ and $\frac{1}{2}\lambda =(2,1,1)$. Suppose $\mu$ and $\nu$ are two partitions. Let $\mu \cup \nu$ denote the partition consisting of all the parts of $\mu$ and $\nu$. The definition of ped-crank is given based on the following theorem.

Theorem 2.1

For integer $k_1\ge -1$, $k_2\ge 1$, there is a bijection $\Delta$ between the set of partitions of n with even parts distinct and the set of vector partitions $(\alpha ,\beta ,\gamma )$ with $|\alpha |+|\beta |+|\gamma |$ equal to n. Here $\alpha$ is an even partition, $\beta$ is a partition of the form $(4k_1+1,\ldots ,9,5,1)$ or $(4k_2-1,\ldots ,11,7,3)$ and $\gamma$ is a distinct even partition.

Proof

The bijection $\Delta$ can be decomposed into six weight preserving steps.

• Step 1. $\lambda \rightarrow (\omega ,\gamma )$: Start with a partition $\lambda$ of n with even parts distinct. Split $\lambda$ into a pair of partitions $(\omega ,\gamma )$ according to the parts odd or even. It is clear that $\omega$ is an odd partition and $\gamma$ is a distinct even partition.

• Step 2. $(\omega ,\gamma )\rightarrow (\xi ,\gamma )$: By Glaisher’s bijection, let $\phi (\omega )=\xi$. One can see that $\xi$ is a distinct partition.

• Step 3. $(\xi ,\gamma )\rightarrow (\mu ^1,\mu ^2,\pi ,\gamma )$: Divide $\xi$ into a triple of partitions $(\mu ^1,\mu ^2,\pi )$ according to the remainder of the parts mod 4. Here $\mu ^1\ (\mu ^2)$ consist of all the parts congruent to 1(3) mod 4 and $\pi$ consists of all the even parts of $\xi$.

• Step 4. $(\mu ^1,\mu ^2,\pi ,\gamma )\rightarrow (\mu ^1,\mu ^2,\zeta ,\gamma )$: Let $\zeta =2\psi (\frac{1}{2}\pi )$ by applying Glaisher’s bijection. Since $\frac{1}{2}\pi$ is a distinct partition, we can say that $\zeta$ is a partition with all parts congruent to 2 mod 4.

• Step 5. $(\mu ^1,\mu ^2,\zeta ,\gamma )\rightarrow (\eta ,\beta ,\zeta ,\gamma )$: Write $\mu ^1$ and $\mu ^2$ as

  $$\begin{aligned} \mu ^1&=(4a_1+1,4a_2+1,\ldots ,4a_{s+m}+1),\\ \mu ^2&=(4b_1+3,4b_2+3,\ldots ,4b_{s}+3), \end{aligned}$$

  where $a_1>a_2>\cdots >a_{s+m}\ge 0$ and $b_1>b_2>\cdots >b_s\ge 0$.

  • Case 1. $m\ge 0$. Using the bijection $\varphi$ established by Seo and Yee [10], a Frobenius symbol

    $$\begin{aligned} \mu =\left( \begin{array}{llll} a_{1+m} &{}\quad a_{2+m} &{}\cdots &{}a_{s+m} \\ b_1 &{} \quad b_2 &{} \cdots &{} b_s \end{array}\right) \end{aligned}$$

    and a partition $\nu =(a_1-m+1,a_2-m+2,\ldots ,a_m)$ can be constructed. Let $\varphi (\mu ^1,\mu ^2)=(\eta ,\beta )$, where $\eta =4(\mu \cup \nu )$ and $\beta =(4(m-1)+1,4(m-2)+1,\ldots ,5,1)$.

  • Case 2. $m<0$. Correspondingly, a Frobenius symbol

    $$\begin{aligned} \mu =\left( \begin{array}{llll} b_{1-m} &{}\quad b_{2-m} &{} \cdots &{} b_s \\ a_{1} &{} \quad a_{2} &{}\cdots &{}a_{s+m} \end{array}\right) \end{aligned}$$

    and a partition $\nu =(b_1+m+1,b_2+m+2,\ldots ,b_{-m})$ can be constructed. Let $\varphi (\mu ^1,\mu ^2)=(\eta ,\beta )$, where $\eta =4(\mu \cup \nu )'$ and $\beta =(4(-m-1)+3,4(-m-2)+3,\ldots ,7,3)$.

• Step 6. $(\eta ,\beta ,\zeta ,\gamma )\rightarrow (\alpha ,\beta ,\gamma )$: Ultimately, let $\alpha =\eta \cup \zeta$ and define $\Delta (\lambda )=(\alpha ,\beta ,\gamma )$.

Furthermore, one sees that the above construction can be reversed. This completes the proof. $\square$

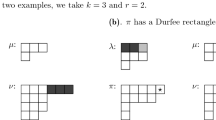
An example of the bijection $\Delta$ is given below.

Example 2.2

[4]

$$\begin{aligned} \lambda =(30,25,18,13,11,9,6,&5,5,5,5,3,3,3,3,3,3,3,1,1,1)\\&\Updownarrow _{\text {Step 1.}} \\ (\omega ,\gamma )=\big ((25,13,11,9,5,5,5,5,&3,3,3,3,3,3,3,1,1,1),(30,18,6)\big )\\&\Updownarrow _{\text {Step 2.}} \\ (\xi ,\gamma )=\big ((25,20,13,12,&11,9,6,3,2,1),(30,18,6)\big )\\&\Updownarrow _{\text {Step 3.}} \\ (\mu ^1,\mu ^2,\pi ,\gamma )=\big ((25,13,9,1),&(11,3),(20,12,6,2),(30,18,6)\big )\\&\Updownarrow _{\text {Step 4.}} \\ (\mu ^1,\mu ^2,\zeta ,\gamma )=\big ((25,13,9,1),(11&,3),(10,10,6,6,6,2),(30,18,6)\big )\\&\Updownarrow _{\text {Step 5.}} \\ (\eta ,\beta ,\zeta ,\gamma )=\big ((20,12,12,8,4),(&5,1),(10,10,6,6,6,2),(30,18,6)\big )\\&\Updownarrow _{\text {Step 6.}} \\ (\alpha ,\beta ,\gamma )=\big ((20,12,12,10,10,&8,6,6,6,4,2),(5,1),(30,18,6)\big )\\ \end{aligned}$$

Now we are ready to give the definition of the ped-crank of a partition with even parts distinct under the bijection $\Delta$.

Definition 2.3

Let $\lambda$ be a partition with even parts distinct and $\Delta (\lambda )=(\alpha , \beta , \gamma )$. The ped-crank of $\lambda$, denoted by $c_{ped}(\lambda )$, is defined as the crank of $\frac{1}{2}\alpha$.

3 Generating function of $M_{ped}(m,n)$

This section focuses on the generating function of $M_{ped}(m,n)$.

According to the bijection $\Delta$, the generating function of $\beta$ can be derived by using Jacobi’s triple product identity.

$$\begin{aligned} \sum _{n=0}^{\infty }q^{4{n \atopwithdelims ()2}+n}+ \sum _{n=-\infty }^{-1}q^{4{n \atopwithdelims ()2}+n} =(-q;q^4)_\infty (-q^3;q^4)_\infty (q^4;q^4)_\infty . \end{aligned}$$

Moreover, it is trivial that the generating function of $\gamma$ is

$$\begin{aligned} (-q^2;q^2)_{\infty }. \end{aligned}$$

Since the ped-crank only relies on the even partition $\alpha$, by (1.2), the generating function of $M_{ped}(m,n)$ can be given as

(3.1)

By considering the transformation that interchanges z and $z^{-1}$ in (3.1), we have

$$\begin{aligned} M_{ped}(m,n)=M_{ped}(-m,n). \end{aligned}$$

Thus, for any positive integer t,

$$\begin{aligned} M_{ped}(m,t,n)=M_{ped}(-m,t,n). \end{aligned}$$

In other words,

$$\begin{aligned} M_{ped}(m,t,n)=M_{ped}(t-m,t,n). \end{aligned}$$

(3.2)

4 Preliminaries

In this section we present some results that will be used in Section 5.

Lemma 4.1

$$\begin{aligned} (-q;-q)_\infty =\frac{f^3_2}{f_1f_4}. \end{aligned}$$

Proof

Replacing q by $-q$ in $(q;q)_\infty$, we have

$$\begin{aligned} (-q;-q)_\infty =\,&(-q;q^2)_\infty (q^2;q^2)_\infty \\ = \,&\frac{(-q;q)_\infty (q^2;q^2)_\infty }{(-q^2;q^2)_\infty }\\ =\,&\frac{(q;q)_\infty (-q;q)_\infty (q^2;q^2)^2_\infty }{(q;q)_\infty (-q^2;q^2)_\infty (q^2;q^2)_\infty }\\ =\,&\frac{(q^2;q^2)^3_\infty }{(q;q)_\infty (q^4;q^4)_\infty }. \end{aligned}$$

$\square$

Lemma 4.2

( [4, Entry 22, p. 36])

$$\begin{aligned} \phi (q)=\sum _{n=-\infty }^{\infty }q^{n^2} =\frac{f_2^5}{f_1^2f_4^2}. \end{aligned}$$

Replacing q by $-q$ in the above equation, we get

$$\begin{aligned} \phi (-q)=2\sum _{n=0}^{\infty }(-1)^nq^{n^2}-1=\frac{f_1^2}{f_2}. \end{aligned}$$

Lemma 4.3

( [4, p. 49])

$$\begin{aligned} \psi (q)=\sum _{n=0}^{\infty }q^{n+1 \atopwithdelims ()2}=\frac{f_2^2}{f_1}=\frac{f_6f_9^2}{f_3f_{18}}+q\frac{f_{18}^2}{f_9}. \end{aligned}$$

Theorem 4.4

( [5, Lemma 2.2])

$$\begin{aligned} \frac{1}{\varphi (-q)}&=\frac{\varphi ^3(-q^9)}{\varphi ^4(-q^3)}\left( 1+2q\omega (q^3)+4q^2\omega ^2(q^3)\right) ,\\ \frac{1}{\psi (q)}&=\frac{\psi ^3(q^9)}{\psi ^4(q^3)}\left( \frac{1}{\omega ^2(q^3)}-q\frac{1}{\omega (q^3)}+q^2\right) , \end{aligned}$$

where

$$\begin{aligned} \omega (q)=\frac{f_1f^3_6}{f_2f^3_3}. \end{aligned}$$

Lemma 4.5

( [13, Lemma 2.5])

$$\begin{aligned} \frac{f_1}{f^3_3}&=\frac{f_2f^2_4f^2_{12}}{f^7_{6}}-q\frac{f^3_2f^6_{12}}{f^2_4f^9_6}. \end{aligned}$$

Lemma 4.6

( [8, p. 5])

$$\begin{aligned} f_1f_2=\frac{f_6f^4_9}{f_3f^2_{18}}-qf_9f_{18} -2q^2\frac{f_3f^4_{18}}{f_6f^2_9}. \end{aligned}$$

Lemma 4.7

( [3, Theorem 3.1])

$$\begin{aligned} \frac{f_4}{f_1}&=\frac{f_{12}f^4_{18}}{f^3_3f^2_{36}}+q\frac{f^2_6f^3_9f_{36}}{f^4_3f^2_{18}}+2q^2\frac{f_6f_{18}f_{36}}{f^3_3}. \end{aligned}$$

The following two theorems are crucial for establishing combinatorial interpretations.

Theorem 4.8

For any fixed n, if

$$\begin{aligned} M_{ped}(0,2,n)&=M_{ped}(1,2,n),\end{aligned}$$

(4.1)

$$\begin{aligned} M_{ped}(0,3,n)&=M_{ped}(1,3,n),\end{aligned}$$

(4.2)

$$\begin{aligned} M_{ped}(0,6,n)+M_{ped}(1,6,n)&=M_{ped}(2,6,n)+M_{ped}(3,6,n), \end{aligned}$$

(4.3)

then

$$\begin{aligned} M_{ped}(m,6,n)=\frac{ped(n)}{6},\ \ m=0,1,2,3,4,5,\ \ \textrm{and}\ \ M_{ped}(3,12,n)=\frac{ped(n)}{12}. \end{aligned}$$

Proof

By (3.2), we have

$$\begin{aligned} M_{ped}(0,2,n)&=M_{ped}(0,6,n)+ 2M_{ped}(2,6,n), \end{aligned}$$

(4.4)

$$\begin{aligned} M_{ped}(1,2,n)&=2M_{ped}(1,6,n)+M_{ped}(3,6,n),\end{aligned}$$

(4.5)

$$\begin{aligned} M_{ped}(0,3,n)&=M_{ped}(0,6,n)+M_{ped}(3,6,n),\end{aligned}$$

(4.6)

$$\begin{aligned} M_{ped}(1,3,n)&=M_{ped}(1,6,n)+M_{ped}(2,6,n). \end{aligned}$$

(4.7)

Substituting (4.4)–(4.7) into (4.1)–(4.2), we have

$$\begin{aligned} M_{ped}(0,6,n)-2M_{ped}(1,6,n)+&2M_{ped}(2,6,n) -M_{ped}(3,6,n)=0,\end{aligned}$$

(4.8)

$$\begin{aligned} M_{ped}(0,6,n)-M_{ped}(1,6,n)-&M_{ped}(2,6,n) +M_{ped}(3,6,n)=0. \end{aligned}$$

(4.9)

Solving system of linear homogeneous equations (4.3), (4.8) and (4.9), we get

$$\begin{aligned} M_{ped}(m,6,n)=\frac{ped(n)}{6},\ \ m=0,1,2,3,4,5. \end{aligned}$$

Moreover,

$$\begin{aligned} M_{ped}(3,6,n)=M_{ped}(3,12,n)+M_{ped}(9,12,n) =2M_{ped}(3,12,n), \end{aligned}$$

(4.10)

which implies

$$\begin{aligned} M_{ped}(3,12,n)=\frac{M_{ped}(3,6,n)}{2}=\frac{ped(n)}{12}. \end{aligned}$$

This completes the proof. $\square$

The following theorem can be checked similarly.

Theorem 4.9

For any fixed n, if

$$\begin{aligned} M_{ped}(0,2,n)&=M_{ped}(1,2,n),\\ M_{ped}(0,6,n)+M_{ped}(1,6,n)&=M_{ped}(2,6,n)+M_{ped}(3,6,n), \end{aligned}$$

then

$$\begin{aligned} M_{ped}(0,6,n)&=M_{ped}(3,6,n),\\ M_{ped}(1,6,n)&=M_{ped}(2,6,n). \end{aligned}$$

5 Proofs of main results

In this section, we give proofs of our main results. Hereafter we always assume $\alpha , n \ge 0$ unless specified otherwise.

Proof of Theorem 1.4

Setting $z=e^{\pi i}=-1$ in (3.1), we get

$$\begin{aligned} \sum _{n=0}^{\infty } \sum _{m=-\infty }^{\infty }M_{ped}(m,n)(-1)^mq^n =\sum _{n=0}^{\infty }\left( M_{ped}(0,2,n)-M_{ped}(1,2,n)\right) q^n =\frac{f_2^4}{f_1f_4}. \end{aligned}$$

(5.1)

Let g(q) be a polynomial of q, observing that the coefficient of $q^n$ in g(q) is zero implies the coefficient of $q^n$ in $g(-q)$ is zero and vice versa. Hence we consider the following equation. By Lemma 4.1, replacing q by $-q$ in (5.1), we have

$$\begin{aligned} \sum _{n=0}^{\infty }\left( M_{ped}(0,2,n)-M_{ped}(1,2,n)\right) (-q)^n=f_1f_2. \end{aligned}$$

(5.2)

According to Lemma 4.6, we find that

$$\begin{aligned} \sum _{n=0}^{\infty }\left( M_{ped}(0,2,n)-M_{ped}(1,2,n)\right) (-q)^n= \frac{f_6f^4_9}{f_3f^2_{18}}-qf_9f_{18} -2q^2\frac{f_3f^4_{18}}{f_6f^2_9}.\nonumber \\ \end{aligned}$$

(5.3)

Extracting those terms associated with powers $q^{3n+1}$ on both sides of (5.3), then dividing by q and replacing $q^3$ by q, we arrive at

$$\begin{aligned} \sum _{n=0}^{\infty }\left( M_{ped}(0,2,3n+1)- M_{ped}(1,2,3n+1)\right) (-1)^{3n+1}q^n =-f_3f_6. \end{aligned}$$

(5.4)

Since the coefficients of $q^{3n+1}$ and $q^{3n+2}$ in (5.4) are both zero, we can conclude that the coefficients of $q^{9n+4}$ and $q^{9n+7}$ in (5.2) are both zero. This yields

$$\begin{aligned} M_{ped}(0,2,9n+4)=M_{ped}(1,2,9n+4),\end{aligned}$$

(5.5)

$$\begin{aligned} M_{ped}(0,2,9n+7)=M_{ped}(1,2,9n+7). \end{aligned}$$

(5.6)

Extracting the terms involving $q^{3n}$ in (5.4) and substituting $q^3$ by q gives

$$\begin{aligned} \sum _{n=0}^{\infty }\left( M_{ped}(0,2,9n+1)-M_{ped}(1,2,9n+1)\right) (-1)^{9n+1}q^n =-f_1f_2. \end{aligned}$$

(5.7)

Since 9n has the same parity as n, (5.7) becomes

$$\begin{aligned} \sum _{n=0}^{\infty }\left( M_{ped}(0,2,9n+1)- M_{ped}(1,2,9n+1)\right) (-q)^n =f_1f_2. \end{aligned}$$

(5.8)

From (5.2), (5.8) and mathematical induction, it follows that

$$\begin{aligned} \sum _{n=0}^{\infty }\left( M_{ped}\left( 0,2,3^{2\alpha }n+\frac{3^{2\alpha }-1}{8}\right) - M_{ped}\left( 1,2,3^{2\alpha }n+\frac{3^{2\alpha }-1}{8}\right) \right) (-q)^n =f_1f_2. \end{aligned}$$

(5.9)

Comparing (5.9) with (5.2), the following equations can be proved by similar arguments for (5.5)–(5.6), and hence the proof is omitted.

$$\begin{aligned} M_{ped}\left( 0,2,3^{2\alpha +2}n+\frac{11\cdot 3^{2\alpha +1}-1}{8}\right)&=M_{ped}\left( 1,2,3^{2\alpha +2}n+\frac{11\cdot 3^{2\alpha +1}-1}{8}\right) , \end{aligned}$$

(5.10)

$$\begin{aligned} M_{ped}\left( 0,2,3^{2\alpha +2}n+\frac{19\cdot 3^{2\alpha +1}-1}{8}\right)&=M_{ped}\left( 1,2,3^{2\alpha +2}n+\frac{19\cdot 3^{2\alpha +1}-1}{8}\right) . \end{aligned}$$

(5.11)

Substituting $z=e^{\frac{\pi i}{3}}$ into (3.1), by (3.2) and $e^{\frac{\pi i}{3}}+e^{\frac{5\pi i}{3}}=-(e^{\frac{2\pi i}{3}}+e^{\frac{4\pi i}{3}})=-e^{\pi i}=1$, we see that

$$\begin{aligned}&\sum \limits _{{n = 0}}^{\infty } {\sum \limits _{{m = 0}}^{5} {M_{{ped}} } } (m,6,n)e^{{\frac{{m\pi i}}{3}}} q^{n} \\&\quad = \sum \limits _{{n = 0}}^{\infty } {\left( {M_{{ped}} (0,6,n)} \right. } n + (e^{{\frac{{\pi i}}{3}}} + e^{{\frac{{5\pi i}}{3}}} )M_{{ped}} (1,6,n)n \\&\qquad \left. { + (e^{{\frac{{2\pi i}}{3}}} + e^{{\frac{{4\pi i}}{3}}} )M_{{ped}} (2,6,n) + e^{{\pi i}} M_{{ped}} (3,6,n)} \right) q^{n} n \\&\quad = \sum \limits _{{n = 0}}^{\infty } {\left( {M_{{ped}} (0,6,n) + M_{{ped}} (1,6,n)} \right. } n \left. { - M_{{ped}} (2,6,n) - M_{{ped}} (3,6,n)} \right) q^{n} n \\&\quad = \frac{{f_{2}^{2} f_{4} }}{{f_{1} }}\prod \limits _{{n = 0}}^{\infty } {\frac{1}{{1 - q^{{2n}} + q^{{4n}} }}} n \\&\quad = \frac{{f_{2}^{2} f_{4} }}{{f_{1} }}\prod \limits _{{n = 0}}^{\infty } {\frac{{1 + q^{{2n}} }}{{1 + q^{{6n}} }}} n \\&\quad = \frac{{f_{2}^{2} }}{{f_{1} }}\frac{{f_{4}^{2} }}{{f_{2} }}\frac{{f_{6} }}{{f_{{12}} }} . \end{aligned}$$

By Lemma 4.3, we have

$$\begin{aligned}&\sum _{n=0}^{\infty }\left( M_{ped}(0,6,n)+M_{ped}(1,6,n)- M_{ped}(2,6,n)-M_{ped}(3,6,n)\right) q^n \nonumber \\&\qquad =\left( \frac{f_6f_9^2}{f_3f_{18}}+q\frac{f_{18}^2}{f_9}\right) \left( \frac{f_{12}f_{18}^2}{f_6f_{36}}+q^2\frac{f_{36}^2}{f_{18}}\right) \frac{f_6}{f_{12}}. \end{aligned}$$

(5.12)

Extracting the terms involving $q^{3n+1}$ in (5.12), then dividing by q and replacing $q^3$ by q, we find that

$$\begin{aligned}&\sum _{n=0}^{\infty }\left( M_{ped}(0,6,3n+1)+M_{ped}(1,6,3n+1)- M_{ped}(2,6,3n+1)\right. \nonumber \\&\qquad \left. -M_{ped}(3,6,3n+1)\right) q^n =\frac{f_6^4}{f_3f_{12}}. \end{aligned}$$

(5.13)

Obviously, the coefficients of $q^{3n+1}$ and $q^{3n+2}$ in (5.13) are both zero, which gives

$$\begin{aligned} M_{ped}(0,6,9n+4)+M_{ped}(1,6,9n+4)=\,&M_{ped}(2,6,9n+4)+M_{ped}(3,6,9n+4),\end{aligned}$$

(5.14)

$$\begin{aligned} M_{ped}(0,6,9n+7)+M_{ped}(1,6,9n+7)=\,&M_{ped}(2,6,9n+7)+M_{ped}(3,6,9n+7). \end{aligned}$$

(5.15)

Considering the terms involving $q^{3n}$ in (5.13), after simplification, we get

$$\begin{aligned}&\sum _{n=0}^{\infty }\left( M_{ped}(0,6,9n+1)+M_{ped}(1,6,9n+1)- M_{ped}(2,6,9n+1)\right. \nonumber \\&\quad \left. -M_{ped}(3,6,9n+1)\right) q^n =\frac{f_2^4}{f_1f_4}. \end{aligned}$$

(5.16)

Comparing (5.16) with (5.1), according to (5.14)–(5.15) and the proofs of (5.10)–(5.11), a simple deduction shows that

$$\begin{aligned}&M_{ped}\left( 0,6,3^{2\alpha +2}n+\frac{11\cdot 3^{2\alpha +1}-1}{8}\right) +M_{ped}\left( 1,6,3^{2\alpha +2}n+\frac{11\cdot 3^{2\alpha +1}-1}{8}\right) \nonumber \\&\quad =M_{ped}\left( 2,6,3^{2\alpha +2}n+\frac{11\cdot 3^{2\alpha +1}-1}{8}\right) +M_{ped}\left( 3,6,3^{2\alpha +2}n+\frac{11\cdot 3^{2\alpha +1}-1}{8}\right) , \end{aligned}$$

(5.17)

$$\begin{aligned}&M_{ped}\left( 0,6,3^{2\alpha +2}n+\frac{19\cdot 3^{2\alpha +1}-1}{8}\right) +M_{ped}\left( 1,6,3^{2\alpha +2}n+\frac{19\cdot 3^{2\alpha +1}-1}{8}\right) \nonumber \\&\quad =M_{ped}\left( 2,6,3^{2\alpha +2}n+\frac{19\cdot 3^{2\alpha +1}-1}{8}\right) +M_{ped}\left( 3,6,3^{2\alpha +2}n+\frac{19\cdot 3^{2\alpha +1}-1}{8}\right) . \end{aligned}$$

(5.18)

Combining (5.10)–(5.11), (5.17)–(5.18) and Theorem 4.9, Theorem 1.4 follows immediately. $\square$

Proof of Corollary 1.5

Corollary 1.5 can be checked easily by (4.6)–(4.7) and Theorem 1.4, hence we omitted the details. $\square$

Proof of Corollary 1.6

By (4.6), (4.10) and Theorem 1.4, one can see that

$$\begin{aligned} M_{ped}\left( 3,12,3^{2\alpha +2}n+\frac{11\cdot 3^{2\alpha +1}-1}{8}\right)&= \frac{M_{ped}\left( 3,6,3^{2\alpha +2}n+\frac{11\cdot 3^{2\alpha +1}-1}{8}\right) }{2}\\&=\frac{M_{ped}\left( 0,3,3^{2\alpha +2}n+\frac{11\cdot 3^{2\alpha +1}-1}{8}\right) }{4},\\ M_{ped}\left( 3,12,3^{2\alpha +2}n+\frac{19\cdot 3^{2\alpha +1}-1}{8}\right)&= \frac{M_{ped}\left( 3,6,3^{2\alpha +2}n+\frac{19\cdot 3^{2\alpha +1}-1}{8}\right) }{2}\\&=\frac{M_{ped}\left( 0,3,3^{2\alpha +2}n+\frac{19\cdot 3^{2\alpha +1}-1}{8}\right) }{4}. \end{aligned}$$

Hence Corollary 1.6 holds.

Proof of Corollary 1.7

By (3.2), we have

$$\begin{aligned} M_{ped}(1,2,n)=M_{ped}(1,4,n)+M_{ped}(3,4,n)=2M_{ped}(1,4,n). \end{aligned}$$

(5.19)

Then Corollary 1.7 follows immediately according to (5.10)–(5.11) and the fact that $ped(n)=M_{ped}(0,2,n)+M_{ped}(1,2,n)$. $\square$

Proof of Theorem 1.8

Substituting $z=e^\frac{\pi i}{2}=i$ into (3.1), by (3.2) and Lemmas 4.2–4.3, we find that

$$\begin{aligned} \sum _{n=0}^{\infty }\sum _{m=-\infty }^{\infty }M_{ped}(m,n)i^mq^n&=\sum _{n=0}^{\infty }\sum _{m=0}^{3}M_{ped}(m,4,n)i^mq^n \nonumber \\&=\sum _{n=0}^{\infty }\left( M_{ped}(0,4,n)+(i+i^3)M _{ped}(1,4,n)\right. \nonumber \\&\quad \left. +i^2M_{ped}(2,4,n)\right) q^n\nonumber \\&=\sum _{n=0}^{\infty }\left( M_{ped}(0,4,n)- M_{ped}(2,4,n)\right) q^n\nonumber \\&=\frac{f_2^2}{f_1}\frac{f_4^2}{f_8}\nonumber \\&=\sum _{n=0}^{\infty }q^{n+1 \atopwithdelims ()2}\left( 2\sum _{n=0}^{\infty }(-1)^nq^{4n^2}-1\right) . \end{aligned}$$

(5.20)

By (3.2), one can see that

$$\begin{aligned} ped(n)=\sum _{m=0}^{3}M_{ped}(m,4,n)= M_{ped}(0,4,n)+2M_{ped}(1,4,n)+2M_{ped}(2,8,n). \end{aligned}$$

In light of (5.20) and the fact that $M_{ped}(0,n)$ has the same parity as $M_{ped}(0,4,n)$, Theorem 1.8 holds. $\square$

We next aim to prove Theorem 1.9.

Proof of Theorem 1.9

Substituting $z=e^{\frac{2\pi i}{3}}$ into (3.1), we obtain

$$\begin{aligned} \sum _{n=0}^{\infty }\sum _{m=0}^{2}M_{ped}(m,3,n)e^{\frac{2m\pi i}{3}}q^n=\frac{(q^2;q^2)_{\infty }}{(\zeta q^2;q^2)_{\infty }(\zeta ^{-1}q^2;q^2)_{\infty }} \frac{(q^4;q^4)_\infty }{(q;q^2)_\infty } =\frac{f_2^2}{f_1}\frac{f_2f_4}{f_6}. \end{aligned}$$

(5.21)

Using Lemmas 4.3, 4.6, by (3.2) and the fact that $1+e^{\frac{2\pi i}{3}}+e^{\frac{4\pi i}{3}}=0$, we get

$$\begin{aligned}&\sum \limits _{{n = 0}}^{\infty } {(M_{{ped}} (} 0,3,n) - M_{{ped}} (1,3,n))q^{n} = \left( {\frac{{f_{6} f_{9}^{2} }}{{f_{3} f_{{18}} }} + q\frac{{f_{{18}}^{2} }}{{f_{9} }}} \right) \\&\quad \left( {\frac{{f_{{12}} f_{{18}}^{4} }}{{f_{6} f_{{36}}^{2} }} - q^{2} f_{{18}} f_{{36}} - 2q^{4} \frac{{f_{6} f_{{36}}^{4} }}{{f_{{12}} f_{{18}}^{2} }}} \right) \frac{1}{{f_{6} }} . \end{aligned}$$

Extracting those terms associated with powers $q^{3n+1}$ on both sides of the above equation, then dividing by q and replacing $q^3$ by q, one can see that

$$\begin{aligned} \sum _{n=0}^{\infty }(M_{ped}(0,3,3n+1)-M_{ped}(1,3,3n+1))q^n =\frac{f_4}{f_2^2}\frac{f_6^6}{f_3f_{12}^2}- 2q\frac{f_2}{f_1f_4}\frac{f_3^2f_{12}^4}{f_6^3}. \end{aligned}$$

(5.22)

Since

$$\begin{aligned} \frac{f_2}{f_1f_4}=\frac{1}{\psi (-q)}, \end{aligned}$$

using Lemma 4.4,

$$\begin{aligned} \begin{gathered} \sum \limits _{{n = 0}}^{\infty } {(M_{{ped}} (} 0,3,3n + 1) - M_{{ped}} (1,3,3n + 1))q^{n} \\ \quad \quad \quad = \frac{{f_{{12}}^{2} f_{{18}}^{6} }}{{f_{3} f_{6}^{2} f_{{36}}^{3} }} - 2q^{3} \frac{{f_{6} f_{9}^{3} f_{{36}}^{3} }}{{f_{3}^{2} f_{{18}}^{3} }} - 2q\frac{{f_{{12}}^{2} f_{{18}}^{9} }}{{f_{6}^{3} f_{9}^{3} f_{{36}}^{3} }} + 4q^{4} \frac{{f_{{36}}^{3} }}{{f_{3} }} \\ \end{gathered} \end{aligned}$$

(5.23)

after simplification.

Clearly, the coefficient of $q^{3n+2}$ in (5.23) is zero. We can conclude that

$$\begin{aligned} M_{ped}(0,3,9n+7)=M_{ped}(1,3,9n+7). \end{aligned}$$

(5.24)

Combining (5.11), (5.18), (5.24) and Theorem 4.8, we complete the proof of Theorem 1.9. $\square$

Remark 1

Andrews, Hirschhorn, and Sellers [3] presented an interesting infinite family of congruences modulo 3 as given by

$$\begin{aligned} ped\left( 3^{2\alpha +1}n+\frac{17\cdot 3^{2\alpha }-1}{8}\right)&\equiv 0\pmod {3}, \ \ \alpha \ge 1, \end{aligned}$$

(5.25)

and deduced that

$$\begin{aligned} ped\left( 3^{2\alpha +1}n+\frac{17\cdot 3^{2\alpha }-1}{8}\right) \equiv 0\pmod {6}, \ \ \alpha \ge 1. \end{aligned}$$

(5.26)

Actually, based on a substantial amount of numerical evidence, we conjecture that the ped-crank can be used to provide a combinatorial interpretation of (5.25), namely

$$\begin{aligned} M_{ped}{} & {} \left( 0,3,3^{2\alpha +1}n+\frac{17\cdot 3^{2\alpha }-1}{8}\right) =M_{ped}\left( 1,3,3^{2\alpha +1}n+\frac{17\cdot 3^{2\alpha }-1}{8}\right) , \\ {}{} & {} \quad \alpha \ge 1. \end{aligned}$$

Here, we only prove the case for $\alpha =1$, and for any $\alpha >1$, we are not able to provide an elementary proof of this conjecture.

Proof

Extracting the terms involving $q^{3n}$ in (5.23) and substituting $q^3$ by q, we obtain

$$\begin{aligned} \sum _{n=0}^{\infty }(M_{ped}(0,3,9n+1)-M_{ped}(1,3,9n+1))q^n =\frac{f_4}{f_1}\frac{f_4}{f_2^2}\frac{f_6^6}{f_{12}^3}- 2q\frac{f_2f_3^3f_{12}^3}{f_1^2f_{6}^3}.\nonumber \\ \end{aligned}$$

(5.27)

From Lemmas 4.4, 4.5, 4.7, considering the terms involving $q^{3n+2}$ in (5.27) leads to

$$\begin{aligned}&\sum _{n=0}^{\infty }(M_{ped}(0,3,27n+19)-M_{ped}(1,3,27n+19))q^n\\&\quad =\frac{f_4f_6^7}{f_1^3f_2f_{12}^2}-\frac{f_3^3f_4^3}{f_1^4} +q\frac{f_2^2f_3^3f_{12}^4}{f_1^4f_4f_6^2}\\&\quad =\frac{f_3^3}{f_1^4}\left( \frac{f_1}{f_3^3} \frac{f_4f_6^7}{f_2f_{12}^2}-f_4^3 +q\frac{f_2^2f_{12}^4}{f_4f_6^2}\right) \\&\quad =\frac{f_3^3}{f_1^4}\left( \left( \frac{f_2f^2_4f^2_{12}}{f^7_{6}}-q\frac{f^3_2f^6_{12}}{f^2_4f^9_6}\right) \frac{f_4f_6^7}{f_2f_{12}^2}-f_4^3 +q\frac{f_2^2f_{12}^4}{f_4f_6^2}\right) \\&\quad =0. \end{aligned}$$

That means

$$\begin{aligned} M_{ped}(0,3,27n+19)=M_{ped}(1,3,27n+19). \end{aligned}$$

$\square$

Unfortunately, the ped-crank cannot be employed to interpret (5.26) even for $\alpha =1$. Hence, it will be interesting to introduce another partition statistic that could combinatorially interpret (5.26).

Remark 2

For ordinary partitions, recall that we define $M(0,1)=-1,\ \ M(-1,1)=M(1,1)=1$. From the definition of ped-crank, one can see that a similar problem will arise when $\Delta (\lambda )=((2), \beta , \gamma )$. So we make the following adjustment to the definition of ped-crank. Let

$$\begin{aligned} \gamma&=(\gamma _1,\gamma _2,\cdots ,\gamma _k),\\ A_n&=\{\lambda | \Delta (\lambda )=((2),\beta ,\gamma ),\ \ |\lambda |=n\},\\ B_n&=\{\lambda | \Delta (\lambda )=((0),\beta ,\gamma ),\ \ |\lambda |=n,\ \ \gamma =(2) \ \ \text {or} \ \ \gamma _1-\gamma _2 \ge 4\}. \end{aligned}$$

Definition 5.1

Let $\lambda$ be a partition of n with even parts distinct. The $c_{mped}(\lambda )$ is given by

$$\begin{aligned} c_{mped}(\lambda )=\left\{ \begin{array}{ll} 1 &{} if\ \ \lambda \in A_n, \\ -1 &{} if\ \ \lambda \in B_n, \\ c_{ped}(\lambda ) &{} otherwise, \\ \end{array}\right. \end{aligned}$$

where $c_{ped}(\lambda )$ is the ped-crank of $\lambda$.

When $\lambda \in A_n$, an injection from $A_n$ to $B_n$ can be constructed by changing $\alpha$ to $\emptyset$ and adding 2 to the largest part of $\gamma$. Another direction is obvious. Hence for any non-negative integer n, there is a bijection between $A_n$ and $B_n$. Let $M_{mped}(m,n)$ denote the number of partitions of n with even parts distinct with $c_{mped}(\lambda )=m$. By the definition of $c_{mped}(\lambda )$, one can check $M_{mped}(m,n)=M_{ped}(m,n)$ for any integer m and non-negative integer n.

For example, if $\lambda =(6,5,4,1,1,1),\Delta (\lambda )=((2),(5,1),(6,4))$, then $c_{mped}(\lambda )=1$ and if $\lambda =(8,5,4,1),\Delta (\lambda )=((0),(5,1),(8,4))$, then $c_{mped}(\lambda )=-1$.

Table 1 The case for $n=7$

Table 1 gives the 12 partitions of 7 with even parts distinct. It is easy to check that these partitions are divided into six equinumerous subsets by ped-crank. Moreover,

$$\begin{aligned} M_{ped}(1,4,7)=3=\frac{ped(7)}{4},\\ M_{ped}(3,12,7)=1=\frac{ped(7)}{12}. \end{aligned}$$

6 Closing remarks

In 2014, Xia [12] proved the following congruence modulo 4 for ped(n).

Theorem 6.1

[12, Equation (9), Theorem 1] For $\alpha ,n\ge 0$,

$$\begin{aligned} ped\left( 3^{2\alpha }n+\frac{3^{2\alpha }-1}{8}\right) \equiv ped(n) \pmod {4}. \end{aligned}$$

Note that comparing (5.4) with (5.13), a simple deduction gives

$$\begin{aligned} M_{ped}(1,6,3n+1)=M_{ped}(2,6,3n+1). \end{aligned}$$

Thus

$$\begin{aligned} ped(3n+1)=M_{ped}(0,3,3n+1)+4M_{ped}(1,6,3n+1). \end{aligned}$$

Since for all $\alpha >0,n\ge 0$, $3^{2\alpha }n+\frac{3^{2\alpha }-1}{8}\equiv 1\pmod {3}$, a refinement of Theorem 6.1 can be given as

$$\begin{aligned} M_{ped}\left( 0,3,3^{2\alpha }n+\frac{3^{2\alpha }-1}{8}\right) \equiv ped(n) \pmod {4}. \end{aligned}$$