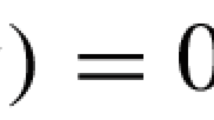Abstract
Some global solvability criteria for the scalar Riccati equations are used to establish new reducibility criteria for systems of two linear first-order ordinary differential equations. Some examples are presented.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let a(t), b(t), c(t) and d(t) be real valued continuous and bounded functions on \([t_0,+\infty )\). Consider the linear system of ordinary differential equations
Introduce new unknowns by equalities
where \(\phi _1, \psi _1\) are new unknowns, \(z_{jk}(t), j,k =1,2\) are the coefficients of a transformation. For \(\phi _1\) and \(\phi _2\) from (1.1) and (1.2) we obtain a new linear system of equations
Definition 1.1
The system (1.1) is called reducible if there exists a bounded matrix function \(Z(t)\equiv (z_{jk}(t))_{j,k=1}^2\) of transformation (1.2) for the system (1.1) such that \(Z'(t), Z^{-1}(t)\) exist and are bounded with \(det Z^{-1}(t)\) and the coefficients \(a_1(t), b_1(t), c_1(t)\) and \(d_1(t)\) of the system (1.3) are constants.
Study the reducibility behavior of systems of linear ordinary differential equation, in particular of the system (1.1), is an important problem of qualitative theory of differential equations and many works are devoted to it (see [1,2,3,4,5,6], and cited works therein) The reducible systems (see [7]) play an important role in the study of stability of solutions of nonlinear systems, for which the first approximation contains the time. They play also an important role in the ’.... study of stability of quasi-periodic motion and preservation of invariant tori in Hamiltonian mechanics (where the reducibility of linear equations with quasi-periodic coefficients play an important role)” (see [1]). In this paper some new reducibility criteria for the system (1.1) are obtained.
2 Auxiliary propositions
Let f(t), g(t), h(t) be real valued continuous functions on \([t_0,+\infty )\). Consider the Riccati equation
In this section we represent some global existence criteria for Eq. (2.1) proved in [8] and [9]. They will be used in the Sect. 3 to obtain new reducibility criteria for the system (1.1).
Theorem 2.1
Let \(f_i(t)\) and \(h_i(t)\) be continuously differentiable functions on \([t_0, + \infty )\) such that \((-1)^i f_i(t)> 0, (-1)^i h_i(t) > 0, \quad t\ge t_0, i=1,2.\) If \(f_1(t) \le f(t) \le f_2(t), h_1(t) \le h(t) \le h_2(t), g(t) \ge \frac{1}{2}\biggl (\frac{f_i'(t)}{f_i(t)} - \frac{h_i'(t)}{h_i(t)}\biggr ) + 2 (-1)^i\sqrt{f_i(t) h_i(t)}, i=1,2, \quad t\ge t_0,\) then for every \(y_{(0)} \in \biggl [-\sqrt{\frac{h_2(t_0)}{f_2(t_0)}}, \sqrt{\frac{h_1(t_0)}{f_1(t_0)}}\biggr ]\) Eq. (2.1) has a solution y(t) on \([t_0,+\infty )\) with \(y(t_0) = y_{(0)}\) and
See the proof in [8].
Theorem 2.2
Let \(f_i(t)\) and \(h_i(t)\) be continuously differentiable functions on \([t_0, + \infty )\) such that \((-1)^i f_i(t)> 0, (-1)^i h_i(t) > 0, \quad t\ge t_0, i=1,2.\) If \(f_1(t) \le f(t) \le f_2(t), h_1(t) \le h(t) \le h_2(t), g(t) \le \frac{1}{2}\biggl (\frac{f_i'(t)}{f_i(t)} - \frac{h_i'(t)}{h_i(t)}\biggr ) - 2 (-1)^i\sqrt{f_i(t) h_i(t)}, i=1,2, \quad t\ge t_0,\) then Eq. (2.1) has a solution y(t) on \([t_0,+\infty )\) and
Proof
In Eq. (2.1) substitute \(y = y(t) = z(-t), t \ge t_0\). We come to the equation
where \(\widetilde{f}(t) \equiv -f(-t), \widetilde{g}(t) \equiv -g(-t), \widetilde{h}(t) \equiv -h(-t), t \le -t_0\). Set: \(\widetilde{f}_i(t) \equiv -f_i(-t), \widetilde{h}_i(t) \equiv -h_i(-t), t \le -t_0, i=1,2.\) From the condition of the theorem it follows
Then by Theorem 2.1 for evwry \(T > t_0\) and for every \(z_{(0)} \in \biggl [\sqrt{\frac{\widetilde{h}_1(-T)}{\widetilde{f}_1(-T)}}, \sqrt{{\frac{\widetilde{h}_2(-T)}{\widetilde{f}_2(-T)}}}\biggr ]\) Eq. (3.3) has a solution \(z_0(t)\) on \([-T, - t_0]\) with \(z_0(-T) = z_{(0)}\) and
Denote by \(I_T\) the set of that values \(z(-t_0)\) of of the solutions z(t) of Eq. (2.3) for which
Obviously \(I_T\) is a finite and close interval and if \(T_1> T_2 > t_0\) then
Let \(t_0< T_1< T_2< ....< T_n < ...\) be a infinitely large sequence. By (2.4) we have
Take \(y_{(0)} \in I\). Then (by already proven) for every \(n=1,2, ...\) Eq. (2.2) has a solution \(z_n(t)\) on \([-T_n, -t_0]\) with \(z_n(-t_0) = y_{(0)}\) and
Therefore \(y_n(t) \equiv z_n(-t)\) is a solution of Eq. (2.1) on \([t_0, T_n]\) with \(y_n(t_0) = y_{(0)}\) and
By virtue of the uniqueness theorem from here it follows that Eq. (2.1) has a solution \(y_0(t)\) on \([t_0,+\infty )\) and (2.2) is valid. The theorem is proved. \(\square \)
Theorem 2.3
Let \(f_1(t)\) and \(h_1(t)\) be continuously differentiable functions on \([t_0,+\infty )\) such that \(f_1(t)> 0, h_1(t) > 0, t\ge t_0.\) If \(0 \le f(t) \le f_1(t), h(t) \le h_1(t), g(t) \le \frac{1}{2}\biggl [\frac{f_1'(t)}{f_1(t)} - \frac{h_1'(t)}{h_1(t)}\biggr ] - 2 \sqrt{f_1(t) h_1(t)}, t\ge t_0\) then for every \(y_{(0)} \ge \sqrt{\frac{h_1(t_0)}{f_1(t_0)}}\) Eq. (2.1) has a solution y(t) on \([t_0,+\infty )\) with \(y(t_0) = y_{(0)}\) and
See the proof in [9].
Theorem 2.4
Let \(f_1(t)\) and \(h_1(t)\) be the same as in Theorem 2.2. If \(0 \le f(t) \le f_1(t), h(t) \le h_1(t), g(t) \ge \frac{1}{2}\biggl [\frac{f_1'(t)}{f_1(t)} - \frac{h_1'(t)}{h_1(t)}\biggr ] + 2 \sqrt{f_1(t) h_1(t)}, f(t) f_1(t) + 2 f_1(t) h_1(t) + h_1(t) h(t) \ge 0, \quad t\ge t_0,\) then for every \(y_{(0)} \in \biggl [-\sqrt{\frac{h_1(t_0)}{f_1(t_0)}}, \sqrt{\frac{h_1(t_0)}{f_1(t_0)}}\biggr ]\) Eq. (2.1) has a solution y(t) on \([t_0,+\infty )\) with \(y(t_0) = y_{(0)}\) and
See the proof in [9].
Theorem 2.5
Let \(f_1(t), g_1(t)\) and \(h_1(t)\) be real valued continuous functions such that \(f_1(t) > 0, \frac{g_1(t)}{f_1(t)}\) is continuously differentiable on \([t_0, +\infty )\). If \(0 \le f(t) \le f_1(t), \lambda (g(t) - g_1(t)) g_1(t) \ge 0, h(t) \le \lambda \biggl [\biggl (\frac{g_1(t)}{f_1(t)}\biggr ) + (1 - \lambda )\frac{g_1^2(t)}{f_1(t)}\biggr ], \lambda = const,\quad t\ge t_0,\) then for every \(y_{(0)} \ge - \lambda \frac{g_1(t_0)}{f_1(t_0)}\) Eq. (2.1) has a solution y(t) on \([t_0,+\infty )\) with \(y(t_0) = t_{(0)}\) and
See the proof in [9].
Theorem 2.6
Let \(f_1(t)\) and \(h_1(t)\) be continuous functions on \([t_0, + \infty )\). If \(0 \le f(t) \le ~ f_1(t), \biggl [\lambda + \int \nolimits _{t_0} {t}h_1(\tau ) d \tau \biggr ]\biggl (f_1(t)\biggl [\lambda + \int \nolimits _{t_0}{t}h_1(\tau ) d \tau \biggr ] - g(t)\biggr ) \le 0, h(t) \le h_1(t), \lambda =~ const,\quad t\ge t_0,\) then for every \(y_{(0)} \ge -\lambda \) Eq. (2.1) has a solution y(t) with \(y(t_0) = y_{(0)}\) and
If in addition for some \(\mu \le \lambda \) the inequality \(\biggl [\mu + \int \nolimits _{t_0}{t}h_1(\tau ) d \tau \biggr ]\biggl (f_1(t)\biggl [\mu + \int \nolimits _{t_0}{t}h_1(\tau ) d \tau \biggr ] - g(t)\biggr ) \ge 0, t\ge t_0\) is satisfied and \(y_{(0)} \le - \mu \), then
See the proof in [9].
Theorem 2.7
Let for some \(\lambda \in \mathbb {R}\) and continuous on \([t_0,+\infty )\) functions \(g_1(t)\) and \(h_1(t)\) the following conditions be satisfied.
\(f(t) \ge 0, \int \nolimits _{t_0}{t}\exp \biggl \{\int \nolimits _{t_0}{\tau }\Bigl [f(s)\bigl (\eta _0(s) + \eta _1(s)\Bigr ) + g(s)\Bigr ]d s\biggr \} \biggl [f(\tau ) \eta _1^2(\tau ) + (g(\tau ) - g_1(\tau )) \eta _1(\tau ) + h(\tau ) - h_1(\tau )\biggr ] d \tau \le 0,\quad t\ge t_0,\) where
Then for every \(y_{(0)} \ge \lambda \) Eq. (2.1) has a solution \(y_0(t)\) on \([t_0,+ \infty )\) with \(y_0(t_0) = y_{(0)}\) and \(y_0(t) \ge \eta _1(t), t \ge t_0\).
See the proof in [9].
3 Reducibility criteria for the system (1.1)
Consider the Riccati equation
where \(E(t) \equiv a(t) - d(t), \quad t\ge t_0.\) In [2] it was established that the system (1.1) is reducible provided:
\(\alpha \)) Eq. (3.1) has a bounded solution on \([t_0,+\infty )\)
or
\(\beta \)) Eq. (3.1) has a solution y(t) on \([t_0,+\infty )\) such that \(\lim \nolimits _{t \rightarrow + \infty } y(t) = \infty \).
We will use this fact with the theorems from Sect. 2 to prove reducibility criteria for the system (1.1).
Theorem 3.1
Let \(b_i(t)\) and \(c_i(t)\) be continuously differentiable functions on \([t_0,+\infty )\) such that \((-1)^ib_i(t)> 0, (-1)^i c_i(t) > 0, \quad t\ge t_0, i=1,2\). If \(b_1(t) \le b(t) \le b_2(t), c_1(t) \le - c(t) \le c_2(t), E(t) \ge \frac{1}{2}\biggl (\frac{b_i'(t)}{b_i(t)} - \frac{c_i'(t)}{c_i(t)}\biggr ) + 2 (-1)^i\sqrt{b_i(t) c_i(t)}, i=1,2,\quad t\ge t_0,\)
\(A_1\)) \(\frac{c_i(t)}{b_i(t)}\) is bounded on \([t_0,+\infty ), i=1,2,\)
then the system (1.1) is reducible.
Proof
By virtue of Theorem 2.1 from the conditions of the theorem it follows that Eq. (3.1) has a solution y(t) on \([t_0,+\infty )\) such that
From here and from the condition \(A_1\)) it follows that y(t) is bounded. Then by \(\alpha \)) the system (1.1) is reducible. The theorem is proved. \(\square \)
Example 3.1
Let \(\nu (t)\) be a continuous and bounded function on \([t_0,+\infty )\). Consider the system
It is not difficult to verify that for \(b_i(t) = c_i(t) = (-1)^i, i=1,2,\quad t\ge t_0\) the conditions of Theorem 3.1 for this system are satisfied.
By analogy using Theorem 2.2 in place of Theorem 2.1 can be proved
Theorem 3.2
Let \(b_i(t)\) and \(c_i(t)\) be continuously differentiable functions on \([t_0,+\infty )\) such that \((-1)^ib_i(t)> 0, (-1)^i c_i(t) > 0, \quad t\ge t_0, i=1,2\). If \(b_1(t) \le b(t) \le b_2(t), c_1(t) \le - c(t) \le c_2(t), E(t) \le \frac{1}{2}\biggl (\frac{b_i'(t)}{b_i(t)} - \frac{c_i'(t)}{c_i(t)}\biggr ) - 2 (-1)^i\sqrt{b_i(t) c_i(t)}, i=1,2,\quad t\ge t_0,\) the function \(\frac{c_i(t)}{b_i(t)}\) is bounded on \([t_0,+\infty ), i=1,2,\) then the system (1.1) is reducible.
Example 3.2
Let \(\nu (t)\) be the same as in Example 3.1. Consider the system
One can readily check that for \(b_i(t) = c_i(t) = (-1)^i, i=1,2, \quad t\ge t_0\) the conditions of Theorem 3.2 for this system are satisfied.
Theorem 3.3
Let \(b_1(t)\) and \(c_1(t)\) be continuously differentiable functions on \([t_0,+\infty )\) such that \(b_1(t)> 0, c_1(t) > 0 , t\ge t_0.\) If \(0 \le b(t) \le b_1(t), - c(t) \le c_1(t), E(t) \le \frac{1}{2}\biggl (\frac{b_1'(t)}{b_1(t)} - \frac{c_1'(t)}{c_1(t)}\biggr ) - 2 \sqrt{b_1(t) c_1(t)}, t\ge t_0.\)
\(A_2\)) \(\lim \nolimits _{t \rightarrow + \infty }\frac{c_1(t)}{b_1(t)} = + \infty \),
then the system (1.1) is reducible.
Proof
In virtue of Theorem 2.3 from the conditions of the thorem it follows that Eq. (3.1) has a solution y(t) on \([t_0,+\infty )\) such that
From here and from \(A_2\)) it follows that
By \(\beta \)) from here it follows the reducibility of the system (1.1). The theorem is proved. \(\square \)
Example 3.3
Let \(\nu (t)\) be the same as in Example 3.1. Consider the system
One can readily check that for \(b_1(t) =\frac{1}{t}, c_1(t) = 1, t \ge 1\) the conditions of Theorem 3.3 for this system are satisfied.
Theorem 3.4
Let \(b_1(t)\) and \(c_1(t)\) be the same as in Theorem 3.3. If \(0 \le b(t) \le b_1(t), -c(t) \le c_1(t), E(t) \ge \frac{1}{2}\biggl (\frac{b_1'(t)}{b_1(t)} - \frac{c_1'(t)}{c_1(t)}\biggr ) + 2 \sqrt{b_1(t) c_1(t)}, b(t) b_1(t) + 2 b_1(t) c_1(t) - c_1(t) c(t) \ge 0,\quad t\ge t_0,\)
\(A_3\)) \(\frac{c_1(t)}{b_1(t)}\) is bounded on \([t_0,+\infty )\),
then the system (1.1) is reducible.
Proof
By Theorem 2.4 from the conditions of the theorem it follows that Eq. (3.1) has a solution y(t) on \([t_0,+\infty )\) such that
From here and from \(A_3\)) it follows that y(t) is bounded on \([t_0,+\infty )\). Then by \(\alpha \)) the system (1.1) is reducible. The theorem is proved. \(\square \)
Example 3.4
Consider the system
where \(\nu (t)\) is the same as in Example 3.1. It is not difficult to verify that for \(b_1(t) = e^{\sin 2 t}, c_1(t) = e^{- \sin 2 t}, \quad t\ge t_0\) the conditions of Theorem 3.4 for this system are fulfilled. Hence this system is reducible.
Remark 3.1
The reducibility of the system (3.2) in the case when \(\nu (t) \equiv 0\) is evident.
Theorem 3.5
Let \(b_1(t)\) and \(E_1(t)\) be continuous functions on \([t_0,+\infty )\) such that \(b_1(t) > 0, \quad t\ge t_0, \frac{E_1(t)}{b_1(t)}\) is continuously differentiable on \([t_0,+\infty )\). If \(0 \le b(t) \le b_1(t), \lambda (E(t) - E_1(t)) E_1(t) \ge 0, - c(t) \le \lambda \biggl [\biggl (\frac{E_1(t)}{b_1(t)}\biggr )' + (1- \lambda )\frac{E_1^2(t)}{b_1(t)}\biggr ], \lambda = const, \quad t\ge t_0,\)
\(A_4\)) \(\lim \nolimits _{t\rightarrow + \infty } - \lambda \frac{E_1(t)}{b_1(t)} = + \infty ,\)
then the system (1.1) is reducible.
Proof
In virtue of Theorem 2.5 from the conditions of the theorem it follows that Eq. (3.1) has a solution y(t) on \([t_0,+\infty )\) such that \(y(t) \ge - \lambda \frac{E_1(t)}{b_1(t)}, \quad t\ge t_0.\) From here and from the condition \(A_4\)) it follows that
Consequently by \(\beta \)) the system (1.1) is reducible. The theorem is proved. \(\square \)
Example 3.5
Let \(\nu (t)\) be the same as in Example 3.1. Consider the system
It is not difficult to verify that for \(b_1(t) =\frac{100}{t}, E_1(t) = 10, \lambda = -1\) the conditions of Theorem 3.5 for this system are satisfied.
Theorem 3.6
Let \(b_1(t)\) and \(c_1(t)\) be continuous functions on \([t_0,+\infty )\) such that \(\int \nolimits _{t_0}{t} c_1(\tau ) d \tau ,\quad t\ge t_0,\) is bounded on \([t_0,+\infty )\). If \(0 \le b(t) \le b_1(t), \biggl [\lambda + \int \nolimits _{t_0}{t} c_1(\tau ) d \tau \biggr ]\biggl (b_1(t) \biggl [\lambda + \int \nolimits _{t_0}{t} c_1(\tau ) d \tau \biggr ] - E(t)\biggr ) \le 0, -c(t) \le c_1(t), \biggl [\mu + \int \nolimits _{t_0}{t} c(\tau ) d \tau \biggr ]\biggl (b(t) \biggl [\mu + \int \nolimits _{t_0}{t} c(\tau ) d \tau \biggr ] - E(t)\biggr ) \ge ~ 0, \lambda = const, \mu = const, \mu \le \lambda ,\quad t\ge t_0,\) then the system (1.1) is reducible.
Proof
By Theorem 2.6 from the conditions of the theorem it follows that Eq. (3.1) has a solution y(t) such that
Then since \(\int \nolimits _{t_0}{t}c_1(\tau ) d \tau \) is bounded y(t) is also bounded. Therefore according to \(\alpha \)) the system (1.1) is reducible. The theorem is proved. \(\square \)
Example 3.6
Let \(\nu (t)\) be the same as in Example 3.1. Consider the system
One can readily check that for \(c_1(t) = 2 \cos t, b_1(t) \equiv 1, \lambda = \sin t_0\) the conditions of Theorem 3.6 for this system are satisfied.
Theorem 3.7
Let for some \(\lambda \in \mathbb {R}\) and continuous functions \(E_1(t)\) and \(c_1(t)\) the following conditions be satisfied
\(b(t) \ge 0,\)
\( \lim \nolimits _{t \rightarrow + \infty }\chi _1(t) = + \infty ,\) where
Then the system (1.1) is reducible.
Proof
By virtue of Theorem 2.7. from the conditions of the theorem it follows that Eq. (2.1) has a solution \(y_0(t)\) on \([t_0,+\infty )\) such that \(\lim \nolimits _{t \rightarrow + \infty } y_0(t) = + \infty \). By \(\beta )\) from here it follows the reducibility of the system (1.1). The theorem is proved. \(\square \)
Remark 3.2
The condition (3.3) of Theorem 3.7 is satisfied if in particular \(\lambda = 0\) and
where \(I_{E_1, c_1}(t) \equiv \int \nolimits _{t_0}{t}\exp \biggl \{-\int \nolimits _{\tau }{t} E_1(s) d s\biggr \} c_1(\tau ) d \tau , \quad t \ge t_0\).
Example 3.7
Let \(\nu (t)\) be the same as in Example 3.1. Consider the system
Using Remark 3.2 one can readily check that for \(c_1(t) \equiv 1, E_1(t) \equiv 0, \lambda =0\) the conditions of Theorem 3.7 for this system are satisfied.
References
Pug, J.: Reducibility of linear equations with quasi-periodic coefficients. A survey. (May, 2002)
Hou, X., You, J.: Almost reducibility and non-perturbative reducibility of quasi-periodic linear systems. Inventions Mathematica 190, 208–260 (2012)
Yuan, X., Nunes, A.: A note on the reducibility of linear differential equations with quasi-periodic coefficients. IJMMS 64, 4071–4083 (2003)
Li, J., Zu, Ch.: On the reducibility of a class of finitely differentiable quasi-periodic linear systems. J. Math. Anal. Appl. 413(1), 69–83 (2014)
Xu, J., Kun, W., Min, Zh: On the reducibility of 2-dimensional linear quasi-periodic systems with small parameters. Proc. Am. Math. Soc 144(11), 4793–4805 (2016)
Erugin, N.P.: “Reducible systems” Trudy Mat. Inst. Steklov. 13, (1946). (In Russian)
Lyapunov, A.M.: Stability of motion , Acad. Press (1966) (Translated from Russian) Reducible systems. Trudy Mat. Inst. Steklov. 13, (1946). (In Russian)
Grigoryan, G.A.: Boundedness and stability criteria for linear ordinary differential equations of the second order. Izv. Vyssh. Uchebn. Zaved. Mat. 12, 11–18 (2013)
Grigoryan, G.A.: Two comparison criteria for scalar Riccati equations and their applications. Izv. Vyssh. Uchebn. Zaved. Mat. 11, 20–35 (2012)
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Adrian Constantin.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Grigorian, G.A. On the reducibility systems of two linear first-order ordinary differential equations. Monatsh Math 194, 513–522 (2021). https://doi.org/10.1007/s00605-020-01456-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00605-020-01456-x