The structure of the space of ergodic measures of transitive partially hyperbolic sets

Abstract

We provide examples of transitive partially hyperbolic dynamics (specific but paradigmatic examples of homoclinic classes) which blend different types of hyperbolicity in the one-dimensional center direction. These homoclinic classes have two disjoint parts: an “exposed” piece which is poorly homoclinically related with the rest and a “core” with rich homoclinic relations. There is an associated natural division of the space of ergodic measures which are either supported on the exposed piece or on the core. We describe the topology of these two parts and show that they glue along nonhyperbolic measures. Measures of maximal entropy are discussed in more detail. We present examples where the measure of maximal entropy is nonhyperbolic. We also present examples where the measure of maximal entropy is unique and nonhyperbolic, however in this case the dynamics is nontransitive.

1 Introduction

An important task in ergodic theory is to describe the topology of the space of invariant and/or ergodic measures which are supported on a given invariant set. Here in many cases the weak$*$ topology is considered, though one also studies convergence in the weak$*$ topology and entropy. Recently there happened a certain revival of this type of problems in the context of nonhyperbolic dynamical systems [2, 12, 16, 17], most of them revisiting the pioneering work of Sigmund on topological dynamical systems satisfying the specification property [27, 28].

For a general continuous map F on a metric space $\Lambda$, consider the set of F-invariant Borel probability measures $\mathcal {M}(\Lambda )$ and denote by $\mathcal {M}_{\mathrm{erg}}(\Lambda )$ the subset of ergodic ones. If $\Lambda$ is compact then $\mathcal {M}=\mathcal {M}(\Lambda )$ is a Choquet simplex whose extremal elements are the ergodic measures. Density of ergodic measures in $\mathcal {M}$ implies that either $\mathcal {M}$ is a singleton (when F is uniquely ergodic) or a nontrivial simplex whose extreme points are dense. In the latter case, it is the so-called Poulsen simplex and by [23] it has immediately a number of further strong properties such as arcwise connectedness. Sigmund [27, 28] addressed first the questions on the density of ergodic measures and also the properties of generic invariant measures. He showed that for a map F satisfying the so-called periodic specification property the periodic measures (and thus the ergodic ones) are dense in $\mathcal {M}$. Here a measure is periodic if it is the invariant probability measure supported on a periodic orbit. Moreover, the sets of ergodic measures and of measures with entropy zero are both residual in $\mathcal {M}$. For an updated discussion and more references, see [16].

Observe that Sigmund’s results [27, 28] immediately apply to any basic set of a smooth Axiom A diffeomorphism. In a (more) general context, to address the general question if the space $\mathcal {M}$ has dense extreme points or at least is connected, some natural requirements are to be satisfied. An important one is certainly topological transitivity, which is however far from being sufficient as for example there exist minimal systems with exactly two ergodic measures.

Nowadays arguments which provide the connectedness of $\mathcal {M}$ are largely based on the approximation of invariant measures by periodic measures or Markov ergodic measures supported on horseshoes (a specific type of basic set). This demands that the periodic orbits involved are hyperbolic and somehow dynamically related among themselves. A natural relation introduced by Newhouse [24], and used in this context, is the homoclinic relation, that is, the un-/stable invariant sets of these orbits intersect cyclically and transversally.

A natural strategy is to study the components of the space of measures which each are candidate to correspond to one of the “elementary” undecomposable pieces of the dynamics. One of the possibilities to define properly what is meant by elementary is the homoclinic class, that is, the closure of the hyperbolic periodic orbits which are homoclinically related to the orbit of a hyperbolic periodic point P and denoted by H(P). Note that one of the fundamental properties is that the dynamics on each class is topologically transitive. Basic sets of the hyperbolic theory mentioned above are the simplest examples of homoclinic classes.

Notice that, when defining a homoclinic class, taking the closure can incorporate other orbits which are dynamically related but which are of different type of hyperbolicity. In this way, homoclinic classes may fail to be hyperbolic, contain saddles of different types of hyperbolicity (different $\mathrm{u}$-index, that is, dimension of unstable manifold), exhibit internal cycles, and support nonhyperbolic measures (also with positive entropy). Homoclinic classes of periodic points of different indices may even coincide. Furthermore, there are examples where a homoclinic class H(P) of a periodic point P properly contains another class $H(P')$ of a periodic point $P'$ of the same index as P. Note that this precisely occurs if $P'\in H(P)$ was not homoclinically related to P. One sometimes refers to $H(P')$ as an exposed piece of H(P) [10]. This type of phenomenon is a key ingredient in this paper. This gives only a rough idea what complicated structure these classes may have, see also [3, Chapter 10.4] for a more complete discussion.

To be more precise for the following, we say that an ergodic measure $\mu$ is hyperbolic if its Lyapunov exponents are nonzero. Moreover, almost all points have the same number $u=u(\mu )$ of positive Lyapunov exponents and we call this number u the $\mathrm{u}$-index of$\mu$ (analogously to hyperbolic periodic measures above). Given u, we denote by denote by $\mathcal {M}_{\mathrm{erg},u}$ the set of ergodic measures of $\mathrm{u}$-index u. Note that in general one may have $\mathcal {M}_{\mathrm{erg},u}(H(P))\ne \varnothing$ for several values of u.

For the following let us study the topological structure of $\mathcal {M}_{\mathrm{erg},u}(H(P))$ for u being the index of P. Assuming that H(P) is locally maximal and that all the saddles of index u are homoclinically related, in [17] it is shown that $\mathcal {M}_{\mathrm{erg},u}(H(P))$ is path connected with periodic measures being dense and that its closure is a Poulsen simplex. Note that $\mathcal {M}_{\mathrm{erg},u}(H(P))$ may only capture some part of $\mathcal {M}_{\mathrm{erg}}(H(P))$. Indeed this occurs when H(P) contains saddles of different indices. Still in this context, assume now that there coexists a saddle Q of index $v\ne u$ and having the property that $H(Q)\subset H(P)$ (in an extreme case, these classes can even coincide as sets) and assume that all the saddles of index v in H(Q) are homoclinically related with Q and consider $\mathcal {M}_{\mathrm{erg},v}(H(Q))$. Though the interrelation between $\mathcal {M}_{\mathrm{erg},u}(H(P))$ and $\mathcal {M}_{\mathrm{erg},v}(H(Q))$ is not addressed in [17], note that, by the very definition, they are disjoint. Nevertheless, their closures may intersect or may not. Indeed, the space $\mathcal {M}_{\mathrm{erg}}(H(P))$ may be connected or may not. To address this point is precisely the goal of this paper.

We introduce a class of examples of saddles P and Q of different indices whose homoclinic classes coincide $H(P)=H(Q)=\Lambda$ such that $\Lambda$ is the disjoint union of two invariant sets $\Lambda _{\mathrm {ex}}$ (a compact set that is a topological horseshoe) and $\Lambda _{\mathrm {core}}$. Moreover, these sets satisfy the following properties: (i) $P, Q\in \Lambda _{\mathrm {core}}$ and the closure of $\Lambda _{\mathrm {core}}$ is the whole homoclinic class, (ii) every pair of saddles of the same index in $\Lambda _{\mathrm {core}}$ (respectively, $\Lambda _{\mathrm {ex}}$) are homoclinically related, and (iii) no saddle in $\Lambda _{\mathrm{core}}$ is homoclinically related to any one in $\Lambda _{\mathrm{ex}}$. We refer to $\Lambda _{\mathrm {ex}}$ as the exposed piece of $\Lambda =H(P)=H(Q)$ and to $\Lambda _{\mathrm{core}}$ as its core. We study the space $\mathcal {M}_{\mathrm{erg}}(\Lambda )$ and show that it has an interesting topological structure: the set $\mathcal {M}_{\mathrm{erg}}(\Lambda )$ has three pairwise disjoint parts $\mathcal {M}_{\mathrm{erg},u}(\Lambda )$, $\mathcal {M}_{\mathrm{erg},v}(\Lambda )$, $v=u+1$ and u, v are the indices of P and Q, and $\mathcal {M}_{\mathrm{erg}}(\Lambda _{\mathrm {ex}})$, such that

$$\begin{aligned} \mathcal {M}_{\mathrm{erg}}(\Lambda )= \mathcal {M}_{\mathrm{erg},u}(\Lambda ) \cup \mathcal {M}_{\mathrm{erg},u}(\Lambda ) \cup \mathcal {M}_{\mathrm{erg}}(\Lambda _{\mathrm {ex}}) \cup \mathcal {M}_{\mathrm{erg, nhyp}}(\Lambda ) \end{aligned}$$

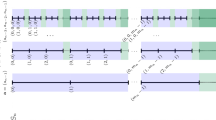
where $\mathcal {M}_{\mathrm{erg, nhyp}}(\Lambda )$ is the set of of nonhyperbolic ergodic measures of $\Lambda$. Note that $\mathcal {M}_{\mathrm{erg}}(\Lambda _{\mathrm {ex}})$ and $\mathcal {M}_{\mathrm{erg, nhyp}}(\Lambda )$ may intersect. Moreover, the sets $\mathrm {closure}(\mathcal {M}_{\mathrm{erg},u}(\Lambda ))$, $\mathrm {closure}(\mathcal {M}_{\mathrm{erg},v}(\Lambda ))$, and $\mathrm {closure}(\mathcal {M}_{\mathrm{erg}}(\Lambda _{\mathrm {ex}}))$, are Poulsen simplices whose intersection is contained in $\mathcal {M}_{\mathrm{erg, nhyp}}(\Lambda )$, see Theorem 2.5. Figure 1 below illustrates the interrelation between the measure space components.

Fig. 1

The space $\mathcal {M}_{\mathrm{erg}}(\Lambda )$

Let us say a few additional words about the topological structure of the set $\Lambda =H(P)=H(Q)$. There are two exposed saddles $P_{\mathrm {ex}}, Q_{\mathrm {ex}} \in \Lambda _{\mathrm {ex}}$ of the same indices such as P and Q, respectively, which are involved in a heterodimensional cycle (i.e., the invariant sets of these saddles meet cyclically), Indeed, the intersections of these invariant sets give rise to the exposed piece of dynamics that satisfy $\Lambda _{\mathrm {ex}}=H(P_{\mathrm {ex}})=H(Q_{\mathrm {ex}})\subsetneq \Lambda$. We are aware that on one hand this is a quite specific dynamical configuration, on the other hand it provides paradigmatic examples. We also observe that this dynamical configuration resembles in some aspects the so-called Bowen eye (a two dimensional vector field having two saddle singularities involved in a double saddle connection) in [15, 30] and the examples due to Kan of intermingled basins of attractions (where an important property is that the boundary of an annulus is preserved) [19]. Finally, if we considered systems satisfying some boundary conditions or preserving a boundary, the conditions considered are quite general.

A particular emphasize is given to the measures of maximal entropy. In some cases, these measures can be nonhyperbolic. We give a (non-transitive) example where the unique measure of maximal entropy is nonhyperbolic.

Finally, we state our results for step skew products (these examples have differentiable realizations as partially hyperbolic sets with one dimensional central direction) and throughout the paper we do not aim generality, on the contrary our goal is to make the construction in the simplest setting emphasizing the key ingredients behind the constructions.

This paper is organized as follows. In Sect. 2 we state precisely our setting and our examples and state our main results. In Sect. 3 we study the “symmetries” between certain measures and investigate entropy. In Sect. 4 we study the approximation of “boundary measures”. In Sect. 5 we study the measures supported in $\Lambda _{\mathrm {core}}$. In “Appendix A” we provide details on transitivity and homoclinic relations in our examples and we analyze examples with nonhyperbolic measures of maximal entropy.

2 Setting and statement of results

We now define precisely the dynamics that we will study. Consider $C^1$ diffeomorphisms $f_0,f_1:[0,1]\rightarrow [0,1]$ satisfying the following properties:

• (H1) The map $f_0$ has (exactly) two fixed points $f_0(0)=0$ and $f_0(1)=1$, satisfies $f_0'(0)=\beta >1$ and $f_0'(1)=\lambda \in (0,1)$.

• (H2) The map $f_1$ has negative derivative and satisfies $f_1(0)=1$ and $f_1(1)=0$.

The simplest (and also paradigmatic) example occurs when $f_1(x)=1-x$.

Let $\sigma :\Sigma _2 \rightarrow \Sigma _2$ be the standard shift map on the shift space $\Sigma _2=\{0,1\}^{{\mathbb {Z}}}$ of two-sided sequences, endowed with the usual metric. Consider the one step-skew product map F associated to $\sigma$ and the maps $f_0$ and $f_1$ defined by

$$\begin{aligned} F:\Sigma _2\times [0,1]\rightarrow \Sigma _2 \times [0,1],\quad ( \xi , x) \mapsto \big ( \sigma (\xi ) , f_{\xi _0}(x) \big ). \end{aligned}$$

(2.1)

We consider the following F-invariant subsets of $\Lambda {\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}\Sigma _2\times [0,1]$

$$\begin{aligned} \Lambda _{\mathrm{{ex}}}{\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}\Sigma _2\times \{0,1\}, \quad \Lambda _{\mathrm{{core}}} {\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}( \Sigma _2\times [0,1]){\setminus }\Lambda _{\mathrm{{exc}}} =\Sigma _2\times (0,1). \end{aligned}$$

(2.2)

We say that $\Lambda _{\mathrm{{ex}}}$ is the exposed piece of $\Sigma _2\times [0,1]$ and that $\Lambda _{\mathrm{{core}}}$ is the core of $\Sigma _2\times [0,1]$ (these denominations are justified below). Note that $\Lambda _{\mathrm{{ex}}}$ is closed while $\Lambda _{\mathrm{{core}}}$ is not. Moreover, $F|_{\Lambda _{\mathrm{ex}}}$ is topologically transitive. In fact, $F|_{\Lambda _{\mathrm{ex}}}$ is conjugate to a subshift of finite type, one may think this dynamical system as a horseshoe in a “plane”, in that plane any pair of saddles are “homoclinically related”.

Remark 2.1

(Topological dynamics on $\Sigma _2\times [0,1]$) Note again that $F|_{\Lambda _{\mathrm{ex}}}$ is conjugate to a subshift of finite type. While the dynamics in $\Lambda _{\mathrm{ex}}$ is completely characterized, in our quite general setting very few can be said about the dynamics of F in $\Lambda _{\mathrm{core}}$. The most interesting case certainly occurs when $F|_{\Lambda _{\mathrm{core}}}$ is topologically transitive. Below we will see more specific examples where this transitivity indeed holds and, moreover, hyperbolic periodic orbits of positive and negative Lyapunov exponent are both dense in $\Sigma _2\times [0,1]$ and homoclinically related. We will see that nevertheless the measure space $\mathcal {M}(\Lambda _{\mathrm{ex}})$ is “semi-detached” from $\mathcal {M}(\Lambda _{\mathrm{core}})$.

Consider now more specific hypotheses on the $C^1$ diffeomorphisms interval maps $f_0,f_1:[0,1]\rightarrow [0,1]$:

• (H2’) $f_1(x)=1-x$.

• (H3) The derivative $f_0^\prime$ is decreasing. Considering the point $c\in (0,1)$ defined by the condition $f_0^\prime (c)=1$, it holds $f_1 \circ f_0^2(c)> f_0^2(c).$

• (H4) The numbers $\lambda$ and $\beta$ given in (H1) satisfy

  $$\begin{aligned} \varkappa {\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}\frac{\lambda ^2\, (1-\lambda )}{\beta \, (\beta -1)}>1. \end{aligned}$$

Observe that for fixed $\lambda$, the inequality in (H4) holds whenever $\beta$ is close enough to 1.

Fig. 2

Fiber maps of the example in Remark 2.4

Proposition 2.2

Assume that F defined in (2.1) satisfies the hypotheses (H1), (H2’), (H3), and (H4). Then F is topologically transitive. Moreover, every pair of fiber expanding hyperbolic periodic orbits and every pair of fiber contracting hyperbolic periodic orbits in $\Lambda _{\mathrm{core}}$ are homoclinically related, respectively.

Remark 2.3

(Discussion of hypotheses) Homoclinic relations for skew products are recalled in “Appendix A”, where also the above proposition is proved. Condition (H4) will provide so-called expanding itineraries which in turn imply the homoclinic relations and their density for expanding points, while condition (H3) takes care of so-called contracting itineraries and the corresponding homoclinic relations. Thus, we conclude transitivity. The proof follows largely blender-like standard arguments used in [8]. Condition (H2’) is only used for simplicity and also to follow more closely the model in [14]. The key facts remain true assuming only (H2), in particular we never use the fact that for (H2’) the map $f_1$ is an involution.

We observe that (H3) and (H4) demand a certain “asymmetry” of the fiber map $f_0$. In Sect. A.4 we will provide a “symmetric” example which satisfies (H1) and for which the associated skew product fails to be transitive and its only measure of maximal entropy is nonhyperbolic and supported on $\Lambda _{\mathrm{ex}}$.

Remark 2.4

(Examples in $\Sigma _3\times \mathbb {S}^1$ and $\Sigma _2\times \mathbb {S}^1$) We can produce a transitive example in $\Sigma _3\times \mathbb {S}^1$ with properties analogous to the one in Proposition 2.2 as follows. Obtain $\mathbb {S}^1$ by identifying the boundary points of [0, 2]. Define $g_0,g_1,g_2:\mathbb {S}^1\rightarrow \mathbb {S}^1$ as follows

• $g_0(x)=f_0(x)$ if $x\in [0,1]$ and $g_0(x)=2-f_0 (2-x)$ if $x\in (1,2)$.

• $g_1(x)=f_1(x)=1-x$ if $x\in [0,1]$ and $g_1(x)=3-x$ if $x\in (1,2)$,

• $g_2(x)=2-x \mod 2$ (or any appropriate map preserving $\{0,1\}$ and interchanging the intervals (0, 1) and (1, 2)).

These maps are depicted in Fig. 2. In this case, $\Lambda _{\mathrm {ex}}=\Sigma _3\times \{0,1\}$ and $\Lambda _{\mathrm {core}}=\Sigma _3\times ((0,1)\cup (1,2))$. We observe that the IFS $\{g_0,g_1,g_2\}$ does not satisfy the axioms stated in [11] which would prevent the existence of exposed pieces of dynamics. Although the Axioms Transitivity and CEC (controlled expanding forward/backward covering) can be verified, the Axiom Accessibility is not satisfied (the points $\{0,1,2\}$ cannot “be reached from outside”).

Note that the skew product on $\Sigma _2\times {\mathbb {S}}^1$ generated by the fiber maps $\{g_0,g_1\}$ as above is not transitive and has two open “transitive” components $\Lambda _{\mathrm{core}}^-$ and $\Lambda _{\mathrm{core}}^+$ contained in $\Sigma _2\times (0,1)$ and $\Sigma _2\times (1,2)$, respectively, which are glued at the “exposed” piece $\Sigma _2\times \{0,1\}$. The additional map $g_2$ in the previous example just mixes the two components $\Lambda _{\mathrm{core}}^\pm$ while preserving the exposed piece.

Let $\mathcal {M}$ be the space of all F-invariant measures and equip it with the weak$*$ topology. It is well known that it is a compact metrizable topological space [31, Chapter 6.1]. Denote by $\mathcal {M}_{\mathrm{erg}}=\mathcal {M}_{\mathrm{erg}}(\Sigma _2\times [0,1])$ the subset of ergodic measures. We denote by $\mathcal {M}_{\mathrm{erg}}(\Lambda _{\mathrm{ex}})$ the ergodic measures supported on $\Lambda _{\mathrm{ex}}$ and by $\mathcal {M}_{\mathrm{erg}}(\Lambda _{\mathrm{core}})$ the ergodic measures supported on $\Lambda _{\mathrm{core}}$. Observe that

$$\begin{aligned} \mathcal {M}_{\mathrm{erg}} =\mathcal {M}_{\mathrm{erg}}(\Lambda _{\mathrm{core}})\cup \mathcal {M}_{\mathrm{erg}}(\Lambda _{\mathrm{ex}}). \end{aligned}$$

We will study this system by separately looking at measures supported on these two sets. A crucial point for us is how these two components “glue”.

Given $X=(\xi ,x)\in \Sigma _k\times [0,1]$, we consider the (fiber) Lyapunov exponent of the map F at X which is defined by

$$\begin{aligned} \chi (X) {\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}\lim _{n\rightarrow \pm \infty }\frac{1}{ n}\log \,|(f^n_\xi )'(x)|, \quad \text { where }\quad f_\xi ^n{\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}f_{\xi _{n-1}}\circ \cdots \circ f_{\xi _0}, \end{aligned}$$

where we assume that both limits exist and are equal. Note that it is nothing but the Birkhoff average of a continuous function. Given an invariant measure $\mu \in \mathcal {M}(\Lambda )$, define its Lyapunov exponent by

$$\begin{aligned} \chi (\mu ) {\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}\int \log \,|(f_\xi ^n)'(x)|\,d\mu (\xi ,x). \end{aligned}$$

For every F-ergodic Borel probability measure $\mu$ the Lyapunov exponent is almost everywhere well defined and constant equal to $\chi (\mu )$. An ergodic measure $\mu$ is nonhyperbolic if $\chi (\mu )=0$ and hyperbolic otherwise.¹

Accordingly, we split the set of all ergodic measures in $\Lambda _{\mathrm{core}}$ and consider the decomposition

$$\begin{aligned} \mathcal {M}_{\mathrm{erg}}(\Lambda _{\mathrm{core}}) =\mathcal {M}_{\mathrm{erg,<0}}(\Lambda _{\mathrm{core}})\cup \mathcal {M}_{\mathrm{erg,0}}(\Lambda _{\mathrm{core}}) \cup \mathcal {M}_{\mathrm{erg,>0}}(\Lambda _{\mathrm{core}}) \end{aligned}$$

into measures with negative, zero, and positive fiber Lyapunov exponent, respectively. Analogously, we consider

$$\begin{aligned} \mathcal {M}_{\mathrm{erg}}(\Lambda _{\mathrm{ex}}) =\mathcal {M}_{\mathrm{erg,<0}}(\Lambda _{\mathrm{ex}})\cup \mathcal {M}_{\mathrm{erg,0}}(\Lambda _{\mathrm{ex}}) \cup \mathcal {M}_{\mathrm{erg,>0}}(\Lambda _{\mathrm{ex}}). \end{aligned}$$

Properties of the space of measures are summarized in the next theorem. Given $\mathcal {N}\subset \mathcal {M}$, its closed convex hull is the smallest closed convex set containing $\mathcal {N}$.

Theorem 2.5

Assume that F defined in (2.1) satisfies the hypotheses (H1) and (H2). Then the space $\mathcal {M}(\Sigma _2\times [0,1])$ has the following properties:

• 1. Periodic orbit measures are dense in the closed convex hull of $\mathcal {M}_{\mathrm{erg}}(\Lambda _{\mathrm{ex}})$.

• 2. Every measure $\mathcal {M}(\Lambda _{\mathrm{ex}})$ with $\chi (\mu )\ne 0$ has positive weak$*$ distance from $\mathcal {M}(\Lambda _{\mathrm{core}})$.

• 3. Every measure $\mu \in \mathcal {M}(\Lambda _{\mathrm{ex}})$ with $\chi (\mu )=0$ can be weak$*$ approximated by periodic measures in $\mathcal {M}_{\mathrm{erg}}(\Lambda _{\mathrm{core}})$.

• 4. Each of the components $\mathcal {M}_{\mathrm{erg,\star }}(\Lambda _{\mathrm{ex}})$, $\star \in \{<0,0,>0\}$ is nonempty.

Moreover, if hypotheses (H2’), (H3), and (H4) additionally hold, then

• 5. The set $\mathcal {M}_{\mathrm{erg,\star }}(\Lambda _{\mathrm{core}})$, $\star \in \{<0,>0\}$, is nonempty.

• 6. The set $\mathcal {M}_{\mathrm{erg,<0}}(\Lambda _{\mathrm{core}})$ and the set $\mathcal {M}_{\mathrm{erg,>0}}(\Lambda _{\mathrm{core}})$ are arcwise connected, respectively.

Fig. 3

Porcupine-like horseshoes

The fact that there are ergodic measures with zero Lyapunov exponent and positive entropy in $\mathcal {M}_{\mathrm{erg}}(\Lambda _{\mathrm{core}})$ can be shown using methods in [1], we refrain from discussing this here. We also refrain from studying how such measures are approached by hyperbolic ergodic measures in $\mathcal {M}_{\mathrm{erg}}(\Lambda _{\mathrm{core}})$ as this is much more elaborate and will be part of an ongoing project (see [11] for techniques in a slightly different but technically simpler context).

Fig. 4

Fiber maps in (2.1)

Remark 2.6

(Porcupine vs. totally spiny porcupine) Let us compare the porcupine-like horseshoes corresponding to the interval maps in Fig. 3 with the “totally spiny porcupine” discussed here (corresponding to Fig. 4). Porcupine-like horseshoes were introduced in [13] as model for internal heterodimensional cycles in horseshoes. Later these horseshoes were generalized and studied in a series of papers from various points of view: topological [8,9,10], thermodynamical [10, 22, 25, 26] and fractal [14].² This line of research is also closely related to the study of so-called bony attractors and sets (see [18] for a survey and references). One important motivation to study those models is that they serve as a prototype of partially hyperbolic dynamics.

Let us consider the map $F_t$ defined as in (2.1) but with the maps $f_0,f_{1,t}$ as in Fig. 3 in the place of $f_0,f_1$ in Fig. 4. Let $\Gamma ^t$ be the maximal invariant set of $F_t$. In the above cited porcupine-like horseshoes, one also splits the maximal invariant set $\Gamma ^t$ (which is nonhyperbolic and transitive) into two parts $\Gamma ^t_{\mathrm{ex}}$ and $\Gamma ^t_{\mathrm{core}}$ in the same spirit as in (2.2) (and with analogous properties as in Proposition 2.2). In that case $\Gamma ^t_{\mathrm{ex}}$ consists only of one fiber expanding point $Q=(0^{\mathbb {Z}},0)$ and $\Gamma ^t_{\mathrm{core}}$ is its complement that contains the fiber contracting point $P=(0^{\mathbb {Z}},1)$. The space of ergodic measures of $\Gamma ^t$ splits into two components, each of them connected but at positive distance from each other, which are $\{\delta _Q\}$ and $\mathcal {M}_{\mathrm{erg}}(\Gamma ^t_{\mathrm{core}})$ (see, in particular, [22]). In the transition from a porcupine to a totally spiny porcupine (which occurs at $t=1$), the space of ergodic measures becomes connected (stated in Theorem 2.5) and this happens as follows. The measures $\delta _Q$ and $\delta _P$ form part of the space of ergodic measures of an abstract horseshoe $\Lambda _{\mathrm{ex}}$. At the same time, the measure $\delta _P$ detaches from $\mathcal {M}_{\mathrm{erg}}(\Lambda _{\mathrm{core}})$ which is a consequence of the fact that the saddle P is not homoclinically related to any saddle in $\Lambda _{\mathrm{core}}$, similarly for Q. The components $\mathcal {M}_{\mathrm{erg}}(\Lambda _{\mathrm{ex}})$ and $\mathcal {M}_{\mathrm{erg}}(\Lambda _{\mathrm{core}})$ become glued through nonhyperbolic measures.

Theorem 2.7

Assume that F defined in (2.1) satisfies the hypotheses (H1) and (H2). Then there is a unique measure $\mu _{\mathrm{max}}^{\mathrm{ex}}$ of maximal entropy $\log 2$ in $\mathcal {M}_{\mathrm{erg}}(\Lambda _{\mathrm{ex}})$ and its Lyapunov exponent is given by

$$\begin{aligned} \chi (\mu _{\mathrm{max}}^{\mathrm{ex}}) = \frac{1}{4}\left( \log \, f_0'(0)+\log \, f_0'(1) +\log \, |f_1'(0)|+\log \, |f_1'(1)|\right) . \end{aligned}$$

Moreover, if the measure $\mu _{\mathrm{max}}^{\mathrm{ex}}$ is hyperbolic then there exists at least one measure of maximal entropy in $\mathcal {M}_{\mathrm{erg}}(\Lambda _{\mathrm{core}})$. More precisely, if the measure $\mu _{\mathrm{max}}^{\mathrm{ex}}$ has positive (negative) Lyapunov exponent then there exists a measure of maximal entropy with nonpositive (nonnegative) exponent in $\mathcal {M}_{\mathrm{erg}}(\Lambda _{\mathrm{core}})$.

Note that the topological structure of $\mathcal {M}(\Lambda _{\mathrm{ex}})$ (items 1. and 4. in Theorem 2.7) are immediate consequences of the fact that the dynamics of F on $\Lambda _{\mathrm{ex}}$ is conjugate to a subshift of finite type (see Sect. 3 for details).

Note that the under the hypotheses of the above theorem, we do not know if the measure of maximal entropy in $\Lambda _{\mathrm{core}}$ is hyperbolic or not.

Remark 2.8

In view of Theorem 2.7, choosing the derivatives of the fiber maps at 0 and 1 appropriately, one obtains one measure of maximal entropy $\mu _{\mathrm{max}}^{\mathrm{ex}}$ which is nonhyperbolic. Note that condition (H4) is incompatible with such a choice, and hence it is unclear if the system is transitive (compare Proposition 2.2).

Similar arguments apply to the examples discussed in Remark 2.4. It is interesting to compare to the results in [29] where ergodic measures with “sufficiently high entropy” are always hyperbolic, though there a key ingredient is accessibility which is missing here.

In “Appendix A.3”, we provide examples where the system is transitive and exhibits a nonhyperbolic measure of maximal entropy in $\mathcal {M}_{\mathrm{erg}}(\Lambda _{\mathrm{ex}})$, proving the following theorem.

Theorem 2.9

There are maps ${\tilde{F}}$ defined as in (2.1) whose fiber maps ${\tilde{f}}_0,{\tilde{f}}_1$ satisfy

• 1. ${\tilde{f}}_0$ has (exactly) two fixed points ${\tilde{f}}_0(0)=0$ and ${\tilde{f}}_0(1)=1$, with ${\tilde{f}}_0'(0)=1={\tilde{f}}_0'(1)$,

• 2. ${\tilde{f}}_1(x)=1-x$,

such that ${\tilde{F}}$ is topologically transitive and that every pair of fiber expanding hyperbolic periodic orbits and every pair of fiber contracting hyperbolic periodic orbits in $\Lambda _{\mathrm{core}}$ are homoclinically related, respectively. In particular, the unique measure of maximal entropy in $\mathcal {M}_{\mathrm{erg}}(\Lambda _{\mathrm{ex}})$ is nonhyperbolic.

Note that in the above theorem this measure is also a measure of maximal entropy in $\mathcal {M}_{\mathrm{erg}}(\Lambda )$, however we do not know if there is some hyperbolic measure of maximal entropy in $\mathcal {M}_{\mathrm{erg}}(\Lambda )$.

Mutatis mutandi, we can perform a version of the map ${\tilde{F}}$ in $\Sigma _3\times \mathbb {S}^1$ as in Remark 2.4.

Finally, in “Appendix A.4” we present an example with a unique measure of maximal entropy which is nonhyperbolic and supported on $\Lambda _{\mathrm{ex}}$. However this example fails to be transitive.

Theorem 2.10

There are maps F defined as in (2.1) whose fiber maps $f_0, f_1$ satisfy

• 1. $f_0$ has (exactly) two fixed points $f_0(0)=0$ and $f_0(1)=1$, with $f_0'(0)=1=f_0'(1)$,

• 2. $f_1(x)=1-x$.

such that F is not topologically transitive and has a unique (hence ergodic) measure of maximal entropy supported on $\Lambda _{\mathrm{ex}}$, which is nonhyperbolic.

One of the key properties of the class of examples in the above theorem is that $f_0$ is conjugate to its inverse $f_0^{-1}$ by $f_1$. The proof of the result is based on an analysis of random walks on ${\mathbb {R}}$ and of somewhat different flavor.

3 Symmetric, mirror, and twin measures

Recalling well-known facts about shift spaces, we will see that there is a unique measure of maximal entropy for $F|_{\Lambda _{\mathrm{ex}}}$ and we will deduce that, in the case this measure is hyperbolic, there is (at least) one “twin” measure in $\Lambda _{\mathrm{core}}$ with the same (maximal) entropy. The latter is either hyperbolic with opposite sign of its exponent or nonhyperbolic.

Recall that on the full shift $\sigma :\Sigma _2\rightarrow \Sigma _2$ there is a unique measure ${\widehat{\nu }}_{\mathrm{max}}$ of maximal entropy $\log 2$ which is the $(\frac{1}{2},\frac{1}{2})$-Bernoulli measure.

To study the structure of the invariant set $\Lambda _{\mathrm{ex}}$, consider the “first level” rectangles ${\mathbb {C}}_k{\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}\{\xi \in \Sigma _2:\xi _0=k\}$ and the subsets

$$\begin{aligned} {\widehat{{\mathbb {C}}}}_{0_L}{\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}{\mathbb {C}}_0\times \{0\} ,\quad {\widehat{{\mathbb {C}}}}_{1_L}{\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}{\mathbb {C}}_1\times \{0\} ,\quad {\widehat{{\mathbb {C}}}}_{0_R}{\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}{\mathbb {C}}_0\times \{1\} ,\quad {\widehat{{\mathbb {C}}}}_{1_R}{\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}{\mathbb {C}}_1\times \{1\} , \end{aligned}$$

of $\Sigma _2 \times [0,1]$. Consider the transition matrix A given by

$$\begin{aligned} A{\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}\left( \begin{matrix} 1&{}\quad 1&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 1&{}\quad 1\\ 0&{}\quad 0&{}\quad 1&{}\quad 1\\ 1&{}\quad 1&{}\quad 0&{}\quad 0 \end{matrix}\right) . \end{aligned}$$

This matrix codes the transitions between the symbols $\{0_L,1_L,0_R,1_R\}$ modelling the transitions between the sets ${\widehat{{\mathbb {C}}}}_{0_L}, {\widehat{{\mathbb {C}}}}_{1_L}, {\widehat{{\mathbb {C}}}}_{0_R}, {\widehat{{\mathbb {C}}}}_{1_R}$ by the map F. More precisely, note that the restriction of $F|_{\Lambda _{\mathrm{ex}}}$ is topologically conjugate to the subshift of finite type $\sigma _A:\Sigma _A\rightarrow \Sigma _A$ by means of a map $\varpi :\Lambda _{\mathrm {ex}}\rightarrow \Sigma _A$. Note that there is a unique measure of maximal entropy $\nu ^{\mathrm{ex}}_{\mathrm{max}}$ for $\sigma _A:\Sigma _A\rightarrow \Sigma _A$.³ Note that $h_{\nu ^{\mathrm{ex}}_{\mathrm{max}}}(\sigma )=\log 2$. Hence, by conjugation, the measure $\mu ^{\mathrm{ex}}_{\mathrm{max}}=(\varpi ^{-1})_*\nu ^{\mathrm{ex}}_{\mathrm{max}}$ is the unique measure of maximal entropy $\log 2$ for $F:\Lambda _{\mathrm{ex}}\rightarrow \Lambda _{\mathrm{ex}}$.

We define the following projection

$$\begin{aligned} \begin{aligned} \Pi :\Sigma _A\rightarrow \Sigma _2, \quad \Pi (\ldots i_{-1}.i_0\ldots )&{\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}(\ldots \xi _{-1}.\xi _0\ldots ),\\ \xi _k&{\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}{\left\{ \begin{array}{ll} 0&{}\quad \text {if }i_k\in \{0_L,0_R\}\\ 1&{}\quad \text {if }i_k\in \{1_L,1_R\}. \end{array}\right. } \end{aligned} \end{aligned}$$

It is immediate to check that

$$\begin{aligned} {\widehat{\nu }}_{\mathrm{max}} = \Pi _*\nu ^{\mathrm{ex}}_{\mathrm{max}}. \end{aligned}$$

We say that the symbols $i_R$, $j_L$ are the mirrors of $i_L$ and $j_R$, respectively, for i and j in $\{0,1\}$ and denote $i_R=\bar{i_L}$ and $j_L=\bar{j_R}$. Given a sequence $\xi =(\ldots \xi _{-1}.\xi _0\ldots )\in \Sigma _A$, we define by $\bar{\xi }=(\ldots \bar{\xi _{-1}}.\bar{\xi _0}\ldots )$ the mirrored sequence of $\xi$. Note that ${\bar{\xi }}\in \Sigma _A$. Given a subset $B\subset \Sigma _A$, we denote by ${\bar{B}}{\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}\{{\bar{\xi }}:\xi \in B\}$ its mirrored set.

Now we are ready to define symmetric sets and measures.

Definition 3.1

(Symmetric sets and measures) A measurable set $B\subset \Sigma _A$ is symmetric if $B={\bar{B}}$. We say that B is symmetric$\nu$-almost surely if $\nu (B\Delta {\bar{B}})=0$. A measure $\nu \in \mathcal {M}(\Sigma _A)$ is symmetric if $\nu (\bar{B})=\nu (B)$ for every $B\subset \Sigma _A$. If a measure is not symmetric then we call it asymmetric. A measure $\mu \in \mathcal {M}(\Lambda _{\mathrm {ex}})$ is symmetric if $\varpi _*\mu$ is symmetric, otherwise we call it asymmetric.

We denote by $\mathcal {M}_{\mathrm{erg}}^{\mathrm{sym}}(\Lambda _{\mathrm{ex}})$ and $\mathcal {M}_{\mathrm{erg}}^{\mathrm{asym}}(\Lambda _{\mathrm{ex}})$ the sets of symmetric and asymmetric ergodic measures in $\Lambda _{\mathrm{ex}}$, respectively.

We will use the following lemma.

Lemma 3.2

Let $\nu \in \mathcal {M}(\Sigma _A)$ be a symmetric measure. Then any set $B\subset \Sigma _A$ which is $\nu$-almost symmetric satisfies

$$\begin{aligned} \nu ((\Pi ^{-1}\circ \Pi )(B) ) = \nu (B). \end{aligned}$$

Proof

Indeed, by $\nu$-almost symmetry of B, setting $C{\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}B\cap {\bar{B}}$, $D{\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}{\bar{B}}{\setminus }C$, and $E{\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}B{\setminus }C$, we have $B=E\cup C$, $\nu (C)=\nu ({\bar{C}})=\nu (B)=\nu ({\bar{B}})$, and $\nu (D)=\nu (E)=0$. Hence $\nu ({\bar{D}})=\nu (D)=0$. Observing that

$$\begin{aligned} (\Pi ^{-1}\circ \Pi )(B) =B\cup {\bar{B}} = E\cup C\cup D \end{aligned}$$

the claim follows. $\square$

Lemma 3.3

For every $\nu \in \mathcal {M}_{\mathrm{erg}}(\Sigma _A)$, there exist at most one measure ${\bar{\nu }}\in \mathcal {M}_{\mathrm{erg}}(\Sigma _A)$, ${\bar{\nu }}\ne \nu$, such that $\Pi _*{\bar{\nu }}=\Pi _*\nu$. There is no such measure if, and only if, $\nu$ is symmetric.

Proof

It suffices to observe that the product $\sigma$-algebra of Borel measurable sets of $\Sigma _A$ is generated by the semi-algebra generated by the family of all finite cylinder sets $\{[i_k\ldots i_\ell ]\}$. Note also that the mirror ${\bar{C}}$ of a cylinder C in $\Sigma _A$ is again a cylinder in $\Sigma _A$. Now given $\nu \in \mathcal {M}_{\mathrm{erg}}(\Sigma _A)$, define a measure ${\bar{\nu }}$ by setting ${\bar{\nu }}(C){\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}\nu ({\bar{C}})$ for every cylinder C and extend it to the generated $\sigma$-algebra.

By definition, we immediately obtain that $\Pi _*{\bar{\nu }}=\Pi _*\nu$ and that $h_{{\bar{\nu }}}(\sigma _A)=h_\nu (\sigma _A)$.

To prove that $\nu$ and ${\bar{\nu }}$ are the only ergodic measures satisfying $\Pi _*{\bar{\nu }}=\Pi _*\nu$, by contradiction assume that there exists ${\widehat{\nu }}\in \mathcal {M}_{\mathrm{erg}}(\Sigma _A)$, ${\bar{\nu }}\ne {\widehat{\nu }}\ne \nu$ satisfying $\Pi _*{\widehat{\nu }}=\Pi _*\nu$. Consider the measure ${\widetilde{\nu }}{\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}\frac{1}{2}(\nu +{\bar{\nu }})$. Note that ${\widetilde{\nu }}$ is symmetric. Also note that $\Pi _*{\widetilde{\nu }}=\Pi _*{\widehat{\nu }}$. Finally note that ${\widetilde{\nu }}$ is singular with respect to ${\widehat{\nu }}$ and hence there is a set $B\subset \Sigma _A$ satisfying ${\widetilde{\nu }}(B)=0={\widehat{\nu }}(B^c)$. Since ${\widetilde{\nu }}$ is symmetric, we have ${\widetilde{\nu }}({\bar{B}})={\widetilde{\nu }}(B)$. So we obtain ${\widetilde{\nu }}({\bar{B}}\triangle B)=0$ and hence B is ${\widetilde{\nu }}$-almost symmetric. Hence, we have

$$\begin{aligned} \begin{aligned} 0&= {\widetilde{\nu }}(B) \\ (\text {by Lemma}~3.2)&= {\widetilde{\nu }}((\Pi ^{-1}\circ \Pi )(B)) = \Pi _*{\widetilde{\nu }}(\Pi (B)) \\ (\text {since }\Pi _*{\widetilde{\nu }}=\Pi _*{\widehat{\nu }}\,)&= \Pi _*{\widehat{\nu }}(\Pi (B)) = {\widehat{\nu }}((\Pi ^{-1}\circ \Pi )(B)) \ge {\widehat{\nu }}(B) =1, \end{aligned} \end{aligned}$$

a contradiction. This proves that ${\bar{\nu }}$ is uniquely defined.

By definition, $\nu$ is symmetric if, and only if, ${\bar{\nu }}=\nu$. $\square$

Definition 3.4

(Mirror measure) We call the measure ${\bar{\nu }}$ provided by Lemma 3.3 the mirror measure of $\nu$. We call the measure $\varpi ^{-1}_*{\bar{\nu }}\in \mathcal {M}(\Lambda _{\mathrm {ex}})$ the mirror measure of $\mu =\varpi ^{-1}_*\nu$ and denote it by ${\bar{\mu }}$.

The following is an immediate consequence of Lemma 3.3 and the uniqueness of the measure of maximal entropy.

Corollary 3.5

The measure of maximal entropy $\mu ^{\mathrm{ex}}_{\mathrm{max}}$ is symmetric.

Lemma 3.6

If ${\bar{\mu }}$ is a mirror measure of $\mu \in \mathcal {M}_{\mathrm{erg}}(\Lambda _{\mathrm{ex}})$ then $h_{{\bar{\mu }}}(F)=h_\mu (F)$. Moreover, we have

$$\begin{aligned} \chi ({\bar{\mu }})+\chi (\mu ) =N(0)\log ( f_0'(0)\cdot f_0'(1)) +N(1)\log ( f_1'(0)\cdot f_1'(1)), \end{aligned}$$

where $N(0){\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}\mu (\Sigma _2\times \{0\})$ and $N(1){\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}\mu (\Sigma _2\times \{1\})$.

Proof

Let $\nu =\varpi _*\mu$. It suffices to observe that a sequence $\xi$ is $\nu$-generic if, and only if, ${\bar{\xi }}$ is ${\bar{\nu }}$-generic and to do the straightforward calculation. $\square$

Definition 3.7

Given an ergodic measure $\mu \in \mathcal {M}_{\mathrm{erg}}(\Sigma _2\times [0,1])$, an ergodic measure ${\widetilde{\mu }}\in \mathcal {M}_{\mathrm{erg}}(\Sigma _2\times [0,1])$, ${\widetilde{\mu }}\ne \mu$, is called a twin measure of $\mu$ if $\pi _*{\widetilde{\mu }}=\pi _*\mu$.

Note that the above immediately implies that if $\mu \in \mathcal {M}_{\mathrm{erg}}(\Lambda _{\mathrm{ex}})$ is symmetric then all its twin measures are in $\mathcal {M}_{\mathrm{erg}}(\Lambda _{\mathrm{core}})$.

Lemma 3.8

(Existence of twin measures) For every measure $\lambda \in \mathcal {M}(\Sigma _2)$ there exist a measure $\mu _1\in \mathcal {M}(\Sigma _2\times [0,1])$ satisfying $\pi _*\mu _1=\lambda$ and $\chi (\mu _1)\ge 0$ and a measure $\mu _2\in \mathcal {M}(\Sigma _2\times [0,1])$ satisfying $\pi _*\mu _2=\lambda$ and $\chi (\mu _2)\le 0$.

Moreover, if $\lambda$ was ergodic then $\mu _1$ and $\mu _2$ can be chosen ergodic.

Note that the measures $\mu _1$ and $\mu _2$ in the above lemma may coincide.

Proof

First observe that $\lambda \in \mathcal {M}(\Sigma _2)$ is weak$*$ approximated by measures $\lambda _\ell \in \mathcal {M}(\Sigma _2)$ supported on periodic sequences.

For each such measure $\lambda _\ell$ there exists a measure $\mu _\ell \in \mathcal {M}(\Sigma _2\times [0,1])$ which is supported on a F-periodic orbit in $\Sigma _2\times [0,1]$ and satisfies $\pi _*\mu _\ell =\lambda _\ell$ and $\chi (\mu _\ell )\ge 0$. Indeed, assume that $\lambda _\ell$ is supported on the orbit of a periodic sequence $\xi \in \Sigma _2$ of period n. Recall that the fiber maps $f_0$ and $f_1$ and hence the map $f_\xi ^n$ preserve the boundary $\{0,1\}$. Hence, this map $f_\xi ^n$ has a fixed point $x\in [0,1]$ satisfying $|(f_\xi ^n)'(x)|\ge 1$. Now observe that the orbit of $(\xi ,x)$ is F-periodic of period n and taking the measure $\mu _\ell$ supported on it we have $\frac{1}{n}\log \,|(f_\xi ^n)'(x)|=\chi (\mu _\ell )$.

Now take any weak$*$ accumulation point $\mu$ of the sequence $(\mu _\ell )_\ell$. Note that by continuity of $\pi _*$ we have $\pi _*\mu =\lambda$.

If $\lambda$ was ergodic, $\mu$ might not be ergodic. However, any ergodic measure in the ergodic decomposition of $\mu$ also projects to $\lambda$ and hence there must exist one measure $\mu '$ in this decomposition satisfying $\chi (\mu ')\ge 0$.

The same arguments work for the case $\chi (\cdot )\le 0$. $\square$

Corollary 3.9

For every hyperbolic symmetric ergodic measure $\mu \in \mathcal {M}_{\mathrm{erg}}(\Lambda _{\mathrm{ex}})$ there exists an ergodic twin measure ${\widetilde{\mu }}\in \mathcal {M}_{\mathrm{erg}}(\Sigma _2\times (0,1))$, ${\widetilde{\mu }}\ne \mu$, satisfying $h_{{\widetilde{\mu }}}(F)=h_\mu (F)$.

Proof

Assume that $\chi (\mu )>0$, the other case $\chi (\mu )<0$ is analogous. Let $\lambda {\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}\pi _*\mu$. By Lemma 3.8, there exists a twin measure ${\widetilde{\mu }}\in \mathcal {M}_{\mathrm{erg}}(\Sigma _2\times [0,1])$ of $\mu$ satisfying $\chi ({\widetilde{\mu }})\le 0$. Note that $h_{\pi _*{\widetilde{\mu }}}(\sigma )\le h_{{\widetilde{\mu }}}(F)$ and $h_{\pi _*\mu }(\sigma )\le h_\mu (F)$. On the other hand, by [21]

$$\begin{aligned} \max \{h_\mu (F),h_{{\widetilde{\mu }}}(F)\}\le & {} \sup _{m:\pi _*m=\pi _*\mu }h_m(F) = h_{\pi _*\mu }(\sigma )\\&+\int h_{\mathrm{top}}(F,\pi ^{-1}(\xi ))\,d\pi _*\mu (\xi ). \end{aligned}$$

Since $\pi$ is 2–1, we have $h_{\mathrm{top}}(F,\pi ^{-1}(\xi ))=0$ for every $\xi$. Thus, we conclude $h_\mu (F)=h_{{\widetilde{\mu }}}(F)=h_{\pi _*\mu }(\sigma )$.

By conjugation $\varpi$ between $F|_{\Lambda _{\mathrm{ex}}}$ and $\sigma _A|_{\Sigma _A}$, there can be at most one other ergodic measure in $\mathcal {M}_{\mathrm{erg}}(\Lambda _{\mathrm{ex}})$ which project to the same measure on $\Sigma _2$, namely $\varpi ^{-1}_*{\bar{\nu }}$, where $\nu =\varpi ^{-1}_*\mu$ and ${\bar{\nu }}$ is the mirror measure of $\nu$. For symmetric $\mu$, no such mirror exists. Hence, we must have ${\widetilde{\mu }}\in \mathcal {M}_{\mathrm{erg}}(\Sigma _2\times (0,1))$. $\square$

By Corollary 3.5, the above applies in particular to $\mu _{\mathrm{max}}^{\mathrm{ex}}$.

Corollary 3.10

If the measure of maximal entropy $\mu _{\mathrm{max}}^{\mathrm{ex}}\in \mathcal {M}_{\mathrm{erg}}(\Lambda _{\mathrm{ex}})$ is hyperbolic then there exists an ergodic twin measure of maximal entropy ${\widetilde{\mu }}\in \mathcal {M}_{\mathrm{erg}}(\Lambda _{\mathrm{core}})$ such that $\chi ({\widetilde{\mu }})\chi (\mu _{\mathrm{max}}^{\mathrm{ex}})\le 0$.

Proof of Theorem 2.7

As recalled already, there is a unique measure of maximal entropy for $F|_{\Lambda _{\mathrm{ex}}}$ and its Lyapunov exponents can be easily calculated. The fact that there may exist another measure of maximal entropy for $F|_{\Lambda _{\mathrm{core}}}$ follows immediately from Corollary 3.10. $\square$

4 Approximations of boundary measures

This section discusses the approximation of measures in $\mathcal {M}(\Lambda _{\mathrm{ex}})$ by (ergodic) measures in $\mathcal {M}(\Lambda _{\mathrm{core}})$. In particular, we will complete the proof of Theorem 2.5. We will always work with the system satisfying hypotheses (H1) and (H2).

Remark 4.1

Recall again that $\mathcal {M}$ equipped with the weak$*$ topology it is a compact metrizable topological space [31, Chapter 6.1]. Recall that $X\in \Sigma _2\times [0,1]$ is a generic point of a measure $\mu \in \mathcal {M}(\Sigma _2\times [0,1])$ if the sequence $\frac{1}{n}(\delta _X+\delta _{F(X)}+\cdots +\delta _{F^{n-1}(X)})$ converges to $\mu$ in the weak$*$ topology, where $\delta _Y$ denotes the Dirac measure supported on Y. Recall that for every ergodic measure there exists a set of generic points with full measure. Note that $F|_{\Lambda _{\mathrm{ex}}}$ is conjugate to a subshift of finite type (see Remark 2.1). Hence, by [27, Corollary to Theorem 4], for every invariant measure $\mu \in \mathcal {M}(\Lambda _{\mathrm{ex}})$ there exists a $\mu$-generic point.

Given $\delta \in (0,1/2)$, we consider the local distortion map

$$\begin{aligned} \Delta (\delta ) {\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}\max _{i=0,1} \left\{ \max _{z\in [0,\delta ]}\left|\log \frac{|f_i'(z)|}{|f_i'(0)|}\right|, \max _{z\in [1-\delta ,1]}\left|\log \frac{|f_i'(z)|}{|f_i'(1)|} \right|\right\} . \end{aligned}$$

(4.1)

Note that $\Delta (\delta )\rightarrow 0$ as $\delta \rightarrow 0$. We state the following simple facts without proof.

Lemma 4.2

For every $\delta \in (0,1/2)$ and every $x\in [0,\delta ]$ we have

$$\begin{aligned} e^{-\Delta (\delta )} \le \frac{ f_i'(x)}{ f_i'(0)}, \frac{ f_i'(1-x)}{ f_i'(1)} \le e^{\Delta (\delta )} \end{aligned}$$

and

$$\begin{aligned} e^{-\Delta (\delta )} \le \frac{|f_i(x)-f_i(0)|}{|x||f_i'(0)|}, \frac{|f_i(1-x)-f_i(1)|}{|1-(1-x)||f_i'(1)|} \le e^{\Delta (\delta )} . \end{aligned}$$

Proposition 4.3

For every $\mu \in \mathcal {M}(\Lambda _{\mathrm{ex}})$ satisfying $\chi (\mu )=0$ there exists a sequence $(\mu _k)_k\subset \mathcal {M}_{\mathrm{erg}}(\Lambda _{\mathrm{core}})$ of measures supported on periodic orbits which converge to $\mu$ in the weak$*$ topology.

Proof

Let $\mu$ be an invariant measure supported in $\Lambda _{\mathrm{ex}}$ and satisfying the hypothesis $\chi (\mu )=0$ and let $X=(\xi ,x)\in \Lambda _{\mathrm{ex}}$ be a $\mu$-generic point. By Remark 4.1 such point indeed exists. Hence $\chi (X)=0$. Note that $\xi$ hence has infinitely many symbols 1 by our hypothesis $f_0'(0)\ne 1\ne f_0'(1)$. Hence, without loss of generality, we can assume that $x=1$.

Given the sequence $\xi =(\ldots \xi _{-1}.\xi _0\xi _1\ldots )$, for $n\ge 1$ define

$$\begin{aligned} \begin{aligned} p_n&{\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}{{\,\mathrm{card}\,}}\big \{i\in \{0,\ldots ,n-1\}:\xi _i=0, {{\,\mathrm{card}\,}}\{j<i:\xi _j=1\}\text { even}\big \},\\ q_n&{\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}{{\,\mathrm{card}\,}}\big \{i\in \{0,\ldots ,n-1\}:\xi _i=0, {{\,\mathrm{card}\,}}\{j<i:\xi _j=1\}\text { odd}\big \},\\ r_n&{\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}{{\,\mathrm{card}\,}}\big \{i\in \{0,\ldots ,n-1\}:\xi _i=1, {{\,\mathrm{card}\,}}\{j<i:\xi _j=1\}\text { even}\big \},\\ s_n&{\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}{{\,\mathrm{card}\,}}\big \{i\in \{0,\ldots ,n-1\}:\xi _i=1, {{\,\mathrm{card}\,}}\{j<i:\xi _j=1\}\text { odd}\big \}. \end{aligned} \end{aligned}$$

Note that $n=p_n+q_n+r_n+s_n$. Let

$$\begin{aligned} \phi (n) {\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}p_n\log \,|f_0'(1)|+q_n\log \,|f_0'(0)|+r_n\log \,|f_1'(1)|+ s_n\log \,|f_1'(0)|. \end{aligned}$$

(4.2)

Observe that $\phi (n)=\log \,|(f_\xi ^n)'(1)|$ and hence $\chi (X)=0$ implies

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{\phi (n)}{n}=0. \end{aligned}$$

Let

$$\begin{aligned} \psi (n) {\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}\max _{i=1,\ldots ,n}|\phi (i)|\end{aligned}$$

and note that

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{ \psi (n)}{n}=0. \end{aligned}$$

(4.3)

Let $B=\{0,1\}$. Given a fiber point $x_0\in (0,1)$ let us use the following notation of its orbit under the fiber dynamics determined by the sequence $\xi$:

$$\begin{aligned} x_i {\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}f_\xi ^i(x_0). \end{aligned}$$

(4.4)

Partially affine case To sketch the idea of the proof, assume for a moment that $f_0|_{I_\delta }$ and $f_1|_{I_\delta }$ are affine, where $I_\delta =[0,\delta ]\cup [1-\delta ,1]$ for some small $\delta >0$. Note that for given n and a point $x_0 \in [1-\delta , 1)$ satisfying

$$\begin{aligned} x_i\in I_\delta \quad \text { for all }\quad i\in \{0,\ldots ,n-1\} \end{aligned}$$

(4.5)

we have

$$\begin{aligned} \frac{{{\,\mathrm{Dist}\,}}(x_{i+1},B)}{{{\,\mathrm{Dist}\,}}(x_i,B)} = e^{\phi (i+1)-\phi (i)}, \end{aligned}$$

(4.6)

where ${{\,\mathrm{Dist}\,}}(x,B)$ denotes the distance of x from a set B. Hence

$$\begin{aligned} \frac{{{\,\mathrm{Dist}\,}}(x_n,B)}{{{\,\mathrm{Dist}\,}}(x_0,B)} = e^{\phi (n)}. \end{aligned}$$

This implies

$$\begin{aligned} e^{-\psi (n)} \le \frac{{{\,\mathrm{Dist}\,}}(x_i,B)}{{{\,\mathrm{Dist}\,}}(x_0,B)} \le e^{\psi (n)} \quad \text { for all }\quad i\in \{0,\ldots ,n\}. \end{aligned}$$

(4.7)

Note that (4.5) is satisfied provided $x_0$ was chosen to satisfy ${{\,\mathrm{Dist}\,}}(x_0,B)<\delta e^{-\psi (n)}$.

Note that $e^{-\psi (n)}$ may not converge to 0. For this reason, let us choose

$$\begin{aligned} \delta (n) {\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}\delta e^{-2\max \{\psi (n),\sqrt{n}\}}. \end{aligned}$$

(4.8)

Note that

$$\begin{aligned} \lim _{n\rightarrow \infty }\delta (n)e^{\psi (n)}=0. \end{aligned}$$

(4.9)

Let now n be a sufficiently large integer such that ${{\,\mathrm{card}\,}}\{j\le n-1:\xi _j=1\}$ is odd. Note that this implies $f_\xi ^n$ is orientation reversing. Let N(n) be the smallest positive integer such that $x_0{\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}f_0^{N(n)}(1/2)\in [1-\delta (n),1)$. Note that

$$\begin{aligned} N(n) \sim |\log \delta (n)|, \end{aligned}$$

(4.10)

where the approximation is up to some universal multiplicative factor, independent on n. Note that $f_0^{N(n)}$ is orientation preserving. We now apply the above arguments to the chosen point $x_0$. We consider the sequence $(x_i)_{i=0}^n$ as defined in (4.4). First, note that ${{\,\mathrm{Dist}\,}}(x_0,B)\sim \delta (n)$ and with (4.7) we have

$$\begin{aligned} \delta (n) e^{-\psi (n)} \le x_i \le {{\,\mathrm{Dist}\,}}(x_0,B) e^{\psi (n)} \le \delta (n) e^{\psi (n)} \quad \text { for all }\quad i\in \{0,\ldots ,n\}. \end{aligned}$$

Further note that $x_n$ by our choice of n is close to 0. Then let M(n) be the smallest positive integer such that $f_0^{M(n)}(x_n)\ge 1/2$. Note that $f_0^{M(n)}$ is orientation preserving. Note that

$$\begin{aligned} M(n) \sim |\log \delta (n)+\psi (n)|. \end{aligned}$$

(4.11)

Now consider the map $g{\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}f_0^{M(n)}\circ f_\xi ^n\circ f_0^{N(n)}$ and note that it reverses orientation. Hence, there exists a point y in the fundamental domain $[1/2,f_0(1/2))$ such that $g(y)=y$. Note that by the estimates of N(n) and M(n) in (4.10) and (4.11) and our choice of $\delta (n)$ in (4.8) and by (4.3) we have

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{N(n)+M(n)}{n} =0. \end{aligned}$$

(4.12)

We now consider the (invariant) measure $\mu _{n,\delta }$ supported on the periodic orbit of the point $Y=(\eta ,y)$, where $\eta =(0^{N(n)}\xi _0\ldots \xi _{n-1}0^{M(n)})^{\mathbb {Z}}$. It remains to show that this measure is close to $\mu$ in the weak$*$ topology provided that n was big. Note that we can write $\mu _{n,\delta }$ as

$$\begin{aligned} \begin{aligned} \mu _{n,\delta }=&\,\frac{N(n)}{N(n)+n+M(n)}\mu _1+\frac{n}{N(n)+n+M(n)}\frac{1}{n}\sum _{k=0}^{n-1}\delta _{F^{N(n)+k}(Y)} \\&+ \frac{M(n)}{N(n)+n+M(n)}\mu _2, \end{aligned} \end{aligned}$$

where $\mu _1$ and $\mu _2$ are some probability measures. Note that by (4.12) the first and the last term converges to 0 as n tends to $\infty$. The second term is close to $\mu$ because X was a $\mu$-generic point and the orbit piece $\{F^{N(n)}(Y),F^{N(n)+1}(Y),\ldots ,F^{N(n)+n}(Y)\}$ is $\delta (n)e^{\psi (n)}$-close to the orbit piece $\{X,F(X),\ldots ,F^{n}(X)\}$. Recalling (4.9), this completes the proof in the affine case.

General case In the nonaffine case the proof goes similarly. Applying Lemma 4.2, we choose the number $\delta (n)$ in an appropriate way. First note that instead of (4.6) by this lemma we have

$$\begin{aligned} \frac{{{\,\mathrm{Dist}\,}}(x_{i+1},B)}{{{\,\mathrm{Dist}\,}}(x_i,B)} \le e^{\phi (i+1)-\phi (i)} e^{\Delta (\delta )}. \end{aligned}$$

Arguing as above, let now

$$\begin{aligned} \delta (n) {\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}\delta e^{-2\max \{\psi (n),\sqrt{n}\}} e^{-n\Delta (\delta e^{-\sqrt{n}})}. \end{aligned}$$

Observe that with this choice, for every $x_0\in [1-\delta (n),1)$ for every $i\in \{1,\ldots , n\}$ we have

$$\begin{aligned} {{\,\mathrm{Dist}\,}}(x_i,B) \le \delta (n)e^{\phi (i)}e^{i\Delta (\delta e^{-\sqrt{n}})} \le \delta e^{-\sqrt{n}} \end{aligned}$$

provided that ${{\,\mathrm{Dist}\,}}(x_j,B)\le \delta e^{-\sqrt{n}}$ for all $j\in \{0,\ldots ,i-1\}$. By induction, we will get that for all $i\in \{0,\ldots , n\}$ we have

$$\begin{aligned} {{\,\mathrm{Dist}\,}}(x_i,B) \le \delta e^{-\sqrt{n}}. \end{aligned}$$

Note that with the above definition of $\delta (n)$ the estimates of N(n) and M(n) in (4.10) and (4.11) remain without changes. And the rest of the proof is analogous to the partially affine case. $\square$

We now prove the converse to Proposition 4.3.

Proposition 4.4

For every $\mu \in \mathcal {M}(\Lambda _{\mathrm{ex}})$ for which there exists a sequence $(\nu _k)_k\subset \mathcal {M}(\Lambda _{\mathrm{core}})$ of measures which converge to $\mu$ in the weak$*$ topology we have $\chi (\mu )=0$.

The proof of the above proposition will be an immediate consequence of the following lemma. Recall the definition of $\Delta (\cdot )$ in (4.1).

Lemma 4.5

There exist constants $K_1,K_2>0$ such that for every $\delta \in (0,1/2)$ and every measure $\nu \in \mathcal {M}(\Lambda _{\mathrm{core}})$ we have

$$\begin{aligned} |\chi (\nu )|\le K_1\nu (\Sigma _2\times [\delta ,1-\delta ])+K_2\Delta (\delta ). \end{aligned}$$

Proof

Note that it is enough to prove the claim for $\nu \in \mathcal {M}(\Lambda _{\mathrm{core}})$ being ergodic. Indeed, for a general invariant measure $\nu \in \mathcal {M}(\Lambda _{\mathrm{core}})$ with ergodic decomposition $\nu =\int \nu _\theta \,d\lambda (\nu _\theta )$, applying the above claim to any (ergodic) $\nu _\theta$ in this decomposition we have

$$\begin{aligned} \chi (\nu ) = \int \chi (\nu )\,d\lambda (\nu _\theta ) \le K_1\nu (\Sigma _2\times [\delta ,1-\delta ]) + K_2\Delta (\delta ) \end{aligned}$$

with the analogous lower bound.

Let us hence assume that $\nu \in \mathcal {M}(\Lambda _{\mathrm{core}})$ is ergodic. Since $\nu$ is not supported on $\Lambda _{\mathrm{ex}}$, there exists $\delta '\in (0,\delta )$ such that $\nu (\Sigma _2\times [\delta ',1-\delta '])>0$. Let $X=(\xi ,x)$ be a generic point for $\nu$ satisfying $x\in [\delta ',1-\delta ']$ and consider the sequence of points $x_i{\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}f_\xi ^i(x)$ for $i\ge 0$. Since $\nu$ is ergodic, there are infinitely many $n\ge 0$ such that $x_n\in [\delta ',1-\delta ']$ and hence

$$\begin{aligned} 2\delta ' \le \frac{{{\,\mathrm{Dist}\,}}(x_n,B)}{{{\,\mathrm{Dist}\,}}(x_0,B)} \le \frac{1}{2\delta '}, \end{aligned}$$

(4.13)

where $B=\{0,1\}$. Because X is a generic point, given any $\varepsilon$, for n large enough we have

$$\begin{aligned} \Big |\frac{1}{n}\log \,|(f_\xi ^n)'(x)|- \chi (\nu )\Big |\le \varepsilon \end{aligned}$$

and also

$$\begin{aligned} \Big |\frac{1}{n}{{\,\mathrm{card}\,}}\{i\in \{0,\ldots ,n-1\}:x_i\in [\delta ,1-\delta ]\} -\nu (\Sigma _2\times [\delta ,1-\delta ])\Big |\le \varepsilon .\nonumber \\ \end{aligned}$$

(4.14)

Applying Lemma 4.2, we have

$$\begin{aligned}&e^{\omega (i+1)}e^{-\Delta (\delta )} \le \frac{{{\,\mathrm{Dist}\,}}(x_{i+1},B)}{{{\,\mathrm{Dist}\,}}(x_i,B)} \le e^{\omega (i+1)}e^{\Delta (\delta )} \quad \text { if }x_i\in (0,\delta ]\cup [1-\delta ,1),\\&e^{\omega (i+1)}K^{-1} \le \frac{{{\,\mathrm{Dist}\,}}(x_{i+1},B)}{{{\,\mathrm{Dist}\,}}(x_i,B)} \le e^{\omega (i+1)}K \quad \text { if }x_i\not \in (0,\delta ]\cup [1-\delta ,1), \end{aligned}$$

where $K>1$ is some universal constant and

$$\begin{aligned} \omega (i) {\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}{\left\{ \begin{array}{ll} \log \,|f'_{\xi _i}(0)|&{}\quad \text {if }x_{i-1}\in (0,\delta ],\\ \log \,|f'_{\xi _i}(1)|&{}\quad \text {if }x_{i-1}\in [1-\delta ,1),\\ 0 &{}\text { otherwise}. \end{array}\right. } \end{aligned}$$

By a telescoping sum, we have

$$\begin{aligned} \begin{aligned} \frac{{{\,\mathrm{Dist}\,}}(x_{n},B)}{{{\,\mathrm{Dist}\,}}(x_0,B)} = \prod _{i=0}^{n-1}\frac{{{\,\mathrm{Dist}\,}}(x_{i+1},B)}{{{\,\mathrm{Dist}\,}}(x_i,B)}. \end{aligned} \end{aligned}$$

We split the index set $\{0,\ldots ,n-1\}=I_1\cup I_2$ according to the rule that $x_i\in [\delta ,1-\delta ]$ for all $i\in I_1$ and $x_i\not \in [\delta ,1-\delta ]$ for all $i\in I_2$. Let

$$\begin{aligned} \phi (n) {\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}\sum _{i=1}^n\omega (i) \end{aligned}$$

and note that this function was also used in the previous proof, see (4.2). By the above estimates, we hence have

$$\begin{aligned} e^{\phi (n)}K^{-{{\,\mathrm{card}\,}}I_1} \cdot e^{-\Delta (\delta ){{\,\mathrm{card}\,}}I_2} \le \frac{{{\,\mathrm{Dist}\,}}(x_{n},B)}{{{\,\mathrm{Dist}\,}}(x_0,B)} \le e^{\phi (n)}K^{{{\,\mathrm{card}\,}}I_1} \cdot e^{\Delta (\delta ){{\,\mathrm{card}\,}}I_2}. \end{aligned}$$

This implies

$$\begin{aligned} e^{\phi (n)} \le \frac{{{\,\mathrm{Dist}\,}}(x_{n},B)}{{{\,\mathrm{Dist}\,}}(x_0,B)} K^{{{\,\mathrm{card}\,}}I_1} \cdot e^{\Delta (\delta ){{\,\mathrm{card}\,}}I_2}. \end{aligned}$$

(4.15)

Again applying Lemma 4.2, if ${{\,\mathrm{Dist}\,}}(x_i,B)<\delta$ then we have

$$\begin{aligned} |(f_{\xi _{i+1}})'(x_i)|\le e^{\omega (i+1)} e^{\Delta (\delta )} \end{aligned}$$

and if ${{\,\mathrm{Dist}\,}}(x_i,B)\ge \delta$ then we have

$$\begin{aligned} |(f_{\xi _{i+1}})'(x_i)|\le e^{\omega (i+1)} L \end{aligned}$$

for some universal $L>1$. Hence, decomposing the orbit piece $(x_i)_{i\ge 0}^{n-1}$ as above into index sets $I_1$ and $I_2$, we obtain

$$\begin{aligned} |(f_\xi ^n)'(x)|\le e^{\phi (n)}L^{{{\,\mathrm{card}\,}}I_1}\cdot e^{\Delta (\delta ){{\,\mathrm{card}\,}}I_2} \end{aligned}$$

with the analogous lower bound.

By (4.14), we have ${{\,\mathrm{card}\,}}I_1\le n(\nu (\Sigma _2\times [\delta ,1-\delta ])+\varepsilon )$.

Substituting the estimate for $e^{\phi (n)}$ in (4.15) we obtain

$$\begin{aligned} |(f_\xi ^n)'(x)|\le \frac{{{\,\mathrm{Dist}\,}}(x_{n},B)}{{{\,\mathrm{Dist}\,}}(x_0,B)} (KL)^{{{\,\mathrm{card}\,}}I_1} \cdot e^{2\Delta (\delta ){{\,\mathrm{card}\,}}I_2} \le \frac{1}{2\delta '} (KL)^{{{\,\mathrm{card}\,}}I_1} \cdot e^{2\Delta (\delta ){{\,\mathrm{card}\,}}I_2}, \end{aligned}$$

where we also used (4.13). Hence

$$\begin{aligned} \frac{1}{n}\log \,|(f_\xi ^n)'(x)|\le \frac{1}{n}|\log (2\delta ')|+\log (KL)\big (\nu (\Sigma _2\times [\delta ,1-\delta ])+\varepsilon \big ) +2\Delta (\delta ), \end{aligned}$$

with the analogous lower bound. Since $|\log \,|(f_\xi ^n)'(x)|/n-\chi (\nu )|\le \varepsilon$, passing $n\rightarrow \infty$ and then $\varepsilon \rightarrow 0$ this ends the proof of the lemma. $\square$

Proof of Theorem 2.5

Item 1 is a well-known fact, see for example [27, Proposition 2 item (a)]. This fact implies that $\mathcal {M}_{\mathrm{erg}}(\Lambda _{\mathrm{ex}})$ is a Poulsen simplex (see [23] or in the particular case of the shift space [28]). Item 4 is then an immediate consequence from the facts that $\mu \mapsto \chi (\mu )$ is continuous and that the Dirac measure on $(0^{\mathbb {Z}},0)$ has Lyapunov exponent $\log \,f_0'(0)>0$ and the Dirac measure on $(0^{\mathbb {Z}},1)$ has Lyapunov exponent $\log \,f_0'(1)<0$ together with the fact that $\mathcal {M}_{\mathrm{erg}}(\Lambda _{\mathrm{ex}})$ is path-connected.

Item 2 follows from Proposition 4.4.

Item 3 follows from Proposition 4.3.

Let us now assume (H1), (H2’), (H3), and (H4). By Lemmas A.4 and A.6 there exist hyperbolic periodic points in $\Lambda _{\mathrm{core}}$ with positive and negative exponent, respectively. This proves item 5. By Proposition 2.2 we can apply 5.1. This implies item 6. $\square$

5 The core measures

In this section we will investigate a bit further the topological structure of $\mathcal {M}_{\mathrm{erg}}(\Lambda _{\mathrm{core}})$. The overall hypotheses are again (H1) and (H2), and we will discuss further additional conditions under which we are able to say more than in the previous sections.

Proposition 5.1

Assume that every pair of fiber expanding hyperbolic periodic orbits in $\Lambda _{\mathrm{core}}$ are homoclinically related. Then the set $\mathcal {M}_{\mathrm{erg,>0}}(\Lambda _{\mathrm{core}})$ is arcwise-connected. The analogous result holds true for fiber contracting hyperbolic periodic orbits in $\Lambda _{\mathrm{core}}$ and the set $\mathcal {M}_{\mathrm{erg,<0}}(\Lambda _{\mathrm{core}})$.

A map F whose fiber maps $f_0,f_1$ satisfy the hypotheses (H1), (H2’), (H3), and (H4) will satisfy the hypotheses of the above proposition.

We will several times refer to a slightly strengthened version of [6, Proposition 1.4] which, in fact, is contained in its proof in [6] and which can be seen as an ersatz of Katok’s horseshoe construction (see [20, Supplement S.5]) in the $C^1$ dominated setting. We formulate it in our setting. Note that to guarantee that the approximating periodic orbits are indeed contained in $\Sigma _2\times (0,1)$ it suffices to observe that in the approximation arguments one can consider any sufficiently large (in measure $\mu$) set and hence restrict to points which are uniformly away from the “boundary” $\Sigma _2\times \{0,1\}$. Indeed, the projection to [0, 1] of the support of $\mu$ can be the whole interval [0, 1] but it does not “concentrate” in $\{0,1\}$.

Lemma 5.2

Let $\star \in \{<0,>0\}$ and $\mu \in \mathcal {M}_{\mathrm{erg,\star }}(\Lambda _{\mathrm{core}})$.

Then for every $\rho \in (0,1)$ there exist $\alpha >0$ and a set $\Gamma _\rho \subset \Sigma _2\times (2\alpha ,1-2\alpha )$ and a number $\delta =\delta (\rho ,\mu )>0$ such that $\mu (\Gamma _\rho )>1-\rho$ and for every point $X\in \Gamma _\rho$ there is a sequence $(p_n)_n\subset \Sigma _2\times (\alpha ,1-\alpha )$ of hyperbolic periodic points such that:

• $p_n$ converges to X as $n\rightarrow \infty$;

• the invariant measures $\mu _n$ supported on the orbit of $p_n$ are contained in $\mathcal {M}_{\mathrm{erg,\star }}(\Lambda _{\mathrm{core}})$ and converge to $\mu$ in the weak$*$ topology;

Proof of Proposition 5.1

Similar results were shown before, though in slightly different contexts (see [17] and [12, Theorem 3.2]). For completeness, we sketch the proof.

Assume that $\mu ^0,\mu ^1\in \mathcal {M}_{\mathrm{erg,>0}}(\Lambda _{\mathrm{core}})$. By Lemma 5.2, $\mu ^i$ is accumulated by a sequence of hyperbolic periodic measures $\nu _n^i\in \mathcal {M}_{\mathrm{erg,>0}}(\Lambda _{\mathrm{core}})$ supported on the orbits of fiber expanding hyperbolic periodic points $P_n^i\in \Lambda _{\mathrm{core}}$, $i=0,1$. Since, by hypothesis, $P_1^0$ and $P_1^1$ are homoclinically related, there exists a horseshoe $\Gamma _1^{0,1}\subset \Lambda _{\mathrm{core}}$ containing these two points. Hence, since $\mathcal {M}(\Gamma _1^{0,1})$ is a Poulsen simplex [23, 28], there is a continuous arc $\mu _0:[1/3,2/3]\rightarrow \mathcal {M}_{\mathrm{erg,>0}}(\Gamma _1^{0,1})\subset \mathcal {M}_{\mathrm{erg,>0}}(\Lambda _{\mathrm{core}})$ joining the measures $\nu _1^0$ and $\nu _1^1$. For any pair of measures $\nu _n^0,\nu _{n+1}^0$, the same arguments apply and, in particular, there exists a continuous arc $\mu _n^0:[1/3^{n+1},1/3^n]\rightarrow \mathcal {M}_{\mathrm{erg,>0}}(\Lambda _{\mathrm{core}})$ joining the measure $\nu _n^0$ with $\nu _{n+1}^0$. Using those arcs and concatenating their domains (or appropriate parts of), we can construct an arc ${\bar{\mu }}_n^0:[1/3^{n+1},1/3]$ joining $\nu _{n+1}^0$ and $\nu _{1}^0$. The same applies to the measures $\nu _n^1$, defining arcs ${\bar{\mu }}_n^1 :[1-1/3^n,2/3]\rightarrow \mathcal {M}_{\mathrm{erg,>0}}(\Lambda _{\mathrm{core}})$ joining $\nu _{n+1}^1$ and $\nu _{1}^1$. Defining $\mu _\infty |_{(0,1)}:(0,1)\rightarrow \mathcal {M}_{\mathrm{erg,>0}}(\Lambda _{\mathrm{core}})$ by concatenating (appropriate parts of) the domains of those arcs, we complete the definition of the arc $\mu _\infty$ by letting $\mu _\infty (0)=\lim _{n\rightarrow \infty }{\bar{\mu }}_n^0(1/3^n)$ and $\mu _\infty (1)=\lim _{n\rightarrow \infty }{\bar{\mu }}_n^1(1-1/3^n)$, joining $\mu ^0$ and $\mu ^1$. Note that in the last step we assume that $\mu ^1,\mu ^2$ do not belong to the image of $\mu _\infty$, if one of these measures belongs it is enough to cut the domain of definition of $\mu _\infty$ appropriately. $\square$

Appendix A: Transitivity and homoclinic relations—proof of Proposition 2.2

In this appendix we prove Proposition 2.2. Hence, we will always assume that hypotheses (H1), (H2’), (H3), (H4) are satisfied.

1.1 The underlying IFS

Studying the iterated function system (IFS) associated to the maps $\{f_0,f_1\}$, we use the following notations. Every sequence $\xi =(\ldots \xi _{-1}.\xi _0\xi _1\ldots )\in \Sigma _2$ is given by $\xi =\xi ^-.\xi ^+$, where $\xi ^+\in \Sigma _2^+{\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}\{0,1\}^{{\mathbb {N}}_0}$ and $\xi ^-\in \Sigma _2^-{\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}\{0,1\}^{-{\mathbb {N}}}$. Given finite sequences $(\xi _0\ldots \xi _n)$ and $(\xi _{-m}\ldots \xi _{-1})$, we let

$$\begin{aligned} \begin{aligned} f_{[\xi _0\ldots \,\xi _n]}&{\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}f_{\xi _n} \circ \cdots \circ f_{\xi _1}\circ f_{\xi _0} \quad \text { and }\quad \\ f_{[\xi _{-m}\ldots \,\xi _{-1}.]}&{\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}(f_{\xi _{-1}}\circ \cdots \circ f_{\xi _{-m}})^{-1} =(f_{[\xi _{-m}\ldots \,\xi _{-1}]})^{-1}. \end{aligned} \end{aligned}$$

1.1.1 Expanding itineraries

Under hypotheses (H1) and (H4) there are a positive number $\varepsilon$ arbitrarily close to 0, a positive integer $N(\varepsilon )$, and fundamental domains $I_0(\varepsilon )= [\varepsilon , f_0(\varepsilon )]$ and $I_1(\varepsilon )= [1-\varepsilon , f_0(1-\varepsilon )]$ of $f_0$ having the following properties⁴

$$\begin{aligned} f_0^{N(\varepsilon )} (I_0(\varepsilon ))=I_1(\varepsilon ) \quad \text{ and }\quad (f_0^{N(\varepsilon )})^\prime (x) \ge \lambda ^{-1} \varkappa >1 \quad \text {for all }x\in I_0 (\varepsilon ). \end{aligned}$$

(A.1)

In what follows we fix small $\varepsilon >0$ satisfying the above conditions and for simplicity we write $I_0$, $I_1$, and N instead of $I_0(\varepsilon )$, $I_1(\varepsilon )$, and $N(\varepsilon )$.

Our construction now is analogous to the one in [9]. We sketch the main steps for completeness. Assuming additionally (H2’), given an interval $H\subset f_0^{-1}(I_0)\cup I_0$ we let $N(H)=N$ if $H\subset I_0$ and $N(H)=N+1$ otherwise and consider the interval $f_{[0^{N(H)}1]}(H)$. By construction, this interval is contained in $[\delta (\varepsilon ),\varepsilon ]$, where $\delta (\varepsilon )=1-f_0^2 (1-\varepsilon )$. Note that, by construction, $\delta (\varepsilon )<\varepsilon$. Therefore there is a first M(H) such that

$$\begin{aligned} f_{ [0^{N(H)}10^{M(H)} ]}(H)\cap (\varepsilon ,f_0(\varepsilon )]\ne \varnothing . \end{aligned}$$

The expanded successor of H is the interval $H'{\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}f_{ [0^{N(H)}10^{M(H)} ]}(H)$. The expanding return sequence of H is the finite sequence $0^{N(H)}10^{M(H)}$ By construction the interval $H'$ intersects the interior of $I_0$ and is contained in $[\delta (\varepsilon ), f_0(\varepsilon )]$. Also observe that there is M such that $M(H)\in \{1,\ldots , M\}$ for every subinterval H in $f_0^{-1}(I_0)\cup I_0$. The following lemma justifies our terminology expanded successor.

Lemma A.1

(Expanding itineraries [9, Lemma 2.3]) For every closed subinterval H of $f_0^{-1}(I_0)\cup I_0$ and every $x\in H$ it holds

$$\begin{aligned} \big | \big (f_{[0^{N(H)}10^{M(H)}]}\big )'(x) \big | \ge \varkappa >1. \end{aligned}$$

Proof

By (A.1) and the choice of H we have $\big |(f_{[0^{N(H)}]})^\prime (x) \big |\ge \varkappa$ for all $x\in H$. The assertion follows noting that $f_1(x)=1-x$, $(f_{[0^{N(H)}1]})(x)\in [0,\varepsilon ]$ if $x\in H$, and $f_0^\prime (y)>1$ if $y\in [0,\varepsilon ]$. $\square$

Lemma A.1 and an inductive argument immediately implies the following:

Lemma A.2

([9, Lemma 2.3]) For every closed subinterval H of $f_0^{-1}(I_0)\cup I_0$ there is a finite sequence $(\xi _0\ldots \xi _{\ell (H)})$ such that

• 1. $\big | \big ( f_{ [\xi _0\ldots \,\xi _{\ell (H)}]}\big )'(x) \big |\ge \varkappa$ for every $x\in H$ and

• 2. $f_{[\xi _0\ldots \, \xi _{\ell (H)]}} (H)\supset f_0^{-1}(I_0)$.

Proof

Write $H_0$ and let $H_1=H_0'$ be its expanding successor. We argue recursively, if $H_1$ contains $f_0^{-1}(I_0)$ we stop the recursion, otherwise we observe that $|H_1|\ge \varkappa |H_0|$ and consider the expanding successor $H_2=H'_1$. Since $H_i\ge \varkappa ^i |H_0|$ there is a first i such that $H_i$ contains $f_0^{-1}(I_0)$. We let $(\xi _0\ldots \xi _{\ell (H)})$ be the concatenation of the successive expanding returns. $\square$

Given a set $H\subset [0,1]$ denote its forward orbit by the IFS by

$$\begin{aligned} \mathcal {O}^+(H){\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}\bigcup _{k\ge 0} \, \bigcup _{(\xi _0\ldots \, \xi _k) \in \{0,1\}^{k+1} } f_{[\xi _0\ldots \, \xi _k]} (H). \end{aligned}$$

A special case occurs when the set H is a point.

Remark A.3

By the very definition of the IFS we have $\mathcal {O}^+(f_0^{-1}(I_0))=(0,1)$. In fact, the same holds for the forward orbit of any open interval containing the closed fundamental domain $f_0^{-1}(I_0)$. Also note that every point in (0, 1) has some forward iterate by the IFS in ${{\,\mathrm{int}\,}}(f_0^{-1}(I_0)\cup I_0)$.

Applying Lemma A.2 to $H=f_0^{-1}(I_0)$, we obtain a finite sequence $(\xi _0\ldots \xi _\ell )$ such that $H'{\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}f_{[\xi _0\ldots \,\xi _\ell ]}(H)\supset f_0^{-1}(I_0)$. Note that it follows from the expansion claimed in item 1. of this lemma that, in fact, there is an open interval $H''\subset H'$ containing $f_0^{-1}(I_0)$.

In what follows we let

$$\begin{aligned} \alpha {\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}\min \{f_0'(x),|f_1'(x)|:x\in [0,1]\}. \end{aligned}$$

(A.2)

Lemma A.4

For every pair of points $p,q\in (0,1)$, every $\kappa >1$, and every $\varepsilon >0$ sufficiently small there is $\delta _0>0$ such that for every $\delta \in (0,\delta _0)$ there is a finite sequence $(\eta _{0}\ldots \eta _{r})$ such that

• (1) $f_{[\eta _{0}\ldots \eta _{r}]}(p-\delta ,p+\delta )\supset (q-\varepsilon ,q+\varepsilon )$,

• (2) $\big | \big (f_{[\eta _{0}\ldots \eta _{r}]})^\prime (x)\big | >\kappa$ for all $x\in (p-\delta ,p+\delta )$, and

• (3) $\mathcal {O}^+((p-\delta ,p+\delta ))=(0,1)$.

Proof

Given $p,q\in (0,1)$, by Remark A.3, there are finite sequences $(\beta _1\ldots \beta _m)$ such that $f_{[\beta _1\ldots \,\beta _m]}(p)\in {{\,\mathrm{int}\,}}(f_0^{-1}(I_0)\cup I_0)$ and $(\eta _1\ldots \eta _n)$ such that $q\in f_{[\eta _1\ldots \,\eta _n]}(H'')$. Assume that $\varepsilon >0$ is so small that

$$\begin{aligned} I(q){\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}(q-\varepsilon ,q+\varepsilon )\subset f_{[\eta _1\ldots \,\eta _n]}(H''), \end{aligned}$$

where $H''$ is as in Remark A.3. Choose now $\delta _0$ small enough such that

$$\begin{aligned} f_{[\beta _1\ldots \,\beta _m]}((p-\delta _0,p+\delta _0))\subset {{\,\mathrm{int}\,}}(f_0^{-1}(I_0)\cup I_0). \end{aligned}$$

In particular, for $\delta \in (0,\delta _0)$ and $I(p){\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}(p-\delta ,p+\delta )$ we have

$$\begin{aligned} J(p) {\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}f_{[\beta _1\ldots \,\beta _m]}(I(p))\subset {{\,\mathrm{int}\,}}(f_0^{-1}(I_0)\cup I_0). \end{aligned}$$

Recalling (A.2), let

$$\begin{aligned} M {\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}\kappa \alpha ^{-n}. \end{aligned}$$

Applying Lemma A.2 to the interval J(p), we get a sequence $(\theta _1\ldots \theta _s)$ such that $f_{[\theta _1\ldots \theta _s]}(J(p))$ covers $f_0^{-1}(I_0)$ in an expanding way. Concatenating this sequence with the sequence $(\xi _1\ldots \xi _\ell )$ provided by Remark A.3, we get

$$\begin{aligned} ( f_{[\xi _1\ldots \xi _\ell ]} \circ f_{[\theta _1\ldots \theta _s]})(J(p)) \supset H'' \end{aligned}$$

and hence

$$\begin{aligned} g(I(p)) \supset H'', \quad \text { where } g {\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}f_{[\beta _1\ldots \beta _m\theta _1\ldots \theta _s\xi _1\ldots \xi _\ell ]}. \end{aligned}$$

If $|g'|$ in the interval I(p) is bigger than M, then the map $f_{[\eta _1\ldots \eta _n]}\circ g$ applied to I(p) covers I(q) in an expanding way with derivative in absolute value bigger than $\kappa$ [recall the definition of $\alpha$ in (A.2)] and the claim follows. Note that in this process we may need to shrink $\delta$ keeping the above covering properties. Otherwise, concatenating the map $f_{[\xi _0\ldots \xi _\ell ]}$ several times instead of just once we can obtain the desired expansion $>M$ for a map of the form $g= f_{[\beta _1\ldots \beta _m\theta _1\ldots \theta _s(\xi _1\ldots \xi _\ell )^t]}$ for some $t\ge 2$ and then argue as before. This gives properties (1) and (2) in the lemma.

Finally, as by construction g(I(p)) covers the fundamental domain $f_0^{-1}(I_0)$, by Remark A.3 property (3) follows. $\square$

1.1.2 Contracting itineraries

For the contracting itineraries we will now in particular focus on (H3), which plays the role of (H4) in the previous subsection. Recall that $c\in (0,1)$ is given by the condition $f_0^\prime (c)=1$. Note that, since $f_0'$ is decreasing, we have $f_0^\prime (f_0(c))<1$ and hence

$$\begin{aligned} \upsilon {\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}\frac{1}{f_0^\prime (f_0(c))}>1. \end{aligned}$$

(A.3)

In what follows, for notational simplicity let $g_0{\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}f_0^{-1}$ and $g_1{\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}f_1^{-1}$($=f_1$) and below consider the IFS generated by $\{g_0,g_1\}$.

Next lemma is a variation of [9, Lemma 2.6], where an important difference is that in our case $g_1$ is not expanding.

Lemma A.5

(Contracting itineraries) Let H be a closed subinterval of $[c,f_0^2(c)]$. Then there are a subinterval $H_0$ of H and a sequence $\xi _0\dots \xi _k$ such that

$$\begin{aligned} g_{[\xi _0\dots \xi _k]}(H_0)\supset [f_0(c), f_0^2(c)] \quad \text{ and } \quad |g^\prime _{[\xi _0\dots \xi _k]}(x)|\ge \upsilon \quad \text{ for } \text{ every } x\in H_0. \end{aligned}$$

Proof

Note that for every $x\in [f_0(c), f_0^2(c)]$ it holds $|g_{[01]}^\prime (x)| \ge \upsilon$. Condition $f_1 \circ f_0^2(c)> f_0^2(c)$ implies that $g_{[01]}(x)> f_0^2(c)$. Thus, there is a first $i\ge 0$ such that $g_{[010^i]}(x)\in [f_0(c), f_0^2(c)]$. Note that $|g_{[010^i]}'(x)|\ge \upsilon$. Now the result follows arguing as in Lemma A.2. $\square$

Define the backward orbit$\mathcal {O}^-(\cdot )$ by the IFS of a set in the natural way. Arguing as in the expanding case, we have the following version of Lemma A.4.

Lemma A.6

For every pair of points $p,q\in (0,1)$, every $\kappa >1$, and every $\varepsilon >0$ sufficiently small there is $\delta _0>0$ such that for every $\delta \in (0,\delta _0)$ there is a finite sequence $(\nu _{0}\ldots \nu _{r})$ such that

• (1) $f_{[.\nu _{0}\ldots \nu _{r}]}((p-\delta ,p+\delta ))\supset (q-\varepsilon ,q+\varepsilon )$,

• (2) $\big | \big (f_{[.\nu _{0}\ldots \nu _{r}]})^\prime (x)\big | >\kappa$ for all $x\in (p-\delta ,p+\delta )$, and

• (3) $\mathcal {O}^-((p-\delta ,p+\delta ))=(0,1)$.

1.1.3 Almost forward and backward minimality

Corollary A.7

(Almost minimality) For every $x\in (0,1)$ the sets $\mathcal {O}^+(x)$ and $\mathcal {O}^-(x)$ are both dense in [0, 1].

Proof

Fix any $x\in (0,1)$. To prove the backward minimality fix $p\in (0,1)$ and an arbitrarily small neighborhood J(p) of it. By Lemma A.6 item (3) we have that $x\in \mathcal {O}^-(J(p))$ and hence $J(p) \cap \mathcal {O}^+(x)\ne \varnothing$. The proof of the forward minimality is analogous using Lemma A.4 item (3). $\square$

1.2 Transitive dynamics: homoclinic relations

To prove that F is topologically transitive, we use the notion of a homoclinic class adapted to the skew product setting. For that we need some definitions. Observe that if $P=(\xi ,p)$ is a periodic point of F of period $k+1$, then $\xi =(\xi _0\ldots \xi _{k})^{{\mathbb {Z}}}$ and $f_{[\xi _0\ldots \,\xi _k]}(p)=p$. Note that

$$\begin{aligned} \frac{1}{k+1}\log \,|f_{[\xi _0\ldots \,\xi _k]}^\prime (p)|= \chi (P). \end{aligned}$$

If $\chi (P)\ne 0$ then we call P(fiber) hyperbolic. There are two types of such points: if $\chi (P)>0$ then we call P(fiber) expanding, otherwise $\chi (P)<0$ and we call P(fiber) contracting. We denote by ${{\,\mathrm{Per}\,}}_{\mathrm {hyp}}(F)$ the set of all fiber hyperbolic periodic points of F and by ${{\,\mathrm{Per}\,}}_{>0}(F)$ and ${{\,\mathrm{Per}\,}}_{<0}(F)$ the (fiber) expanding and (fiber) contracting periodic points, respectively. Clearly, $\mathrm {Per}_{\mathrm {hyp}}(F)= \mathrm {Per}_{>0}(F)\cup \mathrm {Per}_{<0}(F)$. Given a fiber hyperbolic periodic point P we consider the stable and unstable sets of its orbit $\mathcal {O}(P)$ denoted by $W^s\big ( \mathcal {O}(P_1), F\big )$ and $W^u\big ( \mathcal {O}(P_1), F\big )$.

Two periodic points $P_1,P_2 \in \mathrm {Per}_{\mathrm {hyp}}(F)$ of the same type of hyperbolicity (that is, either both points are fiber expanding or both are fiber contracting) with different orbits $\mathcal {O}(P_1)$ and $\mathcal {O}(P_2)$ are homoclinically related if the stable and unstable sets of their orbits intersect cyclically:

$$\begin{aligned} W^s\big ( \mathcal {O}(P_1), F\big ) \cap W^u\big ( \mathcal {O}(P_2), F\big ) \ne \varnothing \,\,\text{ and }\,\, W^u\big ( \mathcal {O}(P_1), F\big ) \cap W^s\big ( \mathcal {O}(P_2), F\big ) \ne \varnothing . \end{aligned}$$

A point $X\not \in \mathcal {O}(P)$ is a homoclinic point of P if

$$\begin{aligned} X\in W^s\big ( \mathcal {O}(P), F\big ) \cap W^u\big ( \mathcal {O}(P), F\big ). \end{aligned}$$

Observe that our definitions do not involved any transversality assumption (indeed in our context of a skew product such a transversality does not make sense, see also [7, Section 3] for more details on homoclinic relations for skew products). However, due to the fact that the maps $f_0$ and $f_1$ have no critical points, the homoclinic points behave as the transverse ones in the differentiable setting.

The homoclinic classH(P) of a fiber hyperbolic periodic point P is the closure of the orbits of the periodic points of the same type as P which are homoclinically related to P. As in the differentiable setting, the set H(P) coincides with the closure of the homoclinic points of P. This set is transitive.

Let us introduce some notation. For $\star \in \{<0,>0\}$, define

$$\begin{aligned} \mathrm {Per}_{\mathrm{{core}},\star }(F){\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}\mathrm {Per}_\star (F) \cap \Lambda _{\mathrm{{core}}} \quad \text{ and } \quad \mathrm {Per}_{\mathrm{{ex}},\star }(F){\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}\mathrm {Per}_\star (F) \cap \Lambda _{\mathrm{{ex}}}. \end{aligned}$$

Proposition A.8

(Homoclinic relations) Let $\star \in \{<0,>0\}$.

• (1) Every pair of points $R_1,R_2 \in \mathrm {Per}_{\mathrm{{core}},\star }(F)$ are homoclinically related.

• (2) Every pair of points $R_1,R_2 \in \mathrm {Per}_{\mathrm{{ex}},\star }(F)$ are homoclinically related and their homoclinic classes coincide with $\Lambda _{\mathrm{{ex}}}$.

• (3) No point in $\mathrm {Per}_{\mathrm{{core}},\star }(F)$ is homoclinically related to any point of $\mathrm {Per}_{\mathrm{{ex}},\star }(F)$.

• (4) The set $\Sigma _2\times [0,1]$ is the homoclinic class of any $R\in \mathrm {Per}_{\mathrm{{core}},\star }(F)$. As a consequence, the set $\mathrm {Per}_{\mathrm{{core}},\star }(F)$ is dense in $\Sigma _2\times [0,1]$.

Proof

As the arguments in this proof are similar to the ones in [8, Section 2] we willl just sketch them. We prove (1) for fiber contracting periodic points only. Fix $P= ((\xi _0\ldots \xi _k)^\mathbb {Z}, p)$ and $R= ((\eta _0\ldots \eta _\ell )^\mathbb {Z}, r)$, $r,p\in (0,1)$. Take an open interval I(r) containing r such that $I(r)\subset W^s_{\mathrm {loc}} (r, f_{[\eta _0\ldots \eta _\ell ]})$. By Corollary A.7, there is $\rho _0\ldots \rho _m$ such that $f_{[\rho _0\ldots \rho _m]} (p)\in I(r)$. Take $X= ( (\xi _0\ldots \xi _k)^{-{{\mathbb {N}}}}. \rho _0\ldots \rho _m (\eta _0\ldots \eta _\ell )^{{\mathbb {N}}},p)$. By construction, $X\in W^u(\mathcal {O}(P),F) \cap W^s(\mathcal {O}(R),F)$. Reversing the roles of P and R we obtain a point in $W^u(\mathcal {O}(R),F) \cap W^s(\mathcal {O}(P),F)$, proving that P and R are homoclinically related.

The proof of (2) is an immediate consequence of the fact that $F_{\Lambda _{\mathrm{ex}}}$ can be seen as an “abstract horseshoe”.

To prove item (3) note that $\mathcal {O}^\pm (0),\mathcal {O}^\pm (1)\subset \{0,1\}$. This prevents any periodic point with fiber coordinate 0 or 1 to be homoclinically related to points in $\Lambda _{\mathrm {core}}$.

We prove item (4) for expanding points only. Fix an expanding periodic point $R\in \Lambda _{\mathrm {core}}$. Consider any point $X=(\xi ,x)$, $x\in (0,1)$. Fix any $m\ge 1$. Let $q{\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}f_{[\xi _{-m}\ldots \xi _{-1}.]}(x)$ and $p{\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}f_{[\xi _{0}\ldots \xi _{m}]}(x)$. Given any $\varepsilon >0$, apply Lemma A.4 to the points p, q, the constant $\kappa =2\alpha ^{-(2m+1)}$, where $\alpha$ was defined in (A.2). Let $\delta _0$ the constant given by the lemma and pick $\delta <\delta _0$ such that

$$\begin{aligned} (p-\delta , p+\delta ) \subset f_{[\xi _{-m}\ldots \xi _{m}]} (q-\varepsilon , q+\varepsilon ) . \end{aligned}$$

By this lemma applied to $\delta$ we get a finite sequence $(\eta _0\ldots \eta _k)$ such that the map $f_{[\xi _{-m}\ldots \xi _m \eta _0 \ldots \eta _k]}$ has a fixed expanding point $r\in (q-\varepsilon , q+\varepsilon )$. By construction, the point $R_m=\big ((\xi _{-m}\ldots \xi _m \eta _0 \ldots \eta _k)^{\mathbb {Z}}, r\big )$ is periodic, expanding, and $F^m(R_m)$ is close to X. In this way we get expanding periodic points arbitrarily close to X. By item (1), any such periodic point is homoclinically related to R. As a consequence, we have X is accumulated by periodic points homoclinically related to R and hence $X\in H(R,F)$. $\square$

1.3 The parabolic case

In this section we will prove Theorem 2.9. For that we see how the constructions above can be modified to construct examples where the set $\Lambda$ has an ergodic measure of maximal entropy which is nonhyperbolic. For this we modify the map $f_0$ satisfying conditions (H1), (H3), and (H4) to get a new map ${\tilde{f}}_0$ such that the points 0 and 1 are parabolic (0 is repelling and 1 is attracting) and consider the skew product ${\widetilde{F}}$ associated to ${\tilde{f}}_0$ and $f_1(x)=x-1$.

Proof of Theorem 2.9

We start with a map $f_0$ satisfying hypotheses (H1), (H3), and (H4) and consider exactly as in Appendix A.1 the fundamental domains $I_0(\epsilon )=[\varepsilon ,f_0(\varepsilon )]$ and $I_1(\epsilon )=[1-\varepsilon , f_0(1-\varepsilon ))$ (for small $\varepsilon >0$) and the natural number $N(\varepsilon )$ with $f_0^{N(\varepsilon )} (I_0(\varepsilon ))=I_1(\varepsilon )$. Note that the estimate in (A.1) holds. We define for a subinterval H of $f_0^{-1}(I_0(\varepsilon )) \cup I_0(\varepsilon )$ the number $N(H)\in \{N(\varepsilon ), N(\varepsilon )+1\}$. Similarly we define $M(H)\in \{0,\dots , M\}$ (M independent of H).

Assume not that $f_1$ satisfies (H2’). Let

$$\begin{aligned} a_1 {\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}\min \{f_0^{-1}(\varepsilon ),1-f_0^{N(\varepsilon )+1} (\varepsilon )\}, \quad b_1{\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}f_0^{N(\varepsilon )+1} (\varepsilon ). \end{aligned}$$

Note also that the definition of the expanding successors only involves iterates in the set

$$\begin{aligned}{}[f_0^{-1}(\varepsilon ), f_0^{N(\varepsilon )+1} (\varepsilon )] \cup f_1 \big ([f_0^{-1}(\varepsilon ), f^{N(\varepsilon )+1} (\varepsilon )]\big )= [a_1,b_1]\subset [\delta , 1-\delta ], \end{aligned}$$

for some small $\delta >0$. We now fix very small $\tau \ll \delta$ and consider a new map ${\tilde{f}}_0$ such that

• (i) ${\tilde{f}}_0=f_0$ in $[\delta ,1-\delta ]$,

• (ii) $({\tilde{f}}_0)'(0)=1$ and 0 is repelling,

• (iii) $({\tilde{f}}_0)'(1)=1$ and 1 is attracting, ${\tilde{f}}_0$ has no fixed points in (0, 1),

see Fig. 5. Note that for this new map ${\tilde{f}}_0$ we can define expanding returns in $I_0(\varepsilon )$ as before. Note also that every point $x\in (0,1)$ has some forward and some backward iterate in $I_0(\varepsilon )$ by the IFS associated to $\{{\tilde{f}}_0, f_1\}$ (here we use that 0 is repelling, 1 is attracting and ${\tilde{f}}_0$ has no fixed points in (0, 1). We now have versions of Lemmas A.1, A.2, and A.4 for the IFS associated to $\{{\tilde{f}}_0, f_1\}$. This concludes the part corresponding to the expanding itineraries.

Fig. 5

Fiber maps: the parabolic case

It remains to check that the arguments corresponding to the contracting itineraries in Appendix A.1.2 also hold. Recall the definition of the point c in hypothesis (H3), see also (A.3). Let $g_0=f_0^{-1}$ and $g_1=f_1^{-1}$. Note that if $\delta$ is small we can assume that $\delta< g_0(c)< 1-g_0(c)]<1-\delta$. Note that for closed intervals $H\subset [c,f_0^2(c)]$ the definition of their expanding successor only involves iterations in the set $[g_0(c), 1-g_0(c)]$. Since in this interval ${\tilde{g}}_0=g_0$ we obtain versions of Lemmas A.5 and A.6 for the IFS associated to $\{{\tilde{g}}_0, g_1\}$. In the same way we recover Corollary A.7 for the IFS associated to $\{{\tilde{f}}_0, f_1\}$.

We can now consider the skew product ${\widetilde{F}}$ associated to ${\tilde{f}}_0, f_1$ and prove Proposition A.8 for ${\tilde{F}}$, obtaining, in particular, that the set $\Sigma _2\times [0,1]$ is a homoclinic class of ${\tilde{F}}$. By Theorem 2.7 the unique measure $\mu _{\mathrm{max}}^{\mathrm{ex}}$ of maximal entropy $\log 2$ in $\mathcal {M}_{\mathrm{erg}}(\Lambda _{\mathrm{ex}})$ is nonhyperbolic. $\square$

1.4 Nontransitive case with a unique measure of maximal entropy

In this section we prove Theorem 2.10 by presenting an example which is not transitive and for which there exists just one measure of maximal entropy, which is nonhyperbolic. This measure is supported on $\Lambda _{\mathrm{ex}}$ and there is no measure of maximal entropy in $\Lambda _{\mathrm{core}}$.

Proof of Theorem 2.10

Let us consider a $C^1$ orientation preserving homeomorphism $\phi :{\mathbb {R}}\rightarrow (0,1)$ satisfying

$$\begin{aligned} \phi (y) = 1-\phi (-y) \end{aligned}$$

(A.4)

and

$$\begin{aligned} \lim _{y\rightarrow \infty } \frac{\phi '(y+1)}{\phi '(y)} {\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}1 \in (0,\infty ). \end{aligned}$$

(For example, $\phi (y) = \frac{1}{\pi }\arctan y + \frac{1}{2}$ satisfies the conditions above.) Now define $f_0:[0,1]\rightarrow [0,1]$

$$\begin{aligned} f_0(x) {\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}{\left\{ \begin{array}{ll} \phi (\phi ^{-1}(x)+1)&{}\quad \text {if }x\in (0,1),\\ 0&{}\quad \text {if }x=0,\\ 1&{}\quad \text {if }x=1, \end{array}\right. } \end{aligned}$$

and $f_1:[0,1]\rightarrow [0,1]$ by $f_1(x)=1-x$. Note that $f_0$ is a $C^1$ map which satisfies

$$\begin{aligned} f_0'(0)=1 = f_0'(1). \end{aligned}$$

(A.5)

Moreover, note that $f_0\circ \phi =\phi \circ \theta$, where $\theta :{\mathbb {R}}\rightarrow {\mathbb {R}}$ denotes the unit translation on the real line defined by $\theta (y){\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}y+1$. The symmetry assumption (A.4) means that $f_1\circ \phi =\phi \circ \gamma$ where $\gamma :{\mathbb {R}}\rightarrow {\mathbb {R}}$ is defined by $\gamma (y){\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}-y$. Observe that $\phi (-\phi ^{-1}(x))=1-x$ implies

$$\begin{aligned} f_0 f_1 = f_1 f_0^{-1}, \end{aligned}$$

(A.6)

that is, $f_0$ is conjugate to its inverse by $f_1$. This provides us fiber maps $f_0,f_1$ satisfying item 1. and 2. in the theorem.

Proposition A.9

F is not topologically transitive.

Proof

It suffices to prove that for any $x\in [0,1]$ the set $\mathcal {O}^+(x){\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}\{f_{[\omega _1\ldots \,\omega _n]}(x):\omega _i\in \{0,1\}, i\in \{1,\ldots ,n\}\}$ is not dense in [0, 1]. This is obvious if $x\in \{0,1\}$. Thus, in what follows, we let $x\in (0,1)$.

Given $n\in {\mathbb {N}}$, consider some finite sequence $(\omega _1\ldots \omega _n)\in \{0,1\}^n$. First, recall that $f_1^2(x)=x$ we can replace this sequence by one in which we eliminated all blocks 11. Hence, without loss of generality, we can assume that the sequence $(\omega _1\ldots \omega _n)$ does not contain two consecutive 1s. Assume first that this sequence contains an even number of symbols 1, that is, we can divide it into a finite number of pieces of the form $0^k10^\ell 10^m$. By (A.6), $f_{[0^k10^\ell 10^m]}(x) = f_0^{k+m-\ell }(x)$. Hence, we have $f_{[\omega _1\ldots \omega _n]}(x)=f_0^j(x)$ for some integer j. Similarly, if this sequence contains an odd number of symbols 1, we can write $\omega _1\ldots \omega _n = 0^k 1 \omega '$ with $\omega '$ containing an even number of symbols 1. As $f_{[0^k1]}(x) = f_0^{-k}(1-x)$, applying the previous argument, we have that $f_{[\omega _1\ldots \omega _n]}(x)=f_0^j(1-x)$ for some integer j.

This proves that the full forward orbit of x by the IFS, $\mathcal {O}^+(x)$, is contained in two sets $\{f_0^j(x):j\in {\mathbb {Z}}\}$ and $\{f_0^j(1-x):j\in {\mathbb {Z}}\}$, each of which has just two accumulation points: 0 and 1. This proves the proposition. $\square$

Proposition A.10

F has a unique measure of maximal entropy, which is nonhyperbolic.

Proof

By Theorem 2.7, the measure $\mu _{\mathrm{max}}^{\mathrm{ex}}$ is unique and nonhyperbolic by our choice (A.5). Hence, it is enough to prove that there cannot exist a measure of maximal entropy supported on $\Sigma _2\times (0,1)$.

Arguing by contradiction, assume that such a measure exists, denote it by $\mu$. Its projection to $\Sigma _2$ must be the measure ${\widehat{\nu }}_{\mathrm{max}}$ of maximal entropy for $\sigma :\Sigma _2\rightarrow \Sigma _2$, that is, the (1 / 2, 1 / 2)-Bernoulli measure (recall Sect. 3). We shortly write $\nu ={\widehat{\nu }}_{\mathrm{max}}$. The measure $\mu$ admits a disintegration, that is, there exists a family $\{\mu _\xi :\xi \in \Sigma _2\}$ of probabilities such that $\xi \mapsto \mu _\xi$ is measurable and every $\mu _\xi$ is supported on $\{\xi \}\times (0,1)$ and satisfies

$$\begin{aligned} \mu (E) = \int \mu _\xi (E)\, d\nu (\xi ) \end{aligned}$$

for any measurable set E. With a slight lack of precision we will consider each $\mu _\xi$ as a measure on (0, 1).

To investigate what happens to $\mu _\xi$ under our dynamics, we will use the following result whose proof we postpone. Recall our notation $f_\omega ^n{\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}f_{\omega _{n-1}}\circ \cdots \circ f_{\omega _0}$.

Lemma A.11

For $\nu$-almost every $\omega \in \Sigma _2$, for every $\varepsilon >0$ and for every measure $\mu$ supported on (0, 1) we have

$$\begin{aligned} \lim _{n\rightarrow \infty } \frac{1}{n} \sum _{i=1}^n (f_{\omega }^i)_*\mu ((\varepsilon , 1-\varepsilon )) =0. \end{aligned}$$

We postpone the proof of the above lemma to the following subsection. Assuming that the above lemma was proven, we can now complete the proof of the theorem. In particular, we can, for a $\nu$-generic $\omega$, apply Lemma A.11 to the measure $\mu = \mu _\omega$. Thus, recalling that $\mu$ is F-invariant, for every $n\ge 1$ we have

$$\begin{aligned} \begin{aligned} \mu ( \Sigma _2\times (\varepsilon , 1-\varepsilon ))&= F_*\mu ( \Sigma _2\times (\varepsilon , 1-\varepsilon )) = \frac{1}{n} \sum _{i=1}^n (F^i)_*\mu ( \Sigma _2\times (\varepsilon , 1-\varepsilon ))\\&= \frac{1}{n} \sum _{i=1}^n \int (f_\omega ^i)_*(\mu _\omega )((\varepsilon , 1-\varepsilon )) d\nu (\omega )\\&=\int \frac{1}{n} \sum _{i=1}^n (f_\omega ^i)_*(\mu _\omega )((\varepsilon , 1-\varepsilon )) d\nu (\omega ). \end{aligned} \end{aligned}$$

Now, by Lemma A.11, taking the limit $n\rightarrow \infty$ and applying the dominated convergence theorem, we obtain $\mu ( \Sigma _2\times (\varepsilon , 1-\varepsilon )) =0$. As $\varepsilon$ is arbitrary, this implies $\mu (\Sigma _2\times (0,1))=0$, contradiction to the fact that we assumed that $\mu$ was supported on $\Sigma _2\times (0,1)$. This finishes the proof of the proposition. $\square$

This proves the theorem. $\square$

1.4.1 Random walks: Proof of Lemma A.11

To prove Lemma A.11 we need to introduce several auxiliary objects in order to reduce it to well-known results. Heuristically, a $\nu$-typical $\omega \in \Sigma _2$ can be treated as a random process with no memory, and then the dynamics generated by $f_\omega ^i$ is given by a certain random walk. The result we will prove below is a version of a well-known statement that a random walk does not stay in any bounded region.

For what we study below, we will consider the one-sided shift space $\Sigma _2^+$ only and by a slight abuse of notation continue to denote the (1 / 2, 1 / 2)-Bernoulli measure on it by $\nu$. We consider a $\nu$-typical $\omega = (\omega _1\omega _2\ldots )\in \Sigma _2^+$ and interpret the values $\omega _i$ as random variables, with $\nu$ giving their joint distribution. That is, each $\omega _i$ takes values 0 and 1 with probabilities 1/2 each, independently of any other $\omega _j$’s. Denoting $\omega ^n=\omega _1\ldots \omega _n$, let $\Omega _n$ be the $\sigma$-algebra generated by the cylinders $[\omega ^1],\ldots ,[\omega ^n]$.

We first introduce the following auxiliary IFS of maps $g_0,g_1$. Let $\Omega =(0,1)\times \{+1,-1\}$ and define $g_0,g_1:\Omega \rightarrow \Omega$ by

$$\begin{aligned} g_0(x,+1){\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}(f_0(x),+1),\quad g_0(x,-1){\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}(f_0^{-1}(x),-1), \end{aligned}$$

and

$$\begin{aligned} g_1(x,+1){\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}(x,-1),\quad g_1(x,-1){\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}(x,+1). \end{aligned}$$

Consider the projections $\pi _1,\pi _2:\Omega \rightarrow (0,1)$ defined as follows

$$\begin{aligned} \pi _1(x,k) {\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}{\left\{ \begin{array}{ll} x&{}\quad \text {if }k=+1,\\ 1-x&{}\quad \text {if }k=-1, \end{array}\right. } \quad \quad \pi _2(x,k) {\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}x. \end{aligned}$$

One immediately checks that $\pi _1\circ g_i = f_i\circ \pi _1$, $i=0,1$, that is, the original IFS $\{f_0,f_1\}$ on (0, 1) is a factor of the IFS $\{g_0, g_1\}$ on $\Omega$ under $\pi _1$. Note that, given $x\in (0,1)$, for every $n\ge 1$ we have

$$\begin{aligned} (\pi _1\circ g_{[\omega ^n]})(x,+1) = f_{[\omega ^n]}(x), \end{aligned}$$

(A.7)

that is, we can consider (0, 1) as $(0,1)\times \{+1\}$, apply the maps $g_i$ instead of $f_i$ and then project back the results by $\pi _1$ and get the same result as if we applied maps $f_i$ and never left (0, 1). Indeed, this is a consequence of our symmetry assumptions on $f_0$ and (A.6).

To model the claimed random walk, we consider now $(0,1)\times \{+1\}$ instead of (0, 1) and apply the maps $g_i$ instead of $f_i$ and then project the results by $\phi ^{-1}\circ \pi _2$. That is, let

$$\begin{aligned} R_i(x) = R_i(x,\omega ) {\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}(\phi ^{-1} \circ \pi _2 \circ g_{[\omega ^{i}]})(x,+1). \end{aligned}$$

This defines a random walk on ${\mathbb {R}}$. The main aim of this section is to prove the following result.

Lemma A.12

For every probability measure $\mu$ on ${\mathbb {R}}$ and for any bounded $A\subset {\mathbb {R}}$, $\nu$-almost surely we have

$$\begin{aligned} \lim _{n\rightarrow \infty } \frac{1}{n}\sum _{i=1}^{n}(R_i)_*\mu (A)=0. \end{aligned}$$

The above result now will provide the

Proof of Lemma A.11

Note that, for any $\varepsilon >0$ we have

$$\begin{aligned} \pi _1^{-1}((\varepsilon ,1-\varepsilon )) = \pi _2^{-1}((\varepsilon ,1-\varepsilon ))=(\varepsilon ,1-\varepsilon )\times \{0,1\}. \end{aligned}$$

Hence, by (A.7) for $A=\phi ^{-1}((\varepsilon ,1-\varepsilon ))$ we have

$$\begin{aligned} (f_{[\omega ^i]})_*\mu (\varepsilon ,1-\varepsilon ) = (\pi _1\circ g_{[\omega ^i]})_*\mu (\varepsilon ,1-\varepsilon ) =(R_i)_*\mu (A). \end{aligned}$$

Applying now Lemma A.12 implies the assertion, proving Lemma A.11. $\square$

1.4.2 Random walks: analysis of the random walk $R_i$

This random process has a complicated behavior. We will introduce a sequence of simpler auxiliary random processes which will help us prove Lemma A.12.

Without loss of generality, we assume $\omega _1=0$. Given $\omega$, let $n_i$, $i\ge 0$, enumerate the positions at which in the sequence $\omega$ there appears the symbol 0. With this notation, we have the following relation

$$\begin{aligned} \begin{aligned}&R_{n_i}(x,\omega ) =\phi ^{-1}\circ \,\pi _2\circ g_{[\omega ^{n_i}]})(x,+1)\\&\quad = {\left\{ \begin{array}{ll} (\phi ^{-1}\circ \pi _2\circ g_{[\omega ^{n_{i-1}}]})(x,+1)+1 &{}\quad \text { if }\#\{k\in \{n_{i-1},\ldots ,n_i\}:\omega _k=1\}\text { is even},\\ (\phi ^{-1} \circ \pi _2\circ g_{[\omega ^{n_{i-1}}]})(x,+1)-1 &{}\quad \text { if }\#\{k\in \{n_{i-1},\ldots ,n_i\}:\omega _k=1\}\text { is odd}. \end{array}\right. } \end{aligned} \end{aligned}$$

An elementary calculation shows that the number of 1’s between any two consecutive 0’s is even with probability 2 / 3 and odd with probability 1 / 3. That is, the random variable $n_i-n_{i-1}$ takes an even value with probability 1/3 and an odd value with probability 2/3, moreover this random variable is independent from $\Omega _{n_{i-1}}$. Considering then the subsequence $(n_i)_i$, we will now pass from the random walk $R_i$ to the following “induced” walk $S_i$, which is defined by

$$\begin{aligned} S_i(x) {\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}(\phi ^{-1} \circ \pi _2 \circ g_{[\omega ^{n_i}]})(x,+1). \end{aligned}$$

The latter is a random walk on the real line composed by translations

$$\begin{aligned} S_i(x) ={\left\{ \begin{array}{ll} S_{i-1}(x)+1&{} \quad \text { if } \#\{k\in \{n_{i-1},\ldots ,n_i\}:\omega _k=1\}\text { is even},\\ S_{i-1}(x)-1&{} \quad \text { if }\#\{k\in \{n_{i-1},\ldots ,n_i\}:\omega _k=1\}\text { is odd}, \end{array}\right. } \end{aligned}$$

where each step being independently and identically distributed: in the same direction as the previous one with probability 2/3 and in the opposite direction with probability 1/3 (with the convention that the ‘zeroth step’ was in the positive direction).

Since $S_i$ does not encode explicitly the information in which direction the walk is moving (it does not carry the second coordinate), we will instead consider the following auxiliary walk. Let $U_i$ be a random walk on ${\mathbb {R}}\times \{-1, +1\}$ given by

$$\begin{aligned} U_i(x,j) {\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}{\left\{ \begin{array}{ll} (x+j,j) &{} \quad \text { with probability } 2/3,\\ (x-j,-j) &{} \quad \text { with probability } 1/3. \end{array}\right. } \end{aligned}$$

which is just $S_i$ adding the information about the direction of the last step: there exists a measure preserving isomorphism under which the first coordinate of $U_i(x,+1)$ is equal to $S_i(x)$.

Recall that we want to show that the evolution of a measure under the application of the fiber maps of the IFS is eventually moving to the boundary of (0, 1), that is, to $\pm \infty$ for the walk lifted by $\phi ^{-1}$ to ${\mathbb {R}}$. For that reason, let us now consider an “induced” walk that only looks at times immediately after we moved in positive direction. Let $V_i^+$ denote the random walk which is the first return of $U_i$ to ${\mathbb {R}}\times \{+1\}$. That is,

$$\begin{aligned} V_i^+(x) {\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}{\left\{ \begin{array}{ll} x+1 &{} \quad \text { with probability } 2/3,\\ x-k, k=0,1,\ldots &{} \quad \text { with probability }2^k/3^{k+2}. \end{array}\right. } \end{aligned}$$

At last we got an usual random walk. Note that the walk $V_i^+$ is recurrent. Indeed, an elementary calculation gives that its expected displacement is zero, that is ${\mathbb {E}}(V_i^+(x)-x)=0$. Given $A\subset {\mathbb {R}}$, let us define $\mathbb {1}_A(y)=1$ if $y\in A$ and $\mathbb {1}_A(y)=0$ otherwise.

The Chung and Erdös Theorem [4] immediately implies

Lemma A.13

For any bounded $A\subset {\mathbb {R}}$, $\nu$-almost surely

$$\begin{aligned} \lim _{n\rightarrow \infty } \frac{1}{n} \sum _{i=1}^n\mathbb {1}_A(V_i^+(0))=0. \end{aligned}$$

Proof

By [4, Theorem 3.1], for any $a,b\in {\mathbb {Z}}$ we have

$$\begin{aligned} \lim _{i\rightarrow \infty }\frac{{\mathbb {P}}(V_i^+(0)=a)}{{\mathbb {P}}(V_i^+(0)=b)} =1. \end{aligned}$$

Hence, for any bounded set $A\subset {\mathbb {Z}}$ for every $a\in A$ we have

$$\begin{aligned} \lim _{i\rightarrow \infty }{\mathbb {P}}(V_i^+(0)=a)\le \frac{1}{|A|}, \end{aligned}$$

where $|A|$ denotes the cardinality of A and hence

$$\begin{aligned} \lim _{i\rightarrow \infty }{\mathbb {P}}(V_i^+(0)\in A) =0. \end{aligned}$$

In particular, for every $a\in {\mathbb {Z}}$ we have

$$\begin{aligned} \lim _{i\rightarrow \infty }{\mathbb {P}}(V_i^+(0)=a) =0. \end{aligned}$$

(A.8)

Let $T_k$ denote the kth return time of $V_i^+(0)$ to 0. Note that $T_k$ equals the sum of k independent copies of $T_1$.

Claim 1

${\mathbb {E}}(T_1)=\infty$.

Proof

By contradiction, assume that ${\mathbb {E}}(T_1)$ would be finite. Hence, by the strong law of large numbers, almost surely we would have $\lim _{n\rightarrow \infty }\frac{1}{n}T_n={\mathbb {E}}(T_1)$. Hence, by Egorov’s theorem, for any $\varepsilon \in (0,1)$ there would exist $N\ge 1$ such that for all $k\ge N$ with probability at least $1-\varepsilon$ we would have $\frac{1}{k}T_k\le {\mathbb {E}}(T_1)+\varepsilon$. This would imply

$$\begin{aligned} \sum _{i=1}^{k({\mathbb {E}}(T_1)+\varepsilon )}{\mathbb {P}}(V_i^+(0)=0) =\int d\omega \sum _{i=1}^{k({\mathbb {E}}(T_1)+\varepsilon )}\mathbb {1}_{\{0\}}(V_i^+(0)) \ge (1-\varepsilon )k({\mathbb {E}}(T_1)+\varepsilon ), \end{aligned}$$

which would imply $\limsup _{i\rightarrow \infty } {\mathbb {P}}(V_i^+(0)=0)>0$. Contradiction with (A.8). $\square$

Analogously, given $a\in {\mathbb {Z}}$, let $T_1^a$ denote the first hitting time of $V_i^+(0)$ at a. Observe that the return times of $V_{i+T_1^a}^+(0)$ to a have the same distribution as the return times of $V_i^+(0)$ to 0. Hence, if $T_k^a$ denotes the kth return time of $V_i^+(0)$ to a, then analogously to the above claim we conclude ${\mathbb {E}}(T_1^a)=\infty$. Hence, by the strong law of large numbers almost surely we have $\frac{1}{k}T_k^a\rightarrow \infty$, which in turn implies

$$\begin{aligned} 0 = \limsup _{k\rightarrow \infty }\frac{k}{T_k^a} = \limsup _{n\rightarrow \infty }\frac{1}{n}\sum _{i=1}^n\mathbb {1}_{\{a\}}(V_i^+(0)). \end{aligned}$$

Writing now $\mathbb {1}_A=\sum _{a\in A}\mathbb {1}_a$, we obtain

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{1}{n}\sum _{i=1}^n\mathbb {1}_{A}(V_i^+(0)) =0 \end{aligned}$$

almost surely. This proves the lemma. $\square$

Looking at the random walk $U_i$, we get the corresponding statement for the set $A\times \{+1\}$, that is

$$\begin{aligned} \lim _{n\rightarrow \infty } \frac{1}{n}\sum _{i=1}^n\mathbb {1}_{A\times \{+1\}}(U_i(0,+1))=0. \end{aligned}$$

The proof for $A\times \{-1\}$ is similar, only instead of $V_i^+$ we need to take the first return to ${\mathbb {R}}\times \{-1\}$. Recalling that the projection of $U_i$ to the first coordinate is just $S_i$, we obtain the following corollary.

Corollary A.14

For any bounded $A\subset {\mathbb {R}}$, $\nu$-almost surely

$$\begin{aligned} \lim _{n\rightarrow \infty } \frac{1}{n} \sum _{i=1}^n\mathbb {1}_A(S_i(0))=0. \end{aligned}$$

Recall that $S_i$ takes into account only the steps of the initial walk when the symbol 0 appeared. Vaguely speaking, $S_i$ takes only into account whether $n_i-n_{i-1}$ is even or odd. Let $\Omega '$ be the $\sigma$-algebra generated by $S_i$. We will consider the following auxiliary random variable $d_i$ defined by

$$\begin{aligned} d_i {\mathop {=}\limits ^{\scriptscriptstyle \mathrm{def}}}{\left\{ \begin{array}{ll} n_i-n_{i-1} &{} \quad \text {if }n_i - n_{i-1} \text { is odd,}\\ n_i-n_{i-1}-1 &{}\quad \text {if } n_i - n_{i-1} \text { is even.} \end{array}\right. } \end{aligned}$$

Below we will argue that $d_i$ is independent of $\Omega '$. The remaining information (needed to recover $\Omega = \bigcap _n \Omega _n$) is in exact values of $n_i-n_{i-1}$. Knowing $(S_i)_{i=1}^n$ and $(d_i)_{i=1}^n$, we can recover $(R_i)_{i=1}^n$. Note that $d_i$ being independent from $\Omega '$ means that we can decompose the measure $\nu$ (the (1 / 2, 1 / 2)-Bernoulli measure on $(\Sigma _2,\Omega )$) as $\mu _s \times \mu _d$, where $\mu _s$ is the distribution of $(S_i)$ and $\mu _d$ is the joint distribution of the i.i.d. random variables $d_i$. Hence then we can conclude that if for $\mu _s$-almost every realization $(S_i)$ for $\mu _d$-almost every realization $(d_i)$ an event holds, then it holds for $\nu$-almost every $\omega$.

Lemma A.15

The random variable $(d_i)$ is independent of $\Omega '$ and has finite expectation ${\mathbb {E}}(d_i)$.

Proof

Whether $n_i-n_{i-1}$ is even or odd, $d_i$ always has the same distribution

$$\begin{aligned} {\mathbb {P}}(n_i-n_{i-1}=2k-2| n_i-n_{i-1}\text { even}) = {\mathbb {P}}(n_i-n_{i-1}=2k+1| n_i-n_{i-1}\text { odd}) = \frac{3}{4^{k+1}}, \end{aligned}$$

which follows from an elementary calculation. Hence, in particular, the expected value of $d_i$ is finite. This proves the lemma. $\square$

With the above, we now return to the random walk $R_i$.

Corollary A.16

For any bounded $A\subset {\mathbb {R}}$, $\nu$-almost surely,

$$\begin{aligned} \lim _{n\rightarrow \infty } \frac{1}{n}\sum _{i=1}^n \mathbb {1}_A(R_i(0)) =0. \end{aligned}$$

Proof

Note that $R_n(0)=R_{n_{i-1}}(0)=S_{i-1}(0)$ for every $n\in \{n_{i-1},\ldots , n_i-1\}$. Hence, we have

$$\begin{aligned} \frac{1}{n_i} \sum _{k=0}^{n_i-1}\mathbb {1}_A(R_k(0)) =\frac{1}{n_i} \sum _{\ell =0}^{i-1} (n_{\ell +1}-n_\ell ) \mathbb {1}_A(S_\ell (0)). \end{aligned}$$

In particular, to show the claim, it is enough to consider the specific subsequence from above proving that

$$\begin{aligned} 0=\lim _{i\rightarrow \infty } \frac{1}{n_i}\sum _{k=0}^{n_i-1}\mathbb {1}_A(R_k(0)) = \lim _{i\rightarrow \infty } \frac{1}{n_i} \sum _{\ell =0}^{i-1} (n_{\ell +1}-n_\ell ) \mathbb {1}_A(S_\ell (0)). \end{aligned}$$

Thus, we have

$$\begin{aligned} \begin{aligned}&\limsup _{n\rightarrow \infty } \frac{1}{n} \sum _{k=0}^{n-1} \mathbb {1}_A(R_k(0))\\&\quad = \limsup _{i\rightarrow \infty } \frac{1}{n_i} \sum _{k=0}^{n_i-1} \mathbb {1}_A(R_k(0)) \\&\quad = \limsup _{i\rightarrow \infty } \frac{1}{n_i} \sum _{\ell =0}^{i-1} (n_{\ell +1}-n_\ell ) \mathbb {1}_A(S_\ell (0)) \\&\quad = \limsup _{i\rightarrow \infty }\frac{i}{n_i} \cdot \frac{\sum _{\ell =0}^{i-1} \mathbb {1}_A(S_\ell (0))}{i}\cdot \frac{\sum _{\ell =0}^{i-1} (n_{\ell +1}-n_\ell ) \mathbb {1}_A(S_\ell (0))}{\sum _{\ell =0}^{i-1} \mathbb {1}_A(S_\ell (0))}\\&\quad \le \limsup _{i\rightarrow \infty }\frac{i}{n_i} \cdot \limsup _{i\rightarrow \infty } \frac{\sum _{\ell =0}^{i-1} \mathbb {1}_A(S_\ell (0))}{i}\cdot \limsup _{i\rightarrow \infty }\frac{\sum _{\ell =0}^{i-1} (n_{\ell +1}-n_\ell ) \mathbb {1}_A(S_\ell (0))}{\sum _{\ell =0}^{i-1} \mathbb {1}_A(S_\ell (0))}\\&\quad =: L_1\cdot L_2\cdot L_3. \end{aligned} \end{aligned}$$

Claim

Almost surely, we have that $L_1$ and $L_3$ are finite and $L_2=0$.

With this claim and also using Lemma A.15, obtain that $\nu$-almost surely we have $L_1\cdot L_2\cdot L_3=0$ and we conclude that $\nu$-almost surely

$$\begin{aligned} \limsup _{n\rightarrow \infty } \frac{1}{n} \sum _{k=0}^{n-1} \mathbb {1}_A(R_k(0)) =0, \end{aligned}$$

proving the corollary. What remains is to prove the claim.

To estimate these latter terms, first observe that almost surely

$$\begin{aligned} \frac{n_i}{i} = \frac{(n_i-n_{i-1})+\cdots +(n_1-0)}{i} \rightarrow {\mathbb {E}}(n_i-n_{i-1}). \end{aligned}$$

Hence

$$\begin{aligned} {\mathbb {E}}(n_i-n_{i-1}) = \sum _{i\ge 1}\Big (d_i{\mathbb {P}}(n_i-n_{i-1}\text { even}) +(d_i+1){\mathbb {P}}(n_i-n_{i-1}\text { odd})\Big ) \ge {\mathbb {E}}(d_i) \end{aligned}$$

and therefore $L_1\le ({\mathbb {E}}(d_i))^{-1} <\infty$. Moreover, this calculation also gives

$$\begin{aligned} {\mathbb {E}}(n_i-n_{i-1}) \le {\mathbb {E}}(d_i)+1. \end{aligned}$$

(A.9)

By Corollary A.14, we have $L_2=0$.

To estimate $L_3$, first observe that, as the expected value of $d_i$ is finite, if we fix $(S_i)$ then, by the law of large numbers, almost surely the average of $\{d_i:S_i(0)\in A\}$ and the average of $\{d_i:S_i(0)\notin A\}$ converge to the same limit ${\mathbb {E}}(d_i)$. Thus, almost surely

$$\begin{aligned} \lim _{i\rightarrow \infty }\frac{\sum _{\ell =0}^{i-1} (n_{\ell +1}-n_\ell ) \mathbb {1}_A(S_\ell (0))}{\sum _{\ell =0}^{i-1} \mathbb {1}_A(S_\ell (0))} =\lim _{i\rightarrow \infty }\frac{ \sum _{\ell =0}^{i-1} (n_{\ell +1}-n_\ell )}{i} \le {\mathbb {E}}(d_i)+1, \end{aligned}$$

where the latter follows from (A.9). Thus, $L_3$ is finite. This proves the claim. $\square$

The statement for random walk starting from 0 can be generalized to any starting distribution which allows us to finally prove Lemma A.12.

Proof of Lemma A.12

Fix $\mu$. For any $\varepsilon >0$ we can find some N such that $\mu ([-N,N])>1-\varepsilon$. As $\phi ^{-1}\circ \pi _2\circ g_i$ is a translation, if $R_n(0) \notin B_N(A)$ then $(R_n)_*\mu (A) < \varepsilon$. Hence,

$$\begin{aligned} \limsup _{n\rightarrow \infty } \frac{1}{n} (R_n)_*\mu (A)\le \varepsilon + \lim _{n\rightarrow \infty } \frac{1}{n} \mathbb {1}_{B_N(A)}(R_n(0))=\varepsilon . \end{aligned}$$

Passing with $\varepsilon$ to 0 ends the proof. $\square$

We end this section by providing an alternative proof which we owe to the referee. It is based on an argument which nowadays one also refers to as the invariance principle.

Alternative proof of Proposition A.10

Again, as in our first proof, we observe that it is enough to prove that there cannot exist a measure of maximal entropy supported on $\Sigma _2\times (0,1)$.

Claim

Every ergodic measure supported on $\Sigma _2\times (0,1)$ has zero Lyapunov exponent.

Proof

Denoting by $\varrho :\Sigma _2\times (0,1)\rightarrow (0,1)$ the natural projection $\varrho (\xi ,x)=x$, relation (A.6) implies that for every $X=(\xi ,x)$, $x\in (0,1)$, the projected orbit $x,f_\xi ^1(x),\ldots ,f_\xi ^n(x),\ldots$ is “discrete” in the sense that it only may have accumulation points at 0 and 1.

Consider now an ergodic measure $\mu$ and a $\mu$-generic point $X=(\xi ,x)$. Without loss of generality, we can assume that X is in the support of $\mu$ and hence, by the Poincaré recurrence theorem, for any $\varepsilon >0$, $F^n(X)$ returns for infinitely many n to the set $\Sigma _2\times (x-\varepsilon ,x+\varepsilon )$. By the above observation, we must have $f_\xi ^n(x)=x$ for infinitely many n. By our hypothesis, if $f_\xi ^n$ preserves orientation, this implies that $f_\xi ^n$ is in fact the identity. There are only two possibilities: either it preserves or it reverses orientation, one of the two will occur infinitely many times. In case $f_\xi ^{n_k}$ is orientation reversing for some sequence $(n_k)_k$, then $f_\eta ^{n_k-n_1}$, with $\eta =\sigma ^{n_1}(\xi )$, will preserve orientation. Hence, there exist infinitely many times n when indeed $f_\eta ^n$ is the identity and $f_\eta ^n(x)=x$. In particular, $(f_\eta ^n)'(x)=1$. Since $(\xi ,x)$ was $\mu$-generic, $(\eta ,x)$ is also $\mu$-generic, and we can conclude that $\chi (\mu )=0$. $\square$

By contradiction, assume now that there exists an ergodic F-invariant probability measure $\mu$ of maximal entropy $\log 2$ which is supported on $\Sigma _2\times (0,1)$. By the above Claim, $\chi (\mu )=0$. Note that the projection of $\mu$ to $\Sigma _2$ is the $(\frac{1}{2},\frac{1}{2})$-Bernoulli measure. Hence, we can invoke for example [5, 8.6 Theorem] and conclude that there must exist a Borel probability measure $\rho$ on (0, 1) which is fixed under all fiber maps simultaneously in the sense that

$$\begin{aligned} (f_\xi ^1)_*\rho =\rho \end{aligned}$$

almost surely, and hence, since we consider a step-skew product, we must have $(f_0)_*\rho =\rho =(f_1)_*\rho$. But this is a contradiction. $\square$