Periodic representations in algebraic bases

Abstract

We study periodic representations in number systems with an algebraic base $\beta$ (not a rational integer). We show that if $\beta$ has no Galois conjugate on the unit circle, then there exists a finite integer alphabet $\mathcal A$ such that every element of $\mathbb Q(\beta )$ admits an eventually periodic representation with base $\beta$ and digits in $\mathcal A$.

1 Introduction

A well known result by Schmidt [10] states that if $\beta >1$ is a Pisot number, then the set of numbers with eventually periodic (greedy) $\beta$-expansions equals precisely to $\mathbb Q(\beta ).$ On the other hand, the only bases allowing eventually periodic $\beta$-expansions of $\mathbb Q(\beta )$ are Pisot and Salem numbers. However, no Salem base has been proved to possess this property.

In [2], Baker, Masáková, Pelantová, and the second author studied the $(\beta ,\mathcal A)$-representations, i.e., the expressions of the form $\sum _{k\ge -L}^{+\infty } a_k\beta ^{-k},$ $a_k\in \mathcal A$, without the greedy condition. One of the problems studied in [2] was the following: Given an algebraic base $\beta \in \mathbb C$, $|\beta |>1$, is there a finite alphabet of digits $\mathcal A\subset \mathbb Q(\beta )$, such that

$$\begin{aligned} \mathbb Q(\beta )={\text {Per}}_\mathcal A(\beta ):=\left\{ \sum _{k\ge -L}^{+\infty } a_k\beta ^{-k}\ : \ a_k\in \mathcal A,\ (a_k)_{k\ge -L} \text { is eventually periodic}\right\} . \end{aligned}$$

(1)

This property indeed holds for the Pisot numbers, and their complex analogy. Our main result is the following theorem.

Theorem 1.1

Let $\beta$ be an algebraic number such that $|\beta |>1$, and let $|\beta '|\ne 1$ for each Galois conjugate $\beta '$ of $\beta$. Then there exists $\mathcal A\subset \mathbb Z$ finite such that ${\text {Per}}_\mathcal A(\beta )=\mathbb Q(\beta ).$

Note that this is a stronger version of Theorem 25 of [2], as an additional condition was required there, namely that $\tfrac{1}{a}\in \mathbb Z[\beta ,\beta ^{-1}]$, where a is the leading coefficient of the minimal polynomial of $\beta$ over $\mathbb Z$. This additional condition is not typically satisfied; the full classification of such bases is also given in [2].

We will see that our result follows from the fact that $\tfrac{1}{n}\in {\text {Per}}_\mathcal A(\beta )$ for all $n\in \mathbb N$. To obtain this statement we first prove a generalized form of the Fermat’s little theorem. Namely, for any $\beta$ algebraic, and for any $n\in \mathbb N$, we show the existence of $i,j\in \mathbb Z$ such that $\beta ^i-\beta ^j \in n\mathbb Z[\beta ]$, see Theorem 3.4. This is surprisingly non-trivial for an non-integer element $\beta$.

An important role in our proofs is played by parallel addition algorithms, see [5]. We use these algorithms for the reduction of the alphabet while preserving periodicity. This approach fails if $\beta$ has a conjugate on the unit circle because we then cannot make use of parallel addition algorithms. Nevertheless, we will show that $\tfrac{1}{n}\in {\text {Per}}_\mathcal A(\beta )$ for all $n\in \mathbb N$ even in these cases, see Sect. 4. We are unable, however, to use our technique to extend the periodicity to the whole $\mathbb Q(\beta )$.

The technique used to prove the main result is rather non-constructive. However, we provide a tool allowing the computation of a $(\beta ,\mathcal A)$-representation for any element of $\mathbb Q(\beta )$ with certain alphabet of digits. These results are contained in Sect. 5.

2 Preliminaries

Let us provide precise definitions of the basic notions mentioned in the introduction.

Definition 2.1

Let $\beta \in \mathbb C$, $|\beta |>1$, and let $\mathcal A\subset \mathbb C$ be a finite set containing 0. An expression

$$\begin{aligned} x = \sum _{k= -L}^{+\infty } a_k\beta ^{-k},\quad a_i\in \mathcal A\end{aligned}$$

is called a $(\beta ,\mathcal A)$-representation of x.

One of possible constructions of $(\beta ,\mathcal A)$-representations is the following one given by Thurston in [11]. Assume we have a set $V\subset \mathbb C$ such that $\beta V \subseteq \bigcup _{a\in \mathcal A}(V+a),$ then all the elements of V have a $(\beta ,\mathcal A)$-representation of the form $\sum _{k=1}^{+\infty } a_k\beta ^{-k}$. Moreover, as a consequence, every $x\in \bigcup _{n\in \mathbb N} \beta ^{n}V$ has a $(\beta ,\mathcal A)$-representation. Here we can see that if $0\in {\text {int}}(V)$, then there exist $(\beta ,\mathcal A)$-representations for all the real (or complex) numbers. It has been shown that the assumption of each element of $\mathbb Q(\beta )$ having an eventually periodic $(\beta ,\mathcal A)$-representation arising from such a construction is very restrictive. In particular, if $\beta \in \mathbb R$, then necessarily $|\beta |$ is a Pisot number, see [2]. More on finding $(\beta ,\mathcal A)$-representations can be found for example in [1, 3, 6, 8, 9].

Given two $(\beta ,\mathcal A)$-representations, one can study their behaviour under elementary arithmetic operations. In [4, 5], the authors proved that if $\beta$ has no conjugates on the unit circle, then there exists $\mathcal A\subset \mathbb Z$ such that $(\beta ,\mathcal A)$-representations allow a parallel addition algorithm defined as follows.

Definition 2.2

For a base $\beta \in \mathbb C$, $|\beta |>1$, and an alphabet $\mathcal A\subset \mathbb C$, denote $\mathcal B=\mathcal A+\mathcal A$. We say that $(\beta ,\mathcal A)$ allows parallel addition if there exist $t,r\in \mathbb N$ and $\Phi :\mathcal B^{t+r+1}\rightarrow \mathcal A$ such that

• $\Phi (0^{t+r+1})=0$;

• For every $x=\sum _{k\in \mathbb Z}x_k\beta ^{-k}$ with $x_k=0$ for $k< L$ for some L and $x_k\in \mathcal B$, it holds that $x=\sum _{k\in \mathbb Z}z_k\beta ^{-k}$, where $z_k=\Phi (x_{k-t}\ldots x_kx_{k+1}\ldots x_{k+r})\in \mathcal A$.

Theorem 2.3

[4, 5] Let $\beta \in \mathbb C$, $|\beta |>1$. Then there exists an alphabet $\mathcal A\subset \mathbb C$ such that $(\beta ,\mathcal A)$ allows parallel addition if and only if $\beta$ is an algebraic number and $|\beta '|\ne 1$ for every conjugate $\beta '$ of $\beta$. Moreover, we can choose $\mathcal A= \{-M,\ldots , 0,\ldots ,M\}\subset \mathbb Z.$

We can thus see a parallel addition algorithm as an algorithm that reduces representations over some large (but finite) alphabet into a $(\beta ,\mathcal A)$-representation using only a bounded neighbourhood of each digit. Therefore it rewrites finite (eventually periodic) representations over $\mathbb Z$ into finite (eventually periodic) $(\beta ,\mathcal A)$-representations. The following statement is thus an easy corollary.

Corollary 2.4

[2] Let $\beta \in \mathbb C$, $|\beta |>1$, and let $\mathcal A$ be a symmetric alphabet such that $(\beta ,\mathcal A)$ allows parallel addition. Let ${\text {Per}}_\mathcal A(\beta )$ be as in (1), and let

$$\begin{aligned} \mathrm{Fin}_\mathcal A(\beta ) = \left\{ \sum _{k\in I} a_k\beta ^{-k} : a_k\in \mathcal A,\ I\subset \mathbb Z\text { is finite}\right\} . \end{aligned}$$

Then

• (1) $\mathrm{Fin}_\mathcal A(\beta )\cdot \mathrm{Per}_\mathcal A(\beta )\subset \mathrm{Per}_\mathcal A(\beta )$;

• (2) $\mathrm{Fin}_\mathcal A(\beta ) = \mathbb Z[\beta ,\beta ^{-1}]$.

In the rest of the text we denote by $\mathbb Z_n$ the factorring $\mathbb Z/ n\mathbb Z$.

3 The main theorem

The following proposition was one of the ingredients used in the proof of Theorem 25 of [2]. Since the proposition appeared as a part of the proof, we include it here for completeness.

Proposition 3.1

Let $\beta >1$ have no conjugate on the unit circle. Then the existence of $\mathcal A$ such that $\tfrac{1}{n}\in \mathrm{Per}_\mathcal A(\beta )$ is equivalent to the existence of $i>j\in \mathbb Z$ such that $\beta ^i-\beta ^j\in n\mathbb Z[\beta ].$

Proof

Suppose that $\tfrac{1}{n}$ has an eventually periodic $(\beta ,\mathcal A)$-representation

$$\begin{aligned} \frac{1}{n} = \sum _{k\ge -L}^{+\infty } a_k\beta ^{-k},\quad \text {with } a_{n}=a_{n+p} \text { for } n > N. \end{aligned}$$

By summing the period as a geometric series we obtain

$$\begin{aligned} \frac{1}{n} =\frac{z_1}{\beta ^N} + \frac{z_2}{\beta ^{N+p}(\beta ^p-1)}\quad \text {for some }z_1,z_2\in \mathbb Z[\beta ], \end{aligned}$$

which can be easily rewritten in the desired form.

Assume that $\beta ^i-\beta ^j\in q\mathbb Z[\beta ]$ with $i>j$. Then we have that

$$\begin{aligned} \frac{1}{n} = z\cdot \frac{1}{\beta ^j}\cdot \frac{1}{\beta ^{i-j}-1}, \quad \text {for some } z\in \mathbb Z[\beta ]. \end{aligned}$$

(2)

Then by Corollary 2.4 we know that $z\cdot \frac{1}{\beta ^j}\in \mathrm {Fin}_\mathcal A(\beta )$. Furthemore,

$$\begin{aligned} \frac{1}{\beta ^{i-j}-1}=-\sum _{k=0}^\infty {\beta ^{-k(i-j)}}\in \mathrm {Per}_\mathcal A(\beta ), \end{aligned}$$

thus the expression (2) belongs to $\mathrm {Fin}_\mathcal A(\beta )\cdot \mathrm {Per}_\mathcal A(\beta )\subset \mathrm {Per}_\mathcal A(\beta ).$ $\square$

Theorem 3.2

Let $\beta$ be an algebraic number with the minimal polynomial $m(x)=a_dx^d+\cdots +a_1x+a_0\in \mathbb Z[x]$, and let $n\in \mathbb N$. If $\gcd (a_d,n)=\gcd (a_0,n)=1$, then $\beta ^i-1\in n\mathbb Z[\beta ]$ for some $i\in \mathbb N.$

Proof

Let $m(x)\in \mathbb Z[x]$ be the minimal polynomial of $\beta .$ Define sequences $z^{(k)}=(z_0^{(k)},\ldots ,z_{d-1}^{(k)})\in \mathbb Z_n^d$ and $p_k\in \mathbb Z_n$ for $k\in \mathbb N_0$ by the relation

$$\begin{aligned} \sum _{i=0}^{d-1} z_i^{(k)}x^i + p_km(x) \equiv \sum _{i=0}^{d-1}z_i^{(k+1)} x^{i+1}\pmod {n\mathbb Z[x]}\quad \text {with}\quad z^{(0)} = (1,0,\ldots ,0). \end{aligned}$$

(3)

The sequences $\{z^{(k)}\}$ and $\{p_k\}$ are uniquely defined. Indeed, each $z^{(k)}$ enforces that $p_k:=-z^{(k)}_0m(0)^{-1}\pmod n$ (using the invertibility of $m(0)=a_0$), and consequently $z^{(k+1)}$ is also defined. Conversely, note that to each $z^{(k+1)}$ there are unique $z^{(k)}$ and $p_k$, as $a_d$ is invertible modulo n.

Clearly, the sequence $\{z^{(k)}\}$ can take only finitely many values. Let r be the smallest index such that $z^{(r)}=z^{(s)}$ for some $s<r.$ Then because of the uniqueness of the followers and predecessors in $\{z^{(k)}\}$ we have $z^{(r)}=z^{(0)}=(1,0,\ldots ,0)$, whence necessarily $z^{(r-d+1)} = (0,\ldots ,0,1).$ Then by (3) we have

$$\begin{aligned} \sum _{k=0}^{r-d} x^kp_km(x)\equiv x^{r}-1\pmod {n\mathbb Z[x]}, \end{aligned}$$

(4)

because $z^{(0)}=(1,0,\ldots ,0),\ z^{(r)}=(0,\ldots ,0,1),$ and the rest of the summands cancel out. We obtain the statement by applying the homomorphism $x\mapsto \beta : \mathbb Z[x]\rightarrow \mathbb Z[\beta ]$ on (4). $\square$

We will need the following lemma to generalize Theorem 3.2 also to the cases $\gcd (a_d,n)\ne 1$ or/and $\gcd (a_0,n)\ne 1.$ We will denote the leading coefficient of the minimal polynomial of $\beta$ over $\mathbb Z$ as $c(\beta )$.

Lemma 3.3

Let $m_i(x)$ be the minimal polynomial for $\beta ^i$, and let $c_i=c(\beta ^i)$ be the leading coefficient of $m_i(x)$. If $p\mid c_1$ for a prime p, then for each j there is i such that $p^j \mid c_i$.

Proof

Let us first assume that $c_1=p^k$ for some k, and that there is j such that $p^j\not \mid c_i$ for each i.

Observe that if $b\beta$ is an algebraic integer for some $b\in \mathbb Z$, then $c(\beta )\mid b$. Also $c(\beta )\beta$ is always an algebraic integer. Hence $p^k\beta$ is an integer, and so also $p^{ik}\beta ^i$ is an integer. Thus $c_i\mid p^{ik}$ and $c_i$ is a power of p. Since $p^j\not \mid c_i$, it is at most $(j-1)$st power. Since $c_i\beta ^i$ is an integer, we see that also $p^{j-1}\beta ^i$ is an integer for each i.

We conclude that $\mathbb Z[\beta ]\subset \frac{1}{p^{j-1}}\mathcal O_K$ (where $K=\mathbb Q(\beta )$). But $\frac{1}{p^{j-1}}\mathcal O_K$ is a finitely generated $\mathbb Z$-module and $\mathbb Z$ is noetherian, and so also $\mathbb Z[\beta ]$ is finitely generated $\mathbb Z$-module. But this implies that $\beta$ is an algebraic integer. This is a contradiction with $c_1>1$.

For the general case, let $a_1=p^k b$ with $p\not \mid b$ and consider $\gamma :=b\beta$. Let $b_i:=c(\gamma ^i)$; by the assumption we have that $b_1=p^k$ (because a candidate for the minimal polynomial for $\gamma$ is $b^{d-1}m(x/b)$; we may need to divide by the gcd of coefficients, but not by p, because p was coprime to b).

By the first part of the proof, we know that for each j there is i such that $p^j\mid b_i$. Let now $n_i(x)$ be the minimal polynomial for $\gamma ^i=b^i\beta ^i$. Then $n_i(b^ix)$ is a candidate for the minimal polynomial for $\beta ^i$; we may need to divide by the gcd of coefficients, but again not by p, as it is coprime to $b^i$. Thus $p^j\mid b_i$ implies that $p^j\mid a_i$. $\square$

Note that we get the same statement for constant coefficients just by considering $\beta ^{-1}$.

Now we are ready to prove the main technical result of this section, which can be viewed as a generalized version of little Fermat’s theorem. There is a number of these in the literature, including some that do not require $\beta$ to be an algebraic integer (e.g., Chapter 23 in [7]), but we could not locate our version, which seems to be in a somewhat different vein than the others.

Theorem 3.4

Let $\beta$ be an algebraic number of degree d. Then for each $n\in \mathbb N$ there exist $i>j\in \mathbb Z$ such that $\beta ^i-\beta ^j\in n\mathbb Z[\beta ]$.

Proof

Let us first prove that if the statement holds for coprime $n_1,n_2\in \mathbb N$, then it also holds for $n_1n_2$. Assuming its validity for $n_1, n_2$, we can suppose that $1-\beta ^{i_1}\in n_1\mathbb Z[\beta ]$, and $1-\beta ^{i_2}\in n_2\mathbb Z[\beta ].$ Then it is also true that for all $k\in \mathbb N$ we have $1-\beta ^{ki_1}\in n_1\mathbb Z[\beta ]$ and $1-\beta ^{ki_2}\in n_2\mathbb Z[\beta ]$. From $\gcd (n_1,n_2)=1$ it follows that $1-\beta ^{i_1i_2}\in n_1n_2\mathbb Z[\beta ],$ i.e., the statement is true for $n=n_1n_2$.

Hence it remains to prove the theorem when $n=p^\ell$ for a prime p and $\ell \in \mathbb N.$ The case $\gcd (a_0,p)=\gcd (a_d,p)=1$ is solved in Theorem 3.2. Thus assume w.l.o.g. that $p|a_d$, otherwise we consider $\beta ^{-1}$. We will proceed by induction on the degree of $\beta$. According to Lemma 3.3 we can find $k\in \mathbb N$ such that $\beta ^k$ has the minimal polynomial $m_k(x)$, such that n divides its leading coefficient $c(\beta ^k)$. Roots of $m_k(x)-c(\beta ^k)x^d$ are of a smaller degree, therefore by the induction we have that

$$\begin{aligned} {p}(x)(m_k(x)-c(\beta ^k)x^d)=x^i-x^j-nz(x) \end{aligned}$$

for some $p(x),z(x)\in \mathbb Z[x]$. Then after a simple rearrangement, and under the map $x\mapsto \beta ^k$ we obtain

$$\begin{aligned} \beta ^{ki}-\beta ^{kj}=nz(\beta ^k)-\beta ^{kd}c(\beta ^k){p}(\beta ^k)\in n\mathbb Z[\beta ^k]\subset n\mathbb Z[\beta ]. \end{aligned}$$

The induction is complete by realizing that the statement is true for $\beta \in \mathbb Z.$ $\square$

Proof of Theorem 1.1

Each $x\in \mathbb Q(\beta )$ can be written as $x = \tfrac{z}{n}$ with $z\in \mathbb Z[\beta ]$, and $n\in \mathbb N.$ By Theorem 3.4 together with Proposition 3.1 we have that $\tfrac{1}{n}\in {\text {Per}}_\mathcal A(\beta ).$ Then by Corollary 2.4 we have that $z\in {\text {Fin}}_\mathcal A(\beta )$, and subsequently also that $x\in {\text {Per}}_\mathcal A(\beta ).$

$\square$

4 Bases with conjugates on the unit circle

In the previous section, a necessary tool for obtaining our results was the existence of the parallel addition in base $\beta .$ The reason was that we were then able to convert eventually periodic representations over the infinite alphabet $\mathbb Z$ to a finite one. However, the existence of the parallel algorithms is possible only if there is no conjugate of $\beta$ lying on the unit circle. Nevertheless, finding periodic representations of $\tfrac{1}{n}$ is possible if one proceeds more carefully. In this section we prove the following theorem.

Theorem 4.1

Let $\beta$ be an algebraic number such that $|\beta '|=1$ for a conjugate $\beta '$. Then $\tfrac{1}{n}\in {\text {Per}}_\mathcal A(\beta )$ for some $\mathcal A\subset \mathbb Z$ finite.

Lemma 4.2

Let $\beta$ be an algebraic number. Then for each $n\in \mathbb N$ one can find $i(n)>j(n)\in \mathbb Z$ such that $\beta ^{i(n)}-\beta ^{j(n)} = n\sum _{k=0}^{m(n)} d_k(n)\beta ^k = z(n)$, such that

• (1) $m(n) < 2(i(n)-j(n))$,

• (2) there exists $C>0$ such that $|d_k(n)|<C$ for any k, n.

Proof

Fix an $n\in \mathbb N$; the existence of $i>j$ and $d_k$’s satisfying $\beta ^i-\beta ^j = n\sum _{i=0}^{m}d_k\beta ^k$ is given by Theorem 3.4. Multiplying both sides of this equation by $\beta ^{r(i-j)}$ and summing for $r=0,1,\ldots ,s$ we obtain

$$\begin{aligned} \beta ^{(s+1)i-sj}-\beta ^j=n \sum _{k=0}^{(s+1)i-sj+m} \widetilde{d_k}\beta ^k. \end{aligned}$$

We can satisfy item (1) by setting $i(n) = (s+1)i-sj$, $j(n)=j$, $d_k(n) = \widetilde{d_k}$, and $m(n) = (s+1)i-sj+m$ for an appropriate value s.

Thus we have

$$\begin{aligned} x^{i(n)}-x^{j(n)}-n\sum _{k=0}^{m(n)} {d_k}(n)x^k = p_n(x)m(x) \end{aligned}$$

for some $p_n(x)\in \mathbb Z[x].$ We can reduce the coefficients of $p_n(x)$ modulo n to assume that they are all between 0 and n. Let M be the maximum of absolute values of coefficients of m(x). Then the polynomial $p_n(x)m(x)$ has all coefficients less than $nM(\deg m+1)$ in absolute value. Consequently, we see that in item (2) we can take $C=M(\deg m+1)$. $\square$

Remark 4.3

Note that one can replace the factor 2 in item (1) by $1+\varepsilon$ for any $\varepsilon >0$.

Proof of Theorem 4.1

For fixed $n\in \mathbb N$ apply Lemma 4.2, i.e., we have that $\beta ^i-\beta ^j = nz$ for some $i>j$ and $z=\sum _{k=0}^{m}d_k(n)\beta ^k\in \mathbb Z[\beta ]$. Then

$$\begin{aligned} \frac{1}{n} = \frac{1}{\beta ^i}\frac{z}{1-\beta ^{j-i}} = \frac{1}{\beta ^i}\sum _{k=0}^{+\infty }z\beta ^{-k(i-j)}. \end{aligned}$$

The latter is indeed a periodic representation over an integer alphabet that is bounded by $2\max \{|d_k(n)| : 0\le k\le m\}$ (here we used that $m<2(i-j)$). Since $d_k(n)$ are bounded independently of n, we can choose a common alphabet for all $n\in \mathbb N.$ $\square$

5 Computational point of view

The results so far showed the existence of the eventually periodic $(\beta ,\mathcal A)$-representations. Because of the induction, the proof of Theorem 3.4 does not give an explicit way of finding i, j such that $\beta ^i-\beta ^j\in n\mathbb Z[\beta ].$ In this section we show how to compute the pair i, j. The method we use is in fact in the background of the proof of Theorem 3.2.

From now on we will handle elements of $\mathbb Z[\beta ]$ as elements of the quotient ring $\mathbb Z[x]/{m(x)}\cong \mathbb Z[\beta ]$, where m(x) is the minimal polynomial of $\beta ,$ through the isomorphism $x\mapsto \beta .$

Let us start with an example which is not covered by the results of [2].

Example 5.1

Consider $m(x)=3x^2+2x+3$ and $n=6.$ Then we have

$$\begin{aligned} 0\equiv (2x^2+3x+4)m(x)=6x^4+13x^3+24x^2+17x+12\pmod {m(x)}, \end{aligned}$$

hence

$$\begin{aligned} x^3-x \equiv -6x^4-12x^3-24x^2-18x-12\in n(\mathbb Z[x]/(m(x)), \end{aligned}$$

or equivalently,

$$\begin{aligned} \beta ^3-\beta = -6\beta ^4-12\beta ^3-24\beta ^2-18\beta -12\in n\mathbb Z[\beta ]. \end{aligned}$$

Let us show how such i, j can be found in general. Assume that $x^i-x^j\equiv np(x)$ in $\mathbb Z[x]/m(x)$ for some $p(x)\in \mathbb Z[x]$. This is equivalent to the existence of $r(x)\in \mathbb Z[x]$ such that

$$\begin{aligned} x^i-x^j-qp(x) = r(x)m(x)\quad \text {in }\mathbb Z[x]. \end{aligned}$$

(5)

The product r(x)m(x) can be viewed (roughly speaking) as a “sum of shifted multiples of m(x)”. This idea is illustrated in the following table, where we continue with Example 5.1.

$$\begin{aligned} \begin{array}{rc@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 2x^2m(x)=&{}6&{}4&{}6&{} &{} \\ 3xm(x)=&{} &{}9&{}6&{}9&{} \\ 4m(x)=&{} &{} &{}12&{}8&{}12 \\ \hline (2x^2+3x+4)m(x)=&{}6&{}13&{}24&{}17&{}12 \end{array} \end{aligned}$$

In each row lies a multiple of the minimal polynomial, the power of x corresponds to the shift. In order to satisfy (5) for some p(x), we want the tuple of the sums of the columns (in our case (6, 13, 24, 17, 12)) to be equivalent $\pmod n$ to a vector with the only two non-zero entries being 1 and $-\,1$. In fact, we can also consider the table to live in $\mathbb Z_n$ to directly obtain the result

$$\begin{aligned} \begin{array}{rc@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 2x^2m(x)=&{}0&{}4&{}0&{} &{} \\ 3xm(x)=&{} &{}3&{}0&{}3&{} \\ 4m(x)=&{} &{} &{}0&{}2&{}0 \\ \hline (x^2+2x+1)m(x)=&{}0&{}1&{}0&{}-1&{}0 \end{array} \end{aligned}$$

When constructing r(x), we can proceed from higher powers of x to lower (or from left to right in the table) wanting to add an appropriate multiple of the minimal polynomial such that the left most digit sums to zero (or 1 at one position and $-1$ at another position) during each step. However, we do not have prior knowledge of where the digits 1 and $-1$ should be created.

Definition 5.2

Let $m(x)=\sum _{i=0}^d a_ix^i$ and let $n\in \mathbb N.$ The graph $G(m,n)=(V,E)$ is the oriented graph with vertices $V = \mathbb Z_n^d\times \{A,B,C\}$, and with the set E of labeled edges $(y_d,\ldots , y_1;\gamma )\xrightarrow {k}(z_d,\ldots ,z_1;\delta ), k\in \mathbb Z_n,$ if

• (1) $\gamma =\delta$ and $\sum _{i=1}^d y_ix^i+k\sum _{i=0}^d{a_ix^i} \equiv \sum _{i=1}^{d}z_ix^{i-1}\quad \pmod { n\mathbb Z[x]},$

• (2) $\gamma =A,\delta =B$ and $\sum _{i=1}^d y_ix^i+k\sum _{i=0}^d{a_ix^i} \equiv x^d+\sum _{i=1}^{d}z_ix^{i-1}\quad \pmod {n\mathbb Z[x]},$

• (3) $\gamma =B,\delta =C$ and $\sum _{i=1}^d y_ix^i+k\sum _{i=0}^d{a_ix^i} \equiv -x^d+\sum _{i=1}^{d}z_ix^{i-1} \quad \pmod {n\mathbb Z[x]}.$

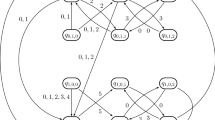
The graph G(m, n) has the following meaning. Consider again Example 5.1. The labels of edges correspond to the coefficients of $r(x)=2x^2+3x+4,$ i.e., we have a path

$$\begin{aligned} (0,0;A)\xrightarrow {2}(4,0;A)\xrightarrow {3}(0,3;B)\xrightarrow {4}(5,0;B)\xrightarrow {0}(0,0;C) \end{aligned}$$

Note that the change of the third entry of a vertex from A to B corresponds to the situation that we created the digit 1, while the change from B to C means that the digit $-1$ was produced.

Theorem 5.3

Let $\beta$ be an algebraic number with no conjugate on the unit circle, let m(x) be the minimal polynomial of $\beta$, and let $n\in \mathbb N$. Then $\tfrac{1}{n}\in \mathrm{Per}_\mathcal A(\beta )$ for some $\mathcal A\subset \mathbb C$ if and only if in the graph G(m, n) there exists a path from $(0,\ldots ,0;A)$ to $(0,\ldots ,0;C)$.

Moreover, if this path has labels $c_0,c_1,\ldots ,c_{s-1}$, then

$$\begin{aligned} (c_0x^{s-1}+c_1x^{s-2} + \cdots + c_{s-1})m(x)\equiv x^i-x^j\quad \pmod {n\mathbb Z[x]} \end{aligned}$$

for some $i,j\in \mathbb Z.$

Proof

Let

$$\begin{aligned} (z^{(0)},\gamma ^{(0)})\xrightarrow {c_0}(z^{(1)},\gamma ^{(1)})\xrightarrow {c_1}\cdots \xrightarrow {c_{s-1}}(z^{(s)},\gamma ^{(s)}), \end{aligned}$$

where $z^{(k)}=(z^{(k)}_d,\ldots ,z^{(k)}_1)$, $z^{(0)}=z^{(s)}=(0,\ldots ,0)$ and $\gamma ^{(0)}=A,\gamma ^{(s)}=C$ be a path in G(m, n).

Fig. 1

The graph G(m, n) for $m(x) = 3x^2+2x+3,\ n=6$ as in Example 5.1

According to the definition of G(m, n) we have that

$$\begin{aligned} c_{k}m(x)\equiv \alpha _k x^d - \sum _{i=1}^dz_i^{(k)}x^i+\sum _{i=1}^dz_i^{(k+1)}x^{i-1}\quad \pmod {n\mathbb Z[x]}, \end{aligned}$$

(6)

where

$$\begin{aligned} \alpha _k={\left\{ \begin{array}{ll} 1&{}\text {if } \gamma ^{(k)}=A, \gamma ^{(k+1)}=B,\\ -1&{}\text {if } \gamma ^{(k)}=B, \gamma ^{(k+1)}=C, \\ 0&{}\text {otherwise.}\end{array}\right. } \end{aligned}$$

Then by multiplying (6) by $x^{s-k-1}$, and summing for each $k=0,\ldots ,s-1$, we obtain

$$\begin{aligned} m(x)\sum _{k=0}^{n-1}x^{s-k-1}c_k\equiv \sum _{k=0}^{s-1}x^{s-k-1}\alpha _k\quad \pmod {n\mathbb Z[x]}. \end{aligned}$$

The right side is of this form because $z^{(0)}=z^{(s)}=(0,\ldots ,0)$, and the rest of the summands cancel out.

Thus we have $c(x)m(x)=x^i-x^j+np(x)$ with $c(x),p(x)\in \mathbb Z[x]$, $i=s-k_1-1$ and $j=s-{k_2}-1$ if $(z^{(k_1)},A)\xrightarrow {k_1}(z^{(k_1+1)},B)$ and $(z^{(k_2)},B)\xrightarrow {k_2}(z^{(k_2+1)},C).$ Hence $x^i-x^j\equiv -np(x)\pmod {\mathbb Z[x]/m(x)}$, and using the isomorphism $\mathbb Z[x]/m(x)\rightarrow \mathbb Z[\beta ]$ we obtain $\beta ^i-\beta ^j=-np(\beta )\in n\mathbb Z[\beta ].$ The graph G(m, n) for Example 5.1 is shown in Fig. 1.$\square$

For a given base $\beta$, set $\mathcal A$ such that $(\beta ,\mathcal A)$ allows parallel addition. Then computing an eventually periodic $(\beta ,\mathcal A)$-representation of $x:=\tfrac{z}{n}\in \mathbb Q(\beta )$, $z\in \mathbb Z[\beta ]$ can be done by the following steps:

• (1) construct the graph G(m, n), and find $i,j\in \mathbb Z$, and $z\in \mathbb Z[\beta ]$ such that $\beta ^i-\beta ^j = nz$ using Theorem 5.3;

• (2) construct an eventually periodic $(\beta ,\mathcal A)$-representation of $\tfrac{1}{n}$ as

  $$\begin{aligned} \frac{1}{n} = -\frac{\widetilde{z}}{\beta ^j}\sum _{k=0}^\infty {\beta ^{-k(i-j)}} \end{aligned}$$

  (see the proof of Proposition 3.1);

• (3) use a parallel addition algorithm (see [5]) to reduce the digits of the eventually periodic $(\beta ,\mathcal A)$-representation

  $$\begin{aligned} x = -\frac{z\widetilde{z}}{\beta ^j}\sum _{k=0}^\infty {\beta ^{-k(i-j)}} \end{aligned}$$

  into the digit alphabet $\mathcal A$.