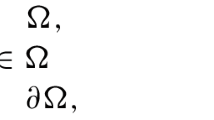Existence and multiplicity of solutions for a class of elliptic problem with critical growth

Abstract

In this paper we show the existence and multiplicity of positive solutions for a class of elliptic problem of the type

$$\begin{aligned} -\,\Delta u+\lambda V(x)u=\mu u^{q-1}+u^{2^*-1},\quad \text{ in } \quad \mathbb {R}^N, \qquad {(P)_{\lambda , \mu }} \end{aligned}$$

where $\lambda , \mu >0$, $q \in (2,2^*)$ and $V:\mathbb {R}^N \rightarrow \mathbb {R}$ is a continuous function verifying some conditions. By using variational methods, we have proved that the above problem has at least $cat(int(V^{-1}) (\{0\}))$ of positive solutions if $\lambda$ is large and $\mu$ is small.

1 Introduction and main result

In this paper we study the existence and multiplicity of positive solutions for the problem

$$\begin{aligned} -\,\Delta u+\lambda V(x)u=\mu u^{q-1}+u^{2^*-1},\quad \text{ in } \quad \mathbb {R}^N, \qquad \qquad \qquad \qquad {(P)_{\lambda , \mu }} \end{aligned}$$

where $\lambda , \mu >0$, $2<q<2^*=\frac{2N}{N-2}$ with $N \ge 3$ and $V:\mathbb {R}^N \rightarrow \mathbb {R}$ is a continuous function verifying

$(V_{1})$ :

$V(x) \ge 0, \,\, \forall x \in \mathbb {R}^N.$

$(V_{2})$ :

There exists $M_0>0$ such that the set $\mathcal {L}=\{x\in \mathbb {R}^N: V(x) \le M_0\}$ is nonempty and $|\mathcal {L}| <\infty$, where |A| denotes the Lebesgue measure of A on $\mathbb {R}^N$.

$(V_{3})$ :

$\Omega := int (V^{-1}(\{0\}))$ is a non-empty bounded open set with smooth boundary $\partial \Omega$.

In [9], Bartsch and Wang have established the existence and multiplicity of positive solutions for the problem

$$\begin{aligned} \begin{array}{lll} -\,\Delta u + (\lambda V(x)+1)u = u^{p-1},\quad \text{ in } \quad \mathbb {R}^N, \\ \end{array} \end{aligned}$$

(1.1)

for $N\ge 3$, $\lambda >0$, $p \in (2, 2^{*})$ and V verifying $(V_1){-}(V_3)$. In that paper, the authors combined variational methods with the Lusternik–Schnirelman category to show that (1.1) has at least $cat(\Omega )$ positive solution when p is close to $2^*$ and $\lambda$ is large. We recall that if Y is a closed subset of a topological space X, the Lusternik–Schnirelman category $cat_{X}(Y)$ is the least number of closed and contractible sets in X which cover Y. Hereafter, cat(X) denotes $cat_{X}(X)$. The reader can find in Bartsch et al. [6] and Bartsch and Tang [7] and their references other results for related problems with (1.1).

Later, Ding and Tanaka [11] have considered the existence and multiplicity of solutions for the problem

$$\begin{aligned} \left\{ \begin{array}{l} -\,\Delta u +(\lambda V(x)+Z(x))u = u^p, \quad \text{ in } \quad \mathbb {R}^{N}, \\ u>0,\ \text{ in }\ \mathbb {R}^N, \end{array} \right. \end{aligned}$$

(1.2)

by supposing that the first eigenvalue of $-\,\Delta +Z(x)$ on $\Omega _j$ under Dirichlet boundary condition is positive for each $j\in \{1,2,\ldots ,k\}$, $p \in \left( 1,\frac{N+2}{N-2}\right)$ and $N \ge 3$. In that paper, it was showed that (1.2) has at least $2^k-1$ solutions for $\lambda$ large enough, which are called multi-bump solutions. These solutions have the following characteristics:

For each non-empty subset $\Gamma \subset \{1,2,\ldots ,k\}$ and $\varepsilon >0$ fixed, there is $\lambda ^*>0$ such that (1.2) possesses a solution $u_{\lambda }$, for $\lambda \ge \lambda ^*=\lambda ^*(\varepsilon )$, satisfying:

$$\begin{aligned} \left| \int _{\Omega _j}\left[ \left| \nabla u_{\lambda }\right| ^2+(\lambda V(x)+Z(x))u_{\lambda }^2\right] -\left( \frac{1}{2}-\frac{1}{p+1}\right) ^{-1}c_j\right| < \varepsilon ,\ \forall j \in \Gamma \end{aligned}$$

and

$$\begin{aligned} \int _{\mathbb {R}^N{\setminus } \Omega _{\Gamma }}\left[ \left| \nabla u_{\lambda }\right| ^2+ u_{\lambda }^2\right] dx< \varepsilon , \end{aligned}$$

where $\Omega _{\Gamma }= \bigcup \nolimits _{j \in \Gamma }\Omega _j$ and $c_j$ is the minimax level of the energy functional related to the problem

$$\begin{aligned} \left\{ \begin{array}{l} - \Delta u +Z(x)u = u^p, \,\, \text{ in } \,\, \Omega _j, \\ u>0, \,\, \text{ in } \,\, \Omega _j, \\ u=0,\ \text{ on }\ \partial \Omega _j . \end{array} \right. \end{aligned}$$

(1.3)

Motivated by study made in [11], Alves et al. [2] and Alves and Souto [4] have considered a problem of the type (1.2), by assuming that the nonlinearity has a critical growth for the case $N \ge 3$ and exponential critical growth when $N = 2$ respectively. Other results involving multi-bump solutions can be found in Alves et al. [3], Guo and Tang [14], Gui [13] and Wang [17] and their references.

In [10], Clapp and Ding have established the existence and multiplicity of positive solutions for the problem

$$\begin{aligned} \begin{array}{lll} -\,\Delta u + \lambda V(x)u =\mu u+ u^{2^*-1},\quad \text{ in } \quad \mathbb {R}^N, \\ \end{array} \end{aligned}$$

(1.4)

for $N \ge 4$, $\lambda ,\mu >0$ and V verifying $(V_1){-}(V_3)$. By using variational methods, the authors were able to show that if $\lambda$ is large and $\mu$ is small, (1.4) has a positive solution that is concentrated near of the potential well.

The present paper has been motivated by results found in [9] and [10] and our intention is to prove that the same type of result holds for problem $(P)_{\lambda ,\mu }$. The problem $(P)_{\lambda ,\mu }$ aroused the interest of all due to the lack of compactness in the inclusion of $H^{1}(\mathbb {R}^N)$ in $L^{s}(\mathbb {R}^N)$ for all $s \in [2,2^{*}]$ and by the fact that we are considering a nonlinearity with critical growth. These fact bring a lot of difficulties to apply variational methods, for example the associated energy functionals do not satisfy in general the Palais–Smale condition at all level. Here, we overcome this difficulty by exploring the parameters $\lambda$ and $\mu$.

Our main result is the following

Theorem 1.1

Assume that $(V_1){-}(V_3)$ hold. If

$$\begin{aligned} N\ge 4\ \text {and}\ 2<q<2^* \quad \text {or} \quad N=3\ \text {and}\ 4<q<6, \end{aligned}$$

then there are $\lambda ^*,\mu ^*>0$ such that $(P)_{\lambda ,\mu }$ has at least $cat(\Omega )$ positive solutions for $\lambda \ge \lambda ^*$ and $\mu \le \mu ^*$.

We would like point out that Theorem 1.1 completes the study made in [9] and [10] in the following sense: In [9], the nonlinearity has a subcritical growth, while in our paper the nonlinearity has a critical growth, then we need to be careful to prove the Palais–Smale for the energy functional. Related to the [10], we have observed that only the case $q=2$ was considered, while in the present paper we have considered the case $2<q<2^*$. The reader is invited to observe that our approach is totally different from what can already be found in [10].

In the proof of Theorem 1.1 we have used variational methods by adapting for our case some arguments explored in [9]. Moreover, another important paper in the proof of our main theorem is due to Alves and Ding [1] where the existence of multiple solutions has been established for the limit problem, for more details see Sect. 2.

The plan of the paper is as follows: In Sect. 2 we will recall some facts involving the limit problem, while in Sect. 3 we will focus our attention to prove our main theorem.

Notation In this paper, we have used the following notations:

• The usual norms in $H^{1}(\mathbb {R}^N)$ and $L^{p}(\mathbb {R}^N)$ will be denoted by $\Vert \;\;\;\Vert$ and $|\;\;\;|_{p}$ respectively.

• C denotes (possible different) any positive constant.

• $B_{R}(z)$ denotes the open ball with center z and radius R in $\mathbb {R}^N$.

• $B^{c}_R(z)=\mathbb {R}^{N} {\setminus } B_R(z)$.

• We say that $u_n \rightarrow u$ in $L_{loc}^{p}(\mathbb {R}^N)$ when

  $$\begin{aligned} u_n \rightarrow u \quad \text{ in } \quad L^{p}(B_R(0)), \quad \forall R>0. \end{aligned}$$

• If g is a measurable function, the integral $\int _{\mathbb {R}^N}g(x)\,dx$ will be denoted by $\int g(x)\,dx$.

2 The limit problem

In this section, we recall some results proved by Alves and Ding [1] involving the functional $I_\mu :H_0^{1}(\Omega ) \rightarrow \mathbb {R}$ given by

$$\begin{aligned} I_\mu (u)=\int _{\Omega }|\nabla u|^{2}\,dx-\frac{\mu }{q}\int _{\Omega }|u|^{q}\,dx-\frac{1}{2^*}\int _{\Omega }|u|^{2^*}\,dx, \end{aligned}$$

whose the critical points are weak solutions of the problem (limit problem)

$$\begin{aligned} \left\{ \begin{array}{l} -\,\Delta u = \mu |u|^{q-2}u+|u|^{2^*-2}u, \quad \text{ in } \quad \Omega , \\ u=0, \quad \text{ on } \quad \partial \Omega . \end{array} \right. \qquad \qquad \qquad \qquad {(P)_\infty } \end{aligned}$$

In the above mentioned paper, Alves and Ding have established the existence of at least $cat(\Omega )$ positive solutions for problem $(P)_{\infty }$. If $c_{\mu }$ denotes the mountain pass level associated with $I_\mu$, it is possible to show the estimate below

$$\begin{aligned} 0<c_\mu < \frac{1}{N}S^{{N}/{2}}, \quad \forall \mu >0, \quad ( \hbox {see Miyagaki} \,\, [15]) \end{aligned}$$

(2.1)

by supposing that

$$\begin{aligned} q \in (2,2^*) \quad \text{ if } \quad N\ge 4 \quad \text {or} \quad q \in (4,6) \quad \text{ if } \quad N=3, \end{aligned}$$

(2.2)

where S is the best Sobolev constant of the embedding $H_0^{1}(\Omega ) \hookrightarrow L^{2^*}(\Omega )$ given by

$$\begin{aligned} S=\inf \left\{ \int _{\Omega }|\nabla u|^{2}\,dx\,:\, u \in H_0^{1}(\Omega ), \,\, \int _{\Omega }|u|^{2^*}\,dx=1 \right\} . \end{aligned}$$

(2.3)

By using well known results, we have

$$\begin{aligned} c_{\mu }=\inf _{u \in \mathcal {M}}I_{\mu }(u), \end{aligned}$$

where

$$\begin{aligned} \mathcal {M}=\{u \in H^{1}_{0}(\Omega )\,\;:\; u\not =0 \quad \text{ and } \quad I_{\mu }'(u)u=0\}. \end{aligned}$$

The set $\mathcal {M}$ is called of Nehari manifold of the functional $I_{\mu }$.

In what follows, without loss of generality, we assume that $0 \in \Omega$. Moreover, since $\Omega$ is a smooth bounded domain, we can fix $r>0$ such that $B_r(0) \subset \Omega$ and the sets

$$\begin{aligned} \Omega _r^+ = \left\{ x \in \mathbb {R}^N \, ; \, d(x, {\Omega }) \le r\right\} \end{aligned}$$

and

$$\begin{aligned} \Omega _r^- = \left\{ x \in \Omega \, ; \, d(x, \partial \Omega ) \ge r\right\} \end{aligned}$$

are homotopically equivalent to $\Omega$. In the sequel, we denote by $m(\mu )$ the mountain pass level associated with the functional

$$\begin{aligned} I_{\mu ,r}(u)=\int _{B_r(0)}|\nabla u|^{2}\,dx-\frac{\mu }{q}\int _{B_r(0)}|u|^{q}\,dx-\frac{1}{2^*}\int _{B_r(0)}|u|^{2^*}\,dx. \end{aligned}$$

As above, we also have

$$\begin{aligned} 0<m(\mu ) < \frac{1}{N}S^{{N}/{2}}, \end{aligned}$$

(2.4)

and

$$\begin{aligned} m({\mu })=\inf _{u \in \mathcal {M}_r}I_{\mu ,r}(u), \end{aligned}$$

(2.5)

with

$$\begin{aligned} \mathcal {M}_r=\{u \in H^{1}_{0}(B_r(0))\,\;:\; u\not =0 \quad \text{ and } \quad I_{\mu ,r}'(u)u=0\}. \end{aligned}$$

(2.6)

Below we define $\beta _0: H^{1}_0(\Omega ) {\setminus } \{0\} \rightarrow \mathbb {R}^N$ by setting

$$\begin{aligned} \beta _0(u)=\frac{\int _{\Omega }|u|^{2^*}x\,dx}{\int _{\Omega }|u|^{2^*}\,dx}. \end{aligned}$$

The next three lemmas can be found in [1] and we will omit their proofs.

Lemma 2.1

$\lim _{\mu \rightarrow 0}c_\mu =\lim _{\mu \rightarrow 0}m(\mu )=\frac{1}{N}S^{N/2}$.

Lemma 2.2

If u is a critical point of $I_\mu$ on $\mathcal {M}$, then u is a critical point of $I_{\mu }$ in $H_0^{1}(\Omega )$.

Lemma 2.3

There is $\mu ^*>0$ such that if $\mu \in (0, \mu ^*)$ and $u \in \mathcal {M}$ with $I_\mu (u) \le m(\mu )$, then $\beta _0(u) \in \Omega _{r/2}^+$.

Here and throughout this work we are assuming that $\mu \in (0,\mu ^*)$ and (2.2) holds.

3 Preliminary results

From now on, we fix the space $E\subset H^1(\mathbb {R}^N)$ given by

$$\begin{aligned} E=\Big \{u \in H^{1}(\mathbb {R}^{N}): \ \int V(x)|u|^{2}\,dx<+ \infty \Big \} \end{aligned}$$

endowed with inner product

$$\begin{aligned} \langle u,v\rangle _\lambda =\displaystyle \int (\nabla u \nabla v + \lambda V(x)uv)\,dx. \end{aligned}$$

The induce norm by this inner product will be denoted by $\Vert \;\;\; \Vert _\lambda$, that is,

$$\begin{aligned} ||u||_\lambda =\left( \displaystyle \int (|\nabla u|^2 + \lambda V(x)|u|^2)\,\,dx\right) ^{\frac{1}{2}}. \end{aligned}$$

From now on, we denote by $E_\lambda$, the space E endowed with the norm $\Vert \;\;\;\Vert _{\lambda }$.

The conditions $(V_1){-}(V_2)$ yield $E_{\lambda }$ is a Hilbert space. Moreover, these conditions also imply that there is $\Upsilon >0$ satisfying

$$\begin{aligned} \Vert u\Vert _{\lambda } \ge \Upsilon \Vert u\Vert , \quad \forall u \in E_\lambda \quad \text{ and } \quad \forall \lambda \ge 1. \end{aligned}$$

This inequality says that the embedding $E_\lambda \hookrightarrow H^{1}(\mathbb {R}^N)$ is continuous for $\lambda \ge 1$. Hence, the embedding

$$\begin{aligned} E_\lambda \hookrightarrow L^{s}(\mathbb {R}^N), \quad \forall s \in [2,2^*], \end{aligned}$$

are also continuous for $\lambda \ge 1$.

Using the above notations, we define the functional $I_{\lambda ,\mu }:E_\lambda \rightarrow \mathbb {R}$ given by

$$\begin{aligned} I_{\lambda ,\mu }(u)=\displaystyle \frac{1}{2}||u||^2_\lambda -\displaystyle \frac{\mu }{q}\displaystyle \int |u|^q\,\,dx-\displaystyle \frac{1}{2^*}\displaystyle \int |u|^{2^*}\,\,dx, \end{aligned}$$

which belongs to $C^{1}(E_\lambda ,\mathbb {R})$ with

$$\begin{aligned} I_{\lambda ,\mu }'(u)v=\langle u,v\rangle _\lambda - \mu \int |u|^{q-2}uv\,dx- \int |u|^{2^*-2}uv\,dx, \quad \forall u,v \in E_\lambda , \end{aligned}$$

or equivalently

$$\begin{aligned} I_{\lambda ,\mu }'(u)v=\int (\nabla u \nabla v + \lambda V(x)uv)\,dx - \mu \int |u|^{q-2}uv\,dx- \int |u|^{2^*-2}uv\,dx. \end{aligned}$$

From this, we see that critical points of $I_{\lambda ,\mu }$ are weak solutions of $(P)_{\lambda ,\mu }$.

Next, we recall the definitions of (PS) sequence and Palais-Smale condition.

Definition 3.1

A sequence $(u_n) \subset E_\lambda$ is a (PS) sequence at level $c \in \mathbb {R}$ for $I_{\lambda ,\mu }$, or simply $(PS)_c$ sequence for $I_{\lambda ,\mu }$, if

$$\begin{aligned} I_{\lambda ,\mu }(u_n)\rightarrow c \,\,\,\, \text {and} \,\,\,\, I_{\lambda ,\mu }'(u_n)\rightarrow 0. \end{aligned}$$

Definition 3.2

The functional $I_{\lambda ,\mu }$ satisfies the (PS) condition if any (PS) sequence of $I_{\lambda ,\mu }$ possesses a convergent subsequence. Moreover, we say that $I_{\lambda ,\mu }$ satisfies the $(PS)_d$ condition if any $(PS)_d$ sequence possesses a convergent subsequence.

In what follows, we will show that $I_{\lambda ,\mu }$ verifies the mountain pass geometry.

Lemma 3.3

The functional $I_{\lambda ,\mu }$ satisfies the mountain pass geometry, that is,

(a)   There are constants $r,\rho >0$, which are independent of $\lambda$ and $\mu$, such that

$$\begin{aligned} I_{\lambda ,\mu }(u) \ge \rho \quad \text{ for } \quad \Vert u\Vert _{\lambda }=r. \end{aligned}$$

(b)   There is $e \in C_0^{\infty }(\Omega )$ with $\Vert e\Vert _{\lambda } >r$ verifying $I_{\lambda , \mu }(e)<0$.

Proof

By using the Sobolev embedding

$$\begin{aligned} H^1(\mathbb {R}^N)\hookrightarrow L^s(\mathbb {R}^N), \ \ \text {for} \ \ 2\le s\le 2^*, \end{aligned}$$

(3.1)

it follows that

$$\begin{aligned} I_{\lambda ,\mu }(u)\ge \displaystyle \frac{1}{2}||u||^2_\lambda -C||u||^q_\lambda -C||u||^{2^{*}}_\lambda . \end{aligned}$$

As $2<q<2^*$, there are $\rho , r>0$ such that

$$\begin{aligned} I_{\lambda ,\mu }(u)\ge \rho >0, \ \ \text {for} \ \ ||u||_\lambda =r, \end{aligned}$$

showing (a). In order to prove (b), fix $\Psi \in C_0^{\infty }(\Omega )$ with $supp \,\Psi \subset \Omega$. Then,

$$\begin{aligned} I_{\lambda ,\mu }(t\Psi )=\displaystyle \frac{t^2}{2}\displaystyle \int _{\Omega }(|\nabla \Psi |^2+|\Psi |^2)\,dx-\displaystyle \frac{t^q \mu }{q}\displaystyle \int _{\Omega } |\Psi |^q\,dx-\displaystyle \frac{t^{2^*}}{2^*}\displaystyle \int _{\Omega } |\Psi |^{2^*}\,dx. \end{aligned}$$

Since $2<q<2^*$,

$$\begin{aligned} I_{\lambda ,\mu }(t \Psi ) \rightarrow -\infty \quad \text{ as } \quad t\rightarrow \infty . \end{aligned}$$

Thereby, (b) follows by taking $e=t^{*}\Psi$ with $t^*>0$ large enough. $\square$

Now, by using a version of the mountain pass theorem found in Willem [17], there is a $(PS)_{c_{\lambda ,\mu }}$ sequence $(u_n)$ for $I_{\lambda ,\mu }$, that is,

$$\begin{aligned} I_{\lambda , \mu }(u_n) \rightarrow c_{\lambda , \mu } \quad \text{ and } \quad I'_{\lambda , \mu }(u_n) \rightarrow 0, \end{aligned}$$

(3.2)

where $c_{\lambda ,\mu }$ is the mountain pass level associated with $I_{\lambda ,\mu }$ given by

$$\begin{aligned} c_{\lambda ,\mu }=\inf _{\gamma \in \Gamma }\max _{t\in [0,1]}I_{\lambda ,\mu }(\gamma (t)), \end{aligned}$$

(3.3)

with

$$\begin{aligned} \Gamma =\{\gamma \in C([0,1],E_\lambda ); \gamma (0)=0 \ \text {and} \ \gamma (1)=e\}. \end{aligned}$$

As in Sect. 2, it is possible to prove that

$$\begin{aligned} c_{\lambda , \mu }=\inf _{u \in \mathcal {M}_{\lambda ,\mu }}I_{\lambda ,\mu }(u), \end{aligned}$$

where

$$\begin{aligned} \mathcal {M}_{\lambda ,\mu }=\{u \in E_{\lambda }\,\;:\; u\not =0 \quad \text{ and } \quad I_{\lambda ,\mu }'(u)u=0\}. \end{aligned}$$

By employing standard arguments, there is $\sigma >0$, which does not depend on $\mu$ such that

$$\begin{aligned} \sigma \le \Vert u\Vert _{\lambda }, \quad \forall u \in \mathcal {M}_{\lambda ,\mu }. \end{aligned}$$

(3.4)

The next lemma establishes an important estimate from above involving the level $c_{\lambda ,\mu }$ that is a key point in our argument.

Lemma 3.4

There is $\tau =\tau (\mu ) >0$ such that the mountain pass level $c_{\lambda ,\mu }$ verifies the following inequality

$$\begin{aligned} 0<c_{\lambda ,\mu }<\displaystyle \frac{1}{N}S^{N/2} - \tau , \quad \forall \lambda >0. \end{aligned}$$

(3.5)

Proof

By definition of $c_{\lambda , \mu }$ and $c_{\mu }$, we see that $c_{\lambda ,\mu } \le c_{\mu }$ for all $\lambda , \mu >0$. Then, it is enough to apply (2.1) to get the desired result. $\square$

In the sequel, we will study some properties of the (PS) sequences of $I_{\lambda ,\mu }$, which will be proved in some lemmas.

Lemma 3.5

If $(w_n)$ is a $(PS)_{d}$ sequence for $I_{\lambda ,\mu }$, then $(w_n)$ is bounded in $E_\lambda$. Moreover,

$$\begin{aligned} \limsup _{n\rightarrow +\infty }\Vert w_n\Vert ^2_{\lambda } \le \frac{2qd}{q-2}. \end{aligned}$$

(3.6)

Proof

First of all, note that

$$\begin{aligned} I_{\lambda ,\mu }(w_n)- \displaystyle \frac{1}{q}I'_{\lambda ,\mu }(w_n)w_n\ge \left( \frac{1}{2}-\frac{1}{q}\right) ||w_n||_\lambda ^2, \quad \forall n \in \mathbb {N}. \end{aligned}$$

On the other hand, there is $n_0\in \mathbb {N}$ such that

$$\begin{aligned} I_{\lambda ,\mu }(w_n)- \frac{1}{q}I'_{\lambda ,\mu }(w_n)w_n\le d +o_n(1)+o_n(1)||w_n||_\lambda , \ \ \text {for} \ \ n\ge n_0. \end{aligned}$$

Combining the above inequalities we get

$$\begin{aligned} \left( \frac{1}{2}-\frac{1}{q}\right) ||w_n||_\lambda ^2\le d +o_n(1)+o_n(1)||w_n||_\lambda , \ \ \text {for} \ \ n\ge n_0, \end{aligned}$$

from where it follows the boundedness of $(w_n)$ and (3.6). $\square$

Lemma 3.6

Let $\Theta >0$ be a constant that does not depend on $\lambda$ and $\mu$. If $(w_{n}) \subset E_\lambda$ is a $(PS)_{d}$ for $I_{\lambda ,\mu }$ with $0\le d \le \Theta$, then given $\delta >0$ there are $\lambda _*=\lambda _*(\delta , \Theta )$ and $R=R(\delta ,\Theta )$ such that

$$\begin{aligned} \limsup _{n \rightarrow +\infty }\displaystyle \int _{B^c_R}|w_n|^q \,dx<\delta ,\quad \forall \lambda \ge \lambda _*. \end{aligned}$$

Proof

The proof follows the same arguments found in [9], however we will write it for convenience of the reader. For $R>0$, fix

$$\begin{aligned} X_R=\left\{ x \in \mathbb {R}^N \, : \, |x| > R , \, V(x) \ge M_0\right\} \end{aligned}$$

and

$$\begin{aligned} Y_R=\left\{ x \in \mathbb {R}^N \, : \, |x| > R , \, V(x) < M_0\right\} , \end{aligned}$$

where $M_0$ is given in $(V_2)$. Observe that,

$$\begin{aligned} \int _{X_R}|w_n|^2\,dx \le \frac{1}{\lambda M_0}\int _{X_R}\lambda V(x)|w_n|^2 dx\le \frac{||w_n||^{2}_{\lambda }}{\lambda M_0} \end{aligned}$$

(3.7)

and

$$\begin{aligned} \int _{Y_R}|w_n|^2\,dx \le \left( \int _{Y_R}|w_n|^{2^*} dx\right) ^{\frac{2}{2^*}} |Y_R|^{\frac{2}{N}} \le C ||w_n||^{2}_{\lambda } |Y_R|^{\frac{2}{N}}. \end{aligned}$$

(3.8)

Using interpolation inequality for $2<q<2^*$, we can infer that

$$\begin{aligned} |w_n|^q_{L^q(B^{c}_R)} \le |w_n|^{q\theta }_{L^2( B^{c}_R)} |w_n|^{q(1-\theta )}_{L^{2^*}( B^{c}_R)} \le |w_n|^{q\theta }_{L^2( B^{c}_R)} ||w_n||^{q(1-\theta )}_{\lambda }, \end{aligned}$$

(3.9)

for some $\theta \in (0,1)$. From (3.7)–(3.9) and Lemma 3.5, there exists $K>0$ such that

$$\begin{aligned} \limsup _{n\rightarrow \infty }|w_n|^q_{L^q( B^{c}_R)} \le K \left( \frac{1}{\lambda M_0} + |Y_R|^{\frac{2}{N}}\right) ^{\frac{q\theta }{2}} . \end{aligned}$$

(3.10)

From $(V_2)$, $Y_R \subset \mathcal {L}$, and so,

$$\begin{aligned} \lim _{R\rightarrow \infty }|Y_R|=0. \end{aligned}$$

The last limit together with (3.10) implies that for each $\delta >0$, there are $R>0$ and $\lambda _*>0$ such that

$$\begin{aligned} \limsup _{n\rightarrow \infty }|w_n|^q_{L^q(B^{c}_{R})} < \delta , \quad \forall \lambda \ge \lambda _*. \end{aligned}$$

$\square$

As a byproduct of the last lemma, we have the following corollary

Corollary 3.7

Let $(v_n) \subset E_{\lambda _n}$ be a sequence such that $(\Vert v_n\Vert _{\lambda _n})$ is bounded with $\lambda _n \rightarrow +\infty$. If $v_n \rightharpoonup 0$ in $H^{1}(\mathbb {R}^N)$, then

$$\begin{aligned} v_n \rightarrow 0 \quad \text{ in } \quad L^{q}(\mathbb {R}^N). \end{aligned}$$

The next proposition shows some levels where the function $I_{\lambda ,\mu }$ satisfies the (PS) condition.

Proposition 3.8

There is $\widehat{\lambda }=\widehat{\lambda }(\tau )>0$ such that $I_{\lambda ,\mu }$ verifies the $(PS)_{d_\lambda }$ condition for any $d_\lambda \in \left( 0,\frac{1}{N}S^{N/2}-\tau \right)$ for all $\lambda \ge \widehat{\lambda }$, where $\tau$ was given in Lemma 3.4.

Proof

Let $(w_n)$ be a $(PS)_{d_{\lambda }}$ sequence for $I_{\lambda ,\mu }$, that is,

$$\begin{aligned} I_{\lambda , \mu }(w_n) \rightarrow d_\lambda \quad \text{ and } \quad I'_{\lambda , \mu }(w_n) \rightarrow 0. \end{aligned}$$

By Lemma 3.5, the sequence $(w_n)$ is bounded in $E_\lambda$, then for some subsequence, still denoted by itself, there is $w \in E_\lambda$ such that

$$\begin{aligned}&w_n \rightharpoonup w \quad \text {in} \quad E_\lambda , \\&w_n(x) \rightarrow w(x) \quad \text {a.e in} \quad \ \mathbb {R}^N, \end{aligned}$$

and

$$\begin{aligned} w_n\rightarrow w \quad \text {in} \quad L_{loc}^s(\mathbb {R}^N), \quad 1\le s<2^*. \end{aligned}$$

A straightforward computation gives $I'_{\lambda ,\mu }(w)=0$, and so, $I'_{\lambda ,\mu }(w)w=0$. On the other hand, since

$$\begin{aligned} \displaystyle \int |w_n|^q\,dx=\displaystyle \int |v_n|^q\,dx+ \displaystyle \int |w|^q\,dx + o_n(1) \end{aligned}$$

and

$$\begin{aligned} \displaystyle \int |w_n|^{2^*}\,dx=\displaystyle \int |v_n|^{2^*}\,dx+ \displaystyle \int |w|^{2^*}\,dx + o_n(1), \end{aligned}$$

where $v_n=w_n-w$, we obtain

$$\begin{aligned} \displaystyle \frac{1}{2}||v_n||^2_\lambda -\displaystyle \frac{\mu }{q}\displaystyle \int |v_n|^q\,dx -\displaystyle \frac{1}{2^*}\displaystyle \int |v_n|^{2^*} dx=d_\lambda -I_{\lambda ,\mu }(w)+o_n(1). \end{aligned}$$

(3.11)

Now, by using the fact that $I'_{\lambda ,\mu }(w_n)w_n=o_n(1)$ and $I'_{\lambda ,\mu }(w)w=0$, it follows that

$$\begin{aligned} ||v_n||^2_\lambda -\mu \displaystyle \int |v_n|^q dx -\displaystyle \int |v_n|^{2^*} dx=o_n(1). \end{aligned}$$

(3.12)

From boundedness of $(w_n)$, we can assume that

$$\begin{aligned} ||v_n||^2_\lambda \rightarrow L_\lambda \quad \text {and} \ \ \ \mu \displaystyle \int _{\mathbb {R}^N}|v_n|^q\,dx +\displaystyle \int |v_n|^{2^*}dx \rightarrow L_\lambda . \end{aligned}$$

If $L_\lambda =0$, we deduce that $v_n \rightarrow 0$ in $E_\lambda$, or equivalently, $w_n \rightarrow w$ in $E_\lambda$, which finishes the proof. Next, we will show that $L_\lambda >0$ does not hold for $\lambda$ large enough. To this end, let us assume that

$$\begin{aligned} \displaystyle \int |v_n|^q\,dx\rightarrow A_\lambda \quad \text {and} \quad \displaystyle \int |v_n|^{2^*}dx \rightarrow B_\lambda , \end{aligned}$$

then $\mu A_\lambda +B_\lambda =L_\lambda .$ Arguing as in the proof of Lemma 3.6, we see that

$$\begin{aligned} \limsup _{n \rightarrow +\infty }\displaystyle \int |v_n|^q\,dx=o_\lambda (1), \end{aligned}$$

where $o_\lambda (1) \rightarrow 0$ as $\lambda \rightarrow +\infty$. Therefore,

$$\begin{aligned} A_\lambda =o_\lambda (1) \quad \text{ and } \quad L_{\lambda }=B_\lambda +o_\lambda (1). \end{aligned}$$

(3.13)

From (3.12) and Sobolev embedding

$$\begin{aligned} ||v_n||^2_\lambda \le C\big (||v_n||^q_\lambda +||v_n||^{2^*}_\lambda \big )+o_n(1). \end{aligned}$$

(3.14)

Recalling that there is $C>0$ verifying

$$\begin{aligned} |t|^q\le \frac{1}{2}|t|^2+C|t|^{2^*}, \quad \forall t\in \mathbb {R}, \end{aligned}$$

and supposing by contradiction that $L_\lambda >0$, the last inequality ensures that

$$\begin{aligned} \lim _{n \rightarrow +\infty }||v_n||^{2}_\lambda \ge (1/C)^{2/(2^*-2)}=C_1>0, \end{aligned}$$

or equivalently,

$$\begin{aligned} L_\lambda \ge C_1>0. \end{aligned}$$

(3.15)

On the other hand, we know that

$$\begin{aligned} S\le \displaystyle \frac{||v_n||_\lambda ^2}{\Big (\int |v_n|^{2^*} dx\Big )^{2/2^*}}. \end{aligned}$$

Then, taking the limit of $n \rightarrow +\infty$, we find

$$\begin{aligned} S\le \displaystyle \frac{L_\lambda }{(B_\lambda )^{2/2^*}}=\frac{L_\lambda }{(L_\lambda +o_\lambda (1))^{2/2^*}}. \end{aligned}$$

Now, taking the limit of $\lambda \rightarrow +\infty$ and using (3.15), we get

$$\begin{aligned} S^{N/2}\le \liminf _{\lambda \rightarrow \infty }L_\lambda . \end{aligned}$$

(3.16)

From (3.11),

$$\begin{aligned} \Big (\frac{1}{2}-\frac{1}{2^*}\Big )L_\lambda +o_\lambda (1) \le d_\lambda , \end{aligned}$$

then

$$\begin{aligned} \liminf _{\lambda \rightarrow \infty }d_{\lambda }\ge \left( \frac{1}{2}-\frac{1}{2^*}\right) \liminf _{\lambda \rightarrow \infty }L_\lambda . \end{aligned}$$

The last inequality combines with (3.16) to give

$$\begin{aligned} \liminf _{\lambda \rightarrow \infty }d_{\lambda }\ge \frac{1}{N}S^{N/2}, \end{aligned}$$

(3.17)

which is absurd, because by hypothesis

$$\begin{aligned} \limsup _{\lambda \rightarrow +\infty }d_{\lambda } \le \frac{1}{N}S^{N/2}-\tau < \frac{1}{N}S^{N/2}. \end{aligned}$$

Therefore, there is $\widehat{\lambda }>0$ such that $L_{\lambda }=0$ for all $\lambda \ge \widehat{\lambda }$, finishing the proof. $\square$

Corollary 3.9

There is $\widehat{\lambda }>0$ such that $I_{\lambda ,\mu }$ verifies the $(PS)_{d_\lambda }$ condition on $\mathcal {M}_{\lambda ,\mu }$ for any $d_\lambda \in \left( 0,\frac{1}{N}S^{N/2}-\tau \right)$ and $\lambda \ge \widehat{\lambda }$, where $\tau$ was given in Lemma 3.4.

Proof

The proof is made as in [1, Lemma 4.1] $\square$

Theorem 3.10

There is $\lambda ^*>0$ such that the mountain pass level $c_{\lambda ,\mu }$ is a critical level of $I_{\lambda ,\mu }$ for all $\lambda \ge \lambda ^*$, that is, there is $u_{\lambda ,\mu } \in E_\lambda$ verifying

$$\begin{aligned} I_{\lambda , \mu }(u_{\lambda ,\mu })=c_{\lambda ,\mu } \quad \text{ and } \quad I'_{\lambda , \mu }(u_{\lambda ,\mu })=0. \end{aligned}$$

Proof

Since by Lemma 3.4 $c_{\lambda , \mu }< \frac{1}{N}S^{N/2} - \tau$, the Proposition 3.8 ensures the existence of $\lambda ^*=\lambda ^{*}(\tau )>0$ such that the functional $I_{\lambda ,\mu }$ verifies the $(PS)_{c_{\lambda ,\mu }}$ condition for $\lambda \ge \lambda ^*$. Thus, by mountain pass theorem due to Ambrosetti–Rabinowitz [5], there is $u_{\lambda , \mu }\in E_\lambda$ verifying

$$\begin{aligned} I_{\lambda ,\mu }(u_{\lambda ,\mu })=c_{\lambda ,\mu } \quad \text{ and } \quad I'_{\lambda ,\mu }(u_{\lambda ,\mu })=0, \end{aligned}$$

finishing the proof. $\square$

Remark 3.11

The function $u_{\lambda ,\mu }$ obtained in Theorem 3.10 is called a ground state solution of $(P)_{\lambda ,\mu }$.

Now, our intention is to show an important relation between $c_{\lambda , \mu }$ and $c_\mu$, however to do this we need to study the behavior of the $(PS)_{c,\infty }$ sequences. Hereafter, $(u_n) \subset H^1(\mathbb {R}^N)$ is a $(PS)_{c, \infty }$ if:

$$\begin{aligned}&u_n \in E_{\lambda _n} \ \text{ and }\ \lambda _{n} \rightarrow +\infty ,&\\&I_{\lambda _n,\mu }(u_n)\rightarrow c,\quad \text{ for } \text{ some } \quad c \in \mathbb {R},&\\&\Vert I_{\lambda _n,\mu }'(u_n)\Vert _{(E_{\lambda _n})'} \rightarrow 0.&\end{aligned}$$

where $(E_{\lambda _n})'$ denotes the dual space of $E_{\lambda _n}$.

Proposition 3.12

Let $(u_n)$ be a $(PS)_{c,\infty }$ sequence with $c \in \left( 0, \frac{1}{N}S^{N/2} \right)$. Then, there is a subsequence of $(u_n)$ , still denoted by itself, and $u \in H^1(\mathbb {R}^N)$ such that

$$\begin{aligned} u_n \rightharpoonup u\ \text{ in }\ H^1(\mathbb {R}^N). \end{aligned}$$

Moreover,

• (i) $u\equiv 0$ in $\mathbb {R}^N {\setminus } \Omega$ and u is a solution of

  $$\begin{aligned} \left\{ \begin{array}{l} -\,\Delta u = \mu |u|^{q-2}u+|u|^{2^*-2}u,\text{ in }\ \Omega , \ \\ u=0,\ \text{ on }\ \partial \Omega . \end{array} \right. \qquad \qquad \qquad \qquad {(P)_\infty } \end{aligned}$$

• (ii) $\left| \left| u_n-u\right| \right| ^{2}_{\lambda _{n}} \rightarrow 0.$

• (iii) $(u_n)$ also satisfies

  $$\begin{aligned}&u_n \rightarrow u \quad \text{ in } \quad H^{1}(\mathbb {R}^N),&\\&\lambda _n \int V(x)\left| u_n\right| ^2dx \rightarrow 0,&\\&\int _{\mathbb {R}^N{\setminus } \Omega } (|\nabla u_n|^2+\lambda _nV(x)|u_n|^{2})\,dx\rightarrow 0,&\\&\left| \left| u_n\right| \right| ^2_{\lambda _n } \rightarrow \int _{\Omega }|\nabla u|^2\,dx=\Vert u\Vert ^{2}_{H_0^{1}(\Omega )}.&\end{aligned}$$

Proof

Arguing as in Lemma 3.5,

$$\begin{aligned} \limsup _{n \rightarrow + \infty } \Vert u_n\Vert ^{2}_{\lambda _n} \le \frac{2qc}{q-2}, \end{aligned}$$

(3.18)

implying that $(\left| \left| u_n\right| \right| _{\lambda _n})$ is bounded in $\mathbb {R}$. Since

$$\begin{aligned} \left| \left| u_n\right| \right| _{\lambda _n} \ge \Upsilon \left| \left| u_n\right| \right| \quad \forall n \in \mathbb {N}, \end{aligned}$$

$(u_n)$ is also bounded in $H^1(\mathbb {R}^N)$, and so, there exists a subsequence of $(u_n)$, still denoted by itself, and $u \in H^{1}(\mathbb {R}^{N})$ such that

$$\begin{aligned} u_n \rightharpoonup u\ \text{ in }\ H^1(\mathbb {R}^N). \end{aligned}$$

To show (i), we fix for each $m \in \mathbb {N}^*$ the set

$$\begin{aligned} C_m=\left\{ x\in \mathbb {R}^N/ V(x) > \frac{1}{m}\right\} . \end{aligned}$$

Hence

$$\begin{aligned} \mathbb {R}^N{\setminus } \overline{\Omega }=\bigcup \limits _{m=1}^{+\infty }C_m. \end{aligned}$$

Note that,

$$\begin{aligned} \int _{C_m}\left| u_n\right| ^2dx=\int _{C_m}\frac{\lambda _n V(x)}{\lambda _n V(x)}\left| u_n\right| ^2dx \le \frac{m}{{\lambda _n}}\left| \left| u_n\right| \right| _{\lambda _n}^2 \le \frac{mM}{{\lambda _n}}, \end{aligned}$$

where $M=\sup _{n \in \mathbb {N}}\Vert u_n\Vert _{\lambda _n}^2.$ By Fatou’s Lemma

$$\begin{aligned} \int _{C_m}\left| u\right| ^2dx \le \liminf _{n \rightarrow +\infty }\int _{C_m}\left| u_n\right| ^2dx \le \liminf _{n \rightarrow +\infty }\frac{mM}{{\lambda _n}}=0. \end{aligned}$$

From this, $u=0$ almost everywhere in $C_m$, and consequently, $u=0$ almost everywhere in $\mathbb {R}^N{\setminus } \overline{\Omega }.$ To complete the proof of (i), consider a test function $\varphi \in C_{0}^{\infty }(\Omega )$ and note that

$$\begin{aligned} I'_{\lambda _n}(u_n)\varphi =\int _{\Omega }\nabla u_n \nabla \varphi \,dx-\int _{\Omega }(\mu |u_n|^{q-2}u_n+|u_n|^{2^*-2}u_n)\varphi \,dx. \end{aligned}$$

(3.19)

As $(u_n)$ is a $(PS)_{c,\infty }$ sequence, we derive that

$$\begin{aligned} I'_{\lambda _n}(u_n)\varphi \rightarrow 0. \end{aligned}$$

(3.20)

Recalling that $u_n \rightharpoonup u$ in $H^1(\mathbb {R}^{N})$, we must have

$$\begin{aligned} \int _{\Omega }\nabla u_n \nabla \varphi \,dx \rightarrow \int _{\Omega }\nabla u \nabla \varphi \,dx \end{aligned}$$

(3.21)

and

$$\begin{aligned} \int _{\Omega }(\mu |u_n|^{q-2}u_n+|u_n|^{2^*-2}u_n)\varphi \, dx \rightarrow \int _{\Omega }(\mu |u|^{q-2}u+|u|^{2^*-2}u)\varphi \, dx. \end{aligned}$$

(3.22)

Therefore, from (3.19)–(3.22),

$$\begin{aligned} \int _{\Omega }\nabla u \nabla \varphi \,dx=\int _{\Omega }(\mu |u|^{q-2}u+|u|^{2^*-2}u)\varphi \, dx,\ \forall \varphi \in C_0^{\infty }(\Omega ). \end{aligned}$$

As $C_{0}^{\infty }(\Omega )$ is dense in $H_0^1(\Omega )$, the above equality gives

$$\begin{aligned} \int _{\Omega }\nabla u \nabla v\,dx=\int _{\Omega }(\mu |u|^{q-2}u+|u|^{2^*-2}u)v \,dx,\ \forall v \in H_0^1(\Omega ), \end{aligned}$$

showing that u is a weak solution of the problem

$$\begin{aligned} \left\{ \begin{array}{l} -\,\Delta u = \mu |u|^{q-2}u+|u|^{2^*-2}u,\, \text{ in } \, \Omega , \ \\ u=0,\ \text{ on }\ \partial \Omega . \end{array} \right. \end{aligned}$$

(3.23)

For (ii), note that

$$\begin{aligned} \left| \left| u_n-u\right| \right| _{\lambda _n}^2&= \left| \left| u_n\right| \right| _{\lambda _n}^2+\left| \left| u\right| \right| _{\lambda _n}^2-2\int (\nabla u_n\nabla u+ \lambda _n V(x)u_nu)\,dx.&\end{aligned}$$

(3.24)

From (i),

$$\begin{aligned} \Vert u\Vert _{\lambda _n}^2=\Vert u\Vert ^2_{H_0^1(\Omega )}, \end{aligned}$$

and so,

$$\begin{aligned} \int (\nabla u_n\nabla u+ \lambda _n V(x)u_nu)\,dx=\Vert u\Vert _{H_0^1(\Omega )}^2+o_n(1). \end{aligned}$$

From this, we can rewrite (3.24) as

$$\begin{aligned} \left| \left| u_n-u\right| \right| _{\lambda _n}^2&= \left| \left| u_n\right| \right| _{\lambda _n}^2-\left| \left| u\right| \right| _{H_0^1(\Omega )}^2+o_n(1).&\end{aligned}$$

(3.25)

Gathering the boundedness of $(\Vert u_n\Vert _{\lambda _n})$ with the limit $\Vert I'_{\lambda _n}(u_n)\Vert _{E'_{\lambda _n}}\rightarrow 0,$ we find the limit

$$\begin{aligned} I'_{\lambda _n}(u_n)u_n \rightarrow 0. \end{aligned}$$

Hence,

$$\begin{aligned} \left| \left| u_n\right| \right| _{\lambda _n}^2= I'_{\lambda _n}(u_n)u_n+\int (\mu |u_n|^{q}+|u_n|^{2^*})\,dx =\int (\mu |u_n|^{q}+|u_n|^{2^*})\,dx+o_n(1). \end{aligned}$$

(3.26)

On the other hand, we know that the limit $I'_{\lambda _n}(u_n)u \rightarrow 0$ is equivalent to

$$\begin{aligned} \int _{\Omega }\nabla u_n \nabla u \,dx-\int _{\Omega } (\mu |u_n|^{q-2}u_n u+|u_n|^{2^*-2}u_n u)\,dx=o_n(1), \end{aligned}$$

which leads to

$$\begin{aligned} \int |\nabla u|^{2}\,dx=\int (\mu |u|^{q}+|u|^{2^*})\,dx. \end{aligned}$$

(3.27)

Combining (3.25) with (3.26) and (3.27), we see that

$$\begin{aligned} \left| \left| u_n-u\right| \right| _{\lambda _n}^2=\int (\mu |u_n|^{q}+|u_n|^{2^*})\,dx-\int (\mu |u|^{q}+|u|^{2^*})\,dx+o_n(1), \end{aligned}$$

that is,

$$\begin{aligned} \Vert v_n\Vert _{\lambda _n}^{2}=\mu |v_n|^{q}_{q}+|v_n|^{2^*}_{2^*}+o_n(1) \end{aligned}$$

where $v_n=u_n-u$. Since by Corollary 3.7 $v_n \rightarrow 0$ in $L^{q}(\mathbb {R}^N)$, we derive

$$\begin{aligned} \Vert v_n\Vert _{\lambda _n}^{2}=|v_n|^{2^*}_{2^*}+o_n(1). \end{aligned}$$

Now, the same arguments used in the proof of Proposition 3.8 gives

$$\begin{aligned} \Vert v_n\Vert ^2_{\lambda _n} \rightarrow 0, \end{aligned}$$

finishing the proof of (ii). Finally, in order to prove (iii) it is enough to use the inequality below

$$\begin{aligned} 0 \le \lambda _n\int V(x)\left| u_n\right| ^2dx=\lambda _n\int V(x)\left| u_n-u\right| ^2dx \le \Vert u_n-u\Vert _{\lambda _n}^2 \rightarrow 0. \end{aligned}$$

$\square$

Now, we are able to prove the estimate involving $c_{\lambda , \mu }$ and $c_\mu$

Lemma 3.13

If $\lambda _n \rightarrow +\infty$, then $\lim _{n\rightarrow \infty }c_{\lambda _n,\mu }=c_\mu$.

Proof

By Theorem 3.10, for each $n \in \mathbb {N}$ there is $u_n=u_{\lambda _n,\mu } \in E_{\lambda _n}$ such that

$$\begin{aligned} I_{\lambda _n,\mu }(u_n)=c_{\lambda _n,\mu } \quad \text{ and } \quad I_{\lambda _n,\mu }'(u_n) = 0. \end{aligned}$$

The Lemma 3.3 together with the definition of $c_{\lambda _n,\mu }$ yield

$$\begin{aligned} 0<\rho \le c_{\lambda _n,\mu } \le c_\mu < \frac{1}{N}S^{N/2}, \quad \forall n \in \mathbb {N}, \end{aligned}$$

from where it follows that $(c_{\lambda _n\mu })$ is a bounded sequence and $\Vert u_n\Vert _{\lambda _n} \not \rightarrow 0$. Now, arguing as in the proof Lemma 3.5, we get

$$\begin{aligned} \limsup _{n\rightarrow +\infty }\Vert u_n\Vert ^{2}_{\lambda _n}\le \frac{2qc_\mu }{q-2}, \end{aligned}$$

showing that $(u_n)$ is a bounded sequence in $H^{1}(\mathbb {R}^N)$. Thereby, by Proposition 3.12, there is a subsequence of $(u_n)$, still denoted by itself, and $u \in H_0^{1}(\Omega ){\setminus } \{0\}$ such that

$$\begin{aligned}&\Vert u_n-u\Vert _{\lambda _n}^{2} \rightarrow 0, \\&u_n \rightarrow u \quad \text{ in } \quad H^{1}(\mathbb {R}^N), \\&u_n \rightarrow u \quad \text{ in } \quad L^{s}(\mathbb {R}^N) \quad \forall s \in [2,2^*], \\&I'_{\mu }(u)=0, \end{aligned}$$

and

$$\begin{aligned} I_{\mu }(u) \le c_{\mu }. \end{aligned}$$

As $u \not =0$ and $I'_{\mu }(u)u=0$, we have that $u \in \mathcal {M}$. Thus,

$$\begin{aligned} c_\mu \le I_{\mu }(u). \end{aligned}$$

The last two inequalities imply that $I_{\mu }(u)=c_\mu$ and

$$\begin{aligned} \lim _{n\rightarrow \infty }c_{\lambda _n,\mu }=c_{\mu }, \end{aligned}$$

proving the desired result. $\square$

The last lemma gives us very important informations, which are listed in the corollaries below.

Corollary 3.14

Let $(\lambda _n) \subset (0,+\infty )$ be a sequence verifying $\lambda _n \rightarrow +\infty$ and $u_{\lambda _n,\mu }$ be the ground state solution obtained in Theorem 3.10. Then, there is a subsequence of $(u_{\lambda _n,\mu })$, still denoted by itself, and $u \in H_0^{1}(\Omega )$ such that $u_{\lambda _n,\mu } \rightarrow u$ in $H_0^{1}(\Omega )$ and u is a ground state solution of the limit problem

$$\begin{aligned} \left\{ \begin{array}{l} -\,\Delta u = \mu |u|^{q-2}u+|u|^{2^*-2}u,\text{ in }\ \Omega , \ \\ u=0,\ \text{ on }\ \partial \Omega . \end{array} \right. \qquad \qquad \qquad \qquad {(P)_\infty } \end{aligned}$$

Corollary 3.15

There are $\lambda ^*>0$ large and $\mu ^*>0$ small such that

$$\begin{aligned} m(\mu ) < 2c_{\lambda ,\mu }, \quad \forall \lambda \ge \lambda ^* \quad \text{ and } \quad \forall \mu \in (0,\mu ^*). \end{aligned}$$

Proof

By Lemma 2.1 we can decreasing $\mu ^*$ if necessary, of a such way that

$$\begin{aligned} m(\mu ) < 2 c_{\mu }, \quad \forall \mu \in (0, \mu ^*). \end{aligned}$$

Since by Lemma 3.13 $c_{\lambda ,\mu } \rightarrow c_{\mu }$ as $\lambda \rightarrow +\infty$ for each $\mu >0$ fixed, there is $\lambda ^*=\lambda ^*(\mu )$ such that

$$\begin{aligned} m(\mu ) < 2 c_{\lambda ,\mu }, \quad \forall \lambda \ge \lambda ^{*}, \end{aligned}$$

showing the result. $\square$

Corollary 3.16

Assume that $m(\mu ) < 2 c_{\lambda ,\mu }$ and $u \in E_\lambda$ is a nontrivial critical point of $I_{\lambda ,\mu }$ with $I_{\lambda , \mu }(u) \le m(\mu )$. Then, u is positive or u is negative.

Proof

If $u^{\pm }\not =0$, it is easy to see that $u^{\pm } \in \mathcal {M}_{\lambda ,\mu }$, and so,

$$\begin{aligned} m(\mu ) \ge I_{\lambda , \mu }(u)=I_{\lambda , \mu }(u^{+})+I_{\lambda , \mu }(u^{-}) \ge 2c_{\lambda ,\mu }, \end{aligned}$$

which is absurd. Now the result follows by applying maximum principle [12]. $\square$

Remark 3.17

As $I_{\lambda ,\mu }$ is even, by the last corollary we can assume that the nontrivial critical points of $I_{\lambda ,\mu }$ are positive solutions of $(P)_{\lambda , \mu }$.

In the sequel, let us fix $R > 2 diam (\Omega )$ such that $\Omega \subset B_R(0)$ and consider the function

$$\begin{aligned} \xi (t)= \left\{ \begin{array}{lll} 1,\quad 0\le t \le R, \\ \frac{ R}{t},\quad t \ge R. \end{array} \right. \end{aligned}$$

Moreover, we define $\beta : H^{1}(\mathbb {R}^N){\setminus } \{0\} \rightarrow \mathbb {R}^N$ by

$$\begin{aligned} {\beta }(u) = \frac{\int \xi (|x|)|u|^{2^*}x\, dx}{\int |u|^{2^*} dx}. \end{aligned}$$

Lemma 3.18

There is $\widehat{\lambda }>0$ such that if $u \in \mathcal {M}_{\lambda ,\mu }$ and $I_{\lambda ,\mu }(u) \le m(\mu )$, then $\beta (u) \in \Omega _r^{+}$ for all $\lambda \ge \widehat{\lambda }$.

Proof

Suppose by contradiction that there exist sequences $\lambda _n \rightarrow +\infty$ and $(u_n) \subset \mathcal{M}_{\lambda _n,\mu }$ with $I_{\lambda _n,\mu }(u_n) \le m(\mu )$ and

$$\begin{aligned} {\beta } (u_n) \notin \Omega _r^+, \quad \forall n \in \mathbb {N}. \end{aligned}$$

As $(||u_n||_{\lambda _n})$ is bounded in $\mathbb {R}$, there exists $u \in H_0^{1}(\Omega )$, such that for a subsequence,

$$\begin{aligned} \left\{ \begin{array}{ll} u_n \rightharpoonup u &{} \text{ in } H^{1}(\mathbb {R}^N),\\ u_n(x) \rightarrow u(x) &{} \text{ a.e. } \text{ in } \mathbb {R}^N,\\ u_n \rightarrow u &{} \text{ in } L_{loc}^{t}(\mathbb {R}^N) \quad \text{ for } \quad t \in [1,2^{*}). \end{array}\right. \end{aligned}$$

Moreover,

$$\begin{aligned} \Vert v_n\Vert _{\lambda _n}^{2}=\mu |v_n|_{q}^{q}+|v_n|_{2^*}^{2^*}+o_{n}(1), \end{aligned}$$

where $v_n=u_n-u$. By Corollary 3.7, we know that $v_n \rightarrow 0$ in $L^{q}(\Omega )$, then

$$\begin{aligned} \Vert v_n\Vert _{\lambda _n}^{2}=|v_n|_{2^*}^{2^*}+o_{n}(1). \end{aligned}$$

Arguing as in the proof of Proposition 3.12, we derive

$$\begin{aligned} \Vert v_n\Vert _{\lambda _n} \rightarrow 0 \Leftrightarrow \Vert u_n - u\Vert _{\lambda _n} \rightarrow 0. \end{aligned}$$

This limit combined with (3.4) implies that

$$\begin{aligned} u_n \rightarrow u \quad \text{ in } \quad H^{1}(\mathbb {R}^N), \quad u \ne 0, \quad I'_\mu (u)u=0 \quad \text{ and } \quad I_{\lambda _n,\mu }(u_n) \rightarrow I_{\mu }(u). \end{aligned}$$

(3.28)

Thereby, $u \in \mathcal {M}_\mu$ and $I_{\mu }(u) \le m(\mu ).$ Applying the Lemma 2.3, we get $\beta _0(u) \in \Omega _{r/2}^+$, which is absurd because

$$\begin{aligned} \beta _0(u)=\lim _{n \rightarrow \infty }{\beta }(u_n) \not \in \Omega _{r/2}^{+}. \end{aligned}$$

This completes the proof. $\square$

3.1 Proof of main theorem

In what follows, $u_{r} \in H^{1}_0(B_{{r}}(0))$ is a positive radial ground state solution for the functional $I_{\mu ,r}$, that is,

$$\begin{aligned} I_{\mu ,r}(u_{r}) = m(\mu )= \inf _{{u \in \mathcal M}_{r} }I_{\mu ,r} (u) \,\,\,\, \text{ and } \,\,\, I'_{\mu ,r} (u_{r}) =0. \end{aligned}$$

Using the function $u_{r}$, we define the operator $\Psi _r : \Omega _{r}^{-} \longrightarrow H^{1}_0(\Omega )$ by

$$\begin{aligned} \Psi _r (y)(x)= \left\{ \begin{array}{l} u_{r}(|x-y|),\quad x\in B_{r}(y),\\ 0,\quad x\in \Omega ^{-}_r {\setminus } B_{{r}}(y), \end{array} \right. \end{aligned}$$

which is continuous and satisfies

$$\begin{aligned} \beta (\Psi _r(y)) = y, \,\,\,\,\,\forall \,y \in \Omega _{r}^{-} . \end{aligned}$$

(3.29)

Using the above informations, we are ready to prove the following claim

Claim 3.19

For $0< \mu <\mu ^*$,

$$\begin{aligned} cat(I_{\lambda ,\mu }^{m(\mu )}) \ge cat(\Omega ), \end{aligned}$$

where $I_{\lambda ,\mu }^{m(\mu )}:=\left\{ u \in \mathcal{M}_{\lambda , \mu } \, :\, I_{\lambda , \mu }(u) \le m(\mu )\right\}$ and $\mu ^*$ is given in Lemma 2.3.

Indeed, assume that

$$\begin{aligned} I_{\lambda ,\mu }^{m(\mu )} = F_1 \cup F_2 \cup \cdots \cup F_n, \end{aligned}$$

where $F_j$ is closed and contractible in $I_{\lambda ,\mu }^{m(\mu )}$, for each $j = 1,2,\ldots ,n$, that is, there exist $h_j \in C([0,1]\times F_j , I_{\lambda ,\mu }^{m(\mu )})$ and $w_j \in F_j$ such that

$$\begin{aligned} h_j(0,u) = u \,\,\,\, \text{ and } \,\,\, h_j (1, u) = w_j, \end{aligned}$$

for all $u \in F_j$. Considering the closed sets $B_j : = \Psi _r^{-1}(F_j)$, $1 \le j \le n$, it follows that

$$\begin{aligned} \Omega _{r}^{-} = \Psi _r^{-1} (I_{\lambda ,\mu }^{m(\mu )}) = B_1 \cup B_2 \cup \cdots \cup B_n, \end{aligned}$$

and defining the deformation $g_j : [0,1] \times B_j \rightarrow \Omega _{r}^{+}$ given by

$$\begin{aligned} g_i(t,y) = \beta (h_j(t,\Psi _r(y))), \end{aligned}$$

we conclude that, by Lemma 3.18, $g_i$ is well defined and thus, $B_j$ is contractible in $\Omega _{r}^+$ for each $j= 1,2,\ldots ,n$. Therefore,

$$\begin{aligned} cat(\Omega )=cat_{\Omega _{r}^{+}}(\Omega _{r}^{-})\le n. \end{aligned}$$

finishing the proof of the claim.

Since $I_{\lambda ,\mu }$ satisfies the $(PS)_c$ condition on $\mathcal{M}_{\lambda ,\mu }$ for $c \le m(\mu )$ (see Corollary 3.9), we can apply the Lusternik–Schnirelman category theory and the Claim 3.19 to ensure that $I_{\lambda ,\mu }$ has at least $cat(\Omega )$ critical points in $\mathcal{M}_{\lambda ,\mu }$, and consequently, critical points in $E_\lambda$.