Finiteness results for F-Diophantine sets

Abstract

Diophantine sets, i.e. sets of positive integers A with the property that the product of any two distinct elements of A increased by 1 is a perfect square, have a vast literature, dating back to Diophantus of Alexandria. The most important result states that such sets A can have at most five elements, and there are only finitely many of them with five elements. Beside this, there are a large number of finiteness results, concerning the original problem and some of its many variants. In this paper we introduce the notion of, and prove finiteness results on so called (F, m)-Diophantine sets A, where F is a bivariate polynomial with integer coefficients, and instead of requiring $ab+1$ to be a square for all distinct $a,b\in A$, the numbers F(a, b) should be full m-th powers. The particular choice $F(x,y)=xy+1$ and $m=2$ gives back the original problem.

1 Introduction

A set A of positive integers is called a Diophantine set if the product of any two of its distinct elements increased by 1 is a perfect square. There are many interesting results in the literature concerning Diophantine sets and its generalizations. The first Diophantine quadruple, the set $\{1,3,8,120\}$, was found by Fermat. Baker and Davenport [2] proved that Fermat’s set cannot be extended to a Diophantine quintuple. A folklore conjecture is that there does not exist a Diophantine quintuple. Dujella [9] proved that there are no Diophantine sextuples and only finitely many Diophantine quintuples. Bugeaud and Dujella [5] considered sets of positive integers with the property that the product of any two of its distinct elements increased by 1 is an m-th power, where $m\ge 2$ is an integer, and they obtained absolute upper bounds for the size of such sets (e.g. there are no quadruples with this property for $m\ge 177$). Several authors considered also the sets where the products plus 1 are (arbitrary) perfect powers (see e.g. [3, 15, 18]). For other generalizations of Diophantine sets and corresponding references see [10] and [11, Section D29].

There are some other classical problems of similar shape. Erdős and Moser asked whether for every n there exist n distinct integers such that the sum of any two is a perfect square. There is no known upper bound for the size of such sets, and, on the other hand, several examples of sextuples with that property are known [7, 13] (see also [11, Section D.15]). We also mention that Bugeaud and Gyarmati [6] considered the problem of finding upper bounds for the sets A of integers such that $a^2+b^2$ is a perfect square for all distinct $a,b\in A$. In all mentioned problems, it is known that the corresponding sets are finite (in some cases we even know an explicit upper bound for the size of these sets). However, there are some obvious variants which allow infinite sets (e.g. sets for which ab is a perfect square for all $a,b\in A$).

In this paper, we deal with the following extension of the problem. Let $F\in \mathbb Z[x,y]$ and m be an integer with $m\ge 2$. A set $A \subseteq \mathbb Z$ is called an (F, m)-Diophantine set if F(a, b) is an m-th power for any $a,b \in A$ with $a\ne b$. Further, we call a set $A \subseteq \mathbb Z$ an $(F,*)$-Diophantine set if F(a, b) is a perfect power for any $a,b \in A$ with $a\ne b$. Note that in the latter case the exponents of the powers are allowed to be different. Note that in this generality the assumption $A\subseteq \mathbb Z$ instead of $A\subseteq \mathbb {N}$ is natural. However, as one can easily see, the results concerning the classical case $F(x,y)=xy+1$ and $m=2$ after obvious modifications would remain valid in this context, too.

In the paper we provide various finiteness results for (F, m)-Diophantine sets. First we give general, but non-effective finiteness results for the size of such sets. In fact we give a complete qualitative characterization of all polynomials F for which there exist infinite (F, m)-Diophantine sets. In the case where F is a binary form not of special shape, we provide effective (though not explicit) results for the size of F-Diophantine sets, too. Finally, when F is a quartic polynomial of certain type, we give explicit and numerical results for (F, 2)-Diophantine sets A.

2 Results

As it is well-known, $\mathbb Z[x,y]$ is a unique factorization domain (shortly UFD). This follows from a classical theorem of Gauss, saying that a polynomial ring over a UFD is also a UFD.

Let $F(x,y)\in \mathbb Z[x,y]$ and write

$$\begin{aligned} F(x,y)=P_1(x,y)^{t_1}\ldots P_k(x,y)^{t_k}, \end{aligned}$$

where the polynomials $P_i(x,y)\,(i=1,\ldots ,k)$ are distinct irreducible elements of $\mathbb Z[x,y]$, and $t_1,\ldots ,t_k$ are positive integers. Throughout the paper, we shall write $F_m(x,y)$ for the m-free part of F(x, y), defined as

$$\begin{aligned} F_m(x,y)=P_1(x,y)^{t_1'}\ldots P_k(x,y)^{t_k'} \end{aligned}$$

where $m\ge 2$ is an arbitrary integer, and the exponents $t_i'$ are integers with $0\le t_i'<m$ and $t_i'\equiv t_i\pmod {m}$ $(i=1,\ldots ,k)$. Further, the power-free part $F^*(x,y)$ of F(x, y) is the product of those $P_i(x,y)$ for which $t_i=1$. Finally, $\text {rad}(F(x,y))$ will denote the radical of F, that is, the product of distinct irreducible divisors of F.

Theorem 2.1

Let $F(x,y)\in \mathbb Z[x,y]$.

• (i) Put $G_m(x,y)=\mathrm{{rad}}(F_m(x,y))$. Assume that

  $$\begin{aligned} \max (\deg _x(G_m(x,y)),\deg _y(G_m(x,y)))\ge 3. \end{aligned}$$

  (1)

  Then every (F, m)-Diophantine set is finite.

• (ii) Assume that

  $$\begin{aligned} \max (\deg _x(F^*(x,y)),\deg _y(F^*(x,y)))\ge 3. \end{aligned}$$

  (2)

  Then every $(F,*)$-Diophantine set is finite.

In the next theorem we give a complete characterization of the possible shapes of pairs (F, m) for which an infinite (F, m)-Diophantine set exists.

Theorem 2.2

Let $F(x,y)\in \mathbb Z[x,y]$ be a non-constant polynomial, and m be an integer with $m\ge 2$. Assume that there exists an infinite (F, m)-Diophantine set A. Then we have one of the following cases:

• (i) m is even, and $F_m(x,y)=(ax^2+bx+c)^{m/2}(ay^2+by+c)^{m/2}$, where $a,b,c\in \mathbb Z$ with $a\ne 0$;

• (ii) m is even, and $F_m(x,y)=(ax^2+bx+c)^{m/2}$ or $(ay^2+by+c)^{m/2}$, where $a,b,c\in \mathbb Z$ with $a\ne 0$;

• (iii) m is even, and $F_m(x,y)=(ax+b)^{m/2}(cx+d)^{m/2}(ay+b)^{m/2}$ or $(ax+b)^{m/2}(ay+b)^{m/2}(cy+d)^{m/2}$, where $a,b,c,d \in \mathbb Z$ with $ac\ne 0$;

• (iv) m is even, and $F_m(x,y)=(ax+b)^{m/2}(cy+d)^{m/2}$, where $a,b,c,d \in \mathbb Z$ with $ac\ne 0$;

• (v) $F_m(x,y)=s(ax+b)^{t_1'}(ay+b)^{t_2'}$, where $s,a,b\in \mathbb Z$ with $sa\ne 0$;

• (vi) $F_m(x,y)=s(ax+b)^{t_1'}$ or $s(ay+b)^{t_1'}$, where $s,a,b\in \mathbb Z$ with $sa\ne 0$;.

Remark

We note that for every case (i)–(vi) above, one can construct infinite (F, m)-Diophantine sets. This is demonstrated by the following examples.

• (i)–(ii) Let m be an arbitrary even integer and a, b, c be arbitrary such that the equation $ax^2+bx+c=z^2$ has infinitely many solutions. Writing A for the set of solutions in x, we clearly obtain an infinite (F, m)-Diophantine set in both cases (i) and (ii).

• (iii)–(iv) Let m be arbitrary even integer, and $a=b=d=1$, $c=2$. As it is well-known, there exist infinitely many integers z such that both $z+1$ and $2z+1$ are squares. Then the set A of these integers z is clearly an infinite (F, m)-Diophantine set in both cases (iii) and (iv).

• (v)–(vi) Let $m,t_1',t_2'$ be arbitrary, and $s=a=b=1$. Then the set $A=\{z^m-1:\ z\in \mathbb {N}\}$ is clearly an infinite (F, m)-Diophantine set in both cases (v) and (vi).

Observe that Theorem 2.1 does not give a bound for the size of an (F, m)-Diophantine (or $(F,*)$-Diophantine) set A, it provides only finiteness of such sets A. In the case when F(x, y) is a binary form, we can give an explicit version of Theorem 2.1.

Theorem 2.3

Let $m\ge 2$ be an integer and $F\in \mathbb Z[x,y]$ be a binary form, whose m-free part is not of the form

• (i) $c(x-\alpha y)^a(x-\beta y)^b$;

• (ii) $cg(x,y)^{m/2}$, where g(x, y) has at most four distinct roots;

• (iii) $cg(x,y)^{m/3}$, where g(x, y) has at most three distinct roots;

• (iv) $c(x-\alpha y)^{m/2}g(x,y)^{m/4}$, where g(x, y) has at most two distinct roots;

• (v) $c(x-\alpha y)^a g(x,y)^{m/2}$, where g(x, y) has at most two distinct roots;

• (vi) $c(x-\alpha y)^{m/2}(x-\beta y)^{am/3}(x-\gamma y)^{bm/r}$ where $r\le 6$;

where $\alpha ,\beta ,\gamma$ and c are integers, a, b and r are non-negative integers such that the exponents im / j are always integers, and g(x, y) is a binary form with integer coefficients. Then for any (F, m)-diophantine set A we have

$$\begin{aligned} |A|< C(F,m), \end{aligned}$$

where C(F, m) is a constant depending only on F and m.

Finally, we deal with quartic polynomials of certain types. For stating our results in this direction, we need to introduce some notation. Let

$$\begin{aligned} F(x,y)=(f_1x^2+f_2xy+f_3y^2+f_4x+f_5y+f_6)^2+f_7x+f_8y+f_9, \end{aligned}$$

(3)

where $f_i\in \mathbb {Z},i=1,2,\ldots ,9.$ We define

$$\begin{aligned} P_1(x,y)&=2(f_1x^2+f_2xy+f_3y^2+f_4x+f_5y+f_6) \\&\quad -(f_7x+f_8y+f_9)+1, \\ P_2(x,y)&=2(f_1x^2+f_2xy+f_3y^2+f_4x+f_5y+f_6) \\&\quad +(f_7x+f_8y+f_9)-1. \end{aligned}$$

We assume that the equations $P_1(x,y)=0$ and $P_2(x,y)=0$ define non-degenerate ellipses, that is

$$\begin{aligned}&\Delta _1:= \begin{vmatrix} 2f_1&f_2&\frac{2f_4-f_7}{2} \\ f_2&2f_3&\frac{2f_5-f_8}{2} \\ \frac{2f_4-f_7}{2}&\frac{2f_5-f_8}{2}&2f_6-f_9+1 \end{vmatrix} \ne 0, \nonumber \\&\Delta _2:= \begin{vmatrix} 2f_1&f_2&\frac{2f_4+f_7}{2}\\ f_2&2f_3&\frac{2f_5+f_8}{2}\\ \frac{2f_4+f_7}{2}&\frac{2f_5+f_8}{2}&2f_6+f_9-1 \end{vmatrix} \ne 0 \\&\text{ and } \nonumber \\&\begin{vmatrix} 2f_1&f_2 \\ f_2&2f_3 \end{vmatrix} >0, \quad (2f_1+2f_3)\Delta _1<0, \quad (2f_1+2f_3)\Delta _2<0. \nonumber \end{aligned}$$

(4)

Szalay [19] characterized the structure of the integral solutions of the Diophantine equation

$$\begin{aligned} F(x,y)=z^2. \end{aligned}$$

(5)

He proved the following result.

Lemma 2.1

If $(x, y, z)\in \mathbb {Z}^3$ is a solution of Eq. (5), then $P_1(x, y) > 0$ and $P_2 (x, y) > 0$ implies $f_7x + f_8y + f_9 = 0.$

That is he showed that if $(x,y,z)\in \mathbb {Z}^3$ is a solution of Eq. (5), then either (x, y) is an inner point of the ellipse defined by $P_1,$ that is $P_1(x,y)\le 0,$ or (x, y) is an inner point of the ellipse defined by $P_2,$ that is $P_2(x,y)\le 0,$ or (x, y) is a point on the line $f_7x+f_8y+f_9=0.$ In our theorem we need the equations of the horizontal and vertical tangent lines to the ellipses defined by $P_1(x,y)=0$ and $P_2(x,y)=0.$ The horizontal tangent lines to $P_1$ are defined by

$$\begin{aligned} y = h_1\quad \text{ and } \quad y=h_2, \end{aligned}$$

where $h_1,h_2$ are the roots of the polynomial

$$\begin{aligned}&4 \, {\left( f_{2}^{2} - 4 \, f_{1} f_{3}\right) } x^{2}+ 4 \, {\left( 2 \, f_{2} f_{4} - 4 \, f_{1} f_{5} - f_{2} f_{7} + 2 \, f_{1} f_{8}\right) } x \\&\quad + 4 \, f_{4}^{2} - 16 \, f_{1} f_{6} - 4 \, f_{4} f_{7} + f_{7}^{2} + 8 \, f_{1} f_{9} - 8 \, f_{1}. \end{aligned}$$

Similarly, the horizontal tangent lines to $P_2$ are defined by

$$\begin{aligned} y = h_3 \quad \text{ and } \quad y=h_4, \end{aligned}$$

where $h_3,h_4$ are the roots of the polynomial

$$\begin{aligned}&4 \, {\left( f_{2}^{2} - 4 \, f_{1} f_{3}\right) } x^{2} + 4 \, {\left( 2 \, f_{2} f_{4} - 4 \, f_{1} f_{5} + f_{2} f_{7} - 2 \, f_{1} f_{8}\right) } x \\&\quad + 4 \, f_{4}^{2} - 16 \, f_{1} f_{6} + 4 \, f_{4} f_{7} + f_{7}^{2} - 8 \, f_{1} f_{9} + 8 \, f_{1}. \end{aligned}$$

The vertical tangent lines to $P_1$ are given by

$$\begin{aligned} x = v_1 \quad \text{ and } \quad x=v_2, \end{aligned}$$

where $v_1,v_2$ are the roots of the polynomial

$$\begin{aligned}&4 \, {\left( f_{2}^{2} - 4 \, f_{1} f_{3}\right) } x^{2} - 4 \, {\left( 4 \, f_{3} f_{4} - 2 \, f_{2} f_{5} - 2 \, f_{3} f_{7} + f_{2} f_{8}\right) } x \\&\quad + 4 \, f_{5}^{2} - 16 \, f_{3} f_{6} - 4 \, f_{5} f_{8} + f_{8}^{2} + 8 \, f_{3} f_{9} - 8 \, f_{3}. \end{aligned}$$

In case of $P_2$ the vertical tangent lines are given by

$$\begin{aligned} x = v_3 \quad \text{ and } \quad x=v_4, \end{aligned}$$

where $v_3,v_4$ are the roots of the polynomial

$$\begin{aligned}&4 \, {\left( f_{2}^{2} - 4 \, f_{1} f_{3}\right) } x^{2} - 4 \, {\left( 4 \, f_{3} f_{4} - 2 \, f_{2} f_{5} + 2 \, f_{3} f_{7} - f_{2} f_{8}\right) } x \\&\quad + 4 \, f_{5}^{2} - 16 \, f_{3} f_{6} + 4 \, f_{5} f_{8} + f_{8}^{2} - 8 \, f_{3} f_{9} + 8 \, f_{3}. \end{aligned}$$

Define

$$\begin{aligned} H_1= & {} \min \{h_1,h_2,h_3,h_4\}, \\ H_2= & {} \max \{h_1,h_2,h_3,h_4\}, \\ V_1= & {} \min \{v_1,v_2,v_3,v_4\}, \\ V_2= & {} \max \{v_1,v_2,v_3,v_4\}. \end{aligned}$$

Now we state our theorem for (F, 2)-Diophantine sets in case of the quartic polynomial (3).

Theorem 2.4

If A is an (F, 2)-Diophantine set, where F is defined by (3), then

$$\begin{aligned} |A| \le \max \{\lfloor H_2-H_1\rfloor ,\lfloor V_2-V_1\rfloor \}+2. \end{aligned}$$

Based on the previous theorem we provide some numerical results, too.

Theorem 2.5

Let F(x, y) be a quartic polynomial defined by (3) satisfying conditions given by (4) such that $F(x,y)=F(y,x)$, $f_1>0$ and $|f_i|\le 5$ for $i=1,2,\ldots ,9$. If A is an (F, 2)-Diophantine set having at least four elements then we have

$[f_1,f_2,f_3,f_4,f_5,f_6,f_7,f_8,f_9]$	A	$[f_1,f_2,f_3,f_4,f_5,f_6,f_7,f_8,f_9]$	A
$[1, 0, 1, -2, -2, -4, 4, 4, -4]$	$\{0, 1, 3, -2\}$	$[1, 0, 1, -2, -2, -2, -4, -4, 4]$	$\{0, 1, 2, -1\}$
$[1, 0, 1, -2, -2, 0, 4, 4, -4]$	$\{0, 1, 2, -1\}$	$[1, 0, 1, -1, -1, -4, 4, 4, 0]$	$\{1, 2, -1, -2\}$
$[1, 0, 1, 0, 0, -4, -4, -4, -4]$	$\{0, 1, -1, -2\}$	$[1, 0, 1, 0, 0, -4, 4, 4, -4]$	$\{0, 1, 2, -1\}$
$[1, 0, 1, 0, 0, -2, -4, -4, 4]$	$\{0, 1, 2, -1\}$	$[1, 0, 1, 0, 0, -2, 4, 4, 4]$	$\{0, 1, -1, -2\}$
$[1, 0, 1, 1, 1, -4, -4, -4, 0]$	$\{1, 2, -1, -2\}$	$[1, 0, 1, 2, 2, -4, -4, -4, -4]$	$\{0, 2, -3, -1\}$
$[1, 0, 1, 2, 2, -2, 4, 4, 4]$	$\{0, 1, -1, -2\}$	$[1, 0, 1, 2, 2, 0, -4, -4, -4]$	$\{0, 1, -1, -2\}$
$[1, 1, 1, -4, -4, -3, 4, 4, 0]$	$\{2, 3, 4, -2\}$	$[1, 1, 1, -2, -2, -4, -4, -4, 1]$	$\{0, 2, 4, -2\}$
$[1, 1, 1, 2, 2, -4, 4, 4, 1]$	$\{0, 2, -4, -2\}$	$[1, 1, 1, 4, 4, -3, -4, -4, 0]$	$\{2, -4, -3, -2\}$
$[2, 0, 2, -3, -3, -4, -4, -4, 4]$	$\{0, 1, 2, -1\}$	$[2, 0, 2, -3, -3, -2, 4, 4, -4]$	$\{0, 1, 2, -1\}$
$[2, 0, 2, -1, -1, -4, -4, -4, 4]$	$\{0, 1, 2, -1\}$	$[2, 0, 2, 1, 1, -4, 4, 4, 4]$	$\{0, 1, -1, -2\}$
$[2, 0, 2, 3, 3, -4, 4, 4, 4]$	$\{0, 1, -1, -2\}$	$[2, 0, 2, 3, 3, -2, -4, -4, -4]$	$\{0, 1, -1, -2\}$
$[2, 2, 2, -5, -5, -4, 4, 4, -4]$	$\{0, 1, 3, -1\}$	$[2, 2, 2, 5, 5, -4, -4, -4, -4]$	$\{0, 1, -3, -1\}$
$[3, 0, 3, -4, -4, -4, 4, 4, -4]$	$\{0, 1, 2, -1\}$	$[3, 0, 3, 4, 4, -4, -4, -4, -4]$	$\{0, 1, -1, -2\}$

3 Proofs

3.1 Proof of Theorem 2.1

To prove Theorem 2.1 we need three lemmas. The following result is in fact well-known, however, for the convenience of the reader we indicate the main steps of its proof, as well.

Lemma 3.1

Let H(x, y) be a square-free polynomial in $\mathbb Z[x,y]$, of degree $n\ge 1$ in x. Then apart from finitely many integers u, the polynomials $H(x,u)\in \mathbb Z[x]$ have n distinct roots.

Proof

Write

$$\begin{aligned} H(x,y)=a_n(y)x^n+\cdots +a_1(y)x+a_0(y) \end{aligned}$$

with $a_i(y)\in \mathbb Z[y]$ for $i=0,1,\ldots ,n$ with $a_n(y)$ not identically zero. Excluding finitely many possibilities, we may clearly assume that u is not a root of $a_n(y)$. Let $T:=\mathbb Q(y)$ be the rational function field in y (field of fractions of polynomials in $\mathbb Z[y]$). Then $\mathbb Z[x,y]$ can be embedded into T[x] in a natural way. Suppose that for some $u\in \mathbb Z$ the polynomial H(x, u) has multiple roots. Then u is obviously a solution to the equation

$$\begin{aligned} D(y):=\text {Disc}_x(H(x,y))=0. \end{aligned}$$

(6)

This is equivalent to saying that

$$\begin{aligned} \text {Res}_x(H(x,y),H'(x,y))=0. \end{aligned}$$

Thus D(y) is identically zero if and only if H(x, y) and $H'(x,y)$ have a common root over T. (For details about this and certain forthcoming facts about polynomials in two variables, see e.g. [12].) Here $L'(x,y)$ denotes the derivative of $L(x,y)\in \mathbb Z[x,y]$ with respect to x. This, in a standard way, yields that $H'(x,y)$ and H(x, y) have a common factor in $\mathbb Z[x,y]$. Since H(x, y) is square-free in $\mathbb Z[x,y]$, we can write $H(x,y)=P_1(x,y)\cdots P_r(x,y)$ for some irreducible polynomials in $\mathbb Z[x,y]$. Then we have

$$\begin{aligned} H'(x,y)=\sum \limits _{i=1}^r P_i'(x,y){\underset{j\ne i}{\prod \limits _{j=1}^r}} P_j(x,y). \end{aligned}$$

Thus one can easily check that H(x, y) and $H'(x,y)$ have no common factors in $\mathbb Z[x,y]$, which means that D(y) is not identically zero. Hence our claim follows. $\square$

The next result is a classical theorem of LeVeque [14]. Note that an effective version follows from a result of Brindza [4].

Lemma 3.2

Let $f(x)\in \mathbb Z[x]$, $m\ge 2$, and let $\alpha _1,\ldots ,\alpha _r$ be the (distinct) roots of f, with multiplicities $e_1,\ldots ,e_r$, respectively. Write $m_i=m/\gcd (m,e_i)$ $(i=1,\ldots ,r)$, and assume that the roots are ordered such that $m_1\ge \ldots \ge m_r$. Suppose that $(m_1,\ldots ,m_r)$ is neither of the form $(t,1,\ldots ,1)$, nor of the shape $(2,2,1,\ldots ,1)$. Then the superelliptic equation

$$\begin{aligned} f(x)=z^m \end{aligned}$$

has only finitely many solutions in integers x, z.

Our last lemma needed to prove Theorem 2.1 is due to Schinzel and Tijdeman [16].

Lemma 3.3

Let $f(x)\in \mathbb Z[x]$ with at least two distinct roots. Suppose that the integers x, z, m with $|z|>1$ and $m\ge 0$ satisfy

$$\begin{aligned} f(x)=z^m. \end{aligned}$$

Then m is bounded by a constant depending only on f.

Now we are ready to give the proof of our first result.

Proof of Theorem 2.1

• (i) Assume first that $m=2$. Note that in this case we have $G_m(x,y)=F_2(x,y)$. Without loss of generality, we may assume that $n:=\deg _x(F_2(x,y))\ge 3$. Let Y be the set of integers u for which $F_2(x,u)$ has less than n distinct roots. Then, by Lemma 3.1, we know that Y is finite. Let A be an (F, 2)-Diophantine set, having at least $|Y|+1$ elements. Then there is a $y_0$ in A which is not in Y. Now using a classical theorem of Baker [1], we know that the equation $F_2(x,y_0)=z^2$ has at most N solutions in integers x, where N is an explicitly computable constant depending only on F and $y_0$. Thus A has at most $N+1$ elements, and the theorem follows. Let now $m\ge 3$. Without loss of generality we may assume that $r:=\deg _x(G_m(x,y))\ge 3$. Let again Y denote the set of integers y such that $G_m(x,y)$ has less than r roots (in x). Assume that $|A|>|Y|$. Then there exists a $y_0\in A$ which is not in Y. Consider the polynomial $F_m(x,y_0)$. Obviously, it has $r\ge 3$ distinct roots, $\alpha _1,\ldots ,\alpha _r$, say, having multiplicities $e_1,\ldots ,e_r$, respectively, with $e_i<m$ $(i=1,\ldots ,r)$. Thus, since $r\ge 3$, from Lemma 3.2 we get that the equation

  $$\begin{aligned} F_m(x,y_0)=z^m \end{aligned}$$

  has at most finitely many solutions. This clearly implies the statement also in this case.

• (ii) Suppose that A is an infinite $(F,*)$-Diophantine set. Without loss of generality we may also assume that $\deg _x(F^*(x,y))\ge 3$. By Lemma 3.1, we may choose a $y_0\in A$ such that the polynomial $F(x,y_0)$ has at least three distinct roots. Then, for infinitely many $x\in A$ we have

  $$\begin{aligned} F^*(x,y_0)=z^m \end{aligned}$$

  with $|z|>1$. This by Lemma 3.3 implies that here m is bounded by a constant depending only on F and $y_0$. However, then we get a contradiction by Lemma 3.2, and the statement follows.$\square$

3.2 Proof of Theorem 2.2

Now we give the proof of our second theorem.

Proof of Theorem 2.2

Theorem 2.1 implies that both $\deg _x(G_m(x,y)) \le 2$ and $\deg _y(G_m(x,y))\le 2$, where $G_m(x,y)$ is the radical of $F_m(x,y)$, the m-free part of F(x, y). We distinguish several cases, according to the shape of

$$\begin{aligned} F_m(x,y)=s P_1(x,y)^{t_1'}\ldots P_k(x,y)^{t_k'}. \end{aligned}$$

(7)

Here s is an m-th power free non-zero integer, and we assume that $P_i(x,y)\,(i=1,\ldots ,k)$ is non-constant. We may further assume that the polynomial $P_i(x,y)\,(i=1,\ldots ,k)$ is also primitive (i.e. the $\gcd$ of its coefficients is one). By the degree condition on $G_m(x,y)$ we clearly have $k\le 4$.

In our arguments we shall frequently use the obvious fact that any (F, m)-Diophantine set A is also an $(\hat{F},m)$-Diophantine set, where

$$\begin{aligned} \hat{F}(x,y)=F(x,y)F(y,x). \end{aligned}$$

(8)

Further, throughout the proof we shall assume that A is an infinite (F, m)-Diophantine set.

Suppose first that $k=4$. Then we may assume that

$$\begin{aligned} P_1(x,y)=a_1x+b_1, \quad P_2(x,y)=a_2x+b_2, \\ P_3(x,y)=a_3y+b_3, \quad P_4(x,y)=a_4y+b_4 \end{aligned}$$

with integers $a_i,b_i$, such that $(a_1,b_1)\ne (a_2,b_2)$, $(a_3,b_3)\ne (a_4,b_4)$ and $\gcd (a_i,b_i)=1$, $a_i>0$ $(i=1,2,3,4)$. Further, in a similar manner as in the proof of Theorem 2.1, by Lemma 3.2 we immediately get that m is even and $t_1'=t_2'=t_3'=t_4'=m/2$ is also necessarily valid, otherwise every (F, m)-Diophantine set is finite. Further, using (8), and applying the same argument to $\hat{F}(x,y)$, by Lemma 3.2 without loss of generality we may write $(a_1,b_1)=(a_3,b_3)$ and $(a_2,b_2)=(a_4,b_4)$. Hence (7) can be written as

$$\begin{aligned} F_m(x,y)=s(ax^2+bx+c)^{m/2}(ay^2+by+c)^{m/2}, \end{aligned}$$

with $a>0$. Here obviously $s^2$ is an m-th power, so we can write $s=r^{m/2}$ with some integer r. For $X\in A$, write $u_X$ for the square free part of $aX^2+bX+c$. Then by the shape of $F_m(x,y)$ we have that

$$\begin{aligned} ru_Xu_Y, \quad ru_Yu_Z, \quad ru_Xu_Z \end{aligned}$$

are all squares, for any $X,Y,Z\in A$. Taking the product of these numbers, we obtain that $r^3$ is also a square. This yields that r is also a square, whence s is an m-th power. However, since s is assumed to be m-th power free, this implies $s=\pm 1$. As $a>0$, we have that up to finitely many exceptions, $aX^2+bX+c>0$. Recalling that m is even, this implies that $s=1$ must be valid, and we are in case (i).

Suppose next that $k=3$. Here we have two subcases to distinguish. Assume first that we have

$$\begin{aligned} P_1(x,y)=a_1xy+a_2x+a_3y+a_4, \quad P_2(x,y)=a_5x+a_6, \quad P_3(x,y)=a_7y+a_8, \end{aligned}$$

where $a_1,\ldots ,a_8$ are integers with $\gcd (a_1,a_2,a_3,a_4)=\gcd (a_5,a_6)=(a_7,a_8)=1$, $a_5>0$, $a_7>0$, and one of $a_1,a_2,a_3$ is non-zero. Similarly as before, we readily get again that m is even and $t_1'=t_2'=t_3'=m/2$. Further, if $a_1\ne 0$, then one can easily show that there exist three distinct $y_1,y_2,y_3\in A{\setminus }\{-a_8/a_7\}$ such that $a_1xy_i+a_2x+a_3y_i+a_4$ have distinct roots (in x) for $i=1,2,3$, and none of these roots equals $-a_6/a_5$. Then using Lemma 3.2 we get that the equation

$$\begin{aligned} F(x,y_1)F(x,y_2)F(x,y_3)=z^2 \end{aligned}$$

has only finitely many solutions in x, which contradicts the assumption that A is infinite. Hence we may assume that $a_1=0$. Further, a similar argument shows that $a_2a_3=0$ must also be valid. Assume that $a_3=0$, the case $a_2=0$ is similar. Using now (8), in the usual way we get that $(a_7,a_8)$ is one of $(a_2,a_4),(a_5,a_6)$. So we obtain that $F_m(x,y)$ is of the form

$$\begin{aligned} s(ax+b)^{m/2}(cx+d)^{m/2}(ay+b)^{m/2}. \end{aligned}$$

Here we may assume that a and c are positive. Since s must obviously be an m / 2-th power, merging s into the term $(cx+d)^{m/2}$, we are in the case (iii).

The other case with $k=3$ is when

$$\begin{aligned} P_1(x,y)=a_1x+a_2, \quad P_2(x,y)=a_3x+a_4, \quad P_3(x,y)=a_5y^2+a_6y+a_7, \end{aligned}$$

with integers $a_1,\ldots ,a_7$ such that $a_1,a_3,a_5$ are positive, $(a_1,a_2)\ne (a_3,a_4)$ and $\gcd (a_1,a_2)=\gcd (a_3,a_4)=\gcd (a_5,a_6,a_7)=1$. Note that here the role of x and y could be interchanged. As previously we obtain that m is even and $t_1'=t_2'=t_3'=m/2$. Now using (8), as $P_3(x,y)$ is assumed to be irreducible, we get a contradiction.

Suppose next that $k=2$. Then we need to distinguish several possibilities. Note that in all cases the roles of x and y could be switched.

If $P_1(x,y)=a_1xy+a_2x+a_3y+a_4$ and $P_2(x,y)=a_5xy+a_6x+a_7y+a_8$ with integers $a_1,\ldots ,a_8$ under the usual assumptions, then we have two options. Similarly as earlier, we obtain that either m is even, $t_1'=t_2'=m/2$, and $a_1=a_3=a_5=a_7=0$, or $a_1=a_3=a_5=a_6=0$. In the first case we are in case (ii). In the latter case we distinguish two subcases. Using (8), either m is even and $t_1'=t_2'=m/2$, and we are in case (iv), or we have $(a,b):=(a_2,a_4)=(a_7,a_8)$. Now we have

$$\begin{aligned} F(x,y)=s(ax+b)^{t_1'}(ay+b)^{t_2'}, \end{aligned}$$

and we are in case (v).

In the case $P_1(x,y)=a_1x^2+a_2x+a_3$ and $P_2(x,y)=a_4y+a_5$ we easily get that m is even and $t_1'=m/2$. Then using (8) we get a contradiction.

Finally, in the case $P_1(x,y)=a_1x^2+a_2x+a_3$ and $P_2(x,y)=a_4y^2+a_5y+a_6$ with $a_1>0$ and $a_4>0$, using (8) by a simple calculation we get that we are in case (i).

When $k=1$ then similarly as above, using (8), we easily get that we are in case (ii) or (vi). $\square$

3.3 Proof of Theorem 2.3

To prove our third theorem we need the following lemma, which is a simple consequence of a deep result due to Darmon and Granville [8].

Lemma 3.4

Let $m\ge 2$ be a fixed integer, and let f(x, y) be a binary form with integral coefficients, whose m-free part is not of the form

• (i) $c(x-\alpha y)^a(x-\beta y)^b$;

• (ii) $cg(x,y)^{m/2}$, where g(x, y) has at most four distinct roots;

• (iii) $cg(x,y)^{m/3}$, where g(x, y) has at most three distinct roots;

• (iv) $c(x-\alpha y)^{m/2}g(x,y)^{m/4}$, where g(x, y) has at most two distinct roots;

• (v) $c(x-\alpha y)^a g(x,y)^{m/2}$, where g(x, y) has at most two distinct roots;

• (vi) $c(x-\alpha y)^{m/2}(x-\beta y)^{am/3}(x-\gamma y)^{bm/r}$ where $r\le 6$;

where $\alpha ,\beta ,\gamma$ and c are integers, a, b and r are non-negative integers such that the exponents im / j are always integers, and g(x, y) is a binary form with integer coefficients. Then the equation

$$\begin{aligned} f(x,y)=z^m \end{aligned}$$

has only finitely many solutions in coprime integers x, y.

Now we are ready to give the

Proof of Theorem 2.3

Since F is not of the shape (i) through (vi), by Lemma 3.4 the equation

$$\begin{aligned} F(x,y)=z^m \end{aligned}$$

(9)

has only finitely many solutions in $x,y,z\in \mathbb Z$ with $\gcd (x,y)=1$. Let $n:=n(F,m)$ denote the number of co-prime solutions of (9). Then n is a constant which depends exclusively on F and m. Let $(x_i,y_i)$ for $i=1, \ldots ,n$ denote the co-prime solutions of (9).

Let A be an (F, m)-Diophantine set. Then for each $(a,b) \in A$ we have $(a,b)=(tx_j,ty_j)$ with some $t\in \mathbb Z$ and $j=1, \ldots ,n$. In this case we shall say that the solution (a, b) belongs to the co-prime solution $(x_j,y_j)$.

Now we fix the co-prime solution $(x_1,y_1)$, and we start to list all the pairs (a, b) with $a,b\in A$, belonging to $(x_1,y_1)$, and then we exclude the elements a, b from the set A. We repeat this procedure until either we have excluded $m\ge 2n+1$ pairs, or the remaining set does not contain a pair (a, b) anymore which belongs to $(x_1,y_1)$. Thus we shall get a finite sequence $(t_jx_1, t_jy_1)$ for $j=1, \ldots , m$ consisting of solutions of Eq. (9), with $t_ix_1,t_iy_1\in A$ for $i=1, \ldots ,m$, and with distinct $t_i\in \mathbb Z$ for $i=1, \ldots , m$.

In the next step we prove that $m<2n+1$. Indeed, assume that $m\ge 2n+1$. Then since $t_ix_1\in A$ for $i=1, \ldots , m$ thus the pair $(t_1x_1, t_ix_1)$ for $i=2, \ldots , m$ is a solution of Eq. (9). Thus it has to belong to one of its co-prime solutions, i.e. we have for $i=2,\ldots ,m$

$$\begin{aligned} {\left\{ \begin{array}{ll} t_1x_1=\delta ^{(i)}u^{(i)} \\ t_ix_1=\delta ^{(i)}v^{(i)}, \end{array}\right. } \end{aligned}$$

where $\delta ^{(i)}\in \mathbb Z$ and either $(u^{(i)},v^{(i)})$ or $(v^{(i)},u^{(i)})$ is a co-prime solution of (9). Since we assumed $m\ge 2n+1$ thus by the pigeonhole principle we have two distinct integers $i,j\in \{2, \ldots , m\}$ such that $(u^{(i)},v^{(i)})=(u^{(j)},v^{(j)})$. For these values of i and j we get the system

$$\begin{aligned} {\left\{ \begin{array}{ll} t_1x_1=\delta ^{(i)}u^{(i)} \\ t_ix_1=\delta ^{(i)}v^{(i)} \\ t_1x_1=\delta ^{(j)}u^{(i)} \\ t_jx_1=\delta ^{(j)}v^{(i)}, \end{array}\right. } \end{aligned}$$

which shows that $t_i=t_j$, a contradiction. Thus we have $m<2n+1$.

So for each co-prime solution $(x_j,y_j)$ of (9), the set A can contain at most 2n elements which may be an entry of a solution (a, b) belonging to $(x_j,y_j)$.

So taking in account the possibility $0\in A$ altogether we have $|A|\le 2n^2+1$. $\square$

3.4 Proof of Theorem 2.4

To prove our results concerning quartic polynomials, we do not need any further preparation.

Proof of Theorem 2.4

Let $A=\{a_1,a_2,\ldots ,a_n\}$ be an (F, 2)-Diophantine set with $a_1<a_2<\cdots <a_n.$ So we have that

$$\begin{aligned} F(a_i,a_j)=\square \end{aligned}$$

for all distinct $a_i,a_j\in A.$ The solutions of the Diophantine equation $F(x,y)=z^2$ are characterized by Szalay’s result [19]. If the line $f_7x+f_8y+f_9=0$ is such that $f_7\ne 0$ and $f_8\ne 0,$ then it has one intersection point with a line defined by $x=a_i$ or $y=a_i$ for $a_i\in A, i=1,2,\ldots ,n.$ The number of points $(x,y)\in \mathbb {Z}^2$ contained in the ellipses $P_1$ and $P_2$ and lying on the line $x=a_i$ is at most $\lfloor V_2-V_1\rfloor$. The number of points $(x,y)\in \mathbb {Z}^2$ contained in the ellipses $P_1$ and $P_2$ and lying on the line $y=a_i$ is at most $\lfloor H_2-H_1\rfloor .$ Therefore the elements of A correspond to points of the form $(a_i,r),$ where $r\in [V_1,V_2]$ and $(s,a_i),$ where $s\in [H_1,H_2]$ and possibly an intersection point with the line $f_7x+f_8y+f_9=0.$ Thus we have that

$$\begin{aligned} |A|\le \min \{\lfloor H_2-H_1\rfloor ,\lfloor V_2-V_1\rfloor \}+2. \end{aligned}$$

If $f_7=0$ or $f_8=0,$ then the equation $f_7x+f_8y+f_9=0$ may define a horizontal or a vertical line. We consider the horizontal case only, the vertical is analogous. In this case the elements of A correspond to points of the form $(a_i,r),$ where $r\in [H_1,H_2].$ Clearly, all the points of the form $(r,a_i)$ are lying on the horizontal line $y=a_i,$ hence we have that

$$\begin{aligned} |A|\le \lfloor H_2-H_1\rfloor +1. \end{aligned}$$

In any case we have the following bound for the cardinality of A

$$\begin{aligned} |A| \le \max \{\lfloor H_2-H_1\rfloor ,\lfloor V_2-V_1\rfloor \}+2. \end{aligned}$$

$\square$

3.5 Proof of Theorem 2.5

Proof of Theorem 2.5

From the URL http://www.math.unideb.hu/~tengely/PDioph.sage. one can download a Sage [17] procedure which determines all non-trivial F-Diophantine sets corresponding to $[f_1,f_2,f_3,f_4,f_5,f_6,f_7,f_8,f_9].$ One can use it as follows. One can determine the solutions of the equation $F(x,y)=z^2$ for which (x, y) is an inner point of the ellipse $P_1(x,y)=0$ or the ellipse $P_2(x,y)=0$ using

$$\begin{aligned} \mathtt{w=Epoints}([f_1,f_2,f_3,f_4,f_5,f_6,f_7,f_8,f_9]). \end{aligned}$$

After that

$$\begin{aligned} \mathtt{PDset(w)} \end{aligned}$$

determines the non-trivial F-Diophantine sets. We provide some details of the computation in two cases.

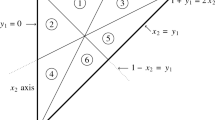
Let $[f_1,f_2,f_3,f_4,f_5,f_6,f_7,f_8,f_9]=[1, 1, 1, 2, 2, -4, 4, 4, 1].$ The two ellipses and the line $4x+4y+1=0$ can be seen in the following figure, also the points (x, y) corresponding to solutions of $F(x,y)=z^2$ are indicated (see below).

There are only finitely many integral solutions of the equation $F(x,y)=z^2$ since $4x+4y+1$ is odd for all $(x,y)\in \mathbb {Z}^2.$ These solutions are as follows

$$\begin{aligned} (x,y)\in&\{(-4, -2), (-4, 0), (-4, 2), (-2, -4), (-2, 0), \\&(-2, 2), (0, -4), (0, -2), (0, 2), (2, -4), (2, -2), (2, 0)\}. \end{aligned}$$

There are several non-trivial (F, 2)-Diophantine sets, e.g. $\{-4, -2, 0, 2\}.$

Now we consider the case

$$\begin{aligned}{}[f_1,f_2,f_3,f_4,f_5,f_6,f_7,f_8,f_9]=[1, 1, 1, 3, 3, -5, 2, 2, -3]. \end{aligned}$$

The set of the solutions can be seen in the figure below.

There exists no integral point lying on the line $2x+2y-3=0,$ hence there are only finitely many solutions. These are given by

$$\begin{aligned} (x,y)\in&\{(-5, -1), (-5, 2), (-3, -3), (-3, 0), (-3, 1), (-1, -5), \\&(-1, 2), (0,-3), (0, 1), (1, -3), (1, 0), (2, -5), (2, -1)\}. \end{aligned}$$

We obtain two disjoint non-trivial (F, 2)-Diophantine sets, namely

$$\begin{aligned} \{-5, -1, 2\} \quad \text{ and } \quad \{-3, 0, 1\}. \end{aligned}$$

$\square$