Experimental and Numerical Study of Phyllite’s Anisotropic Behavior in 3D Space Under Brazilian Test Conditions

Abstract

Phyllite is a kind of typical anisotropic rocks with well-developed foliations. This article aims to study the influence of foliations on the mechanical behaviors of phyllite in three-dimensional (3D) space under Brazilian test conditions. First, the overall behaviors of various anisotropic rocks in 3D space were summarized based on statistical analysis. Then, the acoustic emission signals were investigated in detail to study the micro-fracture process of phyllite. Finally, a new numerical model considering the crystal structures and weak structural planes of phyllite based on the particle discrete element method (PDEM) was developed. The micro-mechanism behind the macro-phenomenon and the failure process of specimens with different fracture patterns were discussed through numerical simulations. The results show that: (1) based on the Brazilian test results of nine kinds of anisotropic rocks in 3D space, the patterns regarding the relationship between the normalized failure strength (NFS) or anisotropic index and fabric-loading angles or orientation angles are obtained; (2) The failure strength of specimens, the temporal distributions of the AE counts and AE energy were closely related to their fracture patterns and the areas of their fracture surfaces. In addition, nine macro-fracture patterns and two distribution patterns of AE signals were obtained; (3) The distribution of micro-cracks has evident accumulation features due to the effect of foliations and the proportions of shear cracks and tensile cracks are influenced by the loading-foliation angles and inclination angles; (4) The calibrated results of phyllite agreed well with the experimental results with regards to failure strength and fracture patterns. During failure process, the intra-grain cracks and inter-grain cracks mainly occurred at the plastic loading stages, and shear cracks along weak planes dominated.

Highlights

• Anisotropic time–space–energy evolution process and accumulation features of microcracks are analysed.

• A numerical model considering crystal structures and weak planes of anisotropic rocks based on the particle discrete element method is developed.

• Failure process and distribution regarding six types of microcracks during tensile failure is explained.

1 Introduction

Layered rocks, such as slate, sandstone phyllite and shale, are featured by significant anisotropies in terms of physico-mechanical properties due to the existence of weak planes (Noori et al. 2023; Zhou et al. 2023; Meng et al. 2022). Engineering practice in the field of oil and gas exploitation, and excavation of underground spaces and tunnels reveal the dominant role of weak planes in determining the fracture patterns of surrounding rocks (Sun et al. 2023; Lee et al. 2019), especially tensile fracture patterns for rocks have lower tensile strengths compared to their compressive strengths. Therefore, understanding the tensile behaviors of rocks has important theoretical and practical value.

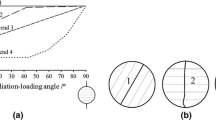
The Brazilian test is a widely adopted method to measure the tensile strength of rocks indirectly (Li and Wong 2013). Unlike the isotropic rocks, the failure strength and patterns of layered rocks are closely related to the angle between the loading direction and weak planes (Cho et al. 2012; Gholamreza et al. 2015; Kundu et al. 2018). The tensile properties of nine different layered rocks were summarized by Vervoort et al. (2014), and four different trends in variation of the relative failure load as a function of foliation-loading angle (θ, the angle between loading direction and foliation planes) and three macro-failure modes were summarized by them (Fig. 1a and Fig. 2a). On the basis of Vervoort’s research, Xu et al. (2018, 2020) find two new tensile strength trends (Fig. 1b) and Tan et al. (2015) classified the macro-failure modes into five types (Fig. 2b). In addition, tensile failure, shear failure, and mixed-mode failure are also obtained according to the mechanical mechanisms (Chen et al. 2013). To study the failure evolution process, high-speed camera (Xu et al. 2018; Mighani et al. 2014), acoustic emission (AE) (Ban et al. 2020; Chu et al. 2023) and digital imaging correlation (DIC) (Yang et al. 2020) are adopted to explain the relation between the macro-behaviors and the micro-failure features. Ban et al. (2020) found the relationship between fracture geometrical morphology and acoustic emission power spectrum characteristics is an effective way to reveal the shale microdamage mechanism. Yang et al. (2020) employed DIC to monitor the deformation of disk faces during the failure process and found that the central deformation is not always at the maximum when the fracture occurs.

Fig. 1

Trends in the variation of the relative failure load as a function of the loading-foliation angle: a. Four trends obtained from Vervoort et al. (2014); b. Two additional trends from Xu et al. (2020)

Fig. 2

Fracture patterns of anisotropic rocks considering the influence of loading-foliation angle: a. three different fracture patterns from Vervoort et al. (2014) (1: layer activation; 2: central fracture; 3: non-central fracture) b. five different fracture patterns from Vervoort et al. (2014)

However, there still exists some limitations in physical tests, such as it is difficult to reveal the influence of mechanical parameters of weak planes on the rock’s behaviors quantitatively. As a supplement, numerical modeling and theoretical analysis can compensate this deficiency to some extent. Dou et al. (2022) investigated the effect of clay minerals on tensile failure characteristics of shale using a particle discrete element method (PDEM) and found that clay distribution has a strong influence on the tensile strength and failure behaviors of shale. Li et al. (2023) analyzed the fracturing mechanism and brittleness characteristics of shale based on the finite–discrete element method (FDEM). Duan and Kwok (2015) revealed the influence of contacted state and strength between particles on the failure patterns of anisotropic rocks under Brazilian splitting. Jiang et al. (2017) investigated the spatial anisotropic deformation properties for jointed rock mass by an analytical deformation tensor. Duveau et al. (1998) evaluated nine failure criteria for typical highly anisotropic rocks. Niandou et al.(2004), Pietruszczak et al. (2004), and Shen and Shao (2015) respectively conducted triaxial compression tests and proposed micromechanical elastoplastic models to analyze the anisotropy of Tournemire shale. Shao et al. (2006) and Chen et al. (2012) built new constitutive models to characterize the induced anisotropic damage and creep deformation behavior of brittle rocks. Qi et al. (2016) developed a three-dimensional micromechanical model to simulate micro-crack propagation and plastic frictional sliding in initially anisotropic quasi-brittle materials under compressive loading. Zhao et al. (2022) introduced a new constitutive model incorporating structural anisotropy to describe elastic, instantaneous, and time-dependent plastic deformation as well as induced damage.

The above research focuses on the effect of foliation-loading angle on the tensile behavior. In other words, the mechanical behaviors of anisotropic rocks are studied in 2D space. Taking tunnel in anisotropic surrounding rocks as an example, only when the bedding plane is perpendicular to the tunnel cross-section (Fig. 3a), the mechanical behaviors in 2D space can be adopted to analyze the tunnel stability. However, the bedding plane intersects diagonally with tunnel cross section is common in most cases and only anisotropic behavior in 3D space can meet the analysis requirement (Figs. 3b and c). However, less attention has been paid regarding the influence of orientation angle (α, the angle between the foliation planes and the test specimen axis). Dan et al. (2013) carried out Brazilian tests on four different rocks ranging from nearly isotropic to anisotropic (one sandstone, two gneiss and one slate), and found that the influence of orientation angle is much larger than that of foliation-loading angle in all the gneiss and slate. Ding et al. (2020) studied the foliation effects on mechanical and failure characteristics of slate under Brazilian test, indicating that the effects of orientation angle should be considered due to its important influences on the mechanical and failure characteristics of anisotropic rocks. Wang et al. (2023) investigated the anisotropic tensile behavior of shale and found that the influence of the orientation angle is slightly stronger than that of the foliation-loading angle. Thus, in this article, the coupling effect of foliation-loading angle and orientation angle on phyllite under Brazilian splitting test is studied through experimental tests and numerical simulations. First, the acoustic emission (AE) system was adopted to record the micro-fracture process and characteristics of AE signals were analyzed. Then, a new numerical model considering the micro-structure of rock matrix and the distribution of weak planes based on the PDEM was put forward to further study the micro-mechanism behind the macro-phenomenon. In addition, the failure process of specimens with different fracture patterns were discussed in detail through numerical simulations.

Fig. 3

The relative location of bedding planes and tunnel cross-section: a. the bedding plane is perpendicular to the tunnel cross section (α = 90°); b. the bedding plane intersects diagonally with tunnel cross section (α = 60°); c. the bedding plane intersects diagonally with tunnel cross section (α = 30°)

2 Statistical Analysis

For isotropic rocks with tensile failure initiating from the center, the tensile strength is derived through Eq. (1):

$$\sigma_{{\text{t}}} = {\text{2F}}/\pi {\text{Dt}}$$

(1)

where σ_t is the tensile strength, F is the peak loading force, D and t are the diameter and thickness of the specimen, respectively. The tensile strength of anisotropic rocks under splitting tests cannot be obtained using this formula for the strict prerequisite. Thus, this formula is adopted in our study only to eliminate the influence of the diameter and thickness on the peak loading force, and the term ‘failure strength’ is more appropriate to describe the calculation results.

A summary of Brazilian test results of anisotropic rocks considering both the foliation-loading angle and orientation angle is given in Table 1. There are evident differences regarding the maximum failure strength of different rocks. Thus, the value of failure strength needs to be normalized for statistical analysis. The normalized failure strength (NFS,ζ) is defined as:

$$\zeta = \sigma_{{\theta |\alpha = {\text{c}}}} /\sigma_{{{\text{max}},\theta |\alpha = {\text{c}}}} \,{\text{or}}\,\zeta = \sigma_{{\alpha |\theta = {\text{c}}}} /\sigma_{{{\text{max}}, \, \alpha |\theta = {\text{c}}}}$$

(2)

where σ_θ|α=c is the failure strength of rock with different foliation-loading angle θ for a specific inclination angle, σ_α|θ=c is the failure strength of rock with different inclination angle α for a specific foliation-loading angle, σ_max,θ|α=c and σ_max,α|θ=c are the maximum failure strength for a specific inclination angle and specific foliation-loading angle, respectively.

Table 1 Failure strength of rock samples

The trends in the variation of NFS as a function of the loading-foliation angle or inclination angles (Figs. 4 and 5) reveal that the six patterns in Fig. 1 can all be found for specimen with different θ and α. For the same case, different rocks show different anisotropic behaviors. Taking specimens with α = 30° as examples, for ①,⑦,⑧ and ⑨ rocks, the strength remains constant when θ < 60° and then it decreases with the increase of θ; For ② rock, the NFS fluctuates slightly, which can be

Fig. 4

The trends in the variation of NFS as a function of the loading-foliation angle: a.α = 0°; b.α = 15°; c.α = 30°; d.α = 45°; e. α = 60°; f. α = 75°; g. α = 90°

Fig. 5

The trends in the variation of NFS as a function of the inclination angle: a. θ = 0°; b. θ = 15°; c. θ = 30°; d. θ = 45°; e. θ = 60°; f. θ = 75°; g. θ = 90°

regarded as a constant through the entire interval. For ③④⑤⑥ rock, the NFS increases non-linearly with the increase of θ.

Two anisotropic indices k₁ and k₂ are adopted to describe the transverse isotropy of rocks:

$$k_{{1}} = \sigma_{{{\text{min}},\alpha |\theta = {\text{c}}}} /\sigma_{{{\text{max}},\alpha |\theta = {\text{c}}}}$$

(3)

$$k_{{2}} = \sigma_{{{\text{min}},\theta |\alpha = {\text{c}}}} /\sigma_{{{\text{max}},\theta |\alpha = {\text{c}}}}$$

(4)

where σ_min,θ|α=c and σ_min,α|θ=c are the minimum failure strength for a specific inclination angle and specific foliation-loading angle, respectively.

The curves of k₂ can be divided into two types (Figs.6 and 7): (1) k₂ fluctuates near 1 with the increase of θ (① and ② rocks); (2) k₂ decreases non-linearly with the increase of θ (other rocks). However, the influence of α is more complicated, that is, the curves of k₁ has four types: (1) k₁ fluctuates near 1 with the increase of α (② rock); (2) k₁ increases non-linearly with the increase of α (⑦ rock); (3) k₂ decreases non-linearly with the increase of α(①③④⑤⑥rocks); (4)k₂ shows a reversed ‘‘U’’ shape distribution over the entire interval(⑧⑨rocks).

Fig. 6

Anisotropic index k₁

Fig. 7

Anisotropic index k₂

3 Engineering Overview

3.1 Engineering Background

China’s traffic network has been developing toward its southwestern area rapidly (Fig. 8). This area is affected by the collision and compression of the Indian and Eurasian plates and featured by complicated geological structures, largely distributed metamorphic rocks, et al. Asymmetric large deformation due to the combined action of high geo-stress field and asymmetric behaviors of surrounding rocks after tunnel excavation is frequently encountered (Fig. 9). Taking the railway from Chengdu to Lanzhou (the total length of line and tunnels are 430 km and 330 km, respectively) and the highway from Wenchuan to Maerkang (the total length of line and tunnels are 174 km and 87 km, respectively) as examples (Fig. 8), carbonaceous phyllite is widely distributed along these two lines. During the tunnel construction, large deformation (Tables 2 and 3) including concrete cracking and spalling, steel arch twist and extruded deformation of side walls puts severe threat to the tunnel safety. All failure phenomena of tunnel structures in these two lines revealed that the inclination angles of weak planes play an important role in controlling the occurring position of failure.

Fig. 8

Typical projects for lines with layered rock tunnels

Fig. 9

Asymmetric large deformation of layered rock tunnels

Table 2 Typical large deformation and surrounding rock characteristics of tunnels in Chengdu–Lanzhou railway

Table 3 Typical large deformation and surrounding rock characteristics of tunnels in Wenchuan–Maerkang Expressway

Fig. 10

Specimen preparation: a. The location of Chengdu–Lanzhou railway; b. The location of Mao county tunnel; c. Tunnel face; d. specimens sampling

3.2 Specimen Preparation

Phyllite specimens were obtained from the Maoxian tunnel, which is located on the railway from Chengdu to Lanzhou. First, cylindrical specimens with diameters of 50 mm were prepared. Then, disks with thickness of 25 mm were cut for the splitting tests (Fig. 10). The results of X-ray diffraction indicated that the main minerals in the phyllite specimens were orthoclase, laumontite, halite, quartz, illite, and plagioclase, which accounted for 68, 12.5, 11.6, 6.4, and 1.5% of the total mass, respectively, as illustrated in Fig. 11a. Well-developed foliation can be observed in the SEM images (Fig. 11b).

Fig. 11

Micro-features of phyllite. a X-ray diffraction results b SEM results

3.3 Experimental Process

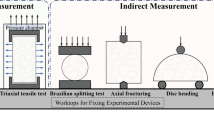
The layout of test devices is shown in Fig. 12a. The tests were conducted using a rock mechanics test system (Model MTS 815). A system for monitoring AE signals, manufactured by the American Physical Acoustic Corporation, was used during the experiment. The AE sensors were Mic 30 sensors that had a resonant frequency of 200 kHz and a recording frequency that ranged from 20 kHz to 1 MHz. Eight AE sensors were uniformly placed at two sides of the disk specimen, as shown in Fig. 12b. The detection threshold of the signal was 40 dB. The time parameters, i.e., peak definition time (PDT), hit definition time (HDT), and hit locking time (HLT), were 50, 200, and 300 s, respectively. For each specimen, the surfaces on which the AE sensors were installed were called surface B or C, and the lateral surface was called surface A.

Fig. 12

Experimental process: a. test apparatus; b. layout of specimens; c. loading cases

Due to the extremely low strength of weak planes, the specimen meeting the test requirement is hardly to get. Thus, only two foliation-loading angles, namely θ = 30°, 60°, were chosen to investigate the anisotropic behavior of phyllite in this test. Three specimens were used for each angle to accommodate outlier results. The loading process was conducted with an increasing axial load at a constant rate of 100 N/s until the specimens failed.

4 Test Results

4.1 Failure Strength

The failure strength is shown in Fig. 13 and Table 4. For α = 60°, the maximum average failure strength was 7.48 MPa when θ was 0°, and the strength decreased to the minimum value of 2.02 MPa at θ = 30°, then the strength increased to 5.7 MPa at θ = 60° and followed by a drop reaching 2.99 MPa at θ = 90°. The anisotropic index k₁ is 3.70 for this case. The trend in the variation of failure strength with foliation-loading angles didn’t fall into the category shown in Fig. 1. For α = 60°, the average failure strength shows a ‘U’ type distribution with the maximum and minimum value occurring at θ = 60° and 90°, respectively. The anisotropic index k₁ is 2.11, which is smaller than that of specimen at α = 60°.

Fig. 13

Strength of specimens: a. Stress–strain curves; b. the relation of failure strength and foliation-loading angle

Table 4 Strength of specimen

The curves also reveal that the strength scatters even for specimens with the same θ and α. For α = 60°, the difference between specimens with the same angle gets smaller with the increase of θ. While for α = 30°, the difference is relatively large for each θ.

4.2 Fracture Pattern

The fracture patterns were regarded as two-dimensional in former tests only considering the influence of foliation-loading angles. Three typical fracture patterns are summarized as layer activation failure, mixed failure, and non-layer activation failure (Fig. 2). Figure 14 displays the ultimate fracture patterns for specimens with different α and θ. It shows that the fracture pattern was essentially three-dimensional, in most cases being different on three surfaces of specimens. In this study, we follow the classification method describing the fracture pattern of each surface (Vervoort et al. (2014)) and nine kinds of patterns can be summarized (Table 5, note that the patterns are not divided strictly and there is a transition over different patterns):

• (1) Type I: layer activation at surface A and non-layer activation at surfaces B and C, such as specimen #1 with α = 30° and θ = 0°.

• (2) Type II: layer activation at surfaces A and B, non-layer activation at surfaces C, such as specimen #3 with α = 60° and θ = 30°.

• (3) Type III: layer activation at three surfaces, such as specimen #1 with α = 30° and θ = 0°.

• (4) Type IV: non-layer activation at three surfaces, such as specimen #2 with α = 30° and θ = 60°.

• (5) Type V: non-layer activation at surfaces A and B, layer activation at surface C, such as specimen #2 with α = 60° and θ = 60°.

• (6) Type VI: non-layer activation at surface A, layer activation at surfaces B and C, such as specimen #3 with α = 30° and θ = 45°.

• (7) Type VII: mixed activation at three surfaces, such as specimen #2 with α = 30° and θ = 45°.

• (8) Type VIII: mixed activation at surfaces A and B, and layer activation at surfaces C, such as specimen #3 with α = 60° and θ = 0°.

• (9) Type IX: mixed activation at surfaces A and B, and non-layer activation at surfaces C, such as specimen #3 with α = 60° and 60 = 0°.

Fig. 14

Fracture of specimens

Table 5 Cracking types

4.3 AE Features

The typical AE parameters and location of AE signals are important for understanding the fracture processes and failure modes of rocks. The AE data of eight sensors have a good consistency for most specimens. Therefore, data from one sensor were presented in this paper for analyzing the AE parameters. The locations of AE signals, AE hits, AE energy, AE frequency and AF-RA features were analyzed.

4.3.1 Location of AE Signals

The relative energy, emerging positions and orders of AE signals is displayed in Fig. 15 with view of X–Y plane, X–Z plane and 3D perspectives. Taking a part of specimens as examples, their specific features are described below.

Fig. 15

Location of micro-cracks

For #2 specimen with α = 30° and θ = 0° (view of X–Y plane), micro-cracks first scattered on and near weak planes at x = 0 along the loading direction. Then, micro-cracks with larger energy occurred around the central part of specimen. Finally, micro-cracks propagated along weak planes and formed a macro-crack. The view of X–Z plane shows that the AE signals concentrated within Z = −15 ~ 0 mm along the thickness direction and two micro-cracks formed across weak planes. The features of micro-cracks agreed well with the macro-fracture patterns. The macro-failure plane passing through one macro-crack on surface A and one macro-crack on surface B.

For #3 specimen with α = 60° and θ = 30° (view of X–Y plane), micro-cracks first occurred near the lower loading point and then appeared upward along the loading direction at X = 0. Then, two micro-crack aggregation zones became evident, one is near surface B with large energy and the axis of the zone intersected with weak planes, the other is near surface C with lower energy and the axis is parallel to weak planes. The view of X–Z plane shows that the micro-cracks near surface C distributed mainly along weak planes.

The energy accumulation characteristics of AE signals are evident in some case. For #3 specimen with α = 60° and θ = 45° or 60° (view of X–Y plane), AE signals with larger energy gathered at upper part of specimen and across weak planes, while AE signals with smaller energy gathered at lower part of specimen and along weak planes. In addition, most AE signals with lower energy appeared earlier than those with larger energy.

As a conclusion, weak planes have a dominant influence on fracture patterns of specimens, (1) In most cases, the macro-cracks propagated wholly or mainly along weak planes, so the AE signals appeared only within a small part along the thickness direction of specimen; (2) AE signals occurring in the rock matrix has larger energy than those appearing along weak planes; (3) In some cases, the AE signals have evident energy accumulation characteristics due to different fracture patterns in different location under the effect of weak planes.

4.3.2 AE Hits and Energy

Figures 16 and 17 display the relationship between the AE counts, AE energy, and strain for different specimens. The pattern of the AE count rate curve during the entire loading process can be divided into two groups:(1) P-I, exponential growth model, for which the AE signals emerged mostly near and after the peak strength point; (2) P-II, normal distribution model, the distribution of the AE count rate shows an inversed shoulder shape with peak point before or near the peak strength point. The pattern of the AE energy rate curve during the entire loading process can also be divided into two groups:(1) M-I, the peak distribution mode, which is the distribution of the AE energy rate presents 1, 2 or finite peak intervals near the peak strength point; and (2) M-II, the uniform distribution mode. That is, the distribution of the AE energy rate presents 1, 2 or finite peak intervals during the whole loading process. The modes of the AE characteristic curves (AE count rate curve and the energy rate curve, “curves” for simplicity) are summarized in Table 6. Note that the modes are not divided strictly and that there is a transition over the two modes.

Fig. 16

The relationship between the AE counts, AE energy, and strain for different specimens with α = 30°: a. θ = 0°; b. θ = 30°; c. θ = 45°; d. θ = 60°; e. θ = 90°

Fig. 17

The relationship between the AE counts, AE energy, and strain for different specimens with α = 60°: a. θ = 0°; b. θ = 30°; c. θ = 45°; d. θ = 60°; e. θ = 90°

Table 6 AE characteristic curves of specimens

Figures 16 and 17 and Table 6 show that the mode of curves is related to angles of specimens and the fracture patterns, and the following features can be drawn:

(1) In most cases, the first small peak point emerging at the transition position from the slow growth to the fast growth of stress, and the second peak point is located near the peak stress for AE count and energy curves.

(2) For specimen with α = 30°, AE count curve is P-I pattern when the cumulative energy is large (θ = 0°, 45°, 60°), indicating that damage occurs at the high-stress level after the specimens have accumulated sufficient energy and the specimen is more prone to brittle failure in this condition. AE count curve is P-II pattern when the cumulative energy is small, indicating that the micro-cracks occurred from the initial loading stage and propagated throughout the entire loading process, making the rock be more prone to plastic failure.

(3) For specimen with α = 60°, a transition exists from a unimodal distribution (θ = 0°) to a multimodal distribution (θ = 30° ~ 90°) for the AE energy rate curves. In addition, AE curve with a unimodal distribution has lower cumulative energy compared to other cases. The reason is that the macro-cracks of specimen with θ = 0° are mainly consisted of micro-cracks occurring on weak planes.

4.3.3 AF-RA Distribution

The density maps of AF (average frequency)-RA (rise-time amplitude) data were drawn to analyze the AF-RA distribution differences of specimens. The analysis results are shown in Figs. 18and 19, in which the white area has lower data density, and the purple area has higher data density. The data distribution changes from sparse to dense with the color changing from light purple to dark purple. The area inside the black square frame was the main data distribution area, and the pink dotted line (AF = 78.728RA + 54.293) was a reference line to determine the location of high-density core data area.

Fig. 18

The AF-RA distribution of different specimens with α = 30°: a. θ = 0°; b. θ = 30°; c. θ = 45°; d. θ = 60°; e. θ = 90°

Fig. 19

The AF-RA distribution of different specimens with α = 30°: a. θ = 0°; b. θ = 30°; c. θ = 45°; d. θ = 60°; e. θ = 90°

The AF of specimens mainly falls within 20 ~ 200 kHz and the value of RA is smaller than 1.5 ms/V in most cases. For specimens with α = 30°, the AF-RA data distributions were mostly in the rectangles with a long side along AF and short side along RA for θ = 45° ~ 90°. On the contrary, the AF-RA data distributions were mostly in the rectangles with a shorter side along AF and longer side along RA for θ = 0° ~ 30°. For specimens with α = 60°, the area of rectangles in which the AF-RA data mainly concentrated is largest for θ = 0° and smallest for θ = 30°, while the area is nearly the same for other angles.

4.3.4 AE Frequency

The distribution of AE frequencies of specimens is displayed in Figs.20 and 21 and has following features:

Fig. 20

The AE frequencies of different specimens with α = 30°: a. θ = 0°; b. θ = 30°; c. θ = 45°; d. θ = 60°; e. θ = 90°

Fig. 21

The AE frequencies of different specimens with α = 60°: a. θ = 0°; b. θ = 30°; c. θ = 45°; d. θ = 60°; e. θ = 90°

(1) The frequencies almost fell between 25 and 350 kHz.

(2) For specimen with α = 30°, the signals with lower frequency first occurred, then the signals with higher frequency emerged when the specimen reached its failure stage for θ = 0° ~ 45°. For θ = 60°, signals with lower and higher frequency emerged at the same loading stage. While for θ = 90°, signals with higher frequency emerged earlier than those with lower frequencies.

(3) For specimen with α = 60°, signals with lower and higher frequency emerged at the same loading stage for all cases. With the increase of θ, the difference between number of signals with lower frequency and that of signals with higher frequency got more notable.

The distribution characteristics of peak frequencies may be determined by the extension speed of cracking and the extension scale (including number and size of micro-cracks). The high extension speed and low extension scale of cracks will induce AE signals with high peak frequencies. Tensile cracking usually has a higher extension speed and lower extension scale than shear cracking (Du et al. 2020).

4.3.5 Classification of Tensile and Shear Cracks

The designated RA value and the average frequency, as depicted in Figs. 18 and 19, have extensive utility in ascertaining failure modes of rocks (Du et al. 2020). AE signals characterized by AF/RA ratio exceeding a certain threshold are classified as indicative of tensile cracks, while the inverse suggests shear types.

For α = 30°, the shear cracks outnumbered tensile cracks when θ = 0° ~ 15°, and the development trends of both types exhibited different trend. The tensile cracks showed a smooth increasing trend while the shear cracks underwent stepwise increase, showing that the cycles of energy accumulation and release for shear cracks were more evident than that of tensile cracks when shear cracks dominate the micro-cracking types. With the increase of θ, the tensile cracks outnumbered shear cracks and the development trends of both types exhibited a similar developmental trend. While for θ = 90°, the shear cracks outnumbered tensile cracks again due to many shear cracks occurred along weak planes.

For α = 60°, the tensile cracks outnumbered shear cracks when θ = 0° ~ 15° and shear cracks became dominant with the increase of θ, which agreed well with the macro-fracture patterns described in Sect. 4.2.

5 Numerical Simulation

To enhance our understanding of how crystal structures and weak structural planes affect rock strength, we introduced a novel modeling approach utilizing Neper and PFC3D software. By employing Voronoi tessellation within Neper, the method creates irregular polyhedra within a cylinder, which is then imported into PFC for detailed segmentation. In addition, flat-joint contact model is used as inter-grain contact and smooth-joint contact is used as intra-grain contact and weak plane contact (Fig. 22d).

Fig. 22

Numerical model: a. Envelope strength of FJM; b. Envelop strength of smooth joint model; c. Voronoi tessellations applied to modeling; d. details of specimens

5.1 Introduction of Key Elements

5.1.1 (1) Flat Joint Model

The flat-joint contact model (Potyondy 2012; Fig. 22a) provides the macroscopic behavior of a finite-size, linear elastic, and either bonded or frictional interface that may sustain partial damage. A flat-joint can be installed when the gap of particles less or equal to the installation gap (g). The installation gap is defined as the multiplication of the installation gap ratio (g_ratio) and the minimum radius of the pairwise connecting particles:

$$g\, = \,g_{{{\text{ratio}}}} {\text{min}}\left( {R_{{1}} ,R_{{2}} } \right)$$

(5)

A larger g_ratio leads to larger coordination number (CN) value, which indicates more contacts for each particle.

The interface of pairwise connecting particles is discretized into elements. The number of elements is N_r N_a (N_r are the number of elements in radial and N_a are the number of circumferential directions). Each element is either bonded or unbonded, and the breakage of each bonded element contributes partial damage to the interface. The behavior of a bonded element is linear elastic until the tensile or shear strength limit is exceeded and the bond breaks:

$$\sigma^{\left( e \right)} \le \overline{\sigma }_{b}$$

(6)

$$\tau^{\left( e \right)} = \overline{c}_{b} - \sigma^{\left( e \right)} \tan \left( {\overline{\phi }_{b} } \right)$$

(7)

When the shear force does not exceed the Mohr–Coulomb envelope, the mechanical behavior of an unbonded element is linear elastic and frictional.

$$\tau^{\left( e \right)} = - \mu \sigma^{\left( e \right)}$$

(8)

The force–displacement law of flat-joint element updates the element force and moment (${\mathbf{F}}^{\left( e \right)}$ and ${\mathbf{M}}^{\left( e \right)}$) and changes the element bond state. The force and moment calculated as follows:

$${\mathbf{F}}^{(e)} = - F_{n}^{\left( e \right)} {\hat{\mathbf{n}}}_{c} + {\mathbf{F}}_{s}^{\left( e \right)}$$

(9)

$${\mathbf{M}}^{\left( e \right)} = - M_{t}^{\left( e \right)} {\hat{\mathbf{n}}}_{c} + {\mathbf{M}}_{b}^{\left( e \right)}$$

(10)

where $F_{n}^{\left( e \right)}$ and ${\mathbf{F}}_{s}^{\left( e \right)}$ are the normal force and shear force vector of each element, respectively; ${\hat{\mathbf{n}}}_{c}$ represent the normal direction of the contact plan; $M_{t}^{\left( e \right)}$ is the twisting moment and a simplifying assumption gives $M_{t}^{\left( e \right)} \equiv 0$;${\mathbf{M}}_{b}^{\left( e \right)}$ represents the bending moment vector.

Moreover, there are three types of flat-joint contacts. Type B represents the contact in bonded state. Type G denotes the contact in unbonded state, including gapped, and type S denotes the slit contact. The proportion of each contact type can be adjusted by changing the value of $\varphi_{B}$, $\varphi_{G}$ and $\varphi_{S}$($\varphi_{B} + \varphi_{G} + \varphi_{S} = 1$).

5.1.2 (2) Smooth Joint Model

The smooth joint model (Pierce et al. 2007) simulates the behavior of a planar interface, where particles located at opposite ends of the plane are able to pass through each other along the plane with dilation. The contact parameters of the smooth joint model are assigned to all contacts traversed by the joint plane.

Similar to flat-joint model, the behavior of the bonded interface is linearly elastic until the strength limit is exceeded and the bond breaks. The force–displacement law for the smooth joint model is calculated as:

$${\mathbf{F}} = - F_{n} {\mathbf{n}}_{j} + {\mathbf{F}}_{s}$$

(11)

where ${\mathbf{F}}$ denotes the force vector, $F_{n}$ is the normal force and ${\mathbf{n}}_{j}$ denotes the normal direction of joint plane;${\mathbf{F}}_{s}$ is the shear force vector. If the smooth joint is unbonded, the ${\mathbf{F}}_{s}$ is calculated as:

$${\mathbf{F}}_{s} = \left\{ {\begin{array}{*{20}c} {{\mathbf{F}}_{s}^{*} } & {\left\| {{\mathbf{F}}_{s}^{*} } \right\| \le F_{s}^{\mu } } \\ {F_{s}^{\mu } ({\mathbf{F}}_{s}^{*} /\left\| {{\mathbf{F}}_{s}^{*} } \right\|} & {otherwise} \\ \end{array} } \right.$$

(12)

where $F_{s}^{\mu }$ is the frictional shear strength limit ($F_{s}^{\mu } = - \mu F_{n}$).

While slip state is true, shear displacements produce an increment in normal force due to dilation:

$$\Delta F_{n} = \left( {\frac{{\left\| {{\mathbf{F}}_{s}^{*} } \right\| - F_{s}^{\mu } }}{{k_{s} }}} \right)k_{n} \tan \psi$$

(13)

where $\mu$ is the friction coefficient, $\psi$ is the dilation angle.

If the smooth joint is bonded, when $F_{n} \ge \sigma_{c} A$, the bonded contact is broken in tension, and if $\left\| {{\mathbf{F}}_{s}^{*} } \right\| > \tau_{c} A$,the bonded contact is broken in shear. $\sigma_{c}$ is the normal strength and $\tau_{c}$ is the bond shear strength, which is calculated as:

$$\tau_{c} = c - \left( {\frac{{F_{n} }}{A}} \right)\tan \phi$$

(14)

5.1.3 (3) Brief Introduction of Neper

Neper creates polycrystalline structures using Voronoi tessellations that consist of convex cells in the spatial domain (Quey et al. 2011). The Voronoi tessellation of 3D space is a collection of 3D entities that fill the space with no overlaps and gaps These polycrystals are typically modeled as tessellations in a vector format, utilizing vertices, edges, faces, and polyhedra (or "cells"), where the cells are usually convex. This “CAD-Type” geometric representation supports the simulation of various polycrystalline microstructures and is compatible with conventional meshing techniques. The tessellation models range from single-scale types suitable for depicting straightforward polycrystals, to multi-scale types designed for detailed representation of polycrystalline microstructures with features within cells or grains (Fig. 22c).

5.2 Modeling Process

The detailed generation process of numerical model is illustrated in Fig. 23: (1) Generated an initial particle-based cylindrical model; (2) Generate Voronoi tessellation of cylinder in Neper; (3) Import the model tessellated by Neper into PFC as geometry information; (4) Utilize geometry information to group particles of an initial cylindrical model; (5) assign flat-joint contact model to same group of particles and assign smooth joint contact model to different group of particles; (6) Generate bedding plane and assign smooth joint contact model for contacts located on the bedding plane.

Fig. 23

Modeling process: a. Initial sample; b. Tessellation in Neper; c. Import as geometry; d. Croup the particles; e. Assign contact for grains; f. Assign contact for bedding planes

5.3 Parameters Calibration

The micro-parameters of FJM and SJM are calibrated by the results of triaxial tests and Brazilian splitting tests with various loading-foliation angles and inclination angles. The specific calibration steps are shown in Fig. 24:

Fig. 24

Flowchart of calibration

6 Determining deformation parameters of DEM model through triaxial compression test results

(a) When θ = 0°and α = 0°, the stiffness of foliation planes has the least influence on Young’s modulus of the specimen. So the stiffness of FJM for intra-grain (normal and shear stiffness $\overline{k}_{n}^{g}$, $\overline{k}_{s}^{g}$) and SJM for inter-grain ($k_{n}^{g}$,$k_{s}^{g}$), and the stiffness of particles (normal and shear stiffness $k^{n}$,$k^{s}$) can be used to match the E₀ (Young’s modulus of triaxial compression test for θ = 0°and α = 0°).

(b) When θ = 90°and α = 0°, the stiffness of bedding plane SJM (normal and shear stiffness $k_{n}^{b}$,$k_{s}^{b}$) can be calibrated based on E₉₀ (Young’s modulus of triaxial compression test for θ = 90°and α = 0) for the stiffness of foliation plane has the largest impact on the rock.

7 Determining strength parameters of DEM model using Brazilian test results

(a) When θ = 90°and α = 0°, the strength parameters of FJM for intra-grain and SJM for inter-grain are determined based on σ_90,0 (strength of Brazilian test for θ = 90°and α = 0) for the strength of bedding plane has the least influence on the strength of rock.

(b) When θ and α are arbitrary angles, the strength of foliation significantly affects the strength of the rock, so the strength parameters of SJM for bedding plane are calibrated based on the strengths at multiple angles obtained from laboratory tests.

The calibrated micro-parameters of FJM and SJM are shown in Tables 7 and 8, respectively. The comparative results are displayed in Figs.25 and 26. The simulated failure strengths are in good agreement with test results for specimens with α = 60°. While for specimens with α = 30°, the trend between numerical results and test results is the same, while the difference in strength when θ = 0° and θ = 60° is relatively large.

Table 7 Micro-parameters of FJM

Table 8 Micro-parameters of SJM

Fig. 25

Failure strength of numerical simulation in comparison with laboratory tests

Fig. 26

Fracture patterns of numerical simulation in comparison with laboratory tests: a. specimens with α = 30°; b. specimens with α = 60°

Figure 26 displays fracture patterns of numerical simulation in comparison with laboratory tests. The location and direction of fractures obtained through test and numerical simulation are closely matched, and the orientation of fracture growth is consistent with the foliation planes. The movement direction of particles on opposite sides of the fracture plane is related to fracture pattern. The directions of velocity field on two sides of fracture surfaces are nearly perpendicular or parallel when θ = 0° and θ = 60° or θ = 30° ~ 45°, respectively. In addition, when θ varies between 30° and 60°, the velocity field shows a clear layering feature, with the velocity on the left side of fracture becoming progressively smaller from top to bottom, while the velocity on the right side of fracture becomes progressively larger from top to bottom. When θ = 90°, the maximum velocity occurs at the top and bottom, while the velocity of particles at middle part is the smallest. When θ = 0°, the particle velocity distribution is different for α = 30° and α = 60°, that is, the maximum velocity at α = 30° occurs in the middle of specimen, whereas the velocity is smaller in the middle portion and larger on the left and right sides at α = 60°.

7.1 Discussion

7.1.1 (1) Effects of Both the Orientation and Loading Angle

After the reliability of numerical model was verified, more cases not covered by laboratory tests were simulated and analyzed to get a full insight into the anisotropic characteristics of phyllite under Brazilian tests. In this simulation, α covers a range of 15° ~ 90° at intervals of 15°, and θ covers a range of 0° ~ 90° at intervals of 15°.

The variation trends of failure strength versus α and θ are illustrated in Fig. 27. The 3D surface of strength was fitted based on the simulation results, as shown in Fig. 27a. Figure 27b shows the variation of strength as a function of θ. For α = 15° ~ 60°, the curve shape can be categorized into Pattern VI (Fig. 1), that is, the strength remains unchanged when θ ≥ 30°, while it undergoes a rapid increase with the further decrease in θ. For α = 75° ~ 90°, the curve shape can be categorized into Pattern V (Fig. 1), that is, the strength shows a ‘‘U’’ shape distribution over the entire interval, and the maximum value occurs at θ = 0°, while the minimum value occurs at θ = 20°–30°.

Fig. 27

Failure strength of specimens: a. contour of failure strength; b. the variation of strength as a function of loading-foliation angles; c. the variation of strength as a function of orientation angles

For θ = 0° or 90°, the strength shows a ‘‘U’’ shape distribution with maximum value occurring at α = 0° or 90° and the minimum value occurring at α = 45° or 60°. For θ = 30°, the curve shape can be categorized into Pattern III (Fig. 1), that is, the failure strength approximately decreases linearly with the increase of α. For θ = 45° ~ 75°, the strength fluctuates when α > 45°, then it undergoes a rapid increase with the further decrease in α.

7.1.2 (2) Fracture Pattern

When the normal or shear stress of a contact exceeds its tensile or shear strength, the contact breaks and a micro-crack is generated. There are six types of micro-cracks including intra-grain shear crack (IGSC), intra-grain tensile crack (IGTC), grain-boundary shear crack (GBSC), grain-boundary tensile crack (GBTC), shear crack on bedding planes (BPSC), and tensile crack on bedding planes (BPTC) may form in our numerical model. Figures 28 shows the distribution of various types of cracks in specimens. Most of the produced cracks are along bedding planes and shear cracks dominate. When θ = 0°, the number of penetrating cracks increases as α increases. The number of cracks is significantly less than other angles when θ is in the range of 30–60°. The maximum number of penetrating macro-cracks occurs at θ = 75° and α = 30°. When θ is small, the macro-cracks mainly appear in the middle part of specimen. As θ gradually increases, the macro-cracks are mainly distributed at the top and bottom ends of specimen.

Fig. 28

Fracture patterns and distribution of various cracking types

The percentage of cracks for each specimen is shown in Fig. 29. Cracks on bedding plane are dominant and shear cracks on bedding planes have the largest proportion. The proportion of crack on bedding planes increases first and then decreases with the increase of θ, while the proportion of grain-boundary crack and intra-grain crack decreases with the increase of θ. When θ is in the range of 30–60°, the proportion of grain-boundary crack and intra-grain crack is below 5% and 10%, respectively. For θ = 0°, the percentage of intra-grain crack decreased while the percentage of tensile cracks on bedding plane increased as the α increased. For specimen with θ = 15° and α = 90°, the shear crack on bedding plane has the largest proportion with value of 95%, and the tensile crack on bedding plane is close to 0%, indicates that the specimen fails due to shear failure along bedding planes.

Fig. 29

Percentage of cracks:. α = 15°; b. α = 30°; c. α = 45°; d. α = 60°; e. α = 75°; f. α = 90°

7.1.3 (3) Failure Process

To further understand the influence of bedding planes and grains on rock failure, three specimens under Brazilian tests were selected for analysis, which are specimen with θ = 45° and α = 0°, specimen with θ = 30° and α = 75° and specimen with θ = 90° and α = 90°, respectively. The stress–strain curves are shown in Figs. 30, 31 and 32. Key points (a, b, c and d) and their corresponding cracking features are displayed. In addition, final cracks at three sections A, B and C (B represents the middle section along the thickness direction of the sample, and A, C represent the Sects. 10 mm before and after the B section, respectively) are also given.

Fig. 30

Failure process of specimen with $\alpha = 45^\circ$ and $\theta = 0^\circ$

Fig. 31

Failure process of specimen with $\alpha = 30^\circ$ and $\theta = 75^\circ$

Fig. 32

Failure process of specimen with $\alpha = 90^\circ$ and $\theta = 90^\circ$

For specimen with θ = 45° and α = 0°, there are a few shear cracks on bedding plane formed at loading point a, and they propagated toward to the top and bottom loading planes. When the specimen is loaded to point b, tensile cracks on bedding planes occurred, and shear cracks along bedding planes penetrated the sample to form a macro-crack in the middle of the specimen. With further increase of the axial loading stress from point b to point c, shear cracks propagated along and across bedding planes, and the intra-grain cracks and inter-grain cracks emerged. During the post-peak stage, the growth rate of tensile cracks and shear cracks on bedding planes slowed down, and cracks in rock matrix began to appear in an accelerated speed. Also, the inter-grain cracks and intra-grain cracks were mainly concentrated in the upper front and lower back of the specimen.

For specimen with θ = 30° and α = 75°, at point a, shear cracks along bedding planes appeared at the bottom and top of the specimen. From point a to point b, shear cracks continued to propagate though the rock, and tensile cracks along bedding planes began to appear. When the specimen is loaded from point b to point c, micro-cracks in grains began to appear in a small amount, centralized in the middle section of the top and bottom of specimen. At point d, shear cracks and tensile cracks along bedding planes in the front and back of the upper and lower parts finally propagated across the specimen and formed a penetrating macro-crack, and tensile cracks along bedding planes were mainly concentrated at both ends of weak planes, while grain-boundary cracks and intra-grain cracks are invisible. In addition, the growth rate of shear cracks and tensile cracks along bedding planes did not slow down in the post-peak stage. In other words, the strength of specimen is controlled by the strength of bedding planes, and the strength of grains has less influence on the failure of specimen in this case.

For specimen with θ = 90° and α = 90°, when the specimen is loaded from point a to point b, shear cracks along bedding planes began to occur in large quantities at the bottom and top of specimen. Afterward, from point b to point c, shear cracks and tensile cracks along bedding planes gathered at the top and bottom region of specimen and formed macro-cracks. During the post-loading stage, some grain-boundary cracks and intra-grain cracks began to appear at the top of the specimen without continuing to propagate downward, indicating that crushing failure occurred at the top area.

8 Conclusions

In this article, the influence of foliations on the mechanical behaviors of phyllite in three-dimensional (3D) space under Brazilian test conditions is studied through laboratory tests and numerical simulations using a new numerical model considering the crystal structures and weak structural planes of phyllite based on the particle discrete element method (PDEM). Following conclusions can be drawn:

(1) Based on the Brazilian test results of nine kinds of anisotropic rocks in 3D space, the patterns regarding the relationship between the normalized failure strength (NFS) or anisotropic index and fabric-loading angles or orientation angles are obtained.

(2) The failure strength of specimens, the temporal distributions of the AE counts and AE energy were closely related to their fracture patterns and the areas of their fracture surfaces, nine macro-fracture patterns and two distribution patterns of AE signals were obtained.

(3) The distribution of micro-cracks has evident accumulation features due to the effect of foliations and the proportion of shear cracks and tensile cracks are influenced by the loading-foliation angles and inclination angles.

(4) The calibrated results of phyllite agreed well with the experimental results with regards to failure strength and fracture patterns. During failure process, the intra-grain cracks and inter-grain cracks mainly occurred at the plastic loading stages, and shear cracks along weak planes dominated.