1 Introduction

Due to various geological, physical, and chemical processes, rock masses often exhibit extensive and intricate fractures and discontinuities. The mechanical and hydraulic properties of rock masses are then significantly impacted by the nature and characteristics of the discontinuities, which could further influence the behavior of geotechnical engineering systems such as rock slopes and rock tunnels (e.g., Priest and Hudson 1976; Vyazmensky et al. 2010; Wu and Kulatilake 2012; Zhou et al. 2023). In practice, measuring the intricate and random discontinuities within rock masses is not a trivial task, making the accurate and quantitative mapping of rock discontinuities a persistent challenge in this field. In an effort to represent the spatial distribution of rock discontinuities, current practices often rely on constructing a three-dimensional (3D) discrete fracture network (DFN), utilizing limited measurements of the visible discontinuities at rock outcrops. In simpler terms, the shape, extent, and other significant features of the discontinuities within the rock masses are then estimated based on these limited measurements. As a result, the selection of an appropriate model to describe the DFN of a rock mass is a crucial factor in ensuring the reliability of slope seepage and stability analyses that involves rock mass discontinuities.

In the literature, studies on computational methods for representing rock discontinuities through the creation of a 3D DFN have been widely conducted, with a significant number of these studies relying on the Baecher circular disc model (Baecher 1983). Despite its popularity, due to its ease of mathematical representation and quick computation (e.g., Liu et al. 2015; Zhan et al. 2017), the Baecher disc model has limitations in simulating slender fractures or joints with complex shapes (e.g., Guo et al. 2020; Zheng et al. 2022). As a result, it may not be suitable for addressing complex geotechnical engineering challenges. To alleviate these limitations, various models have been proposed in the literature, including the parallelogram-based model by Warburton (1980), the polygon-based model by Dershowitz and Einstein (1988) and the rectangle-based model proposed by Decker et al. (2006) for sedimentary rocks. To make the DFN closer to the engineering reality, a method of replacing the disc with the polygon was also proposed by Xu and Dowd (2010). These models offer more flexibility in simulating the complex shapes of rock fractures, but they also have their own limitations and ambiguities, such as the difficulty in choosing the appropriate type of polygon-based model. In a nutshell, both the Baecher disc model and polygon-based model have limitations in realistically representing the complex shapes of rock fractures.

On the other hand, Ivanova et al. (2014) developed a new method for modelling of rock fracture systems with the GEOFRAC three-dimensional stochastic model. With the enhanced GEOFRAC model and MATLAB-based Monte-Carlo Simulation (MCS) program FRACSIM, the applicability of the method was demonstrated. In addition, Zhang et al. (2002) proposed an ellipse-based model in simulating the DFN of rock masses. Jin et al. (2014) further adapted the ellipse-based model to simulate the occurrence of rock discontinuities. Recently, Guo et al. (2020), Zheng et al. (2022), and Guo et al. (2023) developed a new model called the universal elliptical disc (UED) model. The UED model that treats the ratio of major axis to minor axis and rotation angle as uncertain parameters, have been demonstrated to be effective in representing realistic rock fractures. However, the UED model is not widely used in slope engineering practice yet.

In this paper, a framework was proposed for integrating the UED model into 3DEC to construct a more realistic 3D DFN of rock masses for improved stability analysis of jointed rock slopes. The effectiveness of the proposed framework is demonstrated using a rock slope case in Zhejiang Province, China, and the effects of several key parameters in the UED model, including the ratio of major axis to minor axis, rotation angle, and discontinuity density, are investigated through a comparative study with the conventional Baecher disc model. The results show that the proposed framework improves the understanding on the interactive effects of the UED model parameters and discontinuity density on the rock slope stability, and highlight the need for adopting the UED model in constructing realistic DFNs for rock slopes.

2 Universal Elliptical Disc (UED) Model

The conventional Baecher circular disc models originally proposed by Baecher (1983) were formulated based on the size, azimuth, and density characteristics of discontinuities. Specifically, the centroid location, diameter, dip direction, dip angle and discontinuity density are among the important parameters considered in the Baecher disc models. The UED model shares similarities with the conventional Baecher disc model in which the size, azimuth and density of rock fracture discontinuity are important parameters. In this regard, the foundation for the UED model adopted in this paper is established by the principles and findings related to the conventional Baecher disc model. However, the UED model goes beyond the conventional Baecher disc model by including three additional parameters, namely the length of major axis, the ratio of major axis to minor axis and the rotation angle. These added parameters provide the UED model with greater flexibility in representing complex rock fracture topologies (e.g., Guo et al. 2020; Zheng et al. 2022). Figure 1 summarizes the implementation procedures to characterize the DFN models of jointed rock masses using the UED model, which consist of four major steps. Details of the principles and steps illustrated in the figure are described in subsequent sections of the paper.

Fig. 1
figure 1

A summary of the procedure to characterize the DFN models of jointed rock masses using the UED model

Full size image

2.1 Identification and Construction of Equivalent Fracture Planes

The discontinuities in the jointed rocks masses are often three-dimensional and have complex shapes. In some cases, the vertices of a discontinuity surface may not be coplanar, making it necessary to project the vertices onto an optimized two-dimensional (2D) plane before constructing a DFN using the UED model (Guo et al. 2020). This is because the UED model assumes that all fracture surfaces are planar.

Considering a rock slope with q visible discontinuity polygon surfaces, each of which contains n visible vertices at the rock outcrops, the coordinates of the n vertices of the i-th discontinuity polygon surface can be expressed as Pi: V1 (x1, y1, z1), V2 (x2, y2, z2), …, Vn (xn, yn, zn), i = 1, 2, …, q. Following this, the 2D fracture plane in space is optimized by minimizing the sum of the Euclidean distances between the n vertices and this 2D fracture plane. A simplified method is then developed to check whether the 2D fracture plane is a convex or concave polygon and compute its centroid coordinates, (xm, ym, zm). The line segment composed of every two adjacent vertices of the fracture plane is regarded as a vector. In this way, n vectors, \(\overrightarrow {{V_{1} V_{2} }}\), \(\overrightarrow {{V_{2} V_{3} }}\), …, \(\overrightarrow {{V_{n} V_{1} }}\) are obtained. The cross products between any two vectors are then calculated. The fracture plane is deemed as a convex polygon if all cross products have the same sign. Otherwise, it is a concave polygon (Marschner and Shirley 2015). As for the convex polygon, the centroid coordinates (xm, ym, zm) can be evaluated as

$$\left\{ {\begin{array}{*{20}c} {x_{m} = \frac{1}{n}\sum\nolimits_{i = 1}^{n} {x_{n} } } \\ {y_{m} = \frac{1}{n}\sum\nolimits_{i = 1}^{n} {y_{n} } } \\ {z_{m} = \frac{1}{n}\sum\nolimits_{i = 1}^{n} {z_{n} } } \\ \end{array} } \right.$$
(1)

As for the concave polygon, the fracture polygon needs to be first triangulated. Then, the centroid coordinates for each triangle are estimated. The centroid coordinates of the concave polygon are equal to the weighted average of the centroid coordinates across all triangles as follows:

$$\left\{ {\begin{array}{*{20}c} {x_{m} = \frac{{\sum\nolimits_{i = 1}^{j} {A_{i} x_{pi} } }}{{\sum\nolimits_{i = 1}^{j} {A_{i} } }}} \\ {y_{m} = \frac{{\sum\nolimits_{i = 1}^{j} {A_{i} y_{pi} } }}{{\sum\nolimits_{i = 1}^{j} {A_{i} } }}} \\ {z_{m} = \frac{{\sum\nolimits_{i = 1}^{j} {A_{i} z_{pi} } }}{{\sum\nolimits_{i = 1}^{j} {A_{i} } }}} \\ \end{array} } \right.$$
(2)

where j is the number of discretized triangles; Ai is the area of the i-th triangle; (xpi, ypi, zpi) are the centroid coordinates of the i-th triangle.

Thereafter, the matrix H0 that expresses the coordinates of the n vertices with respect to the centroid of the fracture polygon can be computed as follows:

$${\varvec{H}}_{{0}} { = }\left[ {\begin{array}{*{20}c} {x_{1} - x_{m} } \\ {x_{2} - x_{m} } \\ \ldots \\ {x_{n} - x_{m} } \\ \end{array} \, \begin{array}{*{20}c} {y_{1} - y_{m} } \\ {y_{2} - y_{m} } \\ \ldots \\ {y_{n} - y_{m} } \\ \end{array} \, \begin{array}{*{20}c} {z_{1} - z_{m} } \\ {z_{2} - z_{m} } \\ \ldots \\ {z_{n} - z_{m} } \\ \end{array} } \right]$$
(3)

To optimize the 2D fracture plane as described in Guo et al. (2020), the singular value decomposition method is adopted to factorize the matrix H0 as follows:

$${\varvec{H}}_{0} = {\varvec{U}}\Sigma {\varvec{V}}^{{\text{T}}}$$
(4)

In this way, U being a n × n unitary matrix, V being a 3 × 3 unitary matrix, and \({{\varvec{\Sigma}}}\) being a n × 3 diagonal matrix are obtained. The unitary matrix V is then multiplied by a unit column vector (0, 0, 1)T to obtain the normal vector n of the projected plane in a 3D space as follows (Strang 2016):

$${\varvec{n}} = {\varvec{V}}\left[ {\begin{array}{*{20}c} 0 \\ 0 \\ 1 \\ \end{array} } \right]$$
(5)

After obtaining the normal vector n = (a, b, c), the projection of the n vertices can be carried out. Since the line segment between a vertex (x, y, z) and the corresponding vertex \((x^{\prime},y^{\prime},z^{\prime})\) after projection is in parallel with the normal vector n, a proportional relationship can be derived as

$$\frac{{x^{\prime} - x}}{a} = \frac{{y^{\prime} - y}}{b} = \frac{{z^{\prime} - z}}{c} = t$$
(6)

Alternatively, Eq. (6) can be reformulated as

$$\left\{ {\begin{array}{*{20}c} {x^{\prime}_{i} = x_{i} + at} \\ {y^{\prime}_{i} = y_{i} + bt} \\ {z^{\prime}_{i} = z_{i} + ct} \\ \end{array} } \right.$$
(7)

where \((x_{i} ,y_{i} ,z_{i} )\) are the coordinates of an arbitrary vertex on the i-th fracture polygon, and \((x^{\prime}_{i} ,y^{\prime}_{i} ,z^{\prime}_{i} )\) are the coordinates of the companion vertex after projection. The parameter t can be computed as (Strang 2016)

$$t = \frac{{a(x_{m} - x_{i} ) + b(y_{m} - y_{i} ) + c(z_{m} - z_{i} )}}{{a^{2} + b^{2} + c^{2} }}$$
(8)

After processing all vertices following Eqs. (6) to (8), a new matrix H1 that represents the coordinates of the projected vertices can be obtained as

$${\varvec{H}}_{1} = \left[ {\begin{array}{*{20}c} {x^{\prime}_{1} } & {y^{\prime}_{1} } & {z^{\prime}_{1} } \\ {x^{\prime}_{2} } & {y^{\prime}_{2} } & {z^{\prime}_{2} } \\ \cdots & \cdots & \cdots \\ {x^{\prime}_{n} } & {y^{\prime}_{n} } & {z^{\prime}_{n} } \\ \end{array} } \right]$$
(9)

After that, the optimized fracture plane in a 3D space can be further converted to the xoy plane. This conversion starts from computing the parameters \(\delta\) and \(\theta\) as follows when c < 0 and n = (− a, − b, − c):

$$\left\{ \begin{gathered} \delta = \arctan \left( {\frac{{\sqrt {a^{2} + b^{2} } }}{c}} \right) \hfill \\ \theta = \arctan \left( \frac{b}{a} \right) \hfill \\ \end{gathered} \right.$$
(10)

To represent the coordinates in the polar coordinate system, the parameters \(\delta\) and \(\theta\) are further converted into α and β as follows:

$$\left\{ \begin{gathered} \alpha = \left\{ {\begin{array}{*{20}l} {2\uppi - \theta \, (a \ge 0,b \ge 0)} \hfill \\ { - \theta \, (a \ge 0,b < 0)} \hfill \\ {\uppi - \theta { (}a < 0,b < 0 \, or \, a < 0,b \ge 0{) }} \hfill \\ \end{array} } \right. \hfill \\ \beta = \delta \hfill \\ \end{gathered} \right.$$
(11)

Figure 2 illustrates the conversion of the coordinates. First, based on Fig. 2(a), the 2D fracture plane in a 3D space is first rotated with respect to the z-axis by a degree of α in the anti-clockwise direction, and a new matrix \(\varvec{H^{\prime}_{1}}\) can be obtained as

$$\varvec{H^{\prime}_{1}} = \left[ {\begin{array}{*{20}c} {\cos \alpha } & { - \sin \alpha } & 0 \\ {\sin \alpha } & {\cos \alpha } & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]{\varvec{H}}_{1}^{T}$$
(12)
Fig. 2
figure 2

Illustrations of the coordinate transformation from the three-dimensional discontinous planes to the two-dimensionl discontinous planes

Full size image

At the end of this operation, the normal vector n of the converted 2D fracture plane is on the xoz plane. In the next step, the resulting plane is rotated with respect to the y-axis by a degree of β in the clockwise direction, and another matrix \(\varvec{H^{\prime\prime}_{1}}\) can be obtained as

$$\varvec{H^{\prime\prime}_{1}} = \left[ {\begin{array}{*{20}c} {\cos \beta } & 0 & { - \sin \beta } \\ 0 & 1 & 0 \\ {\sin \beta } & 0 & {\cos \beta } \\ \end{array} } \right]\varvec{H^{\prime}_{1}}$$
(13)

Finally, the resulting normal vector n coincides with the z-axis, implying that the converted 2D fracture plane is on the xoy plane. After these two rounds of coordinate transformation, the values corresponding to the z-axis in the matrix \(\varvec{H^{\prime\prime}_{1}}\) are deterministic and known. The corresponding row in \(\varvec{H^{\prime\prime}_{1}}\) can be removed without affecting the subsequent calculations, and a simplified matrix H2 that represents the final coordinates of the vertices on the xoy plane can be expressed as

$${\varvec{H}}_{2} = \left[ {\begin{array}{*{20}c} {x^{\prime\prime}_{1} } & {x^{\prime\prime}_{2} } & \ldots & {x^{\prime\prime}_{n} } \\ {y^{\prime\prime}_{1} } & {y^{\prime\prime}_{2} } & \ldots & {y^{\prime\prime}_{n} } \\ \end{array} } \right]$$
(14)

In the last step, the final coordinates of the vertices are sorted sequentially in the clockwise or anti-clockwise directions as A1 (x1, y1), A2 (x1, y1), …, An (xn, yn), and the Shoelace theorem is employed to calculate the area, SP, of fracture plane as follows (Stewart 2015):

$$S_{P} = \frac{{1}}{{2}}\left| {\sum\limits_{i = 1}^{n - 1} {(x_{i} y_{i + 1} - y_{i} x_{i + 1} )} - (x_{1} y_{n} - y_{1} x_{n} )} \right|$$
(15)

2.2 Determination of the Optimal Ellipse Parameters

The objective of the proposed framework is to realistically depict the rock fractures using ellipses. As shown in Fig. 3, the process starts with aligning the center of a fracture polygon with the center of an ellipse with the same area. In this step, the model parameters that determine the geometry of the ellipse include: the length of major axis e, the length of minor axis f, the ratio of major axis to minor axis k, the semi-latus rectum g and the rotation angle γ. Specifically, the rotation angle γ is the angle between the semi-major axis above the x-axis and the positive x-axis in an anti-clockwise direction, see Fig. 3(b), and has a value between 0 and π. Mathematically, the values of e, f and g can be calculated as follows:

$$\left\{ \begin{gathered} e = \sqrt {\frac{{4kS_{E} }}{\uppi }} \hfill \\ f = \frac{e}{k} \hfill \\ g = \frac{1}{2}\sqrt {e^{2} - f^{2} } \hfill \\ \end{gathered} \right.$$
(16)

where SE is the area of the ellipse. Following the notations explained earlier, the centroid coordinates \(\left( {x^{\prime}_{m} ,y^{\prime}_{m} } \right)\) of the converted fracture plane can also be calculated using Eqs. (1) or (2).

Fig. 3
figure 3

Fitting of a real facture polygon using an ellipse with an arbitrary rotation angle γ

Full size image

To realistically resemble the shape of a real fracture plane, the centroid of an ellipse is first aligned with the centroid of the fracture polygon as shown in Fig. 3. After the matrix H2 obtained through Eq. (14) is processed by removing its centroid coordinates, a new matrix H3 that represents the coordinates of the vertices with respect to the origin of the xoy plane can be obtained as

$${\varvec{H}}_{3} = \left[ {\begin{array}{*{20}c} {x^{\prime\prime}_{1} - x^{\prime}_{m} } & {x^{\prime\prime}_{2} - x^{\prime}_{m} } & \ldots & {x^{\prime\prime}_{n} - x^{\prime}_{m} } \\ {y^{\prime\prime}_{1} - y^{\prime}_{m} } & {y^{\prime\prime}_{2} - y^{\prime}_{m} } & \ldots & {y^{\prime\prime}_{n} - y^{\prime}_{m} } \\ \end{array} } \right]$$
(17)

A computer graphics-based method is then proposed to calculate the union and intersection areas of the fracture polygon and fitted ellipse, which are necessary steps to obtain an optimal ellipse. The proposed method can effectively alleviate the low computational efficiency of the point radial method proposed by Guo et al. (2020). The key steps and equations associated with the computer graphics-based method are summarized as follows:

  1. (1)

    Calculate the area, SP, of the fracture polygon using Eq. (15).

  2. (2)

    Represent the fracture polygon and fitted ellipse in the same coordinate space and digitize both objects. Note that digitization is equivalent to dividing an ellipse or a polygon using grids with unit area. The number of pixels of the digitized ellipse is then denoted as SE, which represents the area of the ellipse (Marschner and Shirley 2015).

  3. (3)

    Overlay the ellipse with the fracture polygon and count the number of pixels in the union area, SU, of the fracture polygon and fitted ellipse.

  4. (4)

    Calculate the intersection area, Scoin, of the fracture polygon and fitted ellipse as follows:

    $$S_{coin} = S_{P} + S_{E} - S_{U}$$
    (18)

Note that numerical errors may also occur in using the computer graphics-based method when some pixels on the polygon boundary cannot be digitized completely. This is because the number of pixels must be an integer. Nevertheless, an adaptive grid-based search is adopted to iteratively sample all possible values of model parameters k and γ. By this means, the fitting results obtained from the computer graphics-based method can still be consistent with those obtained from the point radial method. In addition, for the ease of implementation, the ellipse is often approximated using the polygon with a sufficiently large number of vertices, and the coordinates of the vertices can be obtained as

$$\left\{ \begin{gathered} x = {{(e\cos \theta \cos \gamma - f\sin \theta \sin \gamma )} \mathord{\left/ {\vphantom {{(e\cos \theta \cos \gamma - f\sin \theta \sin \gamma )} 2}} \right. \kern-0pt} 2} \hfill \\ y = {{(e\cos \theta \sin \gamma + f\sin \theta \sin \gamma )} \mathord{\left/ {\vphantom {{(e\cos \theta \sin \gamma + f\sin \theta \sin \gamma )} 2}} \right. \kern-0pt} 2} \hfill \\ \end{gathered} \right.$$
(19)

To determine the optimal ellipse, Intersection over Union (IoU), which represents the ratio of the intersection area to the union area between the fracture polygon and fitted ellipse, is used and evaluated as

$${\text{IoU}} = \frac{{S_{coin} }}{{S_{U} }}$$
(20)

According to Marschner and Shirley (2015), a threshold IoU value of 0.5 is typically used. An optimal ellipse should correspond to an IoU value larger than the threshold value.

As mentioned earlier, the adaptive grid-based search is employed to sample all possible values of k and γ. First, based on a grid resolution of 0.5 and 1° for the two parameters, respectively, the IoU values of all combinations of these two parameters are calculated. After that, the refined search is centred at the combination of model parameters associated with the largest IoU value, denoted as k0 and γ0. Specifically, within the search domain, i.e., (k0 ± 1) and (γ0 ± 5°), based on a refined grid resolution of 0.05 and 0.5°, the IoU values underlying all combinations of model parameters are calculated. Finally, the ellipse model parameters correspond to the one combination associated with the largest IoU value are determined. The process of fitting the optimal elliptical disc is shown in Fig. 4.

Fig. 4
figure 4

Step-by-step illustration of the optimal elliptic disc fitting process

Full size image

2.3 Construction of Optimal Ellipses

The procedures outlined in the previous section are then repeated for all rock fracture planes, and the statistical distributions of the major axis length e, ratio of major axis to minor axis k and rotation angle γ can be obtained. In addition, using the field measurements at the rock outcrops, the statistical distributions of dip direction κ and dip angle φ can also be determined. The remaining model parameters, such as the centroid coordinates of the ellipse (xm, ym, zm), follow a uniform distribution, as reported in Baecher (1983).

After performing the MCS, random samples of the model parameters, such as e, k, γ, κ, φ and (xm, ym, zm), are generated. Based on the equation of a 2D ellipse, the equation of the corresponding 3D ellipse can be derived. The conversion of these coordinates to the 3D space can be performed using the normal vector n and the major axis given a coordinate matrix N on the ellipse as defined in the 2D space by

$${\varvec{N}} = \left[ {\begin{array}{*{20}c} {e\cos \theta /2} \\ {f\sin \theta /2} \\ 0 \\ \end{array} } \right]$$
(21)

Referring to Fig. 5a, assuming that the x-axis points towards the north direction, the ellipse is first rotated by a degree of γ in the anti-clockwise direction around the z-axis, and the resulting coordinate matrix N1 after the rotation can be evaluated as

$${\varvec{N}}_{1} = \left[ {\begin{array}{*{20}c} {\cos \gamma } & { - \sin \gamma } & 0 \\ {\sin \gamma } & {\cos \gamma } & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]{\varvec{N}}$$
(22)
Fig. 5
figure 5

Illustrations of the coordinate transformation from the two-dimensional ellipse to the corresponding ellipse in the three-dimensional space

Full size image

Next, with reference to Fig. 5b, the ellipse is rotated by a degree of φ in the anti-clockwise direction around the y-axis to arrive at another coordinate matrix N2 as follows:

$${\varvec{N}}_{2} = \left[ {\begin{array}{*{20}c} {\cos \varphi } & 0 & {\sin \varphi } \\ 0 & 1 & 0 \\ { - \sin \varphi } & 0 & {\cos \varphi } \\ \end{array} } \right]{\varvec{N}}_{1}$$
(23)

Last, following Fig. 5c, the ellipse is rotated around the z-axis by a degree of κ in the clockwise direction to arrive at the final coordinate matrix N3 as follows:

$${\varvec{N}}_{3} = \left[ {\begin{array}{*{20}c} {\cos \kappa } & {\sin \kappa } & 0 \\ { - \sin \kappa } & {\cos \kappa } & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]{\varvec{N}}_{2}$$
(24)

After these three rounds of coordinate transformation, the 2D ellipse can be transformed into a 3D space, and its transformation equations can be derived as

$$\left\{ {\begin{array}{*{20}l} {x = x_{m} + {{e\cos \theta (\cos \gamma \cos \varphi \cos \kappa + \sin \gamma \sin \kappa )} \mathord{\left/ {\vphantom {{e\cos \theta (\cos \gamma \cos \varphi \cos \kappa + \sin \gamma \sin \kappa )} 2}} \right. \kern-0pt} 2}} \hfill \\ { \, - {{f\sin \theta (\sin \gamma \cos \varphi \cos \kappa - \cos \gamma \sin \kappa )} \mathord{\left/ {\vphantom {{f\sin \theta (\sin \gamma \cos \varphi \cos \kappa - \cos \gamma \sin \kappa )} 2}} \right. \kern-0pt} 2}} \hfill \\ {y = y_{m} + {{e\cos \theta ( - \cos \gamma \cos \varphi \sin \kappa + \sin \gamma \cos \kappa )} \mathord{\left/ {\vphantom {{e\cos \theta ( - \cos \gamma \cos \varphi \sin \kappa + \sin \gamma \cos \kappa )} 2}} \right. \kern-0pt} 2}} \hfill \\ {\begin{array}{*{20}c} { + {{f\sin \theta (\sin \gamma \cos \varphi \sin \kappa + \cos \gamma \cos \kappa )} \mathord{\left/ {\vphantom {{f\sin \theta (\sin \gamma \cos \varphi \sin \kappa + \cos \gamma \cos \kappa )} 2}} \right. \kern-0pt} 2}} \\ {z = z_{m} + {{( - e\cos \theta \cos \gamma \sin \varphi + f\sin \theta \sin \gamma \sin \varphi )} \mathord{\left/ {\vphantom {{( - e\cos \theta \cos \gamma \sin \varphi + f\sin \theta \sin \gamma \sin \varphi )} 2}} \right. \kern-0pt} 2}} \\ \end{array} } \hfill \\ \end{array} } \right.$$
(25)

As described in Eq. (25), each combination of the randomly generated samples, such as e, k, γ, κ, φ, and (xm, ym, zm), corresponds to a unique ellipse in the 3D space. To simulate the DFN of a 3D rock block with a size of L1 × L2 × L3, it is necessary to first calculate the number of fracture planes, D, based on their densities of occurrence (i.e., discontinuity densities). This results in D ellipses that together simulate the DFN of a rock block.

3 Integration of the UED Model in 3DEC

3DEC is a highly advanced 3D numerical simulation software designed for advanced geotechnical analysis (Itasca Consulting Group 2016). Utilizing the discrete element method, the software is particularly well-suited for simulating discontinuous media, such as jointed rock masses, incorporating both continuum and non-continuum mechanics (e.g., Firpo et al. 2011; Bui et al. 2017; Espada et al. 2018). Although 3DEC has the capability to construct the 3D DFN models using the MCS, the current commercial version of the software is developed based on the conventional Baecher disc model. To overcome the limitations of the current commercial release of 3DEC, the present study leverages Python to introduce a subroutine to integrate the UED model into 3DEC. The aim is to construct the 3D DFNs using the UED model. The procedures that involve eight steps are summarized as follows:

  1. (1)

    Generate random samples of ellipse model parameters through the MCS, which results in the construction of the corresponding ellipses on a 2D plane, and convert all 2D ellipses into 3D companion ellipses using Eq. (25).

  2. (2)

    Partition each ellipse into 20 segments with an equal radial angle using the “range” function in Python, and export the coordinates of the 20 vertices in the Cartesian coordinate system as a “DFN.txt” file. Use a polygon with a substantial number of vertices to approximate an ellipse in 3DEC since curves cannot be directly generated in 3DEC. This motivates the partition of all ellipses into 20 segments.

  3. (3)

    Generate a set “s” in 3DEC to store the coordinates of the 3D ellipses using the “geometry set s” command.

  4. (4)

    Use the “call” command available in 3DEC to load the “DFN.txt” file before executing the “geom poly position” command to construct the ellipses. Note that each MCS sample corresponds to an ellipse in the 3D space in 3DEC.

  5. (5)

    Assign all 3D ellipses with the DFN properties using the “DFN gimport geometry s” command, resulting in a complete 3D DFN model.

  6. (6)

    Construct an intact rock mass model in the studied domain, followed by defining a slope surface and a slope base using the “Jset” command. Hide or delete the main slope body and external rock masses using the “hide range group” or “delete range group” commands, respectively, and obtain the rock masses defining the slope model domain. Then, draw two lines to define the slope surface and the slope base following the “seek” command.

  7. (7)

    Merge the DFN with the intact rock slope using the “Jset DFN” command in 3DEC, leading to a jointed rock slope model.

  8. (8)

    Assign the fracture planes and rock masses with the corresponding mechanical properties using the “Change DFN” command. Specifically, the fracture planes follow non-continuum mechanics while the rock masses not belonging to the fracture planes follow continuum mechanics. This command can also remove the duplicate of fracture planes and rock masses generated during the merging process and ensure that partial penetration of elliptical fractures in the neighboring blocks can be considered in the numerical analysis.

4 Discrete Element-Based Strength Reduction Technique

The stability of the 3D jointed rock slopes constructed in the previous section is evaluated using the discrete element-based strength reduction technique embedded in the “solve fos” command in 3DEC (e.g., Firpo et al. 2011; Espada et al. 2018; Liu et al. 2021). This technique, commonly used in the slope stability analysis, involves reducing the strength of the rock mass, such as cohesion, friction angle, normal stiffness and shear stiffness, and iteratively evaluating the slope stability until it becomes disturbed. Cohesion and friction angle are known to be critical strength parameters for slope stability analysis. Therefore, following Espada et al. (2018) and Wang et al. (2020), this study considers these two parameters in the analysis, reducing them according to the following equations:

$$\left\{ {\begin{array}{*{20}l} {C^{\prime} = \frac{C}{{F_{s} }}} \hfill \\ {\phi^{\prime} = \arctan \left( {\frac{\tan \phi }{{F_{s} }}} \right)} \hfill \\ \end{array} } \right.$$
(26)

where C and ϕ represent, respectively, the cohesion and friction angle; Fs represents the reduction factor; \(C^{\prime}\) and \(\phi^{\prime}\) represent, respectively, the reduced cohesion and reduced friction angle. It is important to note that the reduction in the friction angle is based on the tangent of ϕ. When the stability of the slope is disturbed, the Fs is the factor of safety of the slope. However, there are several ways to evaluate whether the slope stability is disturbed. The criterion used in the present study is summarized as follows: If the slope system transitions from a static state to a dynamic state, this is an indication of slope instability. When this occurs, the plastic flow occurs in the materials, causing the discrete element method to be unable to maintain the equilibrium of slope system and constitutive law, resulting in divergence in the calculations (e.g., Bui et al. 2017; Wang et al. 2020). In all subsequent analyses, a maximum of 10,000 iterations are used to evaluate the factor of safety, and an unbalanced force ratio of 10–4 is used to ensure the results with satisfactory accuracy.

5 Illustrative Example

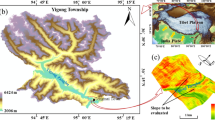
In this section, based on field measurements of a jointed rock slope in Zhejiang Province, China as well as three sets of simulated data, the effectiveness of the UED model in creating the DFNs of jointed rock masses and conducting the 3D discrete element analysis of slope stability is investigated. In addition, the effects of UED model parameters, including the ratio of major axis to minor axis, rotation angle, and discontinuity density on the stability of rock slope are also evaluated. Figure 6 shows the 3D slope model under study. To supplement the sparse field measurements, the statistics of the physical and mechanical properties of the rock masses and discontinuities reported in Lei and Wang (2006) and Jiang et al. (2021) are adopted, which are summarized in Tables 1 and 2, respectively.

Fig. 6
figure 6

Three-dimensional geometric model of a rock slope in Zhejiang Province, China (Unit: m)

Full size image
Table 1 Physical and mechanical properties of the rock mass
Full size table
Table 2 Mechanical properties of the discontinuity
Full size table

5.1 Analysis Based on the Field Measured Data of Discontinuities

Referring the site investigation data and relevant studies, the jointed rock slope mainly consists of limestones. Based on the remote sensing images collected using a widely used unmanned aerial vehicle, Phantom 4 RTK, made by DJI Technology, 90 visible natural fractures that are approximately parallel to the slope are identified at the rock outcrops in Zheng et al. (2022). Each rock fracture contains 3–7 vertices. The discontinuity density is 0.6 trace/m3.

The procedures explained in Sect. 2.2 are then used to process these 90 measured samples. Based on the area, SP, of each fracture plane, the model parameters of the corresponding optimal ellipse, e, k and γ, are calculated. Taking the 9th rock fracture P9 as an example, a step-by-step illustration about the construction of an optimal ellipse based on real rock fracture data is presented as below:


(1) Extract the coordinates of four vertices of P9 as follows:

$$\left\{ \begin{gathered} V_{1} :(11.99, \, 21.37, \, 20555.58) \hfill \\ V_{2} :(45.76, \, 13.24, \, 20484.54) \hfill \\ V_{3} :(38.38, \, 0.15, \, 20484.63) \hfill \\ V_{4} :(1.38, \, 14.58, \, 20568.35) \hfill \\ \end{gathered} \right.$$
(27)

(2) Check and find that P9 is a convex polygon and compute the centroid coordinates of P9 using Eq. (1) as (24.36, 12.34, 20523.28).


(3) Compute the matrix H0 that expresses the coordinates of the four vertices with respect to the centroid of P9 using Eq. (3) as follows:

$${\varvec{H}}_{0} = \left[ {\begin{array}{*{20}c} { - 12.365} \\ {21.315} \\ {14.025} \\ { - 22.975} \\ \end{array} \, \begin{array}{*{20}c} {9.305} \\ {0.905} \\ { - 12.185} \\ {2.245} \\ \end{array} \, \begin{array}{*{20}c} {32.305} \\ { - 38.735} \\ { - 38.645} \\ {45.075} \\ \end{array} } \right]$$
(28)

(4) Compute the unitary matrix V through the singular value decomposition of the matrix H0 using Eq. (4) as follows:

$${\varvec{V}} = \left[ {\begin{array}{*{20}c} {0.41697} \\ { - 0.12123} \\ { - 0.90080} \\ \end{array} \, \begin{array}{*{20}c} { - 0.44604} \\ { - 0.89082} \\ { - 0.08658} \\ \end{array} \, \begin{array}{*{20}c} {0.79195} \\ { - 0.43789} \\ {0.42552} \\ \end{array} } \right]$$
(29)

(5) Compute the normal vector n of the projected plane in a 3D space using Eq. (5) as follows:

$${\varvec{n = }}[0.79195, \, - 0.43789, \, 0.42552]$$
(30)

(6) Project the coordinates of the four vertices of P9 onto the plane in a 2D space using Eqs. (6) to (8), and obtain the matrix H1 that represents the coordinates of the projected four vertices as follows:

$${\varvec{H}}_{1} = \left[ {\begin{array}{*{20}c} {{11}{\text{.992}}} \\ {{21}{\text{.369}}} \\ {{20555}{\text{.581}}} \\ \end{array} \, \begin{array}{*{20}c} {45.669} \\ {{13}{\text{.241}}} \\ {{20484}{\text{.539}}} \\ \end{array} \, \begin{array}{*{20}c} {{38}{\text{.381}}} \\ {{0}{\text{.149}}} \\ {{20484}{\text{.631}}} \\ \end{array} \, \begin{array}{*{20}c} {1.378} \\ {{14}{\text{.581}}} \\ {{20568}{\text{.349}}} \\ \end{array} } \right]$$
(31)

(7) Compute the values of α and β using Eqs. (10) and (11) as α = 0.505 and β = 1.131.


(8) Compute the matrix H2 that represents the final coordinates of the four vertices on the xoy plane through the two rounds of coordinate transformation using Eqs. (12) to (14) as follows:

$${\varvec{H}}_{2} = \left[ {\begin{array}{*{20}c} { - 18601.709} \\ {24.503} \\ \end{array} \, \begin{array}{*{20}c} { - 18523.205} \\ {33.688} \\ \end{array} \, \begin{array}{*{20}c} { - 18523.306} \\ {18.703} \\ \end{array} \, \begin{array}{*{20}c} { - 18615.818} \\ {13.427} \\ \end{array} } \right]$$
(32)

(9) Compute the area of the fracture polygon on the xoy plane using Eq. (15) as Sp = 0.1063 m2.


(10) Compute the matrix H3 that represents the coordinates of the four vertices with respect to the origin of the xoy plane using Eq. (17) as follows:

$${\varvec{H}}_{3} = \left[ {\begin{array}{*{20}c} { - 35.700} \\ {1.923} \\ \end{array} \, \begin{array}{*{20}c} {42.805} \\ {11.108} \\ \end{array} \, \begin{array}{*{20}c} {42.704} \\ { - 3.877} \\ \end{array} \, \begin{array}{*{20}c} { - 49.809} \\ { - 9.153} \\ \end{array} } \right]$$
(33)

(11) Fit the fracture polygon on the xoy plane using an ellipse and set initial ranges for the ellipse model parameters (k and γ). Compute the values of SU and Scoin using the computer graphics-based method and IoU values using Eq. (20) for all combinations of k and γ in the first iteration of the grid-based sampling as shown in Eq. (34) and obtain the optimal combination of k and γ as k0 = 7.5 and γ0 = 7.0°.

$$\left\{ \begin{gathered} k = 1.0{, } \ \gamma = 0^\circ {, }\ S_{U} = 1875, \, S_{coin} = 518,{\text{ IoU = 0}}{.276 } \hfill \\ \, \cdots \hfill \\ k = 7.0{, }\ \gamma = 7.0^\circ {, }\ S_{U} = 1339, \, S_{coin} = 1058,{\text{ IoU = 0}}{.790} \hfill \\ k = 7.5{, } \ \gamma = 7.0^\circ {, }\ S_{U} = 1320, \, S_{coin} = 1061,{\text{ IoU = 0}}{.804} \hfill \\ \, \cdots \hfill \\ \end{gathered} \right. \,$$
(34)

(12) Update the ranges for k and γ, perform the second iteration of the grid-based sampling for k and γ as shown in Eq. (35), and obtain the final optimal combination of k and γ as k0 = 7.4 and γ0 = 7.0°.

$$\left\{ \begin{gathered} k = 6.5{, }\ \gamma = 2.0^\circ , \, S_{U} = 1662, \, S_{coin} = 697,{\text{ IoU = 0}}{.419} \hfill \\ \, \cdots \hfill \\ k = 7.35{, }\ \gamma = 7.0^\circ , \, S_{U} = 1331, \, S_{coin} = 1058,{\text{ IoU = 0}}{.795} \hfill \\ k = 7.40{, }\ \gamma = 7.0^\circ , \, S_{U} = 1312, \, S_{coin} = 1058,{\text{ IoU = 0}}{.806} \hfill \\ \, \cdots \hfill \\ \end{gathered} \right.$$
(35)

(13) Obtain the corresponding IoU value as 0.806 and compute the length of major axis e = 1.001 m, the length of minor axis f = 0.135 m, and the semi-latus rectum g = 0.992 m using Eq. (16) based on SE = SP.

The technique proposed by Jiang et al. (2023a) is then employed for sample augmentation with the original 90 measured samples. A further 4800 samples of e, k and γ are obtained and plotted alongside the original 90 measured samples in Fig. 7. Note that the additional 4800 samples are determined by multiplying the discontinuity density (0.6 trace/m3) with the volume (20 × 20 × 20 m3) of the rock block. The figure shows that the statistics of the additional 4800 samples resemble those of the original 90 measured samples. In addition, 4800 values of dip direction and dip angle are also sampled following a Fisher distribution according to the method reported in Kemeny and Post (2003) based on the statistics as shown in Table 3.

Fig. 7
figure 7

Comparison of the histogram of measured and simulated samples of ellipse model parameters

Full size image
Table 3 Statistics of the azimuth and UED model parameters
Full size table

Figure 8 shows a 3D DFN with a size of 20 m × 20 m × 20 m generated in 3DEC using the UED model and 4800 samples. To show the diagram of the discretization process of rock blocks for a rock slope using 3DEC, the corresponding 3D jointed rock slope model is constructed following the procedures outlined in Sect. 3, as shown in Fig. 9. Note that Fig. 9 should not be interpreted as to reflect the actual cutting situation of a rock slope because only full penetration of structural planes is considered in 3DEC. Then, the factor of safety of the slope calculated using the discrete element-based strength reduction technique is 2.55. Figure 10, which displays the contour of horizontal displacement at the cross-section of x = 8 m, shows that the maximum displacement occurs near the slope surface. It is worth highlighting the horizontal displacement field shown in Fig. 10 corresponds to the iteration results just before the slope fails.

Fig. 8
figure 8

Three-dimensional DFN constructed using the UED model

Full size image
Fig. 9
figure 9

Three-dimensional jointed rock slope model constructed using the UED model

Full size image
Fig. 10
figure 10

Contour of horizontal displacement at the cross-section (x = 8 m) of the jointed rock slope

Full size image

Additionally, the accuracy of (i) the Baecher disc model, (ii) a non-optimal elliptical disc model, and (iii) the optimal elliptical disc model (UED model) for fitting the 90 measured samples is further compared. The means of the optimal elliptical disc model parameters (i.e., k = 2.46 and γ = 112.1°) are taken as the values of the non-optimal elliptical disc model parameters. Figures 11a and b show, respectively, the normalized frequencies of IoU value and the IoU values obtained from fitting the 90 measured samples using these three models. As observed from Fig. 11, the IoU values of the optimal elliptical disc model generally cluster between 0.8 and 0.9. All data exceed the threshold IoU value of 0.5 and are significantly larger than those of the Baecher disc and non-optimal elliptical disc models. The results indicate that the optimal elliptical disc model has the best fitting accuracy. In contrast, the fitting accuracy of the Baecher disc model is poor, especially for slender fractures because the estimated IoU values are generally distributed between 0.3 and 0.7 and exceed the threshold value of 0.5 only for 70% of the cases (63 cases). The non-optimal elliptical disc model cannot accurately represent the spatial distribution of fractures in most cases because the estimated IoU values exceed the threshold value of 0.5 only for 43.3% of the cases (39 cases).

Fig. 11
figure 11

Histograms of IoU Value and IoU Values obtained from fitting the 90 measured samples using three different models

Full size image

5.2 Analysis Based on the Simulated Data of Discontinuities

5.2.1 Case Descriptions

This section presents the implementation of the UED model in the conjunction with three sets of simulated data of discontinuities to investigate the effects of ellipse model parameters, including the ratio of major axis to minor axis and rotation angle, on the characteristics of the resulting DFNs and stability of jointed rock slope. The results associated with the UED model are further compared with those associated with the conventional Baecher disc model. In the subsequent parts of this paper, the three sets of analyses using the UED model are referred to as Group 1, Group 2 and Group 3. Specifically, Group 1 is used to study the sensitivity of slope stability to the UED model parameters. Groups 2 and 3 are assigned with fixed values of discontinuity characteristics. In addition, the total area of the ellipses representing all fracture planes is set to 4 m2 for all these three groups, and the length of major axis is constant across all groups. In this regard, the size of the ellipses is controlled by adjusting the ratio of major axis to minor axis, according to Eq. (16). Lastly, the discontinuity density is set as 0.1 trace/m3 herein.

The statistics of the azimuth and UED model parameters for these three groups of discontinuities, which follow a normal distribution, are shown in Tables 4 and 5, respectively. Table 4 reveal that Group 1 assumes that the dip direction is in parallel with the slope surface, which intuitively results in a low factor of safety as the slip surface of slope is likely to form along the dip direction. With reference to Tables 6 and 7, Group 1 includes twelve cases for sensitivity analysis. Cases 1 to 7 vary the mean of the ratio of major axis to minor axis while keeping its coefficient of variation and the total area of ellipses constant. In these cases, the mean and standard deviation of the rotation angle equal 90° and 5°, respectively. Cases 8 to 12 fix the standard deviation of the rotation angle at 5° while varying the mean from 0° to 150°. In these cases, the mean and standard deviation of the ratio of major axis to minor axis are 5.0 and 1.0, respectively. For comparison purposes, a companion case, Case 13, is designed based on the Baecher disc model, with the total area of the circular discs being the same as the total area (i.e., 4 m2) of the ellipses in Groups 1, 2 and 3. Based on the information presented in Tables 4, 5, 6, 7 and the procedures outlined in Sect. 3, the MCS is utilized to construct the jointed rock slope model in 3DEC for all the cases in these three groups and the case based on the Baecher disc model. The factor of safety of the slope is calculated for each case using the discrete element-based strength reduction technique in 3DEC. The comparative study results of these calculations are discussed in the next section.

Table 4 Statistics of the azimuth of the three groups of discontinuities
Full size table
Table 5 Statistics of the UED model parameters for Group 2 and Group 3
Full size table
Table 6 Sensitivity analysis cases involving the ratio of major axis to minor axis in Group 1
Full size table
Table 7 Sensitivity analysis cases involving the rotation angle in Group 1
Full size table

5.2.2 Comparative Study Results

Figures 12a and b show the variations of the factor of safety of the slope with the ratio of major axis to minor axis and the rotation angle, respectively. The results obtained from the Baecher disc model are also plotted for comparison. Since the Baecher disc model does not involve the ratio of major axis to minor axis and rotation angle, a straight line is observed in Fig. 12. It is evident from the figures that the slope stability can be significantly affected by the ratio of major axis to minor axis and rotation angle. In addition, the effects are not necessarily monotonic. With reference to Fig. 12a, the relationship between the factor of safety and the ratio of major axis to minor axis follows a U-shape curve, with the factor of safety declining as the ratio increases and then bouncing backing once the ratio exceeds 15. With reference to Fig. 12b, a sine-shape curve can be used to describe the relationship between the factor of safety and the rotation angle. In contrast, the conventional Baecher disc model does not account for the effects of the ratio of major axis to minor axis and rotation angle, which could potentially result in inaccurate representation of jointed rock masses and slope stability analysis results. Figure 12a highlighted that the results from the conventional Baecher disc model consistently overestimates the slope stability, potentially leading to inadequate slope reinforcement designs. Figures 13, 14, 15 further compare the three-dimensional DFN models, jointed rock slopes and the contour of horizontal displacement at the cross-section of x = 5 m based on the UED model and the cross-section of x = 10 m based on the Baecher disc model. These figures evidently demonstrate that the UED model, which is a more flexible and generalized model, can produce more realistic stability evaluations of jointed rock slope due to its ability to represent the discontinuities with realistic fracture topology.

Fig. 12
figure 12

Variations of the factor of slope safety with the means of UED model parameters

Full size image
Fig. 13
figure 13

Comparison of the three-dimensional DFNs constructed using the UED model and Baecher disc model

Full size image
Fig. 14
figure 14

Comparison of the three-dimensional jointed rock slopes constructed using the UED model and Baecher disc model

Full size image
Fig. 15
figure 15

Comparison of the contours of horizontal displacement of slope based on the UED model and Baecher disc model

Full size image

With the advantages of the UED model over the conventional Baecher disc model demonstrated, the effect of discontinuity density on the slope stability is further investigated. Ten DFN models with the discontinuity densities ranging from 0.1 to 1.0 trace/m3, are generated. For all the ten cases, the dip direction is parallel with the slope surface. Other parameters are kept the same as those listed in Tables 1, 2, 3, 4. It is also worth noting that except the DFN model with a density of 0.1 trace/m3, which is generated using the MCS, other nine DFN models are generated through adding extra fracture surfaces to the DFN model underlying the preceding density. Figure 16 shows the effects of discontinuity density on the slope stability for the UED model and Baecher disc model.

Fig. 16
figure 16

Variations of the factor of slope safety with the discontinuity density

Full size image

To better understand the impact of the ratio of major axis to minor axis, rotation angle and discontinuity density on the slope stability, a key block model with three stratigraphic units is created because the stability of a rock slope is critically dependent on the size of the sliding surface of the key block. The results are expected to explain the varying trends shown in Fig. 12. Figure 17 shows the schematic diagram of the constructed key block in the rock slope. The top surface is established based on the Group 2 model, while the sliding surface follows the Group 1 model and the two side surfaces are inherited from the Group 3 model. The stability coefficient of the key block can be evaluated as

$$\begin{gathered} K = \frac{mg\cos \theta \tan \phi + CA}{{mg\sin \theta }} \hfill \\ \, = \frac{\tan \phi }{{\tan \theta }} + \frac{CA}{{\rho gA\overline{h}\sin \theta }} \hfill \\ \, = \frac{\tan \phi }{{\tan \theta }} + \frac{C}{\rho gf(A)\sin \theta } \hfill \\ \end{gathered}$$
(36)

where m is the mass of the block (kg); C is the cohesion of the structural surface (kPa); ϕ is the friction angle of the structural surface (o); \(\theta\) is the dip angle of the sliding surface (o); A is the area of the sliding surface (m2); \(\rho\) is the density of rock mass (kg/m3); \(\overline{h}\) is the average height of the key block (m), which is a function of the area of the sliding surface [i.e., \(\overline{h} = f(A)\)]. In this regard, a larger value of A results in a larger value of f(A), which subsequently results in a lower value of K, indicating a large likelihood of instability.

Fig. 17
figure 17

Schematic diagram of a key block model

Full size image

The varying trends observed in Fig. 12 can now be explained with reference to Eq. (36) and Fig. 18. On one hand, the associated sliding area of the key block decreases as the ratio of major axis to minor axis in the UED model increases, as shown in Fig. 18a, improving the slope stability. On the other hand, a large ratio of major axis to minor axis also leads to an increase in the width of the fracture plane, which results in more sliding blocks in the DFN and reduces the stability of the slope. As such, when the mean of the ratio of major axis to minor axis is small, the effects of more sliding blocks are more significant, causing a decrease in the slope stability as the ratio of major axis to minor axis increases. When the mean of the ratio of major axis to minor axis is large, the decrease in the sliding area becomes more dominant, leading to an increase in the slope stability with increasing the ratio of major axis to minor axis. Additionally, the relationship between the sliding area A and rotation angle follows a sine-shape curve in reference to Fig. 18b. Given that the factor of safety is inversely related to the sliding area of the key block based on Eq. (36), the relationship between the factor of safety and rotation angle also follows the sine-shape curve, as observed in Fig. 12b.

Fig. 18
figure 18

Variations of the area of sliding surface for the key block with respect to the means of characteristic parameters of UED model

Full size image

The varying trend observed in Fig. 16 can also be similarly explained. Since the dip direction is in parallel with the slope surface, and the dip angle is larger than the friction angle ϕ of the structural surface, it is reasonable to consider the blocks cut through by the structural surface as the sliding blocks. When the discontinuity density increases, the interruptions within the structural surface increase, reducing the sliding area and thus improving the slope stability following Eq. (36). Referring to the results of the UED model shown in Fig. 19, which illustrates the relationship between the volume of the maximum sliding block (key block) with respect to the discontinuity density, when the discontinuity density increases from 0.1 to 0.3 trace/m3, the volume of the maximum sliding block decreases. As such, the slope becomes more stable (i.e., factor of safety increases). When the volume of the maximum sliding block increases between the discontinuity density of 0.3 to 0.4 trace/m3, the factor of safety reverses the trend accordingly. When the volume of the maximum sliding block remains largely constant between the discontinuity density of 0.4 to 0.7 trace/m3, the factor of safety also remains largely unchanged. Finally, when the volume of the maximum sliding block decreases again between the discontinuity density of 0.8 to 1.0 trace/m3, the factor of safety immediately increases accordingly. These observations are also in line with the conclusion in the block theory that “the factor of safety generally decreases with the increase of the volume of blocks with similar shapes”as stated by Zhang (2004).

Fig. 19
figure 19

Variations of the volume of the maximum sliding block with respect to the discontinuity density

Full size image

6 Discussions

The UED model is a quite useful tool in understanding the behavior and characteristics of jointed rock slopes in various conditions, such as static, dynamic, and seepage conditions. Unlike the Baecher disc model, which lacks the capability to represent realistic characteristics of jointed rock masses, the UED model can provide more accurate slope stability analysis results since it accurately represents the characteristics of jointed rock masses. Although the UED model is viable, and subroutines have been developed to integrate the UED model into 3DEC, the current study only considered a single lithology unit in a rock slope, as the complex procedures of 3DEC to pre-process the generated DFN model made it challenging to analyze the jointed rock slopes with complex geological conditions. To extend the application of the developed framework in engineering practice, there are several key conditions:

  1. (1)

    Construct the geometric model of the jointed rock slope and group the slope bodies using Midas or Rhino software according to their lithology units before importing the model to 3DEC. Then, assign the properties of the lithology units to the corresponding slope body by executing the “prop mat” command. In this way, a jointed rock slope model involving different lithology units can be neatly constructed.

  2. (2)

    A persistence metric should be defined to restrain the probability of discontinuity along the fracture path in 3DEC after uniformly distributing the rock bridges over fracture planes and generating the discrete fractures using the “jset” command. In this way, the effects of rock bridges can be effectively accounted for.

  3. (3)

    In addition to borehole data, it is also crucial to collect more measured data visible at the rock outcrops to improve the accuracy of the relevant statistical estimates. Human inputs and artificial intelligence are also necessary to further refine the jointed rock slope model for achieving the improved prediction accuracy (Jiang et al. 2023b).

7 Conclusions

In this study, a framework is proposed for the stability analysis of jointed rock slopes using a three-dimensional DFNs constructed based on the UED model. The constructed DFNs are successfully integrated into 3DEC for discrete element analysis of the stability of jointed rock slopes. Details of the implementation procedures are outlined in this paper. A 3D jointed rock slope in Zhejiang Province, China is used to illustrate the effectiveness of the proposed framework. In addition, the effects of the UED model parameters (including ratio of major axis to minor axis and rotation angle) and discontinuity density on the stability of jointed rock slopes are investigated. The advantages of the UED model over the Baecher disc model are also demonstrated. The main conclusions and findings are summarized as follows:

  1. (1)

    Python subroutines are successfully developed to incorporate the UED model in 3DEC, allowing the creation of a realistic and accurate 3D DFN model. Furthermore, the DFN constructed based on the UED model is successfully integrated into a 3D slope model, generating a complete jointed rock slope. Based on these, the proposed framework effectively simplifies the 3D stability analysis of jointed rock slopes with the aid of the discrete element-based strength reduction technique in 3DEC.

  2. (2)

    In contrast to the conventional Baecher disc model, the UED model is a more flexible and generalized model that is capable of generating realistic fractures with arbitrary shapes based on a small amount of field measured data. It is also better at representing the random distribution of the discontinuities in the rock masses. These features make the generated slope model resembles the realistic characteristics of jointed rock slopes, providing the improved stability evaluations of jointed rock slopes.

  3. (3)

    The results of parametric sensitivity analyses show that the stability of jointed rock slopes is influenced by the ratio of major axis to minor axis, rotation angle and discontinuity density in a complex manner. The relationship between the slope stability and the ratio of major axis to minor axis follows a convex U-shape relationship while a sine-shape curve can be observed to describe the effects of the rotation angle and discontinuity density on the slope stability. The results are rigorously explained from a mechanical point of view based on a key block model.