1 Introduction

The Biot effective stress coefficient, \(\alpha\), introduced by the pioneering works of Biot (1941) and Biot and Willis (1957), and the Skempton pore pressure coefficient, B, proposed by Skempton (1954), are key parameters in studying the hydro-mechanical (HM) behavior of fluid-saturated elastic geological media. The product \(\alpha B\) defines the effective stress variations in response to undrained loading/unloading, which directly impacts the deformation of the porous material (Biot 1941; Cheng 2016; Zimmerman 2000). These poroelastic coefficients describe the contribution of the fluid in subsurface porous and fractured media to maintain the mechanical equilibrium against perturbations in stress and pore fluid pressure. Fluid in saturated geological media, in fact, holds part of the load, thus the deformation caused by an applied stress is smaller in saturated materials under non-zero pore pressure than in dry materials. This coupled hydro-mechanical behavior has profound implications in both natural processes, such as glaciation (Vidstrand et al. 2008), and geotechnical engineering applications, including reservoir impoundments, underground excavation/construction, geo-energy extraction, and deep geological disposal of used nuclear fuel (Rutqvist and Stephansson 2003).

Although fractures are ubiquitous in rocks, their explicit representation in theoretical or numerical models is challenging and incurs high computational costs. For practical purposes, the assumption of uniform material with poroelastic behavior is extensively adopted in many scientific and engineering applications involving large-scale problems in underground geological media (e.g., Alghannam and Juanes 2020; Chang and Segall 2016; Parisio et al. 2019; Pujades et al. 2014; Rutqvist et al. 2002; Vilarrasa et al. 2010; see also the discussions in Jing 2003; Rutqvist and Stephansson 2003; Viswanathan et al. 2022). In this context, the assessment of equivalent properties is particularly challenging because fractured media are highly heterogeneous and anisotropic, and because sample-scale laboratory tests are not able to represent large-scale behavior. While the definition of equivalent mechanical properties, e.g., elastic moduli, has been extensively discussed (see Grechka and Kachanov 2006 for a review), the estimation of Biot and Skempton poroelastic coefficients for large-scale fractured rocks has received little attention so far.

The Biot effective stress coefficient \(\alpha\) defines the partitioning of total stress between the solid skeleton and the pore fluid, such that an applied external stress, \(\mathrm{d}\sigma\) (total stress), results in an increase of stress applied to the solid phase, \(\mathrm{d}{\sigma }^{\prime}\)(effective stress), and an increase in fluid pore pressure, \(\mathrm{d}p\), which are distributed according to the law

$$d\sigma =d{\sigma }^{\prime}+\alpha dp.$$
(1)

Note that the sign convention for stress is such that compressive stress is positive. From the theory of poroelasticity, it can be derived that \(\alpha\) corresponds to the amount of total stress variation in response to a pressure variation at zero deformation, or alternatively, to the amount of pore pressure that is necessary to counterbalance the deformation caused by an applied external stress (e.g., Cheng 2016; Coussy 2004; Wang 2000). A distinction between Biot coefficient and the effective stress coefficient is considered in cases when inhomogeneities at the scale of the grains lead to non-self-similar deformation of solid and pore space (see the discussion in Cheng 2021; Müller and Sahay 2016a, b; Müller and Sahay 2016a; Sahay 2013). In this case, the Biot coefficient is defined as the fluid volume change induced by bulk volume changes in drained conditions. However, we do not differentiate the two concepts here. The Biot effective stress coefficient expresses the effects of the micromechanical rock characteristics (pore scale) on the behavior at the scale of the representative elementary volume (REV), which is the largest volume over which variables—in this case stress and pore pressure—are constant. The coefficient was originally defined for isotropic materials, taking the nomenclature of the Biot coefficient or Biot-Willis coefficient (Biot and Willis 1957; Biot 1941). In this case, the most recognized theoretical estimation is defined by (Biot and Willis 1957)

$$\alpha =1-\frac{K}{{K}_{s}}.$$
(2)

\(K\) is the porous material stiffness at the REV scale, also called drained bulk modulus, which expresses the volumetric deformation of the saturated material in response to applied stress in dry (zero pore pressure) or drained (constant pore pressure) conditions; a test scheme which was introduced by Biot and Willis (1957) and referred to as the jacketed compressibility test. The drained bulk modulus is dependent on the stress magnitude; it increases with increasing the total stress (e.g., Nur and Byerlee 1971). At the pore scale (micro-scale), the grain stiffness \({K}_{s}\) expresses the deformation of the mineral solid skeleton to an applied stress at constant Terzaghi effective stress conditions, \(\mathrm{d}\sigma -\mathrm{d}p=0\); also introduced by Biot and Willis (1957) and called the unjacketed compressibility test. The grain stiffness does not depend on the stress magnitude in the elastic region (e.g., Nur and Byerlee 1971). According to Eq. 2, \(\alpha\) only depends on the intrinsic properties of bulk skeleton and grains, and not on the fluid properties.

The Skempton coefficient \(B\) (Skempton 1954) also relates pressure and stresses, but it defines the pressure variation in response to an average total stress variation under undrained conditions, e.g., when the volumetric fluid content does not change. Therefore, it reflects a condition (undrained) that is non-permanent in natural aquifers. The coefficient value depends on the hydro-mechanical rock behavior at the bulk scale, i.e., both the rock and fluid properties. For isotropic materials, it can be shown that \(B\) is equal to (Detournay and Cheng 1993; Rice and Cleary 1976)

$$B=\frac{\alpha /K}{\frac{\alpha }{K}+\phi \left(\beta -\frac{1}{{K}_{s}}\right),}$$
(3)

where \(\beta\) represents the fluid compressibility and \(\phi\) is the rock porosity.

Both coefficients depend on the ability of the porous material to deform under loading. They are approximately equal to 1 in highly compressible materials (i.e. soils), whereas they are much smaller than 1 in stiff rocks (Detournay and Cheng 1993). However, experimental and numerical studies have shown that \(\alpha\) and \(B\) may span a broad range of values, and that besides the effect of the applied stress magnitude, macroscale rock heterogeneity and anisotropy play an important role (Cheng 1997; Kachanov 1992; Kasani and Selvadurai 2023; Lockner and Beeler 2003; Lockner and Stanchits 2002; Selvadurai and Suvorov 2020; Tan and Konietzky 2014; Wong 2017).

Although Biot and Skempton coefficients were originally defined as scalars referring to isotropic materials and hydrostatic stress conditions, the concepts have been successively generalized to anisotropic materials undergoing deviatoric stress, leading to the definition of either tensorial coefficients or scalar coefficients that depend on the applied stress. In some cases, the nomenclatures effective stress coefficient and pore pressure coefficient have been adopted to differentiate with respect to the traditional formulation for isotropic homogeneous materials, while in other cases the nomenclatures Biot coefficient and Skempton coefficient have been maintained to underline the connection with the physical meaning of the two coefficients, as we also do in this work.

Biot (1955) extended the poroelasticity theory to the case of anisotropic porous media which was further developed by many other scholars (e.g., Carroll 1979; Skempton 1984; Cheng 1997). The work of Cheng (1997) includes general constitutive laws with 28 independent coefficients, which are reduced to 8 under the assumptions of micro-isotropy (isotropic mineral composition) and transversely isotropic materials, which can be assimilated to fractured media. This allows deriving expressions for anisotropic Biot and Skempton tensors, as a function of the component of the anisotropic elastic stiffness tensor and the solid constituent stiffness \({K}_{s}\). The theory has been later adopted by Wong (2017) to estimate Biot and Skempton tensors in rocks with cracks. The assumption of a porosity-free rock matrix, which is also isotropic and homogeneous at the pore scale, implies that the rock matrix stiffness coincides with the grain stiffness \({K}_{s}\). The anisotropic elastic stiffness tensor for the cracked rock is estimated according to the effective elastic tensor proposed by Kachanov (1992). It depends on the density and orientation of cracks, which are assumed as penny-shaped, dilute and non-interacting with each other. These theoretical predictions are validated against already published results from laboratory triaxial tests on cracked samples of Berea sandstone, showing a not very accurate agreement, the reasons residing in the use of effective parameters and in neglecting the rock matrix porosity.

Tan and Konietsky (2014) analyze the influence of pore cavity shape on the Biot coefficient of fluid-saturated porous rocks. They assume a sample of a solid matrix with a single pore cavity and analyze the case of three different cavity shapes. This structure is considered like a multiphase composite material and they apply the generalized mixture rule to express the composite material stiffness as a function of the solid matrix stiffness, the porosity (cavity volume over total volume) and a shape factor that is empirically derived from numerical simulations. They found that \(\alpha\) is larger for larger porosity, while at equal porosity, \(\alpha\) is larger for long and narrow cracks, than for spherical cavities. The direction of the elliptical cavity with respect to the applied load is key, as the cavity deforms more in the direction perpendicular to the long axes, meaning higher \(\alpha\). These results are consistent with experimental analysis on laboratory scale samples (Selvadurai and Suvorov 2020) and with the assumption that \(\alpha\) is related to the fraction of the surface over which the fluid pressure acts in a given direction (Cheng et al. 2022; Gray 2017; Zhao et al. 2021). They extended the procedure to samples with a random distribution of cavities and they found that elongated cracks have more effect than pores on the Biot coefficient.

While the two previous studies consider fractured (cracked) rocks at the sample scale, Berryman (2012) derives theoretical expressions to estimate \(\alpha\) and \(B\) for fractured media. The porosity of the rock matrix is neglected, and it is also assumed as composed of homogeneous, isotropic grains. Considering poroelasticity laws for anisotropic transversely orthotropic media, the effective elastic moduli of the solid grains and the fractured rock are estimated based on the Reuss average (Reuss 1929), which reflects an arithmetic weighted average over the values of the different components. Afterwards, the average \(\alpha\) and \(B\) are estimated through Eq. 2 and Eq. 3, respectively. The approach is extremely simplified, and it does not consider anisotropy effects, nor the volume occupied by the individual components, which have all the same weight in the average equation. Moreover, the porosity is assumed exclusively within the fractures, while the matrix is assumed as non-porous. Overcoming this latter limitation, Tuncay and Corapcioglu (1995) proposed a double porosity approach to derive an effective stress principle for saturated porous fractured rock. Making use of volume averaging over the rock mass, they write the effective stress principle in terms of macroscopic stresses and two Biot coefficients, one for the porous rock and one for the fractures. While the theory has the value of acknowledging the rock porosity and the fraction of volume occupied by the fractures, it does not consider the effects of fracture orientation. Additionally, the theory is not validated by any numerical or laboratory experiment.

More recently, Chen et al. (2020) estimated the Biot coefficient for fractured media composed of a fracture network embedded in a non-porous intact rock. Three types of network and several fracture and rock properties are analyzed, considering a 2D geometry. They adopt the numerical simulator UDEC (Itasca Consulting Group, 2019), in which fractures are treated as contact interfaces between deformable rock blocks, to reproduce the deformation of such geometries in response to applied stress. Two different methods are employed to estimate \(\alpha\) at the rock mass scale. In the first method, the equivalent bulk modulus \(K\) is estimated from numerical results and directly used to estimate \(\alpha\) by means of Eq. 2. In the second method, \(\alpha\) is indirectly estimated from the comparison of the numerically estimated volumetric deformations in response to an applied stress under dry (\(\varepsilon\)) and saturated drained conditions (\(\varepsilon ^{\prime}\)). Comparison of the two methods shows that the first one is inappropriate to describe the effective stress behavior of the fractured rock mass, mostly because the equivalent bulk modulus is highly influenced by the shear stiffness (Davy et al. 2018), whereas the volumetric deformation, which is strictly related with the effective stress concept, is much influenced by the normal stiffness. Therefore, they adopt the method based on the volumetric deformation to empirically derive a theoretical model. The study represents the best effort so far to define the Biot coefficient for fractured media at the rock mass scale. However, it is limited to 2D plane strain geometries, and the effect of the fracture orientation on the anisotropic \(\alpha\) is not contemplated.

Most of the above studies refer to cracked rocks at the sample scale, and they assume that the porosity is only within the cracks. An established method for estimating Biot and Skempton coefficients in fractured media at the scale of the rock mass is still missing. Consequently, the effects of fracture density, size and orientation on the equivalent parameters have not been analyzed.

In this paper, we investigate the role of the Biot and Skempton coefficients at the scale of a three-dimensional fractured rock mass from a Discrete Fracture Network (DFN) perspective. In the DFN approach, fracture orientation, size, density and aperture are stochastically generated based on field observations or theoretical assumptions. We reduce the geomechanical complexity of fractured rocks by assuming an idealized medium composed of a homogeneous elastic porous rock, which hosts fractures with an elastic behavior. Fracture slip failure is neglected because it does not belong to the elastic regime in which Biot and Skempton coefficients are defined. Both the porous rock and the fracture surfaces are assumed as ideal Gassmann materials with homogeneous grains (Gassmann 1951). Thus, we disregard the effect of micro-structural inhomogeneities to focus on that of the heterogeneity at the scale of the rock mass induced by the population of fractures. Although simplified, this model allows us to analyze the range of variability of the poroelastic coefficients with respect to the complexity of the fracture network structure and with respect to the properties of fractured rocks, which are uncertain and difficult to quantify.

The paper is organized as follows. First, we define the two coefficients for a single fracture, with respect to a load applied normally to the fracture plane. Afterwards, we define formal expressions for the two coefficients for a fractured rock mass, with respect to an average applied stress. Following an approach based on the volumetric deformation, the equivalent coefficients are defined as the ones that reflect the rock mass deformation in fully saturated conditions. In doing so, we consider the contributions of the population of fractures and the porous rock matrix. We find that the equivalent Biot and Skempton coefficients can be analytically estimated based on the geometrical and mechanical properties of the intact rock and of each fracture. These analytical expressions are successively validated against results from coupled hydro-mechanical numerical simulations on systems with explicit representation of fractures and rock blocks. Finally, we make use of these expressions to discuss the sensitivity of the two coefficients to the mechanical properties of intact porous rock and fractures, and to the fracture network parameters.

2 Derivation of Formal Expressions for Equivalent Biot and Skempton Coefficients

2.1 Model for a Single Fracture

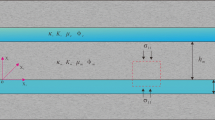
Let a rough fracture with average direction defined by the normal \(N\) and average mechanical aperture \(e\), subject to a generic stress state such that the compressive stress acting normal to the fracture is \({\sigma }_{N}\) (Fig. 1). The fracture is assumed as a fluid-filled void space. Fracture aperture, roughness and stiffness are assumed as homogeneous in the fracture plane. Fracture walls are composed of an ideal material that is homogeneous at both the macro-scale and the micro-scale. The contact between the fracture surface results in an elastic mechanical behavior with the aperture changing proportionally to the normal stiffness \({\kappa }_{N}\), such that

Fig. 1
figure 1

Conceptual sketch of the different scales of the problem, from the fractured rock mass down to the micromechanical characteristics through the scale of the single fracture. Fracture roughness is averaged by considering the average fracture aperture, \(e\), while variability in the local aperture is disregarded. The stress normal to the average fracture orientation, \({\sigma }_{N}\), is considered, while variability in the local stress normal to the fracture wall, \({\sigma }_{n}\), is disregarded

Full size image
$$\mathrm{d}e=-\frac{\mathrm{d}{\sigma }_{N}^\prime\, }{ {\kappa }_{N}}.$$
(4)

Note that this constitutive law is non-linear (e.g., Bandis et al. 1983) because the interface stiffness \({\kappa }_{N}\) increases with the effective stress acting normal to the average fracture plane, which is defined as

$${\sigma }_{N}^\prime={\sigma }_{N}-{\alpha }^{f}p,$$
(5)

where \({\alpha }^{f}\) represents the Biot effective stress coefficient of the fracture and \(p\) is the fluid pressure inside the fracture, considered as homogeneous. Since \({\alpha }^{f}\) expresses the amount of stress variation in response to a pressure variation at zero deformation, it is natural to consider that \({\alpha }^{f}=1\) for a wide-open fracture with no roughness, while for a completely sealed fracture we expect \({\alpha }^{f}=0\), because there is no space for fluid and therefore no fluid pressure. In the general case of a rough fracture, we expect \({\alpha }^{f}<1\) locally, depending on the fracture roughness and aperture, which define the geometry of the porous cavity. This is in agreement with estimations for porous cavities (Tan and Konietzky 2014) and rough fractures (Cheng et al. 2022; Xie et al. 2014; Zhao et al. 2021), and it is also consistent with the physical concept that the effective stress coefficient depends on the fraction of surface that is in contact with the fluid in a specific direction (Gray 2017; Cheng et al. 2022; Zhao et al. 2021). Although the fracture walls are rough and in contact, we consider that on average the effects of the asperities cancel out, and that the contact area of the asperities is small, such that there is no significant reduction of the fracture surface in contact with the fluid. Therefore, we assume that the Biot coefficient of the fracture is \({\alpha }^{f}=1\), with the intention of focusing on the impacts of the fracture average orientation rather than on those of the wall asperities. However, these latter may be included by linking the fracture Biot coefficient with the fracture roughness, which does not alter the method for the estimation of the coefficient at the rock mass scale.

For convenience, we transform the non-linearity of the constitutive law (Eq. 4) into a local linearity. We assume that \({\kappa }_{N}\) changes with the initial stress state, but it is constant for the small variations of stress and pressure that we apply to derive the poroelastic coefficients. This is a reasonable assumption since normal stiffness is not significantly modified by a small reduction of fracture porosity.

Similarly, we define a fracture Skempton coefficient, \({B}^{f}\), which applies in the direction normal to the fracture plane, such as the pore pressure variation in the fracture caused by the total stress acting normal to the fracture in undrained conditions is \(p={B}^{f}{\sigma }_{N}.\) To derive an expression for the fracture Skempton coefficient \({B}^{f}\), we follow the volumetric approach traditionally adopted for the porous medium (Cheng 2021), adapted to consider the fracture capacity of deforming, which gives (Appendix A)

$${B}^{f}={\left(\beta e {\kappa }_{N}+{\alpha }^{f}\right)}^{-1}.$$
(6)

In doing so, we only consider the fracture open volume, assuming the average aperture for the rough fracture and considering that the entire fracture aperture is filled with fluid. However, if the fracture is completely sealed, then \({B}^{f}=0\).

Note that \({\alpha }^{f}\) and \({B}^{f}\) for each fracture are exclusively functions of its mechanical properties and open fraction, i.e., whether the fracture is open or sealed. However, fracture mechanical stiffness intrinsically depends on the remote initial stress, and on the roughness and intensity of contact between asperities (Bandis et al. 1983; Barton et al. 1985). We have defined \({\alpha }^{f}\) and \({B}^{f}\) with respect to the direction normal to the fracture plane. When estimating the equivalent Biot and Skempton coefficients for the fractured rock mass, the orientation of the fracture with respect to an external reference system must be considered, as we explain in the next section (Fig. 1).

2.2 Model for a Fractured Rock Mass

To estimate equivalent Biot and Skempton coefficients for a fractured rock mass, \(\overline{\alpha }\) and \(\overline{B}\), we make the following assumptions. Both the fracture and the rock matrix behaviors are linearly elastic, and they are subject to a compressive stress regime. The intact rock matrix is homogeneous and isotropic, and it is characterized by known values of porosity \(\phi\), drained bulk modulus \({K}^{r}\), and grain stiffness \({K}_{s}\), such that the Biot and Skempton coefficients of the rock composing the matrix, \({\alpha }^{r}\) and \({B}^{r},\) can be estimated according to Eq. 2 and Eq. 3, respectively. For the fractures, we assume the model as detailed in Sect. 2.1, such that each fracture is characterized by known values of \({\alpha }^{f}\) and \({B}^{f}\). The mechanical interactions between fractures, as well as between intact rock and fractures, are such that stress fluctuations can be neglected. No mechanical constraints are applied to the system, which is free to deform. The latter assumptions imply that the total stress variation is homogeneous in space, and equal to the applied stress variation.

Similar to Chen et al. (2020), the formal expressions for \(\overline{\alpha }\) and \(\overline{B}\) are derived considering the effects of the two coefficients on the volumetric deformation of the fractured rock mass in response to an applied stress tensor variation \({\varvec{\upsigma}}\). To do so, volumetric deformations, \(\Delta V/V\), under dry (\(\varepsilon\)), saturated drained (\(\varepsilon ^{\prime}\)) and saturated undrained conditions (\(\varepsilon ^{{\prime}{\prime}}\)) are considered, which are related by the following equivalences

$$\frac{\varepsilon }{{\sigma_{m} }} = { }\frac{{\varepsilon^{\prime}}}{{\sigma_{m} - \overline{\alpha }{ }p}} = { }\frac{{\varepsilon^{\prime\prime}}}{{\left( {1 - \overline{\alpha }{ }\overline{B}} \right) \sigma_{m} }},$$
(7)

where \({\sigma }_{m}=tr({\varvec{\upsigma}})/3\) is the average total stress variation. In Eq. 7, \(p\) represents an equivalent pressure variation in the fractured rock, which is multiplied by \(\overline{\alpha }\) defines the volumetric deformation. Since this equivalent pressure variation is a priori unknown, and the field of pressure variation is in general heterogeneous, to derive the equivalent Biot coefficient we impose a homogeneous pressure variation \({p}^{*}\) over the entire rock mass, and from the first equivalence we derive (see also Chen et al. 2020)

$$\overline{\alpha }=\frac{{\varepsilon -\varepsilon }^{\prime}}{\varepsilon } \frac{{\sigma }_{m}}{{p}^{*}}.$$
(8)

Similarly, the amount of pressure variation in the fractured rock consequent to a load application in undrained conditions is heterogeneous, depending on the rock’s hydraulic properties and fracture connectivity. We consider the equivalent pressure variation, i.e., \(\overline{B} {\sigma }_{m}\), which is responsible for the volumetric deformation. By comparing the first and the third terms of Eq. 7, we obtain

$$\overline{B} = \frac{{\varepsilon - \varepsilon^{\prime\prime}}}{\varepsilon }\frac{1}{{ \overline{\alpha } }}.$$
(9)

For the three hydraulic conditions – dry, drained, undrained – the rock mass volume variation, \(\Delta V\), is the sum of the volume variation of each component, i.e., fractures and intact rock, such that

$$\Delta V=\Delta {V}^{r}+ \mathop \sum \limits_{f}\Delta {V}^{f},$$
(10)

where the summation term refers to all the fractures in the system. Acknowledging the assumption of negligible interactions, each component deforms according to its own mechanical properties. We define \({\gamma }^{i}\) as the volume variation of each component \(i\) for a unitary effective “acting” stress, where “acting” refers to the average stress variation for the rock, \({\sigma }_{m}^{\prime},\) and the normal stress variation for the fractures, \({\sigma }_{N}^{\prime}\). This corresponds to \({\gamma }^{r}={V}^{r}/{K}^{r}\) and \({\gamma }^{f}={S}^{f}/{\kappa }_{N}^{f}\), for the rock and each fracture, respectively, with \({V}^{r}\) representing the rock volume and \({S}^{f}\) the fracture surface area. Therefore, Eq. 10 reads

$$\Delta V={\gamma }^{r}{{\sigma }_{m}^{\prime}}+\mathop \sum \limits_{f}{\gamma }^{f}{\sigma }_{N}^{\prime}.$$
(11)

Substitution of Eq. 11 into Eq. 8 and Eq. 9 allows deriving an explicit expression for the two equivalent poroelastic coefficients as (Appendix B)

$$\overline{\alpha }=\frac{{\gamma }^{r}{\alpha }^{r} +\mathop \sum \limits_{f}{\gamma }^{f}{\alpha }^{f} }{{\gamma }^{r} +\mathop \sum \limits_{f}{{\theta }^{f}\gamma }^{f} }, \overline{B}=\frac{{\gamma }^{r}{\alpha }^{r}{B}^{r} +\mathop \sum \limits_{f}{{\theta }^{f}\gamma }^{f}{\alpha }^{f}{B}^{f}}{{\gamma }^{r}{\alpha }^{r} +\mathop \sum \limits_{f}{\gamma }^{f}{\alpha }^{f}}$$
(12)

\({\theta }^{f}\) is defined for each fracture as the ratio between the component of the applied stress that acts normal to the fracture, \({\sigma }_{N},\) and the average applied stress, \({\sigma }_{m}\), such as

$${\theta }^{f}=\frac{{\sigma }_{N}}{{\sigma }_{m}}=\frac{{{\mathbf{n}}}^{T}{\varvec{\sigma}}\mathbf{n}}{tr({\varvec{\sigma}})/3},$$
(13)

where the vector \(\mathbf{n}\) represents the normal to the fracture plane. According to this formal derivation, both coefficients are defined as weighted averages over the values of the corresponding coefficients of each component, with the weight represented by \(\gamma\) or \(\gamma \alpha\) for \(\overline{\alpha }\) and \(\overline{B}\), respectively. Note that, although the coefficients refer to average stresses, \({\sigma }_{m}^{\prime}=\left(1-\overline{\alpha } \overline{B}\right){\sigma }_{m}\), the term \({\theta }^{f}\), in the denominator of \(\overline{\alpha }\) and in the nominator of \(\overline{B}\), implies that the coefficients depend on the applied stress tensor and on the orientation of the fractures. Fractures sub-parallel to an applied unidirectional stress, i.e., \({\theta }^{f}\approx 0\), tend to increase \(\overline{\alpha }\) (because they require a large fluid pressure acting normally on the fracture walls to counterbalance the stress-induced deformation) and to reduce \(\overline{B}\) (because the stress-induced pressure variation is small, recall the definitions in Sect. 1). The opposite occurs with fractures normal to the applied stress variation. Moreover, \({\gamma }^{f}\) depends on the fracture orientation and the initial stress state, because \({\kappa }_{N}^{f}\) depends on the effective stress acting normally on the fracture before the application of the stress and pressure variations.

3 Validation of Formal Expressions

The theoretical expressions derived above (Eq. 12) are validated against results from hydro-mechanical numerical simulations performed with 3DEC7.0 (Itasca Consulting Group, 2020), which uses the distinct element method (Cundall 1988) in three-dimensional domains. A fractured rock mass is considered, in which fractures and deformable rock blocks are explicitly represented. The volumetric deformation of the rock mass to an applied stress is numerically estimated under the three conditions defined in Sect. 2.2—dry, drained and undrained—which are separately simulated. The equivalent poroelastic coefficients are then estimated by comparing the total volume variation calculated in each condition, according to Eq. 8 and Eq. 9.

The geometry consists of a 1 m side cubic volume comprising an intact rock and a set of embedded fractures. These latter are represented as planar zero-thickness elements that deform according to a linear elastic behavior, defined by assigned values of shear stiffness \({\kappa }_{s}^{f}\) and normal stiffness \({\kappa }_{N}^{f}\). Three different scenarios of fracture networks are analyzed. In scenarios 1 and 2 (Figs. 2, 3, 4, 5), the domain comprises parallel infinite fractures (extending throughout the entire domain) aligned with the \(y\)-direction. They are divided in two sets of crossing fractures, the first set with spacing of 0.2 m and dip orientation equal to 60°, the second set with spacing equal to 0.1 m and dip equal to 100° and 150°, for scenario 1 and scenario 2, respectively. This corresponds to an angle between the crossing fractures equal to 40° in scenario 1, while it is equal to 90° in scenario 2. Scenario 3 (Fig. 6) includes a set of randomly distributed and oriented fractures with finite surface; they are stochastically generated considering uniform distribution of location and orientation, constant fracture length equal to 0.25 m, and percolation parameter equal to 1, which fixes the fracture volumetric intensity as \({p}_{32}=\) 2.54 m−1 (Bour and Davy 1997). Note that, since close and parallel fractures are merged during the generation of the 3DEC block geometry, some fractures are larger than 0.25 m. For the three scenarios, fracture aperture \(e\) is set as equal to \(10\upmu\) m for all fractures, which are also characterized by equal values of normal stiffness and shear stiffness, i.e., \({\kappa }_{N}^{f}={\kappa }_{N}\) and \({\kappa }_{s}^{f}={\kappa }_{s} \forall f.\) Intact rock obeys a linear elastic behavior defined by the Young’s (or elastic) modulus, \(E\), and the Poisson’s ratio, \(\nu ,\) such that \({K}^{r}=E/(3(1-2\nu ))\). For both fractures and rock, the Biot coefficient is equal to 1, according to limitations in the simulator settings. Rock porosity \(\phi\) is equal to 0.1, but for scenarios 1 and 2 we also explore the case in which the intact rock is non-porous (\(\phi =0)\), which implies that \({\alpha }^{r}=0\) because there is no fluid in the rock (Figs. 2, 3).

Fig. 2
figure 2

Comparison between theoretically (full markers) and numerically (empty markers) estimated equivalent Biot and Skempton coefficients, for a non-porous rock hosting two sets of parallel infinite fractures crossing at an angle of 40° (scenario 1), and for different values of fracture normal stiffness, \({\kappa }_{N}\), and intact rock Poisson’s ratio, \(\nu\), and elastic modulus, \(E\). From left to right: loading in x-direction, y-direction, z-direction, and hydrostatic loading conditions

Full size image
Fig. 3
figure 3

Comparison between theoretically (full markers) and numerically (empty markers) estimated equivalent Biot and Skempton coefficients, for a non-porous rock hosting two sets of parallel infinite fractures crossing at an angle of 90° (scenario 2), and for different values of fracture normal stiffness, \({\kappa }_{N}\), and intact rock Poisson’s ratio, \(\nu\), and elastic modulus, \(E\). From left to right: loading in x-direction, y-direction, z-direction, and hydrostatic loading conditions

Full size image
Fig. 4
figure 4

Comparison between theoretically (full markers) and numerically (empty markers) estimated equivalent Biot and Skempton coefficients, for a porous rock hosting two sets of parallel infinite fractures crossing at an angle of 40° (scenario 1), and for different values of fracture normal stiffness, \({\kappa }_{N}\), and intact rock Poisson’s ratio, \(\nu\), and elastic modulus, \(E\). From left to right: loading in x-direction, y-direction, z-direction, and hydrostatic loading conditions

Full size image
Fig. 5
figure 5

Comparison between theoretically (full markers) and numerically (empty markers) estimated equivalent Biot and Skempton coefficients, for a porous rock hosting two sets of parallel infinite fractures crossing at an angle of 90° (scenario 2), and for different values of fracture normal stiffness, \({\kappa }_{N}\), and intact rock Poisson’s ratio, \(\nu\), and elastic modulus, \(E\). From left to right: loading in x-direction, y-direction, z-direction, and hydrostatic loading conditions

Full size image
Fig. 6
figure 6

Comparison between theoretically (full markers) and numerically (empty markers) estimated equivalent Biot and Skempton coefficients, for a porous rock hosting randomly generated finite fractures (scenario 3), and for different values of fracture normal stiffness, \({\kappa }_{N}\), and elastic modulus of intact rock, \(E\). The intact rock Poisson’s ratio, \(\nu\), is equal to 0.25. Only the case of loading in y-direction is shown. The response to loading in other directions is similar, due to the uniform distribution of the orientation of the random set of fractures

Full size image

Although \(\overline{\alpha }\) and \(\overline{B}\) are defined with respect to an average applied stress, they depend on the direction of load (recall Eq. 12). To better understand this behavior, we alternatively apply a compressional load along one of the three principal directions (which gives rise to a deviatoric stress) plus a case in which the load is simultaneously applied along the three principal directions (which results in hydrostatic stress condition). To ensure that the problem is well posed, zero-displacement is assigned to three faces of the volume, which ideally correspond to symmetry planes. The compressional load is therefore applied as a normal stress to one or three external faces of the domain. When the stress is only applied to one face of the domain, the other two are let free to deform. These boundary conditions apply to the three cases (dry, drained, undrained), and they are consistent with the assumption that the domain is free from mechanical constraints (Sect. 2.2). With respect to the hydraulic conditions, in the dry case both fractures and rock are set as non-porous. In the drained case, we apply a constant fixed pressure increase \({p}^{*}\) over the entire volume (together with the applied load). Finally, in the undrained case, we assume that the volume is fluid saturated, and no flow conditions are applied to the entire volume. For the three hydraulic cases, we impose a compressional load of 1 MPa, while the pore pressure imposed in the drained case is equal to 0.5 MPa. Although these amounts are conceptually of small magnitude, to ensure that small strains and elastic behavior are preserved, they are irrelevant in the numerical model because we impose linear elastic behavior of both fractures and rock matrix. Note also that the applied stress and pressure are incremental with respect to a generic initial compressive regime, and the stress variation is such that the regime remains unchanged (no tensile regime is generated).

The analysis considers different values of the parameters\(E\), \(\nu\),\({\kappa }_{N}\), which we vary within a range of realistic values (Figs. 2, 3, 4, 5, 6). Fracture shear stiffness \({\kappa }_{s}\) is not relevant in our theoretical model, but we analyze the sensitivity to this parameter to ensure the validity of our theory (Fig. 7). The hydraulic conductivity is also not relevant because we consider only static problems (fluid flow is not simulated) as either a homogeneous pressure or no-flow conditions are imposed, in the drained and undrained conditions, respectively.

Fig. 7
figure 7

Comparison between theoretically (full markers) and numerically (empty markers) estimated equivalent Biot and Skempton coefficients, for a non-porous rock hosting parallel infinite fractures crossing with an angle of 40°, and for different values of fracture normal and shear stiffness, \({\kappa }_{N}\) and \({\kappa }_{s}\). The case of loading in x-direction is shown

Full size image

In Figs. 2, 3, 4, 5, 6, 7, the equivalent coefficients estimated by directly adopting Eq. 12 are compared with the coefficients estimated from numerical simulations. These latter are derived by introducing the total volume variations estimated for each condition—dry (\(\varepsilon\)), drained (\(\varepsilon ^{\prime}\)) and undrained (\(\varepsilon ^{\prime \prime}\))—into Eq. 8 and Eq. 9, along with the imposed average stress and pressure. Results show a good agreement between the theoretical estimations and the numerical modeling results under different geometrical and parametrical conditions (Figs. 2, 3, 4, 5, 6). In our approach, we have neglected the interactions between fractures, as well as the interaction between the fractures and the rock, which implies that the total stress is homogeneous in the system. This can be untrue because fractures crossing each other and of finite size may generate stress fluctuations and accumulation at the fracture tips (Gao and Harrison 2018). However, results show that these fluctuations have negligible effects on the estimation of the poroelastic coefficients under two different values of the fracture crossing angle (scenarios 1 and 2) and in the case in which the fractures embedded in the rock are of finite size (scenario 3). Minor discrepancies are observed in the estimation of the Skempton coefficient, especially when the intact rock is porous (Figs. 4, 5). They are related to numerical instabilities detected in the numerical simulation of the undrained conditions.

Figures. 2, 3, 4, 5, illustrate the variability of the coefficients with respect to key parameters. First, they are highly anisotropic. \(\overline{\alpha }\) is smaller when the load is approximately normal to the fractures (\(x\)-load) than when it is almost parallel (\(z\)-load) to the fractures, because in the latter case a larger pressure is necessary in the fractures to contrast the increase in load. In the case in which the uniaxial load is parallel to the fractures (\(y\)-load), \(\overline{\alpha }\) tends to values larger than 1 because the required pressure in the fractures to contrast the load virtually tends to infinite. Conversely, the opposite behavior is observed for \(\overline{B}\), i.e., it is larger when the load is approximately normal to the fractures (\(x\)-load) than when it is almost parallel (\(z\)-load) to the fractures, because in the former case a larger pressure increase is observed in the fractures in response to undrained loading. In the case in which the uniaxial load is parallel to the fractures (\(y\)-load), \(\overline{B}\) tends to small values because the pressure variation in the fractures in response to undrained loading tends to 0. Note that the values of \(\overline{B}\) larger than 1 are an artifact due to the definition of the coefficient with respect to the average applied stress, e.g., \({\sigma }_{m}={\sigma }_{x}/3\).

Second, more deformable fractures (smaller normal stiffness) embedded in porous rock yield smaller \(\overline{\alpha }\) and larger \(\overline{B}\) when the load is almost normal to the fractures (\(x\)-load), because more deformable fractures have a major impact on the equivalent behavior (the fracture weight \({\gamma }^{f}\) is larger in the weighted averages of Eq. 12), which tends to move the values far from those of the intact porous rock (\({\alpha }^{r}\) and \({B}^{r}\)) and toward those of the fractures (\({\alpha }^{f}\) and \({B}^{f}\)), corrected by the coefficient \({\theta }^{f}\). Consequently, the opposite occurs when the load is parallel or almost parallel to the fractures, i.e., larger \(\overline{\alpha }\) and smaller \(\overline{B}\) are observed when the fractures are more deformable (Figs. 4, 5). Nevertheless, if the intact rock is not porous, the sensitivity of \(\overline{\alpha }\) to fracture normal stiffness under a load almost normal to the fractures (\(x\)-load) is reversed. In this case, indeed, \(\overline{\alpha }\) is larger for smaller normal stiffness (compare Figs. 2 and 3 with Figs 4 and 5, respectively) because the equivalent behavior is not determined by a weighted average, but it is proportionally impacted by the larger values of \({\gamma }^{f}\) (Eq. 12). This reflects that more deformable fractures need larger pressures than less deformable fractures to counterbalance the deformation induced by the load in a non-porous rock. Note also that in the case of non-porous rock, \(\overline{B}\) is only slightly sensitive to the fracture normal stiffness, which corresponds to the sensitivity of the fracture Skempton coefficient \({B}^{f}\). In fact, if the rock is not porous, the pressure variation in response to undrained load only occurs in the fractures, and the equivalent coefficient is \(\overline{B}={B}^{f}{\theta }^{f}\).

Third, when the load is applied approximately normal to the fractures (\(x\)-load), \(\overline{\alpha }\) is slightly smaller for stiffer porous rocks, while \(\overline{B}\) is slighter larger, except when the fracture normal stiffness is very large. Similar to what observed above, these behaviors express the larger contribution of the porous rock on the equivalent behavior when the rock is softer, corresponding to larger rock weight \({\gamma }^{r}\) in the weighted averages of Eq. 12. As above, the behavior is reversed when the load is applied parallel or almost parallel to the fractures. If the rock is not porous, as also observed above, the variability of \(\overline{\alpha }\) with rock stiffness is reversed for the case of \(x\)-load, because stiffer rocks increase the overall stiffness requiring smaller pressures in the fractures to contrast the deformation induced by the load. This is also shown by setting \({\alpha }^{r}=0\) in Eq. 12, and considering that larger rock stiffness corresponds to smaller \({\gamma }^{r}\), which directly impact \(\overline{\alpha }\). Because the non-porous rock has no impact on the equivalent Skempton coefficient, \(\overline{B}\) is completely insensitive to it. Finally, the effect of the Poisson’s ratio is negligible.

Results for a set of randomly distributed and oriented fractures with finite surface (Fig. 6) exhibit a less pronounced sensitivity of \(\overline{\alpha }\) to both fracture and intact rock stiffness, with respect to what observed above for the scenarios with parallel fractures. This apparently surprising result is the consequence of the small fracture density assumed in the case example (percolation parameter equal to 1), which is due to numerical limitations in the hydro-mechanical simulator. As we will analyze more in detail in the next section, the impact of fracture density on \(\overline{\alpha }\) is smaller than on \(\overline{B}\). In other words, large fracture density is required to get values of \(\overline{\alpha }\) different from those of the intact rock, while this does not happen for \(\overline{B}\). Because the fractures do not play a relevant impact on \(\overline{\alpha }\), this latter is not only almost insensitive to the fracture stiffness, but it is also insensitive to the rock stiffness. In fact, the equivalent behavior is not the result of a volumetric balance between deformation of rock and fractures, but it is essentially determined by rock parameters, i.d., \({\alpha }^{r}=1\) in the example here. Conversely, \(\overline{B}\) is more affected by rock and fracture stiffness, because they impact both rock and fracture contribution in the weighted average through \({\gamma }^{r}\) and \({\gamma }^{f}\), and their values of Skempton coefficient \({B}^{r}\) and \({B}^{f}\).

4 Sensitivity Analysis

Results of the previous section already provided some insights into the variability of the equivalent poroelastic coefficients. Based on these observations, in this section we further investigate the role of fracture orientation and properties, and we also analyze the impact of the intact rock porosity, fracture intensity and fracture size. We perform this analysis in two steps. In the first part, we consider systems with parallel fractures to better explore the effects of the fracture orientation. In the second one, we consider a DFN with randomly oriented fractures and we concentrate on the effects of the fracture size distribution.

4.1 Sensitivity to Rock Porosity and to Fracture Orientation, Density and Mechanical Properties Considering DFNs With Parallel Fractures

Let a set of parallel fractures with different sizes. We analyze the cases in which the fracture set orientation with respect to a unidirectional applied load forms angles of 0°, 45° or 90°, corresponding to values of the coefficient \({\theta }^{f}\) (Eq. 13) equal to 0, 1.5 or 3, respectively. For the sake of simplicity, in this section we also assume that all fractures are characterized by the same values of aperture, \(e\), and normal stiffness, \({\kappa }_{N}\), for which we consider different scenarios of values. Under these conditions, the expressions of Eq. 12 can be modified as the terms \({\kappa }_{N}^{f}\), \({\theta }^{f}\), \({\alpha }^{f}\) and \({B}^{f}\) go out of the summation operator, which can be replaced by introducing the geometrical metrics \({p}_{32}=\frac{1}{V}{\sum }_{f}{S}^{f}\) (total area of fractures per unit volume (Dershowitz and Herda 1992))

$$\overline{\alpha }=\frac{{V}^{-1} {\gamma }^{r}{\alpha }^{r} +{{ p}_{32} {\alpha }^{f} \kappa }_{N}^{-1}}{{V}^{-1} {\gamma }^{r} +{ p}_{32}{\theta }^{f}{\kappa }_{N}^{-1}}, \overline{B}=\frac{{V}^{-1} {\gamma }^{r}{\alpha }^{r}{B}^{r} +{ p}_{32}{\theta }^{f}{\alpha }^{f}{B}^{f}{\kappa }_{N}^{-1}}{{V}^{-1} {\gamma }^{r}{\alpha }^{r} +{ p}_{32}{\alpha }^{f}{\kappa }_{N}^{-1}}.$$
(14)

We thus explore the sensitivity to fracture intensity by considering different values of \({p}_{32}\). Note that, because all the fractures have the same orientation and properties, we perform this analysis regardless of the statistical distribution of the fracture size, which, however, directly impacts the \({p}_{32}.\) In the next section, we illustrate the effects of the fracture size distribution.

Differently from the previous section, where the intact rock Biot coefficient \({\alpha }^{r}\) was either 0 (for the case of non-porous rock) or 1 (for the case of porous rock), here we acknowledge the well-recognized proportionality between rock porosity and \({\alpha }^{r}\) (Nguyen et al. 2018; Selvadurai 2021). In particular, we adopt the relationship proposed by Hashin and Shtrikman (1963), which reads

$${\alpha }^{r}=1-\frac{1-\phi }{1+\frac{1-\nu }{2\left(1-2\nu \right)}\phi }.$$
(15)

Results from this analysis (Figs. 8 and 9)show that the presence of fractures increases \(\overline{\alpha }\) and \(\overline{B}\) with respect to the values of the intact rock, and both coefficients increase with increasing \({p}_{32}\). This trend is not unexpected because both Biot and Skempton coefficients are larger in softer rocks (recall also Eq. 2 and Eq. 3 for isotropic materials), and rock mechanical compliance increases with fracture density because fractures weaken the system (Davy et al. 2018; Grechka and Kachanov 2006; Kachanov 1992). Note that in the case that the fracture is parallel to the load (\(\theta =0),\) \(\overline{B}\) is almost 0, so we do not focus on the sensitivity to \({p}_{32}\) for this case. For larger porosity of the intact rock, \(\overline{\alpha }\) is larger due to the proportionality between \({\alpha }^{r}\) and \(\phi\) (Eq. 15), while \(\overline{B}\) is smaller because \({B}^{r}\) decreases with \(\phi\) (recall Eq. 3). With respect to the orientation, \(\overline{B}\) increases with\(\theta\), i.e., the largest value is met when the load is normal to the fractures, while \(\overline{\alpha }\) appears to be almost insensitive to \(\theta\) (Fig. 8). However, \(\overline{\alpha }\) decreases with\(\theta\), when the fractures are more deformable (compare the values for x-load and y-load when \({k}_{N}\) is small in Figs. 2 to 5). Another impact of fracture stiffness \({k}_{N}\) on both \(\overline{\alpha }\) and \(\overline{B}\) is that these parameters decrease by increasing \({k}_{N}\) (Fig. 9). The behavior of \(\overline{\alpha }\) appears in contradiction with results of Figs. 4 and 5, where smaller \(\overline{\alpha }\) were observed for more deformable fractures (smaller normal stiffness) embedded in porous rock. However, more deformable fractures correspond to major fracture impact on the equivalent behavior rather than smaller or larger values of \(\overline{\alpha }\). In fact, if the fracture stiffness is smaller, the fracture weight \({\gamma }^{f}\) is larger in the weighted averages of Eq. 12, which tends to move the values far from those of the intact porous rock (\({\alpha }^{r}\) and \({B}^{r}\)) and closer to those of the fractures (\({\alpha }^{f}\) and \({B}^{f}\)) corrected by the coefficient \({\theta }^{f}\).

Fig. 8
figure 8

Sensitivity of the equivalent Biot and Skempton coefficients to fracture density (\({p}_{32}\)) and to intact rock porosity (\(\phi\)). The analysis considers a vertical load applied to a porous rock, with E = 60 GPa and \(\nu\)=0.25, hosting a set of parallel fractures with equal e \(=10\mu\) m, \({\kappa }_{N}=\) 5000 GPa/m, and orientation, for which three values of \(\theta\) are analyzed. Colors refer to different values of \(\phi\). The red dashed vertical line defines the case with \({p}_{32}=0\), corresponding to intact rock with no fractures

Full size image
Fig. 9
figure 9

Sensitivity of the equivalent Biot and Skempton coefficients to fracture density (\({p}_{32}\)), aperture, \(e\), and normal stiffness, \({\kappa }_{N}\). The analysis considers a vertical load applied to a porous rock, with E = 60 GPa and \(\nu\)=0.25, hosting a set of parallel fractures with equal e, \({\kappa }_{N}\), and orientation, for which the value of \(\theta\) is equal to 1.5. The red dashed vertical line defines the case with \({p}_{32}=0\), corresponding to intact rock with no fractures

Full size image

For equal values of \({k}_{N}\), \(\overline{B}\) decreases with increasing aperture \(e\), while \(\overline{\alpha }\) is not affected by this factor, as also shown in the first of Eq. 12 or Eq. 14. Although the fracture Skempton coefficient, \({B}^{f}\), does not change if the product \({k}_{N}\cdot e\) is kept constant (Eq. 6), the equivalent coefficient \(\overline{B}\) does change, and it is more sensitive to variations in \({k}_{N}\) than to variation in \(e\) of the same order (Fig. 9), because \({k}_{N}\) intervenes in the weighting factor \({\gamma }^{f}\) (Eq. 12 or Eq. 14).

4.2 Sensitivity to Fracture Size Distribution Considering DFNs with Randomly Oriented Fractures

The purpose of the analysis here is to illustrate the role of the fracture size statistical distribution on \({p}_{32}\), which in turn directly impacts the equivalent poroelastic coefficients, as shown in the previous section. To focus on this aspect, we assume that the population of fractures is randomly oriented following a uniform distribution, which means that the effects of the fracture orientation with respect to the applied load are negligible. Thus, we can assume an average value equal to 1 for the parameter \({\theta }^{f}\) for any unidirectional load.

According to the observations for natural geological media (Bonnet et al. 2001; Davy 1993), we sample the fracture sizes from a power-law distribution of the type \(n\left(\ell\right)=\xi {\ell}^{-\omega }\), where \(n\) is the number of fractures with a certain size \(\ell\), which represents the fracture diameter, and \(\xi\) is a parameter that controls the fracture density per unit volume. We explore the case in which \(\omega\) is equal to 3 and 4, and we consider the size \(\ell\) ranging between a minimum value \({\ell}_{0}\) and a maximum value \(L\). For the latter we assume it as equal to the lateral dimension of the rock mass, i.e., \(L=1\) m considering a unitary rock volume. We set the parameter \(\xi\) such that the maximum \({p}_{32}\) in both scaling models is equal to 10 m−1. For the lower cut-off value, \({\ell}_{0}\), we analyze the results under different values ranging between 1 mm and 1 m, which greatly affects \({p}_{32}\).

Indeed, \({p}_{32}\) increases with decreasing \({\ell}_{0}\) at a rate controlled by the scaling factor \(\omega\). If \(\omega =4,\) then \({p}_{32}={\int }_{{\ell}_{0}}^{L}\pi /4 {\ell}^{2} n\left(\ell\right)\propto {L}^{-1}-{\ell}_{0}^{-1}\), while if \(\omega =3\), then \({p}_{32}\propto \mathrm{ln}(L/{\ell}_{0})\) (Fig. 10). From the estimates of \({p}_{32}\), the coefficients are analytically calculated from Eq. 14, by assuming \({\theta }^{f}=1\). We observe that both poroelastic coefficients increase as \({\ell}_{0}\) decreases, corresponding to the increase of \({p}_{32}\). The increasing rate is larger when \(\omega\) is equal to 4 than when it is equal to 3.

Fig. 10
figure 10

From top to bottom: Equivalent Biot coefficient, equivalent Skempton coefficient, and fracture area per unit volume \({p}_{32}\) for different values of the smallest fracture size in the DFN,\({\ell}_{0}\), under two different scalings of the power law distribution of the fracture size, \(\omega\). Lines represent results derived analytically from Eq. 14, by assuming \({\theta }^{f}=1\) and the values of \({p}_{32}\) derived as described in the text. Markers represent the results obtained by stochastically generating DFN and applying Eq. 12. Results refer to porous rock properties E = 60 GPa, \(\phi =0.01\) and \(\nu\)=0.25, while fracture properties are homogeneous and such that \(e=10\mu\) m and \({\kappa }_{N}=\) 1000 GPa/m

Full size image

We compare the analytical estimates with the ones obtained by applying Eq. 12 on stochastically generated DFNs created by means of DFN.Lab (Le Goc et al. 2019). Direct analytical estimation and stochastic estimations slightly differ, especially for large values of \({\ell}_{0}\), because the assumption of uniformly distributed orientations breaks when the number of fractures is small (compare the markers and the lines in Fig. 10). The impact is larger in the estimations of the Skempton coefficient, which is more sensitive to the fracture orientation, as shown in the previous section.

5 Discussion and Conclusions

We have derived simple expressions that allow estimating equivalent Biot and Skempton coefficients for a saturated fractured rock mass from the properties of the porous intact rock and fracture network that it comprises. To this end, we have first established a meaning for equivalent as corresponding to the volumetric deformation. This definition is applied to define an equivalent pressure variation in the system, where the pressure variation is heterogeneous and depends on the fracture connectivity and on the hydraulic properties of fractures and intact rock. This concept of equivalent is also applied to the Biot and Skempton coefficients, which are therefore the ones that effectively predict the volumetric deformation of the rock mass in response to an applied stress. This approach provides coefficients that describe the HM behavior of a fractured rock mass better than if effective compliances representative of the rock mass (e..g., Davy et al. 2018; Kachanov 1992; Min and Jing 2003) are introduced in Eq. 2 and Eq. 3, as already shown by Chen et al. (2020). In fact, we derive anisotropic expressions of the coefficients that depend on the fracture orientation with respect to the applied load, and on their capacity of changing their volume (or aperture), which depends on fracture normal stiffness. Effective compliance of fractured rock is much affected by fracture shear stiffness (Davy et al. 2018), which instead does not affect the variation of the fracture aperture. It is important to emphasize that the two coefficients depend not only on the characteristics of the fractured rock but also on the initial stress tensor and the applied stress variation.

Given that the presence of deformable fractures weakens the system in the direction orthogonal to the fractures, both the equivalent Biot and Skempton coefficients increase with fracture density and with their normal compressibility (Eq. 14, Fig. 8 and Fig. 9). This agrees with experimental observations that the coefficients are generally larger in soft rocks than in stiff ones (Kasani and Selvadurai 2023), and that they are larger in cracked rocks than in intact rocks (Selvadurai and Suvorov 2020). The implication is not negligible. Let’s consider an external load/unload applied to the system, coinciding with a variation of total stress. In dry conditions, a fractured rock deforms more than an intact rock, as fractures increase the equivalent rock compliance. However, in saturated undrained conditions, the resulting effective stresses are much smaller in a fractured rock than in an intact rock, because the fluid in the fractures bears most of the load, i.e., \({\sigma }_{m}^{\prime}=\left(1-\overline{\alpha } \overline{B}\right){\sigma }_{m}\). Consequently, under the same applied external load and initial conditions, a fractured rock may deform less than an intact rock, depending on the relative impact of fractures on the equivalent rock compliance and on the factor (\(1-\overline{\alpha }\overline{B}\)). Clearly, deformations in a fractured rock are smaller if the fractures are fluid-filled than when they are dry (Berryman 2012).

A natural question arises about the behavior in saturated drained conditions. The time of applicability of the undrained conditions depends on the hydraulic characteristic time of the system, which is strictly related to the hydraulic diffusivity. In conditions where porosity and hydraulic conductivity are much lower in the matrix than in the fractures, we expect large differences in pressure change times for fractures connected to boundary conditions and those that are not. The time of applicability of the undrained conditions therefore depends on the characteristics of the fracture network, in particular its connectivity (Bour and Davy 1997; Maillot et al. 2016), but also on the scale of the rock mass with respect to a potential outlet for the stress-induced pressure change to dissipate. Because there are fractures that are hydraulically disconnected from the main cluster, residual pressure variation will persist in those fractures, meaning that the term \(\overline{\alpha } \overline{B}\) does not vanish in the long-term. A long-term \(\overline{\alpha } \overline{B}\) could be estimated if only the disconnected fractures are included in the summation terms of Eq. 12.

The expressions proposed in this work build on the assumption that the properties of intact rock and embedded fracture network are known. While intact rock properties may be estimated by laboratory experiments on rock samples, the information on the fracture network is often lacking and uncertainties arise from parameters that are not yet constrained by measurements. By using the derived expressions, we have shown the range of variability of the two coefficients with respect to the principal fracture parameters. Fracture aperture \(e\) slightly affects the equivalent Skempton coefficient because it affects the fracture Skempton coefficient \({B}^{f}\), while the equivalent Biot coefficient is insensitive to this parameter (see Eq. 12). An additional uncertainty comes from the mechanical properties, i.e., normal stiffness \({\kappa }_{N}\). Estimates from laboratory tests on fractured samples are not representative of large fractures. The range of uncertainty can be wide, and it may sensibly affect the value of both equivalent coefficients (Fig. 9). Moreover, both \({\kappa }_{N}\) and \(e\) are generally affected by the initial stress regime acting on the fracture (Bandis et al. 1983; Barton et al. 1985), which may be uncertain as well. The fraction of open/sealed fractures is another important parameter because sealed fractures do not contain fluid.

The size of the fractured rock mass is also a critical issue. Although the coefficients are formally independent of the rock mass volume (it cancels out in Eq. 12), they can suffer from scale effects because the estimation of the geometrical and mechanical properties of fracture networks may be affected by the size of the observed domain. Defining a representative elementary volume (REV) for the Biot and Skempton coefficients of fractured rocks (a minimum volume of sampling domain beyond which the coefficients remains mostly constant) is however beyond the scope of this work.

The fracture network geometrical characteristics (fracture density, size, aperture) are in general inferred from borehole observations and assuming a statistical distribution for the fracture size. We have shown the sensitivity of the poroelastic coefficients to the uncertainty in the exponent of the power law distribution, \(\omega\), and in the size of the smallest fracture, \({\ell}_{0}\). Overestimating the smallest fracture size means underestimating the poroelastic coefficients, with an error that increases with the power law exponent. On the other hand, underestimating the power law exponent leads to overestimation of the poroelastic coefficients. The exponent of the power law distribution and the size of the smallest fracture exclusively impact the fracture surface area per unit volume, \({p}_{32}\), which ultimately governs the poroelastic coefficients. In other words, two fractured rocks with the same value of \({p}_{32}\) are characterized by the same poroelastic coefficients, regardless of the values of \(\omega\) and \({\ell}_{0}\). It should be emphasized that this behavior only occurs if the fracture aperture and normal stiffness are homogeneous, as we have assumed in the sensitivity analysis for simplicity. However, fracture aperture and normal stiffness are in general correlated with the fracture size (de Dreuzy et al. 2002; Worthington and Lubbe 2007). It remains unknown whether the role of \(\omega\) and \({\ell}_{0}\) is different if size-dependent aperture and normal stiffness are considered, which will be the focus of future work. Note that Eq. 14 is not valid in the case of heterogeneous fracture aperture and normal stiffness, while Eq. 12 holds.

Similarly, we have analyzed the ideal case with one set of parallel fractures or uniformly distributed fracture orientations. Future work will analyze the variability of the Biot and Skempton coefficients for more realistic fracture networks with different sets of fracture orientations, stress-dependent fracture stiffness, and scaling relationships linking fracture size, aperture and stiffness.