1 Introduction

When the underground engineering below the groundwater table, the engineering is not only affected by the in-site stress, but also affected by the seepage force (De Caro et al. 2020; Li et al. 2022a; Wang et al. 2022a). Vice versa, engineering disturbance will cause mechanical response of surrounding rock and change the initial seepage field. In the above hydraulic–mechanical coupling process, the deformation and failure of the surrounding rock depend on the effective stress (Fransson and Viola 2021; Zhao et al. 2021; Wang et al. 2022b). The study of the hydraulic–mechanical coupling of underground tunnel is of guiding significance for the stability evaluation, support design, and cut-off/drainage design of the tunnel.

The analytical solutions of seepage and mechanics in the surrounding rock of circular tunnel have been studied extensively. Kolymbas and Wagner (2007) deduced the analytical solution of groundwater stable entry into tunnel by means of conformal mapping. Detournay and Cheng (1988) analyzed various coupled pore-elastic processes caused by vertical drilling in saturated formations under non-hydrostatic geostresses. Plastic failure of tunnel caused by high ground stress has attracted the attention of abundant scholars. Shin et al. (2011) studied the elastoplastic mechanical behavior of the tunnel caused by seepage with the MC failure criterion. Taking the seepage force as the volume force to evaluate the influence of pore water pressure on the stability of surrounding rock has been carried out in MC criterion (Bobet 2010; Lee et al. 2007; Shin et al. 2010) and HB materials (Fahimifar and Zareifard 2009; Sharan 2005; Zareifard and Fahimifar 2014) According to the plane strength theory, the intermediate principal stress is ignored in the above studies, and the calculation results of stress tend to be conservative.

Deep-buried circular tunnel is usually accompanied by high ground stress, which will cause the yield failure at the periphery of the tunnel. To simplify the process of fluid–structure coupling modeling, stress superposition or the seepage equation of fixed state is considered. To simplify the process of groundwater hydraulic–mechanical coupling modeling, stress superposition method (Wang and Dusseault 1994) or the specific seepage equation (Zhang et al. 2019) is considered. Zareifard and Fahimifar (2014) deduced the elastoplastic solution of a circular tunnel under steady flow by assuming a constant permeability coefficient. Related to the change of effective stress, the deformation and failure of surrounding rock change the permeability which is consistent with the experimental results of previous study (Chen et al. 2007; Wang et al. 2013; Xu and Yang 2016; Yang et al. 2015; Zhao et al. 2022; Zhang et al. 2023). Fahimifar and Zareifard (2013) deduced the distribution of strain-dependent permeability. According to the method of permeability proportion fraction, Dong et al. (2019) generalized the evolution law of permeability coefficient in elastic zone and plastic zone, so as to establish the hydraulic–mechanical coupling model. When the permeability coefficient changes along the seepage path, the flow velocity often depends on the part with the lowest permeability. However, in the previous studies, this detail is often ignored, which may lead to a larger calculation result.

In this paper, the permeability coefficient is a non-constant parameter in the calculation of coupling. According to the deformation characteristics, the permeability coefficient evolution model and the seepage model in the elastic and plastic zone are established, respectively. Based on the conservation of fluid mass and the physical relation between the equivalent permeability coefficient and the head loss, a new closed solution for circular tunnel with fluid–structure coupling was proposed. Considering the effect of intermediate principal stress, the hydraulic–mechanical coupling model with DP criterion is derived. Finally, the derived stress solution is verified by numerical simulation method.

2 Background Study and General Theory

2.1 General Theory and Assumptions

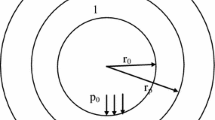
In this study, the mechanical problem of a circular underground tunnel is identified as a two-dimensional plane strain model. Surrounding rock in the range of inner diameter \(r_{0}\) to outer diameter \(r_{R}\) is assumed to be homogeneous isotropic and the plastic volume is considered incompressible. The assumption of incompressibility of the plastic volume is used to simplify the effect of plastic strain on the change in pore volume and thus obtain a solvable differential equation. Such an assumption would neglect the contribution of plastic strain to pore alteration after yielding of the surrounding rock. Changes in porosity are thought to be exponential to permeability. The intermediate principal stress can be represented by two other stress components in the plane, so that the stress differential equation satisfying the DP failure criterion has an analytical solution. The outer boundary is subjected to uniform in-situ stress \(\sigma_{R}\) and pore water pressure \(P_{R}\). Axial stress is considered to be the intermediate value between radial stress and tangential stress. The effective stress is applied in DP yield criterion to determine the plastic zone range and stress distribution of surrounding rock. The DP yield criterion expressed by effective stress can be expressed as follows:

$$F\left( {I_{1}^{\prime } ,\sqrt {J_{2}^{\prime } } } \right) = \sqrt {J_{2}^{\prime } } - \beta I_{1}^{\prime } - K = 0,$$
(1)

where \(I_{1}^{\prime }\) and \(J_{2}^{\prime }\) are the first invariants of stress tensor and the second invariants of deviatoric tensor of stress expressed by effective stress, respectively, which are defined as follows:

$$I_{1}^{\prime } = \sigma_{r}^{\prime } + \sigma_{\theta }^{\prime } + \sigma_{z}^{\prime }$$
(2)
$$J_{2}^{\prime } = \frac{1}{6}\left[ {\left( {\sigma_{r}^{\prime } - \sigma_{\theta }^{\prime } } \right)^{2} + \left( {\sigma_{\theta }^{\prime } - \sigma_{z}^{\prime } } \right)^{2} + \left( {\sigma_{z}^{\prime } - \sigma_{r}^{\prime } } \right)^{2} } \right].$$
(3)

Effective stress is defined as follows:

$$\sigma_{\theta }^{\prime } = \sigma_{\theta } - \alpha P{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \sigma_{r}^{\prime } = \sigma_{r} - \alpha P{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \sigma_{z}^{\prime } = \sigma_{z} - \alpha P,$$
(4)

where α is the Biot coefficient, which generally depends on the volume modulus of surrounding rock and solid granular material (in this solution, α is regarded as a constant); P is pore water pressure; the subscripts θ, r, and z refer to the tangential, radial, and axial directions, respectively. For example, \(\sigma_{r}\) represents radial stress. In DP yield criteria, β and K are strength parameters related to friction angle and cohesion, which are defined as follows (Kabwe et al. 2020):

$$K = \frac{6C\cos \varphi }{{\sqrt 3 \left( {3 - \sin \varphi } \right)}}$$
(5)
$$\beta = \frac{6\sin \varphi }{{\sqrt 3 \left( {3 - \sin \varphi } \right)}},$$
(6)

where φ is the internal friction angle and C is the cohesion force. In the case of the assumption of plasticity incompressible, the plastic incompressible plane strain model has the following relation:

$$\sigma_{z} = \frac{{\sigma_{r} + \sigma_{\theta } }}{2}.$$
(7)

2.2 Governing Equations

The schematic diagram of stress of a deeply buried tunnel in a saturated formation is shown in Fig. 1. In the figure, subscript r is the distance to the center of the circle, and the subscripts 0, y, and R represent the periphery, the elastoplastic interface, and the outer boundary, respectively. The rock skeleton is considered to be elastically compressible and is specified to be positive for compression and negative for tension. Assuming that the pore water pressure only bears positive stresses and has no effect on shear stresses, the constitutive equations can be expressed by the following equation:

$$\left\{ {\begin{array}{*{20}l} {\sigma_{r} = \lambda \varepsilon_{v} + 2G\varepsilon_{r} + \alpha P} \hfill \\ {\sigma_{\theta } = \lambda \varepsilon_{v} + 2G\varepsilon_{\theta } + \alpha P} \hfill \\ \end{array} } \right.,$$
(8)

where λ and G are the Lamé constants, and \(\varepsilon_{r}\), \(\varepsilon_{\theta }\), and \(\varepsilon_{v}\) are the radial, tangential, and volume strain, respectively. The volumetric strain and geometric equations and the equilibrium equation in the plane strain axisymmetric problem have the following form:

$$\varepsilon_{r} = \frac{\partial u}{{\partial r}},{\mkern 1mu} {\mkern 1mu} \varepsilon_{\theta } = \frac{u}{r}$$
(9)
$$\varepsilon_{v} = \varepsilon_{r} + \varepsilon_{\theta } = \frac{\partial u}{{\partial r}} + \frac{u}{r} = \frac{1}{r}\frac{{\partial \left( {ru} \right)}}{\partial r}$$
(10)
$$\frac{{\partial \sigma_{r} }}{\partial r} + \frac{{\sigma_{r} - \sigma_{\theta } }}{r} = 0,$$
(11)

where u is radial displacement.

Fig. 1
figure 1

Hydraulic–mechanical calculation model of a circular tunnel

Full size image

2.3 Basic Problems of Hydraulic–Mechanical Coupling

The key point of hydraulic–mechanical coupling is to establish the dynamic mathematical model of pore volume n and permeability coefficient k. To solve seepage problems in circular cavity, previous studies mainly treat the seepage force of a fixed potential as a volume force (Fahimifar and Zareifard 2013; Li et al. 2022b). This obviously ignores the effect of rock compression on permeability. Assuming that water is incompressible, the change in volume of the rock \(\Delta V\) equals the change in pore volume \(\Delta n\), and also equals the water content of the outflow ϑ. The change in water content has the following expression (Biot 1941):

$$\Delta V = \Delta n = \vartheta = \frac{P}{Q} - \alpha \varepsilon_{v} .$$
(12)

In an isotropic homogeneous porous elastic medium, the permeability is a function of the pore volume. Xu et al. (2000) presented an exponential relationship between the permeability coefficients k and pore volume n

$$k\left( n \right) = k_{0} {\text{e}}^{an} = K_{0} {\text{e}}^{a\Delta n} ,\quad K_{0} = k_{0} {\text{e}}^{{\alpha n_{0} }} ,$$
(13)

where a is an empirical constant and k0 is the initial intrinsic permeability. Substituting Eq. (12) into Eq. (13) yields the following equation, which is the basis for solving the nonlinear seepage and flow coupling problem later:

$$k\left( n \right) = K_{0} {\text{e}}^{{a\left( {\frac{P}{Q} - \alpha \varepsilon_{v} } \right)}} .$$
(14)

The nonlinear Darcy seepage equation and the continuity equation have the following forms:

$$q = k\left( n \right)\frac{\partial P}{{\partial r}}$$
(15)
$$\nabla \left( {\rho k\left( n \right)\frac{\partial P}{{\partial r}}} \right) = n_{0} \frac{\partial P}{{\partial t}} + \frac{1}{Q}\frac{{\partial \left( {\rho P} \right)}}{\partial t} - \alpha \frac{{\partial \left( {\rho \varepsilon_{v} } \right)}}{\partial t},$$
(16)

where ρ denotes water density which is assumed as incompressible (i.e., ρ is a constant). The continuous equation of stable seepage for two-dimensional axisymmetric incompressible fluid can be simplified as follows:

$$\frac{1}{r}\frac{{\text{d}}}{{{\text{d}}r}}\left[ {rk\left( n \right)\frac{{{\text{d}}P}}{{{\text{d}}r}}} \right] = 0.$$
(17)

Substituting the constitutive Eq. (8) into the equilibrium Eq. (11), obtains the equilibrium equation with pore pressure. To solve the equilibrium equation, the basic differential equation for solving stress can be obtained using Eq. (10)

$$\frac{{\text{d}}}{{{\text{d}}r}}\left\{ {\frac{1}{r}\frac{{d\left( {ru} \right)}}{dr}} \right\} = - \frac{\alpha }{\lambda + 2G}\frac{{{\text{d}}P}}{{{\text{d}}r}}.$$
(18)

Equations (17) and (18) are the basic differential equations of seepage and mechanics. Obviously, they are coupled and cannot be solved separately. After obtaining the displacement u and pore water pressure P, the stress and strain can be solved by solving the geometric equation and constitutive equation. When the stress exceeds the yield strength of the surrounding rock, a plastic yield zone is generated first at the periphery of the tunnel. For the case of plastic damage, the fixed solution conditions are more demanding and the boundary conditions on the elastic-plasticity need to be considered. The percolation conditions and mechanical behavior of the plastic zone are altered, and these are discussed in the next section.

2.4 Boundary Conditions

The tangential and radial stresses at the outer boundary are equal to the in-situ stress \(\sigma_{R}\). At the inner boundary, the support force is \(\sigma_{0} = 0\). A constant head boundary is set at outer boundaries, water flowing inwards from the outer boundary. The radial stress and pore water pressure are continuous at the junction of the elastoplastic region. Thus, the boundary conditions can be expressed as follows:

$$\left\{ {\begin{array}{*{20}l} {\sigma_{r} = \sigma_{\theta } = \sigma_{R} {\mkern 1mu} {\mkern 1mu} ,{\mkern 1mu} {\mkern 1mu} P = P_{R} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {r = r_{R} } \right){\mkern 1mu} {\mkern 1mu} } \hfill \\ {\sigma_{r} = \sigma_{r}^{\left( e \right)} = \sigma_{r}^{\left( p \right)} = \sigma_{y} {\mkern 1mu} {\mkern 1mu} ,{\mkern 1mu} {\mkern 1mu} P = P_{y} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {r = r_{y} } \right)} \hfill \\ {\sigma_{r} = \sigma_{0} {\mkern 1mu} = 0{\mkern 1mu} ,{\mkern 1mu} {\mkern 1mu} P = P_{0} = 0{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {r = r_{0} } \right){\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} } \hfill \\ \end{array} } \right..$$
(19)

2.5 Hydraulic Problem

Carrying out one integral calculation of Eq. (18) and combining with the definition of the pore volume increment in Eq. (12) yield

$$\Delta n = \left( {\frac{1}{Q} + \frac{\alpha }{\lambda + 2G}} \right)P + \alpha C_{1} ,$$
(20)

where C1 is the integration constant, which can be obtained using the boundary conditions at \(r_{R}\)

$$C_{1} = \frac{{\sigma_{R} - \alpha P_{R} }}{\lambda + G} + \frac{\alpha }{\lambda + 2G}P_{R} .$$
(21)

The total volume strain of the plastic zone is \(\varepsilon_{v} = \varepsilon_{v}^{\left( e \right)} + \varepsilon_{v}^{\left( p \right)}\). Due to the assumption of plasticity incompressible, the plastic strain has no effect on the change of pore volume. For a completely plastic material, \(\varepsilon_{v}^{\left( e \right)} = const\) after yielding. Substituting Eqs. (20) and (21) into Eq. (13) yields

$$k^{\left( e \right)} \left( n \right) = K_{0} {\text{e}}^{{\left[ {a\left( {\frac{1}{Q} + \frac{\alpha }{\lambda + 2G}} \right)P + \alpha \left( {\frac{{\sigma_{R} - \alpha P_{R} }}{\lambda + G} + \frac{\alpha }{\lambda + 2G}P_{R} } \right)} \right]}} .$$
(22)

Equation (22) is substituted into Eq. (17) to obtain the seepage differential equation in the elastic zone

$$\frac{1}{r}\frac{{\text{d}}}{{{\text{d}}r}}\left[ {r{\text{e}}^{{A_{1} P^{\left( e \right)} }} \frac{{{\text{d}}P^{\left( e \right)} }}{{{\text{d}}r}}} \right] = 0.$$
(23)

Similar to the plastic zone, the equations for permeability coefficient and the differential equations seepage can be obtained as

$$k^{\left( p \right)} \left( r \right) = K_{0} {\text{e}}^{{a\left[ {\frac{P}{Q} + \alpha \varepsilon_{v}^{\left( e \right)} } \right]}}$$
(24)
$$\frac{1}{r}\frac{{\text{d}}}{{{\text{d}}r}}\left[ {r{\text{e}}^{{A_{2} P^{\left( p \right)} }} \frac{{{\text{d}}P^{\left( p \right)} }}{{{\text{d}}r}}} \right] = 0,$$
(25)

where \(A_{1} = a\left( {\frac{1}{Q} + \frac{\alpha }{\lambda + 2G}} \right),\;A_{2} = \frac{\alpha }{Q}\). From the above derivation process, for the elastic and plastic seepage equations under steady-flow conditions, the difference lies mainly in the different permeability coefficients. The pore volume change in the elastic zone is affected by volume strain and pore water pressure, while that in the plastic zone is only affected by pore water pressure. The permeability coefficient k is continuous in the elastic zone and the plastic zone with an inflection point at r elastic–plastic junction. In general, the closer to the periphery of the tunnel, the more rock strain before plastic yielding, resulting in a lower permeability coefficient.

3 Solution of Nonlinear Flow Coupling Problem Based on DP Criterion

3.1 Stress Solution

The stresses in the elastic zone are solved by integrating Eq. (18) twice

$$u^{\left( e \right)} \left( r \right) = - \frac{\alpha }{\lambda + 2G}\frac{1}{r}\int_{{r_{y} }}^{r} {P^{\left( e \right)} \left( {r\prime } \right)} r\prime {\text{d}}r\prime + \frac{{C_{2} }}{2}\left( {r + \frac{{r_{y}^{2} }}{r}} \right) + \frac{{r_{y} }}{r}C_{3} ,$$
(26)

where C2 and C3 are the integration constants, and ry indicates the radius of the plastic area, r` is a integration variable. Bringing the boundary conditions at the outer boundary \(r_{R}\) and the elastoplastic junction \(r_{y}\) into the geometric equations and the intrinsic equations, yields

$$C_{2} = \frac{1}{{\left( {\lambda + G} \right)}}\left[ {\frac{{\sigma_{R} R^{2} - \sigma_{y} r_{y}^{2} }}{{R^{2} - r_{y}^{2} }} - \frac{2\alpha G}{{\lambda + 2G}}\frac{1}{{R^{2} - r_{y}^{2} }}\int_{{r_{y} }}^{R} {P^{\left( e \right)} \left( {r\prime } \right)r\prime {\text{d}}r\prime } } \right]{ ,}$$
(27)

where

$$C_{3} = C_{2} \left[ {1 + \frac{\lambda }{2G}} \right]r_{y} - \frac{{\sigma_{y} r_{y} }}{2G}$$
(28)
$$\sigma_{r}^{\left( e \right)} \left( r \right) = \frac{2\alpha G}{{\lambda + 2G}}\left[ {\frac{1}{{r^{2} }}\int_{{r_{y} }}^{r} {P^{\left( e \right)} \left( {r\prime } \right)r\prime {\text{d}}r\prime - \frac{1}{{R^{2} - r_{y}^{2} }}\left( {1 - \frac{{r_{y}^{2} }}{{r^{2} }}} \right)\int_{{r_{y} }}^{R} {P^{\left( e \right)} \left( {r\prime } \right)r\prime {\text{d}}r\prime } } } \right] + \frac{{\sigma_{R} R^{2} - \sigma_{y} r_{y}^{2} }}{{R^{2} - r_{y}^{2} }} - \frac{{\left( {\sigma_{R} - \sigma_{y} } \right)R^{2} r_{y}^{2} }}{{\left( {R^{2} - r_{y}^{2} } \right)r^{2} }}$$
(29)
$$\sigma_{\theta }^{\left( e \right)} \left( r \right) = \frac{2\alpha G}{{\lambda + 2G}}\left[ {P - \frac{1}{{r^{2} }}\int_{{r_{y} }}^{r} {P^{\left( e \right)} \left( {r\prime } \right)r\prime {\text{d}}r\prime - \frac{1}{{R^{2} - r_{y}^{2} }}\left( {1 + \frac{{r_{c}^{2} }}{{r^{2} }}} \right)\int_{{r_{y} }}^{R} {P^{\left( e \right)} \left( {r\prime } \right)r\prime {\text{d}}r\prime } } } \right] + \frac{{\sigma_{R} R^{2} - \sigma_{y} r_{y}^{2} }}{{R^{2} - r_{y}^{2} }} + \frac{{\left( {\sigma_{R} - \sigma_{y} } \right)R^{2} r_{y}^{2} }}{{\left( {R^{2} - r_{y}^{2} } \right)r^{2} }}.$$
(30)

Equations (29) and (30) are the elastic solutions of the radial and tangential stresses. It is worth mentioning that the first term on the right-hand side of both equations is related to the pore water pressure, and the elastic solutions degenerate to the classical Lamé solution when the pore water pressure P is kept constant equal to 0.

Plastic deformation occurs when the stress in the surrounding rock meets the yield condition of Eq. (1). The simple transformation of yield conditions is made by combining Eqs. (1)–(7)

$$\sigma_{r} - \sigma_{\theta } = - \frac{6\beta }{{1 + 3\beta }}\left( {\sigma_{r} - \alpha P^{\left( p \right)} + \frac{K}{3\beta }} \right).$$
(31)

Substituting Eq. (31) into the equilibrium Eq. (11) yields the differential equation for solving the plastic stress

$$\frac{{{\text{d}}\sigma_{r} }}{{{\text{d}}r}} - \frac{6\beta }{{1 + 3\beta }}\left( {\sigma_{r} - \alpha P^{\left( p \right)} + \frac{K}{3\beta }} \right)\frac{1}{r} = 0.$$
(32)

Integrating the above equation once and making \(M = \frac{6\beta }{{1 + 3\beta }}\) yields

$$\sigma_{r}^{\left( p \right)} \left( r \right) = \left[ {\int {\left( { - \frac{M}{3\beta }\left( {3\alpha P^{\left( p \right)} \beta - K} \right)r^{ - M - 1} } \right){\text{d}}r + C_{4} } } \right]r^{M} .$$
(33)

The constant of integration C4 can be eliminated using the inner boundary condition

$$C_{4} = \frac{{\sigma_{0} }}{{r_{0}^{M} }}.$$
(34)

Then, Eq. (33) can be expressed as

$$\sigma_{r}^{\left( p \right)} \left( r \right) = \left[ { - \alpha M\int_{{r_{0} }}^{r} {P_{r}^{\left( p \right)} r{`}^{{\left( { - M - 1} \right)}} {\text{d}}r\prime - \frac{K}{3\beta }\left( {r^{ - M} - r_{0}^{ - M} } \right) + \frac{{\sigma_{0} }}{{r_{0}^{M} }}} } \right] \cdot r^{M} .$$
(35)

Considering the yield condition Eq. (31), one can obtain the tangential stress in the plastic zone

$$\sigma_{\theta }^{\left( p \right)} \left( r \right) = \sigma_{y} \left( {1 + M} \right) + M\left( {\frac{K}{3\beta } - \alpha P_{y} } \right).$$
(36)

3.2 Hydraulic Solution

The basic differential equations for seepage in the elastic and plastic zones have been discussed above, and this section further solves these differential equations. The solution of the equation for seepage in the elastic zone requires integrating Eq. (23) twice and then eliminating the integration constants using the first and second terms of Eq. (19) (boundary conditions outside the elastic zone and boundary conditions inside the elastic zone). Similarly, Eq. (25) is integrated twice, and then, the integration constants are eliminated using the second and third terms of Eq. (19) (boundary conditions outside the plastic zone and boundary conditions inside the plastic zone).

The seepage equation in the elastic region can be obtained

$$P^{\left( e \right)} \left( r \right) = \frac{1}{{A_{1} }}\ln \left( {\frac{{{\text{e}}^{{A_{1} P_{R} }} - {\text{e}}^{{A_{1} P_{y} }} }}{{\ln \frac{R}{{r_{y} }}}}\ln \frac{r}{{r_{y} }} + {\text{e}}^{{A_{1} P_{y} }} } \right).$$
(37)

Similarly, the seepage equation in the plastic zone is

$$P^{\left( p \right)} \left( r \right) = \frac{1}{{A_{2} }}\ln \left( {\frac{{{\text{e}}^{{A_{2} P_{y} }} - {\text{e}}^{{A_{2} P_{0} }} }}{{\ln \frac{{r_{y} }}{{r_{0} }}}}\ln \frac{r}{{r_{0} }} + {\text{e}}^{{A_{2} P_{y} }} } \right).$$
(38)

Because the second term of Eq. (19) is applied in the solution of both Eqs. (37) and (38), it is obvious to obtain the conclusion that the pore water pressure is equal at the junction of the elastic and plastic zones. Since the pore water pressure P is indicated here to be identical, additional conditions need to be found to seal the coupled system.

3.3 Coupled Equations

After solving seepage equation in the elastoplastic region, the pore water pressure P in the stress Eqs. (29), (30), (35), and (36) has a specific expression. In solving the stress equation for the plastic zone, only the inner boundary conditions are used, so here the following relationship can be obtained using the condition that the radial and tangential stresses at \(r_{y}\) are equal:

$$\sigma_{y} = \left[ { - \alpha M\int_{{r_{0} }}^{{r_{y} }} {P^{\left( p \right)} \left( {r\prime } \right)r\prime^{{\left( { - M - 1} \right)}} } {\text{d}}r\prime - \frac{K}{3\beta }\left( {r_{y}^{ - M} - r_{0}^{ - M} } \right) + \frac{{\sigma_{0} }}{{r_{0}^{M} }}} \right] \cdot r_{y}^{M}$$
(39)
$$\sigma_{\theta }^{\left( e \right)} \left( {r_{y} } \right) = \sigma_{y} \left( {1 + M} \right) + M\left( {\frac{K}{3\beta } - \alpha P_{y} } \right).$$
(40)

The two equations above have three unknown parameters \(r_{y}\), \(\sigma_{y}\), and \(P_{y}\). Obviously, the system of equations is not closed. However, the boundary condition at \(r_{y}\) for pore water P has already been used in the solution of the seepage equation.

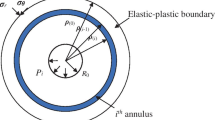
Figure 2 shows the alternating aquifers in the seepage path, each with independent permeability coefficients. In this case, the water flow is equal in each aquifer, the hydraulic slope of each aquifer is different, and the total hydraulic slope is equal to the sum of the head loss of each aquifer

$$Q = k_{i} A\frac{{\Delta P_{i} \rho g}}{{L_{i} }},\quad \Delta P_{i} = \frac{{L_{i} Q}}{{k_{i} A\rho g}}.$$
(41)
Fig. 2
figure 2

“Strung” aquifer seepage model

Full size image

If an equivalent homogeneous aquifer is used to replace the “strung” aquifer, this homogeneous aquifer has an equivalent permeability coefficient of ke

$$k_{e} = \frac{{\sum\nolimits_{i = 1}^{n} {k_{i} L_{i} } }}{{\sum\nolimits_{i = 1}^{n} {L_{i} } }}.$$
(42)

If the aquifer is sufficiently thin and the permeability coefficients of adjacent aquifers are gradually transformed, the equivalent permeability coefficient can be expressed as

$$k_{e} = \frac{1}{M}\int_{0}^{L} {K\left( l \right){\text{d}}l} .$$
(43)

Figure 3 shows the relationship of permeability coefficient k with radius r. The surrounding rock is assumed to be a uniformly homogeneous porous elastic medium, and the pore volume changes with stress and pore water pressure. The seepage behavior no longer satisfies the linear Darcy’s law. In the previous analysis, it was concluded that k is continuous over the elastic and plastic regions, respectively, and equal at \(r_{y}\). Similarly, the elastic zone equivalent permeability coefficient and the plastic zone equivalent permeability coefficient can be defined as follows:

$$k_{e}^{\left( e \right)} = \frac{1}{{R - r_{y} }}\int_{{r_{y} }}^{R} {{\text{e}}^{{A_{1} P^{\left( e \right)} }} {\text{d}}r,{\mkern 1mu} {\mkern 1mu} \quad k_{e}^{\left( p \right)} = \frac{1}{{r_{y} - r_{0} }}\int_{{r_{0} }}^{{r_{y} }} {{\text{e}}^{{A_{2} P^{\left( p \right)} }} {\text{d}}r} } .$$
(44)
Fig. 3
figure 3

Circular continuous aquifer seepage model

Full size image

According to the law of mass conservation, the flow rate at the elastic–plastic junction is equal, so that the following relationship can be obtained by:

$$\frac{{k_{e}^{\left( e \right)} }}{{k_{e}^{\left( p \right)} }} = \frac{{\Delta P^{\left( e \right)} }}{{\Delta L^{\left( e \right)} }} \cdot \frac{{\Delta L^{\left( p \right)} }}{{\Delta P^{\left( p \right)} }} = \frac{{P_{R} - P_{y} }}{{R - r_{y} }} \cdot \frac{{r_{y} - r_{0} }}{{P_{y} - P_{0} }}.$$
(45)

Equation (45) is now supplemented with the relational equation on \(P_{y}\) and \(r_{y}\). The closed system of coupled equations can be formed by combining Eqs. (39) and (40). Since it contains transcendental equations, this system of equations cannot be solved directly and needs to be solved with the help of numerical methods. After solving \(r_{y}\),\(P_{y}\), and \(\sigma_{y}\), the corresponding solutions are obtained by substituting the stress equation and the seepage equation.

When the stress at \(r_{0}\) reaches the yield condition, we have

$$\sigma_{\theta } = \frac{2K}{{1 - 3\alpha }}.$$
(46)

Substituting Eq. (30) into Eq. (46), the in-situ stress at the beginning of yield can be obtained by:

$$\sigma_{R} = \left\{ {\frac{K}{1 - 3\alpha } - \frac{2G}{{\lambda + 2G}}\left[ {P_{0} - \frac{2}{{R^{2} - r_{0}^{2} }}\int_{{r_{0} }}^{R} {P^{\left( e \right)} \left( {r\prime } \right)r\prime {\text{d}}r\prime } } \right]} \right\}\frac{{R^{2} - r_{0}^{2} }}{{R^{2} }}.$$
(47)

4 Model Verification

4.1 Comparison with Numerical Simulation Test Results

In this part, FLAC3D were adopted to conduct numerical tests with the DP failure criterion. The convergence of the numerical results was discussed as follows. Since the numerical model is a planar axisymmetric model, the number of circumferential grids has little effect on the test results, so the sensitivity analysis can be carried out only using the radial grids. The model with different numbers of radial meshes N is calculated to investigate the effect of the discretization number. The number of steps at each computational convergence is recorded, and the unbalanced forces rate is used to mark the convergence. The iteration error en is estimated by calculating the average stress difference. The results of the grid sensitivity analysis are recorded in Table 1.

Table 1 Results of the grid sensitivity analysis
Full size table

Figure 4 shows how the iteration error gradually converges as the number of grids increases, with the party \(e_{n} = 2 \times 10^{ - 3}\) iteration error starting to converge. Taking into account of the computational accuracy and computational cost, the radial grid number of 80 was chosen for this experiment.

Fig. 4
figure 4

Iterative error distribution

Full size image

The numerical model generated 80 × 20 × 4 ‘cshell zone’, and applied 30 and 60 MPa normal stress on the outer boundary, and initialized pore pressure and boundary condition by Eq. (19). The nodal displacements perpendicular to the plane direction were fixed to simulate a plane strain model. The inner boundary of the tunnel is 10 m and the outer boundary is 40 m. Calculated model with friction angle φ = 25°, cohesion C = 6 MPa, and shear modulus G = 2.5 × 103 MPa. DP criterion parameter \(qv = \frac{2\sin \left( \phi \right)}{{\sqrt 3 \left( {3 - \sin \left( \phi \right)} \right)}}\),\(ks = \frac{6C\cos \phi }{{\sqrt 3 \left( {3 - \sin \left( \phi \right)} \right)}}\). The numerical model, plastic-elastic distribution, and colored stress patterns are shown in Fig. 5.

Fig. 5
figure 5

FLAC3D computational model and results

Full size image

Figure 6 shows the stress distribution of surrounding rock obtained from simulation tests and the calculated results under the conditions of 30 MPa and 60 MPa in-situ stress σR. As can be seen from the figure, the simulated and calculated radial stress results are basically the same, no matter in the elastic zone or the plastic zone, while the simulated tangential stress results in the plastic zone are slightly higher than that of calculated tangential stress. Under the condition of σR = 30 MPa, the two obtained results are almost the same. Under the condition of σR = 60 MPa, the plastic zone radius of simulated tests is slightly smaller than that of calculated results. In general, the theoretical calculation results of this paper are in good agreement with the numerical test results.

Fig. 6
figure 6

Comparison of stress distribution between FLAC3D and current work

Full size image

Based on the comparative analysis results of Sects. 4.1 and 4.2, we can preliminarily believe that the theoretical derivation in this paper is reasonable and correct.

4.2 Comparison with the Solution Without Considering the Seepage Effect

The stress distribution diagram of DP and this work is shown in Fig. 7. Both the low and the high in-situ stress show similar feature. In the plastic zone, the stress distribution under the two yield criteria is basically the same, but the solution in this paper shows a larger range of the plastic zone. In the elastic zone, the tangential stress curves of the two solutions are basically parallel. In addition, the radial stress given in this paper is also higher than the solution of DP, but different from tangential stress, the difference of radial stress is the smallest at \(r_{y}\), gradually increases with the increase of radius, and reaches the maximum at \(r_{R}\). This is positively correlated with the distribution of pore water pressure. These differences are magnified in areas of high in-situ stress.

Fig. 7
figure 7

Comparison of stress distribution between DP and current work

Full size image

Based on the comparative analysis results of Sects. 4.1 and 4.2, we can preliminarily believe that the theoretical derivation in this paper is reasonable and correct.

5 Example Analysis

In this part, we make some examples to study the influence of different parameters on the results, and give the following calculation parameters. The inner diameter of the tunnel r0 = 10 m; \(R = 4 \times r_{0}\), the friction angle in the zone φ = 25°, the cohesion C = 6 MPa, the Biot coefficient α = 0.3, the Lamé constant λ = 1.445, the shear modulus G = 2.5 × 103 MPa, and the empirical constant a = 1, Q = 1536 × 103.

(1) The relationship between the in-situ stress and the radius rate of the plastic zone under the same conditions for the four yielding criteria is shown in Fig. 8. Pore water pressure of 10 MPa is applied at the outer boundary. There are some differences in the performance of the initial yield stress and the growth rate of the plastic zone radius. As this work is carried out based on DP criterion, the calculation results are highly familiar to the DP algorithm. However, under the action of pore water pressure, in the solution of current work, the increase of plastic zone radius shows a higher sensitivity to the growth of in-situ stress. It can be seen from the figure that DP, HB, and the solution in this paper have similar slopes, while Kastner’s solution is more sensitive to high ground stress. In addition, due to the intermediate principal stress considered by both DP and this work, the obtained results have higher initial yield stress than HB and Kastner’s solutions. In the HB criterion parameters m = 10 and s = 1; the same parameters are used in the calculation procedure of the DP criterion for uncoupled seepage action as in this study. The solution in this study has an inner boundary water pressure \(P_{0} = 0\). The parameter \(N = \frac{1 + \sin \left( \phi \right)}{{1 - \sin \left( \phi \right)}}\), \(S = \frac{2\sin \left( \phi \right)}{{1 - \sin \left( \phi \right)}}\) in Kastner’s solution.

Fig. 8
figure 8

Influence of confining pressure on radius of plastic zone

Full size image

(2) The relationship between primary rock stress, internal friction angle φ, and outer boundary pore water pressure \(P_{R}\) at yielding condition is shown in Fig. 9. The figure further explains the relationship between the solution in this paper and the solution of DP. The curves are obtained by taking 0, 20, 40, 60, and 80 MPa pore water pressure at \(r_{R}\). This seepage force caused by pressure potential energy is the main difference between the work in this paper and the DP solution. In the case of \(P_{R} = 0\), the obtained curve is the same to that of DP curve. It can be seen from the analysis results that a higher \(P_{R}\) value requires a higher yield stress under the same conditions.

Fig. 9.
figure 9

In-situ stress at initial yield

Full size image

In addition, the internal friction angle has a positive effect on the stability of surrounding rock when φ is less than 40°, and a negative effect on the stability of surrounding rock when φ is over 45°, showing the characteristics of tensile failure.

In the range of 40° < φ < 45°, σR has a high sensitivity to φ. Therefore, the solution proposed in this paper is more reasonable when the internal friction φ < 40°.

(3) The sensitivity analysis between the radius rate of the plastic zone and the internal friction angle of surrounding rock is shown in Fig. 10. According to the proposed criterion, the radius of the plastic zone shows a higher sensitivity at low friction angles, and this sensitivity is more obvious at high stress regions. And the solution presented in this paper shows higher sensitivity. With the increase of in-situ stress, the solution presented in this paper presents a larger range of plastic zone than that presented in the solution of DP. This phenomenon is most obvious at low angles and tends to be equal with the increase of angles.

Fig. 10
figure 10

Relation between internal friction angle and radius of plastic zone

Full size image

(4) Figure 11 shows the relationship between cohesion C and the radius rate of the plastic zone. Similar to the influence of the internal friction angle φ, the radius of the plastic zone shows a high sensitivity when the cohesion is low (mainly when C < 1 MPa). Similarly, due to the effect of pore water pressure, the solution in this paper shows a higher plastic zone range than that of DP, and this enhancement diminishes with increasing cohesion C. No matter the DP criterion or the solution in this paper, it can be seen that the influence of in-situ stress on the plastic radius is linear, which is different from the study of internal friction angle φ.

Fig. 11
figure 11

Relationship between cohesion and radius of plastic zone

Full size image

(5) Figure 12 shows the distribution of permeability under different in-situ rock stress \(\sigma_{R}\) and different water pressure \(P_{R}\). In this example, k0 = 1 × 10–14 m2, n0 = 0.2, inner boundary water head and pressure are set as zero. The outer boundary is applied with water pressure and stress. The distribution of permeability is related to the location of the elastoplastic interface and shows different patterns in different areas. Due to the effect of compressive stress, the closer to the hole, the lower the permeability. The permeability curve has a faster rate of decline in the elastic zone than that in the plastic zone due to the assumption of incompressibility of the plastic volume. In the plastic zone, the volume strain is constant; only the water pressure acts on the volume change of the pores, so that the permeability coefficient decreases slowly. Figure 12a shows a gradual decrease in permeability as \(\sigma_{R}\) increases, with the permeability curves nearly parallel to each other. Figure 12b shows that the permeability decreases as the \(P_{R}\) increases and the slope of the permeability curve increases. Comparison of Fig. 12a, b leads to the conclusion that the in-situ rock stress \(\sigma_{R}\) is the main factor influencing the magnitude of the average permeability and the outer boundary water pressure \(P_{R}\) is the main factor influencing the distribution of permeability along the penetration path.

Fig. 12
figure 12

Distribution of permeability

Full size image

6 Conclusions

Based on DP criterion and effective stress principle, an elastoplastic fluid–solid model of annular cavity with steady flow is proposed. The model considers the dynamic evolution of the permeability coefficient in the fluid–structure coupling and gives the evolution equations of the permeability coefficient in the elastic and plastic zones and the seepage equations. In addition, the physical equation of equivalent permeability coefficient and water head difference is considered. By comparing the analytical solution of DP with the numerical simulation of water-rich surrounding rock, the correctness of the proposed solution is verified.

With the increase of primary rock stress, the plastic radius increases significantly, and the solution presented in this paper shows a faster rate of increase than the solution of DP. Due to the consideration of the influence of intermediate principal stress, the solution presented in this paper and the solution of DP require higher ground stress to make the surrounding rock yield. The increase of pore water pressure leads to a higher yield stress of surrounding rock. However, when the pore water pressure decreases gradually and the region is zero, the solution of the elastic region deforms to the classical Lamé solution, while the solution of the plastic region is consistent with the solution of DP.