1 Introduction

Longwall mining has become the overwhelming coal mining craft worldwide, with the advantages of high production and efficiency, low development ratio and cost. China is the largest coal-producing country globally, with 30%–40% of the recoverable reserves pressed under buildings (Zou et al. 2003). The prediction of mining progressive subsidence and deformation can provide theoretical support for the damage evaluation of the surface buildings, the determination of the corresponding protection and maintenance time nodes, and the reasonable configuration or optimization of mining technology. Therefore, it is of more practical significance to study the prediction method for mining progressive subsidence and deformation instead of focusing only on the final value (Cui et al. 2001).

At present, the approaches of prediction for mining progressive subsidence can be divided into the following four categories: (1) considering the mechanical properties of the rock strata and the surface, such as the visco-elastic rheological model (Hou et al. 2018), elastoplastic finite element model (Sepehri et al. 2017), rheological and unsteady rheological model (Hejmanowski and Malinowska 2017; Wang et al. 2015); (2) mathematical modeling, for instance, grey prediction model (Xu et al. 2014), Cellular Automata (CA) model (Lian et al. 2011), PSO-SVR algorithm (Chen and Deng 2014) and numerical simulation (Li et al. 2019); (3) conducting improvement or optimization for the Knothe time function, to make it suitable for the prediction of mining progressive subsidence under specific conditions; (4) fitting the new time function with the measured data, including the normally distributed time function (Gonzalez-Nicieza et al. 2007; Zhang et al. 2016), Weibull time function (Liu 2013), logistic time function (Roser et al. 2018), arctangent function model (Nie et al. 2017), lognormal function model (Yan et al. 2019) and composite function model (Han et al. 2020).

Among the above approaches, the third category, namely Knothe time function and its derived models, has the most extensive research and practical application. Specifically, Cui et al. (2001) elaborated on the properties and influence results of the Knothe time function parameters, and demonstrated the prediction of progressive subsidence based on the Knothe time function. Luo and Cheng (2009) improved the Knothe time function, and made it suitable for predicting progressive subsidence of inclined coal seams. Liu et al. (2009) presented the power exponent Knothe time function, and the improved Knothe time function is able to express the dynamic process of surface subsidence more accurately. Li et al. (2014) predicted the dynamic three-dimensional surface deformation, based on the AutoCAD platform combined with the Knothe time function. Xiao et al. (2013) performed a dynamic process of mining subsidence by Knothe time function, and land use evolution and its impact on human were quantitatively analyzed under GIS platform. Shortly afterward, Xiao et al. (2014) simulated the dynamic mining subsidence utilizing Knothe time function, and on the basis of these simulations, the topsoil removal time, scope and depth of topsoil were determined. Hu et al. (2015) put forward a model for calculating the parameter of the Knothe time function, taking advantage of probability integral theory and the angle of critical subsidence. Guo et al. (2016) and Zhu et al. (2016) built a dynamic subsidence prediction model for solid backfilling mining, by integrating a dynamic subsidence function in solid backfill mining with Knothe time function, to predict the surface dynamic subsidence process of solid backfill mining and assess mining damage. Wang et al. (2018) modified the Knothe time function, and imposed it suitable for the dynamic subsidence prediction under grouting mining. Chang and Wang (2003) proposed a segmented Knothe time function, and Zhang and Cui (2017) developed it to the optimized segmented Knothe time function (hereafter referred to as the OSK time function).

Summarizing the relevant research on the prediction for mining progressive subsidence using the time function (the above categories 3 and 4), we can found that almost all of them are based on deeming the moment, when the surface point began to subside, as the origin of the time–subsidence coordinate system of the point (Cui et al. 2001; Gonzalez-Nicieza et al. 2007; Wang et al. 2018; Xiao et al. 2014, 2013; Liu 2013; Zhang and Cui 2017). However, because the spatial–temporal relationship of this modeling idea is relatively complicated, and it is hard to estimate the parameters accurately, thus it is inconvenient in practical application. Additionally, most practical applications of time function only focus on several local single points, not on the whole longwall progressive subsidence basin (Gonzalez-Nicieza et al. 2007; Nie et al. 2017; Roser et al. 2018; Zhang et al. 2020; Zhang and Cui 2017). As a result, there are still doubts about the reliability and practical availability of these methods, and the ultimate goals and effects of the prediction for mining subsidence are not achieved.

In this study, aiming at one of the latest research progress of the Knothe time function, i.e., OSK time function, we found that there are still some flaws. After a detailed analysis, we used the moment when the underground extraction had just advanced to the surface point as the origin of the time–subsidence coordinate system of the point, and then proposed the Gompertz time function, constructed the parameters calculation method and the prediction algorithm for the longwall progressive subsidence basin. Subsequently, we applied the method to a practical longwall panel to verify the accuracy. This work can promote the prediction for mining subsidence, serve as a scientific reference for practical engineering, and enable the mining to proceed safely, reasonably, and effectively.

2 OSK Time Function and Its Flaws

2.1 Original Knothe Time Function

In 1953, the Polish scholar Knothe proposed a function model to simulate surface subsidence caused by underground mining, based on the assumption that the instantaneous subsidence velocity of the surface point is proportional to the difference between the final subsidence and the instantaneous subsidence at the point (Knothe 1953), which can be expressed as

$$\frac{dW(t)}{{dt}} = c[W_{0} - W(t)],$$
(1)

where c is the time coefficient, \(W_{0}\) is the final subsidence of the surface point, and \(W(t)\) is the instantaneous subsidence of the surface point at the moment t. Consider the boundary condition \(W(0) = 0\), and integrate Eq. (1) over t to obtain the Knothe time function

$$W(t) = W_{0} (1 - e^{ - ct} ).$$
(2)

2.2 Segmented Knothe Time Function

The original Knothe time function does not conform to the law of dynamic subsidence of the surface point (Cui et al. 2001). In 2003, Chang and Wang (2003) based on the assumption that the maximum subsidence velocity acquired at the moment when is half of the total subsidence time, and the corresponding subsidence at the moment is half of the final subsidence as well (hereafter referred to as the double half condition), proposed the segmented Knothe time function.

$$W(t) = \left\{ \begin{gathered} 0.5W_{0} [e^{ - c(\tau - t)} - e^{ - c\tau } ], \, 0 < t \le \tau \hfill \\ 0.5W_{0} [2 - e^{ - c(t - \tau )} - e^{ - c\tau } ], \, \tau < t < T \hfill \\ \end{gathered} \right.,$$
(3)

where τ is the moment of maximum subsidence velocity of the surface point.

Obviously, the segmented Knothe time function establishes the time–subsidence coordinate system using the moment, when the surface point began to subside, as the origin of the time–subsidence coordinate system of the point, that is, as shown in Fig. 1(a). In Fig. 1, the T-axis, W-axis, and D-axis represent time, subsidence, and the advancing distance of the underground extraction from a certain mining position, respectively; ω and \(l_{{\text{A}}}\) denote the angle and distance of advance influence, respectively.

Fig. 1
figure 1

Two ideas to establish the time–subsidence coordinate system. a Conventional idea and b TOC-based idea

Full size image

2.3 OSK Time Function

In fact, there are some deviations between the segmented Knothe time function value and the boundary conditions of actual surface subsidence. Aiming at the theoretical defects of the segmented Knothe time function, Zhang and Cui (2017) developed the OSK time function, after deeply analyzed the original Knothe time function and the segmented Knothe time function.

$$W(t) = \left\{ \begin{gathered} \frac{1}{2}W_{0} \left[ {\frac{{t - \tau (1 - e^{ct} )}}{{\tau e^{c\tau } }}} \right]{, }0 < t < \tau \hfill \\ W_{0} \left[ {1 - \frac{1}{2}e^{c(\tau - t)} } \right]{, }\tau < t < T \hfill \\ \end{gathered} \right.,$$
(4)

the parameters are calculated by (Zhang 2017; Zhang et al. 2018)

$$\left\{ \begin{gathered} \tau = \frac{L}{2v} \hfill \\ c = \frac{ - 2v\ln 0.04}{L} \hfill \\ \end{gathered} \right.,$$
(5)

where L is the critical mining length, and v is the mean mining velocity.

The OSK time function can rectify the defect that function value at characteristic points is not strictly consistent with the actual value, and it is still based on the double half condition. When \(W_{{0}} = 100\), \(c = 0.07\) and \(\tau = 50\), the curve of the OSK time function is shown in Fig. 2.

Fig. 2
figure 2

Curve of the OSK time function

Full size image

2.4 Flaws of the OSK Time Function

After analysis, due to some simplifications in the modeling process of the OSK time function, it still has the following three flaws.

First, according to a large amount of measured data and related research (Liu 2013), the time–subsidence curve of the surface point is an asymmetrical “S” shape, which had a short acceleration period but a long deceleration period, and the moment of maximum subsidence velocity is in front of the half of the total subsidence time. Unfortunately, the OSK time function is still based on the double half condition, making the time–subsidence curve strictly symmetrical between its first and second half. It is revealed that there are some differences between the OSK time function and the actual surface subsidence.

Second, the OSK time function establishes the time–subsidence coordinate system using the moment, when the surface point began to subside, as the origin of the time–subsidence coordinate system of the point, just as shown in Fig. 1a. Whereas the prediction algorithm introduced in Zhang (2018) reflects that the moment, when the surface point began to subside, is used as the origin, as shown in Fig. 1b. The latter will make the double half condition no longer holds (see Sect. 3.3 for the analysis based on measured data), and then it is corrected by introducing the delay time. Nevertheless, the delay time should be different at each unit, but it is used in Zhang (2018) as an average value, so there is an inevitable error in each unit.

Lastly, the measured data and relevant research (Wang et al. 2015) indicate that when the strike length of the working panel had not reached the critical mining length, the time–subsidence curves at different positions on the strike main section were different, that is, the parameters τ and c of the OSK time function should be different. Regrettably, the model parameters at the different positions given in Zhang (2018) and Zhang et al. (2018) are all the same and equal to the results estimated by Eq. (5), which is derived under the condition of critical mining and would lead to larger error in each prediction stage, especially in the early mining stage (see Sect. 3.3 for the analysis based on measured data).

These flaws will make the predicted longwall progressive subsidence slower and smaller, when the prediction algorithm introduced in Zhang (2018) is performed. To further improve the prediction accuracy of the OSK time function, how to obtain more accurate parameters is an urgent task. It is possible to find the variation law between the distance of advance influence and the strike mining degree of the working panel; then based on the coordinate system in Fig. 1a, obtain the parameters at each position on the strike main section. If the coordinate system is established as Fig. 1b, it can try to find what constraint holds when the double half condition can not be directly applied.

3 TOC-Based Idea and Gompertz Time Function

3.1 TOC-Based Idea

For the longwall panel, the panel width can be regarded as not changing with time, only the advancing length changes with time. Therefore, the models of predicting longwall progressive subsidence using time function, at present, overwhelmingly only consider the impact of the change in panel length (Hou et al. 2018; Zhang et al. 2018, 2020; Wang et al. 2015).

In the past, the prediction combined with the time function was mostly modeled by deeming the moment, when the surface point began to subside, as the origin of the time–subsidence coordinate system of the point (Fig. 1a) (Cui et al. 2001; Gonzalez-Nicieza et al. 2007; Wang et al. 2018; Xiao et al. 2014, 2013; Liu 2013; Zhang and Cui 2017). However, we believe that it is difficult to determine when surface points at different positions began to subside. With this time–subsidence coordinate system, the zero points of the time T, subsidence W and advancing length from a specific mining position D are inconsistent, and the distance of advance influence lA needs to be considered. Nevertheless, the lA also changes during the advancement of underground extraction, which induces the spatial–temporal relationship of this modeling idea is relatively complicated and inconvenient in practical applications. Moreover, the subsidence at the surface points that the underground extraction had not advanced to them was actually conducted by the subsidence of the gob in front of them; in other words, the subsidence of these points was due to them located in the main influence area of the gob in front of them, this is the same as the subsidence principle in the area outside the range of the working panel. Therefore, we assign the moment when the underground extraction had just advanced to this point as a node that this point actually began to subside. That is, the moment when the underground extraction had just advanced to the surface point as the origin of the time–subsidence coordinate system of the point, and we applied this as the basis for modeling, as shown in Fig. 1b. In this way, the three origins of the time T, subsidence W and advancing length from a specific mining position D are consistent and changed synchronously, which is convenient for understanding and mutual derivation. Hereafter, this paper refers to this modeling idea as the TOC-based idea.

Based on the TOC-based idea, after a comprehensive analysis for the measured data and the research results from relative scholars (Xu et al. 2017; Liu 2013; Zhang 2017), we found that the Gompertz time function is able to express the process of surface subsidence sufficiently, and is subject to the dynamic subsidence characteristics of surface point.

3.2 Gompertz Time Function

The expression of the Gompertz time function is

$$W(t) = W_{{\text{f}}} \exp ( - e^{ - k(t - b)} ),$$
(6)

where \(W_{{\text{f}}}\) is the subsidence of the surface point from the underground extraction had just advanced to the point to the maximum subsidence of the point, k is velocity coefficient to reach stabilized status, and b is the moment of maximum subsidence velocity of the surface point since the underground extraction had just advanced to the point. k is the shape parameter, which affects the slope of the curve and the time it takes to reach stabilized status; b is the position parameter, which affects the position of the curve on the abscissa axis. To avoid the nesting of superscripts, which will lead to too small fonts and affect the reading perception, so express \(e^{(*)}\) as \(\exp (*)\) as well. At the moment of maximum subsidence velocity (t = b), the function value \(W(b)\) is \(W_{{\text{f}}} /e\) and equal to 36.8% of \(W_{{\text{f}}}\), at the same time, the slope of the curve at the moment of maximum subsidence velocity has

$$W_{(b)}^{\prime } = k \cdot \frac{{W_{{\text{f}}} }}{e}.$$
(7)

The first and second derivatives of the Gompertz time function are

$$\frac{dW(t)}{{dt}} = v(t) = W_{{\text{f}}} k\exp \left[ { - e^{ - k(t - b)} - k(t - b)} \right],$$
(8)
$$\frac{{d^{2} W(t)}}{{dt^{2} }} = a(t) = \left[ {ke^{ - k(t - b)} - k} \right] \cdot W_{{\text{f}}} k\exp \left[ { - e^{ - k(t - b)} - k(t - b)} \right].$$
(9)

When \(W_{{\text{f}}} = 100\), \(k = 0.08\) and \(b = 30\), the Gompertz time function and its first and second derivative curves are shown in Fig. 3. Their curves shape has the following characteristics: all increase firstly, and subsequently, the subsidence velocity \(v(t)\) gradually increases to its maximum value \(kW_{{\text{f}}} /e\) then slows down to 0; meanwhile, the subsidence \(W(t)\) closes to its up-asymptote \(W_{{\text{f}}}\) and acceleration \(a(t)\) approaches to 0.

Fig. 3
figure 3

Shape characteristics of the Gompertz time function and its first and second derivatives. a Gompertz time function, b first derivative and c second derivative

Full size image

We can see that the Gompertz time function has an asymmetric sigmoidal shape, the moment of maximum subsidence velocity deviates to the front of the curve, the subsidence velocity surges first and then flattens, the extremum of acceleration is higher in the early stage and gentler in the late. These characteristics are in line with the subsidence characteristics of surface point caused by underground mining, for which reason it is very suitable as the time function for the prediction of longwall progressive subsidence under the TOC-based idea.

3.3 Suitability Proof with Measured Data

To specifically illustrate the feasibility and suitability of the Gompertz time function for predicting longwall progressive subsidence under the TOC-based idea, we used the Gompertz time function to fit the measured subsidence data. Randomly selected the feature points across the strike of the working panel 1121 in Xieqiao Coal Mine, which is located in Huainan, China. The relevant parameters of this working panel are mean depth 527 m, mining thickness 4.8 m, seam dip angle 13°, panel length 1588 m, panel width 148 m and mean mining velocity 1.8 m/d.

To eliminate the differences in the amount of subsidence at various points, and highlight the common characteristics about subsidence changing with time, we normalized the subsidence of each point i to the subsidence ratio, which is equal to \(W_{i} /W_{{\text{f}}}\) and the value range is 0–1. Here, the Gompertz time function parameters k and b adopt the Levenberg–Marquardt algorithm to solve the nonlinear least-squares optimal values through loop iteration.

The relationship between time and subsidence ratio, and fitting results of the Gompertz time function at six different feature points are shown in Fig. 4, all of these feature points are on the strike main section of panel 1121 and inside the boundary of panel 1121, and the position of these feature points is represented by the strike critical factor \(x_{i}\), which can be calculated by

$$x_{i} = \frac{{l_{i} }}{{r_{0} }} = \frac{{l_{i} \tan \beta }}{{H_{0} }},$$
(10)

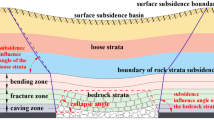
where \(l_{i}\) is the distance from each feature point to the setup entry of the working panel, \(r_{0}\) is the main influence radius of the working panel, \(\tan \beta\) is the tangent of main influence angle \(\beta\), \(H_{0}\) is the mean depth of the working panel. Critical factor is proportional to the degree of mining influence and gob size, which can be classified as strike critical factor and dip critical factor. Illustration of the strike critical factor is shown in Fig. 5. When the strike or dip critical factor of a position reaches 1.5, it can be considered that the mining unit that containing this position has reached critical mining in strike or dip dimension. (for reasons, see Sect. 4.1).

Fig. 4
figure 4

The relationship between time and subsidence ratio and fitting results of the Gompertz time function at different feature points (represented by the strike critical factor \(x_{i}\)). a \(x_{i} = 0.14\), b \(x_{i} = 0.27\), c \(x_{i} = 0.69\), d \(x_{i} = 1.38\), e \(x_{i} = 1.51\) and f \(x_{i} = 1.74\)

Full size image
Fig. 5
figure 5

Illustration of the strike critical factor and lithology parameters

Full size image

In Fig. 4, the zero point on the abscissa axis represents the moment when the underground extraction had just advanced to the feature point. We can see that all time–subsidence ratios are highly consistent with the Gompertz fitting results, and \(\overline{R}^{2}\) (i.e., the adjusted \(R^{2}\)) are all greater than 0.98. These indicate that the Gompertz time function is very suitable for the inversion of dynamic subsidence. Moreover, it is evident that the subsidence at the moment of maximum subsidence velocity is not about half of final subsidence, but about 1/e (0.368), after the underground extraction had just advanced to each feature point. If we assign the subsidence ratio reaches 0.98 as the threshold for subsidence reaching basic stabilized status, and the corresponding time is Ts, then the time of maximum subsidence velocity is less than Ts/2. For example, Fig. 4 (e) and (f) shows that the maximum subsidence velocity was obtained on about 51 d, and the subsidence was basically achieved stabilized status on about 212 d, the time ratio is 0.24 (about 1/4).

Therefore, here it is proved that the double half condition no longer holds if the time–subsidence coordinate system is established as Fig. 1b. Besides, it can also be derived from Fig. 4 that the subsidence curves at different positions are changing with the different geological conditions; in other words, no matter what time function and coordinate system are utilized, when the gob length had not reached the critical length, the parameters at different positions should be different.

4 Parameter Calculation Method and Prediction Algorithm

Because the parameter \(W_{{\text{f}}}\) is the subsidence of a surface point from the underground extraction had just advanced to the point to the final subsidence of the point, based on the summary about observation data of numerous mining areas in China, it can be estimated by (State Bureau of Coal Industry 2000)

$$W_{{\text{f}}} = 0.87W_{{0}} ,$$
(11)

where \(W_{{0}}\) is the final subsidence of the surface point, and can be obtained by the final state prediction method, such as the probability integration method.

Here, we will focus on how to obtain the parameters b and k.

4.1 Law of Parameter Variation

First, we studied the relationship between the parameters of the Gompertz time function and geological mining conditions through a large number of sample data. Specifically, we performed Gompertz time function fitting to the measured data on the strike main section of multiple mining areas in China, using the same method as Sect. 3.3, and obtained parameters b and k at different positions on the strike main section (represented by the strike critical factor \(x_{i}\)) inside each working panel. Here, we randomly selected four representative working panels for the exhibition, which were XQ1121, LD766, HZ1024, and BF3305 respectively, the relevant parameters of each working panel are shown in Table 1. The scatters of parameters b and k are illustrated in Fig. 6a, b, respectively. The lithology P in Table 1 is calculated by

$$P = \frac{{f_{a} }}{{f_{{\text{m}}} }}\left[ {1 - (\frac{{H_{{\text{a}}} }}{{H_{0} }})} \right],$$
(12)

where \(H_{{\text{a}}}\) is the thickness of the alluvium; f is hardness coefficient of the bedrock, an indicator for the hardness of the bedrock, its value is proportional to the hardness of the bedrock and reflects the mechanical properties of the bedrock, and its expression is as follows:

$$f = \frac{{\sum {h_{\eta } R_{\eta } } }}{{10\sum {h_{\eta } } }},$$
(13)

where \(h_{\eta }\) and \(R_{\eta }\) are the normal thickness and uniaxial compressive strength of the ηth overlying stratum, respectively. Part of the parameters in Eqs.  (12) and (13) are illustrated in Fig. 5. The bedrock can be classified as weak (f < 3), medium–hard (3 < f < 8) and hard (8 < f), according to the value of f. The \(f_{{\text{m}}}\) in Eq. (12) refers to the hardness coefficient of medium-hard bedrock, usually choose 5. The \(f_{{\text{a}}}\) in Eq. (12) represents the hardness coefficient of the bedrock under actual geological mining conditions.

Table 1 Geological mining parameters of the representative working panels
Full size table
Fig. 6
figure 6

Parameters of the Gompertz time function at different positions on the strike main section inside representative working panels. a parameter b and b parameter k

Full size image

Combined with Table 1 and Fig. 6, we can see that all working panels obey the following law: before the strike critical factor \(x_{i}\) reaches 1.5, the moment of maximum subsidence velocity b decreases with the increase of \(x_{i}\), and the opposite it is that the velocity coefficient to reach stabilized status k increases with the increase of \(x_{i}\), and after the strike critical factor \(x_{i}\) reaches about 1.5, the two parameters of all working panels almost remain constant.

During the advancing process of underground extraction, it can be considered that the unmined coal pillar is long enough (i.e., semi-infinite mining), and subsequent mining has the same influence on the surface point which above gob and on the strike section. Therefore, the influence on subsidence curves can just consider the variation of gob length during the underground advancement; in brief, only the variation of strike critical factor at different positions needs to be considered. Based on this, the reasons for the law above illustrated are as follows. When the working panel width is fixed and the length is long enough (beyond the length of critical mining), in the early stage of mining (strike critical factor is less than 1.5), with the advance of the underground extraction, the volume of the gob gradually increases, and the stress of rock strata over the gob increases synchronously. The distance more farther between the surface point on the strike main section and the setup entry, the time of maximum subsidence velocity at the point and the time of subsidence stabilized at the point more shorter. This is reflected in that the greater the strike critical factor is, then the smaller the moment of maximum subsidence velocity b is, and the greater the velocity coefficient to reach stabilized status k is, respectively. When the strike critical factor has reached about 1.5, the surface point is only affected by the gob with a length of \(r_{0}\) on the gob side; and the stress of rock strata over the area, where strike critical factor larger than 1.5, reaches constant state substantially. Hence, both the time for reaching the maximum subsidence velocity and the time for reaching the stabilized state are the shortest. This is revealed in that after the strike critical factor reaches about 1.5, the parameter b is the smallest, whereas the parameter k is the largest, and both remain unchanged on the whole. As for why the threshold of strike critical factor is about 1.5 instead of 1, the primary reason is the existence of delay distance of subsidence and offset distance of the inflection point, and they correspond to the strike critical factor of about 0.5.

In addition, from Table 1 and Fig. 6, we can also see that the specific geological mining conditions of different working panels will affect the parameters b and k in the entire panel range, such as the influence of the lithology of the overlying rock strata and the mean mining velocity of the working panel. The harder the lithology, the smaller the mean mining velocity, will induce the faster the b to decrease with the increase of the strike critical factor, that is, the smaller the slope of the fitted line (here is a negative value), and the b is greater on all positions; at the same time, the slower the k to increase with the increase of the strike critical factor, that is, the smaller the slope of the fitted line (here is a positive value) as well, and the k is smaller on all positions.

4.2 Calculation Method of the Parameter b

According to the variation law of the Gompertz time function parameters in Sect. 4.1, under different geological mining conditions and within the interval of the strike critical factor less than 1.5, the parameter b gradually decreases with the increase of the strike critical factor, and after the strike critical factor reaches 1.5, \(b = b_{\min }\) and basically unchanged. Therefore, the parameter \(b_{i}\) of each surface point i (i = 1, 2, 3, …, n) on the strike main section under different geological mining conditions can be calculated by

$$b_{C} \left\{ \begin{gathered} b_{i} = Bx_{i} + b_{C} , \, x_{i} \le 1.5 \hfill \\ b_{i} = b_{\min } , \, x_{i} > 1.5 \hfill \\ \end{gathered} \right.,$$
(14)

where \(x_{i}\) is the strike critical factor corresponding to surface point i, B is the linear slope of \(b_{i}\) with respect to \(x_{i}\) under local geological mining conditions, and \(b_{\min }\) is the minimum value of b under the same conditions.

We first introduce the solution of \(b_{\min }\). Since \(b_{\min }\) represents the moment of maximum subsidence velocity when the working panel reaches critical mining in the strike, it can be derived by

$$b_{\min } = \frac{{l_{{\text{s}}} }}{v},$$
(15)

where \(l_{{\text{s}}}\) is the delay distance of maximsum subsidence velocity of the surface point under critical mining, v is the mean mining velocity of the working panel.

In addition, \(b_{\min }\) can also be obtained through fitting a large number of measured data

$$b_{\min } = 17.089P - 23.752v + {27}{\text{.281}}y + {80}{\text{.413,}}$$
(16)

where P is the lithologic parameter, which can be calculated by Eq. (12), y is the dip critical factor of the working panel, its calculation formula only needs to change the \(l_{i}\) in Eq. (10) to the width of the working panel. When there is no prior data for \(l_{{\text{s}}}\) under local geological mining conditions, Eq. (16) can be adopted.

B can be estimated by

$$B = - 56.57e^{{ - 79.82\frac{mv}{{H_{0} }}}} - 9.987,$$
(17)

where m is the mining thickness of the working panel.

In view of when the strike critical factor is 1.5, the value of b is the minimum value \(b_{\min }\) under the local geological mining conditions, i.e.,

$$b_{{x_{i} = _{1.5}}} = 1.5B + b_{{\text{C}}} = b_{\min },$$
(18)

then the expression of \(b_{{\text{C}}}\) is

$$b_{{\text{C}}} = b_{\min } - 1.5B.$$
(19)

So far, the equation for calculating the parameter b of the Gompertz time function has been established

$$\left\{ \begin{gathered} b_{i} = ( - 56.57e^{{ - 79.82\frac{{mv}}{{H_{0} }}}} - 9.987)(x_{i} - 1.5) + b_{{\min }} ,\;\;x_{i} \le 1.5 \hfill \\ b_{i} = b_{{\min }} ,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x_{i} > 1.5 \hfill \\ \end{gathered} \right.$$
(20)

It is worth noting that the surface point with a strike critical factor less than 1.5 cannot be used to obtain the \(b_{i}\) using a method similar to Eq. (15), because under the subcritical mining condition, the moment of maximum subsidence velocity of the surface point is not equal to the “maximum subsidence velocity” in the delay distance of maximum subsidence velocity. In detail, before the strike of the working panel reaches critical mining, the “maximum subsidence velocity” in the delay distance of maximum subsidence velocity is only a staged maximum subsidence velocity, not the maximum subsidence velocity throughout the entire subsidence period, and it is likely to be less than the latter in fact. Here, the measured subsidence velocity along strike observation line in working panel 8102, Guobei Coal Mine, (Fig. 8) is taken as an example, as shown in Fig. 7. In Fig. 7, there are eight phases of measured data of the subsidence velocity along the strike observation line, represented by different colors. The advancing position of the underground extraction in each phase is illustrated by the vertical dashed line and labeled by the serial number with the same color. We can see that before the penultimate phase (8 ~ 9), the “maximum subsidence velocity” corresponding to the delay distance of maximum subsidence velocity at a surface point, in almost every phase, less than the maximum subsidence velocity in all phases of measured data at the same point, but the last two phases (8 ~ 9, 9 ~ 10), their maximum subsidence velocities are approximately the same, and their strike critical factor \(x_{i}\) is close to 1.5, indicating that the critical mining has been reached.

Fig. 7
figure 7

Eight phases of subsidence velocity along strike observation line in the working panel 8102, Guobei Coal Mine

Full size image

4.3 Calculation Method of the Parameter k

Similar to the method of obtaining the parameter \(b_{i}\), the parameter \(k_{i}\) of each surface point i (i = 1, 2, 3, …, n) on the strike main section under different geological mining conditions can be calculated by

$$\left\{ \begin{gathered} k_{i} = Mx_{i} + k_{{\text{C}}} {\text{,}}\;\;\;\;x_{i} \le 1.5 \hfill \\ k_{i} = k_{{\max }} {\text{,}}\;\;\;\;\;\;\;\;\;\;\;x_{i} > 1.5 \hfill \\ \end{gathered} \right.$$
(21)

where M is the linear slope of \(k_{i}\) concerning \(x_{i}\) under local geological mining conditions, and \(k_{\max }\) is the maximum value of k under the same conditions.

Acquire the \(k_{\max }\) first still. According to Hu et al. 2015; Zhang et al. 2020; Zhang et al. 2018, when the working panel reaches critical mining in the strike, the subsidence of the surface point affected by the critical mining is approximately equal to 0.98 times of the final subsidence, at which time, \(t = L/2v\), L is the gob length when the mining criticality reaching critical mining. This means

$${\text{W}}_{0} \exp \left[ { - e^{{ - k_{\max } (\frac{L}{2v} - b_{\min } )}} } \right]{ = }0.98{\text{W}}_{{0}} ,$$
(22)

thereby we can get

$$k_{\max } = \frac{\ln ( - \ln 0.98)}{{b_{\min } - \frac{L}{2v}}};$$
(23)

substitute L, v and \(b_{\min }\) into Eq. (23) to obtain \(k_{\max }\).

M can be estimated by

$$M = 0.0101(v - 1.3798)^{0.5294} .$$
(24)

Since when the strike critical factor is 1.5, the value of k is the maximum value \(k_{\max }\) under the local geological mining conditions, i.e.,

$$k_{{x_{i} = 1.5}} = 1.5M + k_{{\text{C}}} = k_{\max } ,$$
(25)

then the expression of \(k_{{\text{C}}}\) is.

$$k_{c}=k_{max}-1.5M$$
(26)

Now, the equation for calculating the parameter k of the Gompertz time function has been established

$$\left\{ \begin{gathered} k_{i} = (x_{i} - 1.5)0.0101(v - 1.3798)^{{0.5294}} + k_{{\max }} {\text{,}}\;\;\;\,x_{i} \le 1.5 \hfill \\ k_{i} = k_{{\max }} {\text{,}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\,\,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\,x_{i} > 1.5 \hfill \\ \end{gathered} \right.$$
(27)

It is also worth noting that affected by the mining sufficiency, the subsidence coefficient \(q_{T}\) in predicted time T requires the final state subsidence coefficient q divided by the mining degree coefficient \(n_{x}\) in the strike of the working panel, which means

$$q_{T} = \frac{q}{{n_{x} }}$$
(28)

and the \(n_{x}\) can be estimated by

$$n_{x} = 1.11 - 1.14e^{{ - 1.23x_{T} }} ,$$
(29)

where \(x_{T}\) represents the strike critical factor corresponding to the advancing length \(l_{T}\) of the working panel at the predicted time T, that is,

$$x_{T} = \frac{{l_{T} }}{{r_{0} }}.$$
(30)

4.4 Brief Prediction Algorithm for Longwall Progressive Subsidence Basin

  1. 1)

    Determine the predicted time T, mean mining velocity v and advancing length \(l_{T}\) of the target working panel at the predicted time.

  2. 2)

    According to the unit division length \(l_{{\text{U}}}\) and the advancing length \(l_{T}\), determine the unit number of the working panel at the predicted time, and record the distance from the center of each mining unit j to the setup entry and the corresponding strike critical factor \(x_{j}\).

  3. 3)

    Determine the extracted time of mining unit j, that is \(T_{j}^{{\text{W}}}\), and elapsed time \(T_{j}^{{\text{J}}}\) from the underground extraction had just advanced to the center of the mining unit j to the predicted time T for each mining unit.

  4. 4)

    According to the parameters calculation method introduced in Sects. 4.2 and 4.3, estimate parameters of the Gompertz time function of each mining unit \(b_{j}\) and \(k_{j}\).

  5. 5)

    Calculate the Gompertz time function value of each mining unit \(\Phi_{j} (t)\).

  6. 6)

    Using the probability integration method to predict the whole basin subsidence for each mining unit, then the obtained 0.87 times of predicted subsidence is multiplied by the time function value of each mining unit, which as the actual subsidence contribution of each mining unit to the surface. Other surface movement and deformation can be deduced from the subsidence.

  7. 7)

    Superimposing the actual movement and deformation contribution of each mining unit to the surface.

5 Experiments and Results

5.1 Study Area

The experiment panel is 8102 of Guobei Coal Mine, which is located in the Huaibei mining area, Anhui, China, as is shown in Fig. 8, the mining craft of panel 8102 is longwall fully-mechanized mining with roof caving, the relevant parameters of the working panel 8102 are shown in Table 2, and the predicted parameters of the probability integration method are shown in Table 3. From Fig. 8, we can see that there is a river crossing the surface above panel 8102, and panel 8101 beside the 8102. Panel 8101 is the relay of 8102, due to the panel 8101 started mining on 2008/02/23, thus affected the subsidence of panel 8102 in the late.

Fig. 8
figure 8

Geographical locations of the Huaibei mining area and the working panel 8102 in Guobei Coal Mine

Full size image
Table 2 Parameters of the working panel 8102 in Guobei Coal Mine
Full size table
Table 3 Predicted parameters of the probability integration method
Full size table

5.2 Prediction Results

According to the above-mentioned parameter calculation method and prediction algorithm for longwall progressive subsidence basin, the surface subsidence of the working panel 8102 after 139, 202, 266, 333, 430, 517 and 657 d of mining is predicted. The 430 d is the time of the mining stopped, the advancing distance from setup entry at each predicted time and the corresponding parameters are shown in Table 4, the unit division length \(l_{{\text{U}}}\) is 15 m. Take the predicted time T = 333 d as an example, the key parameters summarized in Table 5.

Table 4 Predicted time and corresponding parameters
Full size table
Table 5 Summary of key parameters in predicted time T = 333 d
Full size table

The obtained three-dimensional longwall progressive subsidence basin at each predicted time and the corresponding two-dimensional plane projection are shown in Figs. 9 and 10, respectively. The coordinate system in Fig. 9 is the local coordinate system. Due to space limitations and redundancy, the progressive deformation here only illustrates curvature along the strike of the working panel, and horizontal strain along the dip of the one, as shown in Figs. 11 and 12, respectively. From Figs. 9, 10, 11, 12, we can derive that the surface subsidence and deformation center gradually move forward and is always biased toward the coal seam downhill, as the underground extraction advances, and the range of surface subsidence and deformation gradually increases. After the mining ceased, the surface subsidence and deformation did not stop immediately, but advanced a certain distance, and the subsidence, curvature, and horizontal strain all increased slightly, which is compatible with the existing characteristics of mining subsidence and deformation (Zou et al. 2003). Additionally, it can be seen from Fig. 11 that the maximum surface curvature appears in the middle phase of the advancement, and does not monotonously increase with the expansion of the gob until reaching critical mining just like subsidence and horizontal strain. These results reveal that the prediction of mining progressive subsidence and deformation is of great value for real-time grasping surface deformation, intensifying understanding of the dynamic surface movement and deformation, rational planning of mining schemes, and protection of vital surface structures.

Fig. 9
figure 9

Three-dimensional longwall progressive subsidence basin at each predicted time. a 139 d, b 202 d, c 266 d, d 333 d, e 430 d, f 517 d and g 657 d

Full size image
Fig. 10
figure 10

Two-dimensional longwall progressive subsidence basin at each predicted time. a 139 d, b 202 d, c 266 d, d 333 d, e 430 d, f 517 d and g 657 d

Full size image
Fig. 11
figure 11

Longwall progressive curvature along the strike of the working panel at each predicted time. a 139 d, b 202 d, c 266 d, d 333 d, e 430 d, f 517 d and g 657 d

Full size image
Fig. 12
figure 12

Longwall progressive horizontal strain along the dip of the working panel at each predicted time. a 139 d, b 202 d, c 266 d, d 333 d, e 430 d, f 517 d and g 657 d

Full size image

5.3 Accuracy Verification

The accuracy of the proposed method was investigated by comparing the predicted subsidence and measured leveling subsidence, along strike and dip observation line in the working panel 8102 at each predicted time. Since the shape of the strike and dip main section can determine the shape of the subsidence basin, and the accuracy of subsidence can represent that of other surface movement and deformation; therefore, the accuracy of the predicted progressive subsidence on the two main sections is competent to represent the predicted accuracy of the whole basin. Furthermore, to more clearly reflect the prediction accuracy and the advantages of the Gompertz time function, the predicted results using the OSK time function at the same predicted time were also compared. The comparison curves are shown in Fig. 13. The advancing position of the underground extraction at each predicted time in Fig. 13 is denoted by vertical dashed line and labeled with the corresponding advancing distance from the setup entry.

Fig. 13
figure 13

Comparison of the predicted progressive subsidence and measured leveling subsidence. a 139 d strike line, b 139 d dip line, c 202 d strike line, d 202 d dip line, e 266 d strike line, f 266 d dip line, g 333 d strike line, h 333 d dip line, i 430 d strike line, j 430 d dip line, k 517 d strike line, l 517 d dip line, m 657 d strike line and n 657 d dip line

Full size image

After the working panel 8102 stopped mining, the surface subsidence basin formed a large seeper area, which made it impossible to observe some observation points on the south bank of the river on 657 d. Meanwhile, the relay panel 8101 (see Fig. 8) had been mined half (513 m) on 657 d, the subsidence of the observation points near the working panel 8101 had been activated again, so in Fig. 13 (m) and (n), these observation points were excluded.

Compared with the two kinds of time function in Fig. 13, the difference between the predicted progressive subsidence using the OSK time function and the leveling subsidence is more distinct. The OSK time function only on 517 d and 657 d, when the working panel had stopped mining for a long time, there is a great consistency with the leveling subsidence. Whereas the results using the Gompertz time function closer to the leveling subsidence at virtually every predicted time. Besides, on the strike observation line, the prediction results of the OSK time function show that the predicted subsidence center lags slightly behind the leveling subsidence center.

To further quantify the accuracy, root mean square error (RMSE) and relative RMSE (RRMSE) of the predicted progressive subsidence using the two time functions in each period are calculated, hereafter also referred to as the RMSE-Gompertz, RRMSE-Gompertz, RMSE-OSK, and RRMSE-OSK.

$${\text{RMSE}} = \sqrt {\frac{{\sum {_{\phi = 1}^{\Phi } } \Delta_{\phi }^{2} }}{\Phi }} = \sqrt {\frac{{\sum {_{\phi = 1}^{\Phi } } (W_{{{\text{P}}_{\phi } }} - W_{{{\text{M}}_{\phi } }} )^{2} }}{\Phi }} ,$$
(31)

where \(W_{{{\text{P}}_{\phi } }}\) and \(W_{{{\text{M}}_{\phi } }}\) denote the predicted subsidence and the leveling subsidence at surface point \(\phi\) (\(\phi\) = 1, 2, 3, …, \(\Phi\)), respectively.

$${\text{RRMSE}} = \frac{{{\text{RMSE}}}}{{W_{\max } }},$$
(32)

where \(W_{\max }\) represents the maximum value of the leveling subsidence.

The accuracies of predicted progressive subsidence using the two time functions are shown in Table 6.

Table 6 Accuracy comparison for predicted progressive subsidence between the two time functions
Full size table

On the strike observation line: (1) the RMSE-Gompertz gradually increases with the increase of surface subsidence, while the RRMSE-Gompertz tends to decreases, and except for the first two periods, the RRMSE-Gompertz of each period is less than 5%; (2) the RRMSE-OSK has a decreasing trend period by period as well, and the remaining six periods are all greater than 5% except the last period; (3) the prediction accuracy using the Gompertz time function in each period is better than that using the OSK time function, and the average RMSE-Gompertz and RRMSE-Gompertz are 50.7 mm and 6.2%, respectively, compared with the average RMSE-OSK and RRMSE-OSK are 86.0 mm and 10.0%, respectively, the accuracy was improved by 41.0% and 38.4%, respectively.

On the dip observation line: (1) the prediction error of Gompertz time function on the dip observation line is larger than that on the strike observation line, but the RRMSE-Gompertz in each period is still less than 10%; (2) the RRMSE-OSK only the last four periods are less than10%; 3) the prediction accuracy using the Gompertz time function is higher than that using the OSK time function except for the last three periods, and the average RMSE-Gompertz and RRMSE-Gompertz are 66.2 mm and 7.6% respectively, compared with the average RMSE-OSK and RRMSE-OSK are 73.0 mm and 9.0% respectively, the accuracy was improved by 9.4% and 16.3%, respectively.

Combined with the analysis on the strike and dip observation lines, we can derive that the predicted longwall progressive subsidence basin using the Gompertz time function has an average RMSE of 58.4 mm, and an average RRMSE of 6.9%, which is less than 10%. This result demonstrates that the accuracy of this paper presented method can achieve centimeter-level and meet the requirements of practical engineering application. Moreover, compared with the OSK time function, in this paper, the Gompertz time function can increase the accuracy by more than 9%, with an average of 27.9%; compared with example in Zhang (2018), which average RRMSE is 8.0%, the accuracy can increase by 14.2%. To a certain extent, the phenomenon that the predicted progressive subsidence is less than the actual subsidence and the predicted subsidence center lags the actual position using the OSK time function has been improved.

In addition, it is worth noting that because the prediction category based on time function is a time function value multiplied by the predicted final subsidence, essentially, the accuracy of the final subsidence prediction algorithm will significantly affect the accuracy of the prediction algorithm for progressive subsidence. Thus, if a more accurate final state prediction algorithm is adopted, the accuracy of the progressive prediction algorithm will be further improved. For example, the accuracy of the OSK time function in this paper is slightly lower than that in Zhang (2018), which is probably caused by this reason.

6 Conclusion

Prediction of longwall progressive subsidence basin is of great significance for production and planning in the mining area. Therefore, the prediction method for longwall progressive subsidence basin was studied in this paper, and the main conclusions drawn from it are summarized below.

We analyzed the OSK time function for prediction of longwall progressive subsidence, and pointed out that there are certain differences between the OSK time function and the actual surface subsidence, the possible improvement directions were given.

After that, we proposed the Gompertz time function for prediction of longwall progressive subsidence basin, based on the modeling idea of three origins are consistent, then proved that the Gompertz time function is highly consistent with the subsidence characteristics of the surface point caused by underground mining and is very suitable for the inversion of dynamic subsidence process. Thereafter, the variation law between parameters of the Gompertz time function and the geological mining conditions was analyzed, within the interval of the strike critical factor less than 1.5, both parameters b and k have a prominent linear relationship with the strike critical factor, and after the strike critical factor reaches 1.5, both are basically unchanged. Then the parameters calculation method and the prediction algorithm for the longwall progressive subsidence basin were elaborated.

Next, we demonstrated the practical application effect of the proposed prediction method, the average RMSE and average RRMSE of predicted results using the Gompertz time function are 58.4 mm and 6.9%, respectively, and compared with using the OSK time function, the accuracy is increased by 27.9% on average with example in this paper and 14.2% with example in Zhang (2018).

The results show that the accuracy of this paper adopted method can achieve centimeter-level and meet the requirements of practical engineering application. It will provide the theoretical foundation for evaluating the damage process of surface structures, determining time nodes of buildings protection and maintenance, calculating the costs associated with rehabilitation, and conducting backfilling to mitigate the overburden and surface deformation. Hence, this method is expected to be extensively applied.

Finally, it should be pointed out that the prediction model mentioned in this work is simplified, which has not comprehensively considering the mining condition of multi-seam, whereas that is a common occurrence and will affect the prediction of surface subsidence. Therefore, predicting the progressive subsidence basin under multi-seam and is our future works.