Introduction

Land subsidence is the movement of the ground due to the loss of support from below. In the majority of cases, this is directly related to human activities which alter the water table or are associated with the mining of coal or economic minerals. With the long wall coal mining method, the ground above the excavated area collapses, is partially compacted and progressively drops as the work of extraction advances. These ground movements may produce damage to buildings, roads, railway lines, oil pipelines or any other infrastructure in the surrounding areas affected by the subsidence trough.

To estimate, quantify and prevent this damage, models must be established which can determine a priori issues such as what the greatest vertical displacement of the surface of the ground will be and where it will be produced, or what the lateral extension of the subsidence will be at any given time. To answer these questions, different methods of modelling have been developed (eg. Whittaker and Reddish 1989; Srivastrava and Bahuguna 1991) including those based on influence functions (Ramirez-Oyanguren and Rambaud-Perez 1986), cross section functions (Rodriguez-Diez and Toraño-Alvarez 2000) or finite elements/finite differences (Coulthard and Dutton 1988). Specifically, the University of Oviedo has developed an n–k–g generalized subsidence function (Alvarez-Fernandez 2004) based on influence functions and adapted to analyzing seams with any dip angle, including vertical seams which are the most common in the coalfields of Northern Spain.

However, these models consider final subsidence without taking time into account. This is important as the final subsidence trough is usually very flat and its differential deformations are practically nil (except at the edges of the trough) whereas if the time effect is considered, different subsidences at practically all the points of the trough would have to be taken into account as the excavated area advances.

The influence functions therefore have to be modified by time functions so as to take this effect into account (Jarosz Karmis Sroka 1990; Cui et al. 2001; Doney Peng Luo 1991). Many of these predictions of progressive subsidence are based on local models, which cannot be extrapolated to mines in other coalfields (Degirmenci Reddish Whittaker 1989; Karmis Jarosz Schilizzi 1987; Doney et al. 1991; Kelly et al. 1998; Stacey Bell 1999). It is therefore necessary to ascertain whether they fit the subsidence behaviour of the Asturian coalfield, or whether it is possible to find better approximations.

In order to study all these issues, the paper briefly describes Knothe’s and Sroka–Schober’s time functions before presenting a new correction function based on the normal distribution function. The correction functions are compared to establish that which best fits field measurements in the Central Asturian Coalfield.

Correction of subsidence over time

Alvarez-Fernandez (2004) proposed a series of formulae to determine the subsidence at the ground surface as a result of an underground cavity. However, all surface movements are not produced immediately after the mining of the cavity, which consequently increases the complexity of the study.

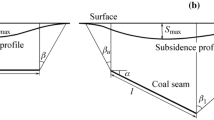
An interval of time called the delay time (tr) elapses from the commencement of underground mining until its effect reaches the surface. This delay time may vary between a few hours and several months. Likewise, once subsidence has commenced, the movements do not take place instantaneously in the majority of cases, but develop over a period of time known as the subsidence time (ts), which may last several years. That part of the displacement which takes place after underground work has finished is called the residual subsidence.

Subsidence has traditionally been obtained at a point on the topographic surface as a function of the time that has elapsed since the opening of the cavity, considering this to be the product of two functions:

  1. 1.

    The spatial function, obtained by means of integration of the influence function extended to the entire seam. This function allows the final subsidence at the surface point to be determined.

  2. 2.

    A time function, which defines the progress of the subsidence over time until it reaches its final value (defined by the spatial function).

Due to the characteristics of the mines in Northern Spain, different spatial influence functions have been developed to estimate the subsidence associated with seams with high dip angles. The static spatial subsidence function at each point P on the topographic surface proposed in Alvarez-Fernandez (2004) must be modified by a time function, thus obtaining the real subsidence function at each instant, given by

$$ \ifmmode\expandafter\vec\else\expandafter\vec\fi{S}{\left( {P,t} \right)} = \ifmmode\expandafter\vec\else\expandafter\vec\fi{S}{\left( P \right)}F{\left( t \right)} $$
(1)

Classical time functions

A number of workers have considered the significance of time functions. This paper considers only two—those of Knothe and Sroka–Schober (Jarosz et al. 1990).

The Knothe time function

One of the most widely used time functions, proposed by Knothe, takes the following form

$$ F_{{{\text{Knothe}}}} {\left( t \right)} = \left\{ \begin{aligned}{} & 1 - {\text{e}}^{{ - \alpha {\left( {t - \tau _{r} } \right)}}} {\text{ }}t > \tau _{r} \\ & 0{\text{ }}t \le \tau _{r} \\ \end{aligned} \right. $$
(2)

where

t is the time elapsed from the opening of the cavity;

τ r is the delay time; and

α is a parameter called the time constant, whose value depends on the characteristics of the ground and on the units in which the time is expressed.

This function varies between 0 and 1, such that

  • when no delay time has elapsed (values of t < τ r ), the time function and hence the subsidence take the value zero, and

  • when the elapsed time is great, the time function tends to 1, and hence the subsidence tends to its final or definitive value. The time needed for the time function to approximate the unit depends on α.

Figure 1 represents the time function for four different values of α (0.1, 0.2, 0.5 and 1) as a function of the time elapsed since the opening of the cavity, in months. A delay time of 2 months has been considered.

Fig. 1
figure 1

Influence of the time constant in Knothe’s time function

Full size image

As can be seen in Fig. 1, the greater α, the sooner the time function reaches the value 1, and therefore the smaller the subsidence interval τ s . For a value of α of 0.1, the subsidence interval is some 48 months, while for α = 1, it is only 8 months.

In order to obtain the evolution of subsidence at any point P on the surface over time, the total subsidence is multiplied by the function FKnothe(t) Thus, for example, a subsidence graph such as that in Fig. 2 is obtained as a function of time, for α = 0.1, τ r  = 2 months and considering a total subsidence at P equal to 1,000 mm.

Fig. 2
figure 2

Subsidence at a point according to Knothe’s time function (α = 0.1)

Full size image

The Sroka–Schober time function

Another time function used to correct subsidence is the one proposed by Sroka–Schober. These authors assume that there are two functions that influence the evolution of subsidence over time:

  • the time during which the convergence of the excavation develops, which is related to a time constant ξ.

  • the time needed for the subsidence to propagate in the overhanging rock mass, which is related to a time constant f.

The time function is expressed as:

$$ F_{{{\text{Sroka}}}} (t) = 1 + \frac{\xi } {{f - \xi }}{\text{e}}^{{ - f(t - \tau _{r} )}} - \frac{f} {{f - \xi }}{\text{e}}^{{ - \xi (t - \tau _{r} )}} $$
(3)

Knothe’s time constant, α, is related to ξ and f by means of the expression

$$ \frac{1} {\alpha } = \frac{1} {\xi } + \frac{1} {f} $$
(4)

The parameters ξ and f act in a similar way; for small values of both, the subsidence time increases, as can be seen in Fig. 3. In this figure, the time function is represented for a value of ξ, of 0.1, with values of 0.15, 0.20, 0.50 and 1.20 assigned to the constant f .The influence of f decreases as its value increases. The subsidence time is around 50 months.

Fig. 3
figure 3

Sroka’s time function for ξ = 0.10

Full size image

As can be seen, these types of Sroka curves, in contrast to those of Knothe, have three clearly differentiated slope sections: the first tangential to the x-axis at the origin, the second where the slope increases, and the third section in which the slope decreases; the curve being tangential to the horizontal straight line of the unit abscissa. This type of curve is a better fit with what actually occurs, as discussed below.

Figure 4 represents the same function for ξ = 0.05 and Fig. 5 for ξ = 100. It can be seen that the subsidence time increases in the former case up to 100 months and decreases in the latter to below 30 months, regardless of the value of f.

Fig. 4
figure 4

Sroka’s time function for ξ = 0.05

Full size image
Fig. 5
figure 5

Sroka’s time function for ξ = 1.00

Full size image

A new time function based on the normal distribution

Neither of the two above functions realistically fits the results obtained in the field. To solve this problem, and in view of the typology of the curves of the evolution of subsidence over time, a new time function is proposed that follows the morphology of a normal-type distribution function, in a similar way to the spatial influence function.

The density function of a normal function in the variable t (time in this case) with mean and standard deviation has the form:

$$ f_{{{\text{Normal}}}} (t) = \frac{1} {{{\sqrt {2\pi \sigma } }}}{\text{e}}^{{ - \frac{1} {2}\frac{{(t - \mu )^{2} }} {{\sigma ^{2} }}}} $$
(5)

and its distribution function:

$$ F_{{{\text{Normal}}}} (t) = \frac{1} {{{\sqrt {2\pi } }\sigma }}{\int\limits_{ - \infty }^t {{\text{e}}^{{ - \frac{1} {2}\frac{{(t - \mu )^{2} }} {{\sigma ^{2} }}}} } }{\text{d}}t $$
(6)

Fig. 6 shows the density function and the normal distribution function. The latter varies between 0 and 1, as a time function should, and presents the appropriate form, with two sections (initial and final) with lesser slope than the central section.

Fig. 6
figure 6

Density and normal distribution functions

Full size image

On the other hand, adopting a normal type distribution function as a time function means that the treatment for the spatial subsidence and time functions is analogous. An exponential influence function is hence defined for spatial subsidence (Alvarez- Fernandez 2004) that is integrated along all the elemental units of the seam and for the treatment of time, an exponential density function is defined that is integrated in time to obtain the total subsidence.

To define the desired density function, it is necessary to establish its mean and standard deviation. In Fig. 7, the time parameters and τ r and τ s have been related to the mean μ and standard deviation σ of the normal density function. Although the density function is defined between −8 and +8, the time function will only be defined for time values between τ r and τ r  + τ s , resulting in an error. In order to evaluate this error, a new parameter δ is defined, such that:

$$ \tau _{r} = \mu - \delta \sigma \quad \Rightarrow \quad \sigma = \frac{{\mu - \tau _{r} }} {\delta } $$
(7)
$$ \tau _{s} = (\mu + \delta \sigma ) - (\mu - \delta \sigma )\quad \Rightarrow \quad \sigma = \frac{{\tau _{s} }} {{2\delta }} $$
(8)

from which we obtain:

$$ \mu = \tau _{r} + \frac{{\tau _{s} }} {2} $$
(9)
Fig. 7
figure 7

Relation between time parameters and the normal distribution function

Full size image

The density function will therefore be:

$$ f_{{{\text{Normal}}}} (t) = \frac{{2\delta }} {{\tau _{s} {\sqrt {2\pi } }}}{\text{e}}^{{\frac{{ - 2\delta ^{2} {\left( {t - \tau _{r} - \frac{{\tau _{s} }} {2}} \right)}^{2} }} {{\tau _{s} ^{2} }}}} $$
(10)

the distribution function of which is:

$$ F_{{{\text{Normal}}}} (t) = \frac{{2\delta }} {{\tau _{s} {\sqrt {2\pi } }}}{\int\limits_{ - \tau _{r} }^t {{\text{e}}^{{\frac{{ - 2\delta ^{2} {\left( {t - \tau _{r} + \frac{{\tau _{s} }} {2}} \right)}^{2} }} {{\tau ^{2}_{s} }}}} } }{\text{d}}t $$
(11)

In order to ascertain the value of the time function in a time t, the density function has to be integrated between τ r and t, provided that t is ≤τ r  + τ s . However, an error would be introduced in this integration, as by not taking into account the density function for values of t ≤ τ r or for values of t ≥ τ r  + τ s (see Fig. 7), the distribution function does not tend to the unit. Figure 8 represents this distribution function for a delay time of zero months (τ r  = 0) and for values of δ of 1, 2 and 5. It can be seen that the lower the value of δ, the greater the error.

Fig. 8
figure 8

The normal distribution function as a function of δ

Full size image

The total error with a certain δ is given by I(δ):

$$ I(\delta ) = \frac{2} {{{\sqrt {2\pi } }}}{\int\limits_{ - \infty }^{ - \delta } {{\text{e}}^{{ - \frac{1} {2}t^{2} }} } }{\text{d}}t $$
(12)

The criterion has been adopted for adding a correction function Δ(t,δ) to Eq. 11 that eliminates this error. This correction function is applied proportionally over time, such that when t is equal to τ r , it must take the value zero and for t > τ r  + τ s , it must take the value I(δ). Thus the correction function Δ(t,δ) is

$$ \Delta (t,\delta ) = \left\{ {\begin{array}{*{20}c} {0} \\ {{\frac{{(t - \tau _{r} )I(\delta )}} {{\tau _{s} }}}} \\ {{I(\delta )}} \\ \end{array} } \right.\quad \begin{array}{*{20}c} {{t \le \tau _{r} }} \\ {{\tau _{r} < t < \tau _{r} + \tau _{s} }} \\ {{t \ge \tau _{r} + \tau _{s} }} \\ \end{array} $$
(13)

Figure 9 represents Δ as a function of time for τ r  = 2 months, τ s  = 2 months and three different values of δ (1, 2 and 3). As can be seen, for δ = 1 the error may be important (up to 16%), whereas for δ = 2 it is reduced to 2.5% and for δ = 3 it is negligible. In view of Fig. 9, it would appear that a value of δ ≥ 2 would be a good approximation.

Fig. 9
figure 9

The correction function Δ for different values of δ

Full size image

Therefore, the corrected time function, and the one that is proposed in this paper, is

$$ F_{{{\text{Normal}}}} (t) = \Delta (t,\delta ) + \frac{{2\delta }} {{\tau _{s} {\sqrt {2\pi } }}}{\int\limits_{\tau _{r} }^t {{\text{e}}^{{\frac{{ - 2\delta ^{2} {\left( {t - \tau _{r} + \frac{{\tau _{s} }} {2}} \right)}^{2} }} {{\tau ^{2}_{s} }}}} } }{\text{d}}t $$
(14)

The form of this function can be seen in Fig. 10, in which it has been represented for subsidence intervals τ s of 12, 24 and 48 months, considering δ = 3 and for a delay time of 2 months.

Fig. 10
figure 10

The normal time function for different values τ s

Full size image

When the subsidence time is 12 months, for t = 14 months, the value of the time function is 0.999, practically 1. The same occurs when the subsidence time is 24 months, since for t = 26 months, the time function already has the value 0.999, and for a subsidence time of 48 months, the time function for t = 50 months takes the value of 1. As can be seen, this value of δ = 3 allows the time function to be adjusted so that the total subsidence is obtained very precisely at the end of the subsidence interval.

Figure 11 shows the time function with a subsidence time τ s of 24 months and assigning values of 1, 2 and 3 to δ. It can be appreciated in this figure how δ allows the slope of the function to be modified.

Fig. 11
figure 11

The normal time function for different values δ

Full size image

Comparative analysis of time functions in the Central Asturian Coalfield

The functions described above have been compared in order to determine which gives the best fit for a real case of mining subsidence in a mine in Northern Spain.

The area of study in the Central Asturian Coalfield

From January 1994 to April 2003, periodic monitoring was carried out of the subsidence related to the underground coalmines in the village of Boo, situated in the River Aller valley in the Autonomous Community of the Principality of Asturias, Northern Spain.

Mining of the seams known as Mariana and Molino has been carried out at Boo since 1992. The average dip angle of the seams is 32° and they vary in thickness between 0.8 and 2.0 m. These seams have been mined in the different advance phases shown in Table 1. The mine workings are distributed over 5 levels, named 3rd (130 m above sea level), 4th (98 m above sea level), 5th (23 m above sea level), 7th (84 m above sea level) and 9th (181 m above sea level) and two sub-levels (2nd and 3rd), situated between the 5th and 7th levels, at 8 m and 20 m above sea level, respectively. At present, coal is only being mined in the Molino seam, between the 7th and 9th levels.

Table 1 Characteristics of the mine workings
Full size table

Figure 12 shows the position of the seams in relation to the topographic surface, as well as indicating the location of the buildings in the village of Boo, situated at an average approximate height above sea level of 425 m.

Fig. 12
figure 12

Mined panels in the surroundings of Boo

Full size image

A series of topographic landmarks were positioned to monitor the surface subsidence produced when mining each of the seams. These have been used to take successive levelling and planimetric measurements.

Since January 1994 (when monitoring commenced) until the present day, some 83 landmarks have been positioned, of which only 54 remain active, the rest having been destroyed or replaced. In this respect, it should be noted that of the 54 currently operative landmarks, 21 have been active since the date of the first positioning, thus providing a continuous evolution of the movements that have occurred. The position of these landmarks in relation to Boo is represented in Fig. 13, in which they are drawn in different colours depending on their date of positioning.

Fig. 13
figure 13

Location of the monitoring landmarks

Full size image

With the aim of carrying out an historical analysis of the movements experienced by each landmark since the date it was positioned, graphs similar to those shown in Figs. 14 and 15 were produced. Using this type of representation, it can be seen that the landmarks with the greatest subsidence are distributed around two well-differentiated areas.

  1. 1.

    One area is to the southeast of the village, above the 3rd and 4th levels of the Mariana and Molino seams mined between 1992 and 1996. Figure 14 shows the development of more than 700 mm of subsidence over time for the most significant landmarks (79, 104, 105, 106, 107, 109 and 78505). The subsidence times may be estimated between 3 and 4 years.

  2. 2.

    The other area is situated to the southwest of Boo, above the 4th and 5th levels of the Molino seam which were mined between 1993 and 1999. The present subsidence is of a similar magnitude, as can be seen in Fig. 15.

It can be appreciated from Figs. 14 and 15 that the majority of the subsidences occurred between 1994 and 1999, after which there was a tendency to stabilize. It can also be seen from Figs. 14 and 15 that landmarks 78505 and 123BIS showed hardly any variation in vertical movement. This is explained by the fact that they were positioned after most of the significant movements had taken place.

Fig. 14
figure 14

Evolution of subsidence at the landmarks in the southeastern area

Full size image
Fig. 15
figure 15

Evolution of subsidence at the landmarks in the southwestern area

Full size image

The information from this monitoring of landmarks was used to analyze which of the time functions best fit the results obtained in the Central Coalfield of Asturias. This can be illustrated by landmark 126BIS, whose real subsidence values are shown in Fig. 16.

Fig. 16
figure 16

Real subsidence at landmark 126BIS in mm as a function of time in months

Full size image

Three clearly differentiated sections can be observed in this curve of real subsidence

  1. 1.

    A first section, lasting some 18 months, in which approximately 40% of the subsidence is produced. This period is associated with the progressive failure of the ground as the subsidence develops.

  2. 2.

    A second section, with a much steeper slope and more abrupt movements which accounts for the majority of the remainder of the subsidence. The ground is now completely fractured and subsidence progresses at a greater speed.

  3. 3.

    A third section, with a much gentler slope, in which the movements are less significant, corresponding to the final post-collapse accommodation of the ground.

The Knothe time function in the Central Asturian Coalfield

Figure 17 shows the real subsidence of landmark 126BIS together with that calculated using the Knothe time function with α values of 0.075, 0.050 and 0.025.

Fig. 17
figure 17

Real subsidence and the theoretical subsidence considering Knothe function

Full size image

It can be seen that the third section corresponding to the post-collapse stage, fits the time function with α values of 0.5 and 0.075. However, the real subsidence is very similar to α = 0.025 in the first 18 months.

The Sroka–Schober time function in the Central Asturian Coalfield

Figs. 18, 19 and 20 compare the actual subsidence of landmark 126BIS related to the curves obtained using the Sroka time function. This fit is much better than that obtained using Knothe’s time function, although it can be seen that the first section of the curve, with a gentler slope, is too small for all the considered combinations of ξ, and f. The length of this section may be increased by decreasing ξ, but the subsidence times then become too great. Although this effect may be slightly counteracted by increasing f, the influence of this latter parameter is not sufficient to achieve the desired effect.

Fig. 18
figure 18

Real subsidence and theoretical subsidence considering Sroka function with ξ = 0.075

Full size image
Fig. 19
figure 19

Real subsidence and theoretical subsidence considering Sroka function with ξ = 0.100

Full size image
Fig. 20
figure 20

Real subsidence and theoretical subsidence considering Sroka function with ξ = 0.200

Full size image

The Sroka–Schober time function, which is dependent on the two parameters f and ξ, though more precise than that of Knothe, does not afford a good fit with the real evolution of surface subsidence.

The normal time function in the Central Asturian Coalfield

Figure 21 shows the evolution of real subsidence at landmark 126BIS and the subsidence calculated using the time function based on the normal distribution, assuming a delay time of 2 months and δ = 3. The subsidence was calculated for delay times of 12, 24, 36 and 48 months.

Fig. 21
figure 21

Real subsidence and theoretical subsidence considering normal function with δ = 3

Full size image

It can be seen from Fig. 21 that for δ = 3, the final observed subsidence is close to the final subsidence indicated by the four calculated curves. Of these four curves, the one that best fits the real evolution of subsidence is that corresponding to a subsidence interval of 36 months. The fit is very good in both the second and the third sections although there is a loss in precision in the first section with the calculated subsidence being less than its real counterpart.

Figure 22 presents a similar graph for δ = 2. For this value of δ, the final subsidence is obtained 1 month after the subsidence interval ends, but the curve corresponding to τ s  = 36 months is a very good fit with the first and third sections and an acceptable fit with the second section. In Fig. 23, which represents the curves for subsidence intervals of 30, 32, 34 and 36 months, it can be seen that the best fit corresponds to an interval of 34 months.

Fig. 22
figure 22

Real subsidence and theoretical subsidence considering normal function with δ = 2

Full size image
Fig. 23
figure 23

Real subsidence and theoretical subsidence considering normal function with δ = 2

Full size image

In the first section of the real curve, the subsidence is slightly greater with respect to the curve calculated for τ s  = 34. The fit in the second and third sections is very good.

Figure 24 shows the observed subsidence plotted against subsidence using the three time functions. It can be seen that the curve corresponding to the normal function allows the evolution of subsidence to be predicted with much more precision that is obtained using the Knothe and Sroka time functions.

Fig. 24
figure 24

Real subsidence and subsidence calculated using the three time functions

Full size image

Conclusions

Many of the formulations that are normally employed to model subsidence in the north of Spain are not really applicable as the characteristics of mines in this area differ from those for which the theoretical methods for estimating subsidence have been developed. The mining activity in the Central Asturian Coalfield takes place in relatively deep pits, in the region of 600 m, with seam thicknesses of between 1 and 2 m and relatively high dip angles (from 20 to 40°). Moreover, in many cases, no experimental results are available to calibrate these models. For this reason, the present work was undertaken to compare the subsidence measured at a series of landmarks situated in the area of Boo in Northern Spain with that predicted by the Knothe and Sroka–Schober models.

None of the time functions fitted the experimental values recorded in the field hence a new time function has been proposed, designated as “normal” as it is based on the normal distribution. It is shown that this normal time function affords a better fit with reality, at least for the coal mining in the Central Asturian Coalfield in Northern Spain.