1 Introduction

More than ten super high arch dams have been constructed and projected in the Southwest of China, such as Ertan (240 m), Xiaowan (294.5 m), Xiluodu (285.5 m), Jinping-I (305 m), Maji (290 m), etc. Among these super high arch dams, Jinping-I double-curvature arch dam is the only one higher than 300 m, representing a milestone in the 300 m level high arch dam construction.

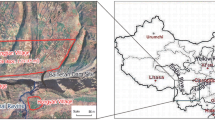
Located on the midstream of Yalong River, Sichuan Province, China, as shown in Fig. 1, the main purpose of Jinping-I project is for electricity generation. The dam crest elevation is 1885 m and the total installed capacity is 3600 MW, while the normal water level is 1880 m and the total storage is \(7.76 \times {10^9}\) m3. Many world-class difficulties, such as geological and geo-morphologic asymmetry, high geo-stress, steep valley, high excavation slope, deep unloading belts and fissures are all encountered and broken through during construction. Without doubt, these difficulties bring many uncertainties and challenges in the evaluation of safety and global stability of dam-abutment.

Fig. 1
figure 1

Location of Jinping-I hydropower station

Full size image

The main methods applied in the analysis for the dam can be divided into two kinds: numerical simulation methods and geomechanical model tests.

In 1930s, the trial load method proposed by the United States Department of the Interior Bureau of Reclamation (Copen et al. 1977) was first used to the analysis of arch dam. The finite element method (Clough 1960), extended finite element method (Daux et al. 2000; Belytschko et al. 2001) and some discontinuous methods such as the discrete element method (Cundall 1971, 1988; Hart et al. 1988) and discontinuous deformation analysis (Shi 1992) allow us to solve the stability and deformation problems of the arch dam foundation and abutment reasonably. Although FEM is limited in the simulation of discontinuities and large deformation, considering its high speed and prominent accuracy at the least number of parameters, it is still widely used in rock engineering. Yang et al. (2008, 2012) proposed the deformation reinforcement theory and achieved unconditional convergence in the nonlinear FEM calculation of failure process, and used unbalanced force and plastic complementary energy norm to judge the cracking and global stability. Deformation reinforcement theory has been implemented in a three-dimensional finite element analysis program, three-dimensional finite element (TFINE), which is developed by Tsinghua University (Liu et al. 2018).

Geomechanical model test was first proposed by the Institute of structure model experiment and simulation (ISMES) in Italy in 1960s (Fumagalli 1966), which can make up for some deficiencies in FEM and has been used in simulating the failure process of complex geotechnical engineering (Fumagalli 1973, 1979). Model material was studied (da Silveira et al. 1979) and the high-density and low-strength material was considered to be suitable. Then several model tests of arch dam were carried out at the National Laboratory for Civil Engineering (LNEC) in Lisbon, Portugal (Lemos et al. 1995; Lemos 1996). In Germany, the feature of failure of dam foundation was studied through model test (Fishman 2008). Meanwhile, model test was applied to studying ground response to tunneling (Meguid et al. 2008). In China, geomechanical model test was also widely used (Liu et al. 2003; Fei et al. 2010; Chen et al. 2015a, b). Through testing and engineering practice, Zhou et al. (2005) established a set of stability analysis criterion based on the overloading method and small block masonry technique. This criterion has been used in more than ten high arch dams in China (Liu et al. 2013; Zhang et al. 2015) and also the cavern engineering (Deng et al. 2015).

Aiming at Jinping-I project, quantities of work have been accomplished by precursors. Hu et al. (2010) explored the effects of concrete replacements and concrete cushion through the analysis of stress and deformation. Song et al. (2013) analyzed the influences of geological defects on Jinping I hydropower station. Chen et al. (2015) derived the safety coefficients and studied the stability of dam and abutment using the temperature-dependent similar material and comprehensive model test. Zhang et al. (2016) studied the Long-term stability of the left bank abutment slope at Jinping I hydropower station.

Generally, the geological condition of Jinping-I project is fairly asymmetric since the left abutment is much more unfavorable than the right. Therefore, the dam body is also designed to be asymmetrical to restrain deformation asymmetry and stress localization, meanwhile, quantities of foundation treatments, such as concrete replacements, grouting and concrete cushion, are arranged, as shown in Fig. 2.

Fig. 2
figure 2

3D view of foundation treatments

Full size image

In this paper, the overall stability of Jinping-I arch dam is studied by geomechanical model test and nonlinear finite element calculation. The stress and displacement of arch dam are compared with the experimental and numerical results. Furthermore, the cracking and failure process of the arch dam is analyzed in detail.

2 Unbalanced Force and Its Correlation with Cracking

In the analysis of the stability of the traditional rock and soil structure, the stability index mainly describes the limit state of the structure, and does not reflect the mechanical behavior after the structural failure. To solve this problem, Yang et al. (2008) put forward the deformation reinforcement theory. The core of the theory is the principle of minimum plastic complementary energy. It is pointed out that elastoplastic structures under given actions deform tending to the limit steady state at which the unbalanced force is minimized according to the principle of minimum plastic complementary energy. The classical elastoplastic theory requires that the mechanical solutions meet the three equations in the whole domain, namely, the equilibrium equation, the constitutive relation and the deformation compatibility. This indicates that the stress state at every point of the structure is inside the yield plane, and the structure is stable at this time. If the external load on the rock and soil structure is over its resistance, the structure will lose its stability, and the difference between the external load and the resistance is called the over stress, and it is also the internal driving force of the structural instability. During the calculation process, the unbalanced force is obtained by condensing the over-stress through the Gauss integral on the model node. The concept of deformation reinforcement theory is explained as follows (Yang et al. 2012; Liu et al. 2017):

$$\dot {\varvec{\varepsilon}}={\dot {\varvec{\varepsilon}}^{\text{e}}}+{\dot {\varvec{\varepsilon}}^{\text{p}}},\;{\dot {\varvec{\varepsilon}}^{\text{e}}}={\varvec{C}}:\dot {\varvec{\sigma}},$$
(1)
$${{\varvec{D}}^{\text{p}}}(\varvec{\sigma},{\dot {\varvec{\varepsilon}}^{\text{p}}}) \geqslant {{\varvec{D}}^{\text{p}}}({\varvec{\sigma}^{{\text{yc}}}},{\dot {\varvec{\varepsilon}}^{\text{p}}}),\quad \forall f({\varvec{\sigma}^{{\text{yc}}}}) \leqslant 0,$$
(2)
$${{\varvec{D}}^{\text{p}}}({\varvec{\sigma}^{{\text{yc}}}},{\dot {\varvec{\varepsilon}}^{\text{p}}})={\varvec{\sigma}^{{\text{yc}}}}:{\dot {\varvec{\varepsilon}}^{\text{p}}}.$$
(3)

In the equation, \({D^{\text{p}}}\), \({\dot {\varepsilon }^{\text{e}}}\), \({\dot {\varepsilon }^{\text{p}}}\), \(\dot {\sigma }\), \(C\), \(f\), \({\sigma ^{{\text{yc}}}}\) are plastic dissipative function, elastic strain rate, plastic strain rate, stress change rate, elastic compliance tensor, yield function and any stress state satisfying the yield criterion, respectively, and the operator “:” means double-dot product between tensors. Inequality (2) is also called the maximum plastic dissipation principle, which includes associated flow rule and the Kuhn–Tucker condition.

Assuming that a strain increment \(\Delta {\varepsilon ^{\text{p}}}\) is generated within a time interval \(\Delta t\), and its plastic strain rate is:

$${\dot {\varvec{\varepsilon}}^{\text{p}}}=\frac{{\Delta {\varvec{\varepsilon}^{\text{p}}}}}{{\Delta t}}=\frac{{{\varvec{C}}:({\varvec{\sigma}^{{\text{eq}}}} - \varvec{\sigma})}}{{\Delta t}}.$$
(4)

In this equation, \({\sigma ^{{\text{eq}}}}\) represents a specific stress field, which is balanced under given external loads, that is, the elastic test stress when \({\dot {\varepsilon }^{\text{p}}}=0\):

$${\varvec{\sigma}^{{\text{eq}}}}={\varvec{\sigma}_0}+{{\varvec{C}}^{ - 1}}:\Delta \varvec{\varepsilon}.$$
(5)

Combining Eqs. (1) and (4), plastic complementary energy \(E({\sigma ^{{\text{yc}}}})\) can be obtained:

$$\begin{gathered} \hbox{min} E({\varvec{\sigma}^{{\text{yc}}}}),\quad\forall f({\varvec{\sigma}^{{\text{yc}}}}) \leqslant 0 \hfill \\ E({\varvec{\sigma}^{{\text{yc}}}})=\frac{1}{2}\left( {{\varvec{\sigma}^{{\text{eq}}}} - {\varvec{\sigma}^{{\text{yc}}}}} \right):{\varvec{C}}:\left( {{\varvec{\sigma}^{{\text{eq}}}} - {\varvec{\sigma}^{{\text{yc}}}}} \right). \hfill \\ \end{gathered}$$
(6)

Equation (6) is also called the nearest point projection method.

The computational precision of the nearest point projection method is one order precision and the algorithm belongs to a special case of the generalized midpoint method (Simo et al. 1988), which has a strong adaptability and unconditional convergence in calculating the large step.

As shown in Fig. 3, considering the complex structure composed of elastic–plastic material, it is assumed that the initial stress in a yield surface at a certain Gauss point is \({\sigma _0}\), that is, the yield condition \(f({\sigma _0}) \leqslant 0\) is satisfied. If the external load is applied to the initial state (that is, applying a tiny perturbation \(\Delta \varvec{\varepsilon}\)), the elastic test stress will change to \({\sigma _1}={\sigma _0}+D:\Delta \varepsilon\) then, where D is the elastic tensor. If \({\sigma _1}\) exceeds the yield surface, that is, \(f\left( {{\sigma _1}} \right)>0\), which is not allowed under the classical elastoplastic mechanics framework, it is necessary to adjust the test stress \({\sigma _1}\) to yield surface \(\varvec{\sigma}\). And the difference between the two is the driving force of the structural deformation, that is \(\Delta {\sigma ^{\text{p}}}=D:\Delta {\varepsilon ^{\text{p}}}\), where \(\Delta {\varepsilon ^{\text{p}}}\) is the plastic strain increment of this loading step. In the finite element calculation, the equivalent nodal force of \(\Delta {\sigma ^{\text{p}}}\) is the unbalanced force:

Fig. 3
figure 3

Elastoplastic stress adjustment diagram (Pan et al. 2013)

Full size image
$$\Delta U=\int_{V} {{B^{\text{T}}}({\sigma ^{{\text{eq}}}} - {\sigma ^{{\text{yc}}}})} {\text{d}}V=F - \int_{V} {{B^{\text{T}}}} \sigma {\text{d}}V.$$
(7)

In the equation, B is the strain matrix and V is the solution domain. From the Eq. (7), it is known that the unbalanced force is the relative relation between the external action and the structural resistance. If a force can be applied to the structure which is equal to the unbalance force and the direction is opposite, the structure balance can be maintained in theory. Similarly, when the crack propagation is studied, the unbalanced force generated by the elastoplastic iteration is the minimum force system to maintain the crack initiation or prevent further expansion.

By comparing the result of block test with the preset crack and the unbalanced force in the numerical calculation, it is concluded that the crack initiation position and the expansion direction are strongly correlated with the distribution of the unbalanced force. Figure 4 shows the process of uniaxial compression and cracking of specimens with preset cracks. The uniaxial pressure increases from 0 to 2 MPa and the loading increment is 0.1 Mpa. When the axial pressure increases to 1.6 MPa, the tip of the preset crack near the free surface of the test block begins to crack first. As the load increases further, the right surface of the test block starts to crack, and cracks in the left side expand further, and the direction of the cracks is approximately perpendicular to the crack trend. When the load increased to 2.0 MPa, the parallel preset cracks gradually penetrated through each other and damaged on both sides of the specimen. Figure 5 shows the corresponding unbalanced force vector map obtained through finite numerical calculation. The unbalanced force first appears at the tip of the preset crack. With the increase of load, the expansion of the unbalanced force is approximately perpendicular to the direction of the preset crack. The experiment shows that it is effective to predict the propagation of cracks through unbalanced forces.

Fig. 4
figure 4

Failure pattern of cube specimen with preset crack during loading (Pan et al. 2013)

Full size image
Fig. 5
figure 5

Unbalanced force vector diagram of cube specimen with preset crack during loading (Pan et al. 2013)

Full size image

3 Model Test Method and Its Application

3.1 Similarity Theorem and Simulation Method

The similarity principle between the prototype and the model is the key to geomechanical model test. On the geometric scale, material parameters (both stiffness and strength) and load intensity need to satisfy the similarity principle. Then stress, displacement and failure process will accordingly satisfy the similarity principle. In general, the similarity coefficient of dimensionless physical quantities is set to 1. However, in actual tests, it is impossible to satisfy the similarity coefficients of all physical quantities. Therefore, only the similarity coefficients of some key physical quantities such as geometry, stress, strength can be satisfied.

At least three basic principles are required (Liu et al. 2013): (1) similar phenomena must occur in the geometric similarity system and follow the same similarity principles; (2) the modulus equations are the same in the similarity physical system; (3) the physical process can be expressed in the same equation and all the similarity coefficients are the same.

The similarity coefficient \({C_{\text{i}}}\) is defined as the ratio of the physical quantity of the prototype \({i_{\text{p}}}\) to that of the model \({i_{\text{m}}}\), as shown in Eq. (8), where i can be different physical quantities.

$${{\varvec{C}}_{\text{i}}}=\frac{{{{\varvec{i}}_{\text{p}}}}}{{{{\varvec{i}}_{\text{m}}}}}.$$
(8)

In the model test of Jinping-I hydropower station, the similarity coefficient of geometric scale \({C_{\text{l}}}\) is set to 250 in consideration of accuracy and costs. Thus, the other similarity coefficients are derived:

$${C_\varepsilon }={C_{\text{v}}}={C_{\text{f}}}={C_\gamma }=1,$$
(9)
$${C_\sigma }={C_{\text{E}}}={C_{\text{c}}}={C_\gamma }{C_l}={C_l}={C_\delta }=250.$$
(10)

In Eqs. (9) and (10), \({C_\varepsilon }\), \({C_\upsilon }\), \({C_{\text{f}}}\), \({C_\gamma }\), \({C_\sigma }\), \({C_{\text{E}}}\), \({C_{\text{c}}}\), \({C_{\text{l}}}\), \({C_\delta }\) are similarity coefficients of strain, of Poisson’s ratio, of friction coefficient, of unit weight, of stress, of Young’s modulus, of cohesion, of geometric and of displacement respectively. However, it is impossible to satisfy all the similarity coefficient simultaneously. In the actual model test, only the most basic similarity coefficient is satisfied, such as \({C_{\text{l}}}\), \({C_\sigma }\), \({C_{\text{E}}}\) and \({C_{\text{f}}}\).

As shown in Eqs. (9) and (10), similarity materials should have some strict conditions, such as high density with low deformation modulus and high friction coefficient with low cohesion. Especially for the faults, the cohesion of model should be less than 0.005 MPa which is hard to realize. In this paper, a kind of mixed powder composed of barite powder, bentonite and diluted poly (vinyl acetal) adhesive is applied (Liu et al. 2013). The mixed powder is compressed into small blocks by a tailor-made equipment, as shown in Fig. 6. To measure the parameters of stiffness and strength, groups of cylinder models with different densities are produced to conduct uniaxial compression tests and shearing tests. Then, proper densities are gained and similarity materials of rock masses with different properties can be manufactured.

Fig. 6
figure 6

The tailor-made compressing equipment and various small blocks

Full size image

Small block masonry technique (Liu et al. 2013) is applied by compacting powder materials into small bricks and constructing model brick by brick. Faults, reinforcement and dam body can all be simulated through this method exquisitely. The model of foundation is constructed by small blocks with different shapes. These blocks are bonded together by a tailor-made glue with proper viscosity to simulate connectivity and surface friction, respectively. The smaller the scale of bricks is, the more exquisite the dam-abutment model will be. More than 100,000 small bricks are used in this test.

The major jointed rock masses are simulated by altering the arrangement and shape of small bricks, and the connectivity of rock mass joints is controlled by the mixture proportion of the tailor-made glues.

A slice of dewatered gypsum (low deformation modulus) with craft papers or iridescent papers (relatively high friction coefficient but low cohesion) on the two sides is used to simulate the faults and crushed zones. Since the thickness are too thin and the deformation modulus is relatively low, the geometrical similarity of the interformational zone is impossible to be achieved absolutely. The principle of equivalent deformation is employed. The deformation modulus can be adjusted through changing the rate of water content to dry gypsum before dewatering, while the cohesion can be neglected since it is quite small. Large numbers of experiments are conducted to obtain the relationship between frictional coefficients and paper selections. Before model construction, shear tests are also needed to ensure the mechanics property.

3.2 Design of Jinping-I Model Test

The model test of Jinping-I arch dam was carried out in a test tank (4.5 m × 4.5 m × 2.5 m) in Tsinghua University, Beijing, as shown in Fig. 7. The steel frame is used to fix the model boundary and the steel channels are employed to fix the displacement gauges.

Fig. 7
figure 7

The model test tank for Jinping-I hydropower station

Full size image

The similarity coefficient of geometric scale \({C_{\text{l}}}\) is 250. The other similarity coefficient are shown in Eqs. (9) and (10). The simulation range of the model is from 160 m upstream (about 0.52 height of dam) to 700 m downstream (about 2.30 height of dam), from 175 m depth under the riverbed (0.57 height of dam) to 0 m above the dam crest, from 537 m of the left (about 1.76 height of dam) to 500 m of the right (about 1.64 height of dam). The large simulation range ensures the accuracy of dominated faults, lamprophyre veins and deep crevices. The boundary fixed constraint condition is also satisfied.

Mechanical parameters of rock masses are shown in Table 1. Five groups of joint rock masses with different material parameters are simulated. Faults f5, f2, F1, f42-9, lamprophyre vein X, deep crevice SL44-1 in the left bank, f13 and f14 in the right bank are simulated in the test. The location and identification of the rock types and of the faults are shown in Fig. 8. Properties and simulated method are shown in Table 2. The column of glues or papers in Table 2 is related to simulation of the friction of connected areas and faults. For instance, smooth papers are selected to simulate low-friction faults while diluted glue is used to simulate relatively high friction faults. Undiluted glue in this research is diluted poly (vinyl acetal) adhesive. The simulations of foundation treatments, including concrete cushion and replacements of vein X, fault f5, f14 and f13, are shown in Fig. 9.

Table 1 Mechanical parameters of concrete and rock masses
Full size table
Fig. 8
figure 8

The location and identification of the rock types and of the faults

Full size image
Table 2 Physical properties and mechanical parameters of faults
Full size table
Fig. 9
figure 9

Simulation of foundation treatments a fault f5; b lamprophyre vein X

Full size image

In the model test, only hydrostatic pressure on the upstream surface of dam is simulated. Overloading process is adopted in this test, resulting in increasing the specific weight of water. Fifty-four tailor-made jacks are divided into eight groups to form an inverted triangle shape array. Meanwhile, eight corresponding sets of oil pumps and pressure control systems are used to control the pushing forces of jacks. Cushion blocks and shims are arranged to avoid inhomogeneous loading. The pushing force and corresponding internal pressure of each group are calculated based on the equivalences of magnitude and moment of the hydrostatic pressure. The model test performs a multi-step incremental loading process. The overloading factor K can be defined as,

$${\varvec{K}}={\varvec{P}}/{{\varvec{P}}_0},$$
(11)

where P is current load on the dam and \({P_0}\) is the normal water load. Under normal condition (the overloading factor equal to 1) and overloading process, cycles of loading and unloading are adopted in the elastic stage, and stepwise continuous loading is adopted in the failure process. The hydrostatic pressure increment is 25% of the design load per step.

Four micro periscopic cameras are arranged near the dam heel and toe to monitor the whole cracking process of dam-abutment in real time. 350 electric resistance strain gages are placed on the upstream and downstream surface of dam to measure the strain and invert the stress of dam body. 180 external displacement gauges are fixed on the steel channels to monitor the absolute displacements of dam body and slops. Meanwhile, 12 internal displacement gauges are set in the abutment to monitor the shear displacements of faults. The layout of strain gages, external displacement gauges are shown in Fig. 10, flowerlike symbols stand for strain gauges while horizontal lines, boxes and circles present displacement gauges.

Fig. 10
figure 10

Layout of strain gauges and displacement gauges

Full size image

Data acquisition system UCAM-70A with high speed and high accuracy is employed to collect and feedback strains and displacements during the overloading process.

4 Model Test Results and Numerical Simulation Verifications

4.1 Deformation Analysis of the Dam Body

Under normal condition (the overloading factor equal to 1), comparison of displacements along the river on the downstream surface of dam between the model test and numerical simulation is shown in Fig. 11. The two displacement fields match each other well, especially the right side of dam body. The displacements show some asymmetry and torsion. For the left side between 1670 and 1800 m, displacements of numerical simulation are larger than those of the model test.

Fig. 11
figure 11

Displacements along the river on the downstream surface of dam (the red curve represents the result of numerical simulation and the blue curve represents the result of the model test, mm). (Color figure online)

Full size image

In the model test, the maximum monitoring displacement on the downstream surface of dam is 85 mm at the top of the crown cantilever while the maximum monitoring displacement on the underside is 20 mm at the right dam toe, 1730 m. Above 1700 m, the right part of dam deforms larger than the left part because of the concrete replacements and concrete cushion in the left abutment. However, the deformation law turns back between 1700 and 1600 m as the existing of fault f2 in the left abutment.

In the numerical simulation, displacements along the dam axis are relatively small as shown in Fig. 12 and obviously torsional deformation can be observed. The maximum displacement along the dam axis is 10.55 mm to the right bank.

Fig. 12
figure 12

Displacements along the dam axis of the downstream surface of dam (mm)

Full size image

In the model test, relationship between overloading factor K and displacements of the crown cantilever is shown in Fig. 13. X-direction is along the dam axis (positive for left bank) and Y-direction is along the river (positive for downstream).

Fig. 13
figure 13

Relationship curves between the displacements (mm) of crown cantilever and the overloading factors a displacements along the river; b displacements along the dam axis

Full size image

For the crown cantilever, displacements above 1730 m are obviously larger than those below 1730 m, and displacements along the river of 1810 m is smaller than those between 1730 and 1885 m. Meanwhile, the magnitude relationship of displacements is not absolutely constant because of the strong nonlinearity of the combined action of dam body and abutment. During the overloading process, the crown cantilever above 1700 m deforms towards left while below 1700 m deforms towards right. The typical asymmetry and torsion results from the asymmetry of dam body and geological conditions. When the overloading factor K is 4.5, almost all of the displacement gauges step into nonlinear stage. With overloading factor over 7, all the displacements increase rapidly and some displacement gauges are even damaged. This is the time for the final failure of dam-abutment.

4.2 Stress Distribution in the Dam

Under normal condition, the stress distribution in the dam is shown in Fig. 14 (downstream) and Fig. 15 (upstream). From the model test, stresses refer to the prototype scale are gained. The maximum principal tensile stress is deduced to be 1.15 MPa at the bottom of dam heel, while the numerical simulation value is 0.66 MPa in the left dam heel at the elevation of 1855 m. There is no prominent tensile stress in downstream surface of dam. The maximum principal compressive stress of two methods are − 9.12 MPa and − 12.85 MPa, respectively, both in the left dam toe near fault f2. Owing to the worse condition of the left foundation, the minimum principal stress (compressive) of the downstream dam surface on the left is larger than that on the right. However, the distribution of stress is bilateral symmetry globally. The stress distribution pattern of two methods are similar and reveal the same regularity that the dam heel is the stress sensitive area. And it is concluded that the design of dam body can overcome the shortcoming of geological asymmetry.

Fig. 14
figure 14

Stress distribution in the downstream surface of dam under normal condition a the model test; b numerical simulation (0.1 MPa)

Full size image
Fig. 15
figure 15

Stress distribution in the upstream surface of dam under normal condition a the model test; b numerical simulation (0.1 MPa)

Full size image

5 Analysis of the Failure Process

5.1 Analysis of the Model Test

Through direct observation and subsequent analysis of all the data recorded, the failure process of dam is analyzed in detail. The failure process and failure mode of the dam are shown in Figs. 16 and 17. It is clear that cracks are mainly concentrated near the dam heel and dam toe instead of the center of the dam.

Fig. 16
figure 16

Schematic diagrams of dam cracks a upstream surface; b downstream surface

Full size image
Fig. 17
figure 17

Photographs of the final failure mode of dam body a upstream surface; b downstream surface

Full size image

Under normal condition, no cracks are found either in the dam body or in the foundation in the model test and no yield zone exists in the numerical simulation as well. When the overloading factor K reaches 2.5, the cracks initiate near the dam heel and tensile cracks appear. Then, more cracks expand around the dam heel while the upstream surface of dam is almost intact during overloading.

As shown in Fig. 16b, the first crack initiates from the center right dam toe to higher elevation vertically when the overloading factor K reaches 3.5, and fault f13 cracks simultaneously. Then tensile cracks perpendicular to the underside develop at 1630 m in the right toe and horizontal cracks develop at 1830 m in the left toe when the overloading factor K reaches 4.0. Meanwhile, the bearing capacity of the foundation treatments in the left foundation decreases, leading to cushion cracking. Some rock masses in high elevation in the right side are dislocated and the dam-abutment enters into the stage of nonlinear deformation.

The cracks appear continuously and expand when the overloading factor K reaches 5.0. At the same time, significant cracks and sliding occur in fault f14 and f5, a long-connected crack appears along the underside from river bottom to the left abutment. When the overloading factor K increases from 5.0 to 7.0, cracks on the right of underside develop at 1790 m and connect with cracks in the left dam body at 1800 m. Large deformation occurs near the resisting force body, especially the transverse joints between f14 and f13 in the right bank.

When the overloading factor K reaches 7.5, cracks interpenetrate on the middle of the downstream surface of dam, concrete cushion in the left bank is also seriously damaged. The cracks expand more than 100 m along the river in the rock masses. The dam body reaches the ultimate bearing capacity and collapses finally.

Above all, according to the model test, the safety factor of cracking K1 is 2.5, the safety factor of nonlinear deformation K2 is 4.0 and the safety factor of the ultimate bearing capacity K3 is 7.5.

5.2 Comparative Numerical Simulation

In the numerical simulation, there is no unbalanced force arising until the overloading factor K reaches 2.0. Figure 18 shows the unbalanced force vector in the dam body under 2 times of overloading. The unbalanced force initials at the bottom of dam heel and the top of the right abutment, while there is no unbalanced force in downstream surface of dam, which matches the result of model test very well.

Fig. 18
figure 18

Unbalanced force vector graphs in the dam body under two times overloading a upstream surface. b Downstream surface

Full size image

Figure 19 shows the yield zone in the downstream surface of dam when the overloading factor K reaches 4.0 and 5.0. When the overloading factor K increases from 4.0 to 5.0, the yield zone in the downstream surface of dam penetrates between 1780 and 1830 m. Significant nonlinear displacement appears on the dam body through linear correlation analysis between displacements of all the nodes on the dam-abutment and the overloading factor K, which means the dam-abutment steps into the nonlinear deformation stage.

Fig. 19
figure 19

Yield zone in the downstream surface of dam aK = 4.0; bK = 5.0

Full size image

When the overloading factor K reaches 8.0, the horizontal sections of yield zone and unbalanced forces vector graphs are shown in Fig. 20. The unbalanced forces in the upstream and downstream surface of dam are connected on 1830 m, while extensive yield zones generate in the dam-abutment, and the final failure occurs.

Fig. 20
figure 20

The horizontal sections of yield zone and unbalanced force vector graphs when K = 8.0, a ∇1830 m; b ∇1670 m

Full size image

Above all, in the numerical simulation, K1, K2 and K3 are 2.0, 4.5 and 8.0, respectively. The results from model test and numerical simulation for the three safety factors are approximately coincident.

6 Engineering Analogy of Global Stability

Geomechanical model test technique has been widely used in the global stability and failure analysis of high arch dams in China. But there are no clear regulatory standards yet. Thus, the engineering analogy method is used in the research. Listed in Table 3 are the safety factors and corresponding information of eight typical super high arch dams in China (Jinping-I project has completed three model tests including scheme without foundation treatments, thin scheme and final scheme).

Table 3 Three safety factors of typical high arch dam in China by model tests
Full size table

The safety factor of crack K1 is often small, of which the essence is the safety degree of dam heel cracking. The initial of nonlinear deformation safety factor K2 is crucial to the overall stability of the arch dam. When the loading reaches multiple times of K2, the dam toe area is destroyed, and then the crack propagation speed is obviously accelerated, and the arch dam has entered the stage of accelerated failure. The reinforcement of dam toe area can obviously improve the K2 of the arch dam. Besides, it can also suppress the cracking of the upstream heel and improve the K1.

7 Conclusions

In this paper, features and test results of Jinping-I, the highest arch dam all over the world, are presented and analyzed. The numerical simulation based on the deformation reinforcement theory is introduced to verify the test results. Some conclusions can be drawn as follows.

  1. 1.

    According to the model test, crack initiates near the dam heel when K = 2.5, then the dam turns into the nonlinear deformation stage at 4.0 times overloading and Jinping-I fails finally when K = 7.5. The solving method of safety factors by the numerical simulation are proposed in this paper, while the results are 2.0, 4.5 and 8.0, respectively, which matches the test results well.

  2. 2.

    The results of model test and numerical calculation show that the unbalanced force is an effective index for predicting cracking. The area where the unbalanced force appears in numerical calculation is also the location of cracking in the model test.

  3. 3.

    Under the failure mode of most high arch dams, the crack first occurred at the upstream of the dam heel. After overloading to a certain number, the compression–shear failure occurred in the dam toe area, then the whole arch dam entered the nonlinear deformation stage. Meanwhile, the number of cracks on the dam increased obviously, but the arch dam still had a definite bearing capacity at this time. With the increase of overload times, ultimate failure of arch dams occurs. The dam heel and dam toe are the key areas in the design of arch dams, of which the reinforcement should be considered minutely.

  4. 4.

    According to the comparison between model test and numerical simulation, and engineering analogy, it is indicated that Jinping-I arch dam has a high inherent safety. Treatment measures such as the concrete replacements and dam fillet are proved to be effective to improve the overall stability of Jinping-I arch dam. However, in this research, only the dominant load, hydrostatic pressure, is simulated. Some other factors such as pore water pressure are not taken into consideration, which may also have an effect on the deformation and cracking of the dam to some extent. To ensure the safety of the dam, visual inspections and observations are still needed during operation.