Statistical Analysis of Rock Fracture Toughness Data Obtained from Different Chevron Notched and Straight Cracked Mode I Specimens

Abstract

In laboratory fracture toughness studies, the crack growth resistance of rock materials may be influenced by different factors such as specimen geometry, loading conditions, and also the type of pre-notch cut in the test sample. In this paper, a large number of mode I fracture toughness experiments are conducted on an Iranian white rock “Harsin marble” with six different mode I specimens. The selected test specimens are in the shape of cylindrical rod, rectangular beam, and circular Brazilian disk containing either chevron notch or straight crack. The effect of specimen geometry and pre-notch type was investigated statistically, and it was found that the average fracture toughness values of notched specimens were higher than those of the similar specimens but containing straight crack. Meanwhile, the scatters of fracture toughness data for chevron notched specimens were smaller than those for the straight cracked samples. For each set of experimental fracture toughness results, probability of fracture was investigated using two- and three-parameter Weibull statistical distributions. Comparison of the Weibull fitted curves for chevron notched and straight cracked samples with the same geometries demonstrated that the discrepancy between the corresponding curves can be described with a good accuracy by a simple shift factor. In addition, using the extended maximum tangential strain criterion which takes into account the influence of both K_I and T-stress terms, the statistical fracture toughness data of chevron notched specimens were predicted in terms of the Weibull distribution parameters of the straight cracked specimens.

1 Introduction

Rock masses contain different types of discontinuities including flaws, fractures, and joints. Due to the mostly elastic behavior of rocks, linear elastic fracture mechanics (LEFM) theory is an appropriate framework to predict the crack growth response of rocks. Based on the LEFM theory, the most important parameter is fracture toughness (K_c) that is considered as the critical value of stress intensity factor (K) (Irwin 1957). This parameter describes the onset of fracture in a cracked specimen under a given loading condition. Hence, it is important to determine the fracture toughness of rocks by employing appropriate testing methods. Since rocks are relatively weak under tensile loads, the mode I (or opening fracture mode) is the major failure mode in the structures made of these materials. So far, several methods and test specimens with different shapes, sizes, loading conditions, and crack geometries have been proposed to determine the mode I fracture toughness of rock materials (Aliha et al. 2013a, b, 2015a, b; Awaji and Sato 1978; Chang et al. 2002; Fowell 1995; Guo et al. 1993; Kavanagh and Pavier 2014; Kuruppu et al. 2013; Matsuki et al. 1991; Ouchterlony 1990; Singh and Pathan 1988; Thiercelin and Roegiers 1986; Xeidakis et al. 1996). It is expected that different specimens of a same material result in an approximately the same value of fracture toughness but, practically, that is not exactly true. Due to the significant discrepancy observed for K_Ic results in a brittle material like rock, this idea was arisen that fracture toughness is dependent on the geometry of tested specimen and loading configuration (Aliha et al. 2012, 2016; Chao et al. 2001; Davenport and Smith 1993; Kataoka et al. 2015; Khan and Al-Shayea 2000; Kumar et al. 2011; Liu and Chao 2003; Sun and Qian 2009; Ueno et al. 2013). Higher-order terms of stress series expansion are proven as affecting factors on the observed difference in the values of apparent fracture toughness (Ayatollahi and Sedighiani 2010; Du and Hancock 1991; Giannakopoulos and Olsson 1992; Melin 2002). Second term in the William’s crack tip stress series expansion (Williams 1957) is called T-stress. This parameter is independent of the distance from the crack tip which is constant and non-singular. In some research works, the inclusion of T-stress in the conventional fracture criteria has been investigated carefully to determine the fracture behavior of materials (Aliha and Ayatollahi 2010; Aliha et al. 2010, 2016; Ayatollahi and Aliha 2009; Erdogan and Sih 1963; Kong et al. 1995; Sedighiani et al. 2011; Sih 1974; Smith et al. 2001; Thomas and Pollard 1993; Yukio et al. 1983). For example, using the extended maximum tangential strain (EMTSN) criterion the dependency of mode I fracture resistance to the T-stress was shown and the obtained experimental rock fracture toughness data were predicted successfully with this criterion (Aliha et al. 2016).

The initial crack in the laboratory-scale rock specimens can be introduced by two common techniques: (1) straight through thickness crack and (2) chevron notch-type crack. However, due to difference in the shape and configuration of these two cracking methods, the geometry and shape of pre-notch may probably affect the value of rock fracture resistance. In some previous researches, a comparison between the fracture toughness values obtained from straight through cracked specimens and chevron notched specimens has been made. Khan and Al-Shayea (2000) investigated the effect of notch type on Brazilian disk made of a limestone rock obtained from Saudi Arabia. According to their results, the fracture toughness of the chevron notched specimen was 0.61 MPa.m^0.5 compared to 0.42 MPa.m^0.5 for the straight through cracked specimen. In addition, Wei et al. (2016) conducted some experimental tests on semi-circular bend specimens with straight crack and chevron notch. Two different rock types (i.e., Dazhou sandstone and Qingdao granite) were tested (Wei et al. 2016). The obtained experimental results indicated that two employed methods yielded different results. However, there is still lack of a comprehensive research on the influence of specimen geometry and notch type on the value of rock fracture toughness.

On the other hand, due to the presence of natural discontinuities (like micro-cracks and flaws) in rock materials, a large scatter in their mechanical properties obtained from the experiments is inevitable (Aliha and Ayatollahi 2014). Indeed, the fracture toughness results obtained from a small number of specimens made of brittle and quasi-brittle materials like rocks, concretes, composites, and ceramics cannot provide a good estimation for the cracking resistance of any given rock material. In such cases, statistical analyses by means of larger number of test data are more reliable. Díaz and Kittl (2013) used a simplified method to determine the fracture toughness for some brittle and ductile materials like glass, cement, steel, and copper. They analyzed the results by Weibull distribution function showing the good ability of this method for predicting the experimental fracture toughness results. In addition, Aliha et al. (2012) predicted the probability of fracture in Guiting limestone by fitting the experimental data to a Weibull model obtained for semi-circular bend specimen. In another work, the test data obtained from some chevron notched Brazilian disks made of white marble were successfully analyzed statistically to predict the Weibull parameters of mode II fracture toughness results in terms of mode I fracture toughness Weibull parameters (Aliha and Ayatollahi 2014). Also, mode I fracture toughness of asphalt mixtures with different air void contents were studied statistically using two- and three-parameter Weibull distribution models (Aliha and Fattahi Amirdehi 2017). Therefore, it has been demonstrated that the Weibull probabilistic distribution is capable to predict the results of fracture resistance for brittle and quasi-brittle materials like rocks.

The aim of this study is to compare the mode I fracture resistance data of a rock material tested with different geometries and notch types by means of Weibull statistical method. Average values of fracture resistance as well as scattering parameters for each set of data are compared in different mode I test specimens. It is shown that there is a meaningful discrepancy between the Weibull statistical parameters of the tested specimens and the notch type has a significant effect on mode I statistical fracture toughness data. Furthermore, using a theory-based framework, the statistical results obtained from the chevron notched specimens are predicted in terms of the Weibull parameters of the straight cracked test specimens.

2 Mode I Fracture Test Specimens

In this section, the geometry and loading configuration of test samples selected for conducting mode I fracture toughness experiments of this research are briefly illustrated.

2.1 SECRBB Specimen

The first specimen utilized for mode I fracture toughness study of rocks in this paper is the single edge cracked round bar bend (SECRBB) specimen as shown in Fig. 1. Some researchers have used this specimen for determining the fracture toughness of rocks and concretes (Barr and Hasso 1986; Bush 1976; Ouchterlony 1981). As shown in Fig. 1, the specimen is a cylinder with diameter D and length L that contains a straight crack of depth a. A three-point bending fixture with span of S is utilized for applying the load on the specimen.

Fig. 1

Geometry and loading configuration of the SECRBB specimen for conducting mode I fracture toughness test

Fracture resistance (K_If) of the SECRBB specimen is determined as follows (Ouchterlony 1981):

$$ K_{\text{If}} = 0.25(S/D)Y^{{\prime }} F_{\hbox{max} } /D^{1.5} $$

(1)

in which

$$ \begin{aligned} Y^{{\prime }} & = 2(D/S)\left\{ {450.8531\rho^{2} (a/D)^{1.5} } \right\}^{0.5} /\left\{ {(a/D) - (a/D)^{2} } \right\}^{0.25} \\ \rho & = (S/D)/3.33 \\ \end{aligned} $$

where as stated before, D is the diameter of rock core specimen, S is the support span, a is the notch length, and F_max is the fracture load that is obtained at the onset of fracture from the test.

2.2 CB Specimen

The other selected mode I specimen is called chevron bend (CB) specimen that has been proposed by International Society for Rock Mechanics (ISRM) as a standard test method for obtaining mode I fracture toughness of rocks (Ouchterlony 1990). The overall shape and dimension of the CB specimen is exactly the same as the SECRBB specimen but a V-shaped chevron notch is introduced in the specimen instead of the straight crack. The configuration and geometric parameters of the CB specimen are presented in Fig. 2. By applying a three-point bend load to the CB specimen, the crack initiation would occur from the tip of chevron notch and then it would propagate stably up to a critical crack length (a = a_m). After that, the crack growth becomes unstable and the sudden failure takes place. The mode I fracture toughness of the CB specimen is obtained from the following relation (Ouchterlony 1990):

$$ \begin{aligned} K_{\text{If}} & = A_{\hbox{min} } F_{\hbox{max} } /D^{1.5} \\ A_{\hbox{min} } & = [1.835 + 7.15a_{0} /D + 9.85(a_{0} /D)^{2} ]S/D \\ \end{aligned} $$

(2)

where F_max is the maximum load (i.e., fracture load) and A_min is the dimensionless critical stress intensity factor of the CB specimen. This parameter (i.e., A_min) is a geometric factor that depends on the ratios of notch length to specimen’s diameter a₀/D and support span to specimen’s diameter S/D.

Fig. 2

Geometry and loading configuration of the CB specimen for conducting mode I fracture toughness test

2.3 SENB Specimen

Another specimen used for rock fracture toughness study of this research is the single edge notched beam (SENB) specimen subjected to three-point bending that its geometry and loading configuration have been shown in Fig. 3. This specimen which contains a straight sharp crack of depth a was firstly proposed by ASTM standard for determining the fracture toughness of metallic material. However, rock fracture mechanics researchers (such as Schmidt 1976) used this specimen to perform mode I fracture toughness test on limestone. The critical mode I stress intensity factor of the SENB specimen is calculated from the following equation suggested by American Society for Testing a Material (Astm 1997):

$$ \begin{aligned} K_{\text{If}} & = \frac{{F_{\hbox{max} } S}}{{BW^{3/2} }}f(a/W) \\ f(a/W) & = \frac{{3\sqrt {\frac{a}{W}} }}{{2\left( {1 + 2\frac{a}{W}} \right)\left( {1 - \frac{a}{W}} \right)^{3/2} }}\left[ {1.99 - \frac{a}{W}\left( {1 - \frac{a}{W}} \right)\left\{ {2.15 - 3.93\left( {\frac{a}{W}} \right) + 2.7\left( {\frac{a}{W}} \right)^{2} } \right\}} \right] \\ \end{aligned} $$

(3)

in which F_max is the fracture load and f(a/W) is a geometry factor that depends on the geometry and loading configuration of the specimen and also crack length. Other parameters are defined in Fig. 3.

Fig. 3

Geometry and loading configuration of the SENB specimen for conducting mode I fracture toughness test

2.4 CNBB Specimen

The fourth mode I specimen is the chevron notched bend beam (CNBB) that has the same configuration of the SENB specimen but instead of straight crack, a V-shaped chevron notch is introduced at the middle of specimen as shown in Fig. 4. The fracture toughness of this specimen was suggested by Wu (1984) as following:

$$ \begin{aligned} K_{\text{If}} & = \frac{{F_{\hbox{max} } }}{B\sqrt W }Y^{*} \left(\frac{{a_{0} }}{W},\frac{{a_{1} }}{W},\frac{a}{W}\right), \\ \alpha_{0} & = \frac{{a_{0} }}{W},\alpha_{1} = \frac{{a_{1} }}{W},\alpha = \frac{a}{W} \\ Y^{*} (\alpha_{0} ,\alpha_{1} ,\alpha ) & = \sqrt {\frac{1}{2}\frac{{(\alpha_{1} - \alpha_{0} )}}{{(\alpha - \alpha_{0} )}}\frac{{{\text{d}}C_{v} (\alpha )}}{{{\text{d}}\alpha }}} \\ \end{aligned} $$

(4)

where F_max is the critical fracture load obtained experimentally at the onset of fracture and the other geometric parameters (such as a₀, a₁, a, B, W, θ) are defined in Fig. 4. C _v (α) is the dimensionless compliance of specimen as C _v  = BE′u/F where E΄ = E/(1 − ν²) for the plane strain condition and u and F are load-point displacement and load, respectively. Wu (1984) calculated the C _v (α) using Bluhm’s slice model (Bluhm 1975) as:

$$ \begin{aligned} \frac{1}{{C_{v} (\alpha )}} & = \frac{{(\alpha - \alpha_{0} )}}{{(\alpha_{1} - \alpha_{0} )}}\frac{1}{{\gamma + \beta \tan^{2} (\frac{\pi \alpha }{2})}} + \frac{k}{{(\alpha_{1} - \alpha_{0} )(\gamma - \beta )}}\left\{ {(\alpha_{1} - \alpha ) - \frac{2}{\pi }\sqrt {\frac{\beta }{\gamma }} } \right. \\ & \quad \times \left. {\left[ {\arctan \left( {\sqrt {\frac{\beta }{\gamma }} \tan \left(\frac{{\pi \alpha_{1} }}{2}\right)} \right) - \arctan \left( {\sqrt {\frac{\beta }{\gamma }} \tan \left(\frac{\pi \alpha }{2}\right)} \right)} \right]} \right\}\, \\ \end{aligned} $$

(5)

where

$$ \begin{aligned} \gamma & = \frac{1}{4}\left( {\frac{S}{W}} \right)^{3} \left[ {1 + 3(1 + \nu )\left( {\frac{S}{W}} \right)^{2} } \right] \\ \beta & = \frac{2}{\pi }\left( {\frac{S}{4W}} \right)^{2} \left[ {7.31 + 0.21\sqrt {\frac{S}{W} - 2.9} } \right]^{2} \\ \end{aligned} $$

(6)

and k is a shear transfer function and is obtained from:

Fig. 4

Geometry and loading configuration of the CNBB specimen for conducting mode I fracture toughness test

$$ \begin{aligned} \phi & = \frac{1}{2}(\pi - \theta ),\quad \theta \,{\text{is}}\,{\text{chevron}}\,{\text{notch}}\,{\text{angle}}\,{\text{ (Fig}}.\,{ 4)} \\ k & = \left\{ {\begin{array}{*{20}l} {1 + 0.444\left( {\alpha_{1} } \right)^{3.12} } \hfill & {\phi \ge 1} \hfill \\ {1 + \left( {\alpha_{1} } \right)^{3.12} (2.236\phi - 4.744\phi^{2} + 4.699\phi^{3} - 1.77\phi^{4} )} \hfill & {\phi < 1} \hfill \\ \end{array} } \right. \\ \end{aligned} $$

(7)

In Eq. 7, ϕ is equal to $\frac{1}{2}(\pi - \theta )$, in which θ is the chevron notch angle as shown in Fig. 4.

2.5 SCCBD Specimen

The straight center cracked Brazilian disk (SCCBD) specimen is another commonly used test configuration for measuring the fracture toughness of brittle and quasi-brittle materials like concretes, rocks, and ceramics (Atkinson et al. 1982). This specimen is a disk of radius and thickness R and B, respectively, that a straight crack is introduced at its center. By applying a diametric compression load to the disk along the crack plane (Fig. 5), the specimen would be subjected to a pure mode I loading condition. The mode I fracture resistance (K_If) of the SCCBD specimen can be obtained from (Atkinson et al. 1982):

$$ K_{\text{If}} = \frac{{F_{\hbox{max} } \sqrt a }}{{\sqrt {\pi RB} }}N_{\text{I}} $$

(8)

in which N_I is the shape or geometry factor that was computed numerically by Ayatollahi and Aliha (2007) or derived theoretically by Atkinson et al. (1982) as following equation for pure mode I loading:

Fig. 5

Geometry and loading configuration of the SCCBD specimen for conducting mode I fracture toughness test

$$ N_{\text{I}} = 0.99 + 0.141\left(\frac{a}{R}\right) + 0.863\left(\frac{a}{R}\right)^{2} + 0.886\left(\frac{a}{R}\right)^{3} $$

(9)

2.6 CCNBD Specimen

The cracked chevron notched Brazilian disk (CCNBD) specimen is another suitable mode I fracture test sample that was suggested in 1995 as a standard ISRM test method (Fowell 1995) for determining fracture toughness of rock materials as illustrated in Fig. 6. A chevron notch of initial length a₀ and final length a₁ is introduced along the disk diameter in the center of CCNBD specimen. Fowell (1995) suggested the following expression to determine the mode I fracture resistance of the CCNBD specimen loaded along the disk diameter:

$$ K_{\text{If}} = \frac{{F_{\hbox{max} } }}{B\sqrt R }Y_{\hbox{min} }^{*} \, $$

(10)

where F_max is the fracture load, Y ^*_min is the normalized critical stress intensity factor that depends on the geometric parameters of initial notch length-to-the radius ratio (a₀/R), final notch length-to-the radius ratio (a₁/R), and the thickness of specimen. Y ^*_min can be obtained either numerically or from available formulations suggested in the literature (Wang et al. 2012).

Fig. 6

Geometry and loading configuration of the CCNBD specimen for conducting mode I fracture toughness test

3 Fracture Toughness Testing

In previous section, different test samples were described in which they can be used for obtaining mode I fracture toughness of wide range of rock materials including sedimentary, metamorphic, and igneous rocks. However, since the geometry, loading condition, and initial crack type differ in the mentioned samples, the fracture toughness results obtained from these mode I test specimens may be different and affected by the geometry and loading conditions. Such possible effects are investigated and examined experimentally in this paper.

3.1 Testing Procedure

In order to investigate the effect of specimen’s configuration and notch type (i.e., chevron notch and straight crack) on the value of mode I fracture resistance of rocks, a large number of test samples in the shape of cylindrical or rectangular type (like SECRBB, CB, SCCBD, CCNBD, SENB, and CNBB specimens illustrated earlier) were manufactured from a coarse-grain white marble rock mass called Harsin marble. This rock is from Harsin area (a region in western of Iran) and contains very few discontinuities, so it could be considered as a homogeneous material and mostly exhibits isotropic properties that is widely used in Iran as a construction material. The crack growth behavior and fracture resistance of this type of rock or other similar marble rocks have already been determined successfully by other researchers by employing the mentioned procedures and specimens described in previous section (Wei et al. 2018, 2017a, b, c; Liu et al. 2018). A rotary diamond circular saw blade (with radius of 35 mm and thickness of 0.6 mm) was utilized to introduce the straight crack and chevron notch in the specimens. The geometry and loading conditions of the manufactured specimens are presented in Table 1.

Table 1 Geometry and span ratio of the test specimens used for mode I fracture toughness testing on the Harsin marble

Fracture toughness tests were conducted using a servo-hydraulic tension–compression test machine (SANTAM/STM-150) with loading capacity of 15 kN. In order to achieve more precise results and study the scatter of experimental data, fracture tests on each sample were also repeated several times (as illustrated in the last column of Table 1). Figure 7 shows the experimental setup employed for testing the CB, CNBB, and CCNBD specimens. The same setup configurations were used for SECRBB, SENB, and SCCBD specimens, respectively. Fracture of whole samples occurred suddenly in brittle manner from the tip of straight crack or chevron notch along the crack plane such that each specimen was split into two same halves after failure. Figure 8 presents the fracture surface of the SENB and CNBB broken samples demonstrating the self-similar and straight path of specimens tested in mode I. The applied load and load-point displacements were recorded continually by the digital data logger of test machine. The results approved dominantly linear elastic fracture behavior of tested samples.

Fig. 7

Loading setup for some of the tested specimens made of Harsin marble rock. a CB specimen, b CNBB specimen, c CCNBD specimen

Fig. 8

Fracture pattern observed for the a straight cracked specimens and b chevron notched specimens

4 Results and Discussion

The corresponding values of mode I fracture toughness data obtained for each test configuration are summarized in Table 2 and also are presented in Fig. 9 in graphical form for better understanding the variations of the results. An inherent scatter can be observed for all six types of rock specimens probably due to the presence of discontinuities and natural flaws in the structure of investigated Harsin marble rock. The average value of fracture resistance (K_If) for each specimen (Fig. 9) reveals the noticeable influence of specimen geometry and the type of crack/chevron on fracture growth resistance of tested marble rock. The minimum and maximum average K_If values were obtained for the SCCBD and CNBB specimens, respectively. This finding demonstrates that the crack growth bearing capacity of rectangular beam specimen subjected to bend-type loading is higher than the circular specimen compressed by diametral load. Moreover, it was found that for similar specimens, the chevron notched specimen results in a greater fracture toughness value in comparison with the same sample containing a straight crack.

Table 2 Summary of fracture resistance values for the tested specimens (all in MPa.m^0.5)

Fig. 9

Experimental results of mode I fracture resistance for the tested samples a SECRBB and CB, b SENB and CNBB, and c SCCBD and CCNBD specimens

In the following section, the scatter of fracture resistance results obtained from the aforementioned six specimens is analyzed statistically using the Weibull model.

4.1 Statistical Analysis of Results

The scatter of the fracture resistance values obtained for different test specimens of this research (i.e., cylindrical and rectangular shape samples containing chevron notch and straight crack) can be studied using a probabilistic failure analysis. To do that, the obtained values for each specimen are plotted in a failure probability (P _f ) graph by sorting the K_If data in an increasing order. Then, the failure probability (P _f ) of the tested samples can be determined from:

$$ P_{f} = \frac{(i - 0.5)}{n}\quad i = 1,2,3, \ldots ,n $$

(11)

in which i is the number of test specimen and n is the total number of tests for each category (i.e., n = 13, 14, or 15 depends on the test specimen according to Table 2). Such failure probability equation has been widely used by researchers (Aarseth and Prestløkken 2003; Aliha et al. 2006; Guo et al. 2017; Quinn and Quinn 2010), but the utilized equation (i.e., Eq. 11) for sorting the fracture toughness results is not necessarily the best one and other failure probability functions have also been used in the literature (e.g., Smith et al. 2006; Wallin 1984; Bass et al. 2001). A stochastic model based on the weakest link theory was suggested by Weibull (1951) to describe the strength distribution of brittle or quasi-brittle materials. This model assumes that the fracture in these materials is locally initiated and propagated due to the failure of largest flaw inside the brittle material. A comparison can thus be made among some sequences, in which the strength is defined by the weakest link. After breaking this critical element, the next weakest element will specify the strength of the other parts (Weibull 1951).

Using a general statistical model, the Weibull-based probability function was proposed by Wallin (1984) for analyzing brittle fracture behavior. Accordingly, the probability of mode I fracture can be estimated using the following two- or three-parameter Weibull distributions (Wallin 1984):

$$ P_{f} (K_{\text{If}} ) = 1 - \exp \left[ { - \left( {\frac{{K_{\text{If}} }}{{K_{0} }}} \right)^{m} } \right]\quad \quad {\text{Two-parameter}}\,{\text{model }}\left( {K_{0} ,m} \right) $$

(12)

$$ P_{f} (K_{\text{If}} ) =\, 1 - \exp \left[ { - \left( {\frac{{K_{\text{If}} - K_{\hbox{min} } }}{{K_{0} - K_{\hbox{min} } }}} \right)^{m} } \right]\quad \quad {\text{Three-parameter}}\,{\text{model }}\left( {K_{\hbox{min} } ,K_{0} ,m} \right) $$

(13)

where K₀ is the scale parameter of the distribution that corresponds to the fracture probability of 0.623, K_min is the location parameter below which the probability of failure is zero, and m is the shape parameter or Weibull modulus for describing the scatter of K_If. While in the simpler two-parameter Weibull distribution model K_min is assumed to be zero, based on the three-parameter Weibull model, this minimum fracture toughness value is not zero and its value depends on the type of tested material. Hence, although both two- and three-parameter Weibull distribution models have widely been used for statistical analysis of strength and failure in brittle and quasi-brittle materials, the three-parameter model which considers such location parameter may provide better statistical predictions for real cracked applications.

In the past, several researchers have shown the applicability of Weibull model for statistical analysis of the fracture phenomenon in brittle materials like rocks, asphalt mixtures, bone, ceramics (Aliha and Ayatollahi 2014; Aliha and Fattahi Amirdehi 2017; Aliha et al. 2012; Quinn and Quinn 2010; Sakin and Ay 2008). Hence, this model is examined here for investigating the statistical rock fracture toughness data obtained from different test geometries and notch types. The Weibull parameters for each specimen of this research were found by fitting a curve to the experimental data of Table 2. For this purpose, MATLAB commercial mathematical software was employed to fit the two- and three-parameter Weibull probability distributions using the least square method.

Figures 10 and 11 show the predicted two- and three-parameter curves, respectively, for the experimental fracture resistance data of Harsin marble obtained from the SECRBB, CB, SENB, CNBB, SCCBD, and CCNBD test specimens. It can be seen from this figure that the relatively appropriate Weibull probabilistic curves can be fitted to each set of data.

Fig. 10

Two-parameter Weibull distributions for the tested samples, a SECRBB and CB, b SENB and CNBB, and c SCCBD and CCNBD specimens

Fig. 11

Three-parameter Weibull distributions for the tested samples, a SECRBB and CB, b SENB and CNBB, and c SCCBD and CCNBD specimens

The Weibull distribution parameters of two- and three-parameter models are presented in Tables 3 and 4, respectively, for the whole tested rock specimens. It can be concluded from Figs. 10 and 11 that reasonably good agreement exists between the experimental data and the predicted Weibull model demonstrating the practical ability of Weibull distribution model in predicting the failure behavior of tested rock materials.

Table 3 Two-parameter Weibull distribution parameters obtained for different mode I test specimens

Table 4 Three-parameter Weibull distribution parameters obtained for different mode I test specimens

4.2 Geometry and Loading Effect on Mode I Fracture Behavior

It is observed that the average values of fracture resistance for specimens with chevron notch (i.e., CB, CNBB, and CCNBD specimens) are higher than that for similar specimens with straight crack (i.e., SECRBB, SENB, and SCCBD specimens, respectively). In addition, it can be found from Tables 3 and 4 that, generally, the m values for specimens with chevron notch are lower than those for specimens with the straight crack demonstrating the lower scatter of fracture resistance results for chevron notched specimens in comparison with the straight-cracked mode I specimens. The Weibull modulus (m) is actually a measure of the distribution of fracture toughness data, and depending on the type of material, manufacturing process and also sample size utilized in the statistical analyses, the value of Weibull modulus may vary in a wide range (Guo et al. 2017; Quinn and Quinn 2010; Smith et al. 2006; Bass et al. 2001). The higher the m value is, the narrower the probability curves of the fracture toughness distribution are. Indeed, one possible reason for the difference in the Weibull modules of the investigated rock samples can be due to different sizes of the highly stressed zones around the notch in which a wider area is stressed for straight cracked specimens than that in the chevron notched specimens. This issue is in agreement with the findings and conclusions of other papers and researchers. For example, according to literature survey (Beremin et al. 1983; da Silva et al. 2004), the Weibull stress is defined in terms of the ratio of effective volume to reference volume and this ratio only depends on the Weibull modulus m; such that when the larger volumes are under load in a specimen, greater m values are obtained. Therefore, probability of fracture initiation for the straight-cracked rock specimens is more than the chevron notched ones. Actually, high stress concentration at the tip of chevron notch results in a lower scatter for fracture toughness data. In the chevron notch-type specimens, the crack initiates at very lower load levels from the chevron tip and grows stably to a critical crack length in which sudden failure occurs.

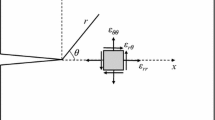
The maximum tangential strain criterion is among the suitable and accurate fracture models for predicting the crack growth in different materials and loading conditions (Mirsayar et al. 2017, 2018a, b). Aliha et al. (2016) employed the extended maximum tangential strain (EMTSN) criterion and showed the dependency of mode I fracture resistance to the geometry and loading condition of tested specimen via considering the influence of non-singular T-stress term. This dependency can also be re-examined here to find the relation between the obtained statistical results for the investigated rock material. By considering r and θ as the polar coordinates with the origin at crack tip as shown in Fig. 12 and based on the maximum tangential strain (MTSN) criterion (Wu 1974), the value of tangential strain along θ₀ (i.e., direction of fracture) and at a critical distance r_c from the crack tip reaches a critical value of ε_c. In this criterion, singular terms of strain components (i.e., stress intensity factors) are considered, but in the extended MTSN (i.e., EMTSN) criterion, the effect of T-stress is also taken into account in addition to the SIFs (Aliha et al. 2016). Hence, the crack initiation occurs based on the following (K_I-T)-based relation:

$$ \varepsilon_{c} \sqrt {2\pi r_{c} } = \beta K_{\text{If}} - \gamma T_{c} \sqrt {2\pi r_{c} } $$

(14)

where T_c is the critical value of T-stress at the onset of fracture and K_If is the critical stress intensity factor of specimen corresponding to the fracture load that was called the mode I fracture resistance. ε_c and r_c can be considered constants (as material properties) for any desired material. Therefore, the value of K_If is linearly dependent on the critical value of T-stress. The other parameters are defined as follows:

$$ \beta = \frac{1 - \nu }{E},\;\;\gamma = \frac{\nu }{E}\quad \quad {\text{for}}\,{\text{plane}}\,{\text{stress}} $$

(15)

$$ \beta = \frac{(1 - 2\nu )(1 + \nu )}{E},\;\;\gamma = \frac{\nu (1 + \nu )}{E}\quad \quad \begin{array}{*{20}l} {{\text{for}}\,{\text{plane}}\,{\text{strain}}} \hfill \\ \end{array} $$

where E and ν are the modulus of elasticity and Poisson’s ratio, respectively, and r is the distance from the crack tip.

Fig. 12

Polar strain components for mode I loading condition

By defining the mode I fracture toughness $K_{\text{Ic}} = {{\varepsilon_{c} \sqrt {2\pi r_{c} } } \mathord{\left/ {\vphantom {{\varepsilon_{c} \sqrt {2\pi r_{c} } } \beta }} \right. \kern-0pt} \beta }$ at T _c  = 0 as a constant material property (that obtained by testing a cracked specimen with zero or negligible T-stress value) and using Eq. 14, the relation between K_If and K_Ic can be obtained as:

$$ K_{\text{Ic}} = K_{\text{If}} - \frac{\gamma }{\beta }T_{c} \sqrt {2\pi r_{c} } $$

(16)

The value of critical distance r_c as the size of fracture process zone (FPZ) in front of the crack tip can be obtained according to the following relation suggested by Schmidt (1980):

$$ r_{c} = \frac{1}{2\pi }\left( {\frac{{K_{\text{If}} }}{{\sigma_{t} }}} \right)^{2} $$

(17)

in which σ_t is the tensile strength of rock material that can be obtained by means of available experimental methods. Biaxiality ratio (B _r ) and normalized critical distance (α _r ) can introduced as normalized factors of T_c and r_c, respectively:

$$ B_{r} = \frac{{T_{c} \sqrt {\pi a} }}{{K_{\text{If}} }} = \frac{{T_{\text{I}}^{*} }}{{Y_{\text{I}}^{*} }} $$

(18)

$$ \alpha_{r} = \sqrt {\frac{{2r_{c} }}{a}} \,\,\,\,\,\,\,\, $$

(19)

where a is the crack length and half-crack length for the edge crack and center crack, respectively. T ^*_I and Y ^*_I are geometry factors in mode I loading condition that can be determined numerically for any given test specimen easily by performing a finite element analysis and considering a reference load (Aliha et al. 2016) and can be defined as:

$$ T_{c} = \sigma T_{\text{I}}^{*} $$

(20)

$$ K_{\text{If}} = \sigma Y_{\text{I}}^{*} \sqrt {\pi a} $$

(21)

where σ is a characteristic stress in the specimen.

Equation 16 can be rewritten in terms of B _r and α_r using Eq. 15 for plain strain condition:

$$ \frac{{K_{\text{Ic}} }}{{K_{\text{If}} }} = 1 - \frac{\nu }{1 - 2\nu }B_{\text{r}} \alpha_{\text{r}} \quad \begin{array}{*{20}l} {{\text{for}}\,{\text{plane}}\,{\text{strain}}} \hfill \\ \end{array} $$

(22)

in which the term B _r α _r represents the contribution of T-stress in mode I fracture resistance.

Based on Eq. 22, a linear relationship would be expected to exist between the mode I fracture results of any two given test specimens with different shapes manufactured from a same material under the plane strain condition as follows (Aliha et al. 2016):

$$ \frac{{K_{{_{\text{If}} }}^{(1)} }}{{K_{{_{\text{If}} }}^{(2)} }} = \frac{{1 - \frac{\nu }{1 - 2\nu }B_{{^{r} }}^{(2)} \alpha_{{^{r} }}^{(2)} }}{{1 - \frac{\nu }{1 - 2\nu }B_{{^{r} }}^{(1)} \alpha_{{^{r} }}^{(1)} }} $$

(23)

Using some cracked and uncracked Brazilian disk specimens, the mechanical properties of Harsin marble were determined experimentally as follows: K_If = 0.947 MPa.m^0.5, σ_t = 5.8 MPa and ν = 0.2. The critical distance r_c was calculated as 4.24 mm from Eq. 17. In Table 5, the values of a, K_If, T_c, Y ^*_I , T ^*_I , B_r, and α_r are presented. To calculate the values of K_Ic for the considered material, the variation of K_If versus T _c is plotted in Fig. 13. Based on Eq. 16, by fitting a linear curve to the (K_If–T_c) data, mode I fracture toughness of Harsin marble was calculated as 1.405 MPa.m^0.5 at T_c = 0.

Table 5 Corresponding values of K_If, T-stress, B, α, Y ^*_I , T^*, and B_rα_r for the tested mode I specimens made of Harsin marble

Fig. 13

Linear relation between K_If and T_c for the tested rock samples

To show the relation between the fracture resistance and B_rα_r, the variation of K_Ic/K_If with B_rα_r is plotted in Fig. 14 based on Eq. 22. As mentioned before, Y ^*_I and T ^*_I values can be obtained for any of the investigated mode I specimens using finite element analyses.

Fig. 14

Relation between K_Ic/K_If and B_rα_r of tested specimens

The aim of this section is to determine the statistical parameters of any desired specimen in terms of the experimental results obtained for a reference specimen (named specimen (1)) without conducting any additional experimental test for another specimen (named specimen (2)). For this purpose, at first by performing some finite element analyses for two specimens with a reference load (for instance 1 N) and finding the value of B_rα_r for them, by substituting the values of B ⁽¹⁾_r α ⁽¹⁾_r , B ⁽²⁾_r α ⁽²⁾_r , and K ⁽¹⁾_If-ave in Eq. 23, the corresponding K ⁽²⁾_If-ave can be estimated. According to the Weibull statistical curves obtained for the cracked and notched specimens, a shift is seen between the two curves, such that as a simple model, the following shift factor can be assumed to correlate the average fracture toughness values of specimens (1) and (2):

$$ \lambda = \frac{{K_{{_{\text{If - ave}} }}^{(2)} }}{{K_{{_{\text{If - ave}} }}^{(1)} }} $$

(24)

By considering above shifting model between the experimental results in order to predict the Weibull distribution parameters of specimen (2) in terms of the Weibull parameters of specimen (1), the Weibull parameters of specimen (2) can be defined by the following relations for two-parameter (2P) Weibull model:

$$ \begin{aligned} m^{(2)} \left| {_{2P} } \right. & = m^{(1)} \left| {_{2P} } \right. \\ K_{0}^{(2)} \left| {_{2P} } \right. & = \lambda K_{0}^{(1)} \left| {_{2P} } \right. \\ \end{aligned} $$

(25)

and for three-parameter (3P) Weibull model:

$$ \begin{aligned} m^{(2)} \left| {_{3P} } \right. & = m^{(1)} \left| {_{3P} } \right. \\ K_{0}^{(2)} \left| {_{3P} } \right. & = \lambda K_{0}^{(1)} \left| {_{3P} } \right. \\ K_{\hbox{min} }^{(2)} \left| {_{3P} } \right. & = \lambda K_{\hbox{min} }^{(1)} \left| {_{3P} } \right. \\ \end{aligned} $$

(26)

Indeed, by considering a constant value of m as scattering parameter and a shift between two sets of results, the Weibull parameters of a specimen with chevron notch can be obtained from the Weibull parameters of the same specimen with straight crack. In order to verify the validity of this model, the Weibull distribution of the CB, CNBB, and CCNBD specimens was predicted from the statistical analysis of SECRBB, SENB, and SCCBD specimens, respectively. As a typical example, the two-parameter Weibull distribution of the CB specimen is calculated here based on the 2P Weibull parameters of the SECRBB specimen according to Eqs. 29–32 as follows:

$$ \begin{aligned} K_{{_{\text{If-ave}} }}^{\text{CB}} & = \frac{{1 - \frac{\nu }{1 - 2\nu }B_{{^{\text{r}} }}^{\text{SECRBB}} \alpha_{{^{r} }}^{\text{SECRBB}} }}{{1 - \frac{\nu }{1 - 2\nu }B_{\text{r}}^{\text{CB}} \alpha_{\text{r}}^{\text{CB}} }}K_{\text{If-ave}}^{\text{SECRBB}} \\ & = \frac{{1 - \frac{0.2}{1 - 2 \times 0.2}( - 1.62)(0.65)}}{{1 - \frac{0.2}{1 - 2 \times 0.2}( - 0.24)(0.71)}} \times 1.010 = 1.290\,{\text{MPa}}\sqrt {\text{m}} \\ \end{aligned} $$

(27)

$$ \lambda = \frac{{K_{{_{\text{If-ave}} }}^{\text{CB}} }}{{K_{{_{\text{If-ave}} }}^{\text{SECRBB}} }} = 1.28 $$

(28)

$$ \begin{aligned} m^{\text{CB}} \left| {_{2P} } \right. & = m^{\text{SECRBB}} \left| {_{2P} } \right. = 8.06 \\ K_{0}^{\text{CB}} \left| {_{2P} } \right. & = \lambda K_{0}^{\text{SECRBB}} \left| {_{2P} } \right. = 1.345\,{\text{MPa}}\sqrt {\text{m}} \\ \end{aligned} $$

(29)

Similarly, for three-parameter Weibull distribution, the following results were found for the CB and SECRBB specimens:

$$ \begin{aligned} m^{\text{CB}} \left| {_{3P} } \right. & = m^{\text{SECRBB}} \left| {_{3P} } \right. = 1.60 \\ K_{0}^{\text{CB}} \left| {_{3P} } \right. & = \lambda K_{0}^{\text{SECRBB}} \left| {_{3P} } \right. = 1.331\,{\text{MPa}}\sqrt {\text{m}} \\ K_{\hbox{min} }^{\text{CB}} \left| {_{3P} } \right. & = \lambda K_{\hbox{min} }^{\text{SECRBB}} \left| {_{3P} } \right. = 1.025\,{\text{MPa}}\sqrt {\text{m}} \\ \end{aligned} $$

(30)

The same manner can be employed to find the 2P and 3P Weibull distributions of the CNBB and CCNBD specimens based on the results of SENB and SCCBD specimens, respectively. Table 6 compares the average values of fracture resistance obtained from the experimental results of chevron notched samples and those predicted using the statistical model (i.e., Eq. 23). As it can be seen, the maximum discrepancy between the experimental results and predicted model is 3.8% for the CB specimen that records quite good ability of employed statistical model in predicting the fracture behavior of rock materials that their mechanical properties are significantly influenced by several natural scatter sources like discontinuities, flaws, and micro-cracks.

Table 6 Comparison of average fracture resistance values for chevron notched specimens obtained from experimental tests and those predicted based on the results of straight cracked specimen

Tables 7 and 8 also compare the 2P and 3P Weibull parameters obtained directly from the experimental results and those predicted using Eq. 23 for all six types of mode I specimens investigated in this research. It can be concluded that there is a good agreement between the results of experimental data and theoretical predictions such that the error percentages are generally lower than 10%, which is reasonable for rock materials.

Table 7 Comparison between 2P Weibull parameters of chevron notched specimens obtained from experimental tests and those predicted from the straight cracked specimens

Table 8 Comparison between 3P Weibull parameters of chevron notched specimens obtained from experimental tests and those predicted from the straight cracked specimens

The predicted two- and three-parameter Weibull statistical models for these specimens are presented in Figs. 15 and 16, respectively. It is seen from these figures that relatively good predictions can be obtained for a chevron notched specimen by knowing the statistical results of a straight cracked one (as a reference specimen). Consequently, by understanding the relation between the crack/notch geometry obtained from Eq. 23 (i.e., the developed statistical model), there is no need to perform any further experiments to find the statistical distribution of specimens with both chevron notch and straight crack and the fracture toughness results of a specimen (i.e., chevron notched specimens) can be predicted quite well in terms of the results of other geometry (i.e., straight cracked specimens).

Fig. 15

Two-parameter Weibull distribution curves predicted for a CB, b CNBB, and c CCNBD specimens in terms of the straight cracked configurations

Fig. 16

Three-parameter Weibull distribution curves predicted for a CB, b CNBB, and c CCNBD specimens in terms of the straight cracked configurations

It is also worth to mention that by rewriting Eqs. 12 and 13, respectively, as:

$$ \ln \left[ {\ln \left[ {\frac{1}{{1 - P_{f} (K_{\text{If}} )}}} \right]} \right] = m\left( {\ln K_{\text{If}} - \ln K_{0} } \right) $$

(31)

$$ \ln \left[ {\ln \left[ {\frac{1}{{1 - P_{f} (K_{\text{If}} )}}} \right]} \right] = m\left( {\ln (K_{\text{If}} - K_{\hbox{min} } ) - \ln (K_{0} - K_{\hbox{min} } )} \right) $$

(32)

A linear relationship is found between the left-hand sides of Eqs. 31 and 32 and the variation of ln(K_If) and ln(K_If − K_min), respectively. In order to find a better comparison between the 2P and 3P Weibull distributions, the plots of these linear variations (i.e., the fitted curves to the experimental data of tested rock specimens) have been presented in Figs. 17 and 18 that show a nearly linear regression between the data presented in the vertical and horizontal axes. In addition, based on these two figures and also as summarized in Table 9, the 3P Weibull distribution model resulted in higher coefficient of determination (R²) in comparison with the 2P model that demonstrates better ability and accuracy of 3P Weibull model in predicting the rock fracture toughness statistical results relative to the 2P Weibull model. In fact, since a threshold value of K_If can be defined and considered in 3P model as K_min under which the failure is not possible, this model can provide more suitable and realistic relation than 2P model in which the failure can be occurred at any K_If value even unrealistic ones. This finding is in good agreement with the results reported by Stefanou and Sulem (2016) as well.

Fig. 17

Predictions of 2P Weibull distribution model for fracture toughness results of a SECRBB and CB, b SENB and CNBB, and c SCCBD and CCNBD specimens

Fig. 18

Predictions of 3P Weibull distribution model for fracture toughness results of a SECRBB and CB, b SENB and CNBB, and c SCCBD and CCNBD specimens

Table 9 Calculated R² values for 2P and 3P Weibull distribution models in the investigated mode I test specimens

Finally, it should be noted that in this research we only examined the ability of Weibull statistical model to predict the influence of notch type (i.e., straight crack and chevron notch) on the distribution of K_If results for the investigated marble rock. As a supplementary future work, it is interesting to perform similar statistical study for prediction of the mode I fracture results of tested specimen in this research (e.g., CB, CNBB, CCNBD, SECRBB, SENB, and SCCBD in terms of other geometries or any reference specimen like CCNBD specimen.

5 Conclusion

• 1. Mode I fracture toughness of Harsin marble was determined using six types of specimens with different configurations and notch types by conducting a large number of experiments for each test specimen.

• 2. The results showed noticeable influence of specimen shape and pre-notch type on mode I fracture resistance. It was observed that similarly for the same geometries, the average fracture toughness of chevron notched samples was higher than those specimens containing straight crack.

• 3. For each type of investigated specimen, the Weibull distribution curves were extracted for K_If data and corresponding two- and three-parameter Weibull distributions were obtained. It was found that the scatter of chevron notched specimens is smaller than that of the straight cracked mode I specimens.

• 4. The main difference between two- and three-parameter (i.e., 2P and 3P) Weibull distribution models is the capability of three-parameter model in predicting a threshold value under which the failure is not possible in comparison with the two-parameter model that anticipates the failure at any value of fracture resistance that may be non-realistic. Thus, it was concluded that the 3P Weibull model can provide more precise estimation and curve fitting for the experimental mode I rock fracture toughness data of this research with different specimens.

• 5. Using the extended maximum tangential strain (EMTSN) criterion, the statistical fracture toughness results obtained for the chevron notched specimens were predicted in terms of the results of straight cracked specimens.