1 Introduction

Rock pillars are used, either temporarily or permanently, as major and important structural elements to support the overburden in mines and many other underground projects (Martin and Maybee 2000; Chen et al. 2009). As time passes, these pillars could become deteriorated under the direct or indirect influence of the atmosphere, underground water, blasting vibration, etc. (Bérest et al. 2008; Poulsen and Shen 2013). When any individual pillar loses its bearing capacity inadvertently, its load transfers to adjacent pillars and overloads those pillars successively. This progressive overloading process leads to a cascading pillar collapse with a ‘domino’ effect, which happens with little or no precursor and poses a serious risk to underground projects (Zipf and Mark 1997).

By now, a great deal of effort has been devoted to the stability study of a single pillar. Pillar strength was firstly estimated based on engineering experience (Hustrulid 1976). Some empirical formulas of pillar strength were then established by analysing the database of failed pillars and considering various factors (Van-der-Merwe 2003a; Esterhuizen et al. 2011). Van-der-Merwe (2003a) analysed the database of failed coal pillars and presented a strength formula for South African coal mines. Esterhuizen et al. (2011) developed a pillar strength equation by considering the potential impact from discontinuities. Meanwhile, Fang and Harrison (2002) developed a local degradation model to describe the pillar strength. Van-der-Merwe (2003b) further developed a method to predict the lifetime of coal pillars. Mortazavi et al. (2009) investigated the relationship between pillar geometry and pillar strength. Poulsen et al. (2014) investigated the strength reduction of coal pillars for water saturation. Recently, probabilistic (Ghasemi et al. 2014), logistic regression (Wattimena 2014) and artificial neural network (Musa et al. 2015) methods have been employed to analyse and predict the pillar stability.

In fact, rock pillars in underground projects are far from being ‘stand-alone’ systems. The supporting function is performed through their multi-interaction effect rather than their individual capacities, which is indicated by the fact that some pillars fail despite being considered stable with a safety coefficient >1 (Esterhuizen et al. 2011). Meanwhile, cascading pillar failure usually occurs when one pillar fails and the overburden is transferred to the adjacent pillars (Cording et al. 2015). Thus, the mechanical behaviour of multi-pillars should be studied. However, there are still few results about this behaviour. Recently, Chen et al. (1997) and Kaiser and Tang (1998) provided a numerical double-rock sample to simulate its progressive failure process. Wang et al. (2011) carried out further numerical analysis on a double-rock sample and revealed that factors including stiffness, elastic modulus and uniaxial compressive strength played important roles in controlling the failure process of pillars. These pioneer works offered good insight to the failure mechanism of multiple rock pillars. However, the existing research was mainly conducted with the numerical method and concentrated on the overall strength. The load transfer and redistribution between pillars, which triggers the massive collapse of a pillar system, has not been investigated.

In this study, load transfer and redistribution between pillars is studied by laboratory compression tests on single-pillar and double-pillar specimens. The information of displacement, load and acoustic emission was recorded, and the load transfer characteristics between pillars were analysed. Numerical analyses with distinct element code PFC2D were also carried out to further reveal the failure mechanism of the multi-pillar system.

2 Laboratory Tests and Results

2.1 Experiment Scheme and Preparation

Single-pillar and double-pillar specimens were prepared for testing. In the single-pillar tests, two types of specimens with different bearing capacities were arranged. There are three specimens in each type, as shown in Table 1. In the double-pillar tests, two sets of tests were arranged. In the first set, two individual pillars of the double-pillar specimen were chosen from the same type and had similar mechanical properties, as shown in Table 2. In the second set, the two pillars were chosen from different types and had different mechanical properties, as shown in Table 3. There are also three specimens in each set of tests.

Table 1 Laboratory results of single-pillar specimens under uniaxial compression
Full size table
Table 2 Laboratory results of double-pillar specimens with pillars with similar properties
Full size table
Table 3 Laboratory results of double-pillar specimens with pillars with different properties
Full size table

All specimens were made of concrete material, which has a similar behaviour to rocks. The size of a single-pillar specimen was 50 × 50 × 100 mm. Each pillar in the double-pillar specimen had the same size as a single-pillar specimen. Specimens with different mechanical properties were made with different mix proportions of concrete. For the first type of pillar specimen, the mix proportion of cement:water:sand was 2:1:10. For the second type, the mix proportion was 3:1:10. The specimens were put in a standard curing chamber for 28 days before tests.

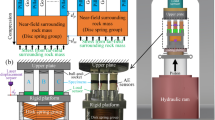
All tests were conducted on an INSTRON1346 servo-control testing machine. As shown in Fig. 1, double-pillar tests were conducted by putting two individual pillars between the indenters in parallel. To monitor the load of each pillar, a pressure sensor was set under each pillar. A displacement-control model was used to give the load. The failure information of the specimens was observed with the help of the acoustic emission (AE) equipment of Physical Acoustics Corporation. Four Nano30 sensors were employed to detect AE signals. The frequency range of the sensors was 125 Hz to 750 kHz. A 40 dB pre-amplification was set, and AE signals whose amplitude exceeds 50 dB were collected. At the same time, the digital speckle correlation method (DSCM) measurement was conducted to analyse the deformation characterization. A side of each pillar specimen was selected to be sprayed with black paint as underpainting and then speckled with white spots according to the DSCM method (Guo et al. 2008). The charge-coupled device of the plane array camera (Basler PiA2400-17gm) was used. Resolution of 2000 × 1500 pixels and a 10-Hz acquisition frame rate of photography were set to catch the deformation image. The size of the region of interest (ROI) of 46 × 48 mm was selected for analysis by a post-processor.

Fig. 1
figure 1

Schematic diagram of test arrangement. ROI-region of interest. a Single-pillar and b double-pillar

Full size image

2.2 Uniaxial Compressive Tests on Single-Pillar Specimens

The single-pillar specimens were tested according to the layout shown in Fig. 1a. Some of the load results are shown in Table 1. Figure 2 shows typical curves of the axial load and cumulative AE counts versus time of the single-pillar specimens. It can be found that the whole deformation process of the single-pillar specimens could be divided into three phases. The first phase was the compaction and elastic deformation stage, which occurred from the compression start to state a. In this phase, only a few AE events could be recorded. The second phase was the plastic deformation stage, which occurred from a to b and from b to c. The stage from a to b was the stress stiffening stage, and the stage from b to c was the stress softening stage. In this phase, the bearing capacity increased to the peak value and then began to decrease. The load–time curve deviated from the straight line gradually, but the cumulative AE events increased slowly. This result indicated that the internal stress of the pillar was still not strong enough to trigger the outburst of the micro-cracks (Martin and Chandler 1994). The third phase was the crack evolution stage, which occurred from c to d and from d to e. In this phase, the inner damage of the pillar developed, which induced the AE counts to increase rapidly. The load curve then declined quickly, and the AE counts accelerated rapidly after point d, which indicated that the ultimate bearing capacity of the pillar decreased rapidly.

Fig. 2
figure 2

Axial load and cumulative AE counts versus time curves of single-pillar specimens. a Specimen A-1 and b Specimen B-1

Full size image

Figure 3 shows some typical strain ɛ x pictures of specimen B-1 from the DSCM measurement. At 890 and 1050 s, the specimen stayed at the first and second phases of the deformation, respectively. The DSCM pictures show that the specimen mainly experienced uniform deformation firstly. At 1150 s, the specimen reached the crack evolution stage, and an obvious shear fracture band could be observed, which indicated that the deformation mode of the specimen changed from the uniform deformation to strain localization. The shear fracture band was mainly caused by the inner crack coalescence, which is also defined as fault nucleation or a fracture process zone (Lockner et al. 1991; Morgan et al. 2013). Finally, with an abrupt stress drop at point d in Fig. 2, a macro-slip occurred at 1210 s as shown in Fig. 3.

Fig. 3
figure 3

Strain ɛ x pictures of specimen B-1 in ROI

Full size image

Figures 2 and 3 also indicate that there is an equilibrium between the external load and the bearing capacity of a pillar. In the deformation process, although the displacement-control model was used by the testing machine during compression, a large amount of strain energy still could be accumulated and stored in the specimen and the indenter of the machine. Once the pillar was not powerful enough to tolerate the external load of the testing machine and failed, the indenter would release the stored strain energy quickly. This action might cause the crack to expand quickly and the pillar to lose its bearing capacity suddenly at the crack evolution stage.

2.3 Compressive Tests of Double-Pillar Specimens with Same Mechanical Property

The compressive tests of the double-pillar specimens with the same mechanical properties were conducted according to the way as shown in Fig. 1b. Figure 4 shows some typical test results of specimen S-1, where the axial load of the overall system and each pillar was demonstrated. The cumulative AE counts–time curve was also recorded, and Fig. 5 shows the corresponding DSCM results.

Fig. 4
figure 4

Load and cumulative AE counts versus time for specimen S-1

Full size image
Fig. 5
figure 5

Failure characteristics of specimen S-1. a The strain ɛ x pictures in ROI and b failure mode

Full size image

During the compression process of the double-pillar specimen with the same mechanical properties, the change tendency of the bearing capacity, the AE evolution and failure model of each individual pillar were similar to that of a single-pillar specimen. The pillar experienced a compaction and elastic deformation stage (from the start to state a I or a II in Fig. 4), plastic deformation stage (from state a I or a II to state c I or c II in Fig. 4) and crack evolution stage (from state c I or c II to state e I or e II in Fig. 4). At the beginning, few AE events occurred. After point c I, the cumulative number of AE counts increased rapidly, and the bearing capacity of pillars declined quickly. Finally, shear bands formed in both pillars of the specimen, as observed at the time of 1170 s in Fig. 5.

In the whole compression process, each individual pillar of the double-pillar specimen seemed to share the load equally. The overall peak load was almost double that of any individual pillar, as shown in Table 2. As each individual pillar deformed simultaneously, when one pillar lost its bearing capacity, the other one failed at once. Thus, abrupt failure of the double-pillar system could be found at its crack evolution stage.

2.4 Compressive Tests of Double-Pillar Specimens with Different Mechanical Properties

The compressive tests of double-pillar specimens with different mechanical properties were also performed according to the layout shown in Fig. 1b. Figures 6 and 7 show the results of the axial load, cumulative AE counts and strain ɛ x pictures of the representative specimen D-1. Some of the load results are shown in Table 3. It can be seen that, during the beginning stage of loading, the strain ɛ x of both pillars was almost uniform in all areas at 683 s, as shown in Fig. 7. Both pillars almost undertook the same external load until point a I. After point a I, the bearing capacity of the individual pillar I-D-1 deteriorated gradually; however, the pillar II-D-1 still remained in the elastic deformation stage. The AE signal also showed the same results. For pillar I-D-1, the cumulative AE counts increased sharply after point \(a_{\text{I}}^{\prime }\), but there were few AE events in pillar II-D-1 until point \(c_{\text{II}}^{\prime }\). Moreover, Fig. 7 shows that a failure zone occurred in pillar I-D-1 at 995 s, while the pillar II-D-1 maintained uniform deformation at this time. Between points c I and c II, when the pillar I-D-1 reached the post-peak stage, the overall bearing force of the specimen D-1 decreased gradually. Because the pillar II-D-1 still remained in the plastic deformation stage, the system did not fail abruptly. After point c II, the pillar II-D-1 also reached its peak strength, the overall bearing capacity began to deteriorate rapidly, and an abrupt drop of the load curve could be monitored. At this time, a shear band formed in both pillars, and the system finally lost its supporting function.

Fig. 6
figure 6

Load and cumulative AE counts versus time for specimen D-1

Full size image
Fig. 7
figure 7

Failure characteristics of specimen D-1. a The strain ɛ x pictures in ROI and b failure mode

Full size image

Figure 6 and Table 3 also show that the overall bearing capacity of the double-pillar system was different from the sum of the peak load of individual pillars. For specimens D-1, D-2 and D-3, the sums of the peak loads of their individual pillars were 234.52, 238.09 and 230.06 kN, while the peak bearing loads of the double-pillar system were 218.75, 209.27 and 203.51 kN, respectively. The systematic bearing load was smaller than the sum of the peak loads of individual pillars. This result indicates that there is an overestimation of the overall bearing capacity of a multiple-pillars support system in the prevailing pillar design practice without considering the system effect.

The pillar I-D-1 of specimen D-1 and specimen A-1 had similar material compositions and design strength, so they should have a similar mechanical behaviour. However, when pillar I-D-1 was compressed together with pillar II-D-1, a difference was observed at the crack evolution stage. The specimen A-1 failed abruptly at the crack evolution stage in Fig. 2a, while pillar I-D-1 of specimen D-1 deteriorated gradually in Fig. 6. This result was also observed in the AE information. In Fig. 2a, the cumulative number of AE counts of specimen A-1 increased rapidly between point c′ and point e′. However, the cumulative AE counts of pillar I-D-1 increased gradually between points \(c_{\text{I}}^{\prime }\) and \(e_{\text{I}}^{\prime }\) in Fig. 6. This result indicates that the mechanical behaviour of an individual pillar in a multi-pillar system may be different from that of a single pillar. And this result can be explained as follows: When there is only one pillar in a system, its failure will cause a direct collapse of the whole system, while in a system with multiple pillars, when one pillar fails, its overburden spreads to the adjacent pillars. In Fig. 6, when pillar I-D-1 reached its peak strength and failed, the load was transferred from pillar I-D-1 to II-D-1 gradually. A gentle decline of bearing capacity other than a sudden catastrophic failure of the system occurred. Only when the bearing capacity of pillar II-D-1 deteriorated greatly, as after point eII in Fig. 6, did overall failure occur.

3 Numerical Analyses

In recent years, the numerical method has shown great advantages in revealing the inner information of complex systems and can yield results more easily and quickly. In this study, a discrete element numerical software PFC2D was used to further investigate the bearing characteristics of pillar systems. PFC2D software could simulate the mechanical behaviour of materials by using a dense packing of non-uniformly sized circular particles bonded together at their contact points. The mechanical behaviour of the PFC model is described and controlled by the movement of each particle and the force and moment acting at each contact. Newton’s laws of motion provide the fundamental relation between particle motion and the resultant forces and moments causing that motion (Itasca 2008). With this code, particles and contacts have been used instead of elements and meshes. Potyondy and Cundall (2004) proved that PFC2D can simulate the formation, growth and eventual interaction of micro-cracks successfully, which govern the mechanical behaviour of rocks.

3.1 PFC2D Model

The double-pillar model shown in Fig. 8 was established by PFC2D. The Augmented PFC FishTank, which is a special language provided by Itasca to help users perform PFC modelling (Itasca 2008), was utilized to automatically record the loads and calculate the elastic modulus. Both pillars were designed to be rectangular with a width of 50 mm and a height of 100 mm. Since the model in the simulation was two-dimensional, a thickness of 50 mm, the same as that of the real specimen in laboratory, was assumed when calculating the load. During the tests, the pillars were loaded by moving the boundary walls towards one another at a specified velocity. The stress in each pillar was measured with measurement circles in it. The load on each pillar was then calculated by multiplying the measured stress and the cross-sectional area. The overall bearing load of the double-pillar system was obtained from the counterforce of the boundary walls.

Fig. 8
figure 8

Numerical model of double-pillar system

Full size image

3.2 Numerical Test Plan

Firstly, the numerical validation test was carried out to calibrate the micro-parameters of the numerical models (Itasca 2008; Li et al. 2014; Zhou et al. 2014). According to the experimental results of specimen B-1 in Fig. 2b, a numerical counterpart (pillar 7 in Table 5) of specimen B-1 was found from the validation procedure. Its basic micro-parameters are listed in Tables 4 and 5 (pillar 7). The other eight pillar specimens were established with different values of strength and modulus for simulation, as shown in Table 5.

Table 4 Some basic micro-parameters for numerical models
Full size table
Table 5 Micro-parameters of specimens for different simulation cases
Full size table

The basic pillar specimens were then combined into different numerical models of double-pillar specimens. In this work, two series of numerical models were investigated. In the first series, the double-pillar system was designed with individual pillars of the same strength but different elastic modulus. One of the pillars was set to have an elastic modulus of 3 GPa and a maximum bearing capacity of 150 kN, and the other pillar, in cases 1–5, was chosen to have the same bearing capacity of 150 kN and elastic modulus of 3, 4, 5, 6 and 7 GPa, respectively. In the second series, pillars of the double-pillar specimen were designed with the same elastic modulus but different bearing capacities. One of the pillars, in cases 6–10, was set to have an elastic modulus of 3 GPa and a maximum bearing capacity of 100 kN, and the other pillar was chosen to have the same elastic modulus of 3 GPa and bearing capacities of 100, 125, 150, 200 and 250 kN, respectively.

3.3 Numerical Results

3.3.1 Numerical Results for the First Series

Figure 9 gives the numerical results of specimens from the first series, where the individual pillars of the specimens have the same bearing capacity but different elastic modulus. For case 1, both pillars of the double-pillar specimen had the same mechanical properties, so they deformed and deteriorated at the same time as in the laboratory tests. When one pillar failed, the other pillar failed simultaneously. Because there was no load transfer between pillars, the overall failure was abrupt and violent.

Fig. 9
figure 9

Load and load-carrying rate versus displacement of pillars for cases 1–5. a Case 1, b case 2, c case 3, d case 4 and e case 5

Full size image

For cases 2–5, pillar I had an elastic modulus of 3 GPa, and pillar II had elastic modulus of 4, 5, 6 and 7 GPa, respectively. Figure 9 shows that the two individual pillars deformed differently and carried different loads during the deformation. The pillar with the higher elastic modulus tended to fail firstly. And the overall bearing capacity increased until the pillar with the higher elastic modulus reached its peak load. This peak load is denoted by point m. The system continued to deform, and the overall bearing capacity decreased gradually. At point n, the pillar with a higher elastic modulus actually lost its supporting function, and the whole overburden of the system was completely transferred to the pillar with a lower elastic modulus.

In order to express the influence of the elastic modulus of pillars, the elastic modulus rate (EMR) is defined as follows:

$${\text{EMR}}_{i} = \frac{{E_{i} }}{{E_{\text{I}} + E_{\text{II}} }} \times 100\% ,\quad i = {\text{I}}\,\,{\text{or}}\,\,{\text{II}}$$
(1)

where E I and E II are the elastic modulus of pillar I and pillar II, respectively.

At the same time, to quantitatively evaluate the load-carrying states of the two pillars in the system, the load-carrying rate (LCR) is defined as follows:

$${\text{LCR}}_{i} = \frac{{L_{i} }}{{L_{\text{I}} + L_{\text{II}} }} \times 100\% ,\quad i = {\text{I}}\,\,{\text{or}}\,\,{\text{II}}$$
(2)

where L I and L II are the load carried by pillar I and pillar II, respectively.

Because a displacement-control model is used in this study, the values of LCR and EMR are the same before any of the individual pillars fails. When pillar failure occurs, the LCR curve instead of the EMR curve is used to evaluate the load-carrying states of the pillar in the system.

With the help of the LCR curves, Fig. 9 shows that before state m, the values of LCRII, the same as those of EMRII, are 0.5, 0.571, 0.625, 0.666 and 0.7 from cases 1–5, respectively. This result indicates that, in a double-pillar system, the higher elastic modulus of a pillar is the larger load it should bear. At the state m, the load of pillar II reached the peak value firstly and damage took place in it. The pillar II then lost its load-carrying capacity gradually. From the state m, the LCRII started to decline while LCRI began to increase. This observation indicates that the load transfer and redistribution process occurred at this stage. After the state n, the majority of the external load is transferred to pillar I. Especially, when the elastic modulus of one pillar is significantly greater than the other one, as shown in cases 4 and 5 in Fig. 9d, e, the pillar with the higher elastic modulus might lose its supporting function totally at this stage with an LCRII value of approximately 0. Meanwhile, pillar I, with a lower elastic modulus, did not fail at this point and would bear most of the external load of the system.

By putting overall load–displacement curves of this series together in Fig. 10, two local maximum load points in the load–displacement curves of cases 2, 3, 4 and 5 are observed. The first local maximum value appeared at point m, where the pillar with a higher elastic modulus reached its peak load. The second maximum value was reached when the pillar with a lower elastic modulus reached its peak load. There is a valley at point n. The first local maximum values of cases 2, 3, 4 and 5 are approximately 265, 245, 226 and 215 kN, respectively, and the second local maximum values have almost the same value, 152 kN.

Fig. 10
figure 10

Overall load–displacement curve of specimens with two pillars of the same strength but different elastic modulus

Full size image

Interestingly, it is found that the maximum bearing capacity of the double-pillar system of this series always occurred at the first local maximum load point of m and could be calculated by the following equation:

$$F_{\text{I+II}} = {\raise0.7ex\hbox{${F_{\text{II}} }$} \!\mathord{\left/ {\vphantom {{F_{\text{II}} } {{\text{EMR}}_{\text{II}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${{\text{EMR}}_{\text{II}} }$}}$$
(3)

where F II is peak load of the pillar with the higher elastic modulus.

3.3.2 Numerical Results for the Second Series

For the second series, individual pillars of the double-pillar specimens had the same elastic modulus but different maximum bearing capacities. In cases 6–10, pillar I of the double-pillar specimen had the bearing capacity of 100 kN, while pillar II had the bearing capacities of 100, 125, 150, 200 and 250 kN.

Figure 11 gives the curves of the load and load-carrying rate versus displacement of each pillar during deformation. For case 6, two individual pillars of the specimen had the same mechanical properties; the bearing characteristics and failure mechanism of the specimen were similar to those of case 1. For cases 7–10, because both individual pillars had the same elastic modulus, they deformed and carried equal loads at the beginning. At point m, the pillar with lower bearing capacity failed firstly. After failure, the system continued to deform and the overall bearing capacity decreased gradually. For cases 8–10, there are also two local maximum load points in the load–displacement curves. The bearing capacity of the double-pillar system reached a local minimum value at point n. After point n, pillar II bores almost all overburden of the system. The stage from state m to state n also can be regarded as a load redistribution process, during which the load on pillar I was gradually transferred to pillar II. This observation is also supported by the change tendency of the LCR curves of both pillars.

Fig. 11
figure 11

Load and load-carrying rate versus displacement of pillars for cases 6–10. a Case 6, b case 7, c case 8, d case 9 and e case 10

Full size image

In the first series of numerical tests shown in Figs. 9 and 10, when the load curve of the system passed point n, the overall load would increase but never surpass the first local maximum load value at point m. However, for the second series of tests shown in Fig. 11, when the load curve of the system passed point n, the overall loads of specimens in case 9 and case 10 would increase and had larger values than that of point m.

By putting all load–displacement curves of the double-pillar specimens of this series together in Fig. 12, two local maximum load points in load–displacement curves are apparent when the two individual pillars have different properties, except in case 6 and case 7. At the first local maximum load point of m, all specimens have the same load value of 200 kN, which is double the peak load value of the pillar (with a lower peak strength) that failed firstly. When one pillar fails, the load is transferred to the other pillar. The bearing capacity of the system would then be determined by the remaining pillar. If the remaining pillar is strong enough, the system still can have good supporting performance even when some of the pillars fail in the system.

Fig. 12
figure 12

Overall load–displacement curve of specimens with two pillars with the same elastic modulus but different strengths

Full size image

4 The Bearing Characteristic of Double-Pillar System

As shown in Fig. 13, a simple double-pillar system was compacted by a rigid indenter that was assumed to maintain its shape during the whole compressive process. Thus, when a vertical displacement increment of u acted on the system, pillar I and pillar II of the system will have vertical displacement increment values of u I and u II, respectively. Static equilibrium gives:

$$u = u_{\text{I}} = u_{\text{II}}.$$
(4)
Fig. 13
figure 13

Schematic of double-pillar system with certain displacement

Full size image

Assuming that the forces acting on pillar I and pillar II are P I and P II, respectively. They can be calculated by the following equations:

$$P_{\text{I}} = f\left( {u_{\text{I}} } \right)u_{\text{I}}$$
(5)
$$P_{\text{II}} = f\left( {u_{\text{II}} } \right)u_{\text{II}}$$
(6)

where f(u I) and f(u II) are the stiffness coefficients of pillar I and pillar II, respectively.

And the bearing load of the double-pillar system can be estimated by

$$P_{\text{I+II}} = P_{\text{I}} + P_{\text{II}} .$$
(7)

As mentioned previously, the individual pillars of the system may not reach their limit bearing capacities simultaneously. Thus, the bearing capacity of the double-pillar system cannot be calculated by adding up the maximum peak loads of individual pillars directly.

Assuming that the limit bearing capacities of the double-pillar system, pillar I and pillar II, are F I+II, F I and F II, respectively, only when the all mechanical properties of the individual pillars are almost the same, the bearing capacity of the system can be estimated by:

$$F_{{{\text{I}}+{\text{II}}}} \approx F_{\text{I}}+F_{\text{II}} .$$
(8)

This assumption can be confirmed by the results shown in Tables 2 and 6. When the mechanical properties of the two individual pillars of the double-pillar specimens were almost the same, they reached their limit bearing capacity and failed simultaneously. The overall bearing capacity of the system is approximately the sum of the peak loads of the individual pillars.

Table 6 Bearing capacity of double-pillar system and individual pillars
Full size table

However, for the pillar system with individual pillars of different mechanical properties (elastic modulus or strength), Eq. (8) cannot be satisfied.

For the series of double-pillar systems with individual pillars of the same strength but different elastic modulus, the load–displacement response of the system can be profiled as shown in Fig. 14. As discussed in Sect. 3.3.1, pillar II with a higher elastic modulus would carry a greater load during the deformation at the beginning stage. When the pillar II reached its peak load (F II), the first local maximum load value of the system occurred. At this time, the pillar I did not yet reach its limit bearing capacity. The load it bears can be determined using Eqs. (4), (5), (6) and (7), as follows:

$$P_{\text{I}} = F_{\text{II}} \frac{{f\left( {u_{\text{I}} } \right)}}{{f\left( {u_{\text{II}} } \right)}} < F_{\text{I}} .$$
(9)
Fig. 14
figure 14

Load–displacement of double-pillar specimen with pillars of the same strength but different elastic modulus. a Individual bearing characteristic and b overall bearing characteristic

Full size image

Consequently, the overall load of the double-pillar system at this time can be estimated by

$$P_{\text{I+II}} = F_{\text{II}} + F_{\text{II}} \frac{{f\left( {u_{\text{I}} } \right)}}{{f\left( {u_{\text{II}} } \right)}}.$$
(10)

The load of the system is then redistributed. The load–displacement curve declines from point A to point B and then increases to point C. At point C, pillar I reaches its limit bearing capacity. At this time, the overall load of the double-pillar system can be expressed by

$$P_{\text{I+II}} = F_{\text{I}} .$$
(11)

Because the two individual pillars have the same peak strength, the overall load of the double-pillar system at point C is lower than that at point A. Thus, the first local maximum load value, as calculated by formula (10), is the peak load of the double-pillar system. That is,

$$F_{\text{I+II}} = P_{\text{I+II}} = F_{\text{II}} + F_{\text{II}} \frac{{f\left( {u_{\text{I}} } \right)}}{{f\left( {u_{\text{II}} } \right)}}.$$
(12)

It can be found that the maximum bearing load of the double-pillar system, F I+II, is smaller than the sum of the values of F I and F II.

Furthermore, as shown in Fig. 9b–d, when the pillar I of the system reached its peak load, the displacements of pillar II were approximately 1.41, 1.17, 0.942 and 0.813 mm. The local maximum load values of the double-pillar system were approximately 265, 245, 226 and 215 kN, respectively. These data indicate that as the elastic modulus of pillar II increases, the time the pillar taken to fail and the load the double-pillar system withstanding both decrease.

Analogously, for the series of a double-pillar system with individual pillars of the same elastic modulus but different strengths, the load–displacement response of the system can be profiled as shown in Fig. 15. As discussed in Sect. 3.3.2, when the strength of pillar II is higher than that of pillar I, during the initial loading stage, the load of the double-pillar system is equally shared by both pillars due to the even deformation. With increasing external load, the pillar I reaches its limit bearing capacity, and the first local maximum load value of the system appears. At this time, the overall load of the double-pillar system can be expressed by:

$$P_{\text{I+II}} = 2 \times F_{\text{I}} .$$
(13)
Fig. 15
figure 15

Load–displacement of double-pillar specimen with pillars of the same elastic modulus but different strengths. a Individual bearing characteristic and b overall bearing characteristic

Full size image

Then there is a load redistribution stage, and the load–displacement curve decreases from point A to point B. After the load adjustment, the overburden of the system is carried by the pillar II, and there is then an increase to point C for the load–displacement curve. Of course, if the peak load of pillar II is far less than 2F I and loses its supporting function in the load redistribution process, the system tends to fail directly, as shown in Fig. 11b. Consequently, only one local maximum load value exists, and it is smaller than the sum of the values of F I and F II. However, if pillar II is strong enough and has a peak load greater than 2F I, the load–displacement curve of the system tends to reach a new local maximum load value at point C, as shown in Fig. 11d, e. The overall load of the double-pillar system at this point is

$$P_{\text{I+II}} = F_{\text{II}} .$$
(14)

The second local maximum load value of the pillar system at point C can even exceed the first local maximum load value at point A. Of course, because the value of F II is smaller than the sum of F I and F II, the maximum bearing load of the double-pillar system, F I+II, is still smaller than the sum of the values of F I and F II. That is, \(F_{{{\text{I}} + {\text{II}}}} < F_{\text{I}} + F_{\text{II}}\).

Based on the above analyses, the peak load of the double-pillar system with individual pillars of the same elastic modulus but different strengths can be expressed as:

$$F_{\text{I+II}} = \left\{ {\begin{array}{*{20}c} {2F_{\text{I}} } \\ {F_{\text{II}} } \\ \end{array} } \right.\begin{array}{*{20}c} {} \\ {} \\ \end{array} \begin{array}{*{20}c} {} \\ {} \\ \end{array} \begin{array}{*{20}c} {F_{\text{II}} \le 2F_{\text{I}} } \\ {F_{\text{II}} > 2F_{\text{I}} } \\ \end{array} .$$
(15)

5 Conclusions

In this study, the bearing and failure characteristics of single-pillar and double-pillar specimens were investigated with laboratory tests and numerical simulation. The following conclusions can be drawn:

  1. 1.

    When the overburden is applied to a single-pillar system, plastic yield and micro-crack evolution will cause the pillar to lose its bearing capacity. The pillar usually fails in an unstable, violent manner. However, when there are two or more pillars with different properties in the supporting system, if one pillar fails, the load it bears can be transferred to the adjacent pillars, and the failure process can occur in a stable, nonviolent manner. As a result, multiple pillars can show system behaviour while playing their supporting functions in underground projects.

  2. 2.

    In the compressive process of a double-pillar system, if two individual pillars have the same mechanical properties, they will bear equal loads and deform similarly. However, once any individual pillar fails, the system will experience unstable failure. When the two individual pillars have different mechanical properties, the pillar with larger elastic modulus or lower peak strength will fail earlier. The system will then fail in a relatively gentle manner. Usually, for a double-pillar supporting system, there are two local maximum load points in the load–displacement curves. When the first pillar fails, the first local maximum value appears. The load transfer and redistribution then occur. If there is a very strong pillar in the system, the second local maximum value may even exceed the first local maximum load.

  3. 3.

    For a pillar system, the overburden is shared by all pillars, but it is not necessary that the bearing capacity of the system equals the sum of the peak strength values of all individual pillars. Only when all individual pillars of a system have identical properties, the bearing capacity of the system is approximately equal to the sum of the peak load of all individual pillars. When the individual pillars of a system have different properties, the bearing capacity of the system is found to be less than the sum of the peak loads of the individual pillars.

  4. 4.

    For a pillar system, the strength, elastic modulus and load state of pillars all have an influence on the supporting effect. When designing pillars to bear the overburden in underground engineering, not only the pillar strength but also the elastic modulus should be considered to avoid the occurrence of large-scale collapse. The load state of pillars should also be paid great attention. When some individual pillars or a small group of pillars fail, the load they bear will be transferred to the adjacent pillars. When all pillars are designed with same size and strength, a violent cascading failure will occur. However, if the pillars are designed with different geometry or material conditions, the failure process of the system will become gentle. Especially, according to Fig. 15, because barrier pillars of a mining panel usually have greater strength than others, they may increase the overall supporting performance of the system even when a pillar fails. Thus, the appropriate layout of barrier pillars is effective in preventing the underground space from sudden large-scale disaster and domino-type collapse.