Experimental Characterization and Micromechanical Modelling of Anisotropic Slates

Abstract

Laboratory tests were performed in this study to examine the anisotropic physical and mechanical properties of the well-foliated Jiujiang slate. The P-wave velocity and the apparent Young’s modulus were found to increase remarkably with the foliation angle θ, and the compressive strength at any confining pressure varies in a typical U-shaped trend, with the maximum strength consistently attained at θ = 90° and the minimum strength at θ = 45°. The slate samples failed in three typical patterns relevant to the foliation angle, i.e. shear failure across foliation planes for θ ≤ 15°, sliding along foliation planes for 30° ≤ θ ≤ 60° and axial splitting along foliation planes for θ = 90°. The stress–strain curves at any given foliation angle and confining pressure display an initial nonlinear phase, a linear elastic phase, a crack initiation and growth phase, as well as a rapid stress drop phase and a residual stress phase. Based on the experimental evidences, a micromechanical damage–friction model was proposed for the foliated slate by simply modelling the foliation planes as a family of elastic interfaces and by characterizing the interaction between the foliation planes and the rock matrix with a nonlinear damage evolution law associated with the inclination angle. The proposed model was applied to predict the deformational and strength behaviours of the foliated slate under triaxial compressive conditions using the material parameters calibrated with the uniaxial and/or triaxial test data, with good agreement between the model predictions and the laboratory measurements.

1 Introduction

Slate is a fine-grained, foliated metamorphic rock derived from shale or tuff through low-grade regional metamorphism. As a pronounced lithological feature, the presence of well-developed slaty structure, cleavage, lamination or bedding planes in slate makes its physical, mechanical and hydraulic properties highly anisotropic or transversely isotropic. Besides its popular uses for materials in building (such as roofing, flooring and flagging), slate is frequently encountered in various engineering applications, such as dam foundation (Özsan and Karpuz 1996; Sharma et al. 1999), tunnelling (Souley et al. 1997; Farrokh and Rostami 2009; An et al. 2012), slope engineering (Chigira 1992; Suwa et al. 2008; Lo and Feng 2014; Weng et al. 2015) and borehole hydrogeology (Jankowski and Acworth 1997; Hunt and Worthington 2000; Lee et al. 2008). Characterization of the mechanical behaviours of slate is therefore of paramount importance in evaluating the deformation and stability of underground openings, dam foundations, slopes and wells (or boreholes) constructed in slate formations.

Over the last few decades, both the microstructure and anisotropic mechanical behaviour of foliated slate have been investigated extensively. The microstructure observed by X-ray diffraction analysis, SEM and TEM technologies (Etheridge and Lee 1975; White and Knipe 1978; Chen 1991; Ho et al. 2001) showed that the anisotropic properties of slate were attributed to the preferred orientation arrangement of mineral grains and microcracks. The anisotropic elastic, strength and failure behaviours of slate rocks were examined under uniaxial, triaxial and Brazilian test conditions in different loading directions with respect to the foliation planes (Donath 1961; McLamore and Gray 1967; Attewell and Sandford 1974; Goshtasbi et al. 2006; Debecker and Vervoort 2009; Alam et al. 2008; Gholami and Rasouli 2014; Tan et al. 2014; Vervoort et al. 2014; Stoeckhert et al. 2015). The test results indicated that the strength, failure modes and elastic properties of slate evidently depend on the loading orientation and confining pressure. The maximum compressive strength occurs when the foliation planes are either perpendicular (θ = 0°) or parallel (θ = 90°) to the loading direction, whereas the minimum compressive strength appears at an approximate angle of θ = 30°–60° (θ is the angle between the normal of foliation planes and the loading direction, which is hereafter also called the inclination angle or foliation angle). The failure modes can be divided into two main categories: one is the sliding mode along the foliation planes on which the compressive strength depends and the other is a non-sliding mode where the material strength governs. With the increase in confining pressure, the anisotropy of the strength and elastic modulus usually reduces and the slate samples tend to be more ductile (Goshtasbi et al. 2006; Gholami and Rasouli 2014).

Based on the experimental observations, considerable efforts have been devoted to formulating appropriate constitutive models for anisotropic rocks. Generally, these constitutive models can be classified into two families. The first family focuses mainly on the anisotropic strength of rocks due to the presence of weak planes, which was developed by an extension of empirical isotropic criteria (Ramamurthy and Arora 1994; Saroglou and Tsiambaos 2008; Asadi and Bagheripour 2015; Singh et al. 2015), by the concept of discontinuous weakness plane or critical plane (Jaeger 1960; Walsh and Brace 1964; Duveau et al. 1998; Tien and Tsao 2000; Mroz and Maciejewski 2002) or more rigorously by a mathematical approach (Karr et al. 1989; Cazacu et al. 1998; Pietruszczak and Mroz 2001). These failure criterion models provide quite a direct interpretation of anisotropic strength for geomaterials, but fail to appropriately describe the anisotropic deformation behaviours and are generally difficult to apply in complex loading conditions encountered in engineering practices. The second family of models overcomes this limitation by taking into account both the anisotropic failure strength and the damage-induced inelastic deformation for initially anisotropic geomaterials (Pietruszczak et al. 2002; Halm et al. 2002; Cazacu et al. 2007; Monchiet et al. 2012; Goidescu et al. 2013, 2015). Among these models, the microstructure tensor approach proposed by Pietruszczak et al. (2002) introduces a scalar anisotropy parameter dependent on the principal stresses and a microstructure tensor for representing the spatial distribution of the microstructure of the material. This formulation has been successfully applied to model the mechanical behaviours of anisotropic geomaterials (Cudny and Vermeer 2004; Chen et al. 2010, 2012a; Hu et al. 2013; Nguyen and Le 2014).

In this study, the mineralogical composition, microstructure and P-wave velocity of a foliated slate taken from a quarry in Jiujiang, Jiangxi Province, China, are examined for evaluating the anisotropic nature of the slate rock. The strength and deformational responses of the slate are tested in uniaxial and triaxial conditions over the entire range of inclination angle (θ) varying from 0° to 90° for understanding the anisotropy of the mechanical behaviour. Based on the experimental observations, a micromechanical damage–friction model is proposed for the foliated slate by considering the influences of the microcracking-induced damage and the foliation planes on the deformation and strength of the slaty rock. The performance of the proposed model is finally evaluated by comparing the model predictions with the triaxial compression test data under various confining pressures.

2 Experimental Study

2.1 Sample Preparation

Two blocks of slate were collected from a slate quarry in Jiujiang, Jiangxi Province, China (Fig. 1). The slate is a metamorphosed Precambrian rock from sedimentary rocks, striking northwest and with a dip angle between 42° and 50°. The slate has a well-developed slaty structure, with the bands displaying dark grey to light grey colours. The dry density of the slate is about 2.55 ± 0.05 g/cm³, and the X-ray diffractometry (XRD) analysis indicated that the slate is composed of 10 % quartz, 35 % chlorite, 33 % sericite, 10 % feldspar, as well as a minor quantity of iron oxides, as shown in Fig. 2. Figure 3 shows a thin section of the slate normal to the foliation planes viewed by an optical microscopy, displaying a layered lattice texture composed of preferred orientation of quartz and sericite, with a fine grain size varying from 0.01 to 0.05 mm.

Fig. 1

Photographs of Jiujiang slate: a the outcrop and b the fresh rock blocks

Fig. 2

X-ray diffractometry of the slate

Fig. 3

Thin sections of the slate viewed in transmitted cross-polarized light

A total of 35 cylindrical specimens of 50 mm in diameter and 100 mm in length were cored from the slate blocks at seven different angles to the foliation planes. The specimens were therefore classified into seven groups, five in each group, with the inclination angle of the foliation planes (θ) being 0°, 15°, 30°, 45°, 60°, 75° and 90°, respectively (Fig. 4), for testing the anisotropic deformation, strength and failure characteristics of the slate under different confining pressures. The errors of length and diameter of the specimens were within ±0.5 mm, and the parallelism of the specimen ends was within ±0.02 mm after being well cut and polished. Table 1 lists the dry density, porosity and P-wave velocity of the specimens. Figure 5 shows the plot of the relation between the P-wave velocity of the specimens and the inclination angle of the foliation planes, showing the anisotropic nature of the slate due to the well-developed foliation. The P-wave velocity increases remarkably with the inclination angle (θ). The velocity normal to foliation (θ = 0°) ranges in 2891–3164 m/s (with a mean of 3017 m/s), which is much lower than that parallel to foliation (θ = 90°) (ranging in 4274–4616 m/s, with a mean of 4434 m/s).

Fig. 4

Slate samples with different foliation angles

Table 1 Physical properties, peak strength and the corresponding axial strain of the slate samples

Fig. 5

Variation of P-wave velocity with the foliation angle (θ)

2.2 Experimental Setup

The mechanical behaviours of the slate were tested using a servo-controlled triaxial equipment (Chen et al. 2014b). The test system consists of a triaxial cell with servo-controlled axial and circumferential loading systems. The triaxial cell is capable of performing conventional triaxial compression tests at confining pressures up to 60 MPa, with a maximum deviatoric stress up to 375 MPa. The axial and confining stresses are applied by hydraulic oil using two high-resolution, servo-controlled fluid pumps. The axial strain is measured by two displacement LVDTs, and the circumferential strain is recorded by an extensometer attached on the middle height of the specimen. The five slate samples at each group were tested under five different confining stresses (σ ₃ = 0, 5, 10, 15 and 20 MPa), respectively, at room temperature (20 °C). Before testing, each slate sample was enclosed in a 3-mm-thick Viton rubber jacket and then assembled in the triaxial cell. Subsequently, the confining stress and the axial stress were simultaneously applied at a rate of 1 MPa/min until the prescribed value of σ ₃, and the axial stress was then increased at a constant strain rate of 10⁻⁵ s⁻¹ until failure.

2.3 Experimental Results

2.3.1 Stress–Strain Curves and Failure Patterns

Figure 6 shows the stress–strain curves of the slate specimens of various inclination angles (θ = 0°–90°) under different confining stresses (σ ₃ = 0–20 MPa). One observes from Fig. 6 that each stress–strain curve at any given inclination angle (θ) and confining stress (σ ₃) displays an initial nonlinear phase due to the closure of pre-existing cracks in the initial deviatoric loading stage, which is followed by a linear elastic phase, a crack initiation and growth phase, as well as a rapid stress drop phase and a residual stress phase after the peak stress is attained. The initial crack closure phase is more pronounced under uniaxial compressive condition (σ ₃ = 0 MPa), because most of the initial cracks have been compressed under triaxial compressive condition as a result of the isotropic compaction to the specified confining stress (i.e. σ ₁ is synchronously applied to the value of σ ₃ before the deviatoric stress is increased). This is also the case for lower inclination angles (θ ≤ 30°) because of the higher compressibility of the foliation planes. With the increase in θ, the stress–strain curve moves closer to the vertical axis passing through the origin, showing a smaller closure of cracks at the initial phase and a larger macroscopic deformation modulus. However, even at θ = 90°, the initial crack closure phase is still visible at moderately large confining stress, indicating that the pre-existing cracks, possibly created both in the geologic history and during the sample collection and preparation, develop in various directions (i.e. not solely along the foliation planes).

Fig. 6

Stress–strain curves of the slate with various foliation angels under different confining pressures: a σ ₃ = 0 MPa, b σ ₃ = 5 MPa, c σ ₃ = 10 MPa, d σ ₃ = 15 MPa and e σ ₃ = 20 MPa

Unlike the macroscopically isotropic rocks (e.g. granitic rocks) on which the initiation and growth of cracks is mainly induced by deviatoric stress (Souley et al. 2001; Chen et al. 2014b), cracking and failure of slate rocks is also highly influenced by the loading direction with respect to the foliation planes. When the foliation planes are horizontally or subhorizontally oriented (e.g. θ = 0°), the increase in the deviatoric stress induces cracking across the foliation planes, leading to a most remarkable phase of crack growth before the peak strength on the stress–strain curves (Fig. 6). The axial stress then drops abruptly from peak to residual, and the rock samples fail by shearing across the foliation planes, together with visible tensile cracks along the axial direction, as shown in Fig. 7. With a moderate increase in the inclination angle (e.g. θ = 15°), the foliation planes start to play a role in the progressive failure of the samples, even though a single failure surface along the foliation planes could not be formed. After the peak stress is attained, a short yield terrace may appear on the stress–strain curves due to coalescence of cracks and foliation planes to form a saw-toothed failure surface (Fig. 7), where a mixed failure mode of shearing across and sliding along the foliation planes takes place.

Fig. 7

Failure modes of the slate observed in the tests, with visible fractures after failure shown with the dash red lines

At θ = 30°–75°, the failure of the samples is mainly controlled by shearing and sliding along the weaker foliation planes, with the lowest peak strength consistently being attained at θ = 45° under various confining stresses. As shown in Fig. 7, the samples may fail along a single foliation plane (e.g. θ = 30°–60° and σ ₃ = 5–20 MPa) or along multiple foliation planes (e.g. θ = 75° or σ ₃ = 0 MPa). An exception appears at θ = 30° under uniaxial compressive condition where shear failure across the foliation planes occurs. It can be concluded from Figs. 6 and 7 that the damage growth phase on the stress–strain curves could be more manifested when the failure surface is rougher. When the deviatoric stress is applied along the foliation planes (θ = 90°), axial splitting along the foliation planes occurs, resulting in the highest peak strength compared to other loading directions.

2.3.2 Anisotropic Properties of the Slate

The P-wave velocity measurements (Fig. 5) and the failure patterns (Fig. 7) clearly show the anisotropic behaviour of the slate rock. In this section, the anisotropic properties of the slate are further examined based on the stress–strain curves (Fig. 6). Figure 8 shows the plot of the peak deviatoric strength of the slate and the corresponding axial strain at the peak against the inclination angle of foliation under various confining stresses. It can be observed from Fig. 8a that the compressive strength increases with the confining stress at any given loading directions. The variation of the compressive strength as a function of the anisotropy angle θ at different confining stresses follows a typical U-shaped trend, which has been widely revealed in various layered or bedded rocks (Donath 1961; McLamore and Gray 1967; Nasseri et al. 2003; Cho et al. 2012; Gholami and Rasouli 2014). The compressive strength at θ = 30°–60° is lower compared to other loading directions, due mainly to the weaker cohesive strength of the foliation planes. At a given confining stress, the maximum compressive strength is obtained when the samples are loaded along the foliation planes (θ = 90°), whereas the minimum compressive strength occurs at θ = 45° as a result of the sliding failure along the foliation planes. Figure 8b indicates that there also exists an approximate U-shape for the variation of the axial strain at the peak stress, but with the largest strain consistently attained at θ = 0°. This phenomenon is attributed to the higher compressibility of the foliation planes and the growth of cracks across the foliation.

Fig. 8

Variations of the peak deviatoric strength and the corresponding axial strain with the foliation angle under various confining pressures: a the peak strength and b the axial strain at the peak

Figure 9 shows the plot of the apparent Young’s modulus E and the Poisson’s ratio ν of the slate against the inclination angle θ under various confining pressures, in which the apparent Young’s modulus and the Poisson’s ratio were measured from the linear slope of the stress–strain curves. The first plot shows that the Young’s modulus almost remains constant for θ < 30°–45° and then increases remarkably for higher inclination angles. This phenomenon results from the higher compressibility of the foliation planes and is rather typical for transversely isotropic rocks (Nasseri et al. 2003; Goshtasbi et al. 2006; Cho et al. 2012). The ratio of modulus at θ = 90° to that at θ = 0° varies between 2.0 and 2.2, with the lowest modulus roughly occurring at θ = 0° and the highest modulus at θ = 90°, which is again rather typical for most of transversely isotropic rocks (Cho et al. 2012). Furthermore, a comparison between Figs. 9a and 5 shows that there is a high correlation between the Young’s modulus and the P-wave velocity. Figure 9b shows that the Poisson’s ratio seems to be more influenced by the heterogeneity of the slate samples, being hard to discern a trend against the confining stress and the loading direction.

Fig. 9

Variation of the apparent elastic properties with the foliation angle: a Young’s modulus and b Poisson’s ratio

3 Formulation of an Anisotropic Damage Model

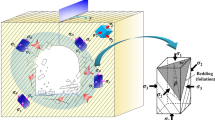
In this section, a constitutive model is developed for the foliated slate by taking into account the alteration in microstructure during the mechanical loading. In the model development, the foliated slate is represented by an isotropic linear elastic solid matrix weakened by arbitrarily distributed penny-shaped microcracks and cut by a set of parallel foliation planes with negligible thickness compared to their spacing, as shown in Fig. 10. Small deformation and rate-independent and isothermal conditions are assumed.

Fig. 10

Illustration of a representative volume element (RVE) of the foliated slate

3.1 Thermodynamic Analysis

Consider a representative volume element (RVE) Ω of the foliated slate (Fig. 10), with ω _j denoting the space occupied by the foliation planes of unit normal n ^j and Ω\ω _j denoting the remaining space occupied by the cracked rock matrix. Let Σ be the uniform macroscopic stress field prescribed on the boundary ∂Ω of the RVE. The local stress σ(x) in Ω can then be related to Σ by defining a fourth-order concentration tensor ${\mathbb{B}}(\varvec{x})$:

$$\varvec{\sigma}\left( \varvec{x} \right) = {\mathbb{B}}(\varvec{x}):\varvec{\varSigma}\quad \forall \varvec{x} \in \varOmega$$

(1)

To avoid the difficulties in the determination of ${\mathbb{B}}(\varvec{x})$, the average stresses of rock matrix and foliation planes are used for further development by taking volumetric average of Eq. (1) on ω _j and Ω\ω _j , respectively:

$$\left\{ \begin{aligned}\varvec{\varSigma}^{j} & = {\mathbb{B}}^{j} :\varvec{\varSigma}\\\varvec{\varSigma}^{r} & = \frac{1}{{f_{r} }}({\mathbb{I}} - f_{j} {\mathbb{B}}^{j} ):\varvec{\varSigma}\\ \end{aligned} \right.$$

(2)

where Σ ^r and Σ ^j are the average stresses acting on rock matrix and foliation planes, respectively, f _r and f _j are the volume fractions of rock matrix and foliation planes, with f _r  + f _j  = 1, ${\mathbb{B}}^{j}$ is the stress concentration tensor for the foliation planes, and ${\mathbb{I}}$ is the fourth-order identity tensor. The derivation of Eq. (2) uses the relation $\left\langle {\mathbb{B}} \right\rangle_{\varOmega } = {\mathbb{I}}$ obtained from the stress average rule $\left\langle {\varvec{\upsigma}} \right\rangle_{\varOmega } =\varvec{\varSigma}$, in which $\langle \cdot \rangle_{\varOmega }$ denotes the volumetric average on Ω. ${\mathbb{B}}^{j}$ is closely related to the geometry and mechanical properties of the foliation planes and their surroundings (Cai and Horii 1992), and it can be approximated by ${\mathbb{B}}^{j} = {\mathbb{I}}$ (i.e. Σ ^j = Σ) for well-foliated slate in which the foliation planes completely cut through the RVE. As mentioned before, when neglecting the thickness of the foliation planes (i.e. f _j  → 0), one approximately has f _r  → 1 and Σ ^r = Σ. This approximation actually leads to a Reuss (or lower-bound) estimate of the effective elastic moduli of the slate.

The macroscopic strain E of the RVE is composed of two components: one is contributed by the cracked rock matrix, E ^r, and the other is contributed by the foliation planes, E ^j:

$$\varvec{E} = \varvec{E}^{r} + \varvec{E}^{j}$$

(3)

$$\varvec{E}^{j} = \frac{1}{\left| \varOmega \right|}\int\limits_{{\omega_{j} }} {\varvec{n}^{j} } \mathop \otimes \limits^{s} \left[\varvec{\xi}\right]\text{d}S = \frac{1}{e}\varvec{n}^{j} \mathop \otimes \limits^{s} \left[\varvec{\xi}\right]$$

(4)

where the operator $\mathop \otimes \limits^{\text{s}}$ denotes the symmetric part of the dyadic product of two vectors, and [ξ] and e are the displacement jump across and the average spacing of the foliation planes, respectively.

The mechanical response of the foliation planes is assumed to be linearly elastic (Singh 1973), given that the failure and sliding of the foliation planes could be modelled later by the microcracking along the foliation. The displacement jump across the foliation planes is then given by:

$$\left[\varvec{\xi}\right] = \varvec{S}^{j} \cdot \varvec{T} = \left( {\frac{1}{{k_{n}^{j} }}\varvec{a} + \frac{1}{{k_{t}^{j} }}\varvec{b}} \right) \cdot \varvec{T}$$

(5)

where T is the stress vector acting upon the foliation planes, with $\varvec{T} =\varvec{\varSigma}^{j} \cdot \varvec{n}^{j} =\varvec{\varSigma}\cdot \varvec{n}^{j}$, $k_{n}^{j}$ and $k_{t}^{j}$ are the normal stiffness and shear stiffness of the foliation planes, a and b are two second-order tensors defined as a = n ^j ⊗ n ^j and b = I - n ^j ⊗ n ^j, I is the second-order identity tensor, and S ^j is the second-order compliance tensor of the foliation planes.

The free enthalpy $W^{j*}$ contributed by the foliation planes can be expressed as:

$$W^{j*} = \frac{1}{e}\int_{\varSigma } {\left[\varvec{\xi}\right] \cdot {\text{d}}(\varvec{n}^{j} \cdot\varvec{\varSigma})} = \frac{1}{e}\int_{\varSigma } {(\varvec{S}^{j} \cdot\varvec{\varSigma}) \cdot \varvec{n}^{j} \cdot {\text{d}}(\varvec{n}^{j} \cdot\varvec{\varSigma})}$$

(6)

The rock matrix, on the other hand, contains arbitrarily distributed penny-shaped microcracks embedded in a homogeneous elastic solid phase. The cracks along any direction (represented by the unit normal vector n) are characterized by three internal variables, d, β and γ, where $d = \mathcal{N}a^{3}$ is the crack density parameter (Budiansky and O’Connell 1976), $\mathcal{N}$ denotes the number of cracks per unit volume, a is the average radius, and β and γ are the volumetric averaging of opening and sliding of the cracks. By virtue of β and γ, the macroscopic strain, E ^c, contributed by cracks could be given by (Zhu et al. 2008a)

$$\varvec{E}^{c} = \frac{1}{4\pi }\int_{{{\text{S}}^{2} }} {\beta (\varvec{n})\varvec{n} \otimes \varvec{n} + \gamma (\varvec{n})\mathop \otimes \limits^{s} \varvec{n}{\text{d}}S}$$

(7)

The free enthalpy of the cracked system developed with the Mori–Tanaka (MT) estimate by applying the Eshelby solution-based homogenization procedure (Zhu et al. 2008b) reads:

$$W^{r*} = \frac{1}{2}\varvec{\varSigma}:{\mathbb{S}}^{s} :\varvec{\varSigma}+\varvec{\varSigma}:\varvec{E}^{c} - \frac{1}{8\pi }\int_{{S^{2} }} {(p_{2} \beta^{2} (\varvec{n}) + p_{4}\varvec{\gamma}(\varvec{n}) \cdot\varvec{\gamma}(\varvec{n})){\text{d}}S}$$

(8)

where ${\mathbb{S}}^{s}$ is the fourth-order elastic compliance tensor of the solid phase (i.e. the undamaged rock matrix), ${\text{S}}^{2} = \{ \varvec{n}||\varvec{n}| = 1\}$ is the surface of a unit sphere, p ₂ and p ₄ are two elastic parameters given in the MT estimate by $p_{2} = \frac{{H_{0} }}{d}$ and $p_{4} = \frac{{H_{1} }}{d}$, with $H_{0} = \frac{{3E^{s} }}{{16\left[ {1 - (\nu^{s} )^{2} } \right]}}$ and $H_{1} = H_{0} (1 - v^{s} /2)$, and E ^s and ν ^s are the elastic modulus and Poisson’s ratio of the solid phase.

The overall free enthalpy W ^*of the foliated slate is finally obtained by summing the components contributed by the foliation planes, Eq. (6), and the cracked rock matrix, Eq. (8):

$$\begin{aligned} W^{*} & = \frac{1}{2}\varvec{\varSigma}:{\mathbb{S}}^{s} :\varvec{\varSigma}+\varvec{\varSigma}:\frac{1}{4\pi }\int_{{S^{2} }} {\beta (\varvec{n})\varvec{n} \otimes \varvec{n} +\varvec{\gamma}(\varvec{n})\mathop \otimes \limits^{s} \varvec{n}{\text{d}}S} \\ & \quad - \frac{1}{8\pi }\int_{{S^{2} }} {(p_{2} \beta^{2} (\varvec{n}) + p_{4}\varvec{\gamma}(\varvec{n}) \cdot\varvec{\gamma}(\varvec{n})){\text{d}}S} + \frac{1}{e}\int_{\varSigma } {(\varvec{S}^{j} \cdot\varvec{\varSigma}) \cdot \varvec{n}^{j} \cdot d(\varvec{n}^{j} \cdot\varvec{\varSigma})} \\ \end{aligned}$$

(9)

Applying the first state law of thermodynamics to Eq. (9) yields the macroscopic strain E of the material:

$$\varvec{E} = \frac{{\partial W^{*} }}{{\partial\varvec{\varSigma}}} = {\mathbb{S}}^{s} :\varvec{\varSigma}+ \frac{1}{4\pi }\int_{{S^{2} }} {\left( {\beta (\varvec{n})\varvec{n} \otimes \varvec{n} +\varvec{\gamma}(\varvec{n})\mathop \otimes \limits^{s} \varvec{n}} \right){\text{d}}S} + \frac{1}{e}[(\varvec{S}^{j} \cdot\varvec{\varSigma}) \cdot \varvec{n}^{j} ]\mathop \otimes \limits^{s} \varvec{n}^{j}$$

(10)

Equation (10) shows that the macroscopic strain of a foliated slate is contributed by the undamaged rock matrix, the microcracks in the cracked rock matrix and the foliation planes, in which the inelastic component is attributed to the microcracks. Directly inverted from Eq. (10), the stress–strain relation can be rewritten as:

$$\varvec{\varSigma}= \left( {{\mathbb{S}}^{s} + {\mathbb{S}}^{j} } \right)^{ - 1} :(\varvec{E} - \varvec{E}^{c} )$$

(11a)

$${\mathbb{S}}^{j} = \frac{1}{{ek_{n}^{j} }}\varvec{a} \otimes \varvec{a} + \frac{1}{{2ek_{t}^{j} }}\left( {\varvec{b}\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\bar{ \otimes }} \varvec{a} + \varvec{a}\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\bar{ \otimes }} \varvec{b}} \right)$$

(11b)

where ${\mathbb{S}}^{j}$ is the compliance tensor for the foliation planes.

3.2 Damage and Friction Evolution

The internal variables, d, β and γ, associated with the cracks in any direction n in Eq. (10) can be determined by their conjugate thermodynamic forces, F ^d, F ^β and F ^γ (Zhu et al. 2008a). The vanishing of F ^β indicates the opening state of cracks so that β and γ can be directly obtained (Chen et al. 2014a). For closed cracks (i.e. F ^β ≤ 0), the sliding and dilatancy behaviours are modelled by an associative Mohr–Coulomb criterion.

$$F = |\varvec{F}^{\gamma } | + \tan \phi_{c} F^{\beta }$$

(12)

where ϕ _c is the friction angle of cracks.

The damage evolution of cracks is guided by a yield criterion suggested by Zhu and Shao (2015) for modelling the material strength and damage softening with the MT homogenization scheme:

$$f(F^{d} ,d) = F^{d} - R(d)$$

(13)

where R(d) is the material resistance to further damage evolution by crack growth, which can be represented as a function of d:

$$R(d) = R_{c} \frac{{2d_{c} d}}{{d_{c}^{2} + d^{2} }}$$

(14)

where R _c is the maximal damage resistance and d _c is the critical damage density, at which the damage resistance reaches its maximal value R _c .

Inspired by the work of Pietruszczak and Mroz (2001), a second-order microstructure tensor (m) in the form of m = m ₁ a + m ₂ b is employed to describe the spatial distribution of the foliation planes, where m ₁ and m ₂ (with m ₃ = m ₂) are the principal values of m normal to and in the foliation planes, respectively. In order to represent the interaction between the cracks and the foliation planes and the resultant anisotropy of deformation and strength for the foliated slate, the following expression modified from Pietruszczak et al. (2002) is suggested for R _c :

$$R_{c} = R_{0} \left[ {1 + M_{ij} l_{i} l_{j} + b\left( {M_{ij} l_{i} l_{j} } \right)^{2} } \right]^{\zeta }$$

(15)

where M _ij is the component of the deviatoric measure of the microstructure tensor m, M _ij  = (m _ij  − m _kk δ _ij /3)/(m _kk /3); l _i is the components of the unit vector along the stress vector acting upon the foliation planes, l _i  = T _i /|T|; R ₀ is the initial damage threshold; and b and ζ are dimensionless material parameters.

It can be inferred from the definition of the tensor M that M can be finally represented in the form of M = M ₁ a +M ₂(I − a), where M ₁ and M ₂ are the principal values of M normal to and in the foliation planes, with M ₁ = −2M ₂. Substituting this relation into Eq. (15) yields:

$$R_{c} = R_{0} \left[ {1 + M_{2} \left( {1 - 3l_{1}^{2} } \right) + bM_{2}^{2} \left( {1 - 3l_{1}^{2} } \right)^{2} } \right]^{\zeta }$$

(16)

Under uniaxial compression test condition, Eq. (16) can be simplified as follows

$$R_{c} = R_{0} \left[ {1 + M_{2} \left( {1 - 3\cos^{2} \theta } \right) + bM_{2}^{2} \left( {1 - 3\cos^{2} \theta } \right)^{2} } \right]^{\zeta }$$

(17)

The evolutions of the internal variables, β, γ and d, that represent the sliding and damage growth of the cracked anisotropic rock, can be readily determined by the Kuhn–Tucker complementary conditions of the sliding and damage criteria; interested readers may refer to Zhu et al. (2008a) for details.

3.3 Computational Aspects

The proposed constitutive model in Eq. (10) is formulated in an integral form on the surface of a unit sphere S² for characterizing the growth of microcracks in any directions induced by deviatoric stress and influenced by slaty structure. This model can be numerically calculated with the Gauss-type numerical integration scheme proposed by Bažant and Oh (1986):

$$\varvec{E} = {\mathbb{S}}^{s} :\varvec{\varSigma}+ \sum\limits_{i = 1}^{m} {w^{i} (\beta \varvec{n} \otimes \varvec{n} + \gamma \mathop \otimes \limits^{s} \varvec{n})_{i} } + \frac{1}{e}[(\varvec{S}^{j} \cdot\varvec{\varSigma}) \cdot \varvec{n}^{j} ]\mathop \otimes \limits^{s} \varvec{n}^{j}$$

(18)

where m is the number of integration points (or equivalently the number of crack families) and w ⁱ is the weighting coefficient at point i. Numerical studies (Chen et al. 2014a) have shown that the integration scheme of m = 33 ensures a good balance between the numerical accuracy and computational cost.

The constitutive model presented in Eq. (18) has been integrated in a finite element computer code, THYME3D (Chen et al. 2009, 2014a). Given the nonlinearity of the coupled damage and friction behaviours of cracks, the stress–strain relation is implemented in an incremental form locally at each Gauss integration point by using a prediction–correction algorithm (Zhu et al. 2008b). As the damage grows, the internal variables d, β and γ in each integration direction are updated using the evolution laws mentioned in Sect. 3.2, and the macroscopic stress–strain behaviour is then determined.

3.4 Parameter Identification

A remaining issue for application of the constitutive model is to determine the material parameters. The proposed model involves 12 parameters, i.e. two elastic coefficients for undamaged rock matrix (Young’s modulus E ^s and Poisson’s ratio ν ^s), three parameters for foliation planes (average spacing e, normal stiffness $k_{n}^{j}$ and shear stiffness $k_{t}^{j}$), two parameters for microcracks (friction angle ϕ _c and initial damage density d ₀) and five parameters for characterizing anisotropic strength and inelastic deformation (R ₀, M ₂, b, ξ and d _c). According to Eq. (11), the equivalent elastic stiffness modulus, E(θ), in the loading direction (denoted by e ₁) can be represented by:

$$E\left( \theta \right) = \left[ {\varvec{e}_{1} \otimes \varvec{e}_{1} :\left( {{\mathbb{S}}^{s} + {\mathbb{S}}^{j} } \right):\varvec{e}_{1} \otimes \varvec{e}_{1} } \right]^{ - 1}$$

(19a)

$$\frac{1}{E\left( \theta \right)} = \frac{1}{{E^{s} }} + \frac{{\cos^{4} \theta }}{{ek_{n}^{j} }} + \frac{{\sin^{2} \theta \cos^{2} \theta }}{{ek_{t}^{j} }}$$

(19b)

Obviously, E(θ) is a function of θ, $k_{n}^{j}$ and $k_{t}^{j}$ and represents the apparent Young’s modulus obtained in the laboratory condition (Sect. 2.3.2). At θ = 90°, E(θ) = E ^s, and therefore, the elastic coefficients E ^s and ν ^s of the undamaged rock matrix could be obtained from conventional triaxial compression tests performed at θ = 90° by measuring the linear slope of the stress–strain curves (i.e. E ^s = Δσ ₁/Δε ₁ and ν ^s = Δε ₃/Δε ₁). Again, at θ = 90°, the average stress of the foliation planes is constantly equal to σ ₃ during the loading process, and therefore the macroscopic strain of the foliated rock is only contributed by the cracked rock matrix and the maximum compressive strength was obtained consistently at this loading orientation for varying confining pressures in the experimental study. Assuming that the presence of foliation planes has negligible influence on the frictional sliding of cracks for this loading orientation and following the treatment by Zhu and Shao (2015) for damage modelling of brittle rocks, the friction angle ϕ _c of cracks could be determined from the envelope of the peak strength under different confining pressures at θ = 90°. The initial damage density, d ₀, can be estimated by the initial fracturing/microcracking status of the slate samples created by tectonic tress, sampling and manufacturing.

The average spacing e of foliation planes can be easily determined from the slate samples. By Eq. (19b), the normal stiffness $k_{n}^{j}$ and shear stiffness $k_{t}^{j}$ can be successively estimated at θ = 0° and θ = 45°, respectively. The parameters R ₀, A ₁, b and ζ in the damage evolution law can be estimated by numerical fitting to the curve of uniaxial compression strength against the loading direction (Pietruszczak et al. 2002; Chen et al. 2010; Hu et al. 2013; Nguyen and Le 2014), which, as shown in Fig. 11, yields a best estimate of R ₀ = 7.7 × 10⁻⁴, M ₂ = 0.87, b = 0.97, and ζ = 3.3 for the foliated slate. The critical damage d _c, which controls the damage kinetics at both pre-peak and post-peak stress stages, is linearly related to the inelastic strain at the peak stress (Lockner 1998; Zhu and Shao 2015), but for simplicity, this study adopts a constant value of d _c.

Fig. 11

Uniaxial compressive strength as a function of the foliation angle (θ)

Figure 12a shows the plot of the variation of the maximal damage resistance R _c calculated by Eq. (17) with the loading orientation θ, showing that R _c follows a U-shaped variation similar to the compressive strength (Fig. 8a), with the minimum value attained at θ = 45° and the maximum value at θ = 90°. This indicates that microcracking is rather easily induced when the foliation angle θ is around 45°, and much more difficultly when the foliation is parallel or perpendicular to the loading direction. Figure 12b shows the plot of the variation of the damage resistance R defined in Eq. (14) with the damage density d at different loading orientations, showing that the damage resistance R increases for d ≤ d _c and then decreases for d ≥ d _c. The combination of Eqs. (17) and (14) enables the proposed model to properly describe both the anisotropic damage growth influenced by the foliation planes and the hardening and softening process during the deviatoric loading (Fig. 6).

Fig. 12

Variations of a the maximum damage resistance R _c with the foliation angle θ and b the damage resistance R with the damage density d at various foliation angles

4 Numerical Simulation

In this section, the performance of the proposed model is assessed by performing numerical simulations on the foliated slate in the test conditions. Table 2 lists the material parameters for the slate rock estimated by using the uniaxial and/or triaxial compression test data (σ ₃ = 0 MPa) with the method presented in Sect. 3.4, where the mean values of E ^s and ν ^s measured at θ = 90° for σ ₃ = 0–20 MPa are taken for simulation. The triaxial compression test data (σ ₃ = 5–20 MPa) are used to validate the effectiveness and assess the performance of the proposed model. In the numerical simulation, each test is assumed to be performed on a representative elementary volume (regarded as a material point) of the slate rock.

Table 2 Values of the model parameters for the foliated slate

4.1 Simulation Results

Figures 13, 14, 15 and 16 show the plots of the simulated and measured stress–strain curves for the foliated slate under varying confining pressures (σ ₃ = 5, 10, 15 and 20 MPa) at varying loading orientations (θ = 0°, 15°, 30°, 45°, 60°, 75° and 90°). Figure 17 shows the plot of the predicted peak strength as a function of the loading orientation at different confining pressures. A comparison between the simulated results and the experimental measurements in Figs. 13, 14, 15, 16 and 17 shows that the proposed constitutive model rather well predicts the anisotropic deformation and strength behaviours of the foliated slate in various triaxial test conditions. The proposed model satisfactorily reproduces the linear elastic phase, the crack initiation and growth phase and the strain softening phase of the stress–strain curves. The influences of the loading orientation and confining pressure on the mechanical responses are also properly modelled. Consistent with the experimental observations, the proposed model successfully predicts more pronounced inelastic deformation at lower inclination angles (θ → 0°) and higher peak stress with less inelastic deformation at higher inclination angles (θ → 90°) as a result of preferential microcrack growth across the foliation planes. Furthermore, the proposed model behaves fairly well to predict the maximum compressive strength occurring at θ = 90° and the minimum one appearing at θ = 45° under various confining pressures.

Fig. 13

Predicted stress–strain curves of the slate under 5 MPa confining pressure at various foliation angles: a θ = 0, 30, 60 and 90° and b θ = 15, 45 and 75°

Fig. 14

Predicted stress–strain curves of the slate under 10 MPa confining pressure at various foliation angles: a θ = 0, 30, 60 and 90° and b θ = 15, 45 and 75°

Fig. 15

Predicted stress–strain curves of the slate under 15 MPa confining pressure at various foliation angles: a θ = 0, 30, 60 and 90° and b θ = 15, 45 and 75°

Fig. 16

Predicted stress–strain curves of the slate under 20 MPa confining pressure at various foliation angles: a θ = 0, 30, 60 and 90° and b θ = 15, 45 and 75°

Fig. 17

Comparison of the predicted and measured peak strength versus foliation angle curves under triaxial test conditions

Some remarkable discrepancies do occur between the model predictions and the experimental measurements, due mainly to the possible inhomogeneity of the slate samples and the damage resistance parameters calibrated in the uniaxial test condition, rather than in the corresponding triaxial test conditions. Another possible reason may be the improper simplifications of the model. For example, the deviatoric peak stress at θ = 30°–60° is underestimated for lower confining pressure (i.e. σ ₃ = 5 MPa), but overestimated for σ ₃ = 15–20 MPa. This discrepancy may be attributed to the negligence of the difference in the damage resistance at different confining pressures. Furthermore, the proposed model predicts larger inelastic deformation at θ = 90° before the samples fail, due to the use of a constant value of d _c in the simulations. A smaller value of d _c would improve the predictions in this orientation, as described in the next section.

4.2 Sensitivities of the Proposed Model with Respect to d _c and R _c

Sensitivity studies have been performed by Chen et al. (2012b, 2014b) to examine the responses of the damage model with respect to some of the model parameters (e.g. E ^s, ν ^s, ϕ _c and d ₀). This section further evaluates the influences of the parameters d _c and R _c in the damage evolution law on the behaviours of the proposed model. The sensitivity study on d _c is conducted at θ = 0° and σ ₃ = 5 MPa by varying d _c from 5 to 50, with the remaining parameters being the same with those listed in Table 2. Figure 18a shows that the critical damage density d _c has a rather significant influence on the stress–strain curves at the damage growth phase and the strain softening phase near the peak stress. A higher value of d _c results in larger inelastic strains due to a larger amount of damage accumulation, whereas a smaller value of d _c predicts a more brittle response. The peak stress, however, almost keeps constant for different values of d _c. The above results indicate that the proposed model could better predict the stress–strain behaviours of the foliated slate by defining d _c as a function of the loading orientation θ.

Fig. 18

Predicted stress–strain curves at θ = 0° and σ ₃ = 5 MPa with different values of a d _c and b R _c

The maximal damage resistance R _c , calibrated in this study with the uniaxial compression test data, is expected to have an important impact on the mechanical behaviours in triaxial test conditions. A numerical simulation is performed to examine the sensitivity of the model response at θ = 0° and σ ₃ = 5 MPa by varying R _c from 0.005 to 0.02. As shown in Fig. 18b, higher peak stress and larger inelastic strain are predicted by adopting a larger value of R _c , which allows a larger amount of crack growth after the initiation of damage. As stated before, defining R _c as a function of the loading orientation θ enables the model to describe the anisotropic mechanical behaviours of the foliated slate.

5 Conclusions

In this study, the anisotropic mechanical behaviours and failure mechanisms of the well-foliated Jiujiang slate were systematically examined by performing a series of uniaxial and triaxial compression tests on the slate specimens with varying inclination angles (θ = 0°–90°) under different confining pressures (σ ₃ = 0–20 MPa). The slate samples were observed to fail in three typical modes, i.e. shear failure across foliation planes, sliding failure along foliation planes and axial splitting from foliation planes, depending on the loading direction (θ) with respect to the foliation. The variation of the compressive strength as a function of the foliation angle θ at different confining pressures follows a typical U-shaped trend, with the maximum strength attained at θ = 90° and the minimum strength at θ = 45°. The apparent Young’s modulus was found to grow with the inclination angle, having a high correlation with the P-wave velocity. The stress–strain curves display an initial nonlinear phase, a linear elastic phase, a crack initiation and growth phase, as well as a rapid stress drop phase and a residual stress phase at any inclination angles and confining pressures, but with the initial crack closure phase being more pronounced under uniaxial compressive condition (σ ₃ = 0 MPa) and at lower inclination angles (θ ≤ 30°).

Based on the experimental observations, a micromechanical damage–friction model was proposed for the foliated slate by characterizing the slaty rock as a homogeneous elastic matrix containing arbitrarily distributed penny-shaped microcracks and a family of parallel foliation planes. The foliation planes were simply modelled with an elastic interface, and the interaction between the foliation planes and the damaged rock matrix was characterized with a nonlinear damage evolution law associated with the inclination angle. The proposed model was applied to predict the anisotropic mechanical responses of the slate rock under triaxial compressive conditions using the material parameters calibrated by the uniaxial and/or triaxial test data. The good agreement between the model predictions and the laboratory measurements shows that the proposed model satisfactorily describes the anisotropic deformational and strength behaviours of the foliated slate.