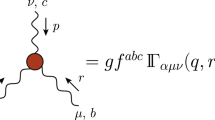1 Introduction

The three-gluon vertex plays a central role in the infrared dynamics of Quantum Chromodynamics (QCD) [1,2,3] and is intimately linked to gluons self-interactions, namely to the non-abelian nature of QCD. The appearance of a three-gluon vertex in the QCD Lagrangian lies at the origin of both asymptotic freedom and confinement in QCD. The study of the non-perturbative features of the three-gluon vertex has attracted attention for the last decades in both Dyson-Schwinger and lattice simulations [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29].

The three-gluon vertex depends on the incoming momenta, q, r and p, with the kinematical constraint \(q+r+p=0\). Most lattice studies focus on the symmetric (\(q^2 = r^2 = p^2\)) and soft-gluon (\(p = 0\), and thus \(q^2=r^2\)) cases, where there is only a single momentum scale [19,20,21]. In both kinematics, the dominant component of the vertex exhibits an infrared zero-crossing at low momentum, motivated by a negative singularity in the vanishing momentum limit which can be understood as the consequence of massless ghost and massive gluons generating the full expansion of the vertex in continuum Schwinger-function methods (CSM)  [30]. The phenomenon of the dynamical generation of a gluon mass has reached a great consensus from both lattice and CSM (see Ref.  [31] for a very recent review, and references therein).

Being its study of paramount theoretical relevance by itself, the three-gluon vertex is also a central component in a great variety of phenomenological studies in the continuum. The infrared suppression displayed by its main form factors is a distinctive feature that plays a crucial role in generating bound states with specific physical properties. The search for such bound states is an ongoing endeavor that relies on the productive synergy between lattice simulations and CSM. This joint effort has resulted in a deeper insight into the intricate patterns underlying the rich dynamics of QCD, establishing remarkable connections with the emergence of a mass scale in the gauge sector of the theory  [30, 32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47]

2 Transversely Projected Three-Gluon Vertex

From the lattice gauge fields in momentum-space, \(\widetilde{A}_\mu ^a (q)\), one begins by evaluating the basic ingredients, namely the gluon propagator

$$\begin{aligned} \Delta _{\mu \nu }^{ab} (q)= \langle \widetilde{A}_\mu ^a (q)\widetilde{A}_\nu ^b (-q)\rangle = \Delta (q^2) \delta ^{ab} P_{\mu \nu }(q) , \end{aligned}$$
(1)

and the three-gluon Green function,

$$\begin{aligned} \mathcal {G}_{\alpha \mu \nu } (q,r,p)= \frac{1}{24} f_{a b c} \langle \widetilde{A}_\alpha ^a (q)\widetilde{A}_\mu ^b (r)\widetilde{A}_\nu ^c (p)\rangle ; \end{aligned}$$
(2)

both specialized in Landau gauge, with \(P_{\mu \nu }(q) = \delta _{\mu \nu } - q_\mu q_\nu /q^2\) for the transverse projector. Note that, in the definition of \(\mathcal {G}_{\alpha \mu \nu } (q,r,p)\), there is an explicit projection over \(f_{a b c}\), the fully anti-symmetric color tensor of SU(3), and we are thus not considering any possible contribution to the symmetric one, \(d_{abc}\). This lattice Green function \(\mathcal {G}_{\alpha \mu \nu } (q,r,p)\) can be expressed as

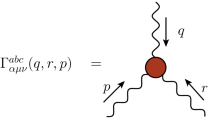
$$\begin{aligned} \mathcal{G}_{\alpha \mu \nu } (q,r,p) = g {\bar{\Gamma }_{\alpha \mu \nu }(q,r,p)} \Delta (q^2) \Delta (r^2) \Delta (p^2), \end{aligned}$$
(3)

in terms of the transversely projected vertex function \(\bar{\Gamma }_{\alpha \mu \nu }(q,r,p)\) which, in its turn, can be related to the full one-particle irreducible (1PI) vertex function \(\Gamma _{\alpha ' \mu ' \nu '}(q,r,p)\),

$$\begin{aligned} {\bar{\Gamma }_{\alpha \mu \nu }(q,r,p)} = \Gamma _{\alpha ' \mu ' \nu '}(q,r,p) {P^{\alpha '}_{\alpha }(q) P^{\mu '}_{\mu }(r) P^{\nu '}_{\nu }(p)}, \end{aligned}$$
(4)

with the use of the transverse projectors defined above.

The full 1PI tensor can be written as a combination of both longitudinal and transverse contributions, \({\Gamma }^{\alpha \mu \nu }(q,r,p) = {\Gamma _L}^{\alpha \mu \nu }(q,r,p) + {\Gamma _T}^{\alpha \mu \nu }(q,r,p)\). Ten out of the fourteen 1PI three-gluon vertex linearly independent tensors are longitudinal, \(\ell _1^{\alpha \mu \nu },\cdots ,\ell _{10}^{\alpha \mu \nu }\), while only four are transverse, \(t_1^{\alpha \mu \nu },\cdots ,t_4^{\alpha \mu \nu }\), using the widely used Ball-Chiu decomposition  [2, 48]. However, as explicitly shown in Refs.  [20], the transverse projection in Eq. (4) results in a rearranging of the longitudinal and transverse components of the former decomposition, mixing them up in four particular combinations. These four combinations correspond to components of a direct decomposition of the transversely projected three-gluon vertex, which are the form factors that can be accessed from Landau-gauge lattice simulations. Indeed, using the Ball-Chiu decomposition, the transversely projected three-gluon vertex can be expanded in terms of the four tensors \(t_i\)’s. However, we have switched to a different basis,

$$\begin{aligned} \lambda _1^{\alpha \mu \nu } \!=&\ P_{\alpha '}^\alpha (q) P_{\mu '}^{\mu }(r) P_{\nu '}^\nu (p) \left[ \ell _1^{\alpha '\mu '\nu '} + \ell _4^{\alpha '\mu '\nu '} + \ell _7^{\alpha '\mu '\nu '}\right] \,, \end{aligned}$$
(5a)
$$\begin{aligned} \lambda _2^{\alpha \mu \nu } \!=&\frac{3}{2 s^2} \,(q-r)^{\nu '} (r-p)^{\alpha '} (p-q)^{\mu '} P_{\alpha '}^\alpha (q) P_{\mu '}^{\mu }(r) P_{\nu '}^\nu (p)\,, \end{aligned}$$
(5b)
$$\begin{aligned} \lambda _3^{\alpha \mu \nu } \!=&\frac{3}{2 s^2} P_{\alpha '}^\alpha (q) P_{\mu '}^{\mu }(r) P_{\nu '}^\nu (p) \left[ \ell _3^{\alpha '\mu '\nu '} + \ell _6^{\alpha '\mu '\nu '} + \ell _9^{\alpha '\mu '\nu '}\right] \,, \end{aligned}$$
(5c)
$$\begin{aligned} \lambda _4^{\alpha \mu \nu } \!=&\left( \frac{3}{2 s^2}\right) ^2 \left[ t_1^{\alpha \mu \nu } + t_2^{\alpha \mu \nu } + t_3^{\alpha \mu \nu }\right] \,, \end{aligned}$$
(5d)

where the four tensors are anti-symmetric under exchange of any pair of gluon momenta and indices. Furthermore, (5a) corresponds to the the tree-level tensor, making thus possible an easier comparison with existing results in the literature for some particular kinematics. Therefore, one is left with

$$\begin{aligned} {\bar{\Gamma }^{\alpha \mu \nu }(q,r,p)} = \bar{\Gamma }_1 \lambda _1^{\alpha \mu \nu } + \bar{\Gamma }_2 \lambda _2^{\alpha \mu \nu } + \bar{\Gamma }_3 \lambda _3^{\alpha \mu \nu } + \bar{\Gamma }_4 \lambda _4^{\alpha \mu \nu }; \end{aligned}$$
(6)

where, as the definition of \(\mathcal{G}_{\alpha \mu \nu }(q,r,p)\) implies a contraction with the anti-symmetric color tensor \(f_{abc}\), Bose symmetry ensures that the scalar form factors \(\overline{\Gamma }_i\) depend only on Bose-symmetric combinations of the three momenta.

The form factors will be extracted projecting the lattice-evaluated three-point Green function over the chosen tensors for the basis:

$$\begin{aligned} \underbrace{\overline{\Gamma }_{\alpha \mu \nu } (q,r,p) \cdot \lambda _j^{\alpha \mu \nu }(q,r,p)}_{b_j} = \sum _i \overline{\Gamma }_i(q^2,r^2,p^2) \underbrace{\lambda ^i_{\alpha \mu \nu } (q,r,p) \lambda _j^{\alpha \mu \nu }(q,r,p)}_{M_{ij}} \end{aligned}$$
(7)

or, calling \(\mathcal {P}_i^{\alpha \mu \nu }=M^{-1}_{ij} \lambda _j^{\alpha \mu \nu }(q,r,p)\) the projector over each element of the basis:

$$\begin{aligned} \overline{\Gamma }_i(q^2,r^2,p^2) = \mathcal {P}_i^{\alpha \mu \nu } \overline{\Gamma }_{\alpha \mu \nu } (q,r,p). \end{aligned}$$
(8)

We will use this general scheme to extract the scalar form factors \(\overline{\Gamma }_i\) from the lattice evaluation of the three-gluon Green function \(\mathcal {G}\).

3 Kinematics of the Three-Gluon Vertex

The three-gluon vertex in its most general form is only restricted by the momentum conservation, i.e. \(q+r+p = 0\), being q, r and p the momenta of the three corresponding gluons. (see Fig. 1).

Fig. 1
figure 1

Schematic representation of the three-gluon vertex. Momentum conservation imposes that the sum of the three incoming momenta q, r and p is zero

Full size image

For some kinematical configurations (i.e. some choices of the three momenta q, r and p), the four tensors in Eqs.(5a) to (5d) are no longer linearly independent, and a careful analysis of the dependence of these tensors on the kinematics is in order. Indeed, the matrix M in Eq.(8) will only be rank 4 in the general case, while in the symmetric configuration (\(q^2=r^2=p^2\)) its rank is reduced to 2 (with our choice only the symmetric limits of \(\lambda _1\) and \(\lambda _2\) survive as linearly independent tensors). In the soft-gluon case (\(p=0\)), which corresponds to an angle between the momenta q and r, \(\theta _{qr}=\pi \), there is only one linearly independent tensor, namely the tree-level one. Finally, in the bisectoral case defined by \(q^2=r^2\) (note that this case contain as particular limits the symmetric and soft-gluon ones), the three first tensors \(\lambda _1\), \(\lambda _2\) and \(\lambda _3\) survive as linearly independent tensors and thus we will have to deal with a 3x3 block of matrix M. The bisectoral case also contains the limit in which the three momenta are parallel with \(q=r\) (and thus, applying momentum conservation, \(p=-2q\)), corresponding to an angle \(\theta _{qr}=0\), termed collinear in table 1. In this case there is no option to build a transverse tensor and the rank of the matrix M is zero. Although there are similarities between the two extreme bisectoral configurations: soft-gluon (\(\theta _{qr}=\pi \)) and collinear (\(\theta _{qr}=0\)), there is a subtle difference between them. In both cases all the momenta that appear are proportional to each other, but the soft-gluon limit \(p\rightarrow 0\) allows to construct a transverse tensor without ambiguity [21, 30].

Table 1 Number of independent tensors for each kinematical configuration. For each one, the angle between the momenta q and r is also shown
Full size table

The different kinematic configurations can be represented in a three-dimensional plot whose axes correspond to \(q^2\), \(r^2\) and \(p^2\) (Fig. 2a). The scalar form factors \(\overline{\Gamma }_i\) will depend Footnote 1 on the squared momenta \(q^2\), \(r^2\), and \(p^2\), and therefore varies within the space defined by these axes. Nevertheless, the choice of the tensors we have made implies that the \(\overline{\Gamma }_i\) are symmetric under exchange of the momenta, and can only depend on symmetric combinations of the momenta [10]. The symmetric combination of the momenta \(s^2=\frac{1}{2}\left( q^2+r^2+p^2\right) \) is a quantity shared by all the points lying on every plane perpendicular to the octant diagonal (see Fig. 2a). Given a fixed \(s^2\), Fig. 2b represents all possible kinematics: the white incircle contains all the kinematic configurations allowed by momentum conservation. The grey line corresponds to the one of the so-called bisectoral regimes, where two of the squared momenta (\(q^2\) and \(r^2\) in this case) are equal. The green dot represents the symmetric case, where all the three squared momenta are the same. Finally, the three dots on the limit of the circle correspond to the three possible soft-gluon cases, where one of the momenta goes to zero.

Fig. 2
figure 2

The kinematic configuration of the three-gluon vertex represented by the Cartesian coordinates \((q^2,r^2,p^2)\) (left picture). All kinematics allowed are contained in a circle around the symmetric case (\(q^2=r^2=p^2\), green dot) (right picture). The bisectoral line (thick gray), and the particular soft-gluon (orange solid circle), and symmetric (green) cases appear depicted. The other two soft-gluon limits (black) are also illustrated

Full size image

4 Results

We have employed a large set of quenched gauge field configurations (See Table 2) using the standard Wilson action and fixed them to the Landau gauge. From these configurations we have computed the gluon propagator and the three-gluon vertex for the symmetric, soft-gluon and bisectoral cases as described above. From the lattice bare inputs, we have implemented the Momentum substraction (MOM) renormalization by introducing the renormalization constants for the gauge field and three-gluon vertex, \(\Delta _{R,\mu }(q^2)=Z_A^{-1}(\mu ^2,a)\Delta (q^2,a)\) and \(\overline{\Gamma }_{R,\mu }(q^2,r^2,p^2)=Z_3(\mu ^2,a)\overline{\Gamma }(q^2,r^2,p^2,a)\); such that the renormalized quantities take the tree-level values at the substraction point \(\mu \). This implies \(\Delta _{R,\mu }(\mu ^2)=1/\mu ^2\), for the gluon propagator; while, particularizing the vertex for the soft-gluon kinematics, one is left with:

$$\begin{aligned} \overline{\Gamma }_{R,\mu }(\mu ^2,\mu ^2,0)=1. \end{aligned}$$
(9)

For the gluon propagator and soft-gluon three-gluon vertex, the H4-extrapolation method described in Refs.  [49, 49,50,51,52] has been applied to reduce the lattice artifacts. In all cases, statistical errors have been estimated using “Jackknife method”.

Table 2 Quenched configurations employed for lattice calculations
Full size table

Although the symmetric and soft-gluon kinematics have been largely studied in the past (see, for example, [16, 19] and references therein.), the so-called planar degeneracy, the fact that the dominant tree-level form factor depends almost exclusively on the Bose-symmetric combination of momenta \(s^2\) [53], implies that

$$\begin{aligned} \overline{\Gamma }_{1,R}^{sym}\left( \frac{2}{3}q^2,\frac{2}{3}q^2,\frac{2}{3}q^2\right) = \overline{\Gamma }_{1,R}^{sg}(q^2,q^2,0)\ ; \end{aligned}$$
(10)

where sym and sg denote the symmetric and soft-gluon cases, respectively. In Fig. 3, both form factors have been represented in terms of the symmetric variable s, and shown to exhibit an impressive overlapping (spoiled by their usual representation in terms of the momentum-scale q) which is a striking indication for the planar degeneracy.

Fig. 3
figure 3

Tree-level form factor \(\overline{\Gamma }_1(s)\) for symmetric (red) and soft-gluon (blue) kinematics, renormalized at \(\mu =4.3 GeV\)

Full size image

Every kinematic configuration belonging to the more general bisectoral case can be represented by moving along the vertical line in Fig. 2b, varying the angle from \(\theta _{qr}=0\), for the collinear case, to \(\theta _{qr}=\pi \) for the soft-gluon case. The symmetric one corresponds to an angle \(\theta _{qr}=2\pi /3\) and is placed between the two extreme cases. In order to show that the planar degeneracy holds true along the bisectoral kinematics, we have plotted in Fig. 4 the dominant form factor for several values of s as a function of the angle \(\theta _{qr}\). From top-left to bottom-right, the values of s correspond to 1, 1.5, 2, and 3 GeV. In each plot, momentum bins of \(s \pm 5\%\) have been considered for the representation, exploiting data from the four data-sets in table 2.

Fig. 4
figure 4

Tree-level form factor \(\overline{\Gamma }_1(q^2,q^2,p^2)\) as a function of the angle \(\theta _{qr}\) for several fixed values of \(s=\sqrt{(q^2+r^2+p^2)/2}\). From top-left to bottom-right, s takes the values 1, 1.5, 2, and 3 GeV. In all subplots, blue symbols represent bisectoral kinematics, red ones show the symmetric case (\(\theta _{qr}=2\pi /3\) and black ones represent the soft-gluon case at \(\theta _{qr}=\pi \). The green band is centered on the weighted average of the soft-gluon values and with its width is three times the average error. Grey points correspond to bisectoral data close to one of the particular cases in table 1

Full size image

Taking as reference the soft-gluon case, we have introduced in Fig. 4 a green band centered in the soft-gluon average for this value of s and width \(3 \sigma \). One can observe that, despite the fact that there is a large spreading of the values for the bisectoral case, the planar degeneracy seems to work as a good approximation; i.e., the data do not present a significant dependence on the angle for any given value of s. The same has been also shown in Ref.  [47].

Besides the fact that planar degeneracy appears to be satisfied at first sight, there are some effects that can be appreciated from the plots in Fig. 4 and deserve a comment. First, the overall uncertainty increases when one approaches the symmetric limit \(\theta _{qr}\rightarrow 2\pi /3\). This is associated to the fact that the rank of matrix M in Eq. (8) is 3 along the bisectoral case and reduces to 2 in the symmetric one. When approaching that limit, the determinant of M approaches a zero and this increasing the numerical noise. Second, and more relevant from a phenomenological point of view, there is a systematic deviation from the planar degeneracy (mostly seen at high momenta) when we approach the soft-gluon limit \(\theta _{qr}\rightarrow \pi \). This effect is indeed expected and can be explained within a simple one-loop analysis with a non-running gluon mass [53].

5 Conclusions

We have presented the lattice calculations of the three-gluon vertex from a large ensemble of quenched gauge-field configurations. We have analysed the transversely projected 1PI vertex beyond the soft-gluon and symmetric kinematical configurations, choosing a suitable tensor basis that makes manifest the Bose symmetry of the vertex. Focusing on the dominant tree-level form factor \(\overline{\Gamma }_1\), we have shown an amazing overlap between the soft-gluon and symmetric cases, when plotted in terms of the symmetric combination of momenta \(s^2=(q^2+r^2+p^2)/2\). This is a strong evidence supporting the planar degeneracy, i.e., the fact that the form-factors only depend on s. To support this evidence, we have also proved that, for all bisectoral kinematics, this dominant form factor has almost no dependence on the angle \(\theta _{qr}\).

This planar degeneracy has also been reported in Dyson-Schwinger studies [10] and is of paramount interest due to the simplifications that introduces in the structure of the three-gluon vertex. In this sense, the planar degeneracy, joint to the dominance of the tree-level tensor contribution [53] allows to approximate the transversely projected three-gluon vertex as:

$$\begin{aligned} \overline{\Gamma }^{\alpha \mu \nu }(q,r,p) \approx \overline{\Gamma }_1^{sg}\left( \frac{q^2+r^2+p^2}{2}\right) \lambda _1^{\alpha \mu \nu }(q,r,p). \end{aligned}$$
(11)

As a first very relevant phenomenogical application of Eq. (11), it has been implemented in Ref.  [47] as an input to deliver a lattice-based estimate of the so-called displacement function, which modifies the three-gluon vertex Slavnov-Taylor identity only when the Schwinger mechanism for the dynamical gluon mass generation is activated. The result entails that the Schwinger mechanism is strongly supported by the momentum running observed from the lattice for the two- and three-point QCD Green’s functions.

At present, we have empirical evidence of the near “planar degeneracy” supported by a large amount of lattice data and a one-loop calculation that incorporates a gluon mass. However, a deeper comprehension of its origin eludes us. It is crucial to uncover the mechanism that underlies this characteristic and to establish any possible connections with other fundamental aspects of QCD.