1 Introduction

Contrary to popular assumption that the outer space is a vast void, the interplanetary or interstellar space is known to be full of Interplanetary or interstellar dust particles (IDPs) of various shapes, sizes, chemical composition and physiochemical properties. These corpuscles have their sources from debris of comets, asteroids, planets and their satellites. Several scientific questions of great importance such as interstellar clouds, proto-nebulae, planetary rings, etc are answered by reasons of the accumulation of the IDPs and micrometeorites in certain regions of space.

Poynting [1, 2] examined the effect of absorption and subsequent re-emission of sunlight by small isolated particles in the solar system. A modification of his studies was carried out by [3] where he modeled the total radiation force by relativistic approach of the first order in the ratio of the velocity of particle to that of light. The study of the P–R effect finds its relevance in the investigation of asteroidal cloud, orbital evolution of cometary meteor streams, interplanetary dust clouds and zodiacal cloud.

Poynting–Robertson (PR) effect is an important tool in the study of dissipation. Reduction in orbital elements such as the semi-major axis of the particle is as a result of external dissipative forces which can cause the particle to spiral toward the Sun. Colombo et al. [4] included the effect of P–R drag in the study of the stability of equilibrium points and they showed that the points are unstable due to such drag force. In discussing the orbital evolution of the Janus and Epimetheus system, Yoder et al. [5] pointed the effects of dissipative processes on stability. Peale [6] studied numerically and analytically the effects of nebular gas drag on Trojan precursors in the orbit of Jupiter; he observed that the leading and trailing triangular equilibrium points could be stable to this drag force. Murray [7]showed that there are certain classes of drag forces for which the displaced triangular points become asymptotically stable, whereas objects displaced from these equilibrium points have resulting paths in the rotating frame that spiral in toward the equilibrium points. Some results on the global dynamics of the regularized restricted three-body problem with dissipation were given by [8]. The equilibrium points and zero velocity surfaces in the restricted four-body problem with solar wind drag was researched by [9]. Likewise, Chakraborty and Narayan [10] considered the effect of Stellar wind and Poynting–Robertson drag on photogravitational elliptic restricted three-body problem and reported that the equilibrium points are unstable due to the presence of drag.

Stokes drag is a form of dissipative force and studies have shown that dissipative forces are responsible for secular changes in orbital angular momentum and energy. In planetary dynamics, there are certain instances where interactions with gas particle can significantly affect the motion of solid particles. Two outstanding examples of this phenomenon are the interactions of planetisimal with the protoplanetary disk during the formation of solar system and the orbital decay of ring particles as a result of drag caused by extended planetary atmospheres. For certain objects having dimensions larger than the mean free path of the gas molecules, they experience Stokes drag \(F_{D}=-C_{d}A\rho v^{2}/2\), where v is the relative velocity of the gas to the body, \(\rho \) is the gas density, A is the projected surface area of the body and \(\hbox {C}_{\mathrm {d}}\) is the dimensionless drag coefficient, which is of order unity.

Lamy and Perrin [11] asserts that the solar radiation force on a particle can be very large compared to the gravitational forces that the particle experiences. The validity of this statement depends upon the size and material composition of the particle and upon the spectral type of the star. Hence, when the motion of the IDPs is considered, the force of radiation, and drag forces on the dust particles must also be put into cognizance along with the impact of the gravitational force. In the light of restricted few body model, Radzievskii [12, 13] investigated the photo-gravitational restricted three-body problem, in which the motion of a test particle is influenced by both the force of gravity and the radiation emitted from one of the primaries. Schuerman [14] further extended the study to include the radiation from both primaries while Simmons et al. [15] examined the problem more holistically with the case of negative radiation parameter. Recently, Sing and Omale [16] investigated the combined effect of Stokes drag, oblateness and radiation pressure on the existence and stability of equilibrium points in the restricted four-body problem.

It is important most times to have the restricted models formulated in a manner that some real physical phenomenon can be captured as much as possible. The bi-circular and bi-elliptic restricted problem attempt to achieve this very goal. Authors such as [17, 18] pioneered this facet of the restricted four-body problem. Others such as [19, 20] have lent their contributions in the area of bi-elliptic restricted four-body problem. The bi-circular restricted four body problem (BCR4BP) is very useful for analytic and application purpose, the effect of the fourth body is included to the restricted three-body problem. In the BCR4BP for instance, the earth and the moon are assumed to move in circular orbits around their centre of mass and their centre of mass also moves in the circular orbit around the Sun in the same plane. Authors such as [21,22,23,24] have used the BCR4BP for applications in the periodic orbit and gravitational capture.

Knowing that dissipative forces are driving evolutionary processes in the solar system, we aim at studying the effect of two of them, namely, the Poynting–Robertson drag and the Stokes drag and on the motion of spacecraft from the Earth–Moon-focused view of the Sun–Earth–Moon system. This work is arranged thus; Sect. 2 is the mathematical formulation of the model using Bi-circular approach, in Sects. 3 and 4 we investigate the Lagrange points and establish the linear stability of the motion around the Lagrange points respectively. Section 5 is the verification of chaos in the system and we draw the conclusion in Sect. 6.

2 Model Formulation and Equations of Motion

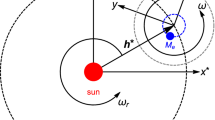
Let \(m_{1}, m_{2}\) and \(m_{3}\) be three primaries of finite masses whose motions are on the same plane along with the fourth body \(m_{4}\) of negligible mass compared to the masses of the three primaries, and its motion is under the gravitational influence of the three finite masses. We set up the configuration of the system in such a way that \(O^{\prime }\) is taken as the centre of mass of \(m_{2}\) and \(m_{3}\) which revolves around O the centre of mass of the integral system. Further, let the distances between \(m_{1}\) and \(OO^{\prime }\) and \(OO^{\prime }\) and \(m_{2}O^{\prime }\) and \( m_{3}\) be \(D_{1}D_{2}\), \(d_{1}\) and \(d_{2}\) respectively (Fig. 1).

Fig. 1
figure 1

The setup of the bi-circular model

Full size image

Now, given a rectangular coordinate system having its origin at \({\underline{O}}\) and its three axes \(\left( {\hat{\xi }}, \hat{\eta },{\hat{\zeta }} \right) \) fixed in space so that the \({\hat{\zeta }}-\)axis is perpendicular to the plane of the masses. Then, the four bodies possess the coordinates \(\left( \xi _{1}, \eta _{1},0 \right) \), \(\left( \xi _{2}, \eta _{2},0 \right) \), \(\left( \xi _{3}, \eta _{3},0 \right) \) and \(\left( \xi , \eta ,\zeta \right) \) respectively. Then the equations of motion for \(m_{4}\) are given as

$$\begin{aligned} \left. {\begin{array}{l} \ddot{\xi }=-\sum \limits _{k=1}^3 \frac{Gm_{k}\left( \xi -\xi _{k} \right) }{r_{k}^{3}} \\ \ddot{\eta }=-\sum \limits _{k=1}^3 \frac{Gm_{k}\left( \eta -\eta _{k} \right) }{r_{k}^{3}} \\ \ddot{\zeta }=-\sum \limits _{k=1}^3 \frac{Gm_{k}\left( \zeta -\zeta _{k} \right) }{r_{k}^{3}} \\ \end{array}} \right\} \end{aligned}$$
(1)

where the dots denote the differentiation with respect to time. Let \(n_{1}\) and \(n_{2}\) be the angular velocities of the system \(m_{2}-m_{3}\) as it moves about \(O^{\prime }\), and as \(O^{\prime }\) moves about O. Then;

$$\begin{aligned} \left. {\begin{array}{ll} \xi _{1}=-D_{1}\cos {(n}_{1}{t)},&{}\quad \eta _{1}=-D_{1}\sin (n_{1}{t)} \\ \xi _{2}=D_{2}\cos {(n}_{1}{t)}-d_{1}\cos {(n}_{2}{t)},&{}\quad \eta _{2}=D_{2}\sin {(n}_{1}{t)}{-d_{1}\sin {(n}_{2}{t)}} \\ \xi _{3}=D_{2}\cos {(n}_{1}{t)}+d_{2}\cos {(n}_{2}{t)},&{}\quad \eta _{3}=D_{2}\sin (n_{1}t){+d_{2}\sin {(n}_{2}{t)}} \\ \end{array}} \right\} \end{aligned}$$
(2)

such that

$$\begin{aligned} D=D_{1}+D_{2}\text { and } d=d_{1}+d_{2} \end{aligned}$$
(3)

From Kepler’s law

$$\begin{aligned} n_{1}^{2}= & {} \frac{G\left( m_{1}+m_{2}+m_{3} \right) }{D^{3}} \end{aligned}$$
(4)
$$\begin{aligned} n_{2}^{2}= & {} \frac{G\left( m_{2}+m_{3} \right) }{d^{3}} \end{aligned}$$
(5)

Transforming \(\left( {\hat{\xi }}, {\hat{\eta }},{\hat{\zeta }} \right) \) to a new coordinate system \(\left( x, y,z \right) \) with its centre \({\underline{O}}\) such that the x-axis revolves with \(m_{2}\) and \(m_{3}\) and the z-axis is parallel to the \({\hat{\zeta }}\)-axis. Then we have

$$\begin{aligned} \left. {\begin{array}{l} {\hat{\xi }}=D_{2}\cos {{(n}_{1})t +x\cos {{(n}_{2})t}}-y\sin {(n_{2})t} \\ {{\hat{\eta }} =D}_{2}\sin ({n_{1})t+x\sin {(n_{2})t+y\cos {(n_{2})t}}} \\ {\hat{\zeta }}=z \\ \end{array}} \right\} \end{aligned}$$
(6)

The new coordinate system of \(m_{1} , m_{2}\) and \(m_{3}\) are respectively

$$\begin{aligned} \left. {\begin{array}{l} \left( x_{1},y_{1}, z_{1} \right) =\left( -D cos\left( n_{2}-n_{1} \right) t, D sin\left( n_{2}-n_{1} \right) t, 0 \right) \\ \left( x_{2},y_{2}, z_{2} \right) =\left( -d_{1}, 0, 0 \right) \\ \left( x_{3},{ y}_{3}, z_{3} \right) =\left( -d_{2}, 0, 0 \right) \\ \end{array}} \right\} \end{aligned}$$
(7)

Substituting equations in systems (2) and (6) into the system (1) and making use of (7) gives the system of equations below

$$\begin{aligned} \left. {\begin{array}{l} \ddot{x}-2n_{2}{\dot{y}}=n_{2}^{2}\left( x-\frac{D_{2}}{D}\frac{n_{1}^{2}}{n_{2}^{2}}x_{1} \right) -\sum \limits _{k=1}^3 \frac{Gm_{k}\left( x-x_{k} \right) }{r_{k}^{3}} \\ \ddot{y}+2n_{2}{\dot{x}}=n_{2}^{2}\left( y-\frac{D_{2}}{D}\frac{n_{1}^{2}}{n_{2}^{2}}y_{1} \right) -\sum \limits _{k=1}^3 \frac{Gm_{k}\left( y-y_{k} \right) }{r_{k}^{3}} \\ \ddot{z}=-\sum \limits _{k=1}^3 \frac{Gm_{k}\left( z-z_{k} \right) }{r_{k}^{3}} \\ \end{array}} \right\} \end{aligned}$$
(8)

with

$$\begin{aligned} r_{k}^{2}=\left( x-x_{k} \right) ^{2}+\left( y-y_{k} \right) ^{2}+\left( z-z_{k} \right) ^{2}, \quad k=1,2,3 \end{aligned}$$
(9)

The system (8) can be expressed as

$$\begin{aligned} \left. {\begin{array}{l} \ddot{x}-2n_{2}{\dot{y}}= W_{x} \\ \ddot{y}+2n_{2}{\dot{x}}= W_{y } \\ \ddot{z}= W_{z} \\ \end{array}} \right\} \end{aligned}$$
(10)

where

$$\begin{aligned} W=n_{2}^{2}\left[ \frac{1}{2}\left( x^{2}+y^{2} \right) -\frac{D_{2}}{D}\frac{n_{1}^{2}}{n_{2}^{2}}\left( x_{1}x+y_{1}y \right) \right] +\sum \limits _{k=1}^3 \frac{{Gm}_{k}}{r_{k}} \end{aligned}$$
(11)

But

$$\begin{aligned} x_{1}x+y_{1}y=rDcos\phi \end{aligned}$$
(12)

Since \(z_{1}=0\) and \(\phi \) is the angle subtended by \(m_{4}\) and \(m_{1}\) at O. Then on using (4), (5) and (12), (11) becomes

$$\begin{aligned} W=\frac{1}{2}\frac{G(m_{2}+m_{3})}{d^{3}}\left( x^{2}+y^{2} \right) - \frac{{Gm}_{1}r}{D^{2}}cos\phi -\frac{G(m_{2}+m_{3})r}{D^{2}}cos\phi +\sum \limits _{k=1}^3 \frac{{Gm}_{k}}{r_{k}} \end{aligned}$$
(13)

Noting that \(\frac{D_{2}}{D}\) is nearly unity since \(\frac{D_{1}}{D}\ll 1\) and \(D\gg r\) is essential for the real motion of \(m_{4}\). Hence using the first three terms of the expansion of the spherical harmonics below

$$\begin{aligned} \frac{1}{r_{1}}=\frac{1}{D}\sum \limits _{n=0}^\infty {\left( \frac{r}{D} \right) ^{n}P_{n}\left( cos\phi \right) } \end{aligned}$$
(14)

we obtain

$$\begin{aligned} \frac{1}{r_{1}}=\frac{1}{D}+\frac{r}{D^{2}}cos\phi +\frac{r^{2}}{2D^{3}}\left( 3{cos}^{2}\phi -1 \right) +\cdots \end{aligned}$$
(15)

Then (13) becomes

$$\begin{aligned} W= & {} \frac{1}{2}\frac{G(m_{2}+m_{3})}{d^{3}}\left( x^{2}+y^{2} \right) +\frac{Gm_{1}}{D}+\frac{{Gm}_{1}r^{2}}{2D^{3}}\left( 3{cos}^{2}\phi -1 \right) \nonumber \\&-\frac{G\left( m_{2}+m_{3} \right) r}{D^{2}}cos\phi + \sum \limits _{k=2}^3 \frac{{Gm}_{k}}{r_{k}} \end{aligned}$$
(16)

We non-dimensionalize by taking the sum of the masses \(m_{2}\) and \(m_{3}\) and the distance d as the units of mass and length, so that the mass parameter \(\mu =\frac{m_{3}}{m_{2}+m_{3}}\) with \(m_{2}=1-\mu \) and \(m_{3}=\mu \). Also taking the unit of time so that the gravitational constant \(G=1.\) More specifically, using the Sun–Earth–Moon system as a case study, \(\mu =\frac{m_{E}}{m_{E}+m_{M}}\) and \(\mu _{S}=\frac{m_{S}}{m_{E}+m_{M}}\) we have,

$$\begin{aligned} W=\frac{1}{2}\left( x^{2}+y^{2} \right) +\frac{\mu _{S}}{D}-\frac{r}{D^{2}}cos\phi +\frac{\mu _{S}r^{2}}{2D^{3}}\left( 3{cos}^{2}\phi -1 \right) +\frac{1-\mu }{r_{2}}+\frac{\mu }{r_{3}} \end{aligned}$$
(17)

Constraining the problem to the xyplane, we can write \(\phi ={\alpha -\alpha }_{0}\), where \(\alpha \) and \(\alpha _{0}\) are the respective angles which the positive x-axis makes with the vectors \({O^{\prime }m}_{4}\) and \(O^{\prime }m_{1}\). Recognizing \(\alpha _{0}\) as a constant in a scale of time for few hours, then (17) becomes

$$\begin{aligned} W= & {} \frac{1}{2}\left( 1+\mathrm {\Gamma } \right) \left( x^{2}+y^{2} \right) +\frac{\mu _{S}}{D}-\frac{xcos{(\alpha }_{0})+ysin(\alpha _{0})}{D^{2}}\nonumber \\&+\frac{3}{2}\mathrm {\Gamma }\left[ \left( x^{2}-y^{2} \right) \cos \left( 2\alpha _{0} \right) +2xysin\left( 2\alpha _{0} \right) \right] +\frac{1-\mu }{r_{2}}+\frac{\mu }{r_{3}} \end{aligned}$$
(18)

where \(\mathrm {\Gamma }=\frac{1}{2}\frac{\mu _{S}}{D^{3}}\) For a particle moving in a gas, the molecules exert a force as the particle collides with gas molecules. This dissipative force is described by stokes drag and it is given by [25]

$$\begin{aligned} \left[ {\begin{array}{l} F_{x}\\ F_{y}\\ \end{array} } \right] =-k_{s}\left[ {\begin{array}{l} \left( {\dot{x}}-y-\frac{3\sigma y}{2r^{7/2}}\right) \\ \left( x+{\dot{y}}+\frac{3\sigma x}{2r^{{7/2}}}\right) \\ \end{array} } \right] \end{aligned}$$
(19)

\(k_{s} \epsilon [0,1)\) is the constant of dissipation due to Stokes drag, \(r=\left( x^{2}+y^{2} \right) ^{1/2}\), \( \sigma \epsilon (0,1)\) is the rate of the gas velocity and the Keplerian velocity \(n_{2}=1\). More so, for a nongravitational force such as the Poynting–Robertson force which is due to the solar radiation incident on the particle, the drag force is given by [25] as

$$\begin{aligned} \left[ {\begin{array}{l} F_{x}\\ F_{y}\\ \end{array} } \right] =-\frac{k}{r_{1}^{2}}\left[ {\begin{array}{l} \left( {\dot{x}}-y+\frac{x}{r_{1}^{2}}(x{\dot{x}}+y{\dot{y}})\right) \\ \left( {\dot{y}}+x+\frac{y}{r_{1}^{2}}(x{\dot{x}}+y{\dot{y}})\right) \\ \end{array} } \right] \end{aligned}$$
(20)

The Eqs. (20) is a combination of two parts that describe the impact of the drag from solar photons and Doppler shift of solar radiation as shown in Eqs. (21) and (22) respectively.

$$\begin{aligned}&-\frac{k}{r_{1}^{2}}\left[ {\begin{array}{l} ({\dot{x}}-y)\\ ({\dot{y}}+x)\\ \end{array} } \right] \end{aligned}$$
(21)
$$\begin{aligned}&-\frac{k}{r_{1}^{2}}\left[ {\begin{array}{l} \frac{x}{r_{1}^{2}}(x{\dot{x}}+y{\dot{y}}) \\ \frac{y}{r_{1}^{2}}(x{\dot{x}}+y{\dot{y}}) \\ \end{array}} \right] \end{aligned}$$
(22)

Now to study the effect of dissipative forces on a test particle in the Sun–Earth–Moon, we substitute \(r_{1}=D\) into (20) and then combine Eqs. (19) and (20) in the system of equations (10) for which \(n_{2}=1\) and W is defined in Eq. (18). Thus, the governing equations of motion our model can be written as:

$$\begin{aligned} \left. {\begin{array}{l} \ddot{x}-2{\dot{y}}= W_{x}-K_{S}\left( {\dot{x}}-y-\frac{3\sigma y}{2r^{7/2}} \right) -\frac{K_{PR}}{D^{2}}({\dot{x}}-y+\frac{x}{D^{2}}(x{\dot{x}}+y{\dot{y}}))\\ \ddot{y}+2{\dot{x}}= W_{y }-K_{S}\left( x+{\dot{y}}+\frac{3\sigma x}{2r^{7/2}} \right) -\frac{K_{PR}}{D^{2}}({\dot{y}}+x+\frac{y}{D^{2}}(x{\dot{x}}+y{\dot{y}}))\\ \end{array}} \right\} \end{aligned}$$
(23)

where \(K_{S}\) and \(K_{PR}\) are the constant of dissipation due to Stokes drag and P–R drag respectively, \(r_{2}^{2}=\left( x+\mu \right) ^{2}+y^{2}\) and \(r_{3}^{2}=\left( x+\mu -1 \right) ^{2}+y^{2}\)

3 Investigation of the Libration Points

It is known that the acceleration and the velocity of the spacecraft at the libration points are zero, so that \(\ddot{x}=\ddot{y}={\dot{x}}={\dot{y}}=0\). Hence the libration points are solutions of equations

$$\begin{aligned}&\left( 1+\mathrm {\Gamma } \right) x-\frac{\left( 1-\mu \right) \left( x+\mu \right) }{r_{2}^{3}}-\frac{\mu \left( x+\mu -1 \right) }{r_{3}^{3}}-\frac{cos{(\alpha }_{0})}{D^{2}}\nonumber \\&\quad +3\mathrm {\Gamma }\left( x\cos {(2\alpha _{0})+y\sin {(2\alpha _{0})}} \right) +K_{S}\left( y+\frac{3\sigma y}{2r^{7/2}} \right) +\frac{{yK}_{PR}}{D^{2}} = 0 \end{aligned}$$
(24)
$$\begin{aligned}&\left( 1+\mathrm {\Gamma } \right) y-\frac{\left( 1-\mu \right) y}{r_{2}^{3}}-\frac{\mu y}{r_{3}^{3}}-\frac{\mathrm {sin}(\alpha _{0})}{D^{2}}\nonumber \\&\quad +3\mathrm {\Gamma }\left( x\sin {(2\alpha _{0})-y\cos {(2\alpha _{0}}}) \right) -K_{S}\left( x+\frac{3\sigma x}{2r^{7/2}} \right) -\frac{{xK}_{PR}}{D^{2}}=0 \end{aligned}$$
(25)

By observation, Eqs. (24) and (25) show that the positions of the primaries varies with \(\alpha _{0}\). Since the functions of \(\alpha _{0}\) are periodic, we will carry out the investigation of the Lagrange points on the scale \({0\le \alpha }_{0}\le \pi \). The libration points are computed by solving Eqs. (24) and (25) simultaneously by Newton–Raphson method with the aid of Mathematica 10.0. To compute the libration points for Sun–Earth–Moon-Spacecraft system from the Earth–Moon-focused view, we use the following values of the parameters \(\mu _{s}=328900.48, \ \mu =0.012151, \ D=389.1724\) The Stokes drag depends on the parameter \(\sigma \) which is the ratio of the gas to the Keplerian velocities, so \(\sigma =0.05, \, { k}_{S}={10}^{-5}\) and in the case of high drag coefficient we can have \(\sigma =0.12, \, { k}_{S}={10}^{-3}\). Beauge and Ferra-Mello [26] stated that in the case of formation of the solar system \(\sigma =0.995\) The results are shown in Tables 1, 2 and 3 and their positions are displayed in Figs. 2, 3, 4, 5, 6, 7 and 8 for three cases, namely; when the Stokes drag is dominant, when the P–R drag is dominant and when both Stokes drag and P–R drag are inaction together. As shown in Table 1, under the effect of Stokes drag, there exist six libration points \(L_{i}, i=\mathrm {1,2,3,4,5,6. }\) Out of these six libration points, \(L_{1,2}\) are collinear, \(L_{3,6}\) are nearly collinear and \(L_{4,5}\) are non-collinear. Unlike the case of restricted four-body problem with Stokes drag (for instance, the studies done by [16]) where there exist eight equilibrium points, in the case of the Bi-circular restricted four-body problem, there are six libration points. Recognizing \(\alpha _{0}\) as a constant in a scale of time for few hours, the positions of the libration points also vacillate periodically with respect to the value of \(\alpha _{0}\)

Table 2 shows the results of the libration points when the Stokes drag is neglected and the effect of the P–R drag is evaluated. In this case there exist only five libration points with \(\hbox {L}_{\mathrm {6}}\) not present. The sixth libration point \(\hbox {L}_{\mathrm {6}}\) is as a result of the Stokes drag. So under the combined effect of the Stokes drag and the P–R drag, there are six libration points as shown in Table 3 and Fig. 7. Moreover, when the effects of the drag forces are neglected, that is, \({ k}_{S}=0,{ k}_{PR}=0\), we found that the system possesses five libration points. Meanwhile, as shown in Fig. 8 below, there is a translation in the position of the libration points notable at \(\hbox {L}_{\mathrm {4,5}}\) as well as increase in the number of the libration points from five to six libration points under the combined effect of the Stokes drag and P–R drag but the sixth libration point is solely as a result of the Stokes drag.

Table 1 Libration points for the Sun–Earth–Moon-Spacecraft System under Stokes drag \({ k}_{S}={10}^{-3}, \sigma =0.12, \, {k}_{PR}=0\)
Full size table
Table 2 Libration points for the Sun–Earth–Moon-Spacecraft System under P–R drag \({ k}_{S}=0, \sigma =0, \, {k_{PR}=10}^{-3}\)
Full size table
Table 3 Libration points for the Sun–Earth–Moon-Spacecraft System under Stokes drag and P–R drag \({{ k}_{S}=10}^{-3}, \sigma =0.12, \, {{ k}_{PR}=10}^{-3}\)
Full size table
Fig. 2
figure 2

Libration points under Stokes drag only when \({k_{S}=10}^{-3}, \sigma =0.12,\varvec{\alpha }_{\mathbf {0}}{=\varvec{0}}\)

Full size image
Fig. 3
figure 3

Libration points under Stokes drag only when \({k_{S}=10}^{-3}, \sigma =0.12,\varvec{\alpha }_{\mathbf {0}}{=}\frac{\varvec{\pi }}{\mathbf {2}}\)

Full size image
Fig. 4
figure 4

Libration points under Stokes drag only when \({k_{S}=10}^{-3}, \sigma =0.12,\varvec{\alpha }_{\mathbf {0}}{=\varvec{\pi } }\)

Full size image
Fig. 5
figure 5

Libration points under P–R drag only when \({k_{PR}=10}^{-3}, \varvec{\alpha }_{\mathbf {0}}{=\mathbf {0}}\)

Full size image
Fig. 6
figure 6

Libration points under P–R drag only when \({{ k}_{PR}=10}^{-3}\varvec{\alpha }_{\mathbf {0}}{=}\frac{\varvec{\pi }}{\mathbf {2}}\)

Full size image
Fig. 7
figure 7

Libration points under Stokes drag and P–R when \({k_{S}=10}^{-3}, \sigma =0.12, {k_{PR}=10}^{-3}{\varvec{\alpha }}_{\mathbf {0}}=\mathbf {0}\)

Full size image
Fig. 8
figure 8

Comparative location of the Libration Points when there is no drag effect and when Stokes drag and P–R drag when \({k_{S}=10}^{-3}, \sigma =0.12, {k_{PR}=10}^{-3}{\mathbf { \alpha }}_{\mathbf {0}}{=\varvec{0}}\)

Full size image

4 Linear Stability of the Lagrange Points

We investigate the linear stability of the motion when a small displacements \(\tau \) and \(\gamma \) are given to the coordinates of the Lagrange point (\(\hbox {x}_{\mathrm {0}}\), \(\hbox {y}_{\mathrm {0}})\) such that

$$\begin{aligned} \tau =x-x_{0}, \, \gamma =y-y_{0} \end{aligned}$$
(26)

Then the variational form of the equations of motion is derived as

$$\begin{aligned} \left. {\begin{array}{l} \ddot{\tau }-2{\dot{\gamma }}=\tau \left( \frac{\partial ^{2}U}{\partial x^{2}} \right) _{0}+{\gamma \left( \frac{\partial ^{2}U}{\partial x\partial y} \right) }_{0}+\left( \frac{\partial ^{2}U}{\partial x\partial {\dot{x}}} \right) _{0}{\dot{\tau }}+\left( \frac{\partial ^{2}U}{\partial x\partial {\dot{y}}} \right) _{0}{\dot{\gamma }} \\ \ddot{\gamma }+2{\dot{\tau }}=\tau \left( \frac{\partial ^{2}U}{\partial y\partial x} \right) _{0}+\gamma \left( \frac{\partial ^{2}W}{\partial y^{2}} \right) _{0}+\left( \frac{\partial ^{2}U}{\partial y\partial {\dot{x}}} \right) _{0}{\dot{\tau }}+\left( \frac{\partial ^{2}U}{\partial y\partial {\dot{y}}} \right) _{0}{\dot{\gamma }} \\ \end{array}} \right\} \end{aligned}$$
(27)

where \(U_{x}=\frac{\partial U}{\partial x}\) and \(U_{y}=\frac{\partial U}{\partial y}\) denote the expression on the right hand side of Eq. (23) respectively. The subscripts 0 implies that the second partial derivatives are evaluated at the equilibrium point (\(\mathrm{x}_0, \mathrm{y}_0\)) and the dots are the derivatives with respect to time t and only the linear terms in \(\tau \) and \(\gamma \) have been considered. We assume

$$\begin{aligned} \tau ={Pe}^{\lambda t}, \qquad \gamma =\mathrm {Q}e^{\lambda t} \end{aligned}$$
(28)

where \(P,\mathrm {Q}\) are constants and \(\lambda \) is a parameter.

Now if Eq. (28) are the solutions of Eq. (27) then

$$\begin{aligned}&\left. {\begin{array}{l} \left( \lambda ^{2}+\lambda U_{x{\dot{x}}}^{0}-U_{xx}^{0} \right) P-\left( 2\lambda +U_{xy}^{0} \right) \mathrm {Q}=0 \\ \left( 2\lambda -U_{yx}^{0} \right) P+\left( \lambda ^{2}+{\lambda U}_{y{\dot{y}}}^{0}-U_{yy}^{0} \right) \mathrm {Q}=0 \\ \end{array}} \right\} \nonumber \\&\quad \left| \begin{array}{ll} {\left( \lambda ^{2}-U_{xx}^{0}-\lambda U_{x{\dot{x}}}^{0} \right) } &{} {-\left( 2\lambda +U_{xy}^{0}+\lambda U_{x{\dot{y}}}^{0} \right) }\\ {\left( 2\lambda -U_{yx}^{0}-\lambda U_{y{\dot{x}}}^{0} \right) } &{} {\left( \lambda ^{2}-U_{yy}^{0}-{\lambda U}_{y{\dot{y}}}^{0} \right) }\\ \end{array}\right| = 0 \end{aligned}$$
(29)

Then the characteristic polynomial of the system (27) is given as

$$\begin{aligned} \lambda ^{4}+R\lambda ^{3}+S\lambda ^{2}+T\lambda +M=0 \end{aligned}$$
(30)

Where

$$\begin{aligned} R= & {} -(U_{x{\dot{x}}}^{0}+U_{y{\dot{y}}}^{0})\nonumber \\ S= & {} 4+U_{x{\dot{x}}}^{0}U_{y{\dot{y}}}^{0}-U_{xx}^{0}-U_{yy}^{0}+2U_{x{\dot{y}}}^{0}-2U_{y{\dot{x}}}^{0}-U_{x{\dot{y}}}^{0}U_{y{\dot{x}}}^{0}\nonumber \\ T= & {} U_{xx}^{0}U_{y{\dot{y}}}^{0}+U_{x{\dot{x}}}^{0}U_{yy}^{0}+2U_{xy}^{0}-2U_{yx}^{0}-U_{xy}^{0}U_{y{\dot{x}}}^{0}-U_{yx}^{0}U_{x{\dot{y}}}^{0}\nonumber \\ M= & {} U_{xx}^{0}U_{yy}^{0}-U_{xy}^{0}U_{yx}^{0} \frac{\partial ^{2}U}{\partial x^{2}}=1+\frac{\mu _{s}}{2D^{3}}+\frac{3\mu \left( x+\mu -1 \right) ^{2}}{r_{3}^{5}}-\frac{\mu }{r_{3}^{3}}\nonumber \\&+\frac{3\left( 1-\mu \right) \left( x+\mu \right) ^{2}}{r_{2}^{5}}-\frac{\left( 1-\mu \right) }{r_{2}^{3}}+\frac{3\mu _{s}\cos {2\alpha _{0}}}{2D^{3}}-\frac{21\sigma K_{s}xy}{4r^{11/2}}- \frac{K_{PR}}{D^{4}}(2x{\dot{x}}+y{\dot{y}}) \end{aligned}$$
(31)
$$\begin{aligned} \frac{\partial ^{2}U}{\partial y^{2}}= & {} 1+\frac{\mu _{s}}{2D^{3}}+\frac{3\mu y^{2}}{r_{3}^{5}}-\frac{\mu }{r_{3}^{3}}+\frac{3\left( 1-\mu \right) y^{2}}{r_{2}^{5}}\nonumber \\&-\frac{\left( 1-\mu \right) }{r_{2}^{3}}-\frac{3\mu _{s}\cos {2\alpha _{0}}}{{2D}^{3}}+\frac{21K_{s}\sigma xy}{4r^{11/ 2}}- \frac{K_{PR}}{D^{4}}(x{\dot{x}}+2y{\dot{y}}) \end{aligned}$$
(32)
$$\begin{aligned} \frac{\partial ^{2}U}{\partial x\partial y}= & {} \frac{3\mu \left( x+\mu -1 \right) y}{r_{3}^{5}}+\frac{3(1-\mu )\left( x+\mu \right) y}{r_{2}^{5}}\nonumber \\&\quad +\frac{3\mu _{s}\sin {2\alpha _{0}}}{2D^{3}}-K_{s}\left( -1-\frac{3\sigma }{2r^{7/ 2}}+\frac{21\sigma y^{2}}{4r^{11/ 2}} \right) - \frac{K_{PR}}{D^{2}}(\frac{x{\dot{y}}}{D^{2}}-1) \end{aligned}$$
(33)
$$\begin{aligned} \frac{\partial ^{2}U}{\partial y\partial x}= & {} \frac{3\mu \left( x+\mu -1 \right) y}{r_{3}^{5}}+\frac{3(1-\mu )\left( x+\mu \right) y}{r_{2}^{5}}\nonumber \\&+\frac{3\mu _{s}\sin {2\alpha _{0}}}{{2D}^{3}} -K_{s}\left( 1+\frac{3\sigma }{2r^{7/2}}-\frac{21\sigma x^{2}}{4r^{11/ 2}} \right) - \frac{K_{PR}}{D^{2}}(\frac{y{\dot{x}}}{D^{2}}+1) \end{aligned}$$
(34)
$$\begin{aligned} U_{x{\dot{x}}}= & {} {-K}_{s}- \frac{K_{PR}}{D^{2}}\left( 1+\frac{x^{2}}{D^{2}}\right) \end{aligned}$$
(35)
$$\begin{aligned} U_{y{\dot{y}}}= & {} -K_{s}- \frac{K_{PR}}{D^{2}}\left( 1+\frac{y^{2}}{D^{2}}\right) \end{aligned}$$
(36)
$$\begin{aligned} U_{x{\dot{y}}}= & {} - \frac{K_{PR}xy}{D^{2}}=U_{y{\dot{x}}} \end{aligned}$$
(37)
Table 4 Linear stability of the Sun–Earth–Moon-Spacecraft Libration points under Stokes drag and P–R drag
Full size table

A Libration point is said to be stable if the characteristic equation (30) has all of its four eigen-roots with negative real parts or are purely imaginary and in geometrical sense that they all lie in the negative half-plane. But as displayed in Table 4, four of the Libration points have at least two characteristic roots with positive real parts. Hence, the motion of the spacecraft is linearly unstable around all these Lagrange points but the motion is stable around \(\hbox {L}_{\mathrm {4,5}}\) Furthermore, the libration points are gotten from the equations of motion is considered at time \(t_{0}=0\), that implies that at time \(t_{1}\ne t_{0}\) there will be a change in the position of the libration points and the test particle will move from position A to position B which brings the possibility of the libration point to potentially “lose hold” of the test particle, depending on the factors such as the strength of the attraction and the speed of the libration point. In that case, the libration point may always be instantaneously stable but effectively unstable. On this regards we infer that the motion around \(\hbox {L}_{\mathrm {4,5}}\) is instantaneously stable and the remaining libration points are effectively unstable.

5 Dynamical Behaviour of the Model

For every dynamical system it is of great interest to establish the regularity or chaoticity of the system. A measure of the system’s sensitivity to change in initial conditions defines its nature. If a dynamical system is very sensitive to change in initial conditions, then it is chaotic and predictability of its future behavior becomes impossible. In particular, if the neighboring orbits separate exponentially fast, then the system possesses irregularity and this irregularity or chaos can be quantified with the aid of Lyapunov characteristic exponents. Given some initial condition \(x_{0}\), consider a nearby point \(x_{0}+\delta _{0}\), where the initial separation \(\delta _{0}\) is very small.

Let \(\delta _{n}\) be the separation after n iterates. if

$$\begin{aligned} \left| \delta _{n} \right| \approx \left| \delta _{0} \right| e^{n\lambda } \end{aligned}$$
(38)

Then \(\lambda \) is called Lyapunov exponent.

Fig. 9
figure 9

Divergence of trajectories for the Sun–Earth–Moon-Spacecraft system underStokes drag and P–R drag after 50 iterations

Full size image
Fig. 10
figure 10

Divergence of trajectories for the Sun–Earth–Moon-Spacecraft system under Stokes drag and P–R drag after 100 iterations

Full size image

A positive Lyapunov exponent is a signature of chaos (see [27]). The first order LCEs is Computed with the help of Mathematica package developed by [28]. For 50 iterations, we found the LCEs as [1.01862, 1.01818, − 0.0193187, − 0.0194755]. While for 100 iterations, the LCEs are [1.0091, 1.00913, − 0.0101028, − 0.0101311]. In each case, two of the LCEs are seen to be positive. Moreover, the Figs. 9 and 10 above show the rate of divergence of the trajectories for the Sun–Earth–Moon-Spacecraft system. They were plotted by first reducing the equations of motion to a first order system and then we used the Mathematica package [28] to generate the divergent. By the rate of divergence shown by the graphs 9 and 10, and the numerical value of the LCEs, we conclude that the orbit of the system is chaotic.

6 Conclusion

A Bi-circular Restricted Four-Body Problem (BCR4BP) was formulated to model the effect of dissipative forces, namely, Stokes drag and P–R drag from the Earth–Moon-focused view in the Sun–Earth–Moon-Spacecraft System. The Earth–Moon-focused view is assumed because in Eq. (24) we substituted D for \(r_{1}\) in the drag equation. More so, \(D=D_{1}+D_{2}\), which implies the approximation of the solar radiation on the test particle as the solar radiation experienced by a test particle near the Earth and moon. This model is nearly coherent in that the orbits of all the primaries were approximated circular. More so, it is a fair model and more realistic than the conventional Restricted Four-Body Problem (R4BP) which has shortcomings in the assumptions of triangular and collinear configurations, two primaries having equal masses (see [29]). We found that the dissipative forces influence the number and location of positions of the Lagrange points. For instance, in the case where only Stokes drag was considered, there exist six equilibrium points where as in the case of only P–R drag, there were five equilibrium points. Furthermore, by observing the y-coordinate of the Lagrange points in Tables 1 and 2, we discovered that P–R drag has greater dissipative influence than the Stokes drag. The linear stability analysis around the Lagrange points under the combined effect of both forces revealed the motion of the spacecraft to be unstable around all the Lagrange points except at \(\hbox {L}_{\mathrm {4,5}}\). Investigating the dynamical behavior of the system showed the exponential divergence in the trajectories of the system and thus we establish the chaotic nature of the system. This model has wide applications to other planetary system other than the Sun–Earth–Moon system because it can incorporate systems that are non-coplanar.