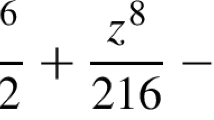Matrix Elements of One Dimensional Explicitly Correlated Gaussian Basis Functions

Abstract

Kinetic, potential and overlap matrix elements of one dimensional correlated Gaussians multiplied by polynomial factors are presented. These matrix elements can be used to calculate energies of one dimensional cold atom systems, or to construct a tensorial product to calculate energies in 2 or 3 dimensional systems with a nonspherical potential.

1 Introduction

The experimental realization of one-dimensional (1D) cold atomic systems [1,2,3,4,5,6,7] has sparked an intense theoretical interest in 1D few particle systems [8,9,10,11,12,13,14]. High accuracy calculations of energies and wave functions of few-body systems have been continuously developed [15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32] for three dimensional system and many of these approaches can be used in 1D as well.

Two- and three-electron atomic systems can be very accurately calculated using Hylleraas-type functions [33, 34], but the extension of the Hylleraas basis approach beyond three electrons is very tedious due to the difficulty of the analytical calculation of their matrix elements [35]. Explicitly Correlated Gaussian (ECG) basis functions have no such restrictions, and have become very popular tools in high accuracy calculations [36,37,38,39,40,41,42,43,44,45,46,47,48,49, 49, 50, 50,51,52,53,54,55,56]. There are several recent reviews illustrating the wide range of applications of ECGs [30, 57, 58].

ECGs as basis functions were first employed in 1960 by Boys [15] and Singer [16]. The simple quadratic form involving inter-particle distances in ECGs permits the reduction of the matrix elements to simple analytic expressions, and the algebraic complexity does not change with the number of particles. These matrix elements depend on the parameters of the ECGs, which should be carefully optimized [41, 59, 60] to get highly accurate variational upper bounds.

In this paper we present detailed derivations of matrix elements of one-dimensional generalized ECGs: ECGs multiplied with a polynomial prefactor formed by the powers of the coordinates of the particles. The polynomial prefactor not only helps the accuracy, but allows for the treatment of spin-orbit interaction or calculation of matrix elements of the dipole operator of a laser field. While the matrix elements presented in this work are in 1D, they can be simply generalized to 2D or 3D by using their tensor products. These tensor products can be used in calculations of systems in nonspherical potentials (e.g. electric or magnetic fields) and can also be used to derive general 3D ECG basis functions with arbitrary angular momentum after suitable angular momentum coupling. In our earlier work [61], we have derived matrix elements of ECGs in 3D for arbitrary angular momentum; the present work extends this to nonspherical potentials and gives a general form for 1D systems.

The outline of the paper is as follows: After the introduction we will introduce our notation and formalism, and will give calculations for different operators, such as overlap, kinetic energy, one-particle and two-particle potentials in later sections.

2 Formalism

We consider a system of N particles in 1D space, with positions in a lab-frame Cartesian coordinate system given by $x_i, i=1,{\ldots } ,N$. To simplify the notation we introduce

$$\begin{aligned} \mathbf {x}=(x_1,{\ldots },x_N). \end{aligned}$$

(1)

The ECG basis functions are defined as

$$\begin{aligned} \varPhi _\mathbf {m}^A(\mathbf {x}) = \left[ \prod _{k=1}^N x_k^{m_k} \right] \exp \left( -\frac{1}{2} {\mathbf {x}}^TA\mathbf {x}\right) , \end{aligned}$$

(2)

where the quadratic form in the exponent is defined as

$$\begin{aligned} {\mathbf {x}}^TA\mathbf {x}{:=} \sum _{i,j=1}^{N} A_{ij}{x}_i\cdot {x}_j . \end{aligned}$$

(3)

Recall that $\mathbf {x}\in \mathbb {R}^N$ is a vector in the configuration space of N particles, each moving in one dimension, $A \in \mathbb {R}^{N \times N}$ is a matrix of variational parameters, and $\mathbf {m}\in \mathbb {Z}_{\ge 0}^N$ is a vector of polynomial exponents. To ensure that these functions are normalizable, we require that A be positive-definite. Without loss of generality we can take A to be symmetric.

We will consider a Hamiltonian in the lab frame defined as

$$\begin{aligned} \begin{aligned} H =~&T+U_{\text {One-Body}}+V_{\text {Two-Body}}\\ =&\sum _{i=1}^{N}{\frac{{p}_{i}^2}{2m_{i}}} + \sum _{i=1}^{N} U(x_i) + \sum _{i<j}^{N} V(x_i-x_j), \end{aligned} \end{aligned}$$

where $p_{k}=-i\hbar {d / d_{x_k}}$ is the momentum operator for the ith particle.

3 Overlap Matrix Elements

In this section we compute the matrix elements of the one-dimensional ECG basis functions.

To evaluate these matrix elements, we introduce the generating function

$$\begin{aligned} G^A_\mathbf {t}(\mathbf {x}) = \exp (-\frac{1}{2}{\mathbf {x}}^TA\mathbf {x}+ {\mathbf {t}}^T\mathbf {x}) \end{aligned}$$

(4)

where $\mathbf {t}\in \mathbb {R}^N$ is a vector of parameters. Observe that the basis functions $\varPhi _\mathbf {m}^A(\mathbf {x})$ can be expressed as derivatives of $G^A_\mathbf {t}(\mathbf {x})$:

(5)

Thus, our strategy will be to first evaluate the matrix elements $\left\langle {G^A_\mathbf {t}}{\hat{\mathcal {O}}}{G^{A'}_{\mathbf {t}'}}\right\rangle$ of the generating functions, and then take derivatives with respect to the parameters $t_k$ to obtain the matrix elements $\left\langle {\varPhi _\mathbf {m}^A}{\hat{\mathcal {O}}}{\varPhi _{\mathbf {m}'}^{A'}}\right\rangle$ of the ECG basis functions.

We first calculate the overlap matrix element. The overlap of two generating functions is simply a multidimensional Gaussian integral:

(6)

Here we have defined $B = A + A'$. (Note that the invertibility of B is guaranteed by A and $A'$ being positive-definite.) This can be written in a more concise form by introducing the 2N-dimensional vector

(7)

and the $2N \times 2N$ block matrix

(8)

(Henceforth we will use underlined symbols to denote 2N-dimensional vectors or matrices obtained in this fashion, by concatenating the N variables in the bra and the N variables in the ket.) By using these notations, we have

(9)

The overlap of the basis functions then can be calculated from

(10)

To evaluate these derivatives, we begin by Taylor-expanding the exponential function in equation (9). This allows us to write

(11)

Now, we expand out the product $\prod _{i,j = 1}^{2N}$ and push all the summation operators to the front, obtaining

(12)

In the preceding equation there are a total of $(2N)^2$ summation operators, one for each variable $k_{ij}$, $i,j = 1, \dots , 2N$. Equivalently, if we let $\mathbb {Z}_{\ge 0}^{2N \times 2N}$ denote the set of $2N \times 2N$ matrices with nonnegative integer entries, we can write this as

(13)

Thus we have:

(14)

This can be evaluated by observing that

$$\begin{aligned} \prod _{i,j=1}^{2N} (\underline{t}_i \underline{t}_j)^{k_{ij}} = \prod _{p=1}^{2N} \underline{t}_p^{\sum _{q=1}^{2N}\left( k_{qp} + k_{pq}\right) } = \prod _{p=1}^{2N} \underline{t}_p^{u_p} \end{aligned}$$

(15)

where we have defined the abbreviation $u_p = \sum _{q=1}^{2N}\left( k_{qp} + k_{pq}\right)$. It follows that

(16)

Now consider what happens when we set $\underline{\mathbf {t}}= \mathbf {0}$. The expression (16) is nonzero only when $u_p = \underline{m}_p$ for all $p = 1, \dots , 2N$, since in this case $\underline{t}_p^{u_p - m_p} = 0^0 = 1$. This means that the infinite sum (14) reduces to a finite sum, since the only terms that contribute are those in which the numbers $\{k_{ij}\}_{i,j=1}^{2N}$ are arranged in such a way that

$$\begin{aligned} \sum _{q=1}^{2N} \left( k_{qp} + k_{pq}\right) = \underline{m}_p \qquad \text {for all } p = 1, \dots , 2N. \end{aligned}$$

(17)

This leads us naturally to the following combinatorial problem:

Definition

Given a vector $\mathbf {m}\in \mathbb {Z}_{\ge 0}^n$ of n nonnegative integers, let $\varOmega (\mathbf {m})$ be the set of $n \times n$ matrices $k \in \mathbb {Z}_{\ge 0}^{n \times n}$ having nonnegative integer entries such that $\sum _{q=1}^{2N} \left( k_{qp} + k_{pq}\right) = m_p$ for all $p = 1, \dots , 2N$.

We will return to this combinatorial problem later in “Appendix A”. For now, let us assume that we know how to compute $\varOmega (\underline{\mathbf {m}})$, and use this to simplify the infinite sum (13). We obtain the formula

(18)

completing the derivation of the overlap matrix element.

4 Kinetic Energy Matrix Elements

The kinetic energy matrix elements can be evaluated using the generating function:

$$\begin{aligned} \langle G^A_t \vert T \vert G^{A'}_{t'}\rangle = {-\sum _{i=1}^N} {\hbar ^2\over 2m} \langle G^A_{{ t}}\vert \frac{\partial ^2}{\partial x_i^2}\vert G^{A'}_{{ t}'} \rangle . \end{aligned}$$

(19)

This can be calculated in two equivalent ways, either taking the second derivative on one side or taking first derivative on both sides.

The first, direct evaluation, gives:

$$\begin{aligned} \frac{\partial ^2 G_t^A}{\partial x_i ^2} = (t_i^2 + (Ax)_i^2 - 2t_i(Ax)_i - A_{ii})G_t^A, \end{aligned}$$

(20)

and

$$\begin{aligned} \langle G_t^A \vert T \vert G_{t'}^{A'} \rangle = -\frac{\hbar ^2}{2m} \langle G_t^A \vert t'^T t' + x^T A'^2 x - 2 t'^T A' x - \hbox {Tr}(A')) \vert G_{t'}^{A'} \rangle \end{aligned}$$

(21)

This can be calculated using the integral given in “Appendix B”, and the final result is:

$$\begin{aligned} -\frac{\hbar ^2}{2m} \langle G_t^A \vert G_{t'}^{A'} \rangle (\mathbf t '^T\mathbf t ' - \hbox {Tr}(A') - 2 \mathbf t '^T A' B^{-1} (\mathbf t + \mathbf t ') + \hbox {Tr}(A'^2 B^{-1}) + (\mathbf t +\mathbf t ')^T B^{-1} A'^2 B^{-1}(\mathbf t + \mathbf t ')). \end{aligned}$$

(22)

Using the second approach, by integration by parts (neglecting the boundary term as $G \rightarrow 0$ as $\mathbf x \rightarrow \infty$), we have

(23)

Using

(24)

we have

$$\begin{aligned} \langle G^A_t \vert T \vert G^{A'}_{t'}\rangle= & {} \frac{\hbar ^2}{2m} \langle {G_t^A} \vert (\mathbf t - A \mathbf x ) \cdot (\mathbf t ' - A' \mathbf x ) \vert G_{t'}^{A'} \rangle \nonumber \\= & {} \frac{\hbar ^2}{2m} \langle {G_t^A} \vert \mathbf t \cdot \mathbf t ' + \mathbf x ^T A A' \mathbf x - (\mathbf t ^T A ' + \mathbf t '^T A)x \vert G^{A'}_{t'}\rangle . \end{aligned}$$

(25)

For the the quadratic term we can use the integral presented in “Appendix B”, for the linear terms we note

(26)

Then, similarly to above, Eq. (25) evaluates to:

$$\begin{aligned}&\frac{\hbar ^2}{2m} \langle G_t^A \vert G_{t'}^{A'} \rangle [\mathbf t \cdot \mathbf t ' \nonumber \\&\quad + \hbox {Tr}(AA'B^{-1}) + (\mathbf t +\mathbf t ')^T B^{-1} A A' B^{-1} (\mathbf t + \mathbf t ') \nonumber \\&\quad - (\mathbf{t}^T A' + \mathbf{t}'^T A) B^{-1} (\mathbf{t} + \mathbf{t'})]. \end{aligned}$$

(27)

Both Eqs. (27) and (22) are valid derivations for the kinetic energy for the generator functions. We have included both because they can be useful in calculations, for example for checking computer codes.

Now, to find the matrix elements of the basis, we apply derivatives to the matrix elements of the generating function:

$$\begin{aligned} \langle \varPhi _{m}^A\vert T \vert \varPhi _{m'}^{A'} \rangle = \left. \prod _{k=1}^{2N} {\partial ^{{\underline{m}}_k}\over \partial {\underline{t}}_k^{{\underline{m}}_k}} \langle G^A_{{ t}}\vert T \vert G^{A'}_{{ t}'} \rangle \right| _{{ t}=0,{ t}'=0}, \end{aligned}$$

(28)

We will use the expression in (27) to find the kinetic matrix elements because it gives a manifestly symmetric result. Expanding Eq. (27) in terms of sums and derivatives:

$$\begin{aligned}&\frac{\hbar ^2}{2m} \langle G_t^A \vert G_{t'}^{A'} \rangle \left( \sum _{i=1}^N (AA'B^{-1})_{ii} + \sum _{i=1}^N t_it'_i -\sum _{i,j=1}^{2N} C_{ij}\underline{t}_i\underline{t}_j + \sum _{i,j=1}^{2N} D_{ij}\underline{t}_i\underline{t}_j\right) \nonumber \\&\quad =\frac{\hbar ^2}{2m}\sqrt{\frac{(2\pi )^N}{\det B}}\Bigg (\sum _{i=1}^N (AA'B^{-1})_{ii} +\sum _{j=1}^{N} {\partial \over \partial {\underline{B}}_{j,j+N}} \nonumber \\&\qquad - \sum _{i,j=1}^{2N} C_{ij} {\partial \over \partial {\underline{B}}_{ij}} + \sum _{i,j=1}^{2N} D_{ij} {\partial \over \partial {\underline{B}}_{ij}}\Bigg )\mathrm{exp}\left\{ {1\over 2} \sum _{i,j=1}^{2N} \underline{B}_{ij} \underline{t}_i \underline{t}_j \right\} \end{aligned}$$

(29)

Where

$$\begin{aligned} C= \left( \begin{array}{cc} A'B^{-1} &{} A'B^{-1} \\ AB^{-1} &{} AB^{-1} \\ \end{array} \right) ,\quad D = \left( \begin{array}{cc} B^{-1}AA'B^{-1} &{} B^{-1}AA'B^{-1} \\ B^{-1}AA'B^{-1} &{} B^{-1}AA'B^{-1} \\ \end{array} \right) \end{aligned}$$

(30)

Pulling the sum out of the exponent and Taylor expanding, (29) takes on the form:

$$\begin{aligned}&={\hbar ^2\over 2m} \sqrt{\frac{(2\pi )^N}{\det B}} \Bigg (\sum _{i=1}^N (AA'B^{-1})_{ii} +\sum _{j=1}^{N} {\partial \over \partial {\underline{B}}_{j,j+N}} \nonumber \\&\quad - \sum _{i,j=1}^{2N} C_{ij} {\partial \over \partial {\underline{B}}_{ij}} + \sum _{i,j=1}^{2N} D_{ij} {\partial \over \partial {\underline{B}}_{ij}}\Bigg ) \prod _{i,j = 1}^{2N} \sum _{k_{ij} = 0}^{\infty } \frac{1}{k_{ij}!} \left( \frac{1}{2} \underline{B}_{ij} \underline{t}_i \underline{t}_j\right) ^{k_{ij}}. \end{aligned}$$

(31)

Expanding the product and pushing all the summations to the front,

$$\begin{aligned}&= {\hbar ^2\over 2m} \sqrt{\frac{(2\pi )^N}{\det B}} \Bigg (\sum _{i=1}^N (AA'B^{-1})_{ii} +\sum _{j=1}^{N} {\partial \over \partial {\underline{B}}_{j,j+N}} \nonumber \\&\quad - \sum _{i,j=1}^{2N} C_{ij} {\partial \over \partial {\underline{B}}_{ij}} + \sum _{i,j=1}^{2N} D_{ij} {\partial \over \partial {\underline{B}}_{ij}}\Bigg ) \sum _{k_{11} = 0}^{\infty } \sum _{k_{12} = 0}^{\infty } \cdots \sum _{k_{2N,2N} = 0}^{\infty } \prod _{i,j=1}^{2N} \frac{1}{k_{ij}!} \left( \frac{1}{2} \underline{B}_{ij} \underline{t}_i \underline{t}_j\right) ^{k_{ij}}. \end{aligned}$$

(32)

This can be written, using the shorthand notation from the overlap evaluation as

$$\begin{aligned}&= {\hbar ^2\over 2m} \sqrt{\frac{(2\pi )^N}{\det B}} \Bigg (\sum _{i=1}^N (AA'B^{-1})_{ii} +\sum _{j=1}^{N} {\partial \over \partial {\underline{B}}_{j,j+N}} \nonumber \\&\quad - \sum _{i,j=1}^{2N} C_{ij} {\partial \over \partial {\underline{B}}_{ij}} + \sum _{i,j=1}^{2N} D_{ij} {\partial \over \partial {\underline{B}}_{ij}}\Bigg ) \sum _{k \in \mathbb {Z}_{\ge 0}^{2N \times 2N}} \prod _{i,j=1}^{2N} \frac{1}{k_{ij}!} \left( \frac{1}{2} \underline{B}_{ij} \underline{t}_i \underline{t}_j\right) ^{k_{ij}}. \end{aligned}$$

(33)

To find the matrix elements of the basis, we apply derivatives to matrix elements of the generating function

(34)

which, similar to the overlap case, becomes:

$$\begin{aligned}&={\hbar ^2\over 2m} \sqrt{\frac{(2\pi )^N}{\det B}} \Bigg (\sum _{i=1}^N (AA'B^{-1})_{ii} +\sum _{j=1}^{N} {\partial \over \partial {\underline{B}}_{j,j+N}} \nonumber \\&\quad - \sum _{i,j=1}^{2N} C_{ij} {\partial \over \partial {\underline{B}}_{ij}} + \sum _{i,j=1}^{2N} D_{ij} {\partial \over \partial {\underline{B}}_{ij}}\Bigg ) \left( \prod _{p=1}^{2N} \underline{m}_p!\right) \sum _{k \in \varOmega (\underline{\mathbf {m}})} \prod _{i,j=1}^{2N} \frac{1}{k_{ij}!} \left( \frac{1}{2} \underline{B}_{ij}\right) ^{k_{ij}}. \end{aligned}$$

(35)

After distributing the terms, we have

$$\begin{aligned}&={\hbar ^2\over 2m} \sqrt{\frac{(2\pi )^N}{\det B}} \left( \sum _{i=1}^N \hbox {Tr}(AA'B^{-1})\left[ \left( \prod _{p=1}^{2N} \underline{m}_p!\right) \sum _{k \in \varOmega (\underline{\mathbf {m}})} \prod _{i,j=1}^{2N} \frac{1}{k_{ij}!} \left( \frac{1}{2} \underline{B}_{ij}\right) ^{k_{ij}}\right] \right. \nonumber \\&\qquad +\sum _{j=1}^{N} {\partial \over \partial {\underline{B}}_{j,j+N}}\left[ \left( \prod _{p=1}^{2N} \underline{m}_p!\right) \sum _{k \in \varOmega (\underline{\mathbf {m}})} \prod _{i,j=1}^{2N} \frac{1}{k_{ij}!} \left( \frac{1}{2} \underline{B}_{ij}\right) ^{k_{ij}}\right] \nonumber \\&\qquad - \sum _{i,j=1}^{2N} C_{ij} {\partial \over \partial {\underline{B}}_{ij}}\left[ \left( \prod _{p=1}^{2N} \underline{m}_p!\right) \sum _{k \in \varOmega (\underline{\mathbf {m}})} \prod _{i,j=1}^{2N} \frac{1}{k_{ij}!} \left( \frac{1}{2} \underline{B}_{ij}\right) ^{k_{ij}}\right] \nonumber \\&\qquad \left. + \sum _{i,j=1}^{2N} D_{ij} {\partial \over \partial {\underline{B}}_{ij}}\left[ \left( \prod _{p=1}^{2N} \underline{m}_p!\right) \sum _{k \in \varOmega (\underline{\mathbf {m}})} \prod _{i,j=1}^{2N} \frac{1}{k_{ij}!} \left( \frac{1}{2} \underline{B}_{ij}\right) ^{k_{ij}}\right] \right) \end{aligned}$$

(36)

Finally, differentiating, we arrive at our final result:

$$\begin{aligned}&\langle \varPhi _{m}^A\vert T \vert \varPhi _{m'}^{A'} \rangle = {\hbar ^2\over 2m} \sqrt{\frac{(2\pi )^N}{\det B}} \left( \hbox {Tr}(AA'B^{-1})\left( \prod _{p=1}^{2N} \underline{m}_p!\right) \sum _{k \in \varOmega (\underline{\mathbf {m}})} \prod _{i,j=1}^{2N} \frac{1}{k_{ij}!} \left( \frac{1}{2} \underline{B}_{ij}\right) ^{k_{ij}} \right. \nonumber \\&\quad +\left( \prod _{p=1}^{2N} \underline{m}_p!\right) \sum _{k \in \varOmega (\underline{\mathbf {m}})} \frac{\prod _{i,j=1}^{2N} \frac{1}{k_{ij}!} \left( \frac{1}{2} \underline{B}_{ij}\right) ^{k_{ij}}}{\prod _{j=1}^N \frac{1}{k_{j,j+N}!} \left( \frac{1}{2}\underline{B}_{j,j+N}^{k_{j,j+N}}\right) }(\prod _{j=1}^N \frac{1}{(k_{j,j+N}-1)!}(\frac{1}{2})^{k_{j,j+N}}(\underline{B}_{j,j+N})^{k_{j,j+N}-1}) \nonumber \\&\quad \left. +\left( \sum _{i,j=1}^{2N} D_{ij} - \sum _{i,j=1}^{2N} C_{ij} \right) \left( \prod _{p=1}^{2N} \underline{m}_p!\right) \sum _{k \in \varOmega (\underline{\mathbf {m}})} \prod _{i,j=1}^{2N} \frac{1}{(k_{ij}-1)!} \left( \frac{1}{2}\right) ^{k_{ij}} (\underline{B}_{ij})^{k_{ij}-1} \right) \end{aligned}$$

(37)

5 Potential Energy Matrix Elements

To calculate the matrix elements of the one-body U and two-body potential V we will use the following expressions

$$\begin{aligned} \sum _{k=1}^N U(x_{k})=\sum _{k=1}^N \int U({ x}) \delta (x_k-{ x})d{ x}= \sum _{k=1}^N \int U({ x}) \delta (w^{(k)}x-{ x}) d { x} \end{aligned}$$

(38)

where

$$\begin{aligned} w^{(k)}x=\sum _{i=1}^N w^{(k)}_i x_i \ \ \ \ \ \ \ \ \ \ \ w^{(k)}_i =\delta _{ki} \end{aligned}$$

(39)

and

$$\begin{aligned} \sum _{k<l}^N V(x_{kl})=\sum _{k<l}^N \int V({ x}) \delta (x_k-x_l-{ x})d{ x}= \sum _{k<l}^N \int V({ x}) \delta (w^{(kl)}x-{ x}) d { x} \end{aligned}$$

(40)

where

$$\begin{aligned} w^{(kl)}x=\sum _{i=1}^N w^{(kl)}_i x_i \ \ \ \ \ \ \ \ \ \ \ w^{(kl)}_i =\delta _{ki}-\delta _{li}. \end{aligned}$$

(41)

These equations show that by calculating the matrix elements of

$$\begin{aligned} \delta (w x-{ x}) \end{aligned}$$

(42)

one can evaluate both the one-body and two-body integrals. The matrix element of $\delta (w x-{ x})$ :

$$\begin{aligned} \langle G^A_{{ t}}\vert \delta (w x-{ x}) \vert G^{A'}_{{ t}'} \rangle = \sqrt{c \over 2\pi } \mathrm{exp}\left\{ -{c \over 2}(x-w B^{-1} ({ t}+{ t'}))^2 \right\} \langle G^A_{{ t}}\vert G^{A'}_{{ t}'} \rangle \end{aligned}$$

(43)

where

$$\begin{aligned} c={1 \over {w}^T B^{-1} w}. \end{aligned}$$

(44)

This matrix element can be written as

$$\begin{aligned}&\langle G^A_{{ t}}\vert \delta (w x-{ x}) \vert G^{A'}_{{ t}'} \rangle = \sqrt{c \over 2\pi } \mathrm{exp} \left\{ -{c\over 2} x^2 \right\} \sqrt{\frac{(2\pi )^N}{\det B}} \times \nonumber \\&\quad \mathrm{exp} \left\{ {1\over 2} \sum _{i,j=1}^{2N} {{\underline{B}}'}_{ij} {\underline{t}}_i {\underline{t}}_j+ \sum _{j=1}^{2N}x c e_j {\underline{t}}_j \right\} , \end{aligned}$$

(45)

where

(46)

and

$$\begin{aligned} {{\underline{B}}'}_{ij}={\underline{B}}_{ij}-c e_i e_j. \end{aligned}$$

(47)

The potential matrix element can be calculated from

$$\begin{aligned} \langle \varPhi _{m}^A\vert \delta (w x-{ x}) \vert \varPhi _{m'}^{A'} \rangle = \left. \prod _{k=1}^{2N} {\partial ^{{\underline{m}}_k}\over \partial {\underline{t}}_k^{{\underline{m}}_k}} \langle G^A_{{ t}}\vert \delta (w x-{ x}) \vert G^{A'}_{{ t}'} \rangle \right| _{{ t}=0,{ t}'=0}, \end{aligned}$$

(48)

which using the general Leibniz rule, can be written as

$$\begin{aligned}&\langle \varPhi _{m}^A\vert \delta (w x-{ x}) \vert \varPhi _{m'}^{A'} \rangle = \nonumber \\&\quad = \sqrt{c \over 2\pi } \mathrm{exp} \left\{ -{c\over 2} x^2 \right\} \sqrt{\frac{(2\pi )^N}{\det B}} \prod _{k=1}^{2N} \sum _{n_k=0}^{m_k} \left( {m_k \atop n_k}\right) \nonumber \\&\qquad \times {\partial ^{{\underline{n}}_k} \over \partial {\underline{t}}_k^{{\underline{n}}_k}} \mathrm{exp} \left\{ {1\over 2} \sum _{i,j=1}^{2N} {{\underline{B}}'}_{ij} {\underline{t}}_i {\underline{t}}_j \right\} \nonumber \\&\qquad {\partial ^{{\underline{m}}_k-{\underline{n}}_k}\over \partial {\underline{t}}_k^{{\underline{m}}_k-{\underline{n}}_k}} \mathrm{exp} \left\{ \sum _{j=1}^{2N}x c e_j {\underline{t}}_j \right\} . \end{aligned}$$

(49)

The derivatives of the first exponent are already calculated in Eq. (18). The derivatives of the second exponent can be calculated in a similar way, which eventually produces the following expression

(50)

where $\mathbf {m},\mathbf n$ are vectors $\in \mathbb {Z}_{\ge 0}^n$ of n nonnegative integers. Now let $\varDelta (\underline{\mathbf {m}}-\underline{\mathbf{n }})$ be the set of n-dimensional vectors k $\in \mathbb {Z}_{\ge 0}^{n}$ having nonnegative integer entries such that $k_p= m_p-n_p$ for all $p = 1, \dots , 2N$, and $\varOmega (\underline{\mathbf {m}})$ is defined as it is in the previous section. This completes the derivation of the potential matrix elements.

To calculate the potential matrix elements one has to integrate

$$\begin{aligned} \int V(x) x^{2n} \mathrm{exp}\left\{ {-\frac{c}{2} x^2}\right\} dx. \end{aligned}$$

(51)

This can easily be calculated analytically or numerically for many potentials of interest.

6 Numerical Example

To show the usefulness of the matrix elements calculated in this work, we present a simple illustrative example: the calculation of the energy of few electron atoms in 1D. As the Coulomb potential is singular in 1D, we use a soft Coulomb potential

$$\begin{aligned} U(x_i)=-{Z\over (a^2+x_i^2)^{1/2}},\ \ \ \ \ \ V(x_i-x_j)={1\over (a^1+(x_i-x_j)^2)^{1/2}} \end{aligned}$$

(52)

for the one and two-body potentials, respectively ($a=1$ a.u.).

The wave function of the system is approximated as linear combination of ECGs,

$$\begin{aligned} \varPsi =\sum _i c_i \mathcal{A}\lbrace \varPhi _\mathbf {m}^{A_i}(\mathbf {x}) \rbrace , \end{aligned}$$

(53)

where $\mathcal{A}$ is an antisymmetrizer. The nonlinear parameters, $A_i$, are optimized with the stochastic variational method [41]. The energy of the 1D atoms are listed in Table 1. These can serve as reference numbers for test calculations in 1D.

We have also calculated the electron density

$$\begin{aligned} d(x)={1\over N}\sum _{i=1}^N \langle \varPsi \vert \delta (x_i-x)\vert \varPsi \rangle , \end{aligned}$$

(54)

and the electron correlation function

$$\begin{aligned} c(x)={2\over N(N-1)}\sum _{i<j}^N \langle \varPsi \vert \delta (x_i-x_j-x)\vert \varPsi \rangle . \end{aligned}$$

(55)

These functions are symmetric with respect to the origin and shown in Figs. 1 and 2.

Table 1 Ground state energies (in a.u.) of 1D atoms. The spins of the electrons arranged in such a way that (N−1)/2 electrons are spin up, the rest is spin down

The densities are very similar for different atoms, except in the $N=3$ case, where it seems that two electrons remains close to the center and the third electron is pushed outside. The $N>3$ correlation functions each have their maxima nearly the same distance from the center, which can be easily explained with electron repulsion. The correlation function of the $N=2$ and $N=3$ atoms have their maxima at the origin (two electrons with spin up and spin down are distinguishable and can stay close to the center). The $N=3$ correlation function has a second maximum, around the same position as the $N=3$ density, showing that the third electron is pushed away from the center.

Fig. 1

Electron density of 1D atoms (in a.u.)

Fig. 2

Electron correlation of 1D atoms (in a.u.)

7 Summary

We have presented the matrix elements of general one dimensional ECGs. These analytical matrix elements can be used in various calculations, for example in 1D cold atom systems. Using these matrix elements, one can also construct matrix elements of 2D or 3D systems by simple tensor products. These matrix elements can be especially useful in calculations where the potential is not spherical, for example in systems in magnetic or electric field. The matrix elements can also be used for spherical system with appropriate angular momentum couplings.

Appendices

Appendix A

In this appendix we show an example how to generate integers satisfying Eq. (17). First we rewrite Eq. (17) as

$$\begin{aligned} k_{1,p} + k_{2,p}+ \cdots + 2k_{p,p} + \cdots + k_{p,2N}= m_{p} \end{aligned}$$

(56)

This equation can be written in form of a linear equation by reindexing $k_{1,p},{\ldots },k_{p,2N}$ to form a vector, q, and defining an S matrix for the the coefficients of q:

$$\begin{aligned} \sum _{i=1}^{2N} q_{i}S_{ip} + \sum _{k=2N+1}^{2N + \frac{2N(2N-1)}{2}} q_{k}S_{kp}=m_{p} \end{aligned}$$

(57)

To illustrate how this can be done we give a $N=2$ example showing the equivalence between Eqs. (56) and (57).

Starting with Eq. (56) for $N=2$,

$$\begin{aligned}&2k_{1,1} + k_{1,2} + k_{1,3} + k_{1,4}=m_{1}\nonumber \\&2k_{2,2} + k_{1,2} + k_{2,3} + k_{2,4}=m_{2}\nonumber \\&2k_{3,3} + k_{1,3} + k_{2,3} + k_{3,4}=m_{3}\nonumber \\&2k_{4,4} + k_{1,4} + k_{2,4} + k_{3,4}=m_{4}\nonumber \\ \end{aligned}$$

(58)

Writing out the summations of Eq. (57),

$$\begin{aligned}&q_{1}S_{1,1} + q_{2}S_{2,1} + q_{3}S_{3,1} + q_{4}S_{4,1} \nonumber \\&\quad + q_{5}S_{5,1}+ q_{6}S_{6,1} + q_{7}S_{7,1} + q_{8}S_{8,1} + q_{9}S_{9,1} + q_{10}S_{10,1} = m_{1} \end{aligned}$$

(59)

$$\begin{aligned}&q_{1}S_{1,2} + q_{2}S_{2,2} + q_{3}S_{3,2} + q_{4}S_{4,2} \nonumber \\&\quad + q_{5}S_{5,2}+ q_{6}S_{6,2} + q_{7}S_{7,2} + q_{8}S_{8,2} + q_{9}S_{9,2} + q_{10}S_{10,2} = m_{2} \end{aligned}$$

(60)

$$\begin{aligned}&q_{1}S_{1,3} + q_{2}S_{2,3} + q_{3}S_{3,3} + q_{4}S_{4,3} \nonumber \\&\quad + q_{5}S_{5,3}+ q_{6}S_{6,3} + q_{7}S_{7,3} + q_{8}S_{8,3} + q_{9}S_{9,3} + q_{10}S_{10,3} = m_{3} \end{aligned}$$

(61)

$$\begin{aligned}&q_{1}S_{1,4} + q_{2}S_{2,4} + q_{3}S_{3,4} + q_{4}S_{4,4} \nonumber \\&\quad + q_{5}S_{5,4}+ q_{6}S_{6,4} + q_{7}S_{7,4} + q_{8}S_{8,4} + q_{9}S_{9,4} + q_{10}S_{10,4} = m_{4} \end{aligned}$$

(62)

To define a mapping between q and k, let $q_i = k_{i,i}$ for $i=1,2N$. This is the diagonal of the matrix k. For $i>2N$, we assign the remaining $q_{i}$ to the elements for which $i<j$, left to right and top to down (with x denoting redundant elements due to symmetry):

$$\begin{aligned} \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} q_1 &{} q_5 &{} q_6 &{} q_{7}\\ x &{} q_2 &{} q_8 &{} q_9\\ x &{} x &{} q_3 &{} q_{10}\\ x &{} x &{} x &{} q_4\\ \end{array} \right) \rightarrow \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} k_{11} &{} k_{12} &{} k_{13} &{} k_{14}\\ x &{} k_{22} &{} k_{23} &{} k_{24}\\ x &{} x &{} k_{33} &{} k_{34}\\ x &{} x &{} x &{} k_{44}\\ \end{array} \right) \end{aligned}$$

(63)

Note that q is not a matrix, it is only illustrated this way for clarity.

The selection matrix S contains integer elements of 0, 1, or 2. This will account for (by setting the value of S equal to 0) the extra terms in Eqs. (59)–(62) that are not in Eq. (58), and account for the coefficient of 2 in front of some terms.

Rewriting Eq. (58) with this mapping,

$$\begin{aligned}&2q_1 + q_5 + q_6 + q_7 = m_1 \nonumber \\&2q_2 + q_5 + q_8 + q_9 = m_2 \nonumber \\&2q_3 + q_6 + q_8 + q_{10} = m_3 \nonumber \\&2q_4 + q_7 + q_9 + q_{10} = m_4 \end{aligned}$$

(64)

The matrix S must then be

$$\begin{aligned} \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 2 &{} 0 &{} 0 &{} 0\\ 0 &{} 2 &{} 0 &{} 0\\ 0 &{} 0 &{} 2 &{} 0\\ 0 &{} 0 &{} 0 &{} 2\\ 1 &{} 1 &{} 0 &{} 0\\ 1 &{} 0 &{} 1 &{} 0\\ 1 &{} 0 &{} 0 &{} 1\\ 0 &{} 1 &{} 1 &{} 0\\ 0 &{} 1 &{} 0 &{} 1\\ 0 &{} 0 &{} 1 &{} 1\\ \end{array} \right) \end{aligned}$$

(65)

Once the S matrix is defined, Eq. (57) can be solved for any given set of $m_p$ by finding the integers satisfying the equation.

Appendix B

In this appendix we show how to calculate a Gaussian integral used in the derivation of the matrix elements. Equations similar to this have been published before (see e.g. in Ref. [41]), but here we prove it for a general complex symmetric matrix.

Let $A \in \mathbb {C}^{N\times N}$ be a complex-symmetric matrix with positive-definite real part. Then for any $Q \in \mathbb {C}^{N \times N}$ and $s \in \mathbb {C}^N$

$$\begin{aligned}&\int _{\mathbb {R}^N} \frac{1}{2} \mathbf x ^T Q \mathbf x \exp \left( -\frac{1}{2} \mathbf x ^T A \mathbf x + \mathbf s ^T \mathbf x \right) d\mathbf x \nonumber \\&\quad =\sqrt{\frac{2\pi }{\det B}}\exp \left( \frac{1}{2} \mathbf s ^T A^{-1} \mathbf s \right) \left[ \frac{1}{2} \hbox {Tr}(Q A^{-1} + \frac{1}{2}(A^{-1} \mathbf s )^T Q (A^{-1} \mathbf s )\right] \end{aligned}$$

(66)

Proof

As in the preceding proof, pick an invertible matrix $V \in \mathbb {R}^{N \times N}$ such that $D \equiv {V^T AV}$ is diagonal, and let $R \equiv {V^T QV}$ and $\mathbf u \equiv {V^T} \mathbf s$. Then by performing a change of variable $\mathbf y = {V}^T \mathbf x$, we can write

$$\begin{aligned}&I \equiv \int _{\mathbb {R}^N} \frac{1}{2} \mathbf x ^T Q \mathbf x \exp \left( -\frac{1}{2} \mathbf x ^T A \mathbf x + \mathbf s ^T \mathbf x \right) d\mathbf x \nonumber \\&\quad = \int _{\mathbb {R}^N} \frac{1}{2} \mathbf x ^T Q \mathbf x \exp \left( -\frac{1}{2} \mathbf x ^T V^{-T} D V^{-1} \mathbf x + \mathbf s ^T \mathbf x \right) d\mathbf x \nonumber \\&\quad = \int _{\mathbb {R}^N} \frac{1}{2} \mathbf y ^T V^T Q V \mathbf y \exp \left( -\frac{1}{2} \mathbf y ^T D \mathbf y + \mathbf s ^T V\mathbf y \right) \det V d\mathbf y \nonumber \\&\quad = \frac{\det V}{2} \int _{\mathbb {R}^N} \mathbf y ^T R \mathbf y \exp \left( -\frac{1}{2} \mathbf y ^T R \mathbf y + \mathbf u ^T \mathbf y \right) d\mathbf y \nonumber \\&\quad = \frac{\det V}{2} \int _{\mathbb {R}^N} \sum _{j,k=1}^N R_{jk} y_j y_k \exp \left( \frac{1}{2} \sum _{l=1}^N d_l y_{l}^2 + \sum _{l=1}^N u_l y_l \right) d\mathbf y \nonumber \\&\quad = \frac{\det V}{2} \sum _{j,k=1}^N R_{jk} \int _{\mathbb {R}^N} y_j y_k \prod _{l=1}^N \exp \left( -\frac{1}{2}d_l y_{l}^2 + u_l y_l \right) d\mathbf y \end{aligned}$$

(67)

At this point, we consider separately the $j=k$ and $j \ne k$ terms. When $j=k$, we want to evaluate the integral

$$\begin{aligned} I_j \equiv \int _{\mathbb {R}^N} y_{j}^2 \prod _{l=1}^N \exp \left( -\frac{1}{2} d_l y_{l}^2 + u_l y_l \right) d\mathbf y \end{aligned}$$

(68)

Observe that each term with $l \ne j$ contributes a factor of

$$\begin{aligned} \int _{-\infty }^\infty \exp \left( -\frac{1}{2} d_l y_{l}^2 + u_l y_l\right) dy_l = \sqrt{\frac{2 \pi }{d_l}} \exp \left( \frac{u_{l}^2}{2d_l} \right) \end{aligned}$$

(69)

while the $l=j$ term contributes a factor of

$$\begin{aligned} \int _{-\infty }^\infty \exp \left( -\frac{1}{2} d_j y_{j}^2 + u_j y_j\right) dy_j = \left( \frac{d_j + u_{j}^2}{d_{j}^2}\right) \sqrt{\frac{2 \pi }{d_j}} \exp \left( \frac{u_{j}^2}{2d_j} \right) \end{aligned}$$

(70)

multiplying these factors gives the result

$$\begin{aligned} I_j = \left( \frac{d_j + u_{j}^2}{d_{j}^2} \right) \prod _{l=1}^N \sqrt{\frac{2 \pi }{d_l}} \exp \left( \frac{u_{j}^2}{2d_j} \right) = \left( \frac{d_j + u_{j}^2}{d_{j}^2}\right) \sqrt{\frac{(2 \pi )^N}{\det D}} \exp \left( \frac{1}{2} \mathbf s ^T A^{-1} \mathbf s \right) \end{aligned}$$

(71)

When $j \ne k$ we want to evaluate the integral

$$\begin{aligned} I_{jk} \equiv \int _{{\mathbb {R}^N}} y_j y_k \prod _{l=1}^N \exp \left( -\frac{1}{2} d_l y_{l}^2 + u_l y_l \right) d\mathbf y \end{aligned}$$

(72)

Again, each term with $l \ne j,k$, contributes a factor of $\sqrt{\frac{2 \pi }{d_l}}\exp (\frac{u_{l}^2}{2d_l})$, while the $l=j,k$ terms contribute a factor of

$$\begin{aligned} \int _{-\infty }^\infty y_j \exp \left( -\frac{1}{2} d_j y_{j}^2 + u_j y_j \right) dy_j = (\frac{u_j}{d_j})\sqrt{\frac{2 \pi }{d_j}} \exp \left( \frac{u_{j}^2}{2d_j} \right) \end{aligned}$$

(73)

Multiplying these factors gives the result

$$\begin{aligned} I_{jk} = \left( \frac{u_j u_k}{d_j d_k}\right) \prod _{l=1}^N \sqrt{\frac{2 \pi }{2d_l}} \exp \left( \frac{u_{j}^2}{2d_j} \right) = \left( \frac{u_j u_k}{d_j d_k}\right) \sqrt{\frac{(2 \pi )^N}{\det D}} \exp \left( \frac{1}{2} \mathbf s ^T A^{-1} \mathbf s \right) \end{aligned}$$

(74)

Returning to the integral, we have

$$\begin{aligned} I= & {} \frac{\det V}{2} \Big [\sum _{j=1}^N R_{jj} I_j + \sum _{j \ne k}^N R_{jk} I_{jk} \Big ] \nonumber \\= & {} \frac{\det V}{2} \sqrt{\frac{(2 \pi )^N}{\det D}} \exp \left( \frac{1}{2} \mathbf s ^T A^{-1} \mathbf s \right) \Big [\sum _{j=1}^N R_{jj} \frac{d_j + u_{j}^2}{d_{j}^2} + \sum _{j \ne k}^N R_{jk} \frac{u_j u_k}{d_j d_k} \Big ] \nonumber \\= & {} \frac{1}{2} \sqrt{\frac{(2 \pi )^N}{\det (V^{-T} D V^{-1})}} \exp \left( \frac{1}{2} \mathbf s ^T A^{-1} \mathbf s \right) \Big [ \sum _{j=1}^N \frac{R_{jj}}{d_j} + \sum _{j,k=1}^N R_{jk} \frac{u_j u_k}{d_j d_k} \nonumber \\= & {} \sqrt{\frac{(2 \pi )^N}{\det D}} \exp \left( \frac{1}{2} \mathbf s ^T A^{-1} \mathbf s \right) \Big [ \frac{1}{2} \hbox {Tr}(R D^{-1}) + \frac{1}{2} \mathbf u ^T D^{-T} T D^{-1} \mathbf u \Big ] \nonumber \\= & {} \sqrt{\frac{(2 \pi )^N}{\det D}} \exp \left( \frac{1}{2} \mathbf s ^T A^{-1} \mathbf s \right) \Big [\frac{1}{2} \hbox {Tr}((V^T Q V)(V^T A V)^{-1}) \nonumber \\&+ \frac{1}{2} \mathbf u ^T (V^T A V)^{-T}(V^T Q V)(V^T A V)^{-1} \mathbf u \Big ] \nonumber \\= & {} \sqrt{\frac{(2 \pi )^N}{\det D}} \exp \left( \frac{1}{2} \mathbf s ^T A^{-1} \mathbf s \right) \Big [ \frac{1}{2} \hbox {Tr}(Q A^{-1}) + \frac{1}{2}(A^{-1}{} \mathbf s )^{T} Q (A^{-1} \mathbf s ) \Big ], \end{aligned}$$

(75)

which is the desired result. $\square$