Two-Pion Exchange Three-Nucleon Force Effects in Elastic Nucleon–Deuteron Scattering Cross Sections

Abstract

Differential cross sections for elastic nucleon–deuteron scattering at intermediate energies are calculated by solving the Faddeev equation in coordinate space using interaction models consisting of a two-nucleon potential and three-nucleon potentials based on the exchange of two pions among three nucleons. Attractive effects of the pion-exchange at medium range region in the three-nucleon potential are taken into account by using a larger cutoff mass parameter and by adding phenomenological repulsive three-nucleon potentials as a counterpart. It is shown that these effects increase the cross sections at backward angles, which tends to reduce discrepancies between theoretical calculations and experimental data.

1 Introduction

In a conventional picture, where atomic nuclei are considered as non-relativistic quantum systems of nucleons, the Hamiltonian of three-nucleon (3N) systems contains two- and three-nucleon potentials. It is widely known that realistic two-nucleon potentials (2NPs) made to reproduce nucleon–nucleon observables underbind 3N bound states, ${}^3$H and ${}^3$He, by about 1 MeV, and that an additional attraction can be obtained by introducing a three-nucleon potential (3NP) based on an exchange process of two pions among three nucleons (2$\pi$E) as shown in Fig. 1 [1,2,3,4,5,6,7]. Since the 2$\pi$E process is considered to be a long-range part in 3NPs and our knowledge of 3NPs at shorter range is still incomplete, combinations of a 2NP and a 2$\pi$E-3NP have been often used in few-nucleon calculations.

In spite of various successful effects of the 2$\pi$E-3NP on 3N observables, there are still unsolved discrepancies between experimental data and theoretical calculations. A typical example of these, which will be discussed in the present paper, is the differential cross section for elastic nucleon–deuteron (N–d) scattering. It has peaks at forward and backward angles along with a minimum at $\theta \approx 120^\circ$, where $\theta$ is the scattering angle in the center of mass system. Calculations with 2NPs underpredict the cross section at this minimum region. The introduction of the 2$\pi$E-3NP increases the cross section successfully, e.g., for $E=65$ MeV as shown in Ref. [8], where E denotes the incident energy in the laboratory system divided by the mass number of the incident particle. However, as the energy increases, say $E > 100$ MeV, 2$\pi$E-3NP effects on the N–d cross sections at the minimum region are not enough to explain experimental data. Relativistic effects on the differential cross section were studied, but found to be small [9].

Here, it is remarked that the 2$\pi$E-3NP produces a strong attraction in the 3N bound states, and thus its contribution at medium and short-range is suppressed to reproduce the 3N binding energy. In this paper, paying attention to this suppression, which could hide an important role of pions at a medium range, I will study effects of 2$\pi$E-3NP at shorter range region by introducing a repulsive 3NP phenomenologically to reproduce the 3N binding energies.

In Sect. 2, three-nucleon calculations and three-nucleon potential models will be described. In Sect. 3, calculations of the N–d elastic cross section will be presented, and effects of the cutoff of 2$\pi$E-3NP will be discussed. Summary will be given in Sect. 4.

2 Calculations and Models

2.1 Three-Nucleon Faddeev Calculations

Three-body calculations in the present paper are performed by solving the Faddeev equations [10] as integral equations in coordinate space using a method developed in Refs. [11,12,13,14,15]. Here, I summarize some characteristics of the calculations.

• Faddeev equations are solved by an iterative method called the method of continued fraction (MCF) [11, 12]. A basic procedure of the algorithm in the MCF is to operate the integral kernel to a function made in a preceding step, as are those in most iterative methods.

• Faddeev components are expanded by a complete set of the spectator particle with respect to relative momenta of the spectator to the interacting pair. In this representation, numerical computations of the integral kernels of the Faddeev equations are performed by solving ordinary differential equations and performing numerical integrations, both of which are well under control [14].

• For systems of charged particles, ${}^{3}$He and p–d scattering in this paper, the Faddeev equation is modified to accommodate the long-range Coulomb interactions, in which the spectator function becomes the Coulomb wave function [13, 15]. This method was successfully applied to systems of three charged particles, such as three $\alpha$-particles [16].

• 3N partial wave states for which 2NPs and 3NPs act, are restricted to those with total two-nucleon angular momenta $j \le 6$ for bound state calculations, and $j \le 5$ for scattering state calculations. For scattering state calculations, 3N partial wave states with the total 3N angular momentum $J \le 27/2$ are taken into account, while 3NPs are switched on for 3N states with $J \le 13/2$.

2.2 Two-Pion Exchange Three-Nucleon Potential

A component of the 2$\pi$E-3NP described by the diagram, Fig. 1, is expressed in the coordinate space representation as

$$\begin{aligned} V^{(3:1,2)}(\mathbf {r}_{13},\mathbf {r}_{23}) = \int d\mathbf {q}_1 d\mathbf {q}_2 e^{ -\imath \mathbf {q}_1\cdot \mathbf {r}_{13} -\imath \mathbf {q}_2\cdot \mathbf {r}_{23}} {\hat{V}}^{(3:1,2)}(\mathbf {q}_1,\mathbf {q}_2), \end{aligned}$$

(1)

where $\mathbf {q}_i~ (i=1,2)$ is defined in Fig. 1 and $\mathbf {r}_{i3}=\mathbf {r}_{i}-\mathbf {r}_{3}$. The momentum space representation ${\hat{V}}^{(3:1,2)}(\mathbf {q}_1,\mathbf {q}_2)$ is given by

$$\begin{aligned} {\hat{V}}^{(3:1,2)}(\mathbf {q}_1,\mathbf {q}_2)= & {} \frac{1}{(2\pi )^6} \left( \frac{g_A}{2f_\pi }\right) ^2 \frac{F(\mathbf {q}_1^2)}{\mathbf {q}_1^2+m_\pi ^2} \frac{F(\mathbf {q}_2^2)}{\mathbf {q}_2^2+m_\pi ^2} (\mathbf {\sigma }_1\cdot \mathbf {q}_1) (\mathbf {\sigma }_2\cdot \mathbf {q}_2) \\&\times \Bigl [ (\mathbf {\tau }_1\cdot \mathbf {\tau }_2) \{a+b(\mathbf {q}_1\cdot \mathbf {q}_2) \} + (\imath \mathbf {\tau }_3\cdot \mathbf {\tau }_1\times \mathbf {\tau }_2) (\imath \mathbf {\sigma }_3\cdot \mathbf {q}_1\times \mathbf {q}_2)d \Bigr ], \end{aligned}$$

(2)

where $m_\pi$ is the pion mass, and $F(\mathbf {q}^2)$ is a form factor, which will be explained below. The coefficients, a, b, and d, which characterize the 2$\pi$E-3NP, are extracted from pion-nucleon scattering amplitudes.

In this paper, I will use a newer version of the Brazil 2$\pi$E-3NP, BR-${{\mathcal {O}}}(q^4)$ in Ref. [7] (BR07), whose coefficients are $\left( a,b,d \right) = \left( 0.981 m_\pi ^{-1}, -2.617 m_\pi ^{-3}, -0.854 m_\pi ^{-3}\right)$.

Fig. 1

(Color online) Diagram that shows a component of the 2$\pi$E-3NP. Total 2$\pi$E-3NP is the sum of cyclic permutations of this diagram

The use of the form factor $F(\mathbf {q}^2)$ in Eq. (2) is a conventional procedure to suppress the short-range contributions of the 2$\pi$E-3NP. A typical functional form of the form factor is the dipole form:

$$\begin{aligned} F(\mathbf {q}^2)= \left( \frac{\varLambda ^2-m_\pi ^2}{\varLambda ^2+\mathbf {q}^2} \right) ^2, \end{aligned}$$

(3)

where $\varLambda$ is a cutoff mass parameter. Calculations with the BR07-3NP adapting the dipole form factor, Eq. (3), with the cutoff parameter $\varLambda$ will be denoted as $\hbox {BR}_{\varLambda }$.

In the present paper, I will use the Argonne $\hbox {V}_{18}$ (AV18) 2NP model [17]. Calculated 3N binding energies for the AV18 are shown in Table 1, which indicates the AV18 calculation underbinds the 3N bound states by about 0.8 MeV. When the BR07-3NP is combined with the AV18-2NP, the cutoff parameter $\varLambda$ determined to reproduce the 3N binding energies is $\varLambda = 660$ MeV ($\hbox {BR}_{660}$) (see Table 1 for numerical values).

The value of $\varLambda$ determined to reproduce the 3N binding energy is quite small compared with ones used in one-boson exchange 2NP models, such as the CD-Bonn potential [18], which are larger than 1000 MeV. This indicates that some medium range contributions in 2$\pi$E-3NP may be reduced.

When the cutoff mass $\varLambda$ larger than 660 MeV is used, calculated 3N binding energies for AV18 + $\hbox {BR}_{\varLambda }$ are too large (e.g., see Table 1 for AV18 + $\hbox {BR}_{1000}$). In order to reproduce the 3N binding energies, I introduce a spin-independent repulsive Gaussian 3NP [19], which will be denoted as C-3NP:

$$\begin{aligned} W_\mathrm {C} =V_\mathrm {C} \sum _{cyclic} e^{-\left( \frac{r_{ik}}{r_\mathrm {C}}\right) ^2 -\left( \frac{r_{jk}}{r_\mathrm {C}}\right) ^2}, \end{aligned}$$

(4)

where $r_{ij}$ is the relative distance between nucleons i and j, $r_\mathrm {C}$ the range parameter, and $V_\mathrm {C}$ the strength parameter. With fixing $r_\mathrm {C}=1.0$ fm, fitted values of $V_\mathrm {C}$ for $\varLambda =1000$ MeV are shown as BR(C)$_{1000}$ in Table 1.

Table 1 Empirical and calculated values of the 3N binding energies and strength parameters of additional 3NPs for models used in this paper. See the text for the description of the models

3 Results and Discussion

3.1 Nd Cross Section at Backward Angles

In Fig. 2, AV18, AV18+$\hbox {BR}_{660}$, and AV18+BR(C)$_{1000}$ calculations of differential cross section for elastic proton-deuteron (p–d) scattering at $E=70$ MeV and $E=170$ MeV are compared with experimental data [20, 21]. The figures demonstrate that the deviation between the AV18 calculation and the data, especially for the minimum region, $90^\circ< \theta < 150^\circ$, is well reduced by introducing the $\hbox {BR}_{600}$ for $E=70$ MeV, but is not for $E=170$ MeV. The introduction of the BR(C)$_{1000}$ gives almost the same effect on the cross section as $\hbox {BR}_{600}$ at $E=70$ MeV, while increases the cross section at backward angles larger than $\hbox {BR}_{600}$ to give a reasonable agreement with the data at $E=170$ MeV.

Fig. 2

(Color online) The p–d cross sections at $E=70$ MeV (a) and $E=170$ MeV (b). Dotted (black), dashed (red), and full (green) curves denote the AV18, AV18+$\hbox {BR}_{660}$, and AV18 +BR(C)$_{1000}$ calculations, respectively. Data are taken from Ref. [20] for $E=70$ MeV, and from Ref. [21] for $E=170$ MeV

To see the situation more clearly and comprehensively, relative differences between some of available experimental data for $E=65$ MeV to $E=250$ MeV [20,21,22,23,24,25,26] and calculations are shown in Fig. 3, where solid circles connected by dotted lines (black) show AV18 calculations, the empty squares connected by dashed lines (red) do AV18+$\hbox {BR}_{660}$ calculations, and the solid diamonds connected by full lines (green) do AV18+BR(C)$_{1000}$ calculations. Furthermore, energy dependence of the relative differences at $\theta = 30^\circ$, $120^\circ$, $140^\circ$, and $165^\circ$ are plotted in Fig. 4. In the figures, experimental data at the corresponding angles are interpolated from the available data points for p–d scattering [20,21,22,23,24,25,26,27,28,29] and for neutron-deuteron (n–d) scattering [30,31,32,33].

As shown in these figures, the AV18 calculations underestimate the cross section at backward angles, roughly for $\theta$ larger than $100^\circ$, and the introduction of the 2$\pi$E-3NP increases the backward cross sections. For lower energies, at least $E<100$ MeV, the introduction works successfully for both of $\hbox {BR}_{660}$ and BR(C)$_{1000}$. For higher energies, while the effects of $\hbox {BR}_{660}$ at backward angles are not enough to explain the experimental data, that of BR(C)$_{1000}$ works well in general.

Fig. 3

(Color online) Relative difference between experimental data and calculations of the p–d cross section. In each figure, solid circles connected by dotted lines (black) denotes for AV18, empty circles connected by dashed lines (red) for AV18+$\hbox {BR}_{660}$, and solid diamonds connected by full lines (green) for AV18+BR(C)$_{1000}$. Experimental data are from Refs. [22] for a; [20] for b; [21] for c, d, e, h, j, and k; [23] for f; [24] for g; [25] for i; and [26] for l

Fig. 4

(Color online) Energy dependence of the relative difference between experimental data and calculations of the p–d and n–d cross section at fixed angles, $\theta =30^\circ$, $120^\circ$, $140^\circ$, and $165^\circ$. The meaning of symbols connected by lines is same as Fig. 3. Experimental data are [22] for $E=65$ MeV; [20] for $E=70$ MeV; [27] for $E=90$ MeV; [30, 31] for $E=95$ MeV; [21] for $E=108$ MeV, 120 MeV, 135 MeV, 150 MeV, 170 MeV, and 190 MeV; [23] for $E=135$ MeV; [24] for $E=135$ MeV; [32] for $E=135$ MeV, 150 MeV, 160 MeV, 170 MeV, 180 MeV, 190 MeV, 200 MeV, 210 MeV, 220 MeV, 230 MeV, 240 MeV, and 250 MeV; [25] for $E=155$ MeV; [29] for $E=146$ MeV, 180 MeV, and 216.5 MeV; [26, 33] for $E=250$ MeV

Fig. 5 shows a comparison between the AV18 + BR(C)$_{1000}$ calculation and the AV18 + $\hbox {BR}_{1000}$ calculation at $E=170$ MeV. It is remarked that the latter is much larger than the former and the experimental data. This indicates that the increase of the cross sections at backward angles is mainly caused by the use of a large cutoff mass value, from which pion contributions at shorter range are taken into account, while the short-range repulsive 3NP plays a role to decrease the cross sections.

Fig. 5

(Color online) The relative difference between experimental data [21] and calculations of the p–d cross section at $E=170$ MeV. Solid circles (black) are for AV18, solid diamonds (green) for AV18+BR(C)$_{1000}$, and solid triangles (blue) for AV18+$\hbox {BR}_{1000}$

3.2 Another Cutoff Procedure

Since the use of the dipole form factor is not unique way to cut off a short-range part of interactions, I will examine other methods: one used in recent the chiral effective field theory ($\chi$EFT) [34,35,36], and one used in the Urbana (UR) [37] and Illinois (IL) 3NP models [38].

In recent calculations of few- and many-nuclear systems [34,35,36], 2NPs based on $\chi$EFT are provided in the coordinate space representation with multiplying a damping function (called as regulator) $f_R(r)$, where R is a parameter representing the range of cutoff. The cutoff procedure used in constructing the 2NP is also applied to 3NP as follows: First, a bare 3NP $V_0^{(3:1,2)}(\mathbf {r}_1,\mathbf {r}_2)$ is introduced by Eq. (1) with setting $F(q^2)=1$ in Eq. (2). Then, the bare potential in the coordinate space is multiplied by the regulator function $f_R(r)$ as

$$\begin{aligned} V_R^{(3:1,2)}(\mathbf {r}_1,\mathbf {r}_2) = V_0^{(3:1,2)}(\mathbf {r}_1,\mathbf {r}_2) f_R(r_1) f_R(r_2). \end{aligned}$$

(5)

In the present work, a bare 2$\pi$E-3NP is made with the coefficients (a, b, d) of the BR07 model, and then a functional form of the regulator used in Refs. [34, 35],

$$\begin{aligned} f_{R}(r) = \left[ 1- \exp \left( -\frac{r^2}{R^2} \right) \right] ^6, \end{aligned}$$

(6)

is applied. (It turns out that the use of different form of the regulator, e.g. one used in Ref. [36], leads to the same conclusion as follows.) The range parameter that is decided to reproduce the 3N binding energy is $R=0.87$ fm. This 3NP will be denoted by $\hbox {BR}_{0.87}$. Range of this regulator may be characterized by a $r_{0.5}$ that satisfies, $f_{R}(r_{0.5}) = 0.5$, which becomes $r_{0.5} \approx 1.5 R$. In this case, $r_{0.5} \approx 1.3$ fm, which indicates rather long-range character of the regulator.

As in the case of the dipole form factor, I will introduce the repulsive C-3NP with taking a smaller value of $R=0.5$ fm. The strength parameter of the C-3NP is determined reproduce the 3N binding energies, which are shown as BR(C)$_{0.5}$ in Table 1.

The UR-3NP [37] and the IL-3NP [38] are often used in few-nucleon calculations with the AV18-2NP. The UR-3NP consists of a long-rang attractive part originating from the $\varDelta$-mediated 2$\pi$E-3NP [b- and d-terms in Eq. (2)] and a shorter range repulsive part. The IL-3NP adds some other 3NP components including a-term in Eq. (2). The cutoff procedure of the long-range parts in UR- and IL-3NPs uses a cutoff function

$$\begin{aligned} \xi (r) = 1- e^{-2.1r^2}, \end{aligned}$$

(7)

but is not the same as in $\chi$EFT. Details are described in Ref. [38].

The short-range parts of the UR-3NP and IL-3NP are as follows:

$$\begin{aligned} V^{R} = U_0 \sum _{cyclic} T^2\left( m_\pi r_{ij}\right) T^2\left( m_\pi r_{jk}\right) , \end{aligned}$$

(8)

where T(x) is the normal tensor function,

$$\begin{aligned} T(x) = \left( 1 + \frac{3}{x} + \frac{3}{x^2} \right) \xi ^2(r). \end{aligned}$$

(9)

I take the bare BR07-3NP following the same cutoff procedure as in Ref. [38], and combine it with the short-range 3NP, Eq. (8) by taking the strength parameter $U_0$ as a fitting parameter to reproduce the 3N binding energies. Thus determined parameter is $U_0=0.022$ MeV, BR(UR-R).

In Fig. 6, the relative difference between experimental data and calculations of p–d scattering at $E=170$ MeV are shown for AV18+$\hbox {BR}_{0.87}$, AV18+BR(C)$_{0.5}$, and AV18+BR(UR-R) calculations. This figure shows a similarity between the AV18+$\hbox {BR}_{0.87}$ and the AV18+$\hbox {BR}_{660}$ calculations. Also, the AV18+BR(C)$_{0.5}$ and AV18+BR(UR-R) calculations almost resolve the difference between the data and calculations as the AV18+BR(C)$_{1000}$ calculations. These indicate that the regulator function $F_{R=0.5}(r)$ and the cutoff function $\xi (r)$ play a similar role as the form factor with $\varLambda =1000$ MeV in the 2$\pi$E-3NP.

In Fig. 7, the functions $F_{R=0.87}(r)$, $F_{R=0.5}(r)$, and $\xi (r)$ are compared. The difference between $F_{R=0.5}(r)$ and $F_{R=0.87}(r)$, as well as that of $\xi (r)$ and $F_{R=0.87}(r)$ demonstrate that the increase of the N–d cross sections at minimum and backward angle regions is caused by effects of the pion-exchange around $r=1$ fm.

Fig. 6

(Color online) The relative difference between experimental data [21] and calculations of the p–d cross section at $E=170$ MeV. Solid circles connected by dotted line (black) are for AV18, empty squares connected by dashed lines (red) for AV18+$\hbox {BR}_{0.87}$, solid diamonds connected by full lines (green) for AV18+BR(C)$_{0.5}$, and solid triangles connected by dotted line (blue) for AV18+BR(UR-R)

Fig. 7

(Color online) Dashed (red), full (green), and dotted (blue) curves denote the regulator functions $F_{R=0.87}(r)$, $F_{R=0.5}(r)$, and the cutoff function $\xi (r)$, respectively

3.3 Spin-Dependent Repulsive 3NP

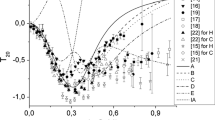
Next, I will consider a possible spin-dependence in the short-range 3NP. In Fig. 8, deuteron vector analyzing power $iT_{11}(\theta )$, and deuteron tensor analyzing powers, $T_{20}(\theta )$, $T_{21}(\theta )$, and $T_{22}(\theta )$, in p–d scattering at $E=3.0$ MeV, just below the 3N breakup threshold, are shown. As these figures show, the AV18 calculations deviate from the experimental data [39] for $iT_{11}(\theta )$, $T_{21}(\theta )$, and $T_{22}(\theta )$. The introduction of the $\hbox {BR}_{660}$-3NP improves $T_{22}(\theta )$ well and $iT_{11}(\theta )$ partially. However, it fails in reproducing the data of $T_{21}(\theta )$ by giving worse agreement between the measured and the calculated as noted in Ref. [19].

In Ref. [40], the following forms of tensor (T)- and spin-orbit (SO)-3NPs, (the latter one was introduced originally in Ref. [41],) in addition to the C-3NP were introduced to explain p–d polarization observables:

$$\begin{aligned} W_\mathrm {T}= & {} V_\mathrm {T} \sum _{cyclic} e^{-\left( \frac{r_{ik}}{r_\mathrm {T}}\right) ^2 -\left( \frac{r_{jk}}{r_\mathrm {T}}\right) ^2} S_\mathrm {T}(ij) {{{\hat{P}}}}_{11}(ij), \\W_\mathrm {SO}= & {} V_\mathrm {SO}~ e^{-\alpha _\mathrm {SO}\rho } \sum _{i < j} \mathbf {L}_{ij} \cdot (\mathbf {S}_i+\mathbf {S}_j) {\hat{P}}_{11}(ij), \end{aligned}$$

(10)

where $S_\mathrm {T}(ij)$ is the tensor operator acting between nucleon pair (i, j), ${\hat{P}}_{11}(ij)$ the projection operator to the spin- and isospin triplet state of the (i, j) pair, $\rho = \sqrt{\frac{2}{3}(r_{12}^2+r_{23}^2+r_{31}^2)}$, $\mathbf {L}_{ij}$ relative angular momentum between nucleon the (i, j) pair, and $\mathbf {S}_i$ spin operator of the nucleon i. It is remarked that very similar forms to Eq. (10) are reported to appear as contact 3NPs at N4LO in $\chi$EFT [42].

In the present work, the range parameter $r_\mathrm {T}$ is taken to be 1.0 fm and $\alpha _\mathrm {SO}$ to be 1.5 fm${}^{-1}$ as in Ref. [40]. The C-, T-, and SO-3NPs are used combined with AV18+$\hbox {BR}_{\varLambda }$, which will be denoted as AV18+BR(CTSO)$_{\varLambda }$. The strength parameters, $V_\mathrm {C}$, $V_\mathrm {T}$, and $V_\mathrm {SO}$, which are determined to reproduce the ${}^3$He binding energy; $iT_{11}(\theta )$ and $T_{21}(\theta )$ in p–d scattering at $E=3.0$ MeV, for $\varLambda =800$ MeV and 1000 MeV, are shown in Table 1¹, and the polarization observables of AV18+BR(CTSO)$_{1000}$ calculations are shown in Fig. 8. It is remarked that the strength of the C-3NP is reduced by introducing the T- and SO-3NPs, which means that these components give a repulsive effect in 3N bound states. Actually, the T-3NP contributes to the repulsive energy by about 0.14 MeV, and the SO-3NP does 0.02 MeV in the 3N bound states.

Fig. 8

(Color online) Polarization observables, $iT_{11}(\theta )$ and $T_{2\kappa }(\theta ) (\kappa =0,1,2)$ in p–d scattering at $E=3.0$ MeV. Dotted (black) curves denote the AV18 calculations, dashed (red) curves the AV18+$\hbox {BR}_{660}$ calculations, and solid (green) the AV18+BR(CTSO)$_{1000}$ calculations. Experimental data are taken from [39]

In Fig. 9, the relative differences between experimental data [20, 23, 43] and AV18+BR(C)$_{1000}$ and AV18+BR(CTSO)$_{1000}$ calculations for the p–d cross sections. Although the spin-dependent 3NPs give some variations in the $\theta$-dependence of the ratios, they are not so large. Thus, it is still essential to use a large cutoff mass in the increasing of the cross section.

Fig. 9

(Color online) The relative difference between experimental data and calculations of the p–d cross section for $E=3$ MeV (a), 70 MeV (b), and 135 MeV (c). Solid circles (black) connected by dotted lines show AV18 calculations, solid diamonds (green) connected by full lines AV18+BR(C)$_{1000}$ calculations, and empty triangles (red) connected by dashed lines AV18+BR(CTSO)$_{1000}$ calculations. Experimental data are taken from Ref. [43] for $E=3$ MeV, and from Refs. [20, 23] for $E=70$ MeV and $E=135$ MeV

In Figs. 10 and 11 , the polarization observables in p-d scattering for AV18, AV18+$\hbox {BR}_{660}$, and AV18+BR(CTSO)$_{1000}$ at $E=70$ MeV and 135 MeV, respectively, are shown with experimental data [20, 44]. It turns out that the present spin-dependent 3NPs are still effective in reproducing at $E=70$ MeV, especially for $T_{22}(\theta )$, but are not enough to reproduce the polarization observables at this energy, which suggests further studies about spin-dependence of 3NPs.

Fig. 10

(Color online) Polarization observables, $iT_{11}(\theta )$ and $T_{2\kappa }(\theta ) (\kappa =0,1,2)$ in p–d scattering at $E=70$ MeV. Curves are the same as Fig. 8. Experimental data are taken from Ref. [20]

Fig. 11

(Color online) Polarization observables, $iT_{11}(\theta )$ and $T_{2\kappa }(\theta ) (\kappa =0,1,2)$ in p–d scattering at $E=135$ MeV. Curves are the same as Fig. 8. Circles (blue) are experimental data from Ref. [20] and solid squares from Ref. [44]

3.4 Short-Range Repulsive 3NP

Recently, the necessity of a short-range repulsive 3NP has been proposed [45,46,47,48] in connection with the stiffness of the neutron-star matter and also with the cross section for nucleus-nucleus scattering. In Ref. [45], a three-baryon repulsive interaction from a viewpoint of the quark confinement mechanism described in a string-junction model was proposed, which has the same form as Eq. (4) but with $r_\mathrm {C}$ = 0.45 fm or 0.5 fm and $V_\mathrm {C}=2000$ MeV. In Refs. [47, 48], a multi-Pomeron exchange potential was introduced, which leads to a triple-pomeron exchange 3NP of the form that

$$\begin{aligned} V_\mathrm {MPP} = V_\mathrm {P} e^{-\rho ^2/a_\mathrm {P}^2}, \end{aligned}$$

(11)

where strength parameter $V_\mathrm {P}$ and range parameter $a_\mathrm {P}$ are given as functions of the mass of the Pomeron, coupling constants, etc. Calculations with these repulsive 3NPs show that they produce repulsive effects at most by about 0.4 MeV in the 3N bound states. These values are smaller than those obtained above, and with the $\hbox {BR}_{\varLambda }$-3NP, the 3N binding energies are reproduced for $\varLambda \approx 720$ MeV. As a result, the increase of the p–d cross section with these models is not so large.

4 Summary

In summary, nuclear interaction models consisting of the AV18-2NP, the BR-2$\pi$E-3NP, and phenomenological short-range 3NPs adjusted to the empirical 3N binding energies equally, are presented. Different ways of the cutoff procedure in the 2$\pi$E-3NP have been examined by fixing the calculated 3N binding energies. It is found that the use of a large cutoff mass or short-range cutoff increases the N–d elastic cross section at minimum and backward angle regions, which tends to improve consistency between calculations and experimental data. Although there is some uncertainty for the spin-dependence of short-range 3NPs to improve polarization observables, the present work demonstrates the importance of the medium range contribution in the 2$\pi$E-3NP in studying few-nucleon systems.