1 Introduction

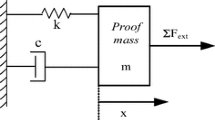
Microelectromechanical system (MEMS) based resonators are used in a wide range of applications in aerospace, satellite, defense, automotive, consumer electronics, and medical instruments for motion, position, stability and navigation purposes (Khan et al. 2020; Khan and Ahamed 2020). The aerospace and satellite industries require high-performance resonators for navigation and guidance systems. These applications demand resonators with higher stability and lower energy loss. Any energy dissipation during vibration will reduce its amplitude of motion and will require additional input energy to keep it vibrating at its resonance. Therefore, the performance of a MEMS resonator highly depends on the rate of vibrational energy dissipation. The Quality factor (Q) is defined as the ratio of maximum stored energy to the total dissipated energy per cycle and can be measured using the time rate of decay of the resonator vibration energy (Ghaffari et al. Jul. 2015). High Q-factor leads to resonance with a sharp peak and high gain, resulting in a more sensitive and efficient sensor. A high performance MEMS resonator with a Q-factor in the range of a million, can be considered as state of the art, was demonstrated in (Senkal et al. 2015). A low Q-factor results in an attenuated amplitude of vibration (low gain and low sensitivity), making the motion of the micro-resonator unstable and not suitable for high performance applications. Many in the literature has explored detailed understanding of energy loss mechanisms and their improvements (Taheri-Tehrani et al. 2017; Santos et al. 2015; Toan et al. 2014; Shmulevich et al. 2013; Ahamed et al. 2014; Du, et al. 2018; Kucera et al. 2013). For example, Q-factor for a damped mass-spring is expressed by the following formula (Ren et al. Sep. 2013; Yang et al. 2017).

$$Q=\frac{{Energy}_{\mathrm{max}\_store}}{{Energy}_{total\_dissipated}}=\frac{m\omega }{c}=\frac{k}{c\omega }=\frac{\sqrt{km}}{c}$$
(1)

where, k is the spring constant of resonator, ω is the radial frequency, c is the coefficient of damping force, and m is the effective mass. There are three primary energy dissipation methods: thermoelastic dissipation (TED), anchor loss, and air damping (Ghaffari et al. 2015; Rodriguez et al. 2019). Among different energy losses, the air pressure is dominating loss for the micro-resonators operated in the open air or at low vacuum (Chiao and Lin 2002). If the resonator is not packaged with a vacuum seal, then it operates in the ambient air at atmospheric pressure. There is significant energy loss, and detected Q-factor is low in the order of 10 to 1000 (Khan et al. 2020). However, if the micro-resonator is encapsulated in vacuum, detected Q-factor is high in the range of hundreds of thousands (Senkal et al. 2014; Li et al. 2018).

Depending on the vacuum level, micro-resonators may experience squeeze film damping and slide film damping against the moving part's motion. This paper addresses which damping mechanism dominates inside the encapsulated cavity under different vacuum regions for vacuum packaged MEMS devices. MEMS packaging techniques can achieve pressures from ~ 0.1 Pa with gettering to ~ 100 Pa without (Lisec and Reinert 2010). Such devices can degrade over time, making the pressures between those regions interesting to study. Sen et al. (2013) have studied a micromachined pressure sensor with an integrated resonator operating at atmospheric pressure, showing that the Q-factor from 1146 to 1772 for a device with a frequency of 34.55 kHz (Ren et al. 2013). Bao (2005) investigated the squeeze-film air damping effect in a MEMS resonator using the Christian model (Rodriguez et al. 2019), the energy transfer model, and the Boltzmann transportation equation (Bao 2005), showing that the effect of air damping is indeed quite constant when air pressure is near atmospheric pressure. However, when the air is rarefied to pressures well below one atmospheric pressure, air damping is reduced appreciably (Christian 1966). Feng (2011) studied the squeeze-damping effect in the molecular regions, showing decreased air damping with the resonator enclosed in a gas evacuated cavity. Gas damping is negligible when ambient pressure is close to 1 pa. Senkal et al. (2014) concluded that viscous effects (evaluated at a pressure of 1.01 × 105 Pa) dominate in low- frequency zone, while the stiffening effect (resisting deformation) dominates in the higher frequency zone for low frequency micro-resonators with resonant frequencies on the order of a few tens of kHz. Zhou et al. (2014) proposed that Q factor strongly depends on the air gap distance between comb fingers. The narrower air gap that exists between the two sides of a capacitive device, the higher the damping coefficient, and the worse the dynamic performance of a micro-resonator (Zhou et al. 2014). Christian’s free molecule model does not consider the influence of fixed walls like the substrate, the fixed comb fingers, and the anchors. However, most MEMS applications have such structures. If there is a substrate near the oscillating structure, Christian’s free molecule model is not suitable. Therefore, Hutcherson and Ye (2004) proposed a direct approach based on the energy transfer model from Bao et al. (2002). This approach considers the effect of nearby walls on damping. Bao et al. assume the reaction between gas molecules and micro-resonator structure, ignoring intermolecular collisions. This energy transfer model uses the conservation of linear momentum and conservation of kinetic energy to calculate the velocity change before and after interactions between the moving structure and the medium. Wang et al. (2013) demonstrated that the dominant air damping mechanism can depend on the direction of motion. For that device, slide- film damping dominates in the driving direction, squeeze-film damping dominates in the sensing direction.

Focusing more on the numerical evaluation of gas damping, a model in Frangi et al. (2009) predicts the effect of gas damping in inertial MEMS by introducing a numerical model for free-molecule flows which advances the modeling approach in near vacuum regime. In the transition regime, on the other hand, the Boltzmann equation with simplified modeling is applied in Frangi et al. (2007) to evaluate the gas damping in silicon inertial MEMS operating at lower frequencies. A numerical 3D integral approach is introduced in Frangi et al. (2016) and used to fabricate and test various structures to validate the prediction of gas damping in MEMS. Later, a simplified model of the gas damping prediction is proposed based on a similar approach in Fedeli et al. (2017).

Air pressure regions and degree of air rarefaction depend on the value of Knudsen number, \({(\mathrm{K}}_{\mathrm{n}}=\frac{\uplambda }{\mathrm{g}}\)), which in a gap-closing comb-drive resonator stands for the ratio of mean free path of the gas molecules to the gap distance between plate and fixed comb fingers. If the Knudsen number is greater than ten which is reasonable for MEMS resonators, air damping is in the free molecular damping region (Hutcherson and Ye 2004) where viscous effects can be ignored. Figure 1 demonstrates the air damping category includes three pressure regions: intrinsic damping, molecular damping, and viscous damping (Bao 2005).

Fig. 1
figure 1

The relationship between pressure and typical quality factor of micro-devices. Pressure regions are classified as intrinsic damping (P < 1 Pa), molecular damping (1 Pa < P < 100 Pa), and viscous damping (P > 100 Pa) (Bao 2005)

Full size image

Figure 1 shows the relationship between pressures and Q-factor for a typical MEMS device. If the device is exposed to lower ambient pressure, the quality factor can be increased. Generally, an assumption is that air acts like a viscous fluid and resists against the micro-resonator’s motion. Viscous damping is dominating near the atmosphere (100–105 Pa) pressure, where the Q value is small due to air damping (Q in the 100 or 1000) (Khan et al. 2020). Therefore, it is studied around atmospheric pressure. At very low pressures, other damping mechanism losses (e.g. TED, anchor loss) is larger than the air damping (Hutcherson and Ye 2004). However, air damping plays an essential role in analyzing capability for improving a MEMS device’s performance even in a low-pressure region to achieve accurate predictions during the design stage. Researchers investigating the low-vacuum region found that air damping dominates energy loss at (about 100–1000 kPa (Bao 2005). In the molecular damping region (1 Pa < P < 100 Pa), molecules strike the micro-resonator and intermolecular collisions are rare enough to be excluded from analysis. In this region, the comb fingers collide with air molecules during the micro-resonator's motion causing kinetic energy loss from the resonator to the surrounding air and the Q factor increases exponentially as pressure decreases. As for the intrinsic damping region, air damping decreases while the Q factor levels off to a constant (typical Q > 105, Kn is high) at a high vacuum (P < 1 Pa). The energy loss is from air damping is no longer significant and dominant energy loss is from TED and anchor loss. Air molecules are far away from each other in this regime and there is no appreciable interaction with the moving mass.

The above-mentioned studies show that even with vacuum seal packaging, several mechanisms limit the obtaining high Q factor. Q factor depends on air gap distance between comb fingers, surrounding walls and gas properties inside the device. The combination of all these damping effects inside vacuum sealed resonators in one single modeling technique has not been explored, thus this paper will present a detailed analysis of air damping effects on sealed micro-resonator at various pressure regions.

The following section aims to perform analysis of the air damping effect on a sealed micro-resonator at various vacuum regions to provide a model to predict the air damping loss and use it to design resonator with low damping. It is critical to present the analytical and numerical modelling techniques to provide a complete understanding of air damping in MEMS resonators. Analytical modelling is developed based on various formulae available in the literature and is presented as a baseline in Sect. 2. Next, Finite Element Analysis (FEA) based numerical modelling of a vacuum-sealed MEMS resonator using the simulation tool COMSOL Multiphysics 5.5 is developed to investigate damping and its relationship with resonator design and cavity pressure parameters by recreating the actual operating environment of the resonator in Sect. 3. Section 3 also compares Q factor in different vacuum regions using both analytical and FEA approaches. In Sect. 4 a qualitative comparison of the model results is presented and compared to previous measurements from literature.

2 Analytical modeling

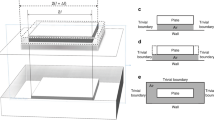
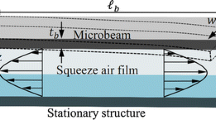
Analytical analyses using various simple formulation are available in the literature to relate air damping on MEMS resonator. These models provide a baseline way to validate the FEA simulation results that should be consistent with analytical results. During the plate’s movement, the viscous air flow dissipates some of the energy and transfers it into heat (Bao et al. 2002). When the movable plate is placed in parallel to the fixed fingers and moving towards the fixed fingers, the air film between movable plate and fixed finger is squeezed so that some of air flows out of the air gaps as shown in Fig. 2. Additional pressure develops in the air gaps due to the viscous flow of the air (Christian 1966). In other words, the air acts as a damper. Gas viscous damping is classified into three categories: slide-film gas damping, squeeze film gas damping, and gas drag damping (Christian 1966). Squeeze-film damping occurs when the moving plates is moving toward to the fixed wall (Fig. 3a) (Itoh et al. 2003; Tang and Zhang 2019). Slide film damping occurs when the movable plate moves parallel to the fixed wall (Fig. 3b) (Dennis et al. 2015; Bao and Yang 2007). Gas drag damping is cause by momentum transfer from gas particles hitting the moving structure, it is negligible at the pressure regions explored in this paper (Boom et al. 2021).

Fig. 2
figure 2

Pressure built-up by squeeze-film motion when the moving plate moves toward fixed fingers. Air gap distances determine the magnitude of squeeze film damping between the movable plate and the fixed wall (Bao 2005)

Full size image
Fig. 3
figure 3

Air damping mechanism in MEMS devices: a squeeze-film damping (movable plate moves toward fixed fingers or fixed wall) and b slide-film damping (movable plate slip to adjacent fixed walls or fixed comb) (Hutcherson and Ye 2004)

Full size image

The damping force of squeeze film air damping is strongly dependent on the air gap distance. The larger the gap, the smaller the damping force generated, and the pressure change between the combs is negligible. When the moving plate moves closer to the fixed finger, smaller air gaps are generated. The pressure build-up in between finger and moving plate create a larger damping force and causes the low-quality factor. Squeeze-film air damping has crucial effects on the dynamic behaviour of micro-structure since our structure comb fingers are used for sensing the capacitance change. There is a trade-off between electrical and mechanical performance. A small gap is desirable to increase capacitance for electrical detection but decreases the Q factor through squeeze-film damping. Modern packaging techniques can achieve low pressures around 1 Pa, but may leak over time (Pickering et al. 2018).

Slide-film coefficient can be derived from the Navier stokes equation (Wang et al. 2013):

$${C}_{Slide,top}={\mu }_{eff}\frac{{A}_{overlap}}{{d}_{pt}}$$
(2)
$${C}_{Slide,bottom}={\mu }_{eff}\frac{{A}_{overlap}}{{d}_{pb}}$$
(3)

where \({C}_{Slide,top},{ C}_{Slide,bottom}\) are the slide film damping coefficient exist in the air cavity above the device and bottom of the device. The air viscosity (μ = 1.75e−5 Pa.s) is the air viscosity constant at room temperature (20 °C), it needs to be converted to effective viscosity due to pressure change \(\left({\mu }_{eff}=\frac{\mu }{\left(1+6{K}_{n}\right)}\right)\)(Jennings 1988) which increases relative to cavity pressure (Wang et al. 2013). \({A}_{overlap}\) \((3.68E-6 {m}^{2})\) is overlapping plate area, \({d}_{pt}\) (50 µm) is the air cavity distance between device wafer and lid wafer. And \({d}_{pb} (20 \mu m)\) is the air cavity distance between device wafer and base wafer (\({d}_{pb}{, d}_{pt}\) are considered as dp shown in Fig. 4, when dp is reduced by 10 µm it will increase the slide film damping by 0.0005 µNs/m slide film damping coefficient).

Fig. 4
figure 4

Three silicon wafers bonded together as one device to create a vacuum encapsulated MEMS device structure. The slide film damping exists in the cavities above (dpt) and bottom (dpb) of device wafer and the squeeze film damping exists between movable plate and fixed comb in the device wafer

Full size image

The squeeze film air damping coefficient can be expressed by the semi-theoretical and semi-empirical expression (Wang et al. 2013):

$${C}_{Squeeze}={\mu }_{eff}\frac{{L}_{x}{{L}_{z}}^{3}}{{g}^{3}}\beta \left(\frac{{L}_{z}}{{L}_{x}}\right)$$
(4)

Beta function β (Lz /Lx) could be represented by Wang et al. (2013):

$$\beta \left(\frac{{L}_{z}}{{L}_{x}}\right)=\left\{1-\frac{192}{{\pi }^{5}}\left(\frac{{L}_{z}}{{L}_{x}}\right){\sum }_{n=\mathrm{1,3},5}^{\infty }tanh\left(\frac{n\pi {L}_{x}}{{L}_{z}}\right)\right\}$$
(5)

where Lx, Ly, Lz are movable finger length, width, and device thickness. Beta function β (Lz /Lx) is equal to 0.85.

This section explains where the slide film damping, and squeeze film damping occur on the micro-resonator. Several geometric parameters can be exploring to optimize the micro-resonator structure to reduce energy loss from the slide film and squeeze film damping effect. Those parameters (comb finger length (Lx), structure thickness (Lz), air gaps (g), overlap area \({A}_{overlap}\), and air cavity (\({d}_{p}\)) need to be analysed for the desired geometry.

A 2D top view of a micro-resonator structure considered in this study is shown in Fig. 5a. A rectangular single mass resonator is selected for this study as it is one of the classical shapes in MEMS resonator involving comb drives, fixed structures, and a moveable mass suspended over a cavity. The device consists of the movable plate (proof mass), 8 pieces of fixed combs and four folded beams (springs) at the top and bottom of the structure. The device is anchored at the edge of the four corners and inner fixed comb fingers. Electrostatic force is applied to actuate the micro-resonator which oscillates in the motion direction at the resonant frequency as shown in Fig. 5b.

Fig. 5
figure 5

a Schematic top view of a micro-resonator. Symmetric structure minimizes anchor loss, air gaps exist between moving fingers and fixed fingers. Each corner is fixed by anchors and folded beams allow moving plate to move up and down to sense the changes in the capacitance between fixed finger and moving fingers. b The desired mode shape of vibration showing the movable structure of the micro-resonator (blue color) allows it to oscillate in the vertical direction at its resonance frequency (784 Hz)

Full size image

The electrostatic force directly depends on the applied voltage, higher voltage creates a larger force. The air gaps exist between the movable comb finger and the fixed comb fingers and between top and bottom spring hinges (Fig. 5a) The device is symmetric in two directions, resulting in equal damping and restoring forces. The gaps between moving and static fingers are 2.6 and 10 µm. When the device moves in one direction, both gap sizes are closing (half of each) and so both must be considered in any analysis.

Several parameters were investigated including the pressure (P), proof mass size, comb size, and spring geometry on device performance. A simple resonating MEMS device shown in Fig. 4 was designed for a commercially available vacuum encapsulated environment known as MicraSilQ (Pickering et al. 2018). Table 1 shows that the resonating structure has proof mass size of (L, W, H) 2430 µm x 2323.6 µm x 60 µm. The length (\({\mathrm{l}}_{\mathrm{cf}}\)), width (Wcf\()\), and thickness (\({t}_{cf}\) of the comb fingers are 240 µm, 18.7 µm, and 60 µm, respectively. The area of plate for slide film damping (Aslide) is 3.68E−6 m2. The overlap area for squeeze film damping (\({A}_{overlap}\) is 2.29 E−6 m2. The dimension of hinge length (\({\mathrm{H}}_{\mathrm{l}}\)), hinge width (\({H}_{w}\)), fold width (\({W}_{c2}\)), and fold height (\({L}_{c2}\)) are 1118 µm, 8.9 µm, 32 µm, and 24.8 µm, respectively, shown in Fig. 6 (Suttisintong and White 2015). The folded beam functions as a spring It allows the resonator to vibrate in the desired vertical direction. The micro-resonator design consists of four pieces of identical dimensions with the beam in each corner of the micro-resonator (Fig. 5a).

Table 1 Various geometry parameters, dimensions and the baseline values
Full size table
Fig. 6
figure 6

Folded beam, showing hinge length and width of 2D view resonator in Fig. 2 (Tang and Zhang 2019)

Full size image

According to Eq. 4, squeeze film damping coefficient is directly proportional to the comb finger length (Lx) and structure thickness (Lz) and inversely proportional to the air gap (g). Using a fixed pressure of 100 Pa and overlap area 3.68 mm2, comb finger length, Lx, (20–200 µm, 2–10 µm) and structure thickness, Lz, (20–80 µm, 1–5 µm) cause the squeeze film damping coefficient to exponentially increase shown in Fig. 7a and b respectively. Smaller air gaps, g (0.5–6.5 µm), between comb fingers generate a larger squeeze film damping coefficient in Fig. 7c. According to Eqs. 2 and 3, the slide film damping coefficient is affected by overlap area \({A}_{overlap}\) and air cavity \({d}_{pb}\). Figure 7d shows the slide film damping coefficient is mainly influenced by overlap area (air cavity have less effect on) with the assumption of Pressure 100 Pa, comb finger length Lx (240 µm), and device thickness Lz (60 µm). In a damped mass-spring system, the quality factor can be expressed as:

$$Q=\frac{1}{2\xi }$$
(6)

where the \(\xi\)=C/2 \(\sqrt{km}\) is the damping ratio.

Fig. 7
figure 7

3D surface plot shows the squeeze film damping coefficient and the slide film damping coefficient versus different parameters: comb finger length (Lx) and structure thickness (Lz) cause an exponential increase in the squeeze film damping coefficient as seen in (a) and (b). c Reducing the air gap results in a higher squeeze film coefficient. d The overlap area influences the slide film damping coefficient linearly

Full size image

The analytical results presented in this section shows the dependence of geometric parameters with damping however it does not provide a detailed dynamic understanding of effect of pressure on Q-factor and frequency which will be presented in the next section with the help of finite element model.

3 Numerical modeling

Numerical simulation gives us the opportunity to explore many design variations for MEMS devices to target better dynamic performance and computationally perform experiments on various design parameters. While the analytical results presented in the previous section can provide general guidance for simple designs, complicated geometry and nonlinear effects require a different approach to produce predictive results. FEA techniques are widely used to perform virtual experimentation of micro-scale devices. In our application, the finite element simulation needs to re-create the surrounding medium inside the sealed cavity and allow simulation of device actuation, damping and dynamic responses. The problem involves solving solid mechanics and viscous damping, creating a multiphysics problem. A Finite Element Analysis (FEA) model was developed for the micro-resonator to simulate its operation at various pressures using simulation tool COMSOL Multiphysics (Manual 1742) which allows solving coupled multiphysics.

FEA simulation allows for quicker and often more efficient and accurate prediction and optimization of the design than analytical techniques. Particularly for expensive MEMS fabrication with the added complication of vacuum sealing, creating a model that can simulate a vacuum sealed environment is useful. The first step of FEA is to define the geometry shown in Fig. 8. The geometry is enclosed by the air with the dimension of 4000 µm × 4000 µm × 920 µm (Fig. 8). The second step is to specify an air domain around the resonator device (include air gaps in between comb fingers and folded beams) as shown in Fig. 8. The air domain around the resonator has cavities providing a space to allow resonator vibration. The air domain is separated into two regions: thermoviscous acoustic and pressure acoustic. These two physics allowed for adjustment of the pressure inside the volume.

Fig. 8
figure 8

Schematic 3D finite element model of micro-resonator, thermoviscous acoustic frequency domain applies in the air domain around micro-resonator, the pressure acoustic frequency domain applies in the outer frame of air domain

Full size image

Thermoviscous acoustic physics defines a volume around the resonator (inner frame of air domain), allowing changes to the equilibrium pressure, which is used to set the air pressure around the device. Setting a lower equilibrium pressure will establish high vacuum. This thermoviscous acoustic physics needs to work with pressure acoustic physics to adjust the acoustic pressure and absolute temperature in the outer frame air domain (Manual 1742), representing atmospheric pressure outside of the vacuum chamber. This pressure acoustic sets 25 °C and one atmosphere as an acoustic pressure.

Furthermore, adding the boundary condition is crucial for the simulation. The acoustic-thermoviscous boundary is set as the surface of the air domain around the resonator and the thermoviscous acoustic structure boundary is automatically selected from the imported geometry as the edge of each air gaps around the comb fingers of the resonator as seen in Fig. 8. Frequency domain analysis was performed to simulate the frequency response and predict the Q value at various pressures. The frequency-domain study adjusts frequency ranges of start frequency, end frequency, and frequency step. Solid mechanics, thermoviscous acoustic, and pressure acoustic and multiple physics couplings like acoustic-thermoviscous acoustic boundary and thermoviscous acoustic structure boundary applies to the model shown in the frequency domain as well. The goal of FEA model is to capture the relationship between the quality factor (Q) and sealing air pressure (P). Figure 9 gives a direct relationship between pressure versus Q factor. This curve of the quality factor illustrates that the quality factor exponentially increases with decrease of pressure.

Fig. 9
figure 9

Combination of Q factor vs varied pressure ranges between 0.0005 and 100 Pa. This finite element model plot classified into intrinsic damping region and molecular damping region

Full size image

The change in pressure can be understood through a few parameters. When the pressure decrease, atmospheric air viscosity \(\left({\mu }_{atm,air}\right)\) changes to the effective air viscosity \(\left({\mu }_{eff,air}\right)\). The squeeze film damping coefficient \({(C}_{Squeeze})\), and the slide-film damping coefficient (\({C}_{Slide}\)) decrease with the pressure decrease (\(Q=\frac{m\omega }{c}=\frac{k}{c\omega }=\frac{\sqrt{km}}{c}\) from Eq. 1).

However, Q factor increases when the pressure decreases (Fig. 9). Another variable impacting Q factor in these pressure regions is the air gap (g) between moving fingers and fixed fingers. Similar behavior was noticed in Hutcherson and Ye (2004). Air gap distances, g, in between comb fingers strongly influence the squeeze film damping coefficient shown in Fig. 10. The larger the air gap, the smaller the squeeze-film air damping coefficient resulting in a higher Q value. To achieve sensitive detection, the gap size should be kept as small as possible which increases capacitance and therefore signal.

Fig. 10
figure 10

Damping due to air gaps between comb fingers. The smaller air gaps generated the larger squeeze-film air damping coefficient, which developed a smaller Q value. In contrast, the larger the air gaps, the smaller squeeze-film air damping coefficient is generated, which developed a higher Q value

Full size image

This section has used FEA techniques to capture amplitude results in three pressure regions and demonstrates the proportionality of the reciprocal of the air pressure to the amplitude and Q factor. The Q factor is also directly proportional to the air gaps (g). To understand the characteristics of air damping at near high vacuum, it is important to perform analysis to capture Q-factor change at near high vacuum damping region (intrinsic damping region). Figure 11 compares Q factor from FEA model simulations and analytical modelling of squeeze film and slide film damping. This figure shows a trend between the Q factor and pressure in the molecular damping (1 < Pa < 100) and intrinsic damping (0.0005 < Pa < 1) regions. As pressure decreases, Q value exponentially increases until it levels off. The red curve is analytical research from Eqs. 2–6. This analytical Q is a combination of squeeze film (blue circle) and slide film analysis (green). The dominant damping at these pressures is squeeze film which closely matches the analytical Q. In this case, slide film damping has less influence on the overall Q factor. Both methods (FEA and analytical model) have a good agreement.

Fig. 11
figure 11

Comparison between FEA model and analytical showing similar relationships between pressures and Q factor

Full size image

Zhou et al. (2014) has discussed the early works of micro-resonator on squeeze-film damping. Bao has developed a direct method, known as energy transfer model, to study squeeze-film damping at low pressure (Bao et al. 2002). The micro-resonator being examined here moves on one axis motion in the vertical direction.

The energy loss from the vibrating plate is absorbed by the air molecules.

$$\Delta {E}_{cycle}=\frac{\pi \overline{{l }^{2}}{{A}_{0}}^{2}\omega }{16}{\rho }_{0}\overline{\nu }\frac{L}{{g}_{0}}$$
(7)

The quality factor for squeeze-film air damping by energy transfer model in low vacuum is

$${Q}_{E,Sq}=\frac{2\pi {E}_{p}}{\Delta {E}_{cycle}}=\frac{2\pi \frac{1}{2}{M}_{p}{{A}_{0}}^{2}{\omega }^{2}}{\frac{\pi }{16}\overline{{l }^{2}}\omega {\rho }_{0}\overline{\nu }\frac{L}{{g}_{0}}}=\frac{16{M}_{p}{g}_{0}\omega }{\overline{{l }^{2}}{\rho }_{0}\overline{\nu }L}$$
(8)

where \({E}_{p}\) is the energy of the plate, Mp is the mass of plate. \({A}_{0}\) is the vibration amplitude. L is peripheral length L = 2(Lx + Lz),\(l\) is the molecule lateral traveling distance between movable fingers and fixed fingers.\({\rho }_{0}\) is the density of the gas. \(\overline{v } (\sqrt{\frac{8KT}{\pi m}})\) is average velocity of molecules. go is the original distance between the movable finger and fixed fingers.

Equations 7 and 8 were used to derive the following Eq. 9. Therefore, the quality factor for squeeze-film air damping by the energy transfer model in medium vacuum (free molecular damping pressure region) related to pressure is

$${Q}_{E,Sq}=\frac{16{M}_{p}*{g}_{0}*\omega {P}_{atm}}{{\rho }_{atm}*\overline{v}*L\overline{{l }^{2}}}\frac{1}{P}$$
(9)

where \({\rho }_{atm}\) is the specific mass of air molecular at atmospheric pressure.

Figure 12 shows the results of the energy transfer model for squeeze-film air damping in low pressures from Bao et al. (2002). This technique yields a Q-factor an order magnitude lower than the Q from finite element modelling for pressures less than 40 Pa. Experimental results will be presented in future work to validate and adjust the available three models.

Fig. 12
figure 12

Combination of the Q-factor from FEA, analytical, and literature model comparing the various model approaches. Analytical Q is combination of Qair, QTED, and QAnchor

Full size image

The numerical simulation results in this section showed how the pressure inside the cavity would impact the device's performance. It showed how to develop the finite element model, provided predicted Q factor for the designed geometry, and explored the relationship between the amplitude versus frequency at pressure regions between 10 and 100 Pa, 1–10 Pa, and below 1 Pa. It also combined the different pressure ranges into one plot, as shown in Fig. 9. Figure 11 compares Q factor from FEA model simulations and analytical modelling techniques to show good agreement on the behavior of Q factor in the same curve trend relationship, concluding that the pressures decrease, the Q factor exponential increase until it levels off (P < 0.1 Pa). Figure 12 compares Q factor from Bao’s energy transfer model with FEA and numerical analysis. Bao’s energy transfer model shows Q-factor an order magnitude lower than the Q from finite element modelling for pressures less than 40 Pa.

4 Comparison of model results with previous experiments

The previous experimental results from the literature (Ghaffari et al. 2015; Candler et al. 2006) use a similar air damping analysis with the MEMS resonator devices. In those experimental setups air is present in the vacuum chamber which is used to adjust the pressure for testing air damping effects on a device in the vacuum chamber. For example, N. Candler (Candler et al. 2006) establishes the MEMS resonator with single-anchored, double-end tuning fork structures, and resonant frequency of near 150 kHz, which shows the quality factor of the sealed encapsulated resonator at pressures ranging between 0.01 and 10 Pa. Ghaffari (Ghaffari et al. 2015) tested the experimental Q of a disk resonator at ~ 247 kHz between 0.1–100 Pa and the highest Q was around 150,000 at 0.6 Pa (Q is level off below 0.6 Pa). To make a comparison between the experimental results, our model and previously reported models (Hutcherson and Ye 2004; Bao et al. 2002), the Q factor values are normalized by the maximum Q factor. Frangi et al. (2016) performed Q factor measurement on comb finger devices and found that around 10–2 mbar the Q factor reaches a plateau near a Q factor of 105. Normalized data from Fig. 11 was used to produce Fig. 13 for comparison with our finite element analysis and analytical analysis with others. Changes in the pressure result in a change of Q/Qmax. This figure illustrates a trend as the pressure decreases, the quantity Q/Qmax exponentially increases. The comparison shows good agreement in estimating the intrinsic Q-factor and similar exponential trend for pressure between 1 to 100 Pa between our FEA model and previous experimental results from other research works.

Fig. 13
figure 13

Normalized Q factor versus pressure of various resonators at low pressures. Comparison between FEA results, an analytical model presented in this paper, along with previously reported experimental and model results

Full size image

5 Conclusion

This paper explores the design of a resonator for vacuum encapsulation using finite element analysis, and analytical analysis, presenting a comparison with the various previous model and experimental results. In this study, the comparison of finite element model simulation, analytical damping analysis and previous experimental results shows good agreement in these three pressure regions. The pressure between 1 and 100 Pa is in the molecular damping region (medium vacuum), and air damping is the dominating loss in low to medium vacuum. However, intrinsic losses, such as anchor loss and thermoelastic damping loss, dominate at a high vacuum in the pressure range of 0.1 to 10–5 Pa. The Q factor from FEA and analytical simulations and previous experiments exponentially increase when the pressure decreases. The amplitude of motion and Q factor increase proportionately with the reciprocal of the air pressure. The Q factor is also directly proportional to the air gap distance (g). The major energy loss for the device being evaluated is from squeeze film damping.