1 Introduction and related work

Mobile robots are utilized in a broad range of applications including the industrial sector, nuclear power plants, space research, underwater investigation, domestic purpose, medical support etc., therefore regarded as smart operating tools (He et al. 2019; Patle et al. 2019; Liao et al. 2021). For a robot to operate effectively, path planning is one of the essential control parameters. Path planning may be considered as an optimization issue whose aim is to identify a path from the initial location to the destination through numerous waypoints in a cluttered environment without colliding with the obstacles (Dolgov et al. 2008). It is divided into two categories such as global path planning and local path planning. In global path planning, the mobile robot must have previous knowledge of the environment such as obstacle location, and target location. On the other hand, local path planning does not need prior knowledge of the surroundings. Global path planning methodology works in an entirely known environment. Whereas, local path planning operates in a partially known or unknown environment. Each of the aforementioned scenarios require distinct path planning approaches.

Path planning research emerged in the late 1960s, and different approaches have been introduced including dynamic programming (DP) (Cesarone and Eman 1989), \({A}^{*}\) approach (Loong et al. 2011), Dijkstra approach (DA) (Wang et al. 2011), roadmap approaches (Clark 2005), and potential field (Xu and Park 2020). The main disadvantages of these approaches are smoothness, local minima issue and high computational costs. Researchers have always been looking for alternative strategies and more effective methods to solve these issues. Various meta-heuristic approaches have been used in previous studies to solve these challenges. These approaches include particle swarm optimization (PSO) (Huang and Tsai 2011), genetic algorithm (GA) (Arora et al. 2014), cuckoo search approach (CS) (Mohanty and Parhi 2016), sparrow search algorithm (Zhang et al. 2021), bacterial foraging optimization (BFO) (Hossain and Ferdous 2015), artificial bee colony (ABC) (Kumar and Sikander 2022), and ant colony optimization (ACO) (Yen and Cheng 2018). In contrast to other approaches, each approach has its own pros and limitations. These algorithms have several advantages such as the capacity to do a global search, need for fewer tuning parameters, the ability to solve unconstrained problems in a short amount of time, and so on. In recent years, some new intelligence path planning algorithms have performed excellently such as DDM (Diversified-path Database driven Multi-robot Path planning) algorithm (Han and Yu 2020), MOD-\({RRT}^{*}\) (Multiobjective dynamic rapidly exploring tree) (Qi et al. 2021) and Self-Adaptive Harmony Search Algorithm (Quan et al. 2021). Han and Yu (2020) introduced a unique DDM algorithm with two alternative strategies, the first of which is to move a collection of robots from their beginning vertices to target vertices as fast as possible, and the second of which is to demand frequent re-planning to account for target configuration changes. This algorithm is not suitable for path planning in narrow passages due to its concise mechanism. Also, Qi et al. (2021) proposed a MOD-\({RRT}^{*}\) algorithm that selects the best node among several nodes by considering the path length and path smoothness. This algorithm suffers from the limitation of longer path length due to the random sampling approach. Similarly, Quan et al. (2021) developed an improved version of the harmony search algorithm to improve the neighbours, self-adaptive and probability disturbance updating strategies. Although this algorithm has better search accuracy, its disadvantages are randomness and instability.

However, many prior literature appreciated the use of Particle swarm optimization (PSO) to solve the path planning issues. A lot of research has been done on PSO due to its concise mechanism and few control parameters. Still, there are some challenging issues such as easily trapped in local minima and lacking guarantee in optimal solutions. To tackle the issues outlined above, numerous updated variants of PSO have been developed to produce a feasible path. A mutation-based technique has been utilized by Gong et al. (2011) to repair the incorrect paths by using the self-adaptive mutation operation. Zhang et al. (2013) developed a multi-objective PSO that depends on a random sampling of particles for mobile robot path planning in the test area with unpredictable danger sources. Also, Deepak et al. (2014) presented a fitness function-based approach that mainly depends on the distance of each particle to the target location. Another recent study on this topic is presented by Li and Chou (2018) and Zhang et al. (2020). Li and Chou (2018) introduced a self-adaptive learning mechanism using different learning strategies and a new bound violation handling scheme to improve the feasibility of the acquired paths. Similarly, Zhang et al. (2020) developed an improved localized PSO that uses the extended Gaussian distribution, inertia weights, and interpolation-based path smoothness principle to enhance the search ability.

The aforementioned researchers conducted a number of experiments to prove the effectiveness of the suggested approach, although there are still some shortcomings:

  • Most studies employ a random sampling strategy. The random sampling strategy does not ensure to provide the global optimal solution every time (Clark 2005; Zhang et al. 2013; Deepak et al. 2014). This will increase the path length.

  • In the case of high dimensional and complex terrains, the existing literature faces various learning ability issues such as slow convergence rate, weak adaptability and weak exploration ability (Huang and Tsai 2011; Deepak et al. 2014; Yen and Cheng 2018).

  • Past study uses the inertia weight factor strategy. Which increases the computational load. Therefore, the processing time of the acquired path increases (Li and chou 2018; Zhang et al. 2020).

  • Most algorithms do not vary the number of particles or samples or populations while calculating the performance indices such as path length and processing time, as variation in samples plays an important role to authenticate the effectiveness of the proposed approach (Huang and Tsai 2011; Deepak et al. 2014; Mohanty and Parhi 2016; Yen and Cheng 2018).

To address these limitations, establishing an intelligent optimum path planning approach in complex terrain would be effective and beneficial, which is the primary goal of this research study. Therefore, this research study presents an intelligent modified particle swarm optimization (IMPSO) approach for resolving mobile robot path planning issues in a complex terrain. The innovations and key contributions of this research work are outlined as follows.

  • A velocity regularized strategy based on regularized coefficients has been applied to balance the exploration and exploitation ability.

  • A neighborhood search strategy based on reward value and utilization probability has been employed, enriching search behaviors and avoiding premature convergence.

  • A path smoothness principle based on hypocycloid curves has been used to smooth the sharp turns.

  • The proposed approach is validated and analyzed against the GA-PSO (Huang and Tsai 2011), Advance PSO (Deepak et al. 2014), FACO (Yen and Cheng 2018), and other conventional approaches in terms of different performance indices.

  • The comparative studies are conducted in four different small and large dimension terrain with different complexity.

  • The performance and effectiveness of the proposed IMPSO are validated using simulation outcomes.

The rest of the research work is outlined in the following ways. The problem formulation and performance indices are presented in Sect. 2. The proposed methodologies for mobile robot path planning are introduced in Sect. 3. In Sect. 4, a set of simulation findings are presented that demonstrate the proposed technique's efficacy compared to prior research. Finally, the conclusion of the research study is presented in Sect. 5.

2 Problem formulation and performance indices

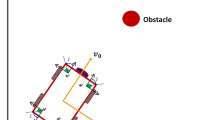
A model should firstly be constructed in order to develop an efficient trajectory path for a mobile robot. Figure 1 shows a two-dimensional corridor like terrains (terrain #1, terrain #2, terrain #3, and terrain #4) with different dimensions. These terrains comprise all entities such as obstacles, mobile robot, number of samples or population size, initial and target locations with different shapes and sizes. The mobile robot is represented as \(R\) (with radius \({r}_{ROB}\)) having its coordinate \(C({x}_{0},{y}_{0})\).

Fig. 1
figure 1

Model of different terrains a terrain #1; b terrain #2; c terrain #3; d terrain #4

Full size image

A green circular object signifies the initial location, which is denoted by \(S({x}_{0},{y}_{0})\). Whereas, a red circular object signifies the target location denoted by \(T({x}_{t}, {y}_{t})\). The mobile robot at the initial location uses a number of samples to find the next best current location. Within the sensor detection range, generate a map that joins the initial and target location. To execute the task of predicting the behaviour and location of obstacles, the sensor range of the mobile robot is divided into four circles having radii \({\mu }_{1}, {\mu }_{2}, {\mu }_{3},\) and \({\mu }_{4}\) as presented in Fig. 2. The range of sensors depends upon its types. There are various types of sensors used in mobile robots such as infrared, ultrasonic, tactile, GPS, etc. The goal of path planning is to discover an effective path without colliding with any obstacle’s regions. If the robot encounters any obstacles in its path, it must move some angles, either left or right, without colliding to reach the desired target location. In order to solve the path planning problem, certain assumptions are taken in this research study.

Fig. 2
figure 2

Sensor range with regards to obstacles location

Full size image

Assumption 1. The obstacles are depicted as rectangular shapes with static in nature.

Assumption 2. The test scenario is partially known or unknown for the robot.

Assumption 3. Robot have some sensor range and it can move in any direction due to its omnidirectional nature.

2.1 Performance indices

Path planning tries to construct the best possible collision-free path while taking into consideration specified performance indices. This study focuses on path length, processing time and smoothness.

(a) Path length

The objective is to acquire the shortest path as much as possible. Suppose, the initial and target locations are \(N_{F0}\, and\, N_{{F\left( {N + 1} \right)}}\), then the path length can be calculated as:

$$P\left( F \right) = \mathop \sum \limits_{i = 0}^{N} N_{{F\left( {i + 1} \right)}} - N_{F\left( i \right)}$$
(1)

where \(N_{{F\left( {i + 1} \right)}} - N_{F\left( i \right)}\) denotes the Euclidean distance between \(N_{F\left( i \right)}\) and \(N_{{F\left( {i + 1} \right)}}\).

(b) Smoothness

The smoothness is computed by summing the robot's turning angles along the predefined path. The formula below can be used to calculate the smoothness.

$$S\left( F \right) = \mathop \sum \limits_{i = 1}^{N} \gamma_{i} = \mathop \sum \limits_{i = 1}^{N} arccos\left( {\frac{{\left( {N_{F\left( i \right)} - N_{{F\left( {i - 1} \right)}} } \right).\left( {N_{{F\left( {i + 1} \right)}} - N_{F\left( i \right)} } \right)}}{{\left| {N_{F\left( i \right)} - N_{{F\left( {i - 1} \right)}} } \right| \times \left| {N_{{F\left( {i + 1} \right)}} - N_{F\left( i \right)} } \right| \times 180}}} \right)$$
(2)

where \(\gamma_{i}\) represents the value of the acquired path’s \(ith\) turning angle (measured in radians ranging from \(0 to \pi\)). \(\left( {F_{i} - F_{i - 1} } \right).\left( {F_{i + 1} - F_{i} } \right)\) are the inner product of two vectors.

(c) Improvement (%)

$$Improvement \left( \% \right) = \left( {\frac{{X_{Conventional} - X_{Proposed} }}{{X_{Conventional} }}} \right) \times 100$$
(3)

where X can be any performance indices.

3 Proposed Methodology

This section outlines the complete path generation process in two stages. The first stage describes the stranded Particle Swarm Optimization (PSO), while the second stage introduces the proposed approach (Intelligent Modified Particle Swarm optimization). Three modules are included in the proposed IMPSO. A velocity regularized strategy is used in the first module, whereas a neighborhood search strategy is utilized in the second module. Lastly, a path smoothness principle is applied in the third module. Figure 3 represents the proposed methodology.

Fig. 3
figure 3

Proposed Methodology

Full size image

3.1 Standard PSO

James Kennedy and Russell Eberhart introduced Particle Swarm Optimization in 1995. PSO is a population-based stochastic optimization approach that is inspired by the social behavior of flocks of birds. Initially, all of the birds travel at random velocities and positions, but after a period, depending on their own flying experience and that of the other birds, all of the birds begin to follow the bird closest to the food. All birds or particles in PSO have two attributes i.e. position and velocity. These particles are introduced into the search space of a problem or function. The fitness values associated to the fitness function are calculated for each particle, and two best fitness values are obtained; the first is the best fitness value a particle has attained so far known as 'pbest'. The second is the best fitness value attained so far by the whole swarm, which is referred to as 'gbest.' In the d-dimensional search space, the ith particle’s velocity and position can be represented as \({V}_{i}=[{v}_{i,1}, {v}_{i,2},\dots , {v}_{i,d}]\) and \({X}_{i}=[{x}_{i,1}, {x}_{i,2}, \dots , {x}_{i,d}]\), respectively. Each particle has its own best position (pbest), \({Pb}_{i}=\left[{p}_{i,1}, {p}_{i,2}\dots ,{p}_{i,d}\right]\) which corresponds to the personal best objective value attained so far at time t and the best one among \({Pb}_{i}\) in a group is designated as the global best particle (gbest) denoted by \(P_{g}\). In each iteration \(t\), the velocity and position of each particle is computed as follows

$$v_{i,j} \left( {t + 1} \right) = wv_{i,j} \left( t \right) + \eta_{1} r_{1} \left( {Pb_{i} - x_{i,j} \left( t \right)} \right) + \eta_{2} r_{2} \left( {P_{g} - x_{i,j} \left( t \right)} \right), j = 1, 2, \ldots d$$
(4)
$$x_{i,j} \left( {t + 1} \right) = x_{i,j} \left( t \right) + v_{i,j} \left( {t + 1} \right),$$
(5)

where \(w\) signifies the inertia weight factor, \(\eta_{1}\) and \(\eta_{2}\) represent the personal and global learning coefficients, \(r_{1}\) and \(r_{2}\) are two random numbers that lies in the range of 0 to 1. To restrict excessive roaming of particles beyond the search space, the value of each component in \(V_{i}\) can be clamped to the range \(\left[ { - v_{max} , v_{max} } \right]\). The following are the main procedures of standard PSO.

Step 1. Generate a population of particles with random velocities and positions, each having d variables.

Step 2. Compute the objective values of all particles; set pbest and its objective value equal to the particle's current location and objective value, and set gbest and its objective value equal to the location and objective value of the best starting particle.

Step 3. Update the velocity and location of each particle by using Eqs. (4) and (5).

Step 4. Compute each particle's objective values.

Step 5. Compare the current objective value of each particle to the pbest objective value. If the current value is superior, then replace pbest and its objective value with the current position and objective value.

Step 6. Find the best particle in the current swarm that has the best objective value. If the current best particle's objective value is higher than gbest, replace gbest and its objective value with the current best particle's position and objective value.

Step 7. If a stopping requirement is fulfilled, generally satisfying the fitness value; otherwise, return to Step 3.

The standard PSO has the advantage of having parameters that are easy to adjust and implement. However, some drawbacks still exist in standard PSO, such as improper balance between exploration and exploitation ability, poor searching behaviour, premature convergence, and being easily stuck into local minima.

3.2 Intelligent Modified Particle Swarm Optimization (IMPSO)

To address the drawbacks of standard PSO, a new approach is introduced, the intelligent modified particle swarm optimization. The IMPSO mainly depends on the velocity regularized strategy, neighborhood search strategy, and path smoothness principle. The velocity regularized strategy is based on regularized coefficients and is used to balance the exploration and exploitation ability. A neighborhood search strategy based on reward value and utilization probability has been employed enriching search behaviors and avoiding premature convergence. A path smoothness principle based on hypocycloid curves has been used to smooth the sharp turns.

3.2.1 Velocity regularized strategy (VRS)

Any optimization technique necessitates a trade-off between exploration and exploitation to determine its efficacy. These contradictory features are ideally balanced by an efficient optimization strategy. In standard PSO, velocities of the particles can readily climb to unacceptable levels and sometimes exceed the bounds of the search region within a few iterations. Therefore, a velocity regularized strategy is applied by introducing regularized coefficients to govern the velocities of the particles as well as to keep inside the boundary constraints. The coefficient governs particle movement and leads it toward convergence. The modified particle velocities can be expressed in the following way:

$$v_{{{\text{max}}\left( {i,j} \right)}} = w_{RF} v_{i,j} \left( t \right) + C_{1} r_{1} \left( {Pb_{i} - x_{{{\text{max}}\left( {i,j} \right)}} \left( t \right)} \right) + C_{2} r_{2} \left( {P_{g} - x_{{{\text{max}}\left( {i,j} \right)}} \left( t \right)} \right),$$
(6)
$$v_{{{\text{min}}\left( {i,j} \right)}} = w_{RF} v_{i,j} \left( t \right) + C_{1} r_{1} \left( {Pb_{i} - x_{{{\text{min}}\left( {i,j} \right)}} \left( t \right)} \right) + C_{2} r_{2} \left( {P_{g} - x_{{{\text{min}}\left( {i,j} \right)}} \left( t \right)} \right),$$
(7)
$$v_{i,j} \left( {t + 1} \right) = \left\{ {\begin{array}{*{20}c} {v_{i,j} \left( {t + 1} \right), } & { if v_{i,j} \left( {t + 1} \right) < v_{{{\text{max}}\left( {i,j} \right)}} } \\ {v_{{{\text{max}}\left( {i,j} \right)}} ,} & {otherwise} \\ \end{array} } \right.$$
(8)

where \(x_{{{\text{min}}\left( {i,j} \right)}}\) and \(x_{{{\text{max}}\left( {i,j} \right)}}\) are the minimum and maximum positions of the particles. Here higher value of \(v_{{{\text{max}}\left( {i,j} \right)}}\) encourages exploration whereas lower value encourages exploitation. Also, \(w_{RF} = w*RF\), and \(C_{1}\), \(C_{2}\) signifies the cognitive and social components that impact exploration and exploitation ability as well as the finding of an optimal point in the search area. The \(C_{1}\) and \(C_{2}\) can be computed as follows:

$$C_{1} = RF*\eta_{1}$$
(9)
$$C_{2} = RF*\eta_{2}$$
(10)

where

$$RF = \frac{2}{{\left| {\eta - 2 + \sqrt {\eta^{2} - 4\eta } } \right|}}$$
(11)
$$\eta = \eta_{1} + \eta_{2}$$
(12)

where \(RF\) and \(\eta\) denotes a regularized factor and co-efficient, respectively. Now the regularized particles can help to converge the process towards the optimal solutions and maintain a proper balance between the exploration and exploitation ability.

3.2.2 Neighborhood search strategy

In IMPSO, neighborhood selection is necessary for enriching search behaviors and avoiding premature convergence. In this study, a neighborhood search strategy is used based on the reward value and utilization probability of each particle. The following equation can be used to calculate the reward value for each particle.

$$\beta = \frac{{\left| {pf - cf} \right|}}{{N\left( {N - 1} \right)}}$$
(13)

where \(N\) signifies the total number of particles in the search space, \(pf\) is the function value of each particle whose coordinate is represented as \(\left( {x_{i} ,y_{i} } \right)\) and \(cf\) is the function value of target particle whose coordinate is denoted as \(\left( {x_{t} ,y_{t} } \right).\) After the reward value is obtained, the utilization probability \(\left( {Prob_{uti} } \right)\) of each particle is calculated with the following formula.

$$Prob_{uti, i} = \frac{{\beta_{i} }}{{\mathop \sum \nolimits_{i = 1}^{N} \beta_{i} }}$$
(14)

where \(\beta_{i}\) is the ith particle's reward value, and N represents the total number of populations or particles. A fit neighborhood will be chosen based on the particle with the highest reward value and utilizing probability. Initially, \(N\) particles are scattered in the search area as shown in Fig. 4a. After applying the proposed strategy, the new neighborhood is \(N_{F1}\), \(N_{F2}\), \(N_{F3}\), \(N_{F4}\), and \(N_{F5}\), as depicted in Fig. 4b.

Fig. 4
figure 4

a Model of the search area, b path attained using proposed neighborhood strategy

Full size image

3.2.3 Path smoothness principle

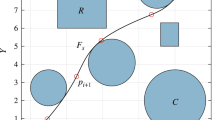
Although the attained path avoids obstacles, still there are too many sharp turns that result in longer path length. To avoid these sharp turns, a path smoothness principle is applied based on hypocycloid curves (Weisstein 2016). The basic steps are outlined as follows.

Step 1. It can be seen from Fig. 5a that a robot traversing form initial (S) to target location (T) encounters sharp turns at points \(N_{F1} ,\) \(N_{F2} ,\) \(N_{F3} ,\) \(N_{F4} ,\) and \(N_{5}\). The complete path from S to T is made up of various line segments labelled \(SN_{F1} ,\) \(N_{F1} N_{F2} ,\) \(N_{F2} N_{F3} ,\) \(N_{F3} N_{F4} ,\) \(N_{F4} N_{F5} ,\) and \(N_{F5} T.\) Each of the six-line segments is represented as

$$y = m_{i} x + c_{i} , i \in \left\{ {1, 2, \ldots 13} \right\}$$
(15)

where \(m_{i}\) and \(c_{i}\) denotes the slopes and the intercepts of the thirteen lines.

Fig. 5
figure 5

a Initial path. b Path after smoothness principle (blue dotted line)

Full size image

Step 2. With respect to line segment \(SN_{F1}\) and \(N_{F1} N_{F2}\), let \(\left( {x_{0} , y_{0} } \right),\) \(\left( {x_{1} , y_{1} } \right)\), and \(\left( {x_{2} , y_{2} } \right)\) be the coordinates of points \(S\), \(N_{F1}\), and \(N_{F2}\). In Fig. 5a, the midpoints of line segments \(SN_{F1}\) and \(N_{F1} N_{F2}\) are \(G\left( {\frac{{x_{0} + x_{1} }}{2},\frac{{y_{0} + y_{1} }}{2}} \right)\) and \(H\left( {\frac{{x_{1} + x_{2} }}{2},\frac{{y_{1} + y_{2} }}{2}} \right)\), respectively. The slope of line \(\overline{{SN_{F1} }} \left( {m_{1} } \right)\) is \(\frac{{y_{1} - y_{0} }}{{x_{1} - x_{0} }}\) and slope of line \(\overline{{N_{F1} N_{F2} }} \left( {m_{2} } \right)\) is \(\frac{{y_{2} - y_{1} }}{{x_{2} - x_{1} }}\). Therefore, the equation of line (\(L_{1} )\) is:

$$y - \frac{{y_{0} + y_{1} }}{2} = - \frac{1}{{m_{1} }}\left( {x - \frac{{x_{0} + x_{1} }}{2}} \right)$$
(16)

For \(L_{2}\), it is

$$y - \frac{{y_{1} + y_{2} }}{2} = - \frac{1}{{m_{2} }}\left( {x - \frac{{x_{1} + x_{2} }}{2}} \right)$$
(17)

Form Eqs. (15) and (16), a first point of turn is determined.

Step 3. Similarly, all point of turn is calculated corresponding to each line segment. Once the point of turn is calculated, the next step is to smooth the path.

Step 4. After calculating the first point of turn corresponding to line segments \(SN_{F1}\) and \(N_{F1} N_{F2}\), the coordinates \(\left( {x_{0} , y_{0} } \right),\) \(\left( {x_{1} , y_{1} } \right)\), and \(\left( {x_{2} , y_{2} } \right)\) are considered as diffused points. From the diffused points \(S\left( {x_{0} , y_{0} } \right),\) \(S_{F1} \left( {x_{1} , y_{1} } \right)\), and \(S_{F2} \left( {x_{2} , y_{2} } \right)\), the angle between the line segments \(\alpha_{max}\) can be calculated by using the cosine rule such as

$$\alpha_{max} = \cos^{ - 1} \left( {\frac{{a^{2} + c^{2} - b^{2} }}{2ac}} \right)$$
(18)

where

$$a = \sqrt {\left( {x_{2} - x_{1} } \right)^{2} + \left( {y_{2} - y_{1} } \right)^{2} }$$
$$b = \sqrt {\left( {x_{2} - x_{0} } \right)^{2} + \left( {y_{2} - y_{0} } \right)^{2} }$$
$$c = \sqrt {\left( {x_{0} - x_{1} } \right)^{2} + \left( {y_{0} - y_{1} } \right)^{2} }$$

For each point of turn, the turns are smoothed by varying the \(\alpha\) from 0 to \(\frac{{\alpha_{max} \pi }}{180}\) by using the following equations

$$x\left( \alpha \right) = \left( {R_{L} - r_{s} } \right)\cos \left( \alpha \right) + r_{s} .\cos \left( {\frac{{R_{L} - r_{s} }}{{r_{s} }}\alpha } \right)$$
(19)
$$y\left( \alpha \right) = \left( {R_{L} - r_{s} } \right)\sin \left( \alpha \right) + r_{s} .\sin \left( {\frac{{R_{L} - r_{s} }}{{r_{s} }}\alpha } \right)$$
(20)

where \(R_{L} = 4 \times r_{s}\). Finally, the smooth path (blue dotted line) has been attained as shown in Fig. 5b. Figure 6 presents the flow chart of path planning using the proposed IMPSO, whereas the pseudo-code of the proposed IMPSO is provided in Algorithm 1.

Fig. 6
figure 6

Flowchart of path planning using the proposed IMPSO

Full size image
figure a

4 Performance evolution

In this part, the outcomes attained by employing the proposed IMPSO are compared by GA-PSO (Huang and Tsai 2011), Advance PSO (Deepak et al. 2014), FACO (Yen and Cheng 2018), and other conventional approaches in terms of different performance metrics. In order to prove the superiority and efficacy of the proposed IMPSO, four distinct terrains with different complexity have been taken into account namely, terrain #1, terrain #2, terrain #3, and terrain #4. The simulation tests of all the techniques were carried out in a corridor-like complex terrains with a size of \(100 \times 100\), \(50 \times 50\), \(400 \times 400\), and \(20 \times 20\) of the literature. The simulation has been carried out using the MATLAB (MATLAB 2020a) programming language with Intel® core i5 4.2 GH processor, hard disk of 500 GB and 6 GB of RAM memory. There is a variation in the number of samples or populations in the search space, such as \(\left[ {N = 40, 80, 120, 160} \right]\) for terrain #1, \(\left[ {N = 50} \right]\) for terrain #2 and \(\left[ {N = 15} \right]\) for terrain #3, and \(\left[ {N = 15} \right]\) for terrain #4. For better performance, the simulation tests were run 50 times with a maximum of 100 iterations. In each terrain, the robot has different initial and target locations. The following are the performance comparison in different terrains:

4.1 Performance comparison in terrain #1

Initially, the mobile robot is standing at the initial location (34, 10) and is required to reach the target location (70, 90). The parameters to be considered are stated in Table 1. As shown in Figs. 7, 8, 9, 10, all the path planning approaches efficiently attained the target without any collision with obstacles. The statistical findings in terms of path length, processing time, and smoothness are graphically presented in Fig. 11 for the different number of samples. As depicted in Fig. 11a, the proposed IMPSO gives the smallest path (112.59, 111.14, 107.50, 106.74) and RRT gives the longest path (237.52, 255.17, 264.34, 285.10) for each value of \(N\). This signifies that the proposed IMPSO easily attain the target location as compared to other approaches. In terms of processing time, the proposed IMPSO surpasses the other approaches, but takes slightly more time (14.07, 17.82, 22.68, 23.07) as compared to PRM (2.20, 3.53, 5.75, 6.01) as displayed in Fig. 11b. In terms of smoothness, the proposed IMPSO provides smoother path (0.8391, 0.8835, 0.8527, 0.7739) as compared to other techniques as shown in Fig. 11c. The reason is that the proposed IMPSO have less sum of turning angles than that of other approaches. This implies that the proposed IMPSO consumes more energy. In addition, the Table 2 clearly illustrate that the proposed IMPSO is more stable as compared to other approaches under the different value of \(N\).

Table 1 Parameters
Full size table
Fig. 7
figure 7

Path found by different path planning approaches when \(N=40\). a \({A}^{*}\) algorithm; b PRM method; c PSO approach; d Dynamic programming; e Dijkstra algorithm; f RRT algorithm; g ABC algorithm; h ABC-EP algorithm; i Proposed IMPSO

Full size image
Fig. 8
figure 8

Path found by different path planning approaches when \(N=80\). a \({A}^{*}\) algorithm; b PRM method; c PSO approach; d Dynamic programming; e Dijkstra algorithm; f RRT algorithm; g ABC algorithm; h ABC-EP algorithm; i Proposed IMPSO

Full size image
Fig. 9
figure 9

Path found by different path planning approaches when \(N=120\). a \({A}^{*}\) algorithm; b PRM method; c PSO approach; d Dynamic programming; e Dijkstra algorithm; f RRT algorithm; g ABC algorithm; h ABC-EP algorithm; i Proposed IMPSO

Full size image
Fig. 10
figure 10

Path found by different path planning approaches when \(N=160\). a \({A}^{*}\) algorithm; b PRM method; c PSO approach; d Dynamic programming; e Dijkstra algorithm; f RRT algorithm; g ABC algorithm; h ABC-EP algorithm; i Proposed IMPSO

Full size image
Fig. 11
figure 11

Comparative analysis of mobile robot path planning using all approaches for different value of \(N\). a Path Length; b Processing time; c Smoothness

Full size image
Table 2 Performance analysis in terms of different performance indices
Full size table

To sum up, it has been clearly analysed from Fig. 11 and Table 2 that the performance parameters of each algorithm change significantly from the initial sample size to final sample size. In case of dynamic programming, A-star, dijkstra, PRM, PSO, and IMPSO, there is reduction in path length as the number of sample increases. Whereas in case of RRT, ABC, and ABC-EP, there is increment in path length as the number of sample increases. The optimal path length acquired by the proposed IMPSO is 106.74 when the sample size is 160. As the number of sample increases, the computational load also increases, which in turn increases the processing time. The minimum processing time taken by the modified IMPSO is 14.07 s when the sample size is 40. In case of smoothness, the proposed IMPSO gives the best smoothness value that is 0.7739 when the number of samples is 160. Overall, the proposed IMPSO performed more efficiently in all path planning performance indices for each number of samples \(N\).

4.2 Performance comparison in terrain #2 \(\left( {50 \times 50} \right)\)

For terrain #2, the mobile robot is at the initial location (1, 1) and is necessary to reach the target (49, 49). The parameters used in GA-PSO (Huang and Tsai 2011) are: global learning coefficient \(\left( {\eta_{1} } \right)\) = 1.5, personal learning coefficient (\(\eta_{2} )\) = 1.5, inertia weight \(\left( w \right)\) = 0.8, crossover probability = 0.7, mutation probability = 0.1, and iterations = 100. The path acquired by the GA-PSO is shown in Fig. 9 in Ref. (Huang and Tsai 2011), whereas the path acquired by the proposed IMPSO is depicted in Fig. 12a.

Fig. 12
figure 12

a Path acquired by proposed IMPSO; b Convergence rate

Full size image

The proposed IMPSO delivers the optimal path length that is 72.18, whereas the optimal path length in GA-PSO is 76.94. It can be observed from Fig. 12b that the proposed IMPSO takes 21 iterations to find the global optimum solutions as compared to GA-PSO, that takes 90 iterations as shown in Fig. 10 in Ref. (Huang and Tsai 2011). This indicates that the proposed IMPSO is more efficient and faster convergence rate to reach the optimal path than GA-PSO. In addition, Table 3 illustrates that the proposed IMPSO is more stable as compared to GA-PSO (Huang and Tsai 2011).

Table 3 Comparison of proposed IMPSO with respect to GA-PSO (Huang and Tsai 2011)
Full size table

4.3 Performance comparison in terrain #3 \(\left( {400 \times 400} \right)\)

For terrain #3, the mobile robot is at the initial location (340, 380) and is necessary to reach the target (10, 10). The parameters used in Advance PSO (Deepak et al. 2014) are: global learning coefficient \(\left( {\eta_{1} } \right)\) = 2, personal learning coefficient (\(\eta_{2} )\) = 2, inertia weight \(\left( w \right)\) = 1.3, population size = 80, and iterations = 100.The path acquired by the Advance PSO is shown in Fig. 13b in Ref. (Deepak et al. 2014), whereas the path acquired by the proposed IMPSO is depicted in Fig. 13a. The proposed IMPSO delivers the optimal path length that is 543.71, whereas the optimal path length in Advance PSO is 659.8. The proposed PSO reduces the path length by 17.59% compared to Advance PSO (Deepak et al. 2014). This signifies that the proposed IMPSO can easily find the optimal path. It can be observed from Fig. 13b that the proposed IMPSO takes 17 iterations to find the global optimum solutions, whereas the algorithm in Ref. (Deepak et al. 2014) does not calculate the convergence rate. In addition, Table 4 demonstrate that the proposed IMPSO surpasses the Advance PSO (Deepak et al. 2014).

Fig. 13
figure 13

a Path acquired by proposed IMPSO; b Convergence rate

Full size image
Table 4 Comparison of proposed IMPSO with respect to Advance PSO (Deepak et al. 2014)
Full size table

4.4 Performance comparison in terrain #4 \(\left( {20 \times 20} \right)\)

For terrain #4, the mobile robot is at the initial location (340, 380) and is necessary to reach the target (10, 10). The parameters used in FACO (Yen and Cheng 2018) are: pheromone factor \(\left( \alpha \right)\) = 1, heuristic factor (\(\beta )\) = 18, pheromone evaporation factor \(\left( \rho \right)\) = 0.4, pheromone intensity coefficient \(\left( Q \right)\) = 1, and population size = 50, and iterations = 100.The path acquired by the FACO is shown in Fig. 14a in Ref. (Yen and Cheng 2018), whereas the path acquired by the proposed IMPSO is depicted in Fig. 14a. The proposed IMPSO delivers the optimal path length that is 27.9647, whereas the optimal path length in FACO is 29.3848. The proposed IMPSO reduce the path length by 4.83% as compared to FACO. It can be observed from the Fig. 14b that the proposed IMPSO takes 19 iterations to find the global optimum solutions as compared to FACO that takes 23 iterations as shown in Fig. 14b in Ref. (Yen and Cheng 2018). The convergence speed of proposed IMPSO increases by 17.39% than that of FACO. This indicates that the proposed IMPSO is more efficient and faster convergence rate to reach the optimal path than FACO. In addition, Table 5 illustrates that the proposed IMPSO surpasses the FACO (Yen and Cheng 2018) in terms of path length and convergence rate.

Fig. 14
figure 14

a Path acquired by proposed IMPSO; b Convergence rate

Full size image
Table 5 Comparison of proposed IMPSO with respect to FACO (Yen and Cheng 2018)
Full size table

5 Conclusion

This research study presents an Intelligent Modified Particle Swarm Optimization (IMPSO) approach with a different strategy to address the path planning issues in a partially known or unknown complex terrain. Firstly, a velocity regularized strategy based on regularized coefficients has been applied to balance the exploration and exploitation ability. Secondly, a neighborhood search strategy based on reward value and utilization probability has been employed enriching search behaviors and avoiding premature convergence. Finally, a path smoothness principle based on hypocycloid curves has been used to smooth the sharp turns. A number of comparison tests have been carried out in a simulation scenario to validate the efficiency and performance of the proposed IMPSO as compared to GA-PSO, Advance PSO, FACO, and other conventional approaches. Moreover, the following results have been achieved:

  • The proposed IMPSO outperforms the conventional approaches in terms of path length and smoothness.

  • In case of processing time, the proposed IMPSO surpasses dynamic programming, \(A^{*}\), dijkstra, PSO, ABC, and ABC-EP, but performs slightly less than PRM.

  • When compared to GA-PSO, Advance PSO, and FACO, the proposed IMPSO reduces path length by 6.18%, 17.59% and 4.83%, respectively.

  • In regards to convergence rate, the proposed IMPSO provides a better convergence rate than GA- PSO and FACO with improvements of 76.66%, 17.39%, respectively.

Form the performance comparison in different terrain, it is clear that the proposed IMPSO perform better in small dimension terrain as well as large dimension terrain. Following this proposed framework, future work will focus on moving obstacles and moving targets in clutter environments.