1 Introduction

Based on the advancement of micro-electro-mechanical system (MEMS) technology, micro-machined vibratory gyroscopes (MVGs) has been becoming popular in technology science and real-life thanks to its advantages over traditional gyroscopes such as small size, light weight, and low power consumption (Yazdi et al. 1998; Dunzhu et al. 2014; Andrei 2006; Acar 2009; Andrei 1999). This device is a kind of micro-sensor used to detect and determine the angular velocity or rotational angle of a body into which the MVG is integrated. The MVG operates based on the “Coriolis effect” to transfer energy from the primary vibration to a secondary one (Acar 2009). These vibrations are in two perpendicular directions and called the driving and sensing direction respectively.

Tuning fork gyroscope (TFG) is known as an anti-phase system with the purpose to cancel the common-mode inputs (Acar 2009). The TFG structure consists of two identical masses connected directly or indirectly by a mechanical frame. The masses are driven in opposite directions but along the same axis (anti-phase mode). When external angular velocity in the vertical axis is applied, the secondary motion of the masses occurs in opposite directions as well. This state increases significantly the performance of TFG (Apostolyuk and Tay 2005; Bumkyoo et al. 2008; Guan et al. 2016). However, the traditional MEMS tuning fork structure with the direct mechanical coupling between two tines likely causes an in-phase vibratory mode (Guan et al. 2016), also could appear some errors in vibration (Yoon et al. 2012), (Weinberg and Kourepenis 2006). Therefore, TFG should be designed with the mechanical frame to guarantee the anti-phase mode in both the driving and sensing direction.

The mechanical frame connecting indirectly two tines in the TFG were designed in a diamond-shaped frame (Guan et al. 2016a, b), a U-shaped bar (Guan et al. 2014), a lozenge-shaped frame (Trinh et al. 2014), a structurally forced lever bar (Trusov et al. 2013), a T-shaped bar (Sharma et al. 2004; Zaman et al. 2008), or a straight linkage bar (Huilin and Yongpeng 2011). These researches focused on simulation and modal analysis to determine the frequency of anti-phase mode and the output characteristics of the TFG model. The results showed that the connecting frame is used to reject the vibration output and take likely the anti-phase mode. However, how the masses of the TFG respond when the external forces applied to them with the considered phase deviation has not been still studied yet. Besides, the response of the sense masses in TFG with the different forms of outside angular velocity should be considered.

This paper presents a TFG model with a connecting diamond-shaped frame to create and guarantee anti-phase mode in the first mode. Besides, the dynamic response of the device in the driving and sensing direction is analyzed to determine the anti-phase frequency and demonstrate the matching phase between two masses in two tines of this TFG. The output mechanical signals of the TFG also are studied by using a numerical analysis method in this research.

2 Configuration

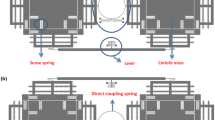
The simple configuration of the proposed TFG is shown in Fig. 1. It consists of two tines. Each tine is defined as a single gyroscope and includes a proof-mass 1 and an outer frame 2. The configuration and dynamic characteristics of every single gyroscope are provided in (Van Vu et al. 2018). This outer frame is connected to the proof-mass by four elastic beams 3 and suspended on substrate thanks to four other elastic beams 4. Each of these beams 4 is linked to the substrate (not be presented in Fig. 1) by an anchor 5 to allow the outer frame and the proof-mass to move freely in two perpendicular directions. Two single gyroscopes are connected through a diamond-shaped frame to create the proposed TFG. This frame has four rigid bars 7 with length L and the rectangular cross-section b × h, where h and b are the thickness and width of each bar, respectively. The bars are connected to the connectors by elastic stems 8 with the width s (where s < b). The configuration and dynamics analysis of this frame is shown in Fig. 2.

Fig. 1
figure 1

3D model of the proposed TFG with a diamond-shaped frame

Full size image
Fig. 2
figure 2

Configuration and dynamic of the connecting frame with the diamond shape

Full size image

Figure 3 describes a physical model of this TFG, where kx1, kx2, ky1, and ky2 are the equivalent stiffness of the elastic beams; cx1, cx2, and cy1, cy2 are damping coefficients in x- and y-direction; mS1 and mS2 are values of the proof-masses; and mf1 and mf2 are masses of the outer frames. The points (e.g. A, B, C, and D) are the nodes of the diamond-shaped frame.

Fig. 3
figure 3

Physical model of the TFG

Full size image

3 FEM analysis

The parameters of this TFG is shown in Table 1, and the specific material parameters of Silicon are shown in Table 2.

Table 1 The parameters of the proposed TFG
Full size table
Table 2 The properties of Silicon
Full size table

The governing equations when carrying out the modal analysis are formed as:

$$[M]\{ \ddot{q}\} + [C]\{ \dot{q}\} + [K]\{ q\} = \{ 0\}$$
(1)

where [M]-masses matrix; [C]-damping matrix; [K]-stiffness matrix; and {q}-deformation vector.

In this paper, the ANSYS software is used to create, analyze and simulate the presented model in Fig. 1. The mesh model for the beams is controlled by using elements with a size of 25 μm, whereas the rest of this MVG is defined by using maple face meshing with 500 µm of an element size to reduce element quantity. The finite element type in this model is SOLID 187 (element 3D with 10 nudes). The element quantity for MVG is 16,915.

3.1 Modal analysis

Three major frequencies of this TFG are shown in Table 3.

Table 3 The major modes of the proposed TFG 
Full size table

The natural vibratory modes of this TFG are displayed in Fig. 4.

Fig. 4
figure 4

Some of the natural vibratory modes of the proposed TFG

Full size image

The harmonic response is carried out to re-determine the resonant frequency of the structure when applying the exciting force on it. The unit forces are applied to the two outer frames of the TFG in the driving direction (1 μN). To reduce time of the calculation, the range of exciting frequency is chosen in 11.2÷12 kHz and the step of the frequency is 10 Hz. The harmonic response of the model is shown in Fig. 4.

The resonant frequency in the driving direction obtained from this analysis is 11,610 Hz (Fig. 5) and match with the result in the modal analysis mentioned above. So, the exciting frequency of the external force applied in this TFG should be chosen following this result.

Fig. 5
figure 5

Harmonic response of the proposed TFG

Full size image

3.2 Equivalent stiffness

The equivalent stiffness of the flexible beams in driving and sensing direction and the connecting frame is determined using simulation analysis in ANSYS. The unit force (1 μN) is applied on the structure, and the equivalent stiffness is defined from the relation between the deformation and the external force as the formula:

$$k = \frac{F}{\delta }$$
(2)

where δ is the deformation of the structure after applying the external force F.

The schemas of applying the external forces on the structures mentioned above are the same and shown in Fig. 6.

Fig. 6
figure 6

Determining the equivalent stiffness of the proposed TFG

Full size image

As follow the formula (2), the equivalent stiffness of the flexible beams in driving, sensing direction and diamond connecting frame is shown in Table 4.

Table 4 The stiffness of the structures
Full size table

4 The differential equation of motion

The bars 7 are assumed as a rigid body. The displacement at the end of the beams (A, B, C, and D) is carried out by the elasticity of stems with the smaller section. When the diamond-shaped frame links two single gyroscopes to create the tuning fork structure, points A and B only displace in x-direction and points C and D only do in the y-direction. The displacement of point A is x1, while point C displaces y1 from the initial position. Points B and D are the same displacements with A and C point except for the direction of motion (Fig. 3). These displacements depend mutually and are related by the followed formulas:

$$\left\{ \begin{aligned} y_{1} = \sqrt {L^{2} - (L_{1} - x_{1} )^{2} } - L_{2} \hfill \\ y_{2} = \sqrt {L^{2} - (L_{1} - x_{2} )^{2} } - L_{2} \hfill \\ \end{aligned} \right.$$
(3)

where L1 = Lcosα0, L2 = Lsinα0, and α0 is the angle to define the initial position of rigid bars of the diamond-shaped frame.

Thence the elastic forces are defined by the followed expressions:

$$F_{Dy} = k_{y} y_{D} /2 = k_{y} y_{1} /2$$
(4)
$$F_{Cy} = k_{y} y_{C} /2 = k_{y} y_{2} /2$$
(5)

The elastic force applied to the outer frames in the x-direction is determined as the followed expression:

$$F_{x} = \frac{1}{2}(F_{Cy} + F_{Dy} ){\text{cotg}}\alpha$$
(6)

with α is an angular rotation of a rigid beam when the diamond-shaped frame operating.

By using the second Newton law, the differential equations of motion for the system are obtained as follows:

$$\left\{ \begin{aligned} m_{1} \ddot{\vec{x}}_{1} = \vec{F}_{L1} + \vec{F}_{C1} + \vec{F}_{x} + \vec{F}_{1} \hfill \\ m_{2} \ddot{\vec{x}}_{2} = \vec{F}_{L2} + \vec{F}_{C2} + \vec{F}_{x} + \vec{F}_{2} \hfill \\ m_{s1} \ddot{\vec{y}}_{1} = \vec{F}_{L1} + \vec{F}_{C1} + \vec{F}_{1}^{C} \hfill \\ m_{s2} \ddot{\vec{y}}_{2} = \vec{F}_{L2} + \vec{F}_{C2} + \vec{F}_{2}^{C} \hfill \\ \end{aligned} \right.$$
(7)

Adding some expressions described the relations between the geometrical parameters of the diamond-shaped frame, the differential equations of motion for the whole TFG system becomes as the followed equations:

$$\left\{ \begin{aligned} m_{1} \ddot{x}_{1} + c_{x1} \dot{x}_{1} + k_{x1} x_{1} + \frac{1}{4}k_{y} \left( {\sqrt {L^{2} - (L_{1} - x_{1} )^{2} } + \sqrt {L^{2} - (L_{1} - x_{2} )^{2} } - 2L_{2} } \right){\text{cotg}}\alpha = F_{1} \hfill \\ m_{2} \ddot{x}_{2} + c_{x2} \dot{x}_{2} + k_{x2} x_{2} + \frac{1}{4}k_{y} \left( {\sqrt {L^{2} - (L_{1} - x_{1} )^{2} } + \sqrt {L^{2} - (L_{1} - x_{2} )^{2} } - 2L_{2} } \right){\text{cotg}}\alpha = F_{2} \hfill \\ m_{s1} \ddot{y}_{1} + c_{y1} \dot{y}_{1} + k_{y1} y_{1} = 2m_{s1} \varOmega \dot{x}_{1} \hfill \\ m_{s2} \ddot{y}_{2} + c_{y2} \dot{y}_{2} + k_{y2} y_{2} = 2m_{s2} \varOmega \dot{x}_{2} \hfill \\ L_{1} = L\cos \alpha_{0} \hfill \\ L_{2} = L\sin \alpha_{0} \hfill \\ \alpha = {\text{atan}}\left( {\frac{{\sqrt {L^{2} - (L_{1} - x_{1} )^{2} } - L_{2} }}{{x_{1} }}} \right) \hfill \\ \end{aligned} \right.$$
(8)

The Eqs. (8) are used to study the response of TFG with every different initial condition.

5 Output mechanical characterization of the TFG

The excited driving forces applied on two outer frames are reversed in the direction (anti-phase) to allow the anti-phase driving mode to appear in this TFG. Two outer frames will oscillate with the same amplitude but reversal phase.

The external forces maybe not completely symmetrical. The phase between them maybe not fully reversal (π radian). Even, there is a difference in the value of the amplitude for them. To express this situation, the deviation phase β is added in the expression of Fl while F-r is kept stably. The deviation phase β describes the non-absolutely opposite level of two exciting forces. Thence, these forces are formed as follow:

$$\begin{aligned} F_{l} = F_{0l} \sin (2\pi ft + \beta ) \hfill \\ F_{r} = F_{0r} \sin (2\pi ft + \pi ) \hfill \\ \end{aligned}$$
(9)

where, F0l and F0r are the value of exciting force amplitude applied on the left and right outer frame, f is the resonant frequency in driving direction (defined in harmonic analysis f = 11,600 Hz). The value of the force is set up to match with the configuration presented in Fig. 1 (i.e. less than 50 μm in this configuration). Thence, the value of the forces, in this case, should be as 60 μN.

In the case of β = 0 and F0r = F0l, two exciting forces are absolutely opposite in the anti-phase situation, and the mechanical response of two outer frames are in the anti-phase mode (shown in Fig. 7).

Fig. 7
figure 7

Mechanical response of two outer frames with deviation phase α = 0

Full size image

The response of the proof-masses appears in the sensing direction when applying the angular velocity Ω thanks to the Coriolis force with the followed expression:

$$F_{C} = 2m_{s} \varOmega \dot{x}$$
(10)

The function of the angular velocity is formed as the constant, the linearity or the impulse (triangular, trapezoid, sinusoidal,… mode). The sensing response with the constant Ω form is revealed in Fig. 8. The border of the amplitude of this vibration is straight line after 0.5 s (0÷0.5 s is a period in which the driving and sensing vibration is unstabilized). The maximal value of the stable amplitude is directly proportional to the applying angular velocity. Besides that, when applying the different forms of the angular velocity on the whole system, the sensing response reflects the form of the applying angular (see Fig. 9). The results show that the TFG model is able to reflect correctly the angular velocity needed to be measured.

Fig. 8
figure 8

Sensing response with the constant angular velocity

Full size image
Fig. 9
figure 9

The sensing response with the different forms of angular velocity

Full size image

The output characterization of this TFG with the constant angular velocity is shown in Fig. 10. The relation between the displacement in the sensing direction and the angular velocity is nearly linear. The variability of the capacity ∆C between the two plates in the TFG depends linearly on the sensing displacement of the proofmass (Acar 2009) as the expression (11). Thence, the variable capacity is directly proportional to the angular velocity.

Fig. 10
figure 10

The linear dependence of the sensing displacement on the angular velocity

Full size image
$$\Delta C = 2N\frac{{\varepsilon_{0} tL}}{{d^{2} }}y$$
(11)

(N is the number of the moveable combs, ε0 is the permittivity of the free space, t and L is the structural thickness and overlap length respectively, d is the plate gap and y is sensing displacement of the proofmass). The result in Fig. 10 shows that the sensitivity of the model is defined as to be 3.8 pm/rad/s.

6 Matching phase in the driving and sensing mode

In this study, the deviation β is considered in range − 100 ÷ 100) to observe the mechanical response of two outer frames and two proof-masses. Besides, the value of the forces is different on two sides. In every case with different equivalent stiffness of the connecting diamond-shaped frame, the vibration of the outer frame and proof-mass in each tine of TFG is considered and thence let us evaluate the influence of the stiffness of the connecting frame to the ability creating the matching phase between two outer frames of the proposed TFG.

The results in Fig. 11 show that the equivalent stiffness of the connecting frame strongly affects the ability to match phase in the driving direction of the connecting diamond-shaped frame. The larger the equivalent stiffness of the connecting frame, the lower the driving phase deviation and the higher the phase deviation compensation ability. In the case of the connecting frame mentioned in this paper, the matching phase between two outer frames is defined to be 89% (1.10/100). Besides that, the ability to compensate for the phase deviation in driving increases up to 95.6% when rising the equivalent stiffness of the connecting frame to 4 times. The influence of the equivalent stiffness of the connecting frame to the matching phase in the driving direction is surveyed and displayed in Table 5 and Fig. 12.

Fig. 11
figure 11

Mechanical phase deviation of the two outer frame

Full size image
Table 5 The phase deviation compensation ability in the driving direction
Full size table
Fig. 12
figure 12

Matching phase in the driving direction

Full size image

The matching phase between two proof-masses in the two tines of TFG structure depends on some factors such as the driving forces, the deflection in the spring coefficient in sensing direction, the noise in the operating process, etc. In this research, the influence of the deflection of the phase between the two driving forces applied to two tines of the TFG model is considered, whereas the others are ignored. The external phase deviation changes in the range mentioned above. The input angular velocity is defined to obtain the required sensing amplitude (according to the survey, this value needs to be about 10 rad/s). The stiffness coefficient of the connecting diamond-shaped frame is still kept to be 4720 N/m as originally. According to the survey, the matching phase in the sensing direction of two proof-masses is displayed in Fig. 13 with the ability to compensate for the sensing phase deviation of the connecting frame as 93.67% (the compensation 0.6330/100).

Fig. 13
figure 13

Mechanical phase deviation in the sensing direction

Full size image

7 Conclusion

This paper presents the model design of a MEMS vibratory gyroscope in tuning fork type with the connecting diamond-shaped frame. The dynamic parameters of this system are determined using the finite element method with ANSYS software. The analysis of the matching phase between two tines of this gyroscope in the driving and sensing direction is carried out to confirm the ability of the connecting frame to compensate for the phase deviation appeared from external forces. The results showed that the equivalent stiffness of the connecting frame considerably affects the matching phase of the system. In this case, the matching phase of the gyroscope is about 89% and 93.67% in the driving and sensing mode, respectively. The ability to compensate for the phase deviation in driving mode increases up to 95.6% when the equivalent stiffness of the connecting diamond-shaped frame rises 4 times. This result is an important basis for further researches to improve the configuration of the TFG model and increase the performance of the sensor with this type.