Transient flow and heat transfer mechanism for Williamson-nanomaterials caused by a stretching cylinder with variable thermal conductivity

Abstract

The utilization of nanometre-sized solid particles in working fluids has been seriously recommended due to their enhanced thermal characteristics. This suspension of solid particles in base fluids can significantly enhance the physical properties, such as, viscosity and thermal conductivity. They are widely used in several engineering processes, like, heat exchangers, cooling of electronic equipment, etc. In this exploration, we attempt to deliver a numerical study to simulate the nanofluids flow past a circular cylinder with convective heat transfer in the framework of Buongiorno’s model. A non-Newtonian Williamson rheological model is used to describe the behavior of nanofluid with variable properties (i.e., temperature dependent thermal conductivity). The leading flow equations for nanofluid transport are mathematical modelled with the assistance of Boussinesq approximation. Numerical simulation for the system of leading non-linear differential equations has been performed by employing versatile, extensively validated, Runge–Kutta Fehlberg scheme with Cash–Karp coefficients. Impacts of active physical parameters on fluid velocity, temperature and nanoparticle concentration is studied and displayed graphically. It is worth to mention that the temperature of non-Newtonian nanofluids is significantly enhanced by higher variable thermal conductivity parameter. One major outcome of this study is that the nanoparticle concentration is raised considerably by an increasing values of thermophoresis parameter.

1 Introduction

It has been experimentally verified that the suspension of nanoparticles in working fluids exhibit several improved thermo-physical features. Such characteristics include higher heat transfer coefficients and thermal conductivity. In addition, viscosity and thermal diffusivity of nanofluids are also of paramount significance for practical applications. Thus, nanofluids offer valuable potential to many fields of science and technology. Beside other industrial and technological applications, the nanofluids are frequently utilized in heat transfer process, solar energy systems, military equipment, industrial cooling circuits, biomedicine, engine cooling systems, electronics, sensing and imaging, Nano-fluid detergents, transportation, nuclear reactor cooling systems, space and defence, cooling of chips, and so forth. The need for an advance technological handling of devices especially those operated on battery is greatly fulfilled by nanofluids. Moreover, application of these suspended nanoparticles in the sensors used in drilling technology and rock penetration methods using lubricants and coolants is likely to lower the production costs. Furthermore, automatic transmission fluids and engine oils have also benefited from the high thermal conductivity presented by these fluids. Another interesting fact that nanofluids display increased performance and stability when exposed to electric fields, widens their usage. Besides, nanofluids in colloidal forms are increasingly being used in biosciences and biomedical engineering these days. The drug delivery microchip, DNA sequencer based on these chips, and hollow micro-needles for transdermal drug delivery are yet other promising applications of nanofluids. Additionally, these have also improved the controlling and monitoring of the cell responses and understanding its activities.

Choi (1995) was the pioneer who introduced the term nanofluid and found the enhanced thermal conductivity of the base liquid imbedded with nanometer sized particles. After that Boungiorno (2006) studied the reasons of enhancement of heat transport of nanofluids and presumed that the impact of thermophoresis and Brownian diffusion are basically responsible for heat transfer improvement. Based on this theory, Nield and Kuznetsove (2009) and Kuznetsove and Nield (2013) have examined the double diffusion free convective boundary layer flow of nanofluids induced by a flat surface. Zaimi et al. (2014) presented the flow of time-dependent viscous nanofluid flow past a contracting cylinder. They analyzed that the skin friction coefficient, rates of heat and mass transfer reduces with a rise in unsteadiness parameter. Sheikholeslami and Ellahi (2015) investigated the nanofluids flow and natural convection heat transfer in a cubic cavity by employing Lattice Boltzmann technique. Imtiaz et al. (2016) have studied the mixed convection flow of Casson nanofluid generated by a stretched cylinder in the presence of applied magnetic field and convective boundary conditions. They acquired the analytical solution by employing homotopy analysis method (HAM) and revealed that the fluid flow depreciates for higher values of Hartman number and Casson fluid parameter. Later, Sheikholeslami (2017) explored the natural convection flow of nanofluids in a porous enclosure. He utilized the Darcy and KKL models for porous media and nanofluid under the influence of magnetic field. Usman et al. (2018) presented a numerical study to discuss the heat transfer of water-based metallic nanofluid flow along a converging/diverging channel. MHD flow of water based SWCNTs with in C-shape cavity has been studied by Haq et al. (2018a). To interpret the physical properties of nanofluids, various experimental and theoretical predictions were proposed by Dogonchi and Ganji (2018), Haq et al. (2018b), Usman et al. (2018a, b, c).

Recently, the researchers have shown great enthusiasms in the MHD flows in context of their vital applications in the fields of medicine, such as tumour treatment, magnetic resonance imaging and a couple of other symptomatic tests. Different experimental and theoretical investigations have been presented in recent past to study the flow of electrically conducting fluids with magnetic field. Ishak et al. (2008) reported a numerical study for MHD flow and heat transport past a stretching cylinder. They utilized the Keller box method to acquire the numerical solutions of governing problem. Mukhopadhyay (2013) investigated the MHD flow caused by a stretched cylinder. Vajravelu et al. (2012) have analysed the axisymmetric MHD flow and heat transfer features of a viscous fluid generated by a non-isothermal stretched cylinder with heat source/sink. Reddy and Das (2016) explored the numerical solution of MHD flow over a porous stretching cylinder with chemical reacting effects by utilizing artificial neural network technique. They examined that ANN approach is reliable and pertinent for simulating heat and mass transfer flow along a stretching cylinder. Acharya et al. (2017) addressed the flow features over a stretched cylinder considering non-uniform heat source. They described that the rate of heat transfer declines for both flat and cylindrical surface with the effects of magnetic field.

The investigation of flow and convective heat transfer phenomenon due to circular cylinder has incredible significance in extrusion forms. Wang (1988) obtained the exact similarity solutions for viscous fluid and heat transfer mechanism induced by a stretching cylinder. Later, Fang et al. (2012) numerically investigated the unsteady flow of viscous fluid on the outside a contracting or expanding cylinder. They study the stability of numerical solutions and observed that unstable solution exists in case of expanding cylinder. In addition, Si et al. (2014) numerically analysed the unsteady flow and heat transport in a viscous fluid caused by through permeable stretching/shrinking cylinder. Hayat et al. (2014) examined the effects of variable thermal conductivity on the flow by an inclined stretched cylinder. They concluded that the fluid temperature rises with higher thermal radiation. Akl (2014) have studied the analytical solution of unsteady flow past a continuously stretching cylinder. In this study, he observed that the curvature parameter enhances the velocity to a certain value then have an opposite trend before decaying to zero. Khan and Malik (2016) obtained analytical solution to explore the heat transfer features in Sisko fluid flow along a permeable cylinder. They found that the thermal relaxation time depreciates the temperature of the liquid. In another paper, Hayat et al. (2016) investigated the convective heat and mass transport during the flow caused by a stretching cylinder. Recently, Hashim et al. (2017) inspected the effects of melting heat transfer during flow of Carreau fluid induced by a stretching cylinder. They explored the numerical solutions for the governing problem.

To the best of author’s knowledge, no attempt has been made yet to investigate the flow and thermal features of a non-Newtonian Williamson nanofluid along a stretching cylinder under the combined effects of variable thermal conductivity and uniform magnetic field. The motivation of the present study is to bring out the effect of convective heat transfer phenomena in presence of Brownian motion and thermophoresis diffusion. Utilizing suitable non-dimensional variables, a third order ordinary differential equation for momentum conservation and a second order ordinary differential equation for energy and concentration conservation equations are modelled. We employing the Runge–Kutta method for the numerical computations. The results obtained are then compared with existing works and found an excellent agreement. Estimation of drag force, heat and mass transfer coefficients are computed and plotted graphically.

2 Physical model and mathematical formulation

2.1 Problem statement

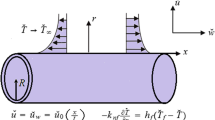
In this article, a comprehensive study for time dependent, laminar and two-dimensional flow along with heat transfer features of a non-Newtonian Williamson nanofluid past an infinitely long circular cylinder is presented. The schematic of current physical model is depicted in Fig. 1. Let $(x,r)$ be the cylindrical polar coordinates such that they represent the direction of axis along horizontal and normal to the cylinder. The flow is induced by stretching of the cylinder is the axial direction and it is electrically conducting such that a uniform magnetic field B₀ is acting along the radial direction. The stretching surface has the velocity $U_{w} (x,t) = \tfrac{ax}{1 - \beta t},$ where a and β are constants. The far field (free stream) temperature and nanoparticles volume fraction are T_∞ and C_∞, respectively. In addition, the surface temperature is controlled by convective process which is characterized by the heat transfer coefficient h_f and temperature of the hot fluid T_f below the surface.

Fig. 1

A Schematic representation for the flow of nanofluid around a circular cylinder

2.2 Governing equations

In view of considered assumptions, the resulting equations for the fluid flow are modelled by employing Oberbeck–Boussineq approximation and can be written in dimensional form as:

Continuity equation:

$$\frac{{{\varvec{\partial }}\left( {ru} \right)}}{{{\varvec{\partial }}x}} + \frac{{{\varvec{\partial }}\left( {rv} \right)}}{{{\varvec{\partial }}r}} = 0,$$

(1)

Momentum equation:

$$\begin{aligned} \frac{{{\varvec{\partial }}u}}{{{\varvec{\partial }}t}} + u\frac{{{\varvec{\partial }}u}}{{{\varvec{\partial }}x}} + v\frac{{{\varvec{\partial }}u}}{{{\varvec{\partial }}r}} = & \frac{\nu }{r}\frac{\partial u}{\partial r}\left[ {\beta^{ * } + \left( {1 - \beta^{ * } } \right)\left( {1 - \varGamma \frac{\partial u}{\partial r}} \right)^{ - 1} } \right] + \nu \frac{{\partial^{2} u}}{{\partial r^{2} }}\left[ {\beta^{ * } + \left( {1 - \beta^{ * } } \right)\left( {1 - \varGamma \frac{\partial u}{\partial r}} \right)^{ - 1} } \right] \\ & + \nu \varGamma \frac{\partial u}{\partial r}\frac{{\partial^{2} u}}{{\partial r^{2} }}\left[ {\left( {1 - \beta^{ * } } \right)\left( {1 - \varGamma \frac{\partial u}{\partial r}} \right)^{ - 2} } \right] - \frac{{\sigma B_{0}^{2} }}{\rho }u, \\ \end{aligned}$$

(2)

Energy equation:

$$\frac{{{\varvec{\partial }}T}}{{{\varvec{\partial }}t}} + u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial r} = \frac{1}{{\rho c_{p} }}\frac{1}{r}\frac{\partial }{\partial r}\left( {k(T)r\frac{\partial T}{\partial r}} \right) + \tau \left[ {D_{B} \frac{\partial C}{\partial r}\frac{\partial T}{\partial r} + \frac{{D_{T} }}{{T_{\infty } }}\left( {\frac{\partial T}{\partial r}} \right)^{2} } \right],$$

(3)

Concentration equation:

$$\frac{{{\varvec{\partial }}C}}{{{\varvec{\partial }}t}} + u\frac{\partial C}{\partial x} + v\frac{\partial C}{\partial r} = \frac{{D_{B} }}{r}\frac{\partial }{\partial r}\left( {r\frac{\partial C}{\partial r}} \right) + \frac{{D_{T} }}{{T_{\infty } }}\frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{\partial T}{\partial r}} \right),$$

(4)

where ρ is density, c_p is specific thermal capacity ν is kinematic viscosity, $\beta^{ * } = \tfrac{{\mu_{\infty } }}{{\mu_{0} }}$ is ratio of viscosities, Γ is material constant, σ is electrical conductivity, T is temperature, D_B and D_T are Brownian and thermophoresis coefficients, C is nanoparticles volume fraction.

For present study, the temperature dependent thermal conductivity k(T) is of the form:

$$k(T) = k_{\infty } \left[ {1 + \varepsilon \left( {\frac{{T - T_{\infty } }}{\Delta T}} \right)} \right].$$

(5)

The conditions applied at different boundaries are as follows:

$$u = U_{w} \left( {x,t} \right),v = 0, - k(T)\frac{\partial T}{\partial r} = h_{f} \left( {T_{f} - T} \right), - D_{m} \frac{\partial C}{\partial r} = k_{m} \left( {C_{f} - C} \right){\text{at }}r = R,$$

(6)

$$u \to 0,\quad T \to T_{\infty } \quad C \to C_{\infty } \quad r \to \infty .$$

(7)

The flow equations can be non-dimensionalized by employing the following variables:

$$\eta = \frac{{r^{2} - R^{2} }}{2R}\left( {\frac{{U_{w} }}{\nu x}} \right)^{1/2} ,\quad \psi = \left( {U_{w} \nu x} \right)^{1/2} Rf\left( \eta \right),\theta \left( \eta \right) = \frac{{T - T_{\infty } }}{{T_{f} - T_{\infty } }},\quad \phi \left( \eta \right) = \frac{{C - C_{\infty } }}{{C_{f} - C_{\infty } }}.$$

(8)

The Stokes stream function ψ is given by the relations $u = \tfrac{1}{r}\tfrac{\partial \psi }{\partial r}$ and $v = - \tfrac{1}{r}\tfrac{\partial \psi }{\partial x}$.

Making use of Eq. (8) into Eqs. (2)–(4), we have a system of ordinary differential equations

$$\begin{aligned} \left( {1 + 2\gamma \eta } \right)\left[ {\beta^{ * } + \left( {1 - \beta^{ * } } \right)(1 - Wef^{\prime\prime})^{ - 2} } \right]f^{\prime\prime\prime} + ff^{\prime\prime} - A\left( {f^{\prime} + \frac{\eta }{2}f^{\prime\prime}} \right) - M^{2} f^{\prime} \hfill \\ + 2\gamma f^{\prime\prime}\left[ {\beta^{ * } + \left( {1 - \beta^{ * } } \right)\left( {1 - \frac{{Wef^{\prime\prime}}}{2}} \right)(1 - Wef^{\prime\prime})^{ - 2} } \right] = 0, \hfill \\ \end{aligned}$$

(9)

$$\begin{aligned} (1 + 2\gamma \eta )[\theta^{\prime\prime} + \varepsilon (\theta \theta^{\prime\prime} + \theta^{\prime 2} )] + 2\gamma (\theta^{\prime} + \varepsilon \theta \theta^{\prime}) + \Pr \,f\theta^{\prime} \hfill \\ + \Pr (1 + 2\gamma \eta )(N_{b} \theta^{\prime}\phi^{\prime} + N_{t} \theta^{\prime 2} ) - \Pr \,A\left( {\theta + \frac{\eta }{2}\theta^{\prime}} \right) = 0, \hfill \\ \end{aligned}$$

(10)

$$\left( {1 + 2\gamma \eta } \right)\phi^{\prime\prime} + 2\gamma \phi^{\prime} + Scf\phi^{\prime} + \frac{{N_{t} }}{{N_{b} }}\left[ {\left( {1 + 2\gamma \eta } \right)\theta^{\prime\prime} + 2\gamma \theta^{\prime}} \right] - ScA\left( {\phi + \frac{\eta }{2}\phi^{\prime}} \right) = 0,$$

(11)

subject to the boundary conditions

$$f(0) = 0,\quad f^{\prime}(0) = 1,\quad \theta^{\prime}(0) = - \gamma_{{_{1} }} \frac{1 - \theta (0)}{1 + \varepsilon \theta (0)},\quad \phi^{\prime}\left( 0 \right) = - \gamma_{{_{2} }} (1 - \phi (0)),$$

(12)

$$f^{\prime}(\infty ) \to 0,\quad \theta (\infty ) \to 0,\quad \phi (\infty ) \to 0,$$

(13)

where primes indicate differentiation with respect to η and $We = \left( {\tfrac{{a^{3} x^{2} r^{2} \varGamma^{2} }}{{(1 - \beta t)^{3} R^{2} \nu }}} \right)^{1/2}$ local Weissenberg number, $\gamma = \left( {\tfrac{\nu (1 - \beta t)}{{aR^{2} }}} \right)^{1/2}$ curvature parameter, $\gamma_{{_{1} }} = \left( {\tfrac{h}{k}\sqrt {\tfrac{\nu }{a}} } \right)^{1/2}$ thermal Biot number, $\gamma_{{_{2} }} = \left( {\tfrac{{k_{m} }}{{D_{m} }}\sqrt {\tfrac{\nu }{a}} } \right)^{1/2}$ concentration Biot number, $M = \left( {\tfrac{{\sigma B_{0}^{2} }}{\rho a}} \right)^{1/2}$ magnetic parameter, $Nt = \left( {\tfrac{{\tau D_{B} (T_{f} - T_{\infty } )}}{{\nu T_{\infty } }}} \right)$ thermophoresis parameter, $Nb = \left( {\tfrac{{\tau D_{B} (C_{f} - C_{\infty } )}}{\nu }} \right)$ Brownian motion parameter, $\Pr = \left( {\tfrac{{\mu c_{p} }}{k}} \right)$ Prandtl number, $Sc = \left( {\tfrac{\nu }{{D_{B} }}} \right)$ Schmidt number and $A = \left( {\tfrac{c}{a}} \right)$ reaction rate parameter.

The three physical parameters are the skin friction coefficients C_f, the local Nusselt number Nu and Sherwood number Sh, which are expressed as

$$C_{f} = \frac{{\left. {\tau_{rx} } \right|_{r = R} }}{{\rho U_w^{2} }},\quad Nu = \frac{{\left. {xq_{w} } \right|_{r = R} }}{{k\left( {T_{f} - T_{\infty } } \right)}},\quad Sh = \frac{{\left. {xq_{m} } \right|_{r = R} }}{{D\left( {C_{f} - C_{\infty } } \right)}},$$

(14)

where τ_rx, q_w and q_m are given by

$$\tau_{rx} = \mu_{0} \frac{{{\varvec{\partial }}u}}{{{\varvec{\partial }}r}}\left[ {\beta^{ * } + (1 - \beta^{ * } )\left( {1 - \varGamma \frac{\partial u}{\partial r}} \right)^{ - 1} } \right],\quad q_{w} = - k\left( {\frac{\partial T}{\partial r}} \right),\quad q_{m} = - D\left( {\frac{\partial C}{\partial r}} \right).$$

(15)

Applying the non-dimensional variables presented in Eq. (8), Eqs. (14) and (15) are reduced to

$$Re^{1/2} C_{f} = f^{\prime\prime}(0)\left[ {\beta^{ * } + (1 - \beta^{ * } )\left( {1 - Wef^{\prime\prime}(0)} \right)^{ - 1} } \right],\,Re^{ - 1/2} Nu = - \theta^{\prime}(0), \, Re^{ - 1/2} Sh = - \phi^{\prime}(0),$$

(16)

where Re = xU_w/ν defines the local Reynolds number.

3 Numerical simulation

3.1 Computational procedure

To solve the modelled problem numerically, the governing Eqs. (9)–(11) are altered into a set of first order differential equation with the associated boundary conditions (12) and (13). Now, Runge–Kutta Fehlberg method and Newton’s techniques are employed to develop a numerical code to solve the first order system. For this purpose, the above-mentioned system of non-linear differential equations is transformed to a set of first order ODEs, by using the following newly defined variables: f = u₁, f′ = u₂, f′′ = u₃, θ = u₄, θ′ = u₅, ϕ = u₆, ϕ′ = u₇.

In view of above defined variables, the governing Eqs. (9)–(11)are regenerated as:

$$\begin{aligned} u^{\prime}_{1} = \,& u_{2} ,u^{\prime}_{2} = u_{3} , \\ u^{\prime}_{3} = \,& \frac{{ - u_{1} u_{3} - 2\gamma u_{3} \left[ {\beta^{ * } + (1 - \beta^{ * } )\left( {1 - \tfrac{We}{2}u_{3} } \right)\left( {1 - {We} u_{3} } \right)^{ - 2} } \right] + A(u_{2} + \tfrac{\eta }{2}u_{3} ) + M^{{^{2} }} u_{2} }}{{\left( {1 + 2\gamma \eta } \right)\left[ {\beta^{ * } + (1 - \beta^{ * } )\left( {1 -W{e} u_{3} } \right)^{ - 2} } \right]}}, \\ \end{aligned}$$

(17)

$$\begin{aligned} u^{\prime}_{4} = \,& u_{5} , \\ u^{\prime}_{5} = \,& \frac{{ - \varepsilon u_{5}^{2} \left( {1 + 2\gamma \eta } \right) - 2\gamma (u_{5} + \varepsilon u_{4} u_{5} ) - \Pr u_{1} u_{5} - \Pr \left( {1 + 2\gamma \eta } \right)\left( {N_{b} u_{5} u_{7} + N_{t} u_{5}^{2} } \right) + \Pr A(u_{4} + \tfrac{\eta }{2}u_{5} )}}{{\left( {1 + 2\gamma \eta } \right)\left[ {1 + \varepsilon u_{4} } \right]}}, \\ \end{aligned}$$

(18)

$$u_{6}^{\prime } = u_{7} ,u_{7}^{\prime } = \frac{{ - 2\gamma u_{7} - \tfrac{Nt}{Nb}\left[ {\left( {1 + 2\gamma \eta } \right)u_{5}^{\prime } + 2\gamma u_{3} } \right] + ScA\left( {u_{6} + \tfrac{\eta }{2}u_{7} } \right)}}{{\left( {1 + 2\gamma \eta } \right)}}$$

(19)

along with the boundary conditions

$$u_{1} \left( 0 \right) = 0,\quad u_{2} \left( 0 \right) = 1,\quad u_{5} \left( 0 \right) = - \gamma_{{_{1} }} \frac{{\left( {1 - u_{4} \left( 0 \right)} \right)}}{{1 + \varepsilon u_{4} \left( 0 \right)}},\quad u_{7} \left( 0 \right) = - \gamma_{{_{2} }} \left( {1 - u_{6} \left( 0 \right)} \right)$$

(20)

$$u_{2} \left( \infty \right) = 0,\quad u_{4} \left( \infty \right) = 0,\quad u_{6} \left( \infty \right) = 0.$$

(21)

We need values for u₃(0), u₅(0) and u₇(0), but no such values are given at the initial condition. The accuracy of the initial guesses for u₃(0), u₅(0) and u₇(0) are verified by comparing the estimated values of u₂(0), u₄(0) and u₆(0) at η = η_max using Newton Raphson method. Finally, the maximum value of η displaying the ambient conditions is taken to be η_∞ = 10, 15 and 20 depending upon the physical parameters. The step size is used to be h = 0.001 and the above proceeding is repeated until the converged results equivalent to the coveted level of precision 10⁻⁶.

3.2 Verification of numerical scheme

To figure out the physical problem more clearly, the numerical technique is implemented to solve governing differential equations, because it provides freedom to choose suitable values of involving flow parameters. The accuracy of the present computations is shown in Table 1 by comparing values of Re^1/2C_f with previously published data for different values of M and neglecting the influences of all other parameters. It can be revealed from table that the result of present investigations is same with previous result calculated by Fathizadeh et al. (2013) and Fang et al. (2009).

Table 1 A comparison of the skin friction Re^1/2C_f for M when $We = 0 = A = \gamma \; {\text {and}} \;\beta^{ * }$

4 Results and discussion

This section manifests the effects of some interesting physical parameters appearing in the problem namely the unsteadiness parameter A, local Weissenberg number We, thermal conductivity parameter ɛ, curvature parameter $\gamma$, thermal Biot number $\gamma_{{_{1} }} ,$ concentration Biot number $\gamma_{{_{2} }} ,$ Prandtl number Pr, Brownian motion parameter Nb, thermophoresis parameter Nt and Schmidt number Sc on Re^1/2C_f, Re^−1/2Nu, Re^−1/2Sh, f′(η), θ(η) and ϕ(η) distributions are presented graphically through Figs. 2, 3, 4, 5, 6, 7, 8, 9 and 10. All the results obtained are presented for two different cases of flat plate and a cylinder. In addition, we pictured the effect of curvature parameter on f′(η) and θ(η) by introducing a comparative study considering the presence and absence of magnetic field. The entire exhibition has been accomplished by taking the default estimations of the governing parameters as We = 1.0, M = 1.0, β^* = 0.1, $\gamma$ = 0.2, A = 0.1, Pr = 3.0, Sc = 2.0, Nt = 0.1, Nb = 0.1, $\gamma_{{_{1} }} = 0.2,$$\gamma_{{_{2} }} = 0.3,$ and ɛ = 3.0 unless otherwise indicated.

Fig. 2

Variation in f′(η), θ(η) and ϕ(η) against A

Fig. 3

Variation in f′(η), θ(η) and ϕ(η) against M

Fig. 4

Variation in f′(η) and θ(η) against We

Fig. 5

Variation in f′(η) and θ(η) against γ

Fig. 6

Variation in θ(η) against Pr and ɛ

Fig. 7

Variation in θ(η) and ϕ(η) against Nt

Fig. 8

Variation in θ(η) and ϕ(η) against γ₁

Fig. 9

Variation in ϕ(η) against Nb and γ₂

Fig. 10

Variation in Re^1/2C_f and Re^−1/2Nu against M and N_t

In Fig. 2a–c the variation of the velocity f′(η), temperature θ(η) and concentration profiles ϕ(η) inside the boundary layer for different values of unsteadiness parameter A is presented for both the flow over a flat plate and cylinder. It is revealed through these figures that f′(η) and θ(η) are the decreasing functions of the unsteadiness for both cases of flat plate (γ = 0) and cylinder (γ ≠ 0) but opposite behaviour is seen for concentration profile ϕ(η). Further, the thicknesses of momentum and thermal boundary layer are diminishing function while solutal boundary layer thickness is the increasing function of the A for both cases. Physically, when unsteadiness enhances the sheet loses more heat because of which temperature of the fluid decreases.

Variation of magnetic parameter M on f′(η), θ(η) and ϕ(η) are depicted in Fig. 3a–c for both cases of flat plate and cylinder. It is evident from these figures that an increment in the strength of magnetic field produces a drag force which slow down the flow and reduce the velocity fields, hence heat generate and enhances the thermal and concentration boundary layers. Hence, the corresponding boundary layer thickness reduces. On the other hand, nanoparticle concentration profiles with in the boundary layer depicts accelerating behaviour for higher magnetic parameter.

Figure 4a, b are plotted for velocity f′(η) and temperature θ(η) distributions for different values of Weissenberg number We. These figures portrayed that the velocity profile reduces by growing the values of We but inverse pattern can be noticed in temperature profiles. According to the definition of Weissenberg number, it is the ratio of relaxation time and a specific process time of the fluid. It develops the thickness of liquid and that is the reason velocity of the liquid declines.

Figure 5a, b illustrate the non-dimensional velocity and temperature profiles inside the boundary layer region for distinct values of curvature parameter. These figures are sketched for two different cases of magnetic parameter i.e., in the presence and absence of magnetic field. From these plots, we observed that the curvature parameter significantly affects the nanofluid velocity and temperature in both the cases. Figure 5a depicts that an increment in the values of γ, has an affinity to the fluid motion along the stretching surface which filled with nanofluids. Moreover, the corresponding boundary layer thickness increases with higher curvature parameter. We can see that there exist an inverse relation between the radius of cylinder and curvature parameter. Therefore, a rise in curvature parameter tends to shrink the radius of cylinder. In such case, the surface area of cylinder becomes smaller and by increasing curvature parameter, the velocity gradient at the surface enhances and consequently boost up the shear stress per unit area. This figure further manifest that both the velocity and boundary layer thickness are higher in the absence of magnetic field. In Fig. 5b, we depict the variation of dimensionless temperature profiles on curvature parameter γ. A dual behaviour is noted for temperature profiles in both the cases. We find that the fluid temperature decreases near the solid boundary as curvature parameter increases, however, an opposite is true for far away the solid boundary. For higher curvature parameter, the radius of the cylinder reduces and the surface area which is close to the solid boundary also decreases. It is noteworthy to mention that heat is exchanged into the fluid modes: conduction at the surface and convection for the domain η > 0. Now, as the surface area of the cylinder decreases, a slight reduction in the temperature profile develops close to the surface of the cylinder, since a thin quantity of heat energy is transferred from the surface to the fluid by means of conduction process. At the same time, thickness of thermal boundary layer increase, because of heat transfer inside the fluid improved convection process all around the cylinder.

The effects of Pr and ɛ have been sketched in Fig. 6a, b. From Fig. 6a, we see that temperature as well as the thickness of thermal boundary layer reduces for increasing Prandtl number Pr. It is clear from the plot fluids with larger Prandtl number speed up the cooling process and fluids with low Pr slow down the cooling process. From this behaviour it is concluded that Prandtl number is used to control the cooling process. Figure 6b depicts the effects of ɛ on temperature profile. It can be observed that temperature of the liquid increases with the growth of thermal conductivity. It is also noticed that temperature profile increases remarkable with the case of flat plate (γ = 0) as comparison with cylinder case (γ ≠ 0).

The thermophoresis parameter Nt is an important parameter for examining the temperature and nanoparticle concentration in nanofluid flow. The effect of thermophoresis parameter Nt on temperature θ(η) and concentration ϕ(η) is portrayed in Figs. 7a, b for both cases γ = 0 and γ ≠ 0. These figures indicate that an increment in Nt yields a decrease in temperature of the fluid while an opposite behaviour is seen for concentration profile. In physical point of view thermophoresis force enhances with the increase in Nt which tends to move nanoparticles from hotter to cool region and hence decreases the fluid temperature and increases the concentration distribution. Further, these results are more significant for (γ = 0).

Figure 8a, b are designed to discuss the impact of thermal Biot number γ₁ on temperature and concentration profile for both cases flat plate (γ = 0) and cylinder (γ ≠ 0). From these plots, it is manifested that higher thermal Biot number correspond to increase in the temperature and concentration profile. Also, thermal and solutal boundary layer thicknesses are the developing functions of the γ₁. We know that thermal Biot number is defined as the ratio between internal thermal resistance of a solid and thermal resistance of the boundary layer. The surface of the cylinder is totally isolated when the value of thermal Biot number is zero. This means that thermal resistance of the surface of cylinder is very strong and there is no convective heat transport form cylinder surface to colder region which is for from the cylinder.

Effect of Brownian motion Nb and concentration Biot number γ₂ on concentration profile is illustrated in Fig. 9a, b. From Fig. 9a, it is seen that nanoparticle concentration of the fluid decreases by enhances the values of Nb. Physically, when Nb increases then the random movement of nanoparticles rises. Since interaction of particles enlarges and kinetic energy is transformed into heat energy which lessens the nanoparticle concentration of fluid. Figure 9b indicate the concentration profile for larger concentration Biot number γ₂. It is manifested that concentration profile is a reducing function of γ₂.

The variation of wall skin friction coefficient Re^1/2C_f and local Nusselt number Re^−1/2Nu are depicted in Fig. 10a, b for both cases flat plate (γ = 0) and cylinder (γ ≠ 0). The results presented in Fig. 10a show that, as the magnetic parameter increases the skin friction decreases. It is to be noticed that Re^1/2C_f is stronger in case of flow past a stretching cylinder (γ ≠ 0). Further, it is observed that higher values of Weissenberg number is to upgrade the wall shear stress. The variation in dimensionless Nusselt number Re^−1/2Nu against the thermal Biot number γ₁ for both cases flat plate (γ = 0) and stretching cylinder (γ ≠ 0) for various values of thermophoresis parameter Nt are displayed in Fig. 10b. In this plot, we observed that with the growth of Nt and thermal Biot number γ₁ the rate of heat transfer enhances at the wall. The thermophoresis particles represent the nanoparticle migration due to imposed temperature gradient across the fluid.

5 Conclusion

In this study, we have examined the unsteady heat and mass transfer mechanisms for Williamson nanofluid flow past a stretching cylinder with variable thermal conductivity and convective boundary conditions. The emerging sets of governing partial differential equations were transformed into ordinary differential equations by using local non-dimensional variables. The dimensionless leading equations of the problem were solved numerically by Runge–Kutta Fehlberg method. Variations of the velocity, temperature and nanoparticle concentration profiles were portrayed graphically for several parameters. The main features of this exploration are listed as:

• The velocity and temperature of the fluid were the decreasing function of the unsteadiness parameter.

• A growth in thermal conductivity parameter leads to enhance the fluid temperature.

• The temperature and concentration were the rising function of the thermophoresis parameter.

• The concentration profile and associated boundary layer thickness was significantly reduced by rising values of Schmidt number.