1 Introduction

It is well known that in thermoelasticity theory the usual theory of heat conduction based on Fourier’s law predicts infinite heat propagation speed proposed by Biot (1956). It is also known that heat transmission at low temperature propagates by means of waves. These aspects have caused intense activity in the field of heat propagation. Extensive reviews on the second sound theories (hyperbolic heat conduction) are given in Lord-Shulman (1967), Joseph and Preziosi (1990), Chandrasekharaiah (1998) or Hetnarski and Ignaczak (1999). The anisotropic case was later developed by Sherief and Dhaliwal (1980) and Ezzat and El-Karamany (2002). Within the theoretical contributions to the subject are the proofs of uniqueness theorems by Ezzat and El Karamany (2003) and the boundary element formulation was done by El Karamany and Ezzat (2002). Among the contributions to this theory are (Lata et al. 2016, Abbas and Kumar 2016, Ezzat et al. 2001, Aatef and Abbas 2016 and Abbas and marin 2017).

Green and Naghdi (1991, 1992, 1993) proposed generalized thermoelasticity theories by suggesting three models which are subsequently referred to as GN-I, II, and III models. Many works were devoted to investigate various theoretical and practical aspects in thermoelasticity, in the context of GN theories. Chandraskharaiah (1996) introduced a note on the uniqueness of solution in the linear theory of thermoelasticity without energy dissipation. Ezzat et al. (2009) introduced a mathematical model of magneto-thermoelasticity based on GN theories. Ciarletta (2009) introduced the theory of micropolar thermoelasticity without energy dissipation and Chirita and Ciarletta (2010) constructed reciprocal and variational principle in thermoelasticity without energy dissipation. El-Karamany, Ezzat (2016) proposed three models of GN generalized thermoelasticity and Alzahrani and Abbas (2016) studied the effect of magnetic field on a thermoelastic fiber-reinforced material under GN-III theory.

Fractional calculus has been used successfully to modify many existing models of physical processes. Caputo and Mainardi (1971) and Caputo (1974) found good agreement with experimental results when using fractional derivatives for description of viscoelastic materials and established the connection between fractional derivatives and the theory of linear viscoelasticity. Povstenko (2009) made a review of thermoelasticity that uses fractional heat conduction equation and proposed and investigated new models that use fractional derivative in Ref. Povstenko (2005). Recently, Sherief et al. (2010) constructed a new theory of fractional thermoelasticity based on Lord-Shulman theory (1967). Ezzat (2011, 2012) established a fraction model for the heat conduction using the Taylor–Riemann series expansion of time-fractional order. More applications of the fractional models in continuum mechanics can be found in the references: El-Karamany and Ezzat (2011a, b), Ezzat and El-Karamany (2011a, b), Ezzat and Fayik (2013), Ezzat and El-Bary (2012, 2017a, b), Ezzat et al. (2013, 2014, 2015, 2017), Hendy et al. (2017) and Abbas (2015).

The constitutive equations with a fractional Maxwell–Cattaneo heat conduction law using the Caputo fractional derivative and the fractional order heat transport equation are obtained El-Karamany and Ezzat (2017). The uniqueness theorem is proved, the reciprocity relation is deduced and the variational characterization of solution is given. Seven thermoelasticity theories result from the given problem as special cases.

In the current work, a modified law of heat conduction including fractional order of time derivative is constructed and replaces the conventional Fourier’s law in Green and Naghdi generalized thermoelasticity. The general solution in the Laplace transform domain is obtained and applied to one-dimensional problem of a thermoelastic spherical cavity which is thermally shocked on its bounding plane in the presence of a constant magnetic field. The inversion of the Laplace transforms is carried out using a numerical approach proposed by Honig and Hirdes (1984). The numerical values of the temperature, displacement and stress will be illustrated graphically.

2 Derivation of fractional heat equation in GN thermoelasticity without energy dissipation

Green and Naghdi (1993) developed a model of thermoelasticity theory without energy dissipation, which includes thermal displacement gradient among the constitutive variables and proposed a heat conduction law as

$$ \vec{q}(\varvec{x},t) = - \,k^{*} \,\vec{\nabla }\upsilon \,(\varvec{x},t), $$
(1)

where \( \dot{\upsilon } = T \) and \( \upsilon \) is the thermal displacement gradient. Here \( k^{*} ( > 0) \) is a material constant characteristic of the theory.

The energy equation in terms of the heat flux vector \( \vec{q} \) is

$$ \frac{\partial }{\partial t}(\rho \,C_{E} T\, + \gamma \,T_{o} \,\gamma \,e) = - \,\vec{\nabla }\, \cdot \,\,\vec{q}\; + \;Q. $$
(2)

By using Taylor–Riemann series expansion of time-fractional order \( \alpha \) to expand \( \vec{q}(x,\;t + \tau_{o} ) \) and retaining terms up to order \( \alpha \) in the thermal relaxation time \( \tau_{o} \), we get

$$ \vec{q}(\varvec{x},\;t + \tau_{o} ) = \vec{q}(\varvec{x},\;t) + \frac{{\tau_{o}^{\alpha } }}{\alpha !}\,\frac{{\partial^{\alpha } \vec{q}(\varvec{x},\;t)}}{{\partial t^{\alpha } }}. $$
(3)

From a mathematical viewpoint, fractional GN heat conduction law is given by

$$ \vec{q}(\varvec{x},\;t) + \frac{{\tau_{o}^{\alpha } }}{\alpha !}\,\frac{{\partial^{\alpha } \vec{q}(\varvec{x},\;t)}}{{\partial t^{\alpha } }} = - \,k^{*} \,\vec{\nabla }\upsilon \,(\varvec{x},t),\quad 0 < \alpha < 1. $$
(4)

Taking the partial time derivative of fraction order \( \alpha \) of Eq. (2), we get

$$ \frac{{\partial^{\alpha + 1} }}{{\partial t^{\alpha + 1} }}(\rho \,C_{E} T\, + \gamma \,T_{o} \,\gamma \,e) = - \,\vec{\nabla }\, \cdot \,\,\frac{{\partial^{\alpha } \vec{q}}}{{\partial t^{\alpha } }}\; + \,\frac{{\partial^{\alpha } Q}}{{\partial t^{\alpha } }}\quad 0 < \alpha < 1. $$
(5)

Multiplying Eq. (5) by \( \tau_{o}^{\alpha } /\alpha ! \) and adding to Eq. (2) we have

$$ \frac{\partial }{\partial t}\left( {1 + \frac{{\tau_{o}^{\alpha } }}{\alpha !}\frac{{\partial^{\alpha } }}{{\partial t^{\alpha } }}} \right)(\rho \,C_{E} T\, + \gamma \,T_{o} \,\gamma \,e) = - \,\vec{\nabla }\, \cdot \,\,\left( {\vec{q} + \frac{{\tau_{o}^{\alpha } }}{\alpha !}\frac{{\partial^{\alpha } \vec{q}}}{{\partial t^{\alpha } }}} \right)\; + \,\,Q\; + \frac{{\tau_{o}^{\alpha } }}{\alpha !}\frac{{\partial^{\alpha } Q}}{{\partial t^{\alpha } }}. $$
(6)

Substituting from Eq. (4), we get

$$ \frac{\partial }{\partial t}\left( {1 + \frac{{\tau_{o}^{\alpha } }}{\alpha !}\frac{{\partial^{\alpha } }}{{\partial t^{\alpha } }}} \right)(\rho \,C_{E} T\, + \gamma \,T_{o} \,\gamma \,e) = k^{*} \,\nabla^{2} \upsilon \; + \,\,Q\; + \frac{{\tau_{o}^{\alpha } }}{\alpha !}\frac{{\partial^{\alpha } Q}}{{\partial t^{\alpha } }},\quad 0 < \alpha < 1. $$
(7)

Differentiating Eq. (7) with respect to time, we have

$$ \frac{{\partial^{2} }}{{\partial t^{2} }}\left( {1 + \frac{{\tau_{o}^{\alpha } }}{\alpha !}\frac{{\partial^{\alpha } }}{{\partial t^{\alpha } }}} \right)(\rho \,C_{E} T\, + \gamma \,T_{o} \,\gamma \,e) = k^{*} \,\nabla^{2} \,T\; + \,\frac{\partial }{\partial t}\,\left( {Q\; + \frac{{\tau_{o}^{\alpha } }}{\alpha !}\frac{{\partial^{\alpha } Q}}{{\partial t^{\alpha } }}} \right),\quad 0 < \alpha < 1 $$
(8)

Equation (8) represents Green-Naghdi heat transfer equation without energy dissipation with time fractional derivative \( \alpha \) and relaxation time \( \tau_{o} \).

2.1 Limiting cases

  1. 1.

    Eq. (8) in the limiting case \( \tau_{o} = 0 \) transforms to Green–Naghdi heat conduction equation of type II (GN).

  2. 2.

    Eq. (8) in the limiting case \( \alpha = 1,\;\tau_{o} \ne 0 \) transforms to the single-phase-lag Green–Naghdi heat conduction equation of type II (SPGN)

  3. 3.

    In the case \( \;0 < \alpha < 1 \), the correspondent equation for the fractional thermoelasticity theories result (FGN).

3 Basic equations

We shall consider a homogeneous, isotropic, perfect conductive thermoelastic medium permeated by an initial magnetic field H. Due to the effect of this magnetic field there arises in the conducting medium an induced magnetic field h and induced electric field E. Also, there arises a force F (the Lorentz Force). Due to the effect of the force, points of the medium undergo a displacement vector u, which gives rise to a temperature. The linearized equations of electromagnetism for slowly moving media

$$ {\text{Curl}}\,h = J + \varepsilon_{o} \frac{{\partial \,\varvec{E}}}{\partial \,t}, $$
(9)
$$ {\text{Curl}}\,E = - \;\mu_{o} \;\frac{{\partial \,\varvec{h}}}{\partial \,t}, $$
(10)
$$ E = - \mu_{o} \,\frac{{\partial \,\varvec{u}}}{\partial \,t}\; \wedge \;{\kern 1pt} \varvec{H} , $$
(11)
$$ {\text{div }}h = \, 0. $$
(12)

The above equations are supplemented by the displacement equations

$$ \sigma_{ij,j} + F_{i} = \rho \ddot{u}_{i} , $$
(13)

where \( F_{i} \) is the Lorentz force given by

$$ F_{i} = \mu_{o} \;(\varvec{J}\, \wedge \,\,\varvec{H})_{i} . $$
(14)

The constitutive equation

$$ \sigma_{ij} = \;\lambda \,e_{kk} \,\delta_{ij} \; + \;2\mu \,e_{ij} \; - \;\gamma \,\left( {T\; - \;T_{o} } \right). $$
(15)

The fractional GN heat equation without energy dissipation in the absence of heat sources has the form

$$ \frac{{\partial^{2} }}{{\partial t^{2} }}(1 + \frac{{\tau_{o}^{\alpha } }}{\alpha !}\frac{{\partial^{\alpha } }}{{\partial t^{\alpha } }})(\rho \,C_{E} T\, + \gamma \,T_{o} \,\gamma \,e) = k^{*} \,\nabla^{2} \,T,\quad 0 < \alpha < 1. $$
(16)

The strain–displacement relations

$$ e_{ij} = \;\frac{1}{2}\,(u_{i,j} \; + \;u_{j,i} ), $$
(17)

together with the previous equations, constitute a complete system of fraction Green-Naghdi (FGN) electro-magneto-thermoelasticity without energy dissipation for a perfect conductive medium.

4 Formulation of the problem

Let \( (r,\vartheta ,\varphi ) \) denote spherical polar coordinates and take the origin of the coordinate system at the center of a spherical cavity with radius \( a \) occupying the region \( a \le r < \infty \). The sphere is placed in a magnetic field with constant intensity \( \varvec{H}\text{ = (0,\,0,}\,H_{o} \text{)} \). We note that due to spherical symmetry, the only non-vanishing displacement component is the radial one \( u_{r} = u(r,t) \) and the induced field components in the sphere are obtained from Eqs. (9)–(12) in the forms

$$ \varvec{E}\text{ = }\;\text{(0,}\,E\,\text{,0) = (0,}\,\mu_{o} H_{o} \frac{\partial u}{\partial t}\text{,\,0),}\quad \varvec{h}\text{ = }\;\text{(0,\,0,\,}h\text{) = (0,\,0,}\, - H_{o} e\text{)}\text{.} $$
(18)

The simplified linear equations of electrodynamics for a perfectly electrically conducting elastic solid are (Ezzat 2006):

$$ J = \;H_{o} \;\left( {\frac{{\partial {\kern 1pt} \,e}}{{\partial {\kern 1pt} r}}\; - \;\varepsilon_{o} \,\mu {\kern 1pt}_{o} {\kern 1pt} \frac{{\partial^{2} u}}{{\partial {\kern 1pt} t^{2} }}} \right), $$
(19)
$$ h = - H_{0} \,e, $$
(20)
$$ E = \mu_{0} H_{0} \frac{\partial \,u}{\partial \,t}. $$
(21)

The components of strain tensor are given by

$$ e_{rr} = \frac{\partial u}{\partial r},\;\;e_{\vartheta \vartheta } = e_{\varphi \varphi } = \frac{u}{r},\;\;e_{r\vartheta } = e_{r\varphi } = e_{\vartheta \varphi } = 0. $$
(22)

The radial component of Lorentz force can be obtained from Eqs. (14) and (18) in the form

$$ F_{rr} = \mu_{o} H_{o}^{2} \left( {\frac{\partial e}{\partial r} - \varepsilon_{o} \mu_{o} \frac{{\partial^{2} u}}{{\partial t^{2} }}} \right). $$
(23)

The equation of motion (13) yield

$$ \left( {\lambda + 2\mu + \mu_{o} H_{o}^{2} } \right)\,\frac{\partial e}{\partial r}\; - \;\;\gamma {\kern 1pt} \frac{\partial T}{\partial r} = \left( {\rho + \varepsilon_{o} \,\mu_{o}^{2} H_{o}^{2} } \right)\;\,\frac{{\partial^{2} u}}{{\partial t^{2} }}. $$
(24)

Applying the div operator to both sides of Eq. (24), we obtain

$$ \left( {\lambda + 2\mu + \mu_{o} H_{o}^{2} } \right)\,\nabla^{2} e\; - \;\;\gamma {\kern 1pt} \nabla^{2} T = \left( {\rho + \varepsilon_{o} \mu_{o}^{2} H_{o}^{2} } \right)\;\,\frac{{\partial^{2} e}}{{\partial t^{2} }}, $$
(25)

where \( \nabla^{2} \) is the 1D Laplace’s operator in spherical polar coordinates, given by

$$ \nabla^{2} = \frac{{\partial^{2} }}{{\partial r^{2} }} + \frac{2}{r}\frac{\partial }{\partial r} = \frac{1}{{r^{2} }}\frac{\partial }{\partial r}\left( {r^{2} \frac{\partial }{\partial r}} \right). $$

The components of the stress tensor are given by

$$ \sigma_{rr} = 2\;\mu \frac{\partial \,u}{\partial \,r} + \lambda e\, - \,\,\gamma \,(T - T_{o} ), $$
(26)
$$ \sigma_{\vartheta \vartheta } = \sigma_{\varphi \varphi } = 2\;\mu \frac{\,u}{\,r} + \lambda e\, - \,\,\gamma \,(T - T_{o} ), $$
(27)
$$ \sigma_{r\vartheta } = \sigma_{r\varphi } = \sigma_{\vartheta \varphi } = 0. $$

In order to solve the problem, we assumed that the initial conditions of the problem are taken to be homogeneous, i.e.,

$$ u(r,0) = \dot{u}(r,0) = \sigma_{rr} (r,0) = \dot{\sigma }_{rr} (r,0) = T(r,0) = \dot{T}(r,0) = 0,\quad t \le 0. $$

while the boundary conditions are taken as follows:

(i) The surface of the cavity are traction free (zero stress) i.e.,

$$ \sigma_{rr} (r,t) = 0,\quad r = a $$
(28)

(ii) The thermal boundary condition is that the surface of the cavity subjected to a thermal shock that is a function of time

$$ T(r,t) = f(t),\quad r = a $$
(29)

Let us introduce the following non-dimensional variables: \( \begin{aligned} r^{\prime } = c_{o} {\kern 1pt} \zeta_{o} r,\quad u^{\prime } = c_{o} {\kern 1pt} \zeta_{o} u,\quad t^{\prime } = c_{o}^{2} {\kern 1pt} \zeta_{o} t,\quad \sigma^{\prime } = \frac{\sigma }{\lambda + 2\mu },\quad \theta^{*} = \frac{{\gamma (T - T_{o} )}}{\lambda + 2\mu },\quad k^{ * \prime } = \frac{{k^{ * } }}{{\rho \,C_{E} c_{o}^{2} }},\quad {\kern 1pt} \hfill \\ J^{\prime } = \frac{J}{{c_{o} H_{o} \zeta_{o} }},\quad h^{\prime } = \frac{h}{{H_{o} }},\quad E^{\prime } = \frac{E}{{\mu_{o} H_{o} c_{o} }},\quad \zeta_{o} = \rho \,C_{E} /k,\quad c_{o}^{2} = \frac{\lambda + 2\mu }{\rho }\quad \hfill \\ \end{aligned} \)

The governing equations, in nondimensional form are given by:

$$ J = \;\frac{{\partial {\kern 1pt} \,e}}{{\partial {\kern 1pt} r}}\;\; - \;\;V^{2} {\kern 1pt} \frac{{\partial^{2} u}}{{\partial {\kern 1pt} t^{2} }}, $$
(30)
$$ h = - \;e, $$
(31)
$$ E = \frac{\partial \,u}{\partial \,t}, $$
(32)
$$ \left( {1 + \frac{{a_{o}^{2} }}{{c_{o}^{2} }}} \right)\,\nabla^{2} e\; - \;\;{\kern 1pt} \nabla^{2} \theta = \left( {1 + \frac{{a_{o}^{2} }}{{c_{{}}^{2} }}} \right)\;\,\frac{{\partial^{2} e}}{{\partial t^{2} }}, $$
(33)
$$ \frac{{\partial^{2} }}{{\partial t^{2} }}(1 + \frac{{\tau_{o}^{\alpha } }}{\alpha !}\frac{{\partial^{\alpha } }}{{\partial t^{\alpha } }})(\theta \, + \varepsilon \,\,e) = k^{*} \,\nabla^{2} \,\theta , $$
(34)
$$ \sigma_{rr} = 2\;\frac{\partial \,u}{\partial \,r} + (\beta^{2} - 2)\,e\, - \,\,\beta^{2} \,\theta , $$
(35)
$$ \sigma_{\vartheta \vartheta } = 2\;\frac{\,u}{\,r} + (\beta^{2} - 2)\,e\, - \,\,\beta^{2} \,\theta = \sigma_{\varphi \varphi } , $$
(36)

where \( a_{o} = \sqrt {\mu_{o} H_{o}^{2} /\rho } \) is Alfven velocity, \( c = \sqrt {1/\varepsilon_{o} \mu_{o} } \) is light speed, \( V = c_{o} {\kern 1pt} /c, \) \( \beta = \sqrt {(\lambda + 2\mu )/\mu } \) and \( \varepsilon = T_{o} \gamma^{2} /(\lambda + 2\mu )\rho \,C_{E} \) is thermoelastic coupling parameter.

5 Solution in the Laplace transform domain

Performing the Laplace transform defined by the relation

$$ \bar{g}(s) = \int\limits_{0}^{\infty } {e^{ - st} g(t)\;dt} , $$

of both sides Eqs. (30)–(36), we get

$$ \bar{J} = \;\frac{{\partial {\kern 1pt} \,\bar{e}}}{{\partial {\kern 1pt} r}}\;\; - \;\;V^{2} s^{2} {\kern 1pt} \bar{u}, $$
(37)
$$ \bar{h} = - \;\bar{e}, $$
(38)
$$ \bar{E} = s\,\bar{u}, $$
(39)
$$ \left( {\nabla^{2} \; - \;\;{\kern 1pt} a_{2} \,s^{2} } \right)\bar{e} = a_{1} \nabla^{2} \theta , $$
(40)
$$ \left( {\nabla^{2} \, - \,\;a_{3} } \right)\bar{\theta } = a_{3} \varepsilon \,\bar{e}, $$
(41)
$$ \bar{\sigma }_{rr} = 2\;\frac{{\partial \,\bar{u}}}{\partial \,r} + (\beta^{2} - 2)\,\bar{e}\, - \,\,\beta^{2} \,\bar{\theta }, $$
(42)
$$ \bar{\sigma }_{\vartheta \vartheta } = 2\;\frac{{\,\bar{u}}}{\,r} + (\beta^{2} - 2)\,\bar{e}\, - \,\,\beta^{2} \,\bar{\theta } = \bar{\sigma }_{\varphi \varphi } , $$
(43)

where \( a_{1} = {1 \mathord{\left/ {\vphantom {1 {\left( {1 + \frac{{a_{o}^{2} }}{{c_{o}^{2} }}} \right)}}} \right. \kern-0pt} {\left( {1 + \frac{{a_{o}^{2} }}{{c_{o}^{2} }}} \right)}}, \) \( a_{2} = {{\left( {1 + \frac{{a_{o}^{2} }}{{c_{o}^{2} }}} \right)} \mathord{\left/ {\vphantom {{\left( {1 + \frac{{a_{o}^{2} }}{{c_{o}^{2} }}} \right)} {\left( {1 + \frac{{a_{o}^{2} }}{{c_{{}}^{2} }}} \right)}}} \right. \kern-0pt} {\left( {1 + \frac{{a_{o}^{2} }}{{c_{{}}^{2} }}} \right)}} \) and \( a_{3} = {{s^{2} \left( {1 + \frac{{\tau_{o}^{\alpha } }}{\alpha !}s^{\alpha } } \right)} \mathord{\left/ {\vphantom {{s^{2} \left( {1 + \frac{{\tau_{o}^{\alpha } }}{\alpha !}s^{\alpha } } \right)} {k^{*} }}} \right. \kern-0pt} {k^{*} }} \)

The boundary conditions (28) and (29) have the form in the Laplace transform

$$ \bar{\theta }(r,s) = \bar{f}(s),\quad r = a, $$
(44)
$$ \bar{\sigma }_{rr} (r,s) = 0,\quad r = a. $$
(45)

By eliminating \( \bar{e} \) between Eqs. (40) and (41), we get

$$ \left\{ {\nabla^{4} - \left[ {a_{3} + a_{2} s^{2} + a_{1} a_{3} \varepsilon } \right]\nabla^{2} + a_{2} a_{3} s^{2} } \right\}\,\bar{\theta } = 0{\kern 1pt} . $$
(46)

The above equation can be factorized as

$$ \left( {\nabla^{2} - k_{1}^{2} } \right)\left( {\nabla^{2} - k_{2}^{2} } \right)\,\bar{\theta } = 0, $$
(47)

where \( k_{1}^{2} {\text{ and}}\;k_{2}^{2} \) are the positive roots of the characteristic equation

$$ k^{4} - \left[ {a_{3} + a_{2} s^{2} + a_{1} a_{3} \varepsilon } \right]k^{2} + a_{2} a_{3} s^{2} = 0. $$
(48)

The solution which satisfies Eq. (46) takes the form

$$ \bar{\theta } = A_{1} \left( {k_{1}^{2} - \;a_{2} s^{2} } \right)\;\frac{{e^{{ - k_{1} r}} }}{r} + A_{2} \left( {k_{2}^{2} - \;a_{2} s^{2} } \right)\;\frac{{e^{{ - k_{2} r}} }}{r}. $$
(49)

By using Eq. (40), we get

$$ \bar{e} = a_{1} \left( {A_{1} k_{1}^{2} \;\frac{{e^{{ - k_{1} r}} }}{r} + A_{2} k_{2}^{2} \;\frac{{e^{{ - k_{2} r}} }}{r}} \right). $$
(50)

Hence, the displacement is given by

$$ \bar{u} = - a_{1} \left[ {A_{1} \left( {k_{1} \; + \frac{1}{r}} \right)\frac{{e^{{ - k_{1} r}} }}{r} + A_{2} \left( {k_{2} \; + \frac{1}{r}} \right)\;\frac{{e^{{ - k_{2} r}} }}{r}} \right]. $$
(51)

The induced electric and magnetic fields can be deduced as

$$ \bar{h} = - \;a_{1} \left( {A_{1} k_{1}^{2} \;\frac{{e^{{ - k_{1} r}} }}{r} + A_{2} k_{2}^{2} \;\frac{{e^{{ - k_{2} r}} }}{r}} \right), $$
(52)
$$ \bar{E} = \, - a_{1} s\left[ {A_{1} \left( {k_{1} \; + \frac{1}{r}} \right)\frac{{e^{{ - k_{1} r}} }}{r} + A_{2} \left( {k_{2} \; + \frac{1}{r}} \right)\;\frac{{e^{{ - k_{2} r}} }}{r}} \right]. $$
(53)

Using the boundary conditions (44) and (45), we obtain the following system of two linear equations

$$ A_{1} \left( {k_{1}^{2} - \;a_{2} s^{2} } \right)\;\frac{{e^{{ - k_{1} a}} }}{a} + A_{2} \left( {k_{2}^{2} - \;a_{2} s^{2} } \right)\;\frac{{e^{{ - k_{2} a}} }}{a} = \bar{f}(s), $$
(52)
$$ a_{1} \left[ {A_{1} \left( {k_{1}^{2} + \frac{4}{{a\beta^{2} }}(k_{1} \; + \frac{1}{a})} \right)\frac{{e^{{ - k_{1} a}} }}{a} + A_{2} \left( {k_{2}^{2} + \frac{4}{{a\beta^{2} }}(k_{2} \; + \frac{1}{a})} \right)\;\frac{{e^{{ - k_{2} a}} }}{a}} \right] = \bar{f}(s). $$
(53)

By solving the above two linear equations, we have

$$ A_{1} = \frac{{a\,\left[ {a_{2} \beta^{2} a^{2} s^{2} + 4a_{1} (ak_{2} + 1)} \right]e^{{ - k_{1} a}} }}{{a_{1} (k_{1} - k_{2} )\left[ {a_{2} \beta^{2} a^{2} s^{2} (k_{1} + k_{2} ) + 4ak_{1} k_{2} + 4(k_{1} + k_{2} + a_{2} a^{2} s^{2} )} \right]}}\;\bar{f}(s), $$
(54)
$$ A_{2} = - \frac{{a\,\left[ {a_{2} \beta^{2} a^{2} s^{2} + 4a_{1} (ak_{2} + 1)} \right]e^{{ - k_{2} a}} }}{{a_{1} (k_{1} - k_{2} )\left[ {a_{2} \beta^{2} a^{2} s^{2} (k_{1} + k_{2} ) + 4ak_{1} k_{2} + 4(k_{1} + k_{2} + a_{2} a^{2} s^{2} )} \right]}}\;\bar{f}(s). $$
(55)

This completes the solution in the Laplace transform domain.

6 Numerical inversion of the Laplace transforms

In order to invert the Laplace transform in the above equations, we adopt a numerical inversion method based on a Fourier series expansion (Honig and Hirdes, 1984). In this method, the inverse g (t) of the Laplace transform \( \bar{g}\,(s) \) is approximated by the relation

$$ g\,(t) = \frac{{e^{{c*t{\kern 1pt} }} }}{{t_{1} }}\,\left[ {\frac{1}{2}\bar{g}\,(c*) + \text{Re} \,\left( {\sum\limits_{k = 1}^{N} {\exp \left( {\frac{{i\,k{\kern 1pt} \pi t}}{{t_{1} }}\,} \right)} \;\bar{g}\,\left( {c* + \frac{{i\,k{\kern 1pt} \pi }}{{t_{1} }}} \right)} \right)} \right],\quad \quad 0 \le t \le 2{\kern 1pt} t_{1} \,, $$
(56)

where c* is an arbitrary constant greater than all the real parts of the singularities of g(t) and N is sufficiently large integer chosen such that,

$$ e^{c*\,t} \text{Re} \;\left[ {\exp \left( {\frac{{i\,N{\kern 1pt} \pi t}}{{t_{1} }}\,} \right)\;\bar{g}\,\left( {c* + \frac{{i\,N{\kern 1pt} \pi }}{{t_{1} }}} \right)} \right] \le \,\;\varepsilon , $$
(57)

where ε is a prescribed small positive number that corresponds to the degree of accuracy required

Using the numerical procedure cited, to invert the expressions of the considered fields in Laplace transform domain. The variation of the temperature, displacement and radial component of stress is plotted for different cases.

7 Numerical results and discussion

In this section, we aim to illustrate the numerical results of the analytical expressions obtained in the previous section and explain the influence of fractional orders on the behavior of the field quantities in GN thermoelasticity theory without energy dissipation.

The method based on a Fourier series expansion proposed by Honig and Hirdes (1984) and developed in detail in many works such as Ezzat (1994) and Ezzat et al. (1996) is adopted to invert the Laplace transform in Eqs. (49)–(53).

Copper material was chosen for the purposes of numerical evaluation. The constant of the problem is given in Table 1 as in Ref. (Ezzat and El-Bary 2017a).

Table 1 Values of the constants
Full size table

Let us consider that f(t) is exponentially decreasing in time described mathematically as:

$$ f(t) = e^{ - t} \quad {\text{or}}\quad \quad \bar{f}(s) = \frac{1}{1 + s}. $$
(58)

The numerical technique outlined above was used to obtain the temperature, strain, displacement and stress. The results are displayed graphically at different positions of x as shown in Figs. 1, 2, 3, 4.

Fig. 1
figure 1

The variation of temperature for different theories

Full size image
Fig. 2
figure 2

The variation of strain for different theories

Full size image
Fig. 3
figure 3

The variation of displacement for different theories

Full size image
Fig. 4
figure 4

The variation of stress for different theories

Full size image

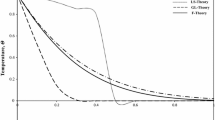
Figure 1 depicts the space variation of temperature with distance x for different values of the fractional order \( \alpha \) at different values of time, namely \( t = 0.05,\;0.15 \). We noticed that the solution corresponding to the GN theory of type II (\( \tau_{o} = 0 \)) that the thermal waves propagate with finite speeds, so the value of the temperature is identically zero for any large value of x (Sherief and Abd El-Latief 2015). While in single phase lag GN theory of type II (SPLGN, \( \alpha = 1 \)), the response to the thermal effect does not reach infinity instantaneously but remains in a bounded region. We observed also that in fractional GN theory of type II (FGN, \( \alpha = 0.2 \)), the temperature field has been affected by the fractional order \( \alpha \), where the decreasing of the value of the parameter \( \alpha \) causes decreasing in the amplitude of the thermal waves.

Figures 2, 3 and 4 show the variation of strain, displacement and stress distributions for different theories in the present (\( a_{o} > 0 \)) or absent (\( a_{o} = 0 \)) of the magnetic field. It was found that the fractional order theory of GN thermoelasticity of type II predicts a value for strain e and displacement u less than that predicted by the generalized GN theory of type II, while the value of the radial component of stress \( \sigma_{rr} \) is greater in the fractional theory.

The Alfven velocity \( a_{o} \) acts to decrease the strain, displacement and magnitude of stress distributions. This is mainly due to the fact that the magnetic field corresponds to a term signifying a positive force that tends to accelerate the charge carries.

8 Conclusions

The magneto–electro thermoelastic analysis in the context of a new consideration of Green-Naghdi heat conduction law without energy dissipation problem of a perfect conducting spherical cavity based upon fractional time derivatives theory is presented. The main contribution in this article is to describe the effects of fractional order on temperature, strain, displacement, and stress distributions. According to this theory we have to construct a new classification for FGN of type II, materials according to their, fractional order where this parameter becomes a new indicator of its ability to conduct heat in conducting medium.