Free vibration and critical angular velocity of a rotating variable thickness two-directional FG circular microplate

Abstract

In this paper, the free vibration of a rotating variable thickness two-directional FG circular microplate is studied. The governing equations of motion for the microplate are extracted utilizing the Hamiltonian’s principle in conjunction with the first shear deformation theory as well as the modified couple stress theory. The solution of equations is presented utilizing the differential quadrature method. In special cases, the natural frequency results obtained by the reduced form of the proposed formulation are compared with those available in the literature, indicating a very good accuracy. The results reveal that there is a non-proportional relation between the natural frequencies of the microplate and the thickness-variations of the section. In contrast, the critical angular velocity of that is not much sensitive with respect to the thickness variation. Moreover, the analyses indicate the significant impact of the two-directionality-variation of the graded material on the natural frequencies as well as the critical angular velocities. A map on the effects of the two-directionality-variation of the material property on the free vibration of the microplate is presented. The results show that the increase of the size dependency would lead to the reduction of the non-dimensional natural frequency as well as the critical angular velocity.

1 Introduction

The increasing demands for the structures bearing the higher mechanical and thermal load lead to introduce the advanced composite structures like functionally graded materials (FGM) in industry. In comparison with competitive materials, the higher strength to weight ratio and the reduction of the delamination failure are the significant advantages that result in the more application of FGM beams, plates and shell in industry. While the FGMs are comprehensively used in macro- micro- and nano-sizes, the tradition applications are limited to those structures that are subjected to thermal and mechanical loads varying in thickness direction only. Since the multi-axial loading on the structures is the frequent ones that are inevitable. In this way, recently, multi-directional FGMs are introduced to use in such structures. In addition, the thickness variability enables the designer to reach the most efficient structures. Since there are many investigations about static (Ghadiri and Shafiei 2015; Salamat-Talab et al. 2012; Eshraghi et al. 2016; Ansari et al. 2015; Duan and Wang 2007; Kadkhodayan and Golmakani 2014; Ma and Wang 2003; Chaht et al. 2015), buckling (Van and Hoa 2013; Jabbari et al. 2014; Bedroud et al. 2013; Mehri et al. 2016; Jin et al. 2014; Özakça et al. 2003; Anjomshoa 2013; Wang et al. 2006; Farajpour et al. 2012; Tsiatas and Yiotis 2014; Gholami et al. 2015, 2016) and vibration (Şimşek and Kocatürk 2009; Wei et al. 2012; Şimşek and Reddy 2013; Huang et al. 2013; Huang and Li 2010; Alshorbagy et al. 2011; Shahba and Rajasekaran 2012; Shahba et al. 2011; Neves et al. 2012a, b, 2013; Şimşek et al. 2012; Aydogdu and Taskin 2007; Şimşek 2010a, b; Khalili et al. 2010; Akgöz and Civalek 2013; Şimşek 2012; Pradhan and Chakraverty 2013; Ghadiri et al. 2015; Ebrahimi et al. 2015; Ghadiri and Hosseini 2014; Shafiei et al. 2016a, b, c, d; Ghadiri and Shafiei 2016a, b; Ghadiri et al. 2016) of one-directional FGMs, the shortcoming of studies on the variable thickness multi-directional FGMs could be seen in the literature. The rarely available studies are only limited to macro-size structures (i.e. beams, plates and shells).

Shariyat and Alipour (2013) and Shariyat et al. (2013) developed a power series solution for the free vibration and the damping analyses of a viscoelastic functionally graded plate with a variable thickness on the elastic foundation. Moreover, Alipour and Shariyat (2013) presented a semi-analytical solution for the buckling analysis of a two-directional FG circular plate with a variable thickness on the elastic foundation. Satouri (2015) studied the free vibration of a two-directional FG sectorial plate with a variable thickness resting on a Winkler–Pasternak elastic foundation. Alinaghizadeh and Shariati (2015, 2016) investigated the static bending of two-directional FG circular/annular sector plates with a variable thickness.

While some investigations were conducted on the macro-size structures, as the best knowledge of the authors, there is not any investigation about the free vibration of a two-directional FG micro-structure with a variable thickness.

In this study, the governing equations of motion for a rotating variable thickness two-directional FG circular microplate are developed considering the modified couple stress. The vibration solution of the equations is presented using differential quadrature method (DQM). In special cases, the results are verified with the available results in the literature. The contributions of size dependency, two-directionality-variation of FG material and thickness variation effects on the first natural frequencies of a micro-plate are studied. The novelty of this study could be summarized as follows:

• The presentation of a formulation for a circular plate considering a variable thickness for the section and a two-directional FG for the material as well as a rotating velocity for the structure, all in the micro-size.

• A parametric study on the contributions of the thickness-variation in the section, two-directionality-variation in the material property and the rotating velocity of the microplate on the natural frequencies as well as the critical angular velocities of a circular microstructure.

2 Formulation

In this section, material assumptions and governing equations of motion in conjunction with associated boundary conditions utilizing first shear deformation theories are presented. Since formulation is derived for a variable thickness two-directional FG circular microplate under rotational velocity condition, the governing equations are enriched with the modified couple stress effects.

2.1 Material

A schematic of a variable thickness two-directional FG circular microplate is represented in Fig. 1. As can be seen in Fig. 1, h₀ and R are the central thickness and the outer radius of the microplate, respectively. The thickness is the maximum in the central point and there is a reduction for the thickness in the radial-direction. It is assumed that the microplate made from a combination of metal and ceramic. The combination changes from the top to the bottom surface of the plate as well as from the center to the outer radius of plates, i.e. the top surface of the plate in central point of the plate (z = h₀/2, r = 0) is ceramic-rich whiles the bottom surface of the plate in central point of the plate (z = − h₀/2, r = 0) is metal-rich. The angular velocity of the rotating microplate is equal with Ω.

Fig. 1

The schematic view of the rotating micro-size tow-directional FGM variable thickness circular plate

Therefore, a two-directional functionally graded material (FGM) character, P, of the circular plate is assumed to vary through the thickness and radius respected to the volume fraction of the constituent components, V _i , as follows (Shariyat and Alipour 2013):

$$ P(r,z) = (P_{t} V_{c} (r,z) + P_{b} V_{m} (r,z))\left( {1 + \alpha \left( {\frac{r}{R}} \right)^{\beta } } \right) $$

(1)

where subscripts b and t denote the bottom and top surfaces of the plate and the subscripts c and m address the ceramic and metal, respectively. α and β denote the coefficient and the power index of the material character variation in the radial-direction of the plate. In each material point of the microplate, it is obvious that:

$$ V_{c} (r,z) + V_{m} (r,z) = 1 $$

(2)

Therefore, one rewrites Eq. (1) as follows:

$$ P(r,z) = (({\rm P}_{t} - {\rm P}_{b} ) {\rm V}_{c} (r,z) + P_{b} )\left( {1 + \alpha \left( {\frac{r}{b}} \right)^{\beta } } \right) $$

(3)

Assuming the origin of the coordinate in the center of the plate (as shown in Fig. 1), the volume fraction of the ceramic, V _c , would define in the power low form as follows:

$$ V(r,z) = \left( {\frac{1}{2} + \frac{z}{h}} \right)^{n} $$

(4)

where n introduces the power index of the volume fraction.

Moreover, the variable thickness function, h(r), is defined as follows:

$$ h(r) = h_{0} \left( {1 - q\left( {\frac{r}{R}} \right)^{m} } \right) $$

(5)

in which q and m denote the coefficient and the power index for thickness-variation in radial-direction. Consequently, one would represent the Young’s modulus expansion of the FGM material as follows:

$$ E(r,z) = \left( {(E_{c} - E_{m} )\left( {\frac{1}{2} + \frac{z}{h}} \right)^{n} + E_{m} } \right)\left( {1 + \alpha \left( {\frac{r}{R}} \right)^{\beta } } \right) $$

(6)

and for the simplicity of the formulation, it is summed that the mass density and the Poisson ratio variation as follows:

$$ \rho (z) = \left( {(\rho_{c} - \rho_{m} )\left( {\frac{1}{2} + \frac{z}{h}} \right)^{n} + \rho_{m} } \right) $$

(7)

$$ \nu (z) = \left( {(\nu_{c} - \nu_{m} )\left( {\frac{1}{2} + \frac{z}{h}} \right)^{n} + \nu_{m} } \right) $$

(8)

2.2 Governing equations of motion

In the three-dimensional first shear deformation plate theory, the displacement components (u _r , u _θ and u _z in cylindrical coordinate) of the circular plates would be written as follows:

$$ u_{r} (r,\theta ,z,t) = u(r,\theta ,t) + z\Phi (r,\theta ,t) $$

(9a)

$$ u_{\theta } (r,\theta ,z,t) = z\Psi (r,\theta ,t) $$

(9b)

$$ u_{z} (r,\theta ,z,t) = w(r,\theta ,z,t) $$

(9c)

where u and w are the radial and the transverse deflection, Φ and Ψ represent the rotations of a transverse normal line about r and θ coordinate, respectively. For the axisymmetric problem, the circumferential displacement, u _θ , is omitted and Φ and w would be independent of the circumferential axis. Hence, displacement field would be rewritten as follows (Leissa 1969):

$$ u_{r} (r,z,t) = u(r,t) + z\Phi (r,t) $$

(10a)

$$ u_{\theta } (r,z,t) = 0 $$

(10b)

$$ u_{z} (r,z,t) = w(r,z,t) $$

(10c)

thereafter, non-zero components of the linear strain tensor are written as follows (Leissa 1969):

$$ \varepsilon_{rr} (r,z,t) = \frac{\partial u}{\partial r} + z\frac{\partial \Phi }{\partial r} $$

(11a)

$$ \varepsilon_{\theta \theta } (r,z,t) = \frac{u}{r} + \frac{z}{r}\frac{\Phi }{r} $$

(11b)

$$ \varepsilon_{rz} (r,z,t) = \frac{1}{2}\left( {\frac{u}{r} + \frac{z}{r}\Phi } \right) $$

(11c)

moreover, a non-zero component of the symmetric curvature tensor is (see “Appendix A”):

$$ \chi_{r\theta } = \frac{1}{4}\left( {\left( { - \frac{{\partial^{2} w}}{{\partial r^{2} }} + \frac{\partial \Phi }{\partial r}} \right) - \left( {\Phi - \frac{\partial w}{\partial r}} \right)} \right) $$

(12)

The strain energy of the circular microplate in axisymmetric condition would obtain by substituting the non-zero strain and the symmetric curvature strain components into Eq. (31) which lead to:

$$ U = \frac{1}{2}\int\limits_{0}^{R} {\int\limits_{{ - \frac{h(r)}{2}}}^{{\frac{h(r)}{2}}} {\left[ \begin{array}{l} \sigma_{rr} \left( {\frac{\partial u}{\partial r} + z\frac{\partial \Phi }{\partial r}} \right) + \sigma_{\theta \theta } \left( {\frac{u}{r} + \frac{z}{r}\frac{\Phi }{r}} \right) + 2\sigma_{rz} \left( {\frac{1}{2}\left( {\frac{u}{r} + \frac{z}{r}\Phi } \right)} \right) \hfill \\ \quad + 2m_{r\theta } \left( {\frac{1}{4}\left( { - \frac{{\partial^{2} w}}{{\partial r^{2} }} + \frac{\partial \Phi }{\partial r}} \right) - \frac{1}{4}\left( {\Phi - \frac{\partial w}{\partial r}} \right)} \right) \hfill \\ \end{array} \right]} } dzdr $$

(13)

Substituting the components of the stress tensor and the deviatoric part of the couple stress tensors (see “Appendix A”) into Eq. (13), one could obtain the strain energy of the micro-plate as follows:

$$ U = \frac{1}{2}\int\limits_{0}^{R} {\left[ \begin{array}{l} N_{rr} \frac{\partial u}{\partial r} + N_{\theta \theta } \frac{u}{r} + M_{rr} \frac{\partial \Phi }{\partial r} + N_{\theta \theta } \frac{\Phi }{r} + N_{rz} \left( {\frac{\partial w}{\partial r} + \Phi } \right) \hfill \\ \quad + \frac{1}{2}\varOmega_{r\theta } \left( {\left( { - \frac{{\partial^{2} w}}{{\partial r^{2} }} + \frac{\partial \Phi }{\partial r}} \right) - \frac{1}{r}\left( {\Phi - \frac{\partial w}{\partial r}} \right)} \right) \hfill \\ \end{array} \right]} dr $$

(14)

where the forces, N _ij, the moments, M _ij, and the couple moment, Ω_ij, are defined in “Appendix B”.

Since the kinetic energy of the plate, T, is extracted as follows:

$$ {\text{T = }}\frac{1}{2}\int\limits_{0}^{R} {\int\limits_{{ - \frac{h(r)}{2}}}^{{\frac{h(r)}{2}}} {\rho (r,z)\left[ {\left( {\frac{\partial u}{\partial t}} \right)^{2} + \left( {\frac{\partial v}{\partial t}} \right)^{2} + \left( {\frac{\partial w}{\partial t}} \right)^{2} } \right]} } dzdr $$

(15)

substituting the displacement components into Eq. (15) would lead to

$$ T = \frac{1}{2}\int\limits_{0}^{R} {\int\limits_{{ - \frac{h(r)}{2}}}^{{\frac{h(r)}{2}}} {\left[ {I_{1} \left( {\frac{\partial u}{\partial t}} \right)^{2} + 2I_{2} \left( {\frac{\partial u}{\partial t}} \right)\left( {\frac{\partial \Phi }{\partial t}} \right) + I_{3} \left( {\frac{\partial \Phi }{\partial t}} \right)^{2} + I_{1} \left( {\frac{\partial w}{\partial t}} \right)^{2} } \right]} } dzdr $$

(16)

where the constants are defined as follows:

$$ \{ I_{1} ,I_{2} ,I_{3} \} = \mathop \int \limits_{{ - \frac{h(r)}{2}}}^{{\frac{h(r)}{2}}} \rho (r,z)\{ 1,{\text{z}}^{1} ,{\text{z}}^{2} \} {\text{dz}} $$

(17)

and the external work, H (due to the rotation) could present as (Bauer and Eidel 2007):

$$ {\text{H = }}\frac{1}{2}\int {N^{Rotation} } \left( {\frac{\partial w}{\partial r}} \right)^{2} dA $$

(18)

where N ^Rotation represents the radial-direction force due to the circumferential acceleration of the angular velocity, Ω, which is defined as follows (Bauer and Eidel 2007):

$$ N^{rotation} = \int\limits_{{ - \frac{h(r)}{2}}}^{{\frac{h(r)}{2}}} {\left( {\frac{{\rho \,\varOmega^{2} }}{8}(2(r)(3 + v))} \right)} dz $$

(19)

The governing equations of motion for a rotating variable thickness two-directional FG circular microplate would be extracted utilizing Hamilton’s principle as follows:

$$ \delta \int\limits_{0}^{t} {( - U + T + H) = 0} $$

(20)

where δ is the variation operator.

Substituting Eqs. (14), (16), and (18) into Eq. (20), the governing equations of motion and the associated boundary conditions would be obtained:

$$ \frac{1}{r}\frac{\partial }{\partial r}(rN_{r} ) - (N_{\theta } ) = I_{1} \frac{{\partial^{2} u}}{{\partial t^{2} }} + I_{2} \frac{{\partial^{2} \Phi }}{{\partial t^{2} }} $$

(21a)

$$ \frac{1}{2r}\frac{{\partial^{2} }}{{\partial r^{2} }}(r\varOmega_{r\theta } ) + \frac{1}{2r}\frac{\partial }{\partial r}(\varOmega_{r\theta } ) + \frac{1}{2r}\frac{\partial }{\partial r}(rN_{rz} ) + \frac{\partial }{r\partial r}\left( {N^{Rotation} r\frac{\partial w}{\partial r}} \right) + F = I_{1} \frac{{\partial^{2} w}}{{\partial t^{2} }} $$

(21b)

$$ \frac{1}{2r}\frac{{\partial^{2} }}{{\partial r^{2} }}(r\varOmega_{r\theta } ) + \frac{{\varOmega_{r\theta } }}{2r} + \frac{1}{r}\frac{\partial }{\partial r}(rM_{r} ) - \frac{{M_{\theta } }}{r} - N_{rz} = I_{2} \frac{{\partial^{2} u}}{{\partial t^{2} }} + I_{3} \frac{{\partial^{2} \Phi }}{{\partial t^{2} }} $$

(21c)

$$ (N_{r} )\delta u = 0\quad {\text{at}}\;{\text{r}} = 0,{\text{R}} $$

(21d)

$$ \left( {\frac{1}{2r}\frac{\partial }{\partial r}(r\varOmega_{r\theta } ) + \frac{{\varOmega_{r\theta } }}{2r} + N_{rz} - N_{r} \frac{\partial w}{\partial r}} \right)\delta w = 0\quad {\text{at}}\;{\text{r}} = 0,{\text{R}} $$

(21e)

$$ \frac{{r\varOmega_{r\theta } }}{2r}\frac{\partial }{\partial r}(\delta w) = 0\quad {\text{at}}\;{\text{r}} = 0,{\text{R}} $$

(21f)

$$ \left( {M_{rr} + \frac{{\varOmega_{r\theta } }}{2}} \right)(\delta \,\Phi ) = 0\quad {\text{at}}\;{\text{r}} = 0,{\text{R}} $$

(21g)

The governing equations of motion and the associated boundary conditions in terms of displacement components are presented in “Appendix C”.

2.3 Solution method

In order to solve the governing equations of motion with the associated boundary conditions (see “Appendix C”) for free vibration of a rotating variable thickness two-directional FG circular microplate, DQ method is utilized. In this method, weight coefficients are computed by an algebraic equation system which confined the usage of large grid numbers. The discretization rule of the method enables one to approximate m-th derivatives of displacement functions, u, w and Φ in respect to r that are defined as the linear sum of the function values (Shu 2012):

$$ \left. {\frac{{\partial^{\varvec{m}} \{ u(r),w(r),\Phi (r)\} }}{{\partial r^{\varvec{m}} }}} \right|_{{\varvec{r} = \varvec{r}_{\varvec{p}} }} = \mathop \sum \limits_{{\varvec{k} = 1}}^{\varvec{n}} C_{{\varvec{ik}}}^{{(\varvec{m})}} \{ u_{\varvec{k}} ,w_{\varvec{k}} ,\Phi_{\varvec{k}} \} $$

(22)

where

$$ u_{\varvec{k}} = u(r_{\varvec{k}} ,t) $$

(23a)

$$ w_{\varvec{k}} = w(r_{\varvec{k}} ,t) $$

(23b)

$$ \Phi_{\varvec{k}} = \Phi (r_{\varvec{k}} ,t) $$

(23c)

n represents the total number of grid points distributed along the r-axis and C ^(m)_ik is the weighting coefficients whose recursive formula can be found in as follows:

$$ C_{{\varvec{ik}}}^{\left( 1 \right)} = \left\{ {\begin{array}{ll} \frac{{M(r_{\varvec{i}} )}}{{(r_{\varvec{i}} - r_{\varvec{k}} )M(r_{\varvec{k}} )}} & i \ne k \\ - \mathop \sum \limits_{{\varvec{k} = 1,\varvec{i} \ne \varvec{k }}}^{\varvec{n}} C_{{\varvec{ik}}}^{\left( 1 \right)} & i = k \\ \end{array} } \right. $$

(24)

where k = 1,2,3, …, n. The more accurate the weight coefficient with an appropriate selection of the grid points, the more accurate the solution of the equations.

In order to improve the mesh point distribution, the cosine pattern, as known Chebyshev–Gauss–Lobatto technique, is used to generate the DQ points as follows:

$$ r_{i} = \frac{1}{2}\left( {1 - \cos \left( {\frac{(i - 1)}{(n - 1)}\pi } \right)} \right) $$

(25)

where i = 1,2,3, …, n. The analysis indicates that the above distribution would accelerate the convergence of the solution. M(r) is defined as follows:

$$ M(\varvec{r}) = \mathop \prod \limits_{{\varvec{k} = 1,\varvec{ k} \ne \varvec{i}}}^{\varvec{n}} (r_{\varvec{i}} - r_{\varvec{k}} ) $$

(26)

The associated weighting coefficient for r-th derivative of displacement functions is written as follows:

$$ C_{{\varvec{ik}}}^{{(\varvec{m})}} = \left\{ {\begin{array}{ll} m\left[ {C_{{\varvec{ik}}}^{{(\varvec{m} - 1)}} C_{{\varvec{ik}}}^{(1)} - \frac{{C_{{\varvec{ik}}}^{{(\varvec{m} - 1)}} }}{{(r_{\varvec{i}} - r_{\varvec{k}} )}}} \right] & i \ne k \ and \ 2 \le m \le n - 1 \\ - \mathop \sum \limits_{{\varvec{k} = 1,\varvec{i} \ne \varvec{k }}}^{\varvec{n}} C_{{\varvec{ik}}}^{{(\varvec{m})}} & i = k \ and \ 1 \le m \le n - 1 \\ \end{array} } \right. $$

(27)

Applying DQ method into the governing equations of the rotating variable thickness two-directional FG circular microplate in terms of displacement components (see “Appendix C”) would lead to the discretized governing equations of motion which are presented in “Appendix D”.

Now, one would rewrite the governing equations of motion in matrix form as follows:

$$ M\frac{{\partial^{2} d}}{{\partial t^{2} }} + K_{e} d = 0 $$

(28)

where M and K _e , are the mass matrix and stiffness matrix, respectively. Utilizing the first shear deformation theory, the dimensions of matrices would be 3N × 3N where the unknown displacement vector, d, is defined as follows:

$$ d = \{ \{ u_{i} \}^{T} ,\{ w_{i} \}^{T} ,\{ \Phi_{i} \}^{T} \} $$

(29)

Equation (28) would be utilized for the free vibration analysis of the rotating variable thickness two-directional FG circular microplate. Moreover, the critical angular velocity of the structure which referred to the unstable condition of the microplate could be obtained in the parametric studies.

3 Results and discussion

In this section, the first natural frequencies results for a rotating variable thickness two-directional FG circular microplate are presented. The non-dimensional angular velocity, Ω^*, of the microplate, is defined as follows:

$$ \varOmega^{*} = \frac{\varOmega }{{\sqrt {D^{c}_{11} /(I^{c}_{1} \times R^{4} )} }} $$

(30)

where, the superscript c is addressed as a ceramic material. The results obtained in this study are verified with the available results in the literature and then the effects of the angular velocity, the thickness variation, the two-directionality of FG material, the size dependency, and the boundary condition on the first non-dimensional natural frequencies are studied.

3.1 Verification

Leissa (1969) presented an analytical solution for the free vibration of a circular classical plate. Moreover Yalcin et al. (2009) and Wu et al. (2002) determined the natural frequencies of the circular classical plates utilizing differential transformation method (DTM) and generalized differential quadrature (GDQ), respectively. In order to compare the results, a reduced form of the proposed formulation would be obtained by assuming that Φ = − ∂w/∂r in Eqs. (10a–10c).

In Table 1, the first five non-dimensional natural frequencies for a circular classical plate obtained in this study are compared with those available results in the literature (Leissa 1969; Yalcin et al. 2009; Wu et al. 2002) The results are presented for different boundary conditions, hinged and clamped. As can be seen, there is a very good agreement between results, indicating the accuracy of the formulation and the solution procedure for the classical plate, neglecting the size dependency effects.

Table 1 The comparison of the first five non-dimensional natural frequencies results, ω, for a circular plate obtained in this study with those presented in the (Leissa 1969; Yalcin et al. 2009; Wu et al. 2002) utilizing the classical theory (R/h = 20)

Moreover, in Table 2, the free vibration results obtained in this study are compared with those available results in the literature (Liew et al. 1997; Irie et al. 1980) for a circular plate utilizing first shear deformation theory, indicating a very good agreement.

Table 2 The comparison of the first five non-dimensional natural frequencies, ω, of a circular plate obtained in this study with those presented in the literature (Liew et al. 1997; Irie et al. 1980) utilizing the first shear deformation theory

In order to evaluate the proposed formulation for a two-dimensional FG material circular plate, a comparison between obtained results in this study and those available results in the literature (Shariyat and Alipour 2013) is conducted in Table 3. The analyses reveal an acceptable agreement between results.

Table 3 The comparison of the first third non-dimensional natural frequencies of two-directional FGM circular plates obtained in this study with those presented in the literature

3.2 Parametric study

In order to perform a parametric study on the free vibration behavior of a variable thickness two-directional FG circular microplate, the verified proposed formulation would be utilized. The effects of the thickness-variation, the two-directionality-variation of the material and the size dependency on the non-dimensional natural frequencies of a circular microplate in terms of the non-dimensional angular velocity are studied.

3.2.1 Thickness-variation effect

In order to evaluate the thickness-variation effects on the non-dimensional natural frequency of a rotating two-directional FG circular microplate, in Table 4, the results for different boundary conditions as well as angular velocities are presented. It can be seen the fact that increasing the angular velocity would lead the reduction in the non-dimensional natural frequencies and, moreover, the non-dimensional natural frequencies of the clamped plates are larger than those of the hinged ones. The both are because of the effective stiffness variation in the plates. As considered in Table 4, the variation of the non-dimensional natural frequencies in terms of the thickness-variation index, m, is not proportional. In the case m = 0, there is a uniform thickness plate (the thickness is equal to h ₀) with a two-directional FG material. Increasing m from 0 to 1, the uniform thickness plate is converting to a plate with a central thickness equal to h ₀ and a linear thickness reduction to h ₀/2 at the outer radius. In this case, due to a large reduction in effective stiffness of the plate in comparison with the mass reduction of that, the non-dimensional natural frequency is decreased with respect to those observed for the first uniform thickness plate. However, it depends on where the thickness is decreased in the section of the plate, the non-dimensional natural frequency might increase or decrease. The fact is that due to two-directionality-variations in the material property (as known non-homogeneous material), there is no a proportional relation between the non-dimensional natural frequency and the thickness variation, unlike the proportional relation could be observed in a homogeneous material plate.

Table 4 The comparison of results obtained by first shear deformation theory for the first non-dimensional natural frequency of a rotating two-directional FG circular microplate for different non-dimensional angular velocities, boundary conditions and thickness variations (h/l = 1, α = 0.5, β = 2, n = 2, R/h = 20, q = 0.5)

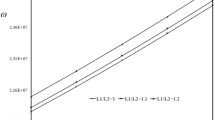
In Figs. 2 and 3, the first two non-dimensional natural frequencies of a rotating two-directional FG circular microplate in terms of the non-dimensional angular velocity for different variations of thickness prescribed by clamp and hinge boundary conditions are presented, respectively. Although, the non-dimensional natural frequencies of the plates vary with respect to the thickness variation, the results reveal that the critical angular velocity would be insensitive in respect to that.

Fig. 2

Free vibration of rotating two-directional FGM circular microplates in terms of the non-dimensional angular velocity for different variations of the thickness with the clamped boundary condition: a the first non-dimensional natural frequencies, ω₁, b the second non-dimensional natural frequencies, ω₂

Fig. 3

Free vibration of rotating two-directional FGM circular microplates in terms of the non-dimensional angular velocity for different variations of thickness with the hinged boundary condition: a the first non-dimensional natural frequencies, ω₁, b the second non-dimensional natural frequencies, ω₂

In Figs. 4 and 5, the first non-dimensional natural frequencies for a two-directional FG circular microplate in terms of the non-dimensional natural frequency for different rates, q, of the linear thickness variation, m = 1, with the clamped and the hinged boundary condition are presented, respectively. As can be seen, the more rate of the linearly increasing the thickness in the microplate, the more enlargement of the effective stiffness. Since the linearly varying the thickness has a significant proportional effect on the critical angular velocity of the clamped microplate, this could be neglect about the hinged ones, as can be seen in Figs. 4 and 5.

Fig. 4

The first non-dimensional natural frequency, ω₁, of a clamped two-directional FG circular microplate in terms of non-dimensional angular velocity for different rates of the linear thickness variation

Fig. 5

The first non-dimensional natural frequency, ω₁, of a hinged two-directional FG circular microplate in terms of non-dimensional angular velocity for different rates of the linear thickness variation

3.2.2 Two-directionality-variation in FG material effect

In order to study the impact of two-directionality-variation of FG material, in Table 5, the first non-dimensional natural frequencies of a rotating variable thickness circular microplate for different size dependencies, h/l, and the material coefficients in radial-direction, α, are presented. The results are evaluated for the hinged and the clamped microplates. As discussed in the literature, there is a critical size dependency in which a significant reduction would occur in the first non-dimensional natural frequencies of the structure. This was known as buckling phenomenon in the literature. For instance, in the case of hinged one-dimensional FG microplate, (i.e. α = 0), in Table 5, h/l close to 1 could know as a critical value. Considering the variation of material in the two-direction, (i.e. α = − 0.5 and 0.5), would lead to the increase or the decrease in the critical values, as can be seen in Table 5. Moreover, it is clear that the non-dimensional natural frequencies of the microplate strongly are depending on how the material is graded in the plate. This could be found that the effects of the material variation in the second direction would lead to non-proportionality of the mechanical response of the plate. Therefore, the nonlinear effects of the material variation on the response of such plates should be predicted to the design of the microdevices.

Table 5 The size dependency effects on the first non-dimensional natural frequency, ω₁, of a rotating variable thickness circular microplate subjected to different boundary conditions and two-direction FG materials (m = 1, Ω ^* = 0.5, β = 2, n = 1.2, R/h = 15, q = 0.5)

Moreover, in Fig. 6, the variation of the first and the second non-dimensional natural frequencies of a rotating variable thickness circular microplate in terms of the non-dimensional angular velocity for one- and two-direction FG materials are presented. Not only the material variation in the second direction has a significant effect on the non-dimensional natural frequencies, but also there is an ineligible impact on the critical angular velocities, as can be found in Fig. 6.

Fig. 6

Free vibration of a rotating variable thickness circular microplate in terms of the non-dimensional angular velocity for one- and two-direction FG materials: a the first non-dimensional natural frequencies, ω₁, b the second non-dimensional natural frequencies, ω₂

In Fig. 7, the first three non-dimensional natural frequencies of rotating variable thickness circular microplate in terms of the FG power index in the thickness direction, n, for homogeneous, one- and two-direction FG materials are presented. The homogeneous material plate is associated with the case of n = α = 0. It can be seen, replacing the homogeneous material with one-directional FG material, α = 0, and n ≠ 0 would lead a reduction in the first non-dimensional natural frequencies. This is because of the effective stiffness reduction in the FG plate in comparison with the first one. Moreover, it can be found in Fig. 7, the effects of two-directionality-variation of FG material, α, is not sensitive in respect to FG power index in the thickness direction, n.

Fig. 7

free vibration of a rotating variable thickness circular microplate in terms of the FG power index for homogeneous, one- and two-direction FG materials: a the first non-dimensional natural frequencies, ω₁, b the second non-dimensional natural frequencies, ω₂, c the third non-dimensional natural frequencies, ω₃

The impact of FG power index in the thickness direction, n, on the first non-dimensional natural non-dimensional frequency in terms of the non-dimensional angular velocity, could be seen in Figs. 8 and 9 for a variable thickness circular microplate prescribed by clamp and hinge boundary conditions, respectively. In the cases of n = 0 and 1000 (infinity), there is only the radially graded material (one-directional FG) with the homogeneous ceramic and metal in thickness direction, respectively. As can be found in Figs. 8 and 9, there is a proportional relation between the FG power index in the thickness direction, n, and the first non-dimensional natural frequency as well as the critical angular velocity.

Fig. 8

The first non-dimensional natural frequency of a clamped variable thickness circular microplate in terms of the non-dimensional angular velocity for one- and two-direction FG materials (the impact of FG power index in thickness direction, n)

Fig. 9

The first non-dimensional natural frequency of a clamped variable thickness circular microplate in terms of the non-dimensional angular velocity for one- and two-direction FG materials (the impact of FG power index in thickness direction, n)

Moreover, the proportional effects of the FG power index in the radial direction, β, on the first non-dimensional natural frequency in terms of the non-dimensional angular velocity could be seen in Fig. 10, where the cases of β = 0 and 1000 (infinity), are known as thickness-dependent graded materials.

Fig. 10

The first natural non-dimensional frequency of a clamped variable thickness circular microplate in terms of the non-dimensional angular velocity for one- and two-direction FG materials (the impact of FG power index in radial direction, β)

In Fig. 11, a comprehensive map for the two-directionality-variation of material effects on the first three non-dimensional natural frequencies of a rotating variable thickness circular microplate is presented. The area between the upper and the lower curves is associated with the non-dimensional natural frequencies for a two-direction FG plate and the boundaries of the area are associated with those for one-direction FG plates.

Fig. 11

A map for the two-directionality-variation of material effects on the first three non-dimensional natural frequencies of a rotating variable thickness circular microplate: a the first non-dimensional natural frequencies, ω₁, b the second non-dimensional natural frequencies, ω₂, c the third non-dimensional natural frequencies, ω₃

3.2.3 Size dependency effect

In Figs. 12 and 13, the impact of the size dependency on the first non-dimensional natural frequency for a variable thickness circular microplate in terms of the non-dimensional angular velocity with clamped and hinged boundary conditions are presented, respectively. As can be seen, the increase of the size dependency would lead to the reduction of the non-dimensional natural frequency as well as critical angular velocity.

Fig. 12

The first non-dimensional natural frequencies, ω₁, of a clamped variable thickness circular microplate in terms of the non-dimensional angular velocity for different size dependencies

Fig. 13

The first non-dimensional natural frequencies, ω₁, of a hinged variable thickness circular microplate in terms of the non-dimensional angular velocity for different size dependencies

4 Conclusion

In this paper, the governing equations of motion for a rotating variable thickness two-directional FG circular microplate were proposed. The equations were derived utilizing the Hamiltonian’s principle as well as the first shear deformation and the modified couple stress theories. The differential quadrature method was used to pursue the solution procedure. The proposed formulation, in special cases, was verified with the available results in the literature. The contributions of the thickness-variation of the section, two-directionality-variation of the material and the size dependency as well as the angular velocity of the plate, on the first natural frequencies were studied.

Appendices

Appendix A

The strain energy, U, in an isotropic linear elastic material would obtain utilizing the modified couple stress theory as follows (Eshraghi et al. 2016; Reddy and Berry 2012; Ke et al. 2012):

$$ {\text{U = }}\frac{1}{2}\int\limits_{V} {(\sigma :\varepsilon + m:\chi )dV} $$

(31)

where ε and σ are the linear strain and the Cauchy stress tensors, respectively. χ and m are the symmetric curvature strain and deviatoric part of the couple stress tensors. The four last tensors are defined as follows (Eshraghi et al. 2016; Reddy and Berry 2012; Ke et al. 2012):

$$ \sigma = \lambda tr(\varepsilon )I + 2\mu \varepsilon $$

(32)

$$ \varepsilon = \frac{1}{2}[\nabla u + (\nabla u)^{T} ] $$

(33)

$$ m = 2l^{2} \mu \chi $$

(34)

$$ \chi = \frac{1}{2}[\nabla \varLambda + (\nabla \varLambda )^{T} ] $$

(35)

where λ and μ are the Lame’s constant, u and l are the displacement vector and the material length scale parameter, respectively, and Λ is a rotation vector defined by:

$$ \varLambda = \frac{1}{2}curl u $$

(36)

Appendix B

$$ N_{rr} (r) = \int\limits_{{ - \frac{h(r)}{2}}}^{{\frac{h(r)}{2}}} {\sigma_{rr} dz = \left( {A_{11} (r)\frac{\partial u}{\partial r} + A_{12} (r)\frac{u}{r}} \right) + \left( {B_{11} (r)\frac{\partial \Phi }{\partial r} + B_{12} (r)\frac{\Phi }{r}} \right)} $$

(37)

$$ N_{\theta \theta } (r) = \int\limits_{{ - \frac{h(r)}{2}}}^{{\frac{h(r)}{2}}} {\sigma_{\theta \theta } dz = \left( {A_{12} (r)\frac{\partial u}{\partial r} + A_{11} (r)\frac{u}{r}} \right) + \left( {B_{12} (r)\frac{\partial \Phi }{\partial r} + B_{11} (r)\frac{\Phi }{r}} \right)} $$

(38)

$$ M_{rr} (r) = \int\limits_{{ - \frac{h(r)}{2}}}^{{\frac{h(r)}{2}}} {\sigma_{rr} zdz = \left( {B_{11} (r)\frac{\partial u}{\partial r} + B_{12} (r)\frac{u}{r}} \right) + \left( {A_{11} (r)\frac{\partial \Phi }{\partial r} + B_{12} (r)\frac{\Phi }{r}} \right)} $$

(39)

$$ M_{\theta \theta } (r) = \int\limits_{{ - \frac{h(r)}{2}}}^{{\frac{h(r)}{2}}} {\sigma_{\theta \theta } zdz = \left( {B_{12} (r)\frac{\partial u}{\partial r} + B_{11} (r)\frac{u}{r}} \right) + \left( {D_{11} (r)\frac{\partial \Phi }{\partial r} + D_{12} (r)\frac{\Phi }{r}} \right)} $$

(40)

$$ M_{rz} (r) = \int\limits_{{ - \frac{h(r)}{2}}}^{{\frac{h(r)}{2}}} {\sigma_{rz} dz = k_{s} A_{55} } (r)\left( {\frac{\partial w}{\partial r} + \Phi } \right) $$

(41)

$$ \varOmega_{r\theta } = \int\limits_{{ - \frac{h(r)}{2}}}^{{\frac{h(r)}{2}}} {m_{r\theta } dz = \frac{1}{2}S(r,z)\left( {\left( {\frac{\partial \Phi }{\partial r} - \frac{{\partial^{2} w}}{{\partial r^{2} }}} \right) - \frac{1}{r}\left( {\Phi - \frac{\partial w}{\partial r}} \right)} \right)} $$

(42)

where ks = π²/12 is known as the shear correction factor and the constants are defined as follows:

$$ \{ A_{11} ,B_{11} ,D_{11} \} = \int\limits_{{ - \frac{h(r)}{2}}}^{{\frac{h(r)}{2}}} {\left( {\frac{E(r,z)}{{1 - v^{2} (r,z)}}} \right)} \{ 1,z,z^{2} \} dz $$

(43)

$$ \{ A_{12} ,B_{12} ,D_{12} \} = \int\limits_{{ - \frac{h(r)}{2}}}^{{\frac{h(r)}{2}}} {\left( {\frac{E(r,z)v(z)}{{1 - v^{2} (r,z)}}} \right)} \{ 1,z,z^{2} \} dz $$

(44)

$$ A_{55} = \int\limits_{{ - \frac{h(r)}{2}}}^{{\frac{h(r)}{2}}} {\left( {\frac{E(r,z)}{2(1 + v(r,z))}} \right)} dz $$

(45)

$$ S = \int\limits_{{ - \frac{h(r)}{2}}}^{{\frac{h(r)}{2}}} {\left( {\frac{{l^{2} (r,z)E(r,z)}}{2(1 + v(r,z))}} \right)} dz $$

(46)

Appendix C

$$ \left[ \begin{aligned} & (A_{11} )\left( {\frac{{\partial^{2} u}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial u}{\partial r} - \frac{u}{{r^{2} }}} \right) \hfill \\ &\quad + r\frac{{\partial A_{11} }}{\partial r}\frac{\partial u}{\partial r} + \frac{{\partial A_{12} }}{\partial r}u \hfill \\ &\quad + (B_{11} )\left( {\frac{{\partial^{2} \Phi }}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial \Phi }{\partial r} - \frac{\Phi }{{r^{2} }}} \right) \hfill \\ &\quad \left( {r\frac{{\partial B_{11} }}{\partial r}\frac{\partial \Phi }{\partial r} + \frac{{\partial B_{12} }}{\partial r}\Phi } \right) \hfill \\ \end{aligned} \right] = \left( {I_{1} \frac{{\partial^{2} u}}{{\partial t^{2} }} + I_{2} \frac{{\partial^{2} \Phi }}{{\partial t^{2} }}} \right) $$

(47)

$$ \left[ \begin{aligned} &\frac{{k_{s} }}{r}\left( {A_{55} r\frac{{\partial^{2} w}}{{\partial r^{2} }} + A_{55} \frac{\partial w}{\partial r} + \frac{{\partial A_{55} }}{\partial r}r\frac{\partial w}{\partial r}} \right) \hfill \\ &\quad + \frac{S}{4r}\left( { - \frac{1}{2}\frac{{\partial^{4} w}}{{\partial r^{4} }} - \frac{1.5}{2r}\frac{{\partial^{3} w}}{{\partial r^{3} }} - \left( {\frac{1.5}{r} - \frac{1}{{r^{2} }}} \right)\frac{{\partial^{2} w}}{{\partial r^{2} }} - \left( {\frac{1}{{r^{3} }} - \frac{3}{{r^{2} }}} \right)\frac{\partial w}{\partial r}} \right) \hfill \\ &\quad - \left( {\frac{1}{2r}\frac{\partial S}{\partial r}} \right)\left( {\frac{{\partial^{3} w}}{{\partial r^{3} }} + \frac{1.5}{r}\frac{{\partial^{2} w}}{{\partial r^{2} }} + \left( {\frac{1.5}{r} - \frac{1}{{r^{2} }}} \right)\frac{\partial w}{\partial r}} \right) \hfill \\ &\quad- \left( {\frac{1}{2r}\frac{{\partial^{2} S}}{{\partial r^{2} }}} \right)\left( {\frac{1}{2}\frac{{\partial^{2} w}}{{\partial r^{2} }} + \frac{1.5}{r}\frac{\partial w}{\partial r}} \right) \hfill \\ &\quad + \frac{{k_{s} }}{r}\left( {A_{55} r\frac{\partial \Phi }{\partial r} + A_{55} \Phi + \frac{{\partial A_{55} }}{\partial r}r\Phi } \right) \hfill \\ &\quad + \frac{S}{4r}\left( {\frac{1}{2}\frac{{\partial^{3} \Phi }}{{\partial r^{3} }} + \frac{1.5}{2r}\frac{{\partial^{2} \Phi }}{{\partial r^{2} }} + \left( {\frac{1.5}{r} - \frac{1}{{r^{2} }}} \right)\frac{\partial \Phi }{\partial r} + \left( {\frac{1}{{r^{3} }} - \frac{3}{{r^{2} }}} \right)\Phi } \right) \hfill \\ &\quad + \left( {\frac{1}{2r}\frac{\partial S}{\partial r}} \right)\left( {\frac{{\partial^{2} \Phi }}{{\partial r^{2} }} + \left( {\frac{1}{r} + 1.5} \right)\frac{\partial \Phi }{\partial r} + \left( {\frac{1.5}{r} - \frac{1}{{r^{2} }}} \right)\Phi } \right) \hfill \\ &\quad + \left( {\frac{1}{2r}\frac{{\partial^{2} S}}{{\partial r^{2} }}} \right)\left( {\frac{1}{2}\frac{\partial \Phi }{\partial r} + \frac{1.5}{r}\Phi } \right) + \frac{\partial }{r\partial r}\left( {N^{Rotation} r\frac{\partial w}{\partial r}} \right) \hfill \\ \end{aligned} \right] = I_{1} \frac{{\partial^{2} w}}{{\partial t^{2} }} $$

(48)

$$ \left[ \begin{aligned} &- k_{s} A_{55} \frac{\partial w}{\partial r} + \left( { - \frac{S}{2}} \right)\left[ {\frac{1}{4}\frac{{\partial^{3} w}}{{\partial r^{3} }} + \frac{1}{r}\frac{{\partial^{2} w}}{{\partial r^{2} }} + \frac{1}{{r^{2} }}\frac{\partial w}{\partial r}} \right] - \left( {\frac{1}{4}\frac{\partial S}{\partial r}} \right)\left( {\frac{{\partial^{2} w}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial w}{\partial r}} \right) \hfill \\ &\quad - k_{s} A_{55} \Phi + D_{11} \left( {\frac{{\partial^{2} \Phi }}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial \Phi }{\partial r} - \frac{1}{{r^{2} }}\Phi } \right) + \left( {\frac{{\partial D_{11} }}{\partial r}} \right)\left( {\frac{\partial \Phi }{\partial r}} \right) + \left( {\frac{{\partial D_{12} }}{\partial r}} \right)\left( {\frac{1}{r}\Phi } \right) \hfill \\ &\quad \frac{1}{2}\left\{ {\left( {\frac{S}{4}} \right)\left( {\frac{{\partial^{2} \Phi }}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial \Phi }{\partial r} - \frac{1}{{r^{2} }}\Phi } \right) + \left( {\frac{\partial S}{\partial r}} \right)\left( {\frac{\partial \Phi }{\partial r}} \right) + \left( {\frac{\partial S}{\partial r}} \right)\left( {\frac{1}{r}\Phi } \right)} \right\} \hfill \\ &\quad \frac{1}{r}\left\{ {(B_{11} )\left( {r\frac{{\partial^{2} u}}{{\partial r^{2} }} + \frac{\partial u}{\partial r} - \frac{1}{r}u} \right) + \left( {\frac{{\partial B_{11} }}{\partial r}} \right)\left( {r\frac{\partial u}{\partial r}} \right) + \left( {\frac{{\partial B_{12} }}{\partial r}} \right)(u)} \right\} \hfill \\ \end{aligned} \right] = I_{2} \frac{{\partial^{2} u}}{{\partial t^{2} }} + I_{3} \frac{{\partial^{2} \Phi }}{{\partial t^{2} }} $$

(49)

$$ \left[ {\left( {A_{11} \left( {r\frac{\partial u}{\partial r}} \right) + A_{12} u} \right) + \left( {B_{11} \left( {r\frac{\partial \Phi }{\partial r}} \right) + B_{12} \Phi } \right)} \right]\delta \,u = 0\quad {\text{at}}\;{\text{r}} = 0,{\text{R}} $$

(50)

$$ \left[ \begin{aligned} &\frac{S}{4}\left( {\frac{{\partial^{2} \Phi }}{{\partial r^{2} }} - \frac{{\partial^{3} w}}{{\partial r^{3} }} + \frac{1}{r}\frac{\partial \Phi }{\partial r} - \frac{1}{r}\frac{{\partial^{2} w}}{{\partial r^{2} }} - \frac{\Phi }{{r^{2} }} + \frac{1}{{r^{2} }}\frac{\partial w}{\partial r}} \right) \hfill \\ &\quad + k_{s} A_{55} \left( {\frac{\partial w}{\partial r} + \Phi } \right) \hfill \\ &\quad + \frac{1}{4}\frac{\partial S}{\partial r}\left( {\frac{\partial \Phi }{\partial r} - \frac{{\partial^{2} w}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial \Phi }{\partial r} + \frac{1}{r} - \frac{\partial w}{\partial r} + \Phi } \right) \hfill \\ \end{aligned} \right]\delta w = 0\quad {\text{at}}\;{\text{r}} = 0,{\text{R}} $$

(51)

$$ \left( {\frac{S}{4}\frac{1}{r}\left( {\left( {\frac{\partial \Phi }{\partial r} - \frac{{\partial^{2} w}}{{\partial r^{2} }}} \right) - \frac{1}{r}\left( {\Phi - \frac{\partial w}{\partial r}} \right)} \right)} \right)\delta \left( {\frac{\partial w}{\partial r}} \right) = 0\quad \,{\text{at}}\;{\text{r}} = 0,{\text{R}} $$

(52)

$$ \left( {B_{{11}} \frac{{\partial u}}{{\partial r}} + B_{{12}} \frac{u}{r} + D_{{11}} \frac{{\partial \Phi }}{{\partial r}} + D_{{12}} \frac{\Phi }{r} + \frac{S}{4}\left( {\left( {\frac{{\partial \Phi }}{{\partial r}} - \frac{{\partial ^{2} w}}{{\partial r^{2} }}} \right) - \frac{1}{r}\left( {\Phi - \frac{{\partial w}}{{\partial r}}} \right)} \right)} \right)\delta \Phi = 0\quad {\text{at}}\;{\text{r}} = 0,{\text{R}} $$

(53)

Appendix D

$$ \left[ \begin{aligned} &(A_{11} )\left( {\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 2 \right)} u_{k} + \frac{1}{{r_{i} }}\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 1 \right)} u_{k} - \frac{{u_{i} }}{{r_{i}^{2} }}} } } \right) \hfill \\ &\quad + \left( {r_{i} \left( {\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 1 \right)} } A_{11} } \right)\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 1 \right)} u_{k} } } \right)\sum\limits_{k = 1}^{{n_{i} }} { + \left( {\left( {\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 1 \right)} A_{12} } } \right)(u_{i} )} \right)} \hfill \\ &\quad + (B_{11} )\left( {\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 2 \right)} \Phi_{k} } + \frac{1}{{r_{i} }}\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 1 \right)} \Phi_{k} - \frac{{\Phi_{i} }}{{r_{i}^{2} }}} } \right) \hfill \\ &\quad + \left( {r_{i} \left( {\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 1 \right)} } B_{11} } \right)\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 1 \right)} \Phi_{k} } } \right) + \left( {\left( {\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 1 \right)} B_{12} } } \right)(\Phi_{i} )} \right) \hfill \\ \end{aligned} \right] = \omega^{2} (I_{1} u_{i} + I_{2} \Phi_{i} ) $$

(54)

$$ \left[ \begin{aligned} &\left( {\frac{S}{{4r_{i} }}} \right)\left[ \begin{aligned} &\frac{1}{2}\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 3 \right)} \Phi_{k} + \frac{1.5}{{2r_{i} }}\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 2 \right)} \Phi_{k} \left( {\frac{1.5}{{r_{i} }} - \frac{1}{{r_{i}^{2} }}} \right)\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 1 \right)} \Phi_{k} } } } \hfill \\ &\quad + \left( {\frac{1}{{r^{3}_{i} }} - \frac{3}{{r_{i}^{2} }}} \right)\Phi_{i} - \frac{1}{2}\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 4 \right)} w_{k} } - \frac{1.5}{{2r_{i} }}\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 3 \right)} w_{k} } \hfill \\ &\quad \left( {\frac{1.5}{{r_{i} }} - \frac{1}{{r_{i}^{2} }}} \right)\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 2 \right)} w_{k} - } \left( {\frac{1}{{r^{3}_{i} }} - \frac{3}{{r_{i}^{2} }}} \right)\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 1 \right)} w_{k} } \hfill \\ \end{aligned} \right] \hfill \\ &\quad + (k_{s} A_{55} )\left( {\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 2 \right)} w_{k} } + \frac{1}{{r_{i} }}\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 1 \right)} w_{k} + \sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 1 \right)} \Phi_{k} + \frac{{\Phi_{i} }}{{r_{i} }}} } } \right) \hfill \\ &\quad \left( {\frac{{k_{s} }}{{r_{i} }}\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 1 \right)} A_{55} } } \right)\left( {r_{i} \sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 1 \right)} w_{k} + r_{i} \Phi_{i} } } \right) \hfill \\ &\quad - \left( {\frac{1}{{2r_{i} }}\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 1 \right)} S} } \right)\left( {\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 3 \right)} w_{k} } + \left( {\frac{1.5}{{r_{i} }}} \right)\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 2 \right)} w_{k} } + \left( {\frac{1.5}{{r_{i} }} - \frac{1}{{r_{i}^{2} }}} \right)\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 1 \right)} w_{k} } } \right) \hfill \\ &\quad + \left( {\left( {\frac{1}{{2r_{i} }}\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 1 \right)} S} } \right)(\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 2 \right)} \Phi_{k} } + \left( {\frac{1}{{r_{i} }} + 1.5} \right)\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 1 \right)} \Phi_{k} } + \left( {\frac{1.5}{{r_{i} }} - \frac{1}{{r_{i}^{2} }}} \right)\Phi_{i} } \right) \hfill \\ &\quad - \left( {\left( {\frac{1}{{2r_{i} }}\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 2 \right)} S} } \right)\left( {\left( {\frac{1}{2}} \right)\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 2 \right)} w_{k} } + \frac{1.5}{{r_{i} }}\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 1 \right)} w_{k} } } \right)} \right) \hfill \\ &\quad + \left( {\left( {\frac{1}{{2r_{i} }}\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 2 \right)} S} } \right)\left( {\left( {\frac{1}{2}} \right)\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 1 \right)} \Phi_{k} } + \left( {\frac{1.5}{{r_{i} }}} \right)\Phi_{i} } \right)} \right) \hfill \\ &\quad + \frac{1}{{r_{i} }}\left( {\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 1 \right)} \left( {N^{Rotation} r\left( {\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 1 \right)} w_{k} } } \right)} \right)} } \right) \hfill \\ \end{aligned} \right] = \omega^{2} I_{1} w_{i} $$

(55)

$$ \left[ \begin{aligned} &- k_{s} A_{55} \left( {\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 1 \right)} w_{k} )} - \Phi_{i} } \right) \hfill \\ &\quad \left( { - \frac{S}{2}} \right)\left( {\frac{1}{4}\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 3 \right)} w_{k} } + \frac{1}{{r_{i} }}\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 2 \right)} w_{k} + \frac{1}{{r_{i}^{2} }}\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 1 \right)} w_{k} } } } \right) \hfill \\ &\quad - \left( {\left( {\frac{1}{4}\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 1 \right)} S} } \right)\left( {\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 2 \right)} w_{k} } + \frac{1}{{r_{i} }}\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 1 \right)} w_{k} } } \right)} \right) \hfill \\ &\quad + \left( {\frac{S}{4}\left( {\frac{1}{2}} \right)} \right)\left( {\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 2 \right)} \Phi_{k} } + \frac{1}{{r_{i} }}\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 1 \right)} \Phi_{k} - \frac{{\Phi_{i} }}{{r_{i}^{2} }}} } \right) \hfill \\ &\quad + \left( {\left( {\frac{1}{2}\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 1 \right)} S} } \right)\left( {\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 1 \right)} \Phi_{k} } + \frac{{\Phi_{i} }}{{r_{i} }}} \right)} \right) \hfill \\ &\quad + (D_{11} )\left( {\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 2 \right)} \Phi_{k} } + \frac{1}{{r_{i} }}\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 1 \right)} \Phi_{k} - \frac{{\Phi_{i} }}{{r_{i}^{2} }}} } \right) \hfill \\ &\quad + \left( {\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 1 \right)} D_{11} } \left( {\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 1 \right)} \Phi_{k} } } \right)} \right) + \left( {\left( {\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 1 \right)} D_{12} } } \right)(\Phi_{i} )} \right) \hfill \\ &\quad + (B_{11} )\left( {\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 2 \right)} u_{k} } + \frac{1}{{r_{i} }}\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 1 \right)} u_{k} - \frac{{u_{i} }}{{r_{i}^{2} }}} } \right) \hfill \\ &\quad + \left( {\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 1 \right)} B_{11} } \left( {\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 1 \right)} u_{k} } } \right)} \right) + \left( {\sum\limits_{k = 1}^{{n_{i} }} {C_{ik}^{\left( 1 \right)} B_{12} } (u_{i} )} \right) \hfill \\ \end{aligned} \right] = \omega^{2} (I_{3} \Phi_{i} + I_{2} u_{i} ) $$

(56)