Small scale effect on the pull-in instability and vibration of graphene sheets

Abstract

In this paper, the small scale effect on the pull-in instability and frequency of graphene sheets subjected to electrostatic and van der Waals forces is studied. Eringen’s nonlocal elasticity theory is used to account for the small scale effect, and the graphene sheet is modeled as a nonlocal plate. Reduce-order model incorporating nonlocal effect and van der Waals force is derived. Results show that nonlocal elasticity reduces the pull-in voltages and fundamental frequencies. The effect of nonlocal parameter on pull-in voltages and fundamental frequencies is more obvious if the size of nanoplate is smaller. In addition, an empirical formula for pull-in voltage is explored. The form of the empirical formula is relatively simple, therefore is convenient for engineers to indicate an experimental method to determine the nonlocal parameters of the materials and to design nano-switches.

1 Introduction

Nanoelectromechanical system (NEMS) is a rapidly growing research field with great potential for future applications (Craighead 2000). Many nanomaterials, such as carbon nanotubes and graphene sheets, have been applied in NEMS with much successfully (Rueckes et al. 2000; Tombler et al. 2000). Therefore, it is important to understand their mechanical and physical properties. There are four main methods of modeling nanomaterials. These are experiment, atomistic modeling, hybrid atomistic–continuum mechanics and continuum mechanics model. At nano-scale, experimental efforts may be formidable and the cost of experiments is tremendous. Continuum mechanical modeling is less computationally expensive than both atomistic modeling and hybrid atomistic–continuum mechanics methods. Therefore, continuum mechanical modeling has been employed as a useful way of simulating mechanical behaviors of nanostructures, such as buckling (Wang et al. 2005; Duan et al. 2010), bending (Wang et al. 2015) and free vibration (Karimi et al. 2015; He et al. 2005). As the sizes of structures reduce to nano-scales, the classical continuum models can not explain the small scale effect discovered in experiments and molecular dynamics (MD) simulations (Lu et al. 2007). Size-dependent continuum models have attracted significant attention in simulating mechanical behaviors of nano-structures and devices. Among these, nonlocal elasticity theory developed by Eringen (1983, 2002) has received wide acceptance. In this theory, small scale effect is introduced by a spatial integral constitutive relation, and the stress at a given reference point depends on the strains at every point in the elastic body.

Due to nano-switches have excellent on–off current characteristics (such as, an abrupt switching and an essentially zero off current), they have been predicted to have an ability for solving some difficulties in complementary metal–oxide–semiconductor devices, such as parasitic leakage currents, short-channel effects (Meindl et al. 2001) and power dissipation. In generally, a nano-switch consists of two parallel electrodes. One is movable electrode which can be modeled as a beam or plate. The other is fixed electrode. When applied voltage across the two electrodes, the movable one will deflect, due to electrostatic force. As the applied voltage reaches a critical value, the upper movable electrode will be unstable and collapses to the fixed electrode. This phenomenon is called as pull-in instability. The critical value of applied voltage is called as pull-in voltage. Size-dependent continuum models have been used to investigate the pull-in instability of nano-switches (Yang et al. 2008; Taghavi and Nahvi 2013; Mousavi et al. 2013; Sahmani and Bahrami 2015; Arani et al. 2013; Ansari et al. 2012). For examples, Yang et al. (2008) and Taghavi and Nahvi (2013) studied the pull-in instability of nano-switches subjected to an electrostatic force and intermolecular force by using nonlocal elasticity theory. Later, Mousavi et al. (2013) investigated the pull-in instability of nonlinear nano-switches based on nonlocal elasticity theory.

On the other hand, graphene sheets have great potential in designs of sensors, mass detection, gas detection, switches and actuators, due to their superior mechanical (Lee et al. 2008, 2009), optical (Nair et al. 2008), electrical and thermal (Balandin et al. 2008) properties. Nonlocal elasticity theory has been widely used to study the buckling and vibrational behaviors of graphene sheets (Pradhan and Murmu 2009, 2010; Murmu and Pradhan 2009; Pradhan and Kumar 2010, 2011; Mandal and Pradhan 2014; Zhang et al. 2015a, b; Arani and Jalaei 2015). In these studied grapheme sheets are modeled as nonlocal plates. Recently, nano-switches based on graphene sheets have been fabricated (Milaninia et al. 2009; Shi et al. 2012). There are a few works which focus on mechanical behaviors of nano-switches based on graphene sheets. For examples, Rokni and Lu (2013) investigated the pull-in instability of curved multilayer graphene/substrate microcantilever electrostatic actuators. Later, they investigated pull-in behavior of graphene nanoribbon electrostatic actuators with consideration of interlayer shear and surface energy effects (Rokni and Lu 2013). It is noted that previous studies about the pull-in behaviour of nano-switches, are limited to one dimensional nanoswitches (the moveable electrode is modeled as an elastic beam). So far, they are no studies on the pull-in instability of 2D graphene sheets nanoswitches (the moveable electrode is modeled as an elastic plate) with consideration of nonlocal effect. In this paper, we study the pull-in behavior of a clamped rectangular graphene sheets subjected to electrostatic and van der Waals forces.

The rest of the present paper is organized as follows. In Sect. 2, based on nonlocal elasticity theory, the governing equation for a rectangular graphene sheets in presence of electrostatic and van der Waals forces is derived. In Sect. 3, the reduced-order model is derived and the procedure for solving the governing equations of the reduced-order model is given. In Sect. 4, the effects of nonlocal parameter and van der Waals forces on the pull-in instability and the fundamental frequency of the rectangular nano-plate are investigated. Conclusions are summarized in Sect. 5.

2 Problem statement

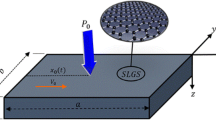
Figure 1 shows a rectangular graphene sheets (modeled as nonlocal plate) with length l, width $\eta l$ ($0 < \eta \le 1$) and thickness h. The initial gap $g_{0}$ between the two sheets (plates) and the thickness h are much smaller than its length l. According to nonlocal elasticity theory (Eringen 1983, 2002), the stress–strain relationship can be represented by.

$$[1 - (e_{0} a)^{2} \nabla^{2} ]\tau_{ij} = 2\mu \varepsilon_{ij} + \lambda \varepsilon_{kk} \delta_{ij}$$

(1)

where $\nabla^{2} = \frac{{\partial^{2} }}{{\partial x^{2} }} + \frac{{\partial^{2} }}{{\partial y^{2} }}$; $\tau_{ij}$ is the nonlocal stress tensor; $\mu$ and $\lambda$ are Lame constants. The nonlocal parameter $e_{0} a$ shows the effect of small scale on the responses of the structure, and can be obtained by MD simulations and matching against experiments (Duan et al. 2007).

Fig. 1

Sketch of the electrostatically actuated device

For thin plate theory, the displacement field is

$$u_{\alpha } = - zw_{,\alpha } \,\,\;{\text{and}}\;\,u_{3} = w\,\,\left( {x,y,t} \right)$$

(2)

where $u_{\alpha }$ ($\alpha = 1,\;2$) and $u_{3}$ are, respectively, displacement components along x-axis, y-axis, and z-axis. The strains are expressed as $\varepsilon_{ij} = (u_{i,j} + u_{j,i} )/2$.

The equation of motion for the plate can be represented by $\sigma_{ij,j} = \rho \frac{{\partial^{2} u_{i} }}{{\partial t^{2} }}$, where $\rho$ is the mass density of the plate. This equation can be expressed in the following forms by multiplying them by $zdz$ and integrating through the thickness direction of the plate:

$$N_{3\alpha ,\alpha } - q = \int_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\rho} {\ddot{u}_{3 }}$$

(3)

$$\, M_{\alpha \beta ,\beta } - N_{3\alpha } \, = 0$$

(4)

Neglecting fringing fields, the electrostatic distributed force per unit area is (Pelesko 2002)

$$F_{e} = \frac{{\varepsilon_{0} V^{2} }}{{2(g_{0} - w)^{2} }}$$

(5)

where $\varepsilon_{0}$ and V are the dielectric constant in vacuum and the applied voltage, respectively. For the gap between the two plates smaller than the retardation length or the wavelength of the virtual transitions responsible for the quantum dipole fluctuations (Bordag et al. 2001), the intermolecular forces can described by van der Waals force. The van der Waals distributed force per unit area is (Israelachvili et al. 1991).

$$F_{vdW} = \frac{A}{{6\pi (g_{0} - w)^{3} }}$$

(6)

where A is the Hamaker constant.

Multiplying Eq. (1) by zdz and integrating through the thickness direction of the plate, we obtained.

$$[1 - (e_{0} a)^{2} \nabla^{2} ]M_{\alpha \beta } = \frac{{h^{3} }}{12}(2\mu w_{,\alpha \beta } + \lambda w_{,kk} \delta_{\alpha \beta } )$$

(7)

Using Eqs. (3)–(7), we obtained.

$$D\nabla^{4} w - [1 - (e_{0} a)^{2} \nabla^{2} ] \left [\frac{{\varepsilon_{0} V^{2} }}{{2(g_{0} - w)^{2} }} + \frac{{\bar{h}c\pi^{2} }}{{240(g_{0} - w)^{4} }} \right] = [1 - (e_{0} a)^{2} \nabla^{2} ] \rho h {\ddot{w}}$$

(8)

where $D = Eh^{3} /[12(1 - v^{2} )]$ is the bending rigidity of the plate, and $E$ and $\upsilon$ are, respectively, the Young’s modulus and Poisson’s ratio. It can be seen that Eq. (8) can be reduced to the classical governing equation by setting $e_{0} a = 0$. The boundary conditions for a clamped plate are:

• (a) At $x = 0$ and $x = l$, $w = 0$, $w_{,x} = 0$,

• (b) At $y = 0$ and $y = l\eta$, $w = 0$, $w_{,y} = 0$.

We introduce the non-dimensional parameters $\bar{x} = \frac{x}{l}$, $\bar{y} = \frac{y}{l}$, $\bar{w} = \frac{w}{{g_{0} }}$, $\alpha = \frac{{e_{0} a}}{l}$, $K = \frac{{\varepsilon_{0} V^{2} l^{4} }}{{2Dg_{0}^{3} }}$, $\xi = \frac{{Al^{4} }}{{6\pi Dg_{0}^{4} }}$, $\tau^{2} = \frac{{\rho hl^{4} }}{D}$ and $\bar{t} = \frac{t}{\tau }$. The non-dimensional form of Eq. (8) is

$$(1 - \alpha^{2} \nabla^{2} )\ddot{\bar{w}} + \nabla^{4} \bar{w} - \left\{ {(1 - \alpha^{2} \nabla^{2} ) \left[\frac{K}{{(1 - \bar{w})^{2} }} + \frac{\xi }{{(1 - \bar{w})^{4} }} \right]} \right\} = 0$$

(9)

It should be noted that K and $\xi$ are indicators of the electrostatically actuated nanoplate stiffening due to coulomb force and van der Waals force, respectively. The associated non-dimensional boundary conditions are

$$\bar{w} = 0\,\;{\text{and}}\,\;\bar{w}_{{,\bar{x}}} = 0\,\;{\text{at}}\;\;\bar{x} = 0, 1$$

(10a)

$$\bar{w} = 0\,\;\,{\text{and}}\,\,\,\bar{w}_{{,\bar{y}}} = 0\,\;{\text{at}}\;\,\bar{y} = 0,\,\;\,\eta (\eta \in [0,1])$$

(10b)

3 Reduced-order model

3.1 Governing equations of the reduced-order model

Getting a closed-form solution for the nonlinear equation Eq. (9) and boundary condition Eq. (10a, 10b) is difficult. Therefore, an approximated solution for the transverse displacement w is constructed as

$$\bar{w}(\bar{x},\bar{y},\bar{t}) = \sum\limits_{n = 1}^{N} {\tilde{w}_{n} } (\bar{x},\bar{y})\chi_{n} (\bar{t}) = {\mathbf{W}}^{T} {\varvec{\upchi}}(t)$$

(11)

where $\tilde{w}_{n}$ and $\chi_{n}$ are, respectively, the orthogonal basis functions and amplitude parameters for the transverse displacement w. The basis functions for the transverse displacement can be expressed as (Batra et al. 2008a)

$$\begin{aligned} \bar{w}_{n} &= \chi_{n} \left( {\frac{{\cosh (\Omega_{n} \bar{x}) - \cos (\Omega_{n} \bar{x})}}{{\cosh (\Omega_{n} ) - \cos (\Omega_{n} )}} - \frac{{\sinh (\Omega_{n} \bar{x}) - \sin (\Omega_{n} \bar{x})}}{{\sinh (\Omega_{n} ) - \sin (\Omega_{n} )}}} \right) \hfill \\ &\quad\times \left( {\frac{{\cosh (\Omega_{n} \bar{y}/\eta ) - \cos (\Omega_{n} \bar{y}/\eta )}}{{\cosh (\Omega_{n} /\eta ) - \cos (\Omega_{n} /\eta )}} - \frac{{\sinh (\Omega_{n} \bar{y}/\eta ) - \sin (\Omega_{n} \bar{y}/\eta )}}{{\sinh (\Omega_{n} /\eta ) - \sin (\Omega_{n} /\eta )}}} \right) \hfill \\ \end{aligned}$$

(12)

where $\Omega_{n}$ (n = 1,…, N) is the nth root of the equation $\cosh \Omega \cos \Omega = 1$. Since the basis functions are symmetric about $\bar{x} = 1/2$ and $\bar{y} = \eta /2$, only the odd number term of the basis functions should be considered (Batra et al. 2008a). Multiplying Eq. (9) with ${\mathbf{W}}$, and substituting Eq. (11) into the result equation, the reduced-order model can be obtained

$$\begin{aligned} \iint {\mathbf{W}}(1 - \alpha^{2} \nabla^{2} ){\mathbf{W}}^{T} {\ddot{\mathbf{\chi }}}dxdy + \iint {\mathbf{W}}\nabla^{4} {\mathbf{W}}^{T} {\varvec{\upchi}}dxdy - K\iint {{\mathbf{W}}(1 - \alpha^{2} \nabla^{2} )\frac{1}{{(1 - {\mathbf{W}}^{T} {\varvec{\upchi}})^{2} }}}dxdy \hfill \\ - \xi \iint {{\mathbf{W}}(1 - \alpha^{2} \nabla^{2} )\frac{1}{{(1 - {\mathbf{W}}^{T} {\varvec{\upchi}})^{3} }}}dxdy = 0 \hfill \\ \end{aligned}$$

(13)

Using the divergence theorem and imposing boundary conditions, we obtained

$${\mathbf{m}{\ddot{\mathbf \chi }}} + {\mathbf{D}}_{1} {\varvec{\upchi}} - K{\mathbf{f}}_{e} ({\varvec{\upchi}}) - \xi {\mathbf{f}}_{v} ({\varvec{\upchi}}) = 0$$

(14)

where

$${\mathbf{m}} = \iint {\mathbf{W}}{\mathbf{W}}^{T} dxdy + \alpha^{2} \iint {{\mathbf{W}}_{{,\bar{x}_{\beta } }} {\mathbf{W}}^{T}_{{,\bar{x}_{\beta } }} }dxdy$$

(15)

$${\mathbf{D}}_{1} = \iint {\nabla^{2} {\mathbf{W}}}\nabla^{2} {\mathbf{W}}^{T} dxdy$$

(16)

$${\mathbf{f}}_{e} ({\varvec{\upchi}}) = \iint {\frac{{{\mathbf{W}} - \alpha^{2} \nabla^{2} {\mathbf{W}}}}{{(1 - {\mathbf{W}}^{T} {\varvec{\upchi}})^{2} }}}dxdy$$

(17)

$${\mathbf{f}}_{vdW} ({\varvec{\upchi}}) = \iint {\frac{{{\mathbf{W}} - \alpha^{2} \nabla^{2} {\mathbf{W}}}}{{(1 - {\mathbf{W}}^{T} {\varvec{\upchi}})^{3} }}}dxdy$$

(18)

From Eqs. (15), (17) and (18), it is found that the nonlocal parameter increased the equivalent mass, coulomb and van der Waals forces. In other words, the nonlocal parameter makes the plate softer.

3.2 Extraction of pull-in parameters from the static problem

Neglecting the inertia term in Eq. (14), the governing equation for static problem can be expressed as

$${\mathbf{D}}_{1} {\varvec{\upchi}} - K{\mathbf{f}}_{e} ({\varvec{\upchi}}) - \xi {\mathbf{f}}_{v} ({\varvec{\upchi}}) = 0$$

(19)

The tangent stiffness matrix of the system is

$${\mathbf{D}}({\varvec{\upchi}},\alpha ,\lambda ,\mu ) = {\mathbf{D}}_{1} - K\frac{{d{\mathbf{f}}_{e} ({\varvec{\upchi}})}}{{d{\varvec{\upchi}}}} - \xi \frac{{d{\mathbf{f}}_{vdW} ({\varvec{\upchi}})}}{{d{\varvec{\upchi}}}}$$

(20)

where

$$\frac{{d{\mathbf{f}}_{e} ({\varvec{\upchi}})}}{{d{\varvec{\upchi}}}} = 2\iint {\frac{{({\mathbf{W}} - \alpha^{2} \nabla^{2} {\mathbf{W}}){\mathbf{W}}^{T} }}{{(1 - {\mathbf{W}}^{T} {\varvec{\upchi}})^{3} }}}dxdy$$

(21)

$$\frac{{d{\mathbf{f}}_{vdW} ({\varvec{\upchi}})}}{{d{\varvec{\upchi}}}} = 3\iint {\frac{{({\mathbf{W}} - \alpha^{2} \nabla^{2} {\mathbf{W}}){\mathbf{W}}^{T} }}{{(1 - {\mathbf{W}}^{T} {\varvec{\upchi}})^{4} }}}dxdy$$

(22)

When pull-in instability occurs, the system’s tangent stiffness matrix ${\mathbf{D}}({\varvec{\upchi}},\beta ,\lambda ,\mu )$ becomes singular. Therefore, at the onset of instability, the system satisfies Eq. (19) and the condition $\det [{\mathbf{D}}({\varvec{\upchi}},\beta ,v,\xi )] = 0$.

Following the procedure as Ref. (Batra et al. 2008a), the displacement iteration pull-in extraction (DIPIE) algorithm (Bochobza-Degani et al. 2002) is used to solve Eq. (19). The complete bifurcation path is constructed by driving the system through the transverse displacement of a pre-chosen point $(\bar{x},\bar{y})$ (it is noted that we chosen $\bar{x} = 1/2 \,\,\;{\text{and}}\;\,$ $\bar{y} = \eta /2$, in this paper), and regarding the load parameters (either $K$ or $\xi$) as unknown.

Introducing a parameter $s$ which is the deflection at the point (1/2, $\eta /2$) and regarding $s$ as a function of both $K$ and $\xi$. Once the solution (${\varvec{\upchi}}_{i - 1}$,$K_{i - 1}$) for ${\mathbf{W}}^{T} (\bar{x},\bar{y})\chi_{i - 1} = s_{i - 1}$ is obtained, the solution $({\varvec{\upchi}}_{i} ,K_{i} ) = ({\varvec{\upchi}}_{i - 1} ,K_{i - 1} ) + (\Delta {\varvec{\upchi}}_{i} ,\Delta K_{i} )$ for $s_{i} = s_{i - 1} + \Delta s_{i}$ can be found by solving the following equations

$${\mathbf{D}}_{1} {\varvec{\upchi}}_{i} - K_{i} {\mathbf{f}}_{e} ({\varvec{\upchi}}_{i} ) - \xi_{i} {\mathbf{f}}_{vdW} ({\varvec{\upchi}}_{i} ) = 0$$

(23)

$${\mathbf{W}}^{T} (\bar{x},\bar{y}){\varvec{\upchi}}_{i} = s_{i}$$

(24)

It is noted that Eqs. (23) and (24) composed a set of nonlinear equations. Solutions of the set of nonlinear equations can be found by using Newton’s iterations. The jth iteration is listed as (Batra et al. 2008a)

$$\left[ {\begin{array}{*{20}c} {{\mathbf{D}}(K_{i}^{j} ,\xi_{i}^{j} ,{\varvec{\upchi}}_{i}^{j} )} & { - {\mathbf{f}}_{e} ({\varvec{\upchi}}_{i}^{j} )} \\ {{\mathbf{W}}^{T} (\bar{x},\bar{y})} & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\Delta {\varvec{\upchi}}_{i}^{j} } \\ {\Delta K_{i}^{j} } \\ \end{array} } \right] = - \left[ {\begin{array}{*{20}c} {{\mathbf{D}}_{1} {\varvec{\upchi}}_{i}^{j} - K_{i}^{j} {\mathbf{f}}_{e} ({\varvec{\upchi}}_{i}^{j} ) - \xi_{i}^{j} {\mathbf{f}}_{vdW} ({\varvec{\upchi}}_{i}^{j} )} \\ {{\mathbf{W}}^{T} (\bar{x},\bar{y}){\varvec{\upchi}}_{i}^{j} - s_{i} } \\ \end{array} } \right]$$

(25)

where ($\Delta {\varvec{\upchi}}_{i}^{j}$, $\Delta K_{i}^{j}$) is the jth solution increment; (${\varvec{\upchi}}_{i}^{j}$, $K_{i}^{j}$) are the updated solution at the (j − 1)th iteration.

$$K_{i}^{j} = K_{i} + \sum\limits_{n = 1}^{j - 1} \Delta K_{i}^{n} \,\;{\text{and}}\,\;{\varvec{\upchi}}_{i}^{j} = {\varvec{\upchi}}_{i} + \sum\limits_{n = 1}^{j - 1} \Delta {\varvec{\upchi}}_{i}^{n}$$

(26)

The iterations are preformed until $\hbox{max} ( {| {\Delta {\varvec{\upchi}}_{i}^{j} }|,\Delta K_{i}^{j} }) \le 10^{ - 7}$.

3.3 Frequencies of the electrostatically actuated nano-plate

The frequencies of a deflected nano-plate at a given solution $({\varvec{\upchi}},\alpha ,K,\xi )$ can be found through the following procedure. If perturbing equilibrium state ${\varvec{\upchi}}$ with a harmonic term $e^{iwt}$ ($i = \sqrt { - 1}$) as ${\varvec{\upchi}} + {\bar{\mathbf{\chi }}}e^{iwt}$($|\bar{\chi }| < < |\chi |$). Substituting ${\varvec{\upchi}} + {\bar{\mathbf{\chi }}}e^{iwt}$ into Eq. (14) and retaining terms linear in ${\varvec{\upchi}}$, we obtain (Batra et al. 2008a)

$$\det ({\mathbf{D}}({\varvec{\upchi}},\alpha ,K,\zeta ) - \omega^{2} {\mathbf{m}}) = 0$$

(27)

When the pull-in occurs, the tangent stiffness matrix satisfies $\det [{\mathbf{D}}({\varvec{\upchi}},\alpha ,K,\xi )] = 0$. This means that at least one natural frequencies of the plate is zero, when the pull-in occurs. This is an alternative method of finding the pull-in parameters of the nanoplate.

4 Numerical results and discussions

4.1 Pull-in parameters from the static analysis

Table 1 lists pull-in parameters extracted for a square clamped plate ($\eta = 1$) with $\xi = 0$ (no van der Waals force) and varying N in the Eq. (12). It is found that convergent solutions for pull-in parameters of the rectangular clamped nanoplate are obtained for $N = 1$.

Table 1 The nondimensional pull-in parameters of a square nanoplate for different number of basis functions used to approximate the transverse deflection

Figure 2 shows the critical van der Waals force parameters $\xi_{cr}$ with variation of the aspect ratio $\eta$. It is found that the critical van der Waals force parameters $\xi_{cr}$ decrease rapidly as the aspect ratio $\eta$ increases. The critical van der Waals force parameters $\xi_{cr}$ decrease with increasing nonlocal parameters. The reason for this is that the nonlocal effect makes equivalent force matrix large (i.e. Eq. 18), and then makes the plate softer. The effect of nonlocal parameter on the critical van der Waals force parameters $\xi_{cr}$ decreases with increasing aspect ratio $\eta$. Figure 3 plots the variation with nonlocal parameters of the critical van der Waals force parameter $\xi_{cr}$. It is noted that $\xi_{cr}^{0}$ is the critical van der Waals force parameter obtained by classical theory (without nonlocal effect). The van der Waals force parameters $\xi_{cr}$ decrease with increasing nonlocal parameters, once again, due to the fact that nonlocal effect makes the plate softer. It is also found that the influence of nonlocal parameter on the critical van der Waals force parameters $\xi_{cr}$ becomes more significant if the aspect ratio is smaller.

Fig. 2

Variation of van der Waals force parameter $\xi_{cr}$ with the aspect ratio $\eta$

Fig. 3

Variation of the critical van der Waals force parameter $\xi_{cr}$ with nonlocal parameter

Figure 4a, b plot the pull-in voltage parameters $K_{PI}$ and pull-in deflection $w_{PI}$ ($\bar{x} = 1/2$ and $\bar{y} = \eta /2$) versus the van der Waals force parameters $\xi$ for a square plate, respectively. The pull-in voltage parameters data (points in Fig. 4a) are fitted with a function which is composited of a one order polynomial in $\xi$ and a two order polynomial in $(e_{0} a/l)^{2}$:

Fig. 4

Pull-in voltage parameter $K_{PI}$ and pull-in deflection $w_{PI}$ versus van der Waals parameter $\xi$ for a square plate

$$K_{PI} = - 1.4\xi + 18067\left( {\frac{{e_{0} a}}{l}} \right)^{4} - 2130\left( {\frac{{e_{0} a}}{l}} \right)^{2} + 171.5$$

(28)

The from of Eq. (28) is relatively simple. Therefore, it is convenient to be used to the design of nano-switches. In addition, Eq. (28) indicates another way to measure the nonlocal parameters of nanomaterials by experiments. It can be seen that the pull-in voltage parameters $K_{PI}$ decreases from its max values $K_{PI}^{\hbox{max} }$ to zero as the van der Waals force parameters $\xi$ increases from zero to its max values $\xi_{cr}$. The pull-in voltage parameter $K_{PI}$ decreases with increasing nonlocal parameter. As the van der Waals force parameter $\xi$ increases, the pull-in deflection $w_{PI}$ decreases from its maximum value to its minimum value. The pull-in deflection decreases with increasing nonlocal parameter. The influence of nonlocal parameter on pull-in voltage parameter $K_{PI}$ and pull-in deflection $w_{PI}$ depends on the size of the plate, and it becomes more significant for a smaller size plate. If $e_{0} a/l \to 0$ (the length of the plate l is more lager than the nonlocal parameter $e_{0} a$) the effect of nonlocal elasticity on the pull-in parameters can be neglected.

Figure 5a, b plot the pull-in voltage parameters $K_{PI}$ and pull-in deflection $w_{PI}$ versus the van der Waals force parameters $\xi$ for a rectangular plate ($\eta = 1/2$), respectively. The pull-in voltage parameters data (points in Fig. 5a) are fitted with a function which is composited of a one order polynomial in $\xi$ and three order polynomial in $(e_{0} a/l)^{2}$:

Fig. 5

Pull-in voltage parameter $K_{PI}$ and pull-in deflection $w_{PI}$ versus van der Waals parameter $\xi$ for a rectangular plate with $\eta = 0.5$

$$K_{PI} = - 1.4\xi - 9367100\left( {\frac{{e_{0} a}}{l}} \right)^{6} + 926500\left( {\frac{{e_{0} a}}{l}} \right)^{4} - 39100\left( {\frac{{e_{0} a}}{l}} \right)^{2} + 1274.3$$

(29)

The similar conclusion as that of Fig. 4 can be drawn. Comparing Figs. 4 with Fig. 5, it is found that the effect of nonlocal parameter is more obvious for a smaller aspect ratio $\eta$.

Figure 6 plots the variation with the nonlocal parameter $e_{0} a/l$ of the pull-in voltage parameter $K_{PI}$ for $\xi = 0$. Here $K_{PI}^{0}$ is the result of the model without considering nonlocal effect and van der Waals force. In Fig. 6, the blue lines are given based on Eqs. (28) and (29), the red points are the results of present model. It can be seen the blue lines match well with the red points. In other words, the accuracy of Eqs. (28) and (29) is great. It is also found that the pull-in voltage parameter $K_{PI}$ decreases with increasing nonlocal parameter, and the influence of nonlocal parameter on the pull-in voltage parameter $K_{PI}$ becomes more significant if the aspect ratio is smaller.

Fig. 6

Variation of the pull-in voltage parameter $K_{PI}$ with nonlocal parameters

4.2 Fundamental frequency of a deformed nanoplate

Figures 7 and 8 display the fundamental frequencies $\omega$ of the deflected nano-plate versus the parameter $K$ for a square (η = 1) and a rectangular nanoplate (η = 0.5), respectively. The fundamental frequencies are normalized with respect to the value $\omega_{0}$ corresponding to the nano-plate with $e_{0} a/l = 0$, $\xi = 0$ and $K = 0$. The values of fundamental frequencies $\omega_{0}$ obtained by the present model are shown in Table 2. From Table 2, it is observed that when $e_{0} a/l = 0$, $\xi = 0$ and $K = 0$, the fundamental frequencies obtained by present model match well with the available results provided by Arenas (2003). Moreover, the results including the effect of van der Waals force parameter ($\xi = 0.3\xi_{cr}$) are also compared with the available results provided by Batra et al. (2008b), it is found that the fundamental frequencies obtained by present model match well with the available results provided by Batra et al. (2008b). The results of Figs. 7 and 8 suggest that the nonlocal parameter reduces the fundamental frequencies. This phenomenon can be explained by the fact that the nonlocal parameter enlarge the equivalent mass, as shown in Eq. (15). On the other hand, neglecting van der Waals force will result in a higher prediction of the fundamental frequencies. Comparing Figs. 7 and 8, it is found the similar conclusions as that from Fig. 2 can be obtained. Such as, the effect of nonlocal parameter on the fundamental frequencies of the nanoplate is more significant if the aspect ratio is smaller. It is noted that the parameter K corresponding to $\omega = 0$ is the pull-in voltage parameter $K_{PI}$. This agrees well with the pull-in voltage parameter $K_{PI}$ from Figs. 4a and 5a. This is an alternative way of finding the pull-in voltage.

Fig. 7

Normalized fundamental natural frequency versus $K$ for a square plate

Fig. 8

Normalized fundamental natural frequency versus $K$ for a rectangular plate with $\eta = 0.5$

Table 2 Values of the fundamental frequencies $\omega_{0}$($e_{0} a/l = 0$ and $K = 0$)

5 Conclusions

The influences of nonlocal effect and van der Waals force on the pull-in instability and fundamental frequency of graphene sheets are investigated. On the basic of nonlocal elasticity theory, the grapheme sheet is modeled as a nonlocal plate. The reduced-order model incorporating nonlocal effect and van der Waals force is derived and solved numerically. Results show that pull-in parameters and frequencies of graphene sheets are size-dependence. The pull-in voltage, pull-in deflection and frequencies decrease with increasing nonlocal parameter, thanks to the contribution of nonlocal parameter to the reduction of plate stiffness. The influence of nonlocal parameter on the pull-in voltage, pull-in deflection and frequencies is more obvious for smaller aspect ratio and size of the sheet (plate). Neglecting the effect of van der Walls force, the pull-in voltage and frequency are overestimated. Moreover, the effect of nonlocal parameter on the critical van der Waals force parameters decreases with increasing aspect ratio of the sheet (plate). In addition, a useful equation is developed to describe the relations between pull-in voltage, van der Waals force and nonlocal parameters. This equation indicates another experimental method to measure the nonlocal parameters.