Linear and nonlinear free vibrations of electrostatically actuated micro-/nanomechanical resonators

Abstract

This paper is concerned with linear and nonlinear free vibrations of an axially stressed clamped–clamped micro-/nanobeam actuated by one-sided electrode configuration. Galerkin procedure and a proper shape function are used to establish a dynamic reduced-order model, where the integral of the electromechanical forcing term is obtained in an explicit and closed form. This model makes the analysis of dynamic behaviors convenient for the micro-/nanobeam. For linear free vibration, the fundamental natural frequency formulas of the system are validated by comparing with published experiment data while the Newton method coupled with the harmonic balance method is developed to obtain analytical approximate period and periodic solution for the nonlinear system. These approximate solutions have explicit expressions and they can readily be used to derive the effects of various physical parameters on dynamic behavior of micro-/nanobeams. Exact solution in an integral form is also presented. For small as well as large amplitudes of nonlinear vibration, the new analytical approximate solutions show excellent agreement with respect to the numerically integrated solutions obtained from the integral-form exact solutions.

1 Introduction

Electrostatically actuated micro-/nanomechanical resonators have been actively developed recently for various applications as sensors and signal processing elements (Eom et al. 2011). For these micro-/nano-systems, their superior characteristics include high sensitivity and resolution, low power consumption and conduciveness to digital output. Such characterizes make these systems more attractive and much better, preferred substitutes that replace the conventional systems without electrostatic actuation. However, by far the electro-mechanical coupling behavior of these systems are largely only known in the sense of numerical analysis without analytical solution, or if do only limited to a grossly approximation extent, accurate approximate analysis of electro-mechanical properties of these resonators is thus of crucial importance for design purposes because the availability of accurate analytical solutions allows mastering of the behavior that meets practical design demands in a global sense. It is precisely the main objective of this paper to formulate and derive new and accurate approximate analytical solutions for such highly nonlinear system where explicit exact analytical solutions are unavailable.

With microelectronics technology now pushing deep into the submicron, a concerted exploration of nanoelectromechanical systems (NEMS) (Roukes 2001; Cleland and Roukes 1996) was embarked upon. The emergence of nanotechnology promotes the development of nanoscale functional devices designed for specific aims such as nanoscale actuation, sensing and detection (Craighead 2000; Roukes 2001; Ekinci 2005). Nanoscale mechanical resonators (Jensen et al. 2008; Chaste et al. 2012) are promising because of their high quality factors, high resonance frequencies, and ultralow masses (Ekinci and Roukes 2005). Nonlinear oscillation has been found in a double-clamped nanowire that is actuated by external field, where fields such as Lorentz force from magnetomotive technique (Feng et al. 2007), electrostatic force (Sazonova et al. 2004), and/or piezoelectric effect (He et al. 2008) have all been utilized to induce the nonlinear vibration. It is extremely difficult to detect the oscillations of such small sensors. Hence, it is important to model the non-linear dynamics of NEMS-based resonant sensors at large amplitudes (Kacem et al. 2011).

In the scope of continuum mechanics, these resonators are often modeled as an electrically actuated micro-/nanobeam. Usually, the beam structures used in micro-/nanoelectromechanical systems devices are simply thin micro-/nanobeams with rectangular cross-sections. A typical resonator consists of an electroded beam structure and there are commonly two different electrode configurations. The first configuration (case I) has a full-length electrode on only one side of the beam (Younis and Nayfeh 2003) while the second (case II) has full-length electrodes on both sides (Kacem et al. 2009; Rhoads et al. 2006).

There are many theoretical and experimental investigations that focused on nonlinear static responses and dynamic behaviors (Ouakad and Younis 2014; Ruzziconi et al. 2013; Wu et al. 2013; Yu and Wu 2014; Jia et al. 2010; Krylov and Dick 2010) of these resonator systems. Precisely, the statics and dynamics of a doubly clamped microbeam are nonlinear in nature because simultaneously large deflections and non-linear electrostatic force are present. For this reason, accurate command and knowledge of nonlinear vibrations near the first natural frequency of a micro-/nanobeam are always of primary concern in nonlinear dynamic analysis and for resonator application designs. The analytical modeling and accurate approximation of these nonlinear systems constitute the main theme of this investigation.

The primary resonance of microbeams was studied by Younis and Nayfeh (2003) by applying the perturbation technique directly to the nonlinear system with distributed-parameter. Abdel-Rahman et al. (2002) reported the boundary-value problem for the static deflection of microbeam subject to electrostatic force in a numerical study. They also solved the natural frequencies and mode shapes of the eigenvalue problem for vibration of microbeam at its statically deflected position. In another study, Nayfeh et al. (2005) reviewed the reduced-order model (ROM) technique using the linear undamped mode shapes of the straight microbeam as the basis functions in the Galerkin procedure. In the reduced-order modeling, a governing partial differential equation of a continuous beam is reduced to a system of ordinary differential equations of finite degree of freedom. The ROM technique was used by Younis et al. (2003) for studying the static and dynamic response of microbeams. However, closed form solution of the integral electromechanical forcing term has to be solved for a continued analytical description of the system response. To deal with this problem, one possible approach is to solve the integral actuation term numerically (Krylov 2007) and to set further analytical investigations aside. Another approach is to expand this term into a Taylor series, but poor accuracy has been reported, even with higher-order terms (Nayfeh et al. 2005; Younis et al. 2003). Younis et al. (2003) introduced a different method by multiplying the equation of motion by the denominator of the electrostatic force prior to discretization. For large displacements, three to five symmetric (linear undamped) modes are able to predict the primary pull-in point accurately. This approach provides a model that allows further analytical investigations. But this method will lead to a high dimensional ROM. On the other hand, the single-mode approximation is sufficient enough to also predict large displacement equilibrium (including pull-in) if the boundary value problem is discretized following the Galerkin method without premultiplication of the denominator of the electrostatic force (Gutschmidt 2010). However, determining the coefficient in such a ROM deduced from the discretization without premultiplication of the denominator requires solving the integral equation by a numerical method. This method faces challenges when the system approaches a singularity, such as the primary and secondary pull-in instability (Gutschmidt 2010).

For nonlinear systems, the response of free undamped and forced damped vibration are closely related under certain conditions. The amplitude–frequency curve of free undamped vibration is also known as the backbone of resonance curve (Nayfeh and Mook 1979). When linear damping and harmonic excitation are present in an oscillator, the primary resonance evolves around its backbone curve (Nayfeh and Mook 1979). An analytical expression for the backbone curve is helpful to determine the nature of this resonance (Nayfeh and Mook 1979). Many analytical techniques for solving free undamped vibrations have been available. Perturbation methods such as Lindstedt–Poincaré (LP) method, method of multiple scales, and averaging methods are applicable to free vibration analysis of a single degree of freedom system with weak nonlinearity (Nayfeh and Mook 1979). For strong nonlinear systems, the analytical studies of such system require more specialized techniques and the harmonic balance (HB) method is a very suitable candidate.

The HB method can be used to derive analytical approximate solutions to nonlinear oscillatory systems for which the nonlinear terms are “not small”, i.e., no perturbation parameter needs to exist (Nayfeh and Mook 1979; Hagedorn 1981; Mickens 1996). However, it is very difficult to construct an analytical approximation of sufficiently high accuracy using HB because it requires analytical solutions to sets of complicated nonlinear algebraic equations. As such, various improved HB methods (Wu et al. 2006; Wu and Lim 2004; Sun and Wu 2008) have been developed.

This paper investigates linear and nonlinear free vibrations of an axially stressed clamped–clamped micro-/nanobeam actuated on one-side by an electrode. In this paper, the single-degree of freedom ROM of the micro-/nanobeam for free undamped vibration is established by using Galerkin method and choosing a proper deflection shape function. The integral of the electromechanical forcing term can be derived in an explicit and closed form without using Taylor series expansion and multiplying by the denominator of the electrostatic force prior to discretization. The resulting ROM makes the analysis of dynamic behaviors convenient for micro-/nanobeam. The influence of static buckling on the system dynamic behavior is addressed. Fundamental natural frequency expressions of the linearized ROM are validated by comparing them with published experimental results (Tilmans and Legtenberg 1994). For the case of nonlinear free vibrations, analytical approximate periods and periodic solutions are systematically constructed. These approximate solutions show very good agreement with respect to the referenced solutions obtained by numerical integration. They are valid for small as well as large geometrically permitted amplitude of oscillation.

2 Reduced order model

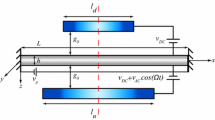
A doubly-clamped undamped micro-/nanobeam made of an elastic material and actuated electrostatically by an electrode with electric force V is shown in Fig. 1. The gap is assumed significantly smaller comparing with the length of the beam. In addition, the residual stress is considered as uniform while the effect of residual stress gradients is neglected.

Fig. 1

An electrically actuated micro-/nanobeam

The dimensionless nonlinear integral–differential governing equation for the electromechanical system can be expressed as (Younis et al. 2003; Gutschmidt 2010)

$$\frac{{\partial^{4} w}}{{\partial s^{4} }} + \frac{{\partial^{2} w}}{{\partial t^{2} }} = N\frac{{\partial^{2} w}}{{\partial s^{2} }} + \alpha_{1} \left[ {\int_{0}^{1} {\left( {\frac{\partial w}{\partial s}} \right)^{2} ds} } \right]\frac{{\partial^{2} w}}{{\partial s^{2} }} + \frac{{\alpha_{2} V^{2} }}{{\left( {1 - w} \right)^{2} }}$$

(1)

with boundary conditions

$$w\left( {0,t} \right) = \frac{\partial w}{\partial s}\left( {0,t} \right) = w\left( {1,t} \right) = \frac{\partial w}{\partial s}\left( {1,t} \right) = 0$$

(2)

where

$$\begin{aligned} s = \frac{x}{L},\quad w = \frac{W}{g},\quad t = \frac{{\hat{t}}}{T},\quad T = \sqrt {\left( {1 - \nu^{2} } \right)\rho bhL^{4} /EI} , \hfill \\ N = \frac{{\left( {1 - \nu^{2} } \right)\hat{N}L^{2} }}{EI},\quad \alpha_{1} = 6\left( {1 - \nu^{2} } \right)\left( {\frac{g}{h}} \right)^{2} ,\quad \alpha_{2} = \frac{{6\left( {1 - \nu^{2} } \right)\varepsilon_{0} L^{4} }}{{Eg^{3} h^{3} }}, \hfill \\ \end{aligned}$$

(3)

Here E is Young’s modulus, ν is Poisson’s ratio, ρ is density of beam, ɛ ₀ is the permittivity of vacuum, b, h(b > h) and L are the width, thickness and length of beam, respectively. The second moment of cross-section is I = bh ³/12, the tensile or compressive axial load is $\hat{N}$, the nominal gap is g, and the fixed electrode potential is V.

In this section, the Galerkin procedure (Nayfeh and Mook 1979; Nayfeh 2000; Younis 2011) is applied to derive a ROM with one degree-of-freedom for investigating the dynamic behavior of system in Eqs. (1) and (2). Such a dynamic model is always of primary interest because it is the case that is used in resonator applications. In the Galerkin procedure, the deflection function w(s, t) is expressed as

$$w(s,t) = a(t)w_{0} (s)$$

(4)

where w ₀(s) is the assumed deflection shape function that satisfies the boundary conditions in Eq. (2) and the coefficient a(t) is the associated amplitude. Based on geometric symmetry considerations, an admissible deflection function that satisfies the conditions in Eq. (2) can be expressed as

$$w_{0} \left( s \right) = \frac{1}{2}\left[ {1 - \cos \left( {2\pi s} \right)} \right],\quad s \in \left[ {0, 1} \right],$$

(5)

Combining Eqs. (4) and (5) shows that the amplitude a(t) of the associated shape is simply the normalized beam-center deflection with a constraint a(t) < 1 according to non-dimensionalization definition in Eq. (3). The shape function in Eq. (5) is used as the basis function in the Galerkin procedure. Substituting Eqs. (4) and (5) into Eq. (1), multiplying by w ₀(s), and integrating from s = 0–1, yield

$$\frac{{d^{2} a}}{{dt^{2} }} + F\left( {a,V} \right) = 0$$

(6)

where

$$F\left( {a,V} \right) = \frac{2}{3}\pi^{2} a\left( {8\pi^{2} + 2N + \pi^{2} \alpha_{1} a^{2} } \right) - \frac{{4\alpha_{2} V^{2} }}{{3\left( {1 - a} \right)^{3/2} }}$$

(7)

It is worth noting that, choosing the shape function in Eq. (5) is extremely important because closed form solution of the integral of the electromechanical forcing can be obtained explicitly. This ROM makes the analysis of dynamic behaviors convenient for the beam. If we use the first undamped beam’s linear vibration mode of the straight microbeam without the electrostatic potential as shape function, the integral cannot be solved analytically and has to be evaluated by numerical method, which leads to some difficulties in the dynamic analyses of the corresponding ROM. In this paper, we use the ROM in Eqs. (6) and (7) to investigate the linear and nonlinear free vibrations of the beam.

3 Analytical formula for fundamental natural frequencies

Analytical expression of fundamental natural frequencies is constructed in this section. Equations (6) and (7) as derived in the previous section represent an ordinary-differential equation with complex nonlinearity. Setting the time derivatives in Eq. (6) to zero, assuming a constant electric load yields the nonlinear algebraic equation governing the static deflection a _s of the beam as follows (Wu et al. 2013):

$$F\left( {a_{s} ,V} \right) = 0$$

(8)

Based on Eqs. (7) and (8), the potential V can be solved and expressed in terms of the normalized static beam-center deflection a _s , as

$$V = V\left( {a_{s} } \right) = \left[ {\frac{{\pi^{2} a_{s} \left( {1 - a_{s} } \right)^{3/2} \left( {8\pi^{2} + 2N + \pi^{2} \alpha_{1} a_{s}^{2} } \right)}}{{2\alpha_{2} }}} \right]^{1/2}$$

(9)

The MEMS beam resonators A210, A310, A410 and A510 in Tilmans and Legtenberg (1994) are referred. The lengths of these microbeams are 210, 310, 410 and 510 μm, respectively; the other parameters are b = 100 μm, h = 1.5 μm, g = 1.18 μm, v = 0.3, $\frac{E}{{1 - \nu^{2} }} = 166 \, {\text{GPa}}$, $\hat{N} = 0.0009{\text{N}}$ and ɛ ₀ = 8.854 × 10⁻¹²F. Microbeam A510 is used as an example to show the change of analytical approximate potential Vwith respect to the normalized static beam-center deflection a _s , as shown in Fig. 2. Here, the stable and unstable solutions are represented by thick solid and dashed lines, respectively.

Fig. 2

Variation of the electric potential V with normalized static beam-center deflection a _s for microbeam A510

In general, the solution curve in Eq. (9) is composed of the left and right branches. In Fig. 2, the highest point is the pull-in one where the corresponding voltage and normalized static beam-center deflection are denoted by V _p and a _p , respectively. For static deflection, the analytical approximate solution was compared with numerical shooting solution and very good agreement was observed for the whole range of normalized static microbeam-center deflection (Wu et al. 2013). In addition, stability analyses of the static deflection have also been performed there. It has been pointed that, the left branch is stable and the right branch is unstable. At pull-in voltage V _p , both branches coincide and it leads to a transition from a stable equilibrium to an unstable one.

For a given potential V(V < V _p ), the dynamic behavior of the beam at stable static deflection a _s in the left branch is investigated. Let deflection

$$a = a_{s} + u$$

(10)

where u is the normalized incremental beam-center deflection measured from stable equilibrium position a = a _s . Substituting Eqs. (10) into (6) results in the equation that governs the dynamic behavior of beam as

$$\frac{{d^{2} u}}{{dt^{2} }} + F\left( {a_{s} + u,V} \right) = 0$$

(11)

where V = V(a _s ).

We determine the fundamental natural frequency of beams at stable equilibrium states. For analysis of linear free vibrations, using Taylor series expansion of F(a _s  + u, V) about u at a = a _s , eliminating the terms representing equilibrium and keeping the linear part of increment u only yields

$$\frac{{d^{2} u}}{{dt^{2} }} + \left[ {\frac{{\partial F\left( {a,V} \right)}}{\partial a}\left| {_{{a = a_{s} }} } \right.} \right]u = 0$$

(12)

Using Eqs. (7), (9) and (12), the fundamental natural frequency of beams can be obtained as

$$\omega_{nf} \left( {a_{s} } \right) = \left[ {\frac{{\partial F\left( {a,V} \right)}}{\partial a}\left| {_{{a = a_{s} }} } \right.} \right]^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} = \left[ {\frac{{4\pi^{4} \alpha_{1} a_{s}^{2} }}{3} + \frac{{\pi^{2} \left( {2 - 5a_{s} } \right){\kern 1pt} \left( {8\pi^{2} + 2N + \pi^{2} \alpha_{1} a_{s}^{2} } \right)}}{{3\left( {1 - a_{s} } \right)}}} \right]^{1/2}$$

(13)

where a _s satisfies 0 ≤ a _s  ≤ a _p .

Let ω ₀ denote the resonance frequency of the system without electromechanical coupling (V = 0, i.e. a _s  = 0). The comparison of the normalized fundamental natural frequency obtained using Eqs. (9) and (13) with experiment by Tilmans and Legtenberg (1994) for microbeams A210, A310, A410 and A510 is shown in Fig. 3. Here, the experimental data for microbeams A210, A310, A410, A510 are marked by symbols ○, △, ◇ and ☆, respectively. It is observed that there is good agreement between the analytical approximate solution derived here and experiment, even when the microbeams approach the stability limitations.

Fig. 3

Comparisons of the normalized fundamental natural frequency ω _nf /ω ₀ obtained from Eqs. (9) and (13) with experiment (Tilmans and Legtenberg 1994)

4 Analytical approximations to nonlinear free vibrations

In view of the effectiveness of the proposed ROM for static and linear free vibration analysis demonstrated above, nonlinear dynamic analysis is further carried out in the following sections.

Based Eq. (11), the equation of undamped motion for ROM at its stable equilibrium state a = a _s can be expressed as

$$\frac{{d^{2} u}}{{dt^{2} }} + f\left( {u,V} \right) = 0,\quad u\left( 0 \right) = A,\quad \frac{du}{dt}\left( 0 \right) = 0,$$

(14)

where

$$f\left( {u,V} \right) = F(a_{s} + u, \, V) = \frac{{2\pi^{2} }}{3}\left( {a_{s} + u} \right){\kern 1pt} \,\left[ {8\pi^{2} + 2N + \pi^{2} \alpha_{1} \left( {a_{s} + u} \right)^{2} } \right] - \frac{{4\alpha_{2} V^{2} }}{{3\left( {1 - a_{s} - u} \right)^{3/2} }}$$

(15)

and A represents the initial normalized incremental beam-center deflection. The corresponding potential energy of this system is

$$\varPi (u,V) = \frac{2}{3}\left[ {\pi^{2} \left( {4\pi^{2} + N} \right)\left( {a_{s} + u} \right)^{2} + \frac{1}{4}\pi^{4} \alpha_{1} \left( {a_{s} + u} \right)^{4} - \frac{{4\alpha_{2} V^{2} }}{{\sqrt {1 - a_{s} - u} }}} \right]$$

(16)

and it reaches its minimum value at u = 0. The system will thus oscillate in an asymmetric interval [−B, A] where both −B(B > 0) and A have the same energy level, i.e.,

$$\varPi ( - B,V) = \varPi (A,V)$$

(17)

and they are left and right limitations of normalized incremental beam-center deflection, respectively, for the vibration. Microbeam A510 is used as an example to illustrate the change of the potential energy Π(u, V)(a _s  = 0.1)with respect to the normalized incremental beam-center deflection u, see Fig. 4.

Fig. 4

Variation of the potential energy Π(u, V)(a _s  = 0.1) with normalized incremental microbeam-center deflection u for microbeam A510

In this study, an analytical approximate periodic solution methodology to the nonlinear Eq. (14) is formulated and solved. With reference to the analytical approximate solutions to general strong nonlinear oscillators (Sun and Wu 2008), the present nonlinear system is more complicated because the elelectrostatic force is a complex function of its incremental displacement. It is hence far more difficult to compute the corresponding coefficients of the Fourier series. At this point, the original governing equation should be expressed such that the previously proposed method (Wu et al. 2006) can be easily applied. The reported methods (Wu et al. 2006; Wu and Lim 2004; Sun and Wu 2008) are to be generalized for constructing analytical approximation to periodic vibrations of the ROM.

The denominator of elelectrostatic force is expended into a Taylor series at u = 0 up to the third order. Further, Eq. (14) is approximated by

$$\frac{{d^{2} u}}{{dt^{2} }} \approx \frac{{C_{1} u + C_{2} u^{2} + C_{3} u^{3} + C_{4} u^{4} + C_{5} u^{5} + C_{6} u^{6} }}{{B_{0} + B_{1} u + B_{2} u^{2} + B_{3} u^{3} }},\quad u\left( 0 \right) = A,\quad \frac{du}{dt}\left( 0 \right) = 0$$

(18)

Where C _i (i = 1, 2, ···, 6) and B _j (j = 0, 1, 2, 3) are listed in the Sect. 6. Introducing a new independent variable τ = ωt, Eq. (18) can be expressed as

$$\varOmega (B_{0} + B_{1} u + B_{2} u^{2} + B_{3} u^{3} )u^{\prime\prime} + C_{1} u + C_{2} u^{2} + C_{3} u^{3} + C_{4} u^{4} + C_{5} u^{5} + C_{6} u^{6} = 0,\quad u\left( 0 \right) = A,\quad u^{\prime } \left( 0 \right) = 0$$

(19)

where Ω = ω ² and (^′) denotes differentiation with respect to τ. The new independent variable is chosen such that the solution of Eq. (19) is a periodic function of τ of period 2π. The corresponding period of nonlinear vibration is given by $T = 2\pi /\sqrt \varOmega$. Here, both periodic solution u(τ) and period T depend on A.

Following Sun et al. (2009) and using Eq. (19), two new nonlinear systems which oscillate between the symmetric bounds [−H, H] is introduced here as

$$\varOmega K\left( {u, \lambda } \right)u^{\prime \prime } + \varPhi \left( {u, \lambda } \right) = 0,\quad u\left( 0 \right) = H,\quad u^{\prime } \left( 0 \right) = 0$$

(20a)

$$\begin{aligned} K(u,\lambda ) = \left\{ \begin{aligned} B_{0} + \lambda B_{1} u + B_{2} u^{2} + \lambda B_{3} u^{3} \, if \, u \ge 0, \hfill \\ B_{0} - \lambda B_{1} u + B_{2} u^{2} - \lambda B_{3} u^{3} \, if \, u < 0 \hfill \\ \end{aligned} \right. \hfill \\ \varPhi (u,\lambda ) = \left\{ \begin{aligned} C_{1} u + \lambda C_{2} u^{2} + C_{3} u^{3} + \lambda C_{4} u^{4} + C_{5} u^{5} + \lambda C_{6} u^{6} \, if \, u \ge 0, \hfill \\ C_{1} u - \lambda C_{2} u^{2} + C_{3} u^{3} - \lambda C_{4} u^{4} + C_{5} u^{5} - \lambda C_{6} u^{6} \, if \, u < 0 \hfill \\ \end{aligned} \right. \hfill \\ \end{aligned}$$

(20b)

And λ = ±1 where H = A for λ = +1, and H = B for λ = −1, respectively.

With reference to the method of single term harmonic balance approximation

$$u_{1}^{\lambda } = H\cos \tau$$

(21)

and it satisfies the initial conditions in Eq. (20a). The functions K(u ^λ₁ , λ) and Φ(u ^λ₁ , λ) can be expanded into the following Fourier series

$$K(u_{1}^{\lambda } ,\lambda ) = D_{10} + D_{12} \cos 2\tau + D_{14} \cos 4\tau + D_{16} \cos 6\tau + \cdots ,$$

(22a)

$$\varPhi (u_{1}^{\lambda } ,\lambda ) = D_{21} \cos \tau + D_{23} \cos 3\tau + \cdots$$

(22b)

where D _1i (i = 0, 2, 4, 6) and D _2j (j = 1, 3) are listed in the Sect. 6. Substituting Eqs. (21) and (22a, 22b) into Eq. (20a) and setting the coefficient of cos τ to zero yield

$$\varOmega_{1}^{\lambda } = \frac{{105\pi (8C_{1} + 6C_{3} H^{2} + 5C_{5} H^{4} ) + 64H\lambda (35C_{2} + 28C_{4} H^{2} + 24C_{6} H^{4} )}}{{840B_{0} \pi + 14H[45B_{2} H\pi + 32\lambda (5B_{1} + 4B_{3} H^{2} )]}}$$

(23)

Therefore, the first approximate solutions to period and periodic solution of Eqs. (20a, 20b) are

$$T_{1}^{\lambda } = {{2\pi } \mathord{\left/ {\vphantom {{2\pi }{\sqrt {\varOmega_{1}^{\lambda } (H)} }}} \right. \kern-0pt} {\sqrt {\varOmega_{1}^{\lambda } (H)} }},\quad u_{ 1}^{\lambda } \left( \tau \right) = H { \cos } \tau ,\quad \tau = \sqrt {\varOmega_{1}^{\lambda } (H)} t.$$

(24)

Using u ^λ₁ and Ω ^λ₁ (H) as the initial approximations to the solution of Eq. (20a), Newton’s method can be combined with the harmonic balance method to further recursively solve Eq. (20a). The first step is the Newton procedure. The periodic solution and the square of frequency of Eq. (20a) can be expressed as

$$u^{\lambda } = u_{ 1}^{\lambda } + \varDelta u_{ 1}^{\lambda } ,\varOmega^{\lambda } = \varOmega_{ 1}^{\lambda } + \varDelta \varOmega_{ 1}^{\lambda }$$

(25)

Substituting Eq. (25) into Eq. (20a) and linearizing with respect to the correction terms Δu ^λ₁ and ΔΩ ^λ₁ lead to

$$\begin{aligned} \left[ {K\left( {u_{1}^{\lambda } ,\lambda } \right) + K_{u} \left( {u_{1}^{\lambda } ,\lambda } \right)\varDelta u_{1}^{\lambda } } \right]\varOmega_{1}^{\lambda } \left( {u_{1}^{\lambda } } \right)^{\prime \prime } + \varOmega_{1}^{\lambda } K\left( {u_{1}^{\lambda } ,\lambda } \right)\left( {\varDelta u_{1}^{\lambda } } \right)^{\prime \prime } + \varDelta \varOmega_{1}^{\lambda } K\left( {u_{1}^{\lambda } ,\lambda } \right)\left( {u_{1}^{\lambda } } \right)^{\prime \prime } \hfill \\ + \varPhi \left( {u_{1}^{\lambda } ,\lambda } \right) + \varPhi_{u} \left( {u_{1}^{\lambda } ,\lambda } \right)\varDelta u_{1}^{\lambda } = 0, \hfill \\ \varDelta u_{ 1}^{\lambda } \left( 0 \right) = 0,\quad \left( {\varDelta u_{ 1}^{\lambda } } \right)^{\prime } \left( 0 \right) = 0 \hfill \\ \end{aligned}$$

(26)

where subscript u denotes differentiation with respect to u. The resulting linear equation in Δu ^λ₁ and ΔΩ ^λ₁ in Eq. (26) will be solved by the harmonic balance method.

Functions K _u (u ^λ₁ , λ) and Φ _u (u ^λ₁ , λ) can be expanded into the following Fourier series

$$K_{u} \left( {u_{1}^{\lambda } ,\lambda } \right) = D_{31} \cos \tau + D_{33} \cos 3\tau + D_{35} \cos 5\tau + D_{37} \cos 7\tau + \cdots ,$$

(27a)

$$\varPhi_{u} \left( {u_{1}^{\lambda } ,\lambda } \right) = D_{40} + D_{42} \cos 2\tau + D_{44} \cos 4\tau + D_{46} \cos 6\tau + \cdots$$

(27b)

where D _3i (i = 1, 3, 5, 7) and D _4j (j = 0, 2, 4, 6) are listed in the Sect. 6. The approximate solution to Eq. (26) can be developed by setting Δu ^λ₁ as

$$\varDelta u_{1}^{\lambda } \left( \tau \right) = x_{1}^{\lambda } \left( {\cos \tau - \cos 3\tau } \right)$$

(28)

which satisfies the initial condition in Eq. (26) at the outset. Substituting Eqs. (21, 22a and 23), (27a, 27b) and (28) into Eq. (26), expanding the resulting expression in a trigonometric series and setting the coefficients of cos τ and cos 3τ to zero, respectively, yield a set of linear equations for ΔΩ ^λ₁ and x ^λ₁ as

$$F_{1}^{\lambda } \varDelta \varOmega_{1}^{\lambda } - F_{2}^{\lambda } x_{1}^{\lambda } = E_{1}^{\lambda }$$

(29a)

$$F_{3}^{\lambda } \varDelta \varOmega_{1}^{\lambda } + F_{4}^{\lambda } x_{1}^{\lambda } = E_{2}^{\lambda }$$

(29b)

where F ^λ _m (m = 1, 2, 3, 4) and E ^λ _n (n = 1, 2) are listed in the Sect. 6. Solving system of Eq. (29a, 29b) leads to

$$\varDelta \varOmega_{1}^{\lambda } \left( H \right) = \frac{{E_{2}^{\lambda } F_{2}^{\lambda } + E_{1}^{\lambda } F_{4}^{\lambda } }}{{F_{2}^{\lambda } F_{3}^{\lambda } + F_{1}^{\lambda } F_{4}^{\lambda } }},\quad x_{1}^{\lambda } \left( H \right) = \frac{{E_{2}^{\lambda } F_{1}^{\lambda } - E_{1}^{\lambda } F_{3}^{\lambda } }}{{F_{2}^{\lambda } F_{3}^{\lambda } + F_{1}^{\lambda } F_{4}^{\lambda } }}$$

(29c)

Therefore, the second approximate solutions to the period and periodic solution of Eq. (20a, 20b) are

$$\begin{aligned} T_{2}^{\lambda } = 2\pi /\sqrt {\varOmega_{2}^{\lambda } \left( H \right)} \equiv 2\pi /\sqrt {\varOmega_{1}^{\lambda } \left( H \right) + \varDelta \varOmega_{1}^{\lambda } \left( H \right)} , \hfill \\ u_{ 2}^{\lambda } \left( t \right) = u_{ 1}^{\lambda } \left( \tau \right) + \varDelta u_{ 1}^{\lambda } \left( \tau \right) = \left[ {H + x_{ 1}^{\lambda } \left( H \right)} \right] { \cos } \tau - x_{ 1}^{\lambda } \left( H \right) { \cos } 3\tau ,\quad \tau = \sqrt {\varOmega_{2}^{\lambda } \left( H \right)t} \hfill \\ \end{aligned}$$

(30)

For brevity, further higher order analytical approximation is omitted. Nevertheless, the procedure can be carried out recursively to any desired order.

By setting λ = +1, H = A, and λ =−1, H = B, respectively, in Eqs. (24) and (30), the corresponding first and second analytical approximate periods and the periodic solutions T ⁺¹ _n (A), u ⁺¹ _n (t) and T ⁻¹ _n (B) , u ⁻¹ _n (t)(n = 1, 2) to the two newly introduced odd oscillating systems in Eqs. (20a) and (20b), respectively, can be obtained. Using these analytical approximate solutions, the corresponding nth (n = 1, 2) analytical approximate period and periodic solution for Eq. (19) can be constructed (Wu and Lim 2004)

$$T_{n} \left( A \right) = \frac{{T_{n}^{ + 1} \left( A \right)}}{2} + \frac{{T_{n}^{ - 1} \left( B \right)}}{2}$$

(31a)

and

$$u_{n} \left( t \right) = \left\{ \begin{aligned} u_{n}^{ + 1} \left( t \right){\text{ for }}0 \le t \le \frac{{T_{n}^{ + 1} \left( A \right)}}{4} \hfill \\ u_{n}^{ - 1} \left( {t - \frac{{T_{n}^{ + 1} \left( A \right)}}{4} + \frac{{T_{n}^{ - 1} \left( B \right)}}{4}} \right){\text{ for}}\frac{{T_{n}^{ + 1} \left( A \right)}}{4} \le t \le \frac{{T_{n}^{ + 1} \left( A \right)}}{4} + \frac{{T_{n}^{ - 1} \left( B \right)}}{2} \hfill \\ u_{n}^{ + 1} \left( {t + \frac{{T_{n}^{ + 1} \left( A \right)}}{2} - \frac{{T_{n}^{ - 1} \left( B \right)}}{2}} \right){\text{ for}}\frac{{T_{n}^{ + 1} \left( A \right)}}{4} + \frac{{T_{n}^{ - 1} \left( B \right)}}{2} \le t \le \frac{{T_{n}^{ + 1} \left( A \right)}}{2} + \frac{{T_{n}^{ - 1} \left( B \right)}}{2} \hfill \\ \end{aligned} \right. \,$$

(31b)

Note that Eqs. (31a, 31b) can easily be used by MEMS/NEMS designers as a quick tool of resonant sensor performance optimization.

On the other hand, direct integration of Eq. (14) yields the exact period T _e (A) as

$$T_{e} (A) = 2\int_{ - B}^{A} {\frac{du}{{\sqrt {2\left[ {\varPi \left( {A,V} \right) - \varPi \left( {u,V} \right)} \right]} }}}$$

(32)

Where B is determined by Eqs. (16) and (17)

Microbeam A510 is again taken as an example and the corresponding parameters can be found in Sect. 2. The “exact” period T _e (A) obtained by Eq. (32) and the approximate periods T ₁(A) and T ₂(A) computed by Eqs. (31a) are listed in Table 1. Note that the maximum amplitude A _m of vibration is determined by the difference between unstable deflection in the right branch and stable static deflection a _s in the left branch at an equal potential V(a _s), see Figs. 2 and 4. Table 1 presents the second approximate period T ₂ derived by Eq. (31a) and it is obvious that very good approximate solutions for different vibration amplitudes have been obtained. In general, the first approximate period T ₁ computed using Eq. (31a) is acceptable.

Table 1 Comparison of approximate and “exact” periods

For V ² = 19.3786, a _s  = 0.1; V ² = 32.6616, a _s  = 0.2; V ² = 40.47, a _s  = 0.3, and different vibration amplitudes, comparisons study of the “exact” periodic solution u _e (t) obtained by directly integrating Eq. (14) and the approximate analytical periodic solutions u ₁(t) and u ₂(t) computed by Eqs. (31b) are presented in Figs. 5, 6, 7, 8, 9 and 10. These figures show that the second analytical approximate periodic solutions in Eq. (31b) provide the very good approximations to the “exact” periodic solutions for the whole range of small and large amplitude of vibration.

Fig. 5

Comparison of approximate periodic solutions with “exact” solution for a _s  = 0.1, V ² = 19.3786, A = 0.45

Fig. 6

Comparison of approximate periodic solutions with “exact” solution for a _s  = 0.1, V ² = 19.3786, A = 0.68

Fig. 7

Comparison of approximate periodic solutions with “exact” solution for a _s  = 0.2, V ² = 32.6616, A = 0.3

Fig. 8

Comparison of approximate periodic solutions with “exact” solution for a _s  = 0.2, V ² = 32.6616, A = 0.44

Fig. 9

Comparison of approximate periodic solutions with “exact” solution for a _s  = 0.3, V ² = 40.47, A = 0.15

Fig. 10

Comparison of approximate periodic solutions with “exact” solution for a _s  = 0.3, V ² = 40.47, A = 0.22

The proposed analytical approximate solutions are also applicable to NEMS beam resonators. Consider a NEMS beam (Kacem et al. 2011), its length, width and thickness are 50, 1 and 1 μm, respectively, and the gap is 400 nm. The other parameters are same as those of microbeam A510. Figure 11 displays amplitude-frequency curves of the NEMS beam resonator at three different stable static equilibrium states a _S = 0.1, 0.2 and 0.3 where Ω₂(A) = 2π/T ₂(A). It can be found that for each static equilibrium state, the vibration frequency decreases with the increase of oscillation amplitude. For saving space, the approximate analytical periodic solutions to the resonator are omitted.

Fig. 11

Amplitude-frequency curves of a NEMS beam resonator at three different static equilibrium states a _S = 0.1, 0.2 and 0.3

5 Conclusions

In this study, a new nonlinear dynamic model for an axially stressed clamped–clamped micro-/nanobeam actuated by one-sided electrode configuration is presented by using ROM and accurate approximate analytical solutions are constructed. The ROM is based on the Galerkin procedure and the choice of a proper shape function from which integral of the electromechanical forcing term is obtained in an explicit and closed form, and its analyses are thus convenient. Fundamental natural frequency of linear free vibration of the beam is established in analytical form. Numerical examples show that the analytical expression is in good agreement with published experimental data. The nonlinear free vibration of the beam is further analytically investigated by combing the Newton method and the harmonic balance method. Two analytical approximations to the period and periodic solution of the beam are constructed. The second analytical approximate period and periodic solutions show very good approximations to the numerical “exact” periodic solutions and they are valid for small as well as large amplitude of vibration. With these analytical expressions, it is possible to perform analytical parametric investigations with respect to various physical quantities that influence the dynamic behavior and to help MEMS and NEMS designers for improving the performances of resonant sensors. Furthermore, the method proposed in this paper may be applied to deal with dynamic electromechanical responses of other nanoscale mechanical resonators. Future work will focus on dynamic behaviors of NEMS actuated by a DC electrostatic load along with an AC harmonic load. The effects of fringing field, interatomic forces including the Casimir and van der Waals forces as well as surface stress need also be considered.

Appendix

The coefficients C _i (i = 1, 2, ···, 6) and B _j (j = 0, 1, 2, 3) in Eq. (18) are given by

$$C_{1} = 32\{ \pi^{2} (1 - a_{s} )^{{{9 \mathord{\left/ {\vphantom {9 2}} \right. \kern-0pt} 2}}} [2N + \pi^{2} (8 + 3a_{s}^{2} \alpha_{1} )] - 3V_{s}^{2} \alpha_{2} (1 - a_{s} )^{2} \} ,$$

$$C_{2} = 24\{ - 2\pi^{2} (1 - a_{s} )^{{{7 \mathord{\left/ {\vphantom {7 2}} \right. \kern-0pt} 2}}} [2N + \pi^{2} (8 - 2\alpha_{1} a_{s} + 5\alpha_{1} a_{s}^{2} )] + V_{s}^{2} \alpha_{2} (1 - a_{s} )\} ,$$

$$C_{3} = 4\pi^{2} (1 - a_{s} )^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0pt} 2}}} \{ 6N + \pi^{2} [24 + \alpha_{1} (8 - 52a_{s} + 53a_{s}^{2} )]\} + 4V_{s}^{2} \alpha_{2} ,$$

$$C_{4} = - 2\pi^{2} (1 - a_{s} )^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} \{ - 2N + \pi^{2} [ - 8 + 3\alpha_{1} (8 - 22a_{s} + 13a_{s}^{2} )]\} ,$$

$$C_{5} = 6\pi^{4} \alpha_{1} (1 - a_{s} )^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} (2 - a_{s} ),$$

$$C_{6} = 2\pi^{4} \alpha_{1} (1 - a_{s} )^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} ,$$

$$B_{0} = 48(1 - a_{s} )^{{{9 \mathord{\left/ {\vphantom {9 2}} \right. \kern-0pt} 2}}} ,$$

$$B_{1} = - 72(1 - a_{s} )^{{{7 \mathord{\left/ {\vphantom {7 2}} \right. \kern-0pt} 2}}} ,$$

$$B_{2} = 18(1 - a_{s} )^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0pt} 2}}} ,$$

$$B_{3} = 3(1 - a_{s} )^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} .$$

The coefficients D _1i (i = 0, 2, 4, 6) and D _2j (j = 1, 3) in Eqs. (22a, 22b) are givens by

$$D_{10} = B_{0} + 2B_{1} H\lambda /\pi + B_{2} H^{2} /2 + B_{3} H^{3} \lambda /(3\pi ),$$

$$D_{12} = 4B_{1} H\lambda /(3\pi ) + B_{2} H^{2} /2 + 8B_{3} H^{3} \lambda /(5\pi ),$$

$$D_{14} = 2B_{3} H^{3} \lambda /(35\pi ) - 4B_{1} H\lambda /(15\pi ),$$

$$D_{16} = 4B_{1} H\lambda /(35\pi ) - 8B_{3} H^{3} \lambda /(315\pi ),$$

$$D_{21} = C_{1} H + 8C_{2} H^{2} \lambda /(3\pi ) + 3C_{3} H^{3} /4 + 32C_{4} H^{4} \lambda /(15\pi ) + 5C_{5} H^{5} /8 + 64C_{6} H^{6} \lambda /(35\pi ),$$

$$D_{23} = C_{3} H^{3} /4 + 5C_{5} H^{5} /16 + 8C_{2} H^{2} \lambda /(15\pi ) + 32C_{4} H^{4} \lambda /(35\pi ) + 64C_{6} H^{6} \lambda /(63\pi ).$$

The coefficients D _3i (i = 1, 3, 5, 7) and D _4j (j = 0, 2, 4, 6) in Eqs. (27a, 27b) are givens by

$$D_{31} = 2B_{2} H + 4B_{1} \lambda /\pi + 2B_{3} H^{2} \lambda /\pi ,$$

$$D_{33} = 8B_{3} H^{2} \lambda /\left( {5\pi } \right) - 4B_{1} \lambda /\left( {3\pi } \right),$$

$$D_{35} = 4B_{1} \lambda /\left( {5\pi } \right) - 8B_{3} H^{2} \lambda /\left( {35\pi } \right),$$

$$D_{37} = 8B_{3} H^{2} \lambda /\left( {105\pi } \right) - 4B_{1} \lambda /\left( {7\pi } \right),$$

$$D_{40} = C_{1} + 3C_{3} H^{2} /2 + 15C_{5} H^{4} /8 + 4C_{2} H\lambda /\pi + 16C_{4} H^{3} \lambda /\left( {3\pi } \right) + 32C_{6} H^{5} \lambda /\left( {5\pi } \right),$$

$$D{}_{42} = 3C_{3} H^{2} /2 + 5C_{5} H^{4} /2 + 8C_{2} H\lambda /\left( {3\pi } \right) + 32C_{4} H^{3} \lambda /\left( {5\pi } \right) + 64C_{6} H^{5} \lambda /\left( {7\pi } \right),$$

$$D_{44} = 5C_{5} H^{4} /8 + 32C_{4} H^{3} \lambda /\left( {35\pi } \right) - 8C_{2} H\lambda /\left( {15\pi } \right) + 64C_{6} H^{5} \lambda /\left( {21\pi } \right),$$

$$D_{46} = 8C_{2} H\lambda /\left( {35\pi } \right) + 32C_{4} H^{3} \lambda /\left( {315\pi } \right) + 64C_{6} H^{5} \lambda /\left( {231\pi } \right).$$

The terms F ^λ _m (m = 1, 2, 3, 4) and E ^λ _n (n = 1, 2) in Eqs. (29a, b) are given by

$$F_{1}^{\lambda } = B_{0} H + 3B_{2} H^{3} /4 + 8B_{1} H^{2} \lambda /\left( {3\pi } \right) + 32B_{3} H^{4} \lambda /\left( {15\pi } \right),$$

$$\begin{aligned} F_{2}^{\lambda } = C_{1} + 3C_{3} H^{2} /2 + 25C_{5} H^{4} /16 + 64C_{2} H\lambda /\left( {15\pi } \right) + 512C_{4} H^{3} \lambda /\left( {105\pi } \right) \\ + 512C_{6} H^{5} \lambda /\left( {105\pi } \right) - B_{0} \varOmega_{1}^{\lambda } + B_{2} H^{2} \varOmega_{1}^{\lambda } /2 + 256B_{3} H^{3} \lambda \varOmega_{1}^{\lambda } /\left( {105\pi } \right), \\ \end{aligned}$$

$$\begin{aligned} E_{1}^{\lambda } = C_{1} H + 3C_{3} H^{3} /4 + 5C_{5} H^{5} /8 + 8C_{2} H^{2} \lambda /\left( {3\pi } \right) + 32C_{4} H^{4} \lambda /\left( {15\pi } \right) \\ + 64C_{6} H^{6} \lambda /\left( {35\pi } \right) - B_{0} H\varOmega_{1}^{\lambda } - 3B_{2} H^{3} \varOmega_{1}^{\lambda } /4 - 8B_{1} H^{2} \lambda \varOmega_{1}^{\lambda } /\left( {3\pi } \right) - 32B_{3} H^{4} \lambda \varOmega_{1}^{\lambda } /\left( {15\pi } \right), \\ \end{aligned}$$

$$F_{3}^{\lambda } = B_{2} H^{3} /4 + 8B_{1} H^{2} \lambda /\left( {15\pi } \right) + 32B_{3} H^{4} \lambda /\left( {35\pi } \right),$$

$$\begin{aligned} F_{4}^{\lambda } = C_{1} + 3C_{3} H^{2} /4 + 5C_{5} H^{4} /16 + 64C_{2} H\lambda /\left( {21\pi } \right) + 512C_{4} H^{3} \lambda /\left( {315\pi } \right) \\ + 512C_{6} H^{5} \lambda /\left( {1155\pi } \right) - 9B_{0} \varOmega_{1}^{\lambda } - 19B_{2} H^{2} \varOmega_{1}^{\lambda } /4 - 2048B_{1} H\lambda \varOmega_{1}^{\lambda } /\left( {105\pi } \right) - 256B_{3} H^{3} \lambda \varOmega_{1}^{\lambda } /\left( {21\pi } \right), \\ \end{aligned}$$

$$\begin{aligned} E_{2}^{\lambda } = C_{3} H^{3} /4 + 5C_{5} H^{5} /16 + 8C_{2} H^{2} \lambda /\left( {15\pi } \right) + 32C_{4} H^{4} \lambda /\left( {35\pi } \right) + 64C_{6} H^{6} \lambda /\left( {63\pi } \right) \\ - B_{2} H^{3} \varOmega_{1}^{\lambda } /4 - 8B_{1} H^{2} \lambda \varOmega_{1}^{\lambda } /\left( {15\pi } \right) - 32B_{3} H^{4} \lambda \varOmega_{1}^{\lambda } /\left( {35\pi } \right). \\ \end{aligned}$$