Abstract
We consider a nematic liquid crystal occupying the three-dimensional domain in the exterior of a spherical colloid particle. The nematic is subject to Dirichlet boundary conditions that enforce orthogonal attachment of nematic molecules to the surface of the particle. Our main interest is to understand the behavior of energy-critical configurations of the Landau–de Gennes Q-tensor model in the limit of vanishing correlation length. We demonstrate existence of configurations with a single Saturn-ring defect approaching the equator of the particle and no other line or point defects. We show this by analyzing asymptotics of energy minimizers under two symmetry constraints: rotational equivariance around the vertical axis and reflection across the horizontal plane. Energy blow-up at the ring defect is a significant obstacle to constructing well-behaved comparison maps needed to eliminate the possibility of point defects. The boundary estimates we develop to address this issue are new and should be applicable to a wider class of problems.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The study of defects in liquid crystals is well-motivated from physical considerations, and is also closely connected to many fundamental questions in analysis and geometry. The intimate connection between nematic liquid crystals and \({\mathbb {S}}^2\)-valued harmonic maps is well-established through director-based models such as Oseen-Frank [25], and a comprehensive study of singularities in nematics will both exploit and expand the rich trove of analytical tools for studying geometrical variational problems. To better describe nematics in settings involving non-orientability, biaxiality, and the presence of line defects, physicists and mathematicians have turned to the tensorial Landau–de Gennes model, which is in some sense a relaxation of the non-convex constraints of director models. Indeed, much recent attention has concentrated on recovering the Oseen-Frank director and energy in the vanishing correlation length limit of Landau–de Gennes (see, e.g., [6, 12, 16, 22, 33, 35].)
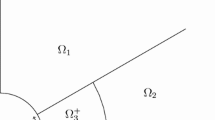
In this paper we revisit an important model problem, that of a spherical colloid particle immersed in a nematic which fills the exterior domain, approaching a constant uniaxial state at infinity. We work within the Landau–de Gennes framework, with homeotropic Dirichlet boundary conditions on the colloid surface. Physicists have long expected that there are two competing candidates for minimizers in this geometry: an orientable solution with dipolar symmetry, consisting of a single satellite point defect lying on the axis of symmetry, and a non-orientable director pattern having a circular “Saturn ring” singularity on the equatorial plane perpendicular to the symmetry axis. The latter configuration exhibits quadrupolar symmetry : in addition to axial symmetry, it is invariant under reflection across the equatorial plane (see (7) for a precise definition). Both configurations are depicted in Fig. 1. In the first mathematical treatment of this problem [1], this expectation is confirmed in the case of very small colloids (for which the quadrupolar Saturn ring solution is minimizing,) or for very large colloids (in which, assuming axial symmetry, the dipolar satellite point defect prevails.) However, Saturn ring defects have been observed both experimentally and numerically in the physics literature (see, e.g., [21, 32, 34, 39, 42]) and appear to be energetically favorable in many settings, even for larger particles. Saturn ring structures are also expected to prevail over radially symmetric point defects in the absence of colloids as well (see [28], and [17, 18, 43] for recent progress around that issue).
1.1 Main results
The goal of this paper is to produce solutions of the spherical colloid problem which exhibit Saturn-ring defects in the limit of small correlation length. To do this, we minimize the Landau–de Gennes energy in a function space enforcing the expected (quadrupolar) symmetries of such a configuration. The symmetry hypothesis will ensure the existence of at least one ring defect on the horizontal plane; a much more difficult issue is to eliminate the possibility of other defects (rings or point defects). Additional ring defects can be excluded by carefully adapting lower bound techniques developed for the Ginzburg–Landau problem [4, 8, 27, 37]. Ruling out point defects, however, presents a new and significant analytical challenge. In general, determining the precise number of point defects in a three dimensional domain is a difficult task: point defects carry only a bounded quantity of energy (see e.g. [11, 33]), which is negligible compared to that of line defects (see [13]), and thus point defects are harder to detect using energy estimates. Moreover, unlike line defects, the number of point defects cannot be deduced from topological considerations as even topologically trivial boundary conditions may give rise to an arbitrary number of point defects [26]. Only very specific examples are known where the number of point defects can be determined (see e.g. [1, 11, 25]). In the present work this task is made even harder due to presence of a line defect approaching the boundary, in that the boundary conditions are “destroyed” by energy blow-up at the ring defect. This considerably complicates the construction of well-behaved comparison maps. We overcome this obstacle by proving a very precise estimate in the blow-up region at the boundary. This estimate appears to be new, even within the context of some well-studied variational problems (such as Ginzburg–Landau with a weight).
Let us now introduce the Landau–de Gennes functional, and the variational framework which we will use in our study. In nondimensional units the colloidal particle is represented by the closed ball of radius one \(B=\lbrace {\vert \cdot \vert }\le 1\rbrace \subset {{\mathbb {R}}}^3\), so that the liquid crystal is contained in the domain \(\Omega ={{\mathbb {R}}}^3\setminus B\). In these units the Landau–de Gennes energy depends on the nematic correlation length \(\xi >0\), and is given by
The map Q takes values into the space \({\mathcal {S}}_0\) of \(3\times 3\) symmetric matrices with zero trace and describes nematic alignment. The nematic potential is given by
where the constant C is such that f satisfies
The correlation length \(\xi \) is typically small and therefore we are going to be interested in the limit \(\xi \rightarrow 0\).
Remark 1.1
We chose specific constants for the potential f(Q) in order to simplify notation. Our results remain valid for any potential of the form
where a, b, c and C(a, b, c) are such that (2) is verified with \({\mathcal {U}}_\star =\left\{ s_\star \left( n\otimes n -\frac{1}{3} I\right) :n\in {\mathbb {S}}^2\right\} \) for some \(s_\star =s_\star (a,b,c)>0\).
Anchoring at the particle surface is assumed to be radial:
At infinity, the effect of the particle is not felt and the alignment is uniform, given by
More precisely, this far field condition is enforced by considering configurations in the space \({\mathcal {H}}\) given by
We denote by \({\mathcal {H}}_b\) the space of such configurations that satisfy in addition the radial anchoring condition at the particle surface:
We seek to construct critical points of \(E_\xi \) with the quadrupolar symmetry of the Saturn ring configuration. This entails two symmetry constraints on the admissible \(Q\in {\mathcal {H}}_b\):
-
rotation symmetry around the vertical axis,
-
and reflection symmetry across the equatorial plane.
See (7) for a precise definition of each, in terms of group actions. We denote the space of maps in \({\mathcal {H}}_b\) satisfying these two symmetry constraints by \({\mathcal {H}}_{sym}\), i.e.
A more complete discussion of the space \({\mathcal {H}}_{sym}\) will be given in Sect. 2. Minimizers of \(E_\xi \) in \({\mathcal {H}}_{sym}\) do exist, because Hardy’s inequality ensures the coercivity of the energy. Moreover, they are critical points of \(E_\xi \) in the full space \({\mathcal {H}}\): this is a consequence of the principle of symmetric criticality [36] (see also [29, Appendix 1]). Our main result shows that the energy of a symmetric minimizer concentrates, as \(\xi \rightarrow 0\), inside a Saturn ring shaped region around the particle. In the limit this region coincides with the equatorial circle
Since the energy will blow up around \({\mathcal {C}}\), the resulting limit configuration will not belong to \({\mathcal {H}}_{sym}\). To define the limit space we cut out a small neighborhood of \({\mathcal {C}}\), consider the exterior domain
and define the limit space \({\mathcal {H}}^\star _{sym}=\bigcap _{\delta >0}{\mathcal {H}}^\star _{sym}(\Omega ^{ext}_\delta )\), where
We may now state our result asserting the existence and asymptotic behavior of solutions with quadrupolar symmetry:
Theorem 1.2
For any \(\xi \in (0,1]\) let \(Q_\xi \) minimize \(E_\xi \) in \({\mathcal {H}}_{sym}\). Then we have:
-
(i)
upper bound: there exists a universal constant \(C>0\) such that
$$\begin{aligned} \frac{1}{2\pi }E_\xi (Q_\xi )\le \pi \ln \frac{1}{\xi }+ \pi \ln \ln \frac{1}{\xi }+ C. \end{aligned}$$ -
(ii)
lower bound: there exists a universal constant \(C>0\) such that for any \(\delta \in (0,1)\),
$$\begin{aligned} \frac{1}{2\pi }E_\xi (Q_\xi ;\Omega _\delta ^{int})\ge \pi \ln \frac{1}{\xi }+ \pi \ln \ln \frac{1}{\xi }- 2\pi \ln \frac{1}{\delta }- C\qquad \text {as }\xi \rightarrow 0, \end{aligned}$$where \(\Omega _\delta ^{int}=\Omega \setminus \Omega _\delta ^{ext} =\Omega \cap \lbrace {{\,\mathrm{dist}\,}}(\cdot ,{\mathcal {C}})\le \delta \rbrace \) is the \(\delta \)-neighborhood of the ring defect \({\mathcal {C}}\).
-
(iii)
limit configuration: there is a subsequence \(\xi \rightarrow 0\) such that \(Q_\xi \) converges in \(C^{1,\alpha }_{loc}({\overline{\Omega }}\setminus {\mathcal {C}})\) to a map \(Q_\star \in {\mathcal {H}}^\star _{sym}\) which is smooth in \({\overline{\Omega }}\setminus {\mathcal {C}}\), and uniaxial,
$$\begin{aligned} Q_\star (x)=n_\star (x)\otimes n_\star (x)-\frac{1}{3} I,\quad n_\star (x)\in {\mathbb {S}}^2, \end{aligned}$$where \(n_\star \) is a smooth \({\mathbb {S}}^2\)-valued locally minimizing harmonic map in \(\Omega \). Furthermore, \(n_\star \) satisfies the additional symmetry property that \(n_\star (x_1,0,x_3)\perp e_2\).
Remark 1.3
-
(a)
The limiting map \(n_\star (\rho ,\varphi ,z)\) is conveniently expressed in cylindrical coordinates \((\rho ,\varphi ,z)\) and is entirely determined by its values \(n(\rho ,z)=n_*(\rho ,0,z)\) in the upper half of the \(\varphi =0\) cross-section,
$$\begin{aligned} D:=\lbrace (\rho ,\varphi ,z) : \ \rho ^2+z^2>1, \ \rho ,z>0, \ \varphi =0\rbrace . \end{aligned}$$Moreover, on the z-axis \(n(0,z)=e_3\), \(\forall z>1\), as well as on the equatorial plane: \(n(\rho ,0)=e_3\), \(\forall \rho >1\). (See Lemma 4.2.)
-
(b)
The additional symmetry statement in Theorem 1.2 (iii) amounts to \(n_\star (\rho ,\varphi ,z)\perp e_\varphi \), i.e. \(n_\star (\rho ,\varphi ,z)\) lies in the azimuthal plane generated by \(e_\rho \) and \(e_z\). (See Proposition 4.4.)
-
(c)
Aside from this symmetry property, in Sect. 4 we obtain rather precise information about \(n_\star \). As \(|x|\rightarrow \infty \), \(n_\star \rightarrow e_3\), in the sense that
$$\begin{aligned} \int _{\Omega } \frac{|n_\star - e_3|^2}{|x|^2}\le \int _{\Omega } \frac{|n_\star - e_3|^2}{x_1^2 +x_2^2} <\infty . \end{aligned}$$Near the ring defect, n resembles a point vortex of degree \(-\frac{1}{2}\), with
$$\begin{aligned} n=n(1+r\cos \theta , r\sin \theta )\approx \sin \theta \, e_1 + \cos \theta \, e_3, \end{aligned}$$in polar coordinates \((r,\theta )\) centered at (1, 0) in the \(\varphi =0\) cross-section. This is a consequence of Lemma 4.7.
-
(d)
Note that we do not prove uniqueness of \(n_\star \), so that in Theorem 1.2 (iii), different subsequences may converge to different maps \(n_\star \) with the above properties.
In proving Theorem 1.2 we rely heavily on the symmetry constraint, which reduces the problem to two dimensions. Indeed, the relevant analogy is to a two-dimensional Ginzburg–Landau energy with a weight \(w=\rho \) arising from cylindrical symmetry. The asymptotic behavior of Ginzburg–Landau energies with weights have been studied in [4, 8]. The principal novelty of this work is that we must deal with Q-tensor-valued maps in an unbounded domain rather than complex-valued maps in a bounded domain. Points (i) and (ii) of Theorem 1.2 follow from careful adaptation of the techniques in [4, 8], along with classical Ginzburg–Landau methods in [27, 37, 41], and more recent arguments for Q-tensor-valued maps in [12, 22].
The most delicate part of Theorem 1.2 is the statement (iii) asserting that the limit is smooth everywhere away from the equatorial ring defect \({\mathcal {C}}\). Proving this statement amounts to eliminating the possibility of point singularities appearing on the z-axis. Indeed, from topological considerations, there is no smooth unit director field in the vertical cross-section D which can satisfy the boundary conditions on the colloid surface and at infinity, and thus the limit must exhibit one or more singularities. This topological constraint is satisfied, for instance, by a single ring defect which is negatively charged, in the sense that it resembles a degree \(-\frac{1}{2}\) vortex in the cross-section. However, a configuration with a positively charged ring defect (a degree \(+\frac{1}{2}\) vortex in the cross-section), combined with a pair of negatively charged point defects (hedgehogs) on the z-axis, is also topologically permissible. The energy comparison between these two configurations turns out to be nontrivial because their energies are the same to leading order in \(\xi ,\) so that more precise, up to o(1), estimates are required. A crucial ingredient in choosing the lowest energy configuration is to show that the energy in the core of a ring defect would be the same, up to terms of order o(1) in \(\xi \), regardless of whether the ring is negatively or positively charged; this is done in Sect. 4.3.2. Once we know the core energies of the two types of ring are essentially the same, the O(1) energy cost in connecting a positive ring to a pair of point defects is shown (in Lemma 4.8) to be strictly greater than that of the single negative degree ring defect.
In calculating the energy of the defect core we encounter an additional difficulty not present in determining the O(1) core energy term for classical Ginzburg–Landau vortices. Indeed, in [9] the authors crucially use the fact that the energy of Ginzburg–Landau vortices scales radially: at scale \(r\gg \xi \), the energy of a vortex goes as \(\ln (r/\xi )=\ln (1/\xi )+\ln r\), and the effect of phase winding is separated from the cost of core formation. Here, on the other hand, proximity to the boundary breaks this scaling invariance and influences the core shape, as seen by the presence of the \(\ln \ln \xi \) term, and makes it much less clear that radial rescaling should reveal a universal O(1) core energy term.
To obtain the core energy estimate, we deform the minimizers in a very narrow wedge domain emanating tangentially from the limiting equatorial defect (see Lemma 4.10). This requires a sharp lower bound on the energy in a small disc tangential to the particle surface at its equator (see Lemma 3.9). The corresponding core energy estimate is new—to the best of our knowledge. Once the core energy is determined, the added energy cost of an anti-hedgehog pair may be computed thanks to ideas in [1] (see Lemma 4.8).
1.2 Background and relevant numerical results
The mathematical study of line defects in nematics was initiated in [13], in the singular limit as the correlation length \(\xi \rightarrow 0\), for domains and boundary values which induce defects along line segments. As mentioned earlier, global minimizers of the spherical colloid problem were first addressed mathematically in [1], in which the size of the colloid plays a determining role. As has long been known by physicists, equatorial ring defects can be observed even around large colloid particles, for example in the presence of external electric or magnetic fields [19, 20, 23, 31, 40] or in confinement [30, 40]. The situation with a magnetic field was studied mathematically in [2], via a Landau–de Gennes energy modified to model interaction with a constant field. The main result of [2] identifies the leading order term in an expansion of the energy, indicating the presence of an equatorial ring defect rather than a satellite point defect, provided the magnetic field is high enough \(h\gg \xi \,\vert \ln \xi \vert \). In the complementary low magnetic field regime \(h\ll \xi \,\vert \ln \xi \vert \), the lower bound established here in Theorem 1.2 directly implies, in view of upper bounds established in [2], that minimizers cannot have quadrupolar symmetry, thus hinting at the presence of a satellite point defect. The asymptotics of that model are further and more precisely explored in [3].
Even in the absence of external factors which appear to favor rings over satellite point defects, much physical evidence, both numerical [21] and formal [32], arguments suggest that there is a range of intermediate particle sizes for which configurations with Saturn ring defects may be stable and coexist with point defect configurations having lower energy.
We do not consider the important question of stability in this paper, but numerical simulations suggest that the solutions found here may be locally stable. To illustrate these observations, in Fig. 1a–c we present the summary of simulations that reproduce and extend the results of [21]. We numerically solved in COMSOL [14] the equations for the gradient flow
for the energy \(E_\xi \) defined in (1) in the domain in the form of a large cylinder with a spherical void of radius 1 with the same center as that of the cylinder. The admissible Q-tensor fields have values in the set of symmetric traceless matrices and are rotationally equivariant with respect to z-axis that is also the axis of the cylinder. The Q-tensors are subject to the initial condition \(Q(\cdot ,0)=Q_{init}\) and the boundary conditions (4) and (3) on the surfaces of the cylinder and the sphere, respectively.
Following [21] and assuming that \((\rho ,\varphi )\) are polar coordinates in a plane perpendicular to the axis of the cylinder, the simulations were run starting from two initial conditions
where \(\mathbf{n}(\psi )=(\cos {\psi }\cos {\varphi },\cos {\psi }\sin {\varphi },\sin {\psi })\) and
Here the second choice of the initial condition represents an approximation of a nematic configuration with a hyperbolic point defect at distance \(z_0\) below the sphere’s center [21, 32]. We assumed that \(z_0=1.4\) in our simulations, although equilibrium configurations attained via the gradient flow are not sensitive to the precise choice of this parameter. Note that, for \(\xi <0.005\), the simulations leading to an equatorial Saturn ring were started from the critical point obtained for \(\xi =0.005\).
Figure 1a–b shows the line fields of the nematic in (r, z)-coordinates when \(\xi =1/70\). For this choice of the correlation length, the critical point approached by the gradient flow simulation depends on the initial condition; the critical point in Fig. 1a has dipolar symmetry, while the critical point Fig. 1b is quadrupolar.
Nematic configurations corresponding to critical points for \(E_\xi \) when \(\xi =1/70\). The red dot marks the location of a Saturn ring. a \(Q_{init}={n}(\psi )\otimes {n}(\psi )-\frac{1}{3}I\) and the critical point is a small hyperbolic ring below the south pole of the particle. The ring shrinks to a hyperbolic point defect on z-axis when \(\xi \rightarrow 0\). b \(Q_{init}={e}_3\otimes {e}_3-\frac{1}{3}I\) and the critical point is the equatorial Saturn ring. The Saturn ring approaches the surface of the colloid when \(\xi \rightarrow 0\). c Energy \(E_\xi \) vs nematic correlation length \(\xi \). The critical point reached from the constant initial condition (blue) is always the equatorial Saturn ring. The critical points with an equatorial Saturn ring and with a small hyperbolic ring coexist and appear to be stable for all values of \(\xi <\xi _c\) for which the simulations were conducted (color figure online)
For larger values of \(\xi \), once it exceeds a critical value \(\xi _c\approx 0.017\), the simulations converge to the equatorial Saturn ring configuration, regardless of the initial conditions. In fact, for the initial condition with a hyperbolic point defect, this defect expands first into a small ring below the south pole of the colloid. This ring then expands and travels up the surface of the colloid, eventually stopping at its equator.
For \(\xi <\xi _c\), the dichotomy between the initial conditions persists for all values of \(\xi \) for which the simulations were run: the hyperbolic point defect expands into a small ring below the colloid and the constant initial condition leads to the equatorial Saturn ring. Even though the energy of the equatorial ring exceeds the energy of the small ring once \(\xi \) becomes sufficiently small, the equatorial ring remains stable. These observations are summarized in Fig. 1c.
Although we do not address the question of their minimality, in the present work we establish that Saturn ring-like critical points of the Landau–de Gennes energy indeed do exist for large particles. Here, rather than varying the radius of the particle, we use an equivalent description in which the size of the particle is fixed and the nematic correlation length is assumed to converge to zero.
This paper is organized as follows. In Sects. 2 and 3 , we establish the upper and lower bounds given by the statements (i) and (ii) of Theorem 1.2. In Sect. 4 we prove the statement (iii) of Theorem 1.2; namely, a sequence of minimizers converges to a limiting map which is smooth away from the ring defect.
2 Upper bound
To obtain the upper bound, i.e. part (i) of Theorem 1.2, we construct an admissible map \(Q\in {\mathcal {H}}_{sym}\) whose energy has the expected behavior.
Let us first describe more explicitly what quadrupolar symmetry means. Symmetries are formalized in terms of the equivariant action of the orthogonal group O(3) on maps \(Q:{{\mathbb {R}}}^3\rightarrow {\mathcal {S}}_0\), given by
The energy \(E_\xi \) is invariant under this action, consistent with the physical requirement of frame invariance. Here we consider the subgroup
This is the largest subgroup of O(3) that maps the space \({\mathcal {H}}\) into itself. Explicitly, \(G_{sym}\) is generated by all rotations around the vertical axis \(e_3\) and by the reflection with respect to the horizontal plane \(\langle e_1,e_2\rangle \), that is,
The critical points we study in this work are minimizers of the energy among symmetric configurations belonging to the space
It is natural to use cylindrical coordinates to describe maps in the space \({\mathcal {H}}_{sym}\), i.e. coordinates \((\rho ,\varphi ,z)\) defined by
In these coordinates the domain \(\Omega \) corresponds to \(\lbrace \rho ^2+z^2 >1\rbrace \), and maps \(Q\in {\mathcal {H}}_{sym}\) can be written in the form
where in addition \({\widetilde{Q}}(\rho ,z)=Q(\rho ,0,z)\) satisfies the mirror symmetry constraint
Written in cylindrical coordinates, the energy of a map \(Q\in {\mathcal {H}}_{sym}\) takes the form
Note that \(\Xi [{\widetilde{Q}}]\le 4\, \mathrm {dist}^2({\widetilde{Q}},{{\mathbb {R}}}Q_\infty ),\) where the distance is induced by the Frobenius norm. We will construct \({\widetilde{Q}}\) in the region
with boundary constraints
and then use the mirror symmetry (10) to extend \({\tilde{Q}}\) to the entire domain \(\Omega \). Note that \({\widetilde{Q}} = S{\widetilde{Q}} S^t\) implies that \(e_3\) is an eigenvector of \({\widetilde{Q}}\) on the horizontal axis \(\lbrace z=0\rbrace \) in order for the mirror symmetry not to create a jump of \({\tilde{Q}}\).
We begin by observing that in all estimates in this and subsequent sections the letter C denotes a generic universal constant. To construct \({\widetilde{Q}}\) we first divide D into 3 subdomains, \({{\overline{D}}}={{\overline{D}}}_1 \cup {{\overline{D}}}_2 \cup {{\overline{D}}}_3,\) where

Let
so that
Then we define a Lipschitz map \(n:\partial D_2\rightarrow {\mathbb {S}}^2\) as follows. We first set
To define n on \(\partial D_2\cap \partial D_3\) we use polar coordinates \((r,\theta )\) centered in (1, 0), that is, given by the relation \(\rho +iz=1+re^{i\theta }\), so that
We set
and in the remaining part of \(\partial D_2\cap \partial D_3\) we interpolate linearly. More precisely, at the point \((1/2,\theta _0)\), continuity of n imposes \(n=(\cos \theta _1,0,\sin \theta _1)\) where \(\theta _1=2\theta _0-\pi = 2\arcsin (1/4)\), so we set

The map \(n:\partial D_2\rightarrow {\mathbb {S}}^2\) thus defined can be written in the form
Thus, considering an \(H^1\) extension of \(\varphi \) to \(D_2\) we obtain \(n:D_2\rightarrow {\mathbb {S}}^2\) with \(\int _{D_2}{\vert \nabla n\vert }^2\le C\) and moreover, thanks to Hardy’s inequality and since \(n=e_3\) on \(\partial D_2\cap \lbrace \rho =0\rbrace \), we have also \(\int _{D_2}\rho ^{-2}{\vert n- e_3\vert }^2\le C\). Then we set
and, since \(f(Q_n)=0\) and \(\Xi [Q_n]\le C {\vert n-e_3\vert }^2\), we have
Next we need to define \({\widetilde{Q}}\) in \(D_3\). We introduce a parameter \(\sigma >0\) with \(\xi<\sigma <1/8\), and further divide \(D_3\) into 3 subdomains:

In the polar coordinates \((r,\theta )\) centered at (1, 0), the domain \(D_4\) is given by
In \(D_4\) we define \({\widetilde{Q}}\) as
for some map \(n:D_4\rightarrow {\mathbb {S}}^2\). The boundary conditions on \(\lbrace \rho ^2+z^2=1\rbrace \) impose
and we define
That way we have
Moreover, in \(D_4\) we have \(f({\widetilde{Q}})=0\) and \(\rho ^{-2}\Xi [Q]\le C\), and therefore
In the subdomain \(D_5\) we are again going to define \({\widetilde{Q}}\) from a unit vector field \(n:D_5\rightarrow {\mathbb {S}}^2\). There we use polar coordinates \((s,\phi )\) centered at \((1+2\sigma ,0)\), that is, given by \(\rho +iz = 1+2\sigma + s e^{i\phi }\). In these coordinates the domain \(D_5\) is of the form
where \({\bar{s}}(\phi )\) is a Lipschitz function of \(\phi \), with \(2\sigma \le {\bar{s}} \le 5\sigma \). On the part of \(\partial D_5\) given by \(\lbrace s={\bar{s}}(\phi )\rbrace \), the values of n are given by the boundary conditions on \(\lbrace \rho ^2+z^2=1\rbrace \) and on \(\partial D_4\), and are of the form
for Lipschitz function \(\alpha :[0,\pi ]\rightarrow {{\mathbb {R}}}\), which satisfies \(\alpha (0)=\pi /2\) and \(\alpha (\pi )=0\). On the part of \(\partial D_5\) given by \(\lbrace s=\sigma \rbrace \), we set
Then we define n in \(\partial D_5\) by interpolating in the s variable, i.e. we set
Note that, by continuity, and since \(n(\sigma ,0)=e_3 = n({\bar{s}}(0),0)\) and \(n(\sigma ,\pi )=e_1 = n({\bar{s}}(\pi ),\pi )\), this forces the trace of n on \(\partial D_5\cap \lbrace z=0\rbrace \), to be given by
Moreover, since it is directly checked that \({\vert \partial _s n\vert } + {\vert \partial _\phi n\vert }\le C\), we deduce
Therefore, setting \({\widetilde{Q}}=Q_n\) in \(D_5\) we obtain
Finally, in \(D_6\) we define \({\widetilde{Q}}\) in polar coordinates \((s,\phi )\) centered at \((1+2\sigma ,0)\) as above, by
Then we have
and therefore, since \(f({\widetilde{Q}}_n)=0\) for \(s>\xi \) and \(\le C\) for \(s< \xi \), we deduce that
Gathering (11)–(16), we obtain
Optimizing in \(\sigma \), we are led to choosing
and conclude that
which, upon applying the mirror symmetry, proves part (i) of Theorem 1.2.
3 Lower bound
In this section we prove the lower bound, part (ii) of Theorem 1.2. The strategy of proof is inspired by vortex ball constructions [9, 27, 37, 41] in the Ginzburg–Landau context, an idea which has been successfully exploited in various previous works on Q-tensors. (See e.g., [12, 22].) Because we expect the ring defect to approach the boundary as \(\xi \rightarrow 0\), we employ methods introduced for Ginzburg–Landau energies with a weight which attains its minimum on the boundary [4, 7, 8]. A considerable sharpening of these results is necessary in order to apply the ideas to the cross-sections of the exterior domain, and this is the aim of the first part of this section. Some of the technical lemmas (such as Lemma 3.9 below) will also be needed in our analysis of singularities of the limit problem in Sect. 4.
We use the notation \(\lesssim \) to denote inequality up to a universal multiplicative constant. We denote by \({\widetilde{Q}}_\xi \) the map defined by
which satisfies in addition the mirror symmetry (10). The map \({\widetilde{Q}}_\xi \) is thus defined in
uniquely determined by its values in the region
and minimizes
under the boundary constraints
For any \(X\in {\widetilde{\Omega }}\) we will denote by B(X, r) the disc of radius \(r>0\) centered at X.
Note that our potential f vanishes quadratically near the manifold \({\mathcal {U}}_\star \): more specifically, given \(C>0\), there exist constants \(c_1,c_2\) with
The upper and lower estimates on f(Q) are proven in [12, Sect. 2.2] for Q in a neighborhood of \({\mathcal {U}}_\star \); by adjusting the constants, the same bounds hold in any compact set of tensors Q. As a consequence, we may fix \(\eta >0\) such that in the region \(\lbrace Q\in {\mathcal {S}}_0:f(Q) < 2 \eta \rbrace \), the nearest neighbor projection \(\pi \) onto the smooth submanifold \({\mathcal {U}}_\star \) is well defined and smooth.
Lemma 3.1
The minimizers \(Q_\xi \) are smooth in \({\widetilde{\Omega }}\), and satisfy the uniform bounds,
Proof
The \(L^\infty \) bound is proved in [1, Lemma 5], and the regularity and gradient bound follow from elliptic estimates. \(\square \)
Away from the vertical axis of symmetry the energy is almost two-dimensional, and we exploit this observation to use \(\eta \)-compactness methods developed for the Ginzburg–Landau functional by Struwe [41].
Lemma 3.2
For any \(\alpha \in (0,1]\) there exists \(C_\alpha >0\) such that for any \(X=(\rho _0,z_0)\in {\widetilde{\Omega }}\cap \lbrace \rho \ge \frac{1}{2}\rbrace \),
Proof
Fix any \(X=(\rho _0,z_0)\in {\widetilde{\Omega }}\cap \lbrace \rho \ge \frac{1}{2}\rbrace \). Define
where \(ds_r\) denotes arclength measure on \(\partial B(X,r)\).
Let \(\beta =\alpha /2 >0\). As in the proof of [41, Lemma 2.3 (i)], by Fubini’s Theorem there exists \(r_\xi \in (\xi ^\alpha ,\xi ^\beta )\) for which
In particular,
To obtain the desired bound we require a version of the Pohozaev identity. We treat our problem as if it were two dimensional, with domain \({\widetilde{\Omega }}\) and a nonconstant weight function \(w=\rho \). Consider a solution u of the equation
For a smooth vector field Y, we multiply by \(Y\cdot \nabla u\) and integrate by parts on \(D\subset {\widetilde{\Omega }}\), to obtain:
In our case, we choose the domain \(D=D_r= B(X,r)\cap {\widetilde{\Omega }}\), and the vector field \(Y=(\rho -\rho _0,z-z_0)\). The Euler-Lagrange equations have the form
where \(L=\frac{1}{6} |{\widetilde{Q}}|^2 {\mathbf {I}}\) is a Lagrange multiplier due to the vanishing trace condition. Since the test functions \(Y\cdot \nabla {\widetilde{Q}}_\xi \) are trace-free, (as observed in [12, Remark 4.3],) \(L({\widetilde{Q}}_\xi )\) plays no role in the resulting identity, and so we may take \(g(x,u)= g(\rho , {\widetilde{Q}}_\xi )= \frac{1}{2\rho ^2}\Xi ({\widetilde{Q}}_\xi ) + \frac{1}{2\xi ^{2}} f({\widetilde{Q}}_\xi )\). Substituting in the above identity, with \(u=\widetilde{Q}_{\xi ,ij}\) and summing over i, j, we obtain:
Recalling \(X=(\rho _0,z_0)\) with \(\rho _0\ge \frac{1}{2}\), we will apply the above identity (here and in the next lemma) for \(r\in (\xi ,\xi ^\beta )\), and so for \(\xi \) sufficiently small the domain \(D_r\) will be strongly starshaped, in the sense that \(Y\cdot \nu \ge \frac{r}{4}\) on \(\partial D_r\). Following [41, Lemma 2.3 (ii)], the right-hand side of (20) may be estimated as:
with constant C independent of X, and recalling \({\widetilde{Q}}_\xi =Q_b\) on \(\partial B(0,1)\). For the left-hand side, we note that in \(D_r\), \(|\rho -\rho _0|<r\le 3\rho \xi ^\beta \), and hence
Thus, we have for any \(r\in (\xi ,\xi ^\beta )\),
Choosing \(r=r_\xi \) as in (18), and noting \(B(X,\xi ^\alpha )\subset B(X,r_\xi )\), the desired inequality is established. \(\square \)
The following is an adaptation of the \(\eta \)-compactness (\(\eta \)-ellipticity) condition to our setting.
Lemma 3.3
There exists \(\gamma >0\) such that, for any \(\alpha \in (0,1]\) there is \(\xi _0(\alpha )>0\) with the following property. If \(\xi \in (0,\xi _0)\) and \(r\in [\xi ,\xi ^\alpha ]\) are such that
then \(f({{{\widetilde{Q}}_\xi }})\le \eta \) in \(B_r(X)\cap {\widetilde{\Omega }}\).
Proof
The proof is as in [41, Lemma 2.3(ii)]. Suppose the contrary: there exists \(X'=(\rho ',z')\in B(X,r)\) for which \(f({\widetilde{Q}}_\xi (X'))>\eta \). By Lemma 3.1, there exists \(c>0\) for which \(f({\widetilde{Q}}_\xi (x))>\eta /2\) for all \(x\in B(X',c\xi )\). Thus, there is a constant \(C_0>0\), independent of \(X,\xi \), for which
On the other hand, by (22) we then have
For any \(\gamma <C_0\) this is impossible, as \(|\rho (X')-\rho (X)| < r \ll 1\), and hence the conclusion must hold. \(\square \)
As in the Ginzburg–Landau case, we may now define the “bad balls” which contain the eventual defects:
Lemma 3.4
There exist \(M_0\in {\mathbb {N}}\) and \(A_0\ge 1\) such that
and for any disjoint collection of balls \(\lbrace B(X_j,\frac{\xi }{5})\rbrace _{j\in J}\) with centers
the cardinality of J must be \(\le M_0\).
Proof
For the first assertion, let \(X'\in \{x\in {\widetilde{\Omega }}: \ f({\widetilde{Q}}_\xi (x))>\eta )\}\). As in the proof of Lemma 3.3, there exists \(c>0\) for which \(f({\widetilde{Q}}_\xi (x))>\eta /2\) in \(B(X',c\xi )\), with the same lower bound (23). Taking \(r=r_\xi \) as in (18), we obtain \(C_0\rho (X')\le CF(r_\xi )\le C'\), and hence \(\rho (X')\) is uniformly bounded in \(\xi \).
The second assertion now follows as in the proof of [41, Lemma 3.2], relying on Lemmas 3.2 and 3.3 . Indeed, thanks to the first assertion, we have \(S_\xi \subset \lbrace 1/2\le \rho \le A_0\rbrace \) and for \(X\in {\widetilde{\Omega }}\cap \lbrace 1/2\le \rho \le A_0\rbrace ,\) the factor \(\rho \) can be replaced by a constant both in the lower bound (23) and in the upper bound appearing in the statement of Lemma 3.3. Hence, the identical arguments as in [41], based on Vitali covering of \(S_\xi \) by balls of radius \(\xi ^{\frac{1}{4}}\), assure the bounded cardinality of the collection of “bad balls” \(\lbrace B(X_j,\frac{\xi }{5})\rbrace _{j\in J}\). \(\square \)
Recall that given any Lipschitz simply connected bounded domain \(R\subset {{\mathbb {R}}}^2\) and any continuous map \(U:\partial R\rightarrow {\mathcal {U}}_\star \) we can consider its homotopy class in \(\pi _1({\mathcal {U}}_\star )\approx {\mathbb {Z}}/2{\mathbb {Z}}\). A loop is trivial in \(\pi _1({\mathcal {U}}_\star )\) if and only if it is orientable, i.e. it is of the form \(\gamma \otimes \gamma -\frac{1}{3} I\), for some continuous loop \(\gamma :{\mathbb {S}}^1\rightarrow {\mathbb {S}}^2\).
Lemma 3.5
Consider for some \(z_0\in (0,1/2]\) and \(\rho _0\ge A_0\) the domain
and assume that \(f({\widetilde{Q}}_\xi )\le \eta \) on \(\partial {{R_0}}\) and that \({\widetilde{Q}}_\xi \) restricted to \(\partial {{R_0}}\) is continuous. Then the projected map
has non trivial homotopy class in \(\pi _1({\mathcal {U}}_\star )\), that is, \(U_\xi \) is non-orientable.
Proof of Lemma 3.5
Recall that \(Q_\xi \in {\mathcal {H}}_{sym}\), hence
In particular, for any \(\xi \in (0,\xi _0)\) and any \(\delta >0\) we may choose \(\rho _1\ge \rho _0\) such that
which implies
We denote by \(R_1\) the domain
and define \(V_\xi =\pi ({\widetilde{Q}}_\xi ):\partial R_1\rightarrow {\mathcal {U}}_\star \). Since \(\pi ({\widetilde{Q}}_\xi )\) is well defined and has finite energy in \(R_1\setminus R_0\), the maps \(U_\xi \) and \(V_\xi \) are homotopically equivalent. To prove Lemma 3.5 it thus suffices to prove that \(V_\xi \) is non orientable. Assume that \(V_\xi \) is orientable: there exists a continuous \(n:\partial R_1\rightarrow {\mathbb {S}}^2\) such that
Since n is uniquely defined up to a sign and \(V_\xi =e_1\otimes e_1-\frac{1}{3} I\) at \((\rho ,z)=(1,0)\), we may assume that \(n(1,0)=e_1\). The symmetry assumption (10) implies that
Evaluating this at \((\rho ,z)=(1,0)\) gives \(e_1=\tau Se_1 =\tau e_1\), hence \(\tau =1\). This implies that at \((\rho ,z)=(\rho _1,0)\) one must have \(n(\rho _1,0)=Sn(\rho _1,0)\), i.e. \(n(\rho _1,0)\perp e_3\), and therefore \({\vert V_\xi (\rho _1,0)-Q_\infty \vert }^2= 2\). For small enough \(\delta \) this contradicts (24). \(\square \)
The next lemmas deal with universal lower bounds in annular regions.
Lemma 3.6
There exists \(C>0\) such that for any \(\xi >0\), for any annulus \(\omega \subset {{\mathbb {R}}}^2\) of the form
and any \(H^1\) map \(Q:\omega \rightarrow {\mathcal {S}}_0\) satisfying \(f(Q)\le \eta \) in \(\omega \) and such that the trace on \(\partial B(0,R)\) of \(U=\pi (Q):\omega \rightarrow {\mathcal {U}}_\star \) is continuous and nonorientable, we have
Proof of Lemma 3.6
Very similar results are proved in [12, Proposition 3.12] and [22, Lemma 7], but for completeness we provide a proof, following the method in [27].
Let \(D={\vert Q-U\vert }={{\,\mathrm{dist}\,}}(Q,{\mathcal {U}}_*)\), and denote by \(P:{\mathcal {U}}_\star \rightarrow {\mathcal {L}}({\mathcal {S}}_0)\) the smooth map given by \(P(u)=P_{(T_u{\mathcal {U}}_\star )^\perp }\) the orthogonal projection onto the normal space to \({\mathcal {U}}_\star \) at u. Note that by definition \(Q-U=P(U)(Q-U)\). Then for any direction k we compute
The last term is zero because \(\partial _k U\in T_U{\mathcal {U}}_\star \) and therefore \(P(U)\partial _k U=0\). So we have
for \(c=2\sup _{{\mathcal {U}}_\star }{\Vert DP(U)\Vert }\). This computation is very similar to [12, Lemma 2.6] and [22, Lemma 4]. Recalling now that \(f(Q)\ge \alpha ^2 D^2\) for some \(\alpha >0\) we find
Hence for any \(s\in (r,R)\) we have, letting \(d(s)=\max _{\partial B(0,s)} D\),
The latter term is bounded from below by
The proof of (26) follows the argument of [27, Lemma 2.3] which we reproduce here for the reader’s convenience. Denoting
Morrey’s inequality gives
Letting \(x_{max}\in \partial B(0,s)\) be such that \(D(x_{max} )=d(s)\), we deduce that
and therefore
This implies
from which (26) follows because \(s\ge r\ge \xi \). Since U is \(H^1\) in \(\omega \) and non orientable on \(\partial B(0,R)\), it is continuous and nonorientable on \(\partial B(0,s)\) for a.e. \(s\in [r,R]\), and for such s we have (see e.g. [12, Corollary 3.8])
and therefore, recalling (25)–(26), there is a constant \({\hat{\alpha }}>0\) such that
Integrating we deduce
\(\square \)
Using Lemma 3.6 and the growing ball construction of Jerrard or Sandier [27, 37] (which is adapted to our setting in [22, Lemma 7]), one obtains the following lower bound on perforated domains:
Lemma 3.7
There exists \(C>0\) such that for any \(\xi \in (0,1]\), for any perforated domain \(\omega \subset {{\mathbb {R}}}^2\) of the form
and any \(H^1\) map \(Q:\omega \rightarrow {\mathcal {S}}_0\) satisfying \(f(Q)\le \eta \) in \(\omega \) and such that the trace on \(\partial B(0,R)\) of \(U=\pi (Q):{\overline{\omega }}\rightarrow {\mathcal {U}}_\star \) is continuous and nonorientable, we have
We will also need a boundary version of Lemma 3.6.
Lemma 3.8
There exists \(C>0\) such that:
-
for any \(\xi >0\), for any annulus \(\omega \subset {{\mathbb {R}}}^2\) of the form
$$\begin{aligned} \omega = B(0,R)\setminus B(0,r),\qquad {\xi \le r<R\le \frac{1}{2},} \end{aligned}$$ -
for any \(H^1\) map \(Q:\omega \rightarrow {\mathcal {S}}_0\) satisfying \(f(Q)\le \eta \) in \(\omega \) and such that the trace on \(\partial B(0,R)\) of \(U=\pi (Q):{\overline{\omega }}\rightarrow {\mathcal {U}}_\star \) is continuous and nonorientable, and such that in addition \(Q=U_0\) on the left half \(\omega _- = \omega \cap \lbrace (x_1,x_2):x_1<0\rbrace \) of the annulus, for some Lipschitz \(U_0:{{\mathbb {R}}}^2\rightarrow {\mathcal {U}}_\star \) with \({\vert \nabla U_0\vert }\le 1\),
-
and for any function w such that \(w(x)\ge 1-{\vert x\vert }^2\),
then:
where \(\omega _+ =\omega \cap \lbrace (x_1,x_2):x_1>0\rbrace \) is the right half of the annulus.
Proof of Lemma 3.8
We claim that
Then, going through the computations in the proof of Lemma 3.6 gives
which proves Lemma 3.8, provided we show (28). We fix \(s\in [r,R]\) such that \(U_{\lfloor \partial B(0,s)}\) is in \(H^1\) and non-orientable. Since \({{\mathbb {R}}}^2\) and \(\partial B(0,s)\cap {\overline{\omega }}_+\) are simply connected we may orient \(U_0\) and U on these domains, i.e. write
Since \(U(se^{-i\frac{\pi }{2}})=U_0(se^{-i\frac{\pi }{2}})\) we may, up to switching the orientation of \(n_0\), assume that
Since \(U(se^{i\frac{\pi }{2}})=U_0(se^{i\frac{\pi }{2}})\) we have \(n_s(\frac{\pi }{2})=\pm n_0(se^{i\frac{\pi }{2}})\), and because U is non-orientable it must be
Note also that, as \({\vert \nabla n_0\vert }=\frac{1}{\sqrt{2}}{\vert \nabla U_0\vert }\le 1\), we have
which implies that
Hence we find
thus proving (28). \(\square \)
In Sect. 4 we will also need the following refinement of Lemma 3.8. In particular, we show that (to O(1)) we obtain the same lower bound in a smaller domain which pulls away from the boundary of the half-disk along a curve \(x_1=\lambda x_2^\beta \) with \(\lambda >0\) and \(\beta >1\). While the statement is quite technical, the result is essential for the very precise control of the energy of the core of the defect demanded in the proof of Lemma 4.10.
Lemma 3.9
Let \(C,\xi ,\omega ,\omega _+,r,R,Q,\eta ,\) and \(U_0\) be as in Lemma 3.8. If Q also satisfies a matching upper bound, in the sense that
for some \(K>0\), then the lower bound (27) is also valid in the slightly smaller domain
in the sense that
Proof of Lemma 3.9
We use the same notations as in the proof of Lemma 3.8, and refine the lower bound obtained on each slice \(\partial B(0,s)\cap \omega _+\). The crucial computation is
This can be interpreted as a stability estimate for geodesics in \({\mathbb {S}}^2\): if the lower bound for the energy of a curve (minimized by constant speed geodesics) is almost saturated, then this curve’s speed must be close to constant. Plugging this back into the estimates performed in Lemma 3.6, we deduce
where recall that \(c>0\) depends only on \({\mathcal {U}}_\star \) and \(0\le d(s)\lesssim \eta \). Hence, possibly lowering \(\eta \) we can assume \(cd(s)\le \frac{1}{2}\), and arguing as in Lemma 3.6 we obtain
Integrating we deduce
Combining this with the assumption that we have a matching upper bound gives
We will use this to show that the part that we “forget” by integrating over \({\tilde{\omega }}_\beta \) instead of \(\omega _+\) is bounded. Indeed we have
Notice that since \(\beta >1\) the last term is summable with respect to s small . Hence upon arguing as above we find
and combining this with (29) enables us to conclude. \(\square \)
We are finally ready to prove the lower bound on the energy stated in Theorem 1.2.
Proof of Part (ii) of Theorem 1.2
First, as in the Ginzburg–Landau problem [9] it will be convenient to extend the minimizers \({\widetilde{Q}}_\xi \) into the colloid. That is we fix a common (ie, \(\xi \)-independent) Lipschitz \({\mathcal {U}}_\star \)-valued map \(U_0\) which is defined in a thin neighborhood \(\{(\rho ,z) \, : \, \frac{1}{4}<\rho ^2+z^2<1\}\) inside the colloid, and such that the extension
is Lipschitz across the colloid surface \(\{\rho ^2+z^2=1\}\). For instance, once could simply choose \(U_0=e_r\otimes e_r -\frac{1}{3} I\). By abuse of notation, we will denote this extension by \({\widetilde{Q}}_\xi \) in the proof. With this understanding, for any circle \(\partial B(a,r)\) with \(a\in \overline{{\widetilde{\Omega }}}\) and \(0<r<3/4\) such that \(f({\widetilde{Q}}_\xi )<\eta \) on \(\partial B(a,r)\cap {\widetilde{\Omega }}\), it makes sense to consider \(U_\xi =\pi ({\widetilde{Q}}_\xi )\) on all of \(\partial B(a,r)\) (even if part of this circle lies outside of \({\widetilde{\Omega }}\)). Moreover \(U_\xi \) is orientable on \(\partial B(a,r)\) if and only if it is orientable on \(\partial (B(a,r)\cap {\widetilde{\Omega }})\).
Step 1: we construct “bad balls” as in [9, 41], and show that at least one must carry topological charge and converge to the equator \(a=(1,0)\) of the colloid. Thanks to Lemma 3.4 and arguing as in [9, Theorem IV.1], there exist \(\lambda >0\) and a family of disjoint balls \(B(x_j^\xi ,\lambda \xi )\) such that
Let us now consider a sequence \(\xi =\xi _n\rightarrow 0\). To keep notation simple we will not write explicitly the dependence on n, and will not relabel subsequences. We may extract converging subsequences of the \(x_j^\xi \) that lie inside \(\lbrace {\vert z\vert }\le \frac{1}{2},\rho \le A_0\rbrace \), and we denote by \(a_1,\ldots ,a_K\) those of the limit points that lie in the axis \(\lbrace z=0\rbrace \), and \(z_1=\min (\frac{1}{2},\frac{d}{2})\), where d is the minimal distance of any other limit point to the axis \(\lbrace z=0\rbrace \) or of any of the \(a_j\)’s to the other \(a_j\)’s. Then for any \(\delta \in (0,z_1)\) the balls \(B(a_j,\delta )\) are disjoint and we have
By Fubini’s theorem we may find \(z_0\in [z_1/2,z_1]\) and \(\rho _0\ge A_0\) such that \({\widetilde{Q}}_\xi \) restricted to \(\partial R\) is continuous, where \(R=\lbrace {\vert z\vert }<z_0,\rho <\rho _0\rbrace \cap {\widetilde{\Omega }}\). By the above \(f({\widetilde{Q}}_\xi )\le \eta \) on \(\partial R\) for small enough \(\xi \), so we may apply Lemma 3.5 to deduce that the \(U_\xi =\pi ({\widetilde{Q}}_\xi )\) is non-orientable on \(\partial R\). As a consequence, \(U_\xi \) must be non-orientable on \(\partial B(a_j,z_1/2)\) for at least one index j.
Relabeling we assume \(j=1\). We claim that \(a_1\) must be the leftmost possible point \(a=(1,0)\). Assume indeed that \(\rho (a_1)>1\) and fix \(\delta \in (0,z_1)\) such that \(\rho (a_1)-\delta >1\). Then applying Lemma 3.7 on \(B(a_1,\delta )\setminus \bigcup _{j} B(x_j^\xi ,\lambda \xi )\) for small enough \(\xi \) we deduce that
but since \(\rho (a_1)-\delta >1\) this implies that \({\widetilde{E}}_\xi ({\widetilde{Q}}_\xi )-\pi \ln \frac{1}{\xi }\rightarrow \infty \) as \(\xi \rightarrow 0\), thus contradicting the upper bound obtained in Sect. 2.
Gathering the above, we have that \(a=(1,0)\) is a limit of some \(x_j^\xi \) and for any \(\delta >0\), if \(\xi \) is small enough then \(U_\xi =\pi ({\widetilde{Q}}_\xi )\) is well defined and non-orientable on \(\partial B(a,\delta )\). Of the above defined \(x_j^\xi \), we now consider only those which converge to a.
Step 2: We identify a critical annulus \(B(a,\mu {\hat{\sigma }}_\xi )\setminus B(a,{\hat{\sigma }}_\xi )\) on which energy concentrates. Since there is a bounded number of \(x_j^\xi \), arguing as in [7, Lemma 2.1] one may find a constant \(\mu >1\) and radii \(\sigma _i^\xi \) such that
(and so \(\mu \sigma _{\ell -1}^\xi <\sigma _{\ell }^\xi \),) and such that each ball \(B({{x}}_i^\xi ,\lambda \xi )\) is contained either in \(B(a,\mu \sigma _0^\xi )\), or for some \(\ell \ge 1\), in the annulus \(B(a,\mu \sigma _{\ell }^\xi )\setminus B(a,\sigma _\ell ^\xi )\) for \(\ell \ge 1\). Inside each annulus \(A_\ell =B(a,\sigma _{\ell }^\xi )\setminus B(a,\mu \sigma _{\ell -1}^\xi )\) the map \(U_\xi \) is well defined and its homotopy class on \(C_s=\partial B(a,s)\) is constant for \(s\in [\mu \sigma _{\ell -1}^\xi ,\sigma _\ell ^\xi ]\). We will refer to this constant homotopy class as the homotopy class of \(U_\xi \) on the annulus \(A_\ell \). For \(\ell =L\) we know that \(U_\xi \) is non-orientable on \(A_L\).
We claim that there exists \(\ell _0\in \lbrace 1,\ldots ,L\rbrace \) such that \(U_\xi \) is orientable on \(A_\ell \). Otherwise, \(U_\xi \) is non-orientable on all annuli \(A_\ell \) which lie outside \(B(a,\mu \xi )\). Thus, flattening the boundary \(\partial {\widetilde{\Omega }}\) we may for small enough \(\delta \) apply Lemma 3.8 on each annulus. We deduce the lower bound
and this contradicts the upper bound obtained in Sect. 2.
Let us then fix the largest \(\ell _0\in \lbrace 1,\ldots ,L-1\rbrace \) such that \(U_\xi \) is orientable on \(A_\ell \), and set \({\hat{\sigma }}_\xi = \sigma _{\ell _0}^\xi \). In particular \(U_\xi \) is non-orientable on \(A_\ell \) for all \(\ell \ge \ell _0+1\), hence arguing as above we find the lower bound
Moreover, since \(U_\xi \) is orientable on \(\partial B(a,{\hat{\sigma }}_\xi )\) and non-orientable on \(\partial B(a,\mu {\hat{\sigma }}_\xi )\), there must be at least one \(x_j^\xi \) such that \(B(x_j^\xi ,\lambda \xi )\subset B(a,\mu {\hat{\sigma }}_\xi )\setminus B(a,{\hat{\sigma }}_\xi )\) and \(U_\xi \) is non-orientable on \(\partial B(x_j^\xi ,\lambda \xi )\).
Step 3: We show that a bad ball must be centered on the plane \(\{z=0\}\), and estimate its contribution to the energy. Now we consider only those \(x_j^\xi \) which are in \(B(a,\mu {\hat{\sigma }}_\xi )\setminus B(a,{\hat{\sigma }}_\xi )\). Considering the balls \(B(x_j^\xi ,c_0{\hat{\sigma }}_\xi )\) for some small enough \(c_0>0\) (depending only on the number of \(x_j^\xi \)’s) and applying the procedure in [9, Theorem IV.1], we obtain a bounded number \(c_0\le \gamma \le \frac{1}{16}\) and a collection of balls \(B(y_j^\xi ,\gamma {\hat{\sigma }}_\xi )\) satisfying the following:
Since all balls \(B(y_j^\xi ,2\gamma {\hat{\sigma }}_\xi )\) are contained in the annulus \(B(a,2\mu {\hat{\sigma }}_\xi )\setminus B(a,{\hat{\sigma }}_\xi /2)\) and for small enough \(\xi \) by the above \(U_\xi \) is non-orientable on \(\partial B(a,2\mu {\hat{\sigma }}_\xi )\) and orientable on \(\partial B(a,{\hat{\sigma }}_\xi /2)\), we deduce that \(U_\xi \) must be non-orientable on \(\partial B(y_j^\xi ,2\gamma {\hat{\sigma }}_\xi )\) for at least one \(y_j^\xi \). Relabeling we assume this is \(y_1^\xi \).
We may apply Lemma 3.7 to obtain a lower bound on the energy in \(B(y_1^\xi ,2\gamma {\hat{\sigma }}_\xi )\). This ball may happen to intersect \(\partial {\widetilde{\Omega }}\), but considering the fixed Lipschitz extension \(U_0\) of \({\widetilde{Q}}_\xi \) outside \({\widetilde{\Omega }}\) we still have the same lower bound.
Let us first assume that this \(y_1^\xi \) does not lie on the axis \(\lbrace z=0\rbrace \). Then, taking into account that \(\rho \ge 1-{\hat{\sigma }}_\xi ^2\) we obtain
By symmetry, if \(y_1^\xi \) lies above the axis \(\lbrace z=0\rbrace \) then the same lower bound will be obtained below the axis, so we deduce
Adding this to the lower bound (30) on \(B(a,\delta )\setminus B(a,2\mu {\hat{\sigma }}_\xi )\), we obtain
Since \({\hat{\sigma _\xi \rightarrow }} 0\) this contradicts the upper bound from Sect. 2.
Thus the point \(y_1^\xi \) must lie on the axis \(\lbrace z=0\rbrace \), hence \(\rho \ge 1+{\hat{\sigma }}_\xi /2\) on \(B(y_1^\xi ,2\gamma {\hat{\sigma }}_\xi )\), and applying Lemma 3.7 we have
Step 4: Completing the lower bound. Together with the lower bound (30) on \(B(a,\delta )\setminus B(a,2\mu {\hat{\sigma }}_\xi )\), this implies
Now notice that
is attained at \(\sigma =2/\ln (\frac{1}{\xi })\), so the above lower bound implies
This is the lower bound we have been after. Now recall we have been arguing on an arbitrary sequence \(\xi =\xi _n\rightarrow 0\) and taking subsequences, so what this proves is that for any \(\delta \in (0,\delta _0)\),
and this is part (ii) of Theorem 1.2. \(\square \)
Remark 3.10
In the above proof, we obtain lower bounds on \(B(a,\delta )\setminus B(a,2\mu {\hat{\sigma }}_\xi )\) and on \(B(y_1^\xi ,2\gamma {\hat{\sigma }}_\xi )\) and realize that their sum corresponds to the upper bound obtained in Sect. 2. Therefore in those sets the lower bounds must be sharp, in the sense that matching upper bounds are valid. In particular we have
and find ourselves in the situation of Lemma 3.9. As a consequence, a lower bound similar to the one in part (ii) of Theorem 1.2 is valid on the slightly smaller set
for any \(\lambda >0\) and \(\beta >1\). Combining this with the upper bound obtained in Sect. 2 then yields
4 Limit configuration
In this section we prove part (iii) of Theorem 1.2. Although in the previous sections we have already established tight upper and lower bounds on the energy away from the equator defect, extracting precise information about the structure of the minimizers and the absence of point singularities will be a multi-step process:
-
In § 4.1 we use standard arguments to establish strong \(H^1\) convergence away from the ring defect.
-
In § 4.2 we then establish the additional symmetry property that the director points inside the azimuthal plane (in the sense of Remark 1.3). The argument of [38] implies that as long as this symmetry is satisfied at the boundary, it should also be satisfied inside the domain. Applying this result in our context is however not straightforward: the limiting map is only minimizing away from the ring defect and it is necessary to cut out a small disc around the defect. The boundary conditions are not fixed there and they need to be carefully estimated using the rigidity imposed by the energy asymptotics (in the spirit of Lemma 3.9).
-
Finally, in § 4.3, we use an argument of [1] to rule out point defects which are not topologically necessary. That argument requires even more precise estimates on the boundary conditions. We can only rule out point defects provided that the ring defect is negatively charged—otherwise a positively charged ring defect would have to be compensated by a pair of point defects. The possibility of a positively charged ring defect is eventually eliminated by establishing that in a small region around the ring, it could not—compared to a negatively charged ring—improve the energy by more than o(1) as \(\xi \rightarrow 0\). Effectively, this amounts to showing that the core energy of a positively or negatively charged ring defect are the same.
4.1 Strong convergence
We start by establishing strong \(H^1\) convergence along a subsequence. The limiting maps \(Q\in {\mathcal {H}}_{sym}^\star \) will be minimizers of the harmonic map energy,
away from the singularity at the defect.
Lemma 4.1
There is a subsequence \(\xi \rightarrow 0\) and \(Q_\star \) such that for all \(\delta >0\), the sequence \(Q_\xi \) converges strongly in \(H^1_{loc}(\Omega ^{ext}_\delta )\) to \(Q_\star \in {\mathcal {H}}^\star _{sym}\) and
as \(\xi \rightarrow 0\). Moreover, in any relatively open subset \(U\subset {\overline{\Omega }}\) where \(Q_\star \) is smooth, we have \(Q_\xi \rightarrow Q_\star \) in \(C^{1,\alpha }_{loc}(U)\) for all \(\alpha \in (0,1)\).
Proof of Lemma 4.1
For any \(\delta >0\), the upper and lower bound imply
By a diagonal argument, this bound implies the existence a limit map \(Q_\star \in {\mathcal {H}}^\star _{sym}\) such that, up to a subsequence, \(Q_\xi \) converges weakly to \(Q_\star \) in \(H^1_{loc}(\Omega ^{ext}_\delta )\) for every \(\delta >0\). We denote by \(T_\delta \) the part of \(\partial \Omega ^{ext}_\delta \) that lies inside \(\Omega \), namely in cylindrical coordinates
By Fubini’s theorem we may (upon extracting a further subsequence) fix \(\delta \) arbitrarily small such that
In particular the trace of \(Q_\xi \) on \(T_\delta \) is bounded in \(H^1(T_\delta )\), and converges therefore also weakly in \(H^1(T_\delta )\). The map \(Q_\xi \) is of the form
and \({\widetilde{Q}}_\xi \) converges weakly in \(H^1_{loc}({\widetilde{\Omega }}^{ext}_\delta )\) and in \(H^1({\widetilde{T}}_\delta )\) to \({\widetilde{Q}}_\star \) such that
where as before, \({\widetilde{\Omega }}^{ext}_\delta \) and \({\widetilde{T}}_\delta \) denote the two-dimensional cross-sections of \(\Omega _\delta ^{ext}\) and \(T_\delta \) corresponding to the \((\rho ,z)\) coordinates. The limiting harmonic map energy is then expressed as
Consider a map \(Q_0\in {\mathcal {H}}_{sym}^\star (\Omega ^{ext}_\delta )\) satisfying
Since \({\widetilde{Q}}_\xi \) converges weakly in \(H^1({\widetilde{T}}_\delta )\) to \( ({\widetilde{Q}}_\star )_{\lfloor {\widetilde{T}}_\delta }=({\widetilde{Q}}_0)_{\lfloor {\widetilde{T}}_\delta }\) and \({\widetilde{T}}_\delta \) is a one-dimensional curve, on this curve \({\widetilde{Q}}_\xi \) converges to \({\widetilde{Q}}_0\) in \(C^{0,\alpha }(T_\delta )\) for any \(\alpha \in (0,1/2)\). We claim that this allows to construct a map \({{\overline{Q}}}_\xi \in {\mathcal {H}}_{sym}\) such that
In order to define \({{\overline{Q}}}_\xi \) in \(\Omega ^{ext}_\delta \) we introduce the cross-sectional domains
and
We use polar coordinates \((r,\theta )\) centered at \((\rho ,z)=(1,0)\). In these coordinates the domains D and \(D^{ext}_\delta \) are given by
Then, the desired map \({{\overline{Q}}}_\xi \) will have the form
and it suffices to define \({\widehat{Q}}_\xi \) in the domain \(D^{ext}_\delta \).
The standard idea is to introduce a thin slice \(\lbrace \delta< r<(1+\lambda )\delta \rbrace \) where we interpolate from \({\widehat{Q}}_\xi ={\widetilde{Q}}_\xi \) at \(r=\delta \) to \({\widehat{Q}}_\xi ={\widetilde{Q}}_0\) at \(r=(1+\lambda )\delta \), and choose \(\lambda \) in order that the energy of \({\widehat{Q}}_\xi \) in that thin slice be negligible. Then we extend by \({\widetilde{Q}}_0\) (slightly rescaled) in \(D_{(1+\lambda )\delta }\). Here, however, we need to be more careful because we have to preserve the boundary condition at \(\rho ^2+z^2=1\), i.e., in polar coordinates at \(\theta =\theta _0(r)=\frac{\pi }{2}+\arcsin \frac{r}{2}\). Hence we interpolate instead in a deformed slice \(S_\lambda \) of the form
for some \(\lambda >0\) to be chosen later. Next we define \({\widehat{Q}}_\xi \) in the deformed slice \(S_\lambda \). As noted in [15, Lemma B.2], with a simple linear interpolation we might fail at controlling the potential part of the energy \(\int f({\widehat{Q}}_\xi )\), and we need to proceed in two steps as in [15], namely first interpolate linearly between \({\widetilde{Q}}_\xi \) and its projection \(\pi ({\widetilde{Q}}_\xi )\) onto \({\mathcal {U}}_\star \), and then interpolate geodesically between \(\pi ({\widetilde{Q}}_\xi )\) and \({\widetilde{Q}}_0\) inside \({\mathcal {U}}_\star \). To this end we denote by
the smooth map such that \(t\mapsto \gamma (t;U_1,U_2)\) is the constant speed geodesic from \(U_1\) to \(U_2\) in \({\mathcal {U}}_\star \), which is indeed unique, well-defined and depends smoothly on \(U_1,U_2\) provided \(U_1,U_2\) are close enough to each other. This map satisfies the bounds
In \(S_\lambda \) we define
Note that \(\pi ({\widetilde{Q}}_\xi (\delta ,\theta ))\) is well-defined for small \(\xi \) because \({\widetilde{Q}}_\xi \) converges uniformly to \({\widetilde{Q}}_0\) on \({\widetilde{T}}_\delta \). Direct computations then show that
Next, we denote by \(\sigma =\sigma (\xi )\) the quantity
and notice that since the boundary conditions on \(\rho ^2+z^2=1\) ensure that \({\widetilde{Q}}_\xi (\delta ,\theta _0(r))={\widetilde{Q}}_0(\delta , \theta _0(r))\), we have
Therefore, the above estimates on the derivatives of \({\widehat{Q}}\) imply
and
For the last inequality we used the fact that, thanks to (31), the \(L^2\) norms of \(\partial _\theta {\widetilde{Q}}_\xi (\delta ,\theta )\) and \(\partial _\theta {\widetilde{Q}}_0(\delta ,\theta )\) are bounded for \(\delta \) fixed. Note moreover that the definition of \({\widehat{Q}}\) ensures that
thanks to the nonegeneracy property (17) of the potential f. Using this pointwise inequality and (31) we infer that
Finally, since \(\rho \approx 1\) and \(\Xi [{\widehat{Q}}]\lesssim 1\) in \(S_\lambda \) we deduce from the above that
Choosing \(\lambda =\sigma \) then implies that
Next we define \({\widehat{Q}}_\xi \) in \(D^{ext}_\delta \setminus S_\lambda \) by setting
Then we have
as \(\xi \rightarrow 0\), since \(\lambda =\sigma \rightarrow 0\). Combining this and the fact that \({\widetilde{E}}_\xi ({\widehat{Q}}_\xi ;S_\lambda )\rightarrow 0\), we deduce that
which implies the desired estimate (33). By minimality of \(Q_\xi \) we then have
and by lower semicontinuity we deduce
It follows that \(Q_\star \) minimizes \(E_\star (\cdot ;\Omega ^{ext}_\delta )\) among all maps \(Q\in {\mathcal {H}}^\star _{sym}(\Omega ^{ext}_\delta )\) such that \(Q=Q_\star \) on \(T_\delta \), and that all above inequalities are in fact equalities. Thus we have
In particular, together with the weak convergence, this implies that \(\nabla Q_\xi \) converges strongly in \(L^2(\Omega ^{ext}_\delta )\) towards \(\nabla Q_\star \), that is, the convergence is in fact strong.
The local \(C^{1,\alpha }\) convergence away from singularities follows from the analysis in [33, 35]. There the authors consider minimizers which are not subject to the constraint of axial symmetry, but they only use the minimizing property to obtain the strong \(H^1\) convergence, which we have just obtained. A close reading of their results reveals that the steps leading to \(C^{1,\alpha }\) convergence apply equally well for smooth critical points, as are \(Q_\xi \). (See Lemma 3.1.)
\(\square \)
4.2 Reduction to a director in a cross-section
The limiting Q-tensor \(Q_*\) inherits the symmetries (8) of the space \({\mathcal {H}}_{sym}\), but it also exhibits further symmetry by virtue of energy minimization. Here we show that the map \(Q_\star \) may be represented by a uniaxial tensor with a unit director field \(n=(n_1(\rho ,z),0,n_3(\rho ,z))\), expressed in cylindrical coordinates in a cross-section of \(\Omega \).
In the sequel, whenever we refer to \(\xi \rightarrow 0\), we will always mean convergence along the subsequence obtained in Lemma 4.1.
Since the limit \(Q_\star \) is symmetric, it is characterized by a map defined in the two-dimensional domain D. To describe \(Q_\star \) further, it will also be convenient to introduce the following notations:
where \(D^{ext}_\delta \) is defined in (34). The symmetry and minimizing property of \(Q_\star \) allow us to express it in terms of a map n which minimizes \({\hat{E}}\) in \(\hat{{\mathcal {H}}}\). Specifically, we have:
Lemma 4.2
The map \(Q_\star \) is given in cylindrical coordinates by
where \(n\in H^1_{loc}({\widetilde{\Omega }})\) satisfies \(n(\rho ,-z)=-Sn(\rho ,z)\) and, when restricted to \(\lbrace z>0\rbrace \), \(n\in \hat{{\mathcal {H}}}\) minimizes \({\hat{E}}(\cdot ;D^{ext}_\delta )\) for all \(\delta >0\), among all maps \(m\in \hat{{\mathcal {H}}}(D^{ext}_\delta )\) such that \(m\otimes m=n\otimes n\) on \(\partial D^{ext}_\delta \cap D\).
Moreover, up to replacing n by \(-n\), we have
for some \(\tau \in \lbrace \pm 1\rbrace \).
Proof (Proof of Lemma 4.2)
Since \(\Omega ^{ext}_\delta \) is simply connected, \(Q_\star \) can be lifted [5, 10]: there exists a map \(n_\star \in H^1_{loc}(\Omega ;{\mathbb {S}}^2)\) such that
As \({\vert \nabla Q_\star \vert }^2=2{\vert \nabla n_\star \vert }^2\), the symmetry of \(Q_\star \) implies that \(n(\rho ,z)= n_\star (\rho ,0,z)\) belongs to \(H^1_{loc}({\widetilde{\Omega }}^{ext}_\delta )\), and we have
Since \(Q_\star \) is minimizing in \({\mathcal {H}}_{sym}^\star (\Omega ^{ext}_\delta )\), we deduce that n minimizes \({\hat{E}}(\cdot ;D^{ext}_\delta )\) among maps \(m:D^{ext}_\delta \rightarrow {\mathbb {S}}^2\) satisfying the boundary conditions
Note that \({\vert m\otimes m-e_3\otimes e_3\vert }^2=2(m_1^2+m_2^2)\), so that the far-field condition which requires \(\int {\vert Q-Q_\infty \vert }^2{\vert x\vert }^{-2}<\infty \) is obsolete here: any map m with finite energy satisfies
The boundary condition on \(\lbrace z=0\rbrace \) comes from the requirement that \(m\otimes m\) can be extended to an \(H^1\) map in \({\widetilde{\Omega }}^{ext}_\delta \) via the mirror symmetry. It is equivalent to \(m_3(\rho ,0)\in \lbrace 0,\pm 1\rbrace \) for almost all \(\rho >1+\delta \). Since the trace \(\rho \mapsto m_3(\rho ,0)\) has \(H^{1/2}_{loc}\) regularity, being integer valued it has to be constant: there exists \(\tau \in \lbrace 0,\pm 1\rbrace \) such that \(m_3(\rho ,0)=\tau \) for almost all \(\rho >1+\delta \). One can rule out \(\tau =0\). Indeed, assume by contradiction that \(\tau =0\), i.e. \(m_3(\rho ,0)=0\). Then we have
and therefore, for almost all \(z_0>0\),
This clearly contradicts the finiteness of \(\int (m_1^2+m_2^2)/\rho \, d\rho dz\). We deduce that \(\tau =\pm 1\), that is,
so that \(m\in \hat{{\mathcal {H}}}(D^{ext}_\delta )\) and, as a consequence, n minimizes \({\hat{E}}(\cdot ;D^{ext}_\delta )\) in \(\hat{{\mathcal {H}}}(D^{ext}_\delta )\) for all \(\delta >0\) with respect to its own boundary conditions on \(\partial D^{ext}_\delta \cap D\).
Moreover, the boundary conditions on \(\partial D^{ext}_\delta \cap \lbrace \rho ^2+z^2=1\rbrace \) require that the \(H^{1/2}\) trace \(n\cdot e_r\) take values into \(\lbrace \pm 1\rbrace \) and thus be constant. Then, up to changing n to \(-n\) and \(\tau \) to \(-\tau \), one obtains the boundary conditions (37).
It remains to show that \(n(\rho ,-z)=-Sn(\rho ,z)\). The mirror symmetry implies that \(n(\rho ,-z)=\pm S n(\rho ,z)\), and therefore the \(H^1\) function \(n(\rho ,-z)\cdot Sn(\rho ,z)\) takes values into \(\lbrace \pm 1\rbrace \) and must be constant. By the above, its trace on \(\lbrace z=0\rbrace \) is equal to \(\tau ^2 e_3 \cdot (-e_3)=-1\). We conclude that \(n(\rho ,-z)=-Sn(\rho ,z)\). \(\square \)
Next we turn to proving the additional symmetry property \(n_2\equiv 0\). The idea is that the use of an appropriate comparison map as in [38] implies that symmetry provided it is satisfied at the boundary. But we can only use energy comparison in \(D^{ext}_\delta \), and then we actually do not know that \(n_2=0\) on the whole boundary, due to the undetermined part \(\partial D^{ext}_\delta \cap D\). This will make the proof quite technical.
To gather more information about the behavior of n on \(\partial D^{ext}_\delta \cap D\), it is natural to use polar coordinates \((r,\theta )\) around \((\rho =1,z=0)\), so that \(\partial D^{ext}_\delta \cap D\) corresponds to fixing \(r=\delta \). In those coordinates, the domain D is given by \(0<\theta <\theta _0(r)\), where \(\theta _0(r)\) is defined in (35). The upper and lower bound, together with strong \(H^1\) convergence, provide the estimate
which for \(n(\rho ,z)\) translates into
In coordinates \((r,\theta )\) this implies
For \(r<\sqrt{2}\), the boundary conditions (37) become
and \(n(r,0)=\tau e_3\). Here, recall (13) that \(\theta _0(r)=\pi /2 + O(r)\) and so \(\theta _1(r)=O(r)\). Remarking (as in Lemma 3.9) that we also have the lower bound
from (38) we deduce
Finiteness of the first integral in (40) tells us that \(\int _0^{\theta _0}|\partial _\theta n|^2d\theta \) is close to the length of the geodesic from n(r, 0) to \(n(r,\theta _0)\) in \({\mathbb {S}}^2\), as this length is \({\vert \tau \pi /2-\theta _1\vert }=\pi / 2 +O(r)\). This implies that n must be close to the actual geodesic, thanks to the following stability estimate for geodesics of length \(\ell <\pi \) on \({\mathbb {S}}^2\).
Lemma 4.3
Let \(\ell \in (0,\pi )\) and \(m_0:[0,\ell ]\rightarrow {\mathbb {S}}^2\) be a geodesic on \({\mathbb {S}}^2\) parametrized with unit speed \(|m_0'|=1\). Then for any \(m\in H^1((0,\ell );{\mathbb {S}}^2)\) such that \(m(0)=m_0(0)\) and \(m(\ell )=m_0(\ell )\), we have
Proof of Lemma 4.3
Using that \(m_0-m\) vanishes at 0 and \(\ell \) we obtain
Note that the geodesic \(m_0\) is smooth and satisfies \(m_0''=-m_0\). Moreover we know that \(m_0-m\) vanishes at 0 and \(\ell \), so integrating by parts in the last term we obtain
Remarking that \(|m -m_0|^2=2-2m_0\cdot m\) we have
by Poincaré inequality, since the lowest positive eigenvalue of the Dirichlet Laplacian on \((0,\ell )\) corresponds to the eigenfunction \(\theta \mapsto \sin (\pi \theta /\ell )\) and is therefore equal to \(\pi ^2/\ell ^2\). Hence we can absorb the last term of (41) into the left-hand side to conclude the proof. \(\square \)
We now define \(m_0:D_1^{int}\rightarrow {\mathbb {S}}^2\) such that for all \(r\in (0,1)\), the map \((0,\theta _0(r))\ni \theta \mapsto m_0(r,\theta )\) is a constant speed geodesic from n(r, 0) to \(n(r,\theta _0(r))\), that is,
Note that \(m_0(r,\cdot )\) is a geodesic of speed \(1+O(r)\) and of length \(\pi /2+O(r)\), so applying Lemma 4.3 to appropriately rescaled versions of \(n(r,\cdot )\) and \(m_0(r,\cdot )\) and invoking (40) we deduce
We are now ready to prove:
Proposition 4.4
We have \(n_2\equiv 0\) in D.
Proof of Proposition 4.4
The starting idea is to use as a comparison map
which has lower energy than n since \(n_1^2+n_2^2={\tilde{n}}_1^2+ {\tilde{n}}_2^2\) and
and to conclude that \(n_2=0\). One just needs to take care of technical difficulties that arise due to the undetermined part of the boundary \(\partial D^{ext}_\delta \cap D\): there, one does not know that \(n_2=0\) and \(n_1\ge 0\), hence \({\tilde{n}}\) cannot be used directly as a comparison map. One does know however thanks to (42) that n is very close to a map satisfying these conditions: (42) implies that the quantity
tends to 0 along a subsequence \(\delta =\delta _k\rightarrow 0\). This readily provides some uniform control on \(n(\delta ,\cdot )-{\tilde{n}}(\delta ,\cdot )\), since by Morrey’s inequality we have
Using that \(m_0={\tilde{m}}_0\) and that the transformation \(n\mapsto {\tilde{n}}\) is Lipschitz, this implies
Next we define a good comparison map \({\bar{n}}\) in \(D_{\delta }^{ext}\). In \(D_{2\delta }^{ext}\) we simply set
and it remains to construct a well-behaved transition layer in \(D_\delta ^{ext}\setminus D_{2\delta }^{ext}\). In polar coordinates \((r,\theta )\), the domain \(D_\delta ^{ext}\setminus D_{2\delta }^{ext}\) is given by \(\delta \le r <2\delta \), \(0<\theta < \theta _0(r)\), and we want to define \({\bar{n}}\) such that \({\bar{n}}=n\) for \(r=\delta \), \({\bar{n}}={\tilde{n}}\) for \(r=2\delta \), and \({\bar{n}}=n={\tilde{n}}\) for \(\theta \in \lbrace 0,\theta _0(r)\rbrace \). To this end we introduce a small parameter \({\hat{\lambda \in }} (0,1/2)\), to be fixed later, and proceed similarly to the construction in the proof of Lemma 4.1. Namely, we interpolate between \(n(\delta ,\cdot )\) and \({\tilde{n}}(\delta ,\cdot )\) in a thin slice \(\delta \le r < (1+{\hat{\lambda }})\delta \), and then slightly rescale \({\tilde{n}}\) in the remaining part \((1+{\hat{\lambda }})\delta \le r <2\delta \). As in Lemma 4.1, this simple picture actually requires a small modification to accomodate the non-constant boundary condition at \(\theta =\theta _0(r)\). To do this, we first define
and partition \(D_\delta ^{ext}\setminus D_{2\delta }^{ext}\) as
Then we set
where \(\pi _{{\mathbb {S}}^2}\) denotes the nearest point projection onto \({\mathbb {S}}^2\), which is well-defined and Lipschitz thanks to the uniform estimate (44) on \(n(\delta ,\cdot )-{\tilde{n}}(\delta ,\cdot )\). With that definition, the map \({\bar{n}}:D_\delta ^{ext}\rightarrow {\mathbb {S}}^2\) agrees with n on \(\partial D_{\delta }^{ext}\) and from the minimizing property of n we have
In order to make use of that inequality, we need to estimate the energy of \({\bar{n}}\) in the transition layer \(D_\delta ^{ext}\setminus D_{2\delta }^{ext}\). We start by estimating the energy in \(R_1\). Recalling the definition of \({\tilde{\lambda }}\) in (45), by direct calculation we have
so, taking into account that \(\int _\delta ^{(1+{\tilde{\lambda }})\delta }r^{-2}\, rdr =\ln (1+{\tilde{\lambda }})\lesssim {\tilde{\lambda }}\) and \(|\partial _\theta {\tilde{n}}|\le |\partial _\theta n|\), we deduce
Using the uniform estimate (44) on \(n(\delta ,\cdot )-{\tilde{n}}(\delta ,\cdot )\) to bound the last term, this implies
Appealing to the facts that \(\sigma ^2=\int _0^{\theta _0}|\partial _\theta n-\partial _\theta m_0|^2\,d\theta \ll 1 \) and \(|\partial _\theta m_0|\lesssim 1\) to bound the first term in the right-hand side, we obtain
From the definition (36) of the energy
and taking into account that \(\rho =1+r\cos \theta =1+O(\delta )\) in \(R_1\), we deduce
Next we turn to estimating the energy in \(R_2\). Direct calculation gives
where it is implicitly understood that all derivatives of \({\tilde{n}}\) appearing in the right-hand sides are evaluated at \(\left( \delta + \frac{r-(1+{\tilde{\lambda }}(\theta ))\delta }{1-{\tilde{\lambda }}(\theta )},\theta \right) \). Integrating and changing variables we deduce
Note that
where we used the fact that \(|\partial _\theta m_0|\lesssim 1\). Therefore, recalling that the two last integrals are finite thanks to (40) and (42), we obtain
The second term in the energy (36) can be estimated in a similar way, so that
Combining this with (47), the estimate on the energy of the transition layer \(D_{\delta }^{ext}\setminus D_{2\delta }^{ext}\) becomes
Choosing \({\hat{\lambda }}=\sigma \), the right-hand side is \(\lesssim \sigma \ll 1\). From the minimizing property (46) of n we thus obtain
Since \(\sigma =\sigma (\delta _k)\rightarrow 0\) as \(\delta =\delta _k\rightarrow 0\), and \({\vert \nabla {\tilde{n}}\vert }\le {\vert \nabla n\vert }\) in D, we deduce that we have in fact \({\vert \nabla {\tilde{n}}\vert }={\vert \nabla n\vert }\) in D, which implies
In particular, for any fixed \(\rho ,z>0\) with \(\rho ^2+z^2=1\), the map \(m:t\mapsto (n_1,n_2)(t\rho ,tz)\) satisfies \(m \wedge \dot{m} =0\), and thus \(\dot{m}= \alpha m\), where \(\alpha =(m\cdot \dot{m}) / {\vert m\vert }^2\) is continuous on \([1,\infty )\) because \({\vert m\vert }^2\) does not vanish there. Since \(m_2(1)=0\) this implies that \(m_2(t)=0\) for all \(t\ge 1\), hence \(n_2\equiv 0\) in D. \(\square \)
Thanks to Proposition 4.4, we can apply the regularity results on symmetric harmonic maps in [25] to deduce that \(n_\star \) is analytic in \({\overline{\Omega }}\setminus ( {\mathcal {C}} \cup Z)\), where \(Z\subset \Omega \cap \lbrace \rho =0\rbrace \) is a discrete set of singular points on the vertical axis. By Lemma 4.1 we therefore have \(Q_\xi \rightarrow Q_\star \) in \(C_{loc}^{1,\alpha }({\overline{\Omega }}\setminus ({\mathcal {C}}\cup Z))\).
4.3 The absence of point defects
To conclude the proof of Theorem 1.2 (iii) it remains to show that Z is empty. The starting idea is to try and apply the argument of [1, Theorem 13] (using reflections of the image in \({\mathbb {S}}^2\) and analyticity) to eliminate all point defects that are not required by topology. If the defect ring is negatively charged, that is \(\tau =+1\) in Lemma 4.2, this argument may be applied to eliminate all point defects, and we carry out this analysis in § 4.3.1. However, if the ring happens to be positively charged—corresponding to \(\tau =-1\)—then an additional pair of point defects would be required. To complete the proof we therefore need to show that the case \(\tau =-1\) can not occur, and this is demonstrated in § 4.3.2.
4.3.1 The case of a negatively charged ring \(\tau =+1\)
The argument of [1, Theorem 13] used to eliminate extraneous point defects relies on the construction of comparison maps, and thus we again face the sticky issue of controlling the boundary conditions on \(\partial D^{ext}_\delta \cap D\). Specifically, we need to know that \(n_3\) does not change sign on that boundary part, and our first step is therefore to gather stronger information about the trace of n there.
Lemma 4.5
There exists \(r_n\rightarrow 0\) such that \(\theta \mapsto n_3(r_n,\theta )\) is strictly monotone on \([0,\theta _0(r_n)]\).
Proof of Lemma 4.5
Since D is simply connected, there exists a lifting \(\varphi \in H^1_{loc}(D;{\mathbb {R}})\) such that
This lifting \(\varphi \) is in fact smooth up to the boundary of D, except at points of the singular set Z and at \((\rho ,z)=(1,0)\). It is defined up to a constant multiple of \(2\pi \), that one may fix by imposing \(\varphi (r,\theta _0(r))=\theta _1(r)\), where we recall the definition (39) of \(\theta _1(r)\). For \(\theta =0\) we then have \(\varphi \equiv \tau \pi /2 + 2N\pi \) for some \(N\in {\mathbb {Z}}\). This implies
Recalling (40), we deduce that necessarily \(N=0\).
Moreover, the estimate (42) suggests that for small \(r>0\), n is close to the map
and hence we expect the same behavior for its lifting, \(\varphi \). More precisely, we have
and since \(\varphi =\tau \varphi _0+O(r)\) at \(\theta =0\) and \(\theta =\theta _0(r)\), together with (40) this shows that
In particular, there are arbitrarily small \(\delta \)’s such that n is very close to \(n_0\) on \(\partial D^{ext}_\delta \cap D\), in \(H^1\) and thus also in \(L^\infty \). Using the equation satisfied by \(\varphi \) one can obtain a stronger estimate. Since \(\varphi \) minimizes
it solves the Euler Lagrange equation
Using also \(\Delta \varphi _0=0\), rescaled elliptic estimates enable us to obtain a stronger control on \(\varphi -\tau \varphi _0\) in the annular domain
Specifically, elliptic estimates in the rescaled domain \(\lambda ^{-1}A_\lambda \) (which is Lipschitz independently of \(\lambda \)) give control on the following scale invariant quantity:
Hence from (49) we deduce
and there exists \(\lambda _n\rightarrow 0\) such that \(g(\lambda _n)\rightarrow 0\). Moreover, by Sobolev embedding, we have
thus we may find \(r_n\in [\lambda _n/2,2\lambda _n]\) such that
Since \(\partial _\theta \varphi _0=-1\), this implies in particular that \(\varphi (r_n,\cdot )\) is strictly monotone for n large enough. \(\square \)
Equipped with Lemma 4.5, we are now in a position to apply an argument similar to the one in [1, Theorem 13]. It enables us to conclude that Z is empty if \(\tau =+1\):
Corollary 4.6
The set of singular points \(Z\cap \lbrace z>1\rbrace \) is empty if \(\tau =1\).
Proof of Corollary 4.6
Assume that \(\tau =+1\). Take \(\delta =r_n\) provided by Lemma 4.5. Then \(n_3>0\) on \(\partial D^{ext}_\delta \cap \lbrace \rho >0\rbrace \). Therefore, the map \({\tilde{n}} =(n_1,n_2,{\vert n_3\vert })\) is an admissible comparison map in \(D^{ext}_\delta \) and has the same energy as n, hence is a minimizer and must be analytic inside \(D^{ext}_\delta \). This implies that \(n_3\ge 0\) inside \(D^{ext}_\delta \). Since Z corresponds to changes of sign of \(n_3\), we deduce that \(Z=\emptyset \). \(\square \)
4.3.2 Ruling out the case of a positively charged ring \(\tau =-1\)
The end of the proof will consist in ruling out the case \(\tau =-1\). This is the most delicate part of the argument, and it has two main steps:
-
In the first step we consider the complement of a small region around the ring defect, and show that the energy cost of a point defect away from this neighborhood is a strictly positive quantity of order O(1). This is done in Lemma 4.8, using a variation of the argument already used in Corollary 4.6, but with more precise boundary estimates.
-
In the second step we derive a more precise estimate of the energy concentrated in a small region around the ring defect, in order to conclude that the O(1) increase obtained in the first step (away from the ring defect) leads to a strict increase of the total energy. Specifically we show that the core energy of the ring defect is independent of the ring’s charge, up to an error of smaller order. To this end, we construct (in Lemma 4.10) a comparison map which modifies boundary values in a singular region between the particle and a curve tangent to it; the error thus introduced can be controlled thanks to Lemma 3.9.
For later use, we derive the following useful estimates, based on those established in the proof of Lemma 4.5; recall \(n=(\cos \varphi ,0,\sin \varphi )\), and \(\varphi _0=\frac{\pi }{2}-\theta \) (the lifting of the comparison map \(n_0\)). Then:
Lemma 4.7
As \(\delta \rightarrow 0\), we have
where \(D^{int}_\delta =D\setminus D^{ext}_\delta =\{(\rho ,z)\in D: \ (\rho -1)^2 + z^2\le \delta ^2\}\).
That is, as we approach the ring defect, the director n resembles \( (\tau \sin \theta ,0,\cos \theta )\), a symmetric vortex of degree \(-\tau /2\).
Proof of Lemma 4.7
It is shown in Lemma 4.5 that
satisfies
We may thus pick \(\lambda _n\in [1/2,1]\) such that
Since \(A_{(2^{-n-1}\lambda _{n+1})}\) overlaps with \(A_{(2^{-n}\lambda _n)}\), we deduce that
as \(N\rightarrow \infty \). \(\square \)
In order to rule out the case \(\tau =-1\), we wish to estimate the difference of total energy between the two cases \(\tau =\pm 1\). To this end, we recall the definition (39) of \(\theta _0(r)\) and \(\theta _1(r)\) in representing the boundary condition on the colloid, and introduce the notation:
Note that \(\phi _0^\tau \) is the phase corresponding to the constant speed geodesic \(m_0\) used in the proof of Lemma 4.4. Then we compare \({\mathbb {E}}^+[\delta ]\) and \({\mathbb {E}}^-[\delta ]\) for small \(\delta \):
Lemma 4.8
we have
Proof (Proof of Lemma 4.8)
We denote by \(\varphi _\delta ^\tau \) the minimizer in \({\mathbb {E}}^\tau [\delta ]\). We claim the following upper bound holds:
Indeed, using a comparison function \({\tilde{\varphi }}\) satisfying
and any admissible Lipschitz extension in the region \(\sqrt{2} \le r \le 2\sqrt{2}\), we find on the one hand the upper bound
On the other hand, for \(0<\delta \le \eta \le \sqrt{2}\), the boundary conditions enforce the lower bound
which, together with the previous upper bound, implies (52). Arguing as in Lemma 4.1 we thus have, up to extracting a further subsequence, a limit \(\varphi _\delta ^\tau \rightarrow \varphi ^\tau \) in \(H^1_{loc}(D)\) as \(\delta \rightarrow 0\), and \(F(\varphi _\delta ^\tau ;D^{ext}_\eta )\rightarrow F(\varphi ^\tau ;D^{ext}_\eta )\) for all \(\eta >0\). The function \(\varphi ^\tau \) satisfies the boundary conditions
and minimizes \(F(\cdot ;D^{ext}_\eta )\) among functions that agree with \(\varphi ^\tau \) on \(\partial D^{ext}_\eta \cap \lbrace \rho >0\rbrace \), for all \(\eta >0\). The arguments in Lemma 4.5 and in Lemma 4.7 carry over, and we find that \(\varphi ^\tau \) is analytic in \({{\overline{D}}} \setminus (Z\cup \lbrace (1,0)\rbrace )\), where \(Z=\emptyset \) if \(\tau =+1\), and \(Z=\lbrace (0,z_0)\rbrace \) for some \(z_0>0\) if \(\tau =-1\). Moreover we have
We set \(\psi = {\vert \varphi ^-\vert }\), so that
for all \(\delta >0\). Next, from the estimates for \(\varphi ^-\) and easy estimates on \(({\vert \varphi _0\vert }-\varphi _0)\) and \((\varphi _0-\phi _0^+)\) we deduce that
Also note that, since \(\varphi ^-\) changes sign at one point of \(\partial D^{ext}_\delta \cap D\) for small enough \(\delta \), \(\psi \) can not be locally analytic inside \(D^{ext}_\delta \). In particular, it is certainly not a minimizer of \(F(\cdot ;D^{ext}_\delta )\) for any \(\delta \) small enough. Therefore, for some small fixed \(\delta _0\) there exists a function \(\xi \) such that \(\xi =\psi \) on \(\partial D^{ext}_{\delta _0}\cap \lbrace \rho >0\rbrace \), and
Let \(\eta <\delta _0/2\). Consistently with its boundary conditions, we may extend \(\xi \) to D by setting
Next we introduce a modified function \(\xi _\eta \) given by
so that \(\xi _\eta =\xi \) in \(D^{ext}_{2\eta }\), \(\xi _\eta =\varphi _\eta ^+\) on \(\partial D^{ext}_\eta \cap \lbrace \rho >0\rbrace \), and
Thanks to (53), we therefore have a function \(R(\eta )\) which tends to zero as \(\eta \rightarrow 0\), such that
The last inequality holds by definition of \({\mathbb {E}}^+\) because \(\xi _\eta =\varphi _\eta ^+\) on \(\partial D^{ext}_\eta \cap \lbrace \rho >0\rbrace \). Recalling the definition of \({\mathbb {E}}^-\) and taking the limit as \(\eta \rightarrow 0\), we find
The lemma will be proven once we show that
To this end we may, consistently with its boundary conditions, extend \(\varphi _\eta ^-\) to D by setting
We also introduce a parameter \(\nu <\eta /2\). We have
where
Next we modify \(\varphi _\eta ^-\) in order to use the minimizing property of \(\varphi ^-\) in \(D^{ext}_\nu \). Similarly to the above definition of \(\xi _\eta \), we set
so that \({\tilde{\varphi }}_\nu =\varphi _\eta ^-\) in \(D^{ext}_{2\nu }\), and \({\tilde{\varphi }}_\nu =\varphi ^-\) on \(\partial D^{ext}_\nu \cap \lbrace \rho >0\rbrace \). Moreover, since \(\varphi _\eta ^-=\phi _0^-\) in \(D^{int}_{2\nu }\), we have
We deduce
The last inequality holds because \({\tilde{\varphi }}_\nu =\varphi ^-\) on \(\partial D^{ext}_\nu \cap \lbrace \rho >0\rbrace \) and \(\varphi ^-\) is minimizing in \(D^{ext}_\nu \). This obviously implies (54). \(\square \)
We would like to use Lemma 4.8 to show that \(\tau \) must be \(+1\). From now on we assume that \(\tau =-1\). We will then construct a map \(P_\xi \in {\mathcal {H}}_{sym}\) with lower energy than \(Q_\xi \), hence contradicting the minimality of \(Q_\xi \) and proving that \(\tau =+1\) and \(Z=\emptyset \). We introduce the notations
where \(\varphi _\delta ^\pm \) are the minimizers corresponding to the minimization problems \({\mathbb {E}}^\pm [\delta ]\). Note in particular that \(n_\delta ^\pm =n_0^\pm \) for \(r=\delta \).
First we show that we may, without messing too much with the energy of \({\widetilde{Q}}_\xi \) inside \(D^{int}_\delta \), replace it with a map that equals \((n_0^-\otimes n_0^--\frac{1}{3} I)\) on \(D\cap \partial D^{ext}_\delta \).
Lemma 4.9
Consider \({\widetilde{R}}_\xi :D^{int}_{\delta }\rightarrow {\mathcal {S}}_0\) minimizing \({\widetilde{E}}_\xi (\cdot ;D^{int}_\delta )\) among all maps R with the boundary constraints
Then we have that
where \(\zeta _1(\delta )\rightarrow 0\) as \(\delta \rightarrow 0\), and \(\sigma _1(\delta ,\xi )\rightarrow 0\) as \(\xi \rightarrow 0\) for all fixed \(\delta >0\).
Proof of Lemma 4.9
We construct a test configuration \(R_\xi \) in \(D^{int}_{\delta }\) and evaluate its energy \({\widetilde{E}}_\xi \). We systematically denote by \(\sigma (\delta ,\xi )\) (resp. \(\zeta (\delta )\)) functions that tend to 0 as \(\xi \rightarrow 0\) for any fixed \(\delta \) (resp. \(\delta \rightarrow 0\)), although they may change from one line to another.
By Fubini’s theorem, we may choose \({\hat{\delta \in }} (\frac{\delta }{4},\frac{\delta }{3})\) such that (possibly along a subsequence)
Arguing exactly as in the proof of (33) in Lemma 4.1, this enables us to construct \(R_\xi \) in \(D^{ext}_{{\hat{\delta }}}\setminus D^{ext}_{\delta /2}\) such that \(R_\xi \) satisfies the boundary conditions of \({\widetilde{R}}_\xi \) for \(z=0\) and \(\rho ^2+z^2=1\), and
for any fixed \(\delta \). In \(D^{int}_{{\hat{\delta }}}\) we set \(R_\xi ={\widetilde{Q}}_\xi \), so that the above estimate combined with Lemma 4.1 implies
Finally, we interpolate in \({\mathcal {U}}_\star \) between \({\widetilde{Q}}_\star =n\otimes n-\frac{1}{3} I\) and \(Q_0^-:=n_0^-\otimes n_0^- -\frac{1}{3} I\) to define \(R_\xi \) in the remaining region \(D^{ext}_{\delta /2}\setminus D^{ext}_{\delta }\). This we do via the phase variables \(\varphi \) and \(\phi _0^-\) which satisfy \(n=(\cos \varphi ,0,\sin \varphi )\) and \(n_0^-=(\cos \phi _0^-,0,\sin \phi _0^-)\): we set
This defines a director \({\hat{n}}:= (\cos {\hat{\phi }}, 0, \sin {\hat{\phi }})\) and an associated uniaxial Q-tensor \(R_\xi ={\hat{n}}\otimes {\hat{n}} -\frac{1}{3} I\). In this way, \(R_\xi \) will be continuous in \(D^{int}_\delta \) and satisfy each of the desired conditions on \(\partial (D^{int}_\delta )\). As \(R_\xi \in {\mathcal {U}}_\star \) in this region, \(f(R_\xi )=0\) and moreover,
Thanks to Lemma 4.7 and the explicit form of \(\varphi _0\) (48) and \(\phi _0^-\) (51), we have
and use this fact to estimate the energy of \(R_\xi \) in \(D^{ext}_{\delta /2}\setminus D^{ext}_{\delta }\). For instance, we have
and similarly,
The estimate (55) ensures that the bracketed terms on the right-hand side of each of the above equations tend to zero in \(L^2(D^{ext}_{\delta /2}\setminus D^{ext}_{\delta })\) as \(\delta \rightarrow 0\). As a consequence we have
where \(\zeta (\delta )\rightarrow 0\) as \(\delta \rightarrow 0\), and we used again (55) for the last inequality. As
we deduce that
Finally,
by Lemma 4.1. Combined with the above estimate in \(D^{int}_{\delta /2}\) this yields
and since \({\widetilde{R}}_\xi \) minimizes \({\widetilde{E}}_\xi \) with the same boundary conditions as \(R_\xi \) this completes the proof of Lemma 4.9. \(\square \)
The final step consists in proving that we may “transform” the boundary conditions on \(D\cap \partial D^{ext}_\delta \) from \(n_0^-\) to \(n_0^+\) without increasing the energy too much. This establishes the crucial core energy estimate mentioned in the Introduction: that the energy of a positively or negatively charged line defect is the same up to o(1).
Lemma 4.10
Consider \({\widetilde{P}}_\xi :D^{int}_{\delta }\rightarrow {\mathcal {S}}_0\) minimizing \({\widetilde{E}}_\xi (\cdot ;D^{int}_{\delta })\) among all maps P with the boundary constraints
Then
where \(\zeta _3(\delta )\rightarrow 0\) as \(\delta \rightarrow 0\).
Proof of Lemma 4.10
We define a map \({\widehat{P}}_\xi \) satisfying the boundary condition of \({\widetilde{P}}_\xi \) and an adequate upper bound on its energy. We do this in two steps: first we define \({\widehat{P}}_\xi \) in the domain
(see Figure 2) as the reflected map \(S{\widetilde{R}}_\xi S\), appropriately rescaled to “fit” into this smaller domain, and then define \({\widehat{P}}_\xi \) on the remaining part by interpolating in \({\mathcal {U}}_\star \) between the boundary values of \(S {\widetilde{R}}_\xi S\) and the boundary values of \({\widetilde{P}}_\xi \).
For the first step we start by defining a bi-Lipschitz change of variables which transforms \(X_\delta \) into
and keeps the subdomain
fixed. Explicitly, we set
Direct computations show that \(\Phi \) is one-to-one from \(X_\delta \) into \(D^{int}_\delta \), that \(\Phi =id\) in \(Y_\delta \), and that
Hence for any function \(u(r,\theta )\), the function \({\tilde{u}}=u\circ \Phi \) satisfies
for some constant \(C>0\). Therefore, setting
and recalling that \(\Phi \) is the identity in \(Y_\delta \), we have
Next, note that the proof of upper and lower bound in Sects. 2 and 3 can be adapted to prove similar bounds on \({\widetilde{R}}_\xi \). Moreover, thanks to Remark 3.10 and the inclusion
the lower bound can actually be obtained in \(Y_\delta \). As a consequence we have the upper bound
and deduce that
On \(\partial X_\delta \cap \lbrace z=0\rbrace \), \({\widehat{P}}_\xi \) satisfies the boundary condition \(S{\widehat{P}}_\xi S ={\widehat{P}}_\xi \), since \({\widetilde{R}}_\xi \) satisfies it as well.
Finally, we define \({\widehat{P}}_\xi \) in the region \(D^{int}_\delta \setminus X_\delta \) to satisfy the desired boundary conditions, via interpolation in this thin region of width \(O(\delta ^{3/2})\). We decompose (up to sets of measure zero),
using the arcs \(\{ r=\delta -\delta ^{3/2}, \ \theta \in (\theta _0(r),{\underline{\theta }}(r))\}\) and \(\{ \theta =\underline{\theta }(r), \ r\in (\delta -\delta ^{3/2}, \delta )\}\), where we denote \(\underline{\theta }(r):= \frac{\pi }{2} - r^{1/2}\). Explicitly, we set
As the boundary data are all taken with values in \({\mathcal {U}}_*\), we may define \({\widehat{P}}_\xi = {\hat{n}}\otimes {\hat{n}} -\frac{1}{3} I\), \({\hat{n}}=(\cos {\hat{\phi }}, 0, \sin {\hat{\phi }})\), by specifying its phase \({\hat{\phi }}\). Similarly, we define the boundary data for \(R_\xi \) in terms of a director characterized by its phase, \(R_\xi |_{\partial X_\delta }= n_R\otimes n_R-\frac{1}{3} I\), \(n_R=(\cos \varphi , 0 ,\sin \varphi )\), with \(\varphi ={\underline{\varphi }}(r)\) on \({\underline{\Gamma }}=\{ \theta ={\underline{\theta }}(r), \ r\in (0,\delta -\delta ^{3/2})\}\), (corresponding to \(n=Se_r\circ \Phi \),) and \(\varphi ={\overline{\varphi }}(\theta )=-\phi _0^-\circ \Phi \) on \({\overline{\Gamma }}=\{ r=\delta -\delta ^{3/2}, \ \theta \in (0,{\underline{\theta }}(r))\}\).
In \(Z^1_\delta =\{ \theta \in ({\underline{\theta }}(r),\theta _0(r)), \ 0<r\le \delta -\delta ^{3/2}\}\), we interpolate in \(\theta \in ({\underline{\theta }}(r),\theta _0(r))\) for each fixed r:
where we recall that \(\theta _1(r)=2\theta _0(r)-\pi \) gives the Dirichlet condition along the circle \(\rho ^2+z^2=1\). As \({\underline{\varphi }}(r)-\theta _1(r)=O(r)\), we calculate
and hence
In \(Z^2_\delta =\{ 0<\theta <\underline{\theta }(r), \ r\in (\delta -\delta ^{3/2}, \delta )\}\) we set
As the phase difference \(|{\overline{\varphi }}(\theta )-\phi _0^+(\theta ,\delta )|=O(\delta )\), we again may estimate the gradient as in (57) to obtain
Lastly, we consider the domain \(Z^3_\delta =\{ r\in (\delta -\delta ^{3/2},\delta ), \ \theta \in ({\underline{\theta }}(r), \theta _0(r))\}\), for which \({\hat{\phi }}\) has already been defined on \(\partial Z^3_\delta \) via the previous two steps. Indeed, \({\hat{\phi }}|_{\partial Z^3_\delta }=\frac{\pi }{2}+h_\delta \), for \(h_\delta \) Lipschitz continuous, with sup norm of order \(\delta \), and \(|\partial _\tau h_\delta |=O(\delta ^{-1/2})\) on each edge. Define \(v_\delta \) as the minimizer of the Dirichlet energy \(\int _{Z^3_\delta } |\nabla v|^2\) with \(v|_{\partial Z^3_\delta }= h_\delta \). The domain \(Z^3_\delta \) is nearly square, with side length \(\delta ^{3/2}\); indeed, after rescaling lengths by \(\delta ^{3/2}\), \(\delta ^{-3/2}Z^3_\delta \) approaches the unit square as \(\delta \rightarrow 0\). In particular elliptic estimates give
Setting \({\hat{\phi }}=\frac{\pi }{2}+ v_\delta \) in \(Z^3_\delta \), we then have that
Together with the previous two constructions, we have defined \({\widehat{P}}_\xi \) in all \(D^{int}_\delta \), satisfying the desired boundary conditions, with
by (56). Using \({\widehat{P}}_\xi \) as a comparison map thus proves Lemma 4.10. \(\square \)
To conclude, we extend \({\widetilde{P}}_\xi \) to \(D^{ext}_\delta \) by setting
From the estimates in Lemma 4.9 and 4.10 we have that
where \(\zeta _4(\delta )\rightarrow 0\) as \(\delta \rightarrow 0\), and \(\sigma _4(\delta ,\xi )\rightarrow 0\) as \(\xi \rightarrow 0\) for all fixed \(\delta >0\). Recalling from the definition of \(n_\delta \) that \({\widetilde{E}}_\xi ({\widetilde{P}}_\xi ;D^{ext}_\delta ) =2{\mathbb {E}}^+[\delta ]\), we also have that
Note that \(\sigma _5(\delta ,\xi )\rightarrow 0\) as \(\xi \rightarrow 0\), thanks to Lemma 4.1. Since \(\varphi \) minimizes \(F(\cdot ;D^{ext}_\eta )\) for every \(\eta >0\) and satisfies the estimates of Lemma 4.7, one can argue exactly as for (54) to prove that \(\max (\zeta _5(\delta ),0)\rightarrow 0\) as \(\delta \) to 0. (In fact similar arguments will show that \(\zeta _5(\delta )\rightarrow 0\), but here we only need the upper bound.)
Gathering the above estimates and recalling Lemma 4.8, we deduce that
and so we can find \(\delta ,\xi >0\) such that the map \({\widetilde{P}}_\xi \) has strictly lower energy than \({\widetilde{Q}}_\xi \). This contradicts minimality of \({\widetilde{Q}}_\xi \) and concludes the proof of Theorem 1.2.
References
Alama, S., Bronsard, L., Lamy, X.: Minimizers of the Landau-de Gennes energy around a spherical colloid particle. Arch. Ration. Mech. Anal. 222(1), 427–450 (2016)
Alama, S., Bronsard, L., Lamy, X.: Spherical particle in nematic liquid crystal under an external field: the Saturn ring regime. J. Nonlinear Sci. 28(4), 1443–1465 (2018)
Alouges, F., Chambolle, A., Stantejsky, D.: The Saturn ring effect in nematic liquid crystals with external field: effective energy and hysteresis. In preparation
André, N., and Shafrir, I.: Asymptotic behavior of minimizers for the Ginzburg-Landau functional with weight. I, II. Arch. Rational Mech. Anal. 142, 1, 45–73, 75–98 (1998)
Ball, J.M., Zarnescu, A.: Orientability and energy minimization in liquid crystal models. Arch. Ration. Mech. Anal. 202(2), 493–535 (2011)
Bauman, P., Park, J., Phillips, D.: Analysis of nematic liquid crystals with disclination lines. Arch. Ration. Mech. Anal. 205(3), 795–826 (2012)
Beaulieu, A., Hadiji, R.: On a class of Ginzburg-Landau equations with weight. PanAmer. Math. J. 5(4), 1–33 (1995)
Beaulieu, A., Hadiji, R.: A Ginzburg–Landau problem with weight having minima on the boundary. Proc. R. Soc. Edinb. Sect. A 128(6), 1181–1215 (1998)
Bethuel, F., Brezis, H., Hélein, F.: Ginzburg–Landau vortices. In: Progress in Nonlinear Differential Equations and their Applications, vol. 13. Birkhäuser Boston Inc, Boston (1994)
Bethuel, F., Chiron, D.: Some questions related to the lifting problem in Sobolev spaces. In: Perspectives in Nonlinear Partial Differential equations, vol. 446 of Contemp. Math. Amer. Math. Soc., Providence, RI, pp. 125–152 (2007)
Brezis, H., Coron, J.-M., Lieb, E.H.: Harmonic maps with defects. Commun. Math. Phys. 107(4), 649–705 (1986)
Canevari, G.: Biaxiality in the asymptotic analysis of a 2D Landau–de Gennes model for liquid crystals. ESAIM Control Optim. Calc. Var. 21(1), 101–137 (2015)
Canevari, G.: Line defects in the small elastic constant limit of a three-dimensional Landau-de Gennes model. Arch. Ration. Mech. Anal. 223(2), 591–676 (2017)
COMSOL Multiphysics® v. 5.3. http://www.comsol.com/. COMSOL AB, Stockholm, Sweden
Contreras, A., Lamy, X.: Singular perturbation of manifold-valued maps with anisotropic energy. Preprint (2019)
Contreras, A., Lamy, X., Rodiac, R.: On the convergence of minimizers of singular perturbation functionals. Indiana Univ. Math. J. 67(4), 1665–1682 (2018)
Dipasquale, F., Millot, V., Pisante, A.: Torus-like solutions for the Landau-de Gennes model. Part II: Topology of \({\mathbb{S}}^1\)-equivariant minimizers. arXiv:2008.13676
Dipasquale, F., Millot, V., Pisante, A.: Torus-like solutions for the Landau-de Gennes Model. Part I: The Lyuksyutov Regime. Arch. Ration. Mech. Anal. 239(2), 599–678 (2021)
Fukuda, J., Stark, H., Yoneya, M., Yokoyama, H.: Dynamics of a nematic liquid crystal around a spherical particle. J. Phys.: Condens. Matter 16(19), S1957 (2004)
Fukuda, J., Yokoyama, H.: Stability of the director profile of a nematic liquid crystal around a spherical particle under an external field. Eur. Phys. J. E 21(4), 341–347 (2006)
Fukuda, J.-I., Yoneya, M., Yokoyama, H.: Nematic liquid crystal around a spherical particle: investigation of the defect structure and its stability using adaptive mesh refinement. Eur. Phys. J. E 13(1), 87–98 (2004)
Golovaty, D., Montero, J.A.: On minimizers of a Landau–de Gennes energy functional on planar domains. Arch. Ration. Mech. Anal. 213(2), 447–490 (2014)
Gu, Y., Abbott, N.: Observation of Saturn-ring defects around solid microspheres in nematic liquid crystals. Phys. Rev. Lett. 85, 4719–4722 (2000)
Hardt, R., Kinderlehrer, D., Lin, F.H.: Stable defects of minimizers of constrained variational principles. Ann. Inst. H. Poincaré Anal. Non Linéaire 5(4), 297–322 (1988)
Hardt, R., Kinderlehrer, D., Lin, F.H.: The variety of configurations of static liquid crystals. In: Variational methods (Paris, 1988), vol. 4 of Progr. Nonlinear Differential Equations Appl. Birkhäuser Boston, Boston, pp. 115–131 (1990)
Hardt, R., Lin, F.-H.: A remark on \(H^1\) mappings. Manuscripta Math. 56(1), 1–10 (1986)
Jerrard, R.L.: Lower bounds for generalized Ginzburg–Landau functionals. SIAM J. Math. Anal. 30(4), 721–746 (1999)
Kralj, S., Virga, E.G.: Universal fine structure of nematic hedgehogs. J. Phys. A 34(4), 829–838 (2001)
Lamy, X.: Bifurcation analysis in a frustrated nematic cell. J. Nonlinear Sci. 24(6), 1197–1230 (2014)
Lavrentovich, O.D.: Transport of particles in liquid crystals. Soft Matter 10(9), 1264–1283 (2014)
Loudet, J.C., Poulin, P.: Application of an electric field to colloidal particles suspended in a liquid-crystal solvent. Phys. Rev. Lett. 87, 165503 (2001)
Lubensky, T.C., Pettey, D., Currier, N., Stark, H.: Topological defects and interactions in nematic emulsions. Phys. Rev. E 57, 610–625 (1998)
Majumdar, A., Zarnescu, A.: Landau-de Gennes theory of nematic liquid crystals: the Oseen–Frank limit and beyond. Arch. Ration. Mech. Anal. 196(1), 227–280 (2010)
Muševič, I.: Liquid Crystal Colloids. Springer, New York (2017)
Nguyen, L., Zarnescu, A.: Refined approximation for minimizers of a Landau–de Gennes energy functional. Calc. Var. Partial Differ. Equ. 47(1–2), 383–432 (2013)
Palais, R.S.: The principle of symmetric criticality. Commun. Math. Phys. 69(1), 19–30 (1979)
Sandier, E.: Lower bounds for the energy of unit vector fields and applications. J. Funct. Anal. 152(2), 379–403 (1998)
Sandier, E., Shafrir, I.: On the symmetry of minimizing harmonic maps in \(N\) dimensions. Differ. Integral Equ.| 6(6), 1531–1541 (1993)
Stark, H.: Physics of colloidal dispersions in nematic liquid crystals. Phys. Rep. 351(6), 387–474 (2001)
Stark, H.: Saturn-ring defects around microspheres suspended in nematic liquid crystals: An analogy between confined geometries and magnetic fields. Phys. Rev. E 66, 032701 (2002)
Struwe, M.: On the asymptotic behavior of minimizers of the Ginzburg–Landau model in \(2\) dimensions. Differ. Integ. Equ. 7(5–6), 1613–1624 (1994)
Terentjev, E.M.: Disclination loops, standing alone and around solid particles, in nematic liquid crystals. Phys. Rev. E 51, 1330–1337 (1995)
Yu, Y.: Disclinations in limiting Landau–de Gennes theory. Arch. Ration. Mech. Anal. 237(1), 147–200 (2020)
Acknowledgements
S.A. and L.B. are supported by NSERC (Canada) Discovery Grants, D.G. was supported in part by NSF grant DMS-1729538, and X.L. by ANR project ANR-18-CE40-0023. We also thank the Erwin Schrödinger International Institute for Mathematics and Physics (Vienna) for their kind hospitality in December 2019, when this work was being completed. Finally, we thank the referees for their careful reading and helpful suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by J. M. Ball.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Alama, S., Bronsard, L., Golovaty, D. et al. Saturn ring defect around a spherical particle immersed in a nematic liquid crystal. Calc. Var. 60, 225 (2021). https://doi.org/10.1007/s00526-021-02091-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00526-021-02091-6