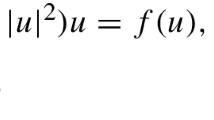Existence and symmetry breaking of ground state solutions for Schrödinger–Poisson systems

Abstract

We study the Schrödinger–Poisson system:

$$\begin{aligned} \left\{ \begin{array}{ll} -\Delta u+u+\lambda \phi u=a\left( x\right) \left| u\right| ^{p-2}u &{} \text { in }{{\mathbb {R}}}^{3}, \\ -\Delta \phi =u^{2} &{} \ \text {in }{{\mathbb {R}}}^{3}, \end{array} \right. \end{aligned}$$

where parameter $\lambda >0$, $2<p<3$ and $a\left( x\right)$ is a positive continuous function in ${{\mathbb {R}}}^{3}$. Assuming that $a\left( x\right) \ge \lim _{\left| x\right| \rightarrow \infty }a\left( x\right) =a_{\infty }>0$ and other suitable conditions, we explore the energy functional corresponding to the system which is bounded below on $H^{1}\left( {{\mathbb {R}}}^{3}\right)$ and the existence and multiplicity of positive (ground state) solutions for $\left[ \frac{A\left( p\right) }{p} a_{\infty }\right] ^{2/\left( p-2\right) }<\lambda \le \left[ \frac{A\left( p\right) }{p}a_{1}\right] ^{2/\left( p-2\right) },$ where $A\left( p\right) :=2^{\left( 6-p\right) /2}\left( 3-p\right) ^{3-p}\left( p-2\right) ^{\left( p-2\right) }$ and $a_{\infty }<a_{1}<a_{\max }:=\sup _{x\in {{\mathbb {R}}} ^{3}}a\left( x\right) .$ More importantly, when $a\left( x\right) =a\left( \left| x\right| \right)$ and $a\left( 0\right) =a_{\max },$ we establish the existence of non-radial ground state solutions.

1 Introduction

Our starting point is the Schrödinger–Poisson systems (SP systems for short):

Such systems, also called Schrödinger-Maxwell equations, can be used to describe the interaction of a charged particle with the electrostatic field in quantum mechanics, where the unknowns u and $\phi$ represent the wave functions associated with the particle and the electric potentials, respectively, and $\rho :{{\mathbb {R}}}^{3}\rightarrow {{\mathbb {R}}}^{+}$ is a measurable function representing a ‘charge’ corrector to the density $u^{2}$ . The nonlinearity $a\left( x\right) \left| u\right| ^{p-2}u$ represents the interaction effect among many particles. For more details on the physical background, we refer the readers to [5, 23].

It is easily seen that system $(SP_{\rho ,a})$ can be transformed into a nonlinear Schrödinger equation with a non-local term, when $\rho \in L^{\infty }\left( {{\mathbb {R}}}^{3}\right) \cup L^{2}\left( {{\mathbb {R}}} ^{3}\right)$ (see [1, 23]). Briefly, the Poisson equation can be solved by using the Lax–Milgram theorem. For all $u\in H^{1}({{\mathbb {R}}}^{3})$, the unique $\phi _{u}\in D^{1,2}({{\mathbb {R}}}^{3})$ is given by

$$\begin{aligned} \phi _{u}(x)=\frac{1}{4\pi }\int _{{{\mathbb {R}}}^{3}}\frac{\rho (x)u^{2}(y)}{ |x-y|}dy, \end{aligned}$$

(1.1)

such that $-\Delta \phi =\rho (x)u^{2}$ and substituting it into the first equation of system $(SP_{\rho ,a})$, gives

Such equation is variational and its solutions are critical points of the corresponding energy functional $J_{\rho ,a}:H^{1}({{\mathbb {R}}} ^{3})\rightarrow {{\mathbb {R}}}$ defined as

$$\begin{aligned} J_{\rho ,a}\left( u\right) =\frac{1}{2}\int _{{{\mathbb {R}}}^{3}}\left( |\nabla u|^{2}+u^{2}\right) dx+\frac{1}{4}\int _{{{\mathbb {R}}}^{3}}\rho \left( x\right) \phi _{u}u^{2}dx-\frac{1}{p}\int _{{{\mathbb {R}}}^{3}}a\left( x\right) \left| u\right| ^{p}dx. \end{aligned}$$

Note that $(u,\phi )\in H^{1}({{\mathbb {R}}}^{3})\times D^{1,2}({{\mathbb {R}}}^{3})$ is a solution of system $\left( SP_{\rho ,a}\right)$ if and only if u is a critical point of $J_{\rho ,a}$ and $\phi =\phi _{u}.$ The pair $(u,\phi )$ is called a ground state solution of system $(SP_{\rho ,a})$, provided u is a solution of Equation $(E_{\rho ,a})$ which has the ground state among all nontrivial solutions of Equation $(E_{\rho ,a}).$

In recent years and in view of this, there has been much attention paid to the SP systems on the existence of positive solutions, nodal solutions, radial solutions and semiclassical states under variant assumptions on $\rho$ and a via variational methods. We refer the readers to [1,2,3, 9, 10, 12, 16, 21, 23,24,25, 27,28,30, 33, 34] and the references therein. More precisely, Ruiz [23] studied a class of autonomous SP systems, namely, system $(SP_{\rho ,a})$ with $\rho (x)\equiv \lambda >0$ and $a\left( x\right) \equiv 1.$ With the help of Strauss inequality in the space of radial functions $H_{r}^{1}$ [26], the author proved that the functional $J_{\lambda ,1}$ is bounded below, $\inf _{u\in H_{r}^{1}}J_{\lambda ,1}\left( u\right) <0$ and satisfies the (PS) condition on $H_{r}^{1}$ for $2<p<3,$ when $J_{\lambda ,1}=J_{\rho ,a}$. For that reason, two positive radial solutions are found for $\lambda >0$ sufficiently small using mountain pass theorem and the global minimizing theory, and $u=0$ is the unique solution for $\lambda \ge 1/4.$ Moreover, by introducing Nehari–Pohozaev manifold, for all $\lambda >0$, one positive radial solution is found when $3<p<6$. The corresponding results have been further improved by Azzollini–Pomponio [3] and Zhao–Zhao [34] by proving the existence of ground state solution (possibly non-radial) when $\lambda =1$ and $3<p<6.$ Their proofs are both based on Nehari–Pohozaev manifold by Ruiz.

Cerami-Varia [9] dealt with a class of non-autonomous SP systems without any symmetry assumptions, i.e., system $(SP_{\rho ,a})$ with $4<p<6.$ By establishing a compactness lemma and using the Nehari manifold method, when the functions $\rho$ and a satisfy some proper assumptions, the existence of ground state and bound state solutions was presented. However, for the case of $2<p\le 4,$ we notice that the (PS) condition on $H^{1}( {{\mathbb {R}}}^{3})$ is still unsolved and that the functional $J_{\rho ,a}$ is not bounded below on both Nehari manifold $\left( 2<p\le 4\right)$ and Nehari–Pohozaev manifold $\left( 2<p<3\right)$ for $\left\| \rho \right\| _{\infty }$ sufficiently small. As a consequence, the standard analysis in variational methods does not work. In [29], the authors proposed a novel constraint approach to study the existence of positive solutions (including ground state solutions) for $2<p\le 4$ and $\left\| \rho \right\| _{\infty }$ sufficiently small filling in the gap in [9] while emphasizing the existence of ground state solutions of system $\left( SP_{\rho ,a}\right)$ for $3.1813\approx \frac{1+\sqrt{73}}{3}<p\le 4$. Again, we refer the interested readers to [28, 29] for further applications on this approach. In an interesting paper recently, Mercuri and Tyler [21], have shown the existence of ground state solutions of system $\left( SP_{\rho ,a}\right)$ for $3<p<4,$ assuming $a(x)\equiv 1$ with different assumptions on $\rho$ at infinity (coercive or non-coercive).

In the present paper, we focus our attention on the symmetry, existence and multiplicity of positive (ground state) solutions for a class of Schrö dinger–Poisson systems:

where parameter $\lambda >0$, $2<p<3$ and $a\left( x\right)$ is a positive continuous function in ${{\mathbb {R}}}^{3}$ satisfying the following assumption:

• $\left( D1\right)$ $a\left( x\right) \ge \lim _{\left| x\right| \rightarrow \infty }a\left( x\right) =a_{\infty }>0\$uniformly on$\ {{\mathbb {R}}}^{3}.$

As mentioned introduced earlier, system $(SP_{\lambda ,a})$ can be transformed into the following nonlinear Schrödinger equation with a non-local term:

and the corresponding energy functional $J_{\lambda ,a}:H^{1}({{\mathbb {R}}} ^{3})\rightarrow {{\mathbb {R}}}$ is defined as

$$\begin{aligned} J_{\lambda ,a}\left( u\right) =\frac{1}{2}\int _{{{\mathbb {R}}}^{3}}\left( |\nabla u|^{2}+u^{2}\right) dx+\frac{\lambda }{4}\int _{{{\mathbb {R}}}^{3}}\phi _{u}u^{2}dx-\frac{1}{p}\int _{{{\mathbb {R}}}^{3}}a\left( x\right) \left| u\right| ^{p}dx. \end{aligned}$$

Furthermore, one can see that $J_{\lambda ,a}$ is a $C^{1}$ functional with the derivative given by

$$\begin{aligned} \left\langle J_{\lambda ,a}^{\prime }(u),\varphi \right\rangle =\int _{ {{\mathbb {R}}}^{3}}\left( \nabla u\nabla \varphi +u\varphi +\lambda \phi _{u}u\varphi -a\left( x\right) |u|^{p-2}u\varphi \right) dx \end{aligned}$$

for all $\varphi \in H^{1}({{\mathbb {R}}}^{3})$ with $J_{\lambda ,a}^{\prime }$ denoting the Fréchet derivative of $J_{\lambda ,a}.$

Then we can deduce the conclusions in [23, 24, 29] that when $2<p<3$ and the weight function $a\left( x\right)$ satisfies condition $\left( D1\right)$, several results are obtained as follows.

• $\left( i\right)$ The functional $J_{\lambda ,a}$ is not bounded below on $H^{1}({{\mathbb {R}}}^{3}),$ Nehari manifold and Nehari–Pohozaev manifold for $\lambda >0$ sufficient small.

• $\left( ii\right)$ There exists $\lambda _{0}>0$ such that $\inf _{u\in H^{1}({{\mathbb {R}}}^{3})}J_{\lambda ,a}\left( u\right) >0$ for all $\lambda >\lambda _{0}.$

• $\left( iii\right)$ When $a\left( x\right) \equiv 1,$ system $\left( SP_{\lambda ,a}\right)$ has at least two positive radial solutions for $\lambda >0$ sufficiently small.

Motivated by the facts mentioned above and the main results in [21], we propose to study the existence and symmetry of ground state solutions to system $\left( SP_{\lambda ,a}\right)$ in the various functional settings corresponding to different hypotheses on parameter $\lambda$ and weight function a. The following are the two main objectives of this paper.

• $\left( I\right)$ When $2<p<3$ and the weight function a satisfies some suitable assumptions, we show that there exist two positive numbers $\lambda _{1}\left( p,a\right)$ and $\lambda _{2}\left( p,a\right)$ such that for every $\lambda _{1}\left( p,a\right)<\lambda <\lambda _{2}\left( p,a\right) ,$ functional $J_{\lambda ,a}$ is coercive and bounded below on $H^{1}({{\mathbb {R}}}^{3})$ and $\inf _{u\in H^{1}({{\mathbb {R}}}^{3})}J_{\lambda ,a}\left( u\right) <0.$ It follows that system $\left( SP_{\lambda ,a}\right)$ has at least two positive solutions including a ground state solution.

• $\left( II\right)$ When $2<p<3$ and the weight function $a\left( x\right) =a\left( \left| x\right| \right)$, we show that there is a non-radial ground state solution in system $\left( SP_{\lambda ,a}\right) .$

To our knowledge, the available literature does not contain any results on the existence of non-radial ground state solutions to system $\left( SP_{\lambda ,a}\right)$ when $2<p<3.$ Before presenting our main results, we first recall a known conclusion (cf. [17]). Let $w_{a_{\max }}$ be the unique radial positive solution of the following nonlinear Schrö dinger equation

Clearly,

$$\begin{aligned} \left\| w_{0}\right\| _{H^{1}}^{2}=\int _{{{\mathbb {R}}}^{3}}a_{\max }\left| w_{0}\right| ^{p}dx=\left( \frac{S_{p}^{p}}{a_{\max }} \right) ^{\frac{2}{p-2}}. \end{aligned}$$

(1.2)

We now summarize our main results in the theorems below.

Theorem 1.1

Suppose that $2<p<3$ and condition (D1) holds. In addition, we assume that$\left( D2\right)$ there exists $a_{\infty }<a_{1}<a_{\max }:=\max _{x\in {{\mathbb {R}}}^{3}}a\left( x\right)$ such that

$$\begin{aligned} a_{\max }>\frac{2A\left( p\right) S_{p}^{p}}{\left( 4-p\right) ^{2}}\left( \frac{4-p}{2\left( p-2\right) {{\overline{S}}}^{2}S_{12/5}^{4}}\right) ^{\left( p-2\right) /2}a_{1}, \end{aligned}$$

where $A\left( p\right) :=2^{\left( 6-p\right) /2}\left( 3-p\right) ^{3-p}\left( p-2\right) ^{p-2},$ and $S_{r}$ and ${{\overline{S}}}$ are the best constants for the embeddings of $H^{1}({{\mathbb {R}}}^{3})$ in $L^{r}({{\mathbb {R}}} ^{3})$ and $D^{1,2}({{\mathbb {R}}}^{3})$ in $L^{6}({{\mathbb {R}}}^{3})$, respectively, for $2\le r<6;$ $\left( D3\right)$ $\int _{{{\mathbb {R}}}^{3}}a\left( x\right) \left| w_{a_{\max }}\right| ^{p}dx>\frac{p\kappa _{0}}{2S_{p}^{p}}\left\| w_{a_{\max }}\right\| _{H^{1}}^{p},$ where $\kappa _{0}:=\frac{A\left( p\right) S_{p}^{p}}{4-p}\left( \frac{4-p}{2\left( p-2\right) {{\overline{S}}} ^{2}S_{12/5}^{4}}\right) ^{\left( p-2\right) /2}a_{1}.$Then for each

$$\begin{aligned} \left[ \frac{A\left( p\right) }{p}a_{\infty }\right] ^{2/\left( p-2\right) }<\lambda \le \left[ \frac{A\left( p\right) }{p}a_{1}\right] ^{2/\left( p-2\right) }, \end{aligned}$$

Equation $(E_{\lambda ,a})$ has two positive solutions $u_{\lambda ,a}^{\left( 1\right) }$ and $u_{\lambda ,a}^{\left( 2\right) }$ such that

$$\begin{aligned} J_{\lambda ,a}\left( u_{\lambda ,a}^{\left( 2\right) }\right)<0<J_{\lambda ,a}\left( u_{\lambda ,a}^{\left( 1\right) }\right) . \end{aligned}$$

Furthermore, $u_{\lambda ,a}^{\left( 2\right) }$ is a ground state solution of Equation $(E_{\lambda ,a}).$

To study the symmetry breaking of ground state solutions, we consider the following equation:

where $a_{\varepsilon }\left( x\right) =a\left( \varepsilon x\right)$ and $\varepsilon >0.$ Then we have the following results.

Theorem 1.2

Suppose that $2<p<3$ and conditions ${(D1)}-{(D2)}$ hold. In addition, we assume that

$\left( D4\right)$ $a\left( x\right) =a\left( \left| x\right| \right)$ for all $x\in {{\mathbb {R}}}^{3}$ and $a\left( 0\right) =a_{\max }.$

Then for each

$$\begin{aligned} \left[ \frac{A\left( p\right) }{p}a_{\infty }\right] ^{2/\left( p-2\right) }<\lambda \le \left[ \frac{A\left( p\right) }{p}a_{1}\right] ^{2/\left( p-2\right) }, \end{aligned}$$

Equation $(E_{\lambda ,a_{\varepsilon }})$ has three positive solutions $u_{\lambda ,a_{\varepsilon }}^{\left( 1\right) },u_{\lambda ,a_{\varepsilon }}^{\left( 2\right) }\in H^{1}\left( {{\mathbb {R}}}^{3}\right)$ and $v_{\lambda ,a_{\varepsilon }}\in H_{r}^{1}$ such that

$$\begin{aligned} J_{\lambda ,a_{\varepsilon }}\left( u_{\lambda ,a_{\varepsilon }}^{\left( 2\right) }\right)<J_{\lambda ,a_{\varepsilon }}\left( v_{\lambda ,a_{\varepsilon }}\right)<0<J_{\lambda ,a_{\varepsilon }}\left( u_{\lambda ,a_{\varepsilon }}^{\left( 1\right) }\right) \end{aligned}$$

for $\varepsilon$ sufficiently small. Furthermore, $u_{\lambda ,a_{\varepsilon }}^{\left( 2\right) }$ is a non-radial ground state solution of Equation $(E_{\lambda ,a_{\varepsilon }}).$

Corollary 1.3

Suppose that $2<p<3$ and conditions ${(D1)}-{(D2)}$ hold. In addition, we assume that$\left( D4^{\prime }\right)$ $a\left( x\right) =a\left( \left| x\right| \right)$ for all $x\in {{\mathbb {R}}}^{3}$ and $a\left( r\right)$ is non-increasing for $r>0.$Then for each

$$\begin{aligned} \left[ \frac{A\left( p\right) }{p}a_{\infty }\right] ^{2/\left( p-2\right) }<\lambda \le \left[ \frac{A\left( p\right) }{p}a_{1}\right] ^{2/\left( p-2\right) }, \end{aligned}$$

Equation $(E_{\lambda ,a_{\varepsilon }})$ has a non-radial ground state solution for $\varepsilon$ sufficiently small.

Remark 1.4

$\left( i\right)$ Suppose that $2<p<3$ and conditions ${(D1)}-{ (D2)}$ hold. Let $w_{a_{\max }}$ be the unique radial positive solution of Equation $(E_{0,a_{\max }}^{\infty })$ and let $a\left( x_{0}\right) =a_{\max }$ for some $x_{0}\in {{\mathbb {R}}}^{3}.$ Define $w_{\varepsilon }\left( x\right) =w_{a_{\max }}\left( x-\frac{x_{0}}{\varepsilon }\right) .$ Then it follows from condition $\left( D2\right)$ and (1.2) with $a_{\max }>\frac{2}{4-p}\kappa _{0}>\frac{p}{2}\kappa _{0}$ for $2<p<3$ that for every $\left[ \frac{A\left( p\right) }{p}a_{\infty } \right] ^{2/\left( p-2\right) }<\lambda \le \left[ \frac{A\left( p\right) }{ p}a_{1}\right] ^{2/\left( p-2\right) },$ we have

$$\begin{aligned} \int _{{{\mathbb {R}}}^{3}}a_{\varepsilon }\left( x\right) \left| w_{\varepsilon }\right| ^{p}dx= & {} \int _{{{\mathbb {R}}}^{3}}a\left( \varepsilon x+x_{0}\right) w_{a_{\max }}^{p}\left( x\right) dx \nonumber \\= & {} \frac{a_{\max }}{S_{p}^{p}}\left\| w_{a_{\max }}\right\| _{H^{1}}^{p}+o\left( \varepsilon \right) \nonumber \\> & {} \frac{p\kappa _{0}}{2S_{p}^{p}}\left\| w_{a_{\max }}\right\| _{H^{1}}^{p}=\frac{p\kappa _{0}}{2S_{p}^{p}}\left\| w_{\varepsilon }\right\| _{H^{1}}^{p}\text { for }\varepsilon \text { sufficiently small.} \qquad \end{aligned}$$

(1.3)

This implies that when $a\left( x\right)$ is replaced by $a\left( \varepsilon x+x_{0}\right) ,$ the condition $\left( D3\right)$ holds for $\varepsilon$ sufficiently small. Therefore, by Theorem 1.1, Equation $(E_{\lambda ,a_{\varepsilon }})$ has two positive solutions $u_{\lambda ,a_{\varepsilon }}^{\left( 1\right) },u_{\lambda ,a_{\varepsilon }}^{\left( 2\right) }\in H^{1}\left( {{\mathbb {R}}}^{3}\right)$ such that

$$\begin{aligned} J_{\lambda ,a_{\varepsilon }}\left( u_{\lambda ,a_{\varepsilon }}^{\left( 2\right) }\right)<0<J_{\lambda }\left( u_{\lambda ,a_{\varepsilon }}^{\left( 1\right) }\right) \text { for }\varepsilon \text { sufficiently small.} \end{aligned}$$

$\left( ii\right)$ Assume that the conditions hold in Theorem 1.2. Since $a\left( x\right) =a\left( \left| x\right| \right)$ and $a\left( 0\right) =a_{\max },$ using an argument similar to that in part $\left( i\right) ,$ we can obtain

$$\begin{aligned} \int _{{{\mathbb {R}}}^{3}}a_{\varepsilon }\left( x\right) \left| w_{a_{\max }}\right| ^{p}dx>\frac{p\kappa _{0}}{2S_{p}^{p}}\left\| w_{a_{\max }}\right\| _{H^{1}}^{p}\text { for }\varepsilon \text { sufficiently small,} \end{aligned}$$

since $x_{0}=0.$ This means that the symmetric case still holds in Theorem 1.1 implying that Equation $(E_{\lambda ,a_{\varepsilon }})$ has two radial positive solutions $v_{\lambda ,a_{\varepsilon }},{{\widetilde{v}}} _{\lambda ,a_{\varepsilon }}\in H^{1}\left( {{\mathbb {R}}}^{3}\right)$ such that

$$\begin{aligned} J_{\lambda ,a_{\varepsilon }}\left( v_{\lambda ,a_{\varepsilon }}\right)<0<J_{\lambda }\left( {{\widetilde{v}}}_{\lambda ,a_{\varepsilon }}\right) \text { for }\varepsilon \text { sufficiently small.} \end{aligned}$$

$\left( iii\right)$ We mainly use energy comparison and constrained minimization to obtain the asymmetry of $u_{\lambda ,a_{\varepsilon }}^{\left( 2\right) }$ in Theorem 1.2, these, however, cannot be applied to $u_{\lambda ,a_{\varepsilon }}^{\left( 1\right) }$, so we cannot confirm the symmetry of the solution $u_{\lambda ,a_{\varepsilon }}^{\left( 1\right) }$ at present.

Remark 1.5

Under the assumption that $\lambda \ne 0,$ Equation $\left( E_{\lambda ,a_{\varepsilon }}\right)$ can be regarded as a perturbation problem of the following nonlinear Schrödinger equation:

When $a\left( x\right) =a\left( \left| x\right| \right)$ and $a\left( r\right)$ is non-increasing for $r>0,$ by [14, 15, 18], it is known that every positive solution of Equation $\left( E_{0,a_{\varepsilon }}\right)$ is radially symmetric for all $\varepsilon >0$. Therefore, by Corollary 1.3, we conclude that under the appropriate effect of non-local term, non-radial positive (ground state) solution can be obtained.

The paper is organized as follows. In Sect. 2, we provide some preliminaries and prove that the energy functional $J_{\lambda ,a}$ is coercive and bounded below in $H^{1}({{\mathbb {R}}}^{3}).$ Moreover, by using the filtration of the Nehari manifold:

$$\begin{aligned} {{\mathbf {M}}}_{\lambda ,a}(c)=\{u\in {{\mathbf {M}}}_{\lambda ,a}:J_{\lambda ,a}(u)<c\}, \end{aligned}$$

where ${{\mathbf {M}}}_{\lambda ,a}$ is the Nehari manifold and c is the energy level of the functional $J_{\lambda ,a}$, we show that there is an appropriate energy level $c_{0}>0$ such that ${{\mathbf {M}}}_{\lambda ,a}(c_{0})$ can be divided into two submanifolds ${{\mathbf {M}}}_{\lambda ,a}^{(1)}$ and ${{\mathbf {M}}}_{\lambda ,a}^{(2)}$, in which each local minimizer of the functional $J_{\lambda }$ restricted on ${{\mathbf {M}}}_{\lambda ,a}^{(i)}$ $(i=1,2)$ is a critical point of $J_{\lambda ,a}$ in $H^{1}({{\mathbb {R}}}^{3}).$ In Sect. 3, we prove that these submanifolds ${{\mathbf {M}}}_{\lambda ,a}^{(i)}$ are non-empty and $\inf _{u\in {{\mathbf {M}}}_{\lambda ,a}^{(2)}}J_{\lambda ,a}\left( u\right) <0.$ In Sect. 4, we show that the Palais-Smale condition of $J_{\lambda ,a}$ on submanifolds ${{\mathbf {M}}}_{\lambda ,a}^{(i)}$ holds and subsequently, we provide the proof for Theorem 1.1. Finally, Sect. 5 is dedicated to the proof of Theorem 1.2.

2 Preliminaries

First, we define the Nehari manifold as follows.

$$\begin{aligned} {{\mathbf {M}}}_{\lambda ,a}:=\{u\in H^{1}({{\mathbb {R}}}^{3})\backslash \{0\}:\left\langle J_{\lambda ,a}^{\prime }\left( u\right) ,u\right\rangle =0\}. \end{aligned}$$

Then, $u\in {{\mathbf {M}}}_{\lambda ,a}$ if and only if $\left\| u\right\| _{H^{1}}^{2}+\lambda \int _{{{\mathbb {R}}}^{3}}\phi _{u}u^{2}dx-\int _{{{\mathbb {R}}} ^{3}}a\left( x\right) |u|^{p}dx=0.$ Using the Sobolev inequality, we have

$$\begin{aligned} \left\| u\right\| _{H^{1}}^{2}\le & {} \left\| u\right\| _{H^{1}}^{2}+\lambda \int _{{{\mathbb {R}}}^{3}}\phi _{u}u^{2}dx=\int _{{{\mathbb {R}}} ^{3}}a\left( x\right) \left| u\right| ^{p}dx \\\le & {} S_{p}^{-p}a_{\max }\left\| u\right\| _{H^{1}}^{p} \end{aligned}$$

for all $u\in {{\mathbf {M}}}_{\lambda ,a}$. Subsequently,

$$\begin{aligned} \int _{{{\mathbb {R}}}^{3}}a\left( x\right) \left| u\right| ^{p}dx\ge \left\| u\right\| _{H^{1}}^{2}\ge \left( \frac{S_{p}^{p}}{a_{\max }} \right) ^{2/\left( p-2\right) }\text { for all }u\in {{\mathbf {M}}}_{\lambda ,a}. \end{aligned}$$

(2.1)

The Nehari manifold ${{\mathbf {M}}}_{\lambda ,a}$ is closely linked to the behavior of the function of the form $h_{\lambda ,u}:t\rightarrow J_{\lambda ,a}\left( tu\right)$ for $t>0.$ Such maps are known as fibering maps and were introduced by Drábek–Pohozaev [11], and further discussed by Brown–Zhang [8] and Brown–Wu [6, 7] and others. For $u\in H^{1}({{\mathbb {R}}}^{3}),$ we find

$$\begin{aligned} h_{\lambda ,u}\left( t\right)= & {} \frac{t^{2}}{2}\left\| u\right\| _{H^{1}}^{2}+\frac{\lambda t^{4}}{4}\int _{{{\mathbb {R}}}^{3}}\phi _{u}u^{2}dx- \frac{t^{p}}{p}\int _{{{\mathbb {R}}}^{3}}a\left( x\right) \left| u\right| ^{p}dx, \\ h_{\lambda ,u}^{\prime }\left( t\right)= & {} t\left\| u\right\| _{H^{1}}^{2}+\lambda t^{3}\int _{{{\mathbb {R}}}^{3}}\phi _{u}u^{2}dx-t^{p-1}\int _{ {{\mathbb {R}}}^{3}}a\left( x\right) \left| u\right| ^{p}dx, \\ h_{\lambda ,u}^{\prime \prime }\left( t\right)= & {} \left\| u\right\| _{H^{1}}^{2}+3\lambda t^{2}\int _{{{\mathbb {R}}}^{3}}\phi _{u}u^{2}dx-\left( p-1\right) t^{p-2}\int _{{{\mathbb {R}}}^{3}}a\left( x\right) \left| u\right| ^{p}dx. \end{aligned}$$

As a direct consequence, we have

$$\begin{aligned} th_{\lambda ,u}^{\prime }\left( t\right) =\left\| tu\right\| _{H^{1}}^{2}+\lambda \int _{{{\mathbb {R}}}^{3}}\phi _{tu}\left( tu\right) ^{2}dx-\int _{{{\mathbb {R}}}^{3}}a\left( x\right) \left| tu\right| ^{p}dx \end{aligned}$$

and so, $u\in H^{1}({{\mathbb {R}}}^{3})\backslash \left\{ 0\right\}$ and $t>0,$ $h_{\lambda ,u}^{\prime }\left( t\right) =0$ holds if and only if $tu\in {{\mathbf {M}}}_{\lambda ,a}$. In particular, $h_{\lambda ,u}^{\prime }\left( 1\right) =0$ holds if and only if $u\in {{\mathbf {M}}}_{\lambda ,a}.$ It becomes natural to split ${{\mathbf {M}}}_{\lambda ,a}$ into three parts corresponding to the local minima, local maxima and points of inflection. Following [31], we define

$$\begin{aligned} {{\mathbf {M}}}_{\lambda ,a}^{+}= & {} \{u\in {{\mathbf {M}}}_{\lambda ,a}:h_{\lambda ,u}^{\prime \prime }\left( 1\right) >0\}, \\ {{\mathbf {M}}}_{\lambda ,a}^{0}= & {} \{u\in {{\mathbf {M}}}_{\lambda ,a}:h_{\lambda ,u}^{\prime \prime }\left( 1\right) =0\}, \\ {{\mathbf {M}}}_{\lambda ,a}^{-}= & {} \{u\in {{\mathbf {M}}}_{\lambda ,a}:h_{\lambda ,u}^{\prime \prime }\left( 1\right) <0\}. \end{aligned}$$

Lemma 2.1

Suppose that $u_{0}$ is a local minimizer for $J_{\lambda ,a}$ on ${{\mathbf {M}}}_{\lambda ,a}$ and $u_{0}\notin {{\mathbf {M}}}_{\lambda ,a}^{0}.$ Then $J_{\lambda ,a}^{\prime }\left( u_{0}\right) =0$ in $H^{-1}({{\mathbb {R}}}^{3}).$

Proof

The proof of Lemma 2.1 is essentially the same as that in Brown–Zhang [8, Theorem 2.3] (or see Binding–Drábek–Huang [4]), so omitted it here. $\square$

For each $u\in {{\mathbf {M}}}_{\lambda ,a},$ we find that

$$\begin{aligned} h_{\lambda ,u}^{\prime \prime }\left( 1\right)= & {} \left\| u\right\| _{H^{1}}^{2}+3\lambda \int _{{{\mathbb {R}}}^{3}}\phi _{u}u^{2}dx-\left( p-1\right) \int _{{{\mathbb {R}}}^{3}}a\left( x\right) \left| u\right| ^{p}dx \nonumber \\= & {} -\left( p-2\right) \left\| u\right\| _{H^{1}}^{2}+\lambda \left( 4-p\right) \int _{{{\mathbb {R}}}^{3}}\phi _{u}u^{2}dx \end{aligned}$$

(2.2)

$$\begin{aligned}= & {} -2\left\| u\right\| _{H^{1}}^{2}+\left( 4-p\right) \int _{{{\mathbb {R}}} ^{3}}a\left( x\right) \left| u\right| ^{p}dx. \end{aligned}$$

(2.3)

For each $u\in {{\mathbf {M}}}_{\lambda ,a}^{-}$, using (2.1) and (2.3) gives

$$\begin{aligned} J_{\lambda ,a}(u)= & {} \frac{1}{4}\left\| u\right\| _{H^{1}}^{2}-\frac{ 4-p}{4p}\int _{{{\mathbb {R}}}^{3}}a\left( x\right) \left| u\right| ^{p}dx> \frac{p-2}{4p}\left\| u\right\| _{H^{1}}^{2} \\\ge & {} \frac{p-2}{4p}\left( \frac{S_{p}^{p}}{a_{\max }}\right) ^{2/\left( p-2\right) }. \end{aligned}$$

Hence, we obtain the following result.

Lemma 2.2

The energy functional $J_{\lambda ,a}$ is coercive and bounded below on ${{\mathbf {M}}}_{\lambda ,a}^{-}.$ Furthermore,

$$\begin{aligned} J_{\lambda ,a}(u)>\frac{p-2}{4p}\left( \frac{S_{p}^{p}}{a_{\max }}\right) ^{2/(p-2)}\text { for all }u\in {{\mathbf {M}}}_{\lambda ,a}^{-}. \end{aligned}$$

The function $\phi _{u}$ defined in (1.1) for $\rho \equiv 1$ possesses the following properties (see [3, 23]).

Lemma 2.3

For each $u\in H^{1}({{\mathbb {R}}}^{3})$, the following two inequalities are true.

• $\left( i\right)$ $\phi _{u}\ge 0;$

• $\left( ii\right)$ $\int _{{{\mathbb {R}}}^{3}}\phi _{u}u^{2}dx\le {{\overline{S}}}^{-2}S_{12/5}^{-4}\Vert u\Vert _{H^{1}}^{4}.$

Lemma 2.4

Suppose that $2<p<3$ and $\lambda ,d>0.$ Let $f_{\lambda ,d}\left( s\right) =\frac{1}{4}+\sqrt{\frac{\lambda }{8}}s-\frac{d}{p}s^{p-2}$ for $s\ge 0.$ Then there exist $d_{\lambda ,p}:=\frac{p}{A\left( p\right) } \lambda ^{\left( p-2\right) /2}$ and $s_{\lambda ,p}\left( d\right) :=\left[ \frac{d\left( p-2\right) }{p}\sqrt{\frac{8}{\lambda }}\right] ^{1/\left( 3-p\right) }$ satisfying$\left( i\right)$ $f_{\lambda ,d}^{\prime }\left( s_{\lambda ,p}\left( d\right) \right) =0$ and $f_{\lambda ,d_{\lambda ,p}}\left( s_{\lambda ,p}\left( d_{\lambda ,p}\right) \right) =0;$ $\left( ii\right)$ for each $d>d_{\lambda ,p}$ there exist $\eta _{d},\xi _{d}>0$ such that $\eta _{d}<s_{\lambda ,p}\left( d\right) <\xi _{d}$ and $f_{\lambda ,d}\left( s\right) <0$ for all $s\in \left( \eta _{d},\xi _{d}\right) ;$ $\left( iii\right)$ for each $0<d<d_{\lambda ,p},$ $f_{\lambda ,d}\left( s\right) >0$ for all $s>0.$

Proof

By a straightforward calculation, we can show that the results are true. $\square$

Following the idea of Lions [19] (or see [23]), we have

$$\begin{aligned} \sqrt{\frac{\lambda }{8}}\int _{{{\mathbb {R}}}^{3}}\left| u\right| ^{3}dx= & {} \sqrt{\frac{\lambda }{8}}\int _{{{\mathbb {R}}}^{3}}\left( -\Delta \phi _{u}\right) \left| u\right| dx=\sqrt{\frac{\lambda }{8}}\int _{ {{\mathbb {R}}}^{3}}\left\langle \nabla \phi _{u},\nabla \left| u\right| \right\rangle dx \nonumber \\\le & {} \frac{1}{4}\int _{{{\mathbb {R}}}^{3}}\left| \nabla u\right| ^{2}dx+ \frac{\lambda }{8}\int _{{{\mathbb {R}}}^{3}}\left| \nabla \phi _{u}\right| ^{2}dx \nonumber \\= & {} \frac{1}{4}\int _{{{\mathbb {R}}}^{3}}\left| \nabla u\right| ^{2}dx+ \frac{\lambda }{8}\int _{{{\mathbb {R}}}^{3}}\phi _{u}u^{2}dx\text { for all }u\in H^{1}({{\mathbb {R}}}^{3}), \end{aligned}$$

(2.4)

this implies that

$$\begin{aligned} J_{\lambda ,a}(u)\ge & {} \frac{1}{4}\left\| u\right\| _{H^{1}}^{2}+\int _{{{\mathbb {R}}}^{3}}\left( \frac{1}{4}u^{2}+\sqrt{\frac{ \lambda }{8}}\left| u\right| ^{3}-\frac{1}{p}a\left( x\right) \left| u\right| ^{p}\right) dx+\frac{\lambda }{8}\int _{{{\mathbb {R}}} ^{3}}\phi _{u}u^{2}dx \nonumber \\= & {} \frac{1}{4}\left\| u\right\| _{H^{1}}^{2}+\int _{\left\{ a(x)>\frac{ p\lambda ^{\left( p-2\right) /2}}{A\left( p\right) }\right\} }u^{2}\left( \frac{1}{4}+\sqrt{\frac{\lambda }{8}}\left| u\right| -\frac{1}{p} a\left( x\right) \left| u\right| ^{p-2}\right) dx \nonumber \\&+\int _{\left\{ a\left( x\right) \le \frac{p\lambda ^{\left( p-2\right) /2} }{A\left( p\right) }\right\} }u^{2}\left( \frac{1}{4}+\sqrt{\frac{\lambda }{8 }}\left| u\right| -\frac{1}{p}a\left( x\right) \left| u\right| ^{p-2}\right) dx \nonumber \\&+\frac{\lambda }{8}\int _{{{\mathbb {R}}}^{3}}\phi _{u}u^{2}dx. \end{aligned}$$

(2.5)

Then by Lemma 2.4 and (2.5), for each

$$\begin{aligned} \left[ \frac{A\left( p\right) }{p}a_{\infty }\right] ^{2/\left( p-2\right) }<\lambda \le \left[ \frac{A\left( p\right) }{p}a_{1}\right] ^{2/\left( p-2\right) }, \end{aligned}$$

we have

$$\begin{aligned} J_{\lambda ,a}(u)\ge & {} \frac{1}{4}\left\| u\right\| _{H^{1}}^{2}+\int _{\left\{ a(x)>\frac{p\lambda ^{\left( p-2\right) /2}}{ A\left( p\right) }\right\} }u^{2}\left( \frac{1}{4}+\sqrt{\frac{\lambda }{8}} \left| u\right| -\frac{1}{p}a(x)\left| u\right| ^{p-2}\right) dx \nonumber \\\ge & {} \frac{1}{4}\left\| u\right\| _{H^{1}}^{2}+\int _{\left\{ a(x)> \frac{p\lambda ^{\left( p-2\right) /2}}{A\left( p\right) }\right\} }m_{\lambda }\left( x\right) dx, \end{aligned}$$

(2.6)

where $m_{\lambda }\left( x\right) =\inf _{s\ge 0}\left( \frac{1}{4}s^{2}+ \sqrt{\frac{\lambda }{8}}s^{3}-\frac{1}{p}a\left( x\right) s^{p}\right) <0$ for all $x\in \left\{ a\left( x\right) >\frac{p\lambda ^{\left( p-2\right) /2}}{A\left( p\right) }\right\} .$

Note that

$$\begin{aligned} \inf _{x\in \left\{ a\left( x\right) >\frac{p\lambda ^{\left( p-2\right) /2}}{ A\left( p\right) }\right\} }m_{\lambda }\left( x\right) \le \frac{1}{4} s_{\lambda ,p}^{2}\left( a_{\max }\right) +\sqrt{\frac{\lambda }{8}} s_{\lambda ,p}^{3}\left( a_{\max }\right) -\frac{1}{p}a_{\max }s_{\lambda ,p}^{p}\left( a_{\max }\right) <0, \end{aligned}$$

and

$$\begin{aligned} 0>\int _{\left\{ a\left( x\right)>\frac{p\lambda ^{\left( p-2\right) /2}}{ A\left( p\right) }\right\} }m_{\lambda }\left( x\right) dx\ge \left| \left\{ a\left( x\right)>\frac{p\lambda ^{\left( p-2\right) /2}}{A\left( p\right) }\right\} \right| \inf _{x\in \left\{ a\left( x\right) >\frac{ p\lambda ^{\left( p-2\right) /2}}{A\left( p\right) }\right\} }m_{\lambda }\left( x\right) , \qquad \nonumber \\ \end{aligned}$$

(2.7)

where $s_{\lambda ,p}\left( a_{\max }\right) =\left[ \frac{a_{\max }\left( p-2\right) }{p}\sqrt{\frac{8}{\lambda }}\right] ^{1/\left( 3-p\right) }.$ Furthermore, the following results are true.

Theorem 2.5

Suppose that $2<p<3$ and conditions $(D1)-\left( D2\right)$ hold. Then for each $\left[ \frac{A\left( p\right) }{p}a_{\infty }\right] ^{2/\left( p-2\right) }<\lambda \le \left[ \frac{A\left( p\right) }{p}a_{1} \right] ^{2/\left( p-2\right) },$ $J_{\lambda ,a}$ is coercive and bounded below on $H^{1}({{\mathbb {R}}}^{3}).$ Furthermore,

$$\begin{aligned} \inf _{u\in H^{1}({{\mathbb {R}}}^{3})}J_{\lambda ,a}(u)>\int _{\left\{ a\left( x\right)>\frac{p\lambda ^{\left( p-2\right) /2}}{A\left( p\right) }\right\} }m_{\lambda }\left( x\right) dx>-\infty . \end{aligned}$$

Proof

Since

$$\begin{aligned} 0<a_{\infty }<\frac{p}{A\left( p\right) }\lambda ^{\left( p-2\right) /2}\le a_{1}<a_{\max }\text { for all }\left[ \frac{A\left( p\right) }{p}a_{\infty } \right] ^{2/\left( p-2\right) }<\lambda \le \left[ \frac{A\left( p\right) }{ p}a_{1}\right] ^{2/\left( p-2\right) }, \end{aligned}$$

by conditions $\left( D1\right)$ and $\left( D2\right)$, we conclude that

$$\begin{aligned} 0<\left| \left\{ a\left( x\right) >\frac{p\lambda ^{\left( p-2\right) /2} }{A\left( p\right) }\right\} \right| <\infty . \end{aligned}$$

(2.8)

Thus, by (2.6)–(2.8),

$$\begin{aligned} 0>\int _{\left\{ a\left( x\right)>\frac{p\lambda ^{\left( p-2\right) /2}}{ A\left( p\right) }\right\} }m_{\lambda }\left( x\right) dx>-\infty \end{aligned}$$

and

$$\begin{aligned} J_{\lambda ,a}(u)\ge \frac{1}{4}\left\| u\right\| _{H^{1}}^{2}+\int _{\left\{ a\left( x\right) >\frac{p\lambda ^{\left( p-2\right) /2}}{A\left( p\right) }\right\} }m_{\lambda }\left( x\right) dx. \end{aligned}$$

This completes the proof. $\square$

Lemma 2.6

Suppose that $2<p<3.$ Let $\lambda >\left[ \frac{A\left( p\right) }{p}a_{\infty }\right] ^{2/\left( p-2\right) }$ and let $u_{\lambda }$ be a non-trivial solution of the following equation:

Then $J_{\lambda ,a_{\infty }}(u_{\lambda })>0,$ where $J_{\lambda ,a_{\infty }}=J_{\lambda ,a}$ for $a\equiv a_{\infty }.$

Proof

By Lemma 2.4 and (2.4)–(2.5) ,

$$\begin{aligned} J_{\lambda ,a_{\infty }}(u)\ge & {} \frac{1}{4}\left\| u\right\| _{H^{1}}^{2}+\int _{{{\mathbb {R}}}^{3}}u^{2}\left( \frac{1}{4}+\sqrt{\frac{ \lambda }{8}}\left| u\right| -\frac{1}{p}a_{\infty }\left| u\right| ^{p-2}\right) dx \\> & {} 0\text { for all }u\in H^{1}({{\mathbb {R}}}^{3})\setminus \left\{ 0\right\} . \end{aligned}$$

This completes the proof. $\square$

Let $\kappa _{0}:=\frac{A\left( p\right) S_{p}^{p}}{4-p}\left( \frac{4-p}{ 2\left( p-2\right) {{\overline{S}}}^{2}S_{12/5}^{4}}\right) ^{\left( p-2\right) /2}a_{1}.$ Define the filtration of Nehari manifold ${{\mathbf {M}}}_{\lambda ,a}$ as follows.

$$\begin{aligned} {{\mathbf {M}}}_{\lambda ,a}\left[ \frac{p-2}{2p}\left( \frac{S_{p}^{p}}{\kappa _{0}}\right) ^{2/\left( p-2\right) }\right] =\left\{ u\in {{\mathbf {M}}} _{\lambda ,a}:J_{\lambda ,a}\left( u\right) <\frac{p-2}{2p}\left( \frac{ S_{p}^{p}}{\kappa _{0}}\right) ^{2/\left( p-2\right) }\right\} . \end{aligned}$$

Then we have the following results.

Lemma 2.7

Suppose that $2<p<3$ and conditions $(D1)-\left( D2\right)$ hold. Then for each $\left[ \frac{A\left( p\right) }{p}a_{\infty }\right] ^{2/\left( p-2\right) }<\lambda \le \left[ \frac{A\left( p\right) }{p}a_{1} \right] ^{2/\left( p-2\right) },$ there exist two $C^{1}$ submanifolds ${{\mathbf {M}}}_{\lambda ,a}^{(1)}\subset {{\mathbf {M}}}_{\lambda ,a}^{-}$ and ${{\mathbf {M}}}_{\lambda ,a}^{(2)}\subset {{\mathbf {M}}}_{\lambda ,a}^{+}$ such that ${{\mathbf {M}}}_{\lambda ,a}\left[ \frac{p-2}{2p}\left( \frac{S_{p}^{p}}{\kappa _{0}}\right) ^{2/\left( p-2\right) }\right] ={{\mathbf {M}}}_{\lambda ,a}^{(1)}\cup {{\mathbf {M}}}_{\lambda ,a}^{(2)}.$ Furthermore, each local minimizer of the functional $J_{\lambda }$ in the submanifolds ${{\mathbf {M}}} _{\lambda ,a}^{(1)}$ and ${{\mathbf {M}}}_{\lambda ,a}^{(2)}$ is a critical point of $J_{\lambda ,a}$ in $H^{1}({{\mathbb {R}}}^{3}).$

Proof

Let $u\in {{\mathbf {M}}}_{\lambda ,a}$ with $J_{\lambda ,a}\left( u\right) < \frac{p-2}{2p}\left( \frac{S_{p}^{p}}{\kappa _{0}}\right) ^{2/\left( p-2\right) }.$ Then we have

$$\begin{aligned} \frac{p-2}{2p}\left( \frac{S_{p}^{p}}{\kappa _{0}}\right) ^{2/\left( p-2\right) }>J_{\lambda ,a}(u)\ge \frac{p-2}{2p}\left\| u\right\| _{H^{1}}^{2}-\frac{\lambda \left( 4-p\right) }{4p{{\overline{S}}}^{2}S_{12/5}^{4} }\Vert u\Vert _{H^{1}}^{4}. \end{aligned}$$

(2.9)

Now, we consider the quadratic equation as follows

$$\begin{aligned} \frac{\lambda \left( 4-p\right) }{2\left( p-2\right) {{\overline{S}}} ^{2}S_{12/5}^{4}}x^{2}-x+\left( \frac{S_{p}^{p}}{\kappa _{0}}\right) ^{2/\left( p-2\right) }=0. \end{aligned}$$

It is easily seen that one of its solutions is expressed as

$$\begin{aligned} x_{0}=\left( 1\pm \sqrt{1-\frac{2\lambda \left( 4-p\right) }{\left( p-2\right) {{\overline{S}}}^{2}S_{12/5}^{4}}\left( \frac{S_{p}^{p}}{\kappa _{0}} \right) ^{\frac{2}{p-2}}}\right) \frac{\left( p-2\right) {{\overline{S}}} ^{2}S^{4}}{\lambda \left( 4-p\right) }. \end{aligned}$$

(2.10)

Since

$$\begin{aligned} \lambda \le \left[ \frac{A\left( p\right) }{p}a_{1}\right] ^{2/\left( p-2\right) }=\frac{2\left( p-2\right) {{\overline{S}}}^{2}S_{12/5}^{4}}{4-p} \left( \frac{\left( 4-p\right) \kappa _{0}}{pS_{p}^{p}}\right) ^{2/\left( p-2\right) }<\frac{\left( p-2\right) {{\overline{S}}}^{2}S_{12/5}^{4}}{2\left( 4-p\right) }\left( \frac{\kappa _{0}}{S_{p}^{p}}\right) ^{2/\left( p-2\right) } \end{aligned}$$

and

$$\begin{aligned} 4\left( \frac{4-p}{p}\right) ^{2/\left( p-2\right) }<4e^{-2}\approx 0.541\,34<1\text { for all }2<p<3, \end{aligned}$$

it follows from (2.10) and (2.9) that if $\left[ \frac{A\left( p\right) }{p}a_{\infty }\right] ^{2/\left( p-2\right) }<\lambda \le \left[ \frac{A\left( p\right) }{p}a_{1}\right] ^{2/\left( p-2\right) },$ then there exist two positive numbers ${{\widehat{D}}}_{1}$ and ${{\widehat{D}}}_{2}$ satisfying

$$\begin{aligned} \left( \frac{S_{p}^{p}}{a_{\max }}\right) ^{1/\left( p-2\right) }<{{\widehat{D}}} _{1}\le \sqrt{2}\left( \frac{S_{p}^{p}}{\kappa _{0}}\right) ^{1/\left( p-2\right) }<\sqrt{\frac{\left( p-2\right) {{\overline{S}}}^{2}S_{12/5}^{4}}{ \lambda \left( 4-p\right) }}<{{\widehat{D}}}_{2} \end{aligned}$$

(2.11)

such that

$$\begin{aligned} \left\| u\right\| _{H^{1}}<{{\widehat{D}}}_{1}\text { or }\left\| u\right\| _{H^{1}}>{{\widehat{D}}}_{2}. \end{aligned}$$

Thus, we have

$$\begin{aligned} {{\mathbf {M}}}_{\lambda ,a}\left[ \frac{p-2}{2p}\left( \frac{S_{p}^{p}}{\kappa _{0}}\right) ^{2/\left( p-2\right) }\right] ={{\mathbf {M}}}_{\lambda ,a}^{(1)}\cup {{\mathbf {M}}}_{\lambda ,a}^{(2)}, \end{aligned}$$

(2.12)

where

$$\begin{aligned} {{\mathbf {M}}}_{\lambda ,a}^{(1)}:=\left\{ u\in {{\mathbf {M}}}_{\lambda ,a}\left[ \frac{p-2}{2p}\left( \frac{S_{p}^{p}}{\kappa _{0}}\right) ^{2/\left( p-2\right) }\right] :\left\| u\right\| _{H^{1}}<{{\widehat{D}}} _{1}\right\} \end{aligned}$$

and

$$\begin{aligned} {{\mathbf {M}}}_{\lambda ,a}^{(2)}:=\left\{ u\in {{\mathbf {M}}}_{\lambda ,a}\left[ \frac{p-2}{2p}\left( \frac{S_{p}^{p}}{\kappa _{0}}\right) ^{2/\left( p-2\right) }\right] :\left\| u\right\| _{H^{1}}>{{\widehat{D}}} _{2}\right\} . \end{aligned}$$

Moreover, by (2.3) and (2.10) and Lemma 2.3, we have

$$\begin{aligned} h_{\lambda ,u}^{\prime \prime }\left( 1\right)\le & {} -\left( p-2\right) \left\| u\right\| _{H^{1}}^{2}+\lambda \left( 4-p\right) \int _{\mathbb { R}^{3}}\phi _{u}u^{2}dx \\\le & {} \left( p-2\right) \left\| u\right\| _{H^{1}}^{2}\left( \frac{ 2\lambda \left( 4-p\right) }{{{\overline{S}}}^{2}S_{12/5}^{4}\left( p-2\right) } \left( \frac{S_{p}^{p}}{\kappa _{0}}\right) ^{2/\left( p-2\right) }-1\right) \\< & {} 0\text { for all }u\in {{\mathbf {M}}}_{\lambda ,a}^{(1)}; \end{aligned}$$

here we have using $\frac{1}{2^{\left( p-2\right) /2}}-\frac{4-p}{p}>0$ for $2<p<3.$ This implies that ${{\mathbf {M}}}_{\lambda ,a}^{(1)}\subset {{\mathbf {M}}} _{\lambda ,a}^{-}.$ Using (2.10) we derive that

$$\begin{aligned} \frac{1}{4}\left\| u\right\| _{H^{1}}^{2}-\frac{4-p}{4p}\int _{\mathbb {R }^{3}}a\left( x\right) |u|^{p}dx= & {} J_{\lambda ,a}\left( u\right)<\frac{p-2 }{2p}\left( \frac{S_{p}^{p}}{\kappa _{0}}\right) ^{2/\left( p-2\right) } \\< & {} \frac{p-2}{4p}\left\| u\right\| _{H^{1}}^{2}\text { for all }u\in {{\mathbf {M}}}_{\lambda ,a}^{(2)}, \end{aligned}$$

which implies that

$$\begin{aligned} h_{\lambda ,u}^{\prime \prime }\left( 1\right) =-2\left\| u\right\| _{H^{1}}^{2}+\left( 4-p\right) \int _{{{\mathbb {R}}}^{3}}a\left( x\right) \left| u\right| ^{p}dx>0\text { for all }u\in {{\mathbf {M}}}_{\lambda ,a}^{(2)}, \end{aligned}$$

and so ${{\mathbf {M}}}_{\lambda ,a}^{(2)}\subset {{\mathbf {M}}}_{\lambda ,a}^{+}.$ This completes the proof. $\square$

3 Non-emptiness of submanifolds ${{\mathbf {M}}}_{\lambda ,a}^{(i)}$

For $u\in H^{1}({{\mathbb {R}}}^{3})\backslash \left\{ 0\right\} ,$ we define

$$\begin{aligned} T_{a}\left( u\right) =\left( \frac{\left\| u\right\| _{H^{1}}^{2}}{ \int _{{{\mathbb {R}}}^{3}}a\left( x\right) \left| u\right| ^{p}dx}\right) ^{\frac{1}{p-2}}. \end{aligned}$$

Then we have the following results.

Lemma 3.1

Suppose that $2<p<3$ and conditions $(D1)-\left( D2\right)$ hold. Then for each $\left[ \frac{A\left( p\right) }{p}a_{\infty }\right] ^{2/\left( p-2\right) }<\lambda \le \left[ \frac{A\left( p\right) }{p}a_{1} \right] ^{2/\left( p-2\right) }$ and $u\in H^{1}({{\mathbb {R}}}^{3})\backslash \left\{ 0\right\}$ satisfying $\int _{{{\mathbb {R}}}^{3}}a\left( x\right) \left| u\right| ^{p}dx>\kappa _{0}S_{p}^{-p}\left\| u\right\| _{H^{1}}^{p},$ there exists a constant ${{\widehat{t}}}_{\lambda }^{\left( 0\right) }>\left( \frac{p}{4-p}\right) ^{1/\left( p-2\right) }T_{a}\left( u\right)$ such that

$$\begin{aligned} \inf _{t\ge 0}J_{\lambda ,a}\left( tu\right) =\inf _{\left( \frac{p}{4-p} \right) ^{1/\left( p-2\right) }T_{a}\left( u\right)<t<{{\widehat{t}}}_{\lambda }^{\left( 0\right) }}J_{\lambda ,a}\left( tu\right) <0. \end{aligned}$$

(3.1)

Proof

For any $u\in H^{1}({{\mathbb {R}}}^{3})\backslash \left\{ 0\right\}$ and $t>0$, it has

$$\begin{aligned} J_{\lambda ,a}\left( tu\right)= & {} \frac{t^{2}}{2}\left\| u\right\| _{H^{1}}^{2}+\frac{\lambda t^{4}}{4}\int _{{{\mathbb {R}}}^{3}}\phi _{u}u^{2}dx- \frac{t^{p}}{p}\int _{{{\mathbb {R}}}^{3}}a\left( x\right) \left| u\right| ^{p}dx \\= & {} t^{4}\left[ g\left( t\right) +\frac{\lambda }{4}\int _{{{\mathbb {R}}}^{3}}\phi _{u}u^{2}dx\right] \\= & {} h_{\lambda ,u}(t), \end{aligned}$$

where

$$\begin{aligned} g\left( t\right) =\frac{t^{-2}}{2}\left\| u\right\| _{H^{1}}^{2}-\frac{ t^{p-4}}{p}\int _{{{\mathbb {R}}}^{3}}a\left( x\right) \left| u\right| ^{p}dx. \end{aligned}$$

Clearly, $J_{\lambda ,a}\left( tu\right) =0$ if and only if

$$\begin{aligned} g\left( t\right) +\frac{\lambda }{4}\int _{{{\mathbb {R}}}^{3}}\phi _{u}u^{2}dx=0. \end{aligned}$$

It is not difficult to observe that

$$\begin{aligned} g\left( {{\hat{t}}}_{a}\right) =0,\ \ \lim _{t\rightarrow 0^{+}}g(t)=\infty \ \text { and }\ \lim _{t\rightarrow \infty }g(t)=0, \end{aligned}$$

where ${{\hat{t}}}_{a}=\left( \frac{p}{2}\right) ^{1/\left( p-2\right) }T_{a}(u).$ Considering the derivative of g(t), we find

$$\begin{aligned} g^{\prime }\left( t\right)= & {} -t^{-3}\left\| u\right\| _{H^{1}}^{2}+ \frac{\left( 4-p\right) t^{p-5}}{p}\int _{{{\mathbb {R}}}^{3}}a\left( x\right) \left| u\right| ^{p}dx \\= & {} t^{-3}\left( \frac{\left( 4-p\right) t^{p-2}}{p}\int _{{{\mathbb {R}}} ^{3}}a\left( x\right) \left| u\right| ^{p}dx-\left\| u\right\| _{H^{1}}^{2}\right) , \end{aligned}$$

which implies that $g\left( t\right)$ is decreasing when $0<t<\left( \frac{p }{4-p}\right) ^{1/\left( p-2\right) }T_{a}\left( u\right)$ and increasing when $t>\left( \frac{p}{4-p}\right) ^{1/\left( p-2\right) }T_{a}\left( u\right) ,$ and so

$$\begin{aligned} \inf _{t>0}g\left( t\right)= & {} g\left[ \left( \frac{p}{4-p}\right) ^{1/\left( p-2\right) }T_{a}\left( u\right) \right] \nonumber \\= & {} -\frac{p-2}{2\left( 4-p\right) }\left( \frac{\left( 4-p\right) \int _{ {{\mathbb {R}}}^{3}}a\left( x\right) \left| u\right| ^{p}dx}{p\left\| u\right\| _{H^{1}}^{2}}\right) ^{2/\left( p-2\right) }\Vert u\Vert _{H^{1}}^{2}<0. \end{aligned}$$

(3.2)

It follows from Lemma 2.3$\left( ii\right)$ that for each $u\in H^{1}\left( {{\mathbb {R}}}^{3}\right) \backslash \left\{ 0\right\}$ satisfying $\int _{{{\mathbb {R}}}^{3}}a\left( x\right) \left| u\right| ^{p}dx>\kappa _{0}S_{p}^{-p}\left\| u\right\| _{H^{1}}^{p}$ we have

$$\begin{aligned} \inf _{t>0}g\left( t\right)< & {} -\frac{p-2}{2\left( 4-p\right) }\left( \frac{ \left( 4-p\right) \kappa _{0}}{pS_{p}^{p}}\right) ^{2/\left( p-2\right) }\Vert u\Vert _{H^{1}}^{4} \nonumber \\= & {} -\frac{1}{4{{\overline{S}}}^{2}S_{12/5}^{4}}\left( \frac{A\left( p\right) }{p} a_{1}\right) ^{2/\left( p-2\right) }\Vert u\Vert _{H^{1}}^{4} \nonumber \\\le & {} -\frac{\lambda }{4}{{\overline{S}}}^{-2}S_{12/5}^{-4}\left\| u\right\| _{H^{1}}^{4}\le -\frac{\lambda }{4}\int _{{{\mathbb {R}}}^{3}}\phi _{u}u^{2}dx. \end{aligned}$$

(3.3)

This indicates that there exist ${{\widehat{t}}}_{\lambda }^{\left( 0\right) }$ and ${{\widehat{t}}}_{\lambda }^{\left( 1\right) }$ satisfying

$$\begin{aligned} 0<{{\widehat{t}}}_{\lambda }^{\left( 1\right) }<\left( \frac{p}{4-p}\right) ^{1/\left( p-2\right) }T_{a}\left( u\right) <{{\widehat{t}}}_{\lambda }^{\left( 0\right) } \end{aligned}$$

(3.4)

such that

$$\begin{aligned} g\left( {{\widehat{t}}}_{\lambda }^{\left( j\right) }\right) +\frac{\lambda }{4} \int _{{{\mathbb {R}}}^{3}}\phi _{u}u^{2}dx=0\text { for }j=0,1. \end{aligned}$$

That is,

$$\begin{aligned} J_{\lambda ,a}\left( {{\widehat{t}}}_{\lambda }^{\left( j\right) }u\right) =0 \text { for }j=0,1. \end{aligned}$$

Moreover, by (3.2) and (3.3) , for each $\left[ \frac{A\left( p\right) }{p}a_{\infty }\right] ^{2/\left( p-2\right) }<\lambda \le \left[ \frac{A\left( p\right) }{p}a_{1}\right] ^{2/\left( p-2\right) }$ and $u\in H^{1}({{\mathbb {R}}}^{3})\backslash \left\{ 0\right\}$ satisfying

$$\begin{aligned} \int _{{{\mathbb {R}}}^{3}}a\left( x\right) \left| u\right| ^{p}dx>\kappa _{0}S_{p}^{-p}\left\| u\right\| _{H^{1}}^{p}, \end{aligned}$$

we have

$$\begin{aligned} \inf _{t>0}J_{\lambda ,a}\left( tu\right) \le J_{\lambda ,a}\left( \left( \frac{p}{4-p}\right) ^{1/(p-2)}T_{a}\left( u\right) u\right) <0. \end{aligned}$$

Note that

$$\begin{aligned} h_{\lambda ,u}^{\prime }\left( t\right) =4t^{3}\left( g\left( t\right) + \frac{\lambda }{4}\int _{{{\mathbb {R}}}^{3}}\phi _{u}u^{2}dx\right) +t^{4}g^{\prime }(t), \end{aligned}$$

which leads to

$$\begin{aligned} h_{\lambda ,u}^{\prime }\left( t\right) <0\text { for all }t\in \left( {{\widehat{t}}}_{\lambda }^{\left( 1\right) },\,\left( \frac{p}{4-p}\right) ^{1/\left( p-2\right) }T_{a}\left( u\right) \right] \end{aligned}$$

and

$$\begin{aligned} h_{\lambda ,u}^{\prime }\left( {{\widehat{t}}}_{\lambda }^{\left( 0\right) }\right) >0. \end{aligned}$$

Consequently, we arrive at inequality (3.1). $\square$

Lemma 3.2

Suppose that $2<p<3$ and conditions $(D1)-\left( D2\right)$ hold. Then for each $\left[ \frac{A\left( p\right) }{p}a_{\infty }\right] ^{2/\left( p-2\right) }<\lambda \le \left[ \frac{A\left( p\right) }{p}a_{1} \right] ^{2/\left( p-2\right) }$ and $u\in H^{1}({{\mathbb {R}}}^{3})\backslash \left\{ 0\right\}$ satisfying $\int _{{{\mathbb {R}}}^{3}}a\left( x\right) \left| u\right| ^{p}dx>\kappa _{0}S_{p}^{-p}\left\| u\right\| _{H^{1}}^{p},$ there exist two constants $t_{\lambda ,a}^{+}$ and $t_{\lambda ,a}^{-}$ which satisfy

$$\begin{aligned} T_{a}\left( u\right)<t_{\lambda ,a}^{-}<\left( \frac{2}{4-p}\right) ^{\frac{ 1}{p-2}}T_{a}\left( u\right) <t_{\lambda ,a}^{+} \end{aligned}$$

such that

$$\begin{aligned} t_{\lambda ,a}^{\pm }u\in {{\mathbf {M}}}_{\lambda ,a}^{\pm },\quad J_{\lambda ,a}\left( t_{\lambda ,a}^{-}u\right) =\sup _{0\le t\le t_{\lambda ,a}^{+}}J_{\lambda ,a}\left( tu\right) \end{aligned}$$

and

$$\begin{aligned} J_{\lambda ,a}\left( t_{\lambda ,a}^{+}u\right) =\inf _{t\ge t_{\lambda ,a}^{-}}J_{\lambda ,a}\left( tu\right) =\inf _{t\ge 0}J_{\lambda ,a}\left( tu\right) <0. \end{aligned}$$

Proof

Define

$$\begin{aligned} f\left( t\right) =t^{-2}\left\| u\right\| _{H^{1}}^{2}-t^{p-4}\int _{ {{\mathbb {R}}}^{3}}a\left( x\right) \left| u\right| ^{p}dx\text { for } t>0. \end{aligned}$$

Clearly, $tu\in {{\mathbf {M}}}_{\lambda ,a}$ if and only if $f\left( t\right) +\lambda \int _{{{\mathbb {R}}}^{3}}\phi _{u}u^{2}dx=0.$ A straightforward evaluation gives

$$\begin{aligned} f\left( T_{a}\left( u\right) \right) =0,\ \lim _{t\rightarrow 0^{+}}f(t)=\infty \text { and }\lim _{t\rightarrow \infty }f(t)=0. \end{aligned}$$

Since

$$\begin{aligned} f^{\prime }\left( t\right) =t^{-3}\left( -2\left\| u\right\| _{H^{1}}^{2}+\left( 4-p\right) t^{p-2}\int _{{{\mathbb {R}}}^{3}}a\left( x\right) \left| u\right| ^{p}dx\right) , \end{aligned}$$

we find that $f\left( t\right)$ is decreasing when $0<t<\left( \frac{2}{4-p} \right) ^{1/\left( p-2\right) }T_{a}\left( u\right)$ and increasing when $t>\left( \frac{2}{4-p}\right) ^{1/\left( p-2\right) }T_{a}(u).$ This gives

$$\begin{aligned} \inf _{t>0}f\left( t\right) =f\left( \left( \frac{2}{4-p}\right) ^{\frac{1}{ p-2}}T_{a}(u)\right) . \end{aligned}$$

(3.5)

It follows from Lemma 2.3$\left( ii\right)$ that for each $\left[ \frac{A\left( p\right) }{p}a_{\infty }\right] ^{2/\left( p-2\right) }<\lambda \le \left[ \frac{A\left( p\right) }{p}a_{1}\right] ^{2/\left( p-2\right) }$ and $u\in H^{1}({{\mathbb {R}}}^{3})\backslash \left\{ 0\right\}$ satisfying

$$\begin{aligned} \int _{{{\mathbb {R}}}^{3}}a\left( x\right) \left| u\right| ^{p}dx>\kappa _{0}S_{p}^{-p}\left\| u\right\| _{H^{1}}^{p}, \end{aligned}$$

we have

$$\begin{aligned} f\left( \left( \frac{2}{4-p}\right) ^{1/(p-2)}T_{a}\left( u\right) \right)< & {} -\frac{1}{2}\left( \frac{p}{2}\right) ^{2/(p-2)}{{\overline{S}}} ^{-2}S_{12/5}^{-4}\left( \frac{A\left( p\right) }{p}a_{1}\right) ^{2/(p-2)}\left\| u\right\| _{H^{1}}^{4} \\\le & {} -\frac{1}{2}\left( \frac{p}{2}\right) ^{2/(p-2)}\lambda {{\overline{S}}} ^{-2}S_{12/5}^{-4}\left\| u\right\| _{H^{1}}^{4} \\< & {} -\lambda \int _{{{\mathbb {R}}}^{3}}\phi _{u}u^{2}dx. \end{aligned}$$

Thus, there exist two constants $t_{\lambda ,a}^{+}$ and $t_{\lambda ,a}^{-}>0$ which satisfy

$$\begin{aligned} T_{a}\left( u\right)<t_{\lambda ,a}^{-}<\left( \frac{2}{4-p}\right) ^{1/\left( p-2\right) }T_{a}\left( u\right) <t_{\lambda ,a}^{+} \end{aligned}$$

(3.6)

such that

$$\begin{aligned} f\left( t_{\lambda ,a}^{\pm }\right) +\lambda \int _{{{\mathbb {R}}}^{3}}\phi _{u}u^{2}dx=0. \end{aligned}$$

That is, $t_{\lambda ,a}^{\pm }u\in {{\mathbf {M}}}_{\lambda ,a}.$ By a calculation on the second order derivatives, we find

$$\begin{aligned} h_{\lambda ,t_{\lambda ,a}^{-}u}^{\prime \prime }\left( 1\right)= & {} -2\left\| t_{\lambda ,a}^{-}u\right\| _{H^{1}}^{2}+\left( 4-p\right) \int _{{{\mathbb {R}}}^{3}}a\left( x\right) \left| t_{\lambda ,a}^{-}u\right| ^{p}dx \\= & {} \left( t_{\lambda ,a}^{-}\right) ^{5}f^{\prime }\left( t_{\lambda ,a}^{-}\right) <0 \end{aligned}$$

and

$$\begin{aligned} h_{\lambda ,t_{\lambda ,a}^{+}u}^{\prime \prime }\left( 1\right)= & {} -2\left\| t_{\lambda ,a}^{+}u\right\| _{H^{1}}^{2}+\left( 4-p\right) \int _{{{\mathbb {R}}}^{3}}a\left( x\right) \left| t_{\lambda ,a}^{+}u\right| ^{p}dx \\= & {} \left( t_{\lambda ,a}^{+}\right) ^{5}f^{\prime }\left( t_{\lambda ,a}^{+}\right) >0. \end{aligned}$$

This implies that $t_{\lambda ,a}^{\pm }u\in {{\mathbf {M}}}_{\lambda ,a}^{\pm }$ and

$$\begin{aligned} h_{\lambda ,u}^{\prime }\left( t\right) =t^{3}\left( f(t)+\lambda \int _{ {{\mathbb {R}}}^{3}}\phi _{u}u^{2}dx\right) . \end{aligned}$$

One can see that $h_{\lambda ,u}^{\prime }\left( t\right) >0$ holds for all $t\in \left( 0,t_{\lambda ,a}^{-}\right) \cup \left( t_{\lambda ,a}^{+},\infty \right)$ and $h_{\lambda ,u}^{\prime }\left( t\right) <0$ holds for all $t\in \left( t_{\lambda ,a}^{-},t_{\lambda ,a}^{+}\right)$. Subsequently,

$$\begin{aligned} J_{\lambda ,a}\left( t_{\lambda ,a}^{-}u\right) =\sup _{0\le t\le t_{\lambda ,a}^{+}}J_{\lambda ,a}\left( tu\right) \text { and }J_{\lambda ,a}\left( t_{\lambda ,a}^{+}u\right) =\inf _{t\ge t_{\lambda ,a}^{-}}J_{\lambda ,a}\left( tu\right) , \end{aligned}$$

and so $J_{\lambda ,a}\left( t_{\lambda ,a}^{+}u\right) <J_{\lambda ,a}(t_{\lambda ,a}^{-}u).$ Using Lemma 3.1, we conclude

$$\begin{aligned} J_{\lambda ,a}\left( t_{\lambda ,a}^{+}u\right) =\inf _{t\ge 0}J_{\lambda ,a}\left( tu\right) <0. \end{aligned}$$

This completes the proof. $\square$

For $b>0,$ we consider the following nonlinear Schrödinger equation.

From [14, 17], for every real number $b>0,$ Equation $(E_{0,b}^{\infty })$ has a unique radial positive solution $w_{b}$ with $w_{b}\left( 0\right) =\max _{x\in {{\mathbb {R}}}^{3}}w_{b}(x).$ Moreover,

$$\begin{aligned} \alpha _{0,b}^{\infty }:=\inf _{u\in {{\mathbf {M}}}_{0,b}^{\infty }}I_{b}^{\infty }\left( u\right) =I_{b}^{\infty }\left( w_{b}\right) =\frac{p-2}{2p}\left( \frac{S_{p}^{p}}{b}\right) ^{\frac{2}{p-2}}, \end{aligned}$$

where $I_{b}^{\infty }$ is the energy functional of Equation $(E_{0,b}^{\infty })$ in $H^{1}({{\mathbb {R}}}^{3})$ in the form

$$\begin{aligned} I_{b}^{\infty }\left( u\right) =\frac{1}{2}\int _{{{\mathbb {R}}}^{3}}(\left| \nabla u\right| ^{2}+u^{2})dx-\frac{1}{p}\int _{{{\mathbb {R}}} ^{3}}b\left| u\right| ^{p}dx \end{aligned}$$

(3.7)

with the Nehari manifold

$$\begin{aligned} {{\mathbf {M}}}_{0,b}^{\infty }=\{u\in H^{1}({{\mathbb {R}}}^{3})\backslash \left\{ 0\right\} :\left\langle \left( I_{b}^{\infty }\right) ^{\prime }\left( u\right) ,u\right\rangle =0\}. \end{aligned}$$

Let $w_{a_{\max }}$ be a unique radial positive solution of Equation $(E_{0,a_{\max }}^{\infty }).$ Then we have the following results.

Lemma 3.3

Suppose that $2<p<3$ and conditions ${(D1)}-{(D3)}$ hold. Then for each $\left[ \frac{A\left( p\right) }{p}a_{\infty }\right] ^{2/\left( p-2\right) }<\lambda \le \left[ \frac{A\left( p\right) }{p}a_{1}\right] ^{2/\left( p-2\right) }$ there exist two constants ${{\tilde{t}}}_{\lambda ,a}^{+}$ and ${{\tilde{t}}}_{\lambda ,a}^{-}$ satisfying

$$\begin{aligned} T_{a}\left( w_{a_{\max }}\right)<{{\tilde{t}}}_{\lambda ,a}^{-}<\left( \frac{2}{ 4-p}\right) ^{1/\left( p-2\right) }T_{a}\left( w_{a_{\max }}\right) <\tilde{t }_{\lambda ,a}^{+} \end{aligned}$$

such that ${{\tilde{t}}}_{\lambda ,a}^{-}w_{a_{\max }}\in {{\mathbf {M}}}_{\lambda ,a}^{(1)},\ {{\tilde{t}}}_{\lambda ,a}^{+}w_{a_{\max }}\in {{\mathbf {M}}}_{\lambda ,a}^{(2)}$ with

$$\begin{aligned} J_{\lambda ,a}\left( {{\tilde{t}}}_{\lambda ,a}^{-}w_{a_{\max }}\right) =\sup _{0\le t\le {{\tilde{t}}}_{\lambda ,a}^{+}}J_{\lambda ,a}\left( tw_{a_{\max }}\right) \text { and }J_{\lambda ,a}\left( {{\tilde{t}}}_{\lambda ,a}^{+}w_{a_{\max }}\right) =\inf _{t\ge {{\tilde{t}}}_{\lambda ,a}^{-}}J_{\lambda ,a}\left( tw_{a_{\max }}\right) <0. \end{aligned}$$

Proof

Since

$$\begin{aligned} \int _{{{\mathbb {R}}}^{3}}a\left( x\right) \left| w_{a_{\max }}\right| ^{p}dx>\frac{p\kappa _{0}}{2S_{p}^{p}}\left\| w_{a_{\max }}\right\| _{H^{1}}^{p}>\frac{\kappa _{0}}{S_{p}^{p}}\left\| w_{a_{\max }}\right\| _{H^{1}}^{p}, \end{aligned}$$

by Lemma 3.2, for each $\left[ \frac{A\left( p\right) }{p}a_{\infty } \right] ^{2/\left( p-2\right) }<\lambda \le \left[ \frac{A\left( p\right) }{ p}a_{1}\right] ^{2/\left( p-2\right) }$ there exist two constants ${{\tilde{t}}} _{\lambda ,a}^{+}$ and ${{\tilde{t}}}_{\lambda ,a}^{-}$ satisfying

$$\begin{aligned} T_{a}\left( w_{a_{\max }}\right)<{{\tilde{t}}}_{\lambda ,a}^{-}<\left( \frac{2}{ 4-p}\right) ^{1/\left( p-2\right) }T_{a}\left( w_{a_{\max }}\right) <\tilde{t }_{\lambda ,a}^{+} \end{aligned}$$

such that ${{\tilde{t}}}_{\lambda ,a}^{\pm }w_{a_{\max }}\in {{\mathbf {M}}}_{\lambda ,a}^{\pm },$

$$\begin{aligned} J_{\lambda ,a}\left( {{\tilde{t}}}_{\lambda ,a}^{-}w_{a_{\max }}\right) =\sup _{0\le t\le {{\tilde{t}}}_{\lambda ,a}^{+}}J_{\lambda ,a}(tw_{a_{\max }}) \end{aligned}$$

and

$$\begin{aligned} J_{\lambda ,a}\left( {{\tilde{t}}}_{\lambda ,a}^{+}w_{a_{\max }}\right) =\inf _{t\ge {{\tilde{t}}}_{\lambda ,a}^{-}}J_{\lambda ,a}\left( tw_{a_{\max }}\right) =\inf _{t\ge 0}J_{\lambda ,a}\left( tw_{a_{\max }}\right) <0. \end{aligned}$$

Using ${{\tilde{t}}}_{\lambda ,a}^{-}w_{a_{\max }}\in {{\mathbf {M}}}_{\lambda ,a}^{-}$ and condition $\left( D3\right) ,$ we have

$$\begin{aligned} J_{\lambda ,a}\left( {{\tilde{t}}}_{\lambda ,a}^{-}w_{a_{\max }}\right)= & {} \frac{\left( {{\tilde{t}}}_{\lambda ,a}^{-}\right) ^{2}}{4}\left\| w_{a_{\max }}\right\| _{H^{1}}^{2}-\frac{4-p}{4p}\left( {{\tilde{t}}}_{\lambda ,a}^{-}\right) ^{p}\int _{{{\mathbb {R}}}^{3}}a\left( x\right) w_{a_{\max }}^{p}dx \\< & {} \frac{\left( {{\tilde{t}}}_{\lambda ,a}^{-}\right) ^{2}}{4}\left\| w_{a_{\max }}\right\| _{H^{1}}^{2}-\frac{\left( 4-p\right) \kappa _{0}}{ 8S_{p}^{p}}\left( {{\tilde{t}}}_{\lambda ,a}^{-}\right) ^{p}\left\| w_{a_{\max }}\right\| _{H^{1}}^{p} \\\le & {} \frac{p-2}{4p}\left( \frac{4}{p\left( 4-p\right) }\right) ^{2/\left( p-2\right) }\left( \frac{S_{p}^{p}}{\kappa _{0}}\right) ^{2/\left( p-2\right) } \\< & {} \frac{p-2}{2p}\left( \frac{S_{p}^{p}}{\kappa _{0}}\right) ^{2/\left( p-2\right) }. \end{aligned}$$

This implies that ${{\tilde{t}}}_{\lambda ,a}^{-}w_{a_{\max }}\in {{\mathbf {M}}} _{\lambda ,a}^{(1)}$. Since $J_{\lambda ,a}\left( {{\tilde{t}}}_{\lambda ,a}^{+}w_{a_{\max }}\right) <0$, we have ${{\tilde{t}}}_{\lambda ,a}^{+}w_{a_{\max }}\in {{\mathbf {M}}}_{\lambda ,a}^{(2)}.$ This completes the proof. $\square$

4 Proof of Theorem 1.1

First, we define the Palais–Smale (simply by (PS)) sequences and (PS)–conditions in $H^{1}\left( {{\mathbb {R}}}^{3}\right)$ for $J_{\lambda ,a}$ as follows.

Definition 4.1

(i) For $\beta \in {{\mathbb {R}}}\mathbf {,}$ a sequence $\left\{ u_{n}\right\}$ is a $(PS)_{\beta }$–sequence in $H^{1}({{\mathbb {R}}}^{3})$ for $J_{\lambda ,a}$ if $J_{\lambda ,a}(u_{n})=\beta +o(1)\;$and$\;J_{\lambda ,a}^{\prime }(u_{n})=o(1)\;$strongly in $H^{-1}\left( {{\mathbb {R}}}^{3}\right)$ as $n\rightarrow \infty .$(ii) We say that $J_{\lambda ,a}$ satisfies the $(PS)_{\beta }$–condition in $H^{1}({{\mathbb {R}}}^{3})$ if every (PS)$_{\beta }$–sequence in $H^{1}( {{\mathbb {R}}}^{3})$ for $J_{\lambda ,a}$ contains a convergent subsequence.

Proposition 4.2

Suppose that condition (D1) holds. Let $\left\{ u_{n}\right\}$ be a bounded $(PS)_{\beta }$–sequence in $H^{1}({{\mathbb {R}}}^{3})$ for $J_{\lambda ,a}.$ There exist a subsequence $\left\{ u_{n}\right\} ,$ a number $m\in {{\mathbb {N}}}$, a sequences $\left\{ x_{n}^{i}\right\} _{n=1}^{\infty }$ in ${{\mathbb {R}}}^{3}$, a function $u_{0}\in H^{1}({{\mathbb {R}}} ^{3})$ and $0\not \equiv v^{i}\in H^{1}({{\mathbb {R}}}^{3})$ when $1\le i\le m$ such that (i) $|x_{n}^{i}|\rightarrow \infty \$and $|x_{n}^{i}-x_{n}^{j}| \rightarrow \infty$ as $n\rightarrow \infty ,$ $1\le i\ne j\le m;$ (ii) $-\Delta u_{0}+u_{0}+\lambda \phi _{u_{0}}u_{0}=a\left( x\right) \left| u_{0}\right| ^{p-2}u_{0}\text { in }{{\mathbb {R}}}^{3};$(iii) $-\Delta v^{i}+v^{i}+\lambda \phi _{v^{i}}v^{i}=a_{\infty }\left| v^{i}\right| ^{p-2}v^{i}\text { in }{{\mathbb {R}}}^{3};$(iv) $u_{n}=u_{0}+\underset{i=1}{\overset{m}{\sum }}v^{i}\left( \cdot -x_{n}^{i}\right) +o(1)\;$strongly in $H^{1}({{\mathbb {R}}}^{3});$ and(v) $J_{\lambda ,a}(u_{n})=J_{\lambda ,a}(u_{0})+\underset{i=1}{\overset{m}{\sum }}J_{\lambda ,a_{\infty }}(v^{i})+o(1)$.

The proof is similar to that of [9, Lemma 4.1] or [32, Lemma 5.1], so we omit it here.

Corollary 4.3

Suppose that $2<p<3$ and condition $\left( D1\right) -\left( D2\right)$ hold. Then for each

$$\begin{aligned} \left[ \frac{A\left( p\right) }{p}a_{\infty }\right] ^{2/\left( p-2\right) }<\lambda \le \left[ \frac{A\left( p\right) }{p}a_{1}\right] ^{2/\left( p-2\right) } \end{aligned}$$

we have the following results.$\left( i\right)$ If $\left\{ u_{n}\right\} \subset {{\mathbf {M}}}_{\lambda ,a}^{\left( 1\right) }$ is a $(PS)_{\beta }$–sequence in $H^{1}({{\mathbb {R}}} ^{3})$ for $J_{\lambda ,a}$ with $\beta >0,$ then there exist a subsequence $\left\{ u_{n}\right\}$ and a nonzero $u_{0}$ in $H^{1}({{\mathbb {R}}}^{3})$ such that $u_{n}\rightarrow u_{0}$ strongly in $H^{1}({{\mathbb {R}}}^{3})$ and $J_{\lambda ,a}\left( u_{0}\right) =\beta .$ Furthermore, $u_{0}$ is a non-trivial solution of Equation $(E_{\lambda ,a}).$ $\left( ii\right)$ If $\left\{ u_{n}\right\} \subset {{\mathbf {M}}}_{\lambda ,a}^{\left( 2\right) }$ is a $(PS)_{\beta }$–sequence in $H^{1}({{\mathbb {R}}} ^{3})$ for $J_{\lambda ,a}$ with $\beta <0,$ then there exist a subsequence $\left\{ u_{n}\right\}$ and a nonzero $u_{0}$ in $H^{1}({{\mathbb {R}}}^{3})$ such that $u_{n}\rightarrow u_{0}$ strongly in $H^{1}({{\mathbb {R}}}^{3})$ and $J_{\lambda ,a}\left( u_{0}\right) =\beta .$ Furthermore, $u_{0}$ is a non-trivial solution of Equation $(E_{\lambda ,a}).$

Proof

$\left( i\right)$ Let $\left\{ u_{n}\right\} \subset {{\mathbf {M}}}_{\lambda ,a}^{\left( 1\right) }$ be a $(PS)_{\beta }$–sequence in $H^{1}({{\mathbb {R}}} ^{3})$ for $J_{\lambda ,a}$ with $\beta >0.$ Then

$$\begin{aligned} J_{\lambda ,a}\left( u_{n}\right) =\beta +o\left( 1\right) <\alpha _{0,\kappa _{0}}^{\infty }=\frac{p-2}{2p}\left( \frac{S_{p}^{p}}{\kappa _{0}} \right) ^{\frac{2}{p-2}}. \end{aligned}$$

Since $\left\| u_{n}\right\| _{H^{1}}<{{\widehat{D}}}_{1},$ there exist a subsequence $\left\{ u_{n}\right\}$ and $u_{0}\in H^{1}({{\mathbb {R}}}^{3})$ such that $u_{n}\rightharpoonup u_{0}$ weakly in $H^{1}({{\mathbb {R}}}^{3})$ and $\left\| u_{0}\right\| _{H^{1}}<{{\widehat{D}}}_{1}.$ If $u_{0}=0,$ then by Lemma 2.6 and Proposition 4.2, there exist $\left\{ x_{n}\right\} \subset {{\mathbb {R}}}^{3}$ and $v_{0}\in H^{1}({{\mathbb {R}}} ^{3})\setminus \left\{ 0\right\}$ such that $u_{n}\left( \cdot +x_{n}\right) \rightharpoonup v_{0}$ in $H^{1}({{\mathbb {R}}}^{3})$ and $v_{0}$ is a non-trivial solution of equation: $-\Delta u+u+\lambda \phi _{u}u=a_{\infty }\left| u\right| ^{p-2}u$ in ${{\mathbb {R}}}^{3}$ and $0<J_{\lambda ,a_{\infty }}^{\infty }\left( v_{0}\right) \le \beta <\alpha _{0,\kappa _{0}}^{\infty }.$ Moreover, $\left\| v_{0}\right\| _{H^{1}}\le \lim \inf \left\| u_{n}\left( \cdot +x_{n}\right) \right\| _{H^{1}}=\lim \inf \left\| u_{n}\right\| _{H^{1}}<\widehat{ D}_{1}.$ Note that for $2<p<3,$ there holds $\left( h_{\lambda ,v_{0}}^{\infty }\right) ^{\prime }\left( 1\right) =0$ and

$$\begin{aligned} \left( h_{\lambda ,v_{0}}^{\infty }\right) ^{\prime \prime }\left( 1\right)= & {} -\left( p-2\right) \left\| v_{0}\right\| _{H^{1}}^{2}+\lambda \left( 4-p\right) \int _{{{\mathbb {R}}}^{3}}\phi _{v_{0}}v_{0}^{2}dx \\\le & {} \left( p-2\right) \left\| v_{0}\right\| _{H^{1}}^{2}\left( \frac{\lambda \left( 4-p\right) }{{{\overline{S}}}^{2}S_{12/5}^{4}\left( p-2\right) }\Vert v_{0}\Vert _{H^{1}}^{2}-1\right) \\< & {} \left( p-2\right) \left\| v_{0}\right\| _{H^{1}}^{2}\left( \frac{ 2\lambda \left( 4-p\right) }{{{\overline{S}}}^{2}S_{12/5}^{4}\left( p-2\right) } \left( \frac{S_{p}^{p}}{\kappa _{0}}\right) ^{\frac{2}{p-2}}-1\right) \\< & {} 0, \end{aligned}$$

where $h_{\lambda ,v_{0}}^{\infty }=h_{\lambda ,v_{0}}$ for $a=a_{\infty }.$ This implies that $v_{0}\in {{\mathbf {M}}}_{\lambda ,a_{\infty }}^{\left( 1\right) }$ and $h_{\lambda ,v_{0}}^{\infty }\left( t\right)$ is increasing on $\left[ 0,1\right] .$ Since $t_{a_{\infty }}\left( v_{0}\right) v_{0}\in {{\mathbf {M}}}_{0,a_{\infty }}^{\infty },$ where

$$\begin{aligned} 0<t_{a_{\infty }}\left( v_{0}\right) :=\left( \frac{\left\| v_{0}\right\| _{H^{1}}^{2}}{\int _{{{\mathbb {R}}}^{3}}a_{\infty }\left| v_{0}\right| ^{p}dx}\right) ^{1/\left( p-2\right) }<1, \end{aligned}$$

(4.1)

and so

$$\begin{aligned} \left( \frac{p-2}{2p}\right) \left( \frac{S_{p}^{p}}{a_{\infty }}\right) ^{2/\left( p-2\right) }= & {} \alpha _{0,a_{\infty }}^{\infty }\le I_{a_{\infty }}^{\infty }\left( t_{a_{\infty }}\left( v_{0}\right) v_{0}\right)<J_{\lambda ,a_{\infty }}\left( t_{a_{\infty }}\left( v_{0}\right) v_{0}\right)<J_{\lambda ,a_{\infty }}\left( v_{0}\right) \\\le & {} \beta <\alpha _{0,\kappa _{0}}^{\infty }=\left( \frac{p-2}{2p}\right) \left( \frac{S_{p}^{p}}{\kappa _{0}}\right) ^{2/\left( p-2\right) }, \end{aligned}$$

which implies that $a_{\infty }>\kappa _{0},$ a contradiction. Hence $u_{0}$ is a non-trivial solution of Equation $(E_{\lambda ,a}).$ Moreover, by Lemma 2.6 and Proposition 4.2$\left( iv\right) -\left( v\right) ,$ $u_{n}\rightarrow u_{0}$ strongly in $H^{1}({{\mathbb {R}}}^{3})$ and $J_{\lambda ,a}\left( u_{0}\right) =\beta <\alpha _{0,\kappa _{0}}^{\infty }$ which implies that $u_{0}\in {{\mathbf {M}}}_{\lambda ,a}^{\left( 1\right) }.$ $\left( ii\right)$ Let $\left\{ u_{n}\right\} \subset {{\mathbf {M}}}_{\lambda ,a}^{\left( 2\right) }$ be a $(PS)_{\beta }$–sequence in $H^{1}({{\mathbb {R}}} ^{3})$ for $J_{\lambda ,a}$ with $\beta <0.$ By Theorem 2.5, there exist a subsequence $\left\{ u_{n}\right\}$ and $u_{0}\in H^{1}({{\mathbb {R}}} ^{3})$ such that $u_{n}\rightharpoonup u_{0}$ weakly in $H^{1}({{\mathbb {R}}} ^{3})$ and $J_{\lambda ,a}^{\prime }\left( u_{0}\right) =0.$ Moreover, by Lemma 2.6 and Proposition 4.2$\left( iv\right) -\left( v\right) ,$ $u_{n}\rightarrow u_{0}$ strongly in $H^{1}({{\mathbb {R}}}^{3})$ and $J_{\lambda ,a}\left( u_{0}\right) =\beta .$ Thus, $u_{0}\in {{\mathbf {M}}} _{\lambda ,a}^{\left( 2\right) }$ is a non-trivial solution of Equation $(E_{\lambda ,a}).$ This completes the proof. $\square$

Define

$$\begin{aligned} \alpha _{\lambda ,a}^{\left( i\right) }=\inf _{u\in {{\mathbf {M}}}_{\lambda ,a}^{(i)}}J_{\lambda ,a}(u)\text { for }i=1,2. \end{aligned}$$

Then by Theorem 2.5, Lemmas 2.2 and 3.2 , and the facts that ${{\mathbf {M}}}_{\lambda ,a}^{(1)}\subset {{\mathbf {M}}}_{\lambda ,a}^{-}$ and ${{\mathbf {M}}}_{\lambda ,a}^{(2)}\subset {{\mathbf {M}}}_{\lambda ,a}^{+},$ we have

$$\begin{aligned} -\infty<\alpha _{\lambda ,a}^{\left( 2\right) }<0<\frac{2p}{4-p}\left( \frac{S_{p}^{p}}{a_{\max }}\right) \le \alpha _{\lambda ,a}^{\left( 1\right) }<\left( \frac{p-2}{2p}\right) \left( \frac{S_{p}^{p}}{\kappa _{0}} \right) ^{2/\left( p-2\right) }. \end{aligned}$$

(4.2)

Remark 4.4

It is not difficult to prove that

$$\begin{aligned} \alpha _{\lambda ,a}^{\left( 1\right) }=\inf _{u\in {{\mathbf {M}}}_{\lambda ,a}^{(1)}}J_{\lambda ,a}(u)=\inf _{u\in {{\mathbf {M}}}_{\lambda ,a}^{-}}J_{\lambda ,a}(u) \end{aligned}$$

and

$$\begin{aligned} \alpha _{\lambda ,a}^{\left( 2\right) }=\inf _{u\in {{\mathbf {M}}}_{\lambda ,a}^{(2)}}J_{\lambda ,a}(u)=\inf _{u\in {{\mathbf {M}}}_{\lambda ,a}^{+}}J_{\lambda ,a}(u)=\inf _{u\in {{\mathbf {M}}}_{\lambda ,a}}J_{\lambda ,a}(u). \end{aligned}$$

(4.3)

Indeed, it is clear that $\alpha _{\lambda ,a}^{\left( 1\right) }\ge \inf _{u\in {{\mathbf {M}}}_{\lambda ,a}^{-}}J_{\lambda ,a}(u),$ since ${{\mathbf {M}}} _{\lambda ,a}^{(1)}\subset {{\mathbf {M}}}_{\lambda ,a}^{-}.$ Moreover, if

$$\begin{aligned} \inf _{u\in {{\mathbf {M}}}_{\lambda ,a}^{-}}J_{\lambda ,a}(u)\ge \left( \frac{p-2 }{2p}\right) \left( \frac{S_{p}^{p}}{\kappa _{0}}\right) ^{2/\left( p-2\right) }, \end{aligned}$$

then by (4.2), $\inf _{u\in {{\mathbf {M}}}_{\lambda ,a}^{-}}J_{\lambda ,a}(u)>\alpha _{\lambda ,a}^{\left( 1\right) },$ which is a contradiction. Thus, there exists a minimizing sequence $\{u_{n}\}\subset {{\mathbf {M}}} _{\lambda ,a}^{-}$ such that

$$\begin{aligned} J_{\lambda ,a}(u_{n})\rightarrow \inf _{u\in {{\mathbf {M}}}_{\lambda ,a}^{-}}J_{\lambda ,a}(u)<\left( \frac{p-2}{2p}\right) \left( \frac{S_{p}^{p} }{\kappa _{0}}\right) ^{2/\left( p-2\right) }, \end{aligned}$$

which implies $\{u_{n}\}\subset {{\mathbf {M}}}_{\lambda ,a}^{(1)}.$ This indicates that $J_{\lambda ,a}(u_{n})\ge \alpha _{\lambda ,a}^{\left( 1\right) }.$ Hence, $\alpha _{\lambda ,a}^{\left( 1\right) }=\inf _{u\in {{\mathbf {M}}}_{\lambda ,a}^{-}}J_{\lambda ,a}(u).$ Repeating the same argument, we obtain $\alpha _{\lambda ,a}^{\left( 2\right) }=\inf _{u\in {{\mathbf {M}}} _{\lambda ,a}^{+}}J_{\lambda ,a}(u).$ Furthermore, by (4.2 ), we also have $\alpha _{\lambda ,a}^{\left( 2\right) }=\inf _{u\in {{\mathbf {M}}}_{\lambda ,a}}J_{\lambda ,a}(u).$

Following [31], we have the following results.

Lemma 4.5

Suppose that $2<p<3$ and conditions $(D1)-(D3)$ hold. Then for each $i=1,2$ and $u\in {{\mathbf {M}}}_{\lambda ,a}^{(i)},$ there exist a number $\sigma >0$ and a differentiable function $t^{*}:B(0,\sigma )\subset X\rightarrow {{\mathbb {R}}}^{+}$ such that

$$\begin{aligned} t^{*}(0)=1\ \text {and}\ t^{*}(v)(u-v)\in {{\mathbf {M}}}_{\lambda ,a}^{(i)} \end{aligned}$$

for all $v\in B(0,\sigma )$, and

$$\begin{aligned} \langle (t^{*})^{\prime }(0),\varphi \rangle =\frac{2\int _{{{\mathbb {R}}} ^{3}}(\nabla u\nabla \varphi +u\varphi )dx+4\lambda \int _{{{\mathbb {R}}} ^{3}}\phi _{u}u\varphi dx-p\int _{{{\mathbb {R}}}^{3}}a\left( x\right) |u|^{p-2}u\varphi dx}{\Vert u\Vert _{H^{1}}^{2}-(p-1)\int _{{{\mathbb {R}}} ^{3}}a\left( x\right) |u|^{p}dx} \end{aligned}$$

for all $\varphi \in H^{1}({{\mathbb {R}}}^{3}).$

Proof

For any $u\in {{\mathbf {M}}}_{\lambda ,a}^{(i)}$, we define the function $F_{u}: {{\mathbb {R}}}\times X\rightarrow {{\mathbb {R}}}$ by

$$\begin{aligned} F_{u}(t,v)= & {} \langle J_{\lambda ,a}^{\prime }(t(u-v)),t(u-v)\rangle \\= & {} t^{2}\int _{{{\mathbb {R}}}^{3}}[|\nabla (u-v)|^{2}+(u-v)^{2}]dx+\lambda t^{4}\int _{{{\mathbb {R}}}^{3}}\phi _{u}u^{2}dx \\&-t^{p}\int _{{{\mathbb {R}}}^{3}}a\left( x\right) |u-v|^{p}dx. \end{aligned}$$

It is not difficult to verify that $F_{u}(1,0)=\langle J_{\lambda ,a}^{\prime }(u),u\rangle =0$ and

$$\begin{aligned} \frac{\partial F_{u}}{\partial t}(1,0)= & {} 2\Vert u\Vert _{H^{1}}^{2}+4\lambda \int _{{{\mathbb {R}}}^{3}}\phi _{u}u^{2}dx-p\int _{{{\mathbb {R}}} ^{3}}a\left( x\right) |u|^{p}dx \\= & {} -2\Vert u\Vert _{H^{1}}^{2}-(p-4)\int _{{{\mathbb {R}}}^{3}}a\left( x\right) |u|^{p}dx\ne 0. \end{aligned}$$

According to the implicit function theorem, there exist a number $\sigma >0$ and a differentiable function $t^{*}:B(0,\sigma )\subset X\rightarrow {{\mathbb {R}}}$ satisfying $t^{*}(0)=1$ and

$$\begin{aligned}&\langle (t^{*})^{\prime }(0),\varphi \rangle \\&\quad =\frac{2\int _{{{\mathbb {R}}}^{3}}(\nabla u\nabla \varphi +u\varphi )dx+4\lambda \int _{{{\mathbb {R}}}^{3}}\phi _{u}u\varphi dx-p\int _{{{\mathbb {R}}} ^{3}}a\left( x\right) |u|^{p-2}u\varphi dx}{\Vert u\Vert _{H^{1}}^{2}-(p-1)\int _{{{\mathbb {R}}}^{3}}a\left( x\right) |u|^{p}dx} \end{aligned}$$

for all $\varphi \in H^{1}({{\mathbb {R}}}^{3})$ such that

$$\begin{aligned} F_{u}(t^{*}(v),v)=0\text { for all }v\in B(0,\sigma ), \end{aligned}$$

that is,

$$\begin{aligned} \langle J_{\lambda ,a}^{\prime }(t^{*}(v)(u-v)),t^{*}(v)(u-v)\rangle =0\text { for all }v\in B(0,\sigma ), \end{aligned}$$

and together with the continuity of the map $t^{*}$, we deduce that

$$\begin{aligned} h_{\lambda ,t^{*}(v)(u-v)}^{\prime \prime }(1)= & {} -2\Vert t^{*}(v)(u-v)\Vert _{H^{1}}^{2}-(p-4)\int _{{{\mathbb {R}}}^{3}}a\left( x\right) |t^{*}(v)(u-v)|^{p}dx \\< & {} 0 \end{aligned}$$

and

$$\begin{aligned} J_{\lambda ,a}(t^{*}(v)(u-v))<\left( \frac{p-2}{2p}\right) \left( \frac{ S_{p}^{p}}{\kappa _{0}}\right) ^{2/\left( p-2\right) }, \end{aligned}$$

if $\sigma$ is sufficiently small. Hence, $t^{*}(v)(u-v)\in {{\mathbf {M}}} _{\lambda ,a}^{(i)}$ for all $v\in B(0,\sigma ).$ Consequently, we complete the proof. $\square$

Proposition 4.6

Suppose that $2<p<3$ and conditions $(D1)-(D3)$ hold. Then for each $i\in \left\{ 1,2\right\}$ and $\left[ \frac{A\left( p\right) }{p} a_{\infty }\right] ^{2/\left( p-2\right) }<\lambda \le \left[ \frac{A\left( p\right) }{p}a_{1}\right] ^{2/\left( p-2\right) }$ there exists a sequence $\{u_{n}\}\subset {{\mathbf {M}}}_{\lambda ,a}^{(i)}$ such that

$$\begin{aligned} J_{\lambda ,a}(u_{n})=\alpha _{\lambda ,a}^{\left( i\right) }+o(1)\text { and }J_{_{\lambda ,a}}^{\prime }(u_{n})=o(1)\text { in }H^{-1}\left( {{\mathbb {R}}} ^{3}\right) . \end{aligned}$$

(4.4)

Proof

By Theorem 2.5 and the Ekeland variational principle [13], there exists a minimizing sequence $\{u_{n}\}\subset {{\mathbf {M}}}_{\lambda ,a}^{(i)}$ such that

$$\begin{aligned} J_{\lambda ,a}(u_{n})<\alpha _{\lambda ,a}^{\left( i\right) }+\frac{1}{n} \end{aligned}$$

and

$$\begin{aligned} J_{\lambda ,a}(u_{n})\le J_{\lambda ,a}(w)+\frac{1}{n}\Vert w-u_{n}\Vert _{H^{1}}\text { for all }w\in {{\mathbf {M}}}_{\lambda ,a}^{(i)}. \end{aligned}$$

(4.5)

Applying Lemma 4.5 with $u=u_{n}$, there exists a function $t_{n}^{*}:B(0,\sigma _{n})\rightarrow {{\mathbb {R}}}$ for some $\sigma _{n}>0$ such that $t_{n}^{*}(w)(u_{n}-w)\in {{\mathbf {M}}}_{\lambda ,a}^{(i)}.$ Let $0<\delta <\sigma _{n}$ and $u\in H^{1}\left( {{\mathbb {R}}}^{3}\right)$ with $u\not \equiv 0.$ We set

$$\begin{aligned} w_{\delta }=\frac{\delta u}{\Vert u\Vert _{H^{1}}}\text { and }z_{\delta }=t_{n}^{*}(w_{\delta })(u_{n}-w_{\delta }). \end{aligned}$$

Clearly, $z_{\delta }\in {{\mathbf {M}}}_{\lambda ,a}^{(i)}.$ It is deduced from (4.5) that

$$\begin{aligned} J_{\lambda ,a}(z_{\delta })-J_{\lambda ,a}(u_{n})\ge -\frac{1}{n}\Vert z_{\delta }-u_{n}\Vert _{H^{1}}, \end{aligned}$$

together with the mean value theorem, we have

$$\begin{aligned} \langle J_{\lambda ,a}^{\prime }(u_{n}),z_{\delta }-u_{n}\rangle +o(\Vert z_{\delta }-u_{n}\Vert _{\lambda })\ge -\frac{1}{n}\Vert z_{\delta }-u_{n}\Vert _{H^{1}} \end{aligned}$$

and

$$\begin{aligned}&\langle J_{\lambda ,a}^{\prime }(u_{n}),-w_{\delta }\rangle +(t_{n}^{*}(w_{\delta })-1)\langle J_{\lambda ,a}^{\prime }(u_{n}),u_{n}-w_{\delta }\rangle \nonumber \\&\quad \ge -\frac{1}{n}\Vert z_{\delta }-u_{n}\Vert _{H^{1}}+o(\Vert z_{\delta }-u_{n}\Vert _{H^{1}}). \end{aligned}$$

(4.6)

Observe that $t_{n}^{*}(w_{\delta })(u_{n}-w_{\delta })\in {{\mathbf {M}}} _{\lambda ,a}^{(i)}$. From (4.6) it gives

$$\begin{aligned}&-\delta \langle J_{\lambda ,a}^{\prime }(u_{n}),u/\Vert u\Vert _{H^{1}}\rangle +\frac{(t_{n}^{*}(w_{\delta })-1)}{t_{n}^{*}(w_{\delta })}\langle J_{\lambda ,a}^{\prime }(z_{\delta }),t_{n}^{*}(w_{\delta })(u_{n}-w_{\delta })\rangle \\&\qquad +(t_{n}^{*}(w_{\delta })-1)\langle J_{\lambda ,a}^{\prime }(u_{n})-J_{\lambda ,a}^{\prime }(z_{\delta }),u_{n}-w_{\delta }\rangle \\&\quad \ge -\frac{1}{n}\Vert z_{\delta }-u_{n}\Vert _{H^{1}}+o(\Vert z_{\delta }-u_{n}\Vert _{H^{1}}), \end{aligned}$$

which implies that

$$\begin{aligned} \left\langle J_{\lambda ,a}^{\prime }(u_{n}),\frac{u}{\Vert u\Vert _{H^{1}}} \right\rangle\le & {} \frac{\Vert z_{\delta }-u_{n}\Vert _{H^{1}}}{\delta n}+\frac{ o(\Vert z_{\delta }-u_{n}\Vert _{H^{1}})}{\delta } \nonumber \\&+\frac{(t_{n}^{*}(w_{\delta })-1)}{\delta }\langle J_{\lambda ,a}^{\prime }(u_{n})-J_{\lambda ,a}^{\prime }(z_{\delta }),u_{n}-w_{\delta }\rangle . \end{aligned}$$

(4.7)

We choose a number $C>0$ independent of $\delta$ such that

$$\begin{aligned} \Vert z_{\delta }-u_{n}\Vert _{H^{1}}\le \delta +C(|t_{n}^{*}(w_{\delta })-1|) \end{aligned}$$

and

$$\begin{aligned} \lim _{\delta \rightarrow 0}\frac{|t_{n}^{*}(w_{\delta })-1|}{\delta } =\lim _{\delta \rightarrow 0}\frac{|t_{n}^{*}(w_{\delta })-t_{n}^{*}(0)|}{\delta }\le \Vert (t_{n}^{*})^{\prime }(0)\Vert _{H^{-1}}\le C. \end{aligned}$$

Letting $\delta \rightarrow 0$ in (4.7) and using the fact that $\lim _{\delta \rightarrow 0}\Vert z_{\delta }-u_{n}\Vert _{H^{1}}=0,$ we have

$$\begin{aligned} \langle J_{\lambda ,a}^{\prime }(u_{n}),\frac{u}{\Vert u\Vert _{H^{1}}} \rangle \le \frac{C}{n}, \end{aligned}$$

which enables us to arrive at (4.4). Consequently, we complete the proof. $\square$

We are now ready to prove Theorem 1.1 By Proposition 4.6 , there exist two sequences $\{u_{n}^{\left( i\right) }\}\subset {{\mathbf {M}}} _{\lambda ,a}^{(i)}$ such that

$$\begin{aligned} J_{\lambda ,a}(u_{n}^{\left( i\right) })=\alpha _{\lambda ,a}^{\left( i\right) }+o(1)\text { and }J_{\lambda ,a}^{\prime }(u_{n}^{\left( i\right) })=o(1)\text { in }H^{-1}\left( {{\mathbb {R}}}^{3}\right) . \end{aligned}$$

Then by Corollary 4.3, there exist two subsequences $\{u_{n}^{\left( i\right) }\}$ and $u_{\lambda ,a}^{\left( i\right) }\in H^{1}\left( \mathbb {R }^{3}\right) \setminus \{0\}$ such that $u_{n}^{\left( i\right) }\rightarrow u_{\lambda ,a}^{\left( i\right) }$ strongly in $H^{1}\left( {{\mathbb {R}}} ^{3}\right)$ for $i=1,2.$ This indicates that $u_{\lambda ,a}^{\left( i\right) }\in {{\mathbf {M}}}_{\lambda ,a}^{\left( i\right) }$ and

$$\begin{aligned} \alpha _{\lambda ,a}^{\left( i\right) }=J_{\lambda ,a}(u_{\lambda ,a}^{\left( i\right) }), \end{aligned}$$

implying $u_{\lambda ,a}^{\left( i\right) }\in {{\mathbf {M}}}_{\lambda ,a}^{(i)}$ and $J_{\lambda ,a}\left( u_{\lambda ,a}^{\left( 2\right) }\right)<0<J_{\lambda ,a}\left( u_{\lambda ,a}^{\left( 1\right) }\right) .$ Since $J_{\lambda ,a}(u_{\lambda ,a}^{\left( i\right) })=J_{\lambda ,a}(|u_{\lambda ,a}^{\left( i\right) }|)=\alpha _{\lambda ,a}^{\left( i\right) },$ by Lemma 2.1, we may assume that $u_{\lambda ,a}^{\left( i\right) }$ are positive solutions of Equation $(E_{\lambda ,a}).$ Moreover, by (4.3), $u_{\lambda ,a}^{\left( 2\right) }$ is a ground state solution of Equation $(E_{\lambda ,a}).$

5 Proof of Theorem 1.2

By conditions $\left( D1\right)$ and $\left( D2\right) ,$ without loss of generality, we may assume that $B^{3}\left( 0,1\right) \subset \mathrm {int} \left\{ x\in {{\mathbb {R}}}^{3}:a\left( x\right) \ge {{\widehat{\kappa }}} _{0}\right\} ,$ this implies that $B^{3}\left( 0,\frac{1}{\varepsilon } \right) \subset \Omega _{\varepsilon }:=\mathrm {int}\left\{ x\in {{\mathbb {R}}} ^{3}:a\left( \varepsilon x\right) \ge {{\widehat{\kappa }}}_{0}\right\} ,$ where ${{\widehat{\kappa }}}_{0}:=\frac{p\kappa _{0}}{2}.$ Note that

$$\begin{aligned} \kappa _{0}<{{\widehat{\kappa }}}_{0}<\frac{2}{4-p}\kappa _{0}<a_{\max }. \end{aligned}$$

As we know, ${{\widehat{w}}}_{0}$ is the unique radial positive solution with ${{\widehat{w}}}_{0}\left( 0\right) =\max _{x\in {{\mathbb {R}}}^{3}}{{\widehat{w}}} _{0}\left( x\right)$ for Equation $\left( E_{0,{{\widehat{\kappa }}} _{0}}^{\infty }\right) .$ Thus,

$$\begin{aligned} T_{{{\widehat{\kappa }}}_{0}}\left( {{\widehat{w}}}_{0}\right) =\left( \frac{ \left\| {{\widehat{w}}}_{0}\right\| _{H^{1}}^{2}}{\int _{{{\mathbb {R}}}^{3}} {{\widehat{\kappa }}}_{0}\left| {{\widehat{w}}}_{0}\right| ^{p}dx}\right) ^{1/\left( p-2\right) }=1, \end{aligned}$$

and

$$\begin{aligned} \int _{{{\mathbb {R}}}^{3}}{{\widehat{\kappa }}}_{0}\left| {{\widehat{w}}} _{0}\right| ^{p}dx=\frac{{{\widehat{\kappa }}}_{0}}{S_{p}^{p}}\Vert \widehat{ w}_{0}\Vert _{H^{1}}^{p}>\frac{\kappa _{0}}{S_{p}^{p}}\Vert {{\widehat{w}}} _{0}\Vert _{H^{1}}^{p}. \end{aligned}$$

(5.1)

Since $2<p<3,$ by Lemmas 3.1 and 3.2 , there exists a constant $t_{\lambda ,{{\widehat{\kappa }}}_{0}}^{+}>0$ satisfying

$$\begin{aligned} \left( \frac{p}{4-p}\right) ^{1/\left( p-2\right) }<t_{\lambda ,\widehat{ \kappa }_{0}}^{+}<{{\widehat{t}}}_{\lambda }^{(0)} \end{aligned}$$

such that

$$\begin{aligned} J_{\lambda ,{{\widehat{\kappa }}}_{0}}^{\infty }\left( t_{\lambda ,\widehat{ \kappa }_{0}}^{+}{{\widehat{w}}}_{0}\right) =\inf _{\left( \frac{p}{4-p}\right) ^{1/\left( p-2\right) }<t<{{\widehat{t}}}_{\lambda }^{(0)}}J_{\lambda ,\widehat{ \kappa }_{0}}^{\infty }\left( t{{\widehat{w}}}_{0}\right) =\inf _{t\ge 0}J_{\lambda ,{{\widehat{\kappa }}}_{0}}^{\infty }\left( t{{\widehat{w}}}_{0}\right) <0, \end{aligned}$$

(5.2)

where ${{\widehat{t}}}_{\lambda }^{(0)}$ is as in Lemma 3.1. For $R>0,$ we define a cut-off function $\psi _{R}\in C^{1}({{\mathbb {R}}}^{3},\left[ 0,1 \right] )$ as

$$\begin{aligned} \psi _{R}\left( x\right) =\left\{ \begin{array}{ll} 1 &{} \left| x\right| <\frac{R}{2}, \\ 0 &{} \left| x\right| >R, \end{array} \right. \end{aligned}$$

and $\left| \nabla \psi _{R}\right| \le 1$ in ${{\mathbb {R}}}^{3}.$ Let $u_{R}\left( x\right) ={{\widehat{w}}}_{0}\left( x\right) \psi _{R}(x).$ Then,

$$\begin{aligned}&\int _{{{\mathbb {R}}}^{3}}\left| u_{R}\right| ^{p}dx\rightarrow \int _{ {{\mathbb {R}}}^{3}}\left| {{\widehat{w}}}_{0}\right| ^{p}dx\text { as } R\rightarrow \infty , \end{aligned}$$

(5.3)

$$\begin{aligned}&\left\| u_{R}\right\| _{H^{1}}\rightarrow \left\| {{\widehat{w}}} _{0}\right\| _{H^{1}}\text { as }R\rightarrow \infty , \end{aligned}$$

(5.4)

and

$$\begin{aligned} \int _{{{\mathbb {R}}}^{3}}\phi _{u_{R}}u_{R}^{2}dx\rightarrow \int _{{{\mathbb {R}}} ^{3}}\phi _{w_{0}}{{\widehat{w}}}_{0}^{2}dx\text { as }R\rightarrow \infty . \end{aligned}$$

(5.5)

Since $J_{\lambda ,{{\widehat{\kappa }}}_{0}}^{\infty }\in C^{1}(H^{1}({{\mathbb {R}}} ^{3}),\mathbb {R)}$, by (5.1)–(5.5) , there exists $R_{0}>0$ such that

$$\begin{aligned} \int _{{{\mathbb {R}}}^{3}}{{\widehat{\kappa }}}_{0}\left| u_{R_{0}}\right| ^{p}dx>\frac{\kappa _{0}}{S_{p}^{p}}\left\| u_{R_{0}}\right\| _{H^{1}}^{p} \end{aligned}$$

(5.6)

and

$$\begin{aligned} J_{\lambda ,{{\widehat{\kappa }}}_{0}}^{\infty }\left( t_{\lambda ,\widehat{ \kappa }_{0}}^{+}u_{R_{0}}\right) <0. \end{aligned}$$

Let

$$\begin{aligned} u_{R_{0},N}^{\left( i\right) }\left( x\right) ={{\widehat{w}}}_{0}\left( x+iN^{3}e\right) \psi _{R_{0}}\left( x+iN^{3}e\right) \end{aligned}$$

for $e\in {{\mathbb {S}}}^{2}$ and $i=1,2,\ldots ,N$, where $N^{3}>2R_{0}.$ Let $0<\varepsilon _{N}\le \frac{1}{N^{4}+R_{0}}.$ Then we have the following result.

$$\begin{aligned} \mathrm{supp} u_{R_{0},N}^{\left( i\right) }\left( x\right) \subset B^{3}\left( 0,\frac{1}{\varepsilon _{N}}\right) \text { for all }i=1,2,\ldots ,N. \end{aligned}$$

Clearly, $\varepsilon _{N}\rightarrow 0^{+}$ as $N\rightarrow \infty .$ Moreover, by condition $\left( D1\right)$, we deduce that

$$\begin{aligned} \left\| u_{R_{0},N}^{\left( i\right) }\right\| _{H^{1}}^{2}= & {} \left\| u_{R_{0}}\right\| _{H^{1}}^{2}\text { for all }N, \\ \int _{{{\mathbb {R}}}^{3}}a_{\varepsilon _{N}}\left( x\right) \left| u_{R_{0},N}^{\left( i\right) }\right| ^{p}dx\ge & {} \int _{{{\mathbb {R}}}^{3}} {{\widehat{\kappa }}}_{0}\left| u_{R_{0}}\right| ^{p}dx\text { for all }N, \end{aligned}$$

and

$$\begin{aligned} \int _{{{\mathbb {R}}}^{3}}\phi _{u_{R_{0},N}^{\left( i\right) }}\left[ u_{R_{0},N}^{\left( i\right) }\right] ^{2}dx= & {} \int _{{{\mathbb {R}}}^{3}}\int _{ {{\mathbb {R}}}^{3}}\frac{\left[ u_{R_{0},N}^{\left( i\right) }\left( x\right) \right] ^{2}\left[ u_{R_{0},N}^{\left( i\right) }\left( y\right) \right] ^{2} }{4\pi \left| x-y\right| }dxdy \\= & {} \int _{{{\mathbb {R}}}^{3}}\int _{{{\mathbb {R}}}^{3}}\frac{u_{R_{0}}^{2}\left( x\right) u_{R_{0}}^{2}\left( y\right) }{4\pi \left| x-y\right| }dxdy. \end{aligned}$$

Since $a_{\varepsilon _{N}}\left( x\right) \ge {{\widehat{\kappa }}}_{0}$ for all $x\in B^{3}\left( 0,\frac{1}{\varepsilon _{N}}\right) ,$ there exists $N_{0}>0$ with $N_{0}^{3}>2R_{0}$ such that for every $N\ge N_{0},$ we have

$$\begin{aligned} \int _{{{\mathbb {R}}}^{3}}a_{\varepsilon _{N}}\left( x\right) \left| u_{R_{0}}\right| ^{p}dx>\frac{\kappa _{0}}{S_{p}^{p}}\left\| u_{R_{0}}\right\| _{H^{1}}^{p}=\frac{\kappa _{0}}{S_{p}^{p}}\left\| u_{R_{0},N}^{\left( i\right) }\right\| _{H^{1}}^{p}\text { } \end{aligned}$$

and

$$\begin{aligned} \inf _{t\ge 0}J_{\lambda ,a_{\varepsilon _{N}}}\left( tu_{R_{0},N}^{\left( i\right) }\right) \le J_{\lambda ,a_{\varepsilon _{N}}}\left( t_{\lambda , {{\widehat{\kappa }}}_{0}}^{+}u_{R_{0},N}^{\left( i\right) }\right) \le J_{\lambda ,{{\widehat{\kappa }}}_{0}}^{\infty }(t_{\lambda ,{{\widehat{\kappa }}} _{0}}^{+}u_{R_{0}}), \end{aligned}$$

for all $e\in {{\mathbb {S}}}^{2}$ and $i=1,2,\ldots ,N.$ Let

$$\begin{aligned} w_{R_{0},N}\left( x\right) =\sum _{i=1}^{N}u_{R_{0},N}^{\left( i\right) }. \end{aligned}$$

Observe that $w_{R_{0},N}$ is a sum of translation of $u_{R_{0}}.$ When $N^{3}\ge N_{0}^{3}>2R_{0}$, the summands have disjoint support and

$$\begin{aligned} \mathrm{supp} w_{R_{0},N}\left( x\right) \subset B^{3}\left( 0,\frac{1 }{\varepsilon _{N}}\right) . \end{aligned}$$

In such a case we have

$$\begin{aligned}&\left\| w_{R_{0},N}\right\| _{H^{1}}^{2}=N\Vert u_{R_{0}}\Vert _{H^{1}}^{2}, \end{aligned}$$

(5.7)

$$\begin{aligned}&\int _{{{\mathbb {R}}}^{3}}a_{\varepsilon _{N}}\left( x\right) \left| w_{R_{0},N}\right| ^{p}dx=\sum _{i=1}^{N}\int _{{{\mathbb {R}}} ^{3}}a_{\varepsilon _{N}}\left( x\right) \left| u_{R_{0},N}^{\left( i\right) }\right| ^{p}dx, \end{aligned}$$

(5.8)

and

$$\begin{aligned} \int _{{{\mathbb {R}}}^{3}}\phi _{w_{R_{0},N}}w_{R_{0},N}^{2}dx= & {} \int _{{{\mathbb {R}}} ^{3}}\int _{{{\mathbb {R}}}^{3}}\frac{w_{R_{0},N}^{2}\left( x\right) w_{R_{0},N}^{2}\left( y\right) }{4\pi \left| x-y\right| }dxdy \nonumber \\= & {} \sum _{i=1}^{N}\int _{{{\mathbb {R}}}^{3}}\int _{{{\mathbb {R}}}^{3}}\frac{\left[ u_{R_{0},N}^{\left( i\right) }\left( x\right) \right] ^{2}\left[ u_{R_{0},N}^{\left( i\right) }\left( y\right) \right] ^{2}}{4\pi \left| x-y\right| }dxdy \nonumber \\&+\sum _{i\ne j}^{N}\int _{{{\mathbb {R}}}^{3}}\int _{{{\mathbb {R}}}^{3}}\frac{\left[ u_{R_{0},N}^{\left( i\right) }\left( x\right) \right] ^{2}\left[ u_{R_{0},N}^{\left( j\right) }\left( y\right) \right] ^{2}}{4\pi \left| x-y\right| }dxdy. \end{aligned}$$

(5.9)

After a straightforward calculation, we have

$$\begin{aligned} \sum _{i\ne j}^{N}\int _{{{\mathbb {R}}}^{3}}\int _{{{\mathbb {R}}}^{3}}\frac{\left[ u_{R_{0},N}^{\left( i\right) }\left( x\right) \right] ^{2}\left[ u_{R_{0},N}^{\left( j\right) }\left( y\right) \right] ^{2}}{4\pi \left| x-y\right| }dxdy\le \frac{N^{2}-N}{N^{3}-2R_{0}}\left( \int _{{{\mathbb {R}}} ^{3}}w_{0}^{2}\left( x\right) dx\right) ^{2}, \end{aligned}$$

which implies that

$$\begin{aligned} \sum _{i\ne j}^{N}\int _{{{\mathbb {R}}}^{3}}\int _{{{\mathbb {R}}}^{3}}\frac{\left[ u_{R_{0},N}^{\left( i\right) }\right] ^{2}\left( x\right) \left[ u_{R_{0},N}^{\left( j\right) }\right] ^{2}\left( y\right) }{4\pi \left| x-y\right| }dxdy\rightarrow 0\text { as }N\rightarrow \infty . \end{aligned}$$

(5.10)

We can now adopt the idea of multibump technique by Ruiz [23] (also see [20]) and the following results are obtained.

Lemma 5.1

Suppose that $2<p<3$ and conditions $\left( D1\right) -\left( D2\right)$ and $\left( D4\right)$ hold. Then for each $\left[ \frac{ A\left( p\right) }{p}a_{\infty }\right] ^{2/\left( p-2\right) }<\lambda \le \left[ \frac{A\left( p\right) }{p}a_{1}\right] ^{2/\left( p-2\right) },$ we have

$$\begin{aligned} \alpha _{\lambda ,a_{\varepsilon }}^{\left( 2\right) }\rightarrow -\infty \text { as }\varepsilon \rightarrow 0^{+}. \end{aligned}$$

(5.11)

Proof

For $N\in {{\mathbb {N}}}$ and let

$$\begin{aligned} f_{N}\left( t\right) =t^{-2}\left\| w_{R_{0},N}\right\| _{H^{1}}^{2}-t^{p-4}\int _{{{\mathbb {R}}}^{3}}a_{\varepsilon _{N}}\left( x\right) \left| w_{R_{0},N}\right| ^{p}dx\ \text { for }t>0 \end{aligned}$$

and

$$\begin{aligned} f_{0}\left( t\right) =t^{-2}\left\| w_{R_{0}}\right\| _{H^{1}}^{2}-t^{p-4}\int _{{{\mathbb {R}}}^{3}}{{\widehat{\kappa }}}_{0}\left| w_{R_{0}}\right| ^{p}dx\ \text { for }t>0. \end{aligned}$$

By (5.7) and (5.8), we get

$$\begin{aligned} f_{N}\left( t\right)= & {} t^{-2}N\left\| u_{R_{0}}\right\| _{H^{1}}^{2}-t^{p-4}\sum _{i=1}^{N}\int _{{{\mathbb {R}}}^{3}}a_{\varepsilon _{N}}\left( x\right) \left| u_{R_{0},N}^{\left( i\right) }\right| ^{p}dx \nonumber \\\le & {} t^{-2}N\left\| u_{R_{0}}\right\| _{H^{1}}^{2}-t^{p-4}N\int _{ {{\mathbb {R}}}^{3}}{{\widehat{\kappa }}}_{0}\left| u_{R_{0}}\right| ^{p}dx \nonumber \\= & {} Nf_{0}(t). \end{aligned}$$

(5.12)

It can be readily seen that $tw_{R_{0},N}\in {{\mathbf {M}}}_{\lambda ,a_{\varepsilon _{N}}}$ if and only if

$$\begin{aligned} f_{N}\left( t\right) +\lambda \int _{{{\mathbb {R}}}^{3}}\phi _{w_{R_{0},N}}w_{R_{0},N}^{2}dx=0. \end{aligned}$$

An evaluation on $f_{0}(t)$ gives

$$\begin{aligned} f_{0}\left( T_{{{\widehat{\kappa }}}_{0}}\left( u_{R_{0}}\right) \right) =0,\ \lim _{t\rightarrow 0^{+}}f_{0}(t)=\infty \text { and }\lim _{t\rightarrow \infty }f_{0}(t)=0, \end{aligned}$$

where

$$\begin{aligned} T_{{{\widehat{\kappa }}}_{0}}\left( u_{R_{0}}\right) =\left( \frac{\left\| u_{R_{0}}\right\| _{H^{1}}^{2}}{\int _{{{\mathbb {R}}}^{3}}\frac{p\kappa _{0}}{2 }\left| u_{R_{0}}\right| ^{p}dx}\right) ^{1/\left( p-2\right) }. \end{aligned}$$

Since $2<p<3$ and

$$\begin{aligned} f_{0}^{\prime }\left( t\right) =-2t^{-3}\left\| u_{R_{0}}\right\| _{H^{1}}^{2}+\left( 4-p\right) t^{p-5}\int _{{{\mathbb {R}}}^{3}}{{\widehat{\kappa }}} _{0}\left| u_{R_{0}}\right| ^{p}dx, \end{aligned}$$

thus f is decreasing on $0<t<\left( \frac{2\left\| u_{R_{0}}\right\| _{H^{1}}^{2}}{\left( 4-p\right) \int _{{{\mathbb {R}}}^{3}} {{\widehat{\kappa }}}_{0}\left| u_{R_{0}}\right| ^{p}dx}\right) ^{1/\left( p-2\right) }$ and increasing on $t>\left( \frac{2\left\| u_{R_{0}}\right\| _{H^{1}}^{2}}{\left( 4-p\right) \int _{{{\mathbb {R}}}^{3}} {{\widehat{\kappa }}}_{0}\left| u_{R_{0}}\right| ^{p}dx}\right) ^{1/\left( p-2\right) }.$ By (5.6) we derive that

$$\begin{aligned} \inf _{t>0}f_{0}\left( t\right)= & {} f_{0}\left( \left( \frac{2\left\| u_{R_{0}}\right\| _{H^{1}}^{2}}{\left( 4-p\right) \int _{{{\mathbb {R}}}^{3}} {{\widehat{\kappa }}}_{0}\left| u_{R_{0}}\right| ^{p}dx}\right) ^{1/\left( p-2\right) }\right) \\= & {} -\frac{p-2}{2\left( 4-p\right) }\left( \frac{\left( 4-p\right) \int _{ {{\mathbb {R}}}^{3}}{{\widehat{\kappa }}}_{0}\left| u_{R_{0}}\right| ^{p}dx}{ 2\left\| u_{R_{0}}\right\| _{H^{1}}^{2}}\right) ^{2/\left( p-2\right) }\left\| u_{R_{0}}\right\| _{H^{1}}^{2} \\< & {} -\frac{p-2}{2\left( 4-p\right) }\left( \frac{\left( 4-p\right) \widehat{ \kappa }_{0}}{pS_{p}^{p}}\right) ^{2/\left( p-2\right) }\Vert u_{R_{0}}\Vert _{H^{1}}^{4}. \end{aligned}$$

For $\left[ \frac{A\left( p\right) }{p}a_{\infty }\right] ^{2/\left( p-2\right) }<\lambda \le \left[ \frac{A\left( p\right) }{p}a_{1}\right] ^{2/\left( p-2\right) }$, it follows from Lemma 2.3 and (5.12) that

$$\begin{aligned} \inf _{t>0}f_{N}\left( t\right)= & {} f_{N}\left( \left( \frac{2\left\| w_{R_{0},N}\right\| _{H^{1}}^{2}}{\left( 4-p\right) \int _{{{\mathbb {R}}} ^{3}}a_{\varepsilon _{N}}\left( x\right) \left| w_{R_{0},N}\right| ^{p}dx}\right) ^{1/\left( p-2\right) }\right) \\< & {} -\frac{N}{{{\overline{S}}}^{2}S_{12/5}^{4}}\frac{1}{2}\left( \frac{p}{2} \right) ^{2/\left( p-2\right) }\left( \frac{A\left( p\right) }{p} a_{1}\right) ^{2/\left( p-2\right) }\left\| u_{R_{0}}\right\| _{H^{1}}^{4} \\< & {} -\lambda N{{\overline{S}}}^{-2}S_{12/5}^{-4}\left\| u_{R_{0}}\right\| _{H^{1}}^{4} \\< & {} -\lambda N\int _{{{\mathbb {R}}}^{3}}\int _{{{\mathbb {R}}}^{3}}\frac{ u_{R_{0}}^{2}\left( x\right) u_{R_{0}}^{2}\left( y\right) }{4\pi \left| x-y\right| }dxdy. \end{aligned}$$

Using (5.10), we further obtain

$$\begin{aligned} \inf _{t>0}f_{N}\left( t\right)< & {} -\lambda N\int _{{{\mathbb {R}}}^{3}}\int _{ {{\mathbb {R}}}^{3}}\frac{u_{R_{0}}^{2}\left( x\right) u_{R_{0}}^{2}\left( y\right) }{4\pi \left| x-y\right| }dxdy-\lambda \sum _{i\ne j}^{N}\int _{{{\mathbb {R}}}^{3}}\int _{{{\mathbb {R}}}^{3}}\frac{u_{R_{0},N}^{\left( i\right) }\left( x\right) u_{R_{0},N}^{\left( j\right) }\left( y\right) }{ 4\pi \left| x-y\right| }dxdy \\= & {} -\lambda \int _{{{\mathbb {R}}}^{3}}\phi _{w_{R,N}}w_{R,N}^{2}dx\ \text { for sufficiently large }N. \end{aligned}$$

Thus, when $\left[ \frac{A\left( p\right) }{p}a_{\infty }\right] ^{2/\left( p-2\right) }<\lambda \le \left[ \frac{A\left( p\right) }{p}a_{1}\right] ^{2/\left( p-2\right) },$ there exist two constants $t_{\lambda ,N}^{\left( 1\right) }$ and $t_{\lambda ,N}^{\left( 2\right) }$ satisfying

$$\begin{aligned} 1<t_{\lambda ,N}^{\left( 1\right) }<\left( \frac{2\left\| u_{R_{0}}\right\| _{H^{1}}^{2}}{\left( 4-p\right) \int _{{{\mathbb {R}}} ^{3}}a_{\varepsilon _{N}}\left( x\right) \left| u_{R_{0}}\right| ^{p}dx}\right) ^{1/\left( p-2\right) }<t_{\lambda ,N}^{\left( 2\right) } \end{aligned}$$

such that

$$\begin{aligned} f_{N}\left( t_{\lambda ,N}^{\left( i\right) }\right) +\lambda \int _{\mathbb {R }^{3}}\phi _{w_{R,N}}w_{R,N}^{2}dx=0 \end{aligned}$$

for $i=1,2$ and for all $N\in {{\mathbb {N}}}$. That is, $t_{\lambda ,N}^{\left( i\right) }w_{R,N}\in {{\mathbf {M}}}_{\lambda ,a_{\varepsilon _{N}}}$ for $i=1,2$ and for all $N\in {{\mathbb {N}}}.$ A direct calculation on the second order derivatives gives

$$\begin{aligned} h_{\lambda ,t_{\lambda ,N}^{\left( 1\right) }w_{R,N}}^{\prime \prime }\left( 1\right)= & {} -2\left\| t_{\lambda ,N}^{\left( 1\right) }w_{R,N}\right\| _{H^{1}}^{2}+\left( 4-p\right) \int _{{{\mathbb {R}}} ^{3}}a_{\varepsilon _{N}}\left( x\right) \left| t_{\lambda ,N}^{\left( 1\right) }w_{R,N}\right| ^{p}dx \\= & {} \left( t_{\lambda ,N}^{\left( 1\right) }\right) ^{5}f_{N}^{\prime }\left( t_{\lambda ,N}^{\left( 1\right) }\right) <0, \end{aligned}$$

and

$$\begin{aligned} h_{\lambda ,t_{\lambda ,N}^{\left( 2\right) }w_{R,N}}^{\prime \prime }\left( 1\right)= & {} -2\left\| t_{\lambda ,N}^{\left( 2\right) }w_{R,N}\right\| _{H^{1}}^{2}+\left( 4-p\right) \int _{{{\mathbb {R}}} ^{3}}a_{\varepsilon _{N}}\left( x\right) \left| t_{\lambda ,N}^{\left( 2\right) }w_{R,N}\right| ^{p}dx \\= & {} \left( t_{\lambda ,N}^{\left( 2\right) }\right) ^{5}f_{N}^{\prime }\left( t_{\lambda ,N}^{\left( 2\right) }\right) \\> & {} 0. \end{aligned}$$

This enables us to conclude that

$$\begin{aligned} t_{\lambda ,N}^{\left( 1\right) }w_{R,N}\in {{\mathbf {M}}}_{\lambda ,a_{\varepsilon _{N}}}^{-}\text { and }t_{\lambda ,N}^{\left( 2\right) }w_{R,N}\in {{\mathbf {M}}}_{\lambda ,a_{\varepsilon _{N}}}^{+}. \end{aligned}$$

Moreover, by (5.7)–(5.10) we obtain

$$\begin{aligned} J_{\lambda ,a_{\varepsilon _{N}}}\left( t_{\lambda ,N}^{\left( 2\right) }w_{R,N}\right)= & {} \inf _{t>0}J_{\lambda ,a_{\varepsilon _{N}}}\left( tw_{R,N}\right) \le J_{\lambda ,a_{\varepsilon _{N}}}\left( t_{\lambda , {{\widehat{\kappa }}}_{0}}^{+}w_{R,N}\right) \\\le & {} NJ_{\lambda ,{{\widehat{\kappa }}}_{0}}^{\infty }\left( t_{\lambda , {{\widehat{\kappa }}}_{0}}^{+}u_{R_{0}}\right) +C_{0}\ \text { for some }C_{0}>0 \end{aligned}$$

and

$$\begin{aligned} J_{\lambda ,a_{\varepsilon _{N}}}\left( t_{\lambda ,N}^{\left( 2\right) }w_{R,N}\right) \rightarrow -\infty \text { as }N\rightarrow \infty . \end{aligned}$$

Therefore, we arrive at (5.11). $\square$

Lemma 5.2

Suppose that $2<p<3$ and conditions ${(D1)}-{(D2)}$ and $\left( D4\right)$ hold. Then for each $\left[ \frac{A\left( p\right) }{p}a_{\infty }\right] ^{2/\left( p-2\right) }<\lambda \le \left[ \frac{A\left( p\right) }{p}a_{1}\right] ^{2/\left( p-2\right) },$ there exists $M_{0}>0$ independent of $\varepsilon$ such that $0>\inf _{u\in H_{r}^{1}}J_{\lambda ,a_{\varepsilon }}\left( u\right) >-M_{0}$ for $\varepsilon$ sufficiently small.

Proof

Since $a\left( x\right) =a\left( \left| x\right| \right)$ and $a\left( 0\right) =a_{\max },$ by Lemma 3.1 and Remark 1.4,

$$\begin{aligned} \inf _{u\in H_{r}^{1}}J_{\lambda ,a_{\varepsilon }}\left( u\right) <0\text { for }\varepsilon \text { sufficiently small.} \end{aligned}$$

Moreover,

$$\begin{aligned} \inf _{u\in H_{r}^{1}}J_{\lambda ,a_{\varepsilon }}\left( u\right) \ge \inf _{u\in H_{r}^{1}}\left[ \frac{1}{2}\int _{{{\mathbb {R}}}^{3}}\left( |\nabla u|^{2}+u^{2}\right) dx+\frac{\lambda }{4}\int _{{{\mathbb {R}}}^{3}}\phi _{u}u^{2}dx-\frac{1}{p}\int _{{{\mathbb {R}}}^{3}}a_{\max }\left| u\right| ^{p}dx\right] \end{aligned}$$

and $\left[ A\left( p\right) a_{\infty }\right] ^{2/\left( p-2\right) }<\lambda \le \left[ A\left( p\right) a_{1}\right] ^{2/\left( p-2\right) },$ by Lemma 2.4,

$$\begin{aligned} \inf _{u\in H_{r}^{1}}\left[ \frac{1}{2}\int _{{{\mathbb {R}}}^{3}}\left( |\nabla u|^{2}+u^{2}\right) dx+\frac{\lambda }{4}\int _{{{\mathbb {R}}}^{3}}\phi _{u}u^{2}dx-\frac{1}{p}\int _{{{\mathbb {R}}}^{3}}a_{\max }\left| u\right| ^{p}dx\right] <0. \end{aligned}$$

Thus, applying similar argument to that in Ruiz [23, Theorem 4.3], there exists $M_{0}>0$ such that

$$\begin{aligned} \inf _{u\in H_{r}^{1}}\left[ \frac{1}{2}\int _{{{\mathbb {R}}}^{3}}\left( |\nabla u|^{2}+u^{2}\right) dx+\frac{\lambda }{4}\int _{{{\mathbb {R}}}^{3}}\phi _{u}u^{2}dx-\frac{1}{p}\int _{{{\mathbb {R}}}^{3}}a_{\max }\left| u\right| ^{p}dx\right] =-M_{0}, \end{aligned}$$

and so $\inf _{u\in H_{r}^{1}}J_{\lambda ,a_{\varepsilon }}\left( u\right) >-M_{0}.$ This completes the proof. $\square$

Next, we define the radial symmetry Nehari manifold

$$\begin{aligned} {{\mathbf {N}}}_{\lambda ,a_{\varepsilon }}:=\{u\in H_{r}^{1}\setminus \{0\}:\left\langle J_{\lambda ,a_{\varepsilon }}^{\prime }\left( u\right) ,u\right\rangle =0\}. \end{aligned}$$

If the weight function $a\left( x\right)$ satisfies condition $\left( D4\right) ,$ then by Remark 1.4 and Lemma 3.3, we can obtain $H_{r}^{1}\cap {{\mathbf {M}}}_{\lambda ,a_{\varepsilon }}^{\left( 2\right) }\ne \emptyset$ and $H_{r}^{1}\cap {{\mathbf {M}}}_{\lambda ,a_{\varepsilon }}^{\left( 2\right) }\subset {{\mathbf {N}}}_{\lambda ,a_{\varepsilon }}.$ By an argument similar to the proof of Lemma 2.7 and Palais criticality principle (cf. [22]), we conclude that the set ${{\mathbf {N}}}_{\lambda ,a_{\varepsilon }}^{\left( 2\right) }:=H_{r}^{1}\cap {{\mathbf {M}}}_{\lambda ,a_{\varepsilon }}^{\left( 2\right) }$ is a $C^{1}$ submanifold and each local minimizer of the functional $J_{\lambda ,a_{\varepsilon }}$ in ${{\mathbf {N}}}_{\lambda ,a_{\varepsilon }}$ is a critical point of $J_{\lambda ,a_{\varepsilon }}$ in $H^{1}({{\mathbb {R}}}^{3}).$

Define

$$\begin{aligned} \theta _{\lambda ,a_{\varepsilon }}:=\inf _{u\in {{\mathbf {N}}}_{\lambda ,a_{\varepsilon }}^{\left( 2\right) }}J_{\lambda ,a_{\varepsilon }}\left( u\right) . \end{aligned}$$

Repeating the argument in Remark 4.4, we have

$$\begin{aligned} \theta _{\lambda ,a_{\varepsilon }}:=\inf _{u\in {{\mathbf {N}}}_{\lambda ,a_{\varepsilon }}^{\left( 2\right) }}J_{\lambda ,a_{\varepsilon }}\left( u\right) =\inf _{u\in {{\mathbf {N}}}_{\lambda ,a_{\varepsilon }}}J_{\lambda ,a_{\varepsilon }}\left( u\right) . \end{aligned}$$

(5.13)

Moreover, by Lemmas 5.1 and 5.2 ,

$$\begin{aligned} \alpha _{\lambda ,a_{\varepsilon }}^{\left( 2\right) }<\theta _{\lambda ,a_{\varepsilon }}<0\text { for }\varepsilon >0\text { sufficiently small.} \end{aligned}$$

(5.14)

Then by an argument similar to the proof of Proposition 4.6 and Palais criticality principle (cf. [22]), for $\varepsilon$ small enough, there exists a sequence $\{u_{n}\}\subset {{\mathbf {N}}}_{\lambda ,a_{\varepsilon }}^{(2)}$ such that

$$\begin{aligned} J_{\lambda ,a_{\varepsilon }}(u_{n})=\theta _{\lambda ,a_{\varepsilon }}+o(1) \text { and }J_{_{\lambda ,a_{\varepsilon }}}^{\prime }(u_{n})=o(1)\text { in } H^{-1}\left( {{\mathbb {R}}}^{3}\right) . \end{aligned}$$

(5.15)

We are now ready to prove Theorem 1.2 Given $\{u_{n}\}\subset {{\mathbf {N}}}_{\lambda ,a_{\varepsilon }}^{(2)}$ satisfying

$$\begin{aligned} J_{\lambda ,a_{\varepsilon }}(u_{n})=\theta _{\lambda ,a_{\varepsilon }}+o(1) \text { and }J_{\lambda ,a_{\varepsilon }}^{\prime }(u_{n})=o(1)\text { in } H^{-1}\left( {{\mathbb {R}}}^{3}\right) , \end{aligned}$$

then by Theorem 2.5, $\{u_{n}\}$ is bounded. Without loss of generality, we can assume that there exists $v_{\lambda ,a_{\varepsilon }}\in H_{r}^{1}$ such that $u_{n}\rightharpoonup v_{\lambda ,a_{\varepsilon }}$ weakly in $H^{1}\left( {{\mathbb {R}}}^{3}\right) .$ Moreover, by Ruiz [23, Lemma 2.1], $J_{_{\lambda ,a_{\varepsilon }}}^{\prime }(v_{\lambda ,\varepsilon })=0$ in $H^{-1}\left( {{\mathbb {R}}}^{3}\right)$ and $u_{n}\rightarrow v_{\lambda ,a_{\varepsilon }}$ strongly in $H^{1}\left( {{\mathbb {R}}}^{3}\right) ,$ which implies that $J_{\lambda ,a_{\varepsilon }}(v_{\lambda ,a_{\varepsilon }})=\theta _{\lambda ,a_{\varepsilon }}$ and $v_{\lambda ,a_{\varepsilon }}\in {{\mathbf {N}}}_{\lambda ,a_{\varepsilon }}^{(2)}.$ Thus, by (5.13), $v_{\lambda ,\varepsilon }$ is a radial ground state solution of Equation $(E_{\lambda ,a_{\varepsilon }}).$ Since $J_{\lambda ,a_{\varepsilon }}(v_{\lambda ,a_{\varepsilon }})=J_{\lambda ,a_{\varepsilon }}(|v_{\lambda ,a_{\varepsilon }}|)=\theta _{\lambda ,a_{\varepsilon }},$ by Lemma 2.1, we may assume that $v_{\lambda ,a_{\varepsilon }}$ is a positive solution of Equation $(E_{\lambda ,a_{\varepsilon }}).$ Therefore, by Theorem 1.1 and (5.14), Equation $(E_{\lambda ,a_{\varepsilon }})$ has three positive solutions $u_{\lambda ,a_{\varepsilon }}^{\left( 1\right) },u_{\lambda ,a_{\varepsilon }}^{\left( 2\right) }\in H^{1}\left( {{\mathbb {R}}} ^{3}\right)$ and $v_{\lambda ,a_{\varepsilon }}\in H_{r}^{1}$ such that

$$\begin{aligned} \alpha _{\lambda ,a_{\varepsilon }}^{\left( 2\right) }=J_{\lambda ,a_{\varepsilon }}\left( u_{\lambda ,a_{\varepsilon }}^{\left( 2\right) }\right)<\theta _{\lambda ,a_{\varepsilon }}=J_{\lambda ,a_{\varepsilon }}\left( v_{\lambda ,a_{\varepsilon }}\right)<0<\alpha _{\lambda ,a_{\varepsilon }}^{\left( 1\right) }=J_{\lambda ,a_{\varepsilon }}\left( u_{\lambda ,a_{\varepsilon }}^{\left( 1\right) }\right) \end{aligned}$$

for $\varepsilon$ sufficiently small. Since

$$\begin{aligned} \alpha _{\lambda ,a_{\varepsilon }}^{\left( 2\right) }=\inf _{u\in {{\mathbf {M}}} _{\lambda ,a_{\varepsilon }}}J_{\lambda ,a_{\varepsilon }}\left( u\right) <\theta _{\lambda ,a_{\varepsilon }}=\inf _{u\in {{\mathbf {N}}}_{\lambda ,a_{\varepsilon }}}J_{\lambda ,a_{\varepsilon }}\left( u\right) \text { for } \varepsilon \text { sufficiently small} \end{aligned}$$

and $v_{\lambda ,a_{\varepsilon }}$ is a radial ground state solution of Equation $(E_{\lambda ,a_{\varepsilon }}),$ we can conclude that $u_{\lambda ,a_{\varepsilon }}^{\left( 2\right) }$ is a non-radial ground state solution of Equation $(E_{\lambda ,a_{\varepsilon }}).$