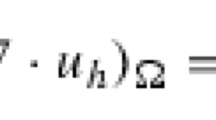Abstract
This paper focuses on the following Keller–Segel–Navier–Stokes system with rotational flux:

in a bounded domain \(\Omega \subset {\mathbb {R}}^3\) with a smooth boundary, where \(\kappa \in {\mathbb {R}}\) is a given constant, \(\phi \in W^{1,\infty }(\Omega )\), \(|S(x,n,c)|\le C_S(1+n)^{-\alpha }\), and the parameter \(\alpha \ge 0\). If \(\alpha >\frac{1}{3}\), then, for all reasonable regular initial data, a corresponding initial-boundary value problem for (KSNF) possesses a globally defined weak solution. This result improves upon the result of Wang (Math Models Methods Appl Sci 27(14):2745–2780, 2017), in which the global very weak solution for the system (KSNF) is obtained. In comparison with the result of the corresponding fluid-free system, the optimal condition on the parameter \(\alpha \) for global (weak) existence is established. Our proofs rely on a variant of the natural gradient-like energy functional.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Chemotaxis, the biased movement of cells (or organisms) in response to chemical gradients, plays an important role in coordinating cell migration in many biological phenomena (see Hillen and Painter [8]). Let n denote the density of the cells and c present the concentration of the chemical signal. In the 1970s, Keller and Segel [12] proposed a mathematical system for chemotaxis through a system of parabolic equations. The mathematical model reads as
where S is a given chemotactic sensitivity function, which can either be a scalar function or, more generally, a tensor-valued function (see, e.g., Xue and Othmer [42]). During the past four decades, Keller–Segel models (1.1) and their variants have attracted extensive attention, withthe main issue of investigation focusing on whether the solutions of the models are bounded or blow up (see Winkler et al. [1], Hillen and Painter [8] and Horstmann [9]). For instance, if \(S:=S(n)\) is a scalar function satisfying \(S(s)\le C(1 + s)^{-\alpha }\) for all \(s\ge 1\), \(\alpha > 1 -\frac{2}{N}\), and \(C>0\), then all solutions to the corresponding Neumann problem are global and uniformly bounded (see Horstmann and Winkler [10]). However, if \(N\ge 2\), \(\Omega \) (a ball) \(\subset R^N\), and \(S(s) > cs^{-\alpha }\) for some \(\alpha < 1-\frac{2}{N}\) and \(c>0\), then the solution to problem (1.1) may blow up (see Horstmann and Winkler [10]). Therefore,
is the critical blow-up exponent, which is related to the presence of a so-called volume-filling effect. For related works in this direction, we mention that a corresponding quasilinear version, the logistic damping or the signal consumed by the cells, has been deeply investigated by Cieślak and Stinner [4, 5], Tao and Winkler [20, 31, 41] and Zheng et al. [44,45,46, 50, 51].
As in the classical Keller–Segel model where the chemoattractant is produced by bacteria, the corresponding chemotaxis–fluid model then becomes the following Keller–Segel(–Navier)–Stokes system:
where n and c are defined as before and \(\Omega \subset {\mathbb {R}}^3\) is a bounded domain with a smooth boundary. Here u, \(P,\phi \), and \(\kappa \in {\mathbb {R}}\) denote, respectively, the velocity field, the associated pressure of the fluid, the potential of the gravitational field, and the strength of nonlinear fluid convection. S(x, n, c) is a chemotactic sensitivity tensor satisfying
and
with some \(C_S > 0\) and \(\alpha > 0\). Problem (1.3) is proposed to describe the chemotaxis-fluid interaction in cases when the evolution of the chemoattractant is essentially dominated by production through cells (see Winkler et al. [1] and Hillen and Painter [8]).
Before delving into our mathematical analysis, we recall some important progress on system (1.3) and its variants. The following chemotaxis-fluid model,which is closely related to the variation of (1.3), was proposed by Tuval et al. [24]:
where f(c) is the consumption rate of oxygen by the cells. In the past few years, by making use of the energy-type functionals, system (1.6) and its variants have attracted extensive attention (see, e.g., Chae et al. [3], Duan et al. [6], Liu and Lorz [13, 15], Tao and Winkler [23, 33, 34, 37], Zhang and Zheng [43] and references therein). For example, Winkler [37] established the global existence of a weak solution in a three-dimensional domain when \(S(x, n, c) \equiv 1\) and \(\kappa \ne 0\). Recently, if \(S(x,n,c):=S(c),\) the long-term behavior of eventual smoothness of the weak solution was investigated by Winkler [38], in which the weak solution became smooth on some interval \([T,\infty )\) and uniformly converged in the large-time limit. For more literature related to this model, we can refer to Tao and Winkler [21, 22, 39] and the references therein. For example, Winkler [39] proved that the chemotaxis–Stokes system (with nonlinear diffusion) admits a global bounded weak solution under the assumption \(m > \frac{9}{8}\). Furthermore, he also showed that the obtained solution approached the spatially homogeneous steady state in the large-time limit.
If the chemotactic sensitivity S(x, n, c) is regarded as a tensor rather than a scalar one (see Xue and Othmer [42]), (1.6) turns into a chemotaxis(–Navier)–Stokes system with rotational flux. Owing to the presence of the tensor-valued sensitivity, the corresponding chemotaxis–Stokes system loses some energy structure, which has played a key role in previous studies for the scalar sensitivity case (see Cao [2] and Winkler [36]). Therefore, very few results appear to be available on chemotaxis-Stokes systems with such tensor-valued sensitivities (see, e.g., Ishida [11], Wang et al. [26, 28] and Winkler [36]). In fact, assuming that \(f(c)=c\) and that (1.4) and (1.5) hold, Ishida [11] proved that (1.6) admits a bounded global weak solution in two dimensions with nonlinear diffusion, whereas, in three dimensions, Winkler [36] showed that the chemotaxis-Stokes system [\(\kappa =0\) in the first equation of (1.6)] with nonlinear diffusion (where the coefficient of diffusion satisfies \(m > \frac{7}{6}\)) possesses at least one bounded weak solution that stabilizes to a spatially homogeneous equilibrium \((\frac{1}{|\Omega |}\int _{\Omega }n_0, 0, 0)\).
In contrast to the large number of existing results ofor (1.6), the mathematical analysis of (1.3) with regard to global and bounded solutions is far from trivial. On the one hand, as its subsystem, the Navier–Stokes system lacks a complete existence theory (see Wiegner [30]). On the other hand, the previously mentioned properties for the Keller–Segel system can still emerge (see Wang et al. [17, 25, 27,28,29] and Zheng [48, 49]). In fact, in two dimensions, if \(S=S(x, n, c)\) is a tensor-valued sensitivity fulfilling (1.4) and (1.5), Wang and Xiang [28] proved that the Stokes version [\(\kappa =0\) in the first equation of (1.3)] of system (1.3) admits a unique global classical solution that is bounded. Recently, Wang et al. [27] extended the above result [28] to the Navier–Stokes version (\(\kappa \ne 0\) in the first equation of (1.3)). In both papers [27] and [28], the condition \(\alpha >0\), corresponding to the condition (1.2) with \(n=2\), is optimal for the existence of the solution. Furthermore, similar results are also valid for the three-dimensional Stokes version [\(\kappa =0\) in the first equation of (1.3)] of system (1.3) with \(\alpha >\frac{1}{2}\) (see Wang and Xiang [29]). In the three dimensional case, Wang and Liu [14] showed that the Keller–Segel–Navier–Stokes [\(\kappa \ne 0\) in the first equation of (1.3)) system (1.3] admits a global weak solution for tensor-valued sensitivity S(x, n, c) satisfying (1.4) and (1.5) with \(\alpha > \frac{3}{7}\). Recently, because of the lack of enough regularity and compactness properties for the first equation, by using the idea proposed by Winkler [35], Wang [25] presented the existence of global very weak solutions for the system (1.3) under the assumption that S satisfies (1.4) and (1.5) with \(\alpha > \frac{1}{3}\), which, in light of the known results for the fluid-free system mentioned above, is an optimal restriction on \(\alpha \) [see (1.2)]. However, the existence of global (stronger than the result of [25]) weak solutions is still open. In this paper, we try to obtain enough regularity and compactness properties (see Lemmas 3.4, 5.1, and 5.2), then show that system (1.3) possesses a globally defined weak solution (see Definition 2.1), which improves the result of [25].
Throughout this paper, we assume that
and that the initial data \((n_0, c_0, u_0)\) fulfill
where \(A_{r}\) denotes the Stokes operator with domain \(D(A_{r}) := W^{2,{r}}(\Omega )\cap W^{1,{r}}_0(\Omega ) \cap L^{r}_{\sigma }(\Omega )\) and \(L^{r}_{\sigma }(\Omega ) := \{\varphi \in L^{r}(\Omega )|\nabla \cdot \varphi = 0\}\) for \({r}\in (1,\infty )\) (similar to that in [19]).
Our main result assert the existence of the global weak solution for system (1.3).
Theorem 1.1
Let \(\Omega \subset {\mathbb {R}}^3\) be a bounded domain with a smooth boundary. (1.7) and (1.8) hold, and suppose that S satisfies (1.4) and (1.5) with some
Then problem (1.3) possesses at least one global weak solution (n, c, u, P) in the sense of Definition 2.1.
Remark 1.1
(i) From Theorem 1.1, we conclude that \(\alpha > \frac{1}{3}\) is sufficient to guarantee the existence of global (weak) solutions. Compared with the results (1.2), we know such a restriction on \(\alpha \) seems to be optimal.
(ii) Obviously, \( \frac{3}{7}>\frac{1}{3}\), so Theorem 1.1 improves the results of Liu and Wang [14], which showed the global weak existence of solutions in cases S(x, n, c) satisfying (1.4) and (1.5) with \(\alpha > \frac{3}{7}\).
(iii) If \(S:=S(n)=C_S(1+n)^{-\alpha }\) is a scalar function which satisfies that \(\alpha >\frac{1}{3},\) the boundedness of solution to Keller–Segel–Stokes [\(\kappa =0\) in the first equation of (1.3)] system (1.3) is obtained by Winkler (see [40]). Recalling the condition (1.2) for global existence in the fluid-free setting, as implied by the previously mentioned studied (see Horstmann and Winkler [10]), this result appears to be optimal with respect to \(\alpha \).
This paper is organized as followed. In Sect. 2, we give the definition of weak solutions to (1.3), the regularized problems of (1.3), and some preliminary properties. Sections 3 and 4 will be devoted to an analysis of regularized problems of (1.3). Next, on the basis of the compactness properties thereby implied, in Sects. 5 and 6, we can pass to the limit along with an adequate sequence of numbers \(\varepsilon = \varepsilon _j{\searrow }0\) and thereby verify Theorem 1.1.
2 Preliminaries
In light of the strong nonlinear term \((u \cdot \nabla )u\), problem (1.3) has no classical solutions in general, thus we consider its weak solutions.
Definition 2.1
Let \(T > 0\) and assume that \((n_0, c_0, u_0)\) fulfills (1.8). Then a triple of functions (n, c, u) is called a weak solution of (1.3) if the following conditions are satisfied:
where \(n\ge 0\) and \(c\ge 0\) in \(\Omega \times (0, T)\) as well as \(\nabla \cdot u = 0\) in the distributional sense in \(\Omega \times (0, T)\). Moreover,
and
for any \(\varphi \in C_0^{\infty } ({\bar{\Omega }}\times [0, T))\) satisfying \(\frac{\partial \varphi }{\partial \nu }= 0\) on \(\partial \Omega \times (0, T)\), as well as
for any \(\varphi \in C_0^{\infty } ({\bar{\Omega }}\times [0, T))\) and
for any \(\varphi \in C_0^{\infty } ({\bar{\Omega }}\times [0, T);{\mathbb {R}}^3)\) fulfilling \(\nabla \varphi \equiv 0\) in \(\Omega \times (0, T)\).
If (n, c, u) : \(\Omega \times (0,\infty )\longrightarrow {\mathbb {R}}^5\) is a weak solution of (1.3) in \(\Omega \times (0, T)\) for all \(T > 0\), then (n, c, u) is called a global weak solution of (1.3).
To obtain the solution of system (1.3), we first consider the following approximate system of (1.3):
where
as well as
and
is a standard Yosida approximation and A is the realization of the Stokes operator (see [19]). Here, \((\rho _\varepsilon )_{\varepsilon \in (0,1)} \in C^\infty _0 (\Omega )\) is a family of standard cutoff functions satisfying \(0\le \rho _\varepsilon \le 1\) in \(\Omega \) and \(\rho _\varepsilon {\nearrow }1\) in \(\Omega \) as \(\varepsilon {\searrow }0\).
The local solvability of (2.6) can be derived by a suitable extensibility criterion and a slight modification of the well-established fixed-point arguments in Lemma 2.1 of [37] (see also [36] and Lemma 2.1 of [16]), so here we omit the proof.
Lemma 2.1
Assume that \(\varepsilon \in (0,1).\) Then there exist \(T_{max,\varepsilon }\in (0,\infty ]\) and a classical solution \((n_\varepsilon , c_\varepsilon , u_\varepsilon , P_\varepsilon )\) of (2.6) in \(\Omega \times (0, T_{max,\varepsilon })\) such that
classically solving (2.6) in \(\Omega \times [0,T_{max,\varepsilon })\). Moreover, \(n_\varepsilon \) and \(c_\varepsilon \) are nonnegative in \(\Omega \times (0, T_{max,\varepsilon })\), and
where \(\gamma \) is given by (1.8).
Lemma 2.2
[32, 47] Let \((e^{\tau \Delta })_{\tau \ge 0}\) be the Neumann heat semigroup in \(\Omega \) and \(p>3\). Then there exist positive constants \(c_1:=c_1(\Omega ),\) \(c_2:=c_2(\Omega ),\) and \(c_3:=c_3(\Omega )\) such that for all \(\tau >0\) and any \(\varphi \in W^{1,p}(\Omega )\),
and for all \(\tau > 0\) and each \(\varphi \in L^\infty (\Omega )\)
as well as for all \(\tau > 0\) and all \(\varphi \in C^{1}({\bar{\Omega }}; {\mathbb {R}}^3)\) fulfilling \(\varphi \cdot \nu =0~\text{ on }~\partial \Omega \)
3 Some a priori estimates for the regularized problem (2.6) that is independent of \(\varepsilon \)
In this section, we are going to establish an iteration step to develop the main ingredients of our result. The iteration depends on a series of a priori estimates. To proceed, first, we recall some properties of \(F_\varepsilon \) and \(F'_\varepsilon \), which play an important role in demonstrating Theorem 1.1.
Lemma 3.1
Assume \(F_{\varepsilon }\) is given by (2.7). Then
as well as
and
Proof
Recalling (2.7), by tedious and simple calculations, we can derive (3.1)–(3.3). \(\square \)
The proof of this lemma is very similar to that of Lemmas 2.2 and 2.6 of [23] (see also Lemma 3.2 of [25]), so we omit it here.
Lemma 3.2
There exists \(\lambda > 0\) independent of \(\varepsilon \) such that the solution of (2.6) satisfies
Lemma 3.3
Let \(\alpha >\frac{1}{3}\). Then there exists \(C>0\) independent of \(\varepsilon \) such that the solution of (2.6) satisfies
Moreover, for \(T\in (0, T_{max,\varepsilon })\), one can find a constant \(C > 0\) independent of \(\varepsilon \) such that
Proof
The proof consists of two cases.
Case \(2\alpha \ne 1\): We first obtain from \(\nabla \cdot u_\varepsilon =0\) in \(\Omega \times (0, T_{max,\varepsilon })\) and straightforward calculations that
for all \(t\in (0, T_{max,\varepsilon }).\) Therefore, from (3.1), in light of (1.5) and (2.7), we can estimate the right-hand side of (3.7) as follows:
by using Young’s inequality, where in the last inequality we have used the fact that \( n_{\varepsilon }^{2\alpha -2}n_{\varepsilon }^2(1 + n_{\varepsilon })^{-2\alpha }\le 1\) for all \(\varepsilon \ge 0\) and \((x,t)\in \Omega \times (0, T_{max,\varepsilon }).\) Inserting (3.8) into (3.7), we conclude that
To track the time evolution of \(c_\varepsilon \), taking \({c_{\varepsilon }}\) as the test function for the second equation of (2.6) and using \(\nabla \cdot u_\varepsilon =0\) and (3.3) together with Hölder’s inequality yields
By applying Sobolev embedding \(W^{1,2}(\Omega ){\hookrightarrow }L^6(\Omega )\) in the three-dimensional setting, in view of (3.4), there exist positive constants \(C_1\) and \(C_2\) such that
Thus, by means of Young’s inequality and (3.11), we proceed to estimate
and some positive constant \(C_3\) independent of \(\varepsilon \). Therefore,
To estimate \(\Vert n_{\varepsilon }\Vert _{L^{\frac{6}{5}(\Omega )}}\) for all \(t\in (0, T_{max,\varepsilon })\), we should notice that \( \alpha >\frac{1}{3}\) ensures that \(\frac{2}{6\alpha -1}<2\), so that, in light of (3.4), the Gagliardo–Nirenberg inequality and Young’s inequality allow us to estimate that
with some positive constants \(C_4\) and \(C_5\) independent of \(\varepsilon \). This together with (3.13) contributes to
and some positive constant \(C_6\). Taking an evident linear combination of the inequalities provided by (3.9) and (3.15), one can obtain
and some positive constant \(C_7.\) Since \(\mathrm{sign}(2\alpha -1)\displaystyle \frac{2\alpha -1}{2}=\displaystyle \frac{|2\alpha -1|}{2},\) (3.16) implies that
If \(2\alpha >1\), then \(\mathrm{sign}(2\alpha -1)=1>0,\) thus, integrating (3.17) over time, we can obtain
and
and some positive constant \(C_8.\) If \(2\alpha <1\), then \(\mathrm{sign}(2\alpha -1)=-1<0\); hence, in view of (3.4), integrating (3.17) over time and employing Hölder’s inequality, we also conclude that there exists a positive constant \(C_9\) such that
and
Case \(2\alpha =1\): Using the first equation of (2.6) and (2.7), integrating by parts, and applying (1.5) and (3.1), we obtain
which combined with Young’s inequality and \(2\alpha =1\) implies that
However, since \(2\alpha =1\) yields \(\alpha >\frac{1}{3}\), by employing almost exactly the same arguments as in the proof of (3.10)–(3.16) (with the minor necessary changes being left as an easy exercise to the reader), we conclude an estimate of
and
Now, multiplying the third equation of (2.6) by \(u_\varepsilon \), integrating by parts, and using \(\nabla \cdot u_{\varepsilon }=0\) give
Here we use Hölder’s inequality, Young’s inequality, (1.7), and the continuity of the embedding \(W^{1,2}(\Omega )\hookrightarrow L^6(\Omega )\) to find \(C_{11} \) and \(C_{12}> 0\) such that
Next, in view of (3.4) and \(\alpha >\frac{1}{3}\), (3.14) and Young’s inequality along with the Gagliardo–Nirenberg inequality yields
and some positive constant \(C_{13}.\) Now, inserting (3.25) and (3.26) into (3.24) and using (3.21) and (3.23), one has
and
and some positive constant \(C_{14}.\) Finally, collecting (3.20)–(3.21), (3.22)–(3.23), and (3.27)–(3.28), we can get (3.5) and (3.6). \(\square \)
With the help of Lemma 3.3, based on the Gagliardo–Nirenberg inequality and an application of well-known arguments from parabolic regularity theory, we can derive the following lemmas:
Lemma 3.4
Let \(\alpha >\frac{1}{3}\). Then there exists \(C>0\) independent of \(\varepsilon \) such that, for each \(T\in (0, T_{max,\varepsilon })\), the solution of (2.6) satisfies
as well as
and
Proof
Case \(\frac{1}{3}<\alpha \le \frac{1}{2}\): From (3.4), (3.5), and (3.6), in light of the Gagliardo–Nirenberg inequality, for some \(C_1\) and \(C_2> 0\) that are independent of \(\varepsilon \), one may verify that
Therefore, employing Hölder’s inequality (with two exponents \(\frac{4}{3\alpha +1}\) and \(\frac{4}{3-3\alpha }\)), we conclude that there exists a positive constant \(C_3\) such that
Case \(\frac{1}{2}<\alpha <1\): Again by (3.4), (3.5), and (3.6) and the Gagliardo–Nirenberg inequality and Hölder’s inequality (with two exponents \(\frac{3+2\alpha }{5\alpha }\) and \(\frac{3+2\alpha }{3-3\alpha }\)), we derive that there exist positive constants \(C_4\), \(C_5\), and \(C_6\) such that
and
Case \(\alpha \ge 1\): Multiplying the first equation in (2.6) by \( n_{\varepsilon }\), in view of (2.7) and using \(\nabla \cdot u_\varepsilon =0\), we derive
Recalling (1.5) and (2.7) and using \(\alpha \ge 1\), via Young’s inequality, we derive
Here we have used the fact that
by using (1.5). Therefore, collecting (3.37) and (3.38) and using (3.6), we conclude that
and
Hence, from (3.39)–(3.40) and (3.5)–(3.6), in light of the Gagliardo–Nirenberg inequality, we derive that there exist positive constants \(C_{8}\), \(C_{9}\), \(C_{10}\), \(C_{11}\), \(C_{12}\), \(C_{13}\), \(C_{14}\), \(C_{15}\), \(C_{16}\) and \(C_{17}\) such that
as well as
and
where the last inequality we have used the embedding \(W^{1,2}_{0,\sigma } (\Omega ) {\hookrightarrow } L^6 (\Omega )\) and the Poincaré inequality. Finally, combining (3.33)–(3.36) with (3.40)–(3.44), we can obtain the results. \(\square \)
Lemma 3.5
Let \(\frac{1}{3}<\alpha \le \frac{8}{21}\). Then there exist \(\gamma =\frac{2\alpha +\frac{2}{3}}{\alpha +1}\in (1,2)\) and \(C > 0\) independent of \(\varepsilon \) such that, for each \(T\in (0, T_{max,\varepsilon })\), the solution of (2.6) satisfies
Proof
To this end, we first prove that for all \(p\in (1,6\alpha ) \), then there exists a positive constant \(C_1\) independent of \(\varepsilon \) such that, for each \(T\in (0, T_{max,\varepsilon })\), the solution of (2.6) satisfies
In fact, by (3.4) and (3.6), we derive that for some positive constants \(C_{2}\) and \(C_3\) independent of \(\varepsilon \) such that
Therefore, (3.46) holds. Next, by \(\alpha \in (\frac{1}{3},\frac{8}{21}],\) we may choose \(\gamma =\frac{2\alpha +\frac{2}{3}}{\alpha +1}\) such that
as well as
and
Collecting (3.46)–(3.49), one can derive (3.45) by using the Young inequality. \(\square \)
4 Global solvability of the regularized problem (2.6)
The main task of this section is to prove the global solvability of the regularized problem (2.6). To this end, first, we need to establish some \(\varepsilon \)-dependent estimates for \(n_{\varepsilon }\), \(c_{\varepsilon },\) and \(u_{\varepsilon }\).
4.1 A priori estimates for the regularized problem (2.6) that depend on \(\varepsilon \)
In this subsection, we obtain some regularity properties for \(n_\varepsilon ,\) \(c_\varepsilon ,\) and \(u_\varepsilon \) in the following form on the basis of Lemma 3.3.
Lemma 4.1
Let \(\alpha >\frac{1}{3}\). Then there exists \(C=C(\varepsilon )>0\) depending on \(\varepsilon \) such that the solution of (2.6) satisfies
In addition, for each \(T\in (0, T_{max,\varepsilon }]\) with \(T < \infty \), one can find a constant \(C > 0\) depending on \(\varepsilon \) such that
Proof
In view of (2.7), we derive
so that, by multiplying the first equation in (2.6) by \( n_{\varepsilon }^{1+2\alpha }\), using \(\nabla \cdot u_\varepsilon =0\), and applying the same argument as in the proof of (3.7)–(3.20), one can obtain that there exist positive constants \(C_1\) and \(C_2\) depending on \(\varepsilon \) such that
and
Now, from \(D(1 + \varepsilon A) :=W^{2,2}(\Omega ) \cap W_{0,\sigma }^{1,2}(\Omega )\hookrightarrow L^\infty (\Omega )\) and (3.5), it follows that, for some \(C_3> 0\) and \(C_4 > 0\),
Next, testing the projected Stokes equation \(u_{\varepsilon t} +Au_{\varepsilon } = {\mathcal {P}}[-\kappa (Y_{\varepsilon }u_{\varepsilon } \cdot \nabla )u_{\varepsilon }+n_{\varepsilon }\nabla \phi ]\) by \(Au_{\varepsilon }\), we derive
However, in light of the Gagliardo–Nirenberg inequality, Young’s inequality, and (4.4), there exists a positive constant \(C_5\) such that
Here we have used the well-known fact that \(\Vert A(\cdot )\Vert _{L^{2}(\Omega )}\) defines a norm equivalent to \(\Vert \cdot \Vert _{W^{2,2}(\Omega )}\) on D(A) (see Theorem 2.1.1 of [19]). Now, recall that \(\Vert A^{\frac{1}{2}}u_{\varepsilon }\Vert ^{{{2}}}_{L^{{2}}(\Omega )} = \Vert \nabla u_{\varepsilon }\Vert ^{{{2}}}_{L^{{2}}(\Omega )}.\) Substituting (4.6) into (4.5) yields
Since \(\alpha >\frac{1}{3}\) yields \(2\alpha +2>\frac{8}{3}>2,\) by collecting (4.3) and (4.7) and performing some basic calculations, we can get the results. \(\square \)
Lemma 4.2
Under the assumptions of Theorem 1.1, one can find that there exists \(C=C(\varepsilon )> 0\) depending on \(\varepsilon \) such that
and
Proof
First, testing the second equation in (2.6) against \(-\Delta c_{\varepsilon }\), employing Young’s inequality, and using (3.3) yields
for all \(t\in (0,T_{max,\varepsilon })\). Next, one needs to estimate the last term on the right-hand side of (4.10). Indeed, in view of Sobolev’s embedding theorem (\(W^{1,2}(\Omega )\hookrightarrow L^6(\Omega )\)) and applying (4.1) and (3.5), we derive from Hölder’s inequality, the Gagliardo–Nirenberg inequality, and Young’s inequality that there exist positive constants \(C_1\), \(C_2\), \(C_3\), and \(C_4\) such that
Inserting (4.11) into (4.10) and using (4.1), one obtains (4.8) and (4.9). This completes the proof of Lemma 4.2. \(\square \)
Lemma 4.3
Let \(\alpha >\frac{1}{3}\). Assume that the hypothesis of Theorem 1.1 holds. Then there exists a positive constant \(C=C(\varepsilon )\) depending on \(\varepsilon \) such that, for any \(3<q<6,\) the solution of (2.6) from Lemma 2.1 satisfies
as well as
and
where \(\gamma \) is the same as in (1.8).
Proof
Let \(h_{\varepsilon }(x,t)={\mathcal {P}}[n_{\varepsilon }\nabla \phi -\kappa (Y_{\varepsilon }u_{\varepsilon } \cdot \nabla )u_{\varepsilon } ]\). Because \(\alpha >\frac{1}{3}\), then , along with (4.1), (1.7), and (4.4), there exist positive constants \(q_0>\frac{3}{2}\) and \(C_{1}\) such that
and
Hence, because \(q_0>\frac{3}{2}\), we pick an arbitrary \(\gamma \in (\frac{3}{4}, 1)\) and, then, \(-\gamma -\frac{3}{2}(\frac{1}{q_0}-\frac{1}{2})>-1\). Therefore, in view of the smoothing properties of the Stokes semigroup [7], we derive that, for some \(\lambda \), \(C_{2} > 0,\) and \(C_{3} > 0\),
Observe that \(\gamma >\frac{3}{4},\) \(D(A^\gamma )\) is continuously embedded into \(L^\infty (\Omega )\). Therefore, we derive that there exists a positive constant \(C_{4}\) such that
from (4.17). However, from (4.8), with the help of Sobolev’s imbedding theorem, it follows that, for any fixed \({\tilde{q}}\in (3,6)\),
Now, involving the variation-of-constants formula for \(c_{\varepsilon }\) and applying \(\nabla \cdot u_{\varepsilon }=0\) in \(x\in \Omega , t>0\), we have
so that, for any \(3<q <\min \{\frac{3q_0}{(3-q_0)_{+}},{\tilde{q}}\}\), we have
To address the right-hand side of (4.21), in view of (1.8), we first use Lemma 2.2 to get
Since (4.15) and (4.19) yields
together with this and (3.3), by using Lemma 2.2 again, the second term of the right-hand side is estimated as
Finally, we will address the third term on the right-hand side of (4.21). To this end, we choose \(0< \iota < \frac{1}{2}\) satisfying \(\frac{1}{2} + \frac{3}{2}(\frac{1}{{\tilde{q}}}-\frac{1}{q}) <\iota \) and \({\tilde{\kappa }}\in (0, \frac{1}{2}-\iota )\). In view of Hölder’s inequality, we derive from Lemma 2.2, (4.19), and (4.18) that there exist constants \(C_{9}\), \(C_{10}\), \(C_{11}\), and \(C_{12}\) such that
Here we have used the fact that
Finally, collecting (4.21)–(4.24), we can obtain that there exists a positive constant \(C_{13}\) such that
The proof of Lemma 4.3 is complete. \(\square \)
Then we can establish global existence in the approximate problem (2.6) by using Lemmas 4.1 and 4.2 .
Lemma 4.4
Let \(\alpha >\frac{1}{3}\). Then, for all \(\varepsilon \in (0,1),\) the solution of (2.6) is global in time.
Proof
Assume that \(T_{max,\varepsilon }\) is finite for some \(\varepsilon \in (0,1)\). Fix \(T\in (0, T_{max,\varepsilon })\), and let \(M(T):=\sup _{t\in (0,T)}\Vert n_{\varepsilon }(\cdot ,t)\Vert _{L^\infty (\Omega )}\) and \({\tilde{h}}_{\varepsilon }:=F'_{\varepsilon }(n_{\varepsilon })S_\varepsilon (x, n_{\varepsilon }, c_{\varepsilon })\nabla c_{\varepsilon }+u_\varepsilon \). Then, by Lemma 4.3, (1.5), and (3.1), there exists \(C_1 > 0\) such that
Hence, because \(\nabla \cdot u_{\varepsilon }=0\), we can derive
by means of an associate variation-of-constants formula for n, where \(t_0 := (t-1)_{+}\). If \(t\in (0,1]\), by virtue of the maximum principle, we can derive
while if \(t > 1\) then, with the help of the \(L^p\)–\(L^q\) estimates for the Neumann heat semigroup and Lemma 3.2, we conclude that
Finally, we fix an arbitrary \(p\in (3,q)\) and then once more invoke known smoothing properties of the Stokes semigroup (see Page 201 of [7]) and Hölder’s inequality to find \(C_4 > 0\) such that
where \(b:=\frac{pq-q+p}{pq}\in (0,1)\) and
Since \(p>3\), we conclude that \(-\frac{1}{2}-\frac{3}{2p}>-1\). In combination with (4.27)–(4.30) and using the definition of M(T), we obtain \(C_6 > 0\) such that
Hence, in view of \(b<1\), with some basic calculation, since \(T\in (0, T_{max,\varepsilon })\) was arbitrary, we can obtain there exists a positive constant \(C_7\) such that
To prove the boundedness of \(\Vert \nabla c_{\varepsilon }(\cdot , t)\Vert _{L^\infty (\Omega )}\), we rewrite the variation-of-constants formula for \(c_{\varepsilon }\) in the form
Now, we choose \(\theta \in (\frac{1}{2}+\frac{3}{2q},1),\) where \(3<q<6\) [see (4.25)], then the domain of the fractional power \(D((-\Delta + 1)^\theta )\hookrightarrow W^{1,\infty }(\Omega )\) (see [10]). Hence, in view of \(L^p\)–\(L^q\) estimates associated with the heat semigroup, (4.13), (4.14), and (3.3), we derive that there exist positive constants \(\lambda \), \(C_{8}\), \(C_{9}\), \(C_{10}\), and \(C_{11}\) such that
Here we have used Hölder’s inequality as well as
In view of (4.12), (4.33), and (4.32), we apply Lemma 2.1 to reach a contradiction. \(\square \)
5 Regularity properties of time derivatives
In preparation of an Aubin–Lions type compactness argument, we will rely on an additional regularity estimate for \(n_\varepsilon F'_{\varepsilon }(n_{\varepsilon })S_\varepsilon (x, n_{\varepsilon }, c_{\varepsilon })\nabla c_\varepsilon \), \(u_\varepsilon \cdot \nabla c_\varepsilon \), \(n_\varepsilon u_\varepsilon \), and \(c_\varepsilon u_\varepsilon \).
Lemma 5.1
Let \(\alpha >\frac{1}{3}\), and assume that (1.7) and (1.8) hold. Then one can find \(C > 0\) independent of \(\varepsilon \) such that, for all \(T\in (0,\infty )\),
as well as
and
Proof
First, by (1.5), (3.1), and (2.8), we derive
with \((1-\alpha )_{+}=\max \{0,1-\alpha \}.\) Case \(\frac{8}{21}<\alpha \le \frac{1}{2}\): It is not difficult to verify that
and
so that, recalling (3.29), (3.44), and Hölder’s inequality, we can obtain (5.2). While if \(\frac{1}{3}<\alpha \le \frac{8}{21}\), in light of (3.6), (3.29), (3.32), (3.45), an employment of the Hölder and Young inequalities to shows that
where \(\gamma =\frac{2\alpha +\frac{2}{3}}{\alpha +1}\) is given by Lemma 3.5.
Other cases can be proved very similarly. Therefore, we omit their proofs. \(\square \)
To prepare our subsequent compactness properties of \((n_\varepsilon , c_\varepsilon ,u_\varepsilon )\) by means of the Aubin–Lions lemma (see Simon [18]), we use Lemmas 3.2–3.4 to obtain the following regularity property with respect to the time variable.
Lemma 5.2
Let \(\alpha >\frac{1}{3}\), and assume that (1.7) and (1.8) hold. Then there exists \(C>0\) independent of \(\varepsilon \) such that
as well as
and
Proof
Firstly, testing the first equation of (2.6) by certain \(\varphi \in C^{\infty }({\bar{\Omega }})\), we have
for all \(t>0\).
Observe that the embedding \(W^{2,4 }(\Omega )\hookrightarrow W^{1,\infty }(\Omega )\), so that, in view of \(\alpha >\frac{1}{3}\), Lemmas 3.4 and 5.1, we deduce from the Young inequality that for some \(C_1\) and \(C_2\) such that
where
and
Likewise, given any \(\varphi \in C^\infty ({\bar{\Omega }})\), we may test the second equation in (2.6) against \(\varphi \) to conclude that
for all \(t>0\). Thus, from Lemmas 3.4 and 5.1 again, in light of \(\alpha >\frac{1}{3}\), we invoke the Young inequality again and obtain that there exist positive constant \(C_{3}\) and \(C_{4}\) such that
with
Finally, for any given \(\varphi \in C^{\infty }_{0,\sigma } (\Omega ;{\mathbb {R}}^3)\), we infer from the third equation in (2.6) that
Now, by virtue of (3.6), Lemmas 3.4 and 5.1 , we also get that there exist positive constants \(C_{5},C_{6}\) and \(C_{7}\) such that
which implies (5.8). Here \(r_3\) is the same as (5.10). \(\square \)
6 Passing to the limit: Proof of Theorem 1.1
Based on the above lemmas and by extracting suitable subsequences in a standard way, we can prove Theorem 1.1.
Lemma 6.1
Let (1.4), (1.5), (1.7) and (1.8) hold, and suppose that \(\alpha >\frac{1}{3}.\) There exists \((\varepsilon _j)_{j\in {\mathbb {N}}}\subset (0, 1)\) such that \(\varepsilon _j{\searrow } 0\) as \(j{\rightarrow }\infty \) and such that as \(\varepsilon = \varepsilon _j{\searrow } 0\) we have
as well as
and
and
with some triple (n, c, u) that is a global weak solution of (1.3) in the sense of Definition 2.1.
Proof
First, from Lemma 3.4 and (5.6), we derive that there exists a positive constant \(C_0\) such that
where r is given by (6.1). Hence, from (6.9) and the Aubin–Lions lemma (see, e.g., [18]), we conclude that
so that, there exists a sequence \((\varepsilon _j)_{j\in {\mathbb {N}}}\subset (0, 1)\) such that \(\varepsilon =\varepsilon _j{\searrow }0\) as \(j{\rightarrow }\infty \) and
where r is the same as (6.1). Now, in view of Lemmas 3.3, 3.4, 5.1, and 5.2, employing the same arguments as in the proof of (6.9)–(6.11), we can derive (6.1)–(6.3) and (6.5)–(6.8) holds. Next, let \(g_\varepsilon (x, t) := -c_\varepsilon +F_{\varepsilon }(n_{\varepsilon })-u_{\varepsilon }\cdot \nabla c_{\varepsilon }.\) With this notation, the second equation of (2.6) can be rewritten in component form as
Case \(\frac{1}{3}<\alpha \le \frac{1}{2}\): Observe that
Thus, recalling (3.29), (3.32), and (5.5) and applying Hölder’s inequality, we conclude that, for any \(\varepsilon \in (0,1)\), \( g_\varepsilon \) is bounded in \(L^{\frac{5}{4}} (\Omega \times (0, T))\), and we may invoke the standard parabolic regularity theory to (6.12) and infer that \((c_{\varepsilon })_{\varepsilon \in (0,1)}\) is bounded in \(L^{\frac{5}{4}} ((0, T); W^{2,\frac{5}{4}}(\Omega ))\). Hence, by virtue of (5.7) and the Aubin–Lions lemma, we derive the relative compactness of \((c_{\varepsilon })_{\varepsilon \in (0,1)}\) in \(L^{\frac{5}{4}} ((0, T); W^{1,\frac{5}{4}}(\Omega ))\). We can pick an appropriate subsequence that is still written as \((\varepsilon _j )_{j\in {\mathbb {N}}}\) such that \(\nabla c_{\varepsilon _j} \rightarrow z_1\) in \(L^{\frac{5}{4}} (\Omega \times (0, T))\) for all \(T\in (0, \infty )\) and some \(z_1\in L^{\frac{5}{4}} (\Omega \times (0, T))\) as \(j\rightarrow \infty \). Therefore, by (5.7), we can also derive that \(\nabla c_{\varepsilon _j} \rightarrow z_1\) a.e. in \(\Omega \times (0, \infty )\) as \(j \rightarrow \infty \). In view of (6.6) and Egorov’s theorem, we conclude that \(z_1=\nabla c\) and hence (6.4) holds. Next, we pay attention to the case \(\frac{1}{2}<\alpha <1\): By straightforward calculations, and using relation \(\frac{1}{2}<\alpha <1\), one has
Consequently, based on (3.30), (3.32), and (5.5), it follows from Hölder’s inequality that
Employing almost exactly the same arguments as in the proof of the case \(\frac{1}{3}<\alpha \le \frac{1}{2}\), and taking advantage of (6.13), we conclude the estimate (6.6). The proof of case \(\alpha \ge 1\) is similar to that of case \(\frac{1}{3}<\alpha \le \frac{1}{2}\), so we omit it.
In the following proof, we shall prove that (n, c, u) is a weak solution of problem (1.3) in Definition 2.1. In fact, by \(\alpha >\frac{1}{3}\), we conclude that
where r is given by (6.1). Therefore, with the help of (6.1)–(6.3) and (6.5)–(6.7), we can derive (2.1). Now, by the nonnegativity of \(n_\varepsilon \) and \(c_\varepsilon \), we obtain \(n \ge 0\) and \(c\ge 0\). Next, from (6.7) and \(\nabla \cdot u_{\varepsilon } = 0\), we conclude that \(\nabla \cdot u = 0\) a.e. in \(\Omega \times (0, \infty )\). However, in view of (5.2), (5.3), and (5.4), we conclude that
where r is given by (6.1). However, it follows from (1.4), (2.8), (3.2), (6.1), (6.3), and (6.4) that
Again by Egorov’s theorem, we gain \(z_2=nS(x, n, c)\nabla c\), and therefore (6.14) can be rewritten as
which together with \(r>1\) implies the integrability of \(nS(x, n, c)\nabla c\) in (2.2) as well. It is not difficult to check that
Thereupon, recalling (5.2), (5.3), and (5.4), we infer that, for each \(T\in (0, \infty ),\)
(6.17) together with (6.1) and (6.5) implies
(6.17) along with (6.18) and Egorov’s theorem guarantees that \(z_3=nu\), whereupon we derive from (6.17) that
for each \(T\in (0, \infty )\).
As a straightforward consequence of (6.3) and (6.5), it holds that
Thus, the integrability of nu and cu in (2.2) is verified by (6.3) and (6.5).
Next, by (6.5) and the fact that \(\Vert Y_{\varepsilon }\varphi \Vert _{L^2(\Omega )} \le \Vert \varphi \Vert _{L^2(\Omega )}(\varphi \in L^2_{\sigma }(\Omega ))\) and \(Y_{\varepsilon }\varphi {\rightarrow } \varphi \) in \(L^2(\Omega )\) as \(\varepsilon {\searrow }0\), we can get that there exists a positive constant \(C_1\) such that, for any \(\varepsilon \in (0,1)\),
and
so that, by the dominated convergence theorem, we also find that
Therefore,
Now, combining (6.5) with (6.21), we derive
Therefore, the integrability of \(nS(x,n,c)\nabla c\), nu, cu, and \(u\otimes u\) in (2.2) is verified by (6.16), (6.19), (6.20) and (6.22). Finally, for any fixed \(T\in (0, \infty )\), applying (6.1), one can get
where r is the same as in (6.1). Besides that, we also deduce from (3.3) and \(r>1\) that
for each \(t\in (0, T)\), which together with (6.1) shows the integrability of \(\left\| F_{\varepsilon }(n(\cdot ,t))\right. \left. -n(\cdot ,t)\right\| _{L^r(\Omega )}^r \) on (0, T). Thereupon, by virtue of (3.2), we infer from the dominated convergence theorem that
for each \(T\in (0, \infty )\). Inserting (6.24) into (6.23) and using (6.1) and (3.1), we can see clearly that
Finally, according to (6.1)–(6.3), (6.5)–(6.7), (6.16), (6.19), (6.20), (6.21), (6.22), and (6.25), we may pass to the limit in the respective weak formulations associated with the regularized system (2.6) and obtain the integral identities (2.3)–(2.5). \(\square \)
References
Bellomo, N., Belloquid, A., Tao, Y., Winkler, M.: Toward a mathematical theory of Keller–Segel models of pattern formation in biological tissues. Math. Models Methods Appl. Sci. 25(9), 1663–1763 (2015)
Cao, X.: Global classical solutions in chemotaxis(-Navier)–Stokes system with rotational flux term. J. Differ. Equ. 261(12), 6883–6914 (2016)
Chae, M., Kang, K., Lee, J.: Global existence and temporal decay in Keller–Segel models coupled to fluid equations. Commun. Partial Differ. Equ. 39, 1205–1235 (2014)
Cieślak, T., Stinner, C.: Finite-time blowup and global-in-time unbounded solutions to a parabolic-parabolic quasilinear Keller–Segel system in higher dimensions. J. Differ. Equ. 252, 5832–5851 (2012)
Cieślak, T., Stinner, C.: New critical exponents in a fully parabolic quasilinear Keller–Segel system and applications to volume filling models. J. Differ. Equ. 258, 2080–2113 (2015)
Duan, R., Lorz, A., Markowich, P.A.: Global solutions to the coupled chemotaxis-fluid equations. Commun. Partial Differ. Equ. 35, 1635–1673 (2010)
Giga, Y.: Solutions for semilinear parabolic equations in \(L^p\) and regularity of weak solutions of the Navier–Stokes system. J. Differ. Equ. 61, 186–212 (1986)
Hillen, T., Painter, K.: A user’s guide to PDE models for chemotaxis. J. Math. Biol. 58, 183–217 (2009)
Horstmann, D.: From \(1970\) until present: the Keller–Segel model in chemotaxis and its consequences. I. Jahresberichte der Deutschen Mathematiker-Vereinigung 105, 103–165 (2003)
Horstmann, D., Winkler, M.: Boundedness vs. blow-up in a chemotaxis system. J. Differ. Equ. 215, 52–107 (2005)
Ishida, S.: Global existence and boundedness for chemotaxis-Navier–Stokes system with position-dependent sensitivity in \(2d\) bounded domains. Discrete Contin. Dyn. Syst. Ser. A 32, 3463–3482 (2015)
Keller, E., Segel, L.: Model for chemotaxis. J. Theor. Biol. 30, 225–234 (1970)
Liu, J.-G., Lorz, A.: A coupled chemotaxis-fluid model: gGobal existence. Ann. Inst. H. Poincaré Anal. Non Linéaire 28(5), 643–652 (2011)
Liu, J., Wang, Y.: Global weak solutions in a three-dimensional Keller–Segel–Navier–Stokes system involving a tensor-valued sensitivity with saturation. J. Differ. Equ. 262(10), 5271–5305 (2017)
Lorz, A.: Coupled chemotaxis fluid equations. Math. Models Methods Appl. Sci. 20, 987–1004 (2010)
Painter, K., Hillen, T.: Volume-filling and quorum-sensing in models for chemosensitive movement. Can. Appl. Math. Q. 10, 501–543 (2002)
Peng, Y., Xiang, Z.: Global existence and boundedness in a 3D Keller–Segel–Stokes system with nonlinear diffusion and rotational flux. Z. Angew. Math. Phys. 68, 68 (2017)
Simon, J.: Compact sets in the space \(L^{p}(O, T;B)\). Annali di Matematica Pura ed Applicata 146(1), 65–96 (1986)
Sohr, H.: The Navier–Stokes Equations: An Elementary Functional Analytic Approach. Birkhäuser, Basel (2001)
Tao, Y., Winkler, M.: Boundedness in a quasilinear parabolic-parabolic Keller–Segel system with subcritical sensitivity. J. Differ. Equ. 252, 692–715 (2012)
Tao, Y., Winkler, M.: Global existence and boundedness in a Keller–Segel–Stokes model with arbitrary porous medium diffusion. Discrete Contin. Dyn. Syst. Ser. A 32, 1901–1914 (2012)
Tao, Y., Winkler, M.: Locally bounded global solutions in a three-dimensional chemotaxis-Stokes system with nonlinear diffusion. Ann. Inst. H. Poincaré Anal. Non Linéaire 30, 157–178 (2013)
Tao, Y., Winkler, M.: Boundedness and decay enforced by quadratic degradation in a three-dimensional chemotaxis-fluid system. Z. Angew. Math. Phys. 66, 2555–2573 (2015)
Tuval, I., Cisneros, L., Dombrowski, C., et al.: Bacterial swimming and oxygen transport near contact lines. Proc. Natl. Acad. Sci. USA 102, 2277–2282 (2005)
Wang, Y.: Global weak solutions in a three-dimensional Keller–Segel–Navier–Stokes system with subcritical sensitivity. Math. Models Methods Appl. Sci. 27(14), 2745–2780 (2017)
Wang, Y., Cao, X.: Global classical solutions of a \(3d\) chemotaxis-Stokes system with rotation. Discrete Contin. Dyn. Syst. Ser. B 20, 3235–3254 (2015)
Wang, Y., Winkler, M., Xiang, Z.: Global classical solutions in a two-dimensional chemotaxis-Navier-Stokes system with subcritical sensitivity. Annali della Scuola Normale Superiore di Pisa-Classe di Scienze. XVII I, 2036–2145 (2018)
Wang, Y., Xiang, Z.: Global existence and boundedness in a Keller–Segel–Stokes system involving a tensor-valued sensitivity with saturation. J. Differ. Equ. 259, 7578–7609 (2015)
Wang, Y., Xiang, Z.: Global existence and boundedness in a Keller–Segel–Stokes system involving a tensor-valued sensitivity with saturation: the 3D case. J. Differ. Equ. 261, 4944–4973 (2016)
Wiegner, M.: The Navier–S-tokes equations: a neverending challenge? Jahresber. Deutsch. Math.-Verein. 101(1), 1–25 (1999)
Winkler, M.: Does a volume-filling effect always prevent chemotactic collapse? Math. Methods Appl. Sci. 33, 12–24 (2010)
Winkler, M.: Aggregation vs. global diffusive behavior in the higher-dimensional Keller–Segel model. J. Differ. Equ. 248, 2889–2905 (2010)
Winkler, M.: Global large-data solutions in a chemotaxis-(Navier–)Stokes system modeling cellular swimming in fluid drops. Commun. Partial Differ. Equ. 37, 319–351 (2012)
Winkler, M.: Stabilization in a two-dimensional chemotaxis-Navier–Stokes system. Arch. Ration. Mech. Anal. 211, 455–487 (2014)
Winkler, M.: Large-data global generalized solutions in a chemotaxis system with tensor-valued sensitivities. SIAM J. Math. Anal. 47, 3092–3115 (2015)
Winkler, M.: Boundedness and large time behavior in a three-dimensional chemotaxis-Stokes system with nonlinear diffusion and general sensitivity. Calculus Var. Partial Differ. Equ. 54, 3789–3828 (2015)
Winkler, M.: Global weak solutions in a three-dimensional chemotaxis-Navier–Stokes system. Ann. Inst. H. Poincaré Anal. Non Linéaire 33(5), 1329–1352 (2016)
Winkler, M.: How far do chemotaxis-driven forces influence regularity in the Navier–Stokes system? Trans. Am. Math. Soc. 369(5), 3067–3125 (2017)
Winkler, M.: Global existence and stabilization in a degenerate chemotaxis-Stokes system with mildly strong diffusion enhancement. J. Differ. Equ. 264(10), 6109–6151 (2018)
Winkler, M.: Does fluid interaction affect regularity in the three-dimensional Keller–Segel System with saturated sensitivity? J. Math. Fluid Mech. 20(4), 1889–1909 (2018)
Winkler, M., Djie, K.C.: Boundedness and finite-time collapse in a chemotaxis system with volume-filling effect. Nonlinear Anal. TMA 72, 1044–1064 (2010)
Xue, C., Othmer, H.G.: Multiscale models of taxis-driven patterning in bacterial populations. SIAM J. Appl. Math. 70(1), 133–167 (2009)
Zhang, Q., Zheng, X.: Global well-posedness for the two-dimensional incompressible chemotaxis-Navier–Stokes equations. SIAM J. Math. Anal. 46, 3078–3105 (2014)
Zheng, J.: Boundedness of solutions to a quasilinear parabolic-elliptic Keller–Segel system with logistic source. J. Differ. Equ. 259(1), 120–140 (2015)
Zheng, J.: Boundedness of solutions to a quasilinear parabolic-parabolic Keller–Segel system with logistic source. J. Math. Anal. Appl. 431(2), 867–888 (2015)
Zheng, J.: A note on boundedness of solutions to a higher-dimensional quasi-linear chemotaxis system with logistic source. Z. Angew. Math. Mech. 97(4), 414–421 (2017)
Zheng, J.: Boundedness and global asymptotic stability of constant equilibria in a fully parabolic chemotaxis system with nonlinear logistic source. J. Math. Anal. Appl. 450(2), 1047–1061 (2017)
Zheng, J.: A new result for global existence and boundedness in a three-dimensional Keller–Segel(–Navier)–Stokes system with nonlinear diffusion, Preprint
Zheng, J.: An optimal result for global existence and boundedness in a three-dimensional Keller–Segel–Stokes system with nonlinear diffusion. J. Differ. Equ. https://doi.org/10.1016/j.jde.2019.03.013
Zheng, J., Wang, Y.: Boundedness and decay behavior in a higher-dimensional quasilinear chemotaxis system with nonlinear logistic source. Comput. Math. Appl. 72(10), 2604–2619 (2016)
Zheng, J., Wang, Y.: A note on global existence to a higher-dimensional quasilinear chemotaxis system with consumption of chemoattractant. Discrete Contin. Dyn. Syst. Ser. B 22(2), 669–686 (2017)
Acknowledgements
This work is partially supported by the National Natural Science Foundation of China (No. 11601215) and the Shandong Provincial Science Foundation for Outstanding Youth (No. ZR2018JL005).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by L. Caffarelli.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Ke, Y., Zheng, J. An optimal result for global existence in a three-dimensional Keller–Segel–Navier–Stokes system involving tensor-valued sensitivity with saturation. Calc. Var. 58, 109 (2019). https://doi.org/10.1007/s00526-019-1568-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00526-019-1568-2