Two dimensional solitary waves in shear flows

Abstract

In this paper we study existence and asymptotic behavior of solitary-wave solutions for the generalized Shrira equation, a two-dimensional model appearing in shear flows. The method used to show the existence of such special solutions is based on the mountain pass theorem. One of the main difficulties consists in showing the compact embedding of the energy space in the Lebesgue spaces; this is dealt with interpolation theory. Regularity and decay properties of the solitary waves are also established.

1 Introduction

Shear flows appear in natural and engineering environments, and in many physical situations. It is connected with a shear stress in solid mechanics, and with the flow induced by a force in fluid dynamics, for instance. In this context, the evolution of essentially two-dimensional weakly long waves is, usually, described by simplified models using the paraxial approximation. In [30], Shrira described a model for the propagation of nonlinear long-wave perturbations on the background of a boundary-layer type plane-parallel shear flow without inflection points. Within the model, the amplitude v of the longitudinal velocity of the fluid is governed by the equation

$$\begin{aligned} v_t+\gamma v_x+\alpha vv_x-\beta Q(v_x)=0, \end{aligned}$$

(1.1)

where $\alpha$, $\beta$, and $\gamma$ are parameters expressed through a profile of the shear flow and Q is the Cauchy–Hadamard integral transform given by

$$\begin{aligned} Q(f)(x,y)=\frac{1}{2\pi }{\mathrm{p.v.}}\int _{{\mathbb {R}}^2}\frac{f(z,w)}{\big ((x-z)^2+(y-w)^2\big )^{3/2}}dzdw. \end{aligned}$$

The model also describes the amplitude of the perturbation of the horizontal velocity component of a sheared flow of electrons (see [18]). For additional applications see also [1, 26, 27].

When considering nearly one-dimensional waves, in the dimensionless form $u(x',y',t')=\alpha v(x-\gamma t,\sqrt{2}y,\beta t)/2\beta$, Eq. (1.1) can be reduced to the so called Shrira equation (see [26])

$$\begin{aligned} u_t-\mathscr {H}\Delta u+2uu_x=0, \end{aligned}$$

(1.2)

where we omitted the primes. Here, $\Delta$ denotes the two-dimensional Laplacian operator and $\mathscr {H}$ is the Hilbert transform defined by

$$\begin{aligned} \mathscr {H}u(x,y,t)=\frac{1}{\pi }{\mathrm{p.v.}}\int _{\mathbb {R}}\frac{u(z,y,t)}{x-z} dz. \end{aligned}$$

In particular, at least from the mathematical viewpoint, Eq. (1.2) can be seen as a two-dimensional extension of the well-known Benjamin–Ono (BO) equation

$$\begin{aligned} u_t-\mathscr {H}\partial _x^2 u+2uu_x=0, \quad x,t\in {\mathbb {R}}. \end{aligned}$$

(1.3)

The study of multi-dimensional extension of BO equation has received considerable attention in recent years (see e.g., [7, 8, 14,15,16,17, 22, 25, 28], and references therein). However, when a suitable result is available for (1.3), it is not completely clear how to extend such a result for (1.2) and, in general, it demands extra efforts.

To the best of our knowledge, not so much is known about Eqs. (1.1) and (1.2) and a few papers are available in the current literature. In particular, numerical results concerned with the instability of one-dimensional solitons of the BO equation were presented in [18, 26]. It is to be observed that these equations presents a strong anisotropic character of the dispersive part, which turns out to be one of the main difficulties to be dealt with.

In this paper we are interested in studying existence, regularity and decay properties of solitary waves for the generalized two-dimensional Shrira equation, namely,

$$\begin{aligned} u_t-\mathscr {H}\Delta u+(f(u))_x=0, \end{aligned}$$

(1.4)

where $u=u(x,y,t)$, $(x,y)\in {{\mathbb {R}}^2}$, $t\ge 0$, and f is a real-valued continuous function. Observe that if $f(u)=u^2$ then Eq. (1.4) reduces to (1.2).

For one hand, from the physical point of view, a solitary wave is a wave that propagates without changing its profile along the temporal evolution, usually it has one global peak and decays far away from the peak. On the other hand, from the mathematical point of view, a solitary wave is a special solution of a partial differential equation belonging to a very particular function space. Nowadays, existence and properties of solitary waves have become one of the major issues in PDEs. The interested reader will find a large number of good texts in the current literature, which we refrain from list them at this moment.

The solitary-wave solutions of interest in the context of Eq. (1.4) have the form

$$\begin{aligned} u(x,y,t)=\varphi (x-ct,y), \end{aligned}$$

where $c> 0$ is the wave speed and $\varphi$ is a real-valued function with a suitable decay at infinity. Substituting this form into (1.4), it transpires that $\varphi$ must satisfy the nonlinear equation

$$\begin{aligned} -c\varphi _x-\mathscr {H}\Delta \varphi +(f(\varphi ))_x=0, \end{aligned}$$

(1.5)

where we have replaced the variable $z=x-ct$ by x. This last equation can be rewritten in the following form

$$\begin{aligned} -c\varphi -\mathscr {H}\partial _x^{-1}\Delta \varphi +f(\varphi )=0. \end{aligned}$$

(1.6)

Hence, in order to show the existence of solitary waves, it suffices to show that (1.5), or equivalently (1.6), has a solution.

Remark 1.1

Note that the wave speed c can be normalized to 1 at least if f is homogeneous of degree $p+1$ such as $f(u)=u^{p+1}$. Indeed, the scale change

$$\begin{aligned} \phi (x,y)=a\varphi \left( bx,dy\right) , \end{aligned}$$

(1.7)

transforms (1.5) in $\varphi$, into the same in $\phi$, but with $c=1$, where $a=c^{-1/p}$ and $b=d=c^{-1}$.

By multiplying (1.6) by $\varphi$ and integrating by parts, one sees that the natural space to study (1.6) is

$$\begin{aligned} \mathscr {Z}=\left\{ u\in L^2({{\mathbb {R}}^2});\;D^{1/2}_xu,\;D^{-1/2}_xu_y\in L^2({{\mathbb {R}}^2})\right\} , \end{aligned}$$

equipped with the norm

$$\begin{aligned} \Vert u\Vert _\mathscr {Z}=\left( \int _{{\mathbb {R}}^2}(cu^2+|D^{1/2}_xu|^2+|D^{-1/2}_xu_y|^2){d}x\;{d}y\right) ^{1/2}, \end{aligned}$$

where $c>0$ is a fixed constant and $D_x^{\pm 1/2}$ denotes the fractional derivative operators of order $\pm 1/2$ with respect to x, defined via Fourier transform by $({D^{\pm 1/2}_xu})^{\wedge }(\xi ,\eta )=|\xi |^{\pm 1/2}\widehat{u}(\xi ,\eta )$. Note that $\mathscr {Z}$ is a Hilbert space with the scalar product

$$\begin{aligned} (u,v)_\mathscr {Z}=\int _{{\mathbb {R}}^2}\left( cuv+D^{1/2}_xuD^{1/2}_xv+D^{-1/2}_xu_yD^{-1/2}_xv_y\right) dxdy. \end{aligned}$$

Also, $\mathscr {Z}$ is an anisotropic space including fractional negative derivatives, which, for one hand, brings many difficulties when applying analytical methods.

The paper is organized as follows. We start Sect. 2 by showing a suitable Gagliardo–Nirenberg-type inequality, which ensures that the space $\mathscr {Z}$ is embedded in suitable Lebesgue spaces. In order to show that indeed we have a compact embedding we use interpolation theory. Thus, we are able to see $\mathscr {Z}$ as an interpolation space between two compatible pairs of Hilbert spaces containing only integer derivatives. With the compact embedding in hand, we use the mountain pass theorem without the Palais-Smale condition, in order to show the existence of at least one nontrivial solution. Variational characterizations of such a solutions are also provided. In Sect. 3 we study regularity and decay properties of the solitary waves. Our regularity result is based on the so called Lizorkin lemma, which gives a sufficient condition to a function be a Fourier multiplier on $L^p({\mathbb {R}}^n)$. The decay properties are obtained once we write the equation as a convolution equation and get some suitable estimates on the corresponding kernel. Of course, the anisotropic structure of the kernel also brings many technical difficulties. Finally, in Sect. 4 we present a nonexistence result of positive solitary waves.

The issue of orbital stability/instability of solitary waves of (1.4) will be studied in a future work.

Notation Otherwise stated, we follow the standard notation in PDEs. In particular, we use C to denote several positive constants that may vary from line to line. In order to simplify notation in some places where the constant is not important, if a and b are two positive numbers, we use $a\lesssim b$ to mean that there exists a positive constant C such that $a\le Cb$. By $L^p=L^p({{\mathbb {R}}^2})$ we denote the standard Lebesgue space. Sometimes we use subscript to indicate which variable we are concerned with; for instance, $L^p_x=L^p_x({\mathbb {R}})$ means the space $L^p({\mathbb {R}})$ with respect to the variable x; thus given a function $f=f(x,y)$, the notation $\Vert f\Vert _{L^p_x}$ means we are taking the $L^p$ norm of f only with respect to x. Also, if no confusion is caused, we use $\int _{{{\mathbb {R}}^2}}f$ instead of $\int _{{{\mathbb {R}}^2}}f(x,y){d}x{d}y$.

2 Existence of solitary waves

In this section we provide the existence of solitary-wave solutions for (1.4). As we already said, our main tool in doing so will be the mountain pass theorem.

2.1 A Gagliardo–Nirenberg-type inequality and embeddings

First, we are going to obtain an embedding of the space $\mathscr {Z}$, which is appropriate to study Eq. (1.6). For the sake of simplicity, in this subsection, we assume that the constant c in the definition of $\mathscr {Z}$ is normalized to 1.

Lemma 2.1

(Gagliardo–Nirenberg-type inequality) Assume $0\le p\le 2$. Then there is a constant $C>0$ (depending only on p) such that for any $\varphi \in \mathscr {Z}$,

$$\begin{aligned} \Vert \varphi \Vert _{L^{p+2}}^{p+2}\le C\Vert \varphi \Vert _{L^2}^{2-p}\left\| D_x^{-1/2}\varphi _y\right\| _{L^2}^{p/2}\left\| D_x^{1/2}\varphi \right\| _{L^2}^{3p/2}. \end{aligned}$$

(2.1)

As a consequence, it follows that there is a constant $C>0$ such that for all $\varphi \in \mathscr {Z}$,

$$\begin{aligned} \Vert \varphi \Vert _{L^{p+2}}\le C\Vert \varphi \Vert _{\mathscr {Z}}, \end{aligned}$$

which is to say $\mathscr {Z}$ is continuously embedded in $L^{p+2}$.

Proof

It suffices to assume $0<p\le 2$. The lemma will be established only for $C_0^\infty ({{\mathbb {R}}^2})$ functions; a standard limit method then can be used to complete the proof. By the Gagliardo–Nirenberg inequality (see, for instance, [2, 19]), there exists $C>0$ such that, for all $g\in H^{1/2}({\mathbb {R}})$,

$$\begin{aligned} \Vert g\Vert _{L^{p+2}({\mathbb {R}})}\le C\Vert g\Vert _{L^2({\mathbb {R}})}^{\frac{2}{p+2}}\Vert D_x^{1/2}g\Vert _{L^2({\mathbb {R}})}^{\frac{p}{p+2}}. \end{aligned}$$

Assume for the moment that $0<p<2$. Integrating on the y variable, it follows that

$$\begin{aligned} \begin{aligned} \Vert \varphi \Vert _{L^{p+2}({{\mathbb {R}}^2})}^{p+2}&\le C\int _{{\mathbb {R}}}\Vert \varphi (\cdot ,y)\Vert _{L^2({\mathbb {R}})}^2\;\Vert D_x^{1/2}\varphi (\cdot ,y)\Vert _{L^2({\mathbb {R}})}^p\;{d}y\\&\le C \left\| \Vert \varphi (\cdot ,y)\Vert ^2_{L^2({\mathbb {R}})}\right\| _{L^{\frac{2}{2-p}}({\mathbb {R}})}\; \Vert D_x^{1/2}\varphi \Vert _{L^2({{\mathbb {R}}^2})}^p\\&\le C\Vert \varphi \Vert _{L^2({{\mathbb {R}}^2})}^{2-p}\; \sup _{y\in {\mathbb {R}}}\Vert \varphi (\cdot ,y)\Vert _{L^2({\mathbb {R}})}^p\; \Vert D_x^{1/2}\varphi \Vert _{L^2({{\mathbb {R}}^2})}^p. \end{aligned} \end{aligned}$$

(2.2)

We now estimate the middle term in (2.2). Fixed $y\in {\mathbb {R}}$, from Hölder’s inequality, we deduce

$$\begin{aligned} \begin{aligned} \Vert \varphi (\cdot ,y)\Vert _{L^2({\mathbb {R}})}^2&=2\int _{{\mathbb {R}}}\int _{-\infty }^y\varphi (x,z)\varphi _y(x,z){d}z{d}x\\&=2\int _{-\infty }^y\int _{{\mathbb {R}}}D^{1/2}_x\varphi (x,z)D^{-1/2}_x\varphi _y(x,z){d}x{d}z\\&\le 2\int _{{\mathbb {R}}^2}|D^{1/2}_x\varphi (x,y)||D^{-1/2}_x\varphi _y(x,y)| {d}x{d}y\\&\le 2\Vert D^{1/2}_x\varphi \Vert _{L^2({{\mathbb {R}}^2})}\Vert D^{-1/2}_x\varphi _y\Vert _{L^2({{\mathbb {R}}^2})}. \end{aligned} \end{aligned}$$

(2.3)

As a consequence,

$$\begin{aligned} \sup _{y\in {\mathbb {R}}}\Vert \varphi (\cdot ,y)\Vert _{L^2({\mathbb {R}})}\le C\Vert D_x^{1/2}\varphi \Vert _{L^2({{\mathbb {R}}^2})}^{1/2}\Vert D^{-1/2}_x\varphi _y\Vert _{L^2({{\mathbb {R}}^2})}^{1/2}. \end{aligned}$$

(2.4)

A combination of (2.4) with (2.2) yields the first statement if $0<p<2$. For $p=2$, from the first inequality in (2.2) and (2.4), we deduce

$$\begin{aligned} \begin{aligned} \Vert \varphi \Vert _{L^{4}({{\mathbb {R}}^2})}^{4}&\le C\int _{{\mathbb {R}}}\Vert \varphi (\cdot ,y)\Vert _{L^2({\mathbb {R}})}^2\;\Vert D_x^{1/2}\varphi (\cdot ,y)\Vert _{L^2({\mathbb {R}})}^2\;{d}y\\&\le C \sup _{y\in {\mathbb {R}}}\Vert \varphi (\cdot ,y)\Vert _{L^2({\mathbb {R}})}^2\; \Vert D_x^{1/2}\varphi \Vert _{L^2({{\mathbb {R}}^2})}^2\\&\le C\Vert D^{-1/2}_x\varphi _y\Vert _{L^2({\mathbb {R}})}\Vert D^{1/2}_x\varphi _y\Vert _{L^2({\mathbb {R}})}^3, \end{aligned} \end{aligned}$$

which is the desired. The lemma is thus proved. $\square$

Remark 2.2

An argument similar to that in Lemma 2.1 gives the continuous embedding $\mathscr {Z}\hookrightarrow L_y^qL_x^r({{\mathbb {R}}^2})$, for any $q,r\ge 2$ satisfying $\frac{1}{q}+\frac{1}{r}\ge \frac{1}{2}$.

As is well known in the theory of critical points, in order to rule out the trivial solution, a compactness result is usually necessary. Here, we will prove the following.

Lemma 2.3

(Compact embedding) If $0\le p<2$ then the embedding $\mathscr {Z}\hookrightarrow L^{p+2}_{loc}({{\mathbb {R}}^2})$ is compact.

Due to the anisotropic property of $\mathscr {Z}$ involving negative fractional derivatives, some difficulties appear in the proof of Lemma 2.3. In particular, we are not able to use truncation by using a cut-off function as it was performed in [9]. To circumvent this problem, we will identify $\mathscr {Z}$ as an interpolation space by using the real interpolation method and construct a suitable extension operator.

For any real number $s\ge 0$, we introduce the space

$$\begin{aligned} X^s:=\Big \{f\in \mathcal {S}'({{\mathbb {R}}^2}); \; (1+|\xi |+|\xi |^{-1}\eta ^2)^{s}\widehat{f}\in L^2({{\mathbb {R}}^2})\Big \}. \end{aligned}$$

The space $X^s$ is a Hilbert space endowed with the scalar product

$$\begin{aligned} (f,g)_{X^s}:=\int _{{\mathbb {R}}^2}(1+|\xi |+|\xi |^{-1}\eta ^2)^{2s}\widehat{f}(\xi ,\eta )\,\overline{\widehat{g}}(\xi ,\eta )\;d\xi d\eta . \end{aligned}$$

In particular, from Plancherel’s theorem we have $X^0=L^2$ and $X^{1/2}=\mathscr {Z}$. If $0\le s_1\le s_2$ then $X^{s_2}\subset X^{s_1}$. The space $X^1$ is a suitable space that involves only integer derivatives and, moreover, it can be defined as the closure of $\partial _x(C_0^\infty ({\mathbb {R}}^2))$ for the norm (see [9])

$$\begin{aligned} \Vert \varphi _x\Vert _{X^1}=\left( \Vert \varphi _x\Vert _{L^2}^2+\Vert \varphi _{xx}\Vert _{L^2}^2+\Vert \varphi _{yy}\Vert _{L^2}^2\right) ^{1/2}. \end{aligned}$$

So, our idea is to look $\mathscr {Z}$ as an interpolation space between $L^2$ and $X^1$.

In what follows, if $(H_0,H_1)$ is a compatible pair of Hilbert spaces and $\theta \in (0,1)$, we denote by $(H_0,H_1)_{\theta }$ the space $(H_0,H_1)_{\theta ,2}$. Here, for $q\in (1,\infty )$, $(H_0,H_1)_{\theta ,q}$ denotes the intermediate space with respect to the couple $(H_0,H_1)$ using either the J-method or the K-method (see e.g., [5, 21, 31]). For our purposes, the following results will be useful.

Lemma 2.4

Let $(X_0,X_1)$ and $(Y_0,Y_1)$ be two compatible pairs of Hilbert spaces. Then, for $0<\theta <1$, $((X_0,X_1)_\theta , (Y_0,Y_1)_\theta )$ is a pair of interpolation spaces with respect to $((X_0,X_1), (Y_0,Y_1))$, which is exact of exponent $\theta$.

In particular, if A is a bounded linear operator from $X_0$ to $Y_0$ and from $X_1$ to $Y_1$, then it is also bounded from $(X_0,X_1)_\theta$ to $(Y_0,Y_1)_\theta$.

Proof

See, for instance, [31, Chapter 1] or [21, Appendix B]. $\square$

Lemma 2.5

Let $(H_0,H_1)$ be a compatible pair of Hilbert spaces, let $(X,\mathcal {M},\mu )$ be a measure space and let $\mathcal {Y}$ denote the set of measurable functions from X to ${\mathbb {C}}$. Suppose that there exist a linear map $\mathcal {A}:H_0+H_1\rightarrow \mathcal {Y}$ and, for $j= 0, 1$, functions $w_j \in \mathcal {Y}$, with $w_j > 0$ almost everywhere, such that the mappings $\mathcal {A}:H_j\rightarrow L^2(X, \mathcal {M},w_j\mu )$ are unitary isomorphisms. For $\theta \in (0,1)$, define

$$\begin{aligned} H_\theta =\Big \{ \phi \in H_0+H_1; \Vert \phi \Vert _{H_\theta }:=\left( \int _X |w_\theta \mathcal {A}\phi |^2\;d\mu \right) ^{1/2}<\infty \Big \}, \end{aligned}$$

where $w_\theta =w_0^{1-\theta }w_1^\theta$. Then $H_\theta =(H_0,H_1)_\theta$ with equality of norms.

Proof

See [6, Corollary 3.2]. $\square$

As an application of the above lemma, we have.

Lemma 2.6

The space $\mathscr {Z}$ is such that

$$\begin{aligned} \mathscr {Z}=X^{1/2}=(X^1,L^2)_{1/2}. \end{aligned}$$

Proof

It suffices to apply Lemma 2.5 with $X={\mathbb {R}}^2$, $w_0=1$, $w_1=(1+|\xi |+|\xi |^{-1}\eta ^2)$, and $\mathcal {A}$ being the Fourier transform. $\square$

For any open set $\Omega \subset {\mathbb {R}}^2$ and $s\ge 0$, we define

$$\begin{aligned} X^s(\Omega ):=\Big \{u\in L^2(\Omega ); \;u=f|_\Omega , \;\hbox {for some}\;f\in X^s\Big \}. \end{aligned}$$

Endowed with the norm

$$\begin{aligned} \Vert u\Vert _{X^s(\Omega )}:=\inf \Big \{\Vert f\Vert _{X^s};\;u=f|_\Omega \;\hbox {with}\; f\in X^s \Big \}, \end{aligned}$$

the space $X^s(\Omega )$ is a Hilbert space.

The next step is the construction of an extension operator from $X^1(\Omega )$ to $X^1$, where $\Omega$ is a rectangle. This construction was essentially given in [24], but for the sake of completeness we bring the details.

Lemma 2.7

Let $\Omega =(a,b)\times (c,d)$. Then, there exists a bounded (extension) linear operator, say, E, from $X^1(\Omega )$ to $X^1$ such that, for any $u\in X^1(\Omega )$, $Eu=u$ in $\Omega$, $\Vert Eu\Vert _{L^2}\le C\Vert u\Vert _{L^2(\Omega )}$ and $\Vert Eu\Vert _{X^1}\le C\Vert u\Vert _{X^1(\Omega )}$, where C is a constant depending only on $\Omega$.

Proof

Take any $u\in X^1(\Omega )$ and, without loss of generality, assume that $u=\partial _xf$ in $\Omega$, for some smooth function $f\in C_0^\infty ({\mathbb {R}}^2)$ with $\Vert \partial _xf\Vert _{X^1}\le 2\Vert u\Vert _{X^1(\Omega )}$. Define

$$\begin{aligned} f_0(x,y)=f(x,y)-\frac{1}{b-a}\int _a^bf(x,y)\,dx. \end{aligned}$$

In $\Omega$ it is clear that $u=\partial _xf_0$. From Poincaré’s inequality,

$$\begin{aligned} \int _a^b\left| f(x,y)-\int _a^bf(z,y)\,dz \right| ^2\,dx\le (b-a)^2\int _a^b|\partial _xf(x,y)|^2\,dx. \end{aligned}$$

Hence, integrating with respect to y on (c, d),

$$\begin{aligned} \Vert f_0\Vert _{L^2(\Omega )}\le (b-a)\Vert \partial _xf\Vert _{L^2(\Omega )}=(b-a)\Vert u\Vert _{L^2(\Omega )}. \end{aligned}$$

(2.5)

Now we extend $f_0$ to the rectangle $[2a-b,2b-a]\times [c,d]$ by using a generalized reflection argument. Indeed, let

$$\begin{aligned} f_1(x,y) = \left\{ \begin{array}{ll} f_0(x,y), &{} {\mathrm{if}}\; x\in [a,b],\\ {\displaystyle \sum _{i=1}^4a_if_0\Big (\frac{i+1}{i}b-\frac{1}{i}x,y\Big )}, &{}\quad \text {if}\; x\in [b,2b-a],\\ {\displaystyle \sum _{i=1}^4a_if_0\Big (\frac{i+1}{i}a-\frac{1}{i}x,y\Big ),} &{}\quad \text {if}\; x\in [2a-b,a], \end{array} \right. \end{aligned}$$

where the coefficients $a_i$ are such that

$$\begin{aligned} \left\{ \begin{array}{ll} a_1+a_2+a_3+a_4=1,\\ \\ {\displaystyle a_1+\frac{a_2}{2}+\frac{a_3}{3}+\frac{a_4}{4}=-1},\\ \\ {\displaystyle a_1+\frac{a_2}{4}+\frac{a_3}{9}+\frac{a_4}{16}=1},\\ \\ {\displaystyle a_1+\frac{a_2}{8}+\frac{a_3}{27}+\frac{a_4}{64}=-1}.\\ \\ \end{array} \right. \end{aligned}$$

It is clear that $f_1$ is a $C^2$ function on $(2a-b,2b-a)\times (c,d)$ with

$$\begin{aligned} \Vert \partial ^\alpha f_1\Vert _{L^2((2a-b,2b-a)\times (c,d))}\le C\Vert \partial ^\alpha f_0\Vert _{L^2(\Omega )}, \end{aligned}$$

for all multi-indices $\alpha \in {\mathbb {N}}^2$ with $|\alpha |\le 2$. By using the same argument we can extend $f_1$ to the rectangle $\widetilde{\Omega }=(2a-b,2b-a)\times (2c-d,2d-c)$ by defining a $C^2$ function $f_2$ such that

$$\begin{aligned} \Vert \partial ^\alpha f_2\Vert _{L^2(\widetilde{\Omega })}\le C\Vert \partial ^\alpha f_0\Vert _{L^2(\Omega )}, \end{aligned}$$

(2.6)

for all multi-indices $\alpha \in {\mathbb {N}}^2$ with $|\alpha |\le 2$.

Now take a smooth function $\eta$ such that $\eta \equiv 1$ on $\Omega$ and $\eta \equiv 0$ on ${\mathbb {R}}^2{\setminus }\widetilde{\Omega }$. Finally, define the extension operator E by setting $Eu=\partial _x(\eta f_2)$. Let us estimate Eu in the $X^1$ norm. First of all, note that from (2.5) and (2.6), we have

$$\begin{aligned} \begin{aligned} \Vert Eu\Vert _{L^2}&\le C\Big ( \Vert f_2\Vert _{L^2(\widetilde{\Omega })}+\Vert \partial _x f_2\Vert _{L^2(\widetilde{\Omega })} \Big )\\&\le C\Big ( \Vert f_0\Vert _{L^2({\Omega })}+\Vert \partial _x f_0\Vert _{L^2({\Omega })} \Big )\\&\le C\Vert u\Vert _{L^2({\Omega })}. \end{aligned} \end{aligned}$$

(2.7)

Also, by using (2.7) and (2.6),

$$\begin{aligned} \begin{aligned} \Vert \partial _xEu\Vert _{L^2}&\le C\Big ( \Vert f_2\Vert _{L^2(\widetilde{\Omega })}+\Vert \partial _x f_2\Vert _{L^2(\widetilde{\Omega })}+\Vert \partial _x^2f_2\Vert _{L^2(\widetilde{\Omega })} \Big )\\&\le C\Big (\Vert u\Vert _{L^2({\Omega })}+ \Vert \partial _x(\partial _xf_0)\Vert _{L^2({\Omega })} \Big )\\&\le C\Big (\Vert u\Vert _{L^2({\Omega })}+\Vert \partial _xu\Vert _{L^2({\Omega })}\Big ). \end{aligned} \end{aligned}$$

(2.8)

It remains to estimate $\partial _x^{-1}\partial _y^2Eu$. In this case, we have

$$\begin{aligned} \begin{aligned} \Vert \partial _x^{-1}\partial _y^2Eu\Vert _{L^2}&\le C\Big ( \Vert f_2\Vert _{L^2(\widetilde{\Omega })}+\Vert \partial _y f_2\Vert _{L^2(\widetilde{\Omega })}+\Vert \partial _y^2f_2\Vert _{L^2(\widetilde{\Omega })} \Big )\\&\le C\Big (\Vert u\Vert _{L^2({\Omega })}+\Vert \partial _y f _0\Vert _{L^2({\Omega })}+ \Vert \partial _y^2f_0\Vert _{L^2({\Omega })} \Big )\\&\le C\Big (\Vert u\Vert _{L^2({\Omega })}+\Vert \partial _y f _0\Vert _{L^2({\Omega })}+ \Vert \partial _x^{-1}\partial _y^2u\Vert _{L^2({\Omega })} \Big ). \end{aligned} \end{aligned}$$

(2.9)

Note that

$$\begin{aligned} \partial _yf_0(x,y)=\int _c^d\partial _y^2f_0(x,z)\,dz. \end{aligned}$$

Hence, from the Cauchy–Schwarz inequality,

$$\begin{aligned} |\partial _yf_0(x,y)|^2\le (y-c)\int _c^d|\partial _y^2f_0(x,z)|^2\,dz. \end{aligned}$$

This last inequality now implies

$$\begin{aligned} \Vert \partial _yf_0\Vert _{L^2(\Omega )}\le \frac{d-c}{\sqrt{2}}\Vert \partial _y^2f_0\Vert _{L^2(\Omega )}\le \frac{d-c}{\sqrt{2}}\Vert \partial _x^{-1}\partial _y^2u\Vert _{L^2({\Omega })}. \end{aligned}$$

(2.10)

Gathering together (2.9) and (2.10), we obtain

$$\begin{aligned} \Vert \partial _x^{-1}\partial _y^2Eu\Vert _{L^2}\le C\Big (\Vert u\Vert _{L^2({\Omega })}+ \Vert \partial _x^{-1}\partial _y^2u\Vert _{L^2({\Omega })} \Big ). \end{aligned}$$

The proof of the lemma is thus completed. $\square$

Remark 2.8

A simple inspection in the proof of Lemma 2.7 reveals that the positive constant C depends only on the difference $b-a$ and $d-c$, but not on the rectangle $\Omega$ itself.

With the extension operator in hand, we can also prove that the space $X^{1/2}(\Omega )$ is also the interpolation of $L^2(\Omega )$ and $X^1(\Omega )$. Results of this type are well known in the context of the standard Sobolev spaces, see, for instance, [6, Lemma  4.2].

Lemma 2.9

Let $\Omega =(a,b)\times (c,d)$. Then, $X^{1/2}(\Omega )=(L^2(\Omega ),X^1(\Omega ))_{1/2}$, with equivalence of norms.

Proof

From Lemma 2.6 we know that $X^{1/2}=(X^1,L^2)_{1/2}$. Note that, for any $s\ge 0$, the restriction operator $R:X^s\rightarrow X^s(\Omega )$ is bounded. Thus, from Lemma 2.4,

$$\begin{aligned} X^{1/2}(\Omega )=R(X^{1/2})\subset (L^2(\Omega ),X^1(\Omega ))_{1/2}. \end{aligned}$$

(2.11)

On the other hand, the extension operator E constructed in Lemma 2.7 is bounded from $L^2(\Omega )$ to $L^2$ and from $X^1(\Omega )$ to $X^1$. Thus, another application of Lemma 2.4 gives $E((L^2(\Omega ),X^1(\Omega ))_{1/2})\subset (X^1,L^2)_{1/2}=X^{1/2}$. Hence,

$$\begin{aligned} (L^2(\Omega ),X^1(\Omega ))_{1/2}=RE((L^2(\Omega ),X^1(\Omega ))_{1/2})\subset R(X^{1/2})=X^{1/2}(\Omega ). \end{aligned}$$

(2.12)

A combination of (2.11) and (2.12) yields the desired. $\square$

Proposition 2.10

Let $\{\Omega _i\}_{i\in {\mathbb {N}}}$ be a covering of ${\mathbb {R}}^2$, where $\Omega _i$ is an open square with edges parallel to the coordinate axis and side-length $\ell$, and such that each point of ${\mathbb {R}}^2$ is contained in at most three squares. Then, there exists a constant $C>0$, such that

$$\begin{aligned} \sum _{i=0}^\infty \Vert u\Vert _{X^{1/2}(\Omega _i)}^2\le C\Vert u\Vert _{X^{1/2}}^2, \end{aligned}$$

for any $u\in X^{1/2}$.

Proof

Let $E_i$ be the extension operator from $X^1(\Omega _i)$ to $X^1$ as constructed in Lemma 2.7. Thus, from Lemma 2.7,

$$\begin{aligned} \Vert E_iu\Vert ^2_{X^1}\le C \int _{\Omega _i}\left( |u|^2+|\partial _x u|^2+|\partial _x^{-1}\partial _y^2 u|^2\right) . \end{aligned}$$

(2.13)

As observed in Remark 2.8, the constant C in (2.13) depends only on $\ell$ but not on $i\in {\mathbb {N}}$. By observing that the restriction operator $R_i:X^1\rightarrow X^1(\Omega _i)$ is bounded with norm 1 and the composition $R_iE_i$ is the identity operator, we obtain

$$\begin{aligned} \Vert u\Vert _{X^1(\Omega _i)}\le \Vert E_iu\Vert _{X^1}. \end{aligned}$$

(2.14)

Hence, (2.13) and (2.14) imply

$$\begin{aligned} \sum _{i=0}^\infty \Vert u\Vert ^2_{X^1(\Omega _i)}\le C\sum _{i=0}^\infty \int _{\Omega _i}\left( |u|^2+|\partial _x u|^2+|\partial _x^{-1}\partial _y^2 u|^2\right) \le 3C\Vert u\Vert ^2_{X^1}. \end{aligned}$$

This means that the restriction operator is bounded from $X^1$ to $\ell ^2(X^1(\Omega _i))$. On the other hand, the trivial inequality,

$$\begin{aligned} \sum _{i=0}^\infty \Vert u\Vert ^2_{L^2(\Omega _i)}\le 3\Vert u\Vert _{L^2}^2, \end{aligned}$$

implies that the restriction operator is also bounded from $L^2$ to $\ell ^2(L^2(\Omega _i))$. Then, Theorem 1.18.1 in [31] combined with Lemmas 2.4, 2.6, and 2.9 gives that the restriction is bounded from $X^{1/2}$ to $\ell ^2(X^{1/2}(\Omega _i))$, which is the desired conclusion. $\square$

Now we are ready to prove Lemma 2.3.

Proof of Lemma 2.3

Let $\{\varphi _n\}$ be a bounded sequence in $\mathscr {Z}=X^{1/2}$ and select a constant $C_0>0$ such that $\Vert \varphi _n\Vert _\mathscr {Z}\le C_0$. It is sufficient to show that $\{\varphi _n\}$ has a convergent subsequence in $L^2_{loc}({\mathbb {R}}^2)$, because if this is true then Lemma 2.1 implies that $\{\varphi _n\}$ also has a convergent subsequence in $L^{p+2}_{loc}({\mathbb {R}}^2)$, $0<p<2$. To do that, it suffices to show that $\{\varphi _n\}$ converges, up to a subsequence, in $L^2(\Omega _R)$, where $\Omega _R$ is a square with center at the origin, edges parallel to the coordinate axis, and side-length $R>0$. Let $E_R$ be the extension operator constructed in Lemma 2.7. By construction, if $u\in X^{1/2}$ then $E_R(u)=u$ in $\Omega _R$ and $E_R(u)=0$ in ${\mathbb {R}}^2{\setminus }\Omega _{3R}$. Thus, without loss of generality, we can assume that $\varphi _n=E_R(\varphi _n)$ for all $n\in {\mathbb {N}}$. Now, since $X^{1/2}$ is a Hilbert space, there exists $\varphi \in X^{1/2}$ such that $\varphi _n\rightharpoonup \varphi$ weakly in $X^{1/2}$. In addition, replacing $\varphi _n$ by $\varphi _n-\varphi$, if necessary, we can assume $\varphi =0$, that is, $\varphi _n\rightharpoonup 0$ in $X^{1/2}$.

Fixed $\rho >0$ to be chosen later, define

$$\begin{aligned} \begin{aligned}&Q_0=\{(\xi ,\eta )\in {\mathbb {R}}^2;\,|\xi |\le \rho ,\;|\eta |\le \rho \},\\&Q_1=\{(\xi ,\eta )\in {\mathbb {R}}^2;\,|\xi |\le \rho ,\;|\eta |\ge \rho \},\\&Q_2=\{(\xi ,\eta )\in {\mathbb {R}}^2;\,|\xi |\ge \rho \}. \end{aligned} \end{aligned}$$

Plancherel’s identity and the fact that $\varphi _n=0$ outside the square $\Omega _{3R}$ yield

$$\begin{aligned} \int _{\Omega _{3R}}|\varphi _n|^2= \int _{{\mathbb {R}}^2}|\varphi _n|^2 =\int _{{\mathbb {R}}^2}|\widehat{\varphi }_n|^2=\sum _{i=0}^2\int _{Q_i}|\widehat{\varphi }_n|^2. \end{aligned}$$

(2.15)

From the definitions of $Q_1$ and $Q_2$, it is clear that

$$\begin{aligned} \int _{Q_1}|\widehat{\varphi }_n|^2 =\int _{Q_1}\frac{|\xi |}{|\eta |^2}\left| \widehat{D_x^{-1/2}\partial _y\varphi }_n\right| ^2 \le \frac{1}{\rho }\left\| D_x^{-1/2}\partial _y\varphi _n\right\| _{L^2({\mathbb {R}}^2)} \le \frac{C_0}{\rho } \end{aligned}$$

and

$$\begin{aligned} \int _{Q_2}|\widehat{\varphi }_n|^2 =\int _{Q_2}\frac{1}{|\xi |}\left| \widehat{D_x^{1/2}\varphi }_n\right| ^2 \le \frac{1}{\rho }\left\| D_x^{1/2}\varphi _n\right\| _{L^2({\mathbb {R}}^2)} \le \frac{C_0}{\rho }. \end{aligned}$$

Fix $\varepsilon >0$; then choosing $\rho >0$ sufficiently large leads to

$$\begin{aligned} \int _{Q_1}|\widehat{\varphi }_n|^2+\int _{Q_2}|\widehat{\varphi }_n|^2\le \varepsilon /2. \end{aligned}$$

Since $\varphi _n\rightharpoonup 0$ in $L^2({\mathbb {R}}^2)$, then $\widehat{\varphi }_n$ tends to zero as $n\rightarrow \infty$ and

$$\begin{aligned} |\widehat{\varphi }_n(\xi ,\eta )|\le \Vert \varphi _n\Vert _{L^1(\Omega _{3R})}\le C\Vert \varphi _n\Vert _{L^2}. \end{aligned}$$

(2.16)

Lebesgue’s dominated convergence theorem implies that

$$\begin{aligned} \lim _{n\rightarrow \infty }\int _{Q_0}|\widehat{\varphi }_n|^2=0. \end{aligned}$$

Thus we have proved that, up to a subsequence, $\varphi _n\rightarrow 0$ in $L^2_{\mathrm{loc}}({\mathbb {R}}^2)$, which concludes the proof of the lemma. $\square$

We conclude this section by observing that Lemma 2.1 also holds when norms are restricted to a rectangle.

Lemma 2.11

Assume $0\le p\le 2$. Let $\Omega =(a,b)\times (c,d)$ be a rectangle. There exist a constant $C>0$ such that, for any $\varphi \in X^{1/2}(\Omega )$,

$$\begin{aligned} \Vert \varphi \Vert _{L^{p+2}(\Omega )}\le C\Vert \varphi \Vert _{X^{1/2}(\Omega )}. \end{aligned}$$

Proof

From Lemmas 2.7 and 2.4 we know that the extension operator is bounded from $X^{1/2}(\Omega )$ to $X^{1/2}$. Now it suffices to note that the identity operator is continuous from $X^{1/2}$ to $L^{p+2}({{\mathbb {R}}^2})$ and the restriction operator is continuous from $L^{p+2}({{\mathbb {R}}^2})$ to $L^{p+2}(\Omega )$. $\square$

2.2 Pohojaev-type identities and nonexistence of solitary waves

As usual, let us first to get an insight for which class of nonlinearities, solutions of (1.6) are expected. This is done with integration by parts.

Theorem 2.12

Assume $c>0$. Equation (1.4) does not possess solitary-wave solutions of the form $u(x,y,t)=\varphi (x-ct,t)$, $\varphi \in \mathscr {Z}$, whether

• (i) ${\displaystyle \int _{{\mathbb {R}}^2} \varphi f(\varphi )\;{d}x{d}y\le 2\int _{{\mathbb {R}}^2}F(\varphi )\;{d}x{d}y}$; or

• (ii) ${\displaystyle \int _{{\mathbb {R}}^2} \left( \varphi f(\varphi )+2F(\varphi )\right) \;{d}x{d}y\le 0}$.

Proof

Formally, by multiplying Eq. (1.6) by $\varphi$ and $y\varphi _y$, respectively, and integrating over ${\mathbb {R}}^2$, we deduce the identities

$$\begin{aligned}&\int _{{\mathbb {R}}^2}\left[ -c\varphi ^2-\varphi \mathscr {H}\varphi _x- \left( D_x^{-1/2}\varphi _y\right) ^2 +\varphi f(\varphi )\right] \;{d}x{d}y=0, \end{aligned}$$

(2.17)

$$\begin{aligned}&\int _{{\mathbb {R}}^2}\left[ c\varphi ^2+\varphi \mathscr {H}\varphi _x- \left( D_x^{-1/2}\varphi _y\right) ^2- 2F(\varphi )\right] \;{d}x{d}y=0. \end{aligned}$$

(2.18)

For smooth functions decaying to 0 at infinity, these formulas follow from integration by parts together with elementary properties of the Hilbert transform. The identities can be justified for functions of the minimal regularity required for them to make sense by the truncation argument put forward in [9]. The proof is completed by subtracting and adding (2.17) and (2.18). $\square$

Remark 2.13

Unfortunately, Theorem 2.12 is not strong enough to rule out the existence of solitary waves even in the case of a power-law nonlinearity. This is mainly because, in view of the nonlocal operator $\mathscr {H}$, we are not able to prove a Pohojaev-type identity on the x-variable for (1.6), i.e., (see [17] for similar calculations)

$$\begin{aligned} \int _{{\mathbb {R}}^2}\left[ c\varphi ^2+2 \left( D_x^{-1/2}\varphi _y\right) ^2-2F(\varphi )\right] \;{d}x{d}y=0. \end{aligned}$$

(2.19)

Indeed, if (2.19) were valid. Then subtracting (2.19) and (2.18) leads to

$$\begin{aligned} \int _{{\mathbb {R}}^2}\left( \varphi \mathscr {H}\varphi _x -3\left( D_x^{-1/2}\varphi _y\right) ^2\right) \;{d}x{d}y=0. \end{aligned}$$

(2.20)

Adding (2.17) and (2.18), there appears

$$\begin{aligned} \int _{{\mathbb {R}}^2}\left( -2\left( D_x^{-1/2}\varphi _y\right) ^2+\varphi f(\varphi )-2F(\varphi )\right) \;{d}x{d}y=0. \end{aligned}$$

(2.21)

Finally, plugging (2.21) in (2.19), there obtains

$$\begin{aligned} c\int _{{\mathbb {R}}^2}\varphi ^2\;{d}x{d}y=\int _{{\mathbb {R}}^2}\left( 4F(\varphi )-\varphi f(\varphi )\right) \;{d}x{d}y. \end{aligned}$$

(2.22)

Therefore, there would exist no nontrivial solitary-wave solutions of (1.4) provided

$$\begin{aligned} 4\int _{{\mathbb {R}}^2} F(\varphi )\;{d}x{d}y\le \int _{{\mathbb {R}}^2}\varphi f(\varphi )\;{d}x{d}y. \end{aligned}$$

(2.23)

To fix ideas, if we assume $f(\varphi )=\varphi ^{p+1}$ and that $\int \varphi ^{p+2}\ge 0$, (2.23) implies that solitary waves do not exist if $p>4$. This seems to be consistent with our embedding in Lemma 2.1. $\square$

2.3 Existence of solitary waves

In this subsection we will prove the existence of solution for (1.6) under suitable conditions on the nonlinearity f. Having in mind Lemma 2.1, we assume the following.

• ($\mathrm{A}_1)$ $f:{\mathbb {R}}\rightarrow {\mathbb {R}}$ is continuous and $f(0)=0$;

• ($\mathrm{A}_2)$ There exists $C>0$ such that $|f(u)|\le C(|u|+|u|^{p-1})$, $p\in (2,4)$ and $f(u)=o(|u|)$ as $|u|\rightarrow 0$;

• ($\mathrm{A}_3)$ There exists $\mu >2$ such that $\mu F(u)\le uf(u)$ for every $u\in {\mathbb {R}}$, where F is the primitive function of f;

• ($\mathrm{A}_4)$ There exists $\omega \in \mathscr {Z}$ such that $\lambda ^{-2}F(\lambda \omega )\rightarrow +\,\infty$ as $\lambda \rightarrow +\,\infty$.

The above assumptions are the ones suitable to apply minimax theory (see e.g. [32]). Probably, assumptions $(A_1)-(A_4)$ can be weakened to establish the existence of solitary waves. However, since our main interest is the study of (1.4) with a power-law nonlinearity, this will be enough to our purposes. Note that, clearly, our original nonlinearity $f(u)=u^2$ given in (1.2) satisfies $(A_1)-(A_4)$.

We start with the following vanishing property.

Lemma 2.14

If $\{u_n\}$ is a bounded sequence in $\mathscr {Z}$ and there is $r>0$ such that

$$\begin{aligned} \lim _{n\rightarrow +\,\infty }\sup _{(x,y)\in {{\mathbb {R}}^2}}\int _{B_r(x,y)}|u_n|^2{d}x{d}y=0, \end{aligned}$$

then, for $2<p<4$,

$$\begin{aligned} \lim _{n\rightarrow \infty }\Vert u_n\Vert _{L^p({{\mathbb {R}}^2})}=0, \end{aligned}$$

where $B_r(x,y)\subset {{\mathbb {R}}^2}$ is the open ball centered at (x, y) with radius r.

Proof

Let $\{\Omega _i\}_{i\in {\mathbb {N}}}$ be a covering of ${\mathbb {R}}^2$, where $\Omega _i$ is an open square with edges parallel to the coordinate axis and side-length r, and such that each point of ${\mathbb {R}}^2$ is contained in at most three squares. By the Hölder inequality and Lemma 2.11, there holds, for any $u\in \mathscr {Z}=X^{1/2}$,

$$\begin{aligned} \begin{aligned} \Vert u\Vert _{L^3(\Omega _i)}^3&\le \Vert u\Vert _{L^2(\Omega _i)} \Vert u\Vert _{L^4(\Omega _i)}^2\\&\lesssim \Vert u\Vert _{L^2(\Omega _i)} \Vert u\Vert _{X^{1/2}(\Omega _i)}^2. \end{aligned} \end{aligned}$$

Thus, in view of Proposition 2.10,

$$\begin{aligned} \Vert u_n\Vert _{L^3({{\mathbb {R}}^2})}^3\lesssim \sum _{i=0}^\infty \int _{\Omega _i}|u_n|^3dxdy\lesssim \sup _{(x,y)\in {{\mathbb {R}}^2}} \Vert u_n\Vert _{L^2(B_r(x,y))}\Vert u_n\Vert _\mathscr {Z}^2. \end{aligned}$$

Since $\{u_n\}$ is bounded, the assumption implies that $u_n\rightarrow 0$ in $L^3({{\mathbb {R}}^2})$. Finally, by interpolation and Lemma 2.1, there are $\theta _1,\theta _2\in (0,1)$, such that

$$\begin{aligned} \Vert u_n\Vert _{L^p({{\mathbb {R}}^2})}\le \Vert u_n\Vert _{L^2({{\mathbb {R}}^2})}^{\theta _1}\Vert u_n\Vert _{L^3({{\mathbb {R}}^2})}^{1-\theta _1}\lesssim \Vert u_n\Vert _\mathscr {Z}^{\theta _1}\Vert u_n\Vert _{L^3({{\mathbb {R}}^2})}^{1-\theta _1}, \qquad p\in (2,3), \end{aligned}$$

(2.24)

and

$$\begin{aligned} \Vert u_n\Vert _{L^p({{\mathbb {R}}^2})}\le \Vert u_n\Vert _{L^4({{\mathbb {R}}^2})}^{\theta _2}\Vert u_n\Vert _{L^3({{\mathbb {R}}^2})}^{1-\theta _2}\lesssim \Vert u_n\Vert _\mathscr {Z}^{\theta _2}\Vert u_n\Vert _{L^3({{\mathbb {R}}^2})}^{1-\theta _2}, \qquad p\in (3,4). \end{aligned}$$

(2.25)

The fact that $u_n\rightarrow 0$ in $L^3({{\mathbb {R}}^2})$ and (2.24)–(2.25) then imply that $u_n\rightarrow 0$ in $L^p({{\mathbb {R}}^2})$, for all $p\in (2,4)$, and the proof of the lemma is complete. $\square$

Now we are able to prove our main theorem in this section.

Theorem 2.15

(Existence) Assume $c>0$. Under assumptions ($\hbox {A}_1$)–($\hbox {A}_4$), Eq. (1.5) possesses a nontrivial solution $\varphi \in \mathscr {Z}$.

Proof

We will use the well known mountain pass lemma without the Palais-Smale condition (see [3]). Let

$$\begin{aligned} S(u)=\frac{1}{2}\Vert u\Vert _\mathscr {Z}^2-\int _{{\mathbb {R}}^2}F(u)\;{d}x{d}y \end{aligned}$$

(2.26)

and note that critical points of S are weak solutions of (1.6).

We claim that, for some constant $C_0>0$,

$$\begin{aligned} |F(u)|\le \frac{1}{4}|u|^2+C_0|u|^p. \end{aligned}$$

(2.27)

Indeed, from assumption ($\hbox {A}_2$), there exists $\varepsilon >0$ such that $|f(u)|\le \frac{1}{2} |u|$, when $|u|\le \varepsilon$. Hence, in this case

$$\begin{aligned} |F(u)|=\left| \int _0^uf(s)ds\right| \le \frac{1}{4}|u|^2. \end{aligned}$$

(2.28)

On the other hand, choose a constant $\widetilde{C}>0$ such that $(1/\widetilde{C})^{1/(p-2)}\le \varepsilon$. Thus, if $|u|\ge \varepsilon$, we immediately see that $|u|^2\le \widetilde{C}|u|^p$. Hence, in this case,

$$\begin{aligned} |F(u)|=\left| \int _0^uf(s)ds\right| \le C(|u|^2+|u|^p)\le C_0|u|^p. \end{aligned}$$

(2.29)

Collecting (2.28) and (2.29) yield (2.27).

Now, an application of Lemma 2.1 gives, for any $u\in \mathscr {Z}$,

$$\begin{aligned} S(u)\ge \frac{1}{2}\Vert u\Vert _\mathscr {Z}^2-\int _{{\mathbb {R}}^2}\left( \frac{1}{4}|u|^2+C_0|u|^p\right) {d}x{d}y \ge \frac{1}{4}\Vert u\Vert ^2_\mathscr {Z}-C_1\Vert u\Vert _\mathscr {Z}^p, \end{aligned}$$

where $C_1>0$. Hence, there are $\delta >0$, independent of u, and $r>0$ small enough with the property that $S(u)\ge \delta$ if $\Vert u\Vert _\mathscr {Z}=r$. On the other hand, it follows from assumption ($\hbox {A}_4$) that $S(\lambda u)\rightarrow -\infty$ as $\lambda \rightarrow +\,\infty$. Thus there exists $e_1\in \mathscr {Z}$ such that $\Vert e_1\Vert _\mathscr {Z}>r$ and $S(e_1)<0$.

Let d be the mountain-pass level, that is,

$$\begin{aligned} d=\inf _{\gamma \in \Gamma }\max _{t\in [0,1]}S(\gamma (t)), \end{aligned}$$

where

$$\begin{aligned} \Gamma =\{\gamma \in C([0,1];\mathscr {Z});\;\gamma (0)=0,\;S(\gamma (1))<0\}. \end{aligned}$$

Clearly $d\ge \inf _{\Vert u\Vert _\mathscr {Z}=r}S(u)>0$. Therefore, from the Mountain-Pass Lemma without the Palais-Smale condition there is a sequence $\{u_n\}\subset \mathscr {Z}$ such that $S'(u_n)\rightarrow 0$ and $S(u_n)\rightarrow d$, as $n\rightarrow +\,\infty$ (see e.g. [32, Theorem 2.9]). For n large enough, we obtain from assumption ($\hbox {A}_3$) that

$$\begin{aligned} \left( \frac{1}{2}-\frac{1}{\mu }\right) \Vert u_n\Vert _\mathscr {Z}^2\le S(u_n)-\frac{1}{\mu }\langle S'(u_n),u_n\rangle \le d+o(1)+\Vert u_n\Vert _\mathscr {Z}. \end{aligned}$$

Since $\mu >2$, we obtain that $\{u_n\}$ is bounded.

We now claim that there is no $r>0$ such that

$$\begin{aligned} \lim _{n\rightarrow +\,\infty }\sup _{(x,y)\in {{\mathbb {R}}^2}}\int _{B_{r}(x,y)}|u_n|^2{d}x{d}y\rightarrow 0. \end{aligned}$$

(2.30)

Indeed, assume the contrary, that is, (2.30) holds for some $r'>0$. Then, from Lemma 2.14,

$$\begin{aligned} \Vert u_n\Vert _{L^p}\rightarrow 0, \qquad \hbox {for}\;\;\; p\in (2,4), \end{aligned}$$

(2.31)

and there is a sequence $\epsilon _n\rightarrow 0$ such that

$$\begin{aligned} \begin{aligned} d&=S(u_n)-\frac{1}{2}\langle S'(u_n),u_n\rangle _{L^2}+\epsilon _n\\&=\int _{{\mathbb {R}}^2}\left( \frac{1}{2}f(u_n)u_n-F(u_n)\right) {d}x{d}y+\epsilon _n\\&\lesssim \Vert u_n\Vert _{L^2}^2+\Vert u_n\Vert _{L^p}^p. \end{aligned} \end{aligned}$$

(2.32)

Since $d>0$, taking the limit in (2.32), we get a contradiction with (2.31).

Therefore, by selecting if necessary a subsequence, we can assume that there is a sequence $(x_n,y_n)\subset {{\mathbb {R}}^2}$ such that

$$\begin{aligned} \Vert u_n\Vert _{L^2(B_1(x_n,y_n))}^2\ge \varrho /2>0,\qquad {\hbox {for all}}\;n, \end{aligned}$$

where

$$\begin{aligned} \varrho =\lim _{n\rightarrow \infty }\sup _{(x,y)\in {{\mathbb {R}}^2}}\int _{B_1(x,y)}|u_n|^2\;{d}x{d}y\ne 0. \end{aligned}$$

Then the functions $\varphi _n(x,y)=u_n(x+x_n,y+y_n)$ satisfy

$$\begin{aligned} \Vert \varphi _n\Vert _{L^2(B_1(0))}^2\ge \varrho /2>0, \end{aligned}$$

(2.33)

and $\{\varphi _n\}$ is bounded in $\mathscr {Z}$. Thus, it converges to some $\varphi \in \mathscr {Z}$ weakly in $\mathscr {Z}$ and strongly in $L^2_{\mathrm{loc}}({{\mathbb {R}}^2})$, by Lemma 2.3. From (2.33) it is clear that $\varphi \ne 0$ and for every $\chi \in \mathscr {Z}$, we have

$$\begin{aligned} \langle S'(\varphi ),\chi \rangle =\lim _{n\rightarrow +\,\infty }\langle S'(\varphi _n),\chi \rangle =0. \end{aligned}$$

This shows that $\varphi$ is a nontrivial solution of (1.5) and completes the proof of the theorem. $\square$

Remark 2.16

To the best of our knowledge, the (non)existence of stationary solutions of (1.5) when $c=0$ and $p=4$ remains as an open problem.

2.4 Variational characterization of ground states

In this subsection we will show that the solution obtained in Theorem 2.15 minimizes some variational problems under the additional assumption:

($\hbox {A}_5$) For $u\ne 0$, the function $t\mapsto t^{-1}\int _{{{\mathbb {R}}^2}} uf(tu)\;{d}x{d}y$ is strictly increasing on $(0,+\,\infty )$ and

$$\begin{aligned} \lim _{t\rightarrow \infty }t^{-1}\int _{{{\mathbb {R}}^2}} uf(tu)\;{d}x{d}y=+\,\infty . \end{aligned}$$

Indeed, let

$$\begin{aligned} I(u)=\langle S'(u), u\rangle =\Vert u\Vert _\mathscr {Z}^2-\int _{{\mathbb {R}}^2}uf(u)\;{d}x{d}y. \end{aligned}$$

Consider the Nehari manifold

$$\begin{aligned} \tilde{\Gamma }=\{u\in \mathscr {Z};\;I(u)=0,\;u\ne 0\}, \end{aligned}$$

and the minimization problem

$$\begin{aligned} \tilde{d}=\inf _{u\in \tilde{\Gamma }}S(u). \end{aligned}$$

(2.34)

Also, let $d^*$ be the minimax value

$$\begin{aligned} d^*=\inf _{u\in \mathscr {Z}}\sup _{t\ge 0}S(tu), \end{aligned}$$

(2.35)

Lemma 2.17

For every $u\in \mathscr {Z}{\setminus }\{0\}$ there exists a unique number $t_u>0$, such that $t_uu\in \tilde{\Gamma }$ and

$$\begin{aligned} S(t_uu)=\max _{t\ge 0}S(tu). \end{aligned}$$

In addition, the function $u\mapsto t_u$ is continuous and the map $u\mapsto t_uu$ is an homeomorphism from the unit sphere of $\mathscr {Z}$ to $\tilde{\Gamma }$.

Proof

First we note that since

$$\begin{aligned} S(tu)=\frac{t^2}{2}\Vert u\Vert _{\mathscr {Z}}^2-\int _{{\mathbb {R}}^2} F(tu){d}x{d}y \end{aligned}$$

we have

$$\begin{aligned} \frac{d}{dt}S(tu)=t\left( \Vert u\Vert _{\mathscr {Z}}^2-t^{-1}\int _{{{\mathbb {R}}^2}} uf(tu)\;{d}x{d}y\right) . \end{aligned}$$

Hence, from ($\hbox {A}_5$) the function $t\mapsto \frac{d}{d t}S(tu)=:g(t)$ vanishes at only one point $t_u>0$. In addition, since the function $t\mapsto -t^{-1}\int _{{{\mathbb {R}}^2}} uf(tu)\;{d}x{d}y$ is strictly decreasing on $(0,\infty )$, we see that $g(t)>0$ on $(0,t_u)$ and $g(t)<0$ on $(t_u,\infty )$, which means that $t_u$ is a maximum point for S(tu). The rest of the proof runs, for instance, as in [32, Lemma 4.1]); so we omit the details. $\square$

Lemma 2.18

Under the above notation, there hold $d=\tilde{d}=d^*$.

Proof

We divide the proof into some steps.

Step 1. $d\ge \tilde{d}$.

First we see that, as in the proof of Theorem 2.15, $I(u)>0$ in a neighborhood of the origin, except at the origin. Also, we have from (A$_3$) that, for $v\in \mathscr {Z}$,

$$\begin{aligned} \begin{aligned} 2S(v)&=\Vert v\Vert _\mathscr {Z}^2-2\int _{{{\mathbb {R}}^2}} F(v)\;{d}x{d}y> \Vert v\Vert _\mathscr {Z}^2-\mu \int _{{{\mathbb {R}}^2}} F(v)\;{d}x{d}y\\&\ge \Vert v\Vert _\mathscr {Z}^2-\int _{{{\mathbb {R}}^2}} vf(v)\;{d}x{d}y=I(v). \end{aligned} \end{aligned}$$

Now let $\gamma$ be in $\Gamma$. So $I(\gamma (t))>0$, for small t and $I(\gamma (1))<2S(\gamma (1))<0$. By continuity, $\gamma$ crosses $\tilde{\Gamma }$, that is, there exists $t_0\in (0,1)$ such that $\gamma (t_0)\in \tilde{\Gamma }$. Consequently, $\tilde{d}\le S(\gamma (t_0))\le \max _{t\in [0,1]}S(\gamma (t))$ and this proves Step 1.

Step 2. $d\le {d}^*$.

For any $u\in \mathscr {Z}$, from the proof of Lemma 2.17, there exists $t_0$ sufficiently large such that $S(t_0u)<0$. By defining $\gamma _0(t)=tt_0u$ we immediately see that $\gamma _0\in \Gamma$. Thus,

$$\begin{aligned} d\le \max _{t\in [0,1]}S(\gamma _0(t))=\max _{t\in [0,1]}S(tt_0u)\le \max _{t\ge 0}S(tu). \end{aligned}$$

The arbitrariness of u gives Step 2.

Step 3. $\tilde{d}={d}^*$.

Given any $u\in \mathscr {Z}{\setminus }\{0\}$ we can find $t_u>0$ such that $t_uu\in \tilde{\Gamma }$ and

$$\begin{aligned} \tilde{d}\le \inf _{u\in \tilde{\Gamma }}S(u)\le S(t_uu)=\max _{t\ge 0}S(tu). \end{aligned}$$

This shows that $\tilde{d}\le d^*$. On the other hand, for any $u\in \tilde{\Gamma }$, from Lemma 2.17, there is v in the unit sphere of $\mathscr {Z}$ such that $u=t_vv$. Thus,

$$\begin{aligned} \inf _{u\in \mathscr {Z}}S(t_uu)\le S(t_vv)=S(u), \end{aligned}$$

and, consequently, $\inf _{u\in \mathscr {Z}}S(t_uu)\le \tilde{d}.$ At last, the relation

$$\begin{aligned} d^*=\inf _{u\in \mathscr {Z}}\max _{t\ge 0}S(tu)=\inf _{u\in \mathscr {Z}}S(t_uu)\le \tilde{d} \end{aligned}$$

establishes Step 3.

By combining Steps 1,2, and 3, we have $d\le d^*=\tilde{d}\le d$ and the proof is completed. $\square$

Definition 2.19

A solution $\varphi \in \mathscr {Z}$ of (1.5) is called a ground state, if $\varphi$ minimizes the action S among all solutions of (1.5).

Theorem 2.20

Let ($\hbox {A}_1$)–($\hbox {A}_5$) hold. There exists a minimizer $u\in \tilde{\Gamma }$ of problem (2.34). In addition, u is a ground state solution.

Proof

As in the proof of Theorem 2.15, we can take a bounded Palais-Smale sequence $\{u_n\}\subset \mathscr {Z}$ and a solution $u\in \mathscr {Z}{\setminus }\{0\}$ such that $S(u_n)\rightarrow d$, $S'(u_n)\rightarrow 0$, $S'(u)=0$ and $u_n\rightarrow u$ a.e. and in $L^p_{\mathrm{loc}}({{\mathbb {R}}^2})$, as $n\rightarrow +\,\infty$. This immediately implies that $u\in \tilde{\Gamma }$ and

$$\begin{aligned} \tilde{d}=\inf _{v\in \tilde{\Gamma }}S(v)\le S(u). \end{aligned}$$

(2.36)

On the other hand, because $I(u_n)\rightarrow 0$, Lemma 2.18 and Fatou’s lemma, yield

$$\begin{aligned} \begin{aligned} \tilde{d}&=d=\liminf _{n\rightarrow \infty }\left( S(u_n)-\frac{1}{2}I(u_n)\right) =\liminf _{n\rightarrow \infty }\int _{{\mathbb {R}}^2}\left( \frac{1}{2}u_nf(u_n)-F(u_n)\right) {d}x{d}y\\&\ge \int _{{\mathbb {R}}^2}\left( \frac{1}{2}uf(u)-F(u)\right) {d}x{d}y=S(u)-\frac{1}{2}I(u)=S(u). \end{aligned} \end{aligned}$$

(2.37)

From (2.36) and (2.37) we deduce that $\tilde{d}=S(u)$. Finally, if v is any critical point of S, then $v\in \tilde{\Gamma }$ and $S(u)\le S(v)$, which means that u is a ground state. $\square$

Theorem 2.21

Let ($\hbox {A}_1$)–($\hbox {A}_5$) hold. Suppose also that $f\in C^1({\mathbb {R}})$ and

$$\begin{aligned} \int _{{\mathbb {R}}^2}uf(u)\;{d}x{d}y< \int _{{\mathbb {R}}^2}u^2f'(u)\;{d}x{d}y. \end{aligned}$$

(2.38)

Then for any nonzero $u\in \mathscr {Z}$, the following assertions are equivalent:

• (i) u is a ground state;

• (ii) $I(u)=0$ and $\inf \{G(v);\;v\in \tilde{\Gamma }\}=\tilde{d}=G(u)$, where

  $$\begin{aligned} G(u)=\int _{{\mathbb {R}}^2}\left( \frac{1}{2}uf(u)-F(u)\right) {d}x{d}y. \end{aligned}$$

Proof

$\hbox {(i)}\Rightarrow \hbox {(ii)}$. If u is a ground state, we have $S'(u)=0$, which implies that $I(u)=0$. On the other hand, for any $u\in \tilde{\Gamma }$,

$$\begin{aligned} S(u)=S(u)-\frac{1}{2}I(u)=\int _{{\mathbb {R}}^2}\left( \frac{1}{2}uf(u)-F(u)\right) {d}x{d}y=G(u). \end{aligned}$$

(2.39)

Hence,

$$\begin{aligned} \tilde{d}=S(u)=\inf _{v\in \tilde{\Gamma }}S(v)=\inf _{v\in \tilde{\Gamma }}G(v). \end{aligned}$$

$\hbox {(ii)}\Rightarrow \hbox {(i)}$. Let $u\in \mathscr {Z}$ satisfy (ii). Then, by using (2.39), there is a Lagrange multiplier $\theta$ such that $\theta I'(u)=S'(u)$. Therefore,

$$\begin{aligned} \theta \langle I'(u),u\rangle =\langle S'(u),u\rangle =I(u)=0. \end{aligned}$$

But,

$$\begin{aligned} \begin{aligned} \langle I'(u),u\rangle&=2\Vert u\Vert _\mathscr {Z}^2-\int _{{\mathbb {R}}^2}f'(u) u^2\;{d}x{d}y-\int _{{\mathbb {R}}^2}f(u) u\;{d}x{d}y\\&=2I(u)+\int _{{\mathbb {R}}^2}f(u) u\;{d}x{d}y-\int _{{\mathbb {R}}^2}f'(u) u^2\;{d}x{d}y\\&=\int _{{\mathbb {R}}^2}f(u) u\;{d}x{d}y-\int _{{\mathbb {R}}^2}f'(u) u^2\;{d}x{d}y\\&<0, \end{aligned} \end{aligned}$$

where we used (2.38) in the last inequality. Therefore $\theta =0$ and $S'(u)=0$, which implies that u is a ground state. $\square$

3 Regularity and decay

In this section we will discuss some regularity and spatially decay properties of solitary waves. For simplicity, throughout the section, we assume $c=1$ and f satisfies the grow condition $|f(u)|\le C|u|^{p-1}$, $p\in (2,4)$.

3.1 Regularity

The difficulty in studying regularity properties of the solutions of (1.5) or (1.6), comes from the fact that the operator $\mathscr {H}\Delta$ is nonlocal and non-isotropic. Here, we will adopt the strategy put forward in [9] (see also [25, 33] for applications to multi-dimensional models). The following Hörmander-Mikhlin type theorem will be useful.

Lemma 3.1

(Lizorkin lemma) Let $\Lambda :{\mathbb {R}}^n\rightarrow {\mathbb {R}}$ be a $C^n$ function for $|\xi _j|>0$,$j=1,\ldots ,n$. Assume that there exists a constant $M>0$ such that

$$\begin{aligned} \left| \xi _1^{k_1}\cdots \xi _n^{k_n} \frac{\partial ^k\Lambda (\xi )}{\partial \xi _1^{k_1}\cdots \partial \xi _n^{k_n}} \right| \le M, \end{aligned}$$

where $k_i$ take the values 0 or 1 and $k=k_1+\cdots k_n=0,1,\ldots ,n$. Then $\Lambda$ is a Fourier multiplier on $L^q({\mathbb {R}}^n)$, $1<q<\infty$.

Proof

See [23]. $\square$

Now we can prove the following.

Theorem 3.2

(Regularity) Assume $p\in (2,4)$. Any solitary-wave solution $\varphi \in \mathscr {Z}$ of (1.4) belongs to $W^{1,r}({{\mathbb {R}}^2})$, where $r\in (1,\infty )$. Moreover $\varphi \in W^{m+1,r}({{\mathbb {R}}^2})$, for $m=1,2$, if $f\in C^m({\mathbb {R}})$. In particular, if $f(u)=u^2$ then $\varphi \in H^{\infty }({\mathbb {R}}^2)$.

Proof

We are left to prove the regularity result for the nonlinear equation

$$\begin{aligned} \varphi _x+\mathscr {H}\Delta \varphi =\left( f(\varphi )\right) _x. \end{aligned}$$

(3.1)

Let $\varphi \in \mathscr {Z}$ be a solution of (3.1). By Lemma 2.1, one has $\mathscr {Z}\hookrightarrow L^r({\mathbb {R}}^2)$, $r\in [2,4]$, and therefore $f(\varphi )\in L^{\frac{r}{p-1}}({\mathbb {R}}^2)$. It can be easily checked that multipliers $\frac{|\xi |}{|\xi |+\xi ^2+\eta ^2}$, $\frac{\xi |\xi |}{|\xi |+\xi ^2+\eta ^2}$ and $\frac{|\xi |\eta }{|\xi |+\xi ^2+\eta ^2}$ satisfy the assumptions in Lemma 3.1. Hence $\varphi$, $\varphi _x$, $\varphi _y\in L^{q}({\mathbb {R}}^2)$, where

$$\begin{aligned} q\in {\left\{ \begin{array}{ll} \left[ \frac{2}{p-1},\frac{4}{p-1}\right] ,&{}p\in (2,3),\\ (1,2],&{}p=3,\\ \Big (1,\frac{4}{p-1}\Big ],&{}p\in (3,4). \end{array}\right. } \end{aligned}$$

(3.2)

We now divide the proof into three cases.

Case 1. $2<p<3$. From (3.2) we see, in particular, that $\varphi ,\nabla \varphi \in L^2({\mathbb {R}}^2)$. In view of the Sobolev embedding $H^1({\mathbb {R}}^2)\hookrightarrow L^r({\mathbb {R}}^2)$, $r\in [2,\infty )$, we deduce that $\varphi \in L^r({\mathbb {R}}^2)$, $r\in [\frac{2}{p-1},\infty )$. As a consequence, $f(\varphi )\in L^r({\mathbb {R}}^2)$, $r\in [\frac{2}{p-1},\infty )$. Thus, we can apply Lemma 3.1 to conclude that $\nabla \varphi \in L^r({\mathbb {R}}^2)$, $r\in [\frac{2}{p-1},\infty )$ and, consequently, $\varphi \in W^{1,r}$ with $r\in [\frac{2}{p-1},\infty )$.

Now, let $p_0=\frac{2}{p-1}$ and define $p_1=\frac{p_0}{p-1}$. It is clear that $f(\varphi )\in L^{p_1}({{\mathbb {R}}^2})$ and $p_1\le 1$ if and only if $p\ge \sqrt{2}+1$. Hence, if $p\ge \sqrt{2}+1$ we can apply Lemma 3.1 to conclude that $\varphi ,\nabla \varphi \in L^r({\mathbb {R}}^2)$, $r\in (1,\infty )$. Assume now $p<\sqrt{2}+1$ and define, inductively, $p_n=\frac{p_{n-1}}{p-1}$. Note that $0<p_n<p_{n-1}$ and $p_n\le 1$ if and only if $p\ge {2}^{\frac{1}{n+1}}+1$. The result then follows, using Lemma 3.1 because $p_n\rightarrow 0$ and ${2}^{\frac{1}{n+1}}+1\rightarrow 2$, as $n\rightarrow \infty$.

Case 2. $p=3$. Here we also have $\varphi ,\nabla \varphi \in L^2({\mathbb {R}}^2)$. So, as in Case 1 we obtain $\varphi ,\nabla \varphi \in L^r({\mathbb {R}}^2)$, $r\in [2,\infty )$, which combined with (3.2) gives the desired.

Case 3. $3<p<4$. Here we have $\varphi , \varphi _x, \varphi _y\in L^{{\frac{4}{p-1}}}({\mathbb {R}}^2)$. By using the Gagliardo–Nirenberg inequality

$$\begin{aligned} \Vert u\Vert _{L^s}\le C\Vert \nabla u\Vert _{L^r}^\theta \Vert u\Vert _{L^q}^{1-\theta }, \qquad \frac{1}{s}=\frac{1-\theta }{q}+\theta \Big (\frac{1}{r}-\frac{1}{2}\Big ), \;\;\theta \in [0,1], \end{aligned}$$

(3.3)

with $\theta =1$ and $r=\frac{4}{p-1}$, we deduce that $\varphi \in L^{{\frac{4}{p-3}}}({\mathbb {R}}^2)$ and, consequently, $f(\varphi )\in L^{\frac{4}{(p-1)(p-3)}}({\mathbb {R}}^2)$. An application of Lemma 3.1 yields $\varphi ,\nabla \varphi \in L^{{\frac{4}{(p-1)(p-3)}}}({\mathbb {R}}^2)$. Now we need to use an iteration process. Indeed, let $p_1$ be the positive root of the equation $(p-1)(p-3)-2=0$, that is, $p_1=2+\sqrt{3}\in (3,4)$. Since the function $\mu _1(p)=4/(p-1)(p-3)$ is strictly decreasing on the interval (3, 4) and $\mu _1(p_1)=2$, we have that $\mu _1(p)\ge 2$ in $(3,p_1]$. Consequently, interpolating between $L^{\frac{4}{p-1}}$ and $L^{\mu _1(p)}$, $p\in (3,p_1]$ we obtain $\varphi ,\nabla \varphi \in L^2$. By proceeding as in Case 1 we conclude the result if $p\in (3,p_1]$.

Assume now $p\in (p_1,4)$. Since $\varphi ,\nabla \varphi \in L^{{\frac{4}{(p-1)(p-3)}}}({\mathbb {R}}^2)$, we can use (3.3) to conclude that $\varphi \in L^{\frac{4}{(p-1)(p-3)-2}}$. It is to be noted that because $p\in (p_1,4)$ we have $(p-1)(p-3)-2>0$. Thus we obtain, $f(\varphi )\in L^{\frac{4}{(p-1)^2(p-3)-2(p-1)}}$. Lemma 3.1 again implies $\varphi ,\nabla \varphi \in L^{\frac{4}{(p-1)^2(p-3)-2(p-1)}}$. Let $P_2$ be the polynomial $P_2(p)=(p-1)^2(p-3)-2(p-1)-2$. Since $P_2(p_1)=-2$ and $P_2(4)=1$, it follows that $P_2$ has a root in the interval $(p_1,4)$, which we shall call $p_2$. Again, since the function $\mu _2(p)=4/[(p-1)^2(p-3)-2(p-1)]$ is strictly decreasing on the interval $(p_1,4)$ and $\mu _2(p_2)=2$, we deduce that $\mu _2(p)\ge 2$ on the interval $(p_1,p_2)$. Another interpolation gives $\varphi ,\nabla \varphi \in L^2$ and the proof is also completed for $p\in (p_1,p_2]$.

Following this process, we define inductively the polynomial $P_n$ in the following way: having defined $P_{n-1}$, we define $P_n$ by the relation $P_{n}(p)=(p-1)P_{n-1}(p)-2$. Precisely, $P_n$ has the expression

$$\begin{aligned} P_n(p)=(p-1)^n(p-3)-2(p-1)^{n-1}-2(p-1)^{n-2}-\cdots -2(p-1)-2. \end{aligned}$$

Also, inductively, if $p_{n-1}$ is the root of $P_{n-1}$ in the interval (3, 4), noting that $P_n(p_{n-1})=-2$ and $P_n(4)=1$, we define $p_n$ to be the root of $P_n$ in the interval $(p_{n-1},4)$. Note that $\{p_n\}$ is increasing and bounded by 4. Thus, in order to complete the proof it suffices to show that the sequence $\{p_n\}$ converges to 4, as $n\rightarrow \infty$. But this follows at once because $P_n(p)\rightarrow -\infty$ for any $p\in (0,4)$. This completes the proof in Case 3.

Now suppose that f is $C^1$. Then, for all $2<p<4$, $f'(\varphi )\varphi _x\in L^q({{\mathbb {R}}^2})$, where $1< q<\infty$. On the other hand, (3.1) is equivalent to

$$\begin{aligned} -\Delta \varphi =\mathscr {H}\left( f(\varphi )\right) _x-\mathscr {H}\varphi _x. \end{aligned}$$

Thus $\Delta \varphi \in L^q({{\mathbb {R}}^2})$ by Riesz’s theorem [29] (see also [11]), where $1< q<\infty$. The proof is now completed by iteration. The case of $f\in C^2$ is similar. $\square$

Remark 3.3

It can be seen from Theorem 3.2, Sobolev’s embedding $W^{1,r}({{\mathbb {R}}^2})\hookrightarrow L^\infty ({{\mathbb {R}}^2})$, $r>2$, and Morrey’s inequality that any solitary wave $\varphi \in \mathscr {Z}$ of (1.5) indeed belongs to $L^\infty ({{\mathbb {R}}^2})\cap C({{\mathbb {R}}^2})$ and vanishes at infinity.

Next we prove that the high regularity of f is reflected in the analyticity of the traveling waves.

Theorem 3.4

(Analyticity) Suppose that $f\in C^\infty ({\mathbb {R}})$ and, for any $R>0$, there exists $M>0$ such that

$$\begin{aligned} |f^{(n)}(x)|\le M^{n+1}n!,\qquad \hbox {for all}\,\, |x|<R,\,\, n\in \mathbb {N}. \end{aligned}$$

Then any solitary wave solution $\varphi \in \mathscr {Z}\cap H^\infty ({\mathbb {R}}^2)$ of (1.4) is real analytic in ${\mathbb {R}}^2$.

Proof

Fix any $(x_0,y_0)\in {\mathbb {R}}^2$. To simplify notation, let $P=(x,y)$ and $P_0=(x_0,y_0)$. By Taylor’s formula and the smoothness of $\varphi$, one has for any $N\in \mathbb {N}$,

$$\begin{aligned} \begin{aligned} \varphi (P+P_0)&=\sum _{|\alpha |\le N}\frac{P^\alpha }{\alpha !}\partial ^\alpha \varphi (P_0)+ \sum _{|\alpha |=N+1}\frac{N+1}{\alpha !}\int _0^1(1-t)^NP^\alpha \partial ^\alpha \varphi (tP+P_0)\;{d}t\\&=I+II, \end{aligned} \end{aligned}$$

where for any $\alpha =(\alpha _1,\alpha _2)\in {\mathbb {N}}^2$,

$$\begin{aligned} \partial ^{\alpha }=\frac{\partial ^{\alpha _1+\alpha _2}}{\partial _x^{\alpha _1}\partial _y^{\alpha _2}}, \end{aligned}$$

represents the derivative operator of order $|\alpha |=\alpha _1+\alpha _2$. In order to show the Taylor series is absolutely convergent one needs to estimate the second term. By using the regularity of $\varphi$ and the Sobolev embedding $H^2({{\mathbb {R}}^2})\hookrightarrow L^\infty ({{\mathbb {R}}^2})$, one gets, for any $N>2$,

$$\begin{aligned} \begin{aligned} |II|&\le \sum _{|\alpha |=N+1} \frac{N+1}{\alpha !}|P|^{|\alpha |}\Vert \partial ^\alpha \varphi \Vert _{H^2}\int _0^1(1-t)^N\; {d}t\\&=\sum _{|\alpha |=N+1} \frac{1}{\alpha !}|P|^{|\alpha |}\Vert \partial ^\alpha \varphi \Vert _{H^2}. \end{aligned} \end{aligned}$$

We claim that it suffices to show that there are constants $C>0$ and $A>0$ such that, for any $\alpha \in \mathbb {N}^2$,

$$\begin{aligned} \Vert \partial ^\alpha \varphi \Vert _{H^2}\le CA^{(|\alpha |-1)_+}(|\alpha |-2)_+!, \end{aligned}$$

(3.4)

where $(\cdot )_+=\max \{\cdot ,0\}$. Indeed, assuming (3.4), we deduce

$$\begin{aligned} \begin{aligned} |II|&\le C\sum _{|\alpha |=N+1}\frac{1}{\alpha !}|P|^{|\alpha }A^{(|\alpha |-1)_+}(|\alpha |-2)_+!\\&=CA^N|P|^{N+1}\sum _{|\alpha |=N+1}\frac{(N-1)!}{\alpha !} \end{aligned} \end{aligned}$$

Now by using the elementary inequality (see [20, Lemma 4.5])

$$\begin{aligned} \sum _{|\alpha |=N}\frac{N!}{\alpha !}\le 2^{N+1}, \end{aligned}$$

one gets

$$\begin{aligned} |II|\le \frac{4C|P|}{N(N+1)}(2A|P|)^N. \end{aligned}$$

Thus by taking a small enough R such that $2AR<1$, we conclude that $II\rightarrow 0$, as $N\rightarrow \infty$, which shows that the Taylor series is absolutely convergent and $\varphi$ is real analytic in a neighborhood of $P_0$.

Now it remains to prove (3.4). If $|\alpha |\le 2$, in view of the inequality $\Vert \partial ^\alpha \varphi \Vert _{H^2}\le C \Vert \varphi \Vert _{H^4}$, the proof is direct. For $|\alpha |>2$, the proof is by induction on $|\alpha |$. Assume the statement is true for all multi-indices $\alpha \in {\mathbb {N}}^2$ such that $|\alpha |\le n$. Then, it suffices to show that (3.4) holds with $\partial ^\alpha \varphi$ replaced by $\partial ^\alpha \nabla \varphi$. First we recall that Eq. (1.5) is equivalent to

$$\begin{aligned} \mathscr {H}\varphi _x-\Delta \varphi +\mathscr {H}f(\varphi )_x=0. \end{aligned}$$

(3.5)

Then by using the regularity of $\varphi$, applying the operator $\partial ^\alpha$ and taking the inner product in ${H^2({{\mathbb {R}}^2})}$ with $\partial ^\alpha \varphi$ in (3.5), one derives the identity

$$\begin{aligned} \langle \mathscr {H}\partial ^\alpha \varphi _x,\partial ^\alpha \varphi \rangle _{H^2}- \langle \Delta \partial ^\alpha \varphi ,\partial ^\alpha \varphi \rangle _{H^2} =-\langle \mathscr {H}\partial ^\alpha f(\varphi )_x,\partial ^\alpha \varphi \rangle _{H^2}. \end{aligned}$$

(3.6)

Since $\langle \mathscr {H}\partial ^\alpha \varphi _x,\partial ^\alpha \varphi \rangle _{H^2}=\Vert D^{1/2}_x\partial ^\alpha \varphi \Vert ^2_{H^2}$ and $\langle \Delta \partial ^\alpha \varphi ,\partial ^\alpha \varphi \rangle _{H^2}=-\Vert \nabla \partial ^\alpha \varphi \Vert _{H^2}^2$,we have

$$\begin{aligned}\begin{aligned} \Vert D^{1/2}_x\partial ^\alpha \varphi \Vert ^2_{H^2}+ \Vert \nabla \partial ^\alpha \varphi \Vert _{H^2}^2&\le \Vert \partial ^\alpha \mathscr {H}\varphi _x\Vert _{H^2} \Vert \partial ^\alpha f(\varphi )\Vert _{H^2}\\&\le \frac{1}{2}\Vert D_x^{1/2}\partial ^\alpha \varphi \Vert _{H^2}^2 +\frac{1}{2}\Vert \partial ^\alpha f(\varphi )\Vert _{H^2}^2. \end{aligned} \end{aligned}$$

Hence

$$\begin{aligned} \Vert \nabla \partial ^\alpha \varphi \Vert _{H^2}\lesssim \Vert \partial ^\alpha f(\varphi )\Vert _{H^2}. \end{aligned}$$

(3.7)

Thus, in order to complete the proof one needs to estimate $\Vert \partial ^\alpha f(\varphi )\Vert _{H^2}$. But, by recalling the estimate [20, proof of Lemma 4.4]:

$$\begin{aligned} \Vert \partial ^\alpha f(\varphi )\Vert _{H^2({{\mathbb {R}}^2})}\le CA^{|\alpha |}(|\alpha |-1)!, \end{aligned}$$

(3.8)

we immediately conclude the proof. $\square$

Remark 3.5

It is to be observed that (3.8) was obtained in [20] when studying analyticity of solitary waves for the KP equation. However, a simple inspection in the proof reveals that it does not depend on the solution itself, but only its smoothness and our assumptions on the nonlinearity f.

Remark 3.6

A similar result of analyticity was obtained, in [24], when $f(u)=u^2$. Thus Theorem 3.4 can also be viewed as an extension of that result.

3.2 Decay

This subsection is devoted to the study of decay properties of the solitary waves. Our results are inspired in those in [4] (see also [10, 25, 33]). The difficulty here, once again comes from the fact that the linear part of (1.5) is nonlocal and non-isotropic.

Recall we are assuming $c=1$ and a priori f satisfies $|f(u)|\le C|u|^{p-1}, p\in (2,4)$. However, as we will see in the next result, a further restriction on p must be imposed.

Lemma 3.7

Assume that $p\in (p_0,4)$ where $p_0=(3+\sqrt{5})/2$. Then any solitary wave $\varphi \in \mathscr {Z}$ of (1.5) satisfies

$$\begin{aligned} \int _{{\mathbb {R}}^2}y^2\left( |D^{1/2}_x\varphi |^2+|\nabla \varphi |^2\right) d xd y<\infty . \end{aligned}$$

Proof

Let $\chi _0\in C_0^\infty ({\mathbb {R}})$ be a function such that $0\le \chi _0\le 1$, $\chi (y)=1$ if $|y|\in [0,1]$ and $\chi _0(y)=0$ if $|y|\ge 2$. Set $\chi _n(y)=\chi _0(\frac{y^2}{n^2})$, $n\in \mathbb {N}$. Equation (1.5) is equivalent to

$$\begin{aligned} \mathscr {H}\varphi _x-\Delta \varphi +\mathscr {H}f(\varphi )_x=0. \end{aligned}$$

(3.9)

Multiplying (3.9) by $y^2\chi _n(y)\varphi$ and integrating over ${{\mathbb {R}}^2}$, we obtain after several integrations by parts that

$$\begin{aligned} \int _{{\mathbb {R}}^2}\mathscr {H}\varphi _x\chi _n(y)y^2\varphi= & {} \int _{{\mathbb {R}}^2}\chi _n(y)y^2|D^{1/2}_x\varphi |^2,\\ -\int _{{\mathbb {R}}^2}\varphi _{xx}\chi _n(y)y^2\varphi= & {} \int _{{\mathbb {R}}^2}\chi _n(y)y^2|\varphi _x|^2, \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} -\int _{{\mathbb {R}}^2}\varphi _{yy}\chi _n(y)y^2\varphi = \int _{{\mathbb {R}}^2}\chi _n(y)(y^2\varphi _y^2-\varphi ^2) -\int _{{\mathbb {R}}^2}(2\chi '_n(y)y+\frac{1}{2}\chi ''_n(y)y^2)\varphi ^2. \end{aligned} \end{aligned}$$

Hence,

$$\begin{aligned} \begin{aligned} \int _{{\mathbb {R}}^2}y^2\chi _n\left( |D^{1/2}_x\varphi |^2+|\nabla \varphi |^2\right)&= \int _{{\mathbb {R}}^2}\chi _n\varphi ^2 + \int _{{\mathbb {R}}^2}(2y\chi _n'+\frac{1}{2}y^2\chi ''_n)\varphi ^2\\&\quad - \int _{{\mathbb {R}}^2}y^2\chi _n\mathscr {H}\varphi f(\varphi )_x . \end{aligned} \end{aligned}$$

(3.10)

Let us estimate the last term on the right-hand side of (3.10). By using Hölder’s inequality (in the x variable) and the fractional chain rule, we have

$$\begin{aligned}\begin{aligned} \left| \int _{{\mathbb {R}}^2} y^2\chi _n\mathscr {H} \varphi f(\varphi )_x\right|&= \left| \int _{{\mathbb {R}}^2} y^2\chi _n\mathscr {H}\partial _x\varphi f(\varphi )\right| =\left| \int _{{\mathbb {R}}^2} y^2\chi _n D_x^{1/2}\varphi D_x^{1/2}f(\varphi )\right| \\&\le \int _{{\mathbb {R}}}y^2\chi _n\Vert D_x^{1/2}\varphi \Vert _{L_x^2}\Vert D_x^{1/2}f(\varphi )\Vert _{L_x^2}dy\\&\le C\int _{{\mathbb {R}}}y^2\chi _n\Vert D_x^{1/2}\varphi \Vert _{L_x^2}\Vert D_x^{1/2}\varphi \Vert _{L_x^m}\Vert \varphi \Vert _{L_x^{\ell (p-2)}}^{p-2}dy, \end{aligned} \end{aligned}$$

where $m,\ell \ne \infty$ are such that $1/m+1/\ell =1/2$. Let $\theta =\frac{2(p-2)}{m(p-1)}$, $\lambda =\frac{\ell -2}{\ell (p-1)}$ and take m such that $m>\max \{2,4(p-2)/(p-1)\}$. From the fractional Gagliardo–Nirenberg inequality (see, for instance, [19]), we deduce

$$\begin{aligned} \Vert D_x^{1/2}\varphi \Vert _{L^m_x}\le C\Vert \varphi _x\Vert _{L^2_x}^\theta \Vert \varphi \Vert _{L_x^{2(p-2)}}^{1-\theta },\quad \Vert \varphi \Vert _{L_x^{\ell (p-2)}}\le C\Vert \varphi _x\Vert _{L_x^2}^\lambda \Vert \varphi \Vert _{L_x^{2(p-2)}}^{1-\lambda }. \end{aligned}$$

Note that if $p\in [p_0,4)$ then, from Theorem 3.2, $\varphi (\cdot ,y)\in L^{2(p-2)}_x$ a.e. $y\in {\mathbb {R}}$. In particular note that $2(p-2)\ge 2/(p-1)$ only if $p\ge p_0$ (here is where the restriction on p appears). Therefore,

$$\begin{aligned} \begin{aligned} \left| \int _{{\mathbb {R}}^2} y^2\chi _n\mathscr {H} \varphi f(\varphi )_x\right| \le C\int _{{\mathbb {R}}}y^2\chi _n\Vert D_x^{1/2}\varphi \Vert _{L_x^2}\Vert \varphi _x\Vert _{L_x^2}\Vert \varphi \Vert _{L_x^{2(p-2)}}^{p-2}dy. \end{aligned} \end{aligned}$$

Let $\epsilon \in (0,1)$ be such that $C\epsilon <1/2$. Since $\varphi$ is continuous and tends to zero at infinity, we choose $R>0$ such that $\Vert \varphi (\cdot ,y)\Vert _{L_x^{2(p-2)}}<\epsilon$ for any $|y|>R$. Then, there exists a constant $C_R>0$ such that

$$\begin{aligned} \begin{aligned} \left| \int _{{\mathbb {R}}^2} y^2\chi _n\mathscr {H} \varphi f(\varphi )_x\right|&\le C_R+C\epsilon \int _{|y|>R}y^2\chi _n\Vert D^{1/2}\varphi \Vert _{L_x^2}\Vert \varphi _x\Vert _{L_x^2}dy\\&\le C_R+C\epsilon \Vert y\chi _n^{1/2}D_x^{1/2}\varphi \Vert _{L^2}\Vert y\chi _n^{1/2}\varphi _x\Vert _{L^2}\\&\le C_R+C\epsilon (\Vert y\chi _n^{1/2}D_x^{1/2}\varphi \Vert _{L^2}^2+\Vert y\chi _n^{1/2}\varphi _x\Vert _{L^2}^2)\\&\le C_R+\frac{1}{2}\left( \Vert y\chi _n^{1/2}D_x^{1/2}\varphi \Vert _{L^2}^2+\Vert y\chi _n^{1/2}\varphi _x\Vert _{L^2}^2\right) . \end{aligned} \end{aligned}$$

(3.11)

By replacing (3.11) into (3.10) we obtain

$$\begin{aligned} \int _{{\mathbb {R}}^2}y^2\chi _n\left( |D^{1/2}_x\varphi |^2+|\nabla \varphi |^2\right) \lesssim \int _{{\mathbb {R}}^2}\chi _n\varphi ^2 + \int _{{\mathbb {R}}^2}(2y\chi _n'+\frac{1}{2}y^2\chi ''_n)\varphi ^2+C_R. \end{aligned}$$

(3.12)

The first term on the right-hand side of (3.12) tends to $\Vert \varphi \Vert _{L^2}^2$, as $n\rightarrow \infty$, by the Lebesgue theorem. The second term tends to zero by the Lebesgue theorem and the properties of $\chi _n$. Therefore

$$\begin{aligned} \int _{{\mathbb {R}}^2}y^2\chi _n\left( |D^{1/2}_x\varphi |^2+|\nabla \varphi |^2\right) {d}x{d}y \end{aligned}$$

is uniformly bounded in n. By the Fatou lemma, we get our claim. $\square$

In view of Lemma 3.7 in what follows, otherwise is stated, we assume $p\in (p_0,4)$.

Lemma 3.8

Let $\ell \ge 0$, $\nu >-3/2$ and define $h_\nu$ via its Fourier transform by

$$\begin{aligned} \widehat{h_\nu }(\xi ,\eta )=\frac{|\xi |^{1+\nu }}{|\xi |+\xi ^2+\eta ^2}. \end{aligned}$$

Then,

• (i) $h_\nu \in C^\infty ({\mathbb {R}}^2{\setminus }\{0\})$;

• (ii) $|y|^\ell h_\nu \in L^q({{\mathbb {R}}^2})$, if $1\le q<\infty$ and $\frac{\ell }{3}+\frac{1}{q}<\frac{2}{3}\nu +1$ and $\ell +\frac{2}{q}>\nu +1$;

• (iii) $|y|^{2\nu +3} h_\nu \in L^\infty ({{\mathbb {R}}^2})$.

Proof

We observe that for any $\phi \in \mathcal {S}({{\mathbb {R}}^2})$ (the Schwartz space)

$$\begin{aligned} \begin{aligned} \langle h_{\nu },\phi \rangle _{\mathcal {S},\mathcal {S}'}&=\int _{{{\mathbb {R}}^2}}\frac{|\xi |^{1+\nu }}{|\xi |+\xi ^2+\eta ^2} \int _{{\mathbb {R}}^2}\mathrm{e}^{\mathrm{i}(x\xi +y\eta )}\phi (x,y)\;{d}x{d}y\;{d}\xi {d}\eta \\&=\int _0^{+\,\infty }\int _{{{\mathbb {R}}^2}}\int _{{{\mathbb {R}}^2}}|\xi |^\nu \mathrm{e}^{\mathrm{i}(x\xi +y\eta )}\mathrm{e}^{-t(1+|\xi |+ \eta ^2/|\xi |)}\phi (x,y)\;{d}\xi {d}\eta \; {d}x{d}y\;{d}t\\&=\int _0^{+\,\infty }\frac{\mathrm{e}^{-t}}{\sqrt{t}}\int _{{{\mathbb {R}}^2}}\int _{{\mathbb {R}}}|\xi |^{\nu +\frac{1}{2}}\mathrm{e}^{\mathrm{i}x\xi }\mathrm{e}^{-|\xi |(t+y^2/t)}\phi (x,y)\;{d}\xi \; {d}x{d}y\;{d}t\\&=2\Gamma \left( \nu +\frac{3}{2}\right) \int _0^{+\,\infty }t^{\nu +1}\mathrm{e}^{-t}\int _{{{\mathbb {R}}^2}} \left( t^2x^2+\left( t^2+y^2\right) ^2\right) ^{-\frac{2\nu +3}{4}}\\&\quad \times \cos \left( (\nu +\frac{3}{2})\arctan \left( \frac{t|x|}{t^2+y^2}\right) \right) \phi (x,y)\;{d}x{d}y\;{d}t, \end{aligned} \end{aligned}$$

where in the last equality we used that $\xi \mapsto |\xi |^{\nu +\frac{1}{2}}\mathrm{e}^{-|\xi |(t+y^2/t)}$ is an even function and formula (7) in [12, page 15]. Thus, we deduce that

$$\begin{aligned} \begin{aligned} h_\nu (x,y)&= 2\Gamma \left( \nu +\frac{3}{2}\right) \int _0^{+\,\infty } t^{\nu +1}\mathrm{e}^{-t}\left( t^2x^2+\left( t^2+y^2\right) ^2\right) ^{-\frac{2\nu +3}{4}}\\&\quad \times \cos \left( \left( \nu +\frac{3}{2}\right) \arctan \left( \frac{t|x|}{t^2+y^2} \right) \right) \;{d}t. \end{aligned} \end{aligned}$$

(3.13)

From the above expression, parts (i) and (iii) are obvious. Let us establish (ii). Indeed,

$$\begin{aligned} \Vert |y|^\ell h_\nu \Vert _{L^q}\lesssim \int _0^\infty t^{\nu +1}\mathrm{e}^{-t}\underbrace{\Vert |y|^{\ell }\left( t^2x^2+\left( t^2+y^2\right) ^2\right) ^{-\frac{2\nu +3}{4}}\Vert _{L^q}}_{A}\; {d}t. \end{aligned}$$

(3.14)

But,

$$\begin{aligned} \begin{aligned} A^q&=\int _{{\mathbb {R}}}|y|^{q\ell }\left[ \int _{{\mathbb {R}}}\left( t^2x^2+\left( t^2+y^2\right) ^2\right) ^{-\frac{2\nu +3}{4}q}{d}x\right] {d}y\\&= \int _{{\mathbb {R}}}|y|^{q\ell }\left[ t^{-\frac{2\nu +3}{2}q}\int _{{\mathbb {R}}}\left( x^2+\left( t+\frac{y^2}{t}\right) ^2\right) ^{-\frac{2\nu +3}{4}q}{d}x\right] {d}y\\&= \int _{{\mathbb {R}}}|y|^{q\ell }\left[ t^{-\frac{2\nu +3}{2}q} \left( t+\frac{y^2}{t}\right) ^{1-\frac{2\nu +3}{2}q} \int _{{\mathbb {R}}}\left( z^2+1\right) ^{-\frac{2\nu +3}{4}q}{d}z\right] {d}y, \end{aligned} \end{aligned}$$

(3.15)

where we used a change of variable. Since $\nu >-3/2$ we have

$$\begin{aligned} \frac{1}{q}<\frac{2}{3}\nu +1-\frac{\ell }{3}\le \frac{2}{3}\nu +1<\nu +\frac{3}{2} \end{aligned}$$

and the inner integral in (3.15) is finite. Thus,

$$\begin{aligned} \begin{aligned} A^q&=C t^{-\frac{2\nu +3}{2}q} \int _{{\mathbb {R}}}|y|^{q\ell } \left( t+\frac{y^2}{t}\right) ^{1-\frac{2\nu +3}{2}q} {d}y\\&=Ct^{-1} \int _{{\mathbb {R}}}|y|^{q\ell } \left( t^2+y^2\right) ^{1-\frac{2\nu +3}{2}q}{d}y\\&=Ct^{q\ell +2-(2\nu +3)q}\int _{{\mathbb {R}}}|z|^{q\ell } \left( 1+z^2\right) ^{1-\frac{2\nu +3}{2}q}{d}y. \end{aligned} \end{aligned}$$

(3.16)

Since $\frac{\ell }{3}+\frac{1}{q}<\frac{2}{3}\nu +1$ this last integral is also finite. Consequently,

$$\begin{aligned} \Vert |y|^\ell h_\nu \Vert _{L^q}\lesssim \int _0^\infty t^{\nu +1}\mathrm{e}^{-t}t^{\ell +\frac{2}{q}-(2\nu +3)}{d}t. \end{aligned}$$

The assumption $\ell +\frac{2}{q}>\nu +1$ now implies that this last integral is finite and the proof of the lemma is completed. $\square$

Lemma 3.9

Assume $f\in C^1$ and $p\ge p_0=(3+\sqrt{5})/2$. Let $\varphi \in \mathscr {Z}$ be any solitary wave of (1.5). Then $|y|\varphi \in L^q({{\mathbb {R}}^2})$, for all $3/2< q\le \infty .$

Proof

First we show $y\varphi \in L^\infty ({\mathbb {R}}^2)$. Choose $\beta \in (0,3/4)$ and $q_1,q_2>2$ satisfying

$$\begin{aligned} \frac{1}{2}=\frac{1}{q_1}+\frac{1}{q_2},\qquad \frac{3}{2q_1}<\beta <\frac{2}{q_1}\quad \hbox {and}\quad (p-2)q_2>1, \end{aligned}$$

(3.17)

where $h_{\beta -1}$ is as in Lemma 3.8. Then it follows from

$$\begin{aligned} |y\varphi |\lesssim |yh_{\beta -1}|*|D^{1-\beta }_xf(\varphi )|+|h_{\beta -1}|*|yD^{1-\beta }_xf(\varphi )|, \end{aligned}$$

Young’s inequality and the fractional chain rule that

$$\begin{aligned} \begin{aligned} \Vert y\varphi \Vert _{L^\infty }&\lesssim \Vert yh_{\beta -1}\Vert _{L^{q_1}}\Vert D^{1-\beta }_x\varphi \Vert _{L^2}\Vert \varphi ^{p-2}\Vert _{L^{q_2}}\\&\quad + \Vert h_{\beta -1}\Vert _{L^{q_1}}\Vert yD^{1-\beta }_x\varphi \Vert _{L^2}\Vert \varphi ^{p-2}\Vert _{L^{q_2}}. \end{aligned} \end{aligned}$$

From (3.17), Lemma 3.8, Theorem 3.2, and the fact that $\varphi \in \mathscr {Z}$, the right-hand side of the above inequality is finite if $\Vert yD^{1-\beta }_x\varphi \Vert _{L^2}<+\,\infty$.

We state that $\Vert yD^{1-\beta }_x\varphi \Vert _{L^2}<+\,\infty$. Indeed, if $\varphi$ satisfies (1.5), then

$$\begin{aligned} D^{1-\beta }_x\varphi =h_{\tilde{\beta }}*D^{1/2}_xf(\varphi ), \end{aligned}$$

where $\tilde{\beta }=1/2-\beta$. Now we choose $\widetilde{q}_1,\widetilde{q}_2,r_1$ and $r_2$ such that

$$\begin{aligned} 1=\frac{1}{\widetilde{q}_1}+\frac{1}{\widetilde{q}_2},\quad \frac{2}{\widetilde{q}_1}>\tilde{\beta }>\frac{3}{2\widetilde{q}_1}-1, \quad \widetilde{q}_1>1, \quad (p-2)\widetilde{q}_2>1 \end{aligned}$$

(3.18)

and

$$\begin{aligned} 1=\frac{1}{r_1}+\frac{1}{r_2}, \quad \frac{1}{2}\left( \frac{3}{r_1}-1\right)<1+\tilde{\beta }<\frac{2}{r_1}, \quad r_1>1, \quad (p-2)r_2>1. \end{aligned}$$

(3.19)

Since

$$\begin{aligned} |yD^{1-\beta }\varphi |\lesssim |yh_{\tilde{\beta }}|*|D^{1/2}_xf(\varphi )|+|h_{\tilde{\beta }}|*|yD^{1/2}_xf(\varphi )|, \end{aligned}$$

we have from the fractional chain rule and Young’s inequality

$$\begin{aligned} \begin{aligned} \Vert yD^{1-\beta }\varphi \Vert _{L^2}&\lesssim \Vert yh_{\tilde{\beta }}\Vert _{L^{q_1}}\Vert D^{1/2}_x\varphi \Vert _{L^2}\Vert \varphi ^{p-2}\Vert _{L^{q_2}}\\&\quad + \Vert h_{\tilde{\beta }}\Vert _{L^{r_1}}\Vert yD^{1/2}_x\varphi \Vert _{L^2}\Vert \varphi ^{p-2}\Vert _{L^{r_2}}<+\,\infty . \end{aligned} \end{aligned}$$

Note that since $p\ge p_0$, Lemma 3.7 implies that $\Vert yD^{1/2}_x\varphi \Vert _{L^2}<\infty$. Hence, (3.18), (3.19), Lemma 3.8, Theorem 3.2, and the fact that $\varphi \in \mathscr {Z}$, imply that the right-hand side of the above inequality is finite.

Next we prove that $y\varphi \in L^q({\mathbb {R}}^2)$, $q>3/2$. Because

$$\begin{aligned} |y\varphi |\lesssim |yh_0|*|f(\varphi )|+|h_0|*|y f(\varphi )|, \end{aligned}$$

by choosing $q_1\in (1,2)$, $r_1>3/2$ and $r_2(p-1),q_2(p-2)>1$ satisfying $1+\frac{1}{q}=\frac{1}{q_1}+\frac{1}{q_2}=\frac{1}{r_1}+\frac{1}{r_2}$, we get from $y\varphi \in L^\infty$ that

$$\begin{aligned}\begin{aligned} \Vert y\varphi \Vert _{L^q}&\lesssim \Vert yh_0\Vert _{L^{r_1}}\Vert f(\varphi )\Vert _{L^{r_2}} + \Vert h_0\Vert _{L^{q_1}}\Vert yf(\varphi )\Vert _{L^{q_2}}\\&\lesssim \Vert \varphi \Vert _{L^{r_2(p-1)}}^{p-1}+\Vert y\varphi \Vert _{L^\infty }\Vert \varphi \Vert _{L^{q_2(p-2)}}^{p-2}<+\,\infty , \end{aligned} \end{aligned}$$

where we used Lemma 3.8 and Theorem 3.2 again. This completes the proof of the lemma. $\square$

In view of Lemma 3.9, otherwise stated, we assume that $f\in C^1$. As an immediate consequence we deduce.

Corollary 3.10

Let $\varphi \in \mathscr {Z}$ be any solitary wave of (1.5) and $\theta \in [0,1]$. Then $|y|^\theta \varphi \in L^q({{\mathbb {R}}^2})$, for all $3/2< q\le \infty$.

Proof

It suffices to note that

$$\begin{aligned} \begin{aligned} \int _{{{\mathbb {R}}^2}}|y|^{\theta q}|\varphi |^q{d}x{d}y&=\int _{{\mathbb {R}}}\left( \int _{|y|\le 1}|y|^{\theta q}|\varphi |^q{d}y \right) {d}x+\int _{{\mathbb {R}}}\left( \int _{|y|\ge 1}|y|^{\theta q}|\varphi |^q{d}y \right) {d}x\\&\le \int _{{{\mathbb {R}}^2}}|\varphi |^q{d}x{d}y+\int _{{{\mathbb {R}}^2}}|y|^{q}|\varphi |^q{d}x{d}y \end{aligned} \end{aligned}$$

and apply Theorem 3.2 and Lemma 3.9. $\square$

Next, we observe that Eq. (1.5) may be written in the equivalent form

$$\begin{aligned} \varphi =k*f(\varphi ), \end{aligned}$$

(3.20)

where $k=h_0=\left( \frac{|\xi |}{|\xi |+\xi ^2+\eta ^2}\right) ^\vee$ was defined in Lemma 3.8. We will use the properties of the kernel k to get some decay estimates for the solution $\varphi$ of (1.5). As an immediate consequence of Lemma 3.8 we have the following.

Lemma 3.11

Let $\ell \in [0,3)$. Assume that $1\le q<\infty$ satisfies $\frac{1}{q}+\frac{1}{3}\ell <1$ and $1<\ell +\frac{2}{q}$. Then,

• (i) $k\in C^\infty ({\mathbb {R}}^2{\setminus }\{0\})$;

• (ii) $|y|^\ell k\in L^q({{\mathbb {R}}^2})$;

• (iii) $|y|^{3} k\in L^\infty ({{\mathbb {R}}^2})$.

Concerning decay and integrability with respect to a power of x we have the following result.

Lemma 3.12

Let $\ell \in [0,3/2)$. Assume that $1\le q<\infty$ satisfies $\frac{1}{q}+\frac{2}{3}\ell <1$ and $1<\ell +\frac{2}{q}$. Then,

• (i) $|x|^\ell k\in L^q({{\mathbb {R}}^2})$;

• (ii) $|x|^{3/2} k\in L^\infty ({{\mathbb {R}}^2})$.

Proof

The proof is very similar to that of Lemma 3.8; so we omit the details. We only point out that a power $|z|^{q\ell }$ appears in the inner integral (3.15). Thus, a condition for the integrability is $\frac{3}{2}q-q\ell >1$; but this is true because $\frac{1}{q}+\frac{2}{3}\ell <1$ and $\ell <3/2$. $\square$

The next step is to show that solutions of (1.5) decay to zero at infinity at the same rate as the kernel k.

Theorem 3.13

(Spatial decay in the y variable) Any solitary wave $\varphi \in \mathscr {Z}$ of (1.5) satisfies

• (i) $y^3\varphi \in L^\infty ({{\mathbb {R}}^2})$; and

• (ii) $|y|^\kappa \varphi \in L^\infty ({{\mathbb {R}}^2})$, $0\le \kappa \le 3$.

Proof

It suffices to prove (i), because (ii) follows immediately from (i). First, by using (3.20), we recall the trivial inequality

$$\begin{aligned} |y|^{\ell }|\varphi |\lesssim |y| ^{\ell }|k|*|f(\varphi )|+|k|*||y|^{\ell }|f(\varphi )|, \end{aligned}$$

(3.21)

which holds for any $\ell \ge 0$. Let $\gamma _1=p-1$.

Claim 1. $|y|^{\gamma _1}\varphi \in L^r({{\mathbb {R}}^2})$, for any $1\le r\le \infty$.

Indeed, choose $r_1,r_2,q_1,q_2$ such that $1+\frac{1}{r}=\frac{1}{r_1}+\frac{1}{r_2}=\frac{1}{q_1}+\frac{1}{q_2}$, $r_1\in (1,2)$, $q_2\gamma _1>1$, $r_2\gamma _1>\frac{3}{2}$ and $q_1>\frac{3}{3-\gamma _1}$. From (3.21) with $\ell =\gamma _1$ and the Young inequality it follows that

$$\begin{aligned} \Vert |y|^{\gamma _1}\varphi \Vert _{L^r} \lesssim \Vert |y| ^{\gamma _1}k\Vert _{L^{q_1}}\Vert \varphi \Vert _{L^{q_2\gamma _1}}^{\gamma _1} + \Vert k\Vert _{L^{r_1}}\Vert y\varphi \Vert _{L^{r_2\gamma _1}}^{\gamma _1}. \end{aligned}$$

Thanks to Lemmas 3.11, 3.9, and Theorem 3.2, the right-hand side of the above inequality is finite and the claim is established.

Next we define $\gamma _2=\min \{3,(p-1)^2\}$ and divide the proof into two cases.

Case 1. $\gamma _2=(p-1)^2$.

Here, we observe the following

Claim 2. $|y|^{\gamma _2}\varphi \in L^r({\mathbb {R}}^2)$, for any $\frac{3}{\gamma _1(3-\gamma _1)}<r\le \infty$.

In fact, by using (3.21) with $\ell =\gamma _2$ and an argument similar to that in Claim 1, we have

$$\begin{aligned} \Vert |y|^{\gamma _2}\varphi \Vert _{L^r} \lesssim \Vert |y| ^{\gamma _2}k\Vert _{L^{q_1}}\Vert \varphi \Vert _{L^{q_2\gamma _1}}^{\gamma _1} + \Vert k\Vert _{L^{r_1}}\Vert |y|^{\gamma _1}\varphi \Vert _{L^{r_2\gamma _1}}^{\gamma _1}<+\,\infty , \end{aligned}$$

provided $1+\frac{1}{r}=\frac{1}{r_1}+\frac{1}{r_2}=\frac{1}{q_1}+\frac{1}{q_2}$, $r_1\in (1,2)$, $q_2\gamma _1>1$, $r_2\gamma _2>\frac{3}{2}$ and $q_1>\frac{3}{3-\gamma _2}$. Note we used Claim 1 for the last term. From our choices, $\frac{1}{q_2}<\gamma _1$ and $\frac{1}{q_1}<\frac{3-\gamma _2}{3}$, which implies $\frac{1}{q_1}+\frac{1}{q_2}<1+\frac{\gamma _1(3-\gamma _1)}{3}$. This forces the restriction $r>\frac{3}{\gamma _1(3-\gamma _1)}$ and shows our claim.

Now, since $p\ge p_0=(3+\sqrt{5})/2$, we deduce that $\gamma _1\gamma _2>3>\gamma _2$. Thus,

$$\begin{aligned} \Vert y^3\varphi \Vert _{L^{\infty }}\lesssim \Vert y^3k\Vert _{L^{\infty }}\Vert \varphi \Vert _{L^{\gamma _1}}^{\gamma _1}+ \Vert k\Vert _{L^{a}}\Vert |y|^{\frac{3}{p-1}}\varphi \Vert _{L^{b\gamma _1}}^{\gamma _1}, \end{aligned}$$

(3.22)

where $1=\frac{1}{a}+\frac{1}{b}$. From Theorem 3.2 and Lemma 3.11 the first term on the right-hand side of (3.22) is finite. Also, by choosing $a\in (0,1)$ and b satisfying $b\gamma _2>\frac{3}{3-\gamma _1}$, we obtain $k\in L^a({{\mathbb {R}}^2})$ and

$$\begin{aligned} \Vert |y|^{\frac{3}{p-1}}\varphi \Vert _{L^{b\gamma _1}}^{\gamma _1}\lesssim \Vert \varphi \Vert _{L^{b\gamma _1}}^{\gamma _1}+\Vert |y|^{\gamma _2}\varphi \Vert _{L^{b\gamma _1}}^{\gamma _1}, \end{aligned}$$

(3.23)

where we used $\frac{3}{p-1}=\frac{3}{\gamma _1}<\gamma _2$. The right-hand side of (3.23) is finite thanks to Theorem 3.2 and Claim 2. This proves that the right-hand side of (3.22) is finite and concludes the proof of the theorem in this case.

Case 2. $\gamma _2=3$.

Here, if $\frac{1}{a}+\frac{1}{b}=1$, we write

$$\begin{aligned} \begin{aligned} \Vert y^3\varphi \Vert _{L^{\infty }}&\lesssim \Vert y^3k\Vert _{L^{\infty }}\Vert \varphi \Vert _{L^{\gamma _1}}^{\gamma _1}+ \Vert k\Vert _{L^{a}}\Vert |y|^{3}f(\varphi )\Vert _{L^{b}}\\&\lesssim \Vert y^3k\Vert _{L^{\infty }}\Vert \varphi \Vert _{L^{\gamma _1}}^{\gamma _1}+ \Vert k\Vert _{L^{a}}\left( \Vert \varphi \Vert _{L^{b\gamma _1}}^{\gamma _1}\Vert |y|^{\gamma _1}\varphi \Vert _{L^{b\gamma _1}}^{\gamma _1} \right) \end{aligned} \end{aligned}$$

where we used that $3<(p-1)^2=\gamma _1^2$. By choosing $a\in (0,1)$, $b\gamma _1>1$, using Claim 1, and arguing as in Case 1, we complete the proof of the theorem. $\square$

Interest is now turned to the decay with respect to the variable x. Let us start with the following result.

Lemma 3.14

Let $q_0=2(p-1)$. Then, for any $q\in (q_0,\infty )$ and $\ell \ge 0$ satisfying $\ell q<1/2$, we have $|x|^{\ell }\varphi \in L^q({{\mathbb {R}}^2})$.

Before proving Lemma 3.14 we recall the following.

Lemma 3.15

Let $j\in \mathbb {N}$. Suppose also that $\ell$ and m are two constants satisfying $0<\ell <m-j$. Then there exists $C>0$, depending only on $\ell$ and m, such that for all $\epsilon \in (0,1]$, we have

$$\begin{aligned} \int _{{\mathbb {R}}^j}\frac{|a|^\ell }{(1+\epsilon |a|)^m(1+|b-a|)^m}\;{d}a \le \frac{C\;|b|^\ell }{(1+\epsilon |b|)^m},\qquad \forall \;b\in {\mathbb {R}}^j,\;|b|\ge 1, \end{aligned}$$

(3.24)

and

$$\begin{aligned} \int _{{\mathbb {R}}^j}\frac{{d}a}{(1+\epsilon |a|)^m(1+|b-a|)^m} \le \frac{C}{(1+\epsilon |b|)^m},\qquad \forall \;b\in {\mathbb {R}}^j. \end{aligned}$$

(3.25)

Proof

The proof is quite elementary and it is essentially the same as that of Lemma 3.1.1 in [4] (see also [13]). $\square$

Proof of Lemma 3.14

Fix $r\in (1,2)$ to be chosen later and take $s_1\in (\frac{1}{r'},\frac{3}{2r'})$ and $s_2\in (\frac{1}{r'},3(p-2))$, where $r'$ is the Hölder conjugate of r.

We first claim that, for any $\ell \in [0,s_1-\frac{1}{r'})$, we have $|x|^\ell \langle y\rangle ^{-s_2}\varphi \in L^{r'}({{\mathbb {R}}^2})$. Indeed, for $0<\epsilon \ll 1$, define $g_\epsilon$ by

$$\begin{aligned} g_\epsilon (x,y)=\frac{|x|^\ell }{{\langle x\rangle }^{s_1}_\epsilon {\langle y\rangle }^{s_2}}\varphi (x,y), \end{aligned}$$

where $\langle y\rangle =1+|y|$ and $\langle x\rangle _\epsilon =1+\epsilon |x|$. Since $\varphi \in L^\infty ({{\mathbb {R}}^2})$, from the choices of $\ell$ and $s_j,j=1,2$, it is easy to see that $g_\epsilon \in L^{r'}({{\mathbb {R}}^2})$. Now, given any $\delta > 0$, there exists a constant $N>1$ (depending on $\delta$) such that

$$\begin{aligned} \langle y\rangle ^{\frac{s_2}{p-2}}|\varphi |<\delta , \qquad \hbox {for}\;\; |x|>N. \end{aligned}$$

(3.26)

To see this, choose a number $a\in (0,1)$ satisfying $\frac{s_2}{a(p-2)}<3$ (this is possible because $s_2<3(p-2)$). Then,

$$\begin{aligned} \begin{aligned} \langle y\rangle ^{\frac{s_2}{p-2}}|\varphi |\lesssim |\varphi |+|y|^{\frac{s_2}{p-2}}|\varphi |^a|\varphi |^{1-a}\le \Vert |y|^{\frac{s_2}{ap-2}}\varphi \Vert ^a_{L^\infty }|\varphi |^{1-a}\lesssim |\varphi |^{1-a}, \end{aligned} \end{aligned}$$

where we used Theorem 3.13. Since $\varphi$ goes to zero at infinity (see Theorem 3.2 and Remark 3.3), this last inequality implies (3.26).

Now we decompose

$$\begin{aligned} {\mathbb {R}}=\{|x|>N\}\cup \{|x|\le N\}=:I_1\cup I_2. \end{aligned}$$

Then, by using Eq. (3.20), Hölder’s inequality and Lemma 3.12, we get

$$\begin{aligned} \begin{aligned} \int _{I_1\times {\mathbb {R}}}&|g_\epsilon (x,y)|^{r'}{d}x{d}y\\&\le \int _{I_1\times {\mathbb {R}}}|g_\epsilon (x,y)|^{r'-1}\frac{|x|^\ell }{\langle x\rangle ^{s_1}_\epsilon \langle y\rangle ^{s_2}}k*f(\varphi ){d}x{d}y\\&\le \int _{I_1\times {\mathbb {R}}}|g_\epsilon (x,y)|^{r'-1}\frac{|x|^\ell }{\langle x\rangle ^{s_1}_\epsilon \langle y\rangle ^{s_2}} \Vert k\langle x\rangle ^{s_1}\Vert _{L^r({{\mathbb {R}}^2})}\Vert \langle x\rangle ^{-s_1}*f(\varphi )\Vert _{L^{r'}({{\mathbb {R}}^2})}{d}x{d}y\\&\lesssim \Vert g_\epsilon \Vert _{L^{r'}(I_1\times {\mathbb {R}})}^{r'-1}\left( \int _{I_1\times {\mathbb {R}}}\frac{|x|^{\ell r'}}{\langle x\rangle ^{s_1r'}_\epsilon \langle y\rangle ^{s_2r'}}\Vert \langle x\rangle ^{-s_1}*f(\varphi )\Vert _{L^{r'}({{\mathbb {R}}^2})}^{r'}{d}x{d}y\right) ^{1/{r'}}. \end{aligned} \end{aligned}$$

Since $g_\epsilon \in L^{r'}({{\mathbb {R}}^2})$, we can divide both sides of the above inequality by $\Vert g_\epsilon \Vert _{L^{r'}}^{r'-1}$ to obtain

$$\begin{aligned} \int _{I_1\times {\mathbb {R}}}|g_\epsilon (x,y)|^{r'}{d}x{d}y\lesssim \int _{I_1\times {\mathbb {R}}}\frac{|x|^{\ell r'}}{\langle x\rangle ^{s_1r'}_\epsilon \langle y\rangle ^{s_2r'}}\Vert \langle x\rangle ^{-s_1}*f(\varphi )\Vert _{L^{r'}({{\mathbb {R}}^2})}^{r'}{d}x{d}y. \end{aligned}$$

By using the definition of convolution, Fubini’s theorem and Lemma 3.15,

$$\begin{aligned} \begin{aligned} \int _{I_1\times {\mathbb {R}}}&|g_\epsilon (x,y)|^{r'}{d}x{d}y\\&\lesssim \int _{{\mathbb {R}}^2}|f(\varphi )(x',y')|^{r'} \int _{I_1\times {\mathbb {R}}}\frac{|x|^{\ell r'}}{\langle x\rangle ^{s_1r'}_\epsilon \langle y\rangle ^{s_2r'}\langle x-x'\rangle ^{s_1r'}} {d}x{d}y\;{d}x'{d}y'\\&\lesssim \int _{I_1\times {\mathbb {R}}}|f(\varphi )(x',y')|^{r'}\frac{|x'|^{\ell r'}}{\langle x'\rangle ^{s_1r'}_\epsilon }{d}x'{d}y'\\&\qquad + \int _{I_2\times {\mathbb {R}}}|f(\varphi )(x',y')|^{r'} \int _{I_1\times {\mathbb {R}}}\frac{|x|^{\ell r'}}{\langle x\rangle ^{s_1r'}_\epsilon \langle y\rangle ^{s_2r'}\langle x-x'\rangle ^{s_1r'}} {d}x{d}y\;{d}x'{d}y'\\&\lesssim \delta ^{r'(p-2)} \int _{I_1\times {\mathbb {R}}}|\varphi (x',y')|^{r'}\frac{|x'|^{\ell r'}}{\langle x'\rangle ^{s_1 r'}_\epsilon \langle y'\rangle ^{s_2r'}} {d}x'{d}y'\\&\qquad + \int _{I_2\times {\mathbb {R}}}|\varphi (x',y')|^{r'(p-1)} \int _{{{\mathbb {R}}^2}}\frac{(|x|+2N)^{\ell r'}}{\langle x\rangle ^{s_1 r'}\langle y\rangle ^{s_2 r'}}{d}x{d}y\;{d}x'{d}y'\\&\lesssim \delta ^{r'(p-2)}\int _{I_1\times {\mathbb {R}}}|g_\epsilon (x',y')|^{r'}{d}x'{d}y'+ \int _{I_2\times {\mathbb {R}}}|\varphi (x',y')|^{r'(p-1)}{d}x'{d}y'. \end{aligned} \end{aligned}$$

By choosing $\delta$ sufficiently small, we deduce that

$$\begin{aligned} \int _{I_1\times {\mathbb {R}}}|g_\epsilon (x,y)|^{r'}{d}x{d}y \le C \int _{I_2\times {\mathbb {R}}}|\varphi (x',y')|^{r'(p-1)}{d}x'{d}y'. \end{aligned}$$

Since the constant C appearing in the right-hand side of the preceding estimate is independent of $\epsilon$, an application of Fatou’s lemma gives

$$\begin{aligned} \int _{I_1\times {\mathbb {R}}}\frac{|x|^{\ell r'}}{\langle y\rangle ^{s_2r'}}|\varphi (x,y)|^{r'}{d}x{d}y \lesssim 1. \end{aligned}$$

(3.27)

On the other hand, clearly

$$\begin{aligned} \int _{I_2\times {\mathbb {R}}}\frac{|x|^{\ell r'}}{\langle y\rangle ^{s_2r'}}|\varphi (x,y)|^{r'}{d}x{d}y \lesssim \Vert \varphi \Vert _{L^{r'}({{\mathbb {R}}^2})}^{r'}. \end{aligned}$$

(3.28)

A combination of (3.27) and (3.28) then establishes that $|x|^\ell \langle y\rangle ^{-s_2}\varphi \in L^{r'}({{\mathbb {R}}^2})$ for any $r'\in (2,\infty )$, $\ell \in [0,s_1-1/r')$ and $s_2\in (\frac{1}{r'},3(p-2))$, which is precisely our claim.

In order to complete the proof of the lemma, we fix $q_0=2(p-1)$ and take $q\in (q_0,\infty )$. Let $\nu =\frac{q}{p-1}$ and note that $2<\nu <q$. Now, for any $\ell \ge 0$ and $s>0$, we infer that

$$\begin{aligned} \Vert |x|^{\ell }\varphi \Vert _{L^{q}({{\mathbb {R}}^2})}\le \Vert |x|^{\frac{q\ell }{\nu }}\langle y\rangle ^{-\frac{s}{\nu }}\varphi \Vert _{L^{\nu }({{\mathbb {R}}^2})}^{\frac{\nu }{q}} \Vert \langle y\rangle ^{\frac{s}{q-\nu }}\varphi \Vert _{L^\infty ({{\mathbb {R}}^2})}^{\frac{q-\nu }{q}}. \end{aligned}$$

(3.29)

We claim that by choosing $s\in (1,3\nu (p-2))$, the right-hand side of (3.29) is finite. Indeed, since the function $t\mapsto \frac{t}{p-1}-\frac{1}{q}$ tends to 0, as $t\rightarrow \frac{p-1}{q}$, and to $\frac{1}{2q}$ as $t\rightarrow \frac{3(p-1)}{2q}$, we can find a number $s_1\in \left( \frac{p-1}{q},\frac{3(p-1)}{2q}\right)$ such that

$$\begin{aligned} 0\le \ell <\frac{s_1}{p-1}-\frac{1}{q}. \end{aligned}$$

With this inequality in hand, all assumptions in our claim above hold and the first term in (3.29) is finite. The second one is also finite thanks to Theorem 3.13. Note that $\frac{s}{q-\nu }<3$ in view of our choices of $\nu$ and s. This completes the proof. $\square$

Theorem 3.16

(Spatial decay in the x variable) Any nontrivial solitary wave $\varphi \in \mathscr {Z}$ of (1.5) satisfies $|x|^{3/2}\varphi \in L^\infty ({{\mathbb {R}}^2})$.

Proof

The proof is analogous to that of Theorem 3.13. We divide it into several steps.

Step 1. First we note from (3.21) that $|x|^\ell \varphi \in L^{q}({{\mathbb {R}}^2})$ for any $2<q\le \infty$ and $0\le 2\ell <\frac{1}{2}+\frac{1}{q}$. In fact, by choosing $r_1,r_2>1$, $q_1\in (1,2)$ and $q_2\in (2,\infty )$ such that $1+\frac{1}{q}=\frac{1}{r_1}+\frac{1}{r_2}=\frac{1}{q_1}+\frac{1}{q_2}$, $2\ell q_2<1$ and $\frac{1}{r_1}+\frac{2\ell }{3}<1<\ell +\frac{2}{r_1}$, as in (3.21), we get from the Young inequality,

$$\begin{aligned} \begin{aligned} \Vert |x|^\ell \varphi \Vert _{L^q}&\lesssim \Vert |x|^\ell k\Vert _{L^{r_1}}\Vert \varphi \Vert _{L^{r_2(p-1)}}^{p-1} + \Vert k\Vert _{L^{q_1}}\Vert |x|^\frac{\ell }{p-1} \varphi \Vert _{L^{q_2(p-1)}}^{p-1}<+\,\infty , \end{aligned} \end{aligned}$$

where we used Theorem 3.2, Lemmas 3.12, and 3.14. The restrictions on q and $\ell$ come from

$$\begin{aligned} 1+\frac{1}{2}> 1+\frac{1}{q}=\frac{1}{q_1}+\frac{1}{q_2}>\frac{1}{2}+2\ell , \quad 1+\frac{1}{q}=\frac{1}{q_1}+\frac{1}{q_2}<1+\frac{1}{2}. \end{aligned}$$

In particular, $|x|^\ell \varphi \in L^\infty ({{\mathbb {R}}^2})$, if $0\le \ell <1/4$.

Step 2. We now show that $|x|^\ell \varphi \in L^{q}({{\mathbb {R}}^2})$ for any $\max \{1,\frac{2}{p-1}\}=:\overline{q}<q\le \infty$ and $0\le 2\ell <\frac{p}{2}+\frac{1}{q}$. In fact, by choosing $r_1,r_2>1$, as in Step 1 and $q_1\in (1,2)$ and $q_2\in (\overline{q},\infty )$ such that $1+\frac{1}{q}=\frac{1}{q_1}+\frac{1}{q_2}$ and $\frac{2\ell }{p-1}<\frac{1}{2}+\frac{1}{q_2(p-1)}$, we deduce

$$\begin{aligned}\begin{aligned} \Vert |x|^\ell \varphi \Vert _{L^q}\lesssim \Vert |x|^\ell k\Vert _{L^{r_1}}\Vert \varphi \Vert _{L^{r_2(p-1)}}^{p-1} + \Vert k\Vert _{L^{q_1}}\Vert |x|^\frac{\ell }{p-1} \varphi \Vert _{L^{q_2(p-1)}}^{p-1}<+\,\infty , \end{aligned} \end{aligned}$$

where now to see that the last term in the above inequality is finite we used the result in Step 1. The restrictions on q and $\ell$ follow as in Step 1. In particular, $|x|^\ell \varphi \in L^\infty ({{\mathbb {R}}^2})$, if $0\le \ell <p/4$.

Step 3. We claim that if p satisfies $p(p-1)>5$ then $|x|^{3/2}\varphi \in L^\infty$ and the proof of the theorem is completed in this case. Indeed, by choosing $q_1\in (1,2)$ and $q_2>2$ such that $1=\frac{1}{q_1}+\frac{1}{q_2}$, we write

$$\begin{aligned} \Vert |x|^{3/2}\varphi \Vert _{L^\infty }\lesssim \Vert |x|^{3/2} k\Vert _{L^{\infty }}\Vert \varphi \Vert _{L^{p-1}}^{p-1} + \Vert k\Vert _{L^{q_1}}\Vert |x|^\frac{3}{2(p-1)} \varphi \Vert _{L^{q_2(p-1)}}^{p-1}<+\,\infty . \end{aligned}$$

The last term in the above inequality is finite in view of Step 2. We point out that conditions on q and $\ell$ in Step 2, is equivalent to $0\le 3<\frac{p(p-1)}{2}+\frac{1}{q_2}$, which holds because

$$\begin{aligned} 3=\frac{5}{2}+\frac{1}{2}<\frac{p(p-1)}{2}+\frac{1}{q_2}. \end{aligned}$$

This establishes Step 3.

Assume from now on that p satisfies $p_0\le p\le p_1$, where $p_1$ is the positive root of $p(p-1)=5$.

Step 4. We show that $|x|^\ell \varphi \in L^{q}({{\mathbb {R}}^2})$ for any $1<q\le \infty$ and $0\le 2\ell <\frac{1}{2}+\frac{p(p-1)}{2}+\frac{1}{q}$. Indeed, in order to apply the results in Step 2, we choose $r_1,r_2>1$, as in Step 1 and $q_1\in (1,2)$ and $q_2\in (1,\infty )$ such that $1+\frac{1}{q}=\frac{1}{q_1}+\frac{1}{q_2}$ and $\frac{2\ell }{p-1}<\frac{p}{2}+\frac{1}{q_2(p-1)}$. Consequently,

$$\begin{aligned} \begin{aligned} \Vert |x|^\ell \varphi \Vert _{L^q}&\lesssim \Vert |x|^\ell k\Vert _{L^{r_1}}\Vert \varphi \Vert _{L^{r_2(p-1)}}^{p-1} + \Vert k\Vert _{L^{q_1}}\Vert |x|^\frac{\ell }{p-1} \varphi \Vert _{L^{q_2(p-1)}}^{p-1}<+\,\infty . \end{aligned} \end{aligned}$$

In particular, $|x|^\ell \varphi \in L^\infty ({{\mathbb {R}}^2})$, if $0\le \ell <\frac{1}{4}+\frac{p(p-1)}{4}=:\ell _0$. Note that $\ell _0<3/2$, which is expected at this stage.

Step 5. We finally show that $|x|^{3/2}\varphi \in L^\infty ({{\mathbb {R}}^2})$ if $p\in [p_0,p_1]$. In fact, choosing $q_1\in (1,2)$ and $q_2>2$ satisfying $1=\frac{1}{q_1}+\frac{1}{q_2}$, we get

$$\begin{aligned} \begin{aligned} \Vert |x|^{3/2}\varphi \Vert _{L^\infty }&\lesssim \Vert |x|^{3/2} k\Vert _{L^{\infty }}\Vert \varphi \Vert _{L^{p-1}}^{p-1} + \Vert k\Vert _{L^{q_1}}\Vert |x|^\frac{3}{2(p-1)} \varphi \Vert _{L^{q_2(p-1)}}^{p-1}<+\,\infty . \end{aligned} \end{aligned}$$

To use Step 4 in order to see that last term is finite, we need to check that $3<\frac{p-1}{2}+\frac{p(p-2)^2}{2}+\frac{1}{q_2}$. But note that such a inequality holds trivially if we replace p by $p_0$. Thus the result follows because $p\ge p_0$.

The proof of the theorem is thus completed. $\square$

Remark 3.17

It is worth noting that the solitary wave solution $\varphi \in \mathscr {Z}$ cannot belong to $L^1({{\mathbb {R}}^2})$, since $\hat{k}$ is not continuous at the origin (see (3.20)).

We finish this section with an additional decay property.

Theorem 3.18

Any nontrivial solitary wave of (1.5) satisfies $\varphi \in L_y^rL_x^q({{\mathbb {R}}^2})\cap L_x^q L_y^r({{\mathbb {R}}^2})$ for all $1\le q,r\le \infty$ satisfying

$$\begin{aligned} \frac{1}{r}+\frac{1}{q}>1\quad \hbox {and}\quad \frac{1}{r}+\frac{2}{q}<3. \end{aligned}$$

(3.30)

In particular $\varphi \in L^q_yL^1_x({{\mathbb {R}}^2})\cap L^1_xL^q_y({{\mathbb {R}}^2})\cap L^q_xL^1_y({{\mathbb {R}}^2})\cap L^1_yL^q_x({{\mathbb {R}}^2})$ for any $1<q\le \infty$.

Proof

The proof is deduced from the fact $k\in L_y^rL_x^q({{\mathbb {R}}^2})\cap L_x^q L_y^r({{\mathbb {R}}^2})$ under conditions (3.30). $\square$

Appendix

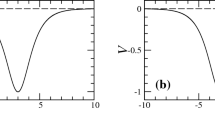
An important question concerning traveling-wave solutions one can ask is about their positivity. In this short appendix we verify that under suitable vanishing conditions at infinity, positive solitary waves do not exist. The numerical result also confirms this fact (see Figure 1).

Fig. 1

The solitary wave of (1.6) and its projection curves for $f(u)=u^2$

Proposition 4.1

(Nonexistence of positive solitary waves) Suppose that f does not change the sign. Then there is no positive solitary-wave solution $\varphi$ of (1.5) satisfying

$$\begin{aligned}&\varphi \rightarrow 0, \quad \hbox {as}\; |(x,y)|\rightarrow +\,\infty , \end{aligned}$$

(4.1)

$$\begin{aligned}&\mathscr {H}\varphi _x\rightarrow 0,\quad \hbox {as}\; |x|\rightarrow +\,\infty , \end{aligned}$$

(4.2)

$$\begin{aligned}&\mathscr {H}\varphi \rightarrow 0, \quad \hbox {as}\; |y|\rightarrow +\,\infty . \end{aligned}$$

(4.3)

Proof

It is straightforward to see that if $\varphi$ is a nontrivial solution of (1.5) satisfying (4.1)–(4.3), then

$$\begin{aligned} \int _{\mathbb {R}}\mathscr {H}\varphi (x,y)\;{d}x=0. \end{aligned}$$

(4.4)

On the other hand, $\mathscr {H}\varphi =\mathscr {H}k*f(\varphi )$, where

$$\begin{aligned} \widehat{\mathscr {H}k}(\xi ,\eta )=-\mathrm{i}\frac{\xi }{|\xi |+\xi ^2+\eta ^2}. \end{aligned}$$

By an argument similar to Lemma 3.8, there holds

$$\begin{aligned} \mathscr {H}k(x,y)=\sqrt{\pi }\int _0^{+\,\infty }t^{5/2}\mathrm{e}^{-t} \left( t^2x^2+\left( t^2+y^2\right) ^2\right) ^{-\frac{3}{2}} \sin \left( \frac{3}{2}\arctan \left( \frac{t|x|}{t^2+y^2}\right) \right) \;{d}t. \end{aligned}$$

The function $\mathscr {H}k$ does not change the sign, since

$$\begin{aligned} \sin \left( \frac{3}{2}\arctan (x)\right) =\frac{\sqrt{2}}{2}\frac{(1+(1+x^2)^{1/2})^{1/2}}{(1+x^2)^{3/4}}\left( 2+(1+x^2)^{1/2}\right) >0. \end{aligned}$$

The proof then follows because if $\varphi$ is positive, $\mathscr {H}\varphi =\mathscr {H}k*f(\varphi )$ has a definite sign, contradicting (4.4). $\square$